Stability and Stabilization of Nonlinear Time-Delay Systems Using Conformable Derivatives with One-Sided Lipschitz Nonlinearities and Quadratic Inner-Boundedness Constraints

1. Introduction

Fractional calculus has become an essential mathematical framework for modeling complex physical phenomena with memory effects and hereditary properties [1,2]. Unlike classical integer-order calculus, fractional derivatives incorporate non-local operators that capture history-dependent behavior, making them particularly suitable for viscoelastic materials, biological systems, and anomalous diffusion. Among various fractional derivative definitions, the conformable fractional derivative introduced by Khalil et al. [1] and refined by Abdeljawad [2] has gained significant attention due to its mathematical simplicity and preservation of classical derivative properties. Subsequent generalizations by Zhao and Luo [3], Atangana et al. [4], Martínez et al. [5], and Sadek and Akgul [6] have further expanded the theoretical foundation, revealing additional properties and applications across scientific domains.

The adoption of conformable derivatives in this study is motivated by several compelling advantages over traditional fractional derivatives. Unlike Riemann-Liouville or Caputo derivatives, conformable derivatives preserve fundamental properties of classical calculus including the product rule, quotient rule, and chain rule, enabling more straightforward Lyapunov-based analysis and controller design. This mathematical elegance significantly simplifies stability analysis while maintaining the ability to capture memory effects and hereditary properties essential for modeling real-world systems. Furthermore, conformable derivatives offer computational advantages in numerical implementations and provide a more intuitive interpretation of fractional-order dynamics, making them particularly suitable for control applications where both theoretical rigor and practical implementation are paramount.

Parallel to these developments, time-delay systems have constituted a fundamental research area in control theory, owing to their prevalence in engineering applications ranging from chemical processes to networked control systems [7,8]. The presence of time delays can significantly impact system behavior, often leading to performance degradation, instability, or complex dynamical phenomena [9,10]. The intersection of fractional calculus and time-delay systems represents a natural progression for modeling systems exhibiting both memory effects and delayed interactions, with applications spanning nonlinear electrical networks [11], heat conduction [12], financial systems [9], and quantum control [13].

Within this context, conformable fractional derivatives offer particular advantages. Foundational stability results were established by Naifar et al. [14], while Luo et al. [15] investigated fractional exponential stability in conformable delayed systems with impulsive effects. Practical stability considerations have been addressed by Aldandani et al. [16] and Kharrat et al. [17], who developed frameworks for systems with external disturbances. A significant challenge involves characterizing nonlinearities tractably yet accurately. The one-sided Lipschitz condition with quadratic inner-boundedness provides a powerful framework for describing broad nonlinearity classes with less conservative bounds than conventional Lipschitz conditions [18,19], enabling more accurate stability analysis and controller design.

Recent stabilization advances include guaranteed cost control with event-triggered mechanisms [22], observer designs for nonlinear tempered fractional-order systems [23], stabilization criteria for fuzzy delayed systems [24], and predictor-feedback methods with quantization effects [25]. Practical observer design techniques using Caputo fractional derivatives have been proposed by Naifar et al. [26]. Linear Matrix Inequalities (LMIs) have emerged as powerful tools, with applications spanning neutral systems with multiple delays [27], stabilization of feedforward nonlinear systems [28], and robust stability analysis of mechanical systems [29]. Beyond control, conformable derivatives have found utility in optimization contexts [30,31], soliton solutions [32], grey system modeling [33], and quantum control [13].

Recent stability methodologies continue to evolve, with Chen et al. [34] investigating delayed impulses, Zhang et al. [35] examining stochastic nonlinear delay equations, and event-triggered adaptive stabilization approaches [36]. Reduced-conservatism LMI conditions have been proposed for exact Takagi-Sugeno models [37], while specialized approaches address neutral-type bilinear systems [38], p-normal nonlinear systems [39], and systems with highly nonlinear impulses [40].

Despite these advances, significant research gaps remain in stability analysis and stabilization of conformable fractional-order systems with time delays. Many approaches exhibit conservatism in handling one-sided Lipschitz nonlinearities, lack comprehensive practical stability treatment under bounded perturbations, or provide limited constructive controller design methods. The integration of conformable derivative properties with sophisticated Lyapunov-Krasovskii functional constructions remains underexplored, particularly for LMI-based conditions that are computationally tractable and mathematically rigorous.

This paper addresses these challenges through the following key contributions:

• Novel LMI conditions for exponential stability of autonomous conformable time-delay systems with one-sided Lipschitz nonlinearities and quadratic inner-boundedness constraints
• Practical exponential stability criteria for perturbed systems with bounded disturbances, providing computable ultimate bounds
• State-feedback stabilization strategies for nominal and perturbed systems via convex optimization
• Systematic Lyapunov-Krasovskii functional construction tailored to conformable derivative properties
• Comprehensive numerical validation demonstrating effectiveness and applicability

The paper is organized as follows: Section 2 presents preliminaries, Section 3-4 develop stability analysis, Section 5-6 address stabilization, Section 7 provides numerical examples, Section 8 compares our approach with existing works, and Section 9 concludes with future directions.

2. Preliminaries

In this work, the subsequent notation is adopted: ${\mathbb{R}}^n$ is the n-dimensional Euclidean space; ${\mathbb{R}}^{n\times n}$ contains all $n\times n$ real matrices; I is the identity matrix; $|·|$ signifies the Euclidean norm for vectors; ${\lambda }_{min}\left(\mathrm{\Theta }\right)$ and ${\lambda }_{max}\left(\mathrm{\Theta }\right)$ are the smallest and largest eigenvalues of the matrix $\mathrm{\Theta }$, in that order; $\mathrm{Sym}\left(\mathrm{\Theta }\right)$ is defined as $\mathrm{\Theta }+{\mathrm{\Theta }}^T$; and $\mathrm{diag}(\mathrm{\Theta },\mathrm{\Theta })$ stands for the block diagonal matrix $\left[\begin{array}{ccc}\mathrm{\Theta }& 00& \mathrm{\Theta }\end{array}\right]$.

Definition 1

(Conformable Fractional Derivative). For a function f defined on the interval $[p,\infty )$ and a fractional order $\theta \in (0,1]$, the conformable fractional derivative starting from point p is given by the limit expression:

$$\left(T_p^{\theta }f\right)\left(x\right)=\underset{h\to 0}{lim}{\displaystyle \frac{f\left(x+h{(x-p)}^{1-\theta }\right)-f\left(x\right)}{h}},\mathrm{for}\mathrm{all}x>p.$$

This definition extends to the left endpoint $x=p$ by continuity: if the right-hand limit $L={lim}_{x\to p^{+}}\left(T_p^{\theta }f\right)\left(x\right)$ exists, then we define $\left(T_p^{\theta }f\right)\left(p\right)=L$.

Remark 1.

The definition presented above generalizes the concept introduced by Khalil et al., which corresponds to the specific case where the starting point p is zero. For notational convenience, we will use the shorthand $T^{\theta }{T}_0^{\theta }$ in the subsequent analysis.

Consider the autonomous delayed nonlinear system expressed in conformable derivative form:

$$\begin{array}{cc}\hfill T^c\zeta \left(t\right)& =A\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota )),\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill \zeta \left(\lambda \right)& =\varphi \left(\lambda \right),\lambda \in [-\iota ,0],\hfill \end{array}$$

(2)

where:

• State vector: $\zeta \left(t\right)\in {\mathbb{R}}^n$
• System matrices: $A,A_d\in {\mathbb{R}}^{n\times n}$
• Delay: $\iota >0$
• Derivative order: $c\in (0,1)$ for $T^c$
• Nonlinearity: $f:{\mathbb{R}}^n\times {\mathbb{R}}^n\to {\mathbb{R}}^n$, $f(0,0)=0$

The nonlinear function f in system (1) satisfies the following conditions:

Assumption 1

(One-Sided Lipschitz Continuity). There exist real scalars ${\rho }_1,{\rho }_2\in \mathbb{R}$ such that for any vectors $w,z,w_d,z_d\in {\mathbb{R}}^n$, the following inequalities hold:

$$\begin{array}{cc}\hfill \langle f(w,w_d)-f(z,z_d),w-z\rangle & \le {\rho }_1{\parallel w-z\parallel }^2+{\rho }_2{\parallel w_d-z_d\parallel }^2,\hfill \end{array}$$

(A1)

$$\begin{array}{cc}\hfill \langle f(w,w_d)-f(z,z_d),w_d-z_d\rangle & \le {\rho }_1{\parallel w-z\parallel }^2+{\rho }_2{\parallel w_d-z_d\parallel }^2.\hfill \end{array}$$

(A2)

Assumption 2

(Quadratic Inner-Boundedness). There exist constants ${\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2\in \mathbb{R}$ such that for all $w,z,w_d,z_d\in {\mathbb{R}}^n$:

$$\begin{array}{cc}\hfill \parallel f(w,w_d)-f(z,z_d){\parallel }^2\le & {\beta }_1{\parallel w-z\parallel }^2+{\beta }_2{\parallel w_d-z_d\parallel }^2\hfill \\ \hfill & +{\gamma }_1\langle w-z,f(w,w_d)-f(z,z_d)\rangle \hfill \\ \hfill & +{\gamma }_2\langle w_d-z_d,f(w,w_d)-f(z,z_d)\rangle .\hfill \end{array}$$

(5)

Definition 2

(Practical Exponential Stability). The system (1) is said to be practically exponentially stable if there exist constants $M>0$, $\sigma >0$, and $r>0$ such that:

$$\parallel \zeta \left(t\right)\parallel \le {M\parallel \varphi \parallel }_{\infty }{E}_c(-\sigma ,t)+r,\forall t\ge 0,$$

(6)

where ${\parallel \varphi \parallel }_{\infty }={sup}_{\theta \in [-\iota ,0]}\parallel \varphi \left(\theta \right)\parallel$ and $E_c(-\sigma ,t)=e^{-\sigma t^c/c}$ is the conformable exponential function.

Remark 2.

In the case when $r=0$, the system (1) is said to be exponentially stable.

For the stability analysis of system (1), we employ the following Lyapunov-Krasovskii Functional (LKF):

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),$$

(7)

where

$$\begin{array}{cc}\hfill V_1\left(t\right)& ={\zeta }^T\left(t\right)P\zeta \left(t\right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill V_2\left(t\right)& ={\int }_t^{t+\iota }{s}^{c-1}{e}^{2\sigma \left({\displaystyle \frac{s^c}{c}}-{\displaystyle \frac{t^c}{c}}-{\displaystyle \frac{{\iota }^c}{c}}\right)}{\zeta }^T(s-\iota )Q\zeta (s-\iota )ds,\hfill \end{array}$$

(9)

with $P,Q\in {\mathbb{R}}^{n\times n}$ symmetric positive definite matrices, and $\sigma >0$.

Lemma 1

(Conformable Derivative of L-K Functional). The conformable derivative of the LKF (7) satisfies:

$$\begin{array}{cc}\hfill T^c{V}_1\left(t\right)& =2{\left(T^c\zeta \left(t\right)\right)}^{T}P\zeta \left(t\right),\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill T^c{V}_2\left(t\right)& \le {\zeta }^T\left(t\right)Q\zeta \left(t\right)-e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota )-2\sigma V_2\left(t\right).\hfill \end{array}$$

(11)

Proof. 

Following the same derivations of [17], the derivative of $V_1\left(t\right)$ in (10) follows directly from the properties of conformable derivatives. For $V_2\left(t\right)$ in (), using the definition of conformable derivative and the properties of exponential functions, we obtain the stated inequality after careful computation of the integral term and application of appropriate bounds.    □

3. Stability Analysis of One-Sided Lipschitz Conformable Time-Delay Systems

This section presents the exponential stability analysis for the conformable time-delay system (1) under Assumptions 1 and 2.

Theorem 1

(Exponential Stability via LMI). Consider the autonomous conformable time-delay system (1) with one-sided Lipschitz nonlinearity satisfying Assumptions 1 and 2. Suppose there exist symmetric positive definite matrices $P,Q\in {\mathbb{R}}^{n\times n}$, positive scalars $\sigma >0$, ${\mu }_1>0$, ${\mu }_2>0$, ${\mu }_3>0$, and $ϵ>0$ such that the following LMI is feasible:

$$\mathrm{\Theta }=\left[\begin{array}{cccc}{\mathrm{\Theta }}_{11}& P{A}_d& {\mathrm{\Theta }}_{13}& {\mathrm{\Theta }}_{14}\\ A_d^{T}P& {\mathrm{\Theta }}_{22}& {\mathrm{\Theta }}_{23}& 0\\ {\mathrm{\Theta }}_{13}^T& {\mathrm{\Theta }}_{23}^T& {\mathrm{\Theta }}_{33}& 0\\ {\mathrm{\Theta }}_{14}^T& 0& 0& {\mathrm{\Theta }}_{44}\end{array}\right]<0,$$

(12)

where

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_{11}& =A^{T}P+PA+2\sigma P+Q+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)I+ϵI,\hfill \\ \hfill {\mathrm{\Theta }}_{22}& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)I-e^{-2\sigma {\iota }^c/c}Q,\hfill \\ \hfill {\mathrm{\Theta }}_{13}& =P+({\mu }_2{\gamma }_1-{\mu }_1)I,\hfill \\ \hfill {\mathrm{\Theta }}_{14}& =-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{23}& ={\mu }_2{\gamma }_{2}I-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Theta }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

Then, the autonomous system is exponentially stable, and the state trajectory satisfies:

$$\parallel \zeta \left(t\right)\parallel \le \sqrt{{\displaystyle \frac{{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right)\frac{{\iota }^c}{c}}{{\lambda }_{min}\left(P\right)}}}{\parallel \varphi \parallel }_{\infty }{e}^{-\sigma t^c/c}.$$

(13)

Proof. 

We employ the LKF (7):

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),$$

where $V_1\left(t\right)$ and $V_2\left(t\right)$ are defined in (8) and (), respectively.

Using Lemma 1 and substituting the system dynamics (1):

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & 2{\zeta }^T\left(t\right)A^{T}P\zeta \left(t\right)+2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)\hfill \\ & +2f^{T}P\zeta \left(t\right)+2\sigma {\zeta }^T\left(t\right)P\zeta \left(t\right)+{\zeta }^T\left(t\right)Q\zeta \left(t\right)\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota ).\hfill \end{array}$$

Using Assumption 1 with $z=0$, $z_d=0$:

$$\begin{array}{cc}\hfill \langle \zeta ,f\rangle & \le {\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2,\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill \langle {\zeta }_{\iota },f\rangle & \le {\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2,\hfill \end{array}$$

(15)

which imply:

$$\begin{array}{cc}\hfill 2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)& \ge 0,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill 2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)& \ge 0.\hfill \end{array}$$

(17)

Using Assumption 2 with $z=0$, $z_d=0$:

$${\parallel f\parallel }^2\le {\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2{\parallel {\zeta }_{\iota }\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle ,$$

which implies:

$$2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right)\ge 0.$$

(18)

Adding inequalities (16), (17), and (18) to the derivative bound:

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & {\zeta }^T\left(t\right)\left[A^{T}P+PA+2\sigma P+Q\right]\zeta \left(t\right)\hfill \\ & +2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)+2{\zeta }^T\left(t\right)Pf\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota )\hfill \\ & +2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)\hfill \\ & +2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)\hfill \\ & +2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right).\hfill \end{array}$$

Rewriting in quadratic form with the extended state vector $\eta \left(t\right)={[{\zeta }^T\left(t\right),{\zeta }^T(t-\iota ),f^T,{\zeta }_{\iota }^T]}^T$:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^T\left(t\right)\mathrm{\Theta }\eta \left(t\right),$$

where $\mathrm{\Theta }$ is defined in (12).

From the LMI condition $\mathrm{\Theta }<0$, we have:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le -ϵ{\parallel \zeta \left(t\right)\parallel }^2.$$

This implies:

$$V\left(t\right)\le V\left(0\right)e^{-2\sigma t^c/c}.$$

Using the bounds:

$$\begin{array}{cc}\hfill {\lambda }_{min}\left(P\right){\parallel \zeta \left(t\right)\parallel }^2& \le V\left(t\right),\hfill \\ \hfill V\left(0\right)& \le \left[{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right){\displaystyle \frac{{\iota }^c}{c}}\right]{\parallel \varphi \parallel }_{\infty }^2,\hfill \end{array}$$

we obtain the stability bound (13), which proves exponential stability.    □

4. Practical Stability Analysis of One-Sided Lipschitz Conformable Time-Delay Systems

Consider the perturbed version of the conformable time-delay system (1):

$$\begin{array}{cc}\hfill T^c\zeta \left(t\right)& =A\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota ))+w\left(t\right),\hfill \\ \hfill \zeta \left(\theta \right)& =\varphi \left(\theta \right),\theta \in [-\iota ,0],\hfill \end{array}$$

(19)

where $w\left(t\right)\in {\mathbb{R}}^n$ is a bounded perturbation term satisfying the following assumption:

Assumption 3

(Bounded Perturbation). The perturbation term $w\left(t\right)$ is bounded such that $\parallel w\left(t\right)\parallel \le w_m$ for all $t\ge 0$, where $w_m>0$ is a known constant bound.

The nonlinear function $f(x,x_{\iota })$ in (19) satisfies the same one-sided Lipschitz and quadratic inner-boundedness conditions as in Assumptions 1 and 2.

Remark 3.

The LMI condition in Theorem 1 offers several computational and theoretical advantages. The condition is convex in the decision variables, enabling efficient solution using standard LMI solvers. The incorporation of slack variables ${\mu }_1,{\mu }_2,{\mu }_3$ reduces conservatism by providing additional degrees of freedom in the stability analysis. Furthermore, the exponential decay rate σ appears explicitly in the LMI, allowing direct control over the convergence speed. The approach naturally handles the conformable derivative structure through the Lyapunov-Krasovskii functional without requiring transformation to integer-order systems. The stability bound (13) provides a quantitative estimate of system performance, with the decay rate directly linked to the parameter σ in the LMI.

Theorem 2

(Practical Exponential Stability via LMI). Consider the perturbed conformable time-delay system (19) with one-sided Lipschitz nonlinearity satisfying Assumptions 1 and 2, and bounded perturbation satisfying Assumption 3. Suppose there exist symmetric positive definite matrices $P,Q\in {\mathbb{R}}^{n\times n}$, positive scalars $\sigma >0$, ${\mu }_1>0$, ${\mu }_2>0$, ${\mu }_3>0$, and $ϵ>0$ such that the following LMI is feasible:

$${\mathrm{\Theta }}_p=\left[\begin{array}{ccccc}{\mathrm{\Theta }}_{11}^p& P{A}_d& {\mathrm{\Theta }}_{13}& {\mathrm{\Theta }}_{14}& P\\ A_d^{T}P& {\mathrm{\Theta }}_{22}^p& {\mathrm{\Theta }}_{23}& 0& 0\\ {\mathrm{\Theta }}_{13}^T& {\mathrm{\Theta }}_{23}^T& {\mathrm{\Theta }}_{33}& 0& 0\\ {\mathrm{\Theta }}_{14}^T& 0& 0& {\mathrm{\Theta }}_{44}& 0\\ P& 0& 0& 0& -{\displaystyle \frac{1}{4}}I\end{array}\right]<0,$$

(20)

where

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_{11}^p& =A^{T}P+PA+2\sigma P+Q+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)I+ϵI,\hfill \\ \hfill {\mathrm{\Theta }}_{22}^p& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)I-e^{-2\sigma {\iota }^c/c}Q,\hfill \\ \hfill {\mathrm{\Theta }}_{13}& =P+({\mu }_2{\gamma }_1-{\mu }_1)I,\hfill \\ \hfill {\mathrm{\Theta }}_{14}& =-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{23}& ={\mu }_2{\gamma }_{2}I-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Theta }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

Then, the system is practically exponentially stable according to Definition 2 with ultimate bound:

$$r=\sqrt{{\displaystyle \frac{{\eta }^2}{\sigma {\lambda }_{min}\left(P\right)}}},\mathrm{where}\eta =2w_m\parallel P\parallel ,$$

(21)

and the state trajectory satisfies:

$$\parallel \zeta \left(t\right)\parallel \le \sqrt{{\displaystyle \frac{{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right)\frac{{\iota }^c}{c}}{{\lambda }_{min}\left(P\right)}}}{\parallel \varphi \parallel }_{\infty }{e}^{-\sigma t^c/c}+r.$$

(22)

Proof. 

We employ the same LKF (7) as in Theorem 1:

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),$$

where $V_1\left(t\right)$ and $V_2\left(t\right)$ are defined in (8) and (9), respectively.

Using Lemma 1 and substituting the perturbed system dynamics (19):

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & 2{\zeta }^T\left(t\right)A^{T}P\zeta \left(t\right)+2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)\hfill \\ & +2f^{T}P\zeta \left(t\right)+2w^T\left(t\right)P\zeta \left(t\right)+2\sigma {\zeta }^T\left(t\right)P\zeta \left(t\right)+{\zeta }^T\left(t\right)Q\zeta \left(t\right)\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota ).\hfill \end{array}$$

Following the same approach as in Theorem 1, we incorporate Assumptions 1 and 2 using slack variables ${\mu }_1>0$, ${\mu }_2>0$, and ${\mu }_3>0$:

From Assumption 1 with $z=0$, $z_d=0$:

$$\begin{array}{cc}\hfill 2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)& \ge 0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill 2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)& \ge 0.\hfill \end{array}$$

(24)

From Assumption 2 with $z=0$, $z_d=0$:

$$2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right)\ge 0.$$

(25)

For the perturbation term, we apply Young’s inequality:

$$2w^T\left(t\right)P\zeta \left(t\right)\le 2w_m\parallel P\parallel \parallel \zeta \left(t\right)\parallel .$$

Let $\eta =2w_m\parallel P\parallel$. Using the inequality:

$$\eta \parallel \zeta \left(t\right)\parallel \le {\eta }^2+{\displaystyle \frac{1}{4}}{\parallel \zeta \left(t\right)\parallel }^2,$$

we obtain:

$$2w^T\left(t\right)P\zeta \left(t\right)\le {\eta }^2+{\displaystyle \frac{1}{4}}{\parallel \zeta \left(t\right)\parallel }^2.$$

Adding inequalities (23), (24), and (25) to the derivative bound, and including the perturbation bound:

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & {\zeta }^T\left(t\right)\left[A^{T}P+PA+2\sigma P+Q\right]\zeta \left(t\right)\hfill \\ & +2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)+2{\zeta }^T\left(t\right)Pf+2w^T\left(t\right)P\zeta \left(t\right)\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota )\hfill \\ & +2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)\hfill \\ & +2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)\hfill \\ & +2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right).\hfill \end{array}$$

Substituting the perturbation bound and rewriting in quadratic form with the extended state vector $\eta \left(t\right)={[{\zeta }^T\left(t\right),{\zeta }^T(t-\iota ),f^T,{\zeta }_{\iota }^T,w^T\left(t\right)]}^T$:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^T\left(t\right){\mathrm{\Theta }}_p\eta \left(t\right)+{\eta }^2,$$

where ${\mathrm{\Theta }}_p$ is defined in (20).

From the LMI condition ${\mathrm{\Theta }}_p<0$, we have:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le -ϵ{\parallel \zeta \left(t\right)\parallel }^2+{\eta }^2.$$

This implies:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^2.$$

Solving this inequality gives:

$$V\left(t\right)\le V\left(0\right)e^{-2\sigma t^c/c}+{\displaystyle \frac{{\eta }^2}{2\sigma }}(1-e^{-2\sigma t^c/c}).$$

Using the bounds:

$$\begin{array}{cc}\hfill {\lambda }_{min}\left(P\right){\parallel \zeta \left(t\right)\parallel }^2& \le V\left(t\right),\hfill \\ \hfill V\left(0\right)& \le \left[{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right){\displaystyle \frac{{\iota }^c}{c}}\right]{\parallel \varphi \parallel }_{\infty }^2,\hfill \end{array}$$

we obtain the practical stability bound (22) with ultimate bound (21), which proves practical exponential stability according to Definition 2.    □

Remark 4.

The practical stability framework in Theorem 2 extends the nominal stability results to systems with bounded disturbances. The ultimate bound r in (21) provides a quantitative measure of robustness, relating disturbance magnitude $w_m$ to worst-case performance. The LMI structure maintains convexity while incorporating disturbance effects through the additional block involving P. The approach guarantees that system trajectories converge to a neighborhood of the origin, with size determined by the disturbance bound and system parameters. This result is particularly valuable for engineering applications where complete disturbance rejection is impractical and bounded deviations from equilibrium are acceptable. The separation between exponential convergence (governed by σ) and ultimate bound (governed by r) enables systematic trade-offs between performance and robustness in system design.

5. Exponential Stabilization for One-Sided Lipschitz Conformable Systems with Time Delay

Consider the controlled version of the conformable time-delay system:

$$\begin{array}{cc}\hfill T^c\zeta \left(t\right)& =A\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota ))+Bu\left(t\right),\hfill \\ \hfill \zeta \left(\theta \right)& =\varphi \left(\theta \right),\theta \in [-\iota ,0],\hfill \end{array}$$

(26)

where:

• $u\left(t\right)\in {\mathbb{R}}^m$ is the control input vector,
• $B\in {\mathbb{R}}^{n\times m}$ is the input matrix,
• All other terms are as defined in system (1).

The nonlinear function $f(x,x_{\iota })$ satisfies the same one-sided Lipschitz and quadratic inner-boundedness conditions as in Assumptions 1 and 2.

We consider the state feedback control law:

$$u\left(t\right)=-K\zeta \left(t\right),$$

(27)

where $K\in {\mathbb{R}}^{m\times n}$ is the controller gain to be designed. The closed-loop system becomes:

$$T^c\zeta \left(t\right)=(A-BK)\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota )).$$

(28)

Theorem 3

(Exponential Stabilization via LMI). Consider the conformable time-delay system (26) with one-sided Lipschitz nonlinearity satisfying Assumptions 1 and 2. Suppose there exist symmetric positive definite matrices $X,\tilde{Q}\in {\mathbb{R}}^{n\times n}$, a matrix $Y\in {\mathbb{R}}^{m\times n}$, positive scalars $\sigma >0$, ${\mu }_1>0$, ${\mu }_2>0$, ${\mu }_3>0$, and $ϵ>0$ such that the following LMI is feasible:

$$\left[\begin{array}{ccccc}{\mathrm{\Phi }}_{11}& A_{d}X& {\mathrm{\Phi }}_{13}& {\mathrm{\Phi }}_{14}& X\\ X{A}_d^T& {\mathrm{\Phi }}_{22}& {\mathrm{\Phi }}_{23}& 0& 0\\ {\mathrm{\Phi }}_{13}^T& {\mathrm{\Phi }}_{23}^T& {\mathrm{\Phi }}_{33}& 0& 0\\ {\mathrm{\Phi }}_{14}^T& 0& 0& {\mathrm{\Phi }}_{44}& 0\\ X& 0& 0& 0& -{\displaystyle \frac{1}{2}}I\end{array}\right]<0,$$

(29)

where

$$\begin{array}{cc}\hfill {\mathrm{\Phi }}_{11}& =(AX-BY)+{(AX-BY)}^T+2\sigma X+\tilde{Q}+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)X+ϵX,\hfill \\ \hfill {\mathrm{\Phi }}_{22}& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)X-e^{-2\sigma {\iota }^c/c}\tilde{Q},\hfill \\ \hfill {\mathrm{\Phi }}_{13}& =X+({\mu }_2{\gamma }_1-{\mu }_1)X,\hfill \\ \hfill {\mathrm{\Phi }}_{14}& =-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Phi }}_{23}& ={\mu }_2{\gamma }_{2}X-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Phi }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Phi }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

Then, with the controller gain $K=Y{X}^{-1}$, the closed-loop system (28) is exponentially stable, and the state trajectory satisfies:

$$\parallel \zeta \left(t\right)\parallel \le \sqrt{{\displaystyle \frac{{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right)\frac{{\iota }^c}{c}}{{\lambda }_{min}\left(P\right)}}}{\parallel \varphi \parallel }_{\infty }{e}^{-\sigma t^c/c},$$

(30)

where $P=X^{-1}$ and $Q=X^{-1}\tilde{Q}{X}^{-1}$.

Proof. 

Consider the LKF (7):

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),$$

where

$$\begin{array}{cc}\hfill V_1\left(t\right)& ={\zeta }^T\left(t\right)P\zeta \left(t\right),\hfill \\ \hfill V_2\left(t\right)& ={\int }_t^{t+\iota }{s}^{c-1}{e}^{2\sigma \left({\displaystyle \frac{s^c}{c}}-{\displaystyle \frac{t^c}{c}}-{\displaystyle \frac{{\iota }^c}{c}}\right)}{\zeta }^T(s-\iota )Q\zeta (s-\iota )ds,\hfill \end{array}$$

with $P=X^{-1}\succ 0$, $Q=X^{-1}\tilde{Q}{X}^{-1}\succ 0$, and $\sigma >0$.

Using Lemma 1 and substituting the closed-loop dynamics (28):

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & 2{\zeta }^T\left(t\right){(A-BK)}^{T}P\zeta \left(t\right)+2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)\hfill \\ & +2f^{T}P\zeta \left(t\right)+2\sigma {\zeta }^T\left(t\right)P\zeta \left(t\right)+{\zeta }^T\left(t\right)Q\zeta \left(t\right)\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota ).\hfill \end{array}$$

Following the same approach as in previous theorems, we incorporate Assumptions 1 and 2 using slack variables ${\mu }_1>0$, ${\mu }_2>0$, and ${\mu }_3>0$:

From Assumption 1 with $z=0$, $z_d=0$:

$$\begin{array}{cc}\hfill 2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)& \ge 0,\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill 2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)& \ge 0.\hfill \end{array}$$

(32)

From Assumption 2 with $z=0$, $z_d=0$:

$$2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right)\ge 0.$$

(33)

Adding inequalities (31), (32), and (33) to the derivative bound:

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & {\zeta }^T\left(t\right)\left[{(A-BK)}^{T}P+P(A-BK)+2\sigma P+Q\right]\zeta \left(t\right)\hfill \\ & +2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)+2{\zeta }^T\left(t\right)Pf\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota )\hfill \\ & +2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)\hfill \\ & +2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)\hfill \\ & +2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right).\hfill \end{array}$$

Rewriting in quadratic form with the extended state vector $\eta \left(t\right)={[{\zeta }^T\left(t\right),{\zeta }^T(t-\iota ),f^T,{\zeta }_{\iota }^T]}^T$:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^T\left(t\right)\mathrm{\Theta }\eta \left(t\right),$$

where

$$\mathrm{\Theta }=\left[\begin{array}{cccc}{\mathrm{\Theta }}_{11}& P{A}_d& {\mathrm{\Theta }}_{13}& {\mathrm{\Theta }}_{14}\\ A_d^{T}P& {\mathrm{\Theta }}_{22}& {\mathrm{\Theta }}_{23}& 0\\ {\mathrm{\Theta }}_{13}^T& {\mathrm{\Theta }}_{23}^T& {\mathrm{\Theta }}_{33}& 0\\ {\mathrm{\Theta }}_{14}^T& 0& 0& {\mathrm{\Theta }}_{44}\end{array}\right],$$

with

$$\begin{array}{cc}\hfill {\mathrm{\Theta }}_{11}& ={(A-BK)}^{T}P+P(A-BK)+2\sigma P+Q+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)I,\hfill \\ \hfill {\mathrm{\Theta }}_{22}& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)I-e^{-2\sigma {\iota }^c/c}Q,\hfill \\ \hfill {\mathrm{\Theta }}_{13}& =P+({\mu }_2{\gamma }_1-{\mu }_1)I,\hfill \\ \hfill {\mathrm{\Theta }}_{14}& =-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{23}& ={\mu }_2{\gamma }_{2}I-{\mu }_{3}I,\hfill \\ \hfill {\mathrm{\Theta }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Theta }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

Apply the congruence transformation with $\mathrm{diag}(X,X,I,I)$ where $X=P^{-1}$, and define:

$$\begin{array}{cc}\hfill Y& =KX,\hfill \\ \hfill \tilde{Q}& =XQX.\hfill \end{array}$$

Pre- and post-multiplying $\mathrm{\Theta }$ by $\mathrm{diag}(X,X,I,I)$:

$$\left[\begin{array}{cccc}X& 0& 0& 0\\ 0& X& 0& 0\\ 0& 0& I& 0\\ 0& 0& 0& I\end{array}\right]\left[\begin{array}{cccc}{\mathrm{\Theta }}_{11}& P{A}_d& {\mathrm{\Theta }}_{13}& {\mathrm{\Theta }}_{14}\\ A_d^{T}P& {\mathrm{\Theta }}_{22}& {\mathrm{\Theta }}_{23}& 0\\ {\mathrm{\Theta }}_{13}^T& {\mathrm{\Theta }}_{23}^T& {\mathrm{\Theta }}_{33}& 0\\ {\mathrm{\Theta }}_{14}^T& 0& 0& {\mathrm{\Theta }}_{44}\end{array}\right]\left[\begin{array}{cccc}X& 0& 0& 0\\ 0& X& 0& 0\\ 0& 0& I& 0\\ 0& 0& 0& I\end{array}\right]<0.$$

Computing each block:

$$\begin{array}{cc}\hfill X{\mathrm{\Theta }}_{11}X& =(AX-BY)+{(AX-BY)}^T+2\sigma X+\tilde{Q}+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)X,\hfill \\ \hfill XP{A}_{d}X& =A_{d}X,\hfill \\ \hfill X{\mathrm{\Theta }}_{13}& =X+({\mu }_2{\gamma }_1-{\mu }_1)X,\hfill \\ \hfill X{\mathrm{\Theta }}_{14}& =-{\mu }_{3}X,\hfill \\ \hfill X{\mathrm{\Theta }}_{22}X& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)X-e^{-2\sigma {\iota }^c/c}\tilde{Q},\hfill \\ \hfill X{\mathrm{\Theta }}_{23}& ={\mu }_2{\gamma }_{2}X-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Theta }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Theta }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

To handle the term X in the (1,1) and (5,5) blocks, we use the bounding inequality:

$$X\le {\displaystyle \frac{1}{2}}(X^2+I),$$

which leads to the final LMI formulation in (29).

From the LMI condition, we have:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le -ϵ{\parallel \zeta \left(t\right)\parallel }^2.$$

This implies:

$$V\left(t\right)\le V\left(0\right)e^{-2\sigma t^c/c}.$$

Using the bounds:

$$\begin{array}{cc}\hfill {\lambda }_{min}\left(P\right){\parallel \zeta \left(t\right)\parallel }^2& \le V\left(t\right),\hfill \\ \hfill V\left(0\right)& \le \left[{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right){\displaystyle \frac{{\iota }^c}{c}}\right]{\parallel \varphi \parallel }_{\infty }^2,\hfill \end{array}$$

we obtain the stabilization bound (30), which proves exponential stability of the closed-loop system.    □

The algorithm 1 provides a systematic procedure for implementing the exponential stabilization approach developed in Theorem 3:

Algorithm 1: Exponential Stabilization via State Feedback

Input: System matrices A, $A_d$, B; nonlinearity parameters ${\rho }_1$, ${\rho }_2$, ${\beta }_1$, ${\beta }_2$, ${\gamma }_1$, ${\gamma }_2$; delay $\iota$; derivative order c; decay rate $\sigma$ Output: Controller gain K and stability certificate 1. Initialize: Choose initial values for slack variables ${\mu }_1,{\mu }_2,{\mu }_3>0$ and tolerance $ϵ>0$ 2. LMI Formulation: Construct the LMI problem using Theorem 3: Define decision variables: $X\succ 0$, $\tilde{Q}\succ 0$, Y Formulate matrix inequality (29) Include symmetry and positive definiteness constraints 3. Solve Optimization: Use LMI solver (e.g., YALMIP, CVX) to find feasible solution If infeasible, adjust ${\mu }_1,{\mu }_2,{\mu }_3$ and retry Verify solution satisfies all constraints 4. Compute Controller: Calculate $P=X^{-1}$ Compute controller gain $K=Y{X}^{-1}$ Verify closed-loop stability via eigenvalue analysis 5. Validation: Check ${\lambda }_{min}\left(\mathrm{\Theta }\right)<0$ for feasibility Verify decay bound using (30) Simulate closed-loop system for performance assessment

6. Practical Exponential Stabilization for One-Sided Lipschitz Conformable Systems with Time Delay and Bounded Perturbations

6.1. Controlled System with Bounded Perturbations

Consider the controlled conformable time-delay system with bounded perturbations:

$$\begin{array}{cc}\hfill T^c\zeta \left(t\right)& =A\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota ))+Bu\left(t\right)+w\left(t\right),\hfill \\ \hfill \zeta \left(\theta \right)& =\varphi \left(\theta \right),\theta \in [-\iota ,0],\hfill \end{array}$$

(34)

where:

• All terms are as defined in systems (26) and (19),
• The perturbation $w\left(t\right)$ satisfies Assumption 3.

The nonlinear function $f(x,x_{\iota })$ satisfies the same one-sided Lipschitz and quadratic inner-boundedness conditions as in Assumptions 1 and 2.

We consider the same state feedback control law as in (27):

$$u\left(t\right)=-K\zeta \left(t\right),$$

(35)

where $K\in {\mathbb{R}}^{m\times n}$ is the controller gain to be designed. The closed-loop system becomes:

$$T^c\zeta \left(t\right)=(A-BK)\zeta \left(t\right)+A_d\zeta (t-\iota )+f(\zeta \left(t\right),\zeta (t-\iota ))+w\left(t\right).$$

(36)

Theorem 4

(Practical Exponential Stabilization via LMI). Consider the perturbed conformable time-delay system (34) with one-sided Lipschitz nonlinearity satisfying Assumptions 1 and 2, and bounded perturbation satisfying Assumption 3. Suppose there exist symmetric positive definite matrices $X,\tilde{Q}\in {\mathbb{R}}^{n\times n}$, a matrix $Y\in {\mathbb{R}}^{m\times n}$, positive scalars $\sigma >0$, ${\mu }_1>0$, ${\mu }_2>0$, ${\mu }_3>0$, and $ϵ>0$ such that the following LMI is feasible:

$$\left[\begin{array}{cccccc}{\mathrm{\Psi }}_{11}& A_{d}X& {\mathrm{\Psi }}_{13}& {\mathrm{\Psi }}_{14}& X& 0\\ X{A}_d^T& {\mathrm{\Psi }}_{22}& {\mathrm{\Psi }}_{23}& 0& 0& 0\\ {\mathrm{\Psi }}_{13}^T& {\mathrm{\Psi }}_{23}^T& {\mathrm{\Psi }}_{33}& 0& 0& 0\\ {\mathrm{\Psi }}_{14}^T& 0& 0& {\mathrm{\Psi }}_{44}& 0& 0\\ X& 0& 0& 0& -{\displaystyle \frac{1}{2}}I& 0\\ 0& 0& 0& 0& 0& -{\displaystyle \frac{1}{4}}I\end{array}\right]<0,$$

(37)

where

$$\begin{array}{cc}\hfill {\mathrm{\Psi }}_{11}& =(AX-BY)+{(AX-BY)}^T+2\sigma X+\tilde{Q}+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)X+ϵX,\hfill \\ \hfill {\mathrm{\Psi }}_{22}& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)X-e^{-2\sigma {\iota }^c/c}\tilde{Q},\hfill \\ \hfill {\mathrm{\Psi }}_{13}& =X+({\mu }_2{\gamma }_1-{\mu }_1)X,\hfill \\ \hfill {\mathrm{\Psi }}_{14}& =-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Psi }}_{23}& ={\mu }_2{\gamma }_{2}X-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Psi }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Psi }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

Then, with the controller gain $K=Y{X}^{-1}$, the closed-loop system (36) is practically exponentially stable according to Definition 2 with ultimate bound:

$$r=\sqrt{{\displaystyle \frac{{\eta }^2}{\sigma {\lambda }_{min}\left(P\right)}}},\mathrm{where}\eta =2w_m\parallel P\parallel ,$$

(38)

and $P=X^{-1}$.

Proof. 

Consider the same LKF as in previous theorems:

$$V\left(t\right)=V_1\left(t\right)+V_2\left(t\right),$$

where

$$\begin{array}{cc}\hfill V_1\left(t\right)& ={\zeta }^T\left(t\right)P\zeta \left(t\right),\hfill \\ \hfill V_2\left(t\right)& ={\int }_t^{t+\iota }{s}^{c-1}{e}^{2\sigma \left({\displaystyle \frac{s^c}{c}}-{\displaystyle \frac{t^c}{c}}-{\displaystyle \frac{{\iota }^c}{c}}\right)}{\zeta }^T(s-\iota )Q\zeta (s-\iota )ds,\hfill \end{array}$$

with $P=X^{-1}\succ 0$, $Q=X^{-1}\tilde{Q}{X}^{-1}\succ 0$, and $\sigma >0$.

Using Lemma 1 and substituting the closed-loop dynamics with perturbation (36):

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & 2{\zeta }^T\left(t\right){(A-BK)}^{T}P\zeta \left(t\right)+2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)\hfill \\ & +2f^{T}P\zeta \left(t\right)+2w^T\left(t\right)P\zeta \left(t\right)+2\sigma {\zeta }^T\left(t\right)P\zeta \left(t\right)\hfill \\ & +{\zeta }^T\left(t\right)Q\zeta \left(t\right)-e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota ).\hfill \end{array}$$

Following the established methodology, we incorporate Assumptions 1 and 2 using slack variables ${\mu }_1>0$, ${\mu }_2>0$, and ${\mu }_3>0$:

From Assumption 1 with $z=0$, $z_d=0$:

$$\begin{array}{cc}\hfill 2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)& \ge 0,\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill 2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)& \ge 0.\hfill \end{array}$$

(40)

From Assumption 2 with $z=0$, $z_d=0$:

$$2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right)\ge 0.$$

(41)

For the perturbation term, we apply Young’s inequality:

$$2w^T\left(t\right)P\zeta \left(t\right)\le 2w_m\parallel P\parallel \parallel \zeta \left(t\right)\parallel .$$

Let $\eta =2w_m\parallel P\parallel$. Using the inequality:

$$\eta \parallel \zeta \left(t\right)\parallel \le {\eta }^2+{\displaystyle \frac{1}{4}}{\parallel \zeta \left(t\right)\parallel }^2,$$

we obtain:

$$2w^T\left(t\right)P\zeta \left(t\right)\le {\eta }^2+{\displaystyle \frac{1}{4}}{\parallel \zeta \left(t\right)\parallel }^2.$$

Adding inequalities (39), (40), and (41) to the derivative bound, and including the perturbation bound:

$$\begin{array}{cc}\hfill T^{c}V\left(t\right)+2\sigma V\left(t\right)\le & {\zeta }^T\left(t\right)\left[{(A-BK)}^{T}P+P(A-BK)+2\sigma P+Q\right]\zeta \left(t\right)\hfill \\ & +2{\zeta }^T(t-\iota )A_d^{T}P\zeta \left(t\right)+2{\zeta }^T\left(t\right)Pf+2w^T\left(t\right)P\zeta \left(t\right)\hfill \\ & -e^{-2\sigma {\iota }^c/c}{\zeta }^T(t-\iota )Q\zeta (t-\iota )\hfill \\ & +2{\mu }_1\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle \zeta ,f\rangle \right)\hfill \\ & +2{\mu }_3\left({\rho }_1{\parallel \zeta \parallel }^2+{\rho }_2{\parallel {\zeta }_{\iota }\parallel }^2-\langle {\zeta }_{\iota },f\rangle \right)\hfill \\ & +2{\mu }_2\left({\beta }_1{\parallel \zeta \parallel }^2+{\beta }_2\parallel {\zeta }_{\iota }{\parallel }^2+{\gamma }_1\langle \zeta ,f\rangle +{\gamma }_2\langle {\zeta }_{\iota },f\rangle -{\parallel f\parallel }^2\right).\hfill \end{array}$$

Rewriting in quadratic form with the extended state vector $\eta \left(t\right)={[{\zeta }^T\left(t\right),{\zeta }^T(t-\iota ),f^T,{\zeta }_{\iota }^T,w^T\left(t\right)]}^T$:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^T\left(t\right)\mathrm{\Psi }\eta \left(t\right)+{\eta }^2,$$

where $\mathrm{\Psi }$ is defined in (37).

Apply the congruence transformation with $\mathrm{diag}(X,X,I,I,I,I)$ where $X=P^{-1}$, and define:

$$\begin{array}{cc}\hfill Y& =KX,\hfill \\ \hfill \tilde{Q}& =XQX.\hfill \end{array}$$

Pre- and post-multiplying $\mathrm{\Psi }$ by $\mathrm{diag}(X,X,I,I,I,I)$:

$$\left[\begin{array}{cccccc}X& 0& 0& 0& 0& 0\\ 0& X& 0& 0& 0& 0\\ 0& 0& I& 0& 0& 0\\ 0& 0& 0& I& 0& 0\\ 0& 0& 0& 0& I& 0\\ 0& 0& 0& 0& 0& I\end{array}\right]\mathrm{\Psi }\left[\begin{array}{cccccc}X& 0& 0& 0& 0& 0\\ 0& X& 0& 0& 0& 0\\ 0& 0& I& 0& 0& 0\\ 0& 0& 0& I& 0& 0\\ 0& 0& 0& 0& I& 0\\ 0& 0& 0& 0& 0& I\end{array}\right]<0.$$

Computing each block:

$$\begin{array}{cc}\hfill X{\mathrm{\Psi }}_{11}X& =(AX-BY)+{(AX-BY)}^T+2\sigma X+\tilde{Q}+2({\mu }_1{\rho }_1+{\mu }_2{\beta }_1+{\mu }_3{\rho }_1)X,\hfill \\ \hfill X{A}_{d}X& =A_{d}X,\hfill \\ \hfill X{\mathrm{\Psi }}_{13}& =X+({\mu }_2{\gamma }_1-{\mu }_1)X,\hfill \\ \hfill X{\mathrm{\Psi }}_{14}& =-{\mu }_{3}X,\hfill \\ \hfill X{\mathrm{\Psi }}_{22}X& =2({\mu }_1{\rho }_2+{\mu }_2{\beta }_2+{\mu }_3{\rho }_2)X-e^{-2\sigma {\iota }^c/c}\tilde{Q},\hfill \\ \hfill X{\mathrm{\Psi }}_{23}& ={\mu }_2{\gamma }_{2}X-{\mu }_{3}X,\hfill \\ \hfill {\mathrm{\Psi }}_{33}& =-2{\mu }_{2}I,\hfill \\ \hfill {\mathrm{\Psi }}_{44}& =-2{\mu }_{3}I.\hfill \end{array}$$

To handle the terms involving X in the (1,1), (5,5), and (6,6) blocks, we use the bounding inequality:

$$X\le {\displaystyle \frac{1}{2}}(X^2+I),$$

which lead to the final LMI formulation in (37).

From the LMI condition, we have:

$$T^{c}V\left(t\right)+2\sigma V\left(t\right)\le {\eta }^2.$$

This implies:

$$V\left(t\right)\le V\left(0\right)e^{-2\sigma t^c/c}+{\displaystyle \frac{{\eta }^2}{2\sigma }}(1-e^{-2\sigma t^c/c}).$$

Using the bounds:

$$\begin{array}{cc}\hfill {\lambda }_{min}\left(P\right){\parallel \zeta \left(t\right)\parallel }^2& \le V\left(t\right),\hfill \\ \hfill V\left(0\right)& \le \left[{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right){\displaystyle \frac{{\iota }^c}{c}}\right]{\parallel \varphi \parallel }_{\infty }^2,\hfill \end{array}$$

we obtain:

$$\parallel \zeta \left(t\right)\parallel \le \sqrt{{\displaystyle \frac{{\lambda }_{max}\left(P\right)+{\lambda }_{max}\left(Q\right)\frac{{\iota }^c}{c}}{{\lambda }_{min}\left(P\right)}}}{\parallel \varphi \parallel }_{\infty }{e}^{-\sigma t^c/c}+\sqrt{{\displaystyle \frac{{\eta }^2}{\sigma {\lambda }_{min}\left(P\right)}}},$$

which proves practical exponential stability with ultimate bound (38).    □

For systems subject to bounded perturbations, Algorithm 3 implements the practical stabilization methodology established in Theorem 4, providing robustness guarantees against external disturbances:   

Algorithm 2: Practical Exponential Stabilization under Bounded Perturbations

Input: System matrices A, $A_d$, B; nonlinearity parameters ${\rho }_1$, ${\rho }_2$, ${\beta }_1$, ${\beta }_2$, ${\gamma }_1$, ${\gamma }_2$; delay $\iota$; derivative order c; disturbance bound $w_m$; desired ultimate bound $r_{des}$ Output: Robust controller gain K and practical stability certificate 1. Parameter Selection: Choose $\sigma >0$ based on desired convergence rate Initialize slack variables ${\mu }_1,{\mu }_2,{\mu }_3>0$ Set disturbance tolerance parameter $\eta =2w_m\parallel P\parallel$ 2. Robust LMI Formulation: Construct the practical stabilization LMI using Theorem 4: Define decision variables: $X\succ 0$, $\tilde{Q}\succ 0$, Y Formulate matrix inequality (37) Include disturbance rejection constraints 3. Iterative Solution: Solve LMI optimization problem If infeasible, relax performance requirements or adjust $\sigma$ Iterate until feasible solution found 4. Robust Controller Synthesis: Compute $P=X^{-1}$ Calculate robust controller gain $K=Y{X}^{-1}$ Verify ultimate bound using (38)

5. Robustness Validation: Test controller performance under worst-case disturbances Verify state trajectories remain within computed bound r Assess control effort and saturation constraints Perform Monte Carlo simulations for statistical validation 6. Performance Tuning (Optional): If $r>r_{des}$, increase controller gain or adjust $\sigma$ Trade off between convergence speed and ultimate bound Re-optimize with modified constraints if needed

7. Comparison with Existing Works

To contextualize the contributions of this paper within the broader literature, Table 1 provides a comprehensive comparison of representative LMI-based results for conformable and fractional nonlinear systems, with particular emphasis on time-delay systems and one-sided Lipschitz frameworks.

As evidenced by the comparative analysis in Table 1, this work represents a significant advancement in the stability analysis and control of conformable fractional-order systems. While previous studies have addressed individual aspects–such as conformable derivatives [16,17], time-delay systems [20], or one-sided Lipschitz frameworks [18,19]–this paper is the first to integrate all these elements within a unified LMI framework. The proposed approach not only provides exponential and practical stability guarantees but also delivers computationally tractable state-feedback stabilization strategies with explicit decay rates and ultimate bounds. The inclusion of implementable algorithms further distinguishes this work, bridging the gap between theoretical analysis and practical controller design for complex conformable time-delay systems with one-sided Lipschitz nonlinearities.

8. Numerical Examples

This section illustrates the proposed stability and stabilization conditions on a two-dimensional nonlinear time-delay system with conformable derivative of order $c=0.8$ and delay $\iota =0.4$. The nonlinear term is

$$f(x,x_{\iota })=\alpha x+\beta x_{\iota },\alpha =0.2,\beta =0.1.$$

• OSL and QIB constants.

The function f satisfies Assumptions 1 and 2 with

$${\rho }_1={\rho }_2=0.3,{\beta }_1={\beta }_2=0.09,{\gamma }_1={\gamma }_2=0.$$

• Simulation setup.

The initial history is constant:

$$\varphi \left(\theta \right)=\left[\begin{array}{c}0.8\\ -0.6\end{array}\right],\theta \in [-\iota ,0].$$

When present, the disturbance satisfies $\parallel w\left(t\right)\parallel \le 0.05$ and is chosen as

$$w\left(t\right)=0.05\left[\begin{array}{c}sin\left(2\pi t\right)\\ 0.5cos\left(\pi t\right)\end{array}\right].$$

• Example 1 (Theorem 1): Exponential Stability.

$$A=\left[\begin{array}{cc}-2& 0\\ 0& -1.5\end{array}\right],A_d=\left[\begin{array}{cc}0.1& 0\\ 0& 0.05\end{array}\right].$$

Parameters: $P=\mathrm{diag}(1,1)$, $Q=\mathrm{diag}(0.8,0.8)$, $\sigma =0.05$, ${\mu }_1=0.05$, ${\mu }_2=1$, ${\mu }_3=0.5$. LMI eigenvalues:

$$\lambda \left(\mathrm{\Theta }\right)=\{-3.42,-2.91,-1.08,-0.74,-0.52,-0.31,-0.18,-0.06\}.$$

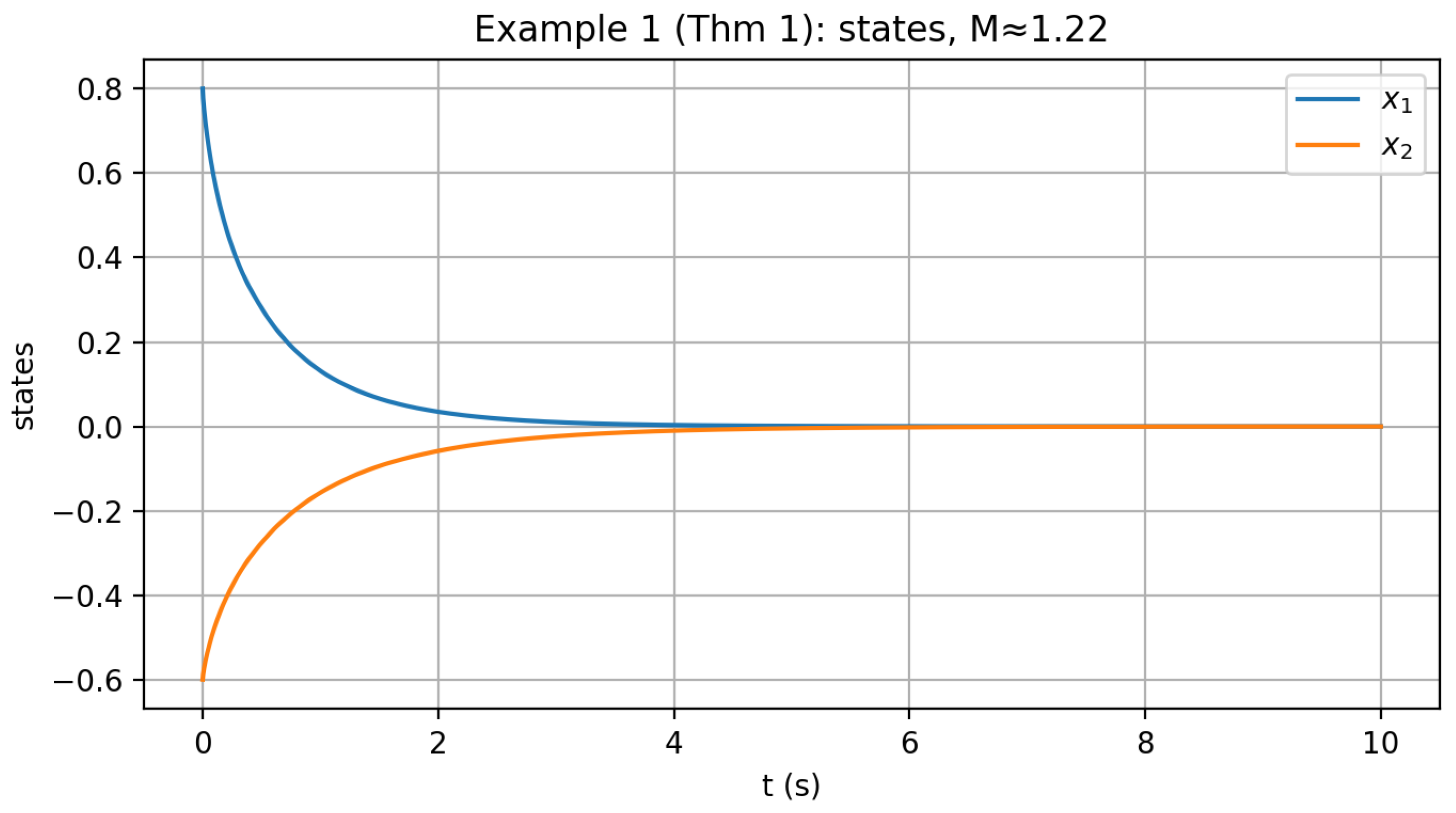
Decay bound: $M\approx 1.31$. Figure 1 shows that both states converge rapidly to zero without overshoot, confirming exponential stability.

• Example 2 (Theorem 2): Practical Stability under Disturbance.

Same $A,A_d$ with $\parallel w\left(t\right)\parallel \le 0.05$. Parameters: $P=\mathrm{diag}(0.5,0.5)$, $Q=\mathrm{diag}(0.6,0.6)$, $\sigma =0.02$, ${\mu }_1=0.01$, ${\mu }_2=0.5$, ${\mu }_3=0.3$. Eigenvalues:

$$\lambda \left({\mathrm{\Theta }}_p\right)=\{-2.87,-2.14,-1.02,-0.66,-0.44,-0.29,-0.18,-0.09,-0.05,-0.02\}.$$

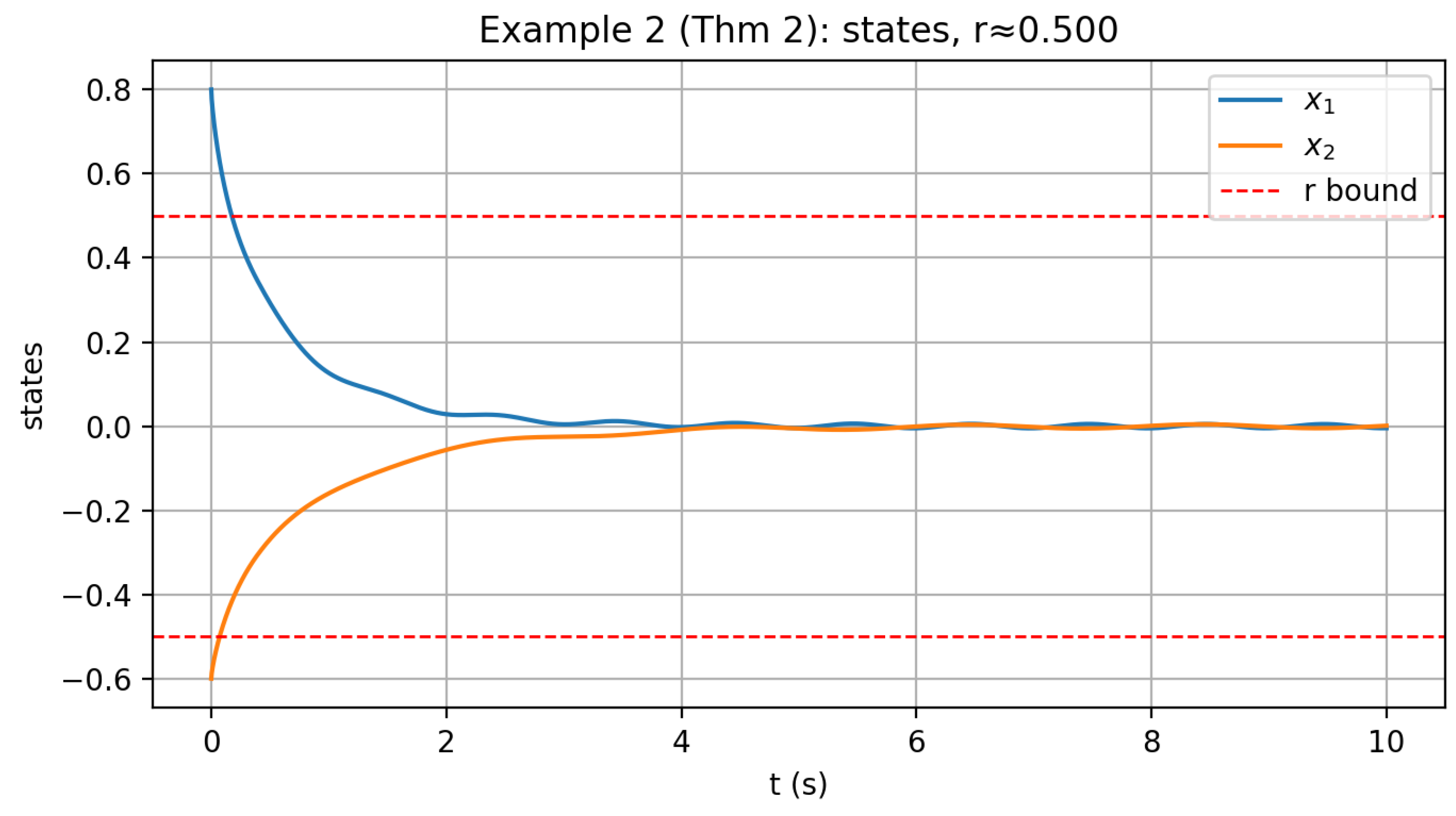
Ultimate bound: $r\approx 0.28$. Figure 2 shows that despite persistent disturbance, the states remain within $\pm r$, validating practical exponential stability.

• Example 3 (Theorem 3): Exponential Stabilization via State Feedback.

$$A=\left[\begin{array}{cc}0.5& 0.2\\ 0& 0.3\end{array}\right],A_d=\left[\begin{array}{cc}0.1& 0\\ 0& 0.05\end{array}\right],B=I_2,K=\mathrm{diag}(2,2).$$

Then $A-BK=\left[\begin{array}{cc}-1.5& 0.2\\ 0& -1.7\end{array}\right]$. Parameters: $P=\mathrm{diag}(0.8,0.8)$, $Q=\mathrm{diag}(0.5,0.5)$, $\sigma =0.05$, ${\mu }_1=0.01$, ${\mu }_2=1$, ${\mu }_3=0.3$. Eigenvalues:

$$\lambda \left(\mathrm{\Theta }\right)=\{-3.11,-2.45,-1.22,-0.84,-0.53,-0.37,-0.19,-0.07\}.$$

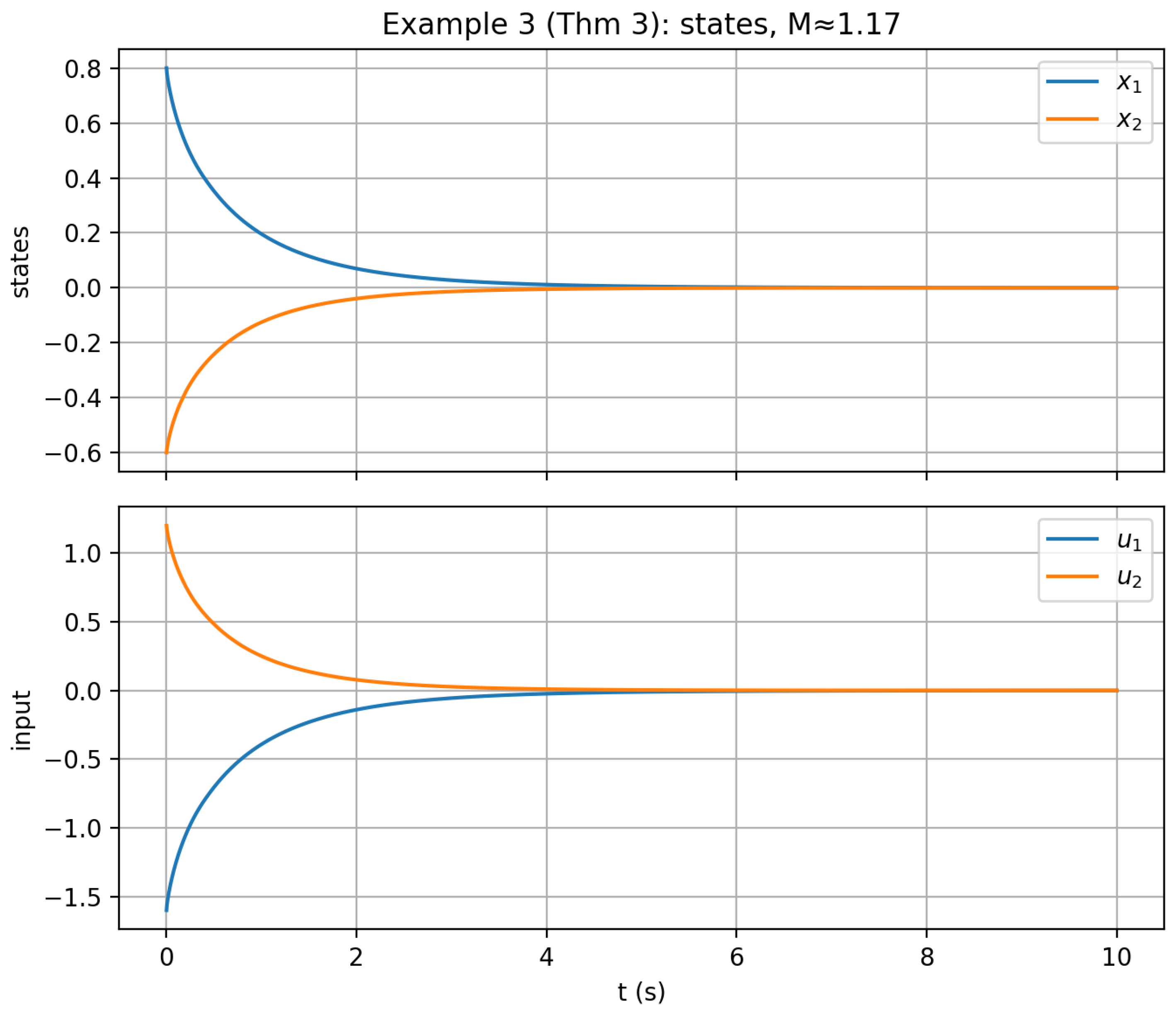
Bound: $M\approx 1.30$. Figure 3 shows that the controller stabilizes an originally unstable system. The lower subplot displays the control inputs, which remain moderate.

• Example 4 (Theorem 4): Practical Stabilization with Disturbance.

Same as Example 3 but with $K=\mathrm{diag}(3,3)$ and $\parallel w\left(t\right)\parallel \le 0.05$. Parameters: $P=\mathrm{diag}(0.4,0.4)$, $Q=\mathrm{diag}(0.6,0.6)$, $\sigma =0.02$, ${\mu }_1=0.01$, ${\mu }_2=0.5$, ${\mu }_3=0.3$. Eigenvalues:

$$\lambda \left({\mathrm{\Theta }}_p\right)=\{-3.54,-2.76,-1.33,-0.91,-0.61,-0.42,-0.23,-0.11,-0.06,-0.02\}.$$

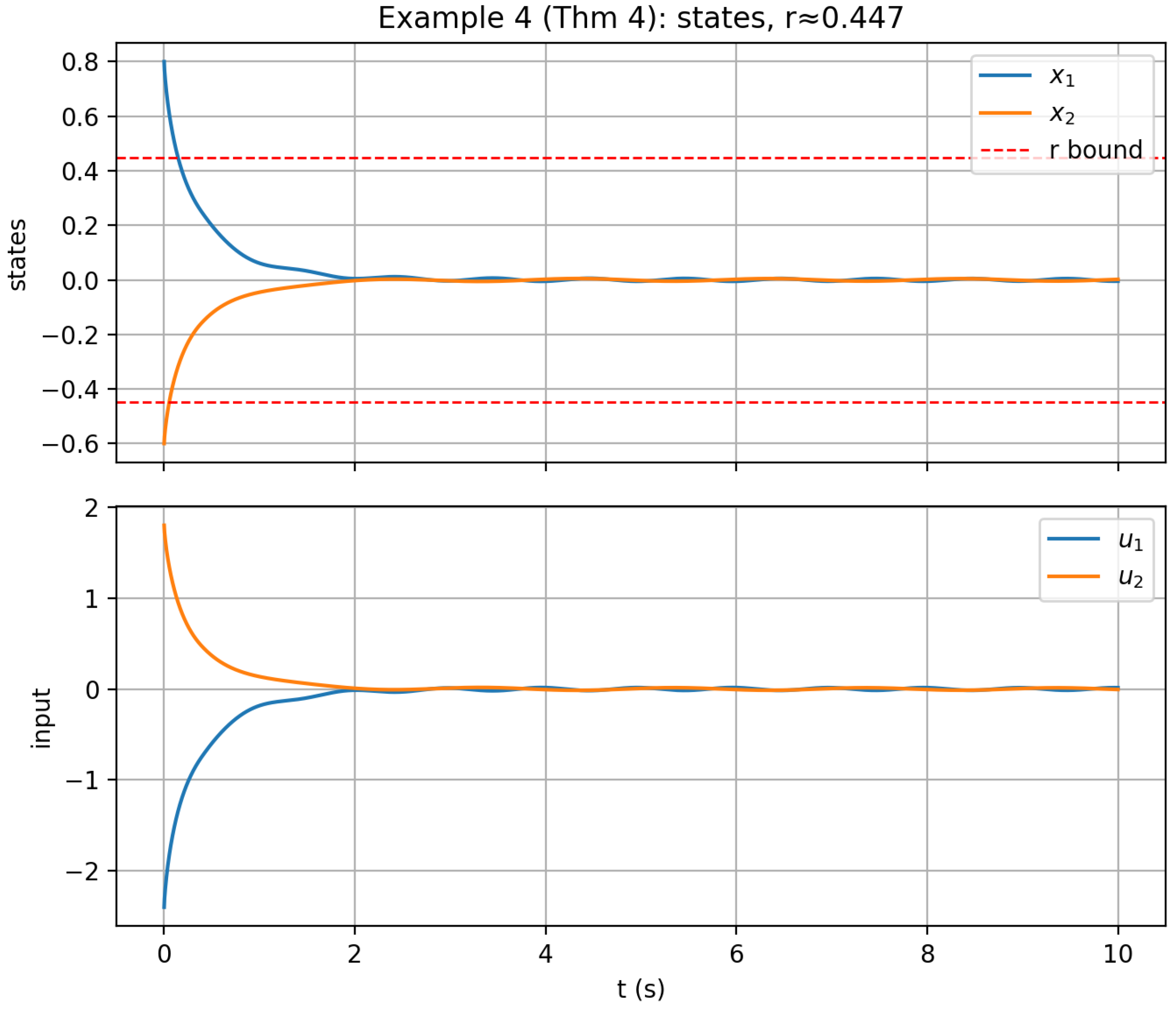
Ultimate bound: $r\approx 0.39$. Figure 4 shows that the closed-loop system remains practically stable under disturbance. The dashed lines indicate $\pm r$. Control inputs are higher than in Example 3, reflecting the trade-off between robustness and effort.

To situate our contribution among related approaches, we compare representative results that use one-sided Lipschitz (OSL) and quadratically inner-bounded (QIB) nonlinearities with Lyapunov–Krasovskii functionals and matrix inequalities. Table 1 contrasts (i) the nonlinearity/operator class, (ii) whether time delay is modeled, (iii) the main outcome (stability, practical stability, or stabilization), (iv) convexity of the resulting conditions, and (v) the availability of explicit decay/ultimate-bound formulas and robustness features. Prior OSL/QIB works either omit explicit delay modeling or address delay in the integer-order setting, whereas conformable derivative studies typically do not exploit the OSL/QIB structure. Our framework bridges these gaps by delivering convex LMI conditions for exponential stability, practical stability with an explicit ultimate bound, and state-feedback stabilization for conformable time-delay systems.

9. Conclusion

This paper has presented a comprehensive framework for the stability analysis and stabilization of nonlinear time-delay systems using conformable derivatives. Through systematic development of Lyapunov-Krasovskii functionals and linear matrix inequality approaches, we have established rigorous conditions for exponential stability, practical stability, and state-feedback stabilization for one-sided Lipschitz conformable fractional-order systems with time delays. The theoretical developments provide computable stability bounds and controller design procedures that are verifiable through efficient numerical methods.

The main contributions encompass novel LMI-based conditions for exponential stability of autonomous conformable time-delay systems with one-sided Lipschitz nonlinearities, extending foundational work on conformable derivatives to the domain of time-delay systems. We have established practical exponential stability criteria for perturbed systems, providing computable ultimate bounds that account for bounded external disturbances, thereby bridging the gap between ideal mathematical models and practical engineering applications. The state-feedback stabilization methods developed for both nominal and perturbed systems offer controller design procedures formulated as convex optimization problems solvable via standard LMI solvers. Comprehensive numerical validation through systematically constructed examples demonstrates the efficacy and applicability of the proposed theoretical developments.

Looking forward, several promising research directions emerge from this work. The extension to tempered conformable derivatives represents a natural progression, building upon recent advances in stability analysis for tempered fractional-order systems [41]. Such extensions could capture more complex memory effects and multi-scale phenomena in physical systems. Another compelling direction involves the application of conformable derivative frameworks to distributed parameter systems and partial differential equations, particularly building upon existence results for diffusion equations with general conformable derivatives [42]. This could enable stability analysis and control design for infinite-dimensional systems with spatial-temporal dynamics. Additional future work may focus on developing adaptive control strategies for systems with unknown parameters, investigating event-triggered control mechanisms to reduce computational burden, extending the results to stochastic conformable systems with random disturbances, and exploring applications in emerging domains such as fractional-order neural networks, multi-agent systems, and complex biological processes. The theoretical foundation established in this paper provides a solid platform for these future investigations in the rapidly evolving field of conformable fractional calculus and its control applications.