Submitted:
28 May 2024
Posted:
29 May 2024
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Three Assumptions of 4G Model of Final Unification
- There exists a characteristic electroweak fermion of rest energy, . It can be considered as the zygote of all elementary particles.
- There exists a nuclear elementary charge in such a way that, = Strong coupling constant [11] and .
-
Each atomic interaction is associated with a characteristic large gravitational coupling constant. Their fitted magnitudes are,
- 1)
- Weak interaction point of view, following our assumptions, Fermi’s weak coupling constant [11] can be fitted with the following relations.
- 2)
- In a unified approach, most important point to be noted is that, Clearly speaking, based on the electroweak interaction, the well believed quantum constant seems to have a deep inner meaning [10]. It needs further study with respect to condensed matter physics.
3. Free Nucleons and Electroweak Term
- 1)
- Nuclear volume can be split into ‘core inner’ and ‘core outer’.
- 2)
- Nucleons residing in nuclear inner core help in increasing nuclear binding energy.
- 3)
- Nucleons residing in outer core will not involve in nuclear binding.
- 4)
- Outer core nucleons can be called as free or electroweak nucleons.
- 5)
- Proportionality coefficient being free nucleon number is proportional to half of the sum of squared proton number and squared mass number.
- 6)
- Considering light and heavy atomic nuclides, by considering a correction factor in our recent publications, we expressed our first approximate relation for free nucleon number as,
4. Nuclear Radius and Radial Term
- 1)
- Interesting observation is that, nuclear binding energy seems to decrease with increasing radius.
- 2)
- As nuclear volume is proportional the mass number, it is possible to understand the decreasing nuclear binding energy with cube root of the mass number .
5. Stable Mass Number and Asymmetry Term
- 1)
- Even though it is not exact stable mass number, we understood that, the ratio of nuclear charge and elementary charge and electroweak interaction seem to play a crucial role in understanding and estimating the approximate stable mass number of any atomic nuclide having a proton number Z. This is one best practical application of our proposed nuclear charge and electroweak fermion.
- 2)
- Stable mass number seems to play a crucial role in estimating the binding energy of other isotopes of Z.
- 3)
- Our estimated mass number close to stability can be called as ‘light house (like) mass number’ where one can find the beginning of relatively long living isotopes of Z.
- 4)
- 1)
- If Z is even and obtained is odd, then,
- 2)
- If Z is even and obtained is even, then,
- 3)
- If Z is odd and obtained is odd, then,
- 4)
- If Z is odd and obtained is even, then,
- 5)
- Number 0.0016 plays a very interesting role in estimating the free nucleon number as,where is a correction factor that needs a review.
- 6)
- Here, very interesting point to be noted is that, the number 0.0016 can also be understood as a ratio of the mean mass of pions to the mean mass of electroweak bosons. It can be expreessed as,
- 7)
-
Independent of proton number, approximate asymmetry term can be expressed as,It may be noted that, even though it is an approximate relation, it greatly helps in estimating the binding energy of isotopes for the entire range of atomic nuclides. It seems essential to work on this kind of relations.
- 8)
- For medium and heavy proton numbers and their isotopes, equality of excess neutron number and free nucleon number can be considered as an index of possible stability. It needs a review at fundamental level.
6. Unique Binding Energy Coefficient
7. Revised and Reference Formulae for Nuclear Binding Energy
8. Discussion
- 1)
- Even though they are having wide scope and very accurate, currently believed semi empirical mass formulae are having many complicated energy coefficients with different terms and different concepts [16,17,18,19,20]. We would like to emphasize the point that, clarity is missing in coupling or interpreting the terms and coefficients with strong and weak interactions. Similarly, energy coefficients associated with recently developed relativistic continuum Hartree-Bogoliubov (RCHB) theory having relativistic density functions are much more complicated [18].
- 2)
- Conceptually, relations (9) and (10) are very simple in understanding and having deep inner meaning. Relation (9) can be expressed as,
- 3)
- Relation (10) can be expressed as,
9. Conclusion
References
- Seshavatharam, U.V.S and Lakshminarayana S.A very brief review on strong and electroweak mass formula pertaining to 4G model of final unification. Proceedings of the DAE Symp. on Nucl. Phys. 67,1173,2023.
- Seshavatharam, U.V.S and Lakshminarayana S. Exploring condensed matter physics with refined electroweak term of the strong and electroweak mass formula. World Scientific News.193(2) 105-13, 2024.
- Seshavatharam, U.V.S and Lakshminarayana S. Inferring and confirming the rest mass of electron neutrino with neutron life time and strong coupling constant via 4G model of final unification. World Scientific News 191, 127-156, 2024.
- Seshavatharam U. V. S., Gunavardhana Naidu T and Lakshminarayana S. 2022. To confirm the existence of heavy weak fermion of rest energy 585 GeV. AIP Conf. Proc. 2451 p 020003. [CrossRef]
- Seshavatharam, U.V.S and Lakshminarayana S. 4G model of final unification – A brief report Journal of Physics: Conference Series 2197 p 012029, 2022. [CrossRef]
- Seshavatharam, U.V.S and Lakshminarayana. Understanding nuclear stability range with 4G model of nuclear charge. World Scientific News. 177, 118-136, 2023.
- Seshavatharam, U.V.S, S. Lakshminarayana, H. K. Cherop and K. M. Khanna, Three Unified Nuclear Binding Energy Formulae. World Scientific News, 163, 30-77, 2022.
- Seshavatharam, U.V.S, Lakshminarayana, S., On the Combined Role of Strong and Electroweak Interactions in Understanding Nuclear Binding Energy Scheme. Mapana Journal of Sciences, 20(1), 1-18, 2021. [CrossRef]
- Seshavatharam, U.V.S and Lakshminarayana S., Strong and Weak Interactions in Ghahramany’s Integrated Nuclear Binding Energy Formula. World Scientific News, 161, 111-129, 2021. [CrossRef]
- Seshavatharam, U.V.S and Lakshminarayana S. Is reduced Planck’s constant - an outcome of electroweak gravity? Mapana Journal of Sciences. 19,1,1, 2020. [CrossRef]
- Workman R.L. et al. (Particle Data Group), Prog. Theor. Exp. Phys. 2022, 083C01, 2022.
- Ghiorso, Albert. Einsteinium and Fermium. Chemical and Engineering News. 81 (36): 174–175, 2003.
- Kondev, F. G.; Wang, M.; Huang, W. J.; Naimi, S.; Audi, G. The NUBASE2020 evaluation of nuclear properties (PDF). Chinese Physics C. 45 (3): 030001, 2021.
- Peter Möller. The limits of the nuclear chart set by fission and alpha decay. EPJ Web Conf. 131, 03002, 2016. [CrossRef]
- Oganessian, Yu & Rykaczewski, Krzysztof. (2015). A beachhead on the island of stability. Physics Today. 68. 32-38. 10.1063/PT.3.2880. [CrossRef]
- Myers W., D. and Swiatecki W. J. Nuclear Properties According to the Thomas-Fermi Model.LBL-36557 Rev. UC-413, 1995. [CrossRef]
- Myers W., D. and Swiatecki W. J. Table of nuclear masses according to the 1994 Thomas-Fermi model. United States: N. p., 1994. Web.
- X.W. Xia, Y. Lim, P.W. Zhao et al. The limits of the nuclear landscape explored by the relativistic continuum Hartree–Bogoliubov theory. Atomic Data and Nuclear Data Tables. 121–122, 1-215, 2018. [CrossRef]
- Bethe H., A. Thomas-Fermi Theory of Nuclei. Phys. Rev., 167(4), 879-907, 1968. [CrossRef]
- Gao, Z.P., Wang, YJ., Lü, HL. et al., Machine learning the nuclear mass. NUCL. SCI. TECH. 32, 109, 2021. [CrossRef]
| Proton number | Estimated stable mass number | Estimated mass number with EO corrections | Proton number | Estimated stable mass number | Estimated mass number with EO corrections | Proton number | Estimated stable mass number | Estimated mass number with EO corrections |
| 5 | 10 | 11 | 43 | 97 | 97 | 81 | 202 | 203 |
| 6 | 12 | 12 | 44 | 100 | 100 | 82 | 205 | 206 |
| 7 | 14 | 15 | 45 | 102 | 103 | 83 | 208 | 209 |
| 8 | 16 | 16 | 46 | 105 | 106 | 84 | 211 | 212 |
| 9 | 18 | 19 | 47 | 107 | 107 | 85 | 214 | 215 |
| 10 | 20 | 20 | 48 | 110 | 110 | 86 | 217 | 218 |
| 11 | 22 | 23 | 49 | 113 | 113 | 87 | 219 | 219 |
| 12 | 24 | 24 | 50 | 115 | 116 | 88 | 222 | 222 |
| 13 | 26 | 27 | 51 | 118 | 119 | 89 | 225 | 225 |
| 14 | 28 | 28 | 52 | 121 | 122 | 90 | 228 | 228 |
| 15 | 30 | 31 | 53 | 123 | 123 | 91 | 231 | 231 |
| 16 | 32 | 32 | 54 | 126 | 126 | 92 | 234 | 234 |
| 17 | 35 | 35 | 55 | 129 | 129 | 93 | 237 | 237 |
| 18 | 37 | 38 | 56 | 131 | 132 | 94 | 240 | 240 |
| 19 | 39 | 39 | 57 | 134 | 135 | 95 | 243 | 243 |
| 20 | 41 | 42 | 58 | 137 | 138 | 96 | 246 | 246 |
| 21 | 43 | 43 | 59 | 140 | 141 | 97 | 249 | 249 |
| 22 | 46 | 46 | 60 | 142 | 142 | 98 | 252 | 252 |
| 23 | 48 | 49 | 61 | 145 | 145 | 99 | 255 | 255 |
| 24 | 50 | 50 | 62 | 148 | 148 | 100 | 258 | 258 |
| 25 | 53 | 53 | 63 | 151 | 151 | 101 | 261 | 261 |
| 26 | 55 | 56 | 64 | 153 | 154 | 102 | 264 | 264 |
| 27 | 57 | 57 | 65 | 156 | 157 | 103 | 268 | 269 |
| 28 | 60 | 60 | 66 | 159 | 160 | 104 | 271 | 272 |
| 29 | 62 | 63 | 67 | 162 | 163 | 105 | 274 | 275 |
| 30 | 65 | 66 | 68 | 165 | 166 | 106 | 277 | 278 |
| 31 | 67 | 67 | 69 | 167 | 167 | 107 | 280 | 281 |
| 32 | 69 | 70 | 70 | 170 | 170 | 108 | 283 | 284 |
| 33 | 72 | 73 | 71 | 173 | 173 | 109 | 286 | 287 |
| 34 | 74 | 74 | 72 | 176 | 176 | 110 | 289 | 290 |
| 35 | 77 | 77 | 73 | 179 | 179 | 111 | 292 | 293 |
| 36 | 79 | 80 | 74 | 182 | 182 | 112 | 295 | 296 |
| 37 | 82 | 83 | 75 | 185 | 185 | 113 | 298 | 299 |
| 38 | 84 | 84 | 76 | 187 | 188 | 114 | 301 | 302 |
| 39 | 87 | 87 | 77 | 190 | 191 | 115 | 304 | 305 |
| 40 | 89 | 90 | 78 | 193 | 194 | 116 | 308 | 308 |
| 41 | 92 | 93 | 79 | 196 | 197 | 117 | 311 | 311 |
| 42 | 94 | 94 | 80 | 199 | 200 | 118 | 314 | 314 |
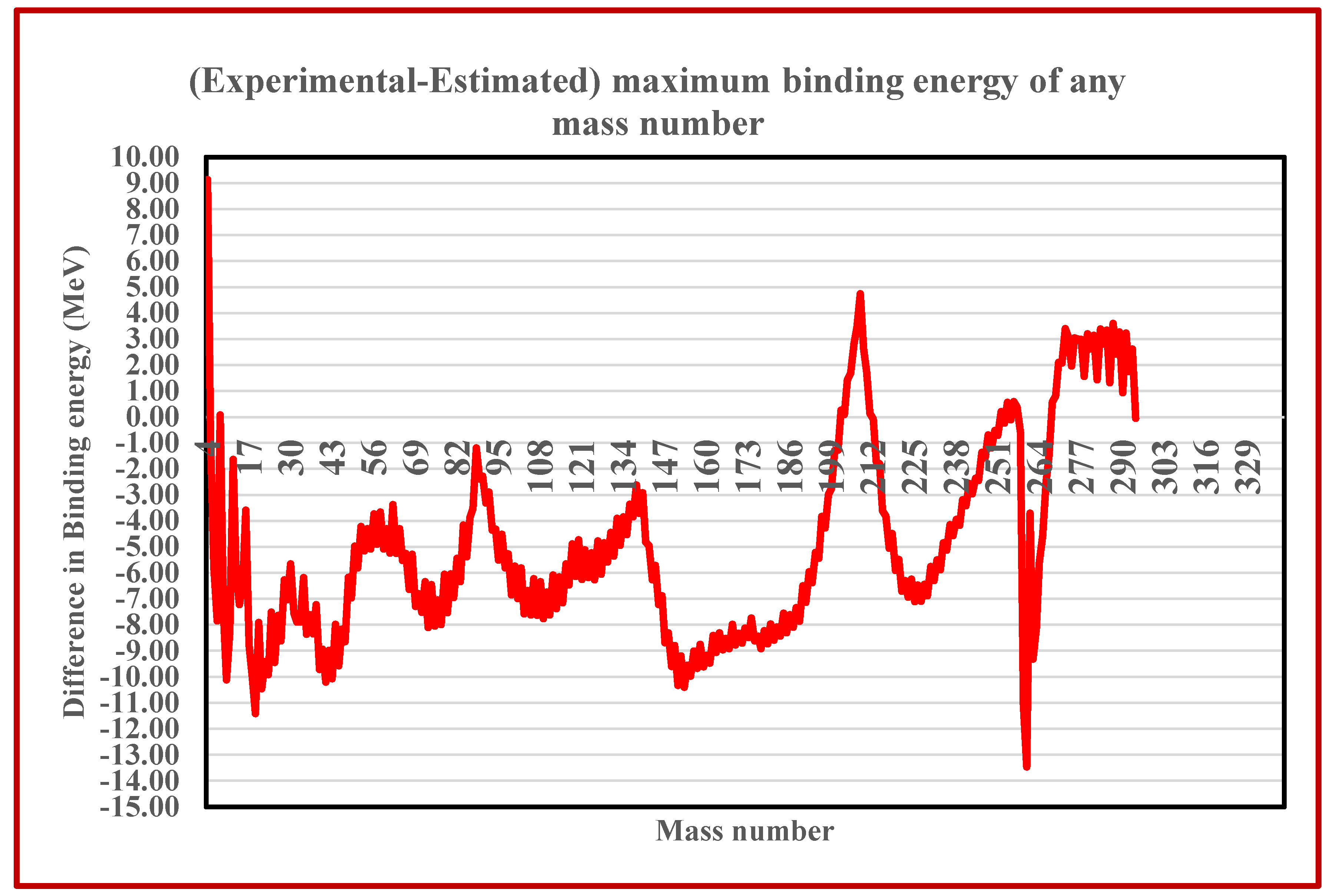
| Assumed mass number A | Estimated Max. Binding energy of A (MeV) | Experimental Max. Binding energy of A(MeV) | (Experimental -Estimated) Binding energy(MeV) |
| 4 | 19.17 | 28.3 | 9.13 |
| 5 | 28.48 | 27.56 | -0.92 |
| 6 | 37.78 | 31.99 | -5.79 |
| 7 | 47.10 | 39.25 | -7.85 |
| 8 | 56.42 | 56.5 | 0.08 |
| 9 | 65.76 | 58.16 | -7.60 |
| 10 | 75.10 | 64.98 | -10.12 |
| 11 | 84.45 | 76.2 | -8.25 |
| 12 | 93.80 | 92.16 | -1.64 |
| 13 | 103.15 | 97.11 | -6.04 |
| 14 | 112.51 | 105.28 | -7.23 |
| 15 | 121.86 | 115.49 | -6.37 |
| 16 | 131.21 | 127.62 | -3.59 |
| 17 | 140.55 | 131.76 | -8.79 |
| 18 | 149.89 | 139.81 | -10.08 |
| 19 | 159.22 | 147.8 | -11.42 |
| 20 | 168.55 | 160.64 | -7.91 |
| 21 | 177.87 | 167.41 | -10.46 |
| 22 | 187.18 | 177.77 | -9.41 |
| 23 | 196.48 | 186.56 | -9.92 |
| 24 | 205.77 | 198.26 | -7.51 |
| 25 | 215.05 | 205.59 | -9.46 |
| 26 | 224.31 | 216.68 | -7.63 |
| 27 | 233.57 | 224.95 | -8.62 |
| 28 | 242.82 | 236.54 | -6.28 |
| 29 | 252.05 | 245.01 | -7.04 |
| 30 | 261.27 | 255.62 | -5.65 |
| 31 | 270.48 | 262.92 | -7.56 |
| 32 | 279.68 | 271.78 | -7.90 |
| 33 | 288.86 | 280.96 | -7.90 |
| 34 | 298.03 | 291.84 | -6.19 |
| 35 | 307.19 | 298.82 | -8.37 |
| 36 | 316.33 | 308.71 | -7.62 |
| 37 | 325.46 | 317.1 | -8.36 |
| 38 | 334.57 | 327.34 | -7.23 |
| 39 | 343.67 | 333.94 | -9.73 |
| 40 | 352.75 | 343.81 | -8.94 |
| 41 | 361.82 | 351.62 | -10.20 |
| 42 | 370.88 | 361.9 | -8.98 |
| 43 | 379.91 | 369.83 | -10.08 |
| 44 | 388.94 | 380.96 | -7.98 |
| 45 | 397.95 | 388.37 | -9.58 |
| 46 | 406.94 | 398.77 | -8.17 |
| 47 | 415.92 | 407.26 | -8.66 |
| 48 | 424.88 | 418.7 | -6.18 |
| 49 | 433.82 | 426.85 | -6.97 |
| 50 | 442.75 | 437.78 | -4.97 |
| 51 | 451.67 | 445.85 | -5.82 |
| 52 | 460.57 | 456.35 | -4.22 |
| 53 | 469.45 | 464.29 | -5.16 |
| 54 | 478.31 | 474.01 | -4.30 |
| 55 | 487.16 | 482.08 | -5.08 |
| 56 | 495.99 | 492.26 | -3.73 |
| 57 | 504.81 | 499.91 | -4.90 |
| 58 | 513.61 | 509.95 | -3.66 |
| 59 | 522.39 | 517.31 | -5.08 |
| 60 | 531.16 | 526.85 | -4.31 |
| 61 | 539.91 | 534.67 | -5.24 |
| 62 | 548.64 | 545.26 | -3.38 |
| 63 | 557.36 | 552.1 | -5.26 |
| 64 | 566.06 | 561.76 | -4.30 |
| 65 | 574.74 | 569.21 | -5.53 |
| 66 | 583.40 | 578.14 | -5.26 |
| 67 | 592.05 | 585.41 | -6.64 |
| 68 | 600.68 | 595.39 | -5.29 |
| 69 | 609.30 | 602 | -7.30 |
| 70 | 617.89 | 611.09 | -6.80 |
| 71 | 626.47 | 618.95 | -7.52 |
| 72 | 635.04 | 628.69 | -6.35 |
| 73 | 643.58 | 635.47 | -8.11 |
| 74 | 652.11 | 645.66 | -6.45 |
| 75 | 660.62 | 652.57 | -8.05 |
| 76 | 669.11 | 662.07 | -7.04 |
| 77 | 677.59 | 669.59 | -8.00 |
| 78 | 686.05 | 679.99 | -6.06 |
| 79 | 694.49 | 686.95 | -7.54 |
| 80 | 702.91 | 696.87 | -6.04 |
| 81 | 711.32 | 704.37 | -6.95 |
| 82 | 719.71 | 714.27 | -5.44 |
| 83 | 728.08 | 721.74 | -6.34 |
| 84 | 736.43 | 732.27 | -4.16 |
| 85 | 744.77 | 739.38 | -5.39 |
| 86 | 753.09 | 749.23 | -3.86 |
| 87 | 761.39 | 757.86 | -3.53 |
| 88 | 769.67 | 768.47 | -1.20 |
| 89 | 777.93 | 775.54 | -2.39 |
| 90 | 786.18 | 783.9 | -2.28 |
| 91 | 794.41 | 791.09 | -3.32 |
| 92 | 802.62 | 799.73 | -2.89 |
| 93 | 810.82 | 806.46 | -4.36 |
| 94 | 818.99 | 814.68 | -4.31 |
| 95 | 827.15 | 821.63 | -5.52 |
| 96 | 835.29 | 830.78 | -4.51 |
| 97 | 843.41 | 837.6 | -5.81 |
| 98 | 851.52 | 846.25 | -5.27 |
| 99 | 859.61 | 852.75 | -6.86 |
| 100 | 867.67 | 861.93 | -5.74 |
| 101 | 875.73 | 868.73 | -7.00 |
| 102 | 883.76 | 877.95 | -5.81 |
| 103 | 891.77 | 884.19 | -7.58 |
| 104 | 899.77 | 893.09 | -6.68 |
| 105 | 907.75 | 900.13 | -7.62 |
| 106 | 915.71 | 909.48 | -6.23 |
| 107 | 923.66 | 916.02 | -7.64 |
| 108 | 931.58 | 925.24 | -6.34 |
| 109 | 939.49 | 931.72 | -7.77 |
| 110 | 947.38 | 940.64 | -6.74 |
| 111 | 955.25 | 947.62 | -7.63 |
| 112 | 963.10 | 957.01 | -6.09 |
| 113 | 970.94 | 963.55 | -7.39 |
| 114 | 978.75 | 972.59 | -6.16 |
| 115 | 986.55 | 979.4 | -7.15 |
| 116 | 994.33 | 988.68 | -5.65 |
| 117 | 1002.10 | 995.62 | -6.48 |
| 118 | 1009.84 | 1004.95 | -4.89 |
| 119 | 1017.57 | 1011.43 | -6.14 |
| 120 | 1025.27 | 1020.54 | -4.73 |
| 121 | 1032.96 | 1026.71 | -6.25 |
| 122 | 1040.64 | 1035.52 | -5.12 |
| 123 | 1048.29 | 1042.1 | -6.19 |
| 124 | 1055.92 | 1050.69 | -5.23 |
| 125 | 1063.54 | 1057.27 | -6.27 |
| 126 | 1071.14 | 1066.37 | -4.77 |
| 127 | 1078.72 | 1072.66 | -6.06 |
| 128 | 1086.28 | 1081.44 | -4.84 |
| 129 | 1093.83 | 1088.24 | -5.59 |
| 130 | 1101.35 | 1096.91 | -4.44 |
| 131 | 1108.86 | 1103.51 | -5.35 |
| 132 | 1116.35 | 1112.45 | -3.90 |
| 133 | 1123.82 | 1118.88 | -4.94 |
| 134 | 1131.28 | 1127.43 | -3.85 |
| 135 | 1138.71 | 1134.18 | -4.53 |
| 136 | 1146.13 | 1142.77 | -3.36 |
| 137 | 1153.53 | 1149.68 | -3.85 |
| 138 | 1160.90 | 1158.29 | -2.61 |
| 139 | 1168.27 | 1164.55 | -3.72 |
| 140 | 1175.61 | 1172.69 | -2.92 |
| 141 | 1182.93 | 1178.12 | -4.81 |
| 142 | 1190.24 | 1185.28 | -4.96 |
| 143 | 1197.53 | 1191.26 | -6.27 |
| 144 | 1204.80 | 1199.08 | -5.72 |
| 145 | 1212.05 | 1204.83 | -7.22 |
| 146 | 1219.28 | 1212.4 | -6.88 |
| 147 | 1226.50 | 1217.8 | -8.70 |
| 148 | 1233.69 | 1225.39 | -8.30 |
| 149 | 1240.87 | 1231.26 | -9.61 |
| 150 | 1248.03 | 1239.24 | -8.79 |
| 151 | 1255.17 | 1244.84 | -10.33 |
| 152 | 1262.30 | 1253.1 | -9.20 |
| 153 | 1269.40 | 1258.99 | -10.41 |
| 154 | 1276.49 | 1266.93 | -9.56 |
| 155 | 1283.55 | 1273.58 | -9.97 |
| 156 | 1290.60 | 1281.59 | -9.01 |
| 157 | 1297.63 | 1287.95 | -9.68 |
| 158 | 1304.65 | 1295.89 | -8.76 |
| 159 | 1311.64 | 1302.02 | -9.62 |
| 160 | 1318.62 | 1309.45 | -9.17 |
| 161 | 1325.57 | 1316.09 | -9.48 |
| 162 | 1332.51 | 1324.1 | -8.41 |
| 163 | 1339.43 | 1330.37 | -9.06 |
| 164 | 1346.33 | 1338.03 | -8.30 |
| 165 | 1353.22 | 1344.25 | -8.97 |
| 166 | 1360.08 | 1351.56 | -8.52 |
| 167 | 1366.93 | 1358 | -8.93 |
| 168 | 1373.76 | 1365.77 | -7.99 |
| 169 | 1380.57 | 1371.78 | -8.79 |
| 170 | 1387.36 | 1379.03 | -8.33 |
| 171 | 1394.13 | 1385.42 | -8.71 |
| 172 | 1400.88 | 1392.76 | -8.12 |
| 173 | 1407.62 | 1399.13 | -8.49 |
| 174 | 1414.34 | 1406.59 | -7.75 |
| 175 | 1421.04 | 1412.41 | -8.63 |
| 176 | 1427.72 | 1419.28 | -8.44 |
| 177 | 1434.38 | 1425.46 | -8.92 |
| 178 | 1441.02 | 1432.8 | -8.22 |
| 179 | 1447.64 | 1438.9 | -8.74 |
| 180 | 1454.25 | 1446.29 | -7.96 |
| 181 | 1460.84 | 1452.24 | -8.60 |
| 182 | 1467.41 | 1459.33 | -8.08 |
| 183 | 1473.96 | 1465.52 | -8.44 |
| 184 | 1480.49 | 1472.94 | -7.55 |
| 185 | 1487.00 | 1478.69 | -8.31 |
| 186 | 1493.50 | 1485.88 | -7.62 |
| 187 | 1499.98 | 1491.88 | -8.10 |
| 188 | 1506.43 | 1499.09 | -7.34 |
| 189 | 1512.87 | 1505.01 | -7.86 |
| 190 | 1519.29 | 1512.8 | -6.49 |
| 191 | 1525.70 | 1518.56 | -7.14 |
| 192 | 1532.08 | 1526.12 | -5.96 |
| 193 | 1538.44 | 1532.06 | -6.38 |
| 194 | 1544.79 | 1539.58 | -5.21 |
| 195 | 1551.12 | 1545.68 | -5.44 |
| 196 | 1557.43 | 1553.6 | -3.83 |
| 197 | 1563.72 | 1559.45 | -4.27 |
| 198 | 1569.99 | 1567 | -2.99 |
| 199 | 1576.25 | 1573.48 | -2.77 |
| 200 | 1582.48 | 1581.18 | -1.30 |
| 201 | 1588.70 | 1587.41 | -1.29 |
| 202 | 1594.90 | 1595.16 | 0.26 |
| 203 | 1601.07 | 1601.16 | 0.09 |
| 204 | 1607.24 | 1608.65 | 1.41 |
| 205 | 1613.38 | 1615.07 | 1.69 |
| 206 | 1619.50 | 1622.32 | 2.82 |
| 207 | 1625.61 | 1629.06 | 3.45 |
| 208 | 1631.69 | 1636.43 | 4.74 |
| 209 | 1637.76 | 1640.37 | 2.61 |
| 210 | 1643.81 | 1645.55 | 1.74 |
| 211 | 1649.84 | 1649.97 | 0.13 |
| 212 | 1655.85 | 1655.77 | -0.08 |
| 213 | 1661.85 | 1660.13 | -1.72 |
| 214 | 1667.82 | 1666.01 | -1.81 |
| 215 | 1673.78 | 1670.16 | -3.62 |
| 216 | 1679.72 | 1675.9 | -3.82 |
| 217 | 1685.64 | 1680.58 | -5.06 |
| 218 | 1691.54 | 1687.05 | -4.49 |
| 219 | 1697.42 | 1691.51 | -5.91 |
| 220 | 1703.28 | 1697.79 | -5.49 |
| 221 | 1709.13 | 1702.42 | -6.71 |
| 222 | 1714.95 | 1708.66 | -6.29 |
| 223 | 1720.76 | 1713.82 | -6.94 |
| 224 | 1726.55 | 1720.3 | -6.25 |
| 225 | 1732.32 | 1725.21 | -7.11 |
| 226 | 1738.07 | 1731.6 | -6.47 |
| 227 | 1743.80 | 1736.71 | -7.09 |
| 228 | 1749.52 | 1743.08 | -6.44 |
| 229 | 1755.21 | 1748.33 | -6.88 |
| 230 | 1760.89 | 1755.13 | -5.76 |
| 231 | 1766.55 | 1760.25 | -6.30 |
| 232 | 1772.19 | 1766.69 | -5.50 |
| 233 | 1777.81 | 1771.93 | -5.88 |
| 234 | 1783.41 | 1778.57 | -4.84 |
| 235 | 1789.00 | 1783.86 | -5.14 |
| 236 | 1794.56 | 1790.41 | -4.15 |
| 237 | 1800.11 | 1795.53 | -4.58 |
| 238 | 1805.64 | 1801.69 | -3.95 |
| 239 | 1811.15 | 1806.97 | -4.18 |
| 240 | 1816.64 | 1813.45 | -3.19 |
| 241 | 1822.11 | 1818.69 | -3.42 |
| 242 | 1827.56 | 1825 | -2.56 |
| 243 | 1833.00 | 1830.03 | -2.97 |
| 244 | 1838.41 | 1836.05 | -2.36 |
| 245 | 1843.81 | 1841.36 | -2.45 |
| 246 | 1849.19 | 1847.82 | -1.37 |
| 247 | 1854.55 | 1852.98 | -1.57 |
| 248 | 1859.89 | 1859.19 | -0.70 |
| 249 | 1865.21 | 1864.02 | -1.19 |
| 250 | 1870.52 | 1869.99 | -0.53 |
| 251 | 1875.80 | 1875.09 | -0.71 |
| 252 | 1881.07 | 1881.27 | 0.20 |
| 253 | 1886.32 | 1886.07 | -0.25 |
| 254 | 1891.55 | 1892.1 | 0.55 |
| 255 | 1896.76 | 1896.64 | -0.12 |
| 256 | 1901.95 | 1902.54 | 0.59 |
| 257 | 1907.12 | 1907.5 | 0.38 |
| 258 | 1912.28 | 1911.69 | -0.59 |
| 259 | 1917.41 | 1906.33 | -11.08 |
| 260 | 1922.53 | 1909.07 | -13.46 |
| 261 | 1927.63 | 1923.93 | -3.70 |
| 262 | 1932.71 | 1923.39 | -9.32 |
| 263 | 1937.77 | 1929.63 | -8.14 |
| 264 | 1942.81 | 1937.23 | -5.58 |
| 265 | 1947.84 | 1943.25 | -4.59 |
| 266 | 1952.84 | 1950.31 | -2.53 |
| 267 | 1957.83 | 1956.31 | -1.52 |
| 268 | 1962.80 | 1963.37 | 0.57 |
| 269 | 1967.74 | 1968.54 | 0.80 |
| 270 | 1972.67 | 1974.78 | 2.11 |
| 271 | 1977.59 | 1979.66 | 2.07 |
| 272 | 1982.48 | 1985.87 | 3.39 |
| 273 | 1987.35 | 1990.44 | 3.09 |
| 274 | 1992.21 | 1994.17 | 1.96 |
| 275 | 1997.05 | 2000.08 | 3.03 |
| 276 | 2001.86 | 2004.86 | 3.00 |
| 277 | 2006.66 | 2009.64 | 2.98 |
| 278 | 2011.44 | 2013 | 1.56 |
| 279 | 2016.21 | 2019.4 | 3.19 |
| 280 | 2020.95 | 2023.56 | 2.61 |
| 281 | 2025.68 | 2028.82 | 3.14 |
| 282 | 2030.38 | 2031.81 | 1.43 |
| 283 | 2035.07 | 2038.45 | 3.38 |
| 284 | 2039.74 | 2042.53 | 2.79 |
| 285 | 2044.39 | 2047.73 | 3.34 |
| 286 | 2049.02 | 2050.33 | 1.31 |
| 287 | 2053.63 | 2057.22 | 3.59 |
| 288 | 2058.22 | 2060.64 | 2.42 |
| 289 | 2062.80 | 2066.06 | 3.26 |
| 290 | 2067.36 | 2068.28 | 0.92 |
| 291 | 2071.89 | 2075.12 | 3.23 |
| 292 | 2076.41 | 2078.16 | 1.75 |
| 293 | 2080.91 | 2083.52 | 2.61 |
| 294 | 2085.39 | 2085.34 | -0.05 |
| 295 | 2089.86 | ||
| 296 | 2094.30 | ||
| 297 | 2098.73 | ||
| 298 | 2103.13 | ||
| 299 | 2107.52 | ||
| 300 | 2111.89 | ||
| 301 | 2116.24 | ||
| 302 | 2120.57 | ||
| 303 | 2124.88 | ||
| 304 | 2129.18 | ||
| 305 | 2133.45 | ||
| 306 | 2137.71 | ||
| 307 | 2141.95 | ||
| 308 | 2146.17 | ||
| 309 | 2150.37 | ||
| 310 | 2154.55 | ||
| 311 | 2158.71 | ||
| 312 | 2162.86 | ||
| 313 | 2166.98 | ||
| 314 | 2171.09 | ||
| 315 | 2175.18 | ||
| 316 | 2179.25 | ||
| 317 | 2183.30 | ||
| 318 | 2187.33 | ||
| 319 | 2191.34 | ||
| 320 | 2195.34 | ||
| 321 | 2199.31 | ||
| 322 | 2203.27 | ||
| 323 | 2207.21 | ||
| 324 | 2211.13 | ||
| 325 | 2215.03 | ||
| 326 | 2218.91 | ||
| 327 | 2222.77 | ||
| 328 | 2226.62 | ||
| 329 | 2230.44 | ||
| 330 | 2234.25 | ||
| 331 | 2238.04 | ||
| 332 | 2241.81 | ||
| 333 | 2245.56 | ||
| 334 | 2249.29 | ||
| 335 | 2253.01 | ||
| 336 | 2256.70 | ||
| 337 | 2260.38 | ||
| 338 | 2264.03 | ||
| 339 | 2267.67 | ||
| 340 | 2271.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





