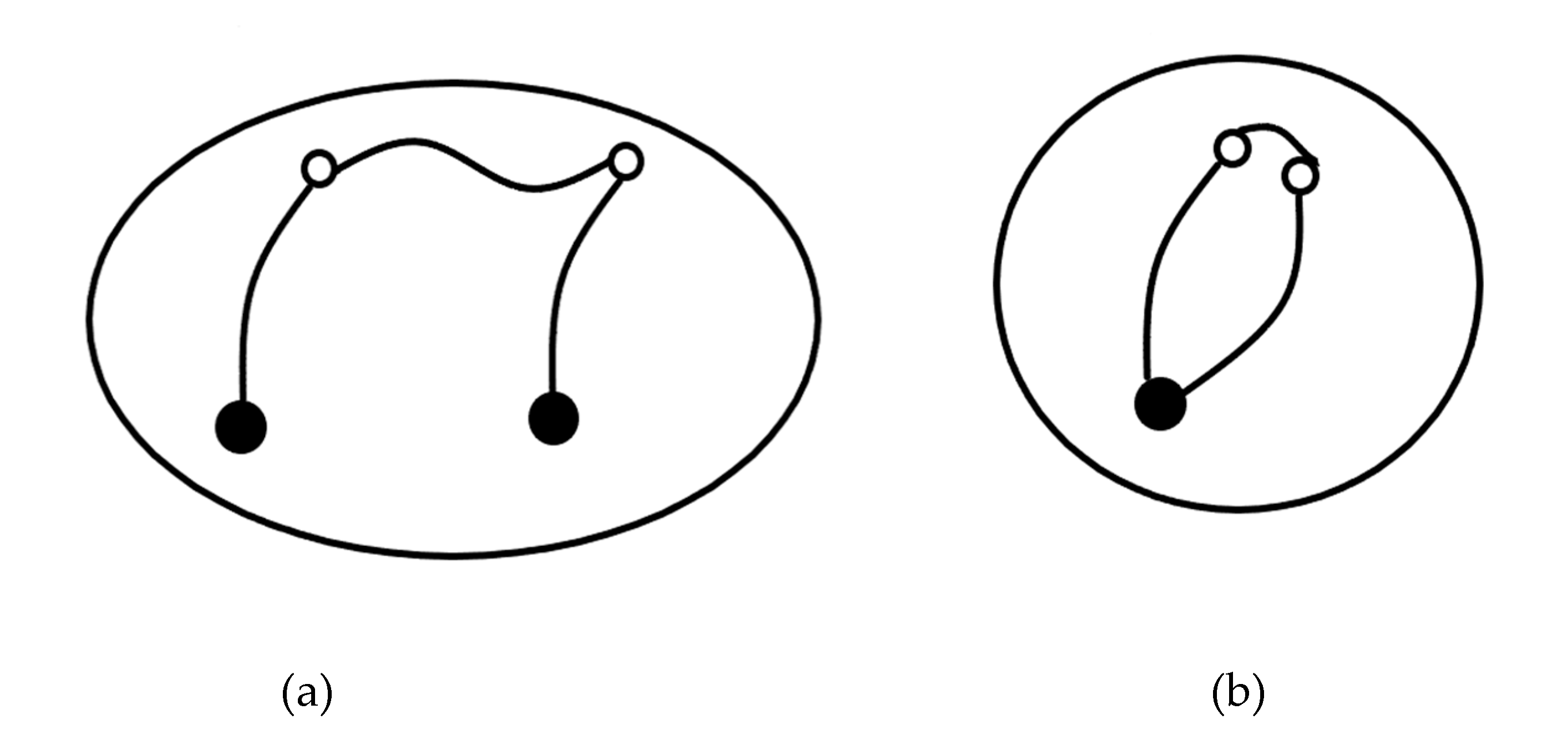Entanglement Swapping Schemes on Intraparticle Entangled States

1. Introduction

Entanglement is one of the most striking features in quantum systems. Initially, it was pointed out as a clue (incompleteness of quantum mechanics) by Einstein et al. It has a miraculous non-classical correlation. Symmetry refers to the property that a system remains unchanged after undergoing certain transformations. Symmetry is an important property in describing natural laws, including spatial, temporal and rotational symmetry, etc. Symmetry is closely related to entanglement in quantum mechanics. For example, in quantum field theory, symmetry can affect the entangled state of particles, and the entangled state can also reflect the symmetry properties of the system.

Today, quantum technology has received worldwide attention and is a major national strategy. Quantum technology is a new interdisciplinary field that combines quantum physics and information technology. Today, it plays a vital role in quantum science and technology. Its non-classical correlation is an essential resource in quantum communication and quantum computing. Many protocols rely on non-classical correlations to achieve, such as quantum teleportation (QT) [1], quantum cryptography [2,3], and quantum random number generators [4].

Two systems not only can entangle on one degree of freedom but also on multiple degrees of freedom [5,6], which is called hybrid entanglement [7]. Diversifying mixed entanglement opens the door to achieving entanglement between various degrees of freedom in a single particle (intraparticle entangled states). The so-called intraparticle entangled states are entanglement states, such as the polarization-momentum entanglement of a single photon [8,9], the spin-path entanglement of a neutron [10,11,12], and so on. Compared with entangled states between multiple particles, intraparticle entangled states are more easily generated and more robust [13]. The non-classical correlations are not shared by two spatially separated subsystems, which do not require temporal correlation between different particles. In addition, only a single particle is needed to generate entangled states, thus intraparticle entangled state consumes fewer resources. These advantages can enable intraparticle entangled states to function better in quantum information protocols.

In similar entangled states between multiple particles, entanglement swapping can also be achieved in intraparticle entangled states, causing two previously unrelated quantities to entangle. Intraparticle entanglement swapping can be applied in super quantum dense encoding [14], quantum information transmission [15,16,17,18], and quantum teleportation [19,20]. This work first analogizes the distinctions and connections between two kinds of entangled states. Then, it analyzes and designs several entanglement swapping methods for intraparticle entangled states, analogizing the entanglement swapping between multiple particles. This work is beneficial for further understanding entanglement and promoting intraparticle entangled states to better application in quantum information transmission.

2. Methods

2.1. The Distinctions and Connections between Two Kinds of Entangled States

Entanglement should be comprehended as involving at least two commuting observables belonging to different particles or the same particle. Thus, entanglement can be divided into two types: the entanglement between multi-partite systems and the entanglement among various degrees of freedom within a single-particle system (intraparticle entangled states). Two types of entanglement have distinctions and connections. This section will analyze and compare their correlation and non-locality, anti-interference ability, mechanisms of generation and separation, and the advantages and drawbacks in practical applications.

2.1.1. Correlation and Non-Locality

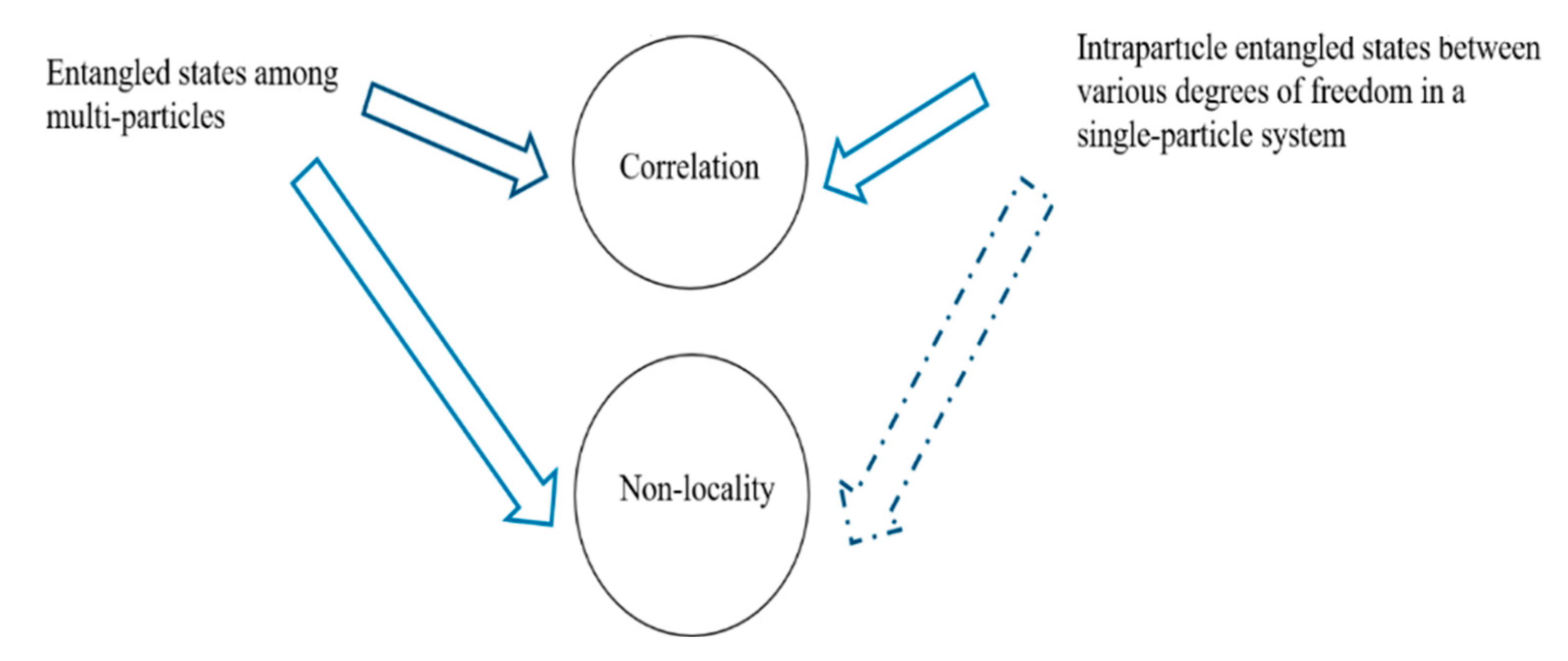
Correlation and non-locality. As shown in Figure 1, the correlation exists in both two types of entanglement. One entangled party’s states changes, regardless of the distance separating them, and another party’s state is correspondingly altered on the entangled states between multiple particles; this kind of entanglement possesses non-local correlations. The non-locality correlation (violation of Bell’s inequality) has been tested in extensive experiments for the entangled states between multiple particles. Intraparticle entangled states do not have non-locality because their entangled states are established on various degrees of freedom within a single particle; non-locality is meaningless; however, it possesses correlation. The corresponding correlations have also been verified in experiments for intraparticle entangled states.

2.1.2. Anti-Interference Ability

Anti-interference ability. Intraparticle entangled states possess a stronger anti-interference ability, which stems from the system of intraparticle entangled states having a smaller interface with the external environment during communication, as shown in Figure 2, this entanglement suffers less interference from the external environment. Quantum systems have a more extensive interface with the external environment for the entangled states between multiple particles. It suffers more significant interference from the external environment, thus its anti-interference ability is relatively weak.

2.1.3. Generation and Separation Methods

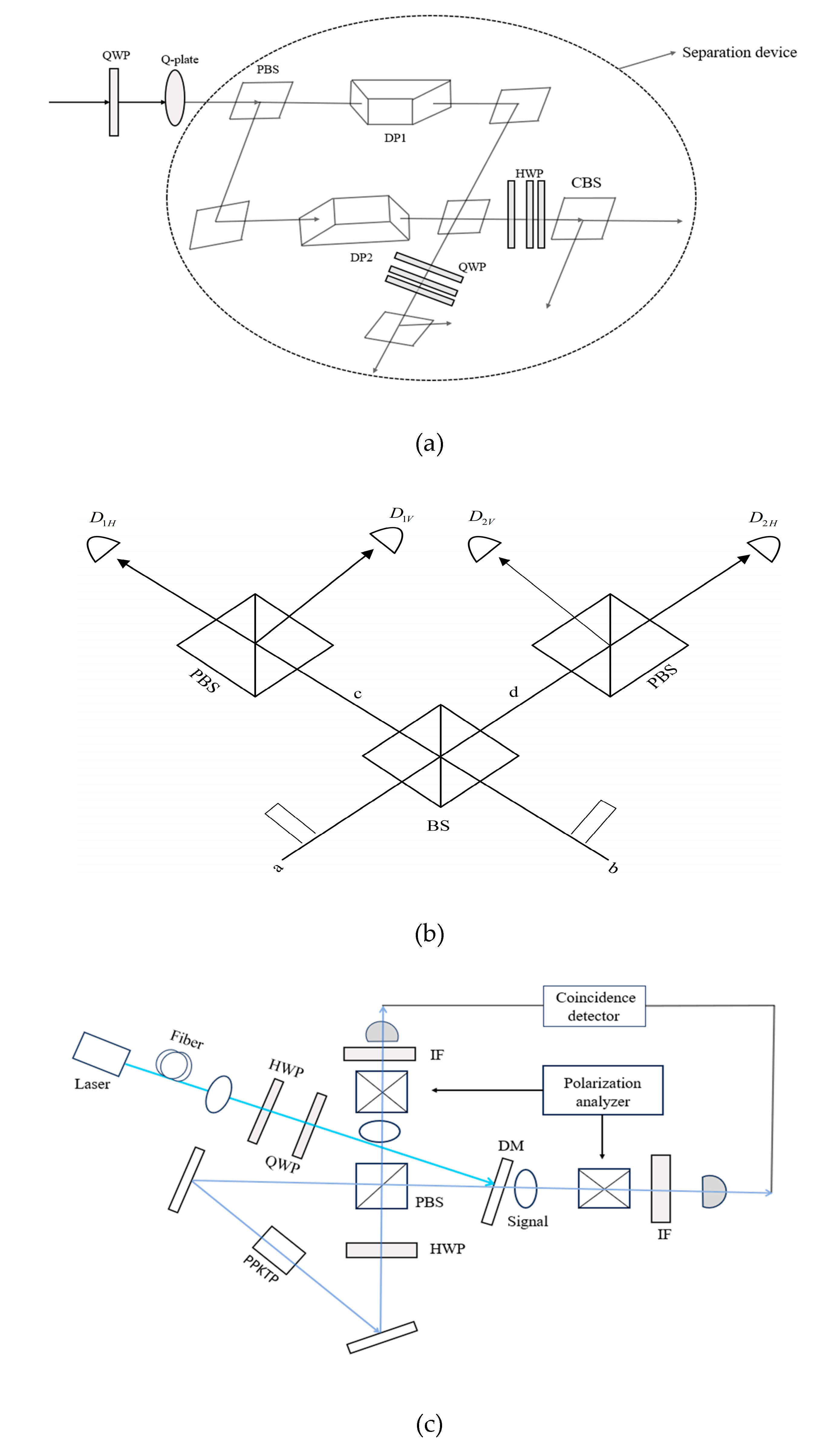
The intraparticle entangled state is established based on various degrees of freedom of a single particle, such as spin-orbital angular momentum, spin-path, path-orbital angular momentum, and so on. This section takes the spin-orbital entangled states of a single photon as an example. Figure 3 is the experimental setup for generating and separating intraparticle entangled states and the entangled state between multiple particles, Figure 3(a) is the experimental setup for intraparticle entangled states; Figure 3(b) and (c) represent the experimental setups for multiple-particle entangled states, respectively.

The generation of intraparticle entangled states is simpler and more convenient than those among multiple particles as shown on the left side of Figure 3(a) [22] and in Figure 3(c). The intraparticle entangled state does not require two or more independent systems. However, as shown on the right side of Figure 3(a), the detection and separation processes are more complicated in intraparticle entangled states than in entangled states among multiple particles as shown in Figure 3(c). Interference and geometrical transformation (diffraction) methods are commonly used to separate and detect the spin-orbital entangled states within a single particle. In principle, continuous separation and detection can be achieved by cascading multiple interferometers and adjusting the corresponding parameters for orbital angular momentum superposition states. This method avoids interference with external beams, and the orbital angular momentum beams can also retain their original phase information [21]. Linear optical elements, such as polarization beam splitters (PBS), half-wave plates, and photodetectors, are generally employed for separating and detecting entangled states among multiple particles [22,23,24].

2.1.4. Application

Entangled states between multiple particles can be utilized in cutting-edge technologies, such as quantum teleportation, quantum key distribution (QKD), quantum dense coding, and quantum secure direct communication (QSDC). Intraparticle entangled states can also be used for quantum teleportation, QKD, entanglement swapping, quantum-dense coding, and so on. The advantages and drawbacks are compared for two types of entangled states in communication processes in Table 1. Compared to entangled states between multiple particles, intraparticle entangled states exhibit stronger robustness (resistance to external environmental disturbances) and a greater capacity for information carrying in the information transmission process; however, it has the drawback of being relatively more challenging to separate and detect. Two kinds of entanglement states both exhibit high levels of security.

2.2. Entanglement Swapping Schemes on Intraparticle Entangled States

This section analyzed and designed three intraparticle entanglement swapping schemes after analyzing the distinctions and connections between two types of entangled states. These schemes are based on Bell state joint measurement, cross-Kerr medium, and linear optical elements.

2.2.1. The Principle of Entanglement Swapping

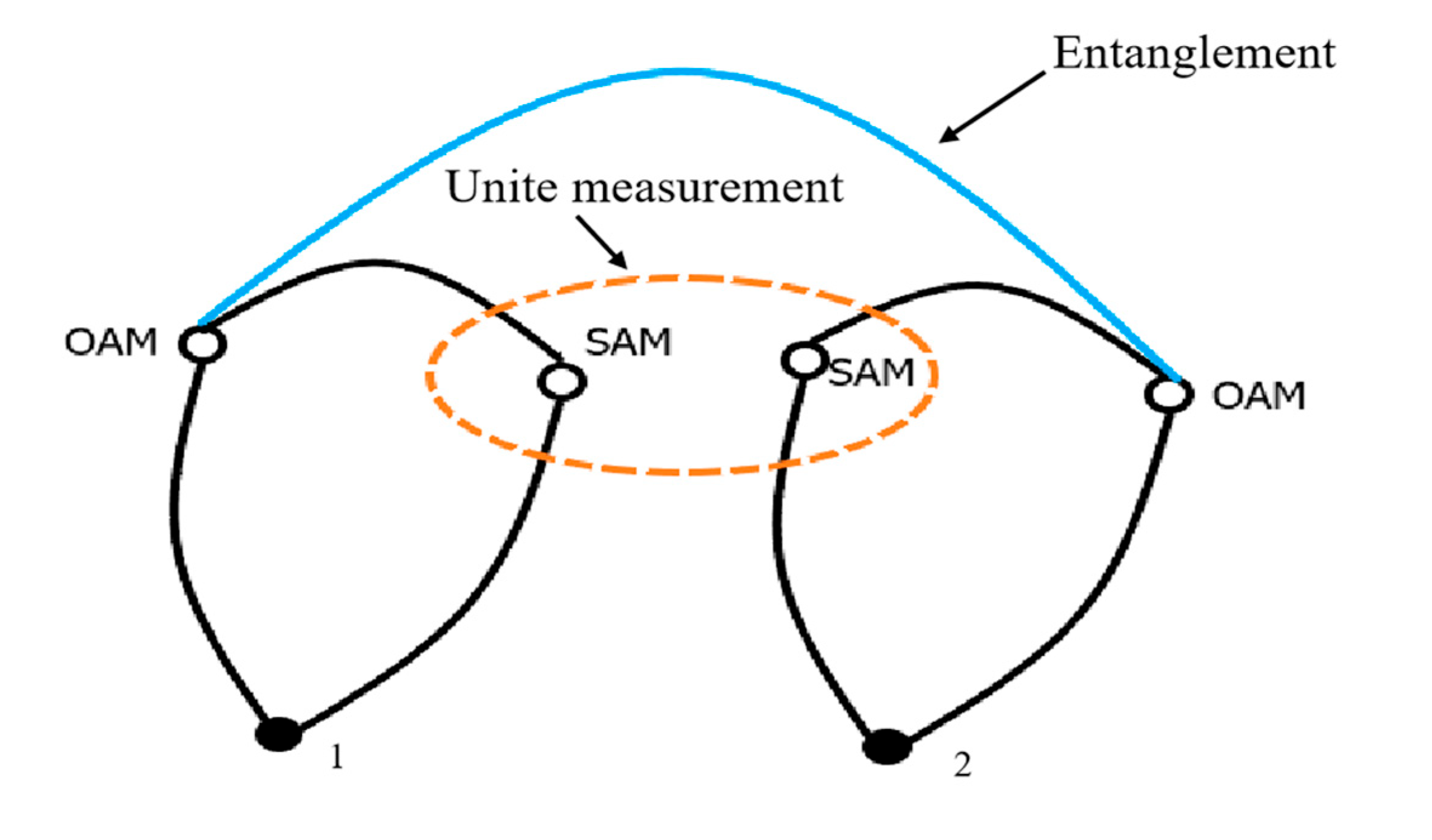
Assuming the light along the z-axis propagating, the projection of the total intrinsic angular momentum of the beams is conserved The principle of entanglement swapping is illustrated in Figure 4. Particles 1 and 2 are entangled in their respective spin-orbit angular momentum degrees of freedom. The intraparticle entanglement swapping can be achieved by united measurement of their spin angular momentum (SAM), the orbital angular momentum (OAM) degrees of freedom of the two particles, the originally unrelated quantities, can be entangled with each other.

2.2.2. Entanglement Swapping Schemes Based on Bell State Joint Measurement

Entanglement swapping can be achieved by utilizing Bell-based joint measurement on intraparticle entangled states. Suppose the entangled states among various degrees of freedom of photons 1 and 2 are as

$${\left|\phi \right.〉}_1={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}_{1s}{\left|0\right.〉}_{1o}+{\left|1\right.〉}_{1s}{\left|1\right.〉}_{1o}\right)$$

(1)

$${\left|\phi \right.〉}_2={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}_{2s}{\left|0\right.〉}_{2o}+{\left|1\right.〉}_{2s}{\left|1\right.〉}_{2o}\right)$$

(2)

The joint state of the above two equations can be written as

$${\left|\phi \right.〉}_3={\displaystyle \frac{1}{2}}\left(\begin{array}{l}{\left|0\right.〉}_{1s}{\left|0\right.〉}_{1o}{\left|0\right.〉}_{2s}{\left|0\right.〉}_{2o}+{\left|0\right.〉}_{1s}{\left|0\right.〉}_{1o}{\left|1\right.〉}_{2s}{\left|1\right.〉}_{2o}\\ +{\left|1\right.〉}_{1s}{\left|1\right.〉}_{1o}{\left|0\right.〉}_{2s}{\left|0\right.〉}_{2o}+{\left|1\right.〉}_{1s}{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2s}{\left|1\right.〉}_{2o}\end{array}\right)$$

(3)

To obtain the orbital angular momentum entangled state between two photons

$$\left|\psi \right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}_{1o}{\left|0\right.〉}_{2o}+{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2o}\right)$$

(4)

Joint measurement spin degree of freedom states of 2 photons by using Bell basis as shown in the following

$$\begin{array}{l}\left|{\mathrm{g}}^{\pm }\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}_{1s}{\left|0\right.〉}_{2s}\pm {\left|1\right.〉}_{1s}{\left|1\right.〉}_{2s}\right)\\ \left|k^{\pm }\right.〉={\displaystyle \frac{1}{\sqrt{2}}}\left({\left|0\right.〉}_{1s}{\left|1\right.〉}_{2s}\pm {\left|1\right.〉}_{1s}{\left|0\right.〉}_{2s}\right)\end{array}$$

(5)

Equation (5) can be rewritten as (6) by the Bell basis

$${\left|\phi \right.〉}_4={\displaystyle \frac{1}{4}}\left[\begin{array}{l}\left|{\mathrm{g}}^{+}\right.〉\left({\left|0\right.〉}_{1o}{\left|0\right.〉}_{2o}+{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2o}\right)+\left|{\mathrm{g}}^{-}\right.〉\left({\left|0\right.〉}_{1o}{\left|0\right.〉}_{2o}-{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2o}\right)\\ +\left|k^{+}\right.〉\left({\left|0\right.〉}_{1o}{\left|1\right.〉}_{2o}+{\left|1\right.〉}_{1o}{\left|0\right.〉}_{2o}\right)+\left|k^{-}\right.〉\left({\left|0\right.〉}_{1o}{\left|1\right.〉}_{2o}-{\left|1\right.〉}_{1o}{\left|0\right.〉}_{2o}\right)\end{array}\right]$$

(6)

From the above equation, the desired entangled swapping state $\left|\psi \right.〉$ can be directly obtained when the joint measurement result is $\left|g^{+}\right.〉$. In other cases, the corresponding unitary operation needs to be performed on the orbital angular momentum degree of freedom of photon 2 to get the desired entangled swapping state. The measurement results and corresponding unitary operation operators needed are shown in Table 2.

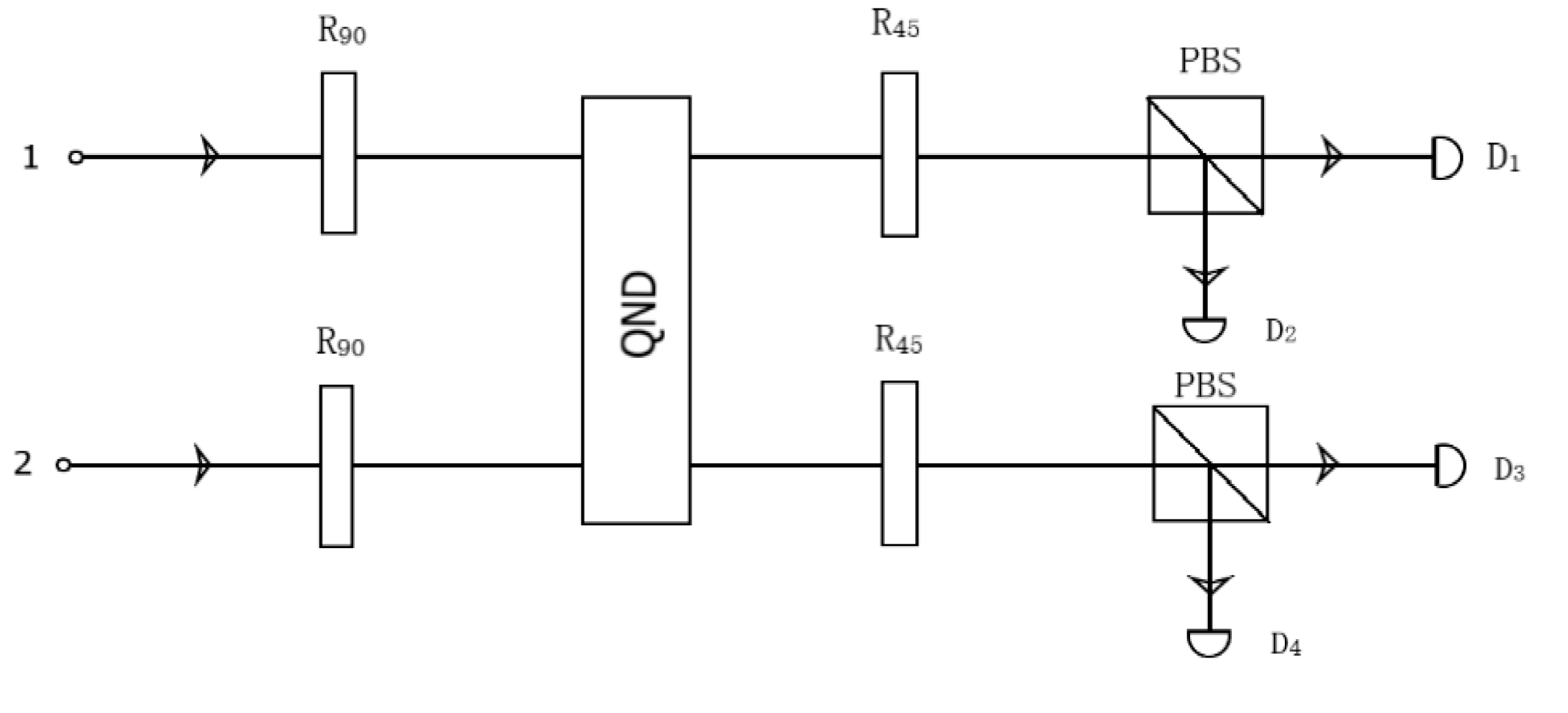
2.2.3. Entanglement Swapping Schemes Based on Cross-Kerr Medium

Entanglement swapping can be achieved based on Cross-Kerr medium. Suppose the entangled states among various degrees of freedom of photons 1 and 2 are as

$${\left|\phi \right.〉}_1^{\text{'}}=\alpha {\left|0\right.〉}_{1s}{\left|0\right.〉}_{1o}+\beta {\left|1\right.〉}_{1s}{\left|1\right.〉}_{1o}$$

(7)

$${\left|\phi \right.〉}_2^{\text{'}}=\alpha {\left|0\right.〉}_{2s}{\left|0\right.〉}_{2o}+\beta {\left|1\right.〉}_{2s}{\left|1\right.〉}_{2o}$$

(8)

where ${\left|\alpha \right|}^2+{\left|\beta \right|}^2=1$.

To obtain the entangled state in equation (9), the scheme, as shown in Figure 5, is used to implement the entanglement swapping.

$${\left|\psi \right.〉}^{\text{'}}={\displaystyle \frac{1}{c}}\left({\left|0\right.〉}_{1o}{\left|0\right.〉}_{2o}+{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2o}\right)$$

(9)

where $c$ represents the coefficient

The joint state ${\left|\phi \right.〉}_3^{\text{'}}$ composed of ${\left|\phi \right.〉}_1^{\text{'}}$ and ${\left|\phi \right.〉}_2^{\text{'}}$ are as

$${\left|\phi \right.〉}_3^{\text{'}}={\alpha }^2{\left|00\right.〉}_{1so}{\left|00\right.〉}_{2so}+\alpha \beta \left({\left|00\right.〉}_{1so}{\left|11\right.〉}_{2so}+{\left|11\right.〉}_{1so}{\left|00\right.〉}_{2so}\right)+{\beta }^2{\left|11\right.〉}_{1so}{\left|11\right.〉}_{2so}$$

(10)

To achieve entanglement swapping, as shown in Figure 5, a half-wave plate ${90}^o$ is used to perform a spin-flip operation on the spin degree of freedom of photons 1 and 2. ${\left|\phi \right.〉}_3^{\text{'}}$ becomes ${\left|\phi \right.〉}_4^{\text{'}}$

$${\left|\phi \right.〉}_4^{\text{'}}={\alpha }^2{\left|10\right.〉}_{1so}{\left|10\right.〉}_{2so}+\alpha \beta \left({\left|10\right.〉}_{1so}{\left|01\right.〉}_{2so}+{\left|01\right.〉}_{1so}{\left|10\right.〉}_{2so}\right)+{\beta }^2{\left|01\right.〉}_{1so}{\left|01\right.〉}_{2so}$$

(11)

Next, letting photons 1 and 2 pass through the QND, ${\left|\phi \right.〉}_4^{\text{'}}$ becomes ${\left|\phi \right.〉}_5^{\text{'}}$

$${\left|\phi \right.〉}_5^{\text{'}}=\left({\alpha }^2{\left|10\right.〉}_{1so}{\left|10\right.〉}_{2so}+{\beta }^2{\left|01\right.〉}_{1so}{\left|01\right.〉}_{2so}\right)\left|c{e}^{i\theta }\right.〉+\alpha \beta \left({\left|10\right.〉}_{1so}{\left|01\right.〉}_{2so}\left|c\right.〉+{\left|01\right.〉}_{1so}{\left|10\right.〉}_{2so}\left|c{e}^{2i\theta }\right.〉\right)$$

(12)

The corresponding operation is performed on the QND to make $\theta =\pi$. If the measurement result is $0$ or $2\pi$, which indicates the polarization states of two photons are different when the photons pass through the QND, ${\left|\phi \right.〉}_5^{\text{'}}$collapses to the state ${\left|\phi \right.〉}_6^{\text{'}}$

$${\left|\phi \right.〉}_6^{\text{'}}=\alpha \beta \left({\left|10\right.〉}_{1so}{\left|01\right.〉}_{2so}+{\left|01\right.〉}_{1so}{\left|10\right.〉}_{2so}\right)$$

(13)

Next, letting photons 1 and 2 pass through a half-wave plate placed at ${45}^{°}$, the half-wave plate acts on the polarization state as shown in the following equation.

$$\left|1\right.〉\to {\displaystyle \frac{1}{\sqrt{2}}}\left(\left|1\right.〉+\left|0\right.〉\right)$$

(14)

$$\left|0\right.〉\to {\displaystyle \frac{1}{\sqrt{2}}}\left(\left|1\right.〉-\left|0\right.〉\right)$$

(15)

After passing through the half-wave plate, ${\left|\phi \right.〉}_6^{\text{'}}$will become ${\left|\phi \right.〉}_7^{\text{'}}$

$${\left|\phi \right.〉}_7^{\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left[\left({\left|01\right.〉}_{1o2o}+{\left|10\right.〉}_{1o2o}\right)\left({\left|00\right.〉}_{1s2s}-{\left|11\right.〉}_{1s2s}\right)+\left({\left|01\right.〉}_{1o2o}-{\left|10\right.〉}_{1o2o}\right)\left({\left|01\right.〉}_{1s2s}-{\left|10\right.〉}_{1s2s}\right)\right]$$

(16)

where $1o2o$represents the orbital angular momentum degree of freedom of photons 1 and 2, $1s2s$represents the spin degree of freedom of photons 1 and 2. Next, photons 1 and 2 pass through a PBS, then four-photon detectors $D_1,D_2,D_3,D_4$are used to detect photons. Based on the detected situation, the entangled states of the two photons are determined. If $D_1,D_2$ or $D_3,D_4$ detectors respond at the same time, the entangled state of photons 1 and 2 collapses as ${\left|\phi \right.〉}_8^{\text{'}}$

$${\left|\phi \right.〉}_8^{\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left({\left|01\right.〉}_{1o2o}+{\left|10\right.〉}_{1o2o}\right)$$

(17)

Performing a unitary operation ${\sigma }_x$ on the orbital angular momentum degree of freedom of photon 2, the entangled state desired will be given

$${\left|\phi \right.〉}_9^{\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left({\left|00\right.〉}_{1o2o}+{\left|11\right.〉}_{1o2o}\right)$$

(18)

If $D_1,D_4$ or $D_2,D_3$detectors respond at the same time, the entangled state of photons 1 and 2 collapses as ${\left|\phi \right.〉}_{10}^{\text{'}}$

$${\left|\phi \right.〉}_{10}^{\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left({\left|01\right.〉}_{1o2o}-{\left|10\right.〉}_{1o2o}\right)$$

(19)

For the same reason, the entangled state desired will be obtained by performing a unitary operation $i{\sigma }_y$on the orbital angular momentum degree of freedom of photon 2.

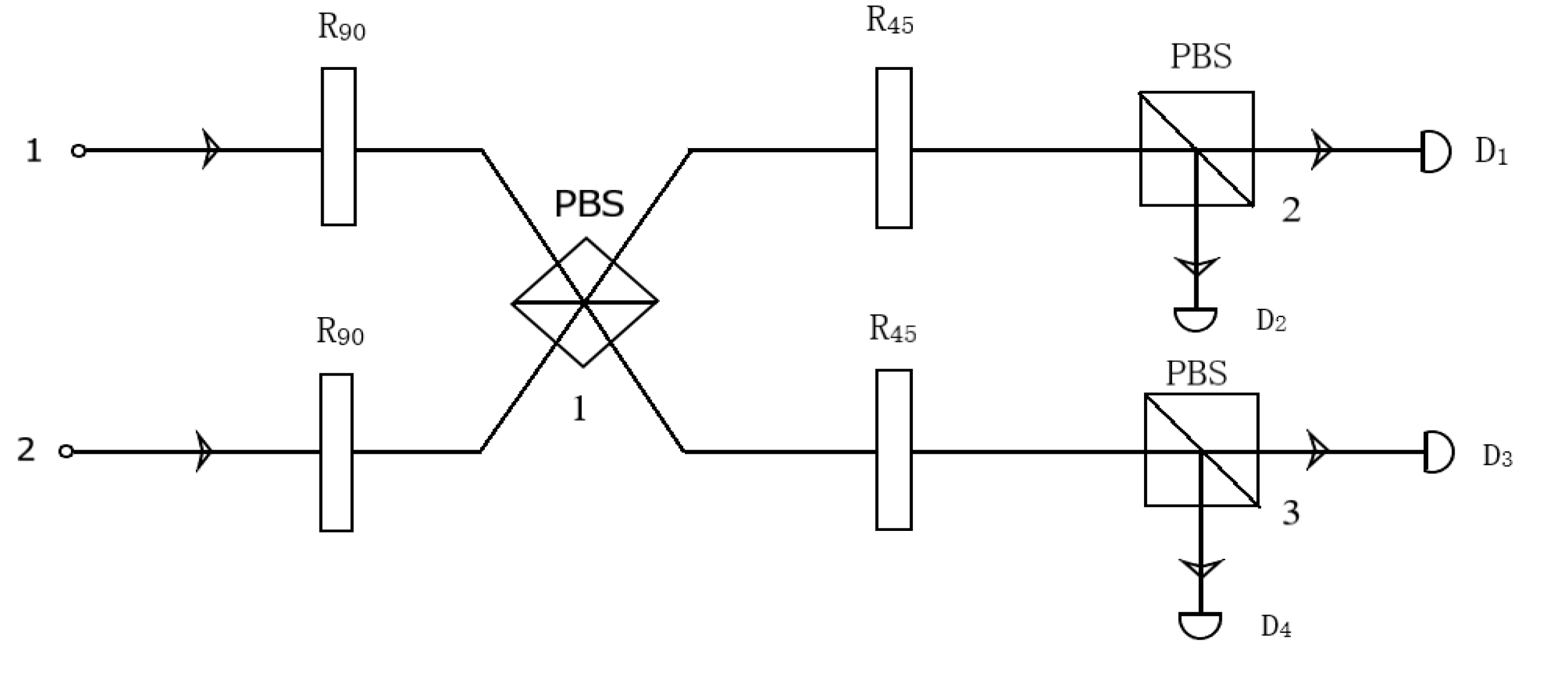
2.2.4. Entanglement Swapping Schemes Based on Linear Optical Elements

Assuming the intraparticle entangled states of photons 1 and 2 are as (7), (8). To obtain the desired entangled state as given in equation (9), the experimental setups, as shown in Figure 6, are used to perform the entanglement swapping. The joint state ${\left|\phi \right.〉}_3^{\text{'}\text{'}}$composed of (7) and (8) is as

$${\left|\phi \right.〉}_3^{\text{'}\text{'}}={\alpha }^2{\left|00\right.〉}_{1so}{\left|00\right.〉}_{2so}+\alpha \beta \left({\left|00\right.〉}_{1so}{\left|11\right.〉}_{2so}+{\left|11\right.〉}_{1so}{\left|00\right.〉}_{2so}\right)+{\beta }^2{\left|11\right.〉}_{1so}{\left|11\right.〉}_{2so}$$

(20)

In Figure 6, R90 is a half-wave plate with ${90}^o$, R45 is a half-wave plate with ${45}^o$ , and $D_i\left(i=1,2,3,4\right)$ are detectors. Using the half-wave plates with ${90}^o$ perform spin-flip operations on the spin degree of freedom of photons 1 and 2, (20) becomes (21).

$$\begin{array}{l}{\left|\phi \right.〉}_4^{\text{'}\text{'}}=\alpha \beta \left({\left|1\right.〉}_{1s}{\left|0\right.〉}_{2s}{\left|0\right.〉}_{1o}{\left|1\right.〉}_{2o}+{\left|0\right.〉}_{1s}{\left|1\right.〉}_{2s}{\left|1\right.〉}_{1o}{\left|0\right.〉}_{2o}\right)\\ {\alpha }^2{\left|1\right.〉}_{1s}{\left|1\right.〉}_{2s}{\left|0\right.〉}_{1o}{\left|0\right.〉}_{2o}+{\beta }^2{\left|0\right.〉}_{1s}{\left|0\right.〉}_{2s}{\left|1\right.〉}_{1o}{\left|1\right.〉}_{2o}\end{array}$$

(21)

In the above equation (21), the first and fourth terms will cause both the transmission and reflection spatial modes of PBS1 to output photons. The second and third terms can only cause one spatial mode (transmission or reflection) of PBS1 to output photons. When the two photons output from the one spatial mode of PBS1, ${\left|\phi \right.〉}_4^{\text{'}\text{'}}$ becomes ${\left|\phi \right.〉}_5^{\text{'}\text{'}}$

$${\left|\phi \right.〉}_5^{\text{'}\text{'}}=\alpha \beta \left({\left|1\right.〉}_{1s}{\left|0\right.〉}_{2s}{\left|0\right.〉}_{1o}{\left|1\right.〉}_{2o}+{\left|0\right.〉}_{1s}{\left|1\right.〉}_{2s}{\left|1\right.〉}_{1o}{\left|0\right.〉}_{2o}\right)$$

(22)

Next, making the photon pass through a half-wave plate with${45}^{°}$, ${\left|\phi \right.〉}_5^{\text{'}\text{'}}$ becomes ${\left|\phi \right.〉}_6^{\text{'}\text{'}}$

$${\left|\phi \right.〉}_6^{\text{'}\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left[\left({\left|01\right.〉}_{1o2o}+{\left|10\right.〉}_{1o2o}\right)\left({\left|00\right.〉}_{1s2s}-{\left|11\right.〉}_{1s2s}\right)+\left({\left|01\right.〉}_{1o2o}-{\left|10\right.〉}_{1o2o}\right)\left({\left|01\right.〉}_{1s2s}-{\left|10\right.〉}_{1s2s}\right)\right]$$

(23)

In the above equation (22-23), the subscript $1o2o$represents the orbital angular momentum degrees of freedom of photons 1 and 2, and the subscript $1s2s$denotes the spin degrees of freedom of photons 1 and 2. Next, the photons are passed through a PBS, then four-photon detectors are used to determine the entangled states of the two photons. If one of the four detectors $D_1,D_2,D_3,D_4$ rings twice, the entangled state of photons 1 and 2 collapses into

$${\left|\phi \right.〉}_7^{\text{'}\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left({\left|01\right.〉}_{1o2o}+{\left|10\right.〉}_{1o2o}\right)$$

(24)

A unitary operation ${\sigma }_x$ is performed on the orbital angular momentum degrees of freedom of photon 1, the desired entangled state will be obtained as

$${\left|\phi \right.〉}_8^{\text{'}\text{'}}={\displaystyle \frac{\alpha \beta }{2}}\left({\left|00\right.〉}_{1o2o}+{\left|11\right.〉}_{1o2o}\right)$$

(25)

If detectors $D_1,D_2$or $D_3,D_4$ is rings twice, the entangled state of photons 1 and 2 will collapsed into

$${\left|\phi \right.〉}_9^{\text{'}\text{'}}={\displaystyle \frac{\alpha \beta }{\sqrt{2}}}\left({\left|01\right.〉}_{1o2o}-{\left|10\right.〉}_{1o2o}\right)$$

(26)

The desired entangled state will be obtained by performing a unitary operation $i{\sigma }_y$ on the orbital angular momentum degree of freedom of photon 2.

This section explained the principle of entanglement swapping and designed three entanglement swapping schemes based on Bell state joint measurement, cross-Kerr medium, and linear optical elements for the intraparticle entangled states.

3. Results

Two kinds of entangled states have distinct distinctions and connections on correlation and non-locality, anti-interference ability, mechanisms of generation and separation, and the advantages and drawbacks in practical applications. According to the entanglement swapping principle, three types of entanglement swapping schemes on intraparticle entangled states are achieved based on Bell state joint measurement, Cross-Kerr medium, and linear optical elements. Bell state joint measurement can only achieve specific-form entanglement swapping of intraparticle entangled states. Various-type target states can be achieved by using cross-Kerr media and linear optical elements. The possibility of implementation is commensurate with the three types of entanglement-swapping schemes mentioned above. The scheme can be chosen based on the specific situation, such as the target states and the experimental equipment available in the laboratory.

4. Conclusions

Firstly, this work analyzed and compared the distinctions and connections between two types of entanglement states on correlation and non-locality, anti-interference ability, generation and separation methods, and advantages and drawbacks in the communication process. Secondly, this work designed three types of schemes of entanglement swapping for intraparticle entangled states analogy entanglement states between multiple particles. These methods include based on Bell state joint measurement, cross-Kerr medium, and linear optical elements. The principle of entanglement swapping was described, and these schemes were elaborated in detail. Finally, the applicability of each scheme of entanglement swapping is discussed. This work can help people further, understand entanglement and promote intraparticle entangled states to apply in quantum information transmission.