Seismic Capacity Evaluation of Reinforced Concrete Moment-Resisting Frames with Steel Damper Columns using Incremental Critical Pseudo-Multi Impulse Analysis

1. Introduction

1.1. Background and Motivation

The peak deformation, cumulative strain energy, and residual deformation are essential parameters in assessing the seismic performance of structural members. Two energy-based seismic intensity parameters—the maximum momentary input energy (Hori et al., 2000; Inoue et al., 2000; Hori and Inoue, 2002) and the total input energy (Akiyama, 1985)—are related to the peak and cumulative responses, respectively. According to a study by Hori and Inoue (2002), the peak displacement of a structure can be evaluated by considering the energy balance during a half cycle of the structural response using the maximum momentary input energy. Meanwhile, the cumulative strain energy of structural members can be evaluated by considering the energy balance during an entire seismic event using the total input energy.

The motivation for using energy dissipation devices (dampers) is to mitigate damage to beams and columns during strong seismic events. A dual system with dampers, e.g., a damage-tolerant structure (Wada et al., 2000), is one solution for creating structures with superior seismic performance. In such a dual system, dampers play important roles (a) to reduce the peak displacement of the system and (b) to reduce the cumulative damage to beams and columns by absorbing seismic energy before it reaches the beams and columns. Accordingly, a building with such a dual system is more resilient than one with a traditional system: in the case of traditional moment-resisting frames (MRFs), most of the seismic energy is absorbed by the plastic hinges at the beam ends. Conversely, in the case of a dual system, most of the seismic energy is absorbed by the dampers; therefore, the seismic energy absorbed by the beams and columns is much smaller than in the case of traditional MRFs. Steel damper columns (SDCs; Katayama et al., 2000) are dampers suitable for reinforced concrete (RC) multistory housing. A SDC consists of a damper panel made of low-yield-strength steel plate, which absorbs the hysteresis energy, and a roll-formed H-section column, which behaves elastically. Numerous studies have been conducted on the seismic rehabilitation of existing RC buildings using SDCs (Fujii and Miyagawa, 2018; Fujii et al., 2019) and the seismic design of new RC MRFs with SDCs (Fujii and Kato, 2021; Mukoyama et al., 2021).

The concept of energy balance is quite useful to understand how such dampers work to improve the seismic performance of buildings. Recent advances in energy-based earthquake engineering can be found in Benavent-Climent and Mollaioli (2021) and Varum et al. (2023). Following Akiyama’s theory (1985, 1999), Benavent-Climent and his research group proposed a simplified seismic retrofitting design method for RC frames using dampers (Benavent-Climent, 2011; Benavent-Climent and Mota-Páez, 2017; Mota-Páez, et al., 2021; Benavent-Climent et al., 2024).

Takewaki and his research group (Kojima et al., 2015; Kojima and Takewaki, 2015a, 2015b, 2015c; Akehashi and Takewaki, 2021, 2022) have introduced the concepts of critical double impulse (DI) and critical multi impulse (MI) as substitutes for near-fault and long-duration earthquake ground motions. First, the concept of the critical DI was introduced to derive the upper bound of the earthquake input energy to a building structure (Kojima et al., 2015). Following this study, the critical response of an undamped elastoplastic single-degree-of-freedom (SDOF) model subjected to near-fault and long-duration earthquake ground motions was examined (Kojima and Takewaki, 2015a, 2015b, 2015c). Then, Akehashi and Takewaki (2021, 2022) introduced pseudo-double impulse (PDI) and pseudo-multi-impulse (PMI) to form a multi-degree-of-freedom (MDOF) model. In PDI and PMI analyses, the MDOF model oscillates predominantly in a single mode, considering the impulsive lateral force corresponding to a certain mode vector. When the impulsive lateral force corresponding to the first mode vector is considered, the MDOF model oscillates predominantly in the first mode.

An energy-based prediction procedure for the peak and cumulative response of RC MRFs with SDCs has been proposed (Fujii and Shioda, 2023). In the presented procedure, the building model is converted to an equivalent SDOF model that represents the first modal response based on a monotonic pushover analysis result. Then, the peak displacement is predicted using the maximum momentary input energy (Hori and Inoue, 2002), while the cumulative energy dissipation demand is predicted using the total input energy (Akiyama, 1985). In this procedure, the accuracy of the equivalent velocity of the maximum momentary input energy of the first modal response ($V_{\mathsf{\Delta }E1}{}^{*}$)–peak equivalent displacement of the first modal response ($D_1{{}^{*}}_{\max }$) relationship is essential for high quality prediction of the peak displacement. This procedure has been verified by comparing nonlinear time-history analysis (NTHA) results using non-pulse-like ground motions (Fujii and Shioda, 2023) and 30 recorded pulse-like ground motions (Fujii, 2023). The accuracy of the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship (seismic capacity curve) has also been verified by comparing the critical PDI analysis results (Fujii, 2024). However, the following issues remain.

• The verification in the previous study (Fujii, 2024) was limited because the number of impulsive inputs is fixed to 2 in a critical PDI analysis. The accuracy of the predicted $V_{\mathsf{\Delta }E1}{}^{*}$ corresponding to $D_1{{}^{*}}_{\max }$ depends on the shape of the assumed half cycle of the structural response. In the case of the critical pseudo-multi impulse (PMI) input, the shape of the half cycle of the structural response depends on the number of impulsive inputs ($N_p$). Therefore, further numerical investigation considering $N_p$ as a parameter is indispensible.
• In the simplified equation using $V_{\mathsf{\Delta }E1}{}^{*}$, the influence of the pinching behavior of the RC members on the energy dissipation is not considered. The severe pinching behavior of RC beam-column connections has been reported in experimental studies (e.g., Gentry and Wight, 1994; Kusuhara et al., 2004; Kusuhara and Shiohara, 2008; Benavent-Climent et al., 2009, 2010). Toyoda et al. (2014) compared the shaking table test results of a 1/4-scaled 20-story RC building model conducted at E-defense with NTHA results. They found that, for a better prediction of the peak response, the influence of the pinching behavior of RC beams should be considered. Following their study, Shirai et al. (2024) demonstrated that the pinching behavior of RC members affects the peak responses of 40-story RC super-high-rise buildings. Therefore, the influence of the pinching behavior of RC members on the seismic capacity curve should be investigated.

The residual displacement (Farrow and Kurama, 2003) is another essential parameter that is important to discuss in the repair of structures after earthquakes. The residual displacement is also important when the seismic sequence is considered (Ruiz-García and Negrete-Manriquez, 2011; Ruiz-García, 2012a, 2012b; Tesfamariam and Goda, 2015; Hoveidae, N., Radpour, 2021; Fujii, 2022). Specifically, Ruiz-García (2012b) pointed out that the residual displacement of a stiffness-degrading SDOF model is smaller than that of an elastoplastic SDOF model, even though the peak displacement of a stiffness-degrading SDOF model is larger than that of an elastoplastic SDOF model. In addition, Hoveidae and Radpour (2021) found that the large residual displacement after a mainshock can significantly increase the peak response under an aftershock. In Fujii (2024), the residual displacement obtained from the critical PDI analysis of RC MRFs with SDCs is larger than that of RC MRFs without SDCs: the residual equivalent displacement reaches close to 30% of the peak equivalent displacement in the case of RC MRFs with SDCs. This is larger than that obtained in the NTHA considering the ground motion records (Fujii, 2022). Therefore, the residual displacement obtained from the critical PDI analysis may be the upper bound. Accordingly, the influence of the number of impulsive inputs ($N_p$) on the residual displacement should be investigated.

1.2. Objectives

Given the above-outlined background, this study addresses the following questions.

(i)

Considering the critical response of an RC MRF with SDCs subjected to critical PMI input, what is the dependence of the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship on the number of impulsive inputs ($N_p$)?

(ii)

How does the pinching behavior of RC members affect the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship of RC MRFs? Can the negative influence of the pinching behavior of the RC members on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{}^{*}$ relationship be improved by installing SDCs?

(iii)

How do $N_p$ and the pinching behavior of RC members affect the ratios of the cumulative energies (cumulative strain energies of the RC MRFs and SDCs) at the end of simulation?

(iv)

How does $N_p$ affect the residual equivalent displacement of RC MRFs?

In this article, the seismic capacities of RC MRFs with and without SDCs are evaluated using incremental critical pseudo-multi impulse analysis (ICPMIA). How the seismic capacity of a structure corresponds to $D_1{{}^{*}}_{\max }$ is defined in terms of $V_{\mathsf{\Delta }E1}{}^{*}$. In the ICPMIA, the structure is subjected to various intensities of pulsive input. From the ICPMIA results, (a) the influence of the number of impulsive inputs ($N_p$) and the pinching behavior of the RC members on $D_1{{}^{*}}_{\max }$ and the residual equivalent displacement and (b) the influence of $N_p$ on the cumulative strain energies of the RC MRFs and SDCs are investigated. Then, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationships (seismic capacity curves) obtained from the ICPMIA results are compared with the predicted results based on the simplified equations.

The rest of this paper is organized as follows. Section 2 outlines the critical PMI analysis and ICPMIA. Section 3 presents four RC MRFs with and without SDCs and the analysis methods. Section 4 describes the responses of the RC MRFs obtained from the critical PDI and PMI analysis results, focusing in particular on (i) the pulse velocity ($V_p$)–peak equivalent displacement ($D_1{{}^{*}}_{\max }$) relationship, (ii) the hysteresis loop and residual displacement of the first modal response, and (iii) the cumulative strain energies of the RC MRFs and SDCs. Section 5 focuses on comparisons with the predicted results based on the study of Fujii and Shioda (2023) and the ICPMIA results. First, the simplified equations for calculating the energy dissipation capacity during a half cycle of the structural response are formulated. Next, the seismic capacity curve is predicted using the pushover analysis results. Then, the predicited seismic capacity curve is compared with the $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ plot obtained from the ICPMIA results. The conclusions drawn from this study and the directions of future research are discussed in Section 6.

2. Incremental Critical Pseudo-Multi Impulse Analysis

2.1. Outline of the Critical Pseudo-Multi Impulse Analysis

First, an outline of the critical PMI analysis is described as follows. Note that this analysis is based on the critical PDI analysis presented in Fujii (2024). Figure 1 outlines the critical PMI analysis.

Following a study by Kojima and Takewaki (2015c), the ground acceleration ($a_g\left(t\right)$) in the case of the critical PDI and PMI analysis can be written as

$$a_g\left(t\right)=-{\displaystyle \sum _{k=1}^{N_p}{}_k\mathsf{\Delta }{V}_g\delta \left(t-{}_{k}t{}_p\right)},$$

(1)

$$\left.\begin{array}{l}\delta \left(t\right)=\underset{\epsilon \to +0}{\lim }\left\{\begin{array}{ll}0\hfill & \left|t\right|>\epsilon \hfill \\ \frac{1}{2\epsilon }\hfill & \left|t\right|\le \epsilon \hfill \end{array}\right.\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta \left(t\right)dt}=1\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta \left(t\right)f\left(t\right)dt}=f\left(0\right)\end{array}\right\}.$$

(2)

In Eq. (1), $N_p$ (≥ 2) is the number of pseudo impulsive lateral forces, ${}_k\mathsf{\Delta }{V}_g$ is the ground motion velocity increment of the $k$-th pulse, ${}_{k}t{}_p$ is the time when the pseudo impulsive lateral force acts, and $\delta \left(·\right)$ is the Dirac delta function that satisfies Eq. (2). In the case of the PDI analysis ($N_p$= 2), ${}_k\mathsf{\Delta }{V}_g$ is defined as in Eq. (3):

$${}_k\mathsf{\Delta }{V}_g={\left(-1\right)}^k{V}_p,$$

(3)

where $V_p$ is the pulse velocity. Similarly in the case of the PMI analysis ($N_p$≥ 3), ${}_k\mathsf{\Delta }{V}_g$ is defined as in Eq. (4):

$${}_k\mathsf{\Delta }{V}_g=\left\{\begin{array}{ll}0.5{\left(-1\right)}^k{V}_p\hfill & :k=1,N_p\hfill \\ {\left(-1\right)}^k{V}_p\hfill & :2\le k\le N_p-1\hfill \end{array}\right..$$

(4)

Next, consider a planer frame building model (number of stories, $N$) subjected to a pseudo impulsive lateral force proportional to the first mode vector. Here, $M$ is the mass matrix of the building model; $d\left(t\right)$, $v\left(t\right)$, and $a\left(t\right)$ are the relative displacement, velocity, and acceleration vector, respectively; and $f_R\left(t\right)$ and $f_D\left(t\right)$ are the restoring and damping force vectors, respectively. The equivalent displacement ($D_1{}^{*}\left(t\right)$), equivalent velocity ($V_1{}^{*}\left(t\right)$), and equivalent relative acceleration ($A_{r1}{}^{*}\left(t\right)$) of the first modal response are defined in Eqs. (5)–(8):

$$D_1{}^{*}\left(t\right)=\frac{{\mathsf{\Gamma }}_1{\phi }_1{}^{T}Md\left(t\right)}{M_1{}^{*}},$$

(5)

$$V_1{}^{*}\left(t\right)={\dot{D}}_1{}^{*}\left(t\right)=\frac{{\mathsf{\Gamma }}_1{\phi }_1{}^{T}Mv\left(t\right)}{M_1{}^{*}},$$

(6)

$$A_{r1}{}^{*}\left(t\right)={\ddot{D}}_1{}^{*}\left(t\right)=\frac{{\mathsf{\Gamma }}_1{\phi }_1{}^{T}Ma\left(t\right)}{M_1{}^{*}},$$

(7)

$$M_1{}^{*}={\mathsf{\Gamma }}_1{}^2{\phi }_1{}^{T}M{\phi }_1,$$

(8)

where $M_1{}^{*}$ is the effective first modal mass. Note that ${\mathsf{\Gamma }}_1{\phi }_1$ and $M_1{}^{*}$ depend on the local maximum equivalent displacement within the range $\left(0,t\right)$. In this study, the first mode vector at time $t$ is updated assuming that ${\mathsf{\Gamma }}_1{\phi }_1$ is proportional to the displacemt vector at the time when the maximum equivalent displacement occurs ($t_{\max }$). The first mode vector at time $t$ is updated via Eq. (9):

$${\mathsf{\Gamma }}_1{\phi }_1\leftarrow \frac{1}{D_1{}^{*}\left(t_{\max }\right)}d\left(t_{\max }\right).$$

(9)

The equivalent acceleration $A_1{}^{*}\left(t\right)$ is defined as in Eq. (10):

$$A_1{}^{*}\left(t\right)=\frac{{\mathsf{\Gamma }}_1{\phi }_1{}^T{f}_R\left(t\right)}{M_1{}^{*}}.$$

(10)

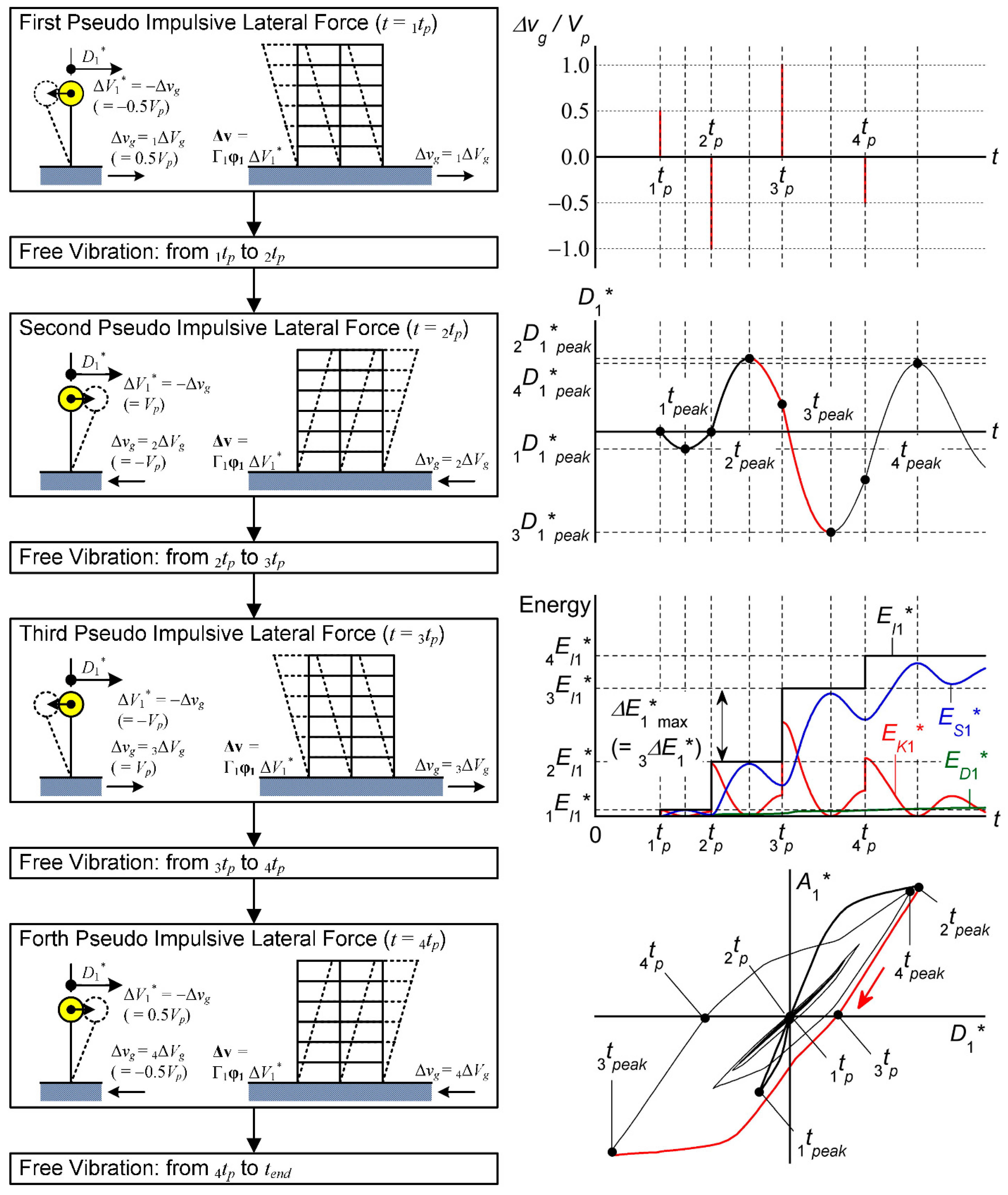
2.1.1. First Pseudo Impulsive Lateral Force

At time $t={}_{1}t{}_p\left({}_{1}t{}_p>0\right)$, the first pseudo impulsive lateral force acts on the building model as shown in Figure 1. Note that, before the action of the first pseudo impulsive force on the building model ($t<{}_{1}t{}_p$), the building model is in a stationary state ($d\left(t\right)=0$, $v\left(t\right)=0$,$a\left(t\right)=0$). The equivalent velocity of the first modal response just after the action of the first pseudo impulsive lateral force (${\tilde{V}}_1{}^{*}\left({}_{1}t{}_p\right)$) is calculated using Eq. (11):

$${\tilde{V}}_1{}^{*}\left({}_{1}t{}_p\right)=-{}_1\mathsf{\Delta }{V}_g,$$

(11)

and the corresponding velocity vector ($\tilde{v}\left({}_{1}t{}_p\right)$) is calculated using Eq. (12):

$$\tilde{v}\left({}_{1}t{}_p\right)={}_1\mathsf{\Gamma }{}_1{}_1\phi {}_1{\tilde{V}}_1{}^{*}\left({}_{1}t{}_p\right)=-{}_1\mathsf{\Gamma }{}_1{}_1\phi {}_1{}_1\mathsf{\Delta }{V}_g,$$

(12)

where ${}_1\mathsf{\Gamma }{}_1{}_1\phi {}_1$ is the first mode vector at the initial stage. The increment of input energy of the first modal response (${}_1\mathsf{\Delta }{E}_1{}^{*}$) is calculated via Eq. (13):

$${}_1\mathsf{\Delta }{E}_1{}^{*}=\frac{1}{2}{}_{1}M{{}_1}^{*}{\left\{{\tilde{V}}_1{}^{*}\left({}_{1}t{}_p\right)\right\}}^2=\frac{1}{2}{}_{1}M{{}_1}^{*}{}_1\mathsf{\Delta }{V}_g{}^2,$$

(13)

where ${}_{1}M{{}_1}^{*}$ is the first modal mass at the initial stage. The cumulative input energy of the first modal response (${}_{1}E{{}_1}^{*}$) is calculated via Eq. (14):

$${}_{1}E{{}_{I1}}^{*}={}_1\mathsf{\Delta }{E}_1{}^{*}.$$

(14)

To calculate the response after the action of the first pseudo impulsive lateral force, the equivalent velocity ($V_1{}^{*}\left(t\right)$) and velocity vector ($v\left(t\right)$) are updated via Eq. (15):

$$V_1{}^{*}\left({}_{1}t{}_p+0\right)\leftarrow {\tilde{V}}_1{}^{*}\left({}_{1}t{}_p\right),v\left({}_{1}t{}_p+0\right)\leftarrow \tilde{v}\left({}_{1}t{}_p\right).$$

(15)

In addition, the counting number of pulsive inputs ($k$) is set to $k$ = 1.

2.1.2. Free Vibration after the First Pseudo Impulsive Lateral Force

After the action of the first pseudo impulsive lateral force, the building model oscillates without external forces (free vibration) until the arrival of the second pseudo impulsive lateral force. The kinetic energy, the damping dissipated energy, the cumulative strain energy, and the cumulative input energy of the first modal response ($E_{K1}{}^{*}$, $E_{D1}{}^{*}$, $E_{S1}{}^{*}$, and $E_{I1}{}^{*}$, respectively) are expressed as shown in Eqs. (16)–(19):

$$E_{K1}{}^{*}\left(t\right)=\frac{1}{2}{M}_1{}^{*}{\left\{V_1{}^{*}\left(t\right)\right\}}^2,$$

(16)

$$E_{D1}{}^{*}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{\mathsf{\Gamma }}_1{\phi }_1{}^T{f}_D\left(t\right)V_1{}^{*}\left(t\right)dt},$$

(17)

$$E_{S1}{}^{*}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{\mathsf{\Gamma }}_1{\phi }_1{}^T{f}_R\left(t\right)V_1{}^{*}\left(t\right)dt},$$

(18)

$$E_{I1}{}^{*}\left(t\right)=\frac{1}{2}{}_{1}M{{}_1}^{*}{}_1\mathsf{\Delta }{V}_g{}^2={}_{1}E{{}_{I1}}^{*}.$$

(19)

The first pseudo impulsive lateral force is proportional to the first mode vector, and thus the building model oscillates predominantly in the first mode. Therefore, the kinetic energy, the damping dissipated energy, the cumulative strain energy, and the cumulative input energy ($E_K$, $E_D$, $E_S$, and $E_I$, respectively) are approximated as shown in Eq. (20):

$$\left\{\begin{array}{l}{E}_K\left(t\right)\approx E_{K1}{}^{*}\left(t\right)\\ E_D\left(t\right)\approx E_{D1}{}^{*}\left(t\right)\\ E_S\left(t\right)\approx E_{S1}{}^{*}\left(t\right)\\ E_I\left(t\right)\approx E_{I1}{}^{*}\left(t\right)\end{array}\right..$$

(20)

Note that the first mode vector (${\mathsf{\Gamma }}_1{\phi }_1$) updates any step according to Eq. (9) until $D_1{}^{*}\left(t\right)$ reaches its local peak (${}_{1}D{{}_1}^{*}{}_{peak}\left(<0\right)$ shown in Figure 1). The effective first modal mass ($M_1{}^{*}$) is then re-calculated according to Eq. (8). The time ${}_{1}t{}_{peak}$ is defined as the time when $D_1{}^{*}\left(t\right)$ reaches ${}_{1}D{{}_1}^{*}{}_{peak}$.

The timing of the action of the second pseudo impulsive lateral force (${}_{2}t{}_p>{}_{1}t{}_p$) is determined from the following conditions:

$${\dot{V}}_1{}^{*}\left({}_{2}t{}_p\right)=A_{r1}{}^{*}\left({}_{2}t{}_p\right)=0.$$

(21)

Equation (21) is equivalent to the condition of critical timing given by Akehashi and Takewaki (2021, 2022).

2.1.3. Pseudo Impulsive Lateral Force

At time $t={}_{k+1}t{}_p$ (1 ≤ $k$ ≤ $N_p$−1), the next pseudo impulsive lateral force acts on the building model, as shown in Figure 1. The equivalent velocity of the first modal response just after the action of the next pseudo impulsive lateral force (${\tilde{V}}_1{}^{*}\left({}_{k+1}t{}_p\right)$) is calculated via Eq. (22):

$${\tilde{V}}_1{}^{*}\left({}_{k+1}t{}_p\right)=V_1{}^{*}\left({}_{k+1}t{}_p-0\right)-{}_{k+1}\mathsf{\Delta }{V}_g.$$

(22)

Here, $V_1{}^{*}\left({}_{k+1}t{}_p-0\right)$ is the equivalent velocity of the first modal response just before the action of the next pseudo impulsive lateral force. Assuming that the velocity vector just before the action of the next pseudo impulsive lateral force ($v\left({}_{k+1}t{}_p-0\right)$) can be approximated by the first modal response, the corresponding velocity vector ($\tilde{v}\left({}_{k+1}t{}_p\right)$) can be expressed as Eq. (23):

$$\tilde{v}\left({}_{k+1}t{}_p\right)=v\left({}_{k+1}t{}_p-0\right)-{\mathsf{\Gamma }}_1{\phi }_1{}_{k+1}\mathsf{\Delta }{V}_g\approx {\mathsf{\Gamma }}_1{\phi }_1{\tilde{V}}_1{}^{*}\left({}_{k+1}t{}_p\right).$$

(23)

The increment of the input energy of the first modal response (${}_2\mathsf{\Delta }{E}_1{}^{*}$) is calculated via Eq. (24):

$${}_{k+1}\mathsf{\Delta }{E}_1{}^{*}=\frac{1}{2}{M}_1{}^{*}\left[{\left\{{\tilde{V}}_1{}^{*}\left({}_{k+1}t{}_p\right)\right\}}^2-{\left\{V_1{}^{*}\left({}_{k+1}t{}_p-0\right)\right\}}^2\right]=\frac{1}{2}{M}_1{}^{*}{}_{k+1}\mathsf{\Delta }{V}_g{}^2\left\{1+\frac{2V_1{}^{*}\left({}_{k+1}t{}_p-0\right)}{{}_{k+1}\mathsf{\Delta }{V}_g}\right\}$$

(24)

The cumulative input energy of the first modal response just after the action of the next pseudo impulsive lateral force (${}_{k+1}E{{}_{I1}}^{*}$) is calculated via Eq. (25):

$${}_{k+1}E{{}_{I1}}^{*}={}_{k}E{{}_{I1}}^{*}+{}_{k+1}\mathsf{\Delta }{E}_1{}^{*}.$$

(25)

To calculate the response after the action of the second pseudo impulsive lateral force, the equivalent velocity ($V_1{}^{*}\left(t\right)$) and the velocity vector ($v\left(t\right)$) are updated via Eq. (26):

$$V_1{}^{*}\left({}_{k+1}t{}_p+0\right)\leftarrow {\tilde{V}}_1{}^{*}\left({}_{k+1}t{}_p\right),v\left({}_{k+1}t{}_p+0\right)\leftarrow \tilde{v}\left({}_{k+1}t{}_p\right).$$

(26)

In addition, the counting number of the pulsive inputs ($k$) is updated such that $k\leftarrow k+1$.

2.1.4. Free Vibration

After the action of the $k$-th pseudo impulsive lateral force, the building model oscillates without external forces (free vibration). The following response depends on $k$ and $N_p$.

In the case in which $k$ is smaller than $N_p$, the free vibration of the building model continues until the action of the next pseudo impulsive lateral force. During the free vibration, the first mode vector (${\mathsf{\Gamma }}_1{\phi }_1$) updates any step according to Eq. (9) until $D_1{}^{*}\left(t\right)$ reaches its local peak (${}_{k}D{{}_1}^{*}{}_{peak}$ shown in Figure 1). The effective first modal mass ($M_1{}^{*}$) is then re-calculated according to Eq. (8). The time ${}_{k}t{}_{peak}$ is defined as the time when $D_1{}^{*}\left(t\right)$ reaches ${}_{k}D{{}_1}^{*}{}_{peak}$. The timing of the action of the next pseudo impulsive lateral force (${}_{k+1}t{}_p>{}_{k}t{}_p$) is determined from the following conditions (Eq. (27)):

$${\dot{V}}_1{}^{*}\left({}_{k+1}t{}_p\right)=A_{r1}{}^{*}\left({}_{k+1}t{}_p\right)=0.$$

(27)

At time $t={}_{k+1}t{}_p$, the next pseudo impulsive lateral force acts as prescribed in Section 2.1.3.

When $k$ equals $N_p$, the free vibration of the building model continues until $t=t_{end}$. The time ${}_{N_p}t{}_{peak}$ is defined as the time when $D_1{}^{*}\left(t\right)$ reaches ${}_{N_p}D{{}_1}^{*}{}_{peak}$. The peak equivalent displacement of the first modal response over the course of the entire seismic event ($D_1{{}^{*}}_{\max }$) is obtained using Eq. (28):

$$D_1{{}^{*}}_{\max }=\max \left(\left|{}_{1}D{{}_1}^{*}{}_{peak}\right|,\left|{}_{2}D{{}_1}^{*}{}_{peak}\right|,\cdots ,\left|{}_{N_p}D{{}_1}^{*}{}_{peak}\right|\right).$$

(28)

The maximum momentary input energy of the first modal response per unit mass ($\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}$) is obtained via Eq. (29):

$$\frac{\mathsf{\Delta }{E}_1{{}^{*}}_{\max }}{M_1{}^{*}}=\max \left\{{}_1\left(\frac{\mathsf{\Delta }{E}_1{}^{*}}{M_1{}^{*}}\right),{}_2\left(\frac{\mathsf{\Delta }{E}_1{}^{*}}{M_1{}^{*}}\right),\cdots ,{}_{N_p}\left(\frac{\mathsf{\Delta }{E}_1{}^{*}}{M_1{}^{*}}\right)\right\}.$$

(29)

The cumulative input energy of the first modal response per unit mass ($E_{I1}{}^{*}/M_1{}^{*}$) is calculated using Eq. (30):

$$\frac{E_{I1}{}^{*}}{M_1{}^{*}}={\displaystyle \sum _{k=1}^{N_p}{}_k\left(\frac{\mathsf{\Delta }{E}_1{}^{*}}{M_1{}^{*}}\right)}.$$

(30)

The equivalent velocity of the maximum momentary input energy of the first modal response ($V_{\mathsf{\Delta }E1}{}^{*}$) is calculated using Eq. (31):

$$V_{\mathsf{\Delta }E1}{}^{*}=\sqrt{2\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}}.$$

(31)

In addition, the equivalent velocity of the cumulative input energy of the first modal response ($V_{I1}{}^{*}$) is calculated using Eq. (32):

$$V_{I1}{}^{*}=\sqrt{2E_{I1}{}^{*}/M_1{}^{*}}.$$

(32)

2.2. Analysis Flow of the Critical PMI Analysis

Figure 2 shows the flow of the critical PMI analysis. This flow is based on the flow of the critical PDI analysis presented in Fujii (2024). The analysis procedure is implemented by the computer code used in Fujii and Miyagawa (2018).

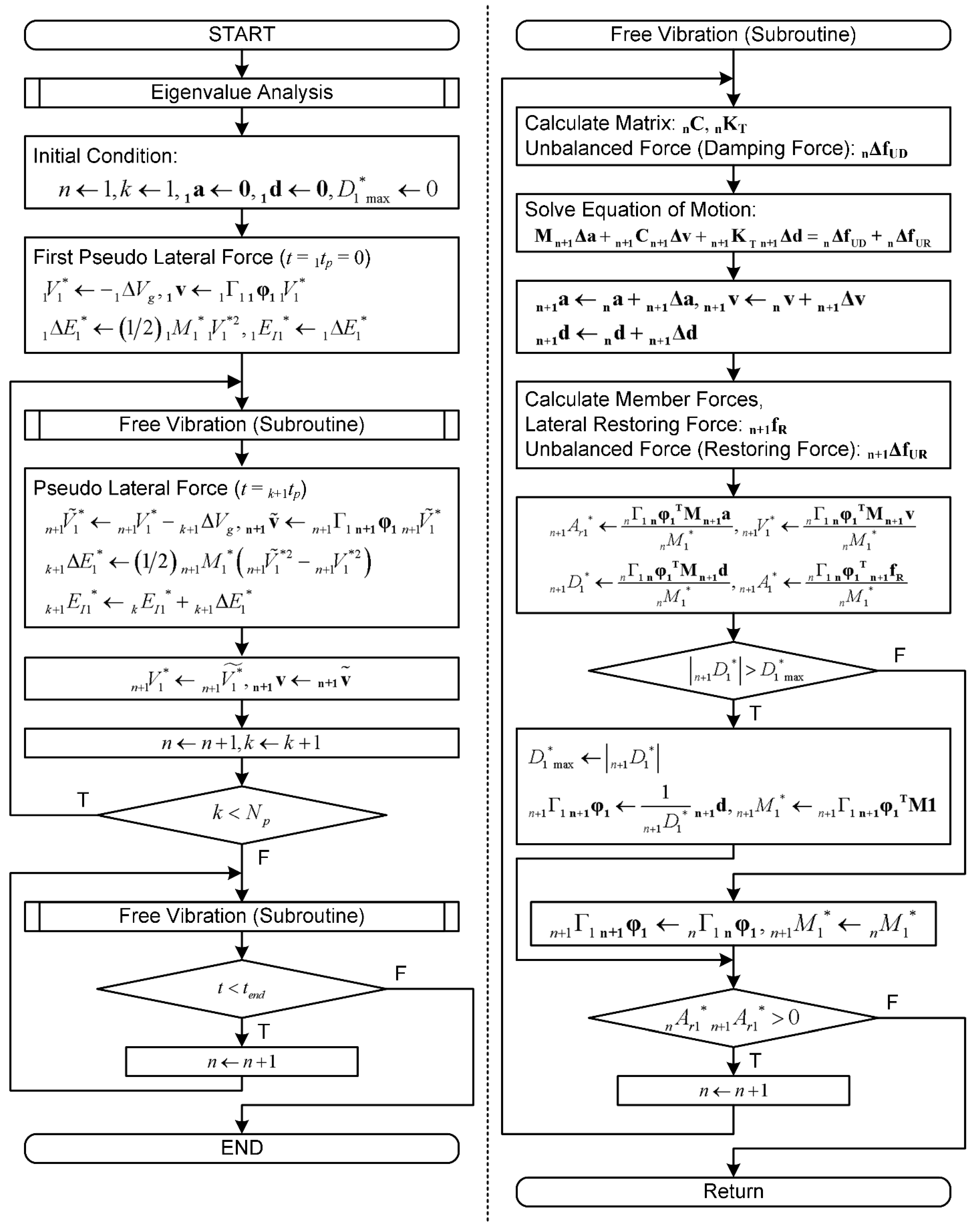
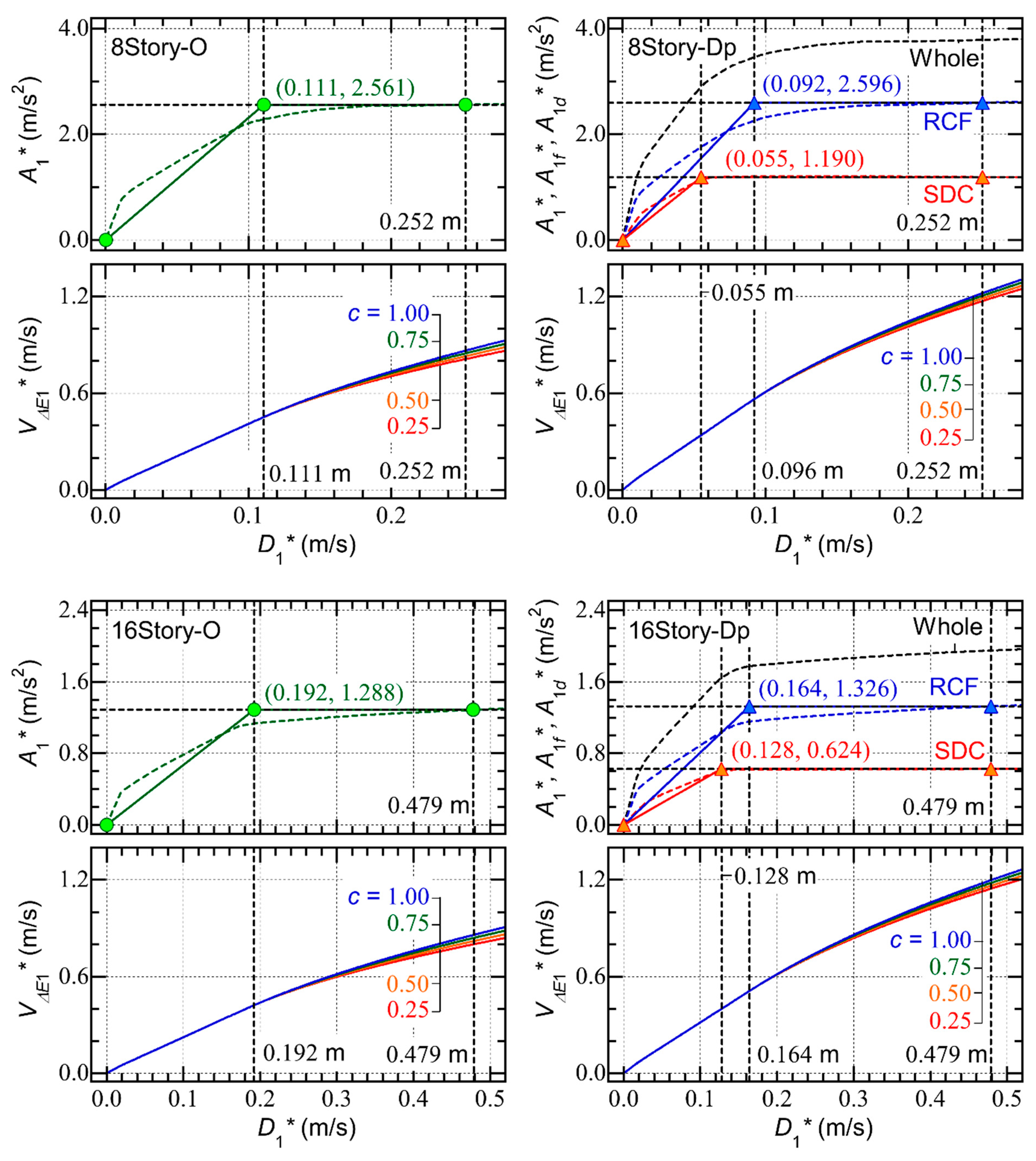
2.3. Calculation of the Seismic Capacity Curve from the Incremental Critical Pseudo-Multi Impulse Analysis (ICPMIA) Results

Incremental critical pseudo-multi impulse analysis (ICPMIA) is a parametric analysis method used to evaluate the nonlinear response of a structure by performing a critical PMI analysis considering various pulse velocities ($V_p$). In the ICPMIA analysis, $V_p$ varies from small to large levels until the structural response reaches a predetermined damage level (e.g., Life Safety of Collapse Prevention). This analysis is similar to the incremental dynamic analysis (IDA) (Vamvatsikos and Cornell, 2002) and the incremental N2 method (Dolšek and Fajfar, 2004). The difference between the three analysis methods is the nonlinear structural analysis method. In IDA, an NTHA of the model is performed using the time-history of the ground accelerations. The IDA results are the most rigorous of the three methods. However, the IDA result is very complex to understand with respect to the nonlinear structural characteristics because the IDA result is intricately intertwined with the nonlinear structural characteristics and the ground motion characteristics. Meanwhile, in IN2, a nonlinear static (pushover) analysis of the model is performed to obtain the nonlinear structural characteristics. Then, the seismic response (the seismic intensity corresponds to a certain peak displacement) is evaluated based on the inelastic spectra. The IN2 result is the most simple and easiest of the three to understand. However, its accuracy strongly depends on several assumptions, that the structure oscillates predominantly in a fundamental mode and that the spectra are inelastic. In ICPMIA, a critical PMI analysis is performed to obtain the nonlinear structural characteristics. Because ICPMIA can directly include the influence of cyclic loading, the influence of the duration of ground motions can be considered in ICPMIA by adjusting the number of pulsive inputs ($N_p$). In addition, because the ground motion in ICPMIA is simplified as the critical pulses determined automatically from the structural response, the ICPMIA result is still simple to understand with respect to the nonlinear structural characteristics.

The $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ plot is obtained from the ICPMIA result. In this study, the $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ curve is referred to as the “seismic capacity curve.” Note that the peak equivalent displacement ($D_1{{}^{*}}_{\max }$) may not occur at the end of the half cycle of the structural response corresponding to the maximum momentary input energy per unit mass ($\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}$). However, because $D_1{{}^{*}}_{\max }$ occurs at the end of a half cycle of the structural response, corresponding to $\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}$ in most cases analyzed herein, the relationship between the as-obtained $V_{\mathsf{\Delta }E1}{}^{*}$ and the as-obtained $D_1{{}^{*}}_{\max }$ is simply plotted in this study.

3. Analysis Data and Methods

3.1. Building Data

The four planar building models analyzed in this study are 8- and 16-story RC MRFs with and without SDCs. Figure 3 shows the simplified plan and elevation of the RC MRF building models. The two models labeled Type Dp (8Story-Dp and 16Story-Dp) are the same as those used in Fujii and Shioda (2023). The two models made from Type Dp by removing all SDCs are referred to as Type O (8Story-O and 16Story-O). All RC MRFs analyzed herein were designed according to the strong-column/weak-beam concept, except at the foundation level beam and in the case of steel damper columns installed in an RC frame. In the latter case, at the joints between an RC beam and a steel damper column, the RC beam was designed to be sufficiently stronger than the yield strength of the steel damper column considering strain hardening. Sufficient shear reinforcement of all RC members was provided to prevent premature shear failure. The failure of beam–column joints is not considered because it is assumed that sufficient reinforcement is provided. The natural periods of the first modal response in the elastic range ($T_{1e}$) of the 8-story models are 0.740 s and 0.561 s for Types O and Dp, respectively. Similarly, the $T_{1e}$ values of the 16-story models are 1.41 s and 1.12 s for Types O and Dp, respectively.

The nonlinear behavior of the RC members and SDCs is modeled as in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023), except the hysteresis rule used for the RC members. Figure 4 shows the nonlinear force–deformation relationship. In this study, the pinching behavior of the RC members is considered. The pinching model is assumed to be a linear combination of perfectly non-pinching and perfectly pinching models. The perfectly non-pinching model is identical to the stiffness degradation model used for RC members in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023). Meanwhile, the perfectly pinching model is a model that has no energy hysteresis energy dissipation in symmetric loading. A parameter $c$ (0 ≤ $c$ ≤ 1) is introduced to control the pinching behavior. When $c$ is 0, its behavior is that of a perfectly pinching model; when $c$ is 1, its behavior is that of a perfectly non-pinching model. In this study, four different pinching behaviors are considered: the parameter $c$ was set to 0.25, 0.50, 0.75, and 1.00, as shown in the bottom of Figure 4. For the damper panel in the SDCs, the same hysteresis model (trilinear model) is used. Other details concerning the four structural models can be found in previous studies (Fujii, 2022; Fujii and Shioda, 2023). In this study, the viscous damping ratio of the first modal response of the RC MRFs in the elastic range ($h_{1f}$) was set to 0.03.

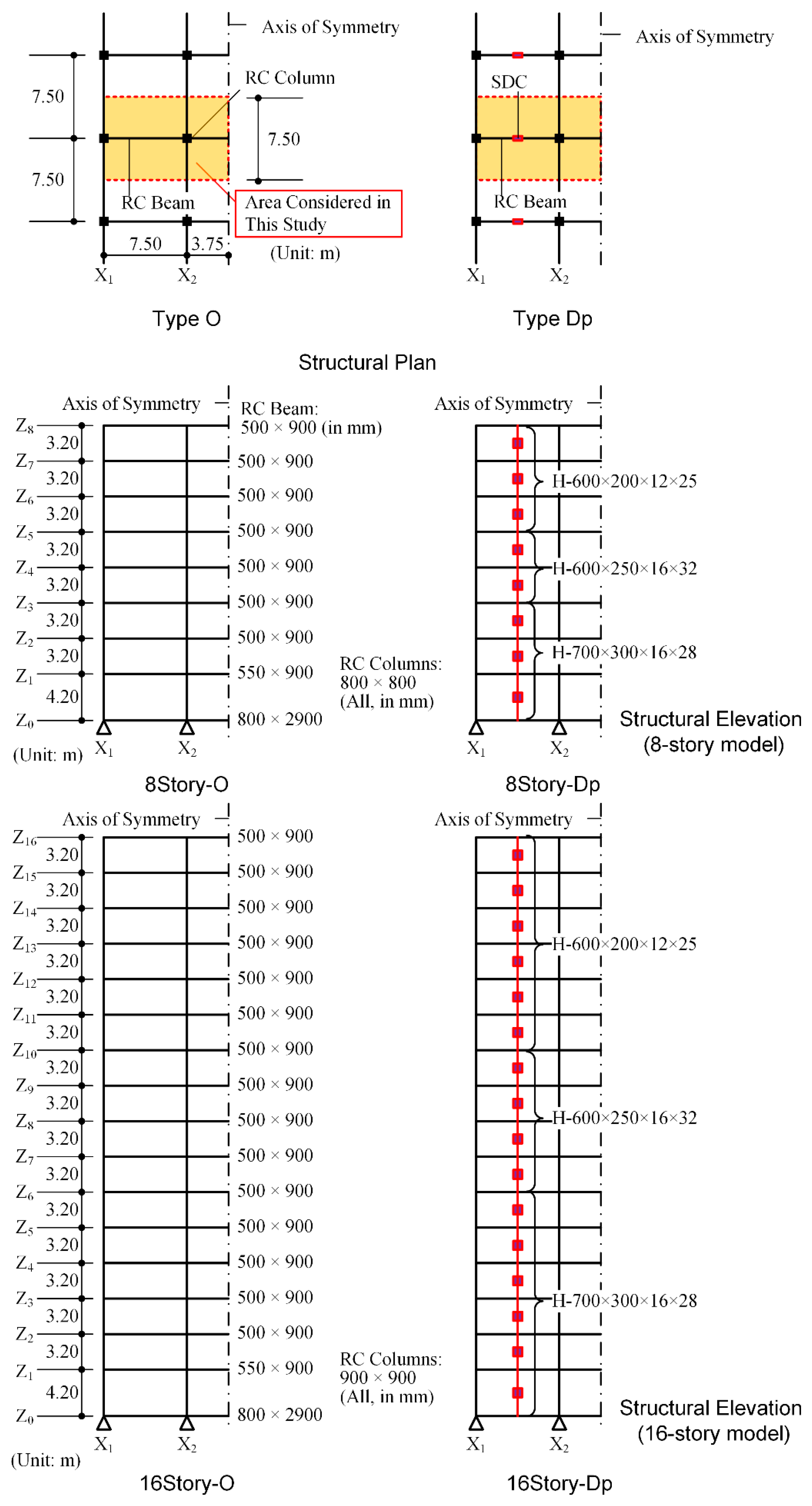
3.2. Analysis Method

In this study, the pulse velocity ($V_p$) was set from 0.10 m/s, with an interval of 0.05 m/s, until $D_1{{}^{*}}_{\max }$ was close to 1/75 of the assumed equivalent height ($H_1{}^{*}$). The target $D_1{{}^{*}}_{\max }$ was set to 0.252 m for the 8-story models, while for the 16-story models the target $D_1{{}^{*}}_{\max }$ was set to 0.479 m. The total number of pseudo impulsive lateral forces ($N_p$) was set to 4, 6, and 8. A critical PDI analysis ($N_p$ = 2) of each model was performed for the comparisons. In each analysis, the ending time of the analysis ($t_{end}$) was determined as the ending of the 32^nd half cycle of free vibration after the action of the second pseudo impulsive lateral force.

4. Analysis Results

This section describes the responses of the RC MRFs obtained from the critical PDI and PMI analysis results, focusing in particular on (i) the pulse velocity ($V_p$)–peak equivalent displacement ($D_1{{}^{*}}_{\max }$) relationship, (ii) the hysteresis loop and residual displacement of the first modal response, and (iii) the cumulative strain energies of the RC MRFs and SDCs.

4.1. Peak Response

Figure 5 compares the relationship between the pulse velocity ($V_p$) and the peak equivalent displacement ($D_1{{}^{*}}_{\max }$). The following conclusions can be drawn.

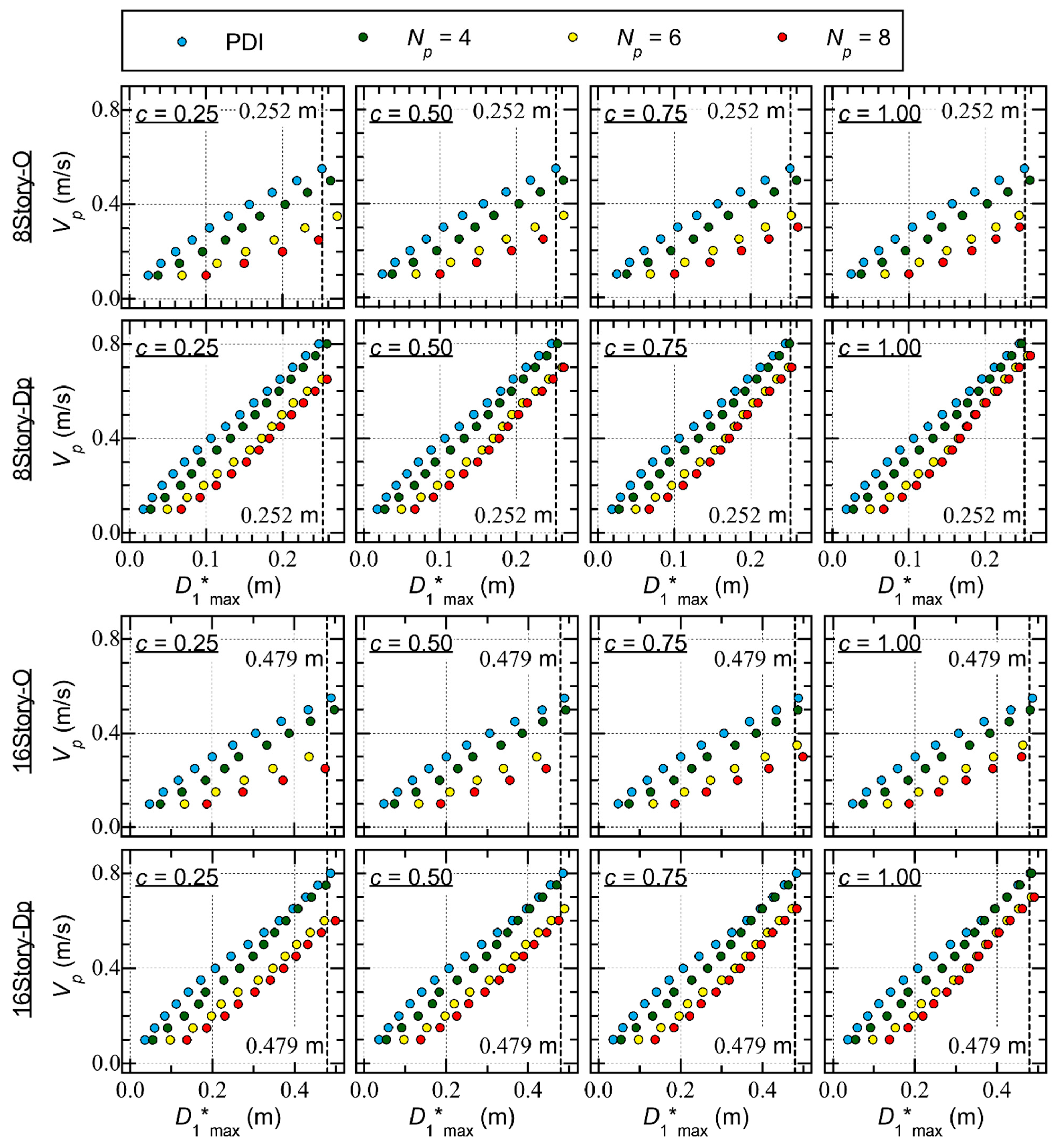
• The peak equivalent displacement ($D_1{{}^{*}}_{\max }$) increases as the pulse velocity ($V_p$) increases. For the same value of $V_p$, the $D_1{{}^{*}}_{\max }$ obtained by PDI is smaller than that obtained by PMI ($N_p$ = 4, 6, and 8).
• For Type O, the increase in $D_1{{}^{*}}_{\max }$ as a result of the increase in $N_p$ is significant. This trend is more pronounced when the pinching behavior of the RC members is significant. Comparing $D_1{{}^{*}}_{\max }$ of 8story-O with $V_p$ = 0.25 m/s and $c$ = 0.25 (significant pinching), $D_1{{}^{*}}_{\max }$ is 0.082 m when $N_p$ = 2 (PDI) and 0.247 m when $N_p$ = 8. Similar observations can be mabe for 16story-O.
• For Type Dp, however, the increase in $D_1{{}^{*}}_{\max }$ as a result of the increase in $N_p$ is less significant than for Type O. Comparing $D_1{{}^{*}}_{\max }$ of 8story-Dp, considering $V_p$ = 0.65 m/s and $c$ = 0.25 (significant pinching), $D_1{{}^{*}}_{\max }$ is 0.196 m when $N_p$ = 2 (PDI) and 0.258 m when $N_p$ = 8. Similar observations can be made for 16story-Dp.

Figure 6 compares the peak story drift. Here, the cases $c$ = 0.25 (significant pinching) and $c$ = 1.00 (perfectly non-pinching) are selected.

The following conclusions can be drawn from Figure 6.

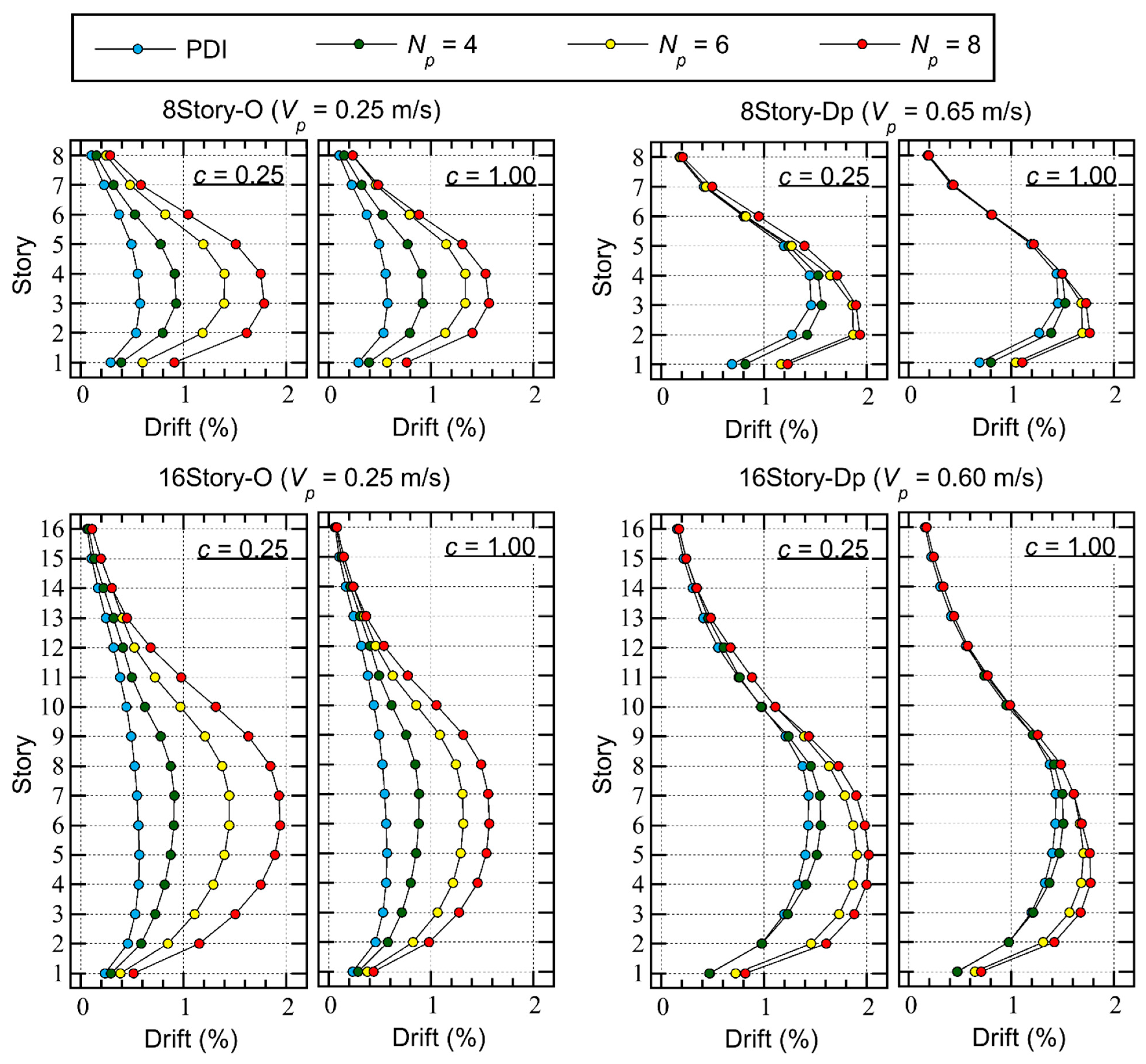
• For Type O, the increase in the peak story resulting from the increase in $N_p$ is significant, as observed in the trend of $D_1{{}^{*}}_{\max }$. This trend is more pronounced when the pinching behavior of the RC members is significant. Comparing the largest peak story drift of 8story-O, considering $V_p$ = 0.25 m/s and $c$ = 0.25 (significant pinching), the largest peak story drift is 0.577% (3^rd story) when $N_p$ = 2 (PDI) and 1.78% (3^rd story) when $N_p$ = 8. Meanwhile, considering $V_p$ = 0.25 m/s and $c$ = 1.00 (perfectly non-pinching), the largest peak story drift is 0.577% (3^rd story) when $N_p$ = 2 (PDI) and 1.57% (3^rd story) when $N_p$ = 8.
• For Type Dp, however, the increase in the peak story drift as a result of the increase in $N_p$ is less significant than for Type O. Comparing the largest peak story drift of 8story-Dp, considering $V_p$ = 0.65 m/s and $c$ = 0.25 (significant pinching), the largest peak story drift is 1.46% (3^rd story) when $N_p$ = 2 (PDI) and 1.94% (2^nd story) when $N_p$ = 8. Meanwhile, considering $V_p$ = 0.65 m/s and $c$ = 1.00 (perfectly non-pinching), the largest peak story drift is 1.46% (3^rd story) when $N_p$ = 2 (PDI) and 1.77% (2^nd story) when $N_p$ = 8. Similar observations can be made for 16story-Dp.

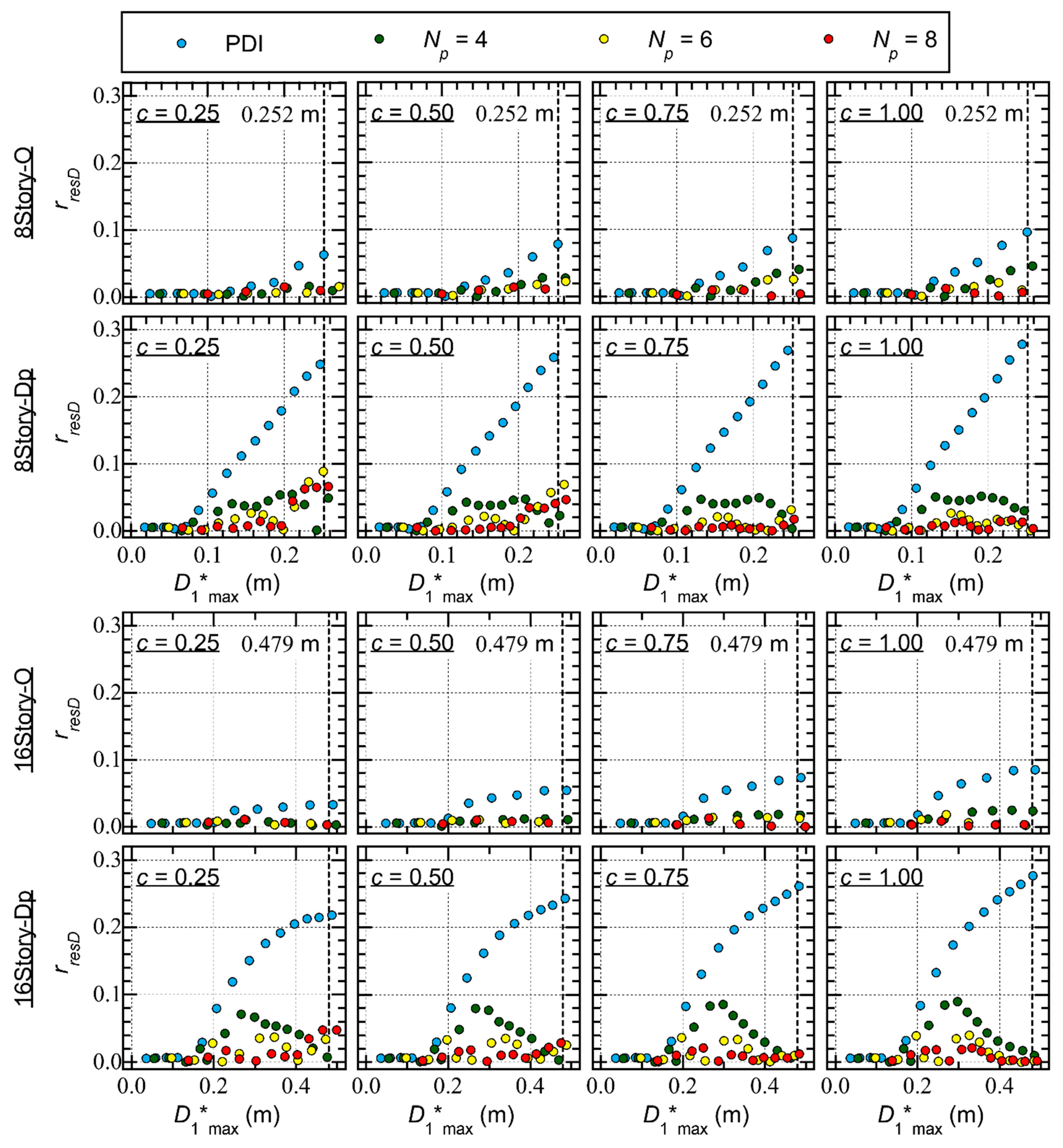
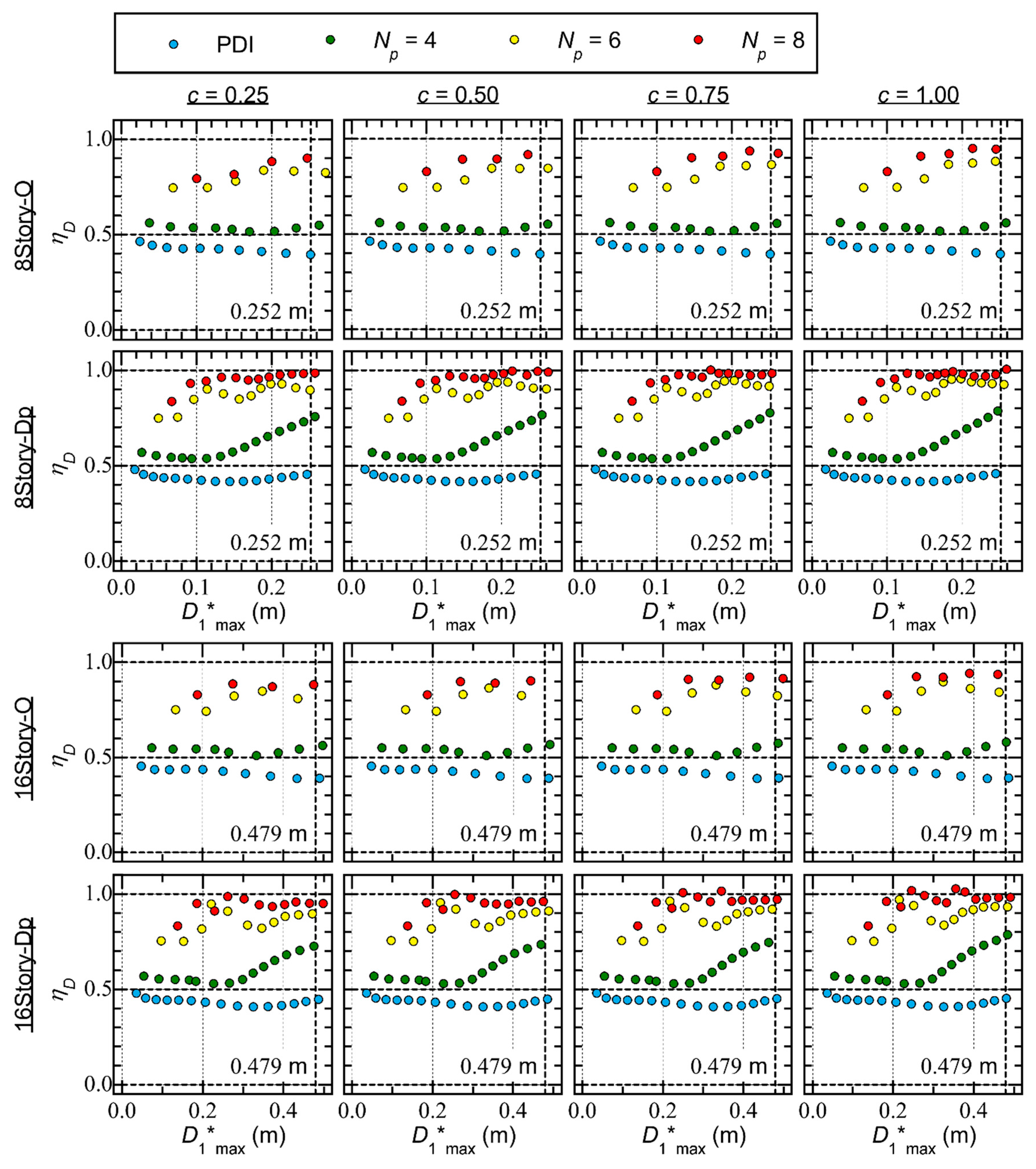
4.2. Hysteresis Loop and Residual Displacement

Figure 7 shows the hysteresis loops of the first modal response ($A_1{}^{*}\left(t\right)$−$D_1{}^{*}\left(t\right)$ relationship) for each model. The hysteresis loops obtained from the critical PDI analysis ($N_p$ = 2) and critical PMI analysis ($N_p$ = 8) are shown in this figure; the hysteresis loops for $c$ = 0.25 (significant pinching) and $c$ = 1.00 (perfectly non-pinching) are compared. In Figure 7, the beginning and ending points of the half cycle of the structural response when the maximum momentary input energy per unit mass ($\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}$) occurs is shown by the red curve. The numbers in the figure indicate the number of the local peak. The points at which the pseudo impulsive lateral force acts ($\mathsf{\Delta }{E}_1{{}^{*}}_{\max }$) and the point at the end of the simulation ($t_{end}$) are also shown.

The following conclusions can be drawn from Figure 7.

• In the critical PDI analysis results ($N_p$ = 2), the difference in the half cycle of the structural response resulting from the pinching behavior is negligibly small. The displacement response is larger in positive directions than in negative directions. A notable residual equiavalent displacement at $t$ = $t_{end}$ is observed, especially for Type Dp.
• In the critical PMI analysis results ($N_p$ = 8), the difference in the half cycle of the structural response resulting from the pinching behavior is noticeable. In the case of $c$ = 0.25 (significant pinching), the pinching behavior in the half cycle of the structural response is clearly observed for both Types O and Dp. The displacement response is almost symmetric in the positive and negative directions. The residual equivalent displacement is negligibly small for both Types O and Dp.

Figure 8 shows the residual equivalent displacement ratio ($r_{resD}$). Here, the $r_{resD}$ ratio is defined as shown in Eq. (33):

$$r_{resD}=\left|D_1{}^{*}\left(t_{end}\right)/D_1{{}^{*}}_{\max }\right|.$$

(33)

The following conclusions can be drawn from Figure 8.

• For Type O, $r_{resD}$ is smaller than 0.1. The $r_{resD}$ ratio is largest in the critical PDI analysis ($N_p$ = 2), and $r_{resD}$ increases as $D_1{{}^{*}}_{\max }$ increases. However in the critical PMI analysis, $r_{resD}$ is small and no regular trend is observed between $r_{resD}$ and $D_1{{}^{*}}_{\max }$: the $r_{resD}$ ratio may decrease when $D_1{{}^{*}}_{\max }$ increases.
• For Type Dp, the $r_{resD}$ ratio increases as $D_1{{}^{*}}_{\max }$ increases in the critical PDI analysis ($N_p$ = 2) and the $r_{resD}$ ratio may be larger than 0.2. The $r_{resD}$ ratio is larger when the parameter $c$ is larger (pinching behavior is not significant). However, in the critical PMI analysis, the $r_{resD}$ ratio is smaller than 0.1. In addition, no regular trend is observed between $r_{resD}$ and $D_1{{}^{*}}_{\max }$: the $r_{resD}$ ratio may decrease when $D_1{{}^{*}}_{\max }$ increases.

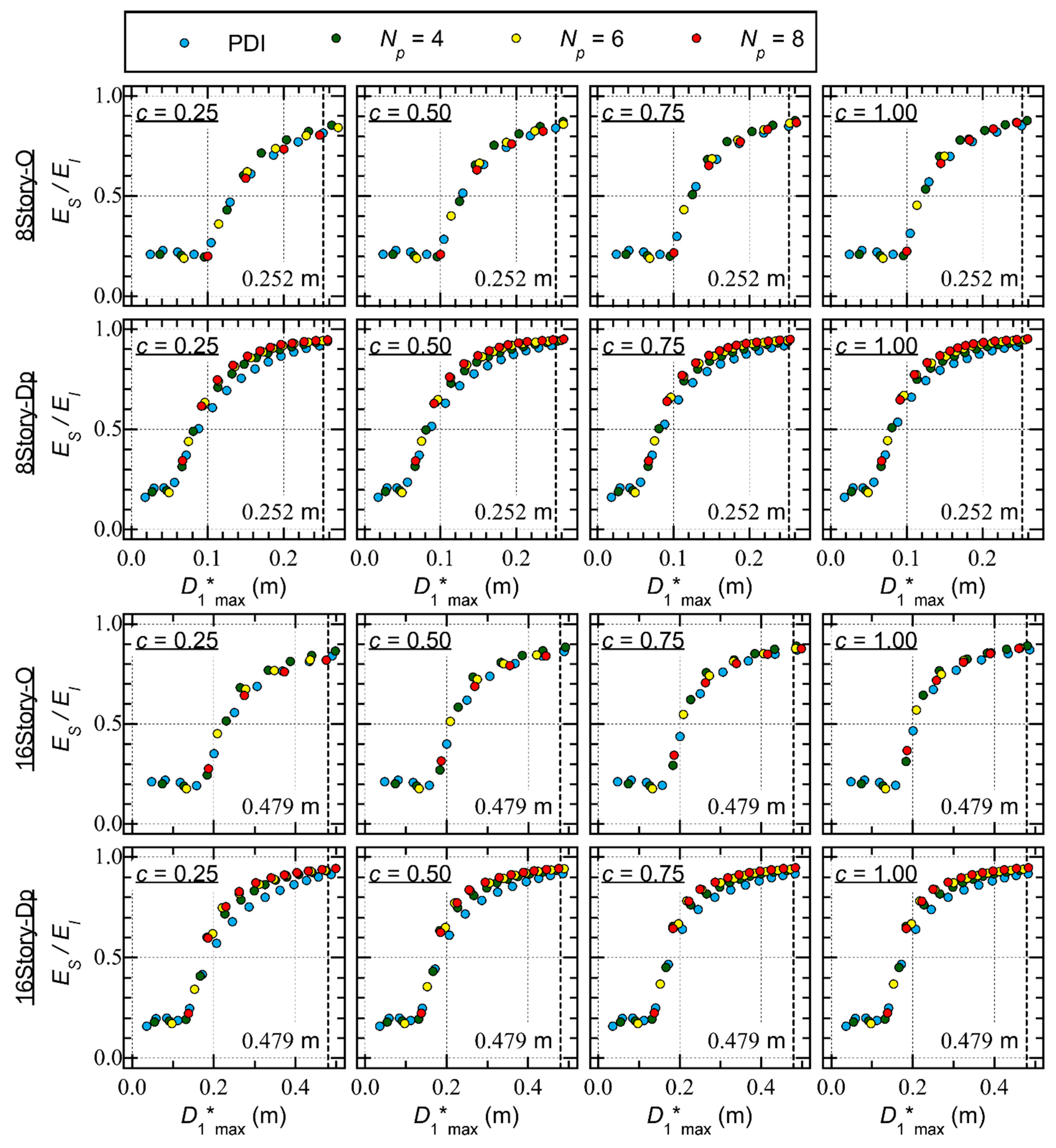
4.3. Cumulative Strain Energy

Figure 9 compares the ratios of the cumulative strain energy of the entire frame model ($E_S/E_I$) at the end of the simulation.

For Type O, the following conclusions can be drawn from Figure 9.

• For 8story-O, the $E_S/E_I$ ratio is close to 0.2 when $D_1{{}^{*}}_{\max }$ is less than 0.1 m. The $E_S/E_I$ ratio increases as $D_1{{}^{*}}_{\max }$ increases when $D_1{{}^{*}}_{\max }$ is larger than 0.1 m. When $D_1{{}^{*}}_{\max }$ is close to 0.25 m, $E_S/E_I$ is between 0.8 and 0.9.
• For 16story-O, the $E_S/E_I$ ratio increases as $D_1{{}^{*}}_{\max }$ increases when $D_1{{}^{*}}_{\max }$ is larger than 0.2 m. When $D_1{{}^{*}}_{\max }$ is larger than 0.4 m, $E_S/E_I$ is between 0.8 and 0.9.
• The difference in the $E_S/E_I$ ratio resulting from the difference in $N_p$ is negligible.

In addition, the following conclusions can be drawn from Figure 9 for Type Dp.

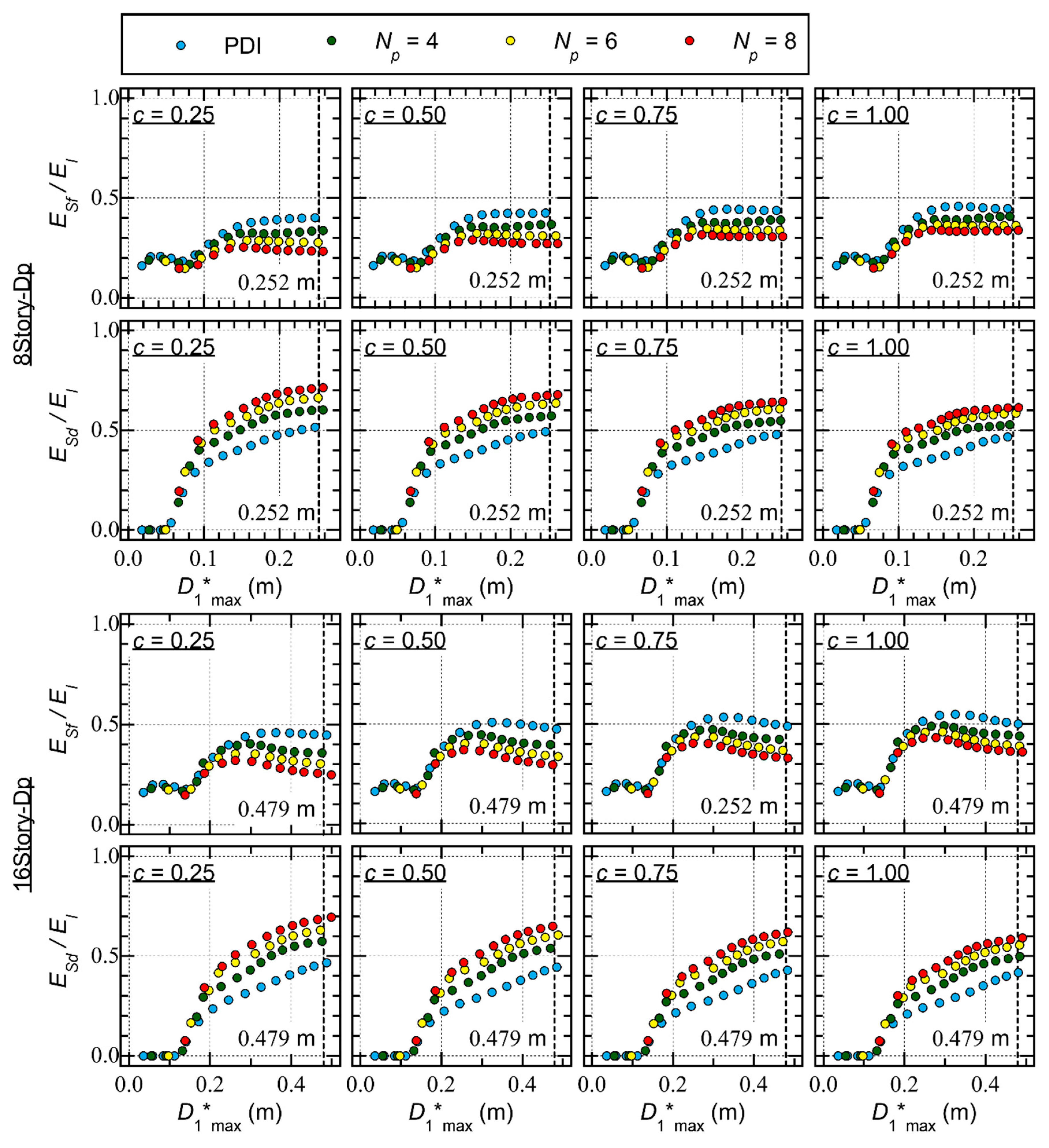
• The $E_S/E_I$ ratio increases rapidly as $D_1{{}^{*}}_{\max }$ increases. For 8story-Dp, the $E_S/E_I$ ratio reaches 0.9 when $D_1{{}^{*}}_{\max }$ is larger than 0.2 m. Meanwhile, for 16story-Dp, the $E_S/E_I$ ratio reaches 0.9 when $D_1{{}^{*}}_{\max }$ is larger than 0.4 m.
• In the PMI analysis results ($N_p$ ≥ 4), the $E_S/E_I$ ratio is larger than that obtained from the PDI analysis results ($N_p$ = 2).

Next, the discussion focuses on the cumulative strain energy ratio of the RC MRF ($E_{Sf}/E_I$) and the cumulative strain energy ratio of the SDCs ($E_{Sd}/E_I$) for Type Dp models. Figure 10 compares the ratios $E_{Sf}/E_I$ and $E_{Sd}/E_I$.

For 8story-Dp, the following conclusions can be drawn from Figure 10.

• The $E_{Sf}/E_I$ ratio is close to 0.2 when $D_1{{}^{*}}_{\max }$ is less than 0.1 m. When $D_1{{}^{*}}_{\max }$ is larger than 0.1 m, $E_{Sf}/E_I$ increases as $D_1{{}^{*}}_{\max }$ increases. However, $E_{Sf}/E_I$ decreases as $N_p$ increases. This trend is pronounced when the parameter $c$ is small (the pinching behavior is significant).
• The $E_{Sd}/E_I$ ratio is negligibly small when $D_1{{}^{*}}_{\max }$ is less than 0.06 m. The $E_{Sd}/E_I$ ratio increases rapidly as $D_1{{}^{*}}_{\max }$ increases. The $E_{Sd}/E_I$ ratio increases as $N_p$ increases. This trend is pronounced when the parameter $c$ is small.

In addition, the following conclusions can be drawn from Figure 10 for 16story-Dp.

• The $E_{Sf}/E_I$ ratio is close to 0.2 when $D_1{{}^{*}}_{\max }$ is less than 0.15 m. When $D_1{{}^{*}}_{\max }$ is larger than 0.15 m, $E_{Sf}/E_I$ increases as $D_1{{}^{*}}_{\max }$ increases. However, $E_{Sf}/E_I$ decreases as $N_p$ increases. Considering $c$ = 0.25, the $E_{Sf}/E_I$ ratio is 0.447 when $D_1{{}^{*}}_{\max }$ is 0.487 m in the PDI analysis results ($N_p$ = 2). Conversely, the $E_{Sf}/E_I$ ratio is 0.248 when $D_1{{}^{*}}_{\max }$ is 0.498 m in the PMI analysis results ($N_p$ = 8).
• The $E_{Sd}/E_I$ ratio is negligibly small when $D_1{{}^{*}}_{\max }$ is less than 0.1 m. The $E_{Sd}/E_I$ ratio increases rapidly as $D_1{{}^{*}}_{\max }$ increases. The $E_{Sd}/E_I$ ratio increases as $N_p$ increases. Considering $c$ = 0.25, the $E_{Sd}/E_I$ ratio is 0.466 when $D_1{{}^{*}}_{\max }$ is 0.487 m in the PDI analysis results ($N_p$ = 2). Conversely, the $E_{Sd}/E_I$ ratio is 0.695 when $D_1{{}^{*}}_{\max }$ is 0.498 m in the PMI analysis results ($N_p$ = 8).

4.4. Summary of the Analysis Results

This section summarizes the responses of the RC MRF models with and without SDCs as obtained from the critical PMI analysis results.

A)

The influence of the number of pseudo impulsive lateral forces ($N_p$) on the $V_p$–$D_1{{}^{*}}_{\max }$ relationship is significant in the case of RC MRFs without SDCs (Type O). For the same value of $V_p$, the $D_1{{}^{*}}_{\max }$ increases as $N_p$ increases. This trend is pronounced when the pinching behaviour is siginificant. In cases of RC MRFs with SDCs (Type Dp), $D_1{{}^{*}}_{\max }$ increases as $N_p$ increases; however, this trend is less pronounced than that observed in the RC MRFs without SDCs. The influence of the pinching behavior of the RC MRFs on the $V_p$–$D_1{{}^{*}}_{\max }$ relationship in the RC MRFs with SDCs is smaller than that in the RC MRFs without SDCs.

B)

In the PMI analysis results ($N_p$ ≥ 4), the difference in the half cycle of the structural response resulting from the pinching behavior is more pronounced than that in the PDI analysis results ($N_p$ = 2). Therefore, the influence of the pinching behavior of the RC members on the peak equivalent displacement ($D_1{{}^{*}}_{\max }$) is more notable in PMI than in PDI.

C)

The residual displacement obtained from the PMI analysis results is smaller than that obtained from the PDI analysis results ($N_p$ = 2). This difference is significant in the case of RC MRFs with SDCs.

D)

The ratio of the cumulative strain energy of the entire frame model ($E_S/E_I$) at the end of the simulation is nearly independent of the number of pseudo impulsive lateral forces ($N_p$), regardless of the presence or absense of SDCs. Meanwhile, the ratio of the cumulative strain energy of the RC MRFs ($E_{Sf}/E_I$) decreases and that of the SDCs ($E_{Sd}/E_I$) increases as $N_p$ increases in the RC MRFs with SDCs (Type Dp). This trend is pronounced when the pinching behavior of the RC members is significant.

5. Prediction of the Maximum Momentary Input Energy of RC MRFs

This section focuses on comparisons with the predicted results based on the study of Fujii and Shioda (2023) and the ICPMIA results. First, simplified equations for calculating the energy dissipation capacity during a half cycle of the structural response are formulated. Next, the seismic capacity curve (the $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ curve) is predicted using the pushover analysis results. Then, the predicted seismic capacity curve is compared with the $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ plot obtained from the ICPMIA results.

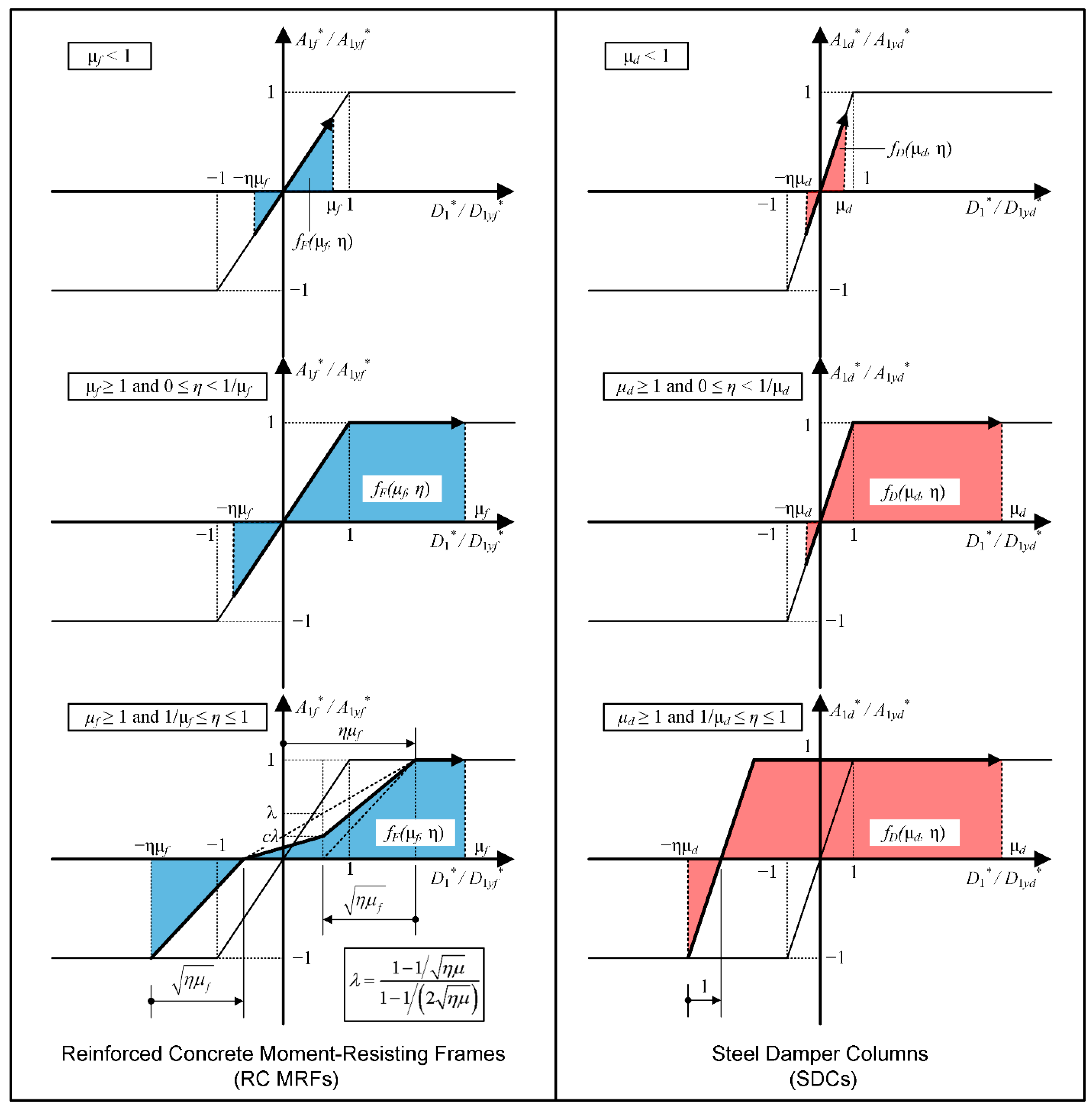
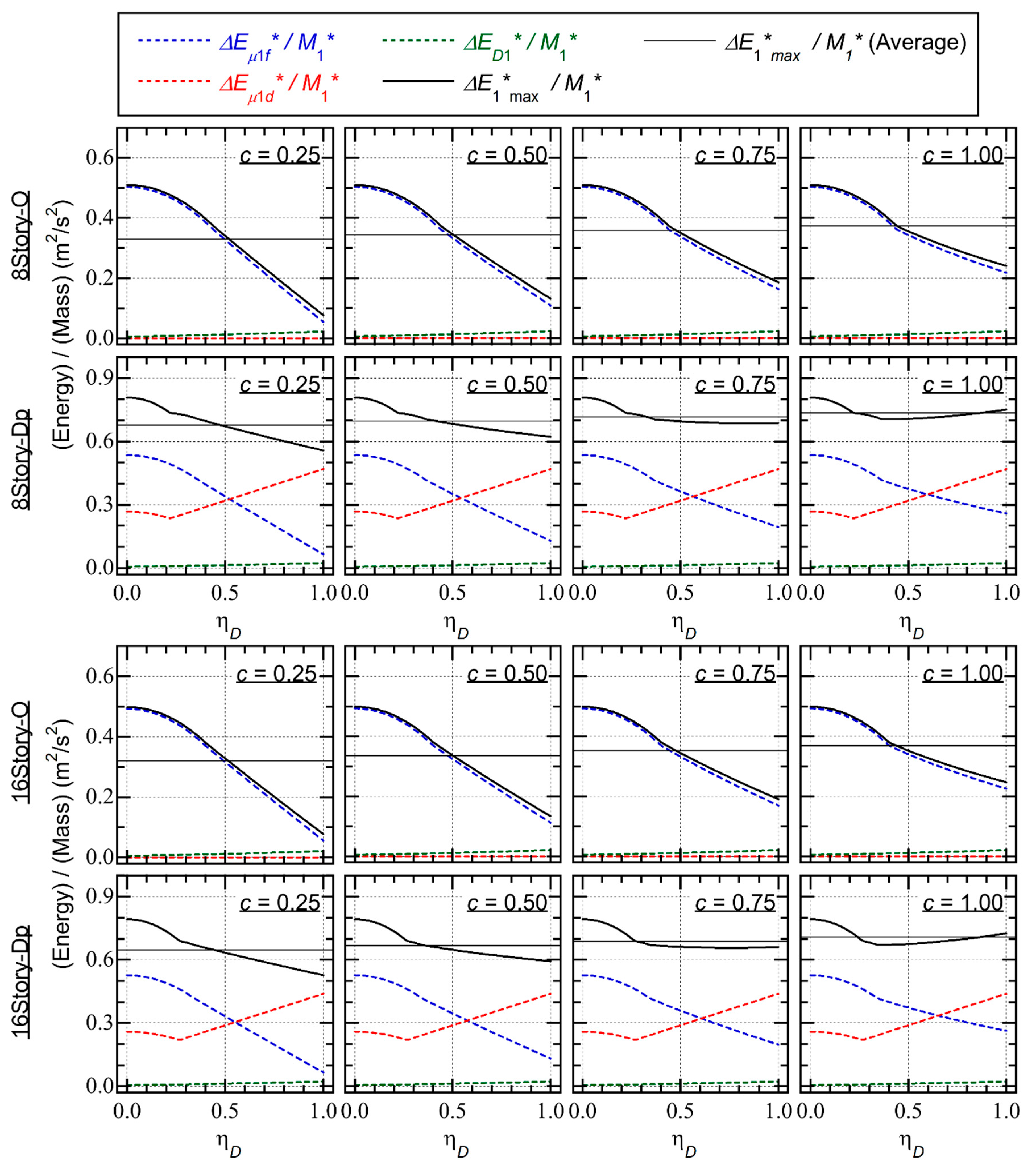
5.1. Simplified Equations for Calculating the Energy Dissipation Capacity during a Half Cycle of the Structural Response

It is assumed that the peak equivalent displacement of the first modal response ($D_1{{}^{*}}_{\max }$) occurs when the maximum momentary energy input ($\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/M_1{}^{*}$) occurs. Following Fujii and Shioda (2023), the energy dissipation capacity during a half cycle of the structural response is expressed as

$$\frac{\mathsf{\Delta }{E}_1{{}^{*}}_{\max }}{M_1{}^{*}}=\frac{\mathsf{\Delta }{E}_{\mu 1f}{}^{*}}{M_1{}^{*}}+\frac{\mathsf{\Delta }{E}_{\mu 1d}{}^{*}}{M_1{}^{*}}+\frac{\mathsf{\Delta }{E}_{D1}{}^{*}}{M_1{}^{*}}.$$

(34)

In Eq. (34), $\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$ and $\mathsf{\Delta }{E}_{\mu 1d}{}^{*}/M_1{}^{*}$ are the contributions from the hysteretic dissipated energies of the RC MRFs and SDCs, respectively, while $\mathsf{\Delta }{E}_{D1}{}^{*}/M_1{}^{*}$ is the contribution from viscous damping.

Figure 11 shows the simplified model for calculating $\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$ and $\mathsf{\Delta }{E}_{\mu 1d}{}^{*}/M_1{}^{*}$. In the figure, $A_{1f}{}^{*}$ and $A_{1d}{}^{*}$ are the contributions of the RC MRFs and SDCs, respectively, to the equivalent acceleration of the first modal response ($A_1{}^{*}$). Here, the $A_{1f}{}^{*}$−$D_1{}^{*}$ and $A_{1d}{}^{*}$−$D_1{}^{*}$ relationships are idealized by bilinear curves, where the “yield” point of the idealized $A_{1f}{}^{*}$−$D_1{}^{*}$ relationship is Y_F($D_{1yf}{}^{*}$, $A_{1yf}{}^{*}$) and that of the idealized $A_{1d}{}^{*}$−$D_1{}^{*}$ relationship is Y_D($D_{1yd}{}^{*}$, $A_{1yd}{}^{*}$). In addition, ${\mu }_f$ and ${\mu }_d$ denote the global ductilities of the RC MRFs and SDCs, respectively, which are defined in Eq. (35):

$${\mu }_f=D_1{{}^{*}}_{\max }/D_{1yf}{}^{*},{\mu }_d=D_1{{}^{*}}_{\max }/D_{1yd}{}^{*}.$$

(35)

The contribution of the hysteretic dissipated energy of the RC MRFs is calculated using Eq (36):

$$\frac{\mathsf{\Delta }{E}_{\mu 1f}{}^{*}}{M_1{}^{*}}=A_{1yf}{}^{*}{D}_{1yf}{}^{*}\widetilde{f_F}\left({\mu }_f\right).$$

(36)

The function $\widetilde{f_F}\left({\mu }_f\right)$ is defined by Eq. (37):

$$\widetilde{f_F}\left({\mu }_f\right)={\displaystyle \underset{0}{\overset{1}{\int }}{f}_F\left({\mu }_f,{\eta }_D\right)d{\eta }_D},$$

(37)

where ${\eta }_D$ is the ratio of the displacements in the positive and negative directions. Given the left panel of Figure 11, $f_F\left({\mu }_f,{\eta }_D\right)$ is calculated as

$$f_F\left({\mu }_f,\eta \right)=\left\{\begin{array}{ll}\frac{1}{2}{\mu }_f{}^2\left(1-{\eta }_D{}^2\right)\hfill & 0\le {\mu }_f\le 1\hfill \\ {\mu }_f-\frac{1}{2}\left\{1+{\left({\eta }_D{\mu }_f\right)}^2\right\}\hfill & {\mu }_f\ge 1\mathrm{and}0\le {\eta }_D\le \frac{1}{{\mu }_f}\hfill \\ {\mu }_f\left(1-{\eta }_D\right)+c\left({\eta }_D{\mu }_f-\sqrt{{\eta }_D{\mu }_f}\right)\hfill & {\mu }_f\ge 1\mathrm{and}\frac{1}{{\mu }_f}\le {\eta }_D\le 1\hfill \end{array}\right..$$

(38)

Note that, in Eq. (38), the influence of the pinching behavior of the RC members on the hysteretic energy dissipation in a half cycle of the structural response is considered by the parameter $c$. This is an updated version of this equation, as compared with previous studies (Fujii, 2022; Fujii and Shioda, 2023). By substituting Eq. (38) into Eq. (37), the function $\widetilde{f_F}\left({\mu }_f\right)$ is calculated as

$$\widetilde{f_F}\left({\mu }_f\right)=\left\{\begin{array}{ll}\frac{1}{3}{\mu }_f{}^2\hfill & 0\le {\mu }_f\le 1\hfill \\ \frac{1}{2}\left(1+c\right){\mu }_f-\frac{2}{3}c\sqrt{{\mu }_f}-\frac{1}{6{\mu }_f}\left(1-c\right)\hfill & {\mu }_f\ge 1\hfill \end{array}\right..$$

(39)

Note that Eq. (39) is consistent with the equation in Fujii and Shioda (2023): by substituting $c$ = 1 into Eq. (39), the same equation for the perfectly non-pinching RC MRFs (Fujii and Shioda, 2023) is obtained. Similarly, the contribution of the hysteretic dissipated energy of the SDCs is calculated using Eq (40):

$$\frac{\mathsf{\Delta }{E}_{\mu 1d}{}^{*}}{M_1{}^{*}}=A_{1yd}{}^{*}{D}_{1yd}{}^{*}\widetilde{f_D}\left({\mu }_d\right).$$

(40)

The function $\widetilde{f_D}\left({\mu }_d\right)$ is defined as in Eq. (41):

$$\widetilde{f_D}\left({\mu }_d\right)={\displaystyle \underset{0}{\overset{1}{\int }}{f}_D\left({\mu }_d,{\eta }_D\right)d{\eta }_D}.$$

(41)

It is assumed that the energy dissipation of SDCs is independent of the pinching behavior of the surrounding RC beams, as shown in the right panel of Figure 11. Therefore, $f_D\left({\mu }_d,{\eta }_D\right)$ is calculated such that

$$f_D\left({\mu }_d,{\eta }_D\right)=\left\{\begin{array}{ll}\frac{1}{2}{\mu }_d{}^2\left(1-{\eta }_D{}^2\right)\hfill & 0\le {\mu }_d\le 1\hfill \\ {\mu }_d-\frac{1}{2}\left\{1+{\left({\eta }_D{\mu }_d\right)}^2\right\}\hfill & {\mu }_d\ge 1\mathrm{and}0\le {\eta }_D\le \frac{1}{{\mu }_d}\hfill \\ \left(1+{\eta }_D\right){\mu }_d-2\hfill & {\mu }_d\ge 1\mathrm{and}\frac{1}{{\mu }_d}\le {\eta }_D\le 1\hfill \end{array}\right..$$

(42)

By substituting Eq. (42) into Eq. (41), the function $\widetilde{f_D}\left({\mu }_d\right)$ is calculated as shown in Eq. (43):

$$\widetilde{f_D}\left({\mu }_d\right)=\left\{\begin{array}{ll}\frac{1}{3}{\mu }_d{}^2\hfill & 0\le {\mu }_d\le 1\hfill \\ \frac{1}{6}\left(9{\mu }_d-12+\frac{5}{{\mu }_d}\right)\hfill & {\mu }_d\ge 1\hfill \end{array}\right..$$

(43)

The contribution of the viscous damping is calculated using Eq. (44), as in Fujii (2022):

$$\frac{\mathsf{\Delta }{E}_{D1}{}^{*}}{M_1{}^{*}}=\frac{7\pi h_{1f\max }}{12}{A}_{1f}{{}^{*}}_{\max }{D}_1{{}^{*}}_{\max },$$

(44)

where $h_{1f\max }$ is the damping ratio corresponding to the peak equivalent displacement ($D_1{{}^{*}}_{\max }$) and $A_{1f}{{}^{*}}_{\max }$ is the contribution of the RC MRF to the equivalent acceleration at $D_1{{}^{*}}_{\max }$.

5.2. Prediction of the Seismic Capacity Curve Based on the Pushover Analysis

Next, the seismic capacity curve (the $V_{\mathsf{\Delta }E1}{}^{*}$−$D_1{{}^{*}}_{\max }$ curve) is predicted based on the formulated equations. First, a pushover analysis of the $N$-story MRF model is performed. Then, the equivalent displacement at loading step $n$ (${}_{n}D{{}_1}^{*}$) and the equivalent acceleration at step $n$ (${}_{n}A{{}_1}^{*}$) are calculated as in Eqs. (45) and (46), given Eq. (47), assuming that the displacement vector at the loading step $n$ (${}_{n}d$) is proportional to the first mode vector at step $n$ (${}_n\mathsf{\Gamma }{}_1{}_n\phi {}_1$):

$${}_{n}D{{}_1}^{*}=\frac{{}_n\mathsf{\Gamma }{}_1{}_n\phi {{}_1}^{T}M{}_{n}d}{{}_{n}M{{}_1}^{*}}=\frac{{}_{n}d{}^{T}M{}_{n}d}{{}_{n}d{}^{T}M1},$$

(45)

$${}_{n}A{{}_1}^{*}=\frac{{}_n\mathsf{\Gamma }{}_1{}_n\phi {{}_1}^{T}M{}_{n}f{}_R}{{}_{n}M{{}_1}^{*}}=\frac{{}_{n}d{}^T{}_{n}f{}_R}{{}_{n}d{}^{T}M1},$$

(46)

$$1={\left\{\begin{array}{ccc}1& \cdots & 1\end{array}\right\}}^T.$$

(47)

In Eq. (46), ${}_{n}f{}_R$ denotes the restoring force of the entire MRF model. The contributions of the equivalent accelerations of the RC MRFs and SDCs (${}_{n}A{{}_{1f}}^{*}$ and ${}_{n}A{{}_{1d}}^{*}$, respectively) are calculated using Eqs. (48) and (49):

$${}_{n}A{{}_{1f}}^{*}=\frac{{}_n\mathsf{\Gamma }{}_1{}_n\phi {{}_1}^{T}M{}_{n}f{}_{Rf}}{{}_{n}M{{}_1}^{*}}=\frac{{}_{n}d{}^T{}_{n}f{}_{Rf}}{{}_{n}d{}^{T}M1},$$

(48)

$${}_{n}A{{}_{1d}}^{*}=\frac{{}_n\mathsf{\Gamma }{}_1{}_n\phi {{}_1}^{T}M{}_{n}f{}_{Rd}}{{}_{n}M{{}_1}^{*}}=\frac{{}_{n}d{}^T{}_{n}f{}_{Rd}}{{}_{n}d{}^{T}M1}.$$

(49)

Here, ${}_{n}f{}_{Rf}$ and ${}_{n}f{}_{Rd}$ denote the restoring forces of the RC MRFs and SDCs, respectively. The restoring force vector ${}_{n}f{}_R$ is equal to the sum of ${}_{n}f{}_{Rf}$ and ${}_{n}f{}_{Rd}$, which are calculated from the shear forces of the RC columns and SDCs, respectively. Then, the ${}_{n}A{{}_{1f}}^{*}$−$D_1{}^{*}$ and ${}_{n}A{{}_{1d}}^{*}$−$D_1{}^{*}$ relationships are idealized by bilinear curves.

Then, the energy dissipation capacity during a half cycle of the structural response of the equivalent SDOF model (${}_n\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/{}_{n}M{{}_1}^{*}$) is calculated using Eq. (50):

$$\frac{{}_n\mathsf{\Delta }{E}_1{{}^{*}}_{\max }}{{}_{n}M{{}_1}^{*}}=\frac{{}_n\mathsf{\Delta }{E}_{\mu 1f}{}^{*}}{{}_{n}M{{}_1}^{*}}+\frac{{}_n\mathsf{\Delta }{E}_{\mu 1d}{}^{*}}{{}_{n}M{{}_1}^{*}}+\frac{{}_n\mathsf{\Delta }{E}_{D1}{}^{*}}{{}_{n}M{{}_1}^{*}}.$$

(50)

The contributions of the hysteretic dissipated energy of the RC MRFs and SDCs are calculated using Eqs. (51) and (52):

$$\frac{{}_n\mathsf{\Delta }{E}_{\mu 1f}{}^{*}}{{}_{n}M{{}_1}^{*}}=A_{1yf}{}^{*}{D}_{1yf}{}^{*}\widetilde{f_F}\left({}_n\mu {}_f\right),$$

(51)

$$\frac{{}_n\mathsf{\Delta }{E}_{\mu 1d}{}^{*}}{{}_{n}M{{}_1}^{*}}=A_{1yd}{}^{*}{D}_{1yd}{}^{*}\widetilde{f_D}\left({}_n\mu {}_d\right).$$

(52)

The values of ${}_n\mu {}_f$ and ${}_n\mu {}_d$ are calculated via Eq. (53):

$${}_n\mu {}_f={}_{n}D{{}_1}^{*}/D_{1yf}{}^{*},{}_n\mu {}_d={}_{n}D{{}_1}^{*}/D_{1yd}{}^{*}.$$

(53)

The contributions of the viscous damping are calculated such that

$$\frac{{}_n\mathsf{\Delta }{E}_{D1}{}^{*}}{{}_{n}M{{}_1}^{*}}=\frac{7\pi h_{1f}}{12}\frac{{}_n\omega {}_{1f}}{{}_1\omega {}_{1f}}{}_{n}A{{}_{1f}}^{*}{}_{n}D{{}_1}^{*},$$

(54)

$${}_n\omega {}_{1f}=\sqrt{{}_{n}A{{}_{1f}}^{*}/{}_{n}D{{}_1}^{*}}.$$

(55)

In Eq. (54), $h_{1f}$ is the viscous damping ratio of the RC MRFs for the first modal response in the elastic range, while ${}_n\omega {}_{1f}$ defined in Eq. (55) is the secant circular frequency of the first mode of the RC MRFs. In this study, it is assumed that $h_{1f\max }$ in Eq. (44) is proportional to the secant circular frequency of the RC MRFs (${}_n\omega {}_{1f}$).

The equivalent velocity of the energy dissipation capacity during a half cycle of the structural response of the equivalent SDOF model corresponding to ${}_{n}D{{}_1}^{*}$ (${}_{n}V{{}_{\mathsf{\Delta }E1}}^{*}$) is calculated via Eq. (56):

$${}_{n}V{{}_{\mathsf{\Delta }E1}}^{*}=\sqrt{2{}_n\mathsf{\Delta }{E}_1{{}^{*}}_{\max }/{}_{n}M{{}_1}^{*}}.$$

(56)

Figure 12 shows the calculated seismic capacity curves (the ${}_{n}V{{}_{\mathsf{\Delta }E1}}^{*}$−${}_{n}D{{}_1}^{*}$ relationships) of the four models calculated from the pushover analysis results. The calculated curves for $c$ = 0.25, 0.50, 0.75, and 1.00 are compared in the figure. As shown here, the differences in the calculated curves resulting from the parameter $c$ are limited.

5.3. Comparisons with ICPMIA Results

Figure 13 shows comparisons between the predicted seismic capacity curves and the ICPMIA analysis results. The following conclusions can be drawn.

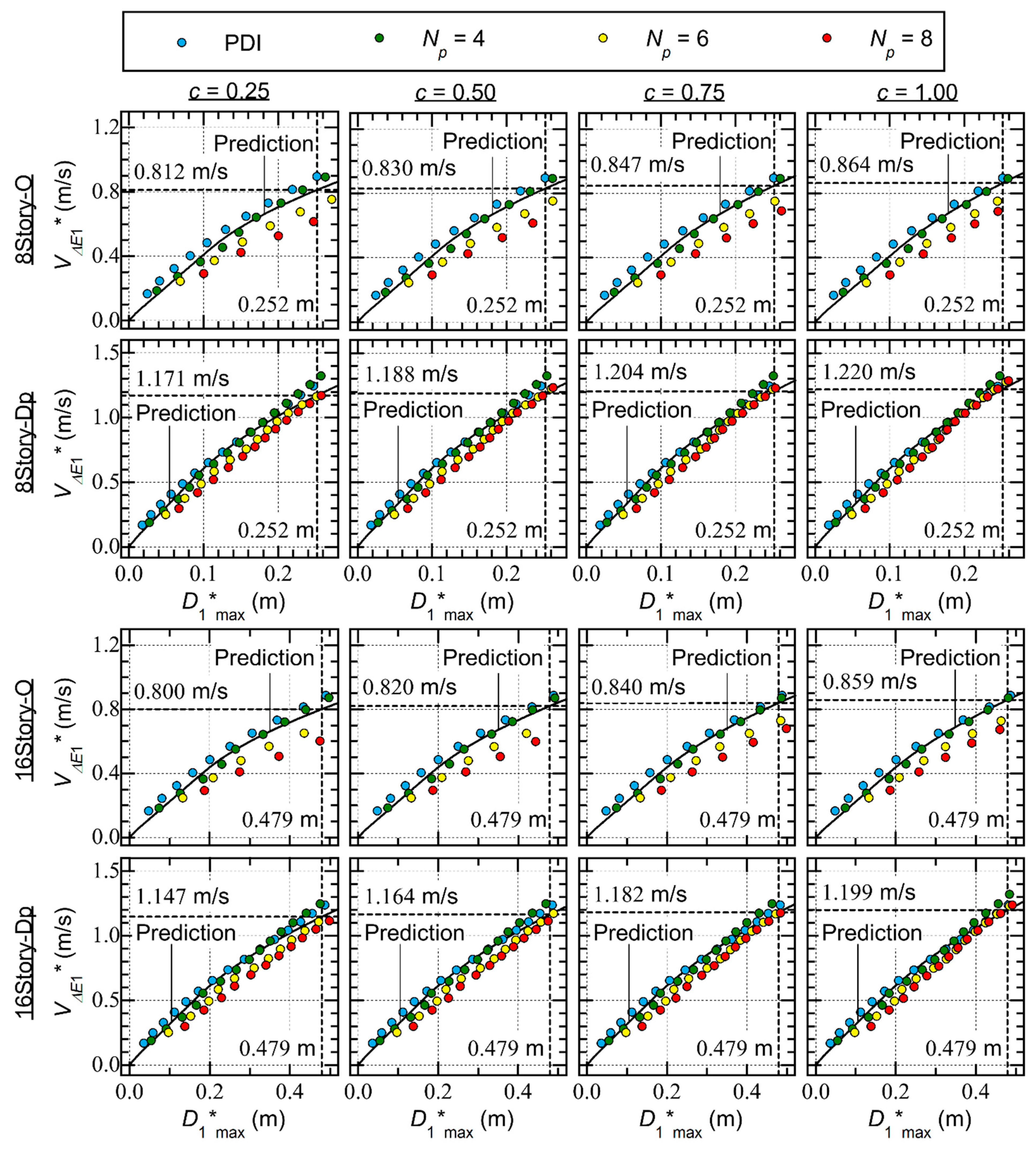
• For Type O, the plots obtained from the PDI and PMI analysis ($N_p$ = 4) results are above the predicted seismic capacity curve. However, the plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are below the predicted curve. Specifically, for 8story-O, with $c$ = 0.25 (significant pinching) and $N_p$ = 8, the $V_{\mathsf{\Delta }E1}{}^{*}$ value corresponding to $D_1{{}^{*}}_{\max }$ = 0.247 m is 0.616 m/s, while the predicted ${}_{n}V{{}_{\mathsf{\Delta }E1}}^{*}$ value corresponding to ${}_{n}D{{}_1}^{*}$ = 0.247 m is 0.802 m/s; this is a 23.1% underestimation of $V_{\mathsf{\Delta }E1}{}^{*}$.
• For Type Dp, the plots obtained from the PDI and PMI analysis ($N_p$ = 4) results agree very well with the predicted seismic capacity curve. In addition, the plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are slightly below the predicted curve. The dependence of the Type Dp $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots on $N_p$ is limited.

The results shown in Figure 13 indicate that the accuracy of the predicted capacity curve is acceptable for Type Dp, while the predicted capacity curve is unacceptably underestimated for Type O for larger $N_p$. As described in Section 5.1, the equation for calculating the energy dissipation capacity during a half cycle of the structural response is simplified by calculating the average in the range of $0\le {\eta }_D\le 1$. Accordingly, the following discussion focuses on the ${\eta }_D$ ratio. First, Figure 14 shows the ${\eta }_D$ ratio obtained from the PDI and PMI analysis results. Here, ${\eta }_D$ is calculated using Eq. (57):

$${\eta }_D=\left|{}_{k-1}D{{}_1}^{*}{}_{peak}/{}_{k}D{{}_1}^{*}{}_{peak}\right|,$$

(57)

where $k$ is the counting number when the maximum momentary energy input occurs. The following conclusions can be drawn from Figure 14.

• For Type O, the ${\eta }_D$ ratio is between 0.4 and 0.5 in the PDI analysis results. Similarly, in the PMI analysis ($N_p$ = 4) results, ${\eta }_D$ is between 0.5 and 0.6. Meanwhile, in the PMI analysis ($N_p$ = 6 and 8) results, ${\eta }_D$ increases as $D_1{{}^{*}}_{\max }$ increases: ${\eta }_D$ is between 0.7 and 0.9 when $N_p$ is 6, while ${\eta }_D$ is larger than 0.8 when $N_p$ is 8.
• For Type Dp, the ${\eta }_D$ ratio is between 0.4 and 0.5 in the PDI analysis results. However, in the PMI analysis ($N_p$ = 4) results, ${\eta }_D$ increases as $D_1{{}^{*}}_{\max }$ increases. For 8story-Dp, ${\eta }_D$ is close to 0.5 when $D_1{{}^{*}}_{\max }$ is close to 0.1 m and ${\eta }_D$ reaches 0.7 when $D_1{{}^{*}}_{\max }$ is close to 0.25 m. In the PMI analysis ($N_p$ = 6 and 8) results, ${\eta }_D$ is larger than 0.7 and increases as $D_1{{}^{*}}_{\max }$ increases; then, ${\eta }_D$ approaches 1.

The results shown in Figure 14 indicate that the ${\eta }_D$ ratio increases as $N_p$ increases for both Types O and Dp. Next, the relationship between the energy dissipation capacity during a half cycle of the structural response and ${\eta }_D$ is investigated. Following the discussion in Section 5.1, the contributions from the hysteretic dissipated energies of the RC MRFs and SDCs ($\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$ and $\mathsf{\Delta }{E}_{\mu 1d}{}^{*}/M_1{}^{*}$, respectively) can be expressed as shown in Eqs. (58) and (59):

$$\frac{\mathsf{\Delta }{E}_{\mu 1f}{}^{*}}{M_1{}^{*}}\left({\mu }_f,{\eta }_D\right)=A_{1yf}{}^{*}{D}_{1yf}{}^{*}{f}_F\left({\mu }_f,{\eta }_D\right),$$

(58)

$$\frac{\mathsf{\Delta }{E}_{\mu 1d}{}^{*}}{M_1{}^{*}}\left({\mu }_d,{\eta }_D\right)=A_{1yd}{}^{*}{D}_{1yd}{}^{*}{f}_D\left({\mu }_d,{\eta }_D\right).$$

(59)

In addition, the contribution from the viscous damping ($\mathsf{\Delta }{E}_{D1}{}^{*}/M_1{}^{*}$) can be expressed as

$$\frac{\mathsf{\Delta }{E}_{D1}{}^{*}}{M_1{}^{*}}\left(D_1{{}^{*}}_{\max },{\eta }_D\right)=\frac{\pi {\left(1+{\eta }_D\right)}^2}{4}\frac{{\omega }_{1f\max }}{{}_1\omega {}_{1f}}{h}_{1f}{A}_{1f}{{}^{*}}_{\max }{D}_1{{}^{*}}_{\max }.$$

(60)

In Eq. (60), ${\omega }_{1f\max }$, the secant circular frequency of the first mode of the RC MRFs, corresponds to $D_1{{}^{*}}_{\max }$ and is calculated from Eq. (55).

Figure 15 shows the relationships between the energy dissipation capacity calculated from Eqs. (58)–(60) and the ${\eta }_D$ ratio. In this figure, $D_1{{}^{*}}_{\max }$ is assumed to be 1/75 of the assumed equivalent height ($H_1{}^{*}$): $D_1{{}^{*}}_{\max }$ is set to 0.252 m for the 8-story models and to 0.479 m for the 16-story models.

The following conclusions can be drawn for Type O from Figure 15.

• The contribution from the hysteretic dissipated energy of the RC MRFs ($\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$) decreases rapidly as ${\eta }_D$ increases. Conversely, the contribution from the viscous damping ($\mathsf{\Delta }{E}_{D1}{}^{*}/M_1{}^{*}$) increases as ${\eta }_D$ increases. However, because $\mathsf{\Delta }{E}_{D1}{}^{*}/M_1{}^{*}$ is much smaller than $\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$, the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ decreases rapidly as ${\eta }_D$ increases: $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ is largest when ${\eta }_D$ is zero and smallest when ${\eta }_D$ is unity.
• The variation in the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ as a result of the ${\eta }_D$ ratio is predominant when the parameter $c$ is 0.25 (significant pinching). For 8story-O and $c$ = 0.25, the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.509 m²/s², while the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.077 m²/s² (only 15.2% of the value when ${\eta }_D$ = 0). Meanwhile, for 8story-O and $c$ = 1.00 (perfectly non-pinching), the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.509 m²/s² (the same value as for $c$ = 0.25) and the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.241 m²/s² (47.3% of the value when ${\eta }_D$ = 0).

The following conclusions can be drawn for Type Dp from Figure 15.

• The contribution from the hysteretic dissipated energy of the SDCs ($\mathsf{\Delta }{E}_{\mu 1d}{}^{*}/M_1{}^{*}$) increases as ${\eta }_D$ increases. Therefore, the variation in the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ of Type Dp resulting from the ${\eta }_D$ ratio is less significant than that of Type O.
• The variation in the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ of Type Dp resulting from the ${\eta }_D$ ratio is much less significant than that of Type O, even for $c$ = 0.25 (significant pinching). For 8story-Dp and $c$ = 0.25, the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.808 m²/s², while the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.557 m²/s² (68.9% of the value when ${\eta }_D$ = 0). Meanwhile, for 8story-Dp and $c$ = 1.00, the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 0 is 0.808 m²/s² (the same value as for $c$ = 0.25) and the calculated $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ corresponding to ${\eta }_D$ = 1 is 0.751 m²/s² (92.9% of the value when ${\eta }_D$ = 0).

The results shown in Figures 14 and 15 can explain why the Type O $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots are influenced significantly by $N_p$ while the dependence of the Type Dp $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots on $N_p$ is limited. As shown in Figure 14, in general, ${\eta }_D$ increases as $N_p$ increases for both Types O and Dp. In addition, $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ decreases significantly as ${\eta }_D$ increases in the case of Type O, as shown in Figure 15. Therefore, in the case of Type O, $V_{\mathsf{\Delta }E1}{}^{*}$ decreases as $N_p$ increases because the increase in $N_p$ leads to an increase in ${\eta }_D$. Conversely, in the case of Type Dp, the variation in $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ resulting from ${\eta }_D$ is less significant, as shown in Figure 15. Therefore, in the case of Type Dp, the variation in $V_{\mathsf{\Delta }E1}{}^{*}$ as a result of the increase in $N_p$ is less significant.

Note that the contribution of the hysteresis energy of the RC MRFs ($\mathsf{\Delta }{E}_{\mu 1f}{}^{*}/M_1{}^{*}$) decreases drastically as ${\eta }_D$ increases, especially when the pinching behavior of the RC members is significant. Therefore, the variation in $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ of RC MRFs without SDCs as a result of ${\eta }_D$ becomes larger. This implies that the variation in the peak displacement ($D_1{{}^{*}}_{\max }$) of RC MRFs without SDCs corresponds to the given $V_{\mathsf{\Delta }E1}{}^{*}$ becoming larger. Conversely, the contribution of the hysteresis energy of the SDCs ($\mathsf{\Delta }{E}_{\mu 1d}{}^{*}/M_1{}^{*}$) increases as ${\eta }_D$ increases. Therefore, the variation in $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ of RC MRFs resulting from ${\eta }_D$ can be reduced by installing SDCs within the MRFs. Consequently, the use of SDCs as supplimental energy dissipating devices in RC MRFs is effective in reducing: (i) the peak displacement; (ii) the cumulative strain energy of RC members; and (iii) the variation in the peak displacement.

5.4. Summary of the Discussion

This section focuses on comparisons with the predicted results based on Fujii and Shioda (2023) and the ICPMIA results. On the basis of these comparisons, the following conclusions can be drawn.

A)

In the case of RC MRFs without SDCs, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots obtained from the PDI and PMI analysis ($N_p$ = 4) results are above the predicted seismic capacity curve. However, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are below the predicted curve. The dependence of the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots of RC MRFs without SDCs on $N_p$ is significant.

B)

In the case of RC MRFs with SDCs, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots obtained from the PDI and PMI analysis ($N_p$ = 4) results agree very well with the predicted seismic capacity curve. In addition, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots obtained from the PMI analysis ($N_p$ = 6 and 8) results are slightly below the predicted curve. The dependence of the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots of the RC MRFs with SDCs on $N_p$ is limited.

C)

The ratio of the displacements in the positive and negative directions (${\eta }_D$) increases as $N_p$ increases. In the case of RC MRFs without SDCs, $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ decreases drastically as ${\eta }_D$ increases, especially when the pinching behavior of the RC members is significant. Meanwhile, in the case of RC MRFs with SDCs, the variation in $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ resulting from ${\eta }_D$ is less significant.

6. Conclusions

In this article, the seismic capacities of RC MRFs with and without SDCs were evaluated using incremental critical pseudo-multi impulse analysis (ICPMIA). From the ICPMIA results, (a) the influence of the number of impulsive inputs ($N_p$) and the pinching behavior of the RC members on $D_1{{}^{*}}_{\max }$ and the residual equivalent displacement and (b) the influence of $N_p$ on the cumulative strain energies of RC MRFs and SDCs were investigated. Then, the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plots obtained from the ICPMIA results were compared with the predicted seismic capacity curves based on the simplified equations. The main results and conclusions can be summarized as follows.

(i)

In the case of RC MRFs without SDCs, the influence of $N_p$ on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship is notable: $V_{\mathsf{\Delta }E1}{}^{*}$ decreases as $N_p$ increases. Meanwhile, in the case of RC MRFs with SDCs, the influence of $N_p$ on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship is limited. This is because the energy dissipation capacity in a half cycle of the structural response decreases drastically in the case of RC MRFs without SDCs when the ratio of the displacements in the positive and negative directions is close to unity.

(ii)

In the case of RC MRFs without SDCs, the influence of the pinching behavior of RC members on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship is small when $N_p$ is small. However, when $N_p$ is larger, the influence of the pinching behavior of RC members on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship is notable. Conversely, the influence of the pinching behavior of RC members on the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ relationship is limited in the case of RC MRFs with SDCs, regardless of $N_p$.

(iii)

For RC MRFs with SDCs, the ratio of the cumulative strain energy of the RC MRFs ($E_{Sf}/E_I$) decreases and that of the SDCs ($E_{Sd}/E_I$) increases as $N_p$ increases. This trend is pronounced when the pinching behavior of the RC members is significant.

(iv)

The residual equivalent displacement ratio ($r_{resD}$), defined as the ratio of the residual equivalent displacement to the peak equivalent displacement ($D_1{{}^{*}}_{\max }$), obtained from the critical PMI analysis results is smaller than that obtained from the critical PDI analysis results. This difference is significant in the case of RC MRFs with SDCs. No regular trend was observed between the $r_{resD}$ ratio and $D_1{{}^{*}}_{\max }$: the $r_{resD}$ ratio may decrease when $D_1{{}^{*}}_{\max }$ increases.

Conclusion (i) supports the accuracy of the prediction procedure (Fujii and Shioda, 2023). Specifically, the predicted $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ curve is sufficiently accurate for RC MRFs with SDCs, regardless of the number of impulsive lateral forces $N_p$. For RC MRFs without SDCs, however, the predicted $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ curve may not be conservative in the case of long-duration earthquake ground motion and resonance. Conclusion (ii) indicates that the installation of SDCs within RC MRFs can effectively reduce the peak displacement, especially when long-duration earthquake ground motion is considered. This conclusion is consistent with the study by Shirai et al. (2024). Conclusion (iii) indicates that the contribution of SDCs in terms of the cumulative strain energy depends on the duration of the input ground motion. Therefore, to better predict the cumulative strain energy of RC members and SDCs, such phenomema should be properly considered. Conclusion (iv) indicates that the residual deformation obtained from the critical PDI analysis results may be the upper bound for RC MRFs with and without SDCs. It is important to consider the extention of the critical PMI analysis as a substitute for seismic sequences because, as shown by Hoveidae and Radpour (2021), the residual displacement after the first earthquake affects the peak response under the second earthquake.

Another finding of interest is the dependence of the calculated energy dissipation capacity ($\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$) on the ratio of the displacement in the positive and negative directions (${\eta }_D$). As discussed in Section 5.3, the variation in the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plot resulting from $N_p$ is small in the case of RC MRFs with SDCs because the variation in $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ resulting from ${\eta }_D$ is less significant. This implies that, if $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ were constant in the range of $0\le {\eta }_D\le 1$, the variation in the $V_{\mathsf{\Delta }E1}{}^{*}$–$D_1{{}^{*}}_{\max }$ plot would be minimized. Such a structural system can be constructed by considering the proper combination of RC MRFs and SDCs or by developing a new energy dissipating system with the proper $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$–${\eta }_D$ relationship. As shown in Section 5.3, the $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$–${\eta }_D$ relationship of RC MRFs indicates that $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ decreases as ${\eta }_D$ increases. Therefore, the $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$–${\eta }_D$ relationship of dampers for RC MRFs should have the opposite behavior with $\mathsf{\Delta }{E}_{1\max }{}^{*}/M_1{}^{*}$ increasing with increasing ${\eta }_D$. Such information is useful when choosing proper dampers considering the characteristics of the main structures (e.g., RC and/or steel MRFs or wood structures).

Note that the results shown in this study are, so far, valid only for RC MRF models with and without SDCs. Therefore, apart from further verifications using additional building models, the following questions remain unanswered, although the list below is not comprehensive.

• How can the number of impulsive inputs $N_p$ as a substitute of recorded ground motions be determined? To the author’s best knowledge, the ratio of the equivalent velocities of the total input energy to the maximum momentary input energy ($V_I/V_{\mathsf{\Delta }E}$) would be the best parameter for this purpose. If the number $N_p$ were chosen to obtain the $V_I/V_{\mathsf{\Delta }E}$ ratio of the considered ground motion, the response obtained from the critical PMI analysis results could represent the peak and cumulative response of the structure subjected to the considered ground motion.
• Can the prediction procedure (Fujii and Shioda, 2023) properly predict the cumulative strain energies of RC MRFs and SDCs obtained by the critical PMI analysis results? As far as the peak response is concerned, the prediction procedure has been validated. However, the prediction procedure has not been validated for the cumulative response. In such a validation, the pinching behavior of the RC members and the number of impulsive inputs $N_p$ would be key parameters.
• Can the ICPMIA be extended for the case of seismic sequences? To the author’s best knowledge, the NTHA is the only method that analyzes the responses of structures subjected to seismic sequences. However, the results obtained from NTHA are too complex to derive general conclusions. This is because the NTHA results are intricately intertwined with the nonlinear structural characteristics and the ground motion characteristics. In the case of a seismic sequence, the complexity increases as a result of the mainshock-aftershock (or foreshock-mainshock) combined ground motions. The nonlinear characteristics of the damaged structure would likely be easier to understand using ICPMIA.