Critical Pseudo-Double Impulse Analysis Evaluating Seismic Energy Input to Reinforced Concrete Buildings with Steel Damper Columns

1. Introduction

1.1. Background and Motivation

A dual system with sacrificial members that absorb the seismic energy prior to the beams and columns, e.g., a damage-tolerant structure (Wada et al., 2000), is one solution for creating structures with superior seismic performance. Unlike traditional earthquake-resistant structures, beams and columns in such dual systems are damage free (or have limited damage) after large earthquakes because most of the seismic energy input is absorbed by the sacrifice members. Therefore, buildings with such dual systems are more resilient than those without sacrificial members.

Steel damper columns (SDCs; Katayama et al., 2000) are energy-dissipating sacrificial members that are suitable for reinforced concrete (RC) buildings and are often used for multistory housing. The purpose of SDCs is to mitigate damage to beams and columns during strong seismic events. The author’s research group has been studying the seismic rehabilitation of existing RC buildings using SDCs (Fujii and Miyagawa, 2018; Fujii et al., 2019) and the seismic design of new RC moment-resisting frames (MRFs) with SDCs (Mukouyama et al., 2021).

The peak deformation and cumulative strain energy are essential parameters in assessing the seismic performance of structural members. Specifically, the peak deformation is an essential parameter for RC members dominated by flexural behavior, as long as the story drift does not exceed 2.0 % (Elwood et al., 2021). Meanwhile, both the peak deformation and the cumulative strain energy are important for the steel damper panels within SDCs. In a previous paper, an energy-based prediction procedure for the peak and cumulative responses of an RC MRF building with SDCs was proposed (Fujii and Shioda, 2023). In this procedure, the building model is converted to an equivalent single-degree-of-freedom (SDOF) model that represents the first modal response. Then, two energy-related seismic intensity parameters are considered, namely, the maximum momentary input energy (Hori and Inoue, 2002) and the total input energy (Akiyama, 1985). The peak displacement is predicted by considering the energy balance during a half cycle of the structural response using the maximum momentary input energy. Meanwhile, the energy dissipation demand of the dampers is predicted considering the energy balance during an entire response cycle using the total input energy.

This procedure has been verified by comparing nonlinear time-history analysis (NTHA) results using non-pulse-like artificial ground motions (Fujii and Shioda, 2023) and 30 recorded pulse-like ground motions (Fujii, 2023). However, the following issues remain.

• In the presented procedure (Fujii and Shioda, 2023), the accuracy of the equivalent velocity of the maximum momentary input energy of the first modal response (${V_{\Delta E1}}^{*}$)–equivalent displacement of the first modal response (${D_1}^{*}$) relationship is essential for high quality predictions of the peak displacement. Accordingly, a monotonic pushover analysis was performed to evaluate the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship. However, the strain hardening effect observed in low-yield steel shear panels subjected to cyclic loading (Nakashima, 1995) cannot be considered in a monotonic pushover analysis.
• For the prediction of the peak equivalent displacement (${{D_1}^{*}}_{\max }$) and cumulative input energy of the first modal response, the equivalent velocities of the maximum momentary input energy (${V_{\Delta E1}}^{*}$) and the total input energy (${V_{I1}}^{*}$) are predicted from the linear elastic spectrum (the $V_{\Delta E}$ and $V_{\Delta E}$ spectra, respectively). In the presented procedure (Fujii and Shioda, 2023), the effective period of the first modal response ($T_{1eff}$) calculated from the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship is used for the predictions of ${V_{\Delta E1}}^{*}$ and ${V_{I1}}^{*}$. Although the accuracies of the predicted ${V_{\Delta E1}}^{*}$ and ${V_{I1}}^{*}$ values have been examined by comparing the predicted results with the NTHA results, the accuracy of $T_{1eff}$ has not yet been examined. The response period of the first modal response ($T_{1res}$), which is defined as twice $\Delta t$ ( where $\Delta t$ is the interval of a half cycle of the structural response), is a good index for evaluating $T_{1eff}$ in NTHA results. However, the value of $\Delta t$ obtained from the NTHA results is unstable because of the complexity of the characteristics of ground motions and the influence of the higher modal responses of a structure.

The relationship between the energy and the peak deformation has been studied by several researchers. There are two main approaches: the first approach is to define a parameter that relates the cumulative input energy (or cumulative strain energy) and the peak deformation and the second approach is to define an energy-based seismic intensity parameter that is directly related to the peak deformation. Akiyama (1988) stated that the cumulative inelastic deformation ratio should be assumed to be 4 times the inelastic deformation ratio for the seismic design of structures with elastic–perfectly plastic behavior, such as ductile steel MRFs. Then, the equivalent number of cycles can be formulated as the ratio of the cumulative inelastic deformation to the peak inelastic deformation in the simplified energy-based seismic design method (Akiyama, 1999). Manfredi et al. (2003) investigated the relationship between the equivalent number of plastic cycles and the seismological parameters in the near field based on 128 near-fault and 122 far-fault records. They concluded that “the relative importance of the cyclic damage for structures grows at the higher distance from the fault, whereas in the near-source conditions structural response is governed by the peak demand, confirming the damage observations after destructive earthquakes.” Mota-Páez et al. (2021) noted that, for the seismic retrofit design of an RC soft-story building with a hysteresis damper under near-fault earthquakes, the equivalent number of cycles should be reduced. This is because, in the case of a near-fault earthquake, a large amount of seismic energy input occurs within a few cycles. Within the first approach, Fajfar (1992) proposed another dimensionless parameter $\gamma$ normalizing the cumulative hysteresis (strain) energy by the peak deformation. This parameter $\gamma$ has been applied to the pushover-based damage analysis method of RC MRFs (Gaspersic et al, 1992; Fajfar and Gaspersic, 1996) and the seismic design procedure of new RC MRFs (Teran-Gilmore, 1998). Decanini et al. (2000) studied the relationship between the cumulative input energy and the peak displacement of RC MRFs subjected to near-source earthquakes; they concluded that a reliable relationship between the cumulative input energy and the peak displacement can be constructed, using either the cumulative hysteretic energy or the cumulative input energy. Mollaioli et al. (2011) analyzed the correlations between the energy and the peak displacement for linear and nonlinear SDOF and multi-degree-of-freedom (MDOF) models; they concluded that the degree of correlation between the energy and the displacement quantities is noticeably more stable when the cumulative input energy is considered, rather than the cumulative hysteresis energy. Following these studies, Angelucci et al. (2023b) studied the relationship between the cumulative input energy and the peak displacement of RC MRFs with infills. Meanwhile, Benavent-Climent (Benavent-Climent et al., 2004; Benavent-Climent, 2011) proposed an energy-based assessment method for existing buildings; they focused on the strain energy under the monotonic loading of stories until the ultimate state, instead of the ultimate story drift.

Inoue and his research group (Hori et al., 2000, Inoue et al., 2000, Hori and Inoue 2002) proposed the maximum momentary input energy as an energy-based seismic intensity parameter that is directly related to the peak displacement of RC structures. Note that a similar energy-based seismic intensity parameter was proposed by Kalkan and Kunnath (2007). The present authors formulated the time-varying function of the momentary energy input of an elastic SDOF mode using Fourier series (Fujii et al, 2019). Then, the concept of the momentary input energy was extended to bidirectional horizontal excitation (Fujii and Murakami, 2021; Fujii 2021). In addition, Fajfar’s $\gamma$ parameter was re-formulated using the maximum momentary input energy and the total input energy for RC structures (Fujii, 2021). Similarly, for base-isolated structures with hysteresis dampers, Akiyama’s equivalent number of cycles was reformulated using the maximum momentary input energy and the total input energy (Fujii, 2023). Angelucci et al. (2023a) studied the relationship between the energy-related seismic intensity parameters proposed by Kalkan and Kunnath (2007) and the peak displacement of bare RC MRFs.

The above-discussed studies are based on NTHA results using recorded ground motions. Conversely, Takewaki and his research group (Kojima et al., 2015; Kojima and Takewaki, 2015a, 2015b, and 2015c; Akehashi and Takewaki, 2021; Akehashi and Takewaki, 2022) studied simplifying the seismic input as a series of impulsive forces. First, Kojima et al. (2015) introduced the concept of the “critical double impulse input,” which represents the upper bound of the earthquake energy input for a given pulse velocity ($V_p$). Next, Kojima and Takewaki introduced the double impulse input as a substitute for the fling-step near-fault ground motion (2015a). Following this study, they introduced the triple impulse input as a substitute for the forward-directivity near-fault ground motion (2015b) and the multiple impulse input as a substitute for long-duration earthquake ground motion (2015c). Then, Akehashi and Takewaki introduced pseudo-double impulse (PDI) (2021) and pseudo-multi impulse (PMI) (2022) analyses. In PDI and PMI analyses, the MDOF model oscillates predominantly in the single mode, considering the impulsive lateral force corresponding to a certain mode vector; when the impulsive lateral force corresponding to the first mode vector is considered, the MDOF model oscillates predominantly in the first mode.

The author believes that PDI is suitable to discuss the above two issues for the following reasons: (i) the momentary input energy can easily be calculated as the energy input because of the acting pseudo lateral force and (ii) the interval of a half cycle of the structural response ($\Delta t$) can easily be evaluated and is expected to be stable because the MDOF model oscillates predominantly in a single mode.

1.2. Objectives

Given the above-outlined background, this study addresses the following questions.

(i)

What is the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ relationship when considering the response of an RC MRF with SDCs subjected to critical PDI input? Does it agree with the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship from the simplified equation proposed in the author’s previous study (Fujii and Shioda, 2023)?

(ii)

What is the relationship between the response period ($T_{1res}$) and the effective period ($T_{1eff}$) calculated from ${{D_1}^{*}}_{\max }$ and ${V_{\Delta E1}}^{*}$ in the case of an RC MRF with SDCs subjected to critical PDI input?

In this study, critical PDI analyses of RC MRF models are performed. These critical PDI analyses are based on studies by Akehashi and Takewaki (2021) with one modification: in this study, the change in the first mode shape in the nonlinear range is considered to maintain consistency with the assumptions applied in the procedure (Fujii and Shioda, 2023). Six 8- and 16-story RC MRFs with and without SDCs are analyzed considering various intensities of the pulse velocity $V_p$. Then, the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ and $T_{1eff}$–${D_1}^{*}$ relationships calculated according to the procedure (Fujii and Shioda, 2023) are compared with those obtained from the critical PDI analysis results.

The rest of this paper is organized as follows. Section 2 outlines the critical PDI analysis based on Akehashi and Takewaki (2021). Section 3 presents the six RC MRFs with and without SDCs and the analysis methods. Section 4 describes the responses of the six RC MRFs obtained from the critical PDI analysis results. Section 5 discusses the comparisons with the predicted results based on the author’s previous study (Fujii and Shioda, 2023) and the critical PDI analysis results, focusing particularly on (i) the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship and (ii) the $T_{1eff}$–${D_1}^{*}$ relationship. The conclusions drawn from this study and the directions of future research are discussed in Section 6.

2. Critical PDI Analysis

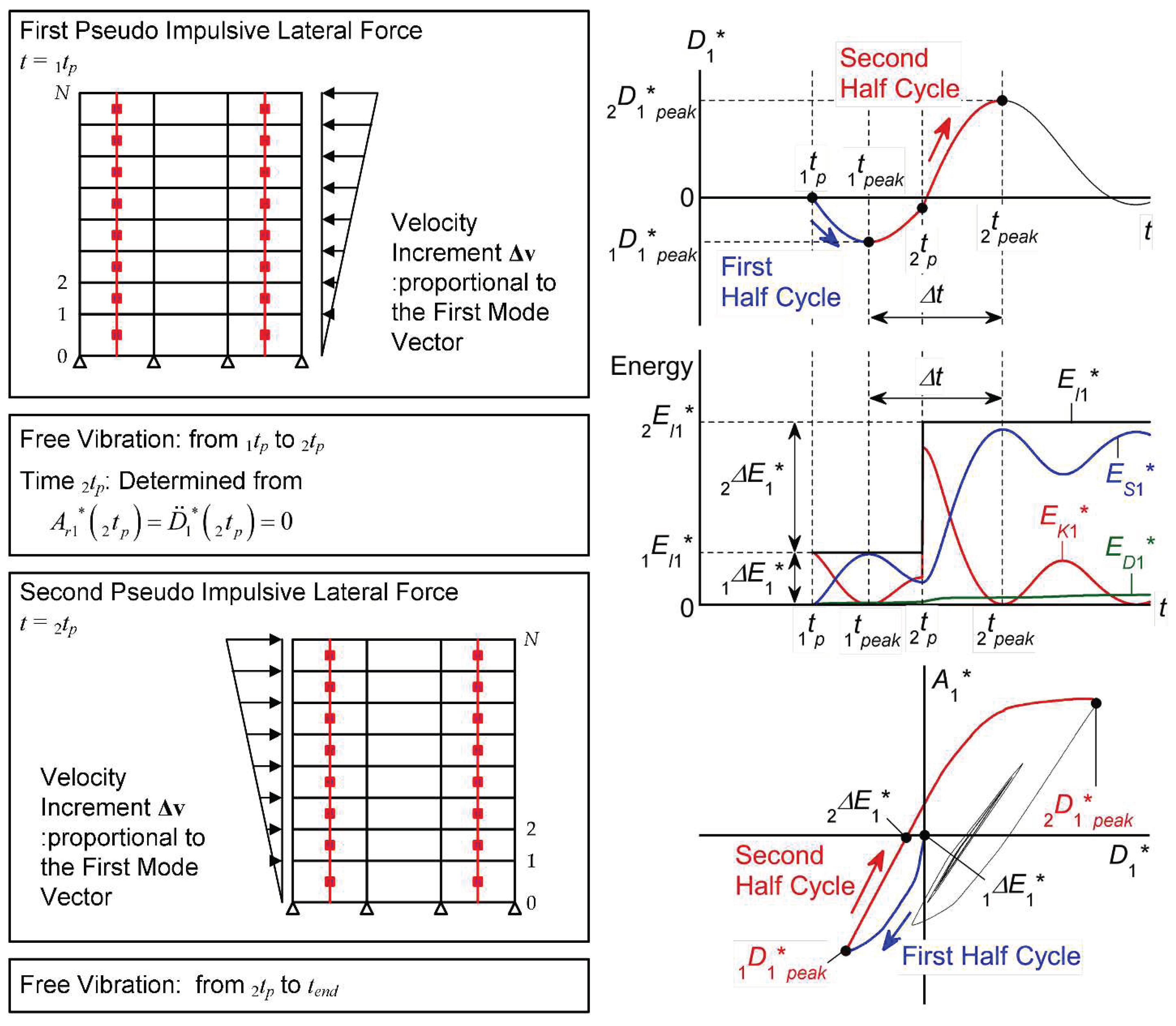
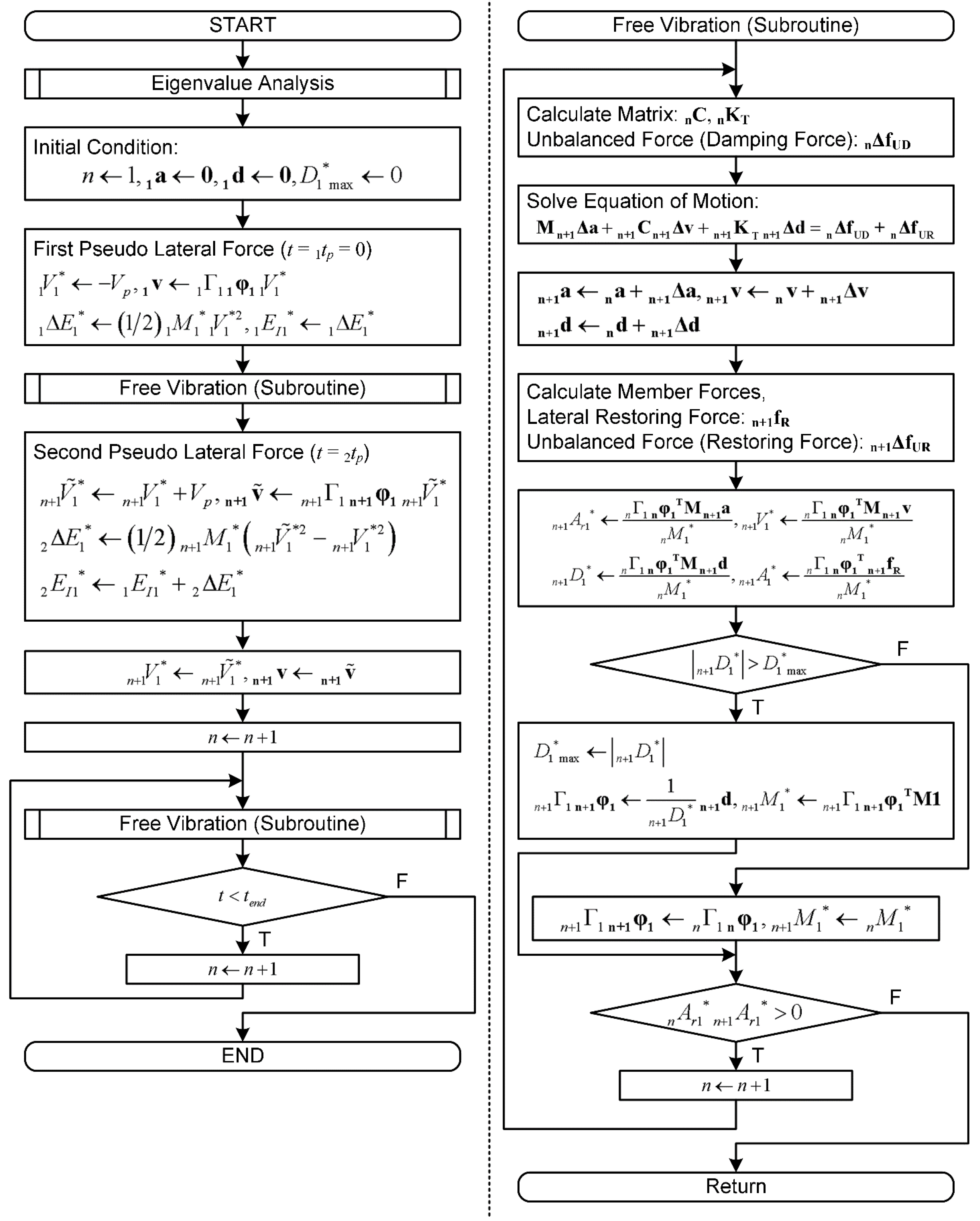
2.1. Outline of the Critical PDI Analysis

Figure 1 outlines the critical PDI analysis. This analysis is based on the studies by Akehashi and Takewaki (2021, 2022), and one modification is made to maintain consistency with the assumptions applied in the procedure (Fujii and Shioda, 2023): in this study, the change in the first mode vector (${\Gamma }_1{\phi }_1$) in the nonlinear range is considered for the calculation of the first modal response at time $t$ and the second pseudo impulsive lateral force.

Consider a planer frame building model (number of stories, $N$) subjected to a pseudo impulsive lateral force proportional to the first mode vector (pulse velocity: $V_p$). Here, $M$ is the mass matrix of the building model; $d\left(t\right)$, $v\left(t\right)$, and $a\left(t\right)$ are the relative displacement, velocity, and acceleration vectors, respectively; and $f_R\left(t\right)$ and $f_D\left(t\right)$ are the restoring force and damping force vectors, respectively. The equivalent displacement (${D_1}^{*}\left(t\right)$), equivalent velocity (${V_1}^{*}\left(t\right)$), and equivalent relative acceleration (${A_{r1}}^{*}\left(t\right)$) of the first modal response are defined as

$${D_1}^{*}\left(t\right)=\frac{{\Gamma }_1{{\phi }_1}^{T}Md\left(t\right)}{{M_1}^{*}},$$

(1)

$${V_1}^{*}\left(t\right)={{\dot{D}}_1}^{*}\left(t\right)=\frac{{\Gamma }_1{{\phi }_1}^{T}Mv\left(t\right)}{{M_1}^{*}},$$

(2)

$${A_{r1}}^{*}\left(t\right)={{\ddot{D}}_1}^{*}\left(t\right)=\frac{{\Gamma }_1{{\phi }_1}^{T}Ma\left(t\right)}{{M_1}^{*}},$$

(3)

$${M_1}^{*}={{\Gamma }_1}^2{{\phi }_1}^{T}M{\phi }_1,$$

(4)

where ${M_1}^{*}$ is the effective first modal mass. Note that ${\Gamma }_1{\phi }_1$ and ${M_1}^{*}$ depend on the local maximum equivalent displacement within the range $\left(0,t\right)$. In this study, the first mode vector at time $t$ is updated assuming that ${\Gamma }_1{\phi }_1$ is proportional to the displacemt vector at the time when the maximum equivalent displacement occurs ($t_{\max }$). The first mode vector at time $t$ is updated such that

$${\Gamma }_1{\phi }_1\leftarrow \frac{1}{{D_1}^{*}\left(t_{\max }\right)}d\left(t_{\max }\right)$$

(5)

The equivalent acceleration ${A_1}^{*}\left(t\right)$ is defined as

$${A_1}^{*}\left(t\right)=\frac{{\Gamma }_1{{\phi }_1}^T{f}_R\left(t\right)}{{M_1}^{*}}.$$

(6)

2.1.1. First pseudo impulsive lateral force

At time $t={{}_{1}t}_p\left({{}_{1}t}_p>0\right)$, the first pseudo impulsive lateral force acts on the building model, as shown in Figure 1. Note that, before the first pseudo impulsive force acts on the building model ($t<{{}_{1}t}_p$), the building model is in the stationary state ($d\left(t\right)=0$, $v\left(t\right)=0$, $a\left(t\right)=0$). The equivalent velocity of the first modal response just after the first pseudo impulsive lateral force acts (${{\tilde{V}}_1}^{*}\left({{}_{1}t}_p\right)$) is calculated such that

$${{\tilde{V}}_1}^{*}\left({{}_{1}t}_p\right)=-V_p,$$

(7)

and the corresponding velocity vector ($\tilde{v}\left({{}_{1}t}_p\right)$) is

$$\tilde{v}\left({{}_{1}t}_p\right)={{}_1\Gamma }_1{{}_1\phi }_1{{\tilde{V}}_1}^{*}\left({{}_{1}t}_p\right)=-{{}_1\Gamma }_1{{}_1\phi }_1{V}_p,$$

(8)

where ${{}_1\Gamma }_1{{}_1\phi }_1$ is the first mode vector at the initial stage. The increment of the input energy of the first modal response (${}_1\Delta {E_1}^{*}$) is calculated such that

$${}_1\Delta {E_1}^{*}=\frac{1}{2}{{{}_{1}M}_1}^{*}{\left\{{{\tilde{V}}_1}^{*}\left({{}_{1}t}_p\right)\right\}}^2=\frac{1}{2}{{{}_{1}M}_1}^{*}{V_p}^2,$$

(9)

where ${{{}_{1}M}_1}^{*}$ is the first modal mass at the initial stage. The cumulative input energy of the first modal response (${{{}_{1}E}_1}^{*}$) is

$${{{}_{1}E}_{I1}}^{*}={}_1\Delta {E_1}^{*}.$$

(10)

To calculate the response following the action of the first pseudo impulsive lateral force, the equivalent velocity (${V_1}^{*}\left(t\right)$) and the velocity vector ($v\left(t\right)$) are updated such that

$${V_1}^{*}\left({{}_{1}t}_p+0\right)\leftarrow {{\tilde{V}}_1}^{*}\left({{}_{1}t}_p\right),v\left({{}_{1}t}_p+0\right)\leftarrow \tilde{v}\left({{}_{1}t}_p\right).$$

(11)

2.1.2. Free vibration after the first pseudo impulsive lateral force

Following the action of the first pseudo impulsive lateral force, the building model oscillates without external forces (free vibration) until the arrival of the second pseudo impulsive lateral force. The kinetic energy, damping dissipated energy, cumulative strain energy, and cumulative input energy of the first modal response (${E_{K1}}^{*}$, ${E_{D1}}^{*}$, ${E_{S1}}^{*}$, and ${E_{I1}}^{*}$, respectively) are expressed as

$${E_{K1}}^{*}\left(t\right)=\frac{1}{2}{M_1}^{*}{\left\{{V_1}^{*}\left(t\right)\right\}}^2,$$

(12)

$${E_{D1}}^{*}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{\Gamma }_1{{\phi }_1}^T{f}_D\left(t\right){V_1}^{*}\left(t\right)dt},$$

(13)

$${E_{S1}}^{*}\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{\Gamma }_1{{\phi }_1}^T{f}_R\left(t\right){V_1}^{*}\left(t\right)dt},$$

(14)

$${E_{I1}}^{*}\left(t\right)=\frac{1}{2}{{{}_{1}M}_1}^{*}{V_p}^2={{{}_{1}E}_{I1}}^{*}.$$

(15)

Because the first pseudo impulsive lateral force is proportional to the first mode vector, the building model oscillates predominantly in the first mode. Therefore, the kinetic energy, damping dissipated energy, cumulative strain energy, and cumulative input energy ($E_K$, $E_D$, $E_S$, and $E_I$, respectively) are approximated as

$$\left\{\begin{array}{l}{E}_K\left(t\right)\approx {E_{K1}}^{*}\left(t\right)\\ E_D\left(t\right)\approx {E_{D1}}^{*}\left(t\right)\\ E_S\left(t\right)\approx {E_{S1}}^{*}\left(t\right)\\ E_I\left(t\right)\approx {E_{I1}}^{*}\left(t\right)\end{array}\right..$$

(16)

Note that the first mode vector (${\Gamma }_1{\phi }_1$) updates any step according to Equation (5) until ${D_1}^{*}\left(t\right)$ reaches its local peak (${{{{}_{1}D}_1}^{*}}_{peak}\left(<0\right)$ shown in Figure 1) and that the effective first modal mass (${M_1}^{*}$) is re-calculated according to Equation (4). The time ${{}_{1}t}_{peak}$ is defined as the time when ${D_1}^{*}\left(t\right)$ reaches ${{{{}_{1}D}_1}^{*}}_{peak}$.

The timing of the second second pseudo impulsive lateral force (${{}_{2}t}_p>{{}_{1}t}_p$) is determined from the following condition:

$${{\dot{V}}_1}^{*}\left({{}_{2}t}_p\right)={A_{r1}}^{*}\left({{}_{2}t}_p\right)=0.$$

(17)

This condition (Equation (17)) is equivalent to the condition of critical timing given by Akehashi and Takewaki (2021, 2022).

2.1.3. Second pseudo impulsive lateral force

At time $t={{}_{2}t}_p$, the second pseudo impulsive lateral force acts on the building model, as shown in Figure 1. The equivalent velocity of the first modal response just after the arrival of the second pseudo impulsive lateral force (${{\tilde{V}}_1}^{*}\left({{}_{2}t}_p\right)$) is calculated such that

$${{\tilde{V}}_1}^{*}\left({{}_{2}t}_p\right)={V_1}^{*}\left({{}_{2}t}_p-0\right)+V_p.$$

(18)

Here, ${V_1}^{*}\left({{}_{2}t}_p-0\right)$ is the equivalent velocity of the first modal response just before the action of the second pseudo impulsive lateral force. Assuming that the velocity vector just prior to the action of the second pseudo impulsive lateral force ($v\left({{}_{2}t}_p-0\right)$) can be approximated by the first modal response, the corresponding velocity vector ($\tilde{v}\left({{}_{2}t}_p\right)$) can be expressed as

$$\tilde{v}\left({{}_{2}t}_p\right)=v\left({{}_{2}t}_p-0\right)+{\Gamma }_1{\phi }_1{V}_p\approx {\Gamma }_1{\phi }_1{{\tilde{V}}_1}^{*}\left({{}_{2}t}_p\right).$$

(19)

The increment of the input energy of the first modal response (${}_2\Delta {E_1}^{*}$) is calculated such that

$${}_2\Delta {E_1}^{*}=\frac{1}{2}{M_1}^{*}\left[{\left\{{{\tilde{V}}_1}^{*}\left({{}_{2}t}_p\right)\right\}}^2-{\left\{{V_1}^{*}\left({{}_{2}t}_p-0\right)\right\}}^2\right]=\frac{1}{2}{M_1}^{*}{V_p}^2\left\{1+\frac{2{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}\right\}$$

(20)

Note that Equation (17) is obtained by differentiating Equation (20) with respect to ${{}_{2}t}_p$ and equating it to zero. Therefore, the timing of the arrival of the second pseudo impulsive lateral force is the timing that maximizes ${}_2\Delta {E_1}^{*}$.

The cumulative input energy of the first modal response immediately following the action of the second pseudo impulsive lateral force (${{{}_{2}E}_{I1}}^{*}$) is calculated such that

$${{{}_{2}E}_{I1}}^{*}={}_1\Delta {E_1}^{*}+{}_2\Delta {E_1}^{*}.$$

(21)

To calculate the response following the action of the second pseudo impulsive lateral force, the equivalent velocity (${V_1}^{*}\left(t\right)$) and the velocity vector ($v\left(t\right)$) are updated such that

$${V_1}^{*}\left({{}_{2}t}_p+0\right)\leftarrow {{\tilde{V}}_1}^{*}\left({{}_{2}t}_p\right),v\left({{}_{2}t}_p+0\right)\leftarrow \tilde{v}\left({{}_{2}t}_p\right).$$

(22)

2.1.4. Free vibration after the second pseudo impulsive lateral force

Following the action of the second pseudo impulsive lateral force, the building model oscillates without external forces (free vibration) until $t=t_{end}$.

The time ${{}_{2}t}_{peak}$ is defined as the time when ${D_1}^{*}\left(t\right)$ reaches its local peak (${{{{}_{2}D}_1}^{*}}_{peak}\left(>0\right)$). The peak equivalent displacement of the first modal response over the course of the entire seismic event (${{D_1}^{*}}_{\max }$) is

$${{D_1}^{*}}_{\max }=\max \left(\left|{{{{}_{1}D}_1}^{*}}_{peak}\right|,\left|{{{{}_{2}D}_1}^{*}}_{peak}\right|\right).$$

(23)

2.2. Momentary Input Energy in the Critical PDI Analysis

Consider the energy response of the equivalent SDOF model representing the first modal response subjected to the ground acceleration ($a_g\left(t\right)$). The cumulative input energy of the first modal response per unit mass over the course of the entire seismic event (${E_{I1}}^{*}/{M_1}^{*}$) is calculated from the time derivative of the equivalent displacement (${{\dot{D}}_1}^{*}\left(t\right)={V_1}^{*}\left(t\right)$) and the ground acceleration ($a_g\left(t\right)$) such that

$$\frac{{E_{I1}}^{*}}{{M_1}^{*}}=-{\displaystyle \underset{0}{\overset{t_{end}}{\int }}{a}_g\left(t\right)}\cdot {{\dot{D}}_1}^{*}\left(t\right)dt=-{\displaystyle \underset{0}{\overset{t_{end}}{\int }}{a}_g\left(t\right)}\cdot {V_1}^{*}\left(t\right)dt.$$

(24)

According to Hori and Inoue (2002), the momentary input energy of the first modal response per unit mass ($\Delta {E_1}^{*}/{M_1}^{*}$) is calculated such that

$$\frac{\Delta {E_1}^{*}}{{M_1}^{*}}=-{\displaystyle \underset{t}{\overset{t+\Delta t}{\int }}{a}_g\left(t\right)}\cdot {V_1}^{*}\left(t\right)dt.$$

(25)

In Equation (25), $t$ and $t+\Delta t$ are the beginning and ending times of a half cycle of the structural response, respectively. The maximum momentary input energy per unit mass ($\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$) is defined as the maximum value of $\Delta {E_1}^{*}/{M_1}^{*}$ over the course of the entire seismic event.

Following the study by Kojima and Takewaki (2015a), the ground acceleration ($a_g\left(t\right)$) in the case of a critical DI analysis can be written as

$$a_g\left(t\right)=V_p\left\{\delta \left(t-{{}_{1}t}_p\right)-\delta \left(t-{{}_{2}t}_p\right)\right\}.$$

(26)

In Equation (26), $\delta \left(·\right)$ is the Dirac delta function, which satisfies

$$\left.\begin{array}{l}\delta \left(t\right)=\underset{\epsilon \to +0}{\lim }\left\{\begin{array}{cc}0& \left|t\right|>\epsilon \\ \frac{1}{2\epsilon }& \left|t\right|\le \epsilon \end{array}\right.\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta \left(t\right)dt}=1\\ {\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\delta \left(t\right)f\left(t\right)dt}=f\left(0\right)\end{array}\right\}.$$

(27)

Next, the momentary input energy of the first modal response per unit mass at the first and second half cycles ${}_1\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ and ${}_2\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ respectively) are calculated from Equations (25) and (26). Assuming that the intervals of the first and second half cycles of the structural response are $\left[0,{{}_{1}t}_{peak}\right]$ and $\left[{{}_{1}t}_{peak},{{}_{2}t}_{peak}\right]$, respectively, as shown in Figure 1, ${}_1\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ and ${}_2\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$can be calculated such that

$${}_1\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)=-{\displaystyle \underset{0}{\overset{{{}_{1}t}_{peak}}{\int }}{a}_g\left(t\right)}\cdot {V_1}^{*}\left(t\right)dt,$$

(28)

$${}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)=-{\displaystyle \underset{{{}_{1}t}_{peak}}{\overset{{{}_{2}t}_{peak}}{\int }}{a}_g\left(t\right)}\cdot {V_1}^{*}\left(t\right)dt.$$

(29)

Note that, in Equation (28), the interval of integration is changed from $\left[{{}_{1}t}_p,{{}_{1}t}_{peak}\right]$ to $\left[0,{{}_{1}t}_{peak}\right]$ to calculate the integrals that contain the Dirac delta fuction. To calculate Equations (28) and (29), the equivalent velocities (${V_1}^{*}\left(t\right)$) at times $t={{}_{1}t}_p$ and $t={{}_{2}t}_p$ are rewritten as

$${V_1}^{*}\left({{}_{1}t}_p\right)=\frac{1}{2}\left\{{V_1}^{*}\left({{}_{1}t}_p-0\right)+{V_1}^{*}\left({{}_{1}t}_p+0\right)\right\}=-\frac{1}{2}{V}_p,$$

(30)

$${V_1}^{*}\left({{}_{2}t}_p\right)=\frac{1}{2}\left\{{V_1}^{*}\left({{}_{2}t}_p-0\right)+{V_1}^{*}\left({{}_{2}t}_p+0\right)\right\}={V_1}^{*}\left({{}_{2}t}_p-0\right)+\frac{1}{2}{V}_p.$$

(31)

Therefore, ${}_1\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ and ${}_2\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ can be calculated such that

$${}_1\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)=-V_p\cdot {V_1}^{*}\left({{}_{1}t}_p\right)=\frac{1}{2}{V_p}^2,$$

(32)

$${}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)=-\left(-V_p\right)\cdot {V_1}^{*}\left({{}_{2}t}_p\right)=\frac{1}{2}{V_p}^2\left\{1+\frac{2{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}\right\}.$$

(33)

The calculated ${}_1\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ and ${}_2\left(\Delta {E_1}^{*}/{M_1}^{*}\right)$ shown in Equations (32) and (33) are consistent with the above-shown increments of the energy input (Equations (9) and (20), respectively). This implies that, in the case of a critical PDI analysis, the momentary input energy is calculated as the increment of the energy input as a result of the pseudo impulsive lateral force.

The maximum momentary input energy of the first modal response per unit mass ($\Delta {{E_1}^{*}}_{\max }/{M_1}^{*}$) is obtained such that

$$\frac{\Delta {{E_1}^{*}}_{\max }}{{M_1}^{*}}=\max \left\{{}_1\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right),{}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)\right\}={}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)=\frac{1}{2}{V_p}^2\left\{1+\frac{2{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}\right\}$$

(34)

The cumulative input energy of the first modal response per unit mass (${E_{I1}}^{*}/{M_1}^{*}$) is calculated such that

$$\frac{{E_{I1}}^{*}}{{M_1}^{*}}={}_1\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)+{}_2\left(\frac{\Delta {E_1}^{*}}{{M_1}^{*}}\right)={V_p}^2\left\{1+\frac{{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}\right\}.$$

(35)

The equivalent velocity of the maximum momentary input energy of the first modal response (${V_{\Delta E1}}^{*}$) is calculated such that

$${V_{\Delta E1}}^{*}=\sqrt{\frac{2\Delta {{E_1}^{*}}_{\max }}{{M_1}^{*}}}=V_p\sqrt{1+\frac{2{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}}.$$

(36)

Similarly, the equivalent velocity of the cumulative input energy of the first modal response (${V_{I1}}^{*}$) is calculated such that

$${V_{I1}}^{*}=\sqrt{\frac{2{E_{I1}}^{*}}{{M_1}^{*}}}=\sqrt{2}\cdot V_p\sqrt{1+\frac{{V_1}^{*}\left({{}_{2}t}_p-0\right)}{V_p}}.$$

(37)

In this study, the response period of the first modal response ($T_{1res}$) is defined as twice the interval between the two local peaks (${{{{}_{1}D}_1}^{*}}_{peak}$ and ${{{{}_{2}D}_1}^{*}}_{peak}$) such that

$$T_{1res}=2\Delta t=2\left({{}_{2}t}_{peak}-{{}_{1}t}_{peak}\right).$$

(38)

2.3. Analysis Flow

Figure 2 shows the flow of the critical PDI analysis. In this flow, the damping force increment resulting from the velocity vector changing at analysis step $n$ (${}_{n}v$) is treated as the unbalanced force to be corrected in the next step. In addition, the timing of the second pseudo impulsive lateral force is determined by checking the sign of the equivalent relative acceleration (${{{}_{n}A}_{r1}}^{*}$). The timing of the second pseudo impulsive lateral force is determined according the following condition:

$${{{}_{n}A}_{r1}}^{*}{{{}_{n+1}A}_{r1}}^{*}\le 0.$$

(39)

When Equation (39) is satisfied, the second pseudo impulsive lateral force acts.

The analysis procedure was implemented in the computer code used in the previous analysis (Fujii and Miyagawa, 2018).

3. Analysis Data and Methods

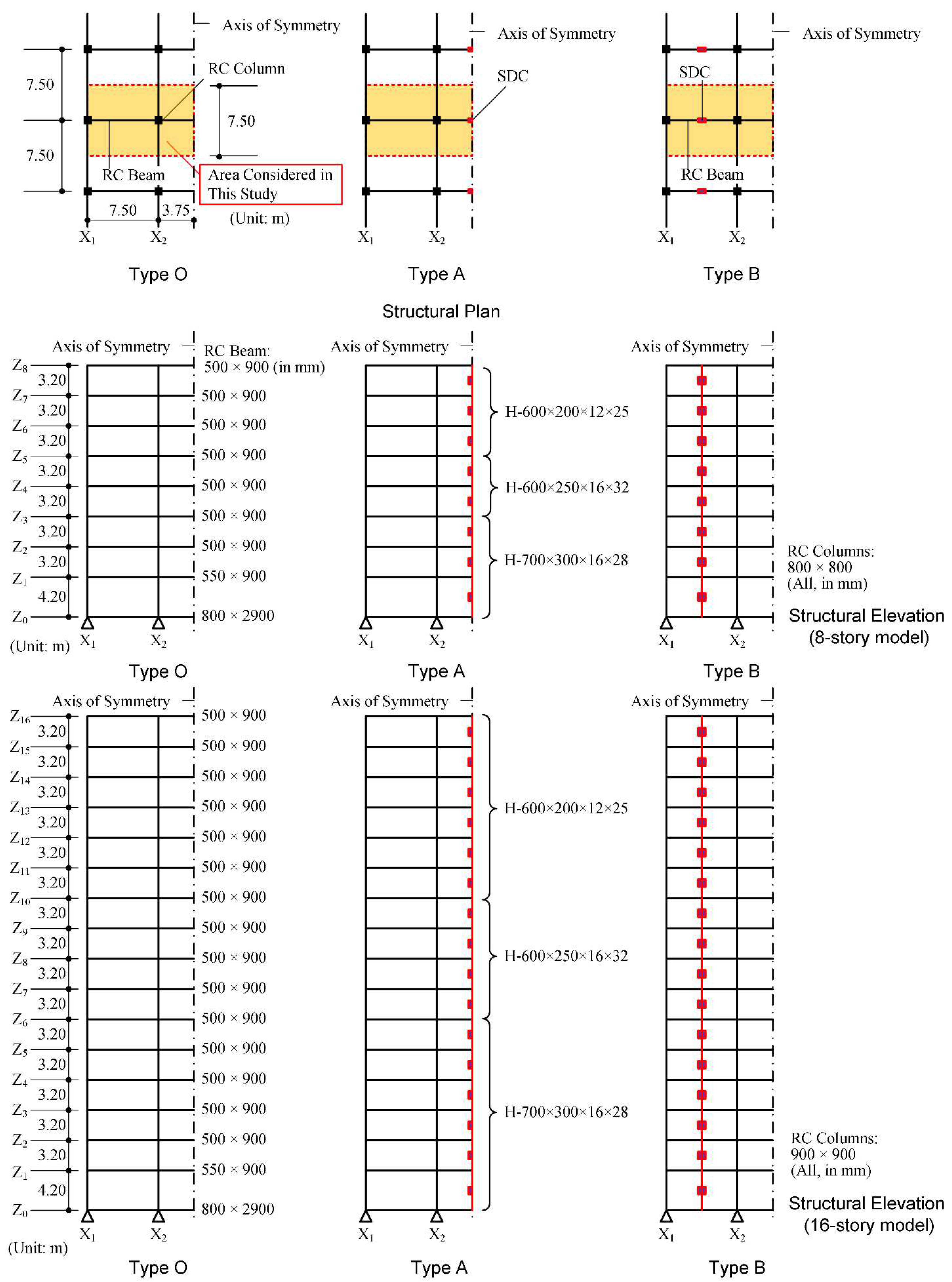
3.1. Building Data

The six planar building models analyzed in this study are 8- and 16-story RC MRFs with and without SDCs. Figure 3 shows the simplified plans and elevations of the RC MRF building models. The two models labeled Type B are the same as those used in the previous study (Fujii and Shioda, 2023). Meanwhile, the two models made from the Type B models by removing all SDCs are referred to as Type O. The models referred to as Type A were made from the Type B models by reducing the number of SDCs. All RC MRFs analyzed herein were designed according to the strong-column/weak-beam concept, except for the foundation level beam and in the case of SDCs installed in an RC frame. In the latter case, at the joints between an RC beam and a steel damper column, the RC beam was designed to be sufficiently stronger than the yield strength of the steel damper column considering strain hardening. Sufficient shear reinforcement of all RC members was provided to prevent premature shear failure. The failure of the beam–column joints was not considered because it was assumed that sufficient reinforcement was provided. The natural periods of the first modal response in the elastic range ($T_{1e}$) of the 8-story models are 0.740 s, 0.627 s, and 0.561 s for the Type O, A, and B models, respectively. Similarly, the $T_{1e}$ values of the 16-story models are 1.41 s, 1.21 s, and 1.12 s for the Type O, A, and B models, respectively.

The nonlinear behavior of the RC members and SDCs was modeled as in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023), except for the hysteresis rule used for the SDCs. Figure 4 shows the hysteresis rule. The same hysteresis model (stiffness degradation model) was used for the flexural springs in the RC members. Meanwhile, for the damper panel in the SDCs, two hysteresis models were considered to investigate the influence of strain hardening on the energy response. The first model was the normal bilinear model (LB); its yield strength is set to the initial yielding strength of the damper panel ($Q_{yDL}$), and the strain hardening effect is neglected. The second model was the trilinear model used in previous studies (Mukoyama et al., 2021; Fujii, 2022; Fujii and Shioda, 2023) with the strain-hardening effect (SH); its upper bound strength ($Q_{yDU}$) was set such that the ratio $Q_{yDU}/Q_{yDL}$ equaled 300/205 = 1.46. Other details concerning the six structural models can be found in previous studies (Fujii, 2022; Fujii and Shioda, 2023). In this study, the viscous damping ratio of the first modal response of the RC MRFs in the elastic range ($h_{1f}$) was set to 0.03.

Figure 5 shows the equivalent acceleration–equivalent displacement relationships of the six models. In this study, a displacement-based mode-adaptive pushover (DB-MAP) analysis (Fujii, 2014) was applied to obtain the relationship between the equivalent acceleration (whole building: ${A_1}^{*}$, RC MRF: ${A_{1f}}^{*}$, and SDCs: ${A_{1d}}^{*}$) and the equivalent displacement (${D_1}^{*}$). The pushover analyses were performed until the equivalent displacement (${D_1}^{*}$) reached 1/75 of the assumed equivalent height (${H_1}^{*}$): the assumed ${H_1}^{*}$ values were 18.9 m and 35.9 m for the 8- and 16-story models, respectively. The target equivalent displacement for the pushover analysis was 0.252 m for the 8-story model, while that for the 16-story model was 0.479 m. Note that, in the pushover analyses of the Type A and B models, the influence of the strain hardening of the SDCs was neglected. The idealized ${A_1}^{*}$–${D_1}^{*}$ curves for the Type O models and the idealized ${A_{1f}}^{*}$–${D_1}^{*}$ and ${A_{1d}}^{*}$–${D_1}^{*}$ curves for the Type A and B models are shown in Figure 5. The values of ${D_1}^{*}$ and ${A_1}^{*}$ at the “yield point” ($\left({D_{1yf}}^{*},{A_{1yf}}^{*}\right)$ for RCF and $\left({D_{1yd}}^{*},{A_{1yd}}^{*}\right)$ for SDC) are also shown. The bilinear idealization of each curve was performed following the methods shown in Fujii (2022).

The following observations can be drawn from Figure 5.

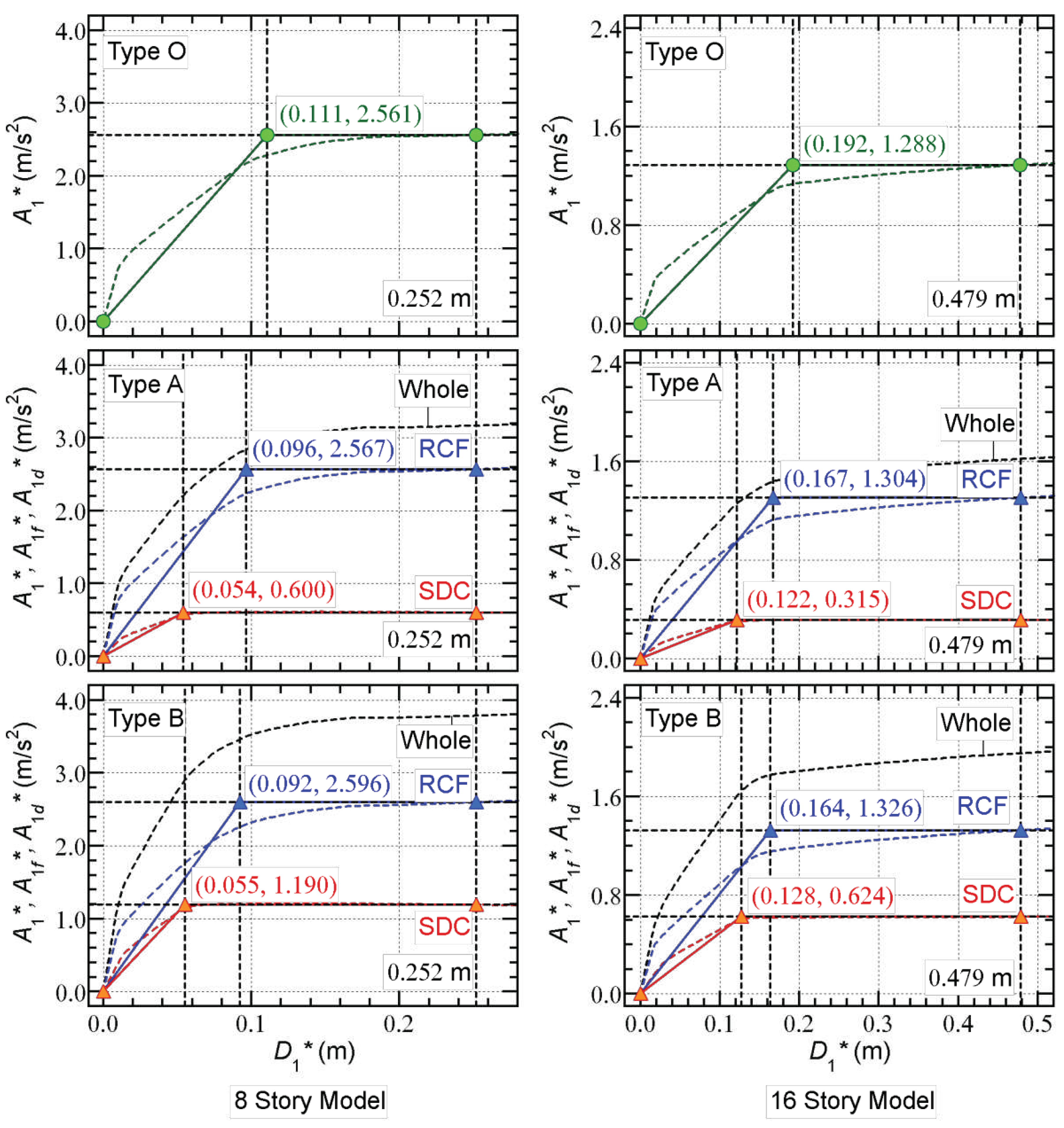
• The “yield displacement” of RCF (${D_{1yf}}^{*}$) in Type A and B models is smaller than that in Type O models. The equivalent drift ratio at the “yielding of RCF” (${D_{1yf}}^{*}/{H_1}^{*}$) of the Type O 8-story model is 1/170, while those of the Type A and B models are 1/196 and 1/205, respectively. Similarly, the ratio ${D_{1yf}}^{*}/{H_1}^{*}$ of the Type O 16-story model is 1/187, while those of the Type A and B models are 1/215 and 1/218, respectively. This is because of the shortening of the beam span resulting from the presence of the SDCs.
• The “yield acceleration” of RCF (${A_{1yf}}^{*}$) in the Type A and B models is nearly the same as that in the Type O models. In case of the 8-story models, the ${A_{1yf}}^{*}$ values of the Type O, A, and B models are 2.561 m/s², 2.567 m/s², and 2.596 m/s², respectively. Similarly, in the case of the 16-story models, the ${A_{1yf}}^{*}$ values of the Type O, A, and B models are 1.288 m/s², 1.304 m/s², and 1.326 m/s², respectively.
• The “yield acceleration” of SDC (${A_{1yd}}^{*}$) in the Type B models is approximately twice of that in the Type A models. The ratio of the “yield acceleration” of SDC to that of RCF (${A_{1yd}}^{*}/{A_{1yf}}^{*}$) of the Type A 8-story model is 0.234, while that of the Type B model is 0.458. Similarly, the ${A_{1yd}}^{*}/{A_{1yf}}^{*}$ ratio of the Type A 16-story model is 0.242, while that of the Type B model is 0.471.
• The ratio of the “yield displacement” of SDC to that of RCF (${D_{1yd}}^{*}/{D_{1yf}}^{*}$) of the 8-story models is smaller than that of the 16-story models. For the 8-story models, the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratios of the Type A and B models are 0.563 and 0.598, respectively. Meanwhile for the 16-story models, the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratios of the Type A and B models are 0.731 and 0.780, respectively.

Note that the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratio influences the effectiveness of the SDCs with respect to seismic energy absorption. This is discussed in the analysis results.

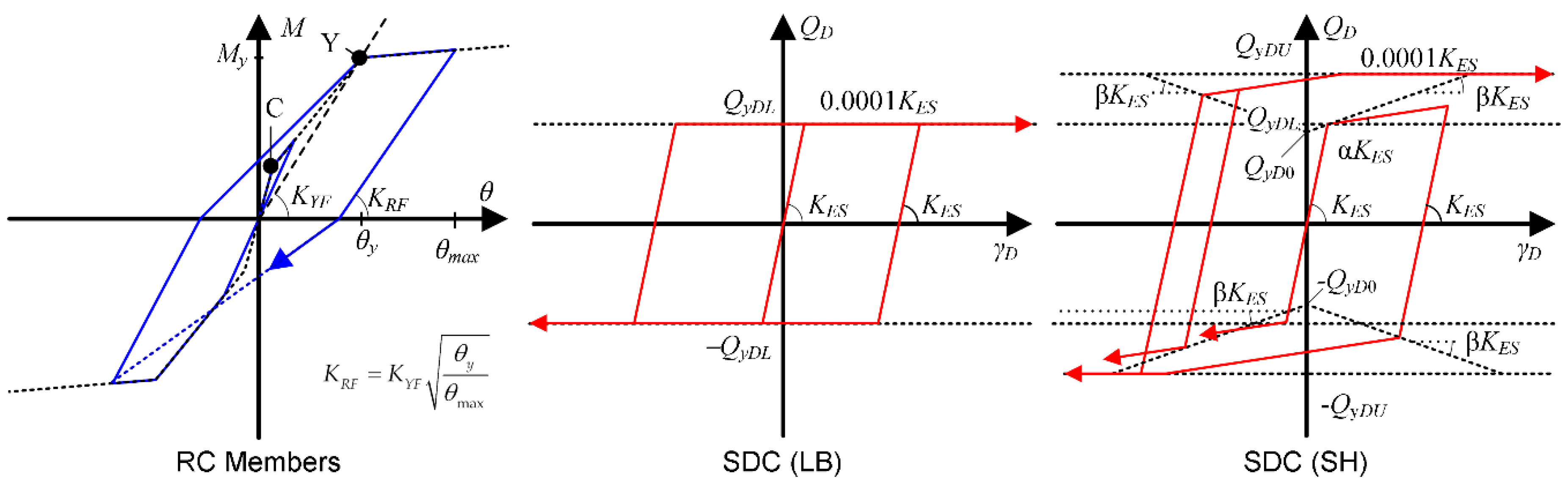
3.2. Analysis Method

In this study, the pulse velocity ($V_p$) was set from 0.10 m/s, with an interval of 0.05 m/s, until ${{D_1}^{*}}_{\max }$ was close to 1/75 of the assumed equivalent height (${H_1}^{*}$). In each analysis, the ending time of the analysis ($t_{end}$) was determined as the ending of the 32^nd half cycle of free vibration following the action of the second pseudo impulsive lateral force.

4. Analysis Results

In this section, the responses of the building models subjected to a pseudo impulsive lateral force proportional to the first mode vector are compared and discussed. For the Type A and B models, only the results considering strain hardening are shown here.

4.1. Response of the Overall Building Model

Figure 6 compares the relationships between the seismic intensity parameters ($V_p$, ${V_{I1}}^{*}$, and ${V_{\Delta E1}}^{*}$) and the peak equivalent displacement (${{D_1}^{*}}_{\max }$).

The following conclusions can be drawn from Figure 6.

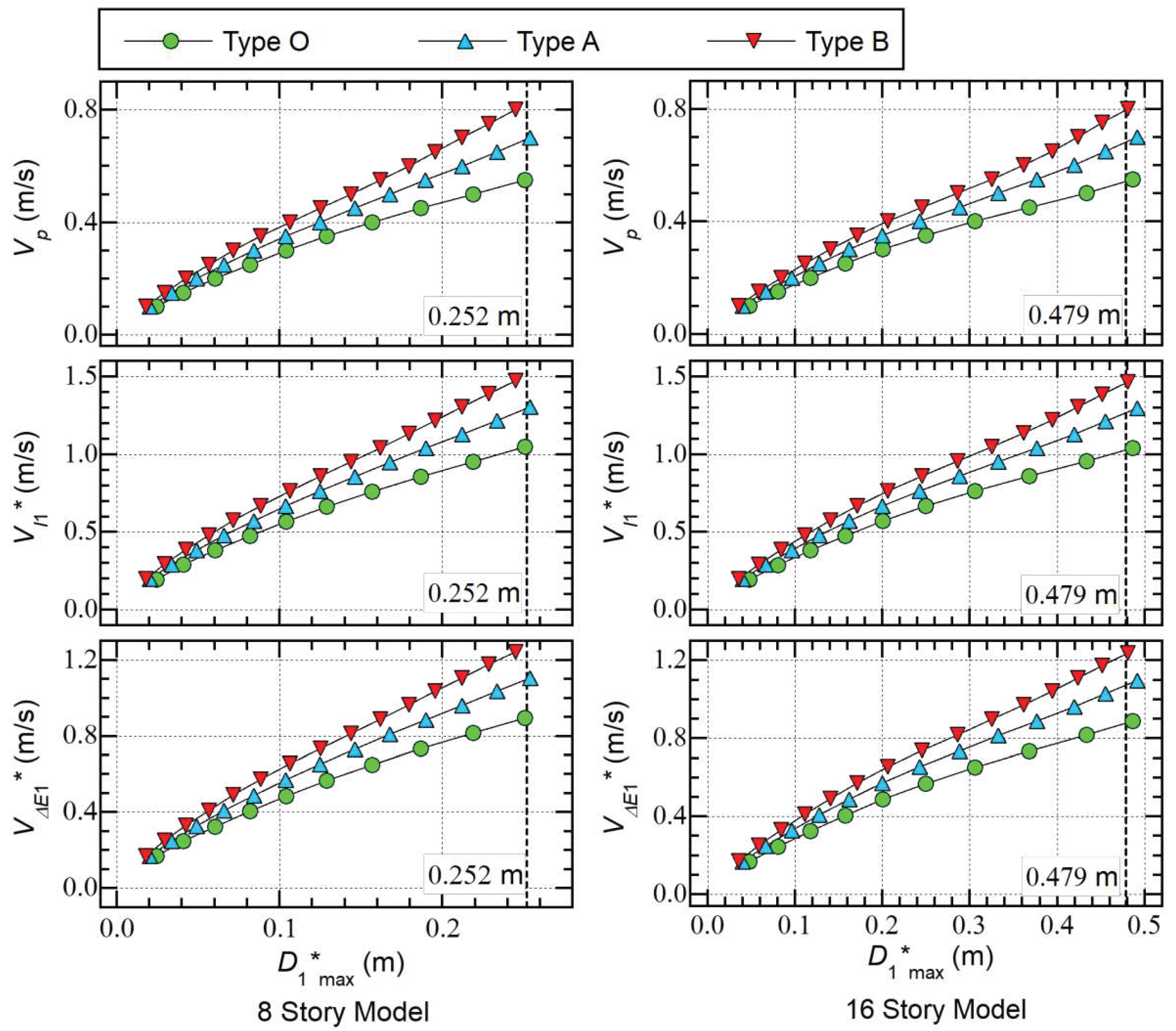
• The seismic intensity parameters ($V_p$, ${V_{I1}}^{*}$, and ${V_{\Delta E1}}^{*}$) increase as ${{D_1}^{*}}_{\max }$ increases. The ${V_{I1}}^{*}$–${{D_1}^{*}}_{\max }$ and ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ curves are very similar to the $V_p$–${{D_1}^{*}}_{\max }$ curve of the same model: the ${V_{I1}}^{*}/V_p$ ratio ranges from 1.8 to 2.0, while the ${V_{\Delta E1}}^{*}/V_p$ ratio ranges from 1.5 to 1.7. The differences in the ${V_{I1}}^{*}/V_p$ and ${V_{\Delta E1}}^{*}/V_p$ ratios between models are very small.
• For the same value of $V_p$, the ${{D_1}^{*}}_{\max }$ values of the Type B models are the smallest while those of the Type O models are the largest. Comparing the ${{D_1}^{*}}_{\max }$ values of the 8-story models considering the case where $V_p$ = 0.55 m/s, the ${{D_1}^{*}}_{\max }$ value for the Type O models is 0.252 m, while those for the Type A and B models are 0.190 m (−24.6 %) and 0.162 m (−35.7 %), respectively. Similarly, comparing the ${{D_1}^{*}}_{\max }$ values of the 16-story models considering the case where $V_p$ = 0.55 m/s, the ${{D_1}^{*}}_{\max }$ value for the Type O models is 0.487 m, while those for the Type A and B models are 0.377 m (−22.6 %) and 0.325 m (−33.3 %), respectively.

Figure 7 compares the ratios of the cumulative energy at the end of the simulation ($t=t_{end}$), i.e., the ratios of the kinetic energy ($E_K/E_I$), damping dissipated energy ($E_D/E_I$), cumulative strain energy of the RC MRF ($E_{Sf}/E_I$), and cumulative strain energy of the SDCs ($E_{Sd}/E_I$). In this figure, the vertical dotted lines indicate the “yield displacement” of the SDCs (${D_{1yd}}^{*}$) and the RC MRF (${D_{1yf}}^{*}$).

The following conclusions can be drawn from Figure 7.

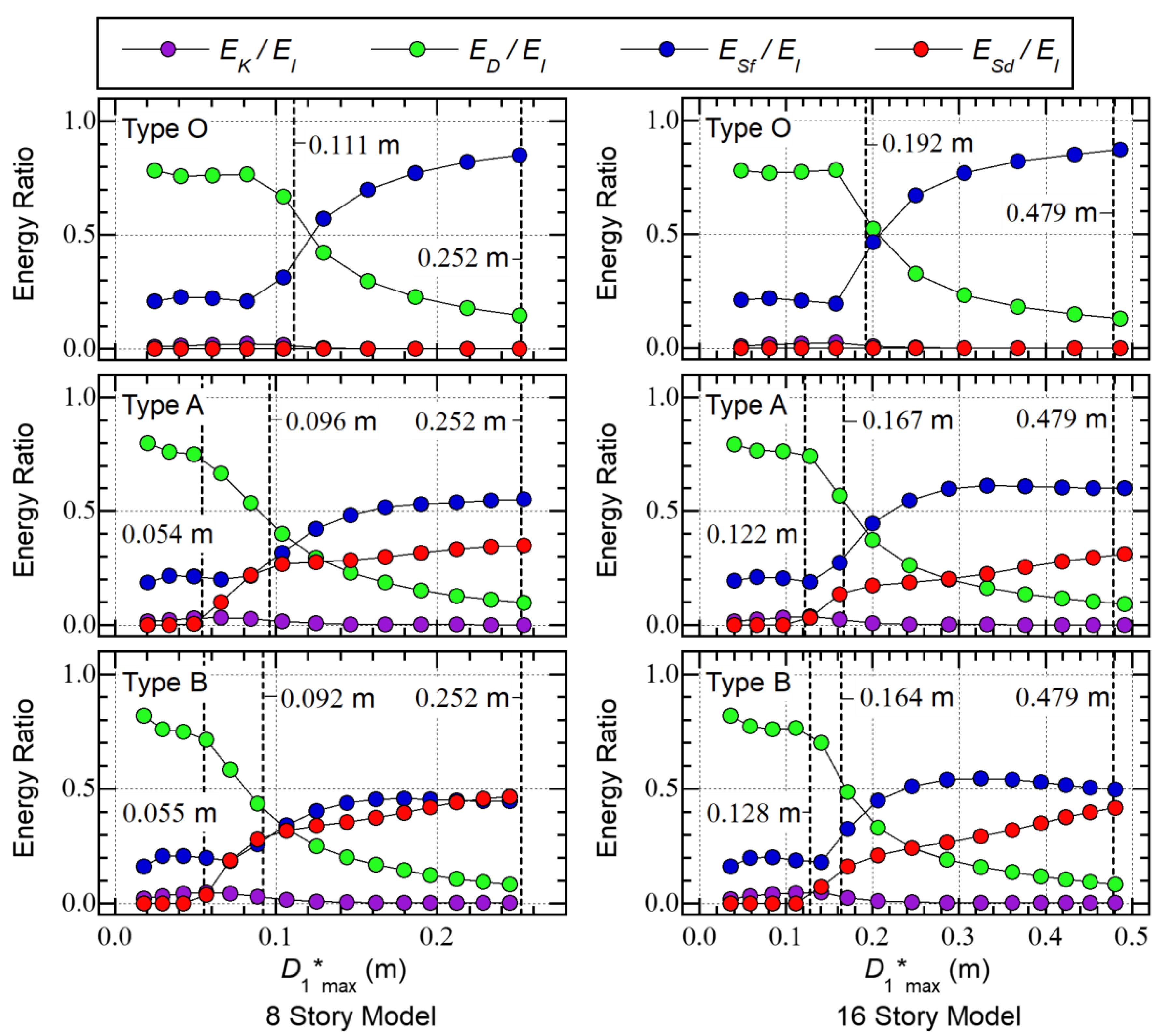
• In all cases, the ratio of the kinetic energy ($E_K/E_I$) is close to zero.
• For the Type O 8-story model, the $E_D/E_I$ ratio is close to 0.8 when ${{D_1}^{*}}_{\max }$ is smaller than 0.111 m (= ${D_{1yf}}^{*}$). Meanwhile, the $E_D/E_I$ ratio decreases and the $E_{Sf}/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.111 m. When ${{D_1}^{*}}_{\max }$ is 0.251 m, $E_D/E_I$ is 0.148 while $E_{Sf}/E_I$ is 0.852. Because no SDCs are installed in the Type O models, the $E_{Sd}/E_I$ ratio is zero.
• For the Type A 8-story model, the $E_{Sd}/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.054 m (= ${D_{1yd}}^{*}$). The $E_{Sf}/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.096 m (= ${D_{1yf}}^{*}$). Meanwhile, the $E_D/E_I$ ratio decreases as ${{D_1}^{*}}_{\max }$ increases. When ${{D_1}^{*}}_{\max }$ is 0.254 m, $E_D/E_I$ is 0.097 while $E_{Sf}/E_I$ is 0.553 and $E_{Sd}/E_I$ is 0.350.
• For the Type B 8-story model, similar observations can be made as for the Type A 8-story model. When ${{D_1}^{*}}_{\max }$ is 0.250 m, $E_D/E_I$ is 0.084 while $E_{Sf}/E_I$ is 0.447 and $E_{Sd}/E_I$ is 0.467.
• For the Type O 16-story model, similar observations can be made as for the Type O 8-story model. When ${{D_1}^{*}}_{\max }$ is 0.487 m, $E_D/E_I$ is 0.129 while $E_{Sf}/E_I$ is 0.871. Because no SDCs are installed in the Type O models, the $E_{Sd}/E_I$ ratio is zero.
• For the Type A 16-story model, the $E_{Sd}/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is larger than 0.122 m (= ${D_{1yd}}^{*}$). The $E_{Sf}/E_I$ ratio increases as ${{D_1}^{*}}_{\max }$ increases when ${{D_1}^{*}}_{\max }$ is between 0.167 m (= ${D_{1yf}}^{*}$) and 0.332 m. However, the $E_{Sf}/E_I$ ratio is nearly constant when ${{D_1}^{*}}_{\max }$ is larger than 0.332 m. When ${{D_1}^{*}}_{\max }$ is 0.492 m, $E_D/E_I$ is 0.091 while $E_{Sf}/E_I$ is 0.600 and $E_{Sd}/E_I$ is 0.310.
• For the Type B 16-story model, similar observations can be made as for the Type A 16-story model. When ${{D_1}^{*}}_{\max }$ is 0.480 m, $E_D/E_I$ is 0.084 while $E_{Sf}/E_I$ is 0.499 and $E_{Sd}/E_I$ is 0.417.

The differences in the $E_{Sd}/E_I$ ratios for the 8- and 16-story models can be explained by the diffrences in the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratios shown in Figure 5. As shown in Figure 5, the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratios in the 8-story models are 0.563 (Type A) and 0.598 (Type B), while those in the 16-story models are 0.731 (Type A) and 0.780 (Type B). Therefore, the effectiveness of the SDCs in 8-story models is better than that in 16-story models because the ${D_{1yd}}^{*}/{D_{1yf}}^{*}$ ratio is smaller for the 8-story models than for the 16-story models.

Figure 8 shows the hysteresis loops of the first modal response (the ${A_1}^{*}\left(t\right)$–${D_1}^{*}\left(t\right)$ relationship) for each model. In this figure, the points at which the first and second pseudo impulsive lateral forces act (${}_1\Delta {E_1}^{*}$ and ${}_2\Delta {E_1}^{*}$, respectively), and the points of the local peak responses (${{{{}_{1}D}_1}^{*}}_{peak}$ and ${{{{}_{2}D}_1}^{*}}_{peak}$, respectively) are shown. The ${A_1}^{*}$–${D_1}^{*}$ curves obtained from the pushover analysis results (as in Figure 5) are also shown Figure 8.

The following conclusions can be drawn from Figure 8.

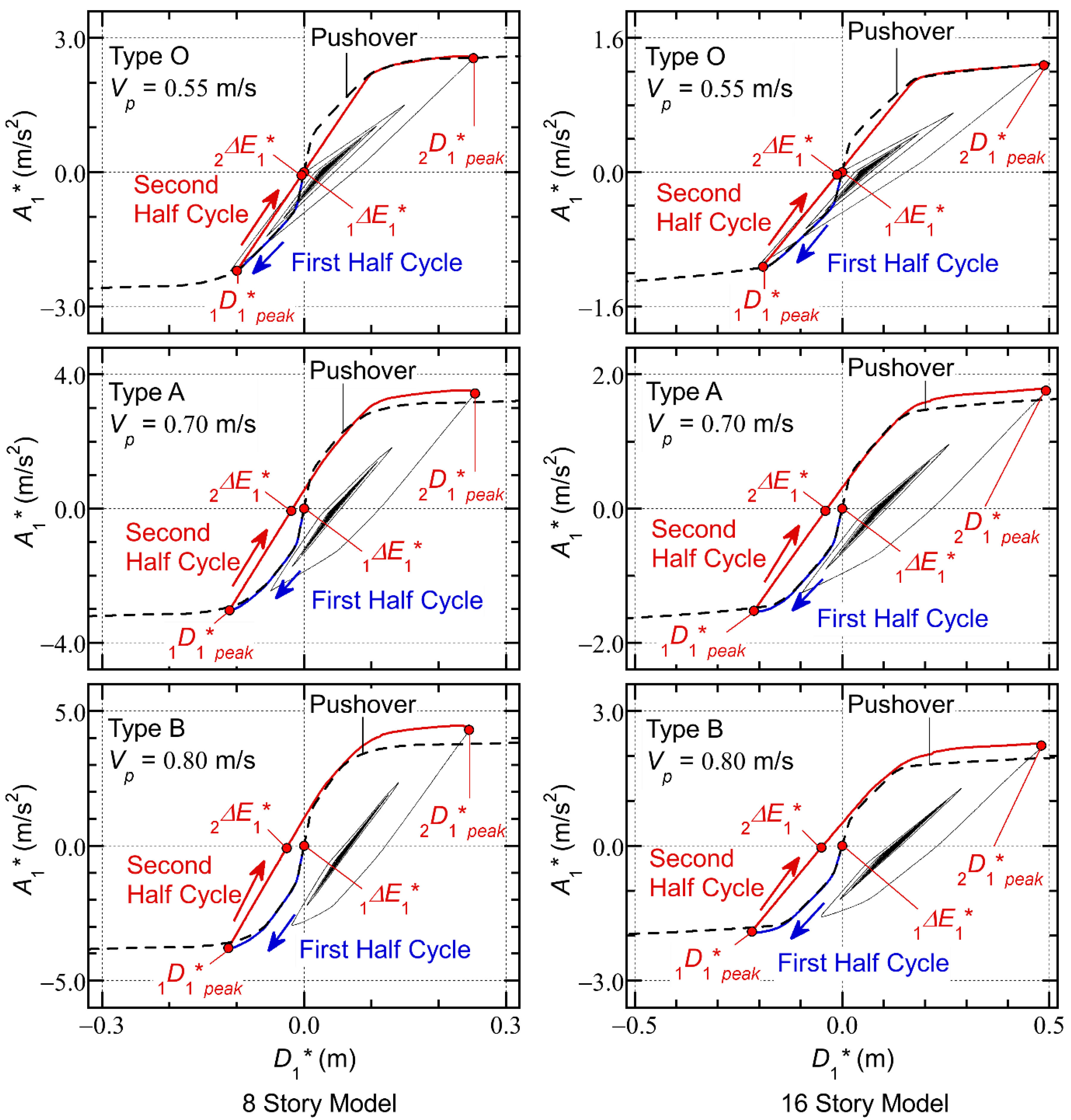
• In all models, larger equivalent displacements occur in the positive direction: $\left|{{{{}_{2}D}_1}^{*}}_{peak}\right|$ is larger than $\left|{{{{}_{1}D}_1}^{*}}_{peak}\right|$. This means that the peak equivalent displacement of the first modal response over the course of the entire seismic event (${{D_1}^{*}}_{\max }$) occurs at the end of the second half cycle of the response, where the momentary energy input ${}_2\Delta {E_1}^{*}$ occurs.
• For the Type O models (both 8- and 16-story), the ${A_1}^{*}$–${D_1}^{*}$ curves obtained from the pushover analysis results (black dotted curve) agree very well with the hysteresis loops obtained via the critical PDI analyses: the points at the local peak response (${{{{}_{1}D}_1}^{*}}_{peak}$ and ${{{{}_{2}D}_1}^{*}}_{peak}$) are on the ${A_1}^{*}$–${D_1}^{*}$ curves obtained from the pushover analysis results.
• For the Type A and B models (both 8- and 16-story), the ${A_1}^{*}$–${D_1}^{*}$ curves obtained from the pushover analyses are slightly different from the hysteresis loops obtained via the critical PDI analyses: the points at the second local peak response (${{{{}_{2}D}_1}^{*}}_{peak}$) are above the ${A_1}^{*}$–${D_1}^{*}$ curve obtained from the pushover analysis results. For the 8-story models, the ratios of the ${A_1}^{*}$ values obtained from the critical PDI analysis and the pushover analysis at the point ${{{{}_{2}D}_1}^{*}}_{peak}$ are 1.086 for the Type A model and 1.141 for the Type B models. Similary, for the 16-story models, the ratios of the ${A_1}^{*}$ values from the critical PDI analysis and the pushover analysis are 1.083 for the Type A model and 1.149 for the Type B model.

Figure 9 shows the ratio of the energy input (${\eta }_E$) to the local peak equivalent displacement (${\eta }_D$). Here, the ${\eta }_E$ ratio is defined as

$${\eta }_E={}_1\Delta {E_1}^{*}/{}_2\Delta {E_1}^{*}.$$

(40)

The ${\eta }_E$ ratio is 1/3 if the structure exhibits undamped linear elastic behavior. Meanhile, the ${\eta }_E$ ratio is 1 if the structure exhibits rigid–perfectly plastic behavior, that is, no strain energy is released after the first local peak (${{{{}_{1}D}_1}^{*}}_{peak}$) occurs.

The ${\eta }_D$ ratio is defined as

$${\eta }_D=\left|{{{{}_{1}D}_1}^{*}}_{peak}/{{{{}_{2}D}_1}^{*}}_{peak}\right|.$$

(41)

The ${\eta }_D$ ratio is 0.5 if the structure exhibitis undamped linear elastic behavior. Meanwhile, the ${\eta }_D$ ratio is 1 if the structural response is symmetric in the positive and negative directions.

The following conclusions can be drawn from Figure 9.

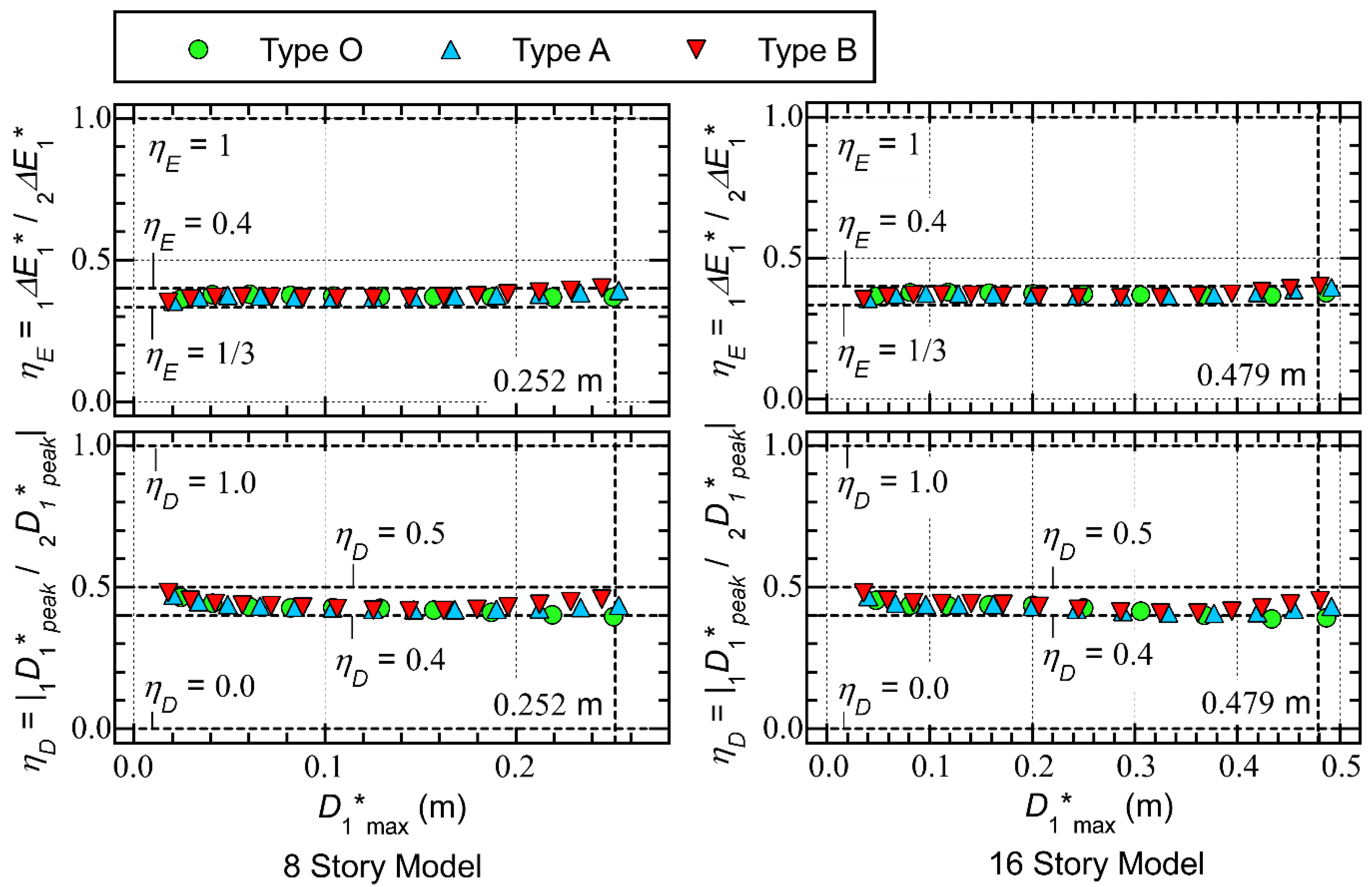
• In all models, the ${\eta }_E$ ratio is nearly constant: most of the plots are distributed within a narrow range between 1/3 and 0.4.
• In all models, the ${\eta }_D$ ratio is nearly constant: most of the plots are distributed within a narrow range between 0.4 and 0.5.

Figure 10 shows the response periods of the first modal response ($T_{1res}$) and the ratios of the effective period of the first modal response ($T_{1eff}$) and the response period ($T_{1res}$). Here, $T_{1eff}$ is defined as in Fujii and Shioda (2023) as

$$T_{1eff}=2\pi \sqrt{\frac{4+7\pi \beta }{6}}\frac{{{D_1}^{*}}_{\max }}{{V_{\Delta E1}}^{*}}.$$

(42)

In Equation (42), $\beta$ is the complex damping ratio of the equivalent linear system. Here, $\beta$ is set to 0.10.

The following conclusions can be drawn from Figure 10.

• In all models, $T_{1res}$ increases as ${{D_1}^{*}}_{\max }$ increases.
• When comparing $T_{1res}$ in the case of similar ${{D_1}^{*}}_{\max }$, $T_{1res}$ of the Type O models is the largest while that of the Type B models is the smallest. This means that $T_{1res}$ becomes smaller as the number of SDCs increases.
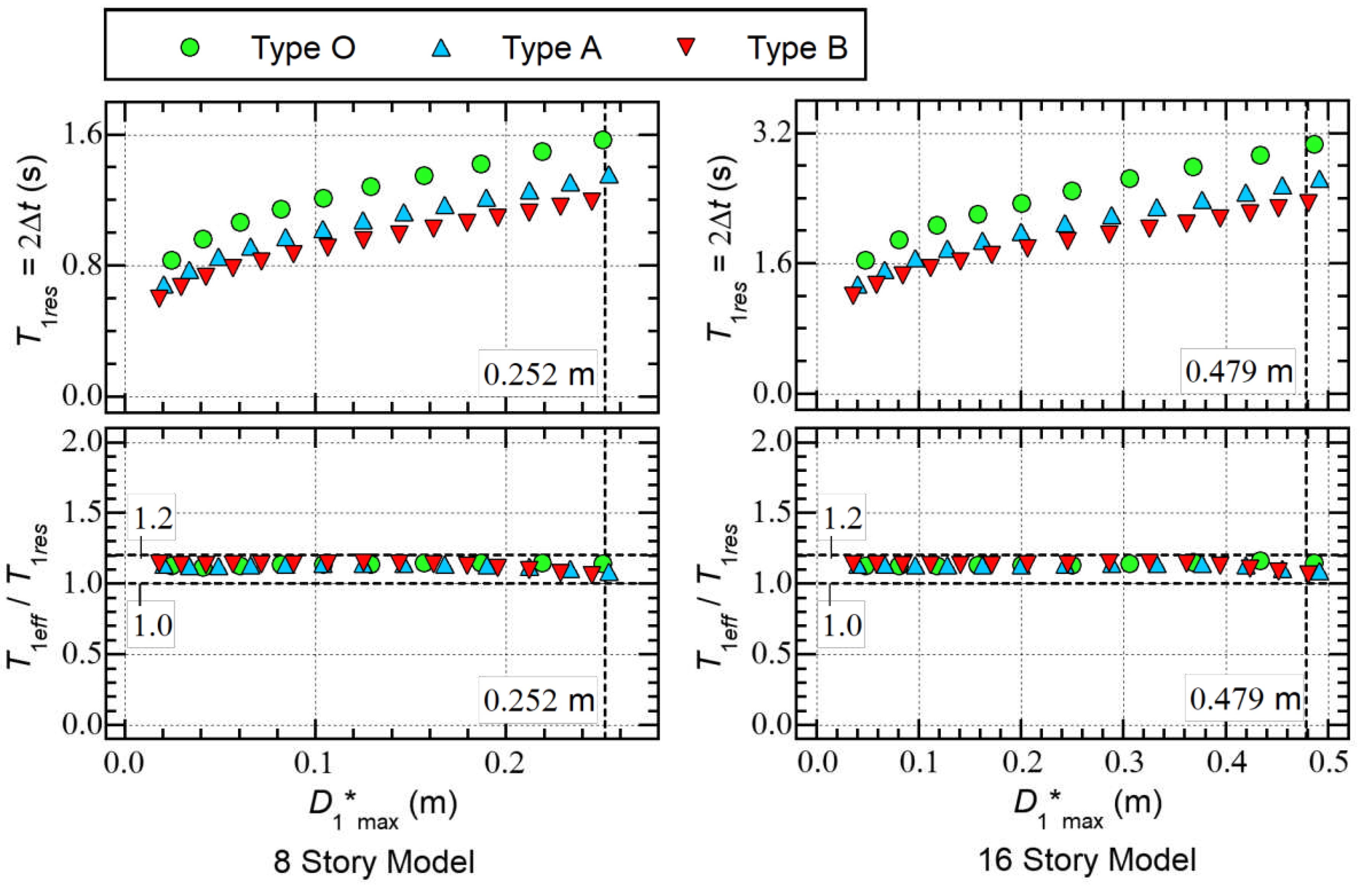
• In all models, the $T_{1eff}/T_{1res}$ ratio is nearly constant: all of the plots are distributed within a narrow range between 1.0 and 1.2.

4.2. Local Response

Figure 11 compares the peak responses of all model types for $V_p$ = 0.55 m/s. The following local response quantities are compared: (i) the peak relative displacement; (ii) the peak story drift; (iii) the peak plastic rotation at the beam end (${\theta }_{p\max }$); and (iv) the peak shear strain of the damper panel (${\gamma }_{D\max }$). Note that, because the span length is different due to the presence of SDCs, ${\theta }_{p\max }$ for the beam end at the right of column X2 is shown for the Type O and B models; meanwhile, ${\theta }_{p\max }$ for the beam end at the left of column X2 is shown for the Type A models. The plot of ${\gamma }_{D\max }$ for the Type O models is not shown because no SDCs were installed in this model type.

The following conclusions can be drawn from Figure 11.

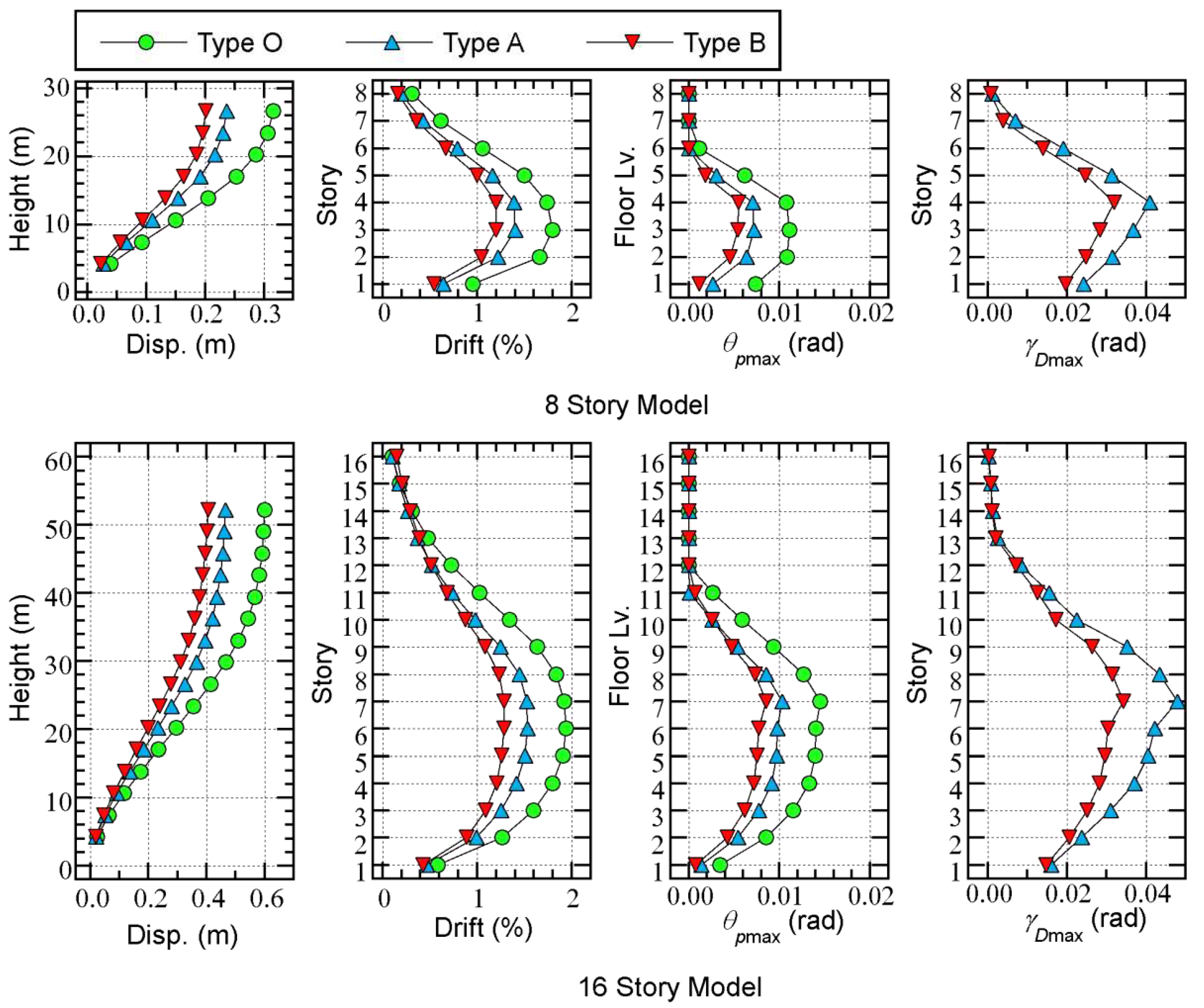
• For both the 8- and 16-story models, the responses of the Type O models are the largest, while those of the Type B models are the smallest.
• For the 8-story models, the largest peak story drift is observed at the third floor level. The largest ${\theta }_{p\max }$ is observed at the third or forth floor levels. The largest ${\gamma }_{D\max }$ is observed at the forth floor level.
• For the 16-story models, the largest peak story drift is observed at the sixth or seventh floor levels. The largest ${\theta }_{p\max }$ is observed at the seventh floor level. The largest ${\gamma }_{D\max }$ is observed at the seventh floor level.

Figure 12 compares the normalized cumulative strain energies of all the model types for $V_p$ = 0.55 m/s. The following local response quantities are compared: (i) the normalized cumulative strain energy at the beam end ($N{E}_{Sb}$) and (ii) the normalized cumulative strain energy of the damper panel ($N{E}_{Sd}$). Here, $N{E}_{Sb}$ is defined as

$$N{E}_{Sb,k}=\frac{E_{Sb,k}}{M_{yb,k}\cdot {\theta }_{yb,k}}.$$

(43)

In Equation (43), $M_{yb,k}$ and ${\theta }_{yb,k}$ are the yield moment and the chord rotation, respectively, at the yielding of the $k$th beam end and $E_{Sb,k}$ is the cumulative strain energy of the $k$th beam end.

$N{E}_{Sd}$ is defined as

$$N{E}_{Sd,k}=\frac{E_{Sd,k}}{Q_{yDL,k}\cdot {\gamma }_{yDL,k}\cdot h_{d0,k}}.$$

(44)

In Equation (44), $Q_{yDL,k}$ and ${\gamma }_{yDL,k}$ are the initial yield shear force and the initial yielding shear strain, respectively, of the $k$th damper panel; $h_{d0,k}$ is the height of the $k$th damper panel; and $E_{Sd,k}$ is the cumulative strain energy of the $k$th damper panel.

The following conclusions can be drawn from Figure 12.

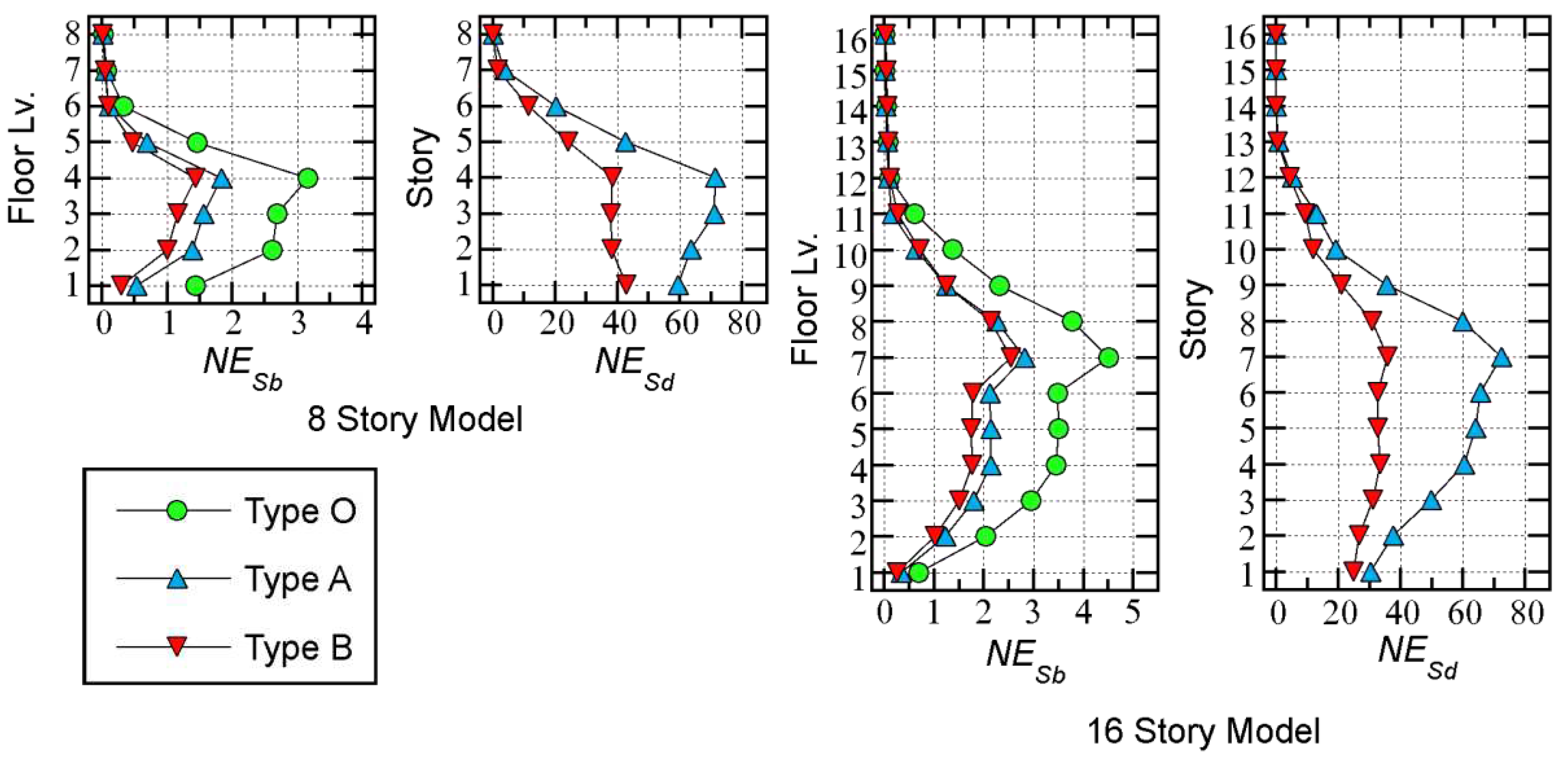
• For both 8- and 16-story models, the $N{E}_{Sb}$ values of the Type O models are the largest, while those of the Type B models are the smallest. The largest $N{E}_{Sb}$ values are observed at the forth floor level in the 8-story models and at the seventh floor level in the 16-story models.
• For both the 8- and 16-story models, the $N{E}_{Sd}$ values of the Type A models are larger than those of the Type B models. In the 8-story models, the largest $N{E}_{Sd}$ is observed at the forth floor level in the Type A models, while it is observed at the first floor level in the Type B models. In the 16-story models, the largest $N{E}_{Sd}$ is observed at the seventh floor level in both model types.

4.3. Summary of the Analysis Results

This section summarizes the responses of the RC frame building models with and without SDCs subjected to a pseudo impulsive lateral force proportional to the first mode vector. The analysis results can be summarized as follows.

A)

In the critical PDI analysis results shown herein, the peak equivalent displacement of the first modal response over the course of the entire seismic event (${{D_1}^{*}}_{\max }$) occurs at the end of the second half cycle of the response, when the second pseudo impulsive lateral force acts. The momentary input energy corresponding to the second pseudo impulsive lateral force (${}_2\Delta {E_1}^{*}$) is larger than that corresponding to the first pseudo impulsive lateral force (${}_1\Delta {E_1}^{*}$).

B)

The equivalent acceleration (${A_1}^{*}$)–equivalent displacement (${D_1}^{*}$) curve obtained from the pushover analysis results agrees very well with the hysteresis loop (the ${A_1}^{*}\left(t\right)$–${D_1}^{*}\left(t\right)$ relationship) obtained by the critical PDI analysis in the case of the Type O models. Meanwhile, in the case of the models with SDCs, the ${A_1}^{*}$–${D_1}^{*}$ curve obtained from the pushover analysis is slightly different from the hysteresis loop obtained by the critical PDI analysis. This is due to the strain hardening effect of the damper panel.

C)

The ratio of the the effective period of the first modal response ($T_{1eff}$), calculated from Equation (42), to the response period of the first modal response ($T_{1res}$), $T_{1eff}/T_{1res}$, is nearly constant: the ratio is within a narrow range between 1.0 and 1.2.

Point (A) is important for discussing the relationship between the maximum momentary input energy ($\Delta {{E_1}^{*}}_{\max }$) and the peak displacement (${{D_1}^{*}}_{\max }$). In the prediction procedure for the peak displacement of Hori and Inoue (2002), as well as that of Fujii and Shioda (2023), the peak displacement is calculated considering the energy balance during the half cycle of the structural response: it is assumed that the peak displacement (${{D_1}^{*}}_{\max }$) occurs at the end of the response, when the maximum momentary energy input occurs. Therefore, point (A) is consistent with the assumption of the prediction procedure.

Point (B) indicates that the ${A_1}^{*}$–${D_1}^{*}$ curve obtained from the pushover analysis results agrees well with the critical PDI analysis results, as far as the model without the strain hardening effect is concerned. This implies that, for the bare RC MRF studied herein, the ${A_1}^{*}$–${D_1}^{*}$ curve constructed from the critical PDI analysis results of various $V_p$ by plotting the peak response point will be the same as the the ${A_1}^{*}$–${D_1}^{*}$ curve obtained from the pushover analysis.

Point (C) indicates that $T_{1eff}$ calculated from ${{D_1}^{*}}_{\max }$ and the equivalent velocity of the maximum momentary input energy of the first modal response (${V_{\Delta E1}}^{*}$) via Equation (42) is clearly related to the response period ($T_{1res}$). This may indicate that Equation (42) is valid for calculating $T_{1eff}$ when evaluating ${V_{\Delta E1}}^{*}$ and ${V_{I1}}^{*}$ from the $V_{\Delta E}$ and $V_I$ spectra as discussed in previous studies (Fujii and Shioda, 2023; Fujii 2023).

5. Comparisons with the Predicted Results

This section focuses on comparisons with the predicted results based on the study of Fujii and Shioda (2023) and the critical PDI analysis results, particularly (i) the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ relationship and (ii) the $T_{1eff}$–${D_1}^{*}$ relationship. Details concerning calculating ${V_{\Delta E1}}^{*}$ and $T_{1eff}$ from the pushover analysis results can be found in Fujii and Shioda (2023).

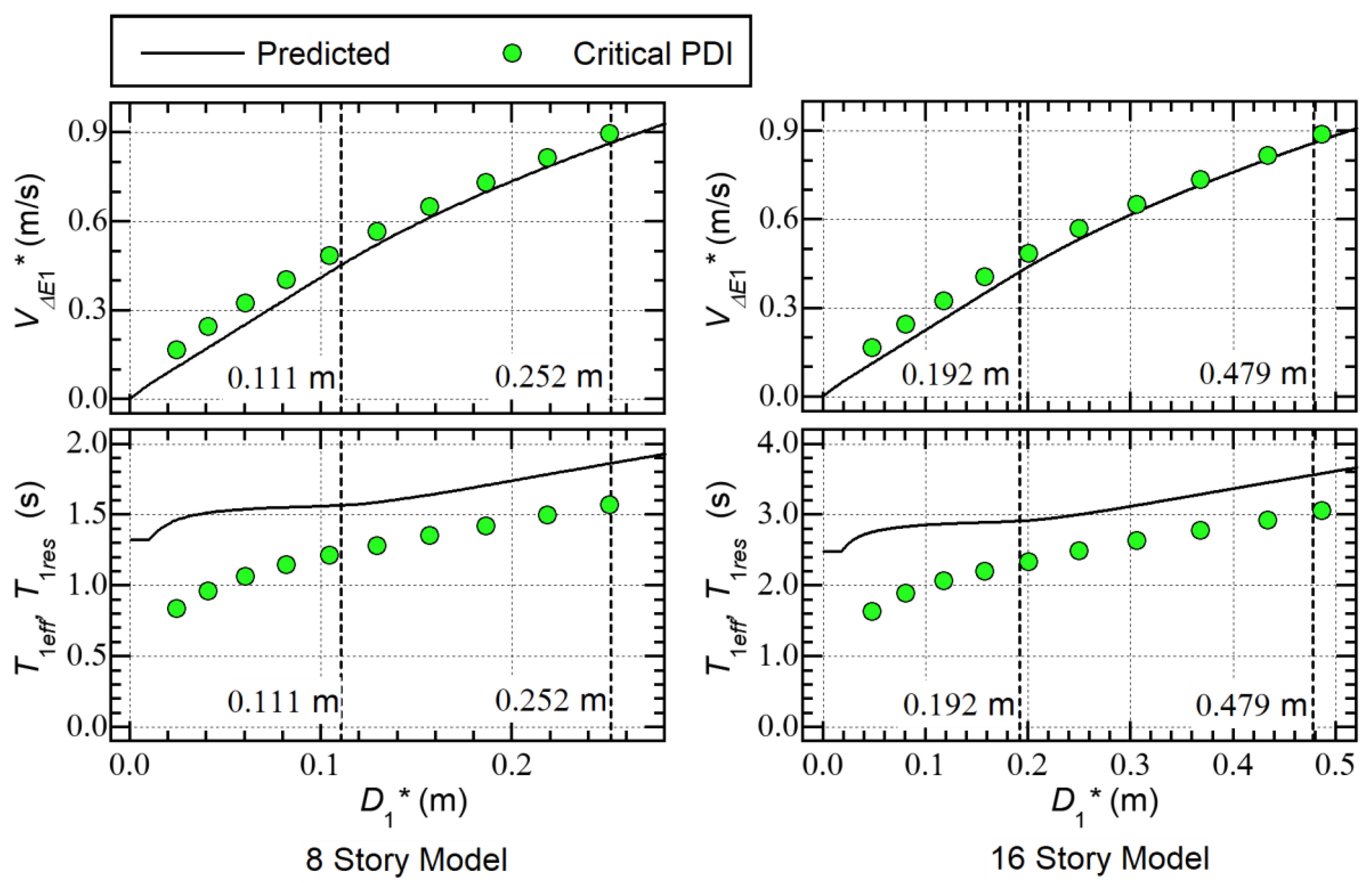
5.1. Bare RC Frame Models

Figure 13 shows comparisons between the predicted results and the critical PDI analysis results for the Type O models. The upper two panels show comparisons of the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve and the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results, while the lower two panels show comparisons of the predicted $T_{1eff}$–${D_1}^{*}$ curve and the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results.

The following conclusions can be drawn from Figure 13.

• The predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves agree well with the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results. More specifically, the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve of the 8-story model agrees very well with the critical PDI results when ${{D_1}^{*}}_{\max }$ is larger than 0.111 m (= ${D_{1yf}}^{*}$). Similarly, the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve of the 16-story model agrees very well with the critical PDI results when ${{D_1}^{*}}_{\max }$ is larger than 0.192 m.
• The predicted $T_{1eff}$–${D_1}^{*}$ curves are above the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results, although its trend is similar. The predicted $T_{1eff}$–${D_1}^{*}$ curves show a gradual increase in $T_{1eff}$ as ${D_1}^{*}$ increases, which is consistent with the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots. However, the difference between $T_{1eff}$ and $T_{1res}$ becomes significant when ${{D_1}^{*}}_{\max }$ is small.

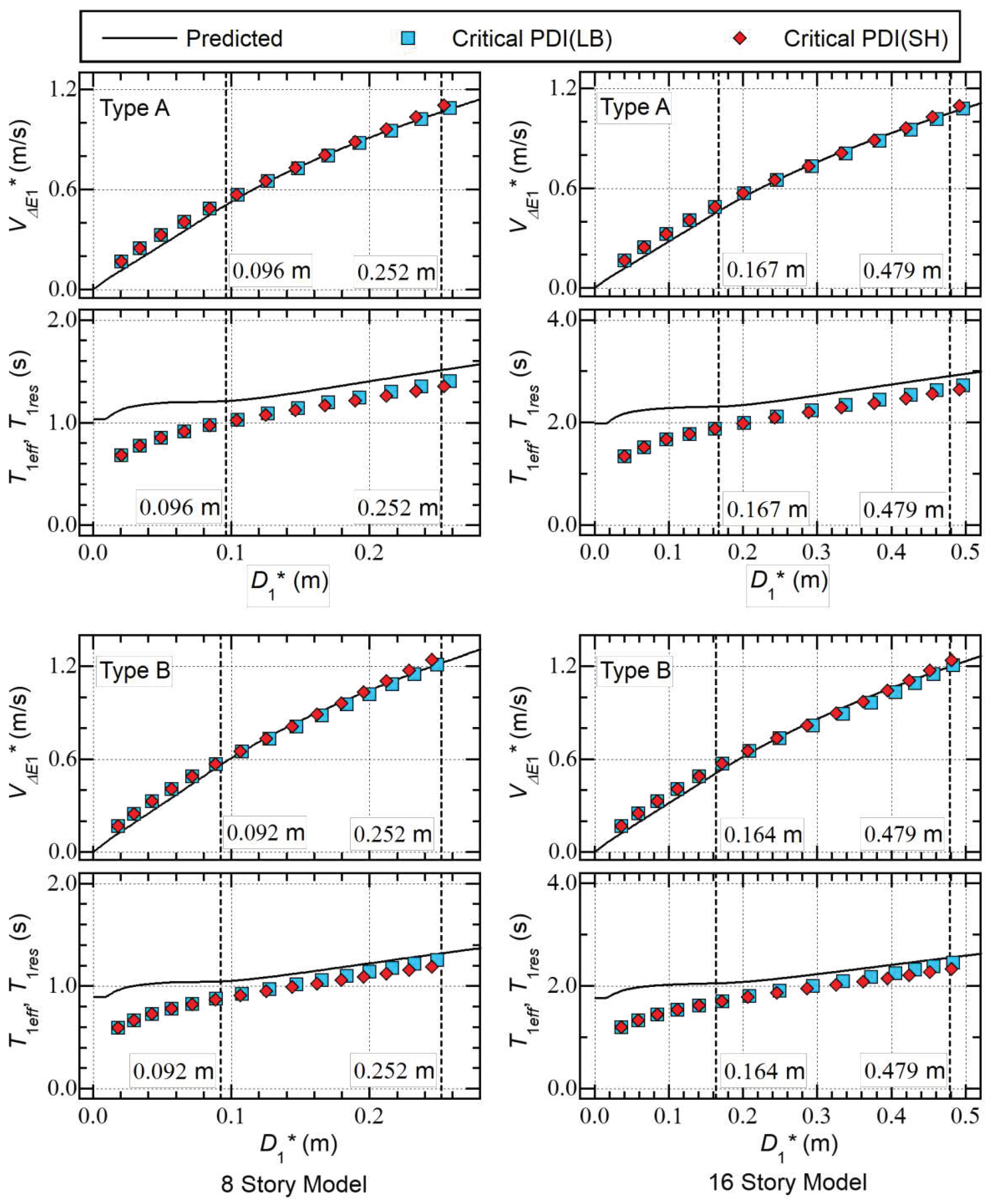
5.2. RC Frame Models with SDCs

Figure 14 shows comparisons between the predicted results and the critical PDI analysis results for the Type A and B models. Similar to Figure 13, the upper two panels show comparisons of the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves with the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results, while the lower two panels show comparisons of the predicted $T_{1eff}$–${D_1}^{*}$ curves with the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results. In this figure, the critical PDI results obtained by the models without the strain hardening effect (LB) and with the strain hardening effect (SH) are shown for comparison.

The following conclusions can be drawn from Figure 14.

• As far as the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ and $T_{1res}$–${{D_1}^{*}}_{\max }$ plots are concerned, the differences between the LB (without strain hardening) and SH (with strain hardening) plots are very small in the critical PDI analysis results shown herein.
• The predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves agree well with the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results for all models shown herein.
• The predicted $T_{1eff}$–${D_1}^{*}$ curves are above the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results, and the difference between the predicted $T_{1eff}$–${D_1}^{*}$ curves and the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots decreases as ${D_1}^{*}$ increases.

5.3. Discussion

This section compares the predicted results based on the study of Fujii and Shioda (2023) with the critical PDI analysis results, focusing on (i) comparisons between the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves and the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results and (ii) comparisons between the predicted $T_{1eff}$–${D_1}^{*}$ curves and the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots. Based on these comparisons, the following conclusions can be drawn.

A)

The predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves agree well with the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results for all models shown herein.

B)

The predicted $T_{1eff}$–${D_1}^{*}$ curves are slightly above the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results. Although their trends are similar, the predicted $T_{1eff}$–${D_1}^{*}$ curves show a gradual increase in $T_{1eff}$ as ${D_1}^{*}$ increases, which is consistent with the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots.

C)

The influence of the strain hardening of the damper panels on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ and $T_{1res}$–${{D_1}^{*}}_{\max }$ plots of the RC MRF models with SDCs is negligibly small.

Conclusion (A) indicates that the accuracy of the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves is satisfactory, as far as the bare RC MRF models and RC MRF models with SDCs are concerned. However, the difference between the predicted $T_{1eff}$ and $T_{1res}$ is not small when ${{D_1}^{*}}_{\max }$ is small, as evident in conclusion (B). The predicted $T_{1eff}$ can be closer to $T_{1res}$ if the idealization of the ${A_{1f}}^{*}$–${D_1}^{*}$ curve is made via a tri-linear curve. Conclusion (C) indicates that the strain hardening effect of the damper panel can be neglected in calculations of the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve.

6. Conclusions

In this study, critical PDI analyses of six RC MRF models with and without SDCs were performed. Then, the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ and $T_{1eff}$–${D_1}^{*}$ relationships calculated according to Fujii and Shioda (2023) were compared with those obtained from the critical PDI analysis results. The main results and conclusions can be summarized as follows.

• The equivalent acceleration (${A_1}^{*}$)–equivalent displacement (${D_1}^{*}$) curves obtained from the pushover analysis results agree very well with the hysteresis loops (${A_1}^{*}\left(t\right)$–${D_1}^{*}\left(t\right)$ relationship) obtained by the critical PDI analysis in the case of models without SDCs. In the case of models with SDCs, the ${A_1}^{*}$–${D_1}^{*}$ curve obtained from the pushover analysis differs slightly from the hysteresis loop obtained by the critical PDI analysis.
• The effective period of the first modal response ($T_{1eff}$), calculated from the equation of the peak equivalent displacement (${{D_1}^{*}}_{\max }$) and the equivalent velocity of the maximum momentary input energy (${V_{\Delta E1}}^{*}$), is clearly related to the response period ($T_{1res}$); the $T_{1eff}/T_{1res}$ ratio is within a narrow range between 1.0 and 1.2.
• The predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves agree well with the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results for all models shown herein. Meanwhile, the predicted $T_{1eff}$–${D_1}^{*}$ curves are slightly above the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots obtained from the critical PDI results. Although their trends are similar, the predicted $T_{1eff}$–${D_1}^{*}$ curves show a gradual increase in $T_{1eff}$ as ${D_1}^{*}$ increases, which is consistent with the $T_{1res}$–${{D_1}^{*}}_{\max }$ plots.
• The influence of the strain hardening of the damper panels on the ${V_{\Delta E1}}^{*}$–${{D_1}^{*}}_{\max }$ and $T_{1res}$–${{D_1}^{*}}_{\max }$ plots of the RC MRF models with SDCs is negligibly small.

The above conclusions support the accuracy of the prediction procedure (Fujii and Shioda, 2023): the predicted ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curves are sufficiently accurate for RC MRFs with and without SDCs. In addition, considering the unavoidable scatter in evaluating ${V_{\Delta E1}}^{*}$ and ${V_{I1}}^{*}$ from the linear spectrum, the accuracy of the predicted $T_{1eff}$–${D_1}^{*}$ curves may be acceptable.

Another finding of interest is that the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve can be directly evaluated from the critical PDI (or PMI) analysis in the case of buildings with a significant cyclic loading effect. In the DB-MAP analysis, there are several limitations imposed to avoid instability problems in the numerical analysis, e.g, the envelope of the force–deformation relationship of members must be symmetric, and a severe strength degredation (severe negative slope) in the force–deformation relationship of brittle members may cause numerical stability. In addition, because the DB-MAP analysis is a monotonic loading analysis, the influence of the cyclic loading effect cannot be directly included. Meanwhile, the critical PDI analysis shown herein has no such limitations; a critical PDI analysis of a structural model can be performed as long as the structural model is stable for NTHA. The flow of the critical PDI analysis shown herein can easily be extended to a critical PMI analysis. Therefore, the influence of the number of cyclic loadings on the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve can easily be evaluated by increasing the number of impulsive inputs in the critical PMI analysis. Therefore, critical PDI analyses have great potential for seismic performance evaluations of structures.

Note that the results shown in this study are, so far, valid only for RC MRF models with and without SDCs. Therefore, apart from further verifications using additional building models, the following questions remain unanswered. This list of questions is not comprehensive.

• What is the dependence of the ${V_{\Delta E1}}^{*}$–${D_1}^{*}$ curve on the number of impulsive inputs? It is expected that the ratio of the amplitude of ${D_1}^{*}$ in the positive and negative directions changes as the number of impulsive inputs increases. Therefore, the relationship between the increment of the energy input in each half cycle and the local peak equivalent displacement should vary depending on the number of impulsive inputs.
• Can the distribution of the cumulative strain energy of the SDCs in the critical PDI analysis at each floor level be properly evaluated from the pushover analysis results? Because the pushover analysis cannot consider the strain hardening effect, the distribution of the deformation of the SDCs may be different from the critical PDI analysis results. It is expected that the influence of the strain hardening effect on the distribution of the cumulative strain energy of the SDCs may be significant when the number of impulsive inputs increases.