Modelling of Texture Development during Metal Forming Using FE-VPSC

1. Introduction

Directional forming processes usually lead to the formation of an anisotropic grain structure in metals, known as texture. This is known to cause multiple effects, the most obvious of which are direction-dependent material properties. Such behaviour is particularly evident in sheet metal as sheets have already undergone highly directional forming during the rolling process. For subsequent deformation steps, the material behavior is strongly dependent on the resulting direction-dependent strength. Therefore, it is essential to take the anisotropy of pre-deformation and the resulting microstructure into account when investigating multi-stage forming processes, e.g. rolling followed by deep drawing.

In finite element (FE) simulations the relationship between the stresses and the direction-dependent deformation behavior is usually described by classical anisotropic material models such as Hill [1], Barlat [2,3] , Cazacu [4], or similar. These models use measured R-values or anisotropy coefficients that are applied the entire component. However, local changes in the anisotropy coefficients during the material deformation are not covered. For this purpose, methods that take the local microstructure evolution into account must be applied.

While multiple approaches have been used to calculate the development of local anisotropy [5], a distinction must be made between approaches for calculating the interactions of individual crystals (full-field single crystal) and mesoscopic (polycrystal) approaches. When using single crystal approaches, only a smaller number of crystals are considered due to the computational intensity of the methods [6,7]. In contrast, the mesoscopic approach also allows larger components to be simulated [8]. A representative of this mesoscopic approach is the VPSC model (Visco-Plastic Self-Consistent [9]), which was developed by the Los Alamos National Laboratory.

Due to the numerical effort involved, texture calculation methods were mainly performed without taking the component geometry into account. Today’s availability of high computing power has made approaches such as CPFE (Crystal Plasticity Finite Element [7]) methods or the implementation of VPSC in finite element calculation routines [8] possible. This means that complex part geometries, manufacturing processes or process chains can now be simulated in terms of texture evolution.

In this paper, the VPSC code for implicit calculations was implemented in the LS-DYNA^® solver and the functionality is demonstrated for texture development calculations by means of compression and deep drawing simulations.

2. Materials & Methods

FE-VPSC is an independent variant of the original VPSC program for implementation in FE solvers [8,10]. For the simulations presented below, FE-VPSC was implemented as a user-defined material subroutine in the LS-DYNA^® FE solver.

2.1. VPSC-Model

As a mesoscopic method, VPSC links macroscopic effects, i.e. plastic deformation, and the resulting microscopic material responses. Namely, the resulting changes in grain orientation and local flow stresses of a polycrystalline structure are calculated in correspondence with the plastic deformation applied. In this context a grain is only defined by its orientation, i.e. three Euler angles, and its size fraction in relation to the whole material structure. Consequently, grain orientations, e.g. from EBSD measurements, descriptions of the slip system activities and the prescribed deformation path are required as input parameters for the material simulation. The simulations are based on the assumption that each grain is embedded in a viscoplastic matrix, which in turn represents the average of all grains present in the material. The forming behavior of each individual grain is controlled by their individual slip system activities, which are derived from the grain orientation and the critical resolved shear stress (CRSS) of the slip systems [11]. The stresses are calculated in VPSC using an elastic predictor-plastic corrector method [12] based on the Voce hardening model. A set of Voce parameters must be assigned for each slip system under consideration. In addition, the crystal orientations are stored so that the texture evolution can be considered.

Thereby the used VPSC approach allows for fast simulation times when compared to full-field methods, but shows rising calculation effort with increasing number of considered grains.

2.2. Implementation of FE-VPSC into LS-DYNA^®

LS-DYNA^® is a widely applied FE solver that allows a direct implementation of FORTRAN-based user-defined material models. As part of the implementation as a material subroutine, the stress response to a specified deformation increment is calculated by the FE-VPSC model in each FE time step and for each relevant element. The results are submitted to LS-DYNA^®, which in turn uses the stresses to determine the local strains for the next time step.

Based on the implementation of the VPSC method in the FE solver Abaqus by Zecevic [13] a tailored interface converts the inputs from LS-DYNA^® into a suitable form for FE-VPSC and then returns the relevant results. Important results from the FE-VPSC calculations are stored for each VPSC instance of each finite element for visualization by LS-DYNA^®.

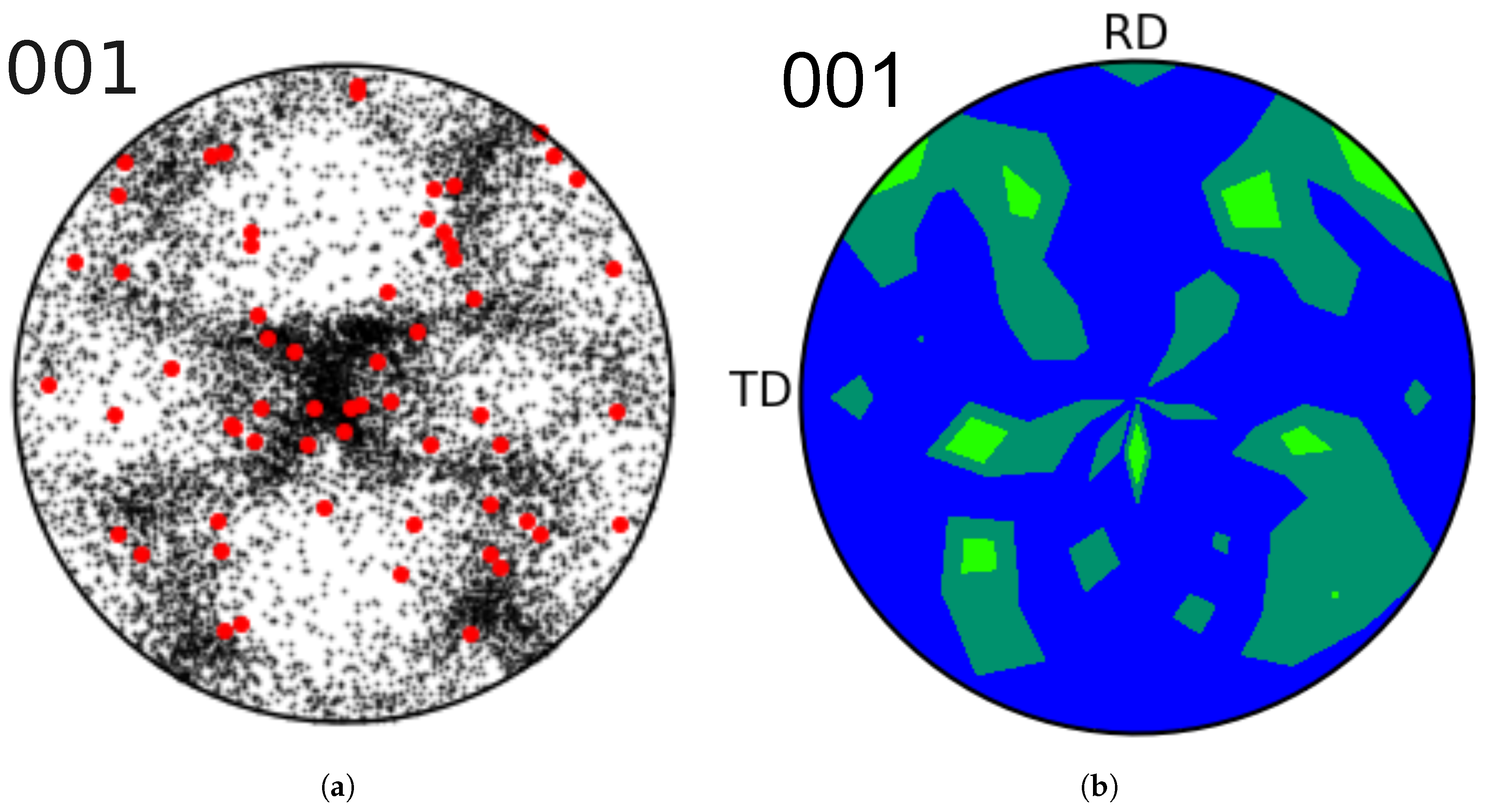
To simplify the interpretation of the texture evolution for the whole simulated part, an algorithm for the macroscopic visualization of the texture was developed and implemented. The grain structure, which is used in each VPSC instance of each FE element, consists of multiple grains with individual orientations. The algorithm calculates the weighted average of all crystal orientations for each element and then colors the element with a color corresponding to the inverse pole figure, see insert in Figure 2. In addition, the texture for selected elements can be exported and displayed as a pole figure, see Figure 1 (b).

2.3. Clustering of Textures

The VPSC (and FE-VPSC) simulations require the proportions of the respective grain orientations of the initial texture as input. In case of FE-VPSC the model recalculates the changes in grain orientation for each FE element. It is therefore useful to reduce the number of grain orientations per element to limit the computational effort. The VPSC approach only considers the ratio of grain orientations compared to the whole input texture instead of each individual grain and its respective location. It is thus feasible to reduce the number of different grain orientations by applying a clustering algorithm. Our algorithm is based on a k-means clustering using weighted input data which merges clusters with similar orientations, according to a preset degree of data reduction (called cluster radius). Details about the clustering algorithm can be found in [14]. In this work a total of 16 effective clusters were determined from approximately 3000 measured grains. A comparison between the original and clustered texture is shown in Figure 1 (a).

Figure 1 (a) shows a comparison between the original pole figure and the clustered texture with a clustering radius of 0.5 (red dots). The contour plot of the clustered texture with the even more severe radius 0.8 is depicted in Figure 1 (b) and shows a fairly good agreement with the original pole figure despite the huge reduction from 3000 grains to only 16 clusters.

2.4. Material

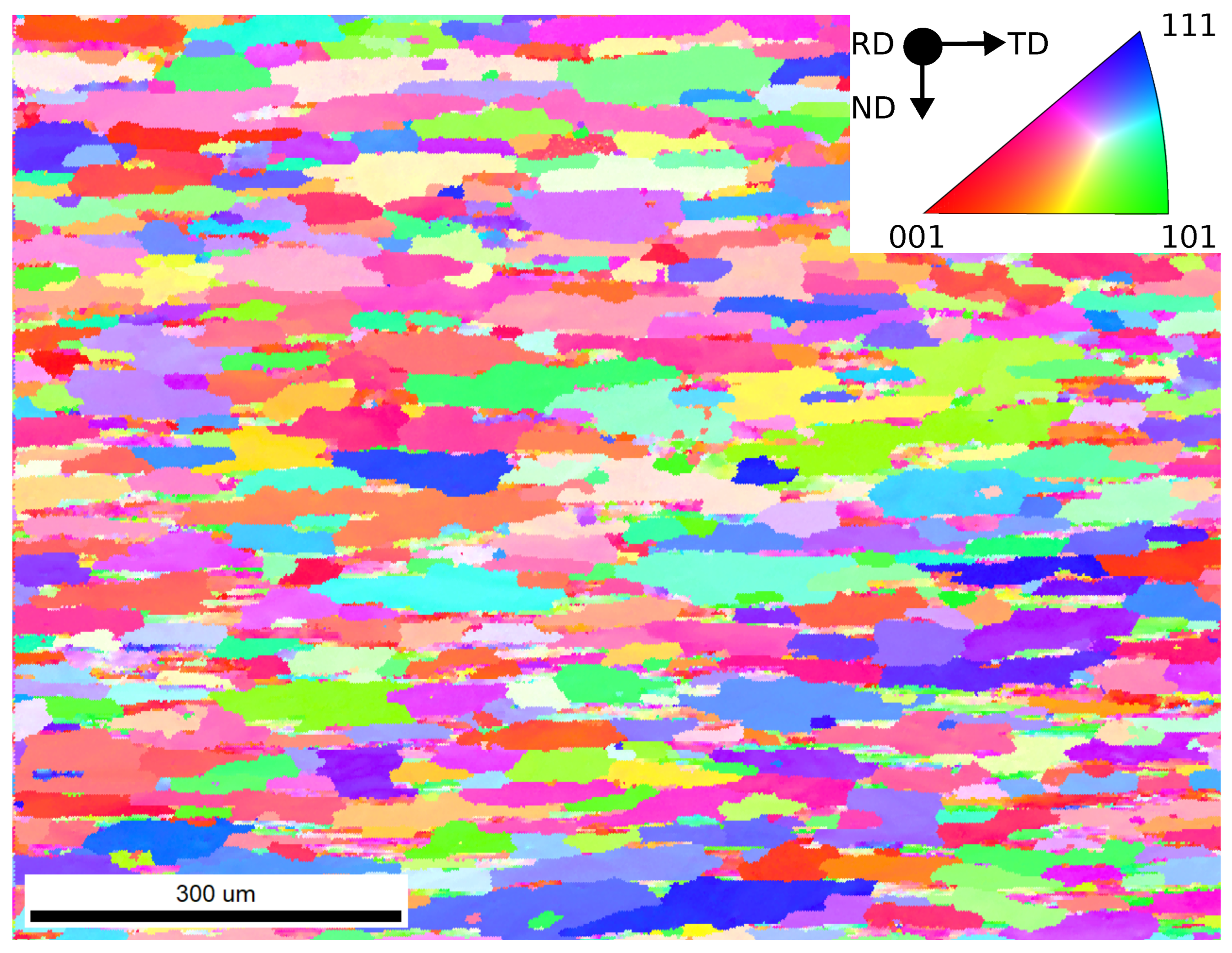
An initial texture is required for a crystal-based simulation of anisotropy and macroscopic material behavior. If semi-finished products are deformed, e.g. a rolled sheet or an extruded profile, it already has an inherent texture due to its production process. The material data used for the simulations in this work stems from a rolled aluminum sheet with 20 mm thickness (EN AW-7075). The necessary microstructure data, e.g. grain orientations and corresponding microstructural components, were determined using a Tescan Mira3 field emission scanning electron microscope equipped with a EDAX Hikari Plus electron back scattered diffraction (EBSD) detector, operated at 20 mm working distance. Figure 2 shows the initial microstructure and the measured texture as an inverse pole figure map (IPF map).

A DIL508 A/D of Texas Instruments was used to perform compression tests in three different directions. By fitting the four parameters of the Voce hardening law to the experimentally determined force/displacement curves, the model was mechanically calibrated. Further information on the material, as well as mechanical characteristics, can be found in the work by Domitner et al. [15].

3. Results & Discussion

To investigate the effects of an existing texture on the material behavior during a simulated forming process, LS-DYNA^® in combination with FE-VPSC was used. The resulting simulations of a compression and a deep drawing test are analyzed and compared with a similar FE setup using an isotropic and anisotropic material model.

The parameters for the experimental setup and the corresponding simulations are given in Table 1 for the compression test and Table 2 for the deep-drawing test. R denotes the sample radius, H the sample height, $\dot{\phi }$ the forming rate in the compression test and $R_I$, $R_O$ represent the inner and outer radius of the punch in the deep drawing test. The number of elements (N), the number of iterations (I) and the simulation time per element and iteration ($T_{sim}$) for the forming simulations are also provided. Due to the uniform distribution of the anisotropy in the rolled aluminum sheet, all FE elements start with the same input texture, see Figure 2.

In the results of the respective simulations, which are presented below, RD refers to the rolling direction of the sheet metal. Furthermore, TD (transversal direction) denotes the sheet width and ND (normal direction) the sheet thickness.

3.1. Compression Test Simulation

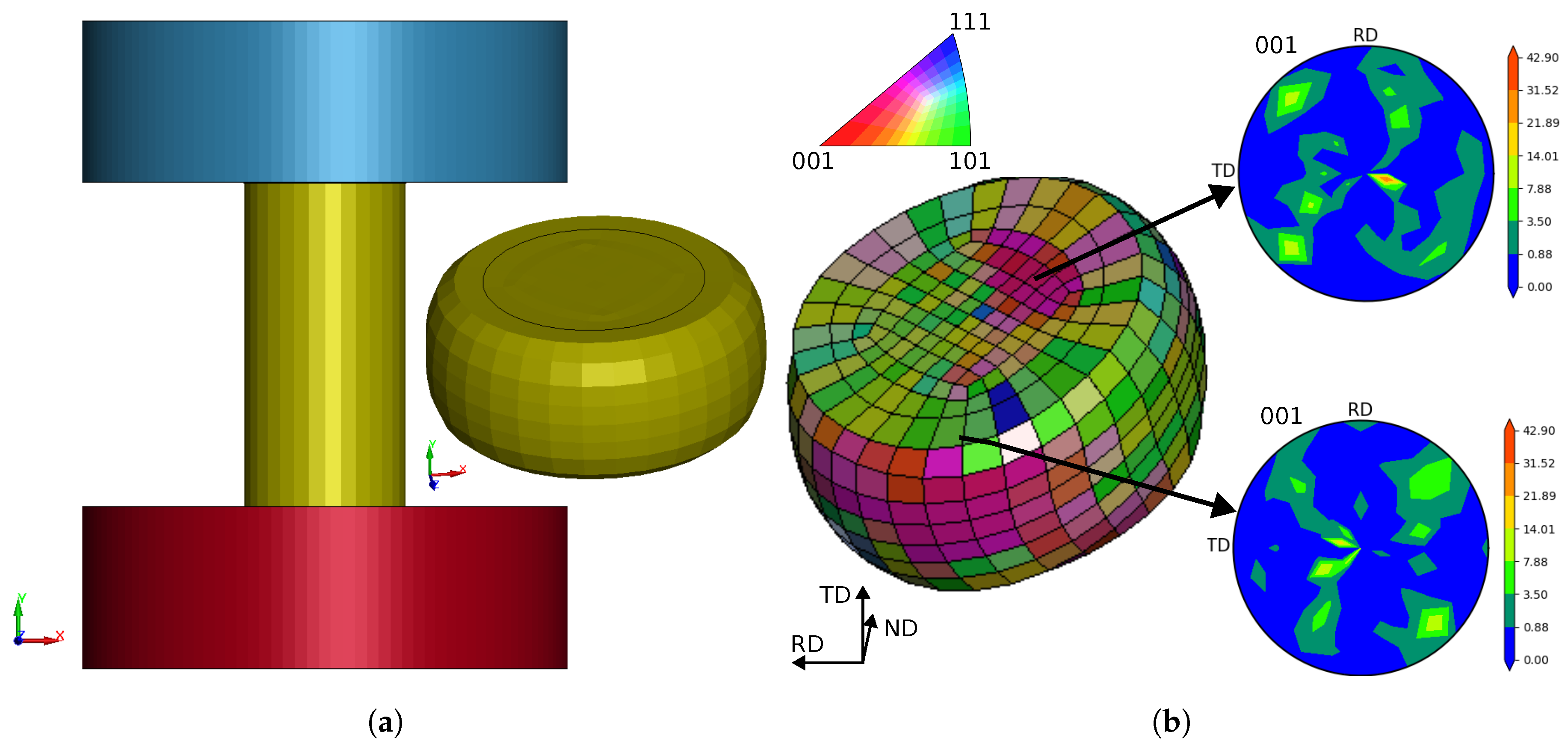
In the compression test, a cylinder was compressed at a constant deformation rate. The test setup is shown in Figure 3 (a) and Table 1 contains the relevant parameters.

The resulting geometry from the reference simulation with an isotropic material model is also shown in Figure 3 (a). Due to the isotropy, the result is completely rotationally symmetrical and has no preferred direction of deformation. However, in reality there is often an ovality when compressing samples made of rolled material [16]. Such a behaviour can be caused by the inherent texture and corresponding mechanical anisotropy of the sample. As the material deforms more easily in directions of low mechanical strength, the sample gets distorted accordingly. The result of the FE-VPSC simulation in Figure 3 also shows such an oval shape, providing proof of the successful interaction of material texture via FE-VPSC and the deformation path superimposed by LS-DYNA^®.

The colors of the FE elements in Figure 3 (b) show different (average) crystal orientations in correspondence to the rolling direction, as briefly described in Section 2.2. As all FE elements start with the same initial texture this is a clear indication for the texture evolution calculated individually for each element. As an example the simulated textures of two selected elements, shown as pole figures, are provided as inserts.

3.2. Deep Drawing Simulation

Deep drawing operations are an important industrial processes, which are used to form metal sheets into various (complex) part geometries, e.g. automotive parts. For our investigation we simulated the cup drawing process, which is relatively simple but a well known test in material characterization. Engler et al. [17] already modeled the earing formation for EN AW-3104 by performing FE-simulations of the cup deep drawing process and used the results to derive boundary conditions for the standalone VPSC computations. The VPSC code afterwards calculates the yield information according to the determined load history for the radial elongation under different in-plane angles. The yield information was afterwards introduced by Hill’s yield criterion [18]. 2D axial symmetric models as well as a 3D model, where earing was already predicted, are presented in [17]. Pronounced earing could be found at 0° and 90° to the rolling direction (RD) for recrystallized sheets and at 45° for the as-rolled state [17].

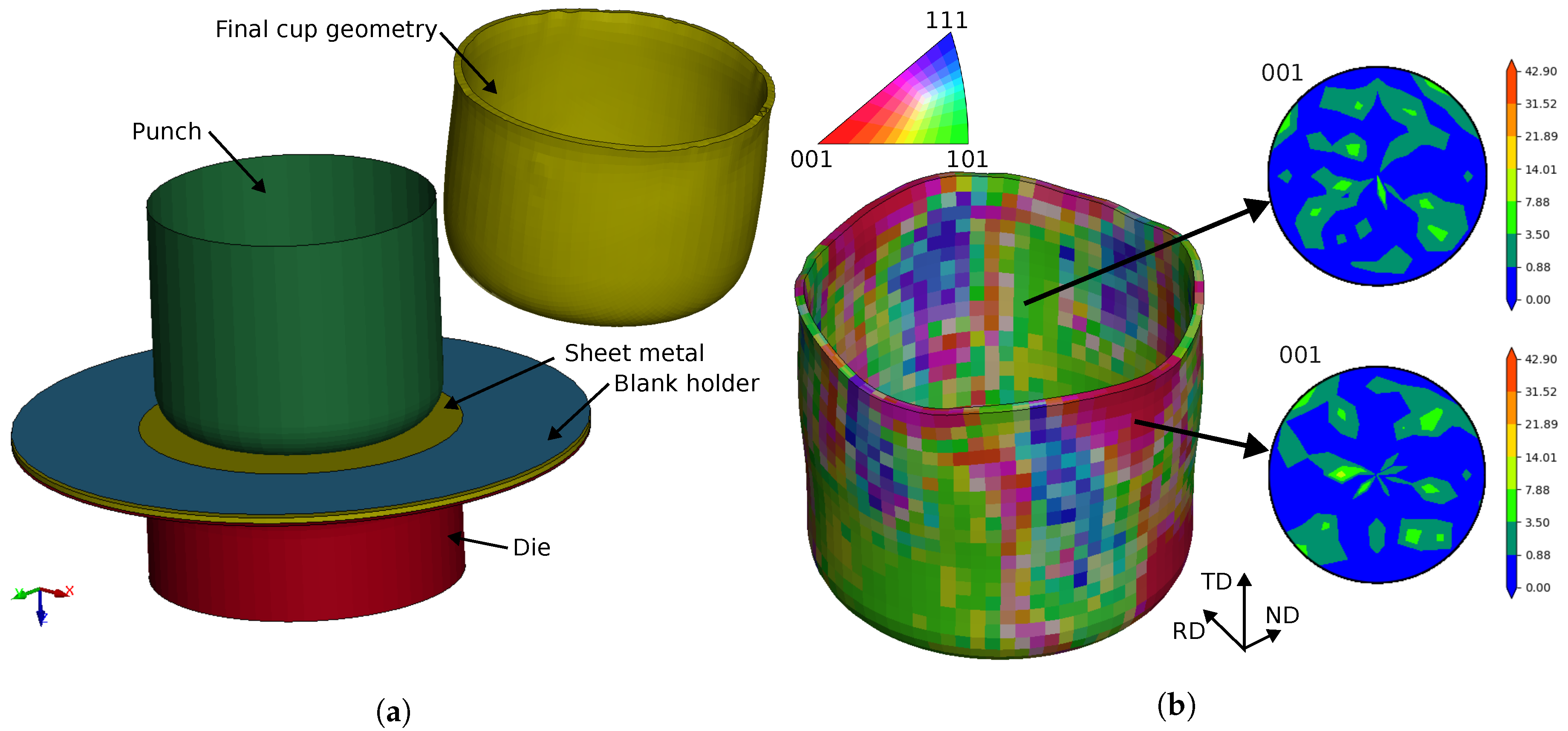
In contrast to Engler et al., we introduced VPSC directly into the FEM code and therefore obtain the anisotropic behavior in a two-way coupling between mechanical calculation and texture evolution. Our test setup and the isotropic reference simulation are shown in Figure 4. The relevant parameters are summarized in Table 2. Punch, blank holder and die were modelled as rigid bodies and meshed with shell elements. However, since FE-VPSC is currently only implemented for solid elements, the workpiece is meshed with three layers of solid elements.

Similar to the compression test, the isotropic material model produces a rotationally symmetrical result, see Figure 4 (a). On the other hand, the result of the FE-VPSC simulation in Figure 4 (b) clearly shows variations in the texture. As the initial texture is identical for all FE elements at the start of the simulation, the texture evolutions are caused by the complex displacement fields of this simulation. The polefigures of two different FE elements, depicted for verification, show that differences exist both between each element and in comparison to the initial texture in Figure 2.

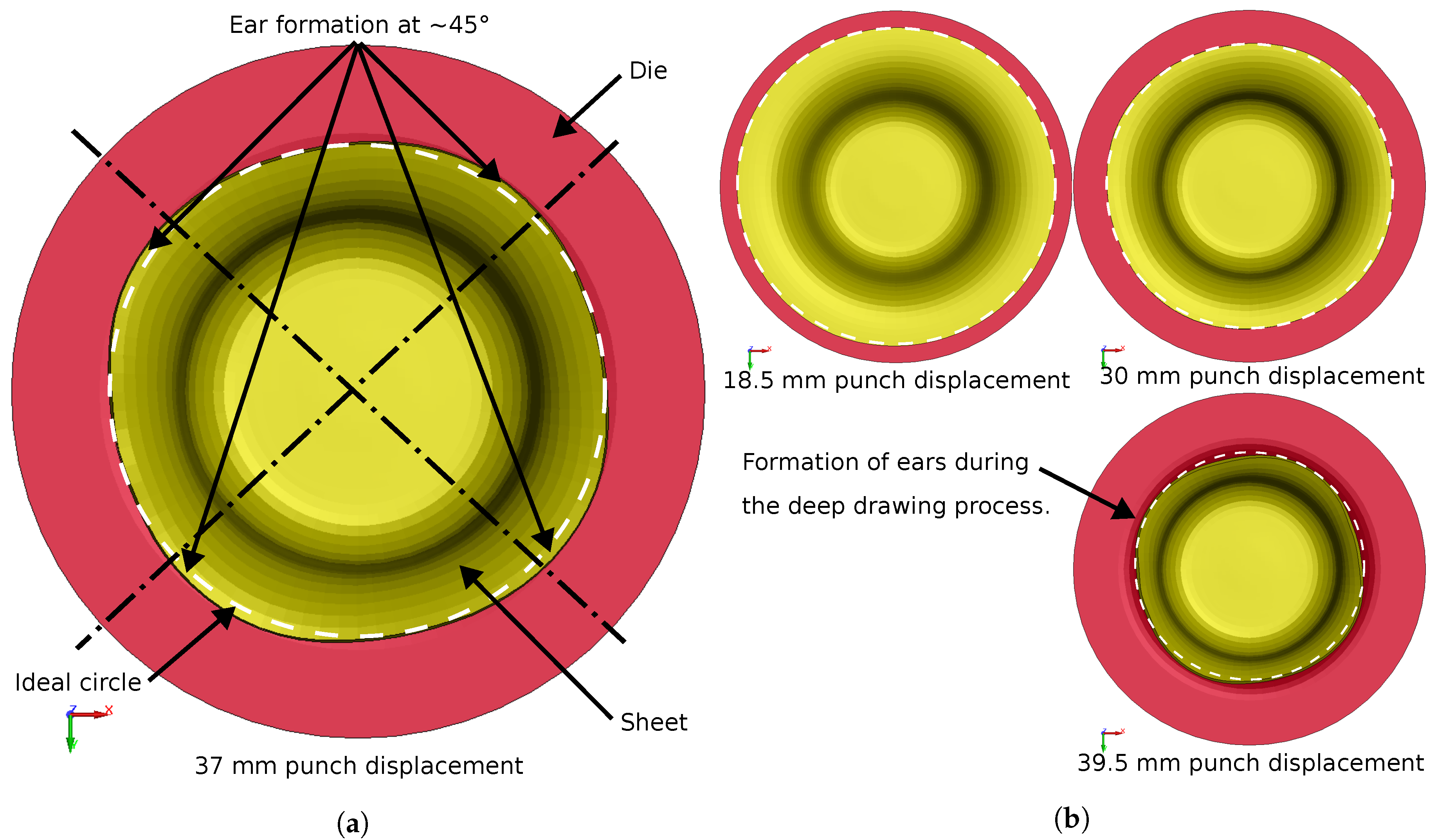
The most striking result of this calculation is the formation of four so-called ears. Earing is a well-known effect of textured materials, which also occurs regularly in experiments [17]. The anisotropic sheet properties, caused by the pronounced texture from the rolling process, lead to earing of the drawn cup. According to Engler et al. [17], the formation of ears occurs in the flange under the blank holder. Material behavior similar to this description was reproduced by the simulation model, where the ears form at approximately 45° to the rolling direction in the as-rolled state, see Figure 5.

4. Conclusions

An efficient way of modelling the local texture development during the deformation of metals by using a mesoscopic approach was presented. The VPSC (Visco-Plastic Self-Consistent) model was used to simulate the texture evolution in an EN AW-7075 aluminum sheet during a simple compression test and in a cup-drawing operation. By implementing the VPSC model in the context of the finite element method, the effects of the material texture on the mechanical material properties as well as the forming behavior for entire components can be shown directly. In contrast to simpler phenomenological approaches to modeling material anisotropy, the evolution of the local texture during forming can be described and investigated.

In our work we have shown that:

• By implementing VPSC in the FEM framework of LS-DYNA^®, even industry relevant part sizes could be simulated in a reasonable time.
• By applying a texture clustering algorithm, the numerical effort could be successfully reduced.
• First results for the compression tests show a oval specimen geometry, similar to the experiments.
• The cup drawing simulation also showed the earing phenomenon which is typical for this kind of test.

It is thought that the prediction and analysis of local correlations in the microstructure with external boundary conditions and process parameters will help to optimize individual processes and process chains. By using mesoscopic (polycrystal) approaches such as the VPSC model, more detailed investigations of forming processes can be carried out on models of real components without having to invest in the enormous computing capacities and elaborate preparation of input data necessary for full-field calculations.

The implementation of FE-VPSC for shell elements should make it more convenient for sheet metal forming processes in the future. This is thought to result in a significant acceleration of the currently considerable calculation times. With further improvements in computational efficiency (e.g. the implementation of the clustering algorithm for the VPSC calculation itself, improvements in the parallelization, ...), phenomenological approaches could be replaced in the future.

The results presented here are still a proof of concept. Subsequently, investigations with additional experiments are to be carried out in order to quantitatively prove the accuracy of the predictions.