Unveiling the True Nature of Sliding Friction through Thermodynamic Principles

1. Introduction

Friction arises due to the relative movement between two objects; hence, frictional force is also considered a dissipative force existing at the interface of friction, converting mechanical kinetic energy into irreversible heat. Frictional fire-making is one of the oldest technology used by humankind [1,2,3,4,5,6], which signifies the active utilization of thermal energy by humans, aiding in the departure from the barbaric era of eating raw meat and drinking blood, and ushering in modern civilization. Friction plays a crucial role in our everyday lives, from walking to driving a car and from energy dissipation to triboelectric nanogenerators (TENG) [7,8].

The study of friction can be traced back to the Renaissance period, when figures such as Leonardo da Vinci, Amontons, and Coulomb proposed the famous laws of friction. The phenomenological Amontons-Coulomb friction law $F={\mu }_{k}N$ states that kinetic friction force F is equal to a kinetic friction coefficient ${\mu }_k$ times the normal load N and is independent of contact area and relative sliding velocity. This description of frictional force is not derived from first principles, but rather an empirical summary of frictional phenomena [9,10,11,12].

As the accuracy of measuring instruments continues to improve, an increasing number of research results indicate that the three models of friction including the Amontons-Coulomb law, the classical Prandtl-Tomlinson (PT)[2,3] and Frenkel-Kontorova (FK)[4,5,6] models are not entirely accurate [9,10,11,12]. The Amontons’ law states that kinetic friction is independent of the sliding velocity while the Prandtl Tomlinson model suggests that damping is proportional to the relative sliding velocity between two contacting objects. To date, no theoretical model can predict the magnitude of frictional force, nor can it accurately predict the vibrations and noise induced by friction, making these aspects still unpredictable and elusive.

Recently, Huang et al. [12] discovered that the interfacial force is not a dissipative force. During the process of sliding friction, the interfacial interaction forces simply convert mechanical kinetic energy into the elastic potential energy of an elastic body, which is a process of conservation of mechanical energy. This potential energy continuously accumulates until it exceeds a specific threshold, at which point some of the accumulated potential energy is released in the form of phonons. The energy dissipation occurs throughout the entire elastic body, not just at the frictional interface. The energy dissipation of the entire elastic body can be described by an equivalent material damping. Therefore, the damping of sliding friction is directly proportional to the vibration velocity of the elastic body in sliding direction, rather than being proportional to the relative velocity of the two sliding interfaces, as assumed in traditional models such as the Prandtl-Tomlinson (PT). Based on this, Huang eta al. [12] has proposed the phonon friction model, which can predict the frictional forces measured by friction force microscopy, and this has been verified by molecular dynamics simulation models. The phonon friction model tries to explain long-standing puzzling tribological phenomena, such as the velocity weakening of frictional forces and the observed dependence of frictional forces on spring stiffness.

The work of Huang et al. [12] has subverted the traditional understanding that friction is a dissipative force at the interface, their phononic friction model deepens our understanding of the mechanism of frictional energy dissipation. However, the Amontons-Coulomb law has not been derived from their phononic friction model. The rational formulation of the Amontons-Coulomb law of friction is still an open problem.

In this Letter, we will take a different approach to considering the problem by treating two objects that are sliding past each other as elastic deformable bodies. The sliding interface is characterized by irregular roughness, and when the objects slide past each other, the irregularities of the rough surface undergo elastic deformation under pressure. The objects in motion obtain elastic potential energy, and then the issue of sliding friction is re-examined from the standpoint of energy conservation, in accordance with the first law of thermodynamics.

2. Thermodynamics of friction force

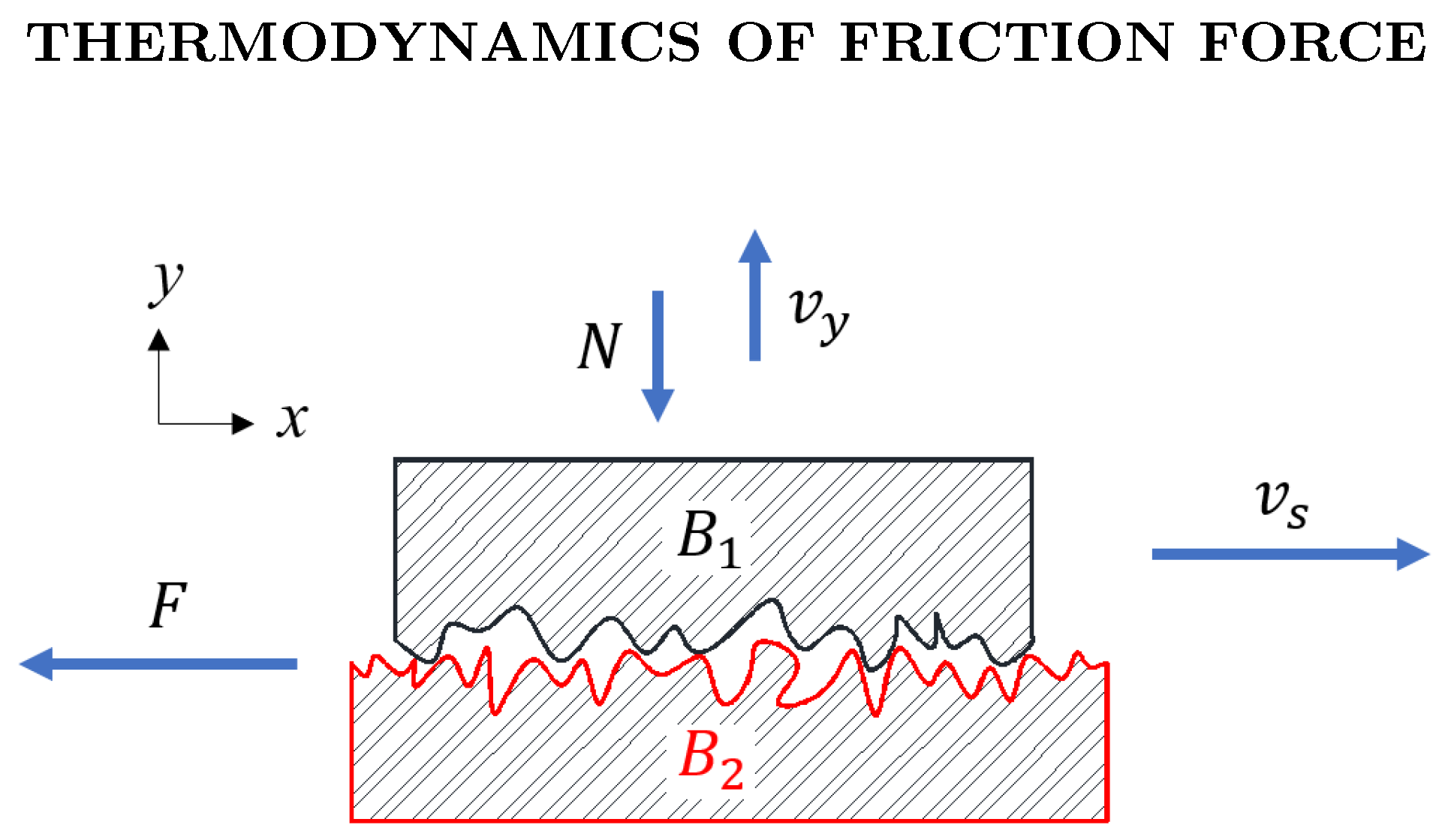
If we consider the two contact elastic objects $B_1$ and $B_2$ as a system $S=B_1+B_2$ as shown in Figure 1, their relative sliding motion with the sliding velocity $v_s$ causes the corrugated surface deformed under the pressure of the normal force N, the friction force F will resist the motion of the top object $B_1$ if we assume the bottom object $B_2$ is fixed. The problem becomes to find the kinetic friction force F under the pressure of N.

According to Huang et al.[12], the energy of sliding friction process is conservative. If the friction force does work $\delta W$, and/or contact bodies absorb heat $\delta Q$ from its surroundings, then this corresponds to a net flow of energy $\delta W-\delta Q$ across the boundary to the surroundings. In order to conserve the total energy E, there must be a counterbalancing change $\delta E=\delta Q-\delta W$ in the internal energy of the bodies. The first law provides a kind of strict energy accounting system in which the change in the energy account $\delta E={\int \int \int }_V\frac{1}{2}\mathit{\sigma }:\mathit{ϵ}dV$ equals the difference between deposits $\delta Q$ and withdrawals $\delta W$. Hence we have the 1st law of thermodynamics for the sliding friction as follows:

$${\int \int \int }_{V_1}\frac{1}{2}\mathit{\sigma }:\mathit{ϵ}dV+{\int \int \int }_{V_2}\frac{1}{2}\mathit{\sigma }:\mathit{ϵ}dV=\delta Q-\mathit{F}·\ell ,$$

(1)

where $V_1$ and $V_2$ are the volume of the friction system $B_1$ and $B_2$, respectively, $\mathit{\sigma }$ is stress tensor, $\mathit{ϵ}$ is strain tensor, ℓ is displacement vector of the friction motion.

Taking the time derivative on both side of Eq.1, noting $\frac{d\mathit{F}·\ell }{dt}=\frac{d\mathit{F}}{dt}·\ell +\mathit{F}·\frac{d\ell }{dt}=\mathit{F}·\frac{d\ell }{dt}$ due to the fact the the derivative $\frac{d\mathit{F}}{dt}$ is orthogonal to the displacement vector ℓ, namely $\frac{d\mathit{F}}{dt}·\ell =0$, therefore we have the rate form of the 1st law of thermodynamics

$${\int \int \int }_{V_1}\mathit{\sigma }:\dot{ϵ}dV+{\int \int \int }_{V_2}\mathit{\sigma }:\dot{ϵ}dV=\delta \dot{Q}-\mathit{F}·{\mathit{v}}_s,$$

(2)

where ${\mathit{v}}_s=d\mathit{l}/dt$ is sliding velocity.

Denoting $\theta$ as the angle between $\mathit{F}$ and $\mathit{v}$, since they are in the opposite direction, hence $\mathit{F}·\mathit{v}=-F{v}_{s}cos\theta =-F{v}_s$ due to the fact $\theta =\pi$ and $cos\pi =-1$. Notice $\mathit{\sigma }:d\dot{ϵ}=\mathit{\sigma }:\mathit{d}$, where the $\mathit{d}=\mathbf{\nabla }\mathit{v}$ is deformation rate [13,14], where $\mathit{v}$ is velocity field of deformable body and ∇ is gradient operator.

Hence Eq.2 becomes

$${\int \int \int }_{V_1}\mathit{\sigma }:\mathit{d}dV+{\int \int \int }_{V_2}\mathit{\sigma }:\mathit{d}dV=\delta \dot{Q}+F{v}_s,$$

(3)

For kinetic sliding friction ($v_s\ne 0$), the kinetic friction force is given by

$$F=\frac{\delta \dot{Q}}{v_s}+\frac{1}{v_s}\left({\int \int \int }_{V_1}\mathit{\sigma }:\mathit{d}dV+{\int \int \int }_{V_2}\mathit{\sigma }:\mathit{d}dV\right),$$

(4)

which reveals that the friction force is weakening as the sliding velocity $v_s$ increasing, which might be the first rational interpretation of the sliding velocity weakening phenomenon in sliding friction. It also shows that the damping of sliding friction is inversely proportional to the relative velocity between the two sliding interfaces, rather than being directly proportional to the relative velocity between the two sliding interfaces as assumed in traditional models. In the same time, Eq.4 indicates that the friction force is proportional to the elastic energy rate that is the ability of the elastic body to absorb the vibration energy caused by sliding motion. It is similar to the situation of a car driving on the bumping road, wheel shock-absorb provides a damping. Eq.4 also indicates that the heat absorbing rate $\delta \dot{Q}$ has impact on the friction force, in particular, frictional heating will reduce the friction force.

For the friction system $B_1+B_2$ in Figure 1, since the fiction force is caused by the contact surface, therefore, the system’s deformation is only happen in a very thin boundary layer of the contact surface between $B_1$ and $B_2$. The rest of the system $B_1+B_2$ can be considered as strain-free. This very thin boundary layer can be considered as a friction boundary layer, and corresponding simplification can be called as friction boundary layer modelling, in which the elastic potential energy cased by the friction force on the contact surface is only stored within a thin layer around the contact surface.

3. Simplification

Based on this perspectives and simplification, we can assume that no friction heat $\delta \dot{Q}=0$ and the elastic energy density rate $\mathit{\sigma }:\mathit{d}$ as constant within the friction boundary layer volume $V=l_x{l}_y{l}_z$, where $l_x,l_y,l_z$ are the length of the friction boundary layer. Noting $\sigma ={\sigma }_{yy}{\mathit{e}}_y\otimes {\mathit{e}}_y=-\frac{N}{l_x{l}_z}{\mathit{e}}_y\otimes {\mathit{e}}_y$ (sign convention: compression stress is defined as negative), and $d=d_{yy}{\mathit{e}}_y\otimes {\mathit{e}}_y=\frac{d{v}_y}{dy}{\mathit{e}}_y\otimes {\mathit{e}}_y$, where $l_x{l}_z$ is the contact area. Thus $\mathit{\sigma }:\mathit{d}={\sigma }_{yy}{d}_{yy}$, Hence, the friction force is given by

$$F=-\frac{N}{v_s}{l}_y\left(\frac{d{v}_y}{dy}\right){|}_{y=0}.$$

(5)

Based on the friction boundary layer, we can assume the elastic body has bumping velocity $v_{{y|}_{y=0}}=v_{y0}$ on the contact surface and decay to zero at $y=\infty$, namely $v_y=v_{yo}{e}^{-y/l_y}$, leads to the velocity gradient $\frac{d{v}_y}{dy}=-\frac{v_{y0}}{l_y}{e}^{-y/l_y}$.

Substitute $\frac{d{v}_y}{dy}=-\frac{v_{y0}}{l_y}{e}^{-y/l_y}$ into Eq.5, we have the sliding fiction force as follows

$$F=\frac{v_{yo}}{v_s}N,v_s\ne 0,$$

(6)

which can be easily understood from the power conservative point of view, that is the dissipation power equal to the potential power of the elastic body, namely $F{v}_s=N{v}_{{y|}_{y=0}}$.

Eq.6 gives the kinetic friction coefficient as follows

$${\mu }_k=\frac{v_{yo}}{v_s}=\frac{\mathrm{bumping}\mathrm{velocity}}{\mathrm{sliding}\mathrm{velocity}},$$

(7)

which provides a clear picture for reducing friction that is to increase the sliding velocity while decreasing the vibration velocity of the object perpendicular to it.

It is worth to mention that the kinetic friction coefficient ${\mu }_k$ is a function of time, and its value is varying with the bumping velocity caused by surface roughness.

4. Conclusions and Perspectives

To the best of the authors’ knowledge, this is the first theoretical formulation of sliding friction force in the context of the physics. This study, which applies thermodynamics of continuum media, provides a clear physical picture about sliding friction and mechanism on how to control friction actively. This marks a significant departure from the traditional models that have failed to accurately predict kinetic friction over a wide range of sliding velocities.

Our findings reveal a surprising inverse relationship between the damping of sliding friction and the relative sliding velocity between the two interfaces. Contrary to the widely accepted belief that friction is directly proportional to the relative velocity, our theoretical model demonstrates that friction force is actually inversely proportional to the sliding velocity. This groundbreaking revelation has the potential to revolutionize our understanding of friction and could lead to the development of new technologies aimed at reducing friction and improving the efficiency of mechanical systems.

To simplify the general result and gain deeper insights into the underlying mechanisms, we introduce the concept of a friction boundary layer. By considering this layer, we derive an approximate expression that sheds light on the strategies for reducing friction. Remarkably, our analysis suggests that one effective way to decrease friction is to increase the sliding velocity while simultaneously reducing the vibration velocity of the object perpendicular to the sliding interface.