Submitted:
25 March 2024
Posted:
26 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
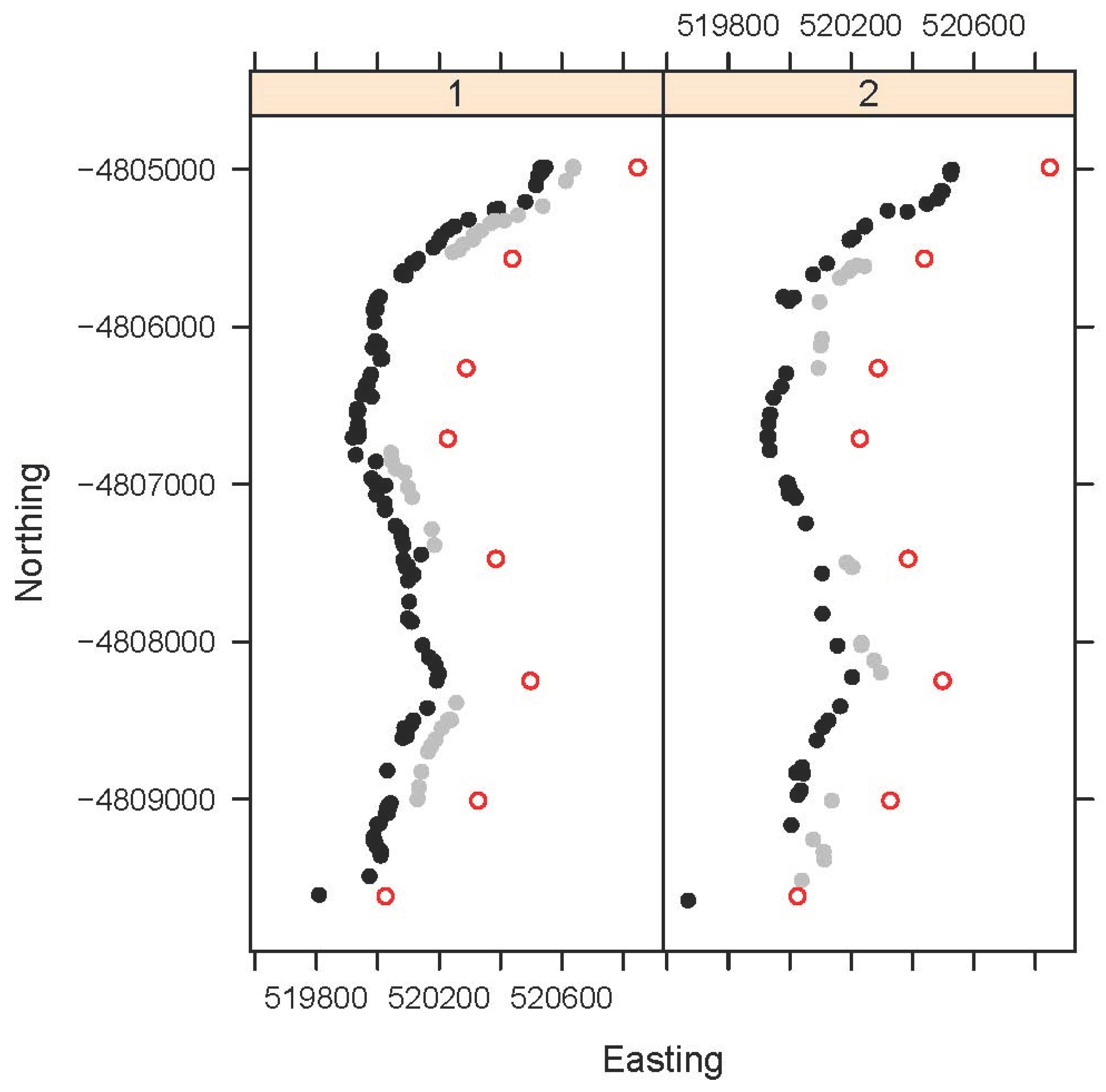
2.1. Study Site and Data Collection
2.2. Experimental Design Including Treatment Allocation (VF Off vs On) and Data Aggregation/Standardisation
2.3. Statistical Analyses
2.3.1. Simple Comparison of Rates
2.3.2. Fitting Poisson GLMs or Negative Binomial Extended GLMs to the MBACI Tables
3. Results
3.1. Data Summary and Simple Comparison of Rates
3.2. Fitting Poisson GLMs or Negative Binomial Extended GLMs to the MBACI Tables
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Baskaran, N.; Boominathan, D. Road kill of animals by highway traffic in the tropical forests of Mudumalai Tiger Reserve, southern India. J. Threat. Taxa 2010, 2, 753–759. [Google Scholar] [CrossRef]
- Fergus, C. The Florida Panther Verges on Extinction. Science 1991, 251, 1178–1180. [Google Scholar] [CrossRef] [PubMed]
- Hobday, A.J.; Minstrell, M.L. Distribution and abundance of roadkill on Tasmanian highways: human management options. Wildl. Res. 2008, 35, 712–726. [Google Scholar] [CrossRef]
- Palazón, S.; Melero, Y.; Gómez, A.; de Luzuriaga, J.L.; Podra, M.; Gosàlbez, J. Causes and patterns of human-induced mortality in the Critically Endangered European mink Mustela lutreola in Spain. Oryx 2012, 46, 614–616. [Google Scholar] [CrossRef]
- Glista, D.J.; DeVault, T.L.; DeWoody, J.A. A review of mitigation measures for reducing wildlife mortality on roadways. Landsc. Urban Plan. 2009, 91, 1–7. [Google Scholar] [CrossRef]
- Muierhead,S. ; Blache,D.; Wykes,B.; Bencini, R. Roo-Guardsuper (registered) sound emitters are not effective at deterring Tammar Wallabies (Macropus eugenii) from a source of food. Wildl. Res. 2006, 33, 131. Animals 2019, 9, 752.
- Valitzski,S.A. Evaluation of Sound as a deterrent for reducing deer-vehicle collisions. Ph.D.Thesis, University of Georgia, Athens, GA, USA, 2007.
- Benten, A.; Hothorn, T.; Vor, T.; Ammer, C. Wildlife warning reflectors do not mitigate wildlife–vehicle collisions on roads. Accid. Anal. Prev. 2018, 120, 64–73. [Google Scholar] [CrossRef]
- Bíl, M.; Andrášik, R.; Bartoniˇ cka, T.; Kˇrivánková, Z.; Sedoník, J. An evaluation of odor repellent effectiveness in prevention of wildlife-vehicle collisions. J. Environ. Manag. 2018, 205, 209–214. [Google Scholar] [CrossRef] [PubMed]
- Umstatter, C. The evolution of virtual fences: A review. Comput. Electron. Agric. 2011, 75, 10–22. [Google Scholar] [CrossRef]
- Fox, S.; Potts, J.M.; Pemberton, D.; Crosswell, D. Roadkill mitigation: trialing virtual fence devices on the west coast of Tasmania. Aust. Mammal. 2019, 41, 205–211. [Google Scholar] [CrossRef]
- Hurlbert, S.H. Pseudoreplication and the Design of Ecological Field Experiments. Ecol. Monogr. 1984, 54, 187–211. [Google Scholar] [CrossRef]
- Coulson, G.; Bender, H. Roadkill mitigation is paved with good intentions: a critique of Fox et al. (2019). Aust. Mammal. 2020, 42, 122–130. [Google Scholar] [CrossRef]
- Fox, S.; Potts, J. Virtual fence devices—a promising innovation: a response to Coulson and Bender (2019). Aust. Mammal. 2020, 42, 131–133. [Google Scholar] [CrossRef]
- Englefield, B.; Candy, S.G.; Starling, M.; McGreevy, P.D. A Trial of a Solar-Powered, Cooperative Sensor/Actuator, Opto-Acoustical, Virtual Road-Fence to Mitigate Roadkill in Tasmania, Australia. Animals 2019, 9, 752. [Google Scholar] [CrossRef]
- Rytwinski, T.; van der Ree, R.; Cunnington, G.M.; Fahrig, L.; Findlay, C.S.; Houlahan, J.; Jaeger, J.A.; Soanes, K.; van der Grift, E.A. Experimental study designs to improve the evaluation of road mitigation measures for wildlife. J. Environ. Manag. 2015, 154, 48–64. [Google Scholar] [CrossRef] [PubMed]
- Candy, S.G.; Englefield, B. Analysis of Roadkill Rates from a Trial of a Virtual Fence for Reducing Wombat Road Mortalities. Are Severely Under-Powered Studies Worth the Effort? Current Journal of Applied Science and Technology, 2022, 41: 1-13.
- Jones, B.; Kenward, M.G. Design and Analysis of Cross-Over Trials; Chapman and Hall/CRC: London, UK, 2014. [Google Scholar]
- Stannard, H.J.; Wynan, M.B.; Wynan, R.J.; Dixon, B.A.; Mayadunnage, S.; Old, J.M. Can virtual fences reduce wombat road mortalities? Ecol. Eng. 2021, 172: 106414.
- Haight, FA. Handbook of the Poisson Distribution, John Wiley & Sons, New York, NY, USA; 1967. ISBN 978-0-471-33932-8.
- McCullagh, P. and J.A. Nelder. 1989. Generalized Linear Models. 2nd Edition. Chapman and Hall/CRC, USA.
- Booth, J.G.; Casella, G.; Friedl, H.; Hobert, J.P. Negative binomial loglinear mixed models. Stat. Model. 2003, 3, 179–191. [Google Scholar] [CrossRef]
- R Core Team R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018.
- Wood, S.N. Generalized additive models, 2nd ed.; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Hobday, A.J. Nighttime driver detection distances for Tasmanian fauna: informing speed limits to reduce roadkill. Wildl. Res. 2010, 37, 265–272. [Google Scholar] [CrossRef]
| Fixed effect | LORP estimates (SE, t-value) | Average LORP (SE, t-value) |
Percentage rate reduction | NB θ Estimate (Poisson deviance,DF) |
||
| 1 | 2 | 3 | ||||
| Rep | 0.326 (0.655, 0.50ns) |
-1.301 (0.804, -1.62ns) |
0.684 (0.807, 0.85ns) |
-0.097 (0.438, -0.22ns) |
9.2 | 4.8 (52.5**, 23) |
| Block | 0.254 (0.433, 0.59ns) |
-0.600 (0.620, -0.97ns) |
-0.172 (0.378, -0.46 ns) |
15.9 | 11.6 (47.7*, 27) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




