Submitted:
25 March 2024
Posted:
25 March 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Model Sensitivity and Uncertainty Analysis Input for the Fourth-Order Maximum Entropy Based Predictive Modeling Methodology (4th-BERRU-PM): Review and Applicability to Energy Systems
2.1. Input to 4th-BERRU-PM Methodology: 4th-Order Sensitivity and Uncertainty Analysis of Model Responses to Model Parameters
- (i)
-
The expected value, denoted as , of a computed response , for ; the vector of the computed responses is defined as follows: . Up to, and including, the fourth-order response sensitivities to parameters, the expected value of a computed response has the following expression obtained by integrating formally Eq. (1) over the unknown distribution of parameters:In Eq. (2), the moments up to and including fourth-order of the unknown distribution of model parameters are assumed to be known. These moments are as follows: (a) the covariances of two model parameters, and , are denoted as , , where denotes the total number of parameters under consideration; the parameter covariance matrix is denoted as ; (b) the triple-correlations of three model parameters , , and , are denoted as , where ; (c) the quadruple-correlations of four model parameters , , , and , are denoted as , where .
- (ii)
- The correlation, denoted as , between a parameter and a computed response , for and ; the correlation matrix between parameters and computed responses is denoted as . Up to, and including, the fourth-order response sensitivities to parameters, the correlation between a parameter and a computed response has the following expression:
- (iii)
- The covariances, denoted as , between two computed responses and , for ; the covariance matrix of computed responses is denoted as . Up to and including the fourth-order response sensitivities to parameters, the covariance between two computed responses has the following expression:
- (iv)
- The triple correlations among three responses, , and , , which are denoted as . Up to and including the fourth-order response sensitivities to parameters, these triple correlations among three responses have the following expression:
- (v)
- The quadruple-correlations among four responses, , , and , for , which are denoted as . Up to and including the fourth-order response sensitivities to parameters, these quadruple correlations among computed responses have the following expression:
- (vi)
- The expressions of the triple and quadruple correlations among parameters and responses are provided by Cacuci [14]; they will not be reproduced here because they are considered to be negligible by comparison to the other terms used within the 4th-BERRU-PM methodology.
2.2. Applicability of the 4th-Order Sensitivity and Uncertainty Analysis to Energy Systems
3. Illustrative High-Order Uncertainty Analysis of the PERP Reactor Physics Benchmark
3.1.“High Precision” Parameters, Having Uniform Relative Standard Deviations
3.2.“Medium Precision” Parameters, Having Uniform Relative Standard Deviations
3.3. Low Precision” parameters, Having Uniform Relative Standard Deviations
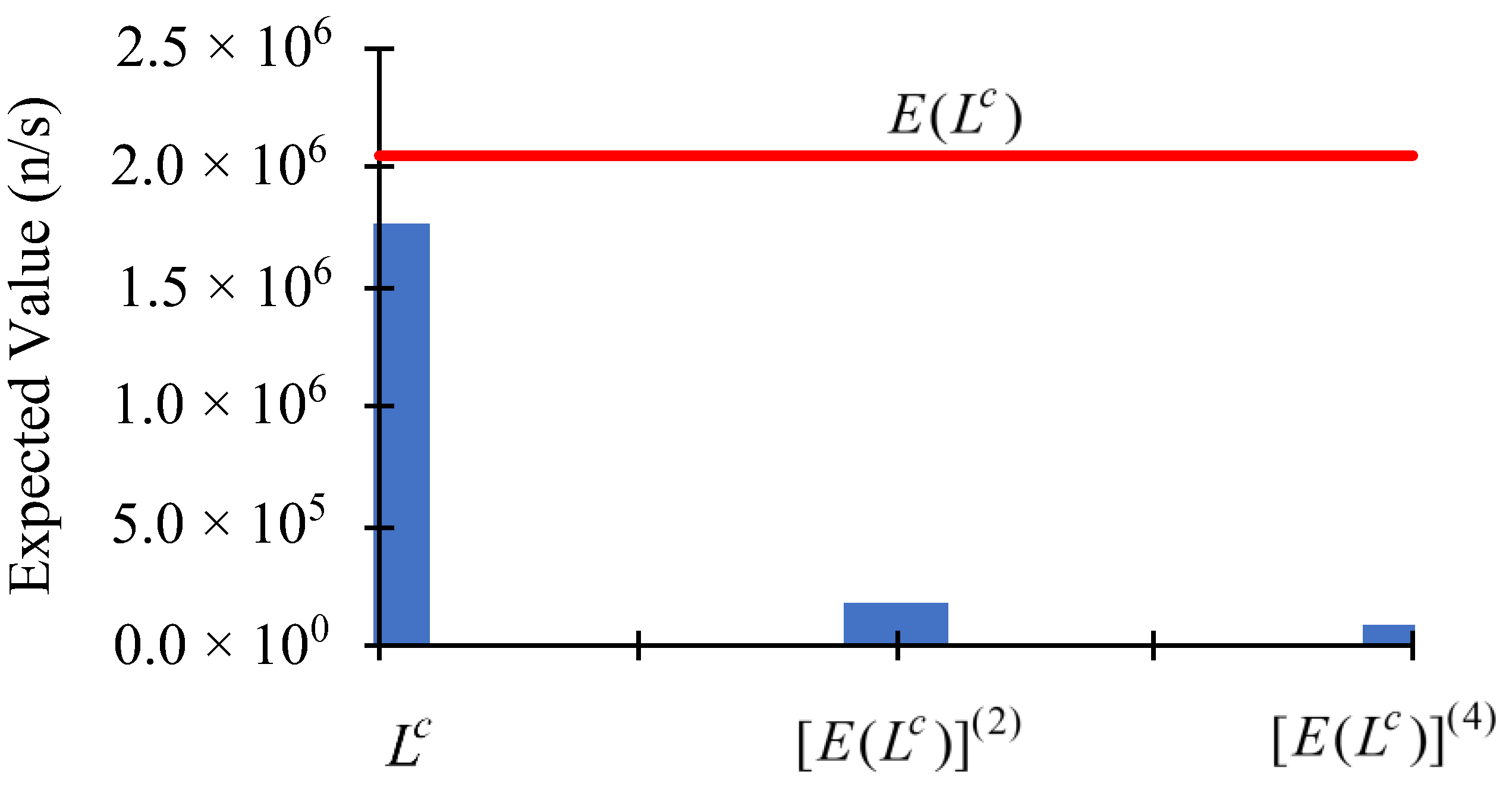
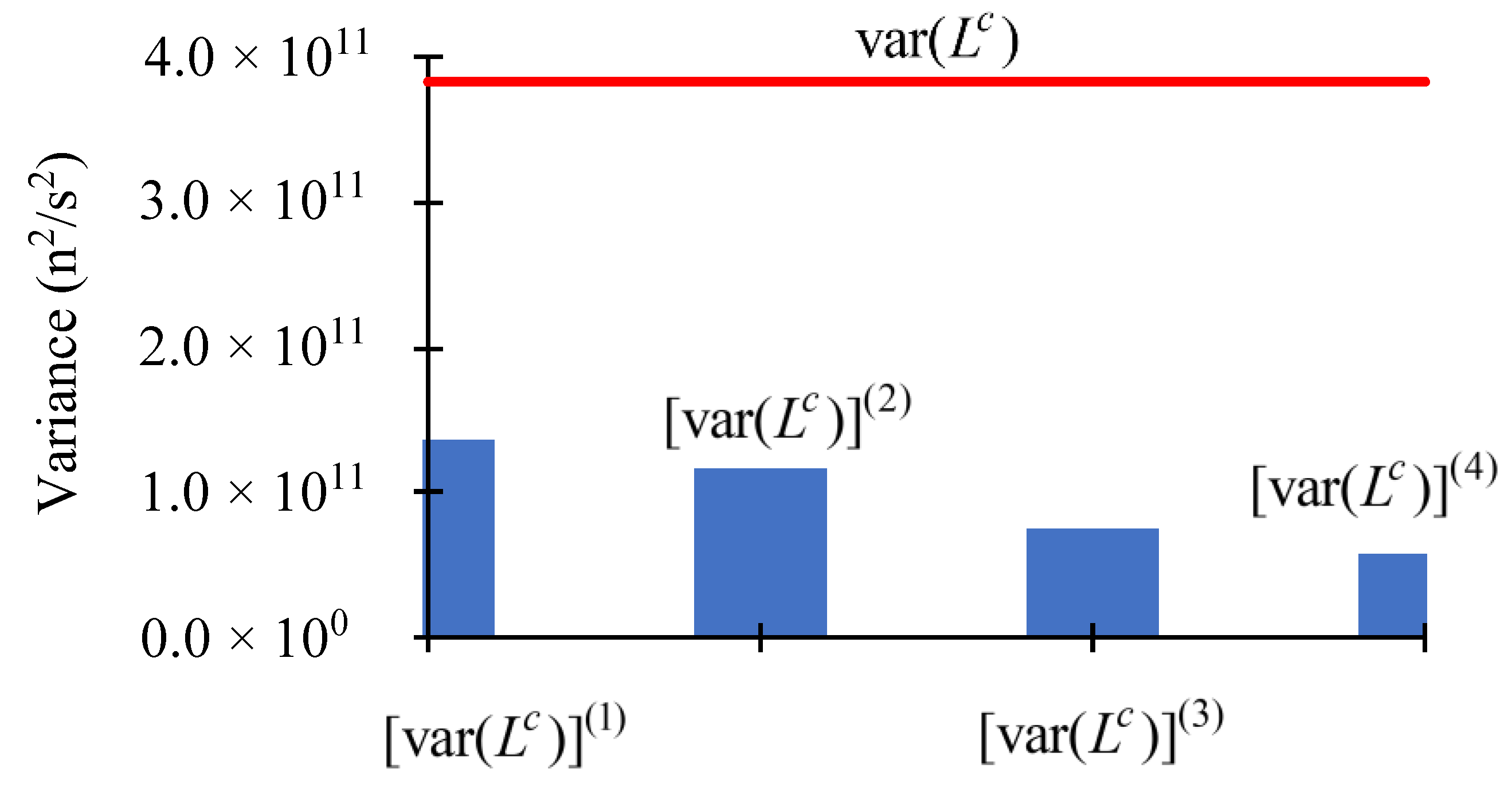
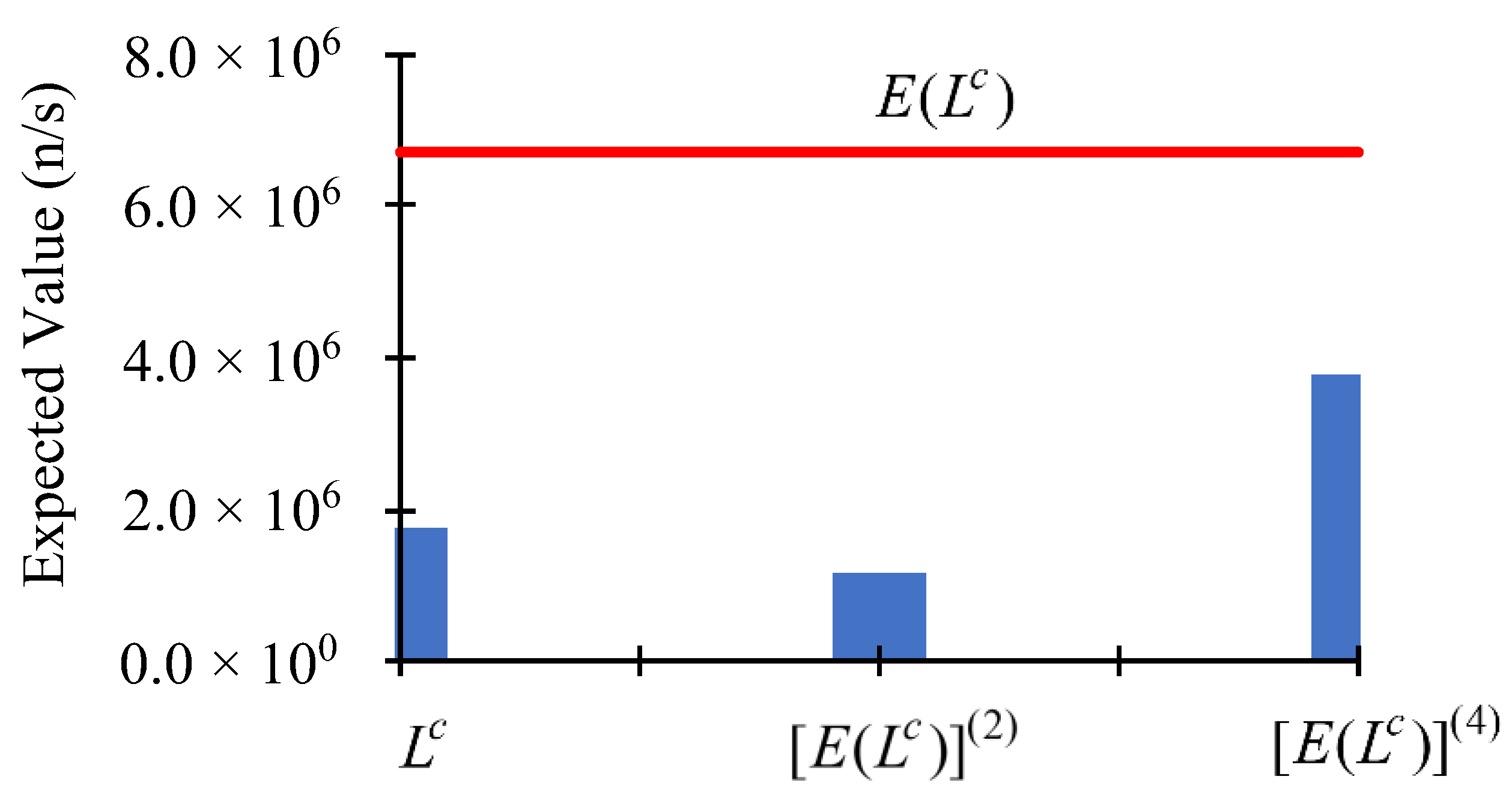
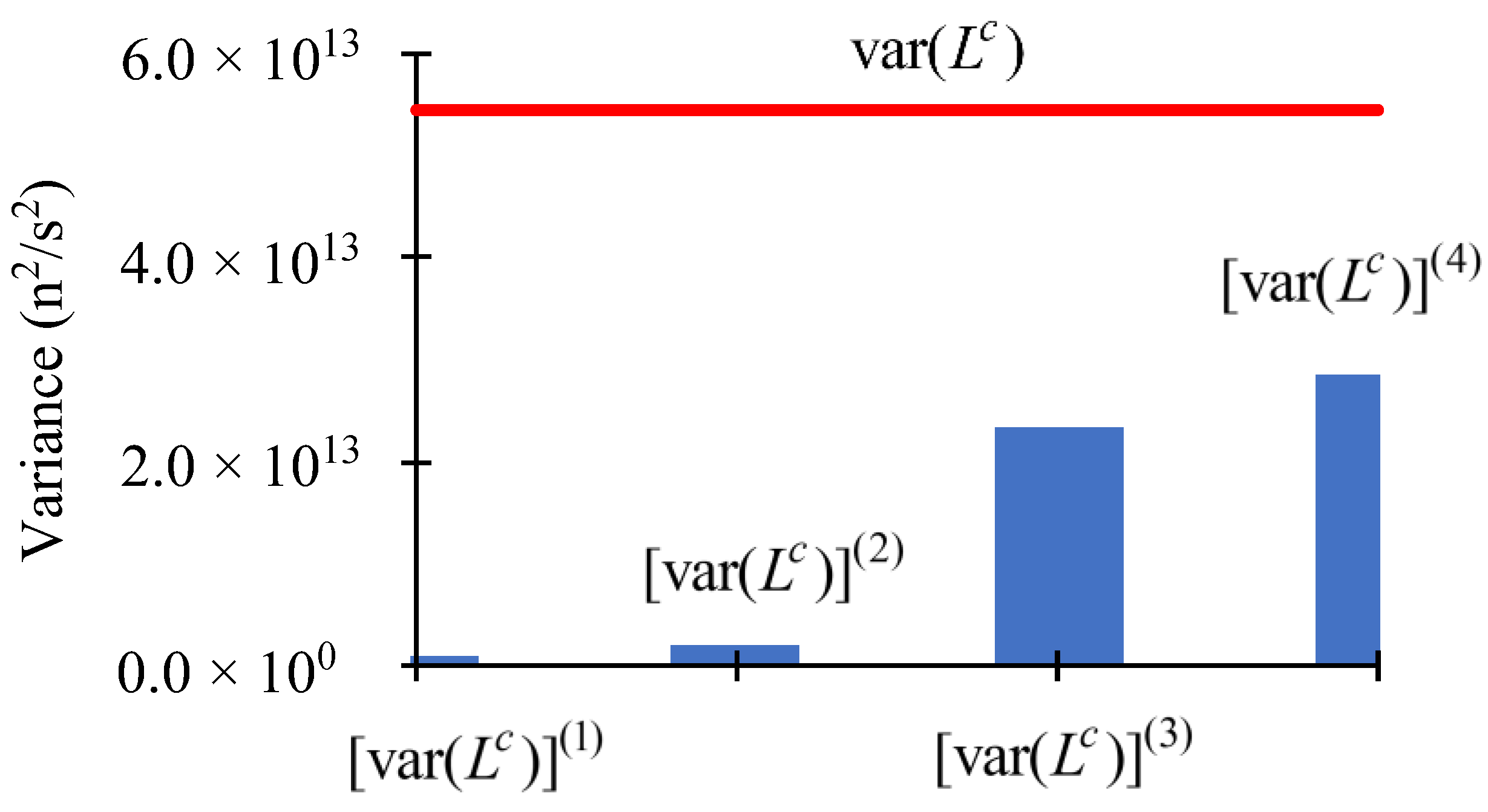
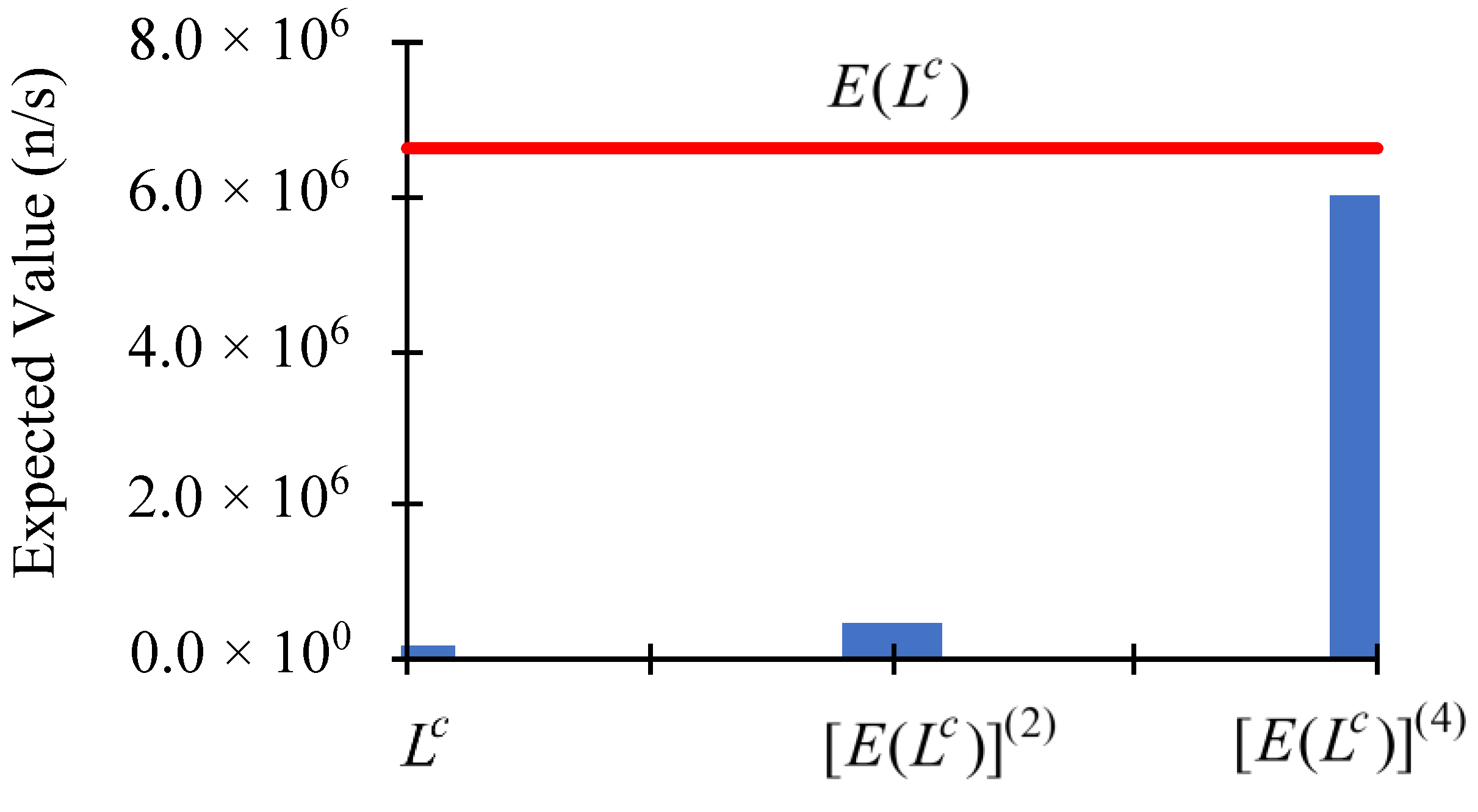
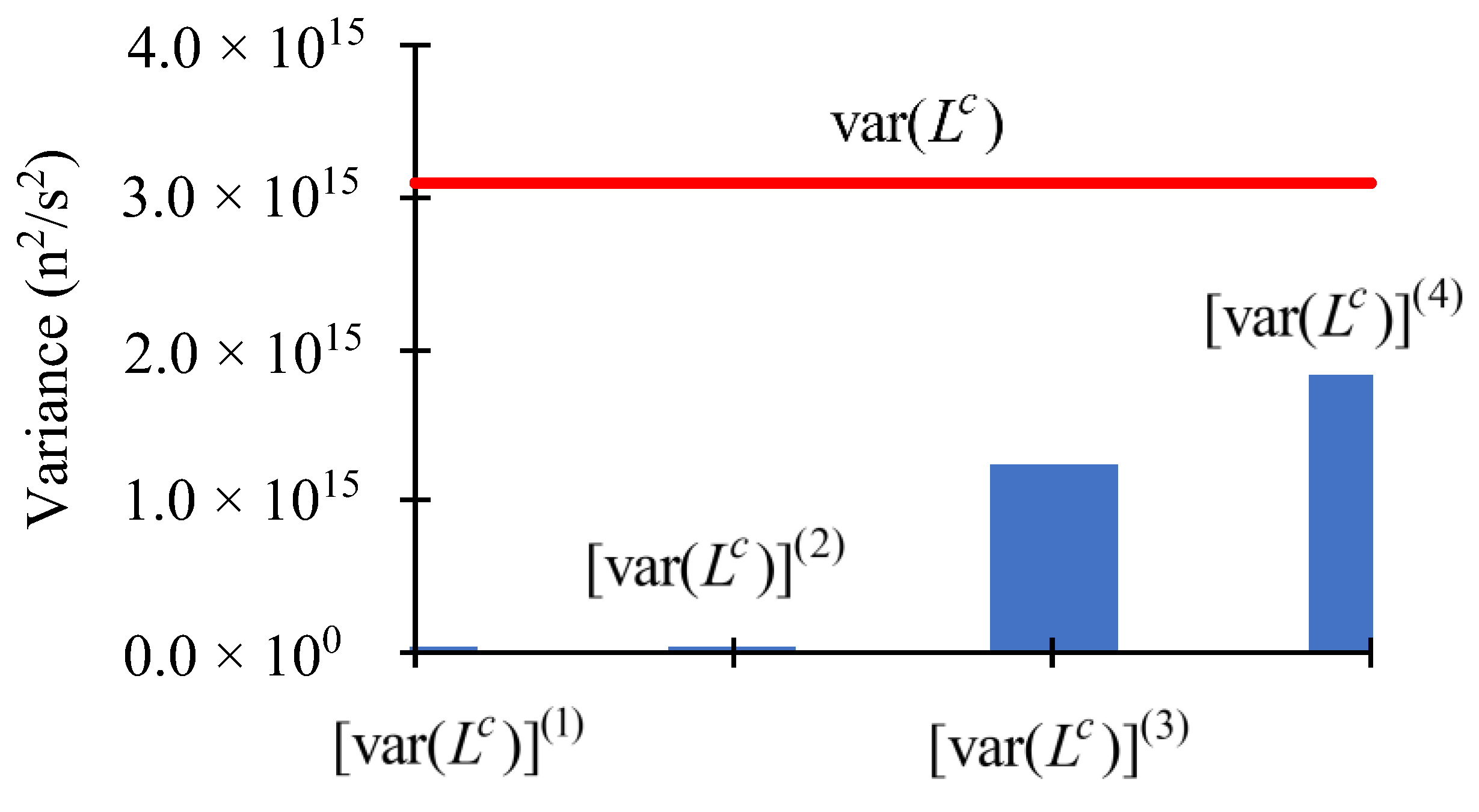
4. Concluding Discussion
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A: Computational Model of the PERP Benchmark
| Materials | Isotopes | Weight Fraction |
Density (g/cm3) |
Zones |
|---|---|---|---|---|
| Material 1 (plutonium metal) |
Isotope 1 (239Pu) | 9.3804 × 10−1 | 19.6 | Material 1 is assigned to zone 1, which has a radius of 3.794 cm. |
| Isotope 2 (240Pu) | 5.9411 × 10−2 | |||
| Isotope 3 (69Ga) | 1.5152 × 10−3 | |||
| Isotope 4 (71Ga) | 1.0346 × 10−3 | |||
| Material 2 (polyethylene) |
Isotope 5 (12C) | 8.5630 × 10−1 | 0.95 | Material 2 is assigned to zone 2, which has an inner radius of 3.794 cm and an outer radius of 7.604 cm. |
| Isotope 6 (1H) | 1.4370 × 10−1 |
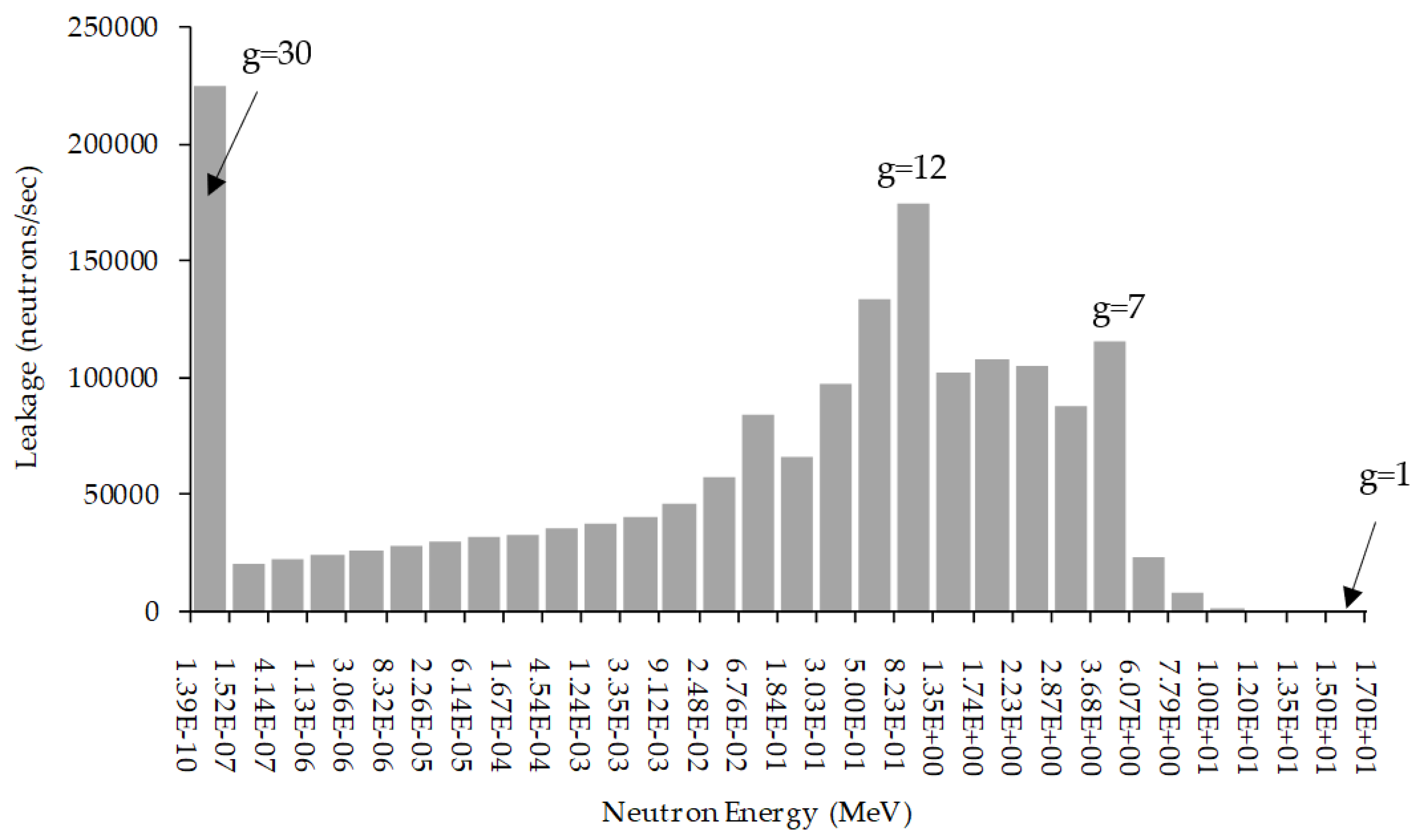
| g | 1 | 2 | 3 | 4 | 5 | 6 |
| 1.50×101 | 1.35×101 | 1.20×101 | 1.00×101 | 7.79×100 | 6.07×100 | |
| 1.70×101 | 1.50×101 | 1.35×101 | 1.20×101 | 1.00×101 | 7.79×100 | |
| g | 7 | 8 | 9 | 10 | 11 | 12 |
| 3.68×100 | 2.87×100 | 2.23×100 | 1.74×100 | 1.35×100 | 8.23×10−1 | |
| 6.07× 100 | 3.68×100 | 2.87×100 | 2.23×100 | 1.74×100 | 1.35×100 | |
| g | 13 | 14 | 15 | 16 | 17 | 18 |
| 5.00×10−1 | 3.03×10−1 | 1.84×10−1 | 6.76×10−2 | 2.48×10−2 | 9.12×10−3 | |
| 8.23×10−1 | 5.00×10−1 | 3.03×10−1 | 1.84×10−1 | 6.76×10−2 | 2.48×10−2 | |
| g | 19 | 20 | 21 | 22 | 23 | 24 |
| 3.35×10−3 | 1.24×10−3 | 4.54×10−4 | 1.67×10−4 | 6.14×10−5 | 2.26×10−5 | |
| 9.12×10−3 | 3.35×10−3 | 1.24×10−3 | 4.54×10−4 | 1.67×10−4 | 6.14×10−5 | |
| g | 25 | 26 | 27 | 28 | 29 | 30 |
| 8.32×10−6 | 3.06×10−6 | 1.13×10−6 | 4.14×10−7 | 1.52×10−7 | 1.39×10−10 | |
| 2.26×10−5 | 8.32×10−6 | 3.06×10−6 | 1.13×10−6 | 4.14×10−7 | 1.52×10−7 |
- Using the notation employed in PARTISN [20], the quantity denotes the “group-flux” for group , and is the unknown state-function obtained by solving Eqs. (A1) and (A2).
- The spontaneous-fission isotopes in the PERP benchmark are “isotope 1” (239Pu) and “isotope 2” (240Pu). The quantity denotes the total number of spontaneous-fission isotopes; for the PERP benchmark, . The spontaneous fission neutron spectra of 239Pu and, respectively, 240Pu, are approximated by Watt’s fission spectra, each spectrum using two evaluated parameters, denoted as and , respectively. The decay constant for actinide nuclide is denoted as , while denotes the fraction of decays that are spontaneous fission (the “spontaneous fission branching fraction”).
- The quantity denotes the atom density of isotope i in material m; , , where denotes the total number of isotopes, and denotes the total number of materials. The computation of uses the following well-known expression:where denotes the mass density of material m, ; denotes the weight fraction of isotope i in material m; denotes the atomic weight of isotope , ; denotes the Avogadro’s number. For the PERP benchmark, and , but since the respective isotopes are all distinct (i.e., are not repeated) in the PERP benchmark’s distinct materials, as specified in Table A1, it follows that only the following isotopic number densities exist for this benchmark: .
- The quantity represents the scattering transfer cross section from energy group into energy group . The transfer cross sections is computed in terms of the th-order Legendre coefficients (of the Legendre-expanded microscopic scattering cross section from energy group into energy group , for isotope ), which are tabulated parameters, using the following finite-order expansion:where denotes the order of the respective finite expansion in Legendre polynomial. The variable will henceforth no longer appear in the arguments of the various cross sections since the cross-sections for every material are treated in the PARTISN [20] computations as being space-independent within the respective material.
- The total cross section for energy group and material , is computed for the PERP benchmark using the following expression:where and denote, respectively, the tabulated group microscopic fission and neutron capture cross sections for group . Other nuclear reactions, including (n,2n) and (n,3n) reactions, are not present in this benchmark. The expressions in Eqs. (A8) and (A9) indicate that the zeroth-order (i.e., ) scattering cross sections must be separately considered from the higher order (i.e., ) scattering cross sections, since the former contribute to the total cross sections, while the latter do not.
-
PARTISN [20] computes the quantity using the quantities , which are provided in data files for each isotope , and energy group , as follows:For the purposes of sensitivity analysis, the quantity , which denotes the number of neutrons that were produced per fission by isotope and energy group , can be obtained by using the relation , where the isotopic fission cross sections are available in data files for computing reaction rates.
- The quantity denotes the fission spectrum in energy group ; it is defined in PARTISN [20] as a space-independent quantity, as follows:where denotes the isotopic fission spectrum in group , while denotes the corresponding spectrum weighting function.
- The vector , which appears in the expression of the Boltzmann-operator , represents the “vector of imprecisely known model parameters,” comprising 21,976 components, which are presented in Table A3, below.
| Symbol | Parameter Name | Number of Parameters |
|---|---|---|
| Multigroup microscopic total cross section for isotope and energy group | 180 |
|
| Multigroup microscopic scattering cross section for -th order Legendre expansion, from energy group into energy group , for isotope | 21,600 |
|
| Multigroup microscopic fission cross section and energy group | 60 |
|
| Average number of neutrons per fission for isotope and energy group | 60 |
|
| Fission spectrum for isotope and energy group | 60 |
|
| Source parameters | 10 | |
| Isotopic number density for isotope and material | 6 |
|
| Total number of parameters: | 21,976 |
References
- Cacuci, D.G. Fourth-Order Predictive Modelling: II. 4th-BERRU-PM Methodology for Combining Measurements with Computations to Obtain Best-Estimate Results with Reduced Uncertainties. Am. J. Comp. Math., 2023, 13, 439-475. [CrossRef]
- Valentine, T.E. Polyethylene-Reflected Plutonium Metal Sphere Subcritical Noise Measurements. SUB-PU-METMIXED-001, International Handbook of Evaluated Criticality Safety Benchmark Experiments; NEA/NSC/DOC(95)03/I-IX; Organization for Economic Co-Operation and Development; Nuclear Energy Agency: Paris, France, 2006.
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev., 1957, 106, pp. 620.
- Cacuci, D.G. Second-Order MaxEnt Predictive Modelling Methodology. I: Deterministically Incorporated Computational Model (2nd-BERRU-PMD). Am. J. Comp. Math., 2013, 13, 236-266. [CrossRef]
- Cacuci, D.G. Second-Order MaxEnt Predictive Modelling Methodology. II: Probabilistically Incorporated Computational Model (2nd-BERRU-PMP). Am. J. Comp. Math., 2023, 13, 267-294. [CrossRef]
- SCALE: a modular code system for performing standardized computer analyses for licensing evaluation, ORNL/TM 2005/39, Version 6, Oak Ridge National Laboratory, Oak Ridge, Tennessee, USA, 2009.
- Venard, C.; Santamarina, A.; Leclainche, A.; Mournier, C. The R.I.B. Tool for the determination of computational bias and associated uncertainty in the CRISTAL criticality safety package. Proceedings of ANS Nuclear Criticality Safety Division Topical Meeting (NCSD 2009), Richland, Washington, USA, 2009.
- Rabier, F. Overview of global data assimilation developments in numerical weather-prediction centers, Q. J. R. Meteorol. Soc., 2005, 131(613), 3215.
- Lewis, J. M.; Lakshmivarahan, S.; Dhall, S.K. Dynamic Data Assimilation: A Least Square Approach. Cambridge University Press, Cambridge, UK, 2006.
- Lahoz, W.; Khattatov, B.; Ménard, R. Eds. Data Assimilation: Making Sense of Observations, Springer Verlag, Heidelberg, Germany, 2010.
- Práger, T.; Kelemen, F. D. Adjoint methods and their application in earth sciences. Chapter 4, Part A, pp 203-275, in Faragó, I.; Havasi, Á.; Zlatev, Z. (Eds.) Advanced Numerical Methods for Complex Environmental Models: Needs and Availability, Bentham Science Publishers, Bussum, The Netherlands, 2013.
- Cacuci, D.G.; Navon, M.I.; Ionescu-Bujor, M. Computational Methods for Data Evaluation and Assimilation. Chapman & Hall/CRC, Boca Raton, USA, 2014.
- Cacuci, D. G.; Fang, R. The nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology: Overcoming the Curse of Dimensionality: Vol. II: Application to a Large-Scale System; Springer Nature Switzerland AG, 6330 Cham, Switzerland, 2023. ISBN 978-3-031-19634-8 ISBN 978-3-031-19635-5. [CrossRef]
- Cacuci, D.G. The nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology: Overcoming the Curse of Dimensionality. Volume I: Linear Systems. Springer Nature Switzerland, Cham, Switzerland, 2022. [CrossRef]
- Cacuci, D. G. The nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology (nth-CASAM): Overcoming the Curse of Dimensionality in Sensitivity and Uncertainty Analysis, Volume III: Nonlinear Systems. Springer Nature Switzerland, Cham, 2023. [CrossRef]
- Bellman, R.E. Dynamic programming. Rand Corporation, Princeton University Press, ISBN 978-0-691-07951-6, USA. 1957.
- Cacuci, D. G.; Fang, R. Review of Fourth-Order Maximum Entropy Based Predictive Modelling and Illustrative Application to a Nuclear Reactor Benchmark: II. Best-Estimate Predicted Values and Uncertainties for Model Responses and Parameters. Energies, 2024, submitted.
- Tukey, J.W. The Propagation of Errors, Fluctuations and Tolerances. Technical Reports No. 10–12; Princeton University. Princeton, NJ, USA, 1957.
- Saltarelli, A.; Chan, K.; Scott, E. M. (Eds.) Sensitivity analysis. J. Wiley & Sons Ltd. Chichester, UK, 2000.
- Alcouffe, R. E.; Baker, R. S.; Dahl, J. A.; Turner, S.A.; Ward, R. PARTISN: A Time-Dependent, Parallel Neutral Particle Transport Code System. LA-UR-08-07258; Los Alamos National Laboratory: Los Alamos, NM, USA, 2008.
- Conlin, J.L.; Parsons, D.K.; Gardiner, S.J.; Gray, M.; Lee, M.B.; White, M.C. MENDF71X: Multigroup Neutron Cross-Section Data Tables Based upon ENDF/B-VII.1X. Los Alamos National Laboratory Report LA-UR-15-29571; Los Alamos National Laboratory: Los Alamos, NM, USA, 2013.
- Chadwick M.B.; Herman M.; Obložinský P.; Dunn M.E.; Danon Y.; Kahler A.C.; Smith D.L.; Pritychenko B.; Arbanas G.; Brewer R. et al. ENDF/B-VII.1: Nuclear data for science and technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets, 2011, 112, 2887–2996. [CrossRef]
- Wilson, W.B.; Perry, R.T.; Shores, E.F.; Charlton, W.S.; Parish, T.A.; Estes, G.P.; Brown, T.H.; Arthur, E.D.; Bozoian, M.; England, T.R.; et al. SOURCES4C: A code for calculating (α,n), spontaneous fission, and delayed neutron sources and spectra. In Proceedings of the American Nuclear Society/Radiation Protection and Shielding Division 12th Biennial Topical Meeting, Santa Fe, NM, USA, 14–18 April 2002.
| g | 1st-order | 2nd-order | 3rd-order | 4th-order |
|---|---|---|---|---|
| 1 | −8.471 × 10−6 | 7.636 × 10−7 | 6.322 × 10−8 | 1.460 × 10−7 |
| 2 | −2.060 × 10−5 | 2.280 × 10−6 | 4.516 × 10−8 | 4.956 × 10−7 |
| 3 | −6.810 × 10−5 | 9.021 × 10−6 | −4.677 × 10−7 | 2.245 × 10−6 |
| 4 | −3.932 × 10−4 | 6.673 × 10−5 | −8.758 × 10−6 | 2.039 × 10−5 |
| 5 | −2.449 × 10−3 | 5.549 × 10−4 | −1.216 × 10−4 | 2.142 × 10−4 |
| 6 | −9.342 × 10−3 | 2.935 × 10−3 | −1.123 × 10−3 | 1.553 × 10−3 |
| 7 | −7.589 × 10−2 | 3.949 × 10−2 | −2.690 × 10−2 | 3.513 × 10−2 |
| 8 | −9.115 × 10−2 | 5.604 × 10−2 | −4.380 × 10−2 | 5.536 × 10−2 |
| 9 | −1.358 × 10−1 | 1.014 × 10−1 | −9.758 × 10−2 | 1.416 × 10−1 |
| 10 | −1.659 × 10−1 | 1.428 × 10−1 | −1.604 × 10−1 | 2.582 × 10−1 |
| 11 | −1.899 × 10−1 | 1.849 × 10−1 | −2.385 × 10−1 | 4.233 × 10−1 |
| 12 | −4.446 × 10−1 | 6.620 × 10−1 | −1.373 × 100 | 3.815 × 100 |
| 13 | −5.266 × 10−1 | 9.782 × 10−1 | −2.590 × 100 | 9.015 × 100 |
| 14 | −5.772 × 10−1 | 1.262 × 100 | −3.991 × 100 | 1.650 × 101 |
| 15 | −5.820 × 10−1 | 1.391 × 100 | −4.581 × 100 | 2.208 × 101 |
| 16 | −1.164 × 100 | 4.460 × 100 | −2.530 × 101 | 1.890 × 102 |
| 17 | −1.173 × 100 | 4.853 × 100 | −2.991 × 101 | 2.432 × 102 |
| 18 | −1.141 × 100 | 4.828 × 100 | −3.049 × 101 | 2.543 × 102 |
| 19 | −1.094 × 100 | 4.619 × 100 | −2.913 × 101 | 2.428 × 102 |
| 20 | −1.033 × 100 | 4.284 × 100 | −2.655 × 101 | 2.175 × 102 |
| 21 | −9.692 × 10−1 | 3.937 × 100 | −2.388 × 101 | 1.915 × 102 |
| 22 | −8.917 × 10−1 | 3.515 × 100 | −2.069 × 101 | 1.609 × 102 |
| 23 | −8.262 × 10−1 | 3.177 × 100 | −1.823 × 101 | 1.382 × 102 |
| 24 | −7.495 × 10−1 | 2.792 × 100 | −1.552 × 101 | 1.140 × 102 |
| 25 | −7.087 × 10−1 | 2.604 × 100 | −1.427 × 101 | 1.033 × 102 |
| 26 | −6.529 × 10−1 | 2.349 × 100 | −1.260 × 101 | 8.932 × 101 |
| 27 | −5.845 × 10−1 | 2.039 × 100 | −1.061 × 101 | 7.288 × 101 |
| 28 | −5.474 × 10−1 | 1.885 × 100 | −9.678 × 100 | 6.565 × 101 |
| 29 | −5.439 × 10−1 | 1.891 × 100 | −9.800 × 100 | 6.705 × 101 |
| 30 | −9.366 × 100 | 4.296 × 102 | −2.966 × 104 | 2.720 × 106 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





