Kinematics of Balls and Light Versus the Theory of Special Relativity

1. Introduction

From 2017 to 2019, we studied Michelson‒Morley’s experiment, Fizeau’s experiment, the observation of binary stars, and other topics related to light as well. These studies were essential in understanding light reflection, emission, and propagation as mechanical phenomena in the following years.

The first part of this article summarizes the kinematics of light, a concept emerging from a series of articles beginning in 2020 on the reflection of balls with and without mass. The study of ball reflection gives the velocity formula for a ball reflected by a wall for any incident angle the moving ball makes with the wall’s moving direction and for any inclination of the wall, not just the known formula for a two-ball frontal collision. A complete study of ball reflection for any incident angle and wall inclination was required when the reflection of hypothetical massless balls was applied to light as a massless entity. We continued with the emission and propagation of balls with and without mass, which, when applied to light, show that the emitted light inherits/possesses the velocity of the source. Until the end of 2023, considering the ballistic law of light, we explained experiments and observations that have been misunderstood for over 100 years.

The kinematics of balls, with and without mass, and light are identical. As such, if we include the massless entities in mechanics, we can state that the ballistic law gives light the mechanical speed of its source besides the emitted speed $c$ of an electromagnetic nature.

The second part of this article examines the Lorentz transformation and special relativity revealing their hidden incorrectness.

2. Kinematics of Balls

2.1. Balls Brought from Rest to Velocity v

A constant force $F$ acts on a ball of mass $m$ in a straight line along a length $d$ from rest to a velocity $v$ at a constant acceleration $a$. In time $t$, while the speed of the ball increases from zero to $v$, the inertial force $F_i$ of the ball acts with the same magnitude in the opposite direction of force $F$ that changes its state. Energy $E$ consumed to overcome $F_i$ is given by the mechanical work created by the force $F$, $L=F\times d=ma\times {\displaystyle \frac{1}{2}}a{t}^2={\displaystyle \frac{1}{2}}m{v}^2$. While the ball is moved from rest to speed $v$, it gains energy $E={\displaystyle \frac{1}{2}}m{v}^2$ stored in its momentum $P=mv$, which opposes any force that changes its new state. Indeed, the integral of momentum $P=mv$, as a linear function with a constant slope $m$ and the variable speed from zero to $v$ gives the energy gained by the ball, ${\int }_0^{v}mv={\displaystyle \frac{1}{2}}m{v}^2=E$. The ball continues traveling at the velocity $v$ when the force $F$ stops.

Suppose a carrier with balls of different masses stops at the velocity $v$. In that case, all balls continue traveling independently from the carrier and one another with velocity $v$, regardless of their mass, including hypothetical massless ones. Differently from balls with mass, the massless balls travel from rest to speed $v$ without the force $F$ to act upon them, $F=0$, without energy consumption, $E=0$, and without momentum after that, $P=0$. Massless balls need a carrier that only consumes energy for itself.

2.2. Balls Emitted at Velocity $V$ by a Moving Source at Velocity $v$

Suppose that in the absolute frame, a hypothetical source traveling at a velocity $v$ emits balls of different masses at a speed $V$. In the instance of emission, the kinematics of an emitted ball of mass $m$ depends on two vector momentums. One momentum is given by $m\mathit{v}$ that the ball already has while moving with the source and another by $m\mathit{V}$. The vector sum of the two momentums is ${\mathit{P}}_{\mathit{s}\mathit{a}}=m\mathit{V}+m\mathit{v}$ where ${\mathit{P}}_{\mathit{s}\mathit{a}}=m{\mathit{V}}_{sa}$ and ${\mathit{V}}_{sa}$ is the propagation ball’s velocity in the frame at absolute rest from the instance of the emission. The vector equation $m{\mathit{V}}_{\mathit{s}\mathit{a}}=m\mathit{V}+m\mathit{v}$ is independent of the bolls’ mass. At the limit when the mass of a ball converges to zero, the equation of the momentums gives the equation of the velocities ${\mathit{V}}_{\mathit{s}\mathit{a}}=\mathit{V}+\mathit{v}$ that applies to balls with and without mass. Thus, if the hypothetical source emits balls of different masses at the same emitted velocity $\mathit{V}$, each ball, including massless ones, has the same velocity ${\mathit{V}}_{\mathit{s}\mathit{a}}=\mathit{V}+\mathit{v}$. Note that ${\mathit{V}}_{\mathit{s}\mathit{a}}$ has different directions and magnitudes according to $\mathit{V}$ directions even if the magnitude of $\mathit{V}$ is the constant speed $V$ in any direction.

2.3. Ballistic Law

Considering Section 2.1 and 2.2, we can understand the phenomenon that acts on emitted balls formulated in the following so-called ballistic law: balls with or without mass inherit the velocity of their source in the absolute frame in the instance of emission. The vector sum of the source velocity and the emitted velocity of a ball in the emission instance gives the mathematical expression of this law in the absolute frame.

A ball with or without mass inherits the velocity $v$ of its source and travels in the absolute frame at propagation velocity ${\mathit{V}}_{\mathit{s}\mathit{a}}=\mathit{V}+\mathit{v}$ applicable for any direction of the speed $V$. The ball travels at the emitted speed $V$ concerning the source in any direction in the source inertial frame.

Suppose that in the absolute frame, a hypothetical source at rest emits balls with or without mass at period $T$ and speed $V$ in all directions uniformly distributed in space. Each spherical ball front has its center at the source. The length between two consecutive balls traveling in the same direction is $\lambda$; this is true for any other direction.

Suppose the same ball source travels at a velocity $v$. The ballistic law acts in the absolute frame on each ball with or without mass making each ball travel at its specific propagation velocity $V_{sa}$ offered by the vector sum of the emitted ball velocity $V$ specific for its direction and the same common source velocity $v$. Therefore, each spherical ball front emitted at period $T$ travels in the absolute frame at velocity $v$ with its center at the source location at all times and continuously expanding with a radius increasing in time with $Vt$. In the inertial frame of the source, each spherical ball front is emitted at period $T$ and speed $V$ with balls uniformly distributed in the space of the source inertial frame having its center at the source at all times; the length between two consecutive balls traveling in the same direction is $\lambda$. The ballistic law acts in the background of the absolute frame and makes the phenomena in inertial frames like those in the absolute frame.

The ballistic law governs the kinematics of balls with mass or massless and it can be extended to massless entities such as light. Therefore, the constant light speed $c$ of an electromagnetic nature given by Maxwell’s equations emitted in any direction in the absolute frame by a source in motion replaces the emitted velocity $V$ from mechanics. The velocity $v$ of the source of a mechanical nature remains the same. Therefore, the propagation velocity of light in the absolute frame is ${\mathit{c}}_{\mathit{s}\mathit{a}}=\mathit{c}+\mathit{v}$ which applies to each wave emitted in any direction in the absolute frame. In the source inertial frame, the phenomenon is like in the absolute frame when the source is at rest and each wavefront has its center at the source at all times; light travels in any direction with the speed $c$, wavelength $\lambda$, period $T$, and frequency $f$.

2.4. Elastic Collision of Two Balls Moving in Opposite Directions

In the absolute frame, two balls, one with mass$m_1$ traveling at velocity$v_1$ and the other with mass$m_2$ traveling at velocity$v_2$, are engaged in a frontal elastic collision, as shown in Figure 1. The velocities of the balls after collision are $v_1^{\text{'}}$ and$v_2^{\text{'}}$, respectively. The equations for the law of conservation of momentum and energy of the balls before and after collision are as follows:

$$m_1{v}_1+m_2{v}_2=m_1{v}_1^{\mathrm{\text{'}}}+m_2{v}_2^{\mathrm{\text{'}}}$$

(1)

and

$${\displaystyle \frac{1}{2}}{m}_1{v}_1^2+{\displaystyle \frac{1}{2}}{m}_2{v}_2^2={\displaystyle \frac{1}{2}}{m}_1{v}_1^{\text{'}2}+{\displaystyle \frac{1}{2}}{m}_2{v}_2^{\text{'}2}$$

(2)

The two equations yield the solution for speed $v_1^{\mathrm{\text{'}}}={\displaystyle \frac{m_1-m_2}{m_1+m_2}}{v}_1+{\displaystyle \frac{2m_2}{m_1+m_2}}{v}_2$ and $v_2^{\mathrm{\text{'}}}={\displaystyle \frac{2m_1}{m_1+m_2}}{v}_1+{\displaystyle \frac{m_2-m_1}{m_1+m_2}}{v}_2.$

For $m_1\gg m_2$, the simplified solution $v_1^{\text{'}}\cong v_1$ and$v_2^{\text{'}}\cong 2v_1-v_2$ are given with approximation. The solutions are offered without considering the direction of the velocities. Considering the direction of $v_1$ positive, the direction of $v_2$ is negative and the directions of $v_1^{\text{'}}$ and $v_2^{\text{'}}$ are positive, as shown in Figure 1. Therefore, the simplified solutions with approximation becomes $v_1^{\text{'}}\cong v_1$ and$v_2^{\text{'}}\cong v_2+2v_1$. At the limit when $m_2$ converges to zero, the simplified solutions are $v_1^{\text{'}}=v_1$ and $v_2^{\text{'}}=v_2+2v_1$.

When the ball of mass $m_1$ travels in the opposite direction, the simplified solutions for the massless balls are $v_1^{\text{'}}=v_1$ and $v_2^{\text{'}}=v_2-2v_1$, considering the same positive direction.

The massless balls obey the law of conservation of momentum $m_1{v}_1=m_1{v}_1^{\mathrm{\text{'}}}$, and the law of energy conservation, ${\displaystyle \frac{1}{2}}{m}_1{v}_1^2={\displaystyle \frac{1}{2}}{m}_1{v}_1^{\text{'}2}$. According to the equations of these two laws, massless balls do not have momentum and no energy is required to change their state.

A rigid wall can replace the ball of mass $m_1$ to study the reflection of balls with mass $m_2$ or without mass in any direction. The solution $v_2^{\text{'}}=v_2+2v_1$ is given in the frame at absolute rest and indicates that $v_2$ adds once to $v_2^{\text{'}}$ and $v_1$ adds twice. In the wall’s inertial frame, the relative incident speed of the massless ball concerning the wall is $v_{ii}=v_2+v_i$, where $v_i$ is the speed of the wall in the opposite direction of the incident velocity $v_2$; in Figure 1, $v_i=v_1$. The speed of the reflected massless ball is $v_{ri}=v_{ii}=v_2+v_i$; velocities $v_{ri}$ and $v_{ii}$ are in opposite directions in Figure 1. In the frame at absolute rest, the speed of the reflected massless balls is $v_2^{\text{'}}=v_{ri}+v_r$, where $v_r$ is the speed of the wall in the direction of the reflected massless ball; in Figure 1, $v_r=v_1$. The expression $v_2^{\text{'}}=v_{ri}+v_r$, where $v_{ri}=v_2+v_i$, yields the following equation:

$$v_2^{\mathrm{\text{'}}}=v_2+v_i+v_r$$

(3)

Equation (3) provides the massless ball’s speeds reflected in the absolute frame $v_2^{\mathrm{\text{'}}}$ where $v_2$ is the emitted velocity by a source of the massless ball coming from any direction concerning the wall. The angles of the incident speed $v_i$ and the reflected speed $v_r$ are measured from the moving direction of the wall. Equation (3) applies to the reflection of light by a moving mirror and with approximation to the reflection of balls by a moving wall to balls with mass in an elastic collision when $m_1\gg m_2$.

2.5. Elastic Reflection of a Ball by a Moving Wall

Figure 2 illustrates in the absolute frame a wall W traveling at a velocity $v$ and a ball traveling at a velocity $V$ hitting the wall in an elastic collision; the wall’s mass is much greater than the ball’s mass $m$. The wall reflects the ball in the instance of collision at point $A$ of the wall in the wall inertial frame and its corresponding point $A_1$ in the absolute frame. The angle of velocity of the incident and reflected ball are equal and measured from the normal at the common points $A$ and $A_1$ at the collision instance according to the law of reflection. One second after the collision, the ball is at point $B_2$ and the wall is at $A_2$.

This section employs Equation (3), $v_2^{\text{'}}=v_2+v_i+v_r$, in which the speed of the ball $V$ replaces $v_2$ and the reflected speed of the ball in the absolute frame $V_{ra}$ replaces $v_2^{\text{'}}$:

$$V_{ra}=V+v_i+v_r$$

(4)

In the inertial frame, the speed of the wall in the opposite direction of the incident ball is $v_i=v\cos a$, and in the absolute frame, the speed of the wall in the direction of the reflected ball is $v_r=v\cos b$. Another form of Equation (4) is

$$V_{ra}=V+v\mathit{cos}a+v\mathit{cos}b$$

(5)

where angles $a$ and $b$ are measured counterclockwise from velocity $v$.

In the absolute frame, the wall moved in one direction; however, the wall inclination reflects a ball in multiple directions. The velocity of the ball in the inertial frame of the wall is $V_i$, given by the vector subtraction of velocity $V$ and $v$. Velocity triangle $A_1{A}_2{B}_2$ applies to the ball at any time. On another scale, $A_1{A}_2{B}_2$ represents the momentum triangle.

2.6. Emission, Propagation, and Reflection of Balls in the Absolute and an Inertial Frame

Figure 3 illustrates the same ball source and rigid wall at rest in the absolute and an inertial frame. The source and wall have the same geometry with respect to the origin of each frame.

In the absolute frame $OXYZ$, the source at the origin $O$ emits a ball at an instant velocity $V_e$ at an angle $a$ from the axis $OX$. After time $t_1$, the ball is at point $A$ on wall $W$. At point $A$, the ball is reflected in an elastic collision at a velocity $V_r$ and then travels along the path $AB$ in time $t_2$. The velocity $V_e$ and $V_r$ have the same magnitude $V$. The ball travels paths $OA$ and $AB$ in time $t=t_1+t_2$ at speed $V$. The ball continues to travel in the $AB$ direction.

The inertial frame $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}{Z}^{\mathrm{\text{'}}}$ travels at velocity $v$, and the source is at the origin $O^{\mathrm{\text{'}}}$. Origin $O^{\mathrm{\text{'}}}$ and points $A$ and $B$ belong to the inertial frame, and their instances in the absolute frame receive the corresponding index. The source at the origin $O^{\mathrm{\text{'}}}$ emits a ball at the instant velocity $V_e$ in direction $O_1^{\mathrm{\text{'}}}{A}_1$ at angle $a$ from the axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$. The ball inherits the velocity $v$ of the source. The ball travels on the propagation path $O_1^{\mathrm{\text{'}}}{A}_2$ at the propagation velocity $V_{sa}$ given by the vector sum of the emitted velocity $V_e$ and source velocity $v$. The velocity $V_e$ does not change its direction and magnitude $V$ along path $O_1^{\mathrm{\text{'}}}{A}_2$. At point $O_2^{\mathrm{\text{'}}}$, the ball is at $A_2$; it has traveled, in the inertial frame, path $O_2^{\mathrm{\text{'}}}{A}_2$ at speed $V_e=V$ in time $t_1$, and the direction $O_2^{\mathrm{\text{'}}}{A}_2$ makes angle $a$ from the axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$. Path $O_2^{\mathrm{\text{'}}}{A}_2$ is path $O^{\mathrm{\text{'}}}A$ in the inertial frame, which is identical to $OA$ in the absolute frame. If the source emits other balls between $O_1^{\mathrm{\text{'}}}$ and $O_2^{\mathrm{\text{'}}}$, all balls are on the path $O_2^{\mathrm{\text{'}}}{A}_2$.

In the elastic collision at point $A_2$, the wall perceives only the magnitude and direction of the velocity $V_e$ of the emitted ball because both the ball and wall have the same velocity $v$. The incident and reflected angles $b$ are measured from the normal to the wall at the collision point to the incident velocity $V_e$ and reflected velocity $V_r$ as in the absolute frame. After reflection, the velocity $v$ keeps the ball moving in the same direction with the same magnitude. The ball travels on the propagation path $A_2{B}_3$ at the propagation velocity $V_{ra}$ given by the vector sum of the reflected velocity $V_r$ and source velocity $v$. The velocity $V_r$ does not change its direction and magnitude $V$ along the path $A_2{B}_3$. At point $O_3^{\text{'}}$, the ball is at $B_3$, the direction $O_3^{\text{'}}{A}_3$ makes angle $a$ from axis $O^{\text{'}}{X}^{\text{'}}$, and the ball has traveled the path $O_3^{\text{'}}{A}_3=O_2^{\text{'}}{A}_2={O_1^{\text{'}}{A}_1=O}^{\text{'}}A$ at speed $V_e=V$ in time $t_1$ and the path $A_3{B}_3$ at speed $V_r=V$ in time $t_2$. Path $A_3{B}_3$ is the path $AB$ in the inertial frame identical to that in the absolute frame. At point $O_3^{\text{'}}$, the ball has traveled the paths $O_3^{\text{'}}{A}_3=OA$ and $A_3{B}_3=AB$ in time $t=t_1+t_2$ at speed $V$, as in the absolute frame.

Newtonian mechanics formulates observations and experiments rationally understood in laws applicable to experiments, phenomena, and needs of everyday life. However, Newtonian laws state nothing about observing these phenomena.

3. Kinematics of Light

The kinematics of light based on the ballistic law arises from a series of articles [1,2,3,4,5,6,7,8,9,10,11,12,13] regarding light emission, propagation, and reflection applied to a few fundamental experiments. The reflection of light as a mechanical phenomenon [1,2,3] was the first step. The experiment regarding the reflection and emission of light [13] summarized in Appendix A was the turning point in our understanding of the kinematics of light.

Differing from Newtonian laws, we employed the expressions “observer in the absolute frame” and “observer in an inertial frame;” these hypothetical observers observe the phenomena as they are in their frames. These terms may be eliminated to state directly how the phenomena are as in mechanics. The expression “local observer” is particularly essential. A local observer perceives the phenomena through light coming directly from a source or reflected by objects from the observer’s frame or others, as well as through partially reflected wavefronts of light by some particles of the transparent medium, such as air, through which light travels. In a vacuum, a beam of light is invisible except when it comes directly to the human eye. Furthermore, the human eye only observes the light emitted from a source and its reflection in a mirror, not necessarily light propagation. Therefore, a local observer perceives a physics phenomenon differently from the reality of Newton’s laws. Nevertheless, we may better understand reality by applying Newtonian laws and local observations of light.

Electromagnetic theory gives the emitted speed of light by a source at rest or in motion in a vacuum of the absolute frame that is the universal constant $c$. The speed of light $c$ behaves similarly to the speed $V$ of a ball, as presented in Section 2.5 and 2.6.

3.1. Reflection of Light by a Moving Mirror

Unlike in References [1] and [2], Figure 4 illustrates the absolute frame in which a mirror $M$ travels at velocity $v$ and the source $S$ of coherent light is at rest.

This section employs Equation (3), $v_2^{\text{'}}=v_2+v_i+v_r$, where the electromagnetic speed $c$ replaces $v_2$ and the reflected speed of the wavefront $c_{ra}$ in the absolute frame replaces $v_2^{\text{'}}$:

$$c_{ra}=c+v_i+v_r$$

(6)

In the absolute frame, the speed of the mirror in the direction opposite to the incident light is $v_i=v\cos a$, and the speed of the mirror in the direction of the reflected light is $v_r=v\cos b$. Another form of Equation (6) is

$$c_{ra}=c+v\mathit{cos}a+v\mathit{cos}b$$

(7)

where angles $a$ and $b$ are measured counterclockwise from velocity $v$.

In the absolute frame, the mirror moves in one direction, but the inclination of the mirror reflects light in multiple directions.

A second after the collision at $A_1$, the wavefront from $A_1$ is at $B_2$ and the mirror is at $A_2$. The wavefronts reflected between $A_1$ and $A_2$ travel in the absolute frame in the direction $A_1{B}_2$ at speed $c_{ra}$. In the inertial frame of the mirror, the wavefronts travel on the path $A_2{B}_2$, forming a continuous wave of light propagating at velocity $c_i$, wavelength ${\lambda }_i$, period $T_i$, and frequency $f_i$. Velocity $c_i$ is given by the vector subtraction of velocity $c_{ra}$ of the wavefronts and $v$ of source, and velocity $c_i$ does not change the direction and magnitude of the velocity $c_{ra}$. A local observer at point $B_2$ perceives the wavefront coming from $A_1$.

In Reference [1], the source is at rest in the inertial frame of the mirror and the emitted velocity of light is considered independent from its source. Wavefronts reflected at point $A$ originate from a single point at the source. In Figure 4, the wavefronts reflected at point $A$ of the mirror belong to the waves originating from the sequential points of the source.

The source may not be at rest; therefore, the speed of light propagation is $c_{sa}\ne c$ in the absolute frame. In this case, the mirror may also perceive the source’s velocity not only the emitted velocity. In Reference [5] we approached this general consideration.

3.2. Emission, Propagation, and Reflection of Light as Mechanical Phenomena in the Absolute and an Inertial Frame

The study of the emission, propagation, and reflection of light is based on that of balls, as described in Section 2.6. The mechanical velocity $v$ is the same as that for balls with or without mass. The emitted velocity $c$ replaces the velocity $V$ for the balls.

Figure 5 illustrates the light source and reflective mirror at rest in the absolute and an inertial frame. The source and mirror have the same geometry concerning the origin of each frame.

In the absolute frame $OXYZ$, the source at the origin $O$ emits a wavefront at velocity $c_e$ at an angle $a$ from the axis $OX$. After time $t_1$, the wavefront is at point $A$ of the mirror $M$. At point $A$, the wavefront is reflected at velocity $c_r$, then travels the path $AB$ in time $t_2$. The velocity $c_e$ and $c_r$ have the magnitude $c$. The light travels paths $OA$ and $AB$ in time $t=t_1+t_2$ at speed $c$, wavelength $\lambda$, period $T$, and frequency $f$.

The inertial frame $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}{Z}^{\mathrm{\text{'}}}$ travels at velocity $v$, and the source is at the origin $O^{\mathrm{\text{'}}}$. Origin $O^{\mathrm{\text{'}}}$ and points $A$ and $B$ belong to the inertial frame, and their instances in the absolute frame receive a corresponding index. The source emits a wavefront at the velocity $c_e$ in direction $O_1^{\mathrm{\text{'}}}{A}_1$ at angle $a$ from axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$. The wavefront travels on the propagation path $O_1^{\mathrm{\text{'}}}{A}_2$ at the propagation velocity $c_{sa}$ given by the vector sum of the emitted velocity $c_e$ and source velocity $v$. The velocity $c_e$ does not change its direction and magnitude $c$ along the path $O_1^{\mathrm{\text{'}}}{A}_2$. At point $O_2^{\mathrm{\text{'}}}$, the wavefront is at $A_2$; it has traveled the path $O_2^{\mathrm{\text{'}}}{A}_2$ at speed $c_e=c$ in time $t_1$, and the direction $O_2^{\mathrm{\text{'}}}{A}_2$ makes angle $a$ from axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$. Path $O_2^{\mathrm{\text{'}}}{A}_2$ is path $O^{\mathrm{\text{'}}}A$ in the inertial frame, which is identical to $OA$ in the absolute frame. The emitted wavefronts between $O_1^{\mathrm{\text{'}}}$ and $O_2^{\mathrm{\text{'}}}$ are on path $O_2^{\mathrm{\text{'}}}{A}_2$.

At point $A_2$ of the reflection, the mirror perceives only the magnitude and direction of the emitted velocity $c_e$ because the wavefront and mirror have the same velocity $v$. The incident and reflected angles $b$ are measured from the normal to the mirror at the collision point to the incident velocity $c_e$ and reflected velocity $c_r$. After reflection, the velocity $v$ keeps the light moving in the same direction with the same magnitude. The wavefront travels on the propagation path $A_2{B}_3$ at the propagation velocity $c_{ra}$ given by the vector sum of the reflected velocity $c_r$ and source velocity $v$. The velocity $c_r$ does not change its direction and magnitude $c$ along path $A_2{B}_3$. At point $O_3^{\text{'}}$, the wavefront emitted from $O_1^{\text{'}}$ is at $B_3$, the direction $O_3^{\text{'}}{A}_3$ makes angle $a$ from axis $O^{\text{'}}{X}^{\text{'}}$, and the wavefront has traveled the path $O_3^{\text{'}}{A}_3=O_2^{\text{'}}{A}_2=O_1^{\text{'}}{A}_1=O^{\text{'}}A$ at speed $c_e=c$ in time $t_1$ and the path $A_3{B}_3$ at speed $c_r=c$ in time $t_2$. Path $A_3{B}_3$ is the path $AB$ in the inertial frame identical to that in the absolute frame. At point $O_3^{\text{'}}$, light has traveled the path $O_3^{\text{'}}{A}_3=OA$ and $A_3{B}_3=AB$ in the time $t=t_1+t_2$ at speed $c$, with wavelength $\lambda$, period $T$, and frequency $f$, as in the absolute frame. A local observer at point $A$ observes the light coming from the origin $O^{\text{'}}$ and another at point $B$ observes the light from point $A$.

3.3. Discussions

Maxwell’s equations give the emitted speed of light, which is the universal constant $c$, by a source at rest or in motion in a vacuum of the absolute frame. The kinematics of light makes the difference between the emitted, propagated, and reflected light velocity.

Suppose a source of light at rest in a vacuum of the absolute frame emits waves in all directions. The spherical wavefront has its center at the source at all times, waves are uniformly distributed in space concerning the source, and waves travel at the emitted speed $c$ with wavelength $\lambda$, period $T$, and frequency $f$ in any direction. The phenomenon is a sphere with the center at source at rest continuously expanding with a radius increasing in time with $ct$. At each point of the spherical wavefront, a local observer observes its wave wavefront coming from the source with a delay according to the time $t$ from its emission. When the source is in motion at a velocity $v$, each emitted wave inherits the velocity of the source in the absolute frame, such that the phenomenon in the inertial frame of the source is like that in the absolute frame when the source is at rest. In the absolute frame, the phenomenon is a sphere traveling at the velocity $v$ and continuously expanding with a radius increasing in time with $ct$. If the source emits intermittent spherical wavefronts, each wavefront has its center at the moving source at all times.

In the inertial frame of a source, a mirror at rest perceives only the emitted directions of the waves that are then reflected accordingly. The reflected waves inherit the source’s velocity such that the waves in the source inertial frame are like when the source is at rest in the absolute frame having the same $c$, $\lambda$, $T$, and $f$.

The ballistic law applicable to balls and light is embedded in mechanics because it is derived from mechanics. It works in the absolute frame which is the background of any source’s inertial frame and acts on each ball and light wave emitted by a source in motion creating in the source’s inertial frame a phenomenon identical to that in the absolute frame when the source is at rest. Therefore, the kinematics of light explains and confirms the principle of relativity, according to which no experiment in an inertial frame can prove its motion. It also explains why the laws of physics have the same form in each inertial frame, and why the speed of light is the constant $c$ in inertial frames when the source and reflected mirror are at rest.

It is convenient to compare the physical phenomena from inertial frames with the frame at absolute rest, which is a hypothetical inertial frame at zero speed. The phenomena in each inertial frame are similar to those in the frame at absolute rest. Therefore, each inertial frame can be considered a local frame at absolute rest for phenomena belonging to that inertial frame. The study of a physics system belonging to an inertial frame can be performed in another frame considered a stationary frame or a local absolute frame where the inertial frame travels at the relative velocity between the two frames.

3.4. Experiments and Observations That Support the Kinematics of Light

The kinematics of light explain experiments and local observations that supported special relativity due to insufficient and incorrect understanding.

3.4.1. Michelson‒Morley Experiment

Light travels through a transparent medium at a specific constant speed independent of the source speed. Michelson and Morley [14] approached their experiment considering the theory of fixed ether. Therefore, the speed of light emitted by a source and reflected by a mirror has the same magnitude in the hypothetical ether at rest in the absolute frame, regardless of whether the source and mirror are at rest or in motion. In ether theory, the speed of light is limited by the ether. The Michelson‒Morley experiment predicted a fringe shift that was not confirmed by the experimental results.

In contrast, the kinematics of light demonstrates that in an inertial frame where a source of light and a mirror are at rest the speed of light is the constant c of electromagnetic nature. Therefore, the kinematics of light predicts a zero fringe shift in the Michelson‒Morley experiment, which agrees with the experimental results.

3.4.2. Experiment Performed at CERN, Geneva

Without rejecting Ritz’s ballistic theory [15], the emission, propagation, and light reflection in inertial frames [4] can explain the experiment performed at CERN, Geneva, in 1964 [16]. Figure 6 illustrates this phenomenon using a simple approach.

When a boson $B$ of mass $m$ is accelerated at a mechanical speed $v$ near the constant speed of light $c$, it decays into particle $A$ of mass $m$ and one massless photon. At speed $v$, particle $A$ changes direction and the photon continues moving free at the speed $v$. Bosons are just carriers that give photons their mechanical speed $v$ near the constant speed of light $c$. Bosons are not sources of light and cannot give photons the speed $c$ of electromagnetic nature. This experimental result confirmed the ballistic law of light.

3.4.3. Observation of a Star in the Universe

Figure 7a illustrates the observation of a star in the universe according to the kinematics of light. Suppose that a star at point $A_1$ and the Earth at point $B_1$ travel at velocity $v$. At the initial instance, the star emits a wavefront of light in the direction $A_1{B}_1$ at the emitted speed $c$.

After a certain time, the star travels the path $A_1{A}_2$ and the Earth travels the path $B_1{B}_2$, which are of equal length $L_1$. Ballistic law makes the wavefront emitted in the direction $A_1{B}_1$ to propagate along $A_1{B}_2$. At $B_2$, the local observer perceives the wavefront as coming from $A_2$. Therefore, the star is observed at its actual location.

Figure 7b illustrates the observation of a star in the universe based on the hypothesis that the speed of light is independent of the source motion. Suppose a star at point $A_1$ and the Earth at point $B_1$ travel at velocity $v$. At the initial instance, the star emits a wavefront of light in the direction $A_1{B}_3$ at the emitted speed $c$.

After a certain time, the star travels the path $A_1{A}_3$ and the Earth travels the path $B_1{B}_3$, which are of equal length $L_2$. The wavefront emitted in the direction $A_1{B}_3$ reaches point $B_3$, where a local observer perceives the wavefront coming from $A_1$. Therefore, the star is observed at the initial location and not at its actual location, which means that the hypothesis of the constancy of the speed of light creates irregularities that are unobserved by astronomers. These irregularities differ from those that De Sitter incorrectly predicted [17,18].

3.4.4. Observation of a Star’s Orbit

Light emission as a mechanical phenomenon [4] has been applied to star orbit observation [5]. Figure 8 depicts an actual star’s orbit with the center at point $O_s$ of radius $R$ in the plane of the paper and an imaginary circle of radius $O{A}^{\text{'}}$ with the center at point $O$ and with its plane parallel to and in the front of the paper plane.

The distance $d=O{O}_s$ is perpendicular to the orbit and imaginary circle planes. The observer at rest is located at point $O$. The observed star orbit of the radius $R_O$ is centered on $O_s$. The view is from the back right of the observer, enabling a clear image of the actual and observed orbits.

The distances in each set of ($A{A}^{\text{'}},A^{\text{'}\text{'}}O,E{E}^{\text{'}},E^{\text{'}\text{'}}O,\dots )$ and ($AO,EO,...$), including all other similar distances corresponding to points $B,C,D,F,G$, and $H,$ are equal.

The waves emitted by the star in motion inherit the velocity v of the star corresponding to each orbital point and travel through different paths to the local observer $O$. At point $A$, the star emits a wavefront of light at the velocity $c$ in the direction $AA\text{'}$, but this wavefront travels along the path $AO$ at the propagation velocity $c_p$. At point $O$, the observer observes the wavefront originating from point $A\text{'}\text{'}$ traveling at speed $c$. At point $E$, the star emits a wavefront of light at the velocity $c$ in the direction $E{E}^{\text{'}}$, $E{E}^{\text{'}}=AA\text{'}$, and this wavefront travels along the path $EO$ , $EO=AO$, at the propagation velocity $c_p$. At point $O$, the observer sees the wavefront coming from point $E\text{'}\text{'}$ traveling at speed $c$ along path $E^{\text{'}\text{'}}O=A\text{'}\text{'}O$. The observer perceives a similar observation for each point in the circular orbit.

Points $A,B,C,D,E,F,G$, and $H$ give the corresponding points $A\mathrm{\text{'}}\mathrm{\text{'}},B\mathrm{\text{'}}\mathrm{\text{'}},C\mathrm{\text{'}}\mathrm{\text{'}},D\mathrm{\text{'}}\mathrm{\text{'}},E\mathrm{\text{'}}\mathrm{\text{'}},F\mathrm{\text{'}}\mathrm{\text{'}},G\mathrm{\text{'}}\mathrm{\text{'}}$, and $H\mathrm{\text{'}}\mathrm{\text{'}}$, which in this particular case give the observed orbit with the center at $O_s$. The local observer sees the star’s orbit rotated; this orbit has a larger diameter than the actual orbit and the observed orbital speed is higher than that of $v$. The speed of light from any point on the observed orbit to the observer is the constant $c$. Therefore, no time irregularities exist to refute Ritz’s ballistic theory [15], as De Sitter did [17,18]. Observing a star’s orbit supports our understanding of the kinematics of light based on the ballistic law.

3.4.5. Miller Experiment

Studying the emission, propagation, and reflection of light in inertial frames [4] helps us to predict zero fringe shifts for any location and altitude in Earth’s inertial frame. This explains Miller’s experiments [19] at the Cleveland Laboratory in 1924, which employed light from local sources, as well as sunlight; the fringe shift with sunlight was of the order of ${10}^{-8}$. The fringe shifts of 0.08 in 1921 and 0.088 in 1925, recorded by Miller using local sources at a high altitude on Mount Wilson, remain unexplained.

3.4.6. Airy Experiment

In addition to the interactions of the emission and reflection of light with matter, there are other examples, such as the velocity of light through a moving medium [8] and the refraction of light when it travels from one medium to another, both at rest, according to Snell’s law. Airy’s experiment is an example of dragging light by a moving medium. Observing the star γ Draconis, Airy [20] expected to adjust the inclination of the telescope after introducing a tube with water along its axis; however, this was unnecessary. Considering the dragging of light by moving water and the experimental results, we obtained the Fresnel dragging coefficient $1-{\displaystyle \frac{1}{n_1^2}}$ from a mechanical perspective, where $n_1$ is the refractive index of the medium.

3.4.7. Majorana Experiment

Majorana’s experiment [21] in Earth’s inertial frame employed a fixed light source. The light traveled through three stages, each consisting of one movable and one fixed mirror, and entered a Michelson interferometer with arms of unequal length. The movable mirrors were fixed on a rotational disk in both directions. A fringe image was observed when the disk was at rest. When the disk was rotated from maximum speed in one direction to another, a shift of 0.71 fringes was observed. Similar to the Michelson interferometer, Majorana’s experimental device offers an outstanding contribution to the physics of light, despite changes in the interpretation of the experiment over time. Majorana misunderstood the phenomenon within the device and the significance of the fringe shift observed during the experiment, explaining the fringe shift favorably to special relativity. The reflection of light as a mechanical phenomenon [1,2,3,4] applied to the Majorana experiment [21] shows that the speed of light changes after each stage, causing a fringe shift in the Michelson interferometer. Reference [12] approximates rotational mirrors as inertial frames and derives a shift of 0.27 fringes. However, the observed fringe shift of 0.71 confirms the kinematics of light, rejecting the constancy of light propagation.

3.5. Galilean Transformation

We studied the Galilean transformation for light like in mechanics that presents the physical phenomena as they are not observed.

When extended to infinite, all the inertial frames overlap. A phenomenon in an inertial frame is instantly shared with any other inertial frame. The inertial frame in which a phenomenon is shared is considered at relative rest/a stationary frame.

The Galilean transformation shows how the physical phenomenon of light emission is instantly shared from a stationary frame in an inertial frame. Figure 9 depicts a stationary frame $OXYZ$ in which an inertial frame $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}{Z}^{\mathrm{\text{'}}}$ travels at velocity $v$ along the $OX$ axis, and the planes $OXY$ and $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}$ coincide.

The kinematics of light proves that a stationary frame/frame at relative rest can be considered a local frame at absolute rest; we do not assume this fact.

Origins $O$ and $O^{\mathrm{\text{'}}}$ coincide at the initial instance when the source, belonging to the origin $O$ of the stationary frame, emits a spherical wavefront of light formed by the individual waves’ wavefronts. After time $t$, the spherical wavefront of light has its center at $O$, and the origin of the inertial frame $O^{\mathrm{\text{'}}}$ is at a distance $vt$ from $O$. Galilean transformation provides in the inertial frame the coordinates of each point on the spherical wavefront. Figure 9 shows the wavefronts at points $A$, $B$, $C$, and $D$ on the circular wavefront in the plane $OXY$ at time $t$ and their coordinates along the axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$ of the frame $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}{Z}^{\mathrm{\text{'}}}$.

The Galilean transformation consists of four equations applicable to each point of the spherical wavefront that can be written as follows:

$$x^{\mathrm{\text{'}}}=x-vt,y^{\mathrm{\text{'}}}=y,z^{\mathrm{\text{'}}}=z,\mathrm{and}{t}^{\mathrm{\text{'}}}=t.$$

(8)

The wavefront emitted at the initial instance in the direction $OB$ travels in this direction at all times. It is on this circular wavefront, which enlarges continuously. This wavefront travels the length $O^{\mathrm{\text{'}}}B$ in the inertial frame at propagation speed $c^{\mathrm{\text{'}}}$. The vector subtraction of velocity $c$ and $v$ gives the velocity $c^{\mathrm{\text{'}}},$ illustrated at points $O$ and $B$. This wavefront travels at the same angles $a$ and $a^{\mathrm{\text{'}}}$ and speed $c^{\mathrm{\text{'}}}$ for any other instance of the circular wavefront. Angles $a$ and $a^{\mathrm{\text{'}}}$ and speed $c^{\mathrm{\text{'}}}$ are different for any other point on the circular wavefront. The speed of wavefronts varies from $c\mathrm{\text{'}}=2.999700000\mathrm{E}+08$ for $a=0°$ to $c\mathrm{\text{'}}=3.000000015\mathrm{E}+08$ for $a=90°$ and to $c\mathrm{\text{'}}=3.000300000\mathrm{E}+08$ for $a=180°$.

Figure 9 and the Galilean transformation applied to a hypothetical ball source when the source emits a circular ball front with the speed of the balls $V>v$.

In Figure 9, the physical phenomenon consists of the source, the light waves, and the circular wavefront; all belonging to the stationary frame and none to the inertial frame. A phenomenon in an inertial frame is unique in the universe; it is independent of any other inertial frame and, though it is instantly shared in any other inertial frame through its coordinates, it is not duplicated. There are no transformations of phenomena that undergo changes from the stationary frame to the inertial frame that may or may not affect the laws of physics. The term “transformation” may be inappropriate; a better wording may be “Galilean coordinates.”

3.6. Discussions

In the Galilean coordinates shown in Figure 9, the phenomenon, which includes the light source, waves, and circular wavefront, belongs to the stationary frame. The circular wavefront has the center at the source located at the origin of the stationary frame. Each point of the circular wavefront is a coordinate to the origin of the inertial frame, given by Equation 8.

The ballistic law was unknown in Einstein’s time; therefore, he had to work with the above case and the following one: In Figure 9, if the source belongs to the origin of the inertial frame $O\text{'}$ and the ballistic law is ignored, the phenomenon, which includes the light source, waves, and circular wavefront, belongs to the inertial frame. The circular wavefront has the center at the origin of the stationary frame $O$ and not at the source. Thus, the circular wavefront is common if the source belongs to either of the two origins. In the inertial frame, each point of the circular wavefront is given by Equation 8.

Einstein hypothesizes that if the source belongs to either of two frames, the common circular wavefront is observed in the inertial frame as a circular wavefront with the center at its origin. To fulfill his hypothesis, he applies a mathematical transformation to the common circular wavefront, for both cases.

Understanding Einstein’s approach to both cases above is sufficient to reject special relativity. However, we chose to do so from within the special relativity presented in Section 4.

4. Einsteinian Theory of Special Relativity

4.1. Einstein Suggestions

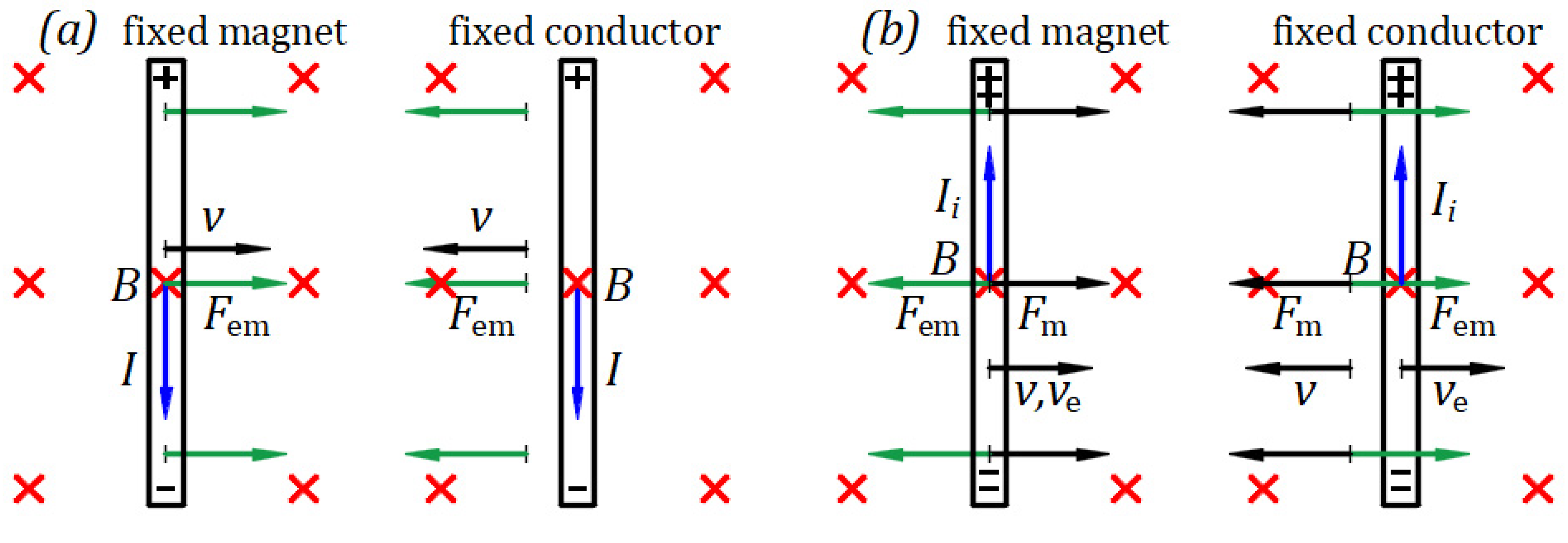
In the first paragraph on page one of his manuscript “On the electrodynamics of moving bodies,” [22] Einstein writes the following: “It is known that Maxwell’s electrodynamics—as usually understood at the present time—when applied to moving bodies, leads to asymmetries which do not appear to be inherent in the phenomena. For example, consider the reciprocal electrodynamic action of a magnet and a conductor. The observable phenomenon here depends only on the relative motion of the conductor and magnet, whereas the customary view draws a sharp distinction between the two cases in which either one or the other of these bodies is in motion. If the magnet is in motion and the conductor is at rest, there arises in the neighborhood of the magnet an electric field with a certain definite energy, producing a current at the places where parts of the conductor are situated. However, if the magnet is stationary and the conductor is in motion, no electric field is generated in the neighborhood of the magnet. In the conductor, however, we find an electromotive force, to which in itself there is no corresponding energy, but which gives rise—assuming equality of relative motion in the two cases discussed—to electric currents of the same path and intensity as those produced by the electric forces in the former case.”

Einstein’s example describes a reciprocal experimental observation of a conductor and magnet in proximity when one is in motion/rest and another is at rest/in motion but only when the magnet is in motion an electrical field arises. He may suggest that observations are sufficient to accept reciprocal phenomena symmetrical even if an electromagnetic quantity, such as an electric field, does not occur when the magnet is at rest. Therefore, it is not necessary to rationally understand physical phenomena. Appendix B shows that in both cases an electric field arises in the conductor, making it an electrical source. Thus, Maxwell’s electrodynamics lead to symmetries when applied to moving bodies; each physical quantity involved in a phenomenon arises and the phenomena can be rationally explained.

Even if the reciprocal phenomena are explained, can we apply the symmetry of phenomena to the symmetry between two inertial frames? Einstein’s example has a magnet and conductor in proximity, and they have reciprocal electromagnetic properties. None of these characteristics applies to a stationary and inertial frame to support special relativity. Origins of the two frames depart from each other and remain nearby for a relatively short time. The frames, including the absolute frame, are hypothetical entities. These tools help us to study and understand physical phenomena. They have no physical properties to transform or duplicate a physical system from one frame to another.

By applying symmetry to two inertial frames, the main idea in special relativity, Einstein unrealistically creates duplicates that lead to irrational conclusions, which are discussed further.

From “Examples of this sort, together with the unsuccessful attempts to discover any motion of the earth relatively to the ‘light medium’,” Einstein concludes with three suggestions in the second paragraph of page 1:

• “… the phenomena of electrodynamics as well as of mechanics possess no properties corresponding to the idea of absolute rest.”

Einstein rejected the idea of absolute rest. However, the inertial frame considered stationary is a local frame at absolute rest for another inertial frame. The stationary frame was a convenient choice to present his transformational understanding of the phenomenon between the two inertial frames.

2.

“… the same laws of electrodynamics and optics will be valid for all frames of reference for which the equations of mechanics hold good.”

The equations/laws of mechanics are valid for phenomena belonging to an inertial frame, but not for the coordinates of phenomena in another inertial frame. However, contrary to the second suggestion, special relativity forces the laws of electrodynamics and optics to hold good for coordinate observations, for which mechanics does not.

3.

“… light is always propagated in a vacuum with a definite velocity $c$, which is independent of the state of motion of the emitting body.”

In a stationary frame/local frame at absolute rest, the emitted wavefronts from a source at rest at an initial instance travel at the velocity $c$ in all directions. The waves wavefronts are on a sphere with the center at the source at all times. However, without considering the ballistic law of light, when the source is in motion at a velocity $v$, the emitted wavefronts at an initial instance travel in the stationary frame at the velocity $c$. In this case, the spherical wavefront has the center at the initial location of the source, which is the origin of the stationary frame, not at the source. Therefore, there are differences in wave propagation if the source belongs to the stationary or inertial frame.

Without understanding the physical phenomena of his example and the comments from the above suggestions, Einstein has chosen to formulate hypotheses based on observations, elevating them to postulates.

4.2. Einstein Postulates

From the three suggestions, Einstein formulates two postulates:

• “The laws by which the states of physical systems undergo change are not affected, whether these changes of state be referred to the one or the other of two systems of co-ordinates in uniform translatory motion.”
• “Any ray of light moves in the “stationary” system of co-ordinates with the determined velocity $c$, whether the ray be emitted by a stationary or by a moving body.”

A phenomenon in a stationary frame is independent of the inertial frame, although instantly shared with the latter through its coordinates. The first postulate forces the shared coordinates in the inertial frame to obey the same laws of physics as those applied in the stationary frame, thereby creating a fictive duplication of a phenomenon from a stationary frame into an inertial frame. The first postulate includes the phenomena of electrodynamics, optics, and mechanics in physical systems; see also Suggestion 2 of Section 4.1 However, in practice, special relativity is applied to light observation.

The second postulate indicates the comments regarding Suggestion 3 of Section 4.1 were not considered in Einstein’s study.

Einstein applied this transformation when the source belonged to a stationary or inertial frame. For clarity presentation, we consider the light source to belong to a stationary frame. If the source belongs to the inertial frame, then this frame is considered stationary. Einstein presented a transformation identical to the well-known Lorentz transformation [23].

4.3. Lorentz Transformation and Einstein Transformation

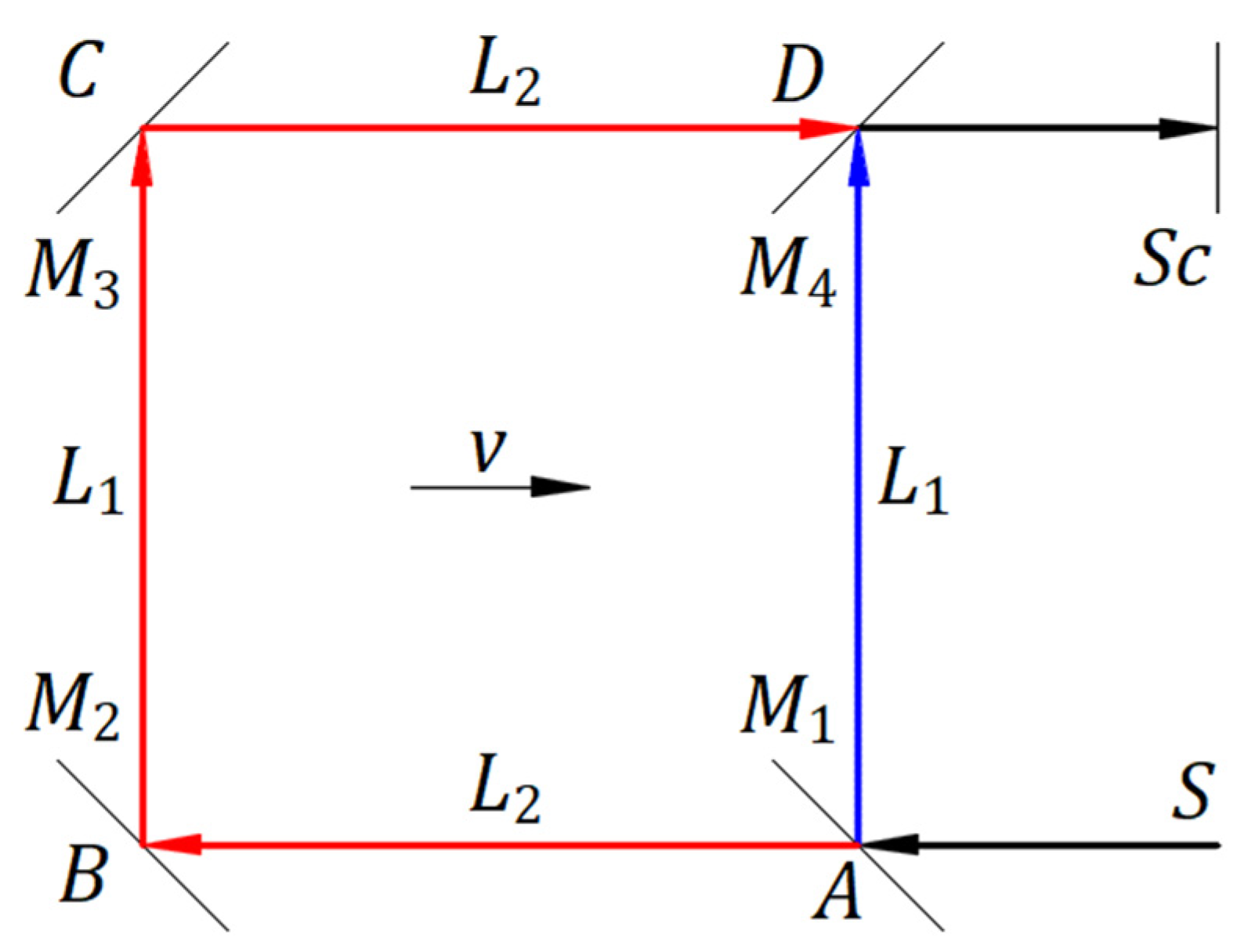
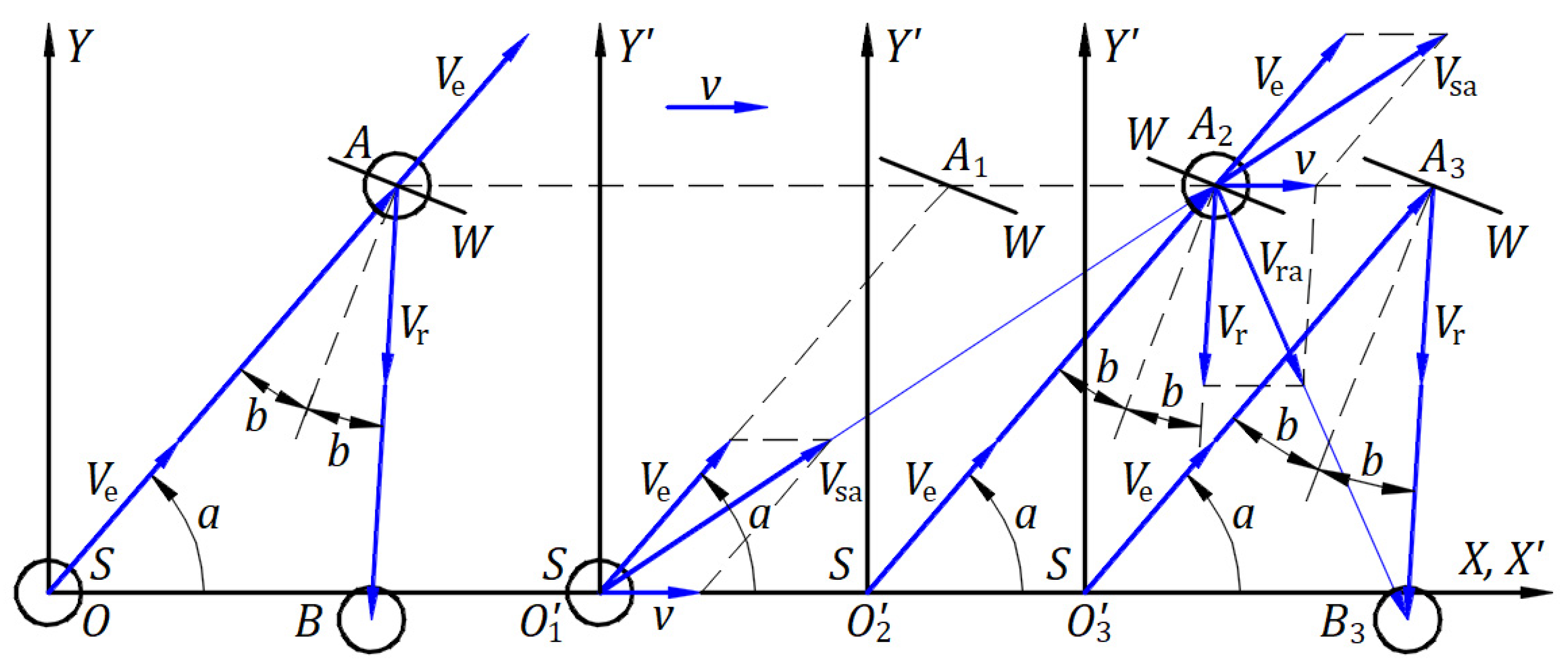
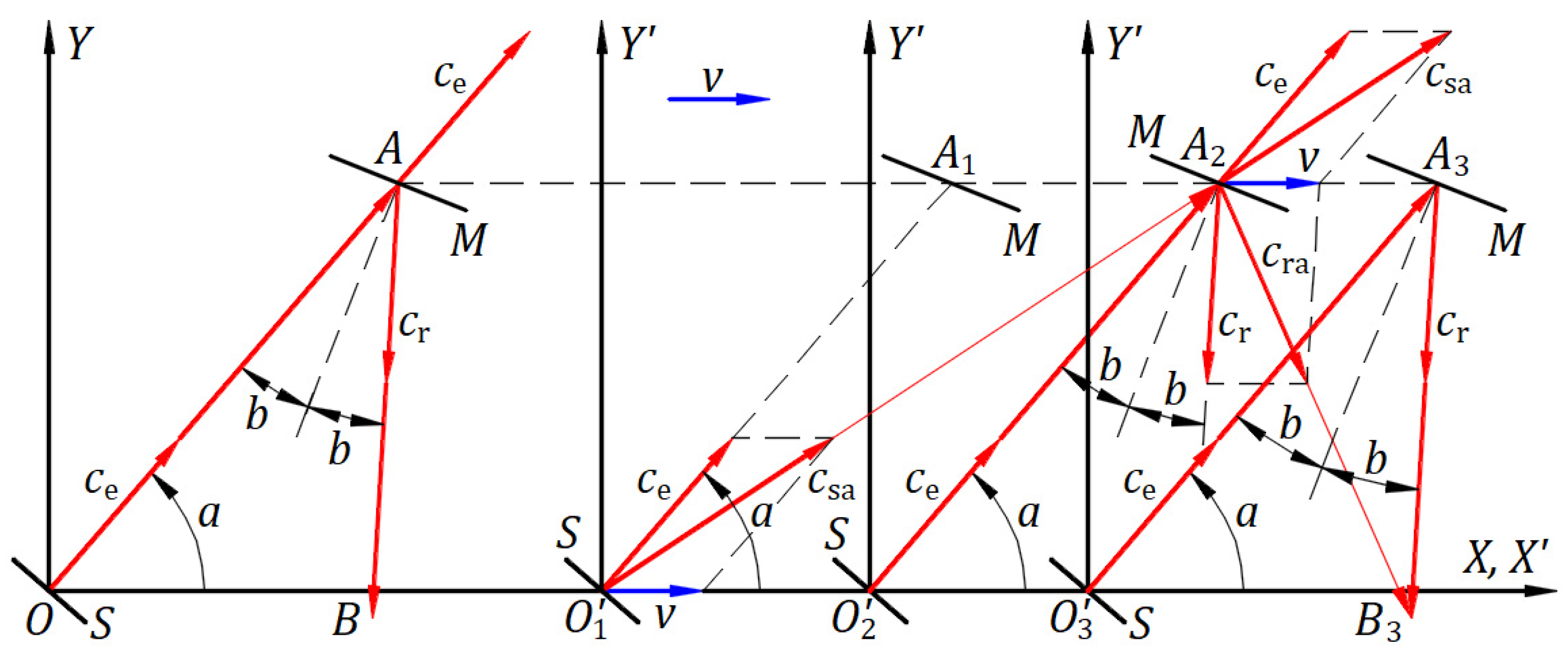
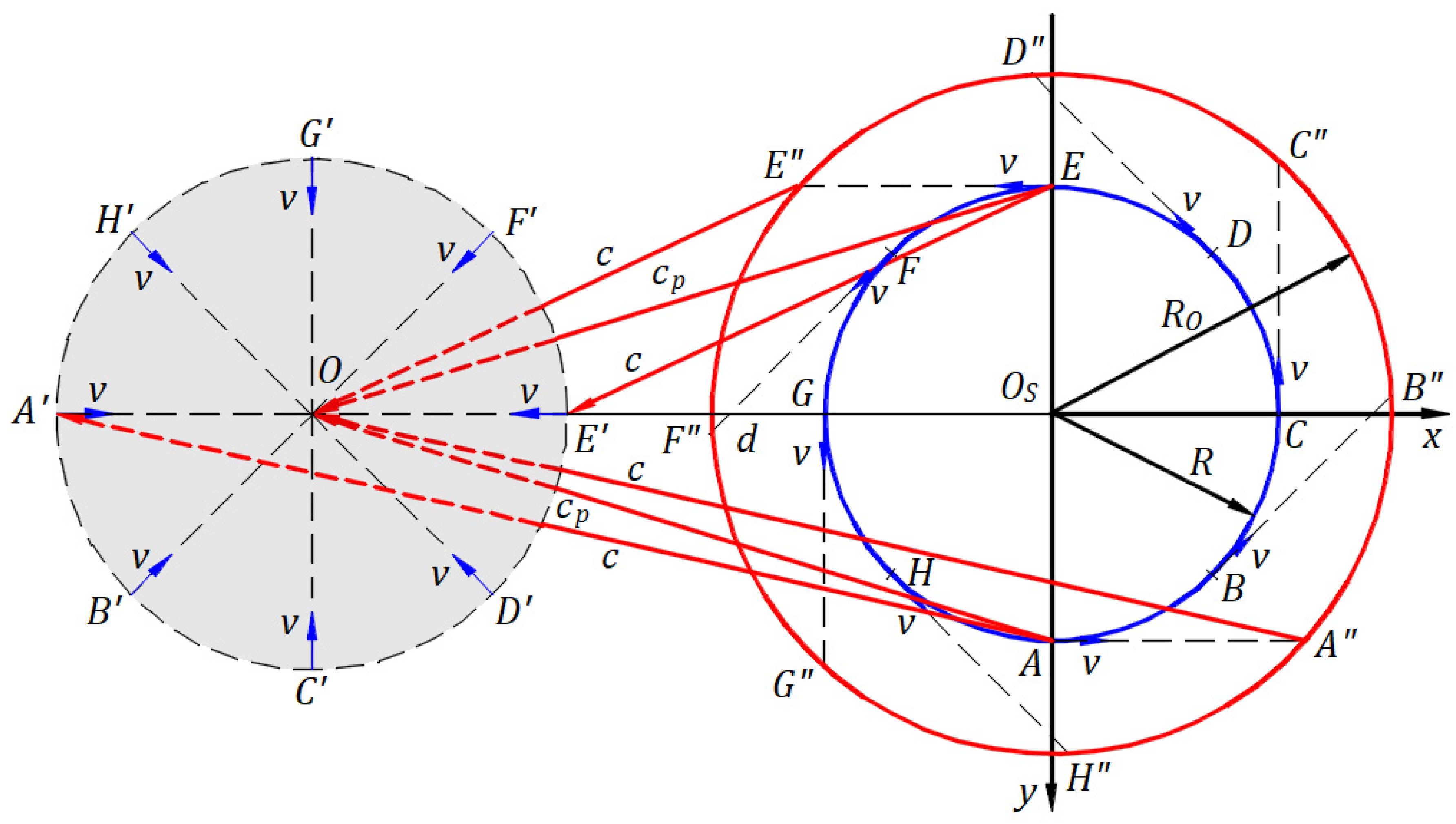
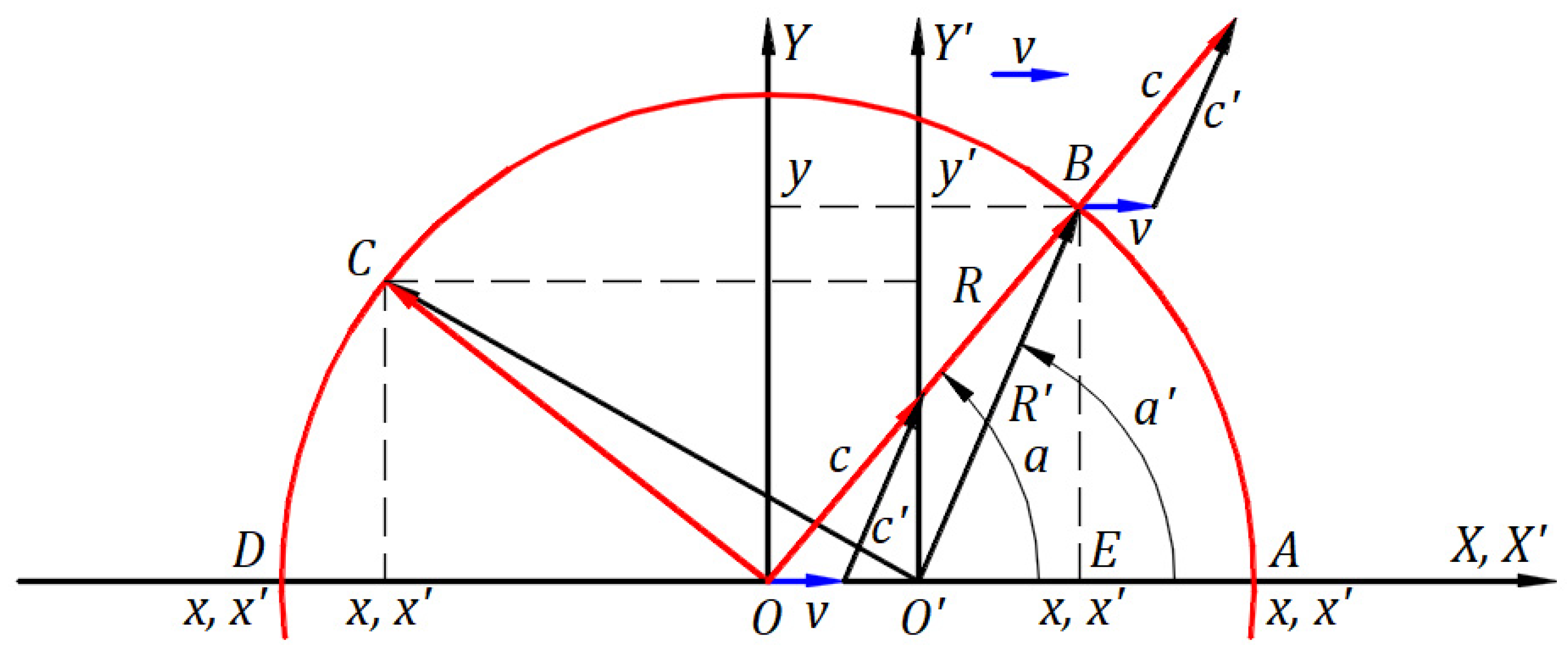
Figure 10 depicts a stationary frame $OXYZ$ in which an inertial frame $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}{Z}^{\mathrm{\text{'}}}$ travels at a velocity $v$ along the $OX$ axis, and the planes $OXY$ and $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}{Y}^{\mathrm{\text{'}}}$ coincide. Origins $O$ and $O^{\mathrm{\text{'}}}$ coincide at the initial instance when a light source belonging to the origin $O$ emits a spherical wavefront. After a time $t$, the spherical wavefront expands in space with a radius of magnitude $ct$, and the origin $O^{\mathrm{\text{'}}}$ is at a distance $vt$ from $O$.

In the theory of the ether at rest in the absolute frame, the speed of light is the constant $c$. Observations and Michelson‒Morley’s experiment can be explained if the speed of light is the constant $c$ in inertial frames. With no explanation of the Michelson‒Morley experiment during his time, FitzGerald [24] wrote the following: “I would suggest that almost the only hypothesis that can reconcile this opposition is that the length of material bodies changes, according to their movement through the ether or across it, by an amount depending on the square of the ratio of their velocity to that of light.”

The projection of each coordinate of the spherical wavefront of the stationary frame gives in the inertial frame along the axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$ a length $x^{\mathrm{\text{'}}}$ measured from $O^{\mathrm{\text{'}}}$. Lorentz’s transformation states that light travels a length $x^{\mathrm{\text{'}}}$ at speed $c$ in a time $t\text{'}$ and consists of four equations that apply to each point of the spherical wavefront as follows:

$$x_{\gamma }^{\mathrm{\text{'}}}=\gamma \left(x-vt\right),y^{\mathrm{\text{'}}}=\mathrm{y},z\mathrm{\text{'}}=z,\mathrm{and}{t}_{\gamma }^{\mathrm{\text{'}}}=\gamma \left(t-{\displaystyle \frac{vx}{c^2}}\right),$$

(9)

where $\gamma ={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}$ is the Lorentz factor, which is comparable to the square of the ratio of velocity $v$ and $c$, as suggested by FitzGerald.

Substituting $x=ct$ at point $A$, $x^{\mathrm{\text{'}}}=x-vt=(c-v)t$is the absolute coordinate in the inertial frame, and $t^{\text{'}}=t-{\displaystyle \frac{vx}{c^2}}=t-{\displaystyle \frac{vct}{c^2}}=t-{\displaystyle \frac{v}{\mathrm{c}}}t={\displaystyle \frac{c-v}{c}}t={\displaystyle \frac{x^{\text{'}}}{c}}$ is the hypothetical contracted time $t$ by ${\displaystyle \frac{v}{\mathrm{c}}}t$ given by Lorentz, in which the wavefront travels length $x^{\mathrm{\text{'}}}$ at speed $c$. $x_{\gamma }^{\mathrm{\text{'}}}=\gamma x^{\mathrm{\text{'}}}$, $t_{\gamma }^{\mathrm{\text{'}}}=\gamma t^{\text{'}}$, and then ${\displaystyle \frac{x_{\gamma }^{\mathrm{\text{'}}}}{t_{\gamma }^{\mathrm{\text{'}}}}}={\displaystyle \frac{x^{\mathrm{\text{'}}}}{t^{\text{'}}}}=c$, which verifies the constancy of light. Because $\gamma >1$ for $v\ne 0$, the length $x_{\gamma }^{\mathrm{\text{'}}}=\gamma x^{\mathrm{\text{'}}}$ is longer than $x^{\mathrm{\text{'}}}$, and point $A$ shifts to $A_{\gamma }$.

Substituting $x=-ct$ at point $D$, $x^{\mathrm{\text{'}}}=-x-vt=-(c+v)t$ is the absolute coordinate in the inertial frame, and $t^{\mathrm{\text{'}}}=t-{\displaystyle \frac{vx}{c^2}}=t+{\displaystyle \frac{vct}{c^2}}=t+{\displaystyle \frac{v}{c}}t={\displaystyle \frac{c+v}{c}}t={\displaystyle \frac{-x^{\mathrm{\text{'}}}}{c}}$ is the hypothetical dilated time $t$ by ${\displaystyle \frac{v}{\mathrm{c}}}t$ given by Lorentz, in which the wavefront travels length $x^{\mathrm{\text{'}}}$ at speed $c$. $x_{\gamma }^{\mathrm{\text{'}}}=\gamma x^{\mathrm{\text{'}}}$, $t_{\gamma }^{\mathrm{\text{'}}}=\gamma t^{\mathrm{\text{'}}}$, and then ${\displaystyle \frac{x_{\gamma }^{\mathrm{\text{'}}}}{t_{\gamma }^{\mathrm{\text{'}}}}}={\displaystyle \frac{x^{\mathrm{\text{'}}}}{t^{\mathrm{\text{'}}}}}=-c$, which verifies the constancy of light. Because $\gamma >1$ for $v\ne 0$, the length $x_{\gamma }^{\mathrm{\text{'}}}=\gamma x^{\mathrm{\text{'}}}$ is longer than $x^{\mathrm{\text{'}}}$, and point $D$ shifts to $D_{\gamma }$.

Lorentz’s transformation makes a duplication but the shift caused by the factor $\gamma$ at points $A$ and $D$ makes the duplication different from the spherical wavefront of the stationary frame, which is not the intention of Lorentz’s transformation or special relativity. The factor $\gamma$ should not be there and can be ignored without affecting the constancy of the speed of light in the two directions of the axis $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$. Eliminating factor $\gamma$, the transformation can be written as follows:

$$x^{\mathrm{\text{'}}}=x-vt,y^{\mathrm{\text{'}}}=\mathrm{y},z\mathrm{\text{'}}=z,\mathrm{and}{t}^{\text{'}}=t-{\displaystyle \frac{vx}{c^2}}.$$

(10)

In Figure 10, the mechanical equation for the wavefront traveling the path $OA=R=O\text{'}A+OO\text{'}$ is $x=x^{\mathrm{\text{'}}}+vt$ ⇒ $x^{\text{'}}=x-vt$ ⇒ $x^{\text{'}}=(c-v)t$ ⇒ $x^{\text{'}}=c\text{'}t$ with $c\text{'}=c-v$. In Lorentz’s transformation, the equation for $x^{\mathrm{\text{'}}}=x-vt$ is identical to that in mechanics for $x^{\text{'}}=x-vt$. The terms from the right of the two equations are identical which indicates that $x^{\mathrm{\text{'}}}$ is as well. If we hypothesize that the speed of light is the constant $c$ in any inertial frame, then $c\text{'}=c-v$ from mechanics becomes the speed $c$ and $x^{\text{'}}=c{t}^{\text{'}}$. Therefore, $c{t}^{\text{'}}=c^{\mathrm{\text{'}}}t$ offers $t^{\text{'}}={\displaystyle \frac{\mathrm{c}-v}{c}}t$ ⇒ $t^{\text{'}}=t-{\displaystyle \frac{vx}{c^2}}$ which is the equation of time in Lorentz’s transformation. For clarity, we can employ $t^{\text{'}}={\displaystyle \frac{c-v}{c}}t$ instead of $t^{\text{'}}=t-{\displaystyle \frac{vx}{c^2}}$. In the relativistic time of Lorentz’s transformation, the speed of light is the constant $c$ but the time contracts or dilates such that $x^{\mathrm{\text{'}}}$ has the same absolute magnitude as in mechanics; therefore, no length contractions or dilations exist.

The following numerical calculation employs the length $x^{\mathrm{\text{'}}}$ offered by Lorentz’s transformation and all others shown in Figure 10 that have absolute values. The speed of light along each length $x^{\mathrm{\text{'}}}$ corresponding to each light ray on the axis $O^{\text{'}}X\text{'}$ is constant $c$ according to the relativistic time in Lorentz’s transformation.

The distance $OB$ is the radius $R$ of the circular wavefront in the stationary frame. At time $t$ radius $R=ct$ and for angle $a$ we can calculate $y=R\sin a$. In triangle $O^{\mathrm{\text{'}}}BE$ of the inertial frame, $x^{\mathrm{\text{'}}}$ at point $E$ gives $x^{\mathrm{\text{'}}}=R\cos a-vt$ according to Lorentz’s transformation, and employing relativistic speed $c$ along $x^{\mathrm{\text{'}}}=O\mathrm{\text{'}}E$, $t^{\mathrm{\text{'}}}={\displaystyle \frac{x^{\mathrm{\text{'}}}}{c}}$ ⇒ $t^{\mathrm{\text{'}}}={\displaystyle \frac{R\cos a-vt}{c}}$. The distance $O^{\mathrm{\text{'}}}B$ is the variable radius $R^{\mathrm{\text{'}}}=\sqrt{x^{\mathrm{\text{'}}2}+y^2}$. The time the light travels along $R^{\mathrm{\text{'}}}=O^{\mathrm{\text{'}}}B$ is equal to the time $t^{\mathrm{\text{'}}}$ the light travels $x^{\mathrm{\text{'}}}=O\mathrm{\text{'}}E$ according to Lorentz’s transformation. Therefore, the speed of light traveling $R^{\mathrm{\text{'}}}=O^{\mathrm{\text{'}}}B$ is $c^{\mathrm{\text{'}}}={\displaystyle \frac{R^{\mathrm{\text{'}}}}{t^{\mathrm{\text{'}}}}}$. Table 1 lists the numerical calculations for the $x^{\mathrm{\text{'}}}$ and $c^{\mathrm{\text{'}}}$ functions of angle $a$ at time $t=1$ s.

Table 1 confirms that Lorentz’s transformation maintains the constancy of the speed of light for the waves in the direction $O^{\text{'}}{X}^{\text{'}}$ and the opposite direction. However, the speed of every other wave direction varies converging to infinite. The second postulate asserts the constancy of the speed of light in the inertial frame regardless of its direction; whereas the transformation drastically concludes otherwise.

4.4. Discussions

1. Is it rational to observe the circular wavefront with its center at the origin $O^{\mathrm{\text{'}}}$ and to keep the speed of light constant along the $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$ axis in both directions or to have a theory that may or may not explain experiments and observations without understanding their physics phenomena? Furthermore, is it reasonable to force the circular wavefront and its observations to follow the same physical laws as those in the stationary frame? Einstein chose this approach, leading to an irrational world. Unlike special relativity, Newtonian laws present phenomena as they are, rationally understood by themselves, and not accepted by observations, hypotheses, or postulates.

2. What natural phenomena can transform each wave from a stationary frame into its unique form, as required by Lorentz’s transformation and shown in Figure 10? Other mathematical transformations can be considered, e.g., ignoring the Lorentz factor $\gamma$ as discussed in Section 4.3, allowing the speed of light to be constant along each wave in the inertial frame, or having the time a constant and the speed of light variable according to its direction [25]. Could there be a phenomenon for each of these hypothetical mathematical transformations to explain the Michelson‒Morley experiment? If so, which one would be correct? If we attempt these transformations, we obtain a theory with irrational conclusions like that for special relativity.

3. A ruler identical to that in the stationary frame is required to measure the lengths involved in phenomena that belong to the inertial frame. We also must have two rulers with different scales required by Lorentz’s transformation to measure the lengths along $O^{\mathrm{\text{'}}}{X}^{\mathrm{\text{'}}}$ according to $x^{\mathrm{\text{'}}}$ positive or negative without considering other directions. The use of multiple rulers is unacceptable. The same conclusion applies to multiple synchronized clocks.

4. Suppose that the inertial frame also has a source at its origin. When the origins coincide, each source emits a circular wavefront of light. Considering factor $\gamma$, imagine the confusion in the inertial frames having two different wavefronts, one of its own and another observed from the stationary frame.

5. When we observe a star that involves astronomical distances, as seen in the example in Section 3.4.4, we observe it in an enlarged orbit without irregularities; however, our observation does not change the actual orbit. There is no need to mention other observations close to our eyes that we know are not factual. These observations can be explained by laws of physics. However, we must distinguish between actual phenomena and their local observation. Therefore, we cannot rely solely on observations. Special relativity focuses on observations but makes no distinction between the emitted and propagated velocities of waves’ wavefronts. It fails to consider that our eyes perceive only the direction of waves emitted by a source and reflected by a mirror, not the direction of wave propagation.

6. Figure 10 illustrates a case in which origins $O$ and $O^{\text{'}}$ coincide at the initial instance. However, origin $O^{\text{'}}$ may be far away from $O$ when the source emits a spherical wavefront at an initial instance. In this case, there is an interval of time when the circular wavefront does not include the origin $O^{\text{'}}$, a time when the circular wavefront is at the origin $O^{\text{'}}$, and an interval of time converging to infinite when the circular wavefront includes the origin $O^{\text{'}}$. How is the circular wavefront observed at $O^{\text{'}}$ at these different times? Do we force the coordinates of the circular wavefront to be observed according to the Lorentz transformation with its center at $O^{\text{'}}$ at any time?

7. Suppose that a source of balls in the stationary frame emits balls of equal mass in all directions at a speed $V$ that is higher than the speed of the inertial frame $v$. As for light, the coordinates of the spherical ball front in the inertial frame at a time $t$ are as in Figure 9. Mechanics does not and cannot force the coordinates of the circular ball front to have its center at $O^{\text{'}}$; in Einstein’s words, “the equations of mechanics do not hold good” in this case. However, special relativity does not respect Suggestion 2 in Section 4.1.

8. The first postulate indicates that the physical systems in the stationary frame change when they are transformed/duplicated into the inertial frame. The physical system mentioned in the first postulate has a source and light rays that create a circular wavefront. However, other systems may contain bodies and living beings involved in a phenomenon. Considering that the origin of inertial frames is relative, their origins can be at the origin of the stationary frame when the source emits a spherical wavefront of light. We can imagine what the physical systems’ duplication from a stationary frame in all other inertial frames means. Moreover, each inertial frame may be arbitrarily stationary; therefore, a phenomenon from another stationary frame can be duplicated in all other inertial frames. Do all these duplications occur just by choosing a stationary frame? All these duplications are irrational and are not observed in the universe or at a local scale.

9. In a stationary frame, as shown in Figure 10, the origin $O^{\text{'}}$ of the inertial frame may travel through a few consecutive points along the $OX$ axis. Suppose that a phenomenon arises in the stationary frame when the origin $O^{\text{'}}$ coincides with each consecutive point. Each of these phenomena is thus transformed at the origin $O^{\text{'}}$. Imagine all of these phenomena involving bodies and living beings at $O^{\text{'}}$.

10. In Figure 10, when the origins coincide, the light source emits in the stationary frame waves in all directions at speed $c$, with wavelength λ, period $T$, and frequency $f$ that are not disturbed by the inertial frame in which the wave propagation is observed. When the wavefront that travels along the $OX$ axis arrives at point $A$ in time $t$, the length $OA$ is given by equation $x=x^{\mathrm{\text{'}}}+vt$ ⇒ $x^{\text{'}}=x-vt$ ⇒ $x^{\text{'}}=(c-v)t$. The equation $x=x^{\mathrm{\text{'}}}+vt$ can be rewritten as $ct=\left(c-v\right)t+vt$ ⇒ ${\displaystyle \frac{t}{T}}={\displaystyle \frac{c-v}{c}}{\displaystyle \frac{t}{T}}+{\displaystyle \frac{v}{c}}{\displaystyle \frac{t}{T}}$ where ${\displaystyle \frac{t}{T}}$, ${\displaystyle \frac{c-v}{c}}{\displaystyle \frac{t}{T}}$, and ${\displaystyle \frac{v}{c}}{\displaystyle \frac{t}{T}}$are the numbers of wavelengths comprised in the lengths $x$, $x^{\mathrm{\text{'}}}$, and $OO\text{'}$. For ${\displaystyle \frac{t}{T}}=N$, $N={\displaystyle \frac{c-v}{c}}N+{\displaystyle \frac{v}{c}}N$ is a fractional relation of a rational number $N$. The number of wavelengths $N$ can be replaced with $\mathsf{\lambda }$ which may mean one wavelength or the length$\mathsf{\lambda }$ as in the Detail of Figure 10 which gives $\mathsf{\lambda }={\displaystyle \frac{c-v}{c}}\mathsf{\lambda }+{\displaystyle \frac{v}{c}}\mathsf{\lambda }$, or the length $x$ which yields $x={\displaystyle \frac{c-v}{c}}x+{\displaystyle \frac{v}{c}}x$, or the speed $c$ which offers $c={\displaystyle \frac{c-v}{c}}c+{\displaystyle \frac{v}{c}}c$. As fractional relations, all these arrangements are correct and meaningful in mechanics.

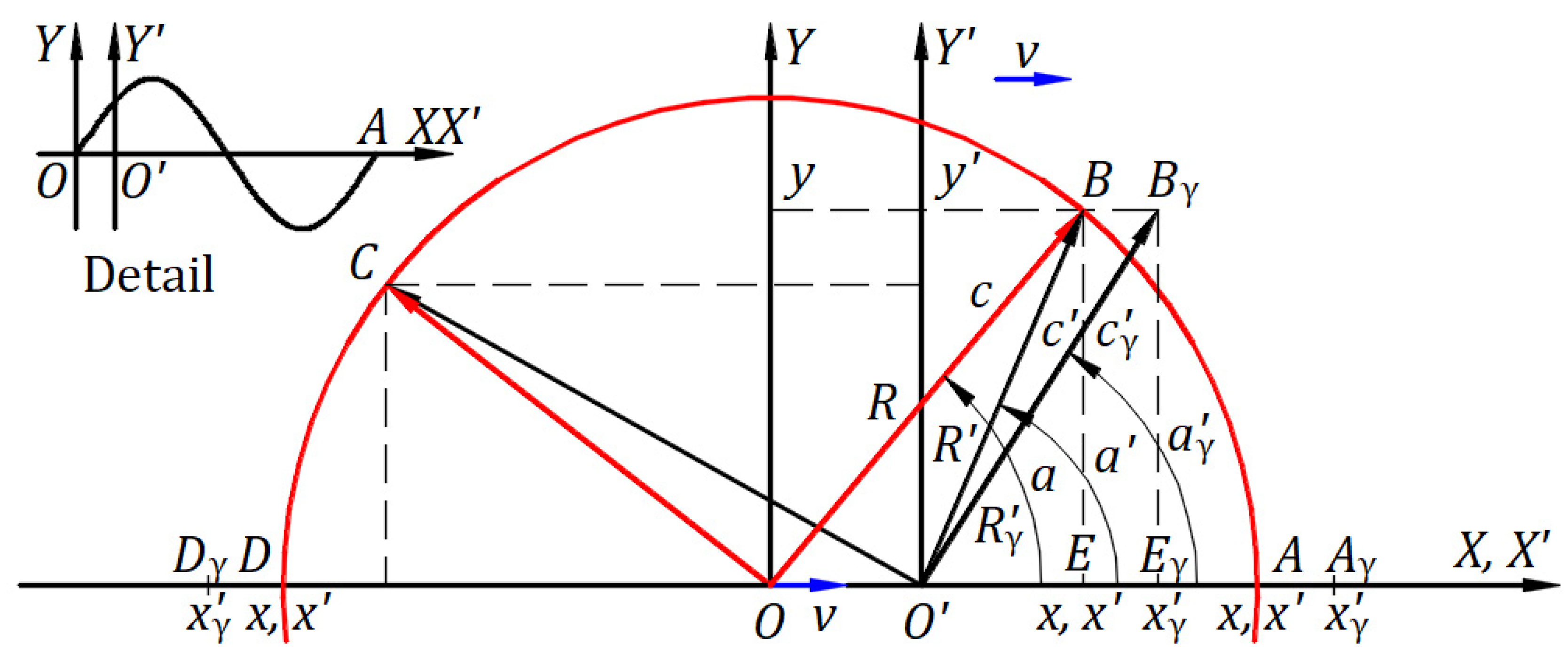
When we replace $N$ with the time $t$, the fractional relation $t={\displaystyle \frac{c-v}{c}}t+{\displaystyle \frac{v}{c}}t$ is susceptible to relativistic time interpretation. The fractional term ${\displaystyle \frac{c-v}{c}}t$ yields $t-{\displaystyle \frac{vt}{c}}=t-{\displaystyle \frac{vx}{c^2}}$ , the equation for time $t^{\text{'}}=t-{\displaystyle \frac{vx}{c^2}}$ in the set of Equations (10) of Lorentz’s transformation. As shown in detail in Figure 10, light travels the fraction ${\displaystyle \frac{c-v}{c}}\lambda$ of wavelength $\lambda$ in time $t^{\text{'}}={\displaystyle \frac{c-v}{c}}T$. This implies that, in the inertial frame, light travels one wavelength ${\lambda }^{\text{'}}=\lambda$ at period $T^{\text{'}}=t^{\text{'}}+{\displaystyle \frac{v}{c}}T={\displaystyle \frac{c-v}{c}}T+{\displaystyle \frac{v}{c}}T$ ⇒ $T^{\text{'}}=T$ , frequency $f^{\text{'}}=f$, and speed $c$, as in the stationary frame. Considering $y^{\mathrm{\text{'}}}=\mathrm{y}$ and $z\mathrm{\text{'}}=z$ as in mechanics, the set of Equations (10) of Lorentz’s transformation is complete, which gives in the inertial frame absolute length $x^{\text{'}}=x-vt$, $y^{\mathrm{\text{'}}}=\mathrm{y}$, $z\mathrm{\text{'}}=z$, and fractional time $t^{\text{'}}={\displaystyle \frac{c-v}{c}}t$, as in Section 4.3. We presented a mechanical derivation of Lorentz’s transformation identical to the hypothesized Lorentz transformation as in Section 4.3. Understanding the incorrectness introduced in this derivation, we know that of Lorentz’s.

We obtained the division of ${\displaystyle \frac{x^{\text{'}}}{t^{\text{'}}}}=c$ for the wavefront in the direction $OA$ as in Section 4.3 where incorrectly considered it to verify Lorentz’s transformation. Here, the speed $c$ does not represent the speed of light in the inertial frame as Lorentz’s transformation and Einstein’s special relativity pretend because the equation $x^{\mathrm{\text{'}}}=x-vt$is correctly a relation between different quantities that gives an absolute length but the term $t^{\text{'}}={\displaystyle \frac{c-v}{c}}t$ belongs to $t={\displaystyle \frac{c-v}{c}}t+{\displaystyle \frac{v}{c}}t$ that is a fractional relation for a quantity, which in this case is time $t$. Indeed, the division can be written as $x^{\text{'}}=c{t}^{\text{'}}$ ⇒ $x^{\text{'}}=c{\displaystyle \frac{c-v}{c}}t$ ⇒ $x^{\text{'}}=(c-v)t$ as in mechanics with variable speed $c^{\text{'}}=c-v$ according to the speed of the inertial frame. This incorrectness in Lorentz’s transformation and Einstein’s special relativity not only refutes them but proves the constancy of time passage in the universe and the variability of light speed in the form of light propagation; light emitted by a source in motion is the constant $c$ in the absolute frame.

The following paragraphs show how different the Doppler observation in an inertial frame is from special relativity.

As shown in detail in Figure 10, light travels the fraction ${\displaystyle \frac{c-v}{c}}\lambda$ of wavelength $\lambda$ in time $T$. This means that, in the inertial frame, light travels one wavelength ${\lambda }^{\text{'}}=\lambda$ at period $T^{\text{'}}={\displaystyle \frac{c}{c-v}}T$, speed $c^{\text{'}}=c-v$, and frequency $f^{\text{'}}={\displaystyle \frac{c-v}{c}}f$ that is the observed frequency offered by the Doppler effect. The number of wavelengths $\lambda$ comprising $x^{\text{'}}=O^{\text{'}}A$ is ${\displaystyle \frac{c-v}{c}}{\displaystyle \frac{t}{T}}$.

In the $O^{\text{'}}D$ direction, light travels the length $\lambda +{\displaystyle \frac{v}{c}}\lambda ={\displaystyle \frac{c+v}{c}}\lambda$ in time $T$ and one wavelength ${\lambda }^{\text{'}}=\lambda$ at period $T^{\text{'}}={\displaystyle \frac{c}{c+v}}T$, speed $c^{\text{'}}=c+v$ , and frequency $f^{\text{'}}={\displaystyle \frac{c+v}{c}}f$ that is the observed frequency offered by the Doppler effect. The number of wavelengths $\lambda$ comprising $x^{\text{'}}=O^{\text{'}}D$ is ${\displaystyle \frac{c+v}{c}}{\displaystyle \frac{t}{T}}$.

5. Conclusions

Lorentz’s transformation is based on observations and duplicates the physics phenomena from a stationary frame into an inertial frame.

The transformation provides the constant speed of light $c$ in both the moving and opposite directions of the inertial frame. Simultaneously, it varies in any other direction, converging to infinite. However, special relativity claims that the speed of light is constant in all directions.

The time contraction in the moving direction of the inertial frame differs from the time dilation in the opposite direction, requiring a ruler and time synchronization in both directions and any others.

There are no length contractions In Lorentz’s transformation to support this fundamental concept of special relativity.

The above unacceptable conclusions derived from calculations and discussions of Section 4 make the theory of special relativity rejectable.

The saga of special relativity started with FitzGerald’s statement that the length of material bodies changes, which was based on a misunderstanding of the Michelson‒Morley experiment. Lorentz continued this with his transformation, and Einstein did so with an entire theory, followed by many others. Special relativity should not have been written or accepted.

Mechanics present phenomena as they are. Special relativity focuses on observations of phenomena instead of understanding them. In contrast to these two approaches, the article presents how the phenomena are, like in mechanics, and how a local observer perceives them, which helps us understand reality.

The kinematics of light explain why the speed of light is constant $c$ in any inertial frame in which light sources and reflective mirrors are at rest, why the laws of physics have the same form in each inertial frame, and why no light experiment in an inertial frame can prove its motion.

Matter creates light and, as a mechanical phenomenon, the kinematics of light naturally present light in its interactions with matter at emission and reflection [1,2,3,4,5,6,7,9,10,12], refraction [11], and when traveling through a moving medium [8]. Light and any other electromagnetic radiation can be considered massless matter/fields and the kinematics of light can thus be included in mechanics.

The following mechanical ballistic law governs the kinematics of balls and electromagnetic radiation: a ball or light emitted by a source inherits the velocity of the source in the absolute frame. The ballistic law has the mathematical expression given by a vector sum of velocities based on a physics phenomenon. It is reasonable, understandable without explanations, and fundamental in mechanics like the Newtonian laws.

The kinematics of light also presents the essential concept of how the human eye reacts to propagated and emitted light. The understanding that the human eye perceives only emitted velocity $c$ by a source and not its propagation is crucial in understanding physics phenomena. Based on the ballistic law, the observation of a star’s orbit as in Section 3.4.4 and Reference [5] with no irregularity requires perceiving only emitted velocity $c$. The peripheral vision may explain this perception. Light travels in its propagation direction and can be more or less perceived by the human eye. To have a good view, the eye has to adjust its direct vision with the direction of the velocity $c$. The perception of the constant velocity of light $c$ emitted by a source in the absolute frame may be a topic for vision and optical science.

There are different theories of light, e.g., ether theory, special relativity theory, Ritz’s ballistic theory, and kinematics theory similar in concept to Ritz’s. We can consider criteria to distinguish which theory is acceptable. For example, a theory must be based on physical phenomena explainable by themself to which a mathematical expression may be applied, be rational according to human understanding, and explain observations and experiments realistically. The kinematics theory of light and the special relativity theory originated from Newtonian physics and Galilean transformation, but they are different in approach and results. Section 2.3 offers details regarding the discrete emission of balls with and without mass and Section 3.3 presents details related to the continuous emission of light. Section 3.6 shows what Einstein had to deal with without knowing the ballistic law. Einstein eliminated the concept of the frame at absolute rest. He hypothesized that the speed of light is constant in each inertial frame when the source belongs to any inertial frame and without distinguishing between the emitted and propagation velocity. Einstein employed Lorentz’s transformation intending to obtain the constancy of light speed in inertial frames which the ballistic law does. The mathematical Lorentz’s transformation without the support of a physics phenomenon cannot deliver Lorentz’s and Einstein’s intent. Nevertheless, Einstein obtained Lorentz’s transformation in his special relativity. With the unintended irrational conclusions, the special relativity is self-negating.