2024 Key Reflections on the 1824 Sadi Carnot’s ‘Réflexions’: Sadi Carnot’s Legacy and 200-Year ‘Réflexions’ Anniversary

1. Introduction

In 2024 the thermodynamic community celebrated Sadi Carnot’s Legacy and the 200^th Anniversary of his only and famous 1824 ‘Réflexions’ publication [1,2,3,4,5]. Here we present this author’s contribution with 2024 ‘Key Reflections’ of his related work and his plenary presentation at Sadi Carnot’s Legacy International Colloquium at École Polytechnique in France [3,6].

Sadi Carnot, at age 28, published in 1824, now famous “Réflexions sur la puissance motrice du feu” (English translation, “Reflections on the Motive Power of Fire [1]”). His ingenious reasoning of reversible processes and cycles, and maximum “heat-to-power efficiency” laid foundations for the Second Law of thermodynamics, before The First Law of energy conservation was even formulated (in 1840s), and long before Thermodynamic concepts were established (in 1850s and later, [7,8] and elsewhere). Sadi Carnot, who died in 1832 at age 36 from cholera epidemic, could not had been aware of immense implications of his ingenious reasoning at that time. No wonder that Sadi Carnot's masterpiece, regardless of flawed assumption of conservation of caloric, was not appreciated at his time, when his ingenious reasoning of ideal “heat engine reversible cycles” was not fully recognized, and may be truly comprehended by a few, even nowadays. We are often trapped in our own thoughts and words (especially if nonnative) and the subtle holistic meanings are to be read “between the lines.”

Before this author’s “2024 Key Reflections on the 1824 Sadi Carnot’s ‘Réflexions’ ” are presented here, the brief introduction, based on his prior publications [9,10,11], is given next to revisit essential concepts.

Sadi Carnot gave a full and accurate reasoning of heat engine cyclic-processes and their limitations of “converting heat to [work] power” at the time when caloric theory was flourishing and almost two decades before equivalency between work and heat was experimentally established [Joule, 1843].

At that time, when the energy conservation law was not known and heat was considered as indestructible caloric, when heat engines were in initial stage of development with efficiency of less than 5%, the confusion and speculations flourished. Can efficiency be improved by different temperatures or pressures, a different working substance than water; or some different mode of operation than pistons and cylinders? With ingenious and far-reaching reasoning, Sadi Carnot answered all of those questions and logically reasoned (thus proved) that maximum, limiting efficiency of heat engine does not depend on medium used in the engine or its design, but only depends on (and increases with) the temperature difference between the heat source and cooling medium or heat sink, similarly to the water-wheel work-power dependence on the waterfall height difference at a given water flowrate, see Eq. (1) and Figure 1 (explicit formulas were developed after Carnot followers’ work [7,8] and elsewhere; see also Key NOVEL-Point 4).

The most importantly, Carnot introduced the reversible processes and cycles and, with ingenious reasoning of “contradiction impossibility”, see Key NOVEL-Point 3, proved that maximum heat engine efficiency is achieved by any reversible cycle, thus, all must have the same maximum-possible efficiency ([1,9,10], see also Key NOVEL-Point 2), i.e.:

“The motive power of heat is independent of the agents employed to realize it; its quantity is fired solely by the temperatures of the bodies between which is effected, finally, the transfer of the caloric.” [1]. Namely,

$$W_C=W_{netOUT}=Q_{IN}\cdot f_C(T_H,T_L);\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\eta }_C={\left.{\displaystyle \frac{W_{netOUT}}{Q_{IN}}}\right|}_{Max}={\left.\underset{\mathrm{Qualitative}\hspace{0.17em}\mathrm{function}\hspace{0.17em}}{\underbrace{f_C(T_H,T_L)}}\right|}_{\mathrm{Rev}.}$$

(1)

Carnot cycle consists of four reversible processes, see Figure 2: isothermal heating and expansion at constant high-temperature T_H (process 1-2); adiabatic expansion to achieve low-temperature T_L (process 2-3); isothermal cooling and contraction at constant low-temperature T_L (process 3-4); and adiabatic compression to achieve high-temperature T_H and complete the cycle (process 4-1).

All processes are reversible; thus, the cycle could be reversed, without additional external intervention, along the same path and with the same quantities of all the heats and works in opposite directions (in-to-out and vice versa), see Figure 3, i.e.:

$$\left\{Q_H,Q_L,W_C\right\}\underset{\mathrm{IF}\mathrm{REVERESED}}{\underbrace{\iff }}\left\{-Q_H,-Q_L,-W_C\right\}$$

(2)

The concept and consequences of a process and cycle reversibility are the most ingenious and far-reaching, see [5,9,10] (see also Key NOVEL-Point 1). Sadi Carnot’s simple and logical reasoning that mechanical work is extracted in heat engine due to the heat passing from high to low temperature (see also Key Point I), led him to a very logical conclusion that any heat transfer from high to low temperature (like in a heat exchanger) without extracting possible work (like in a reversible heat engine) will be a waste of work potential — so he deduced that any heat transfer in ideal, perfect heat engine must be at infinitesimally small temperature difference, achieved by mechanical compression or expansion of the working medium (required temperature adjustment without heat transfer), as Carnot ingeniously advised in full details [1] (see also Key Point II).

Then, Sadi Carnot expended his logical reasoning to conclude that all reversible (ideal) heat engines must have equal and maximum possible efficiency, otherwise if reversed, the impossible “creation of conserved quantities” would be achieved, see all details in [1,9,10] and elsewhere (see also Key Point V and Key NOVEL-Point 2). What a simple and logical ingenious reasoning!

Carnot’s reasoning proves that a reversible cycle cannot have smaller efficiency (power output relative to heat input) than any other cycle, thus all reversible cycles must have the same maximum possible power-efficiency for the given temperature of the two thermal reservoirs, independently from anything else, including the nature of heat-engine design and its agent undergoing the cyclic process (see all relevant specifics in [1,9,10] and elsewhere; see also Key Point V and Key NOVEL-Point 2). Since the irreversible cycles could not be reversed, they may (and do) have lower than maximum reversible efficiency up to zero (no net-work produced, if all work potential is dissipated to heat) or even negative (external work input required to run such a “parasite” engine which will dissipate such work, in addition to original work potential, into heat), i.e.:

$${\eta }_{Irr}<\underset{\mathrm{Reversible}}{\underbrace{{\eta }_{\mathrm{Rev}}={\eta }_{\max }=f_C(T_H,T_L)}}$$

(3)

Carnot did not provide quantitative, but qualitative relation for the ideal heat engine power-efficiency, and accurately specified all conditions that must be satisfied to achieve reversibility and the maximum efficiency: the need for “re-establishing temperature equilibrium for caloric transfer,” i.e. reversible processes, where the reversible heat transfer has to be achieved at negligibly small (in limit zero) temperature difference at both temperature levels, at T_H , high temperature for heat source (reversible heating), and at T_L , low temperature for heat sink (reversible cooling of heat-engine medium), see Figure 3; otherwise the work potential during heat transfer due to temperature difference will be irreversibly lost (the main Carnot’s cause-and-effect reasoning), see also Key Point II.

Sadi Carnot reasoned that mechanical expansion and compression are needed to decrease and increase the temperature of the engine medium to match the temperature of the high- and low-temperature thermal reservoirs, respectively, and thus provide for the reversible heat transfer [1].

Carnot then reasoned that in limiting cases, such as an ideal cycle, it could be reversed using the prior obtained work, to transfer back the caloric (heat) from low- to high-temperature thermal reservoirs, thus laying foundations for the refrigeration cycles (cooling and heat-pumps) as ‘reversed’ heat engine cycles, see Figure 3 and Eq. (2).

Sadi Carnot’s reasoning of “heat engine reversible cycles and their maximum efficiency” is in many ways in par with Einstein’s Relativity theory in modern times, see Eq. (4). It may be among the most important correlations in natural sciences.

(4)

The ‘Key Reflections’ presented next are founded on the Sadi Carnot’s ‘Réflexions’ (English translation by Robert H. Thurston [1]) and on the developments of thermodynamics by the pioneers [7,8] and others, emphasizing this author’s views as an engineering thermodynamicist [5,9,10,11], as a complement to the existing science historians and science philosophers’ analyses [12,13,14,15].

Therefore, a key thermodynamic logic is used to recognize and infer the most probable sequential developments of Sadi Carnot’s ingenious discoveries, as well as to reflect on the related analyses and misconceptions, considering the current state of knowledge, since now, we have the advantage to look at the historical developments more comprehensively and objectively than the pioneers. The sequential ‘Key Points’, where key reasoning infers the next one, along with ‘Miss Points’ (persistent post-misconceptions and fallacies by others), including novel contributions and original generalizations by this author, as ‘Key NOVEL-Points’ with ‘Key Takeaways’, are presented next.

2. Key Points: Most probable sequential developments of Sadi Carnot’s ingenious discoveries

• The source of the heat engine “motive power” is “caloric fall” (“temperature fall” or temperature difference of the caloric)
• The “temperature fall,” as source of engine motive power, should “not be wasted,” but minimized in any “workless heat transfer process”
• All motive frictions and other dissipative processes should be minimized in order to maximize engine power and efficiency
• Reversible Cycles: Isothermal heat transfer and other frictionless processes make an engine process or cycle reversible
• Reversible cycles must all have equal and maximum efficiency

Key Point I: “The source of the heat engine “motive power” is “caloric fall” (“temperature fall” or temperature difference of the caloric)

Hot caloric (heat at high temperature) is the cause and source of the motive power (produced work) by the steam engines (the heat engines in general). Since at the time, the caloric was believed to be conserved (might be a fortunate misconception leading to the critical analogy with the waterwheel, see Figure 1), then Sadi Carnot inferred that its hotness is producing the motive power while being cooled: “motive power due to the [temperature] ‘fall of the caloric’ ” Therefore, all else the same, if temperature of heat is higher than the surrounding’s, the higher ‘temperature fall’ through an engine, the more motive power will be (the more efficient engine, the more power per unit of heat flow), analogous to the more power from more “water-fall” from higher elevation through a water-wheel per unit of water flow. In Sadi Carnot’s words, “The temperature of the fluid should be made as high as possible, in order to obtain a great fall of caloric, and consequently a large production of motive power [1].”

Key Point II: The “temperature fall,” as source of engine motive power, should “not be wasted,” but minimized in any “workless heat transfer process”

This is the most critical and ingenious reasoning by Sadi Carnot, “wherever there exists a difference of temperature, motive power can be produced.” [1], that led to inference of ideal reversible cycles, the most critical concept of Carnot’s discovery. If the temperature difference is the cause and source of motive power, then, if it is “consumed” during the heat transfer without work extraction, then its work potential would be lost, so the temperature difference during heat transfer should be minimized, i.e., be infinitesimal; ideally the heat transfer should be isothermal: “need for re-establishing temperature equilibrium for caloric transfer … in the bodies employed to realize the motive power of heat there should not occur any change of temperature which may not be due to a change of volume [1].”

Key Point III: All motive frictions and other dissipative processes should be minimized in order to maximize engine power and efficiency. Mechanical processes should be ideally frictionless to avoid work waste, i.e., dissipation losses.

Key Point IV:  Reversible Cycles: Isothermal heat transfer and other frictionless processes make an engine process or cycle reversible

This is a monumental and crucial “reversibility concept” with far-reaching consequences. Reversible processes and cycles could effortlessly (without additional external compensation) reverse back-and-forth in perpetuity (like perpetual motion), therefore without any degradation or loss, being perfect and with maximum possible 100% efficiency. They take place at infinitesimal potential difference in either direction (in limit equipotential process, no potential loss of quality), without any quantity nor quality degradation, including conservation of the motive power or work potential. More details at Key NOVEL-Point 1 and elsewhere.

Key Point V: Reversible cycles must all have equal and maximum efficiency.

This “key discovery” (Carnot Theorem) was ingeniously inferred by Sadi Carnot by logical reasoning that otherwise would result in creation of [assumed] conserved caloric and/or perpetual motion: “the maximum of motive power resulting from the employment of steam is also the maximum of motive power realizable by any means whatever [1].” This powerful insight is the most important and ingenious reasoning of Sadi Carnot, and it has far-reaching consequence as demonstrated much later by Kelvin and Clausius, and other Sadi Carnot’s followers. It is further elucidated in Key NOVEL-Point 2, and in Key NOVEL-Point 3 it is further generalized as “Reversible Contradiction impossibility,” see also Figure 4.

The selected and persistent post-misconceptions and fallacies by others are also presented as ‘Miss Points’ next:

3. Miss Points: Persistent post-misconceptions and fallacies by others

• The well-known Carnot efficiency formula,  ${\eta }_{Carnot}=W_{Rev|Max}/Q_H=\left(1-T_L/T_H\right)$, was not established by Sadi Carnot, but much later by Kelvin and Clausius
• The cause and source for motive power is the temperature difference, in principle, but not linearly dependent as misstated by some
• The heat transferred out of the Carnot cycle at lower temperature is “not a waste heat” as often stated, but it is “useful quantity”, necessary for completion of the cycle
• Sadi Carnot could not had been thinking of “any other caloric” but heat, to imply “entropy-like quantity” as speculated by some

Miss Point 1: The well-known Carnot efficiency formula, ${\eta }_{Carnot}=W_{Rev|Max}/Q_H=\left(1-T_L/T_H\right)$, was not established by Sadi Carnot, but much later by Kelvin and Clausius

Sadi Carnot inferred in 1824 the maximum heat-engine power efficiency as implicit function of thermal source-and-sink reservoirs’ High-and-Low temperatures only [${\eta }_{Rev|Max}=W_{Rev|Max}/Q_H=f_C\left(t_H,t_L\right)$]. However, the well-known Carnot efficiency formula, ${\eta }_{Carnot}=W_{Rev|Max}/Q_H=\left(1-T_L/T_H\right)$, sometimes attributed as developed by Sadi Carnot, was actually developed much later in 1850s, first by Kelvin using ideal gas and later by Clausius in general, and named “Carnot efficiency.” Paradoxically, it is shown here that Carnot, Kelvin and Clausius concepts of maximum, reversible cycle efficiency is misplaced, since fundamentally the Carnot cycle efficiency is not the “reversible cycle efficiency” per se, but a thermal energy-source ‘work-potential efficiency’, see Key NOVEL-Point 4 and Figure 6. After all, the Carnot cycle efficiency does not depend on the cycle in any way, but it depends on the thermal reservoirs’ temperatures only.

Miss Point 2:  The cause and source for motive power is the temperature difference, in principle, but not linearly dependent as misattributed by some

Carnot stated that temperature difference is, in principle, cause and source for motive power, but not directly, not linearly dependent as misquoted by some [$W_{Max}=Q_H\cdot f_C\left(t_H,t_L\right)f(t_H-t_L$), not function of Δt =$t_H-t_L\mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y}$]. As stated by Sadi Carnot, “In the fall of caloric the motive power undoubtedly increases with the difference of temperature between the warm and the cold bodies; but we do not know whether it is proportional to this difference. … The fall of caloric produces more motive power at inferior than at superior temperatures” [1].

Miss Point 3: The heat transferred out of the Carnot cycle at lower temperature is “not a waste heat” as often stated, but it is “useful quantity”, necessary for completion of the cycle

The heat transferred out of the ideal Carnot cycle at lower temperature is “not a waste” as often stated but it is necessary for completion of the cycle (the entropy balance), and therefore necessary and useful quantity. As stated by Sadi Carnot, “… without ‘the cold’ the heat would be useless [1].” The only waste is additional heat generated by irreversible work dissipation accompanied by entropy generation in real cycles, that must also be taken out to complete the cycle.

Miss Point 4: Sadi Carnot could not had been thinking of “any ‘other’ caloric” but heat, to imply “entropy-like quantity” as speculated by some

We need to keep in mind that in Sadi Carnot’s time (early 1800s) the steam engines were inefficient (below 5%, so the heat in and out were comparable within experimental uncertainty, as if caloric is conserved), the conservation of caloric flourished, and many critical thermal-concepts, including the conservation of energy (The First Law) were not even established. At that time the entropy concept was not known even remotely. Therefore, Sadi Carnot could not had been thinking of “any ‘other’ caloric” but heat, to imply “entropy-like quantity” as speculated by some.

Novel contributions with deeper physical insights and related generalization by this author are formalized in the following ‘Key NOVEL-Points’:

4. Key NOVEL-Points: Novel contributions and original generalizations

• “Reversible and Reverse” Processes and Cycles Dissected
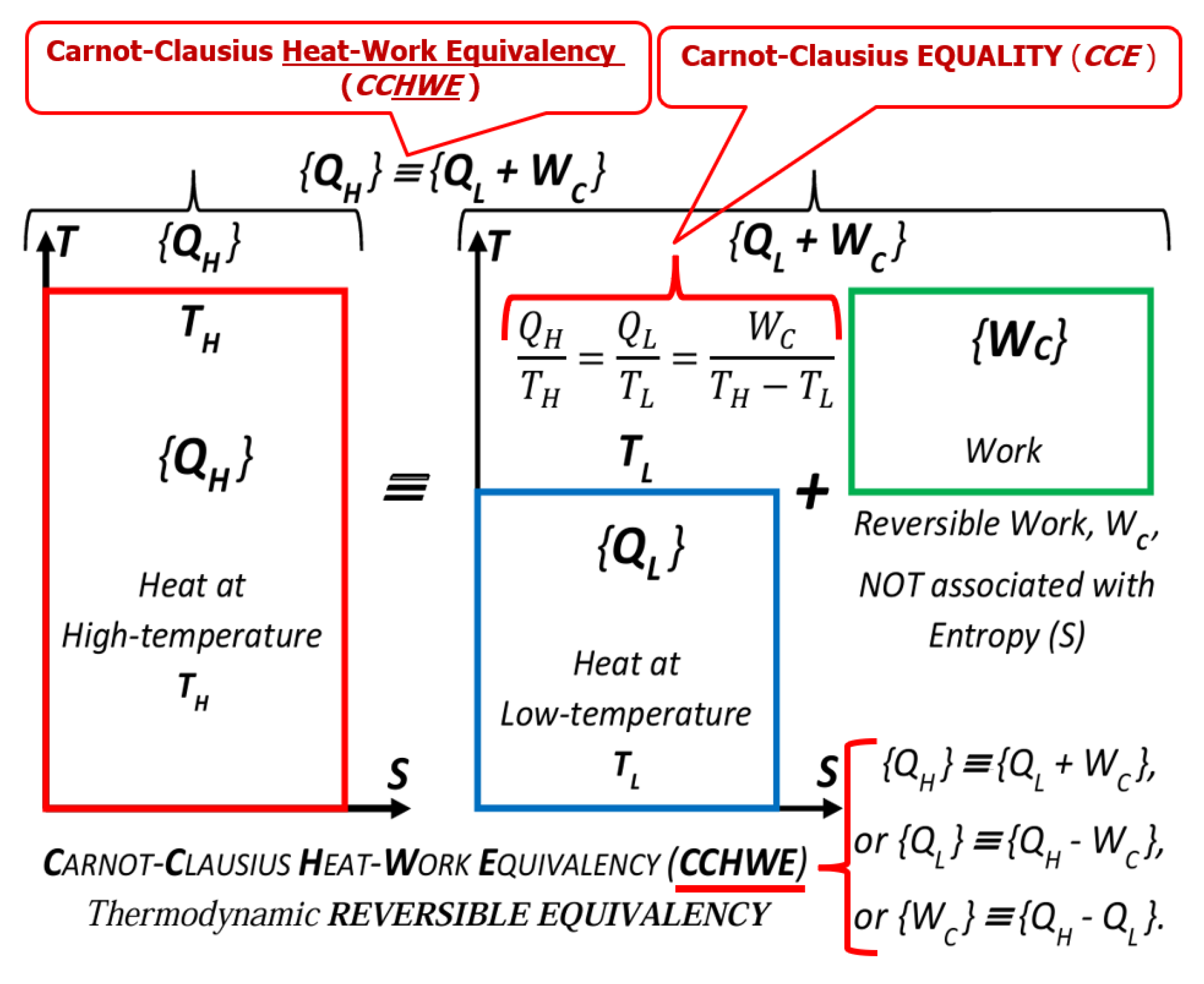
• Maximum Efficiency and “Reversible Equivalency” Scrutinized
• Reversible Contradiction Impossibility (“Reductio ad absurdum”)
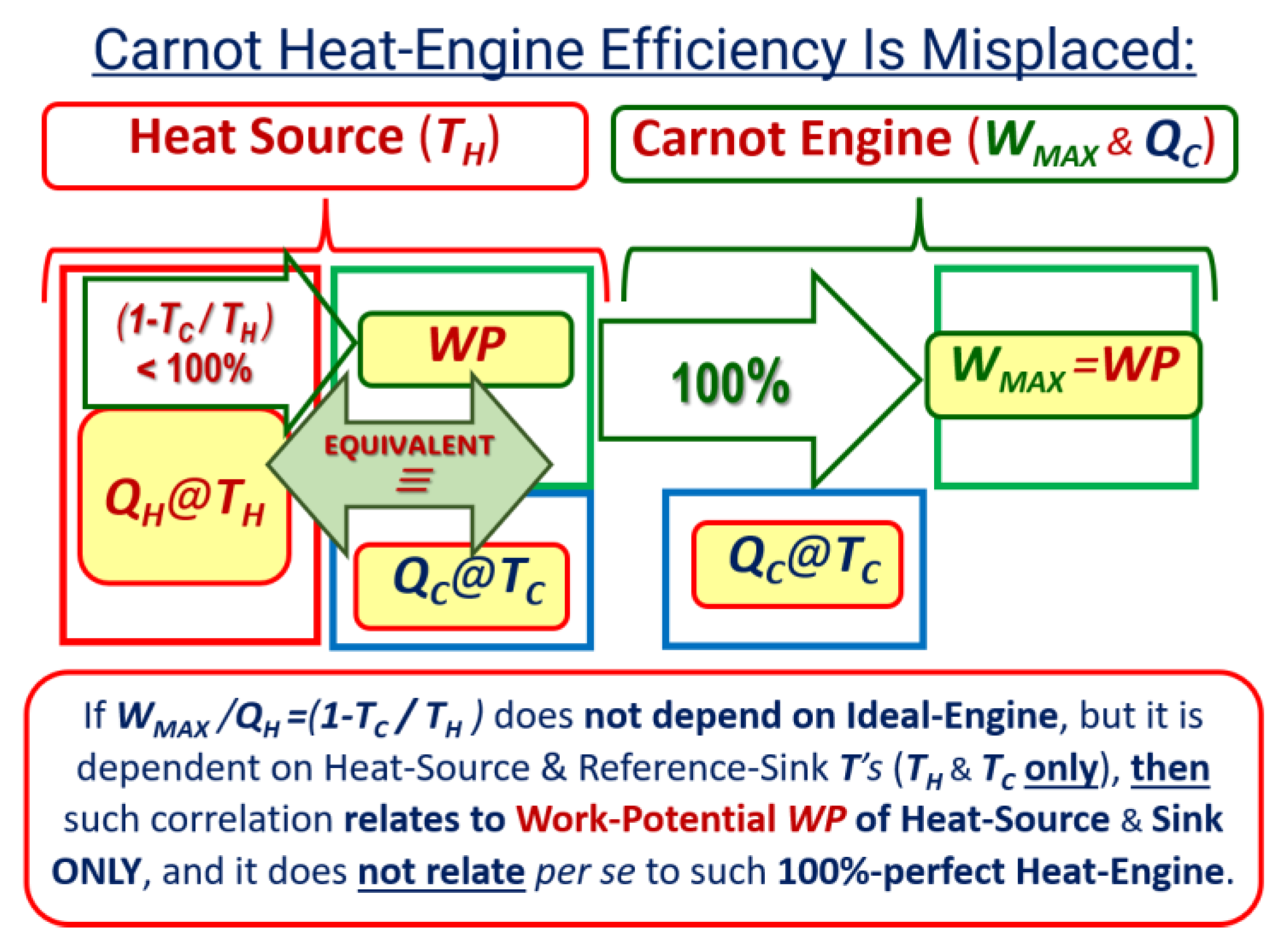
• Reversible Carnot Cycle Efficiency Is Misplaced — It is NOT the “Cycle efficiency” ‘per se’, but a “Thermal energy-source ‘work-potential efficiency’”
• The Carnot-Clausius [Ratio] Equality (CCE) and Clausius Equality (Cyclic integral) are special cases of relevant “Entropy boundary integral” for reversible stationary processes

Key NOVEL-Point 1: “Reversible and Reverse” Processes and Cycles Dissected

Ideal and perfect, “Reversible processes” take place at infinitesimal potential difference (temperature, pressure and similar) at any instant within and between a system and its boundary surroundings, but they may and do change in time (process is a change in time). Namely, the spatial gradients are virtually zero at any instant while time gradients and related fluxes may be arbitrary as driven by ideal boundary surroundings and facilitated by ideal arbitrary (or infinite) transport coefficients. Therefore, the potential qualities of flux quantities (heat and different kinds of works) are not degraded but equipotentially transferred and stored between the system and its boundary surroundings, and thereby ‘truly’ conserved in every way. However, in time, due to unavoidable irreversible dissipation of work to generated-heat, accompanied by generation of entropy, all real processes between interacting systems (including relevant surroundings) are asymptotically approaching common equilibrium with zero mutual work potential and maximum mutual entropy.

Namely, if an elastic, ideal gas or ideal spring is reversibly compressed, then the pressure may change in time but is equal everywhere at any instant across the system and the boundary surroundings (equipotential driving force at any instant). Similarly, if heat is reversibly transferred, the temperature may change in time, but it is equal everywhere within the system at any instant, and if it varies in time, it is driven by varying, but spatially equipotential surrounding temperature, so the energy potential quality is stored and conserved everywhere in every way (it may be reversed back-and-forth in perpetuity without external compensation).

Note that ‘time and energy rates’ are irrelevant per se for the reversible analysis of energy balances and properties between initial and final states, being independent on process type and path of how the final state is achieved, either reversibly or irreversibly, the former being more simple and suitable for analysis than the latter.

A Cycle is a special case of quasi-stationary process when flow inlet and outlet quantities are the same (feed into each other) and close the cycle. Like a stationary process, a cycle does not accumulate flux quantities and may repeat and last in perpetuity (quasi-stationary). Note that all processes, particle-wise, are transient in time (in Lagrangian sense, from inlet to outlet), but for the steady-state or stationary processes (in Eulerian sense) the properties do not change in time (zero temporal gradients) at a fixed location, and for a cyclic process the flow inlet quantities are the same as the outlet’s (since they feed into each other).

A “Reverse” concept is independent from and should not be confused with the reversible concept. If reversible, a reverse-process could be reversed using prior, related process work (with infinitesimal change of potential difference in opposite direction, and without additional external-work compensation), while to reverse an irreversible process it would require an additional, external work compensation.

A “Reverse process” and/or “Reverse cycle” would take place if the driving (forced) potentials of a reversible process or a cycle are reversed (by infinitesimal change in opposite direction), then such a reversible process would be reversed with all quantities changing direction from input to output (and vice versa; e.g., a refrigeration cycle is a “reverse” of a power cycle or vice versa, see Figure 3). For stationary processes, no temporal gradients, there is no accumulation of flux-quantities within a system, and for quasi-stationary cycles no accumulation of flux-quantities after completion of a cycle. The input and output quantities would be conserved and could be reversed back-and-fort in perpetuity like perpetual motion.

In reality, there is a need for at least infinitesimal temperature difference (and/or pressure and similar) to provide a process ‘sense of direction’, and to resolve directional ambiguity by chance. Therefore, every process must be at least infinitesimally irreversible (infinitesimally imperfect), the reversibility being an asymptotic, limiting ideal concept. For this reason, even reversible equilibrium is unachievable, like absolute zero temperature or any other ideal concept, only approached asymptotically.

Key NOVEL-Point 2: Maximum Efficiency and “Reversible Equivalency” Scrutinized

Maximum efficiency of an energy process or cycle entails maximum-possible work extraction from a system while coming to equilibrium with a reference system, usually the surroundings; or minimum-possible work expenditure in a reverse process of formation of original system (from within the same reference state), see Figure 4. Since the reversible processes do not degrade any potential quality and could be reversed without external intervention, the two works must be the same for all reversible processes, and they represent the maximum work potential (WP) for the given conditions. Therefore, the reversible processes are perfect, and equally and maximally 100% efficient. They define the concept of “Reversible Equivalency” — the ‘true quantity and quality equality’ of input and output, where relevant quantities and qualities are conserved in perpetuity. In real processes there will be some work dissipation losses (degradation of work with its dissipative conversion to heat), so that less work would be extracted than the maximum possible, and more work would be needed than the minimum required, thus reducing the maximum possible efficiency for real, irreversible processes, see Eq. (3) and Figure 4.

Since the reversible processes take place at virtual equipotential condition (virtually the same temperature, pressure, etc.; they are equipotential locally at any time, thus being reversible at any time), but they may vary in time with variable system and surrounding properties. Therefore, ‘potential quality’ of all relevant quantities would be equipotentially transferred and stored, i.e., conserved without any degradation (without any dissipation) and could be effortlessly reversed back-and-forth (without additional external compensation).

With infinitesimal reversal of relevant potentials, all flux quantities will change directions while conserving the qualities. Therefore, the work extraction in a reversible cycle would be equal to the expenditure of work in its ‘reverse’ reversible-cycle, see Eq. (2) and Figure 3 and Figure 4. Furthermore, all reversible cycles must have equal and maximum 100% efficiency, otherwise any ‘under-achieving’ reversible cycle (with lower work extraction than another [reference] cycle), when reversed, would consume less work than the reference cycle and thus be ‘over-achieving’ with higher than reference 100% maximum efficiency, resulting in a ‘Contradiction impossibility’, see Key NOVEL-Point 3.

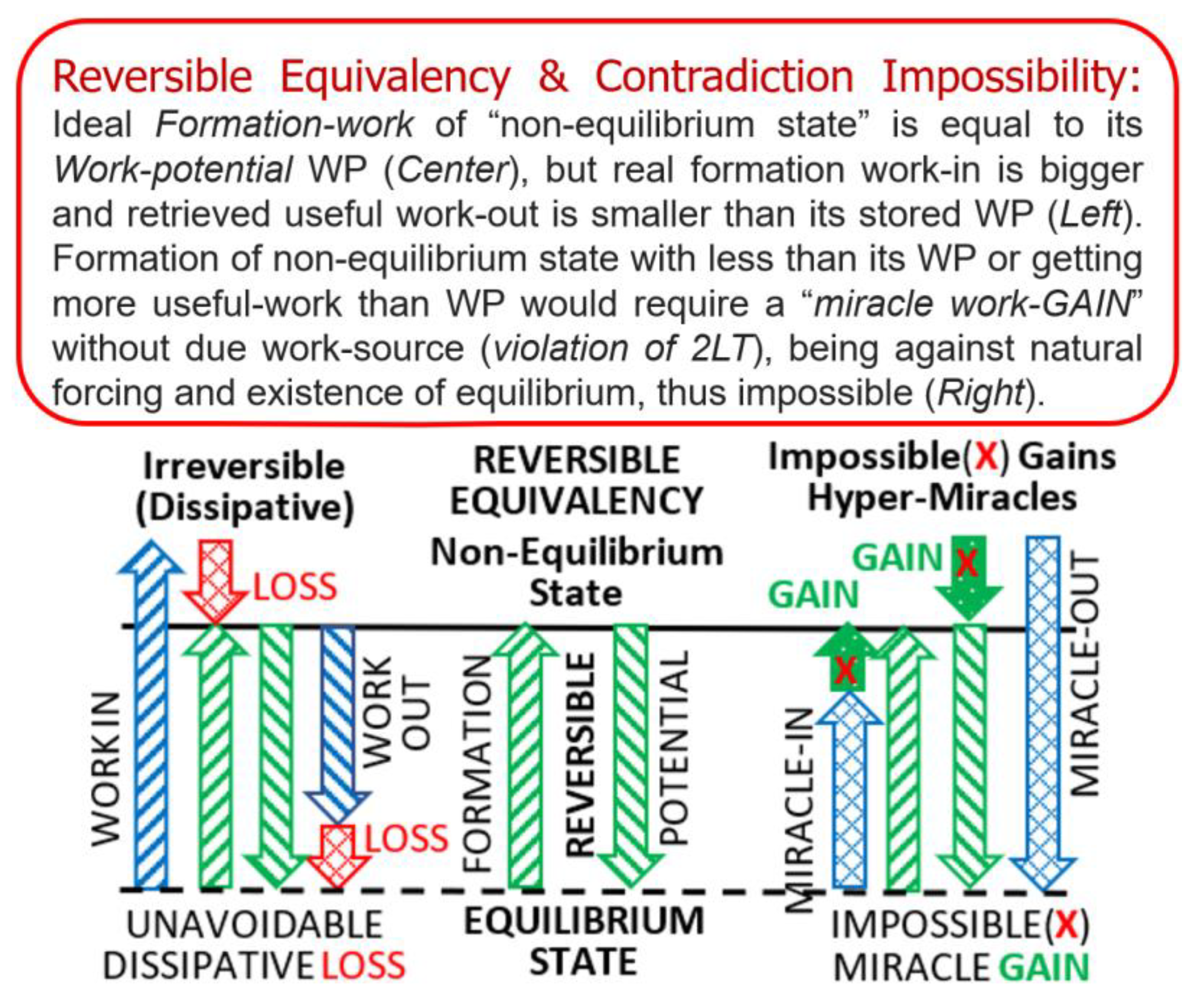
Key NOVEL-Point 3: Reversible Contradiction Impossibility (“Reductio ad absurdum”)

As stated above, the reversible efficiency implies maximum work extraction and minimum work expenditure in the reverse process, thereby the two must be equivalent for given conditions, thus establishing the Reversible Equivalency, see also Key NOVEL-Point 2. Otherwise, any reversible cycle “under-achievement” (getting less than maximum possible) would become an “over-achievement” when such cycle is reversibly ‘reversed’ (accomplishing with less than minimum required), and such “reverse over-achievement” would be physically impossible, would be the “Reversible equivalency violation” and may violate the conservation laws, thus implying the “Reversible Contradiction Impossibility” of a well-known fact, see Figure 4 (impossible ‘miracle GAIN’).

Namely, the “Reversible Contradiction Impossibility” (an under-achieving reversible process when reversed would become an impossible over-achieving reversible process) could result in numerous consequences: Namely, miraculous creation of ‘perpetual motion’ or creation of assumed ‘conserved caloric’, regardless of Sadi Carnot’s misconception, and other impossible processes, like spontaneous heat transfer from lower to higher temperature, etc. The ‘contradiction impossibility’ is so strong and universal a concept that any pertinent or quasi-relevant criteria, even if misunderstood, like conservation of caloric, will be sufficient to reason fundamental inferences [1].

Further consequences of the “Reversible Contradiction Impossibility” would be spontaneous generation of a conserved quantity, or generation of nonequilibrium work potential, or energy transfer from lower to higher potential, like spontaneous heat transfer from lower to higher temperature and generation of thermal nonequilibrium and destruction of entropy, see more details in [9,10,11] and elsewhere. Or in general, spontaneous creation of non-equilibrium from within an equilibrium being the physical contradiction of always observed “spontaneous process direction from non-equilibrium towards mutual equilibrium,” and never experienced otherwise. It will amount to the “forced-directionality contradiction” of the irreversible process-directionality from a higher to lower potential towards mutual equilibrium, as well as impossibility to reverse dissipation.

KEYNOTE 1: It would be logically and otherwise impossible and absurd (“Reductio ad absurdum”) to have a spontaneous process “the one way and/or the opposite way” arbitrarily in opposite directions, as casual by chance (i.e., to have heat transfer “from hot-to-cold or from-cold-to-hot” or “forcing in one direction and accelerating in opposite direction,” by chance). It would be a violation of the Second law of thermodynamics (2LT).

The reversible processes are equipotential and therefore do not degrade nonequilibrium, but store and/or convert one kind to another, like a reversible cycle converts ‘heat at high temperature’ to ‘work plus heat at lower temperature’, and in reverse in perpetuity, defined in [11] as “Carnot-Clausius Heat-Work Equivalency, CCHWE” (‘potential-like’ heat at high temperature to ‘kinetic-like’ work plus heat at lower temperature, and vice versa, analogous to a reversible pendulum converting potential to kinetic energy, and in reverse in perpetuity), see Figure 5. Therefore, all reversible processes are perfectly “equivalent in every way” and the most efficient, without any dissipative degradation.

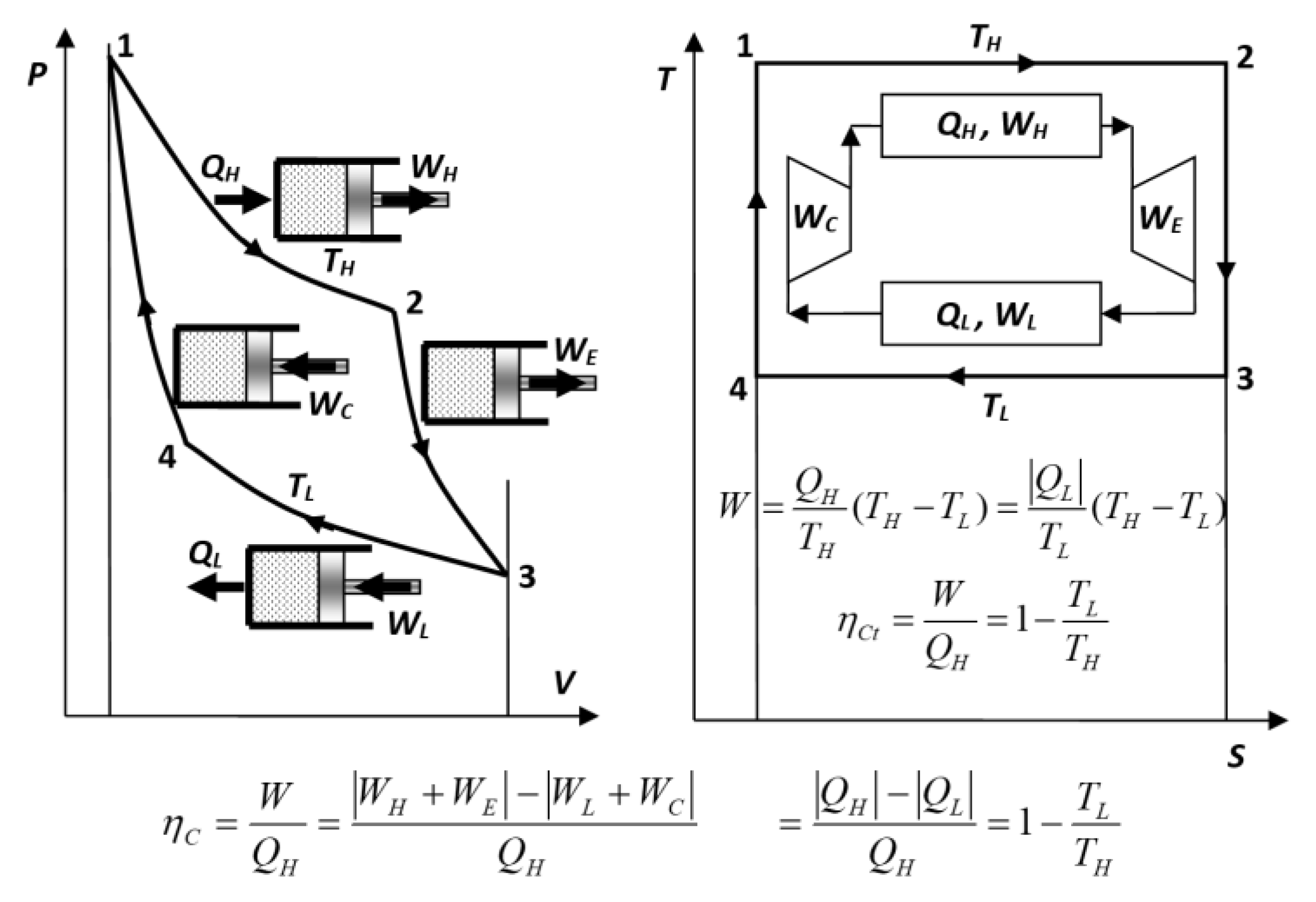
Key NOVEL-Point 4:  Reversible Carnot Cycle Efficiency Is Misplaced − It is NOT the “Cycle efficiency” ‘per se’, but a “Thermal energy-source ‘work-potential efficiency’”

The reversible processes and cycles, as a matter of concept, are 100% perfect without any degradation and must be equally and perfectly (maximally) efficient, not over nor below 100% efficient (would be the Reversible Contradiction Impossibility). Therefore, all reversible processes and cycles have 100% “true quantity and quality” efficiency: they extract 100% of “available work potential” as does any ideal waterwheel and any other reversible engine or motor. The 100% perfect “true reversible efficiency (CCHWE)” [11], see Figure 5, should not be confused with “maximum work-thermal efficiency” of a thermal energy source, that represents the “work potential of heat” or Exergy of heat (or nonequilibrium thermal energy) of the relevant thermal reservoirs [E_x=W_Rev|Max = Q(1-T₀/T_H)], see Figure 6.

Sadi Carnot [1] and his followers, including Kelvin and Clausius [4,5], ironically referred to the maximum heat-engine cycle efficiency (they “agonizingly” developed at the time when most thermal concepts were unknown), with the absurd conclusion, that “it does not depend on the cycle design itself nor its operation mode,” hence, the proof that it is not the efficiency of ideal Carnot cycle per se. Therefore, their attribution is misplaced since the efficiency they developed should had referred to the “maximum motive power or ‘work potential (WP)’ of the thermal reservoirs” since it depends on their temperatures only, and hence, being the logical proof of the claim presented here.

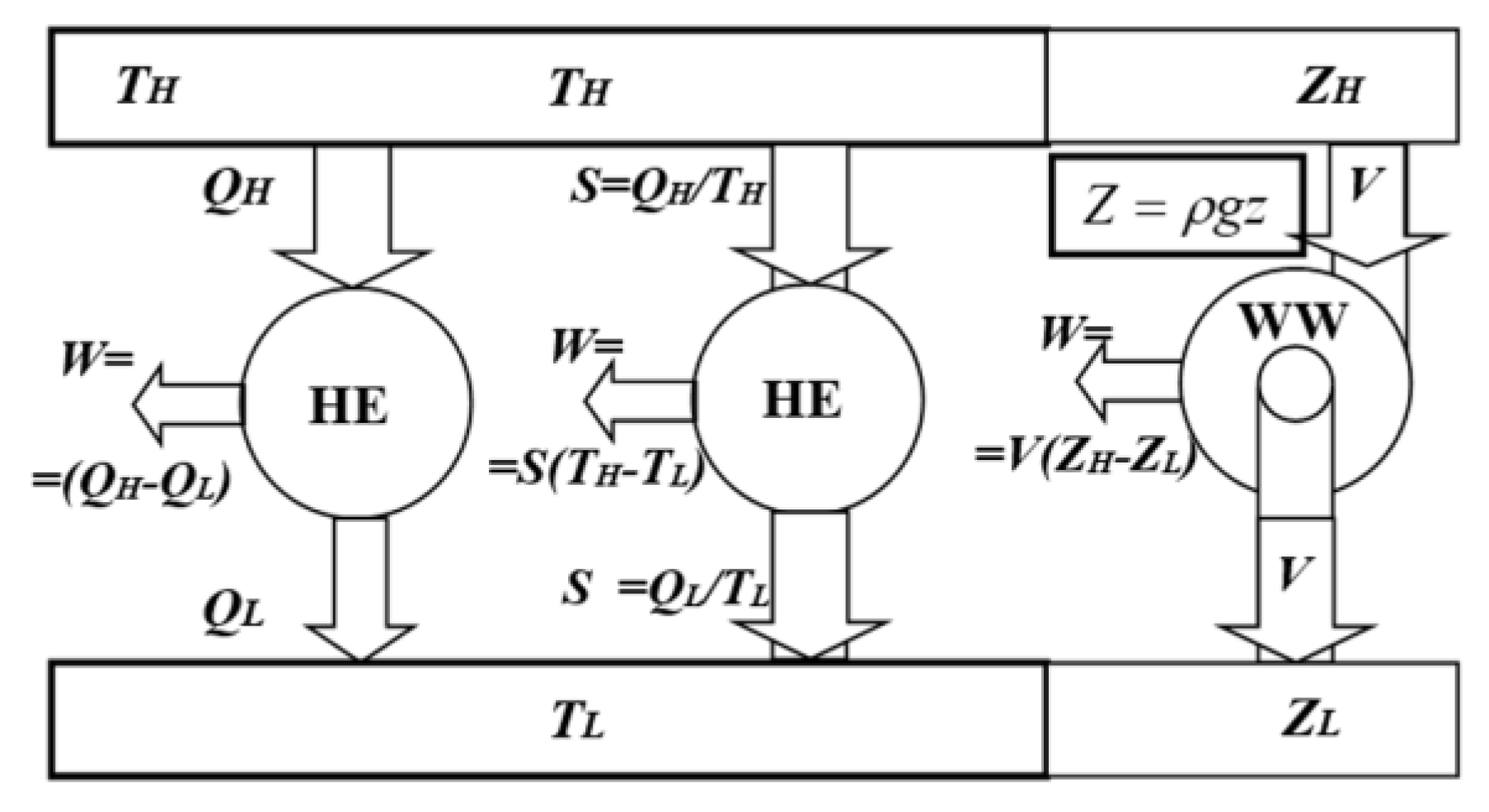
KEYNOTE 2: Carnot heat-engine efficiency dependance on temperatures of the heat reservoirs would be equally misplaced as attribute the maximum efficiency of an ideal water-wheel (water turbine), based on its motive-power per unit of input water-flow, and then it would also mistakenly depend on the water-reservoirs’ elevations only. All reversible devices are equally and maximally 100% efficient.

A motive power efficiency (i.e., a device’s work efficiency) should be consistently based on the work potential of an energy source (not on a “convenient nor arbitrary input quantity,” like heat input or water-flow input, etc.); and then the ‘true’ Carnot cycle efficiency would be 100% as for all other efficiencies for ideal, reversible engines and motors.

We now have the advantage of looking at the historical developments more comprehensively and objectively than the pioneers [5,9,10,11]. Sadi Carnot defined engine cycle efficiency, logically and “empirically,” as “[work] power output per heat input,” long before the concept of “work potential” of an energy-source and energy conservation were established.

An exact “reverse” of the reversible “Power Carnot cycle” is the ideal “Heat-pump cycle” (“Reverse Carnot cycle”) whose efficiency or “performance” is defined ‘in reverse’ as “heat output per work input.” It is always over 100% (as the “fundamental inverse” of the Carnot cycle efficiency, latter always smaller than 100%); and it is named as the “Coefficient of Performance (COP)” since ‘such efficiency’ over 100% would not be fundamentally (nor “politically”) proper.

KEYNOTE 3: For the same fundamental reason, the efficiency of a perfect, ideal Carnot cycle (being below 100%) would also be logically inappropriate (as if there are “some work losses” in the ideal reversible cycles). For the same reason, as for the Heat-pump cycle, it should be called ‘Carnot cycle COP’ but not the ‘Cycle efficiency’. Fundamentally, all ideal, reversible cycles must be “equally and maximally [100%] efficient,” as reasoned by Sadi Carnot [1].

Furthermore, it is fundamentally inappropriate, as often stated, to call the heat transferred out of the Carnot cycle at lower temperature, the “waste heat or loss”, since it is the “useful quantity,” necessary for the completion of the perfect, ideal cycle, and together with the cycle work, they are interchangeable and present the “reversible equivalent” to the heat-input at the high temperature (CCHWE [11]), see also Figure 5. The only “waste or loss” that lower efficiency below 100% would be any ‘irreversible work dissipation’ (converted into generated-heat) and accompanied by entropy generation, that must be also taken out to complete a real cycle. A device’s efficiency should not be higher than 100% and only could be lower for irreversible, dissipative losses.

The “original,” nowadays well-known Carnot cycle efficiency is misplaced and inappropriate, and it should be renamed for what it is: the Work potential (WP) efficiency of a heat-source-and-sink, or Exergy efficiency of a thermal-energy source with respect to the heat-sink reference. We now know that “true” Carnot efficiency, the Second-Law or Exergy efficiency is 100%. It is a goal here to clarify and resolve what is fundamentally misplaced. However, it would be hard “to let go” of the 200 yearlong “habit and addiction.”

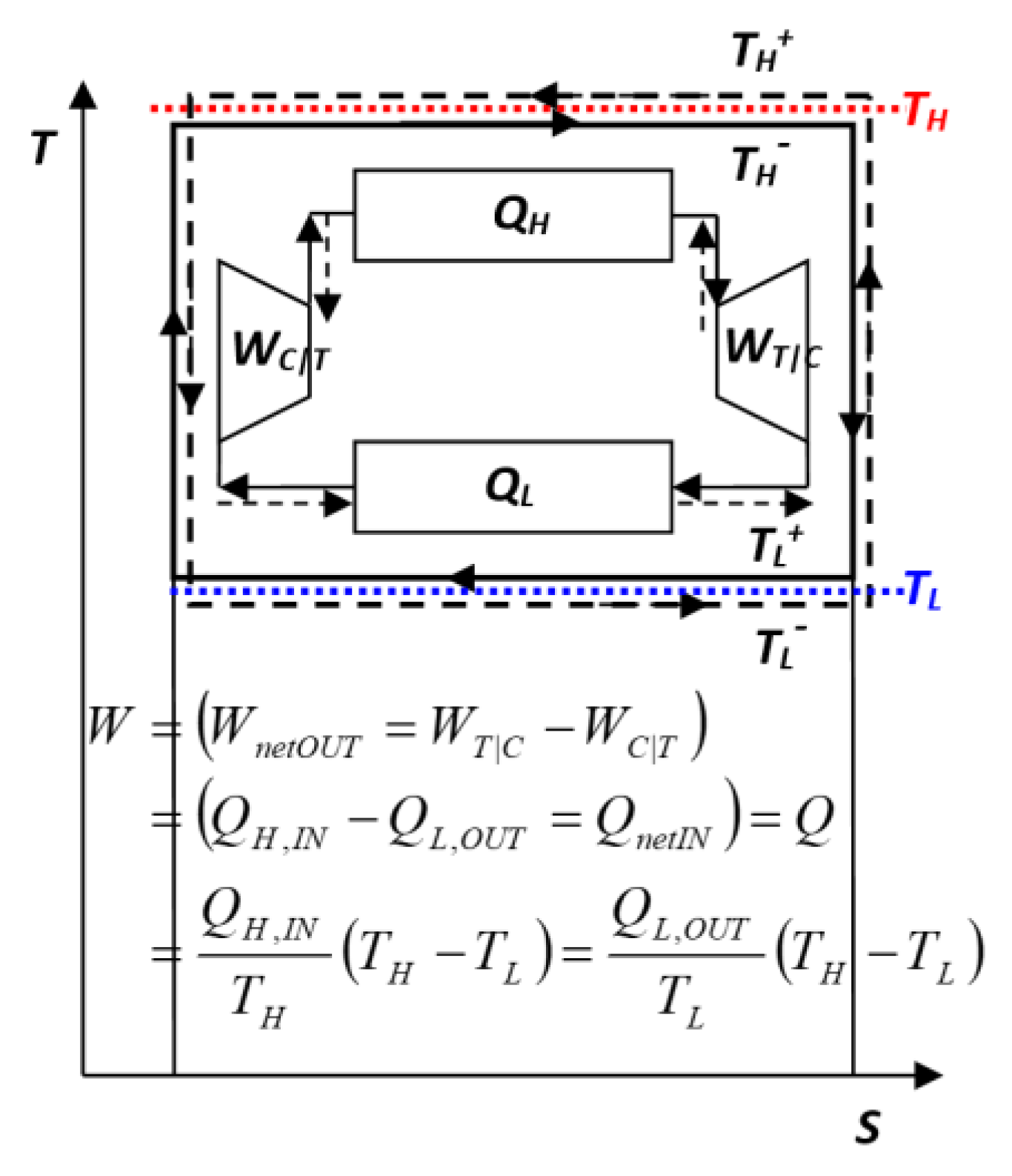
Key NOVEL-Point 5: The Carnot-Clausius [Ratio] Equality (CCE) and Clausius Equality (Cyclic integral) are special cases of related “Entropy boundary integral” for reversible stationary processes

The balance equations (used for definition of a new property, the entropy) were first developed by Clausius, based on Carnot’s discovery of “maximum efficiency and equality for all reversible cycles,” namely Carnot-Clausius Equality, CCE, as ratio Q_H/T_H=Q_L/T_L for constant high- and low-temperature of the thermal reservoirs, to be the precursor for Clausius Equality, as circular integral for a reversible cycle with variable temperatures, $∲\delta Q/T=0$. Then from those correlations a new property, entropy, was inferred by Clausius, to be later generalized with Clausius Inequality as the entropy balance, as “quantification” of the Second Law of thermodynamics.

The Carnot-Clausius Equality (CCE, as renamed hear to reconcile it with cyclic Clausius Equality, was named as Carnot [Ratio] Equality, CtEq, in [11]), is in essence, the entropy balance, i.e., “entropy-in equal to entropy-out” of the reversible Carnot cycle at constant in- and out-temperatures, while the Clausius Equality is also the balance of net-entropy (in-minus-out) of a reversible cycle with varying temperatures, a cyclic integral around the cycle boundary or per cycle time period. They both represent special cases of the entropy balance for the steady-state, stationary processes (including quasi-stationary cyclic processes), and no accumulation of entropy (nor any other system properties).

Note that engines are designed to run and produce power perpetually (except for necessary maintenance and repair). Therefore, their processes have to be either steady-state (stationary processes), or quasi-steady cyclic processes, achieved by rotating or reciprocating piston-and-cylinder machinery, or any similar energy conversion devices. They both, steady-state and/or cyclic processes, do not accumulate mass and energy, but convert input to output while interacting with the energy-reservoirs, an energy source and reference sink, the latter usually a device surrounding.

5. Conclusion and “Key Takeaways”

The most logical and the most probable sequential developments by Sadi Carnot, regarding the reversible cycle maximum efficiency and his ingenious reasoning of the reversible contradiction impossibility, as well as related consequences developed by his followers, and this author’s novel contributions and generalization, are presented above and summarized by the Key Takeaways below.

Key Takeaways:

• Conservation of caloric misconception was probably a fortunate catalyst leading to analogy with the waterwheel and Carnot’s hypothesis that the motive power of steam engine was caused and produced by the “fall of caloric” (cooling of hot caloric) since Carnot believed that there was no “consumption” of the caloric (Key Point I).
• Carnot’s reasoning that “wherever there exists a difference of temperature, motive power can be produced” and not be wasted for workless heat transfer, was the most critical and ingenious reasoning (Key Point II) that led to inference of the most critical concept of Carnot’s discovery (Key Point IV & V).
• The “Key discovery” ingeniously inferred by Sadi Carnot, that Reversible cycles must all have equal and maximum efficiency, by demonstrating that otherwise would result in creation of conserved caloric and/or perpetual motion: “the maximum of motive power resulting from the employment of steam is also the maximum of motive power realizable by any means whatever [1] (Key Point V).”
• The selected and persistent post-misconceptions and fallacies by others are also presented as Miss Points 1-4, including the misconceptions that the heat transferred out of the ideal Carnot cycle at lower temperature is the “waste heat or loss” as often stated. However, it is the “useful and necessary quantity,” required for the entropy balance and completion of a perfect, reversible cycle.
• The “Reversible and Reverse” processes and cycles are re-examined in Key NOVEL-Point 1. Among others, it is emphasized that the potential qualities of flux quantities (heat and different kinds of works) are not degraded but equipotentially transferred and stored between the system and its boundary surroundings, and thus conserved in every way. The spatial gradients are virtually zero at any instant while time gradients and related fluxes may be arbitrary since the time and energy rates are irrelevant for the reversible analysis of energy balances and properties.
• The reversible cycle “Maximum efficiency” and “Reversible equivalency” are scrutinized in Key NOVEL-Point 2. The reversible efficiency implies maximum work extraction and minimum work expenditure in the reverse process, thereby the two must be equivalent for given conditions, thus establishing the ‘Reversible equivalency’. The reversible processes are perfect and “equally and maximally efficient,” and they define the concept of “Reversible Equivalency,” — the ‘true equality’ of input and output, where relevant quantities and qualities are conserved in perpetuity.
• Reversible Contradiction Impossibility (“Reductio ad absurdum”) is scrutinized in Key NOVEL-Point 3. Namely, any reversible cycle “under-achievement” (getting less than maximum possible) would become an “over-achievement” when such cycle is reversibly ‘reversed’ (accomplishing with less than minimum required), and such “‘reversed’ over achievement” would be physically impossible (would be the “‘reversible equivalency’ violation” and may violate the conservation laws), thus establishing the “Reversible Contradiction Impossibility” of established fact with numerous consequences as detailed in Key NOVEL-Point 3 and elsewhere.
• Sadi Carnot [1] and his followers, including Kelvin [7] and Clausius [8], ironically referred to the maximum heat-engine cycle efficiency they developed (at the time when most thermal concepts were unknown), with the absurd conclusion, that it does not depend on the cycle design itself nor its operation mode, therefore, the proof that it is not the efficiency of ideal Carnot cycle ‘per se’. Therefore, their attribution is misplaced since the correlation they developed should had referred to the “maximum motive power or ‘work potential’ of the thermal reservoirs” since it depends on their temperatures only, and hence, being the proof of the claim presented here, see Key NOVEL-Point 4 and Figure 6.
• The Clausius-Carnot [Ratio] Equality and Clausius Equality [Cyclic integral] are elucidated to be the special cases of related “Entropy [balance] boundary integral” for reversible stationary or cyclic processes, see Key NOVEL-Point 5.

In conclusion, even though Sadi Carnot has been often called as the “Father of thermodynamics,” with all farness if conceivable, it might be more appropriate for Clausius and Kelvin to be named as the Fathers of thermodynamics, since they meticulously developed the most critical concepts of thermodynamics, starting from thermodynamic temperature to entropy and to formulation of the Laws of thermodynamics, among others — whereas Sadi Carnot would be the “Forefather of thermodynamics-to-become” in honor of his ingenious discovery and reasoning of heat engines reversible cycles and their maximum efficiencies at the time when steam engines were in initial developments, when the concepts of heat and work where not fully recognized, and even the energy conservation was not established at that time.