Impact of Economic Growth on Environmental Health: Evidence from Argentina, Equatorial Guinea, and South Korea

1. Introduction

The average global temperature has  increased by ~0.6 ºC in the last 100 years and is expected to continue rising  (Baldo et al., 1998). Global warming is an outcome of human  activities on the climate through large-scale consumption of fossil fuels  (coal, oil, and gas) and extensive deforestation. Remarkably, the industrial  revolution formed the impetus for such increased consumption. Each year,  7 billion tonnes of CO2, chlorofluorocarbons, and methane are  released into the atmosphere (Houghton, 2005). In 2018, these emissions reached  an all-time high of 37.1 billion metric tonnes (Thripp, 2019). In addition, from  1900 to 2000, the global population has increased from 1.6 billion to 6.1  billion ‘United Nations, 2001’ . This ever-growing population continues to  increase the demand for industries and industrial goods. As a result,  industrial emissions now account for 29% of greenhouse gases (ASN Bank, 2014).

The Kuznets (1955) hypothesis  postulates that environmental pollution grows faster than a firm’s income level  in the early economic and industrial development stages. This hypothesis is  logically intuitive because individuals at this stage become more interested in  income; they prioritize monetary and output goals over the environment  (Dasgupta et al., 2002). During early industrialization, natural resources and  hazardous pollutants were high, leading to environmental deterioration. Despite  the dangers of emissions, the apathetic attitude of individuals (firms’  governing bodies) toward pollution abatement was more alarming since proper  disposal of hazardous substances is considered too expensive (Dinda, 2004).

Over time, environmental  degradation has become a ‘side effect’ of a development that relies on resource  (air, water, and soil) depletion, ecosystem destruction, wildlife extinction,  and pollution (Johnson et al., 1997). It became crucial to encounter these  negative externalities, especially in developed countries, which generate 79%  of carbon emissions (Kong & Khan, 2019). Beckerman (1992), who studied the  relationship between income and environment, states that being too poor to  green implies that developing countries do not have the resources to protect  the environment.

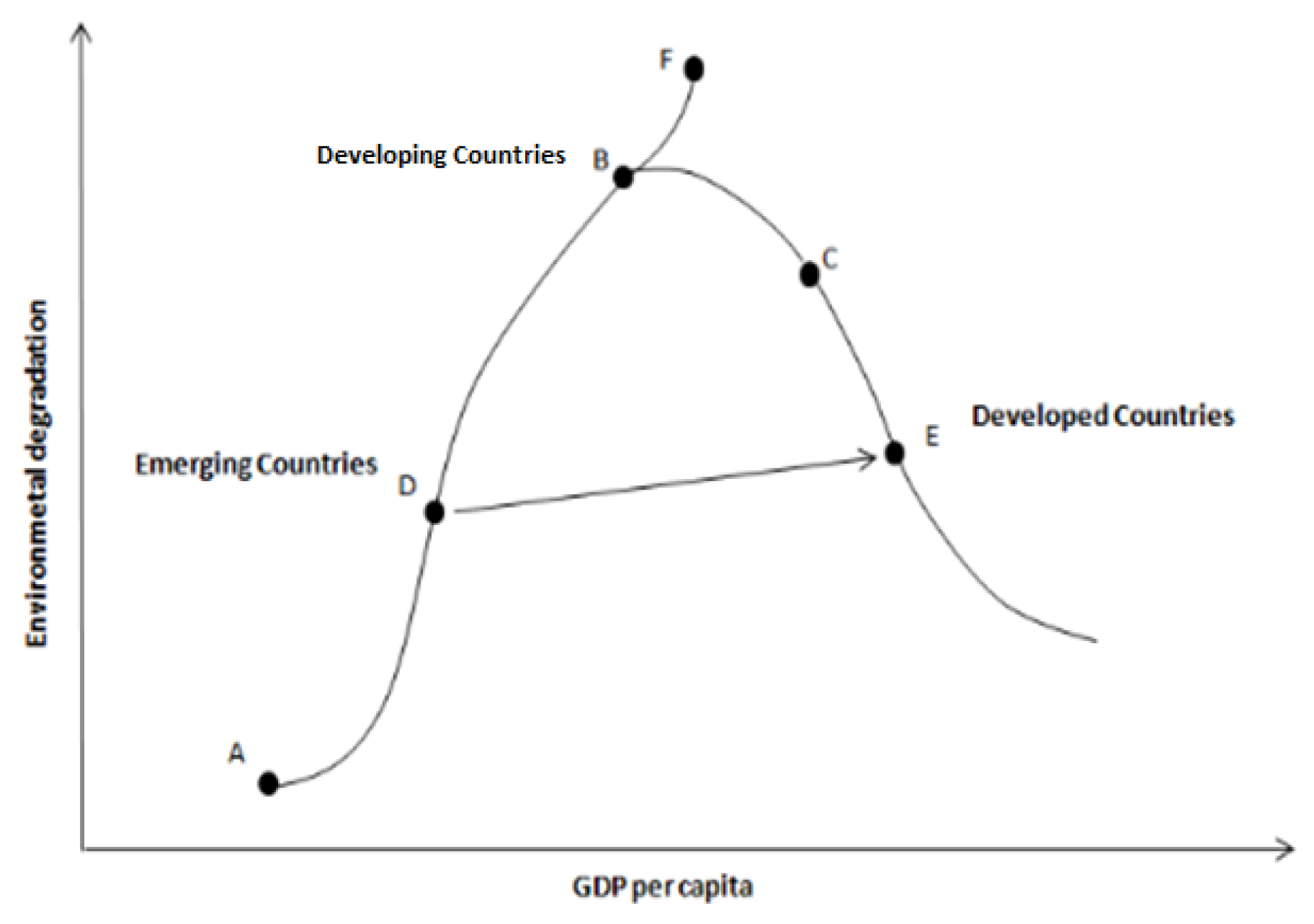
Only rich countries have the  resources to implant green technologies to tackle environmental issues.  Subsequent, a world development report during the same year noted that  environmental issues caused by economic development could be resolved by more  economic development. Studied the status of countries in different ‘income  classes’(developing, emerging, and developed) on the path  of economic growth and level of pollution (environmental Kuznets curve or EKC)  by suggesting the sustainomics hypothesis, which indicates a tunnel  effect between the GDP per capita and resulting environmental quality at  different stages of development (see Figure  1). 

Figure 1. Tunnel Effect.

Figure 1. Tunnel Effect.

In Figure 1 , point B shows the  target economic growth of developing countries that can proceed to point C  through sustainable development policies and clean technologies. The pathway  from point B to F generates more pollutants than financial growth, so it is  less likely to be followed. However, when emerging economies are given  financial support and environmental-friendly technologies, they are better  positioned to progress from point D to E, illustrating the tunnel effect. Thus,  we see a ‘grow now, clean later ’attitude in high-income countries, which  assumes that solutions to environmental problems can be developed at later  stages of economic growth. Therefore, in a dynamic economy, improved  technologies and policies that do not threaten economic growth are considered a  means to recover the environment (Gill et al., 2018).

According to the Global  Environment Outlook, the environment is changing faster, which calls for  governments to save the planet since ‘pollution and global warming are causing  millions of more deaths than conflicts’ are (United Nations, 2016). For  developed countries, this is a zero-sum game: On one hand, they seek more  incredible wealth, while on the other hand, they will have to spend large  amounts of capital on environmental recovery, primarily due to the higher costs  of pollution-abatement technologies. We thus evaluate the existence of the EKC  hypothesis by taking two primary variables: CO₂ emissions and per  capita GDP. Based on the above discussion, the primary purpose of this study is  to examine the countries whose economic status changed from high-income to  previously high-income countries such as (Equatorial Guinea), a new country  entered in the high-income status (Argentina), and stable high-income (South  Korea). Equatorial Guinea is a Sub-Saharan country that changed its status to a  high-income country (2007–2014) ‘after the discovery of huge oil reserves in  1996, with 1.7 billion bbl. and average daily oil production of 0.3 million  BOPD as of December 2013’ (BP, 2014) (Echendu et al., 2015). Cronin et al.  (2015) report that Equatorial Guinea underwent rapid economic growth due to its  oil exports, accounting for 90% of its revenues.

Argentina, the eighth-largest  country globally, defaulted seven times between 1825 and 2001’ (López &  Nahón, 2017). However, it ultimately changed its status to a high-income  country, becoming the third-largest Latin American economy. It is now a member  of the G20 due to its rich reserves of natural resources, export-based  agricultural zones, well-diversified industrial sector, high-technology sector,  literate population, and high Human Development Index rating.

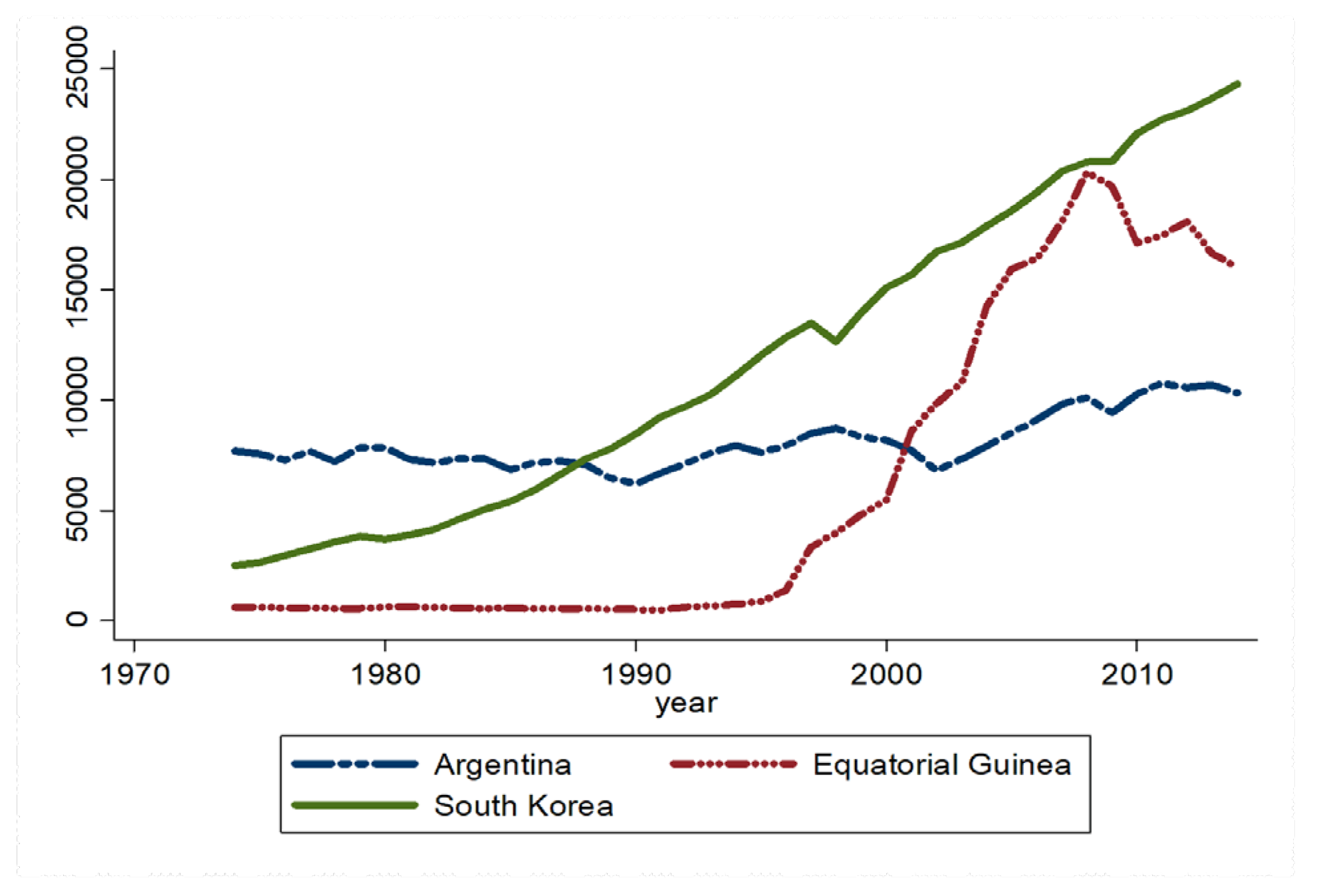
Figure 2 illustrates the real GDP per capita of all three sample countries.  South Korea’s GDP is continuously rising, while Equatorial Guinea experienced a  boom at the end of the nineteenth century, followed by a fall after a decade.  Argentina’s growth traces a zig-zag pattern over the The third sample country  is South Korea. As per the International Monetary Fund, it is a highly  developed country that holds the rank of the world’s 11th largest economy by  nominal GDP and is one of the stable members of the world’s more prosperous  societies. South Korea is also a member of the G20. It moved from the  seventh-largest CO₂ emitter to the twelfth largest in 2018 (World  Resource Institute). The governments’ strategic measures to promote ‘low  carbon-green growth’ under the National Green Growth Strategy (2009–2050) are  mainly responsible for this reduction in emissions (Zhang and Choi, 2013).

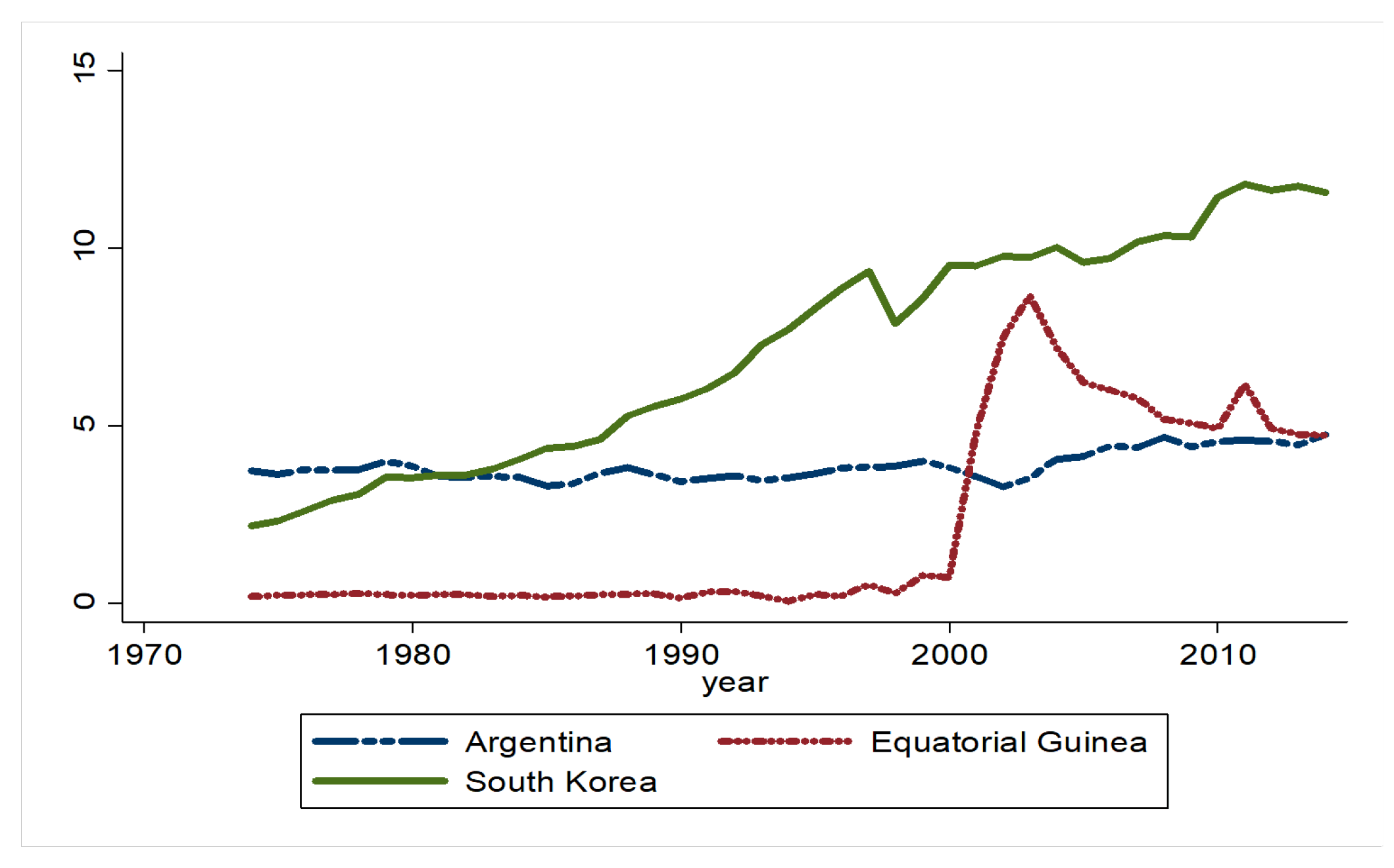
chosen period. The CO₂  emissions of these countries also trace a similar pattern compared with  economic growth ( Figure 3 ): South Korea has higher emissions, the emissions of Equatorial  Guinea peak when the country reaches higher per capita income, while Argentina  once again follows a meandering pattern. Recent years have shown that economic  study and policymaking cannot ignore the reality of the global climate crisis  when assessing the benefits of any given analytical tool or policy strategy. We  are now seeing widespread ecological calamities due to the failure to establish  a viable global climate stabilization program. Due to companies' substantial  involvement in climate change, attempts to stabilize the environment must be  seen as industrial rather than macroeconomic policy. The primary objective of  the climate stabilization endeavor is to significantly expand the renewable  energy industry while simultaneously shutting down the global fossil fuel  business (Pollin, 2021) . Previous studies only analyzed  the nexus between income and pollution. None of the studies have investigated  how the change in the income status from high to low and vice versa has  impacted their environmental health. To our knowledge, despite the importance  of evaluating the level of CO₂ emissions in comparison with  increasing levels of income, the literature comprises no empirical studies on  individual high-income countries, especially those countries which transformed  their economic status, as in this study. Thus, we critically appraise the rise  in income against environmental pollutants for three developed countries from  1974 to 2020. Besides testing the EKC hypothesis, we also check for  co-integration and a causal relationship between GDP growth and CO₂ emissions. 

Figure 2. GDP per Capita.

Figure 2. GDP per Capita.

Figure 3. CO2 Emissions per Capita.

Figure 3. CO2 Emissions per Capita.

The remaining paper is organized  as follows: Section 2 presents the literature survey. Section 3 encloses the data  model and methodology. Section 4 reports the empirical results. Finally, section 5 presents the  conclusion.

2. Literature Review

Energy consumption promotes  economic growth. There is a growing body of literature on the causal  relationship between economic growth and environmental deregulation. This phenomenon was first coined by Kuznets (1955), known as the Kuznets  curve. Furthermore,  Berthier et al., (2010) indicated an inverted  U-shaped relationship between economic growth and income inequality. Later,  Gross man and Krueger 1991 found a similar relationship between environmental  conditions, economic growth, and EKC. It hypothesizes an inverted U-shaped  relationship between real income and environmental pollution. That is, ‘as per  capita income increases, environmental pollution also increases at first and  then starts declining at a turning point.’  Numerous scholars and institutes  have endorsed the EKC model to protect the loss of environmental health from  economic activities. The World Development Report (IBRD, 1992) of the World  Bank, backed by Shafik (1994), states that environmental quality is an  essential element of sustainable development. Thus, numerous studies have  modeled the relationship between economic growth and CO₂ emissions,  one of the highest observed pollutants in environmental economics studies.

Several scholars have tested the  EKC hypothesis against multiple indicators of environmental deterioration. For  example, Mather et al. (1999), Koirala and Mysami (2015),  Bulte and van Soest  (2001), Stern et al. (1996), Ehrhardt-Martinez et al. (2002), Koop and Tole  (1999), and Panayotou (1994) attribute the extensive  deforestation to environmental deregulation. Moreover, sulfur dioxide (SO₂)  was found to be another cause, according to the empirical findings (Brajer et  al., 2008; Arouri et al., 2012; Kaufmann et al., 1998; Selden and Song, 1994;  Zhoumu et al., 2015) and after all municipal waste was analyzed by (Bhattarai  and Hammig, 2001; Khajuria et al., 2011; Mazzanti et al.,2006; 2009).

Most of the literature on the EKC  hypothesis focuses on developed and developing countries  (Cetin, 2018; Iwata  et al., 2012; Liu et al., 2019; Perman and Stern, 2003; Sinha Babu and Datta,  2013). These studies neglect the policy implications of economic growth and  environmental deregulation (Ang, 2008). This limitation necessitates studies  that can help in sustainable development policies at the country level. As  Stern et al. (1996b) believe, ‘A more fruitful approach for analyzing the  relationship between economic growth and environmental impact would be  examining the historical experience of individual countries, using econometric  and qualitative historical analyses. A comprehensive study by Zhang et  al.(2021) indicated a varied influence on nations with a high GDP per capita.

Additionally, the study  demonstrates that public investment in human capital and further developing  green energy technologies fosters a sustainable green economy via  labor-intensive and technology-oriented industrial activities, with varying  consequences in various nations (Sohu et al., 2023).  Taghizadeh-Hesary et al. (2021) examined the amount of investment in green  projects, particularly in the green power sector, is constrained by factors  such as insufficient long-term financing, various hazards, and a poor rate of  return on investment. Iqbal et al. (2021) propose many policy implications or  remedies to assist governments, institutions, companies, and the general people  in reducing environmental pollution through green financing. However, in a  recent study, Taghizadeh-Hesary et al. (2021) found that the COVID-19 epidemic  and worldwide recessions have resulted in a global decline in investments in  green initiatives jeopardizing the attainment of climate-related targets. As a  result, the post-COVID-19 world must transition to a green financial system by  introducing new financial instruments. Green bonds—a loan instrument aimed at  financing sustainable infrastructure projects—are gaining prominence in this  area.

However, scholars have tested the  EKC hypothesis by using time-series data for individual countries (Chen, 2012;  Friedl and Getzner, 2003; Halkos and Tzeremes, 2011; Hussain et al., 2012;  Lindmark, 2002; Mohapatra and Giri, 2009; Roca et al., 2001; Vollebergh et al.,  2011). Decade’s worth of studies have evaluated EKC hypothesis testing using  distinct methodologies, and this stream of research has resulted in a rich  array of perspectives. For instance, computational techniques have shifted the  research focus from simple EKC testing using static ordinary least squares  (OLS) models to a combination of dynamic models. EKC indicators include GDP to  foreign direct investments, population density, agriculture base, electricity  consumption, and trade-related proxies.

Consequently, the findings in the  literature reflect immense heterogeneity, from no existence of EKC to inverted  a U- or N-shaped curve (Yongsung et al., 2011). Further, Egli (2005) tested the  EKC hypothesis with co-integration and the causal  relationship, distinguishing the short- and long-run effects of financial  growth on the concentration of environment-deteriorating elements in the  atmosphere. Considering the vast literature on the EKC that uses multiple  indicators, large datasets, and different econometric methodologies, we  significantly contribute to this discipline by analyzing the existence of the  EKC hypothesis based on economic growth and pollutant emissions in the three  developed countries. In other words, when these countries’ financial status  changes or remains the same, what happens to their CO₂ emissions? A  comprehensive study by Li et al. (2020) and Akbar et  al. (2023) investigate the effect of environmental  diplomacy on a country's carbon emissions. To examine whether environmental  accords resulted in reductions in CO2 emissions. The study concludes that both  developed and developing nations do not adhere to treaty standards in the long  term since CO2 emissions grow as the number of treaties increases. In general,   findings suggest that environmental accords are likely to waste international  diplomacy that does little to address climate change.  One more study by Zakari  and Toplak (2021) emphasized the need for policymakers to consider non-economic  and non-technological elements, such as ethics, to achieve ecologically and  economically sustainable development. Furthermore, countries enact  environmental legislation to safeguard the environment. According to Zakari et  al. (2021), environmental accords have a considerable beneficial impact on the  environment in resource-poor nations that may help them achieve sustainable  development growth by 2030.

Table 1. Descriptive Statistics.

	Argentina			Equatorial Guinea			South Korea
	CO2	GDP	GDP2	CO2	GDP	GDP2	CO2	GDP	GDP2
Mean	1.34	8.98	13.15	-0.29	7.71	17.39	1.84	9.16	16.93
Median	1.32	8.94	13.35	-1.25	6.64	17.77	2.04	9.31	17.62
Maximum	1.55	9.28	15.79	2.15	9.92	18.86	2.46	10.09	18.86
Minimum	1.19	8.73	9.09	-2.69	6.18	13.21	0.78	7.82	10.66
Std. Dev.	0.10	0.14	1.74	1.53	1.52	1.06	0.51	0.71	1.78
Skewness	0.62	0.68	-0.46	0.50	0.37	-1.78	-0.52	-0.36	-1.57
Kurtosis	2.27	2.52	2.52	1.51	1.31	7.07	1.93	1.77	5.31
Jarque–Bera	3.56	3.56	1.88	5.50	5.81	50.05	3.79	3.48	26.12
Probability	0.16	0.16	0.39	0.06	0.05	0.00	0.14	0.17	0.00

Table 1. Descriptive Statistics.

	Argentina			Equatorial Guinea			South Korea
	CO2	GDP	GDP2	CO2	GDP	GDP2	CO2	GDP	GDP2
Mean	1.34	8.98	13.15	-0.29	7.71	17.39	1.84	9.16	16.93
Median	1.32	8.94	13.35	-1.25	6.64	17.77	2.04	9.31	17.62
Maximum	1.55	9.28	15.79	2.15	9.92	18.86	2.46	10.09	18.86
Minimum	1.19	8.73	9.09	-2.69	6.18	13.21	0.78	7.82	10.66
Std. Dev.	0.10	0.14	1.74	1.53	1.52	1.06	0.51	0.71	1.78
Skewness	0.62	0.68	-0.46	0.50	0.37	-1.78	-0.52	-0.36	-1.57
Kurtosis	2.27	2.52	2.52	1.51	1.31	7.07	1.93	1.77	5.31
Jarque–Bera	3.56	3.56	1.88	5.50	5.81	50.05	3.79	3.48	26.12
Probability	0.16	0.16	0.39	0.06	0.05	0.00	0.14	0.17	0.00

3. Data and Methodology

3.1. Data

We  use annual data on per capita CO₂emissions and per capita real GDP  measured in metric tons and constant 2010 US dollars, respectively. Data on  Argentina, Equatorial Guinea, and South Korea data are collected from the World  Development Indicator (2021) of the World Bank, covering 1974 to 2020. The  countries are selected based on data availability and current, previous, and  continued high-income countries.

Carbon  emissions are taken as the dependent variable to capture the nonlinear  relationship between income and CO₂ emissions, with two independent  variables, GDP and EKC term: the square of GDP, to predict the short-run and  long-run elasticities. Table 1 reports the descriptive statistics of the sample time series in a  natural logarithm.

3.2. Model and Methodology

To verify the presence of the  environmental Kuznets curve in the sample countries, we follow three steps.  First, we investigate the long-run relationship among the variables by  employing the autoregressive distributed lag (ARDL) bounds test of co-integration. Second, we use the Granger causality test to test the  causal relationship among the variables' time series. Then, the robustness  analysis is conducted using fully modified ordinary least squares (FMOLS),  dynamic ordinary least squares (DOLS), and canonical co-integrating regression (CCR). Generally, the EKC hypothesis is  specified using the following equation:”

$$E={\mathrm{ƒ}(\mathrm{}\mathrm{Y},\mathrm{}\mathrm{Y}}^2,\mathrm{}\mathrm{Z})$$

Where the dependent variable $E$ is the environmental factor, $Y$ is the income, and $Z$ denotes the variables responsible  for environmental deregulation. Our objective is to assess the causal  relationship between economic growth and environmental stability for the sample  of current, previous, and continued high-income countries. Instead of taking  additional variables, we take only income and CO2 emissions in our model. The  following equation corresponds to the logarithmic form of the model:

$$\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{}\mathrm{l}\mathrm{n}{\left(E\right)}_t={\alpha }_0+{\alpha }_1{lnY}_t+{\alpha }_2{\left({lnY}_t\right)}^2+{\epsilon }_t$$

(1)

Here, each variable is in $log\left(ln\right)$  form,   where $t$ is the time, $E$ is the CO₂ emissions at  the per-capita level, $Y$ is the per capita real GDP, and $e$ is the standard error term. To  validate the existence of the EKC hypothesis and confirm its significance, the  signs of the two coefficients ${\alpha }_1$ and ${\alpha }_2$  should be positive and negative,  respectively. It indicates an inverted U-shaped relationship between real  income and CO₂ emissions.

There are many methods for  conducting the co-integration analysis, including the residual-based approach  by Engle and Granger (1987), the maximum likelihood approach by Johansen and  Juselius (1990), and the fully modified OLS procedure by, and the ARDL by (Pesaran et al., 2001). We use  the ARDL bounds testing approach because it has several advantages over  conventional methods. For instance, the method has better reliability for small  samples, has no endogeneity, and estimates long-and short-run coefficients to  simultaneously capture the independent variables' effect on the dependent  variable. Further, the method allows openness for integration order  irrespective of whether the variables are stationary at  I (0) or I(1) or a mixture of both. To capture the co-integration  relationship between real income growth and CO₂ emissions through  the unrestricted error correction regressions, we estimate as follows:

$${\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}}}={\alpha }_0+{\sum }_{\mathrm{k}=1}^{\mathrm{n}}{\mathsf{\alpha }}_{1\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-\mathrm{k}}}+{\sum }_{k=0}^n{\alpha }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=0}^n{\alpha }_{3\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}})}^2+{\mathsf{\Delta }}_{1{\mathrm{C}\mathrm{o}}_2}{\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-1}}+{\mathsf{\Delta }}_{2{\mathrm{C}\mathrm{o}}_2}{\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1}+{\mathrm{}\mathsf{\Delta }}_{3{\mathrm{C}\mathrm{o}}_2}{{\mathrm{l}\mathrm{n}(\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1})}^2+{\mathrm{\varepsilon }}_{1\mathrm{t}}$$

(2)

$${\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}}={\beta }_0+{\sum }_{k=1}^n{\beta }_{1\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=0}^n{\beta }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}}}+{\sum }_{k=0}^n{\beta }_{3\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}\left)\right(}^2+{\mathsf{\Delta }}_{1\mathrm{G}\mathrm{D}\mathrm{P}}{\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-1}}+{\mathsf{\Delta }}_{2\mathrm{G}\mathrm{D}\mathrm{P}}{\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1}+{\mathrm{}\mathsf{\Delta }}_{3\mathrm{G}\mathrm{D}\mathrm{P}}{{\mathrm{l}\mathrm{n}(\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1})}^2+{\mathrm{\varepsilon }}_{2\mathrm{t}}$$

(3)

$${{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}})}^2={\theta }_0+{\sum }_{k=1}^n{\theta }_{1\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}})}^2+{\sum }_{k=0}^n{\theta }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=0}^n{\theta }_{3\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-\mathrm{k}}}+{\mathsf{\Delta }}_{1{\mathrm{G}\mathrm{D}\mathrm{P}}^2}{\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-1}}+{\mathsf{\Delta }}_{2{\mathrm{G}\mathrm{D}\mathrm{P}}^2}{\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1}+{\mathrm{}\mathsf{\Delta }}_{3{\mathrm{G}\mathrm{D}\mathrm{P}}^2}{{\mathrm{l}\mathrm{n}(\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-1})}^2+{\mathrm{\varepsilon }}_{3\mathrm{t}\mathrm{}}$$

(4)

In equation (2), ${\alpha }_0$is the drift element and ${\mathrm{\varepsilon }}_{1\mathrm{t}}$ is the error term. Further, ${\alpha }_1{\alpha }_2$, and ${\alpha }_3$ are the error correction dynamics,  whereas${\delta }_{1{Co}_2}$, ${\delta }_{2{Co}_2}$, and ${{\delta }_3}_{{C0}_2}$The long-run association and the  same pattern are applied to equations (3) and (4).  In equation (2), following  the first step of the ARDL approach, we test the presence of the long-run co-integrating relationship using the null hypothesis—$H_0:{\delta }_{1{Co}_2}={\delta }_{2{Co}_2}={{\delta }_3}_{{C0}_2}$= 0—against the alternative  hypothesis $H_0:{\delta }_{1{Co}_2}\ne {\delta }_{2{Co}_2}\ne {{\delta }_3}_{{C0}_2}$≠ 0—examined through the F  statistics. We apply the same process to equations (3) and (4).

“Next,  we determine the long-run co-integrating relationship  among the variables by comparing the calculated F statistics with two  sets of critical values found in the literature (Pesaran  et al., 2001b). The first set comprises the lower  critical bound (LCB) values for I(0) variables,  while the second set holds the upper critical bound values (UCB) for I(1)  variables. The null hypothesis of ‘no co-integration’  will be rejected if the calculated F statistics value is higher than the  UCB value, but the hypothesis cannot be rejected if the calculated F  statistics value is smaller than the LCB value. The value between the two  limits, UCB and LCB, will be inconclusive when the long-run association among  the variable series is confirmed with a negative and significant value of the  error correction term (ECT). Moreover, to run the ARDL model, the order of lags  is based on the Schwartz Bayesian criteria (SBC) and  Akaike’s information criteria (AIC), which select the smallest possible and  maximum relevant lag lengths, respectively. Once the existence of a long-run  relationship has been confirmed, we estimate the error correction model (ECM)  and Karagozoglu and Lindell (2000) as follows:”

$${\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}}}={\alpha }_0+{\sum }_{\mathrm{k}=1}^{\mathrm{n}}{\mathsf{\alpha }}_{1\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-\mathrm{k}}}+{\sum }_{k=1}^n{\alpha }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=1}^n{\alpha }_{3\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}})}^2+{\theta ECT}_{t-1}+{\mathrm{\varepsilon }}_{1\mathrm{t}}$$

(5)

$${\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}}={\beta }_0+{\sum }_{k=1}^n{\beta }_{1\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=1}^n{\beta }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}}}+{\sum }_{k=1}^n{\beta }_{3\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}})}^2+{\theta ECT}_{t-1}+{\mathrm{\varepsilon }}_{2\mathrm{t}}$$

(6)

$${{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}})}^2={\theta }_0+{\sum }_{k=1}^n{\theta }_{1\mathrm{k}}{{\mathsf{\Delta }(\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}})}^2+{\sum }_{k=1}^n{\theta }_{2\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{k}}+{\sum }_{k=1}^n{\theta }_{3\mathrm{k}}{\mathsf{\Delta }\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-\mathrm{k}}}+{\theta ECT}_{t-1}+{\mathrm{\varepsilon }}_{3\mathrm{t}}$$

(7)

The  ${ECT}_{t-1}$ equations (5) to (7) indicate the  speed of adjustment, that is, the time taken to restore the long-run  equilibrium. Diagnostic tests such as functional form, serial correlation,  normality, and heteroscedasticity tests are conducted to ensure the model's  fitness. Further, as per (Pesaran et al., 2001b), the long- and short-run stability coefficients are checked using  the cumulative sum and cumulative sum square tests. These tests  confirm the model’s stability if the test statistics value lies within the plot  of two straight lines representing critical bounds at the 5% significance  level. Note that the ARDL method only confirms the presence or non-existence of  co-integration among variables series, so we employ the  (Granger 1969)  test to verify the existence and direction of causality. The  enlarged version of the Granger causality test with the ECM encompassing the  vector error correction model (VECM) and multivariate n^th  order is formulated as follows:

$$\left(1-B\right)\left[\begin{array}{c}\begin{array}{c}{\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}\mathrm{}}}\\ {\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}}\end{array}\\ {\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}}^2\end{array}\right]=\left[\begin{array}{c}{\mathrm{c}}_1\\ {\mathrm{c}}_2\\ {\mathrm{c}}_3\end{array}\right]+\sum _{i=1}^P(1-B)\left[\begin{array}{c}{d}_{11,i}{d}_{12,i}{d}_{13,i}\\ d_{21,i}{d}_{22,i}{d}_{23,i}\\ d_{31,i}{d}_{32,i}{d}_{33,i}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}{\mathrm{l}\mathrm{n}\mathrm{C}\mathrm{o}}_{2_{\mathrm{t}-\mathrm{i}\mathrm{}}}\\ {\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{i}}\end{array}\\ {\mathrm{l}\mathrm{n}\mathrm{G}\mathrm{D}\mathrm{P}}_{\mathrm{t}-\mathrm{i}}^2\end{array}\right]+\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ {\lambda }_3\end{array}\right]\left[{ECT}_{t-1}\right]+\left[\begin{array}{c}{\gamma }_{1t}\\ {\gamma }_{2t}\\ {\gamma }_{3t}\end{array}\right]$$

Where $\left(1-B\right)$ is the lag operator, $d$ denotes the parameters of  estimation, ${\gamma }_t$ denotes the zero mean uncorrelated  random disturbance terms, and ${ECT}_{t-1}$ is the lagged error term. The VECM  determines the direction of the causality, while the  significance value of the lagged ECT, ${ECT}_s$ , verifies  the long-run causal relationship among the variable series. In addition, the  short-run Granger causal relationship can be detected through the significant F  statistics value of the lagged independent variables.

4. Empirical Results

4.1. Unit-Root Tests

Before the ARDL model, we employ  three-unit root tests—augmented Dickey-Fuller, Phillips–Person, and  Lee–Strazicich tests—to confirm the required I (0) or I(1)  integration order of variables series. Because of the  substantial likelihood, the sample data contain structural breaks, thus  avoiding the spurious results of traditional stationarity tests. The  Lee–Strazicich test is used if a structural break(s) occur(s) in the data,  where the augmented Dickey-Fuller (1979) and PHILLIPS- PERRON (1988)  tests  would generate misleading and biased results (Phillips & Perron, 1988).

The existence of a single  structural break that further extends to two and five breaks was proposed by  Zivot and Andrews (1992), Lumsdaine and Papell (1997), and Kapetanios (2005),  respectively. However, these tests bear a linearity assumption limitation under  the null hypothesis.

Therefore, if there is a break  under the null hypothesis, we will observe size distortions that will lead us  to reject the null hypothesis as these results are erroneously estimated  breakpoints (ALTINAY, 2005).  Lee and Strazicich (2004) developed their test to  overcome the assumption that breaks are accommodated under null and alternative  hypotheses. Table 2 reports the empirical findings of the unit root tests, starting  with the augmented Dickey-Fuller and Phillips–Person tests, followed by the  Lee–Strazicich tests with single and double structural breaks. In structural  breaks in the time series, we find three series: CO₂ emissions of  Argentina and South Korea and the GDP of Equatorial Guinea are stationary at  the first difference, while the remaining series are stationary at level.

Table 2. Augmented Dickey–Fuller, Phillips–Person, and Lee and Strazicich (2004) with single and double structural breaks.

Variable	ADF test		PP test		Lee–Strazicich test (One Break)			Lee–Strazicich test (Two Breaks)
	t-Statistic	I(•)	t-Statistic	I(•)	t-Statistic	TB1	I(•)	t-Statistic	TB1	TB2	I(•)
Argentina
CO2	-4.80***	I(1)	-9.32***	I(1)	-4.57** (4)	1993	I(0)	-10.16*** (1)	2007	2010	I(1)
GDP	-5.26***	I(1)	-5.17***	I(1)	-6.32*** (7)	1987	I(0)	-6.23** (7)	1989	2000	I(0)
GDP2	-6.56***	I(1)	-13.37***	I(1)	5.90*** (1)	1995	I(0)	-7.71*** (1)	1991	1995	I(0)
Equatorial Guinea
CO2	-7.78***	I(1)	-7.65***	I(1)	-5.34*** (7)	1998	I(0)	-6.21** (7)	1991	1999	I(0)
GDP	-3.50**	I(1)	-3.48**	I(1)	-5.76*** (7)	1995	I(0)	-10.16*** (1)	2007	2010	I(1)
GDP2	-6.56***	I(1)	-13.3***	I(1)	-4.92*** (7)	1994	I(0)	-7.71*** (1)	1991	1995	I(0)
South Korea
CO2	-6.51***	I(1)	-6.62***	I(1)	-4.84** (4)	2001	I(0)	-7.46*** (4)	1996	2002	I(1)
GDP	-4.56***	I(1)	-5.80***	I(1)	-6.37*** (7)	1998	I(0)	-5.84* (5)	1991	2003	I(0)
GDP2	-6.39***	I(1)	-6.42***	I(1)	-4.25* (8)	1997	I(1)	-6.65** (7)	1992	2004	I(0)

Notes. The numbers in parentheses are t statistics. *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels.

Table 2. Augmented Dickey–Fuller, Phillips–Person, and Lee and Strazicich (2004) with single and double structural breaks.

Variable	ADF test		PP test		Lee–Strazicich test (One Break)			Lee–Strazicich test (Two Breaks)
	t-Statistic	I(•)	t-Statistic	I(•)	t-Statistic	TB1	I(•)	t-Statistic	TB1	TB2	I(•)
Argentina
CO2	-4.80***	I(1)	-9.32***	I(1)	-4.57** (4)	1993	I(0)	-10.16*** (1)	2007	2010	I(1)
GDP	-5.26***	I(1)	-5.17***	I(1)	-6.32*** (7)	1987	I(0)	-6.23** (7)	1989	2000	I(0)
GDP2	-6.56***	I(1)	-13.37***	I(1)	5.90*** (1)	1995	I(0)	-7.71*** (1)	1991	1995	I(0)
Equatorial Guinea
CO2	-7.78***	I(1)	-7.65***	I(1)	-5.34*** (7)	1998	I(0)	-6.21** (7)	1991	1999	I(0)
GDP	-3.50**	I(1)	-3.48**	I(1)	-5.76*** (7)	1995	I(0)	-10.16*** (1)	2007	2010	I(1)
GDP2	-6.56***	I(1)	-13.3***	I(1)	-4.92*** (7)	1994	I(0)	-7.71*** (1)	1991	1995	I(0)
South Korea
CO2	-6.51***	I(1)	-6.62***	I(1)	-4.84** (4)	2001	I(0)	-7.46*** (4)	1996	2002	I(1)
GDP	-4.56***	I(1)	-5.80***	I(1)	-6.37*** (7)	1998	I(0)	-5.84* (5)	1991	2003	I(0)
GDP2	-6.39***	I(1)	-6.42***	I(1)	-4.25* (8)	1997	I(1)	-6.65** (7)	1992	2004	I(0)

Notes. The numbers in parentheses are t statistics. *, **, and *** indicate statistical significance at the 10%, 5%, and 1% levels.

We find that every variable series of each country is non-stationary at the level under the former two tests; when transformed to the first difference, each series rejects the null hypothesis at the 1% significance level. On the other hand, Lee and Strazicich (2004) demonstrated a different integration order; except for South Korea’s GDP square, the remaining series of the three countries are stationary at the level for single the break hypothesis. Finally, for more robust testing, we find three series for two structural breaks in the time series: CO2 emissions of Argentina and South Korea and the GDP of Equatorial Guinea are stationary at the first difference, while the remaining series are stationary at level.

4.2. Cointegration

In the next step, we use the most widely used co-integration measure, ARDL bounds testing, developed (Pesaran et al., 2001b) to capture the long-run equilibrium among the variable series. Bounds testing is advantageous compared with other conventional co-integration techniques for three reasons. First, it can be applied to both a mixed I(0) or I(1) integration order. Second, it performs well with a small or finite sample size(Narayan, 2005). Third, it is a bias-free technique for long-run estimations (Harris and Sollis, 2003). The decision regarding co-integration is based on an F statistics comparison with the UC Band LCB values. The UCB considers all variables at I(1) integration order, while LCB takes level order I(0) for all variables (Pesaran et al., 2001). Therefore, a weaker UCB value than the computed F-statistics would validate co-integration among variables. Therefore, the decision is reserved when the F statistics value is below the LCB value. However, the decision on co-integration presence will be inconclusive if the computed value of the F statistics is less than the UCB value and more than the LCB value. In this case, the lagged ECT decides the long-term relationship. The results in Table 3 present the F statistics of three countries based on the null hypothesis—H₀: ₁= ₂= ₃=0—against the alternative hypothesis—H₁: ₁≠ ₂ ≠ ₃≠0, denoting CO₂ emissions as the dependent variable, while the GDP and GDP square are the independent variables.

The F statistics values for Argentina, Equatorial Guinea, and South Korea are 9.225, 11.463, and 9.250, respectively, which are much higher than the UCB values to reject the null hypothesis at the 1% significance level. Such a rejection implies that the CO₂ emissions, GDP, and GDP square series are mutually co-integrated in Argentina, Equatorial Guinea, and South Korea. After verifying co-integration in the time series, we conduct the causality test by deriving the marginal impact of GDP and GDP square on the CO₂ emissions for the long-and short-run elasticities. That allows us to confirm the existence of the EKC for the sample countries.

As shown in Table 4, the per capita GDP positively and statistically significantly impacts CO₂ emissions. Specifically, a 1% permanent increase in GDP raises CO₂ emissions in the long run by 0.60% and 0.96% in Argentina and Equatorial Guinea, respectively. The same pattern continues for GDP square: A 1% increase in GDP square significantly boosts the CO₂ emissions by 0.01% and 0.28% in that order for both countries. For South Korea, the significant positive and negative long-run elasticities are 0.67% and -0.02% for GDP and GDP square, respectively, which aligns with our expectations. That confirms the existence of EKC in South Korea. We now proceed to short-run results and diagnostic tests (Table 5). The short-run elasticities for each of the three countries are computed using the ECM from equations (5) to (7). The results show a positive and significant relationship between Argentina's economic growth and CO2 emissions.

Their coefficient of the GDP square is less than zero and insignificant; hence, the results do not support the EKC hypothesis in the short run. For Equatorial Guinea, we find a significant and positive relationship between GDP growth and CO₂ emissions but a negative and significant coefficient of GDP square. That indicates the existence of the EKC in the short run at the 1% significance level. Finally, after validating an inverted U-shaped curve between GDP growth and CO₂ emissions in the long run, we confirm the short-run existence of the EKC for South Korea for GDP and at a two-time lag of the GDP square.

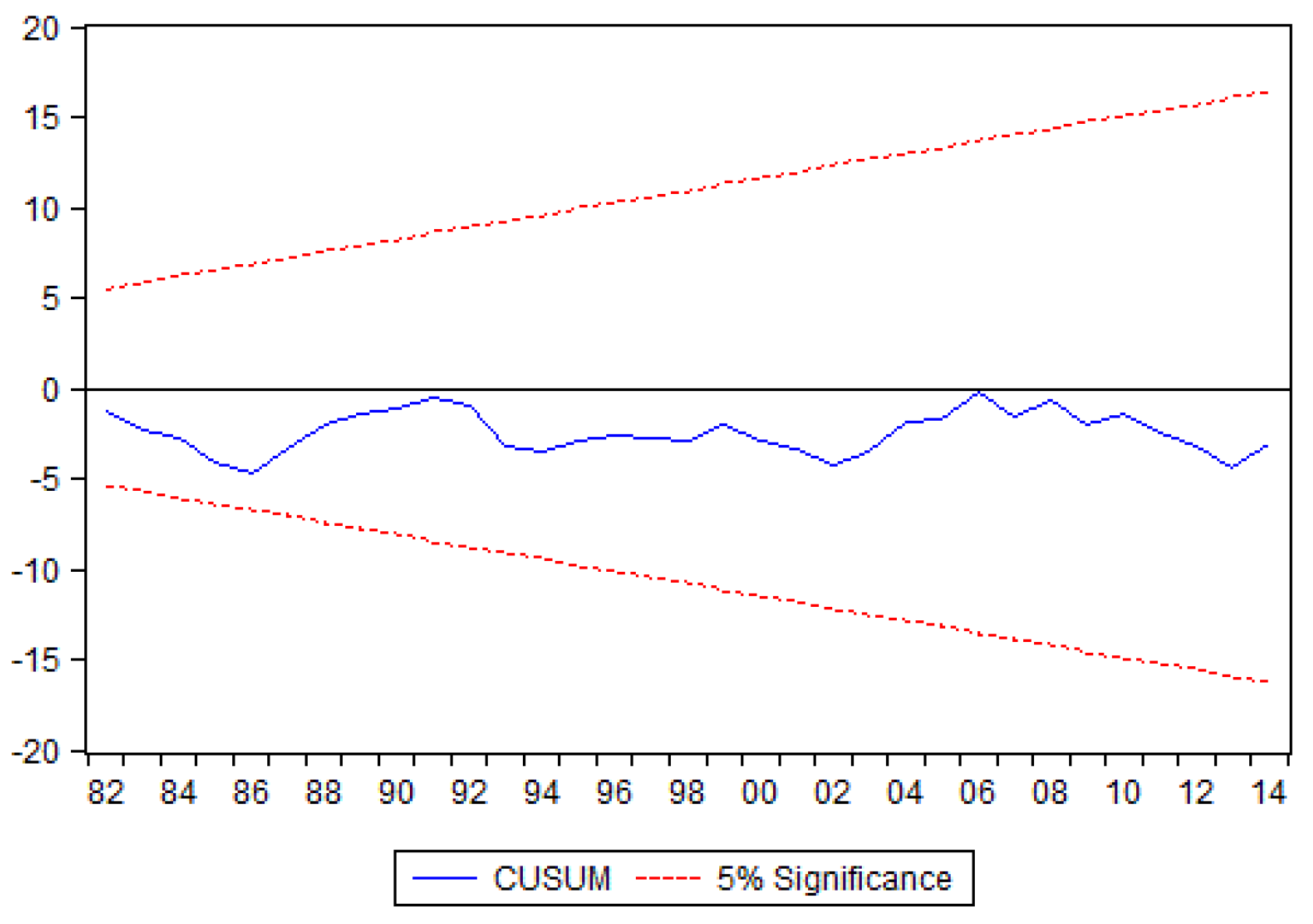
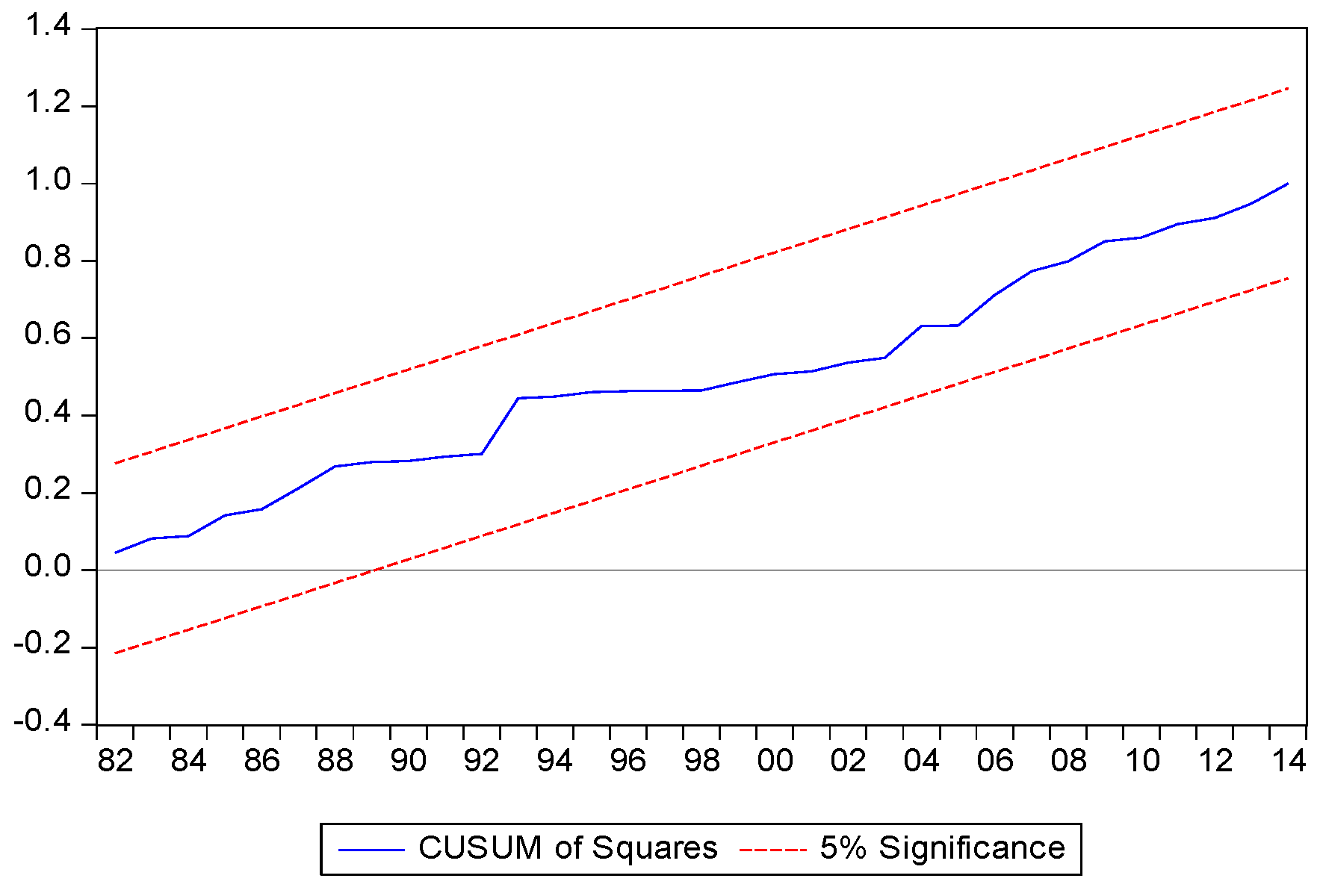
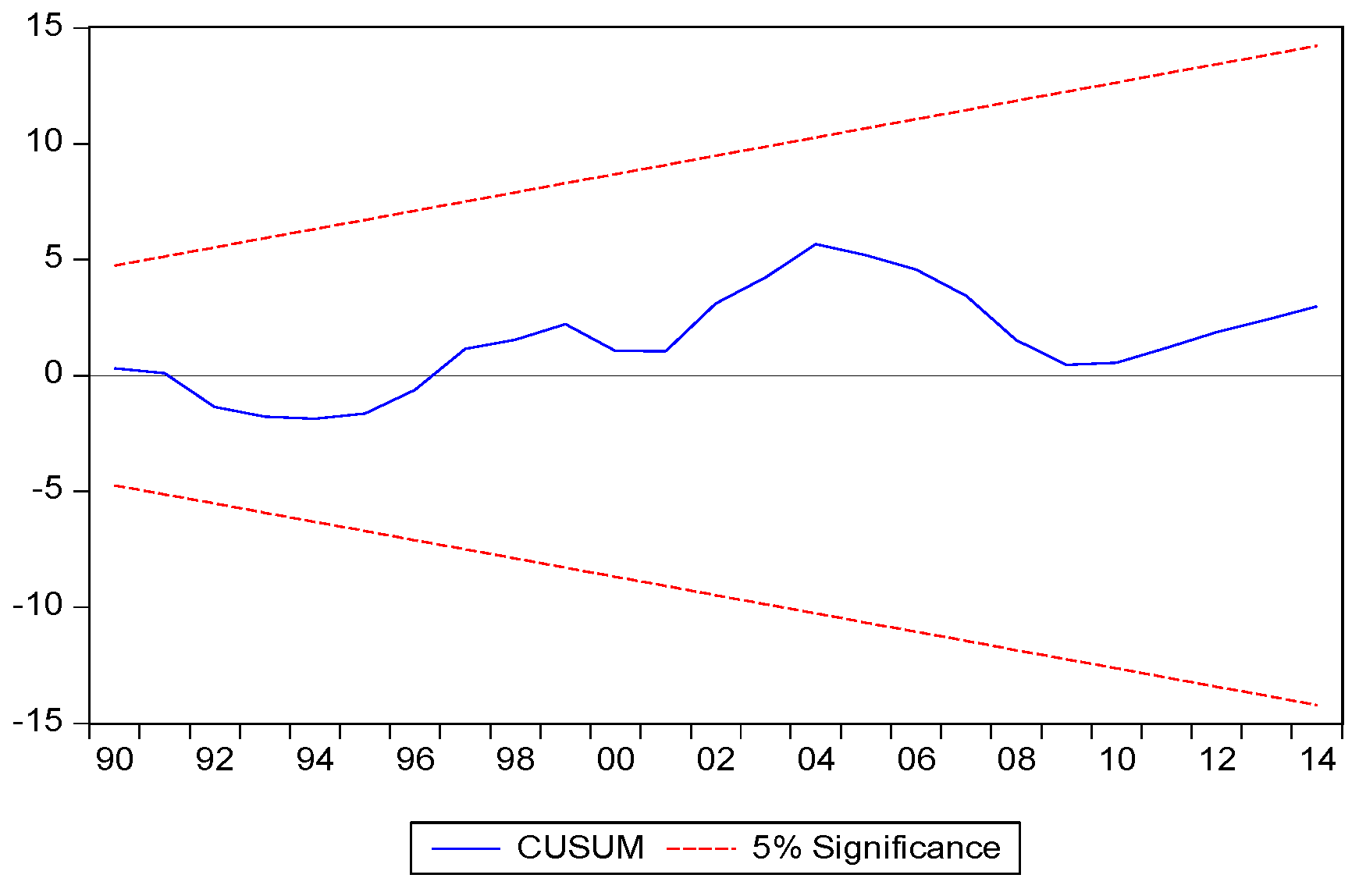
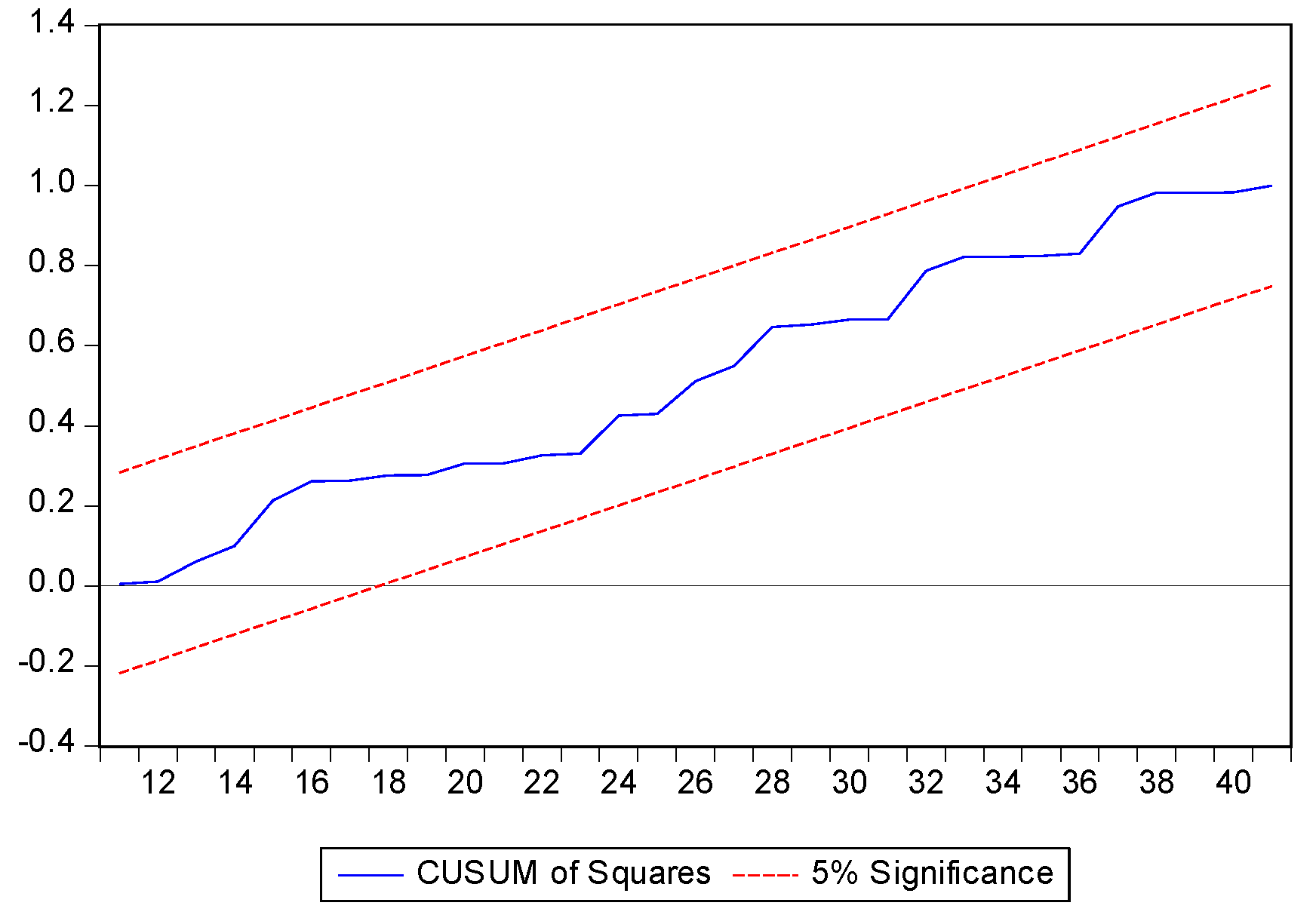
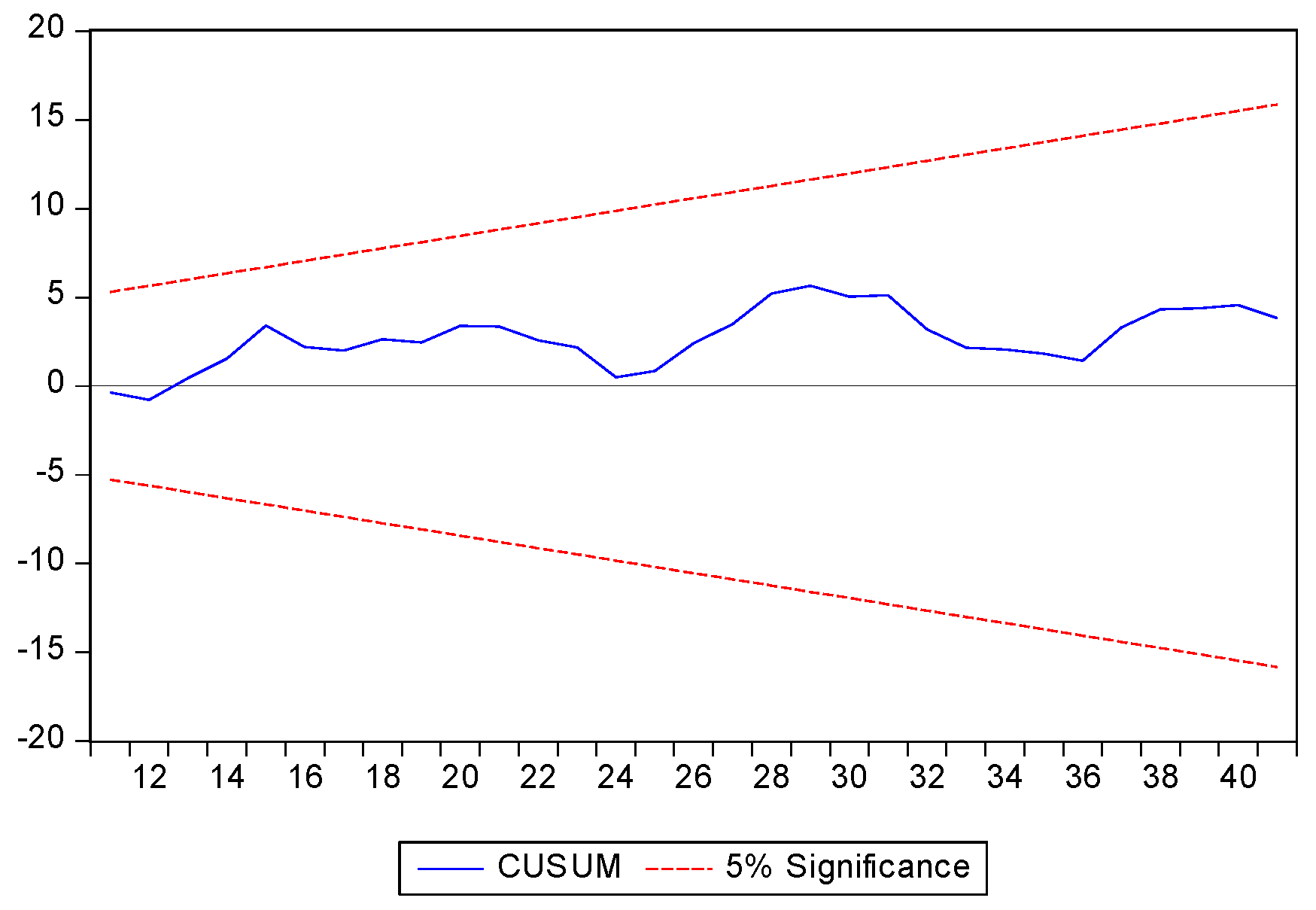
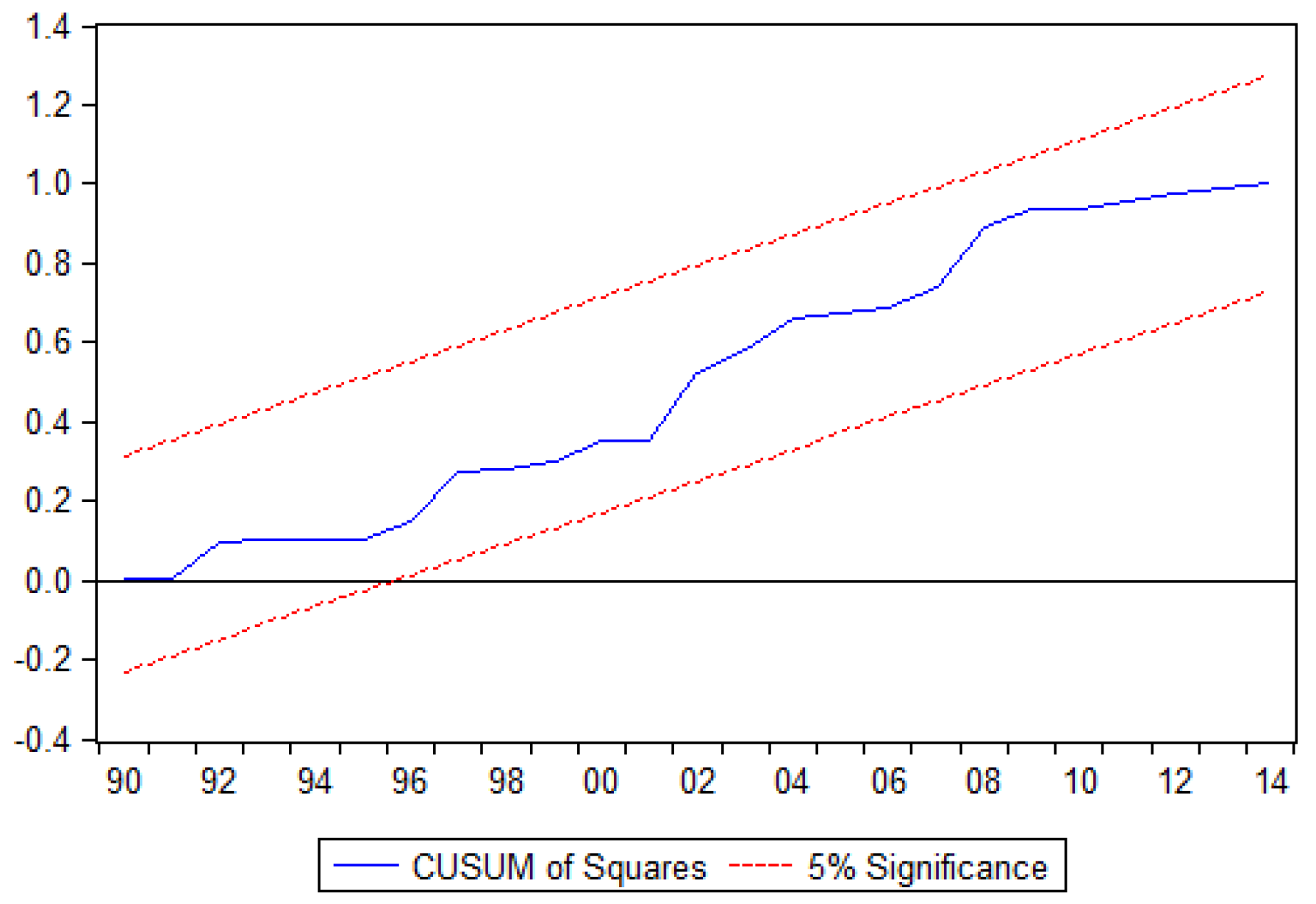
The stability of the ECM coefficients and the long-run goodness of fit for the model are further confirmed with the cumulative sum and cumulative sum square. The two ECMs for the three countries are illustrated in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9: All remain within the critical bounds at the 5% significance level.

After yielding successful results on the cointegrated causal relationship between CO₂emissions and economic growth, we employ the VECM Granger causality test to identify the direction of the relationship among the time series. Table 6 reports the results of the Granger causality test, indicating a significant long-run relationship for all three countries. However, Argentina shows a bidirectional long-run significant relationship between GDP and CO₂ emissions.

In the short run, findings from Argentina reveal a unidirectional negative causal relationship that runs from GDP square to CO₂ emissions. We observe several short-run Granger causalities for Equatorial Guinea; the results reveal a unidirectional positive and significant short-run relationship from GDP to CO₂ emissions. The only bidirectional and significant relationship between GDP square and CO₂ emissions exists at the 5% level. Finally, the results for South Korea indicate a unidirectional short-run negative causality from economic growth to CO₂ emissions.

Table 7 reports the results of the FMOLS, DOLS, and CCR estimators to check the robustness of the model. The robustness of the long-run findings of the ARDL estimations for the three countries is fully validated. The results confirm the absence of the EKC in the long run for Argentina and Equatorial Guinea but a presence for South Korea.

5. Conclusions

We explored the EKC hypothesis's existence, including causal and long-run relationships between CO₂ emissions and economic growth per capita for Argentina, Equatorial Guinea, and South Korea. The period covers 1974 to 2020, and we used the ARDL method proposed by (Pesaran et al. (2001a) and the FMOLS, DOLS, CCR, causality, and stability tests. We found that all three countries exhibit a robust long-run relationship between CO₂ emissions and per capita GDP. An inverted U-shaped curve exists only in the short run for Equatorial Guinea and South Korea. In the long run, only South Korea exhibits the EKC. The FMOLS, DOLS, and CCR estimations confirm the long-run findings of the ARDL approach, which confirms the robustness of the results. The VECM Granger causality test checked the variables' linkage and direction of causality. It specified a significant long-run relationship from GDP to CO₂ emission for each country; except for Argentina, the remaining two countries exhibit a bidirectional long-run significant relationship. This result proves that the decoupling of the two variables is unlikely under the economic policy structure of the sample countries.

In the short run, Argentina has a similar unidirectional negative relationship that runs from GDP square to CO₂ emissions, whereas South Korea exhibits a unidirectional negative causality from GDP to CO₂ emissions. Equatorial Guinea exhibits more causal associations following the long-run path: a significant and negative unidirectional positive relationship from GDP to CO₂ emissions and the only bidirectional and significant negative relationship between GDP square and CO₂ emissions.

Conclusively, in the short run, Argentina’s GDP square has a negative impact on CO₂ emissions. For South Korea, economic growth has a negative impact on CO₂ emissions. Finally, for Equatorial Guinea, the GDP has only a positive impact, while the GDP square has a positive and negative impact on CO₂ emissions. It implies that in the short run, after the turning point on the EKC curve, an increase in the GDP causes a decline in CO₂ emissions in Argentina. In the long run, the unidirectional causality from GDP to CO2 emissions indicates that the Argentinian government must invest more in pollution abatement policies to encourage sustainable development. Pollution reduction strategies such as emissions tax, carbon credit policy, enhanced use of clean energy technologies, and energy efficiency schemes will not harm the long-term economic growth of this newly high-income country but cement its economic status along with better environmental conditions.

In Equatorial Guinea, a former high-income country that once experienced the oil boom, a short-run, bidirectional, positive, and negative relationship runs from GDP square to CO₂ emissions. Thus, the rise and fall in the GDP square align with the economic growth. That is, the EKC hypothesis in the short run is confirmed. Thus, Equatorial Guinea must employ environmentally friendly measures and stringent environmental laws without adversely affecting GDP growth. In South Korea, an increase in GDP does not increase the pollution level in the short run, which is a rare case that might be attributed to the country’s ‘low carbon green growth’ policy(see section 1) and five-year plan for green growth (2009–2013). These short-run causality results for South Korea are in line with Sonnenschein and Mundaca (2016), who revealed a short-term (2008–2012) enhancing effect of GDP per capita on CO₂ emissions with lower emissions. However, the 1971–2012 period is evidence of worsening CO₂ intensity during the early years of the Green Growth Strategy. Therefore, South Korea still requires a more robust low-carbon growth policy that matches its economic growth. It must discard fossil fuels subsidies and increase energy efficiency rather than offer ‘green growth engines.’ In addition, it must implement pricing reforms, carbon energy taxes, and a strict regulatory system. Without good sustainable development policies, stable financial growth in South Korea is impossible without environmental deterioration.

Future researchers may broaden this study to more high-income countries by using large and improved datasets. That would allow an analysis of these countries before and after becoming high-income countries. It would also refine findings to understand long-term policy implications, thus ensuring continuous environmentally sustainable growth.