Submitted:
03 January 2024
Posted:
04 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Basics of femtoscopy with Lévy sources
- Second-order phase transitions [31], where the correlation length diverges near the critical point, and at the critical point the spatial correlations exhibit a power-law tail with exponent ; this is one of the critical exponents, and its value is suggested to be [32] for the 3D Ising model, or for the random external field 3D Ising model [33] – QCD is expected to be in the same universality class as one of them [34,35].
- Resonance decays [9,28,36], where the power-law tail is generated by the set of resonances decaying into pions (or the given investigated particle species); this phenomenon is similar to the decay heat of used fuel rods in power plants, see Fig. 1. of Ref. [37]. Note that the simulations of Refs [9,36] indicate Lévy distributions in EPOS even before resonance decays, hence (at least in EPOS) these cannot be the only reason for the appearance of Lévy distributions.
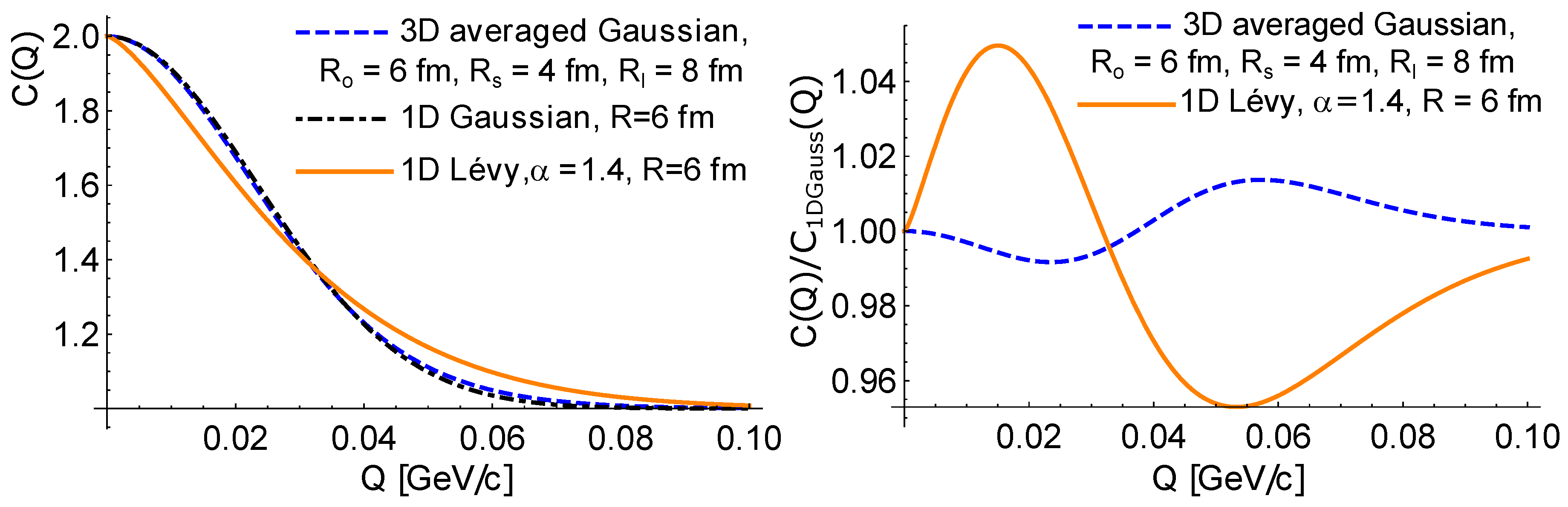
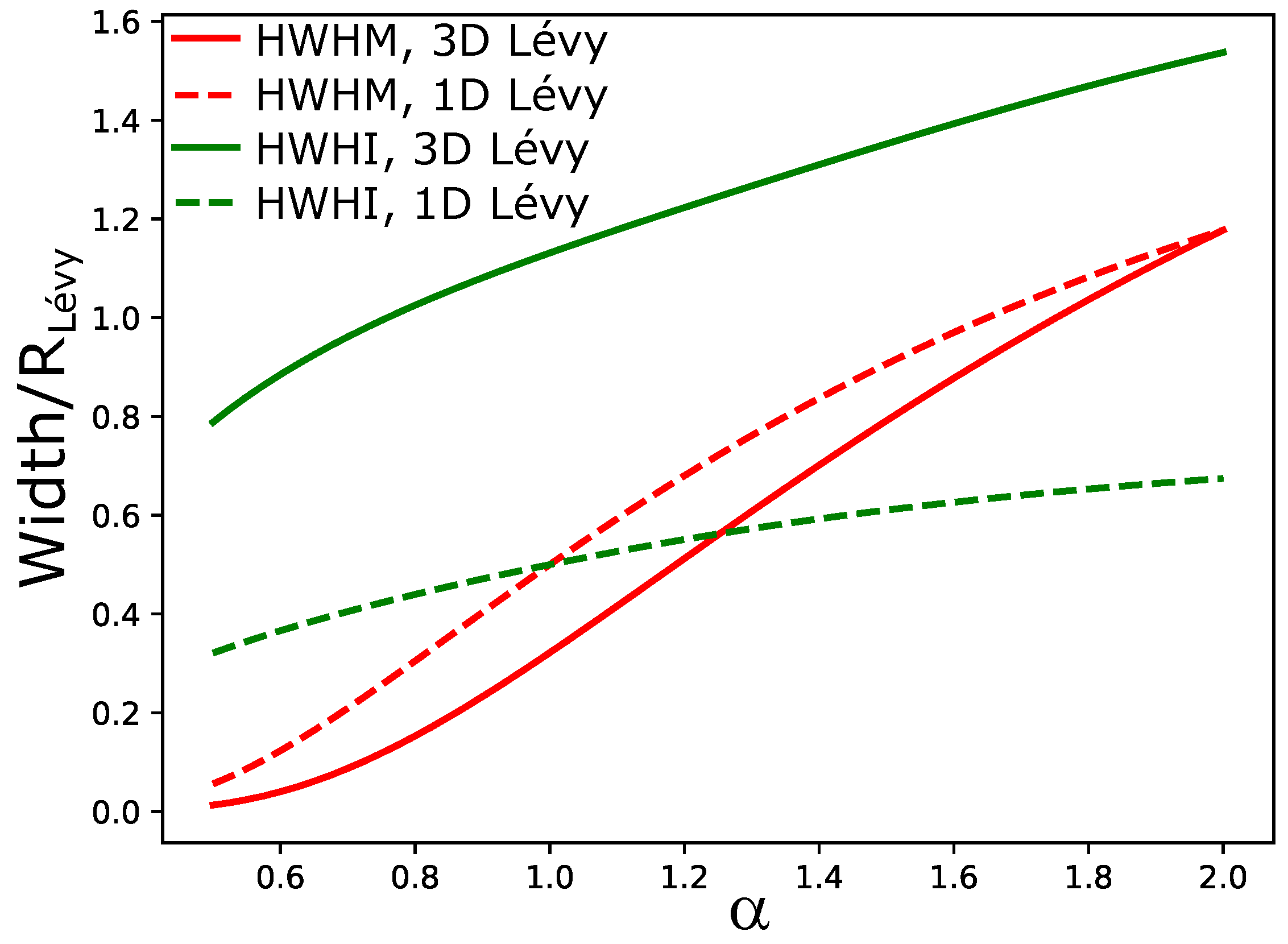
3. Measures of the source extent
- due to a change in size (i.e., the scale), or
- due to a change in shape.
4. Signs of the critical point in femtoscopy
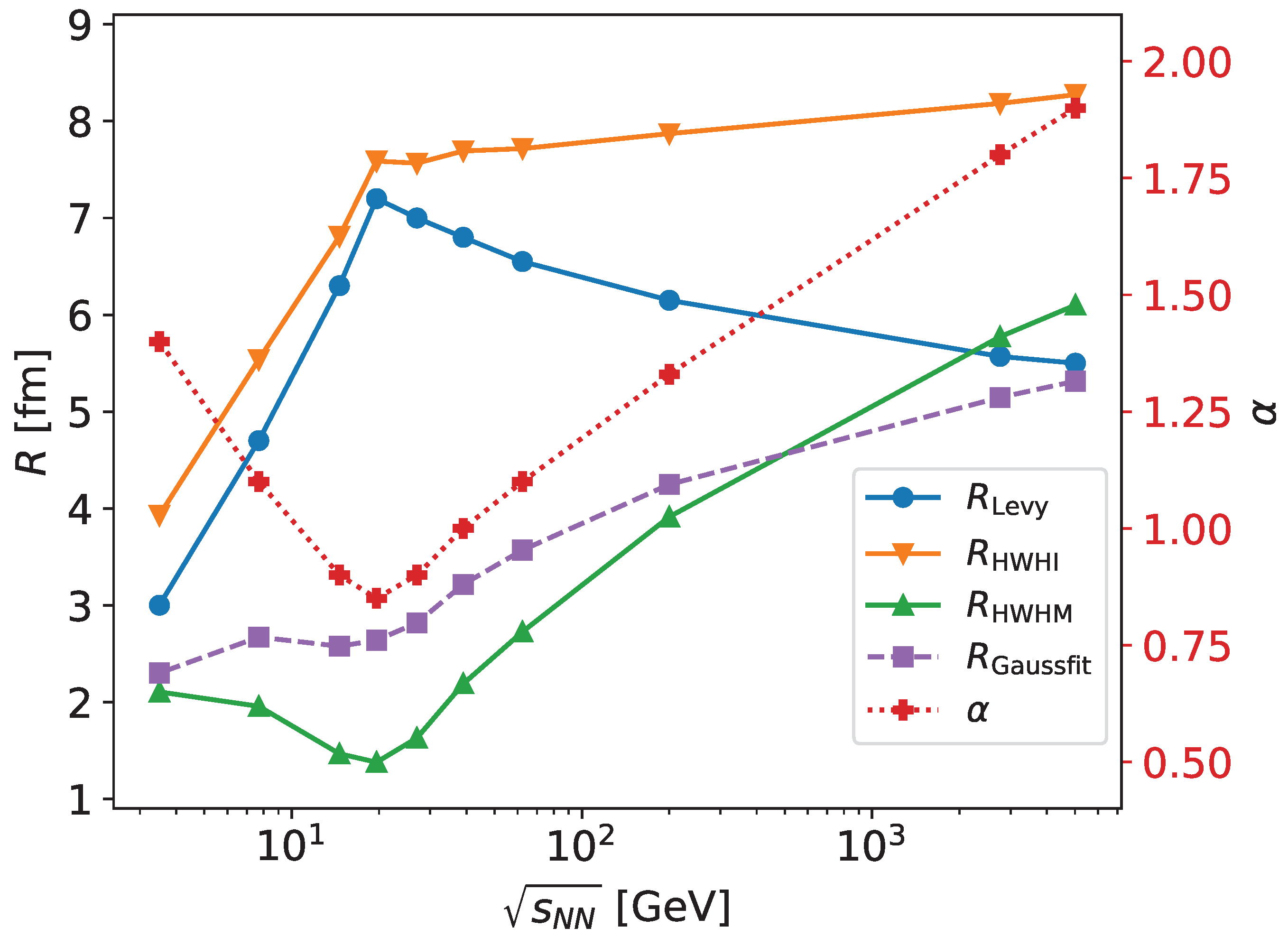
5. Experimental results from SPS through RHIC to LHC
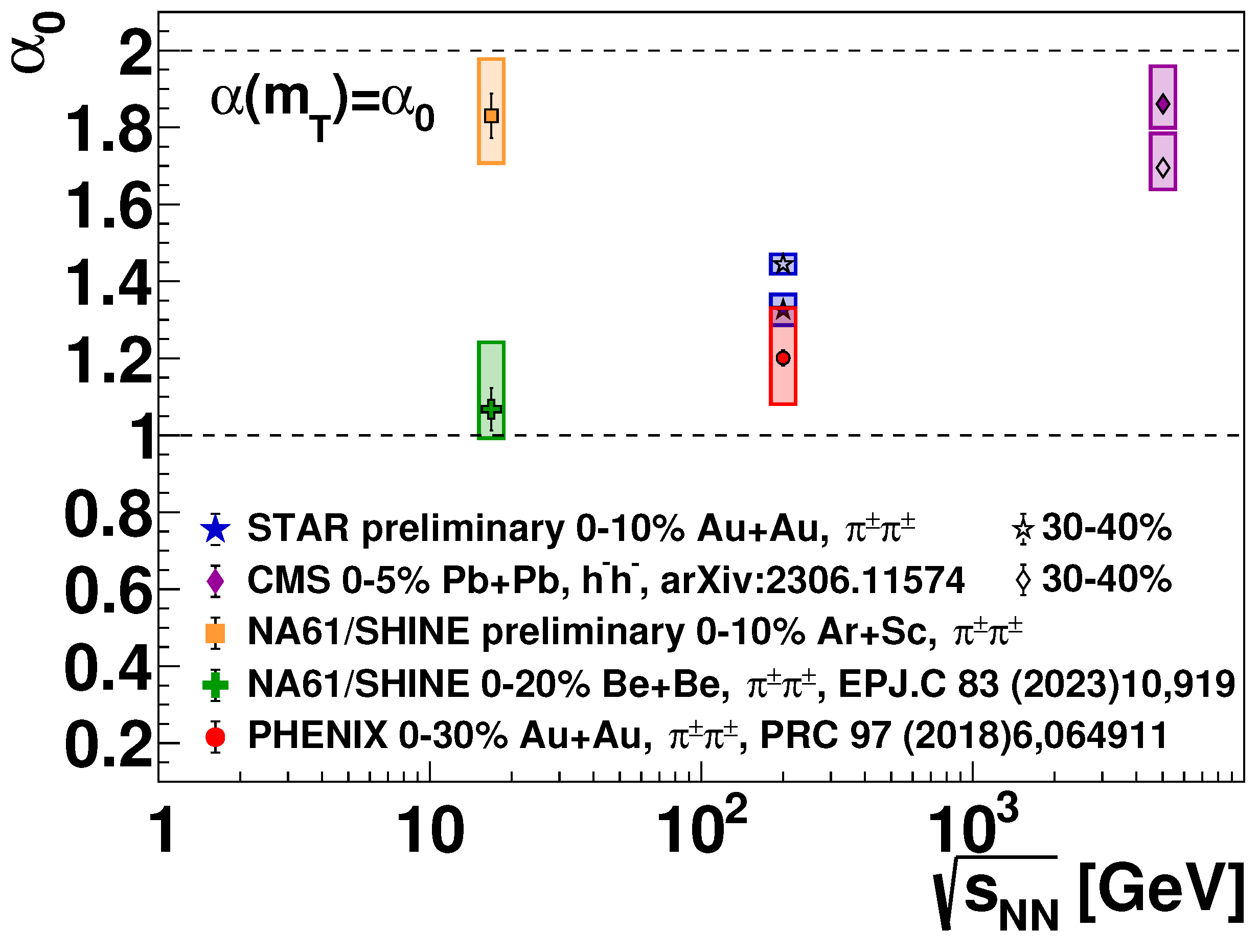
6. Discussion and conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HBT | Hanbury Brown and Twiss |
| QCD | Quantum chromodynamics |
| LCMS | Longitudinally Comoving System |
| SPS | Super Proton Synchrotron |
| RHIC | Relativistic Heavy Ion Collider |
| LHC | Large Hadron Collider |
| HWHM | Half width at half maximum |
| HWHI | Half width at half integral |
References
- Lednicky, R. Femtoscopy with unlike particles. International Workshop on the Physics of the Quark Gluon Plasma, 2001, [nucl-th/0112011].
- Lisa, M.A.; Pratt, S.; Soltz, R.; Wiedemann, U. Femtoscopy in relativistic heavy ion collisions. Ann. Rev. Nucl. Part. Sci. 2005, 55, 357–402, [nucl-ex/0505014]. [CrossRef]
- Hanbury Brown, R.; Jennison, R.C.; K., D.G.M. Apparent Angular Sizes of Discrete Radio Sources: Observations at Jodrell Bank, Manchester. Nature 1952, 170, 1061–1063. [CrossRef]
- Goldhaber, G.; Goldhaber, S.; Lee, W.Y.; Pais, A. Influence of Bose-Einstein statistics on the antiproton proton annihilation process. Phys. Rev. 1960, 120, 300–312. [Google Scholar] [CrossRef]
- Csanád, M. Two- and three-pion Lévy femtoscopy with PHENIX. J. Phys. Conf. Ser. 2018, 1070, 012026, [arXiv:nucl-ex/1806.05745]. arXiv:nucl-ex/1806.05745]. [CrossRef]
- Adare, A.; others. Lévy-stable two-pion Bose-Einstein correlations in sNN=200 GeV Au+Au collisions. Phys. Rev. C 2018, 97, 064911, [arXiv:nucl-ex/1709.05649]. [Erratum: Phys.Rev.C 108, 049905 (2023)]. [CrossRef]
- Kurgyis, B.; Kincses, D.; Nagy, M.; Csanád, M. Coulomb Corrections for Bose–Einstein Correlations from One- and Three-Dimensional Lévy-Type Source Functions. Universe 2023, 9, 328, [arXiv:nucl-th/2007.10173]. [CrossRef]
- Nagy, M.; Purzsa, A.; Csanád, M.; Kincses, D. A novel method for calculating Bose–Einstein correlation functions with Coulomb final-state interaction. Eur. Phys. J. C 2023, 83, 1015, [arXiv:nucl-th/2308.10745]. [CrossRef]
- Kórodi, B.; Kincses, D.; Csanád, M. Event-by-event investigation of the two-particle source function in sNN=2.76 TeV PbPb collisions with EPOS. Phys. Lett. B 2023, 847, 138295, [arXiv:nucl-th/2212.02980]. [CrossRef]
- Csorgo, T.; Lorstad, B.; Zimanyi, J. Bose-Einstein correlations for systems with large halo. Z. Phys. C 1996, 71, 491–497, [hep-ph/9411307]. [CrossRef]
- Csorgo, T. Particle interferometry from 40-MeV to 40-TeV. Acta Phys. Hung. A 2002, 15, 1–80. [Google Scholar] [CrossRef]
- Csanad, M.; Jakovac, A.; Lokos, S.; Mukherjee, A.; Tripathy, S.K., Multi-particle quantum-statistical correlation functions in a Hubble-expanding hadron gas. In Gribov-90 Memorial Volume; World Scientific, 2020; pp. 261–273, [arXiv:hep-ph/2007.07167]. [CrossRef]
- Adam, J.; others. Flow and interferometry results from Au+Au collisions at sNN=4.5 GeV. Phys. Rev. C 2021, 103, 034908. [Google Scholar] [CrossRef]
- Lacey, R.A. Indications for a Critical End Point in the Phase Diagram for Hot and Dense Nuclear Matter. Phys. Rev. Lett. 2015, 114, 142301. [Google Scholar] [CrossRef]
- Adamczyk, L.; others. Beam-energy-dependent two-pion interferometry and the freeze-out eccentricity of pions measured in heavy ion collisions at the STAR detector. Phys. Rev. C 2015, 92, 014904. [Google Scholar] [CrossRef]
- Adare, A.; others. Azimuthal-angle dependence of charged-pion-interferometry measurements with respect to second- and third-order event planes in Au+Au collisions at GeV. Phys. Rev. Lett. 2014, 112, 222301. [Google Scholar] [CrossRef]
- Lökös, S.; Csanád, M.; Tomášik, B.; Csörgo, T. Higher order anisotropies in the Buda-Lund model: Disentangling flow and density field anisotropies. Eur. Phys. J. A 2016, 52, 311. [Google Scholar] [CrossRef]
- Cimerman, J.; Tomasik, B.; Csanad, M.; Lokos, S. Higher-order anisotropies in the Blast-Wave Model - disentangling flow and density field anisotropies. Eur. Phys. J. A 2017, 53, 161. [Google Scholar] [CrossRef]
- Kincses, D.; Nagy, M.I.; Csanád, M. Coulomb and strong interactions in the final state of Hanbury-Brown–Twiss correlations for Lévy-type source functions. Phys. Rev. C 2020, 102, 064912. [Google Scholar] [CrossRef]
- Fabbietti, L.; Mantovani Sarti, V.; Vazquez Doce, O. Study of the Strong Interaction Among Hadrons with Correlations at the LHC. Ann. Rev. Nucl. Part. Sci. 2021, 71, 377–402. [Google Scholar] [CrossRef]
- Kisiel, A.; Zbroszczyk, H.; Szymański, M. Extracting baryon-antibaryon strong interaction potentials from pΛ¯ femtoscopic correlation functions. Phys. Rev. C 2014, 89, 054916. [Google Scholar] [CrossRef]
- Afanasiev, S.; others. Source breakup dynamics in Au+Au Collisions at s(NN)**(1/2) = 200-GeV via three-dimensional two-pion source imaging. Phys. Rev. Lett. 2008, 100, 232301. [Google Scholar] [CrossRef]
- Adler, S.S.; others. Evidence for a long-range component in the pion emission source in Au + Au collisions at s(NN)**(1/2) = 200-GeV. Phys. Rev. Lett. 2007, 98, 132301. [Google Scholar] [CrossRef] [PubMed]
- Csorgo, T.; Hegyi, S.; Zajc, W.A. Bose-Einstein correlations for Levy stable source distributions. Eur. Phys. J. C 2004, 36, 67–78. [Google Scholar] [CrossRef]
- Gnedenko, B.V.; Kolmogorov, A.N.; Chung, K.L. Limit Distributions For Sums Of Independent Random Variables; Addisson-Wesley: Cambridge, MA, 1954. [Google Scholar]
- Nolan, J.P. Univariate Stable Distributions; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, 2020. [Google Scholar] [CrossRef]
- Metzler, R.; Barkai, E.; Klafter, J. Anomalous Diffusion and Relaxation Close to Thermal Equilibrium: A Fractional Fokker-Planck Equation Approach. Phys. Rev. Lett. 1999, 82, 3563–3567. [Google Scholar] [CrossRef]
- Csanad, M.; Csorgo, T.; Nagy, M. Anomalous diffusion of pions at RHIC. Braz. J. Phys. 2007, 37, 1002–1013. [Google Scholar] [CrossRef]
- Csorgo, T.; Hegyi, S.; Novak, T.; Zajc, W.A. Bose-Einstein or HBT correlations and the anomalous dimension of QCD. Acta Phys. Polon. B 2005, 36, 329–337. [Google Scholar]
- Achard, P.; others. Test of the \boldmathτ-Model of Bose-Einstein Correlations and Reconstruction of the Source Function in Hadronic Z-boson Decay at LEP. Eur. Phys. J. C 2011, 71, 1648. [Google Scholar] [CrossRef]
- Csorgo, T.; Hegyi, S.; Novak, T.; Zajc, W.A. Bose-Einstein or HBT correlation signature of a second order QCD phase transition. AIP Conf. Proc. 2006, 828, 525–532. [Google Scholar] [CrossRef]
- El-Showk, S.; Paulos, M.F.; Poland, D.; Rychkov, S.; Simmons-Duffin, D.; Vichi, A. Solving the 3d Ising Model with the Conformal Bootstrap II. c-Minimization and Precise Critical Exponents. J. Stat. Phys. 2014, 157, 869. [Google Scholar] [CrossRef]
- Rieger, H. Critical behavior of the three-dimensional random-field Ising model: Two-exponent scaling and discontinuous transition. Phys. Rev. B 1995, 52, 6659–6667. [Google Scholar] [CrossRef] [PubMed]
- Halasz, A.M.; Jackson, A.D.; Shrock, R.E.; Stephanov, M.A.; Verbaarschot, J.J.M. On the phase diagram of QCD. Phys. Rev. D 1998, 58, 096007. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Rajagopal, K.; Shuryak, E.V. Signatures of the tricritical point in QCD. Phys. Rev. Lett. 1998, 81, 4816–4819. [Google Scholar] [CrossRef]
- Kincses, D.; Stefaniak, M.; Csanád, M. Event-by-Event Investigation of the Two-Particle Source Function in Heavy-Ion Collisions with EPOS. Entropy 2022, 24, 308. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.J.; Lee, J.Y.; Choi, J. Development of geological disposal systems for spent fuels and high-level radioactive wastes in korea. Nuclear Engineering and Technology 2013, 45, 29–40. [Google Scholar] [CrossRef]
- Tomášik, B.; Cimerman, J.; Plumberg, C. Averaging and the Shape of the Correlation Function. Universe 2019, 5, 148. [Google Scholar] [CrossRef]
- Cimerman, J.; Tomášik, B.; Plumberg, C. The Shape of the Correlation Function. Phys. Part. Nucl. 2020, 51, 3. [Google Scholar] [CrossRef]
- Pratt, S. Pion Interferometry of Quark-Gluon Plasma. Phys. Rev. D 1986, 33, 1314–1327. [Google Scholar] [CrossRef] [PubMed]
- Bertsch, G.F. Pion Interferometry as a Probe of the Plasma. Nucl. Phys. A 1989, 498, 173C–180C. [Google Scholar] [CrossRef]
- Kurgyis, B. Three dimensional Lévy HBT results from PHENIX. 13th Workshop on Particle Correlations and Femtoscopy, 2018. [CrossRef]
- Brown, D.A.; Danielewicz, P. Imaging of sources in heavy ion reactions. Phys. Lett. B 1997, 398, 252–258. [Google Scholar] [CrossRef]
- Ballesteros, H.G.; Fernandez, L.A.; Martin-Mayor, V.; Munoz Sudupe, A. Finite size effects on measures of critical exponents in d = 3 O(N) models. Phys. Lett. B 1996, 387, 125–131. [Google Scholar] [CrossRef]
- Fytas, N.G.; Martín-Mayor, V.; Parisi, G.; Picco, M.; Sourlas, N. Finite-size scaling of the random-field Ising model above the upper critical dimension. Phys. Rev. E 2023, 108, 044146. [Google Scholar] [CrossRef]
- Makhlin, A.N.; Sinyukov, Y.M. Hydrodynamics of Hadron Matter Under Pion Interferometric Microscope. Z. Phys. C 1988, 39, 69. [Google Scholar] [CrossRef]
- Csorgo, T.; Lorstad, B. Bose-Einstein correlations for three-dimensionally expanding, cylindrically symmetric, finite systems. Phys. Rev. C 1996, 54, 1390–1403. [Google Scholar] [CrossRef] [PubMed]
- Lisa, M.A.; Pratt, S., Femtoscopically Probing the Freeze-out Configuration in Heavy Ion Collisions. In Landolt-Börnstein - Group I Elementary Particles, Nuclei and Atoms; Springer-Verlag Berlin Heidelberg, 2010; chapter 21. [CrossRef]
- Tumasyan, A.; others. Two-particle Bose-Einstein correlations and their Lévy parameters in PbPb collisions at sNN = 5.02 TeV 2023.
- Adhikary, H.; others. Two-pion femtoscopic correlations in Be+Be collisions at GeV measured by the NA61/SHINE at CERN. Eur. Phys. J. C 2023, 83, 919. [Google Scholar] [CrossRef]
- Porfy, B. Femtoscopic Correlation Measurement with Symmetric Lévy-Type Source at NA61/SHINE. Universe 2023, 9, 298. [Google Scholar] [CrossRef]
- Kovács, L. Charged Kaon Femtoscopy with Lévy Sources in GeV Au+Au Collisions at PHENIX. Universe 2023, 9, 336. [Google Scholar] [CrossRef]
- Mukherjee, A. Kaon femtoscopy with Lévy-stable sources from GeV Au+Au collisions at RHIC. Universe 2023, arXiv:nucl-ex/2306.13668]9, 300. [Google Scholar] [CrossRef]
- Novák, T.; Csörgo, T.; Eggers, H.C.; de Kock, M. Model independent analysis of nearly Lévy correlations. Acta Phys. Polon. Supp. 2016, 9, 289. [Google Scholar] [CrossRef]
- Kisiel, A.; Brown, D.A. Efficient and robust calculation of femtoscopic correlation functions in spherical harmonics directly from the raw pairs measured in heavy-ion collisions. Phys. Rev. C 2009, 80, 064911. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




