Kinematrix Field Theory Unifying Fundamental Forces and Particles

1. Introduction

Particle physics and the quest to understand the fundamental forces of nature have long intrigued scientists. The Standard Model (SM) of particle physics has successfully explained many phenomena but leaves several critical questions unanswered, such as the nature of dark matter [1], the asymmetry between matter and antimatter [2], and the unification of fundamental forces, including gravity [3]. Despite its remarkable success in describing electromagnetic, weak, and strong interactions, the SM does not encompass gravity, nor does it account for the cosmological observations of dark energy and dark matter [4,5].

In recent years, pursuing unifying the fundamental forces under a comprehensive theoretical framework has remained a forefront challenge in theoretical physics [6,7]. This manuscript introduces the Kinematrix Field Theory (KFT), a novel approach that extends beyond the traditional U(1) gauge extensions of the Standard Model [7]. Unlike conventional extensions, KFT introduces a unique gauge boson, termed the kinematon, which serves as a cornerstone for unifying the electromagnetic, weak, and strong forces with gravitational interactions in a coherent quantum framework [8].

The kinematon differentiates itself from the gauge bosons of the Standard Model in several key aspects. Firstly, it exhibits a dual nature in massless and massive forms, akin to photons and W/Z bosons, respectively [9,10]. This dualism allows for a broader range of interactions and implications in both particle physics and cosmology. Secondly, the kinematon’s interactions with fermions and other gauge bosons are governed by a distinct set of quantum numbers, proposing a new layer of complexity and interactions within the quantum realm [11,12]. Our approach aligns with the quest for a Grand Unified Theory (GUT) and addresses several of the Standard Model’s shortcomings [6].

The development of KFT reflects a growing trend in theoretical physics to explore beyond the Standard Model, seeking to reconcile the disparate forces of nature and solve the mysteries that remain unsolved within the current theoretical framework [7,8]. The kinematon’s introduction and its unique properties provide a fresh perspective on these long-standing challenges, offering potential insights and solutions that could reshape our understanding of the universe’s fundamental forces.

2. Background and Theoretical Framework

KFT’s theoretical development is grounded in the principles of quantum field theory and general relativity, with a focus on unification and consistency across different scales and forces. The framework of KFT is built upon a modified gauge symmetry group, which we denote as $G_{\mathrm{KFT}}$. This group extends the Standard Model’s gauge group by incorporating additional U(1) symmetries associated with the kinematon:

$$G_{\mathrm{KFT}}=SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y\times U{\left(1\right)}_{K_m}\times U{\left(1\right)}_{K_0},$$

(1)

where $U{\left(1\right)}_{K_m}$ and $U{\left(1\right)}_{K_0}$ represent the novel gauge symmetries introduced by the kinematon. This extension is not merely an augmentation of gauge groups but represents a fundamental shift in how particles and forces interact at a quantum level.

The Standard Model Lagrangian is a crucial foundation upon which KFT builds. It is given by:

$$L_{\mathrm{SM}}=L_{\mathrm{gauge}}+L_{\mathrm{Higgs}}+L_{\mathrm{fermion}}+L_{\mathrm{Yukawa}},$$

(2)

• $L_{\mathrm{gauge}}$ encapsulates the dynamics of the gauge fields and their interactions.
• $L_{\mathrm{Higgs}}$ represents the dynamics of the Higgs field instrumental for the mechanism of spontaneous symmetry breaking and bestows masses to particles.
• $L_{\mathrm{fermion}}$ describes the free propagation of fermions like quarks and leptons.
• $L_{\mathrm{Yukawa}}$ dictates the interactions between the Higgs field and fermions, leading to their masses post-symmetry breaking.

The Lagrangian for KFT, encompassing these novel interactions, is expressed as an extension of the SM Lagrangian:

$${\mathcal{L}}_{\mathrm{KFT}}=L_{\mathrm{SM}}+{\mathcal{L}}_{\mathrm{kinematon}}+{\mathcal{L}}_{\mathrm{int}},$$

(3)

where ${\mathcal{L}}_{\mathrm{kinematon}}$ represents the kinematic and dynamic terms for the kinematon, and ${\mathcal{L}}_{\mathrm{int}}$ encapsulates the interaction terms between the kinematon and other Standard Model particles.

The kinematon’s potential to bridge the gap between quantum mechanics and gravity while also addressing dark matter and energy mysteries positions KFT as a potential step forward in our understanding of the universe. The theory’s unique construction and implications promise a paradigm shift in comprehending our universe’s fundamental forces and constituents.

2.1. Quantum Numbers and Interaction Terms in KFT

In the Kinematrix Field Theory (KFT), fermions are assigned specific quantum numbers under the newly introduced U(1) gauge symmetries. These quantum numbers are pivotal in defining the interactions between fermions and the kinematon. The interaction Lagrangian involving the kinematon and fermions is expressed as:

$$L_{\mathrm{int}}=g_K\sum _f{Q}_{f,K}{\overline{\psi }}_f{\gamma }^{\mu }{\psi }_f{K}_{\mu },$$

(4)

where:

• $g_K$ is the coupling constant for the kinematon,
• $Q_{f,K}$ denotes the kinematon charge of the fermion f,
• ${\overline{\psi }}_f$ and ${\psi }_f$ represent the fermionic fields, and
• $K_{\mu }$ is the kinematon field.

This formulation underscores the distinct coupling of the kinematon to different fermions, setting the stage for exploring novel phenomena in particle physics and cosmology. Unlike typical U(1) gauge extensions, these interactions suggest potential anomalies and deviations in high-energy processes, offering new avenues for experimental verification.

2.2. Key Concepts and Mathematical Formulations of the Kinematrix Field Theory

The KFT notably expands the Standard Model (SM). The kinematon, a central element of KFT, is a gauge boson appearing in two distinct forms: a massless version analogous to photons and a massive counterpart similar to W and Z bosons. Its association with a new gauge symmetry, denoted as U(1${)}^{\prime }$, enriches the symmetrical framework of the particle world, introducing new force interactions.

An extended Lagrangian density governs the dynamics of KFT:

$$L_{\mathrm{KFT}}=L_{\mathrm{SM}}+L_{K_0}+L_{K_m},$$

(5)

where $L_{K_0}$ and $L_{K_m}$ represent the kinetic energies of the massless and massive kinematon fields. These terms encapsulate their interactions with fermions and gauge bosons:

$$-\frac{1}{4}{F}_{0\mu \nu }{F}_0^{\mu \nu }-\frac{1}{4}{F}_{m\mu \nu }{F}_m^{\mu \nu }+L_{\mathrm{int}0}+L_{\mathrm{intm}},$$

(6)

with $F_{0\mu \nu }$ and $F_{m\mu \nu }$ being the field strength tensors for the respective kinematon fields. The duality of the kinematon’s behavior underlies novel interaction mechanisms, contributing to the understanding of phenomena such as dark energy and neutrino masses.

2.3. Role of the Kinematon as a Gauge Boson in the KFT

The kinematon operates dualistically as both a massless entity and a massive counterpart, coupling with fermionic matter fields. KFT introduces specific interaction terms into the Lagrangian density to capture these interactions, bridging the gap between massless and massive kinematon gauge fields:

$$L_{\mathrm{int}}=g_{K_m}{K}_{m\mu }\overline{\psi }{\gamma }^{\mu }\psi +g_{K_0}{K}_{0\mu }\overline{\psi }{\gamma }^{\mu }\psi ,$$

(7)

where $g_{K_m}$ and $g_{K_0}$ are the coupling constants for the massive and massless kinematons, respectively. This distinction between massless and massive forms offers a unique interaction landscape, contrasting with traditional gauge bosons in the SM. The massless kinematon $K_{0\mu }$ is hypothesized to mediate long-range forces, while its massive counterpart $K_{m\mu }$ might account for short-range effects.

2.4. Unification of Forces and the Relativistic Consistency of KFT

KFT proposes a unified framework for forces, integrating general relativity. We introduce the metric tensor $g_{\mu \nu }$ to describe the gravitational field within the Einstein-Hilbert action:

$$S_{GR}=\frac{1}{16\pi G}\int d^{4}x\sqrt{-g}R,$$

(8)

and transform the KFT Lagrangian into a covariant form:

$${\mathcal{L}}_{KFT}^{\prime }=\sqrt{-g}(L_{SM}+L_{K_0}+L_{K_m}).$$

(9)

This approach incorporates gravity into the KFT framework, offering a comprehensive view of the interplay between gravity and other forces. It aligns with the Standard Model’s Higgs mechanism and extends to include the kinematon’s interactions, paving the way toward a unified quantum theory of gravity.

2.5. Quantum Nature of Gravity and the KFT Approach

KFT addresses the quantum nature of gravity, distinct from the classical description in Einstein’s general relativity. The KFT approach to quantum gravity involves the kinematon fields, offering new insights into spacetime quantization at the Planck scale. The gravitational interaction in the KFT framework is expressed through the Einstein field equations:

$$G_{\mu \nu }=8\pi G{T}_{\mu \nu },$$

(10)

with a quantum gravity treatment involving path integrals over all possible spacetime metrics:

$$Z=\int \mathcal{D}\left[g_{\mu \nu }\right]e^{iS\left[g_{\mu \nu }\right]},$$

(11)

where Z is the partition function. The kinematon fields regularize quantum fluctuations and introduce interaction vertices that make the quantum theory of gravity finite and renormalizable, resolving the issue of non-renormalizable ultraviolet divergences encountered in traditional quantum gravity approaches.

2.6. Black Holes, Information Paradox, and the KFT’s Interpretation

KFT provides a unique perspective on the black hole information paradox. The theory suggests modifications to the Hawking radiation process due to the influence of kinematon fields. The kinematon’s interaction with scalar fields near the event horizon of black holes leads to altered radiation spectra, potentially resolving the paradox of information loss:

$$\mathsf{\Phi }(t,r)=\int \left[a_k{u}_k(t,r)+a_k^{†}{u}_k^{*}(t,r)\right]dk,$$

(12)

where $a_k$ and $a_k^{†}$ are the annihilation and creation operators. The kinematon’s modifications to the Bogoliubov coefficients ${\alpha }_k$ and ${\beta }_k$ in the Hawking radiation process might offer insights into how information is preserved in black hole dynamics.

2.7. Early Universe Cosmology: The Role of the Kinematon

KFT significantly contributes to our understanding of the early universe, particularly during the inflationary epoch. The kinematon’s influence on cosmic inflation and the generation of primordial fluctuations offers a novel explanation for the large-scale structure of the universe:

$$H^2=\frac{8\pi G}{3}\left(\frac{{\dot{\varphi }}^2}{2}+V\left(\varphi \right)+\frac{{\dot{K}}^2}{2}+U\left(K\right)\right),$$

(13)

where $U\left(K\right)$ is the potential associated with the kinematon field. The kinematon’s role in inflationary dynamics and its impact on the Cosmic Microwave Background (CMB) anisotropies can provide testable predictions, differentiating KFT from other cosmological models.

2.8. Literature Review and Novel Contributions of KFT

KFT’s introduction of the kinematon and its associated interactions significantly departs from existing U(1) gauge extensions. This section reviews the literature on U(1) gauge extensions, emphasizing how KFT’s dual nature of the kinematon and its unique interaction mechanisms contribute novel aspects to the field. The theory’s potential to solve longstanding puzzles in particle physics and cosmology, such as dark matter and neutrino masses, is contrasted with existing models, highlighting the innovative contributions of KFT to theoretical physics.

Feynman Diagrams and Loop Corrections in the KFT

Visual representations of particle interactions are crucial for any quantum field theory, and in the context of the KFT, Feynman diagrams fulfill this role [11]. Through these diagrams, the complex web of particle interactions, especially involving kinematons, is decoded and expressed graphically. The diagrams’ power is their ability to simplify complex mathematical constructions, making calculations of probability amplitudes manageable.

2.9. Kinematon Interactions and Their Depiction in Diagrams

The kinematon’s role as a gauge boson in the Kinematrix Field Theory (KFT) is pivotal in orchestrating novel interactions between various particles and fields. Utilizing Feynman diagrams, these interactions are vividly portrayed, emphasizing the unique properties of the kinematon. The corresponding Feynman’s rules, essential for describing the vertices in these diagrams, reflect the kinematon’s interaction with fermions, its interactions with other gauge bosons, and its self-interactions.

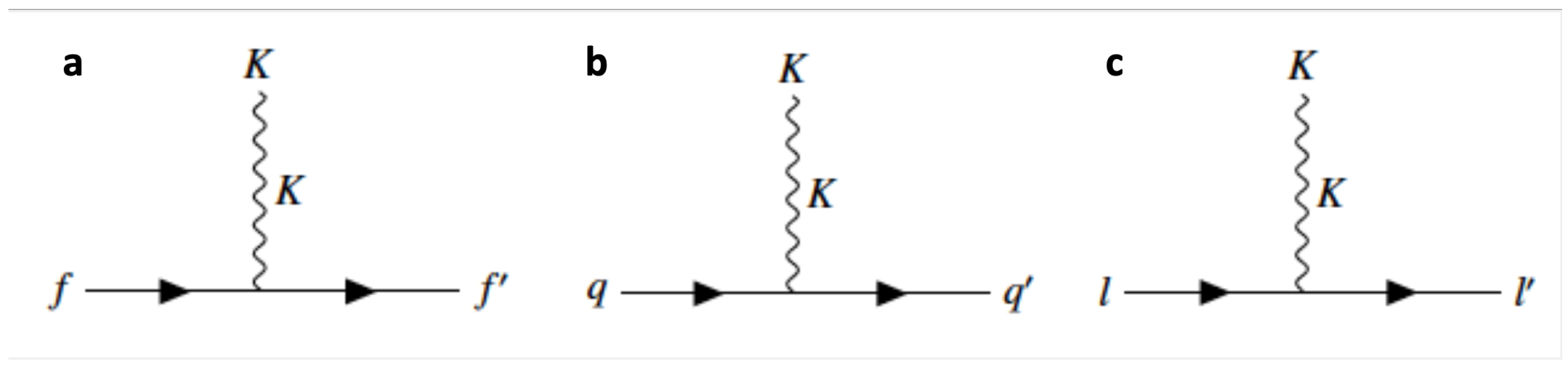
Figure 1. Kinematon-related vertices. a: Kinematon-fermions interaction. b: Kinematon-quarks interaction. c: Kinematon-leptons interaction.

Figure 1. Kinematon-related vertices. a: Kinematon-fermions interaction. b: Kinematon-quarks interaction. c: Kinematon-leptons interaction.

The kinematrix field enables interactions that span both the massless and massive modes of the kinematon, delineated by specific Lagrangians. For instance, the kinematon’s interaction with fermions is given by ${\mathcal{L}}_{K\psi \overline{\psi }}=g_{K\psi \overline{\psi }}{K}^{\mu }\overline{\psi }{\gamma }_{\mu }\psi$. The constants $g_{K\psi \overline{\psi }}$, $g_{KVV}$, and $g_{KKKK}$ represent the coupling strengths for the kinematon’s interactions with fermions, other gauge bosons, and self-interactions, respectively. These mathematical formulations are crucial for understanding the kinematon’s influence within the quantum realm and its potential implications for the Standard Model [11,13].

$${\mathcal{L}}_{K\psi \overline{\psi }}=g_{K\psi \overline{\psi }}{K}^{\mu }\overline{\psi }{\gamma }_{\mu }\psi ,$$

(14)

$${\mathcal{L}}_{KVV}=g_{KVV}{K}^{\mu }{V}_{\mu \nu }{V}^{\mu \nu },$$

(15)

$${\mathcal{L}}_{KKKK}=g_{KKKK}{K}^{\mu }{K}_{\mu }{K}^{\nu }{K}_{\nu }.$$

(16)

Characteristic vertices for these interactions are:

1.

$i{g}_{K\psi \overline{\psi }}{\gamma }^{\mu }$,

2.

$i{g}_{KVV}(g^{\mu \nu }{k}_1^{\rho }-g^{\mu \rho }{k}_1^{\nu }+g^{\nu \rho }{k}_2^{\mu })$,

3.

$2i{g}_{KKKK}{g}^{\mu \nu }$.

The interactions between fermions and the kinematon in both its massless and massive states exhibit distinct characteristics, highlighting the kinematon’s unique role in the quantum realm.

2.10. On the Use of K without an Index

In field theories, it is customary to use indices to denote the spacetime components of fields. However, for certain analyses, it is sufficient to consider only the magnitude or norm of a field, such as the kinematon field, denoted as K without an index. This approach simplifies certain calculations without losing essential information about the field’s behavior.

$$K=\sqrt{K_{\mu }{K}^{\mu }}.$$

(17)

This definition of K is particularly useful in contexts where the detailed spacetime structure of the field is not the primary concern. When necessary, indices can be reintroduced to provide a more detailed description of the field [13].

2.11. Kinematon’s Interactions with Gauge Bosons

The kinematon, as a unique gauge boson in the KFT, interacts with other gauge bosons, including photons, W and Z bosons, and gluons. These interactions are formulated within the framework of quantum field theory and play a crucial role in the theoretical structure of the KFT.

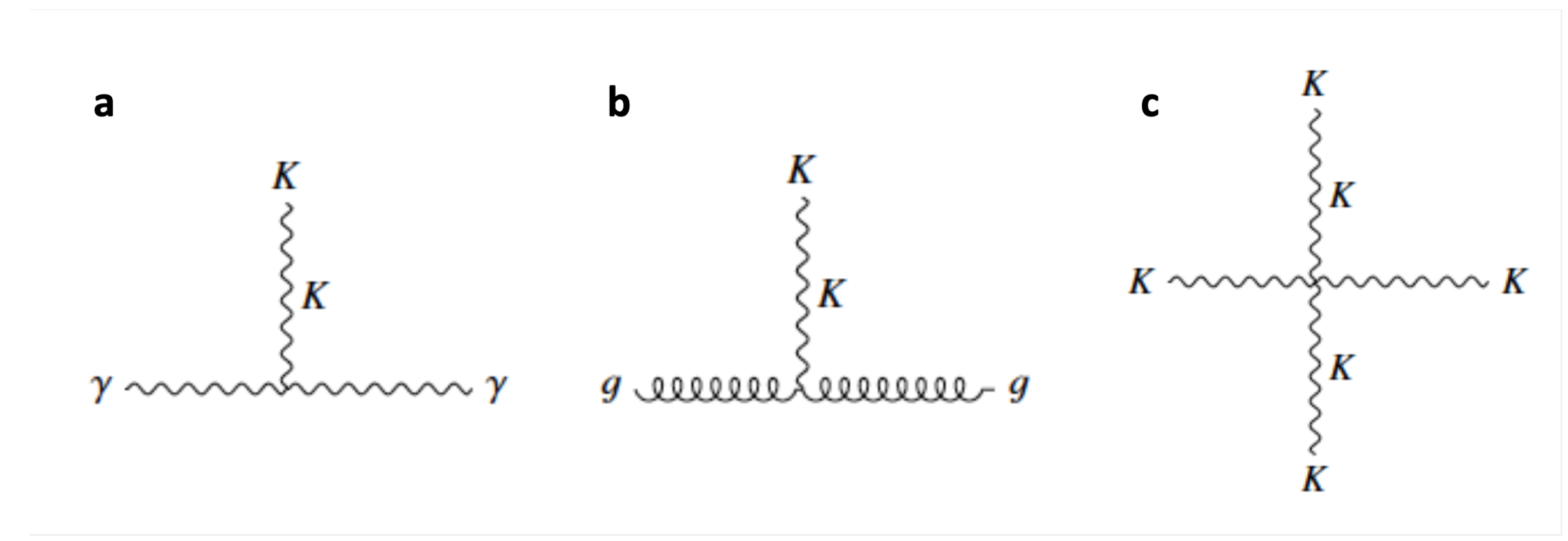
Figure 2. Visual Representations of Kinematon Interactions. a: Kinematon-photon vertex. b: Kinematon-gluon-gluon vertex. c: Kinematon self-interaction.

Figure 2. Visual Representations of Kinematon Interactions. a: Kinematon-photon vertex. b: Kinematon-gluon-gluon vertex. c: Kinematon self-interaction.

The Lagrangian terms describing these interactions, such as ${\mathcal{L}}_{KVV}=g_{KVV}{K}^{\mu }{V}_{\mu \nu }{V}^{\mu \nu }$, provide a basis for analyzing how the kinematon influences and is influenced by the fundamental forces of the Standard Model. These interactions have profound implications for particle physics and cosmology, potentially offering new insights into the unification of forces and the nature of dark matter and energy [13,14,15].

The kinematon’s interactions with gauge bosons are detailed in the Lagrangian of KFT, which incorporates interaction terms explicitly describing these dynamics. The Lagrangian terms accounting for the kinematon’s interactions with various gauge bosons are given by Eq. (15), where $V_{\mu \nu }$ is the field strength tensor for the gauge boson in question, and $g_{KVV}$ is the coupling constant of the kinematon with that gauge boson. This term in the Lagrangian facilitates the study of how the kinematon interacts with electromagnetic, weak, and strong forces, potentially bridging these interactions in novel ways.

Moreover, the kinematon’s massless and massive modes can lead to distinct interaction patterns with gauge bosons, mirroring the behaviors of photons and W/Z bosons, respectively. These interactions are critical for exploring potential phenomenological implications and experimental signatures of the kinematon in high-energy physics.

2.12. Dynamics of Kinematon Self-interactions

Self-interaction is a notable characteristic of gauge bosons, and within the Kinematrix Field Theory (KFT), the kinematon is no exception. The kinematon’s self-interactions, particularly intriguing due to its dual massless and massive nature, provide a fertile ground for theoretical exploration.

In KFT, the self-interaction dynamics of the kinematon are incorporated into the Lagrangian through a term that captures these complex interactions (Eq. (16)). $g_{KKKK}$ is the self-coupling constant of the kinematon. This term suggests non-trivial self-interactions that distinguish the kinematon from other gauge bosons like gluons in Quantum Chromodynamics (QCD). The exploration of these self-interactions is pivotal for understanding the kinematon’s role in particle physics, particularly in processes that the Standard Model does not adequately explain,[13].

Additionally, these self-interactions may have significant implications in the kinematon’s contribution to vacuum polarization effects and higher-order loop corrections. The influence of the kinematon’s self-interactions extends to the modification of the renormalization group flow and potentially introduces new fixed points in the theory, which can have profound consequences for the KFT’s predictions and its unification of fundamental forces [12].

2.13. The Essence and Ramifications of Loop Corrections

Loop corrections are a cornerstone of quantum field theory, representing higher-order processes in Feynman diagram computations. These corrections, involving virtual particle exchanges, are critical in understanding and predicting complex particle interactions. The Kinematrix Field Theory (KFT) leverages these loop corrections to offer deep insights into the subtleties of particle interactions.

Loop corrections can arise from various sources, such as fermion loops, gauge boson loops, and, uniquely in KFT, kinematon loops. These corrections are crucial in deriving parameters like renormalization constants, which ensure the mathematical consistency and physical interpretability of the theory [11,13].

In the context of KFT, loop corrections involving the kinematon are of particular interest. These corrections can manifest in several ways:

• Modifications to the propagators of particles, affecting their observed mass and lifetime.
• Alterations in the coupling strengths between particles, leading to variations in interaction rates and cross-sections.
• Contributions to the anomalous magnetic moments of fermions, providing potential explanations for discrepancies observed in experimental data.

Furthermore, the kinematon’s involvement in loop corrections can influence the vacuum structure of the theory, thereby impacting the Casimir effect and other phenomena related to vacuum energy. The study of loop corrections in KFT not only enhances our understanding of the kinematon’s properties but also aids in scrutinizing the theory’s compatibility with experimental observations and its potential to address unresolved questions in particle physics and cosmology [16].

2.14. Dissecting Loop Corrections within the KFT Framework

The Kinematrix Field Theory (KFT) delves deep into the quantum realm, where loop corrections play a pivotal role in revealing the intricate dynamics of particle interactions. These corrections, essential for understanding the renormalization properties of the KFT, ensure the theory’s consistency across various energy scales [13].

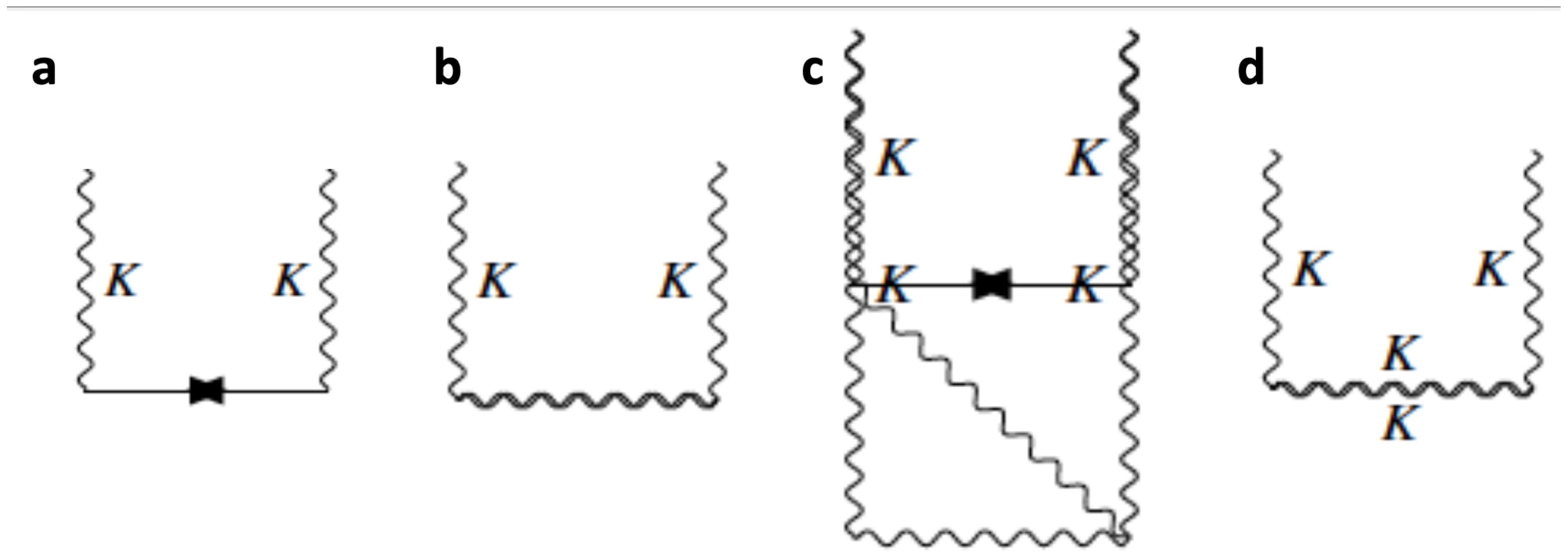
Figure 3. Insights from Feynman Diagrams. a: One-loop correction for the kinematon-fermion interaction. b: Kinematon-gauge boson interactions at one-loop level. c: Probing the kinematon’s self-interactions at one-loop. d: Kinematon loops influencing the primary interaction.

Figure 3. Insights from Feynman Diagrams. a: One-loop correction for the kinematon-fermion interaction. b: Kinematon-gauge boson interactions at one-loop level. c: Probing the kinematon’s self-interactions at one-loop. d: Kinematon loops influencing the primary interaction.

In dissecting the loop corrections due to the kinematon, we encounter a range of complex interactions. For example, the one-loop correction for the kinematon’s interaction with fermions is given by the integral:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{K\psi \overline{\psi }}^{1-\mathrm{loop}}& =\int \frac{d^{4}k}{{\left(2\pi \right)}^4}\mathrm{Tr}\left[{\gamma }^{\mu }\frac{\cancel{k}+\cancel{p}+m_{\psi }}{{(k+p)}^2-m_{\psi }^2+iϵ}{\gamma }^{\nu }\frac{\cancel{k}+m_{\psi }}{k^2-m_{\psi }^2+iϵ}\right]\hfill \\ \hfill & \times K_{\mu }{K}_{\nu }{g}_{K\psi \overline{\psi }}^2.\hfill \end{array}$$

(18)

This integral encapsulates the contributions from virtual particles and is critical in evaluating the interaction strength and the potential modifications to the kinematon’s properties. Similarly, the kinematon’s interactions with gauge bosons at one-loop are described by:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{KVV}^{1-\mathrm{loop}}& =\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\left[i{g}_{K\psi \overline{\psi }}(g^{\mu \nu }{k}_1^{\rho }-g^{\mu \rho }{k}_1^{\nu }+g^{\nu \rho }{k}_2^{\mu })\right]}^2\hfill \\ \hfill & \times \frac{-i}{k^2-m_V^2+iϵ}{K}_{\mu }{K}_{\nu }.\hfill \end{array}$$

(19)

Moreover, the dynamics of the kinematon’s self-interactions at one-loop can be articulated through the expression:

$$\begin{array}{cc}\hfill {\mathcal{M}}_{KKKK}^{1-\mathrm{loop}}& =\int \frac{d^{4}k}{{\left(2\pi \right)}^4}{\left[2i{g}_{K\psi \overline{\psi }}{g}^{\mu \nu }\right]}^2\left(\frac{i\mathrm{Tr}\left(\cancel{k}\right)}{k^2-m_{\psi }^2+iϵ}+\frac{-i}{k^2-m_V^2+iϵ}\right)K_{\mu }{K}_{\nu },\hfill \end{array}$$

(20)

These loop corrections are not merely mathematical constructs but are fundamental in predicting the kinematon’s behavior and its interactions. They serve as a gateway to understanding the deeper quantum mechanical aspects of the KFT and its implications for unifying the fundamental forces [11,16].

2.15. Renormalization in the KFT

Renormalization in the KFT plays a critical role in addressing divergences that arise in the interaction formulas involving the kinematon. This process is akin to the renormalization procedures found in the Standard Model (SM) and other quantum field theories, where divergences are systematically addressed to ensure theoretical consistency and physical plausibility, [11,13].

In the KFT, renormalization is essential to deal with the ultraviolet (UV) behavior exhibited by the kinematon’s interaction terms. These terms, without renormalization, would lead to divergent integrals, particularly evident in higher-order loop corrections. The renormalization process involves the introduction of counter-terms that absorb these divergences, thereby regularizing the theory.

2.16. Illustrative Example: Kinematon Vertex Loop Correction

To elucidate the renormalization process within the KFT, consider a one-loop correction involving a kinematon vertex:

$${\mathcal{M}}_{1-\mathrm{loop},\mathrm{KFT}}=-i{\lambda }^2\int \frac{d^{4}k}{{\left(2\pi \right)}^4}\frac{1}{(k^2-{\mu }^2+iϵ)({(p-k)}^2-{\mu }^2+iϵ)},$$

(21)

where k represents the momentum of the loop, p the external momentum, $\mu$ the kinematon mass parameter, and $\lambda$ the coupling strength. This integral demonstrates the UV divergences encountered in loop calculations, which are typical in quantum field theories and require careful renormalization.

2.17. Introducing Counter-terms in the KFT

Addressing these divergences in the KFT involves the introduction of counter-terms into the Lagrangian. These counter-terms are designed to cancel out the divergent parts of loop diagrams. The renormalization process thus modifies the Lagrangian to include these additional terms, ensuring that the physical quantities, such as scattering amplitudes, remain finite and physically meaningful,[16].

$$\mathcal{M}{1-\mathrm{loop}}^{\mathrm{ren}}=\mathcal{M}1-\mathrm{loop}+\delta \mathcal{M},$$

(22)

In this expression, $\delta \mathcal{M}$ represents the contribution from the counter-terms, which are meticulously calculated to precisely offset the divergences in the loop integrals.

2.18. Renormalization Group Evolution and Implications for the KFT

The renormalization procedure leads to the understanding that coupling constants in quantum field theories, including the KFT, are not fixed but evolve with the energy scale. This energy dependence is described by the renormalization group (RG) equations and quantified by the beta function, [12,13]:

$$\beta \left(g\right)=\frac{dg}{dln\mu }=\frac{\partial g}{\partial ln\mu }+{\beta }_{Z}g,$$

(23)

where $\mu$ is the renormalization scale, and ${\beta }_Z$ is the beta function associated with the renormalization constant Z. The RG equations govern the variation of coupling constants with energy scale:

$$\mu \frac{d}{d\mu }{g}_i=\beta \left(g_i\right),$$

(24)

These equations underscore the dynamic nature of the coupling constants within the KFT, highlighting how they change with varying energy scales. Such changes are crucial for understanding the behavior of the kinematon and its interactions in different energy regimes, and they play a pivotal role in the theoretical structure and predictions of the KFT.

2.19. Vacuum Fluctuations

The vacuum structure in the Kinematrix Field Theory (KFT) is a fundamental aspect that influences the behavior of particles and fields within the theory. In KFT, the dynamics of the vacuum are quantified by the vacuum expectation values (VEVs) of field operators. These VEVs, representing the state of the field in the absence of external influences, capture the inherent fluctuations inherent in the quantum field theory, [11,17]. The significance of the vacuum fluctuations in KFT is mathematically described by the Green’s function, defined as:

$$G(x-y)=\langle 0\left|\widehat{\varphi }\left(x\right)\widehat{\varphi }\left(y\right)\right|0\rangle ,,$$

(25)

where $\widehat{\varphi }\left(x\right)$ is the quantum field operator at point x. This equation reflects the quantum nature of fields in KFT, highlighting the probabilistic and fluctuating characteristics of quantum fields even in their ground state.

2.20. Influence of Loop Corrections on the Kinematon Field

In KFT, the kinematon field, like all quantum fields, is subject to modifications due to higher-order effects, particularly those arising from loop corrections. These corrections are critical in understanding the nuances of the kinematon’s interactions and its propagation. The one-loop correction to the kinematon propagator illustrates the impact of these quantum fluctuations:

$$G_{1-\mathrm{loop}}(x-y)=G_0(x-y)+\int d^{4}z{G}_0(x-z)\mathsf{\Pi }\left(z\right)G_0(z-y),,$$

(26)

In this formulation, $G_0(x-y)$ represents the tree-level kinematon propagator, illustrating the basic interaction and propagation properties of the kinematon. The term $\mathsf{\Pi }\left(z\right)$ denotes the self-energy contribution from one-loop corrections, encapsulating the modifications to the kinematon’s behavior due to quantum effects. This relationship between the bare and corrected propagators is pivotal in KFT for accurately modeling and predicting the kinematon’s interactions and influence in various physical scenarios.

2.21. Consequences and Implications of Vacuum Fluctuations in the KFT

The vacuum fluctuations in KFT are not merely theoretical constructs; they have profound empirical implications. These fluctuations play a crucial role in shaping the behavior and interactions of the kinematon and other particles within the theory. A prime example of the observable consequences of vacuum fluctuations is the Casimir effect, which serves as a direct demonstration of the dynamic nature of the quantum vacuum, [17].

In KFT, the vacuum fluctuations govern the kinematon’s interactions with other particles and fields, thereby influencing the theory’s phenomenological predictions. Understanding and analyzing these fluctuations are crucial for comprehending the kinematon’s role in unifying the fundamental forces and particles. The vacuum structure in KFT is thus a key component in unraveling the mysteries of particle physics and cosmology, offering insights into the unification mechanism proposed by the theory.

2.22. Formulation of Higher-Order Processes

In the Kinematrix Field Theory (KFT), the formulation of higher-order processes is essential for a comprehensive understanding of the kinematon’s interactions and behavior. The incorporation of loop corrections significantly enhances the predictive power of the theory. The Green function, representing the probability amplitude for a particle to propagate from one point to another, evolves with the inclusion of these corrections. A generic two-point Green function, taking into account multiple loop corrections, is expressed as:

$$G_n(x-y)=G_0(x-y)+\sum _{i=1}^n{G}_i(x-y),$$

(27)

Here, $G_0(x-y)$ is the tree-level propagator, depicting the fundamental interaction and propagation properties of the kinematon. Each term $G_i(x-y)$ in the summation represents the contribution from the i-th loop correction. These higher-order corrections are crucial for capturing the intricate dynamics of the kinematon field, including its interactions with fermions, other gauge bosons, and its own self-interactions.

The significance of higher-order processes in KFT extends beyond mathematical sophistication; they provide deep physical insights into the kinematon’s properties and its role within the framework of particle physics:

• Deciphering the Kinematon’s Interactions: Higher-order processes elucidate rare and exotic interactions of the kinematon with other fields, enriching our understanding of its interaction landscape.
• Energy Scale Dependence: These processes reveal how the kinematon’s behavior and interactions evolve across different energy scales, which is fundamental for theoretical consistency and for making predictions in high-energy physics.
• Path Toward Unification: By exploring these nuanced processes, KFT aims to uncover subtle mechanisms by which the kinematon potentially interacts and merges with other fundamental fields, contributing to the unification of forces and particles.

In summary, higher-order processes in KFT are not just theoretical constructs but are pivotal in unraveling the complex tapestry of the subatomic world, shedding light on the kinematon’s role and significance in the broader narrative of the universe’s fundamental forces and particles.

Mathematical Framework of the KFT’s Unification

This section establishes the mathematical rigor of the KFT. We construct the foundation upon which the KFT unifies interactions by incorporating the necessary corrections and feedback.

2.23. Lagrangian Formulation

To centralize the kinematon within the formulated field theory, we define the KFT Lagrangian as

$${\mathcal{L}}_{KFT}={\mathcal{L}}_{\mathrm{kinematon}}+{\mathcal{L}}_{\mathrm{interaction}}+{\mathcal{L}}_{\mathrm{known}-\mathrm{forces}},$$

(28)

where ${\mathcal{L}}_{\mathrm{kinematon}}$ encapsulates the free propagation of the kinematon, ${\mathcal{L}}_{\mathrm{interaction}}$ describes its interactions with other particles, and ${\mathcal{L}}_{\mathrm{known}-\mathrm{forces}}$ incorporates the dynamics of the established forces. To ensure Lorentz invariance and address feedback mechanisms, appropriate indices are assigned to the kinematon fields. Additionally, the mass and interaction terms are carefully crafted to align with theoretical expectations and empirical observations [11,13].

2.24. Gauge Symmetry and Kinematon Unification

To integrate the kinematon within the existing gauge framework, we define the following gauge symmetry group:

$$G_{\mathrm{KM}}=SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y\times U{\left(1\right)}_{K_m}\times U{\left(1\right)}_{K_0}.$$

(29)

The inclusion of $U{\left(1\right)}_{K_m}$ and $U{\left(1\right)}_{K_0}$ terms represents the novel gauge symmetries related to the kinematon, and their integration brings forth a comprehensive exploration of this theoretical extension [12].

2.25. Renormalization and Gauge Invariance

Ensuring gauge invariance, especially in the interactions involving quarks and gluons, is fundamental. The covariant derivative, incorporating the kinematon’s influence, is given by

$$D_{\mu }={\partial }_{\mu }-ig{A}_{\mu }^a{T}^a-i{g}^{\prime }{B}_{\mu }Y-i{g}^{\prime \prime }{K}_{\mu }.$$

(30)

This derivative formulation ensures gauge invariance under the desired transformations. Renormalizability of the interactions, particularly those involving the kinematon, is re-evaluated and refined to ensure theoretical viability within the framework of quantum field theory [14,15].

2.26. The Kinematon Dual Nature

The kinematon’s unique dual nature, existing in both massless and massive forms, presents both theoretical challenges and opportunities for novel physics.

Massless Kinematon: The kinematon functions as a gauge field similar to the photon in its massless form. Its distinct interactions and quantum numbers set it apart from the electromagnetic force mediator

$${\mathcal{L}}_{\mathrm{kinematon}-\mathrm{massless}}=-\frac{1}{4}{K}_{\mu \nu }{K}^{\mu \nu }.$$

(31)

Here, $K_{\mu \nu }$ represents the field strength tensor for the kinematon, akin to $F_{\mu \nu }$ for the photon. This formulation highlights the kinematon’s potential to mediate long-range forces, distinct from conventional electromagnetic interactions [17].

Massive Kinematon: The massive kinematon emerges through a mechanism analogous to the Higgs mechanism but requires additional scalar fields for its mass generation beyond the Standard Model Higgs.

$${\mathcal{L}}_{\mathrm{kinematon}-\mathrm{massive}}=\frac{1}{2}{m}_K^2{K}_{\mu }{K}^{\mu }.$$

(32)

$${\mathsf{\Phi }}_K=\left(\begin{array}{c}{\varphi }^{+}\\ {\varphi }^0+v+h\end{array}\right),$$

(33)

$$V\left({\mathsf{\Phi }}_K\right)={\mu }^2{\mathsf{\Phi }}_K^{†}{\mathsf{\Phi }}_K+\lambda {\left({\mathsf{\Phi }}_K^{†}{\mathsf{\Phi }}_K\right)}^2.$$

(34)

In these expressions, ${\mathsf{\Phi }}_K$ is the kinematon-Higgs field, and $V\left({\mathsf{\Phi }}_K\right)$ is its potential. The expansion of this potential around the vacuum expectation value (VEV), v, leads to the derivation of the kinematon mass term and the couplings influencing its interactions [18].

2.27. Implications and Detectability

The kinematon’s dual nature implies varied interaction strengths across different energy regimes and leads to diverse experimental signatures.

Massless Kinematon. Signatures and Interactions: The massless kinematon could mediate long-range forces distinct from traditional electromagnetic or gravitational interactions.

• Cosmological Footprint: The kinematon may leave observable traces in cosmological phenomena, potentially providing insights into the nature of dark matter and the early universe’s evolution.
• Precision Tests: Deviations from expected interaction patterns at macroscopic scales could be indicative of the kinematon’s presence, necessitating precision measurements in various physical contexts.

Massive Kinematon. Decays and Experimental Searches: The massive kinematon’s potential to decay into known Standard Model particles offers avenues for experimental detection.

• Collider Signatures: In high-energy collisions, such as those in the LHC, the production and subsequent decay of the massive kinematon may lead to detectable anomalies in jet patterns or energy distributions.
• Rare Decay Processes: The kinematon’s involvement in rare decay processes could result in measurable deviations from the Standard Model predictions, thereby hinting at new physics.

Complemented by dedicated experimental investigations, a comprehensive theoretical analysis is essential for unveiling the kinematon’s properties and validating its role within the KFT framework.

2.27.1. The Kinematon vs. Standard Vector Bosons

The kinematon, as posited in the Kinematrix Field Theory (KFT), exhibits unique characteristics that distinguish it from standard vector bosons such as photons or Z bosons. This distinction is pivotal for understanding the kinematon’s role in particle physics and its potential to extend the Standard Model.

2.27.2. Quantum Numbers and Interactions

Contrary to the gauge bosons in the Standard Model, the kinematon’s interactions with fermions might occur through more complex channels or involve higher-dimensional operators, a hypothesis that can be mathematically represented in the Lagrangian:

$${\mathcal{L}}_{\mathrm{kinematon}-\mathrm{interactions}}=g_K\overline{\mathsf{\Psi }}{\mathsf{\Gamma }}^{\mu }\mathsf{\Psi }{K}_{\mu }+\dots ,$$

(35)

Here, $g_K$ denotes the coupling constant of the kinematon, $\mathsf{\Psi }$ signifies the fermionic fields, and ${\mathsf{\Gamma }}^{\mu }$ encapsulates a set of matrices that define the kinematon’s unique interactions. The specificity of ${\mathsf{\Gamma }}^{\mu }$ differentiates the kinematon’s interactions from those characteristic of known bosons, suggesting novel quantum numbers and interaction mechanisms. These unique interactions warrant further theoretical and experimental investigation to elucidate their implications on particle dynamics and the unification of forces.

2.27.3. Field Strength and Self-interactions

The kinematon’s field strength tensor, characterized in the KFT, shows non-traditional self-interaction properties. The self-interaction dynamics are captured in the Lagrangian as:

$${\mathcal{L}}_{\mathrm{kinematon}-\mathrm{self}-\mathrm{interactions}}=-g_K^{\prime }{K}_{\mu \nu }{K}^{\nu \lambda }{K}_{\lambda }^{\mu }+\dots ,$$

(36)

In this Lagrangian term, $g_K^{\prime }$ represents a unique coupling constant for the kinematon’s self-interactions. These self-interactions differentiate the kinematon from photons and gluons, suggesting new avenues for particle interaction and vacuum polarization studies. The exploration of these self-interactions is critical for a comprehensive understanding of the kinematon’s influence in quantum field theories and its potential role in new physics beyond the Standard Model.

2.27.4. Addressing the Mass Term Ambiguity

The mass term of the kinematon has been a subject of extensive theoretical discussion. Diverging from the Higgs mechanism known for imparting mass to W and Z bosons, the kinematon’s mass generation could involve an extended scalar sector. The kinematon’s mass term in the Lagrangian is represented as:

$${\mathcal{L}}_{\mathrm{kinematon}-\mathrm{mass}}=\frac{1}{2}{m}_K^2{K}_{\mu }{K}^{\mu }+{\lambda }^{\prime }{\mathsf{\Phi }}_K^{†}{\mathsf{\Phi }}_K{K}_{\mu }{K}^{\mu },$$

(37)

In this equation, $m_K$ signifies the kinematon’s mass, and ${\lambda }^{\prime }$ is a coupling constant related to the interaction between the kinematon and the kinematon-Higgs field, ${\mathsf{\Phi }}_K$. This mass term implies a unique mechanism for the kinematon’s mass generation, potentially via a process similar to but distinct from the traditional Higgs mechanism. Fully understanding the kinematon’s mass origin is vital for integrating it into particle physics and exploring its contributions to the unification of fundamental forces, as well as for predicting its experimental signatures.

2.27.5. Phenomenological Insights: Dissecting the Kinematon’s Mark on Reality

2.28. The Subtle Dance of Deviations: Kinematon vs Standard Model

The introduction of the kinematon in the Kinematrix Field Theory (KFT) leads to nuanced deviations from the established predictions of the Standard Model (SM) in particle interactions. These deviations can manifest in various aspects such as cross-sections, decay patterns, or specific branching ratios, where the kinematon subtly asserts its influence. Consider the decay sequence of a fermion represented as $f\to f^{\prime }+k$. Any notable disparity between observed decay rates and those predicted by the SM could hint at the kinematon’s existence. However, it is crucial to distinguish these deviations from potential overlooked aspects of the SM. Thus, the identification of the kinematon necessitates a rigorous and comprehensive examination of experimental data.

$$\sigma (pp\to k+X)=\sum _{i,j}\int d{x}_{1}d{x}_2{f}_{i/p}\left(x_1\right)f_{j/p}\left(x_2\right)\widehat{\sigma }(ij\to k+X).$$

(38)

2.29. Kinematon: A Prospective Player at the LHC

The Large Hadron Collider (LHC) presents an ideal platform for the potential observation and study of the kinematon. The hypothesized production cross-section of the kinematon in proton-proton collisions can be mathematically expressed as shown in Equation 38. This theoretical framework suggests a method for the kinematon’s production, where an observable excess of events, differing from SM predictions, could indicate its presence.

Additionally, the kinematon’s potential role in dark matter dynamics and force unification is of significant interest. The kinematon’s theoretical relic density, which can be compared with actual dark matter observational data, provides a promising avenue for gaining insights into its nature and implications in cosmology.

$$\frac{d{n}_k}{dt}+3H{n}_k=-\langle {\sigma }_{\mathrm{ann}}v\rangle (n_k^2-n_{k,\mathrm{eq}}^2).$$

(39)

2.30. Exploring the Kinematon’s Possible Experimental Footprints

The kinematon, if existent, can influence a range of experimental outcomes, not only in collider experiments like the LHC but also in broader cosmological contexts. Potential experimental footprints of the kinematon include:

• Dark Matter Searches: As a potential dark matter component, the kinematon may alter signals in direct and indirect dark matter search experiments, presenting a novel aspect in the quest to understand dark matter.
• Cosmological Imprints: The kinematon’s involvement in the early universe dynamics could manifest in observable effects on large-scale cosmic structures, such as alterations in the cosmic microwave background’s power spectrum or deviations in fundamental constants. However, attributing specific patterns to the kinematon demands rigorous scientific validation.
• Precision Tests of Fundamental Interactions: The kinematon might introduce subtle variations in the characteristics of fundamental forces. Precision tests at various scales are essential for detecting or constraining the kinematon’s properties and interactions.

In conclusion, while the potential discovery of the kinematon holds the promise of fundamentally reshaping our understanding of particle physics and cosmology, it is crucial to approach this exploration with scientific rigor and objectivity. Confirmatory or contradictory findings related to the kinematon will undoubtedly enrich our understanding of the universe’s fundamental forces and components.

3. Conclusions and Discussion

The development of the Kinematrix Field Theory (KFT) represents a significant advancement in our understanding of the fundamental forces of nature. The introduction of the kinematon as a new gauge boson in KFT symbolizes a pivotal step toward unifying all known forces, including the elusive gravitational interaction. The comprehensive unification within the KFT is elegantly encapsulated by the gauge symmetry group:

$$G_{\mathrm{KM}}=SU{\left(3\right)}_C\times SU{\left(2\right)}_L\times U{\left(1\right)}_Y\times U{\left(1\right)}_{K_m}\times U{\left(1\right)}_{K_0}.$$

(40)

Several key developments underpin this theory:

1.

Mathematical Framework: The meticulous construction of the mathematical structure in KFT enhances its predictive power and theoretical robustness. This framework is pivotal in formulating and testing the various hypotheses arising from the theory.

2.

Feynman Rules: The extraction of Feynman rules provides a clear representation of the kinematon’s interactions with fermions and other gauge bosons. This aspect is crucial for visualizing and calculating the complex interaction dynamics within KFT.

3.

Loop Corrections: An exhaustive discourse on loop corrections is integral in fine-tuning the theory. These corrections play a vital role in adjusting and refining the theoretical framework to align with empirical evidence.

4.

Renormalization: The theory’s renormalization ensures that KFT’s predictions remain consistent with current experimental data, highlighting the theory’s credibility and relevance.

Furthermore, the KFT integrates into the Higgs mechanism, leading to the generation of a massive kinematon. This integration provides a cohesive narrative around electroweak symmetry breaking and further bolsters the theory’s coherence. Additionally, the juxtaposition of KFT with general relativity facilitates a step toward a unified quantum theory of gravity, bridging previously divergent theoretical foundations.

Experimental validation stands at the forefront of these theoretical explorations. The potential experimental footprints of the kinematon, as outlined in the KFT, pave the way for an experimental roadmap. This roadmap is instrumental in guiding future endeavors to detect and understand these novel gauge bosons and the profound unification they represent.

However, discerning the kinematon’s signatures amid the plethora of known particles and forces presents a formidable challenge in experimental physics. The path forward requires a synergistic blend of theoretical rigor and experimental innovation to fully appreciate the implications of KFT. Our forthcoming publications aim to delve deeper into the ramifications of KFT in areas such as flavor physics, the mysteries surrounding dark matter and energy, and the complexities of early universe cosmology. Additionally, exploring the technological implications of harnessing the kinematon will be a key focus in future studies.