Substantiation of the Sample Size for Assessing a Diagnostic Accuracy of Software Based on AI Technology for Diagnostic Radiology

1. Introduction

Computer vision and artificial intelligence technologies are beginning to form a decision support system for doctors for detecting pathologies in patients. In the operation of the most computer vision systems, it is customary to distinguish several stages, in particular, image preprocessing, recognition (classification of the detected object by various categories) and the final decision by the system about a presence of the object of interest in the image [1]. Recognition of objects in the image can be assigned to AI-based software (SW) in the medical application of "norm" or "abnormality" [2].

Software based on artificial intelligence technology automates the image classification process, reducing an influence of the human factor on the object detection process (“abnormalities” in medical images). A success of using AI-based software in computer vision applications has been demonstrated in several papers [3,4,5,6,7,8]. Application of software with artificial intelligence technology based on several neural network topologies in the classification of "norm"/"abnormality" in medical X-rays images are covered in the study "Deep Residual Learning for Image Recognition" [9].

When building software with artificial intelligence technology based on neural networks, a dependence of a quality of the classification on the network depth was revealed [3]. When used in medical applications, a result of “abnormality” recognition depends on the quality of training data [8] and requires a large amount of data for pre-training neural networks.

Thus in [7], a recognition of the “abnormality” by means of neural networks trained on a large amount of data – about 100,000 X-ray images obtained from more than 30,000 patients is covered. The authors note that a quality of forecasting the “norm” or “abnormality” strongly depends on data quality on which the neural network was trained (a presence of technological defects in the image that make it difficult to recognize a target “abnormality”). In papers [3,4,5,6,7,8,9], the amount of data on which the neural network was trained exceeded 100 studies. However, the question of data amount necessary and sufficient for training is not covered, as well as the issue of balance between the “norm” and “abnormality” in training data.

The issue of data amount required for a construction and validation of prognostic models was considered on regression models of developing the disease in patients [10,11]. It is noted in [10], that a considerable amount of data is required for the correct construction of a prognostic model of the disease development (the authors used more than 1.5 million data). Whereas for the validation purposes (testing predictive ability), the models recommend a sample size of 100, 200 or more values, which coincides with the results obtained in [11]. The paper [11] notes the importance of the balance between negative outcomes (patient death) and positive outcomes (patient recovery) in a construction of the prognostic model, however, a methodology for assessing a balance required for the model validation has not been proposed. Experimental studies have been conducted to assess diagnostic accuracy on sample sizes much larger than 100 and 200 studies (more than 10000 studies) [12], but this approach cannot always be achieved in clinical practice.

Therefore, when building AI-based software, the quality, quantity, and balance of classes in the data used for training and verifying the model results (validation) are of key importance.

The proposed work considers a methodology for determining a balance of classes "norm"/"abnormality" and proposes a statistical approach to determine the data amount necessary for testing AI-based software (validation).

2. Materials and Methods

For validating the results of training AI-based software, previously approved by the Ethics Committee, and registered at ClinicalTrials (NCT04489992) study was used. Mammograms were classified by the presence of breast cancer ("abnormality") and the absence of breast cancer ("norm"). The general set contains 123,301 unique studies for the period from September 1, 2021 to December 27, 2021. The original balance of classes in the study was "norm" 89.3%/"abnormality" 10.7%. Before use, the data was pre-processed in terms of deleting patients’ personal information (anonymization). The input data were a study containing 4 images – two projections of each breast. As the results of AI-based software (ML-algorithm), a probability of the presence of pathology in the entire study was taken. The following values were used as empirical data (GT): 0 – in case of Bi-RADS [13] classes 1 or 2 diagnosed by a doctor, and 1 – in case of Bi-RADS classes 3,4,5.

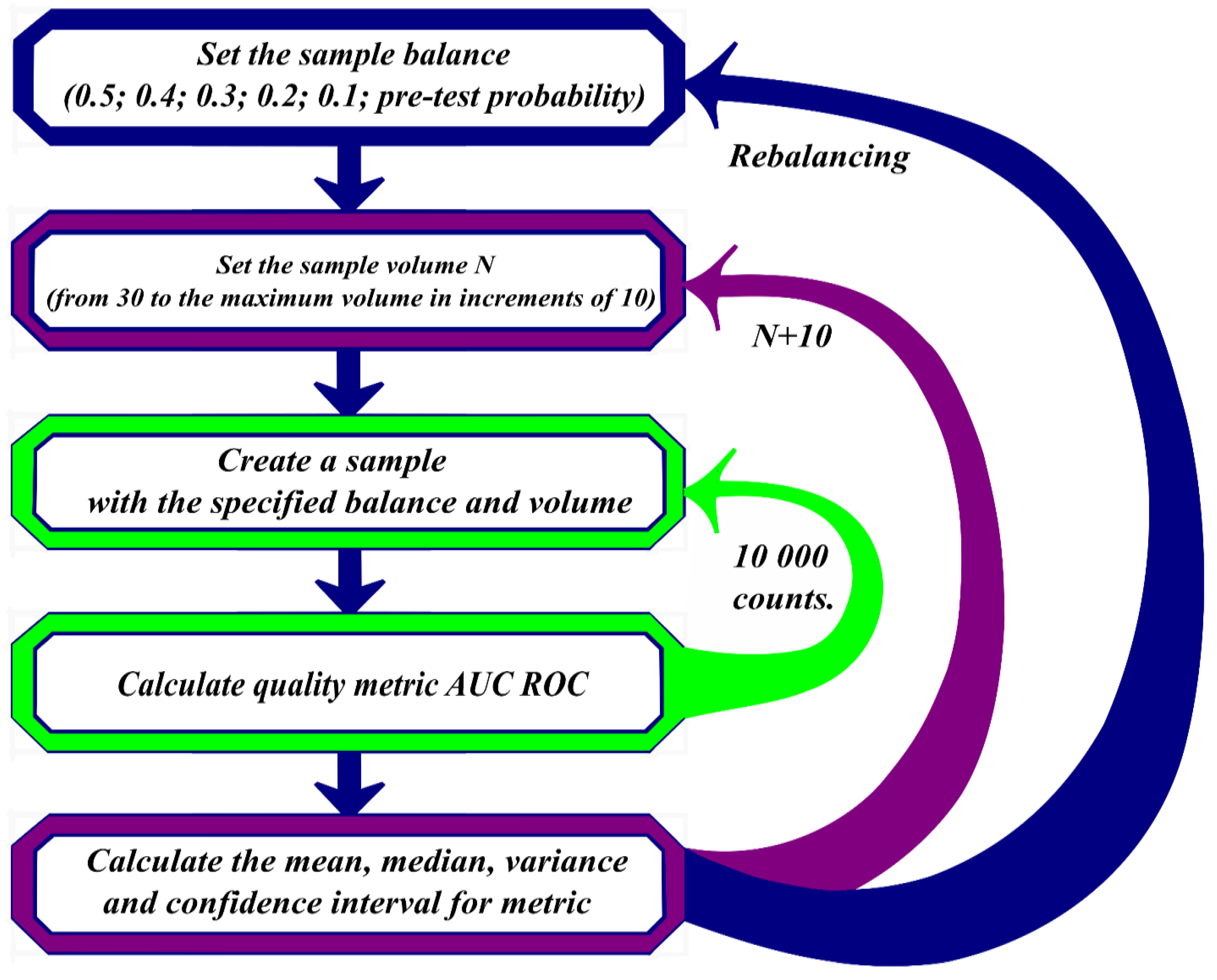
A validation of neural network training results took place in several stages. At the first stage, the data were divided into two groups – norm and abnormality. From the divided data, samples were randomly formed with balances of the "norm"/"abnormality" classes, containing "abnormality" in the amount of 50%, 40%, 30%, 20%, 10%. The minimum sample size formed randomly contained 30 research results, then the data sample size increased in increments of 10, considering the preservation of the "abnormality" share.

Each data sample is transferred to AI-based software for processing. Quality metrics are calculated based on its results: AUC ROC [14,15]. All the described actions were repeated 10,000 times for all the studied balances of "norm"/"abnormality". Based on the results of AUC ROC calculations, mean values were calculated for different random data series with the same balances. Figure 1 shows a block diagram of the described algorithm.

Mean AUC ROC values were subjected to two types of analysis:

• Fourier analysis of the AUC ROC values depending on the amount of data presented to the pre-trained neural network.
• Analysis of the nature of statistical distribution of AUC ROC values, followed by a calculation of the coefficient of variation for the established distribution.

Analysis of the distribution nature was carried out based on a comparison of the minimum of the Akaike [16] and Bayes [17] criteria for a proximity of 10 theoretical distributions to the actual AUC ROC distribution:

• Normal:

$$f\left(AUC\right)=\frac{1}{sd\ast \sqrt{2\pi }}\mathrm{e}\mathrm{x}\mathrm{p}(-\left(\frac{{(\mathrm{A}\mathrm{U}\mathrm{C}-\mu )}^2}{2{\ast sd}^2}\right))$$

(1)

where sd is the mean square deviation of the AUC; μ is the mathematical expectation of the AUC distribution.

2.

Logarithmically normal:

$$f\left(AUC\right)=\frac{1}{\mathrm{A}\mathrm{U}\mathrm{C}·sd·\sqrt{2·\pi }}\exp \left(-\frac{{\left(\mathit{ln}\left(AUC\right)-\mu \right)}^2}{2·{sd}^2}\right)$$

(2)

3.

Exponential:

$$f\left(AUC\right)=\lambda ·exp(-\lambda ·AUC)$$

(3)

where λ= 1/μ is the inverse of the mathematical expectation.

4.

Poisson:

$$f\left(AUC\right)=\frac{{\mu }^k}{k!}·exp(-\mu )$$

(4)

where k is the number of events (studies).

5.

Cauchy:

$$f\left(AUC\right)=\frac{1}{\pi ·s·\left[1+{\left(\frac{\mathrm{A}\mathrm{U}\mathrm{C}-x_0}{s}\right)}^2\right]}$$

(5)

where s is the scale factor; x₀ is the shift factor.

6.

Gamma:

$$f\left(AUC\right)=\frac{1}{{sd}^{\alpha }·\mathsf{\Gamma }\left(\alpha \right)}·{AUC}^{\alpha -1}·\mathit{exp}\left(-\frac{AUC}{sd}\right)$$

(6)

7.

Logistic:

$$f\left(AUC\right)=\frac{1}{s}·\frac{\mathit{exp}\left(-\frac{\left(AUC-\mu \right)}{s}\right)}{{\left(1+\mathit{exp}\left(-\frac{\left(AUC-\mu \right)}{s}\right)\right)}^2}$$

(7)

8.

Binomial:

$$f\left(AUC\right)=\left(\begin{array}{c}n\\ k\end{array}\right){·p}^k·{(1-p)}^{n-k}$$

(8)

Where n – all number of studies; k - number of studies with AUC data;p - probability of a given AUC value;

9.

Geometric:

$$f\left(k\right)=p·{(1-p)}^k$$

(9)

10.

Weibull:

$$f\left(\sigma \right)=\frac{a}{b}{·\left(\frac{AUC}{b}\right)}^{(a-1)}·\mathit{exp}\left(-{\left(\frac{AUC}{b}\right)}^a\right)$$

(10)

Where a is the shape factor of the Weibull distribution; b is the scale factor of the Weibull distribution.

The entire calculation of quality metrics and a formation of subsamples from the general population was carried out in Python, version 3.6. Fourier analysis and analysis of distributions was carried out on software implemented in the R language.

3. Results and Discussion

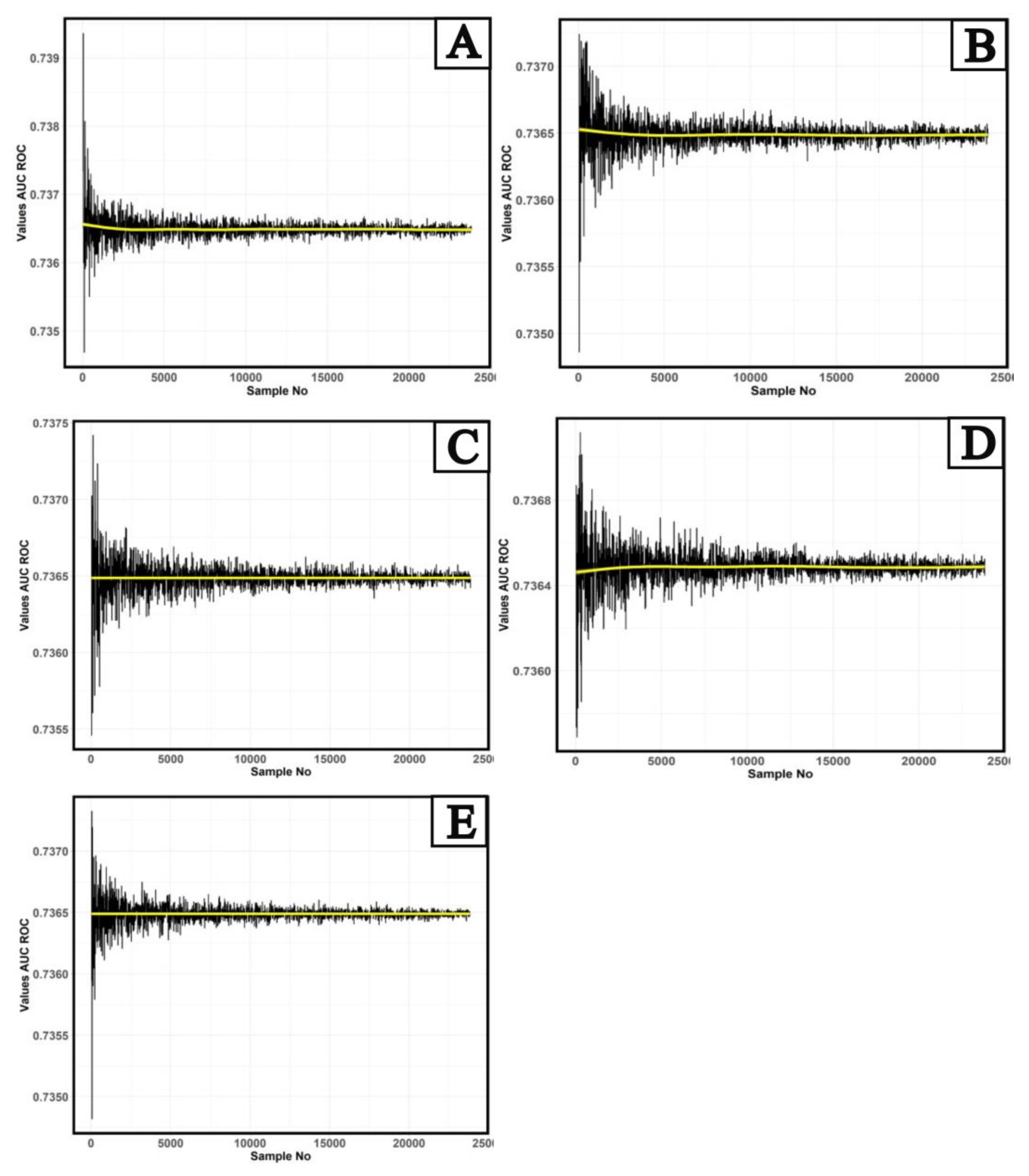
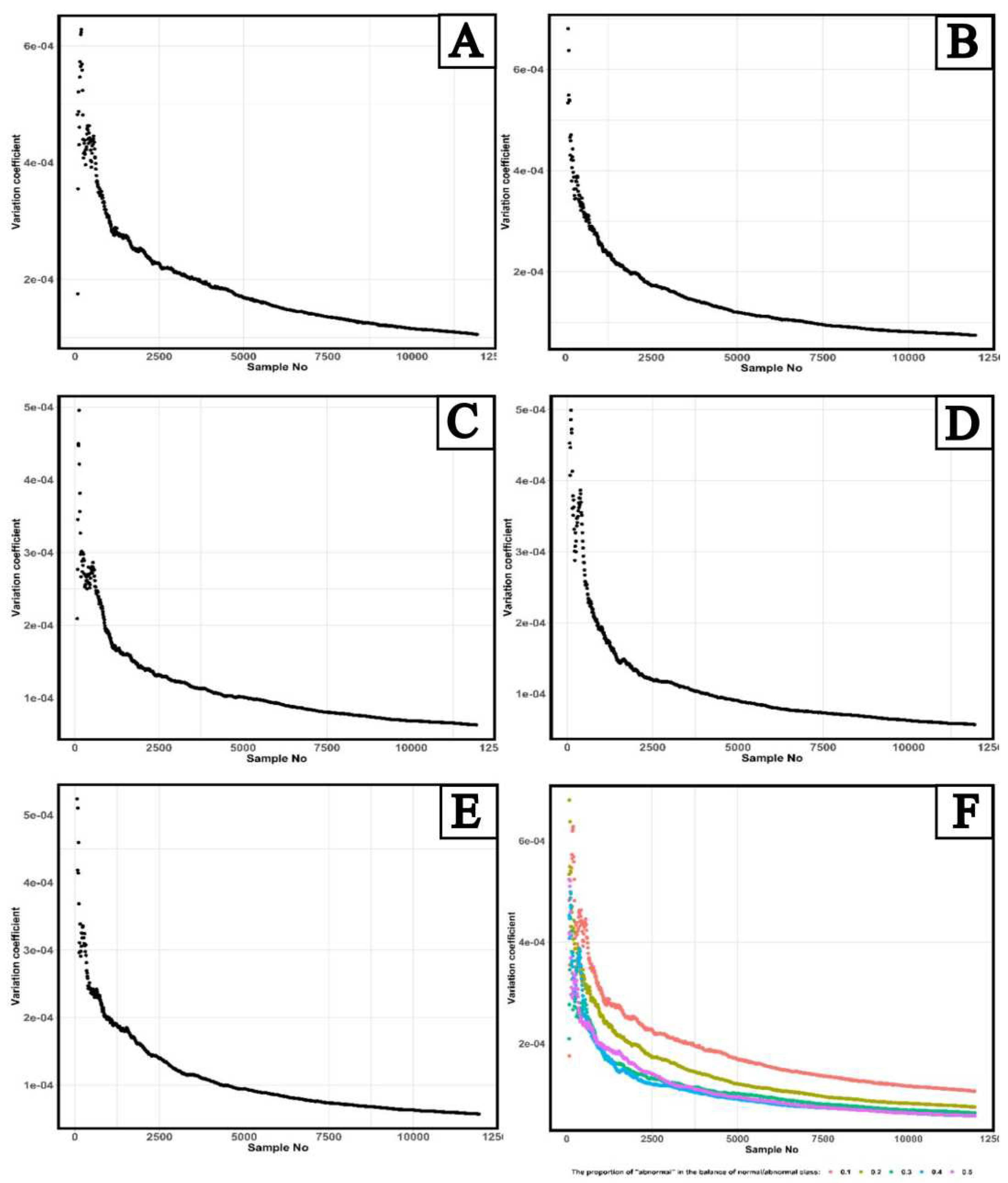
Figure 2 shows the results of calculating the AUC ROC quality metric for the studied AI-based software.

A preliminary analysis of the behavior of AUC ROC values shows a presence of the periodic dependence of a mean value on the sample size. For "norm"/"abnormality" balances with the "abnormality" share of 10%, 20% (Figure 2a and 2b), a downward trend is observed from 30 to 5,000 studies (yellow line), and an upward trend in the dependence of AUC ROC values on the number of studies for the balance with 40% "abnormality" share (Figure 2d). Further, this trend changes to a linear one. A completely linear trend in the dependence of AUC ROC on the number of studies is observed for balances with a proportion of “abnormality” of 30% and 50% (Figure 2c and 2e). It should be noted that the nature of fluctuations in AUC ROC values depending on the number of studies is very similar to the behavior of noise of various electromagnetic signals, and it has a periodical nature. In the most general form, the dependence of AUC on the number of trials can be represented as:

$$\overline{AUC}=F\left(n\right)$$

(11)

Where F(n) - some periodic function depending on the number of trials.

If the function F(n) is continuous and integrable over the whole range of changes in the number of trials, then we can define the spectral density as:

$$\widehat{F\left(n\right)}=\sum _{j=1}^N{F}_j\left(n\right)\ast \mathrm{e}\mathrm{x}\mathrm{p}(-2\pi i(\gamma ,n_j\left)\right)$$

(12)

Where F(n) – function eq. (11); n – number of samples; N - total number of studies; γ - spectral function argument:

$$\gamma =Re\left(\widehat{F\left(n\right)}\right)/Im\left(\widehat{F\left(n\right)}\right)$$

(13)

Where Re($\widehat{F\left(n\right)}$) - the real part of the spectral function; Im($\widehat{F\left(n\right)}$) - Imaginary part of the spectral function.

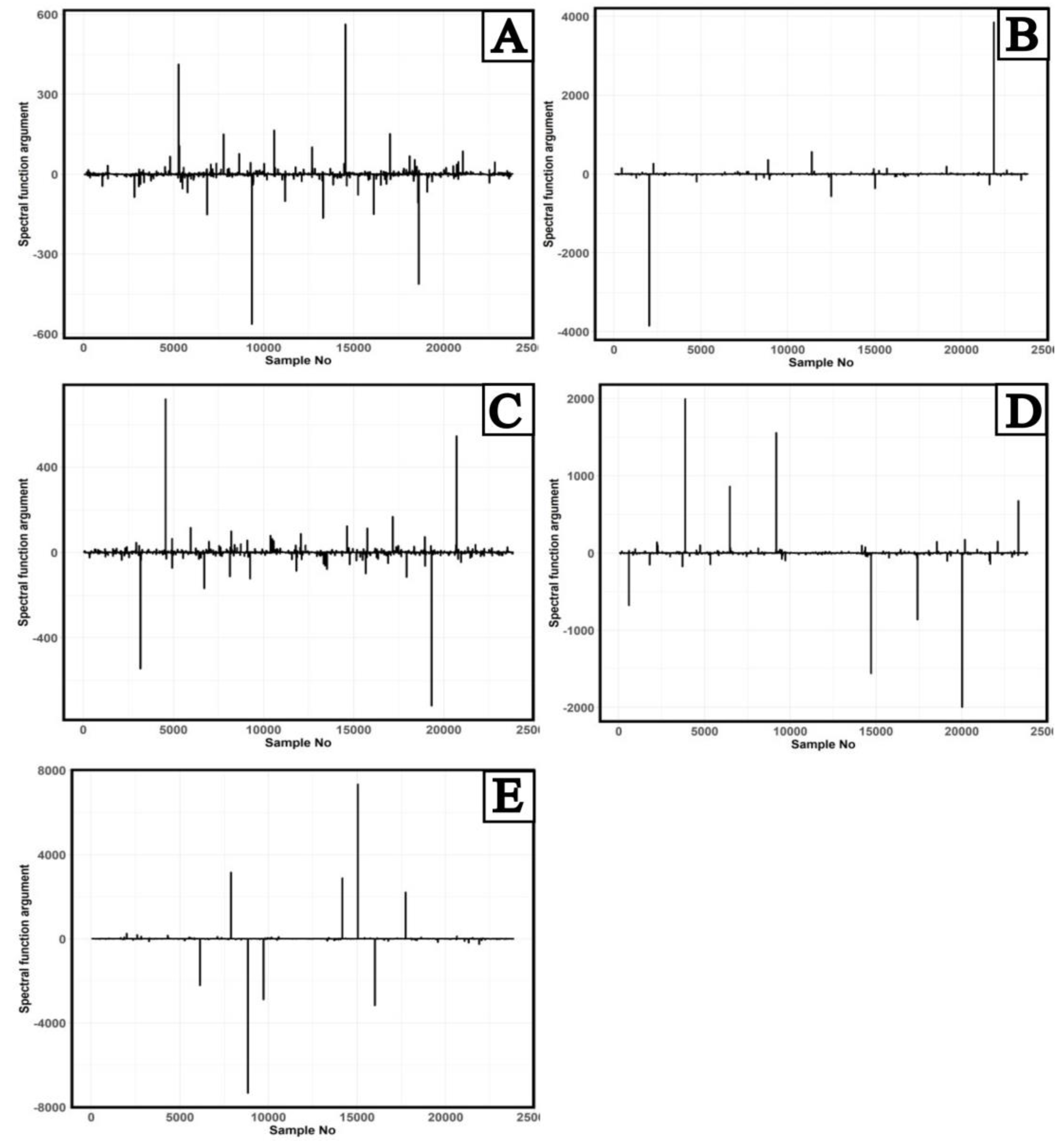
Given the results presented in Figure 2 and equations (12) and (13), a Fourier analysis of the mean AUC ROC values was performed to identify features in the AUC ROC behavior. The results of calculating the argument (13) of the spectral function (12) depending on the number of trials obtained by Fourier analysis are presented in Figure 3.

In Figure 3, for all balances, two main patterns of behavior of the main maxima and minima of the argument of the AUC ROC spectral function can be distinguished. The exception is a behavior of the maxima of the argument of AUC ROC spectral function of the balance of "norm"/"abnormality" classes with 10% "abnormality" share. The values of the main maxima and minima of the AUC ROC spectral function argument were further analyses for the presence of symmetry [16] of the species:

$$\gamma \left(n\right)+\gamma \left(n_T-n\right)=0$$

(14)

Where $n_T$ - symmetry point of the spectral function argument.

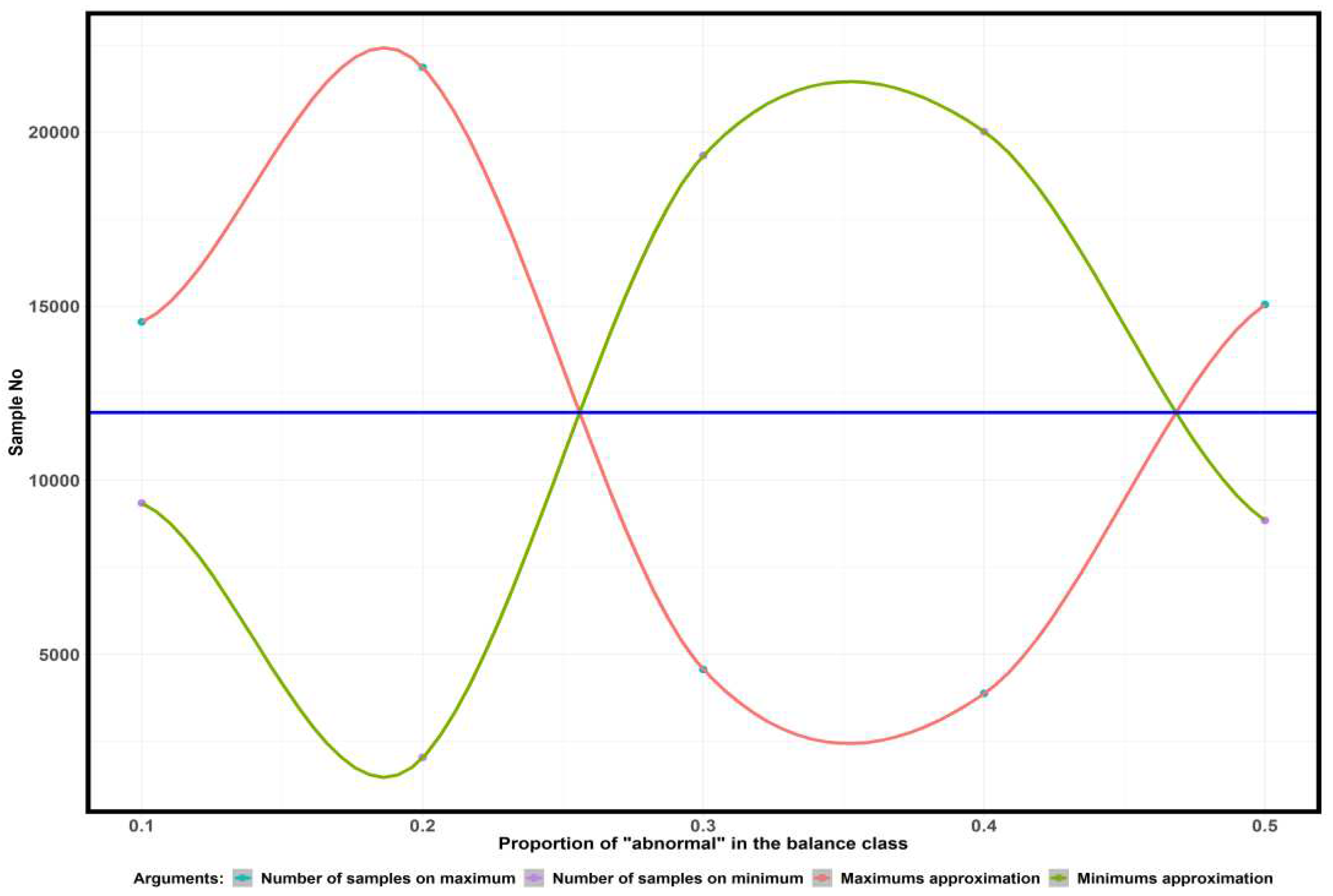
Figure 4 shows the dependence of the number of samples corresponding to the major maxima and minima of the AUC ROC argument function on the proportion of "abnormality" in the balance of the "normal"/"abnormality" classes.

The blue line in Figure 4 indicates the midpoint of the interval between the first maxima and minima of the argument of the AUC ROC spectral functions. For all considered fractions of "abnormality" in the balance of "normal"/"abnormality" classes, the middle of the interval corresponds to the value of 11940 studies. The resulting value is the n_T transition point.

To find the maximum deviation from the trend line (Figure 2) of the average diagnostic accuracy metric to the left and right of the transition point (11940 studies), we determine the closest type of simple distribution (Equations 1 - 10). The closest type of simple distribution is determined by the minimum of the Akaike and Bayesian information criteria. Table 1 shows the results of comparing the distribution of AUC ROC values on the left and right of the transition point.

From the results of the analysis of the behavior of the argument of the AUC ROC spectral function and the analysis of the nearest theoretical distribution, it follows that up to the transition point (11940 trials) the same type of distribution, the Cauchy distribution, is maintained. After the transition point (11940 studies), the type of distribution changes. Normal distribution is observed at 10% and 20% " abnormality", logistic distribution at 30% and 50% " abnormality", and log-normal distribution of AUC ROC values at 40% "abnormality ".

To assess the uniformity of AUC ROC values, analysis of the coefficient of variation depending on the number of studies (up to 11940 studies) was undertaken. In the case of the Cauchy distribution, the coefficient of variation was calculated by the equation:

$$K=\frac{\gamma }{x_0}$$

(15)

where γ – scale parameter in Cauchy distribution; x₀ – shift parameter in Cauchy distribution.

Figure 5 shows results of calculating a dependence of the coefficient of variation of the distribution of AUC ROC values on the number of studies for five “abnormality” shares in the balance of “norm”/ “abnormality” classes.

A maximum value of the coefficient of variation of AUC ROC values for 10% “abnormality” share is achieved at the number of studies equal to 190; for the 20% share, it is 80 studies; for the 30% share – 120 studies, for the 40% share – 110 studies, and for the 50% share – 70 studies. Thus, the maximum deviation of AUC ROC values from the general average is observed in the balance of “norm”/ “abnormality” classes with 10% “abnormality” share and with the number of studies equal to 190.

The application of the Fourier transforms to fluctuations in AUC ROC values allowed identifying several studies, which is a kind of border between two types of statistical distributions. This limit corresponds to the value of 11940 studies. When using less or equal number of studies for validation of AI-based software, the AUC ROC values for all studied “abnormality” shares in the balance of “norm”/ “abnormality” classes are distributed according to the laws close to the Cauchy distribution. And if the number of studies was above this value, the AUC ROC have a normal distribution for 10% and 20% "abnormality" shares, a logistic – for 30% and 50% "abnormality" shares, and a logarithmically normal – for 40% "abnormality" share.

To assess a uniformity of AUC ROC values depending on the number of studies, an analysis of the coefficient of variation of Cauchy distribution was carried out which showed that the most heterogeneous AUC ROC values were observed at 10% “abnormality” share in the balance of “norm”/ “abnormality” classes and the number of studies equal to 190.

The developed approach of determining the number of studies required for validation can be implemented in the software monitoring system based on artificial intelligence technology [19].

5. Conclusions

Summarizing the conducted study results, it can be concluded that when testing AI-based software, it is necessary to consider that the number of studies reflecting the greatest heterogeneity of AUC ROC values (the largest deviation from the mean value) is different for various class balances. If the purpose of validation is to establish the worst-case behavior of AUC ROC values, then for the studied AI-based software, the "abnormality" share should be 10%, and the number of studies 190. If the validation is carried out under conditions of a limited amount of data, then the "abnormality" share should be 50% and the number of studies equal to 70. In this case, there will be a maximum deviation from the mean AUC ROC value for the studied AI-based software. It should also be noted that the deviation of the average value of AUC ROC from the trend line with increasing number of studies decreases, which indicates that when using software based on artificial intelligence technology in clinical practice will demonstrate metrics of diagnostic accuracy different from the diagnostic accuracy obtained in pre-testing, for this reason at the stage of pre-testing and validation of software based on artificial intelligence systems it is necessary to determine the maximum limits of change of diagnostic accuracy metrics.