Analysis of AGVs Routes Considering Disturbances and Unexpected Events

1. Introduction

Automated Guided Vehicles (AGVs) play a pivotal role in flexible manufacturing systems, material transportation, and stock management. Their adoption stems from their ability to enhance productivity, system flexibility, and cost reduction [1]. However, designing efficient AGV systems is intricate due to interrelated decision-making processes and the array of available algorithms and solutions [2].

AGVs employ diverse technologies for workplace navigation, including magnetic or optical guide tracking, Global Positioning System (GPS), and Laser Imaging Detection and Ranging (LIDAR) sensors [3]. Particularly, the organization of the workspace into nodes and arcs, forming a Flow Network Model graph [4], is common in applications where AGVs follow optical or magnetic guides. In this model, nodes denote material pickup and delivery points, and arcs represent predefined paths for AGV movement. The graph-based approach simplifies route planning and optimization.

Algorithms like Bellman-Ford [5], Dijkstra [6] and A* [1] have been applied to determine optimal paths between nodes. While they often prioritize the shortest path, the occurrence of impediments during operation necessitates recalculating routes, potentially leading to costly detours and disruptions of the service. Such scenarios could adversely impact production schedules and necessitate halting manufacturing lines.

This study delves into the emergence of unexpected disruptions in robot trajectories, evaluating the costs associated with rectifying these situations using an approach we named E* analysis. Results make it clear that that the additional cost incurred due to disruptions can be substantial. Therefore, considering this aspect during AGV route identification holds potential for enhancing the resilience of the entire system.

In the subsequent sections, this paper presents a comprehensive analysis of disruptions, explores related works in the field, outlines the proposed methodology for route planning and robustness assessment, and offers insights into the attained results and their implications.

2. Related Work

In the pursuit of optimal paths between origin and destination nodes in a graph, a range of techniques and algorithms have been developed to enhance route planning efficiency and effectiveness. These approaches aim to minimize travel time, prevent collisions with obstacles and other vehicles, and mitigate the likelihood of congestion. A selection of prominent algorithms and their applications in this context are discussed below.

2.1. Dijkstra’s Algorithm

One of the most renowned algorithms for finding the shortest path, Dijkstra’s algorithm was formulated by computer scientist Edsger W. Dijkstra in 1956. It addresses the shortest path problem within a graph with non-negative arcs [7]. By choosing the closest node with the lowest weight (arc value), Dijkstra’s algorithm systematically processes each node in the graph. The speed of finding a solution depends on the number of nodes, and this algorithm treats the shortest path as the optimal outcome [6,8,9,10,11,12,13].

2.2. Yen’s Algorithm

Yen’s algorithm [14,15] can be used to find the k-shortest paths between two nodes. An efficient single shortest path algorithm (like Dijkstra’s algorithm) is repeatedly ran on selectively modified versions of the original graph, producing in this way alternative deviations from the single optimal path solution.

2.3. Bellman-Ford’s Algorithm

The Bellman-Ford algorithm is employed to compute the shortest distance in a weighted flow network [16]. Unlike Dijkstra’s algorithm, Bellman-Ford accommodates negative weights on arcs connecting two vertices. This algorithm is capable of parallel searching and counting of paths, allowing nodes to perform simultaneous processes (multiprocessing). It is especially suitable for scenarios where negative weights are incorporated into the routing decision [5,16,17,18,19,20].

2.4. A Star Algorithm

The A Star (A*) algorithm employs heuristic information to identify an ideal path. Executing node exploration and a heuristic evaluation, this algorithm continually selects the best node for expansion until the destination node is reached [21]. Maintaining both an open list (nodes to be considered) and a closed list (nodes already visited), A* benefits from rapid convergence due to the heuristic approach [1]. A* is extensively utilized for route and path planning problems [22,23,24,25,26,27,28,29].

2.5. Time Enhanced A* Algorithm

A variant of A*, the Time Enhanced A* algorithm, enhances the algorithm’s predictive capability in scenarios involving multiple AGVs. Incorporating time as an additional parameter, this algorithm predicts vehicle movements during runtime [30]. The approach constructs trajectories for each vehicle by considering the movements of other mobile robots. This technique facilitates the creation of collision-free routes while dynamically recalculating paths and updating map information iteratively [1,20,31,32].

2.6. Other Algorithms

Additional algorithms, including Probabilistic Roadmaps [20,33,34,35,36], Rapidly Exploring Random Trees [1,21,29,32,37,38], and Genetic Algorithms [35,39,40,41,42], have been explored for optimal path determination. These algorithms are particularly suited for open spaces and free-form environments.

Ongoing research in this area aims to enhance heuristics and approaches for path selection, especially in graphs with a high number of nodes [11,43].

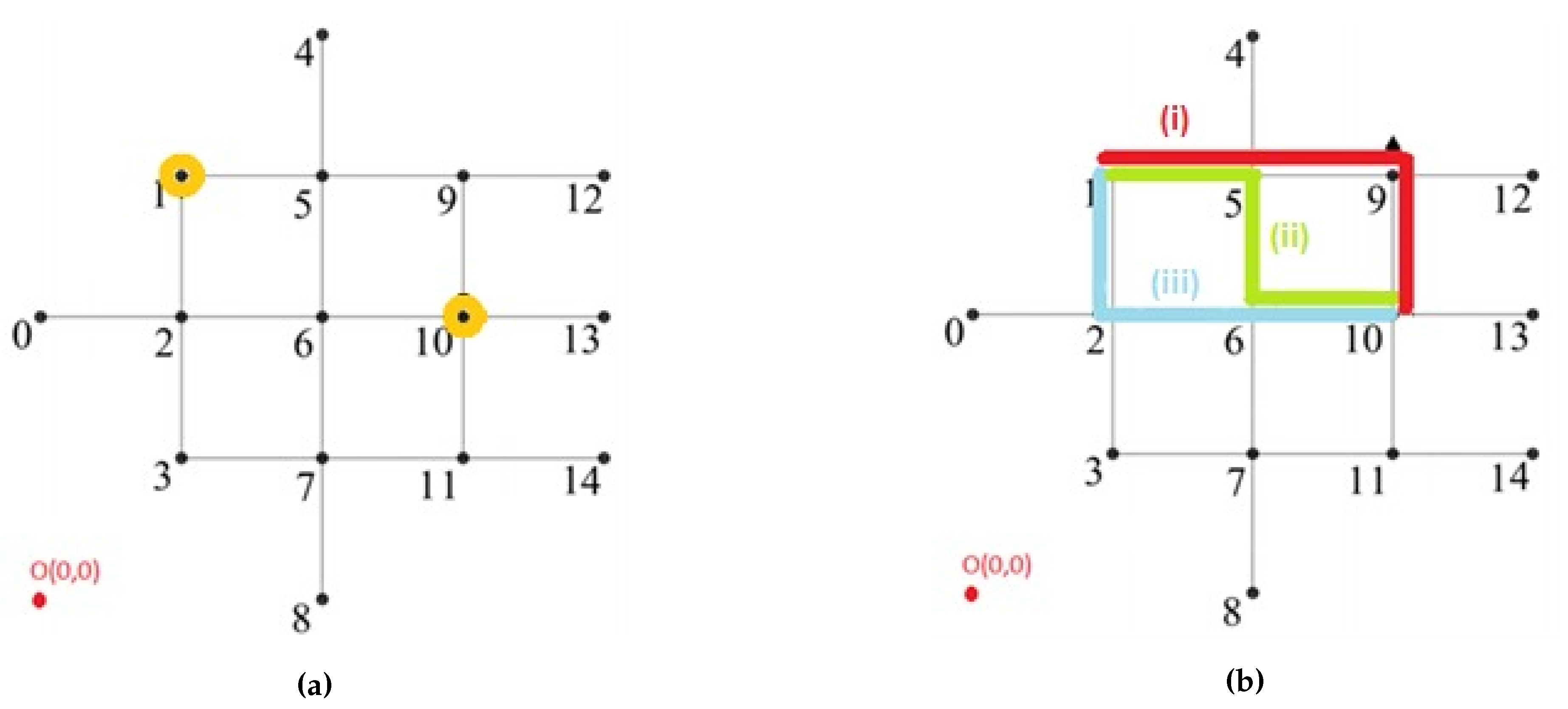
3. Resilience in the Presence of Pre-Planned Path Disturbances

The concept of robustness considered in this work refers to the capacity to reroute an AGV partially along the pre-planned route, when unforeseen disturbances block parts of pre-planned paths, with minor or even no cost in terms of increased distance required to reach the target destination. This concept of robustness is different from the one discussed in [44], which is concerned with algebraic connectivity.

The concept of robustness considered in our work is illustrated using the graph in Figure 1a, adapted from [45].

By applying Dijkstra’s or A* algorithms, three optimal paths between nodes 1 and 10 can be found, namely:

  (i)

1-5-9-10

 (ii)

1-5-6-10

(iii)

1-2-6-10

Because all arcs in Figure 1a correspond to 10 meter segments, these paths correspond to alternative 30 meter routes from origin to destination (Figure 1b).

Although they are equivalent from that perspective, considering some specific scenarios of arc disturbance and AGV positioning:

• Consider path (i), represented in red in Figure 1b, with the AGV in arc 1-5 and arc 5-9 becoming unavailable. In this scenario, the AGV can be rerouted successfully via the arc 5-6 and 6-10, leading to the AGV reaching the destination via the route 1-5-6-10, with total distance 30 meter. In this case, the disturbance did not have any actual impact on the total distance that the AGV must travel to reach the destination.
• Consider path (ii), represented in green in Figure 1b, with the AGV in arc 1-5 and arc 5-6 becoming unavailable. Rerouting through 5-9-10 is possible, resulting in a total travel distance of 30 meters from origin to destination. Again, the disturbance has no negative impact on travelled distance.
• Consider path (iii), represented in blue in Figure 1b, with the AGV in arc 1-2 and arc 2-6 becoming unavailable. Four rerouting possibilities exist, based on the AGV’s current position and the destination, leading to the AGV travelling the path 1-2-3-7-11-10, 1-2-3-7-6-10, 1-2-1-5-9-10 or 1-2-1-5-6-10. In any one of these cases, the total travelled distance is 50 meter. In this case, the disturbance has an actual negative impact on total travelled distance.

This example makes it clear that some paths are more susceptible to being negatively impacted by unforeseen disturbances on the pre-planned route than others. In our example, we describe paths (i) and (ii) as being more robust than path (iii). One interesting metric is to consider the probability of accidental robustness, that is, the probability of randomly selecting a robust path from the entire set of distance-optimal paths. In the example scenario, two paths out of three are robust, so the probability of accidental robustness is 2/3=66.6%. This is the probability of randomly selecting a robust route if the only criteria used to obtain the candidate routes is path length. Similarly, another metric to consider would be the actual impact in travelled distance when path disturbances occur and non-robust paths are being followed. In the example, travelled distance increases to 50 in non-robust reroutes over 30 in robust routes, so robust routes would only travel on average in 30/50=60% the distance of non-robust reroutes when a disturbance occurs1.

4. Methodology

The main objective of this work is to evaluate the robustness of AGV paths using the E* analysis, which verifies the impact of unexpected disturbances and obstructions that might unexpectedly appear along the route during operation. The E* analysis evaluates the robustness of the routes by considering the cost of re-routing the AGVs through a new path. In the context of this work, we consider a route to be more robust than other, of similar cost, if the cost of rerouting the AGVs in the presence of a disturbance is lower in the former than in the latter, in terms of total distance travelled, including re-routing movement.

The E* analysis includes the following steps:

1)

Generating candidate paths. These are the paths that are going to be considered in the analysis.

2)

Generating path disturbances in each candidate path.

3)

Assessing route repair cost for each disturbance, dependent on AGV position.

These steps are described in further detail in the next sections.

4.1. Generating Candidate Paths

The first step of E* entails generating a set of paths among which will be considered in the ensuing resilience analysis. This set of paths should include the shortest path or paths, which are most commonly used to determine the preferred routes, as well as possible alternatives. Two approaches that can be considered for generating the candidate set:

–

An optimal shortest path solution is obtained using a traditional algorithm (e.g., A*). Alternative paths are then obtained by modification of this initial path using a stochastic approach such as mutation followed by hill-climbing search.

–

A k-set of optimal shortest paths is explicitly computed using Yen’s algorithm [14,15]. This set might include all alternative possibilities for shortest paths, or also include sub-optimal solutions within a specified threshold of the optimal solution. A hard limit in the size of the candidate set can be imposed for practical purposes.

The first approach ensures at least one route with optimal distance is included in the candidate set. The stochastic process will then generate other variations of this original path. Because this requires computing only a single optimal path, an efficient single solution algorithm such as A* can be used to compute the initial solution. Advantages of this approach are higher efficiency, even for large networks. However, the stochastic algorithm may fail to identify all optimal paths.

In contrast, the second approach entails the systematic generation of all optimal paths using Yen’s algorithm. While this ensures all these paths are considered in the E* analysis, Yen’s algorithm requires repeated use of Dijkstra’s algorithm, which might result in a performance-intensive operation, especially in large graphs.

4.2. Generating Path Disturbances

Once the candidate paths are found, disturbances will be applied. To do so, different scenarios are generated for each candidate path. In each such scenario, a single arc along the path is made unavailable, representing an unforeseen disturbance during operation. Scenarios will include disturbances for all possible arcs. Furthermore, each possible position (arc-wise) of the AGV along the path up to the unavailable arc is also considered in an independent scenario. In this way, the disturbance scenario set will contemplate all possible combinations of arc unavailability and positioning of the AGV along the path up to the disturbance. It is not necessary to consider AGV positions beyond the disturbance for the purposes of our analysis, because the target node may be reached by following along the pre-planned route in that scenario.

4.3. Assessing Route Repair Cost

On each of the disturbance scenarios that is identified using the approach discussed in Section 4.2, it is no longer possible for the AGV to follow along the pre-planned path towards the destination node, because one of the required path arcs is no longer available.

For the AGV to progress towards the desired destination, it will be necessary to find an alternative path originating at the current position of the AGV. This alternative route can be found by applying one of the standard optimal path algorithms (such as A* or Dijkstra algorithms). It is possible that a new route may be discovered which does not extend the remaining distance to be covered before reaching the destination; however, this is not always guaranteed. In the latter scenario, there is a risk that the AGV could fail to meet the necessary deadlines for ensuring just-in-time distribution of materials. Such a delay could have a detrimental effect on the overall efficiency of the manufacturing plant. Consequently, we calculate the route repair cost as the additional distance that must now be traversed in comparison to the original path.

5. Results

To assess the gains in robustness when the E* analysis is considered, we devised a set of experiments aimed at determining:

a)

What is the magnitude of the improvement obtained by using robust paths vs. non-robust paths, in the presence of disturbances?

b)

What is the likelihood of obtaining a robust path when not specifically looking for it?

c)

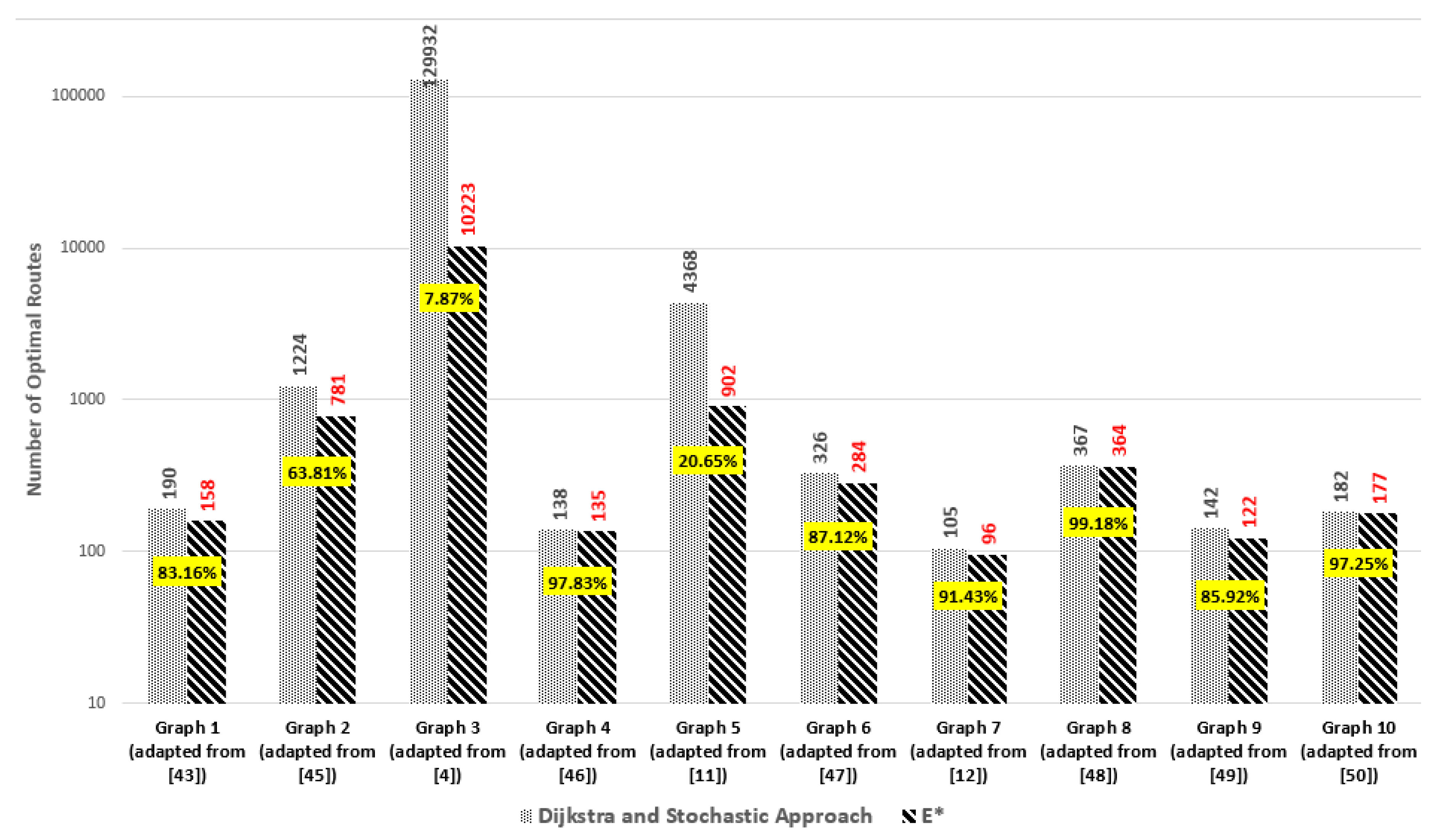
What are the trade-offs of using Yen’s algorithm vs. using the stochastic algorithm, particularly with respect to execution time and result quality?

To answer these questions, we applied the E* approach to two sets of data:

• Input Set A: Ten AGV paths described in the literature (adapted from [4,10,11,45,46,47,48,49,50,51]).
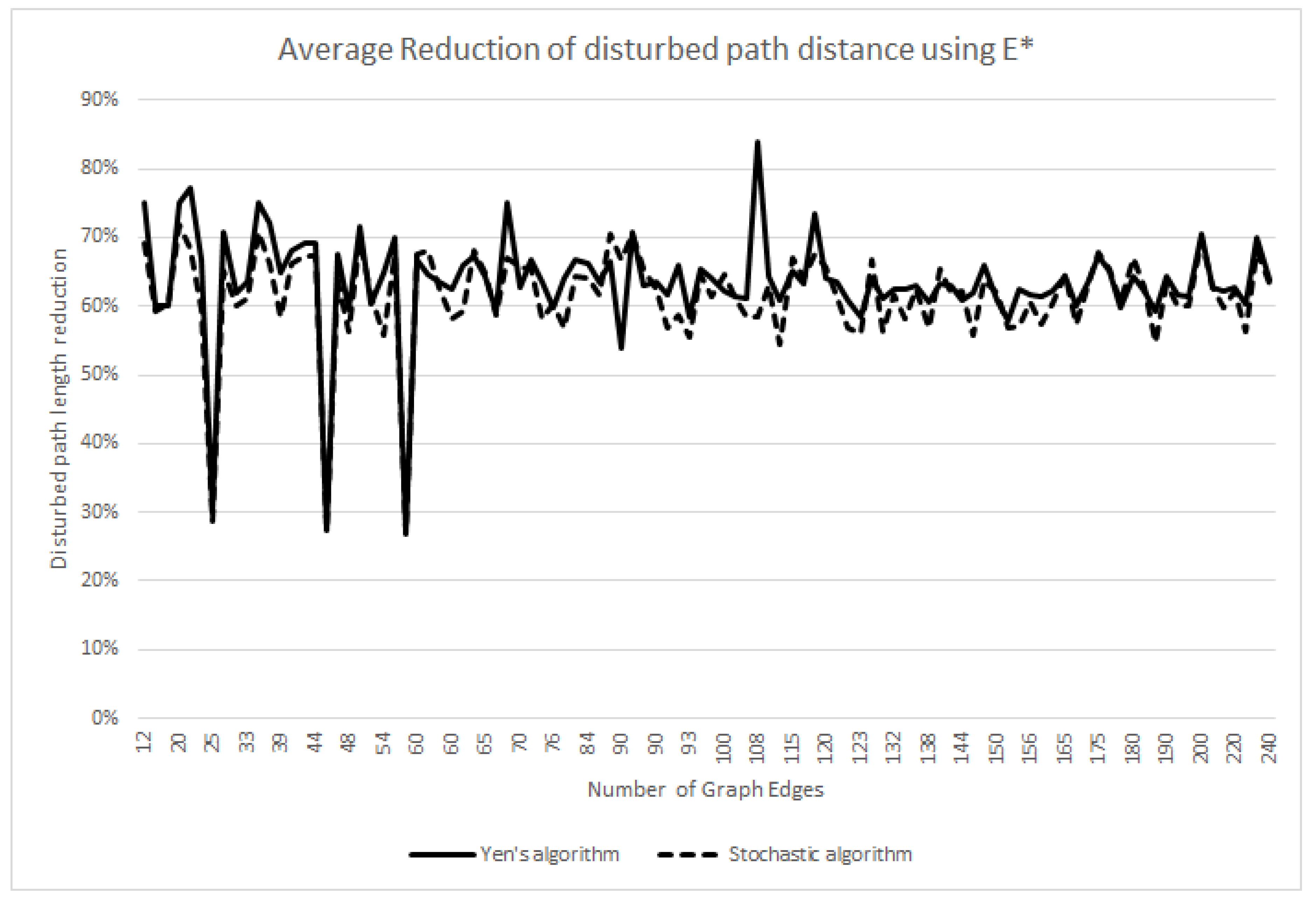
• Input Set B: A set of 100 randomly generated graphs, with varying dimensions ranging up to 240 edges and up to 150 nodes.

5.1. Ratio of Robust vs. Non-Robust Paths

To address the first question, results for input set A are presented in Figure 2, representing the number of optimal paths identified by Dijkstra’s algorithm and stochastic approach (considering only on the route distance), compared to the number of optimal paths identified after the E* analysis (considering not only the route distance but also the costs of rerouting due to disturbances in the path). As it can be expect, not all paths considered optimal in the former sense are optimal when considering the rerouting costs. By comparing the number of optimal solutions found for each metric, we can determine the probability of obtaining a robust path when not specifically looking for it, as indicated by the percentage displayed in each pair of columns in Figure 2.

Similar results can be found for Set B in Figure 3. In this case, both the stochastic approach and Yen’s algorithm were used to compute the optimal path set, and the ratio of robust vs. non-robust paths is obtained.

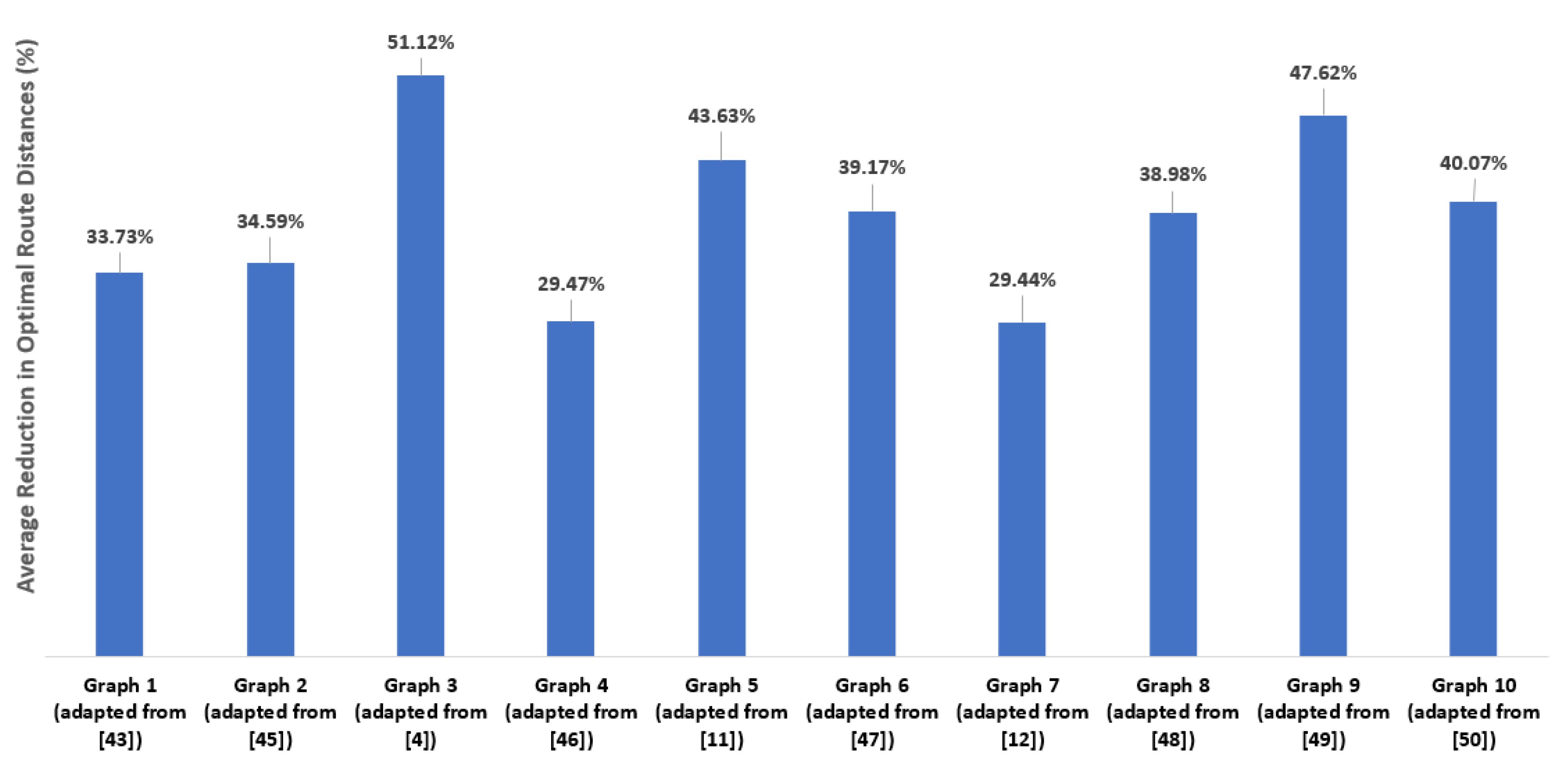
5.2. Magnitude of Improvement Achieved by Robust Paths under the Presence of Disturbances

Figure 4 represents the average values of the ratio of the distance travelled under the presence of disturbances when robust paths are used, with respect to the distance travelled when shortest but non-robust paths are used. To obtain these values, disturbances in all possible arcs of the path between the current AGV position and the target destination were considered, that forced the identification of a new path to the destination starting at the current AGV position. Furthermore, to do this, we considered all possible intermediate location of the AGV along the predetermined path.

To assess the impact of the path generation approach and also to collect results from a wider range of graphs, a similar analysis was applied to the graphs in input set B. Figure 5 presents the reduction in the length of the path when a disturbance occurs, for both path generation algorithms.

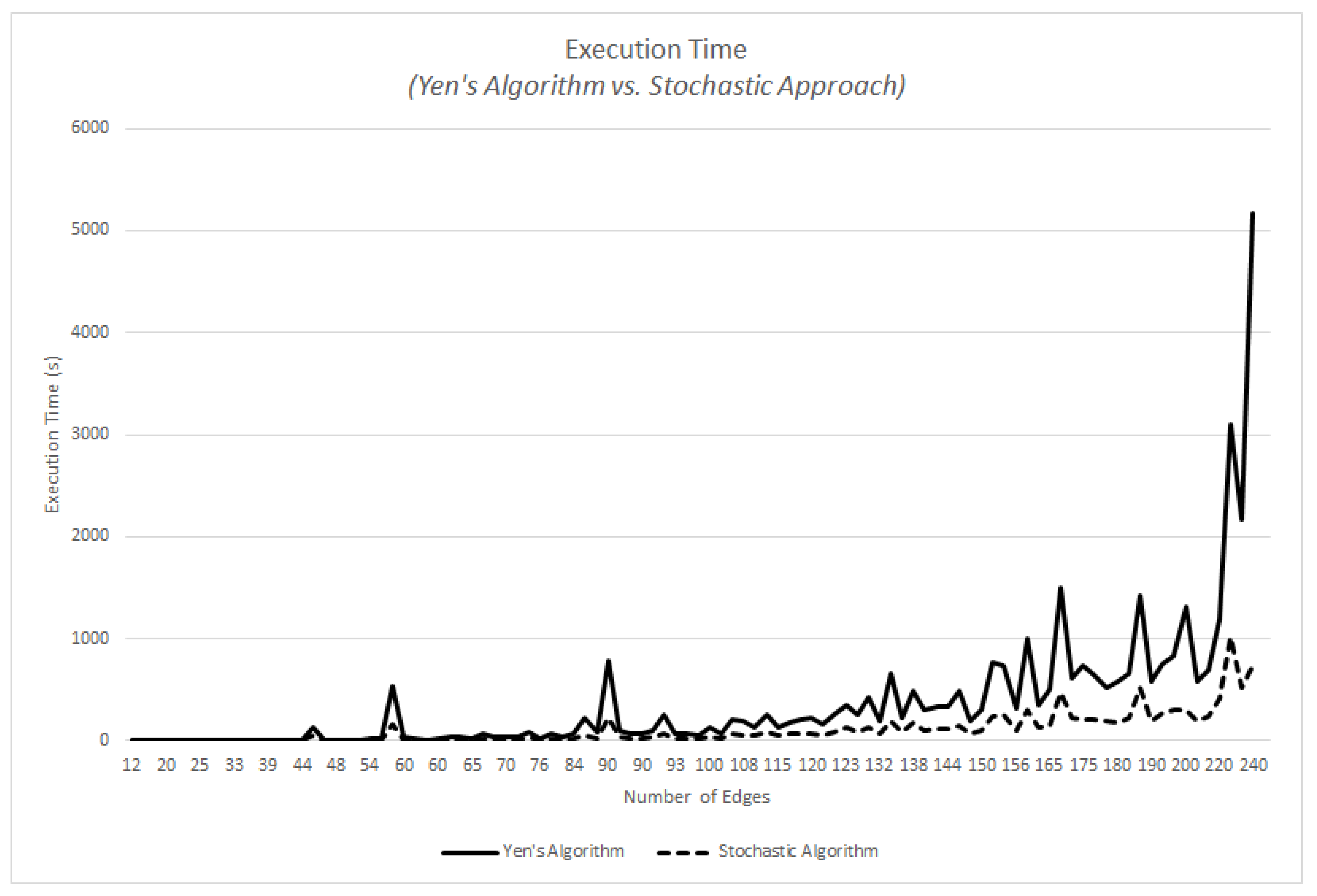
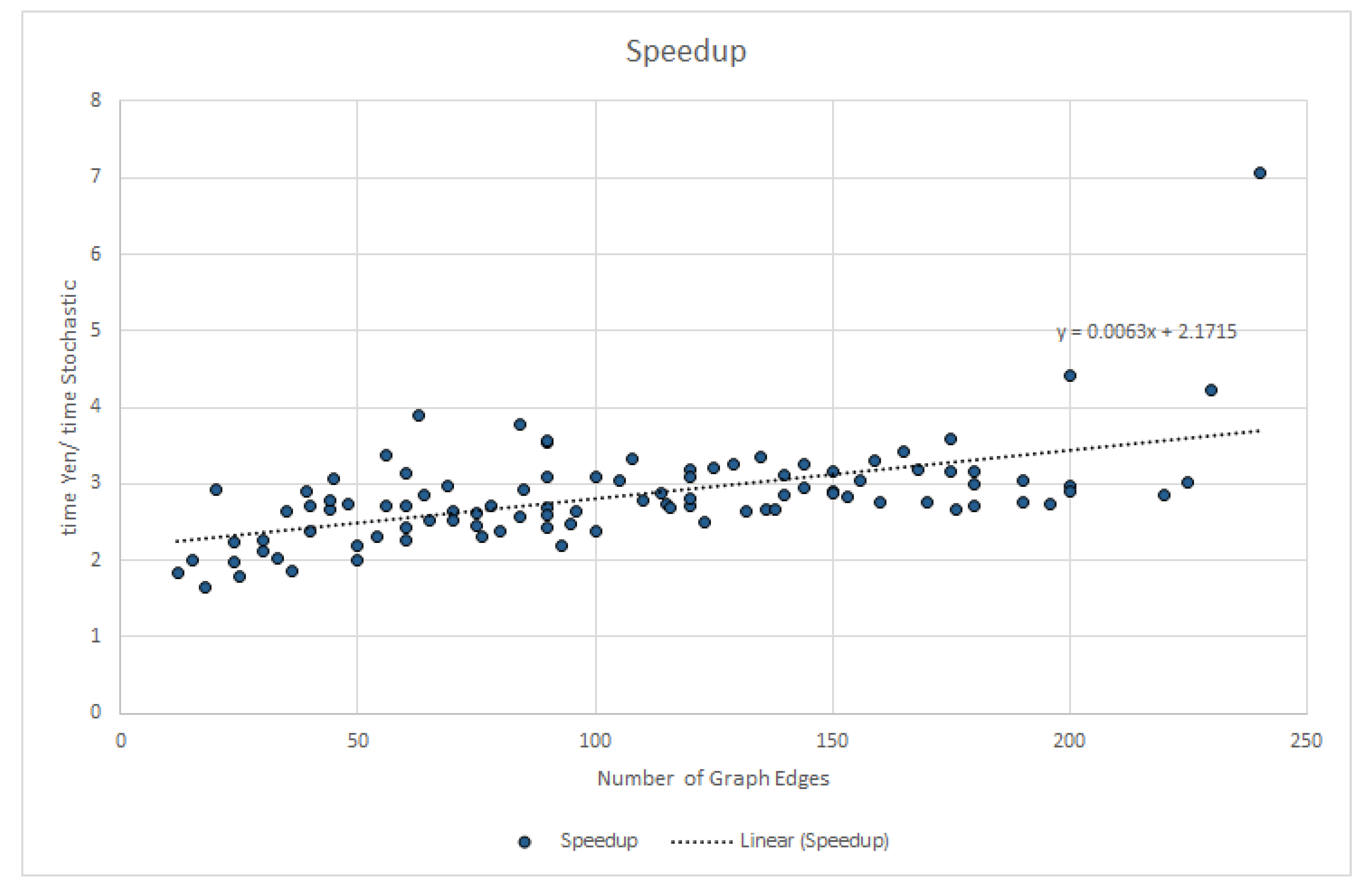
5.3. Execution Time Performance of Yen’s and Stochastic Algorithms

To assess whether there are significant advantages in using the stochastic approach with respect to Yen’s algorithm in terms of execution speed we applied both to the graphs in input set B and collected the results. Input set A was not considered for this purpose because of it mostly includes graphs of low to medium dimension, for which execution time differences are not very meaningful. Execution time for all graphs is presented in Figure 6, while Figure 7 presents a zoomed in view of the results for graphs with a lower number of edges.

6. Discussion

Results in Figure 2, obtained with input set A, demonstrate that path robustness is not ensured if the only criteria for route creating are based on path distance. In average, for all scenarios, 73,42% of all paths generated using only shortest-distance criteria were robust to disturbances. Further analysis of results reveals, however, that while the probability of accidental robustness is reasonably high for simpler graphs with fewer alternative paths, it will decrease rapidly as the complexity of the graph and number of alternative paths increases. In the most complex graph of input set A, only 7.87% of the distance-optimal solutions are also robust. There is, however, a large variance of results, so for definitive conclusions we should also consider similar metrics for input set B, which includes a larger number of randomly generated graphs.

The results disturbed path ratios for input set B can be seen in Figure 3. It can be observed that, when using the stochastic algorithm for generating optimal paths, the observed ratio of robust to non-robust paths was much higher (on average 91%) than those of input set A. In contrast, when Yen’s algorithm is used,the same metric drops to an average value of 47%. The values obtained when using Yen’s algorithm are most likely more representative of the real ratio, because it generates all distance-optimal paths, while the stochastic algorithm can only provide a best-effort approximation of the distance-optimal path set.

Concerning the average improvement of total distance travelled when re-routing is required due to unexpected disturbances, results in Figure 4 indicate that, when using E* with input set A, the length of the paths subjected to disturbances is reduced to only 61.22% of the solutions based only on distance-optimal criteria. For input set B, no significant difference is found when comparing the results using either distance-optimal path generators (61.5% for the stochastic algorithm and 63.5% when using Yen’s algorithm) (See Figure 5). These results are also in line with those that were obtained using input set A. This result demonstrates that significant improvements of performance on disturbance scenarios can be gained if path robustness is considered during route selection.

Results in Figure 6 and Figure 7 demonstrate that, as expected, the stochastic algorithm is faster than Yen’s algorithm. The speedup gained from using the stochastic algorithm instead of Yen’s algorithm is represented in Figure 8. It can be seen that the speedup slowly improves with increasing number of graph edges, with a speedup of approximately 3 for an average sized graph of input set B.

Summarizing our findings, and answering the questions posed at the start of Section 5:

a)

What is the magnitude of the improvement obtained by using robust paths vs. non-robust paths, in the presence of disturbances?

When in the presence to unforeseen disturbances requiring rerouting an AGV from its current route, we found that the length of robust routes was just slightly over 60% of the corresponding values. This improvement of nearly 40% demonstrates the usefulness of considering robustness in route design.

b)

What is the likelihood of obtaining a robust path when not specifically looking for it?

While specific results depend on the input set and route generator being used, data in Figure 2 and Figure 3 demonstrate that accidental robustness is generally unlikely to occur when routing only with optimal distance considerations.

c)

What are the trade-offs of using Yen’s algorithm vs. using the stochastic algorithm, particularly with respect to execution time and result quality?

No discernible difference in effectiveness is found when using either approach (Figure 5). Execution time benefits the stochastic approach, with speedups in the range of 2 to 4 for the tested graphs (Figure 6, Figure 7 and Figure 8). In spite of this improvement, it appears that the benefit is mostly linear which might not be sufficient to scale well for operation in graphs of very high dimension.

7. Conclusions and Future Work

In this paper, we propose the E* analysis approach, that identifies AGV routes with high robustness, in terms of resilience against unexpected disturbances in pre-planned routes. We demonstrated that routes of equivalent distance may have different robustness properties, suggesting that route planning based on distance criteria only may not be generate robust solutions.

High robustness mitigates unforeseen disruptions of planned routes in industrial applications, reducing wasted time and allowing the continued operation of production processes.

Future work can address issues such as improving the efficiency of E*, or exploring its use in other contexts such as scenarios with multiple AGVs and multiple routes.