Submitted:
14 August 2024
Posted:
16 August 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Literature Review
| Model type | author | model | scheduling framework | uncertain times | action consolidation | look-forward | Multi-objective/ Single-objective |
| Xin et al. (2020)[8] |
MVPD | One-time decision | N | S | |||
| Cheng etal. (2023)[9] |
MAGV-SP | One-time decision | N | S* | |||
| Gao et al. (2023)[10] |
MADP | One-time decision | N | S* | |||
| Qiu et al. (2015)[11] |
EHARP | One-time decision | N | S* | |||
| Chen et al. (2023)[12] |
AGVEESC | One-time decision | N | M | |||
| Xin et al. (2022)[13] |
ARP | One-time decision | N | ||||
| Zou et al. (2020)[14] |
AGVDP | One-time decision | N | S* | |||
| Li et al. (2018)[15] |
AGVSP | One-time decision | N | S* | |||
| Wang et al. (2022)[16] |
MARP | One-time decision | N | S | |||
| Liu et al. (2023)[17] |
AGVDP | One-time decision | Y | M | |||
| Xue et al. (2021)[6] |
The pickup and delivery problem, |
One-time decision | N | S | |||
| Ulmer et al. (2021)[7] |
DPDP, SDDP | One-time decision | Y | c | f | S | |
| Reyes et al. (2018)[18] |
MDRP | Rolling decision | N | c | S | ||
| Yildiz et al. (2019)[19] |
DVRPs | Rolling decision | N | c | S | ||
| Zheng et al.(2020)[24] | PDP | One-time decision | Y | S* | |||
| Liao et al. (2020)[25] |
GMDRP, | Rolling decision | N | c | M | ||
| Zheng et al.(2022)[27] | on-demand food delivery | One-time decision | Y | S* | |||
| Non-VRP | Liu et al. (2018)[5] |
Spatial CrowdSourcing | One-time decision | N | S; S* | ||
| Du et al (2019)[20] |
Spatial CrowdSourcing | Rolling decision | N | M | |||
| Zachary (2019)[21] | VFCDP | Rolling decision * | N | f | S | ||
| Sun et al. (2020)[22] |
TRDR | Rolling decision | N | S | |||
| Tu et al. (2019)[23] |
Spatial CrowdSourcing | Rolling decision | N | S* | |||
| Yu et al (2022)[26] |
DRVRP | Rolling decision | N | M | |||
| 本文 | Rolling decision* | Y | C | F | M |
3. Problem Formulation
3.1. Problem Description
3.1.1. Take-Out Delivery Flow
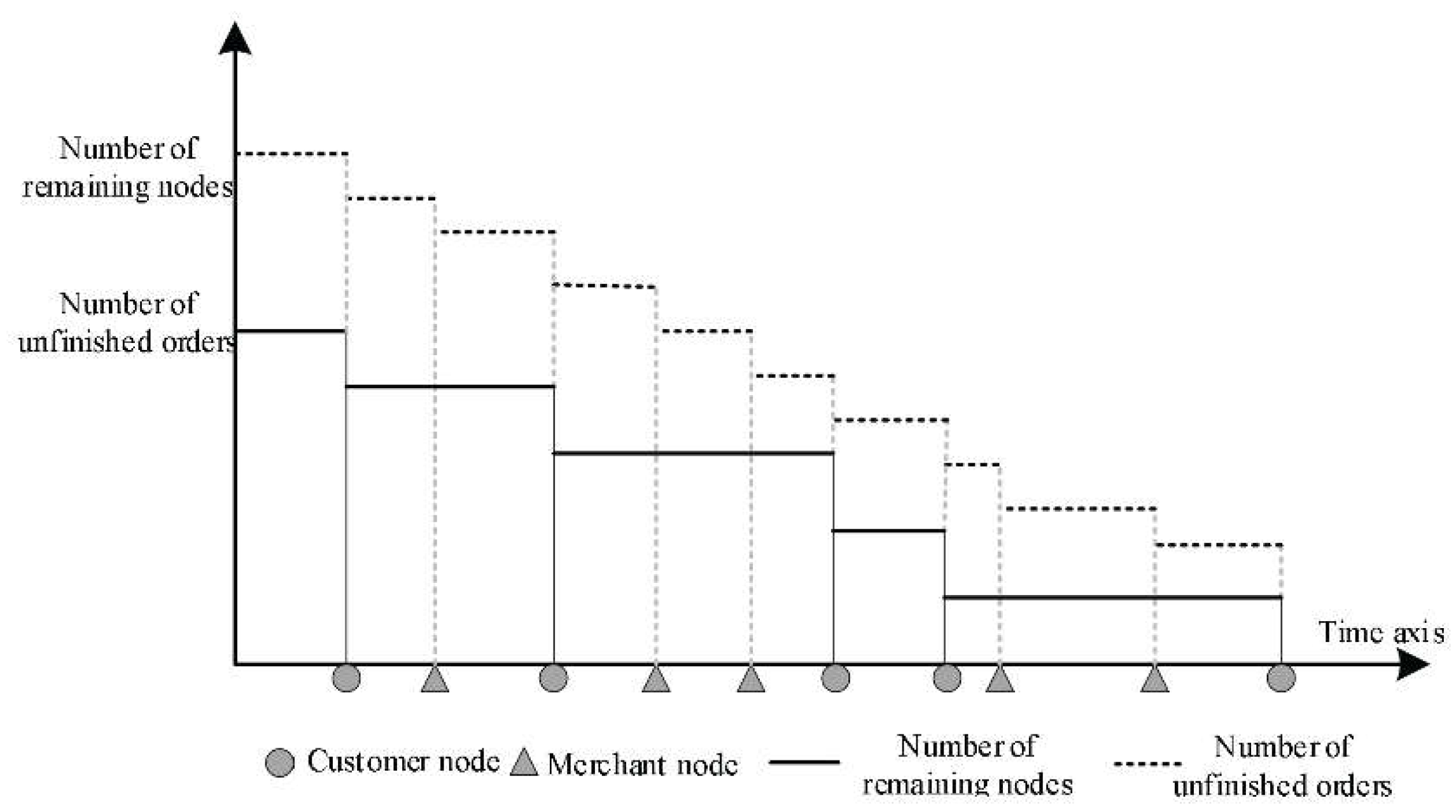
3.1.2. Real-Time Dynamic and Rolling Scheduling
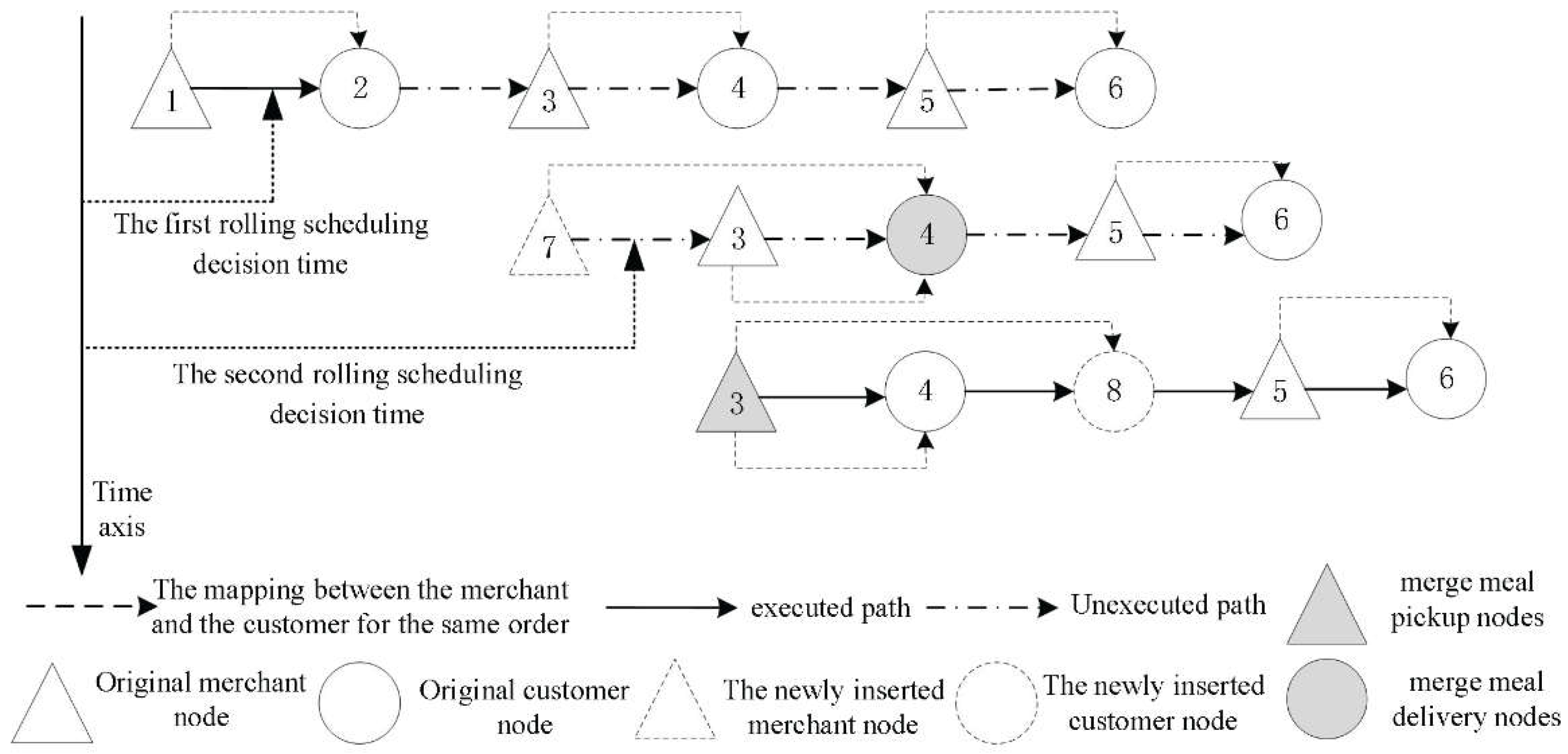
3.1.3. Uncertain Preparation Times
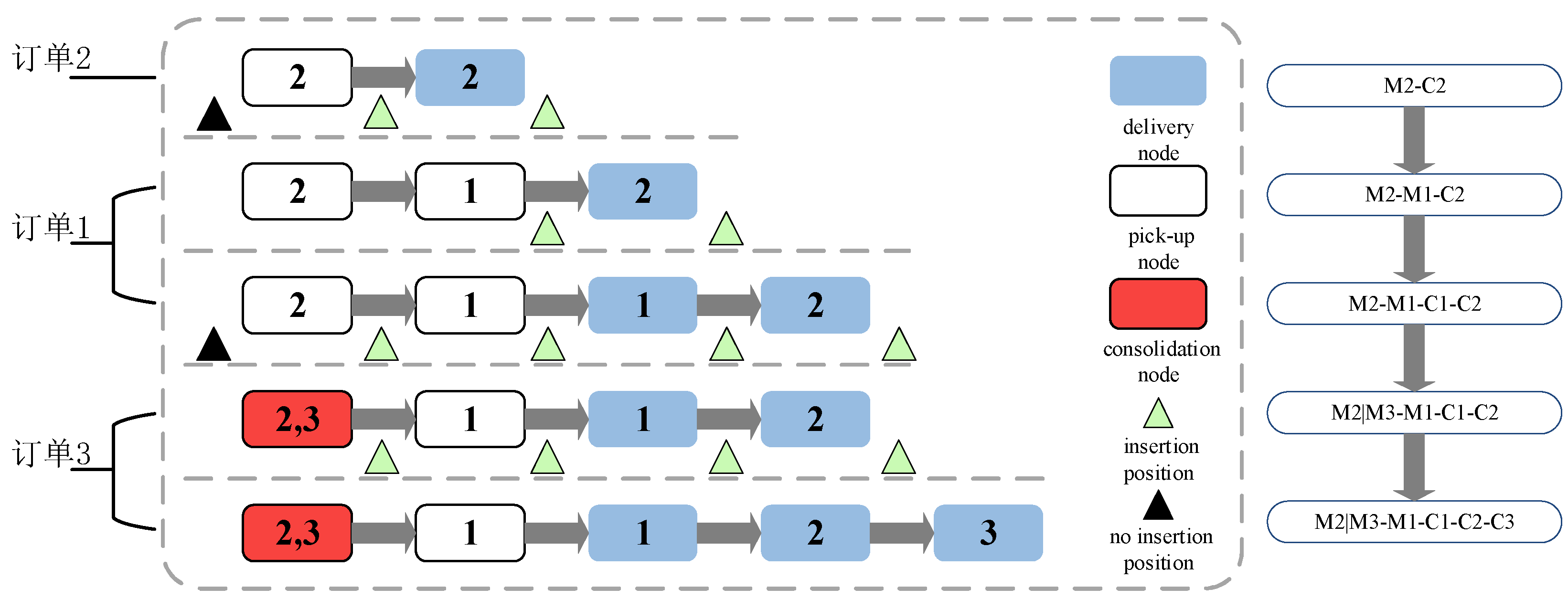
3.1.4. Routing Combination
3.1.5. Look-Forward
3.2. Modeling
- The inertial action currently being executed cannot be changed.
- The preparation time of the restaurant is subject to Gaussian distribution.
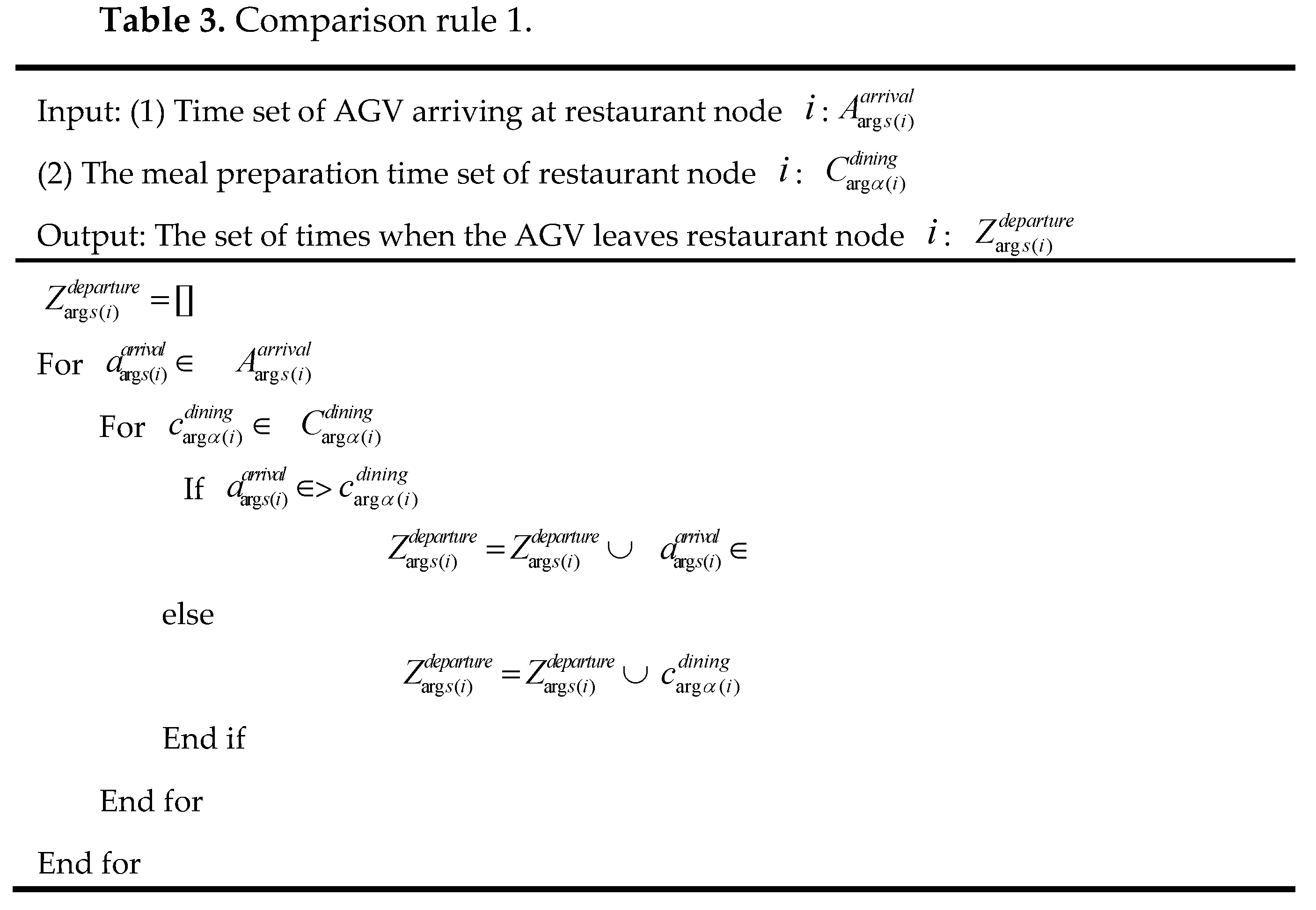
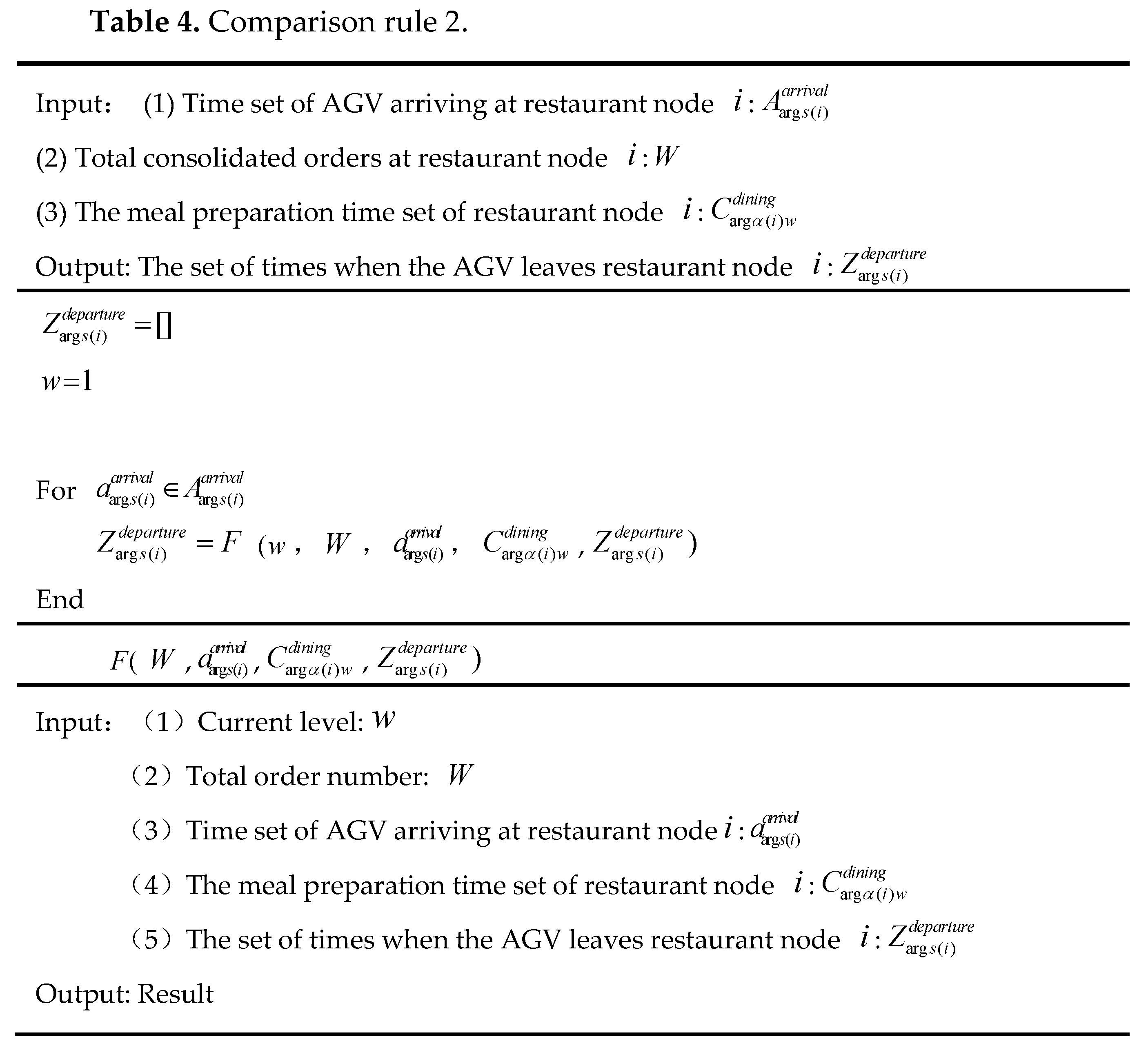
- The AGV's meal pick-up time occupies a small amount of time in the entire delivery process, so it is not considered.



4. The Proposed AC-NSGA-III Algorithm
4.1. NSGA-III
4.2. Operator Design
4.2.1. IRC Coding

4.2.2. Initial Population
4.2.3. Non-Dominant Hierarchical Ranking of Population
4.2.4. Reference Point Evaluation System
4.2.5. Binary Tournament Selection
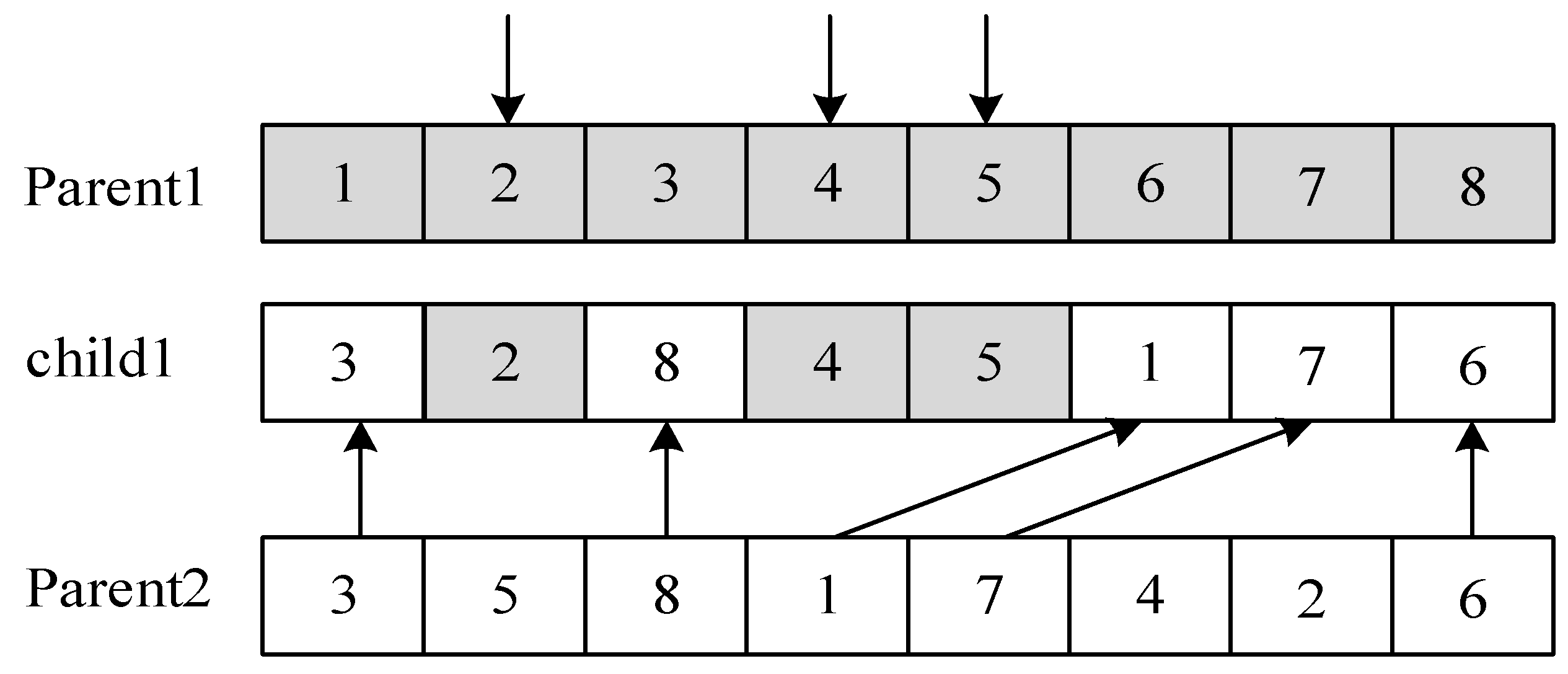
4.2.6. OBX&SBX Mixed Crossover
4.2.7. Mutation Operator
4.2.8. Elite Strategy
4.2.9. Termination Condition of the Algorithm
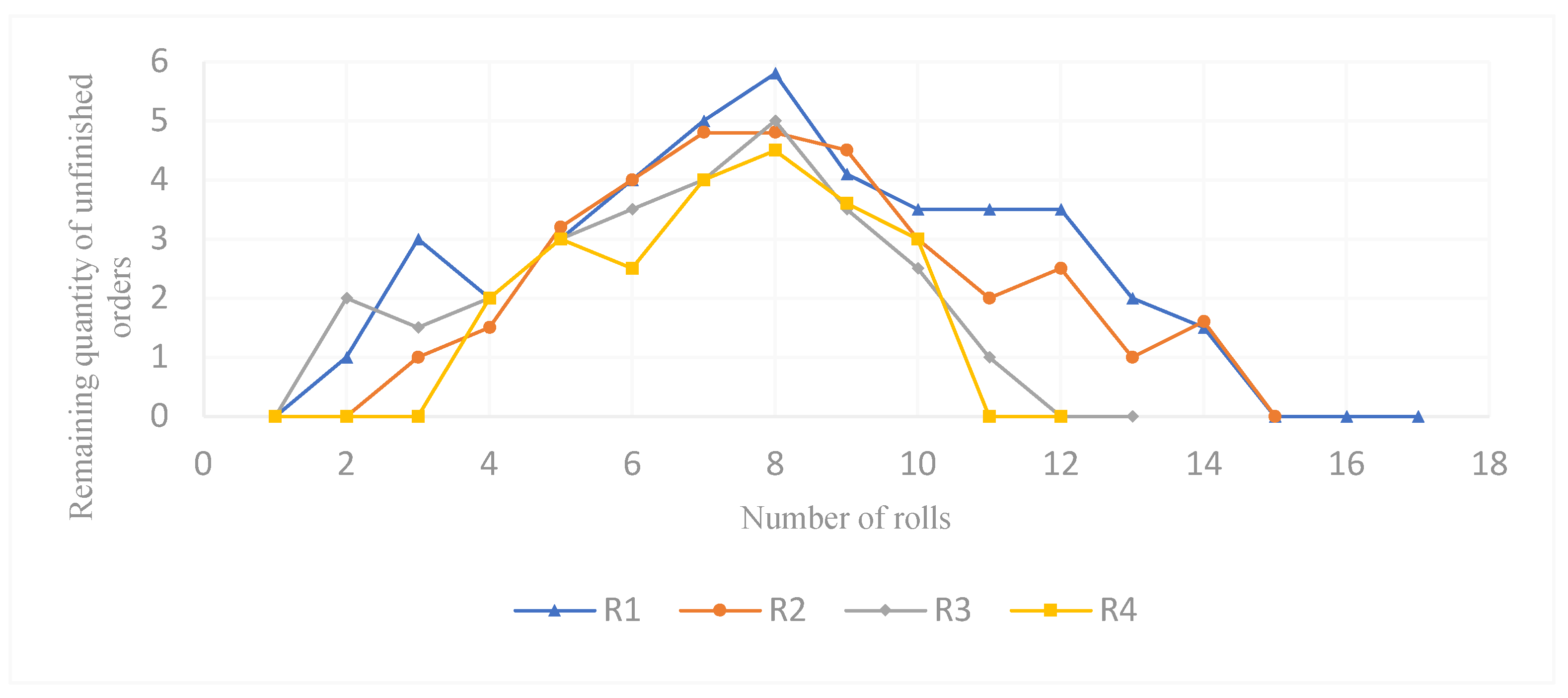
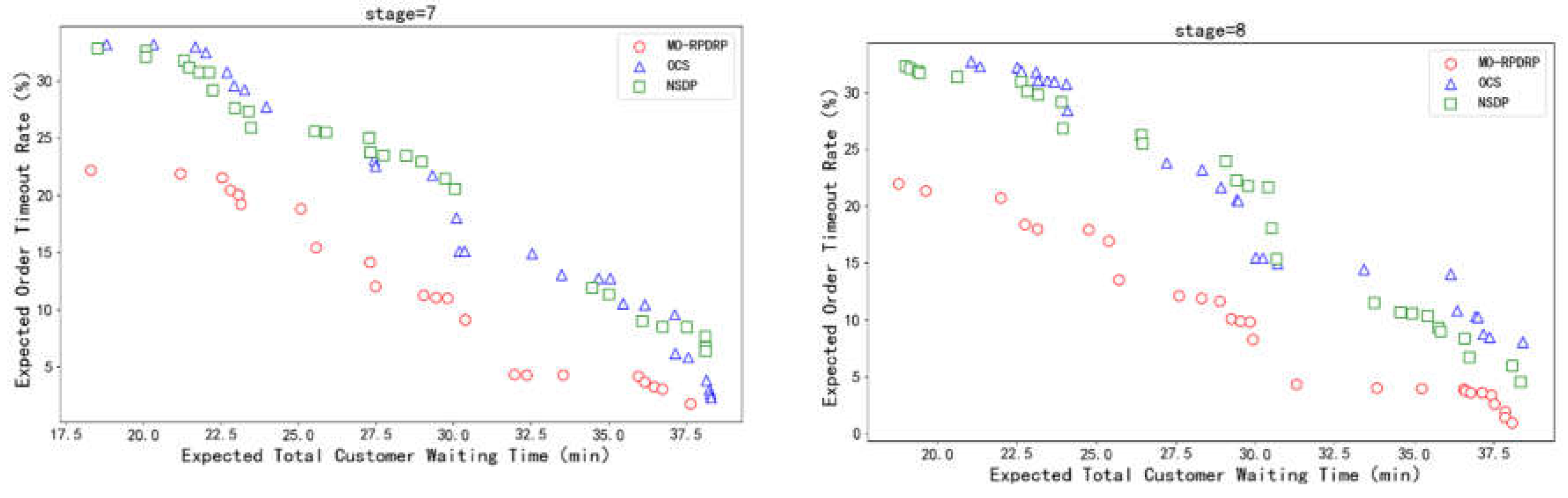
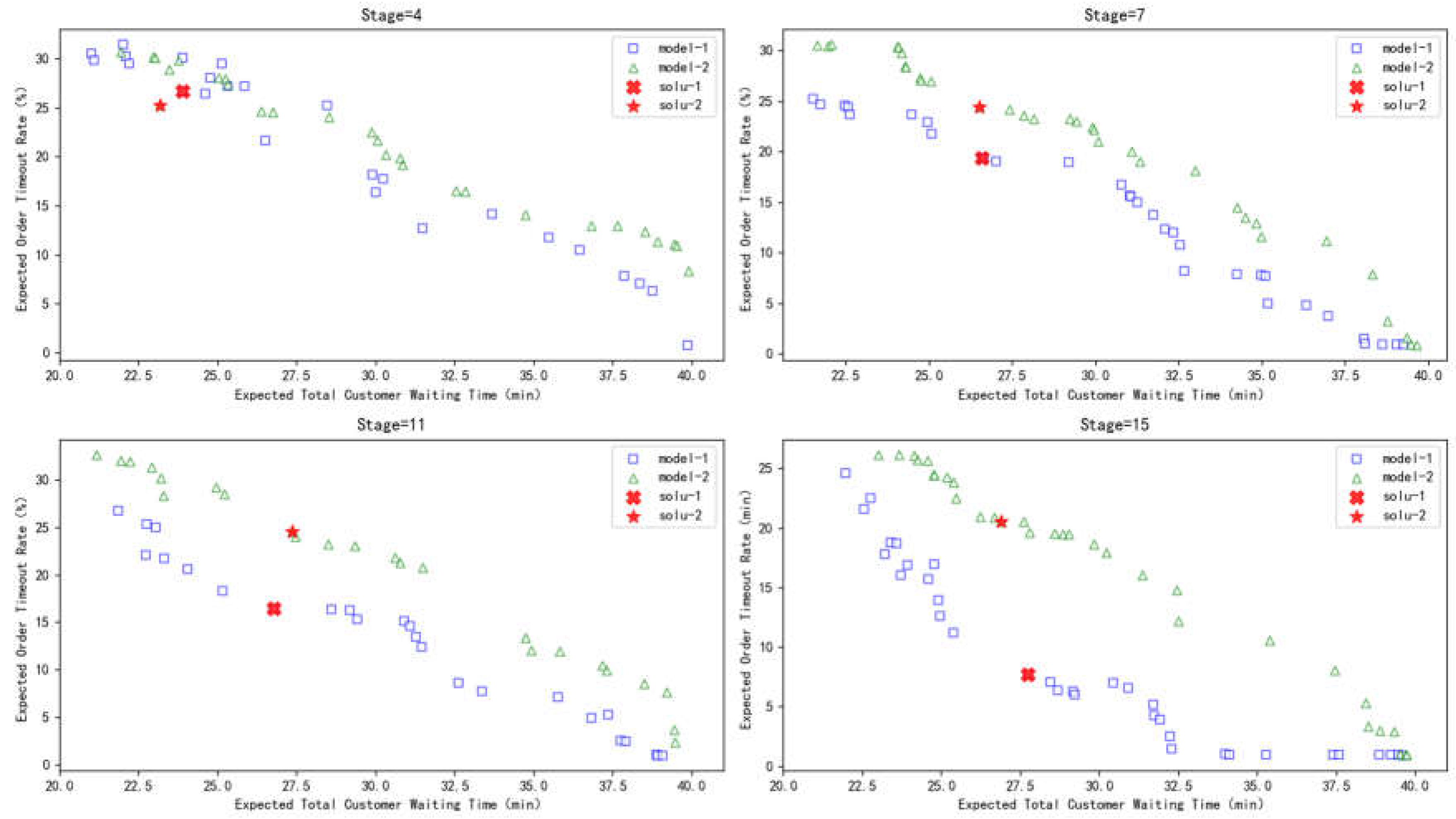
5. Experiments
5.1. Basic Data
4.2. Ex5.2. Experimental Design
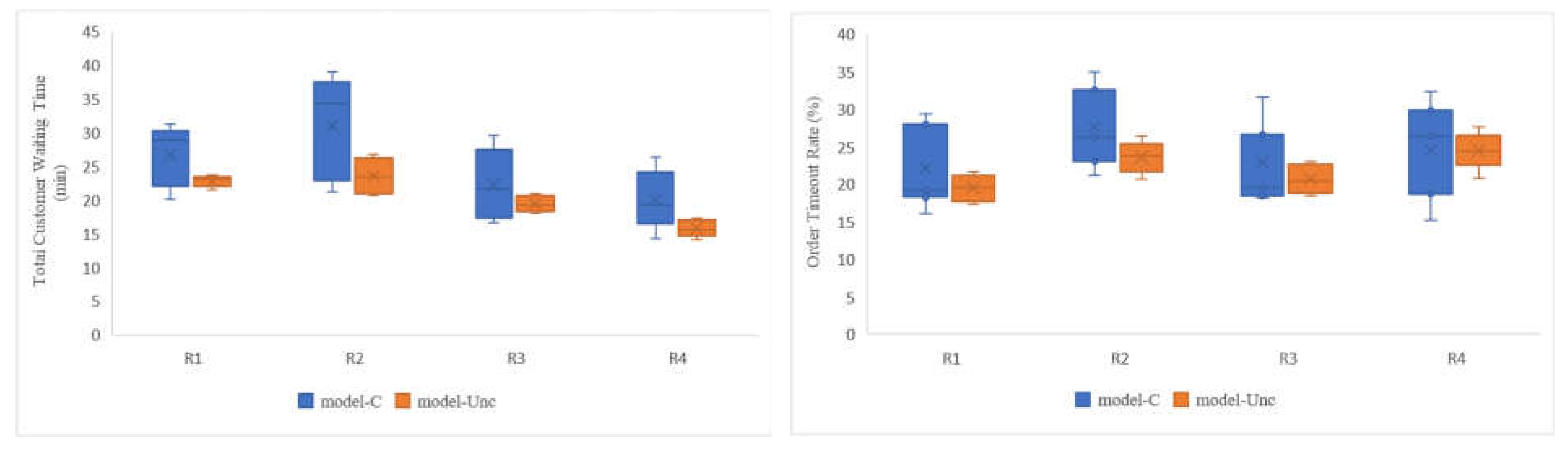
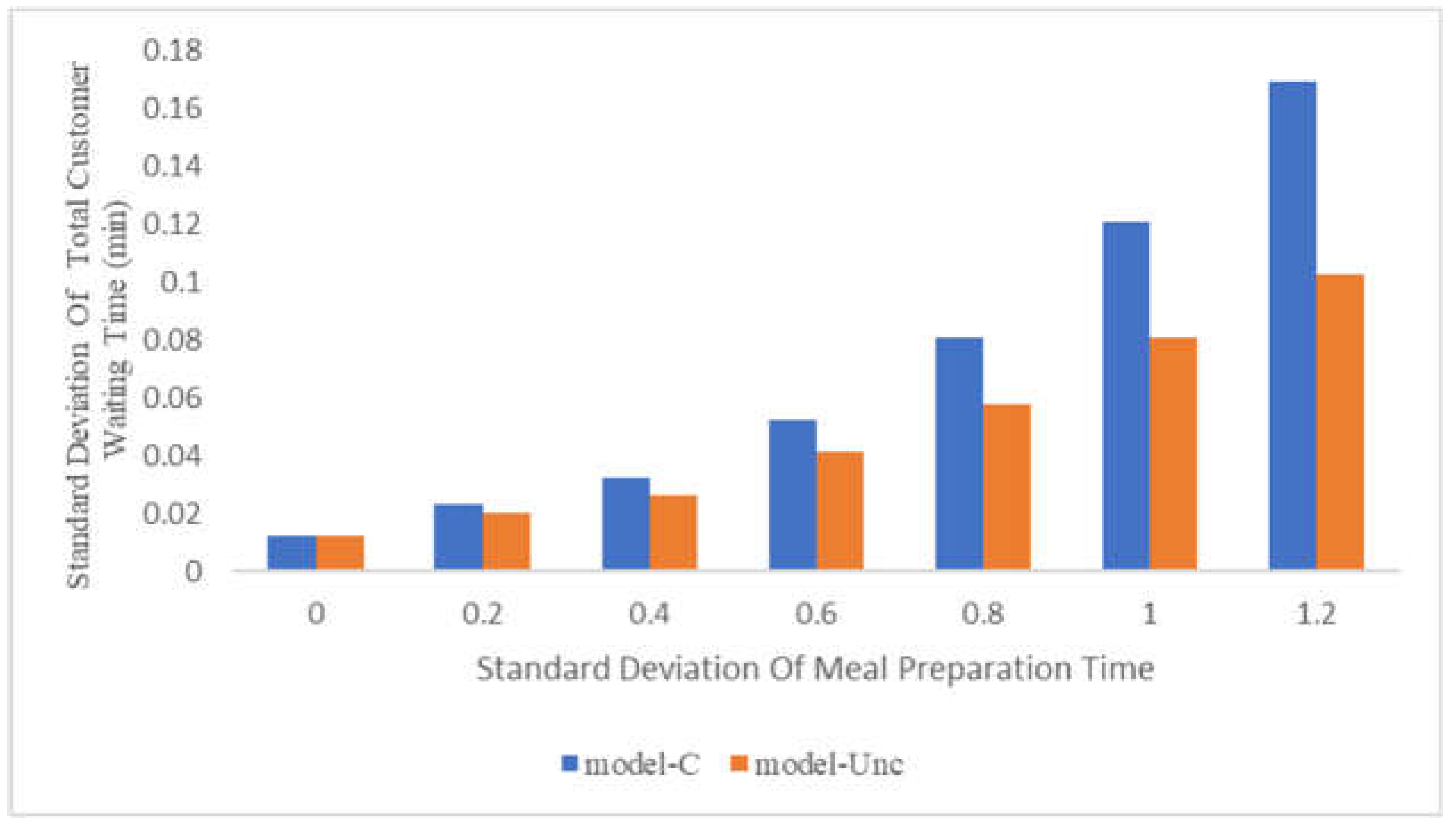
5.3. Comparison of Results
6. Conclusions
Appendix A
| The number of rolling schedules | Order time | Restaurant preparation time is subject to distribution expectations | Restaurant preparation time follows the standard deviation of the distribution | Restaurant node number | Customer node number | The latest delivery time |
| (1) | 11:00:22 | 2 | 0.5 | 1 | 14 | 11:30 |
| (2) | 11:19:58 | 3 | 0.2 | 2 | 15 | 11:45 |
| (3) | 11:23:19 | 2.4 | 1 | 3 | 16 | 11:53 |
| (4) | 11:25:24 | 2.8 | 0.8 | 3 | 17 | 11:55 |
| (5) | 11:31:25 | 2 | 0.6 | 4 | 18 | 12:00 |
| (6) | 11:47:14 | 3.4 | 2 | 5 | 19 | 12:00 |
| (7) | 11:51:54 | 5 | 1.6 | 6 | 20 | 12:20 |
| (8) | 11:56:42 | 5 | 1.5 | 6 | 21 | 12:25 |
| (9) | 11:59:32 | 5 | 0.8 | 6 | 22 | 12:30 |
| (10) | 12:05:49 | 2 | 1 | 7 | 23 | 12:35 |
| (11) | 12:11:36 | 4 | 0.4 | 8 | 24 | 12:40 |
| (12) | 12:20:20 | 2 | 0.6 | 9 | 24 | 12:55 |
| (13) | 12:27:14 | 5.4 | 1.7 | 10 | 25 | 12:55 |
| (14) | 12:30:28 | 3 | 1.3 | 11 | 26 | 13:10 |
| (15) | 12:31:54 | 6.2 | 1 | 12 | 27 | 13:15 |
| (16) | 12:39:42 | 6.2 | 1.2 | 12 | 28 | 13:20 |
| (17) | 12:58:49 | 2.3 | 0.9 | 13 | 29 | 13:30 |
| The number of rolling schedules | Order time | Restaurant preparation time is subject to distribution expectations | Restaurant preparation time follows the standard deviation of the distribution | Restaurant node number | Customer node number | The latest delivery time |
| (1) | 11:04:08 | 2 | 0.9 | 1 | 13 | 11:35 |
| (2) | 11:20:08 | 3 | 0.2 | 2 | 14 | 11:50 |
| (3) | 11:25:58 | 5 | 1.7 | 3 | 15 | 12:00 |
| (4) | 11:28:24 | 3.8 | 0.8 | 4 | 16 | 12:00 |
| (5) | 11:35:19 | 2 | 0.9 | 5 | 17 | 12:10 |
| (6) | 11:46:47 | 3 | 2 | 5 | 18 | 12:15 |
| (7) | 11:50:07 | 5 | 0.4 | 6 | 19 | 12:25 |
| (8) | 11:58:49 | 5.2 | 1.5 | 7 | 20 | 12:30 |
| (9) | 12:20:32 | 2.4 | 1 | 8 | 21 | 12:55 |
| (10) | 12:31:25 | 3 | 1.2 | 9 | 22 | 13:00 |
| (11) | 12:39:36 | 2 | 0.9 | 9 | 23 | 13:20 |
| (12) | 12:40:20 | 4 | 1.7 | 9 | 24 | 13:25 |
| (13) | 12:47:14 | 5.5 | 1 | 10 | 25 | 13:30 |
| (14) | 12:51:28 | 2 | 1 | 11 | 26 | 13:30 |
| (15) | 12:51:54 | 6 | 1 | 12 | 26 | 13:35 |
| The number of rolling schedules | Order time | Restaurant preparation time is subject to distribution expectations | Restaurant preparation time follows the standard deviation of the distribution | Restaurant node number | Customer node number | The latest delivery time |
| (1) | 11:10:42 | 6.2 | 1.2 | 1 | 13 | 11:45 |
| (2) | 11:20:49 | 2.3 | 0.9 | 2 | 13 | 11:50 |
| (3) | 11:25:08 | 2 | 1.7 | 3 | 14 | 11:55 |
| (4) | 11:28:13 | 4.4 | 1.6 | 4 | 15 | 12:00 |
| (5) | 11:31:25 | 4.6 | 0.4 | 5 | 16 | 12:00 |
| (6) | 11:40:59 | 2 | 0.9 | 6 | 17 | 12:15 |
| (7) | 11:55:24 | 3 | 1 | 7 | 18 | 12:30 |
| (8) | 12:10:19 | 2.1 | 0.4 | 8 | 19 | 12:40 |
| (9) | 12:26:17 | 3.7 | 0.2 | 8 | 20 | 12:55 |
| (10) | 12:29:24 | 3 | 2 | 9 | 21 | 13:00 |
| (11) | 12:32:06 | 4 | 1 | 10 | 21 | 13:00 |
| (12) | 12:45:04 | 5.5 | 2.4 | 11 | 22 | 13:25 |
| (13) | 12:50:43 | 5.5 | 1.9 | 12 | 23 | 13:30 |
| The number of rolling schedules | Order time | Restaurant preparation time is subject to distribution expectations | Restaurant preparation time follows the standard deviation of the distribution | Restaurant node number | Customer node number | The latest delivery time |
| (1) | 11:00:36 | 5 | 1.5 | 1 | 12 | 11:30 |
| (2) | 11:05:08 | 4.6 | 0.4 | 2 | 13 | 11:35 |
| (3) | 11:17:47 | 2.4 | 1 | 3 | 14 | 11:50 |
| (4) | 11:29:24 | 4 | 1 | 4 | 15 | 11:55 |
| (5) | 11:39:20 | 2 | 0.6 | 4 | 16 | 12:00 |
| (6) | 11:48:47 | 3.4 | 2 | 5 | 17 | 12:15 |
| (7) | 11:53:07 | 5.5 | 2.4 | 6 | 18 | 12:25 |
| (8) | 12:19:24 | 5 | 1.5 | 7 | 19 | 12:40 |
| (9) | 12:27:32 | 4.6 | 0.4 | 8 | 19 | 12:55 |
| (10) | 12:31:07 | 2 | 1 | 9 | 20 | 13:00 |
| (11) | 12:44:39 | 5 | 2.4 | 10 | 21 | 13:20 |
| (12) | 12:54:20 | 2 | 0.8 | 11 | 22 | 13:30 |
References
- https://bg.qianzhan.com/report/detail/300/211112-19960858.html.
- Giuffrida N, Fajardo-Calderin J, Masegosa A D, et al. Optimization and machine learning applied to last-mile logistics: A review[J]. Sustainability, 2022, 14(9): 5329. [CrossRef]
- Liu, L. , Qu, T., Thurer, M., Ma, L., Zhang, Z., & Yuan, M. (2022). A new knowledge-guided multi-objective optimisation for the multi-AGV dispatching problem in dynamic production environments. International Journal of Production Research.
- https://tech.meituan.com/2020/02/20/meituan-delivery-operations-research.html.
- Yan L, Guo B, Chao C, et al. FooDNet: Toward an Optimized Food Delivery Network based on Spatial Crowdsourcing[J]. IEEE Transactions on Mobile Computing, 2019, PP:1-1. [CrossRef]
- Xue G, Wang Z, Wang G. Optimization of Rider Scheduling for a Food Delivery Service in O2O Business[J]. Journal of Advanced Transportation, 2021, 2021(3):1-15. [CrossRef]
- Marlin W Ulmer,Barrett W Thomas,Ann Melissa Campbell,Nicholas Woyak. The Restaurant Meal Delivery Problem: Dynamic Pickup and Delivery with Deadlines and Random Ready Times[J]. Transportation Science,2021,55(1). [CrossRef]
- Xin, J.; Wei, L.; Wang, D.; Xuan, H. Receding horizon path planning of automated guided vehicles using a time-space network model. Optim. Control. Appl. Methods 2020, 41, 1889–1903. [Google Scholar] [CrossRef]
- Cheng W, Meng W. An efficient genetic algorithm for multi AGV scheduling problem about intelligent warehouse[J]. Robotic Intelligence and Automation, 2023, 43(4): 382-393. [CrossRef]
- Gao Y, Chen C H, Chang D. A Machine Learning-Based Approach for Multi-AGV Dispatching at Automated Container Terminals[J]. Journal of Marine Science and Engineering, 2023, 11(7): 1407. [CrossRef]
- Qiu L, Wang J, Chen W, et al. Heterogeneous AGV routing problem considering energy consump- tion[C].IEEE Int Conf on Robotics and Biomimet- ics, Zhuhai, China, 2015:1894-1899.
- Chen J, Wu Y, Huang S, et al. Multi-objective optimization for AGV energy efficient scheduling problem with customer satisfaction[J]. AIMS Mathematics, 2023, 8(9): 20097-20124. [CrossRef]
- Xin, J.; Wei, L.; D’Ariano, A.; Zhang, F.; Negenborn, R. Flexible time-space network formulation and hybrid metaheuristic for conflict-free and energy-efficient path planning of automated guided vehicles. J. Clean. Prod. 2023, 398, 136472. [Google Scholar] [CrossRef]
- W. Zou, Q. Pan, T. Meng, L. Gao, Y. Wang, An effective discrete artificial bee colony algorithm for multi-AGVs dispatching problem in a matrix manufacturing workshop, Expert Syst. Appl., 161 (2020), 113675. [CrossRef]
- G. Li, B. Zeng, W. Liao, X. Li, L. Gao, A new AGV scheduling algorithm based on harmony search for material transfer in a real-world manufacturing system, Adv. Mech. Eng., 10 (2018),1–13. [CrossRef]
- Wang Y J, Liu X Q, Leng J Y, et al. Study on scheduling and path planning problems of multi-AGVs based on a heuristic algorithm in intelligent manufacturing workshop[J]. Advances in Production Engineering & Management, 2022, 17(4): 505-513 . [CrossRef]
- Liu L, Qu T, Thürer M, et al. A new knowledge-guided multi-objective optimisation for the multi-AGV dispatching problem in dynamic production environments[J]. International Journal of Production Research, 2023, 61(17): 6030-6051. [CrossRef]
- Reyes D, Erera A, Savelsbergh M, et al. The Meal Delivery Routing Problem. 2018.
- Baris Yildiz,Martin Savelsbergh. Provably High-Quality Solutions for the Meal Delivery Routing Problem[J]. Transportation Science,2019,53(5). [CrossRef]
- Du J, Guo B, Liu Y, et al. CrowDNet: Enabling a Crowdsourced Object Delivery Network Based on Modern Portfolio Theory[J]. Internet of Things Journal, IEEE, 2019, 6(5):9030-9041. [CrossRef]
- Zachary Steever,Mark Karwan,Chase Murray. Dynamic courier routing for a food delivery service[J]. Computers and Operations Research,2019,107{5}. [CrossRef]
- Guofeng Sun,Zhiqiang Tian,Renhua Liu,Yun Jing,Yawen Ma,Purushothaman Damodaran. Research on Coordination and Optimization of Order Allocation and Delivery Route Planning in Take-Out System[J]. Mathematical Problems in Engineering,2020,2020{5}. [CrossRef]
- Tu W, Zhao T, Zhou B, et al. OCD: Online Crowdsourced Delivery for On-Demand Food[J]. IEEE Internet of Things Journal, 2019, PP(99). [CrossRef]
- Zheng J, Wang S, Wang L, et al. A two-stage algorithm for fuzzy online order dispatching problem[C]//2020 IEEE Congress on Evolutionary Computation (CEC). IEEE, 2020: 1-8. [CrossRef]
- Liao W, Zhang L, Wei Z. Multi-objective green meal delivery routing problem based on a two-stage solution strategy[J]. Journal of Cleaner Production, 2020, 258:120627-. [CrossRef]
- Yu H, Luo X, Wu T. Online pickup and delivery problem with constrained capacity to minimize latency[J]. Journal of Combinatorial Optimization, 2020: 1-20. [CrossRef]
- Zheng, Jie, et al. "Modeling stochastic service time for complex on-demand food delivery." Complex & Intelligent Systems (2022): 1-15.
- Jiang S, Li X, Zheng Q, et al. Approximate equal frequency discretization method[C]//2009 WRI global congress on intelligent systems. IEEE, 2009, 3: 514-518. [CrossRef]
- Department of Mathematics, Tongji University Advanced Mathematics [M] Beijing: Higher Education Press, 2014.
- Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2013, 18(4): 577-601. [CrossRef]
- Das, Indraneel; Dennis, J. E. (1998). Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM Journal on Optimization, 8(3), 631–657. [CrossRef]
- Sato M, Oyama A. Comparative Study of Crossovers for Decision Space Diversity of Non-Dominated Solutions[C]//2021 IEEE Symposium Series on Computational Intelligence (SSCI). IEEE, 2021: 01-08.
- Park H, Son D, Koo B, et al. Waiting strategy for the vehicle routing problem with simultaneous pickup and delivery using genetic algorithm[J]. Expert Systems with Applications, 2021, 165: 113959. [CrossRef]
- SUN Y N,YEN G G, YI Z, et al, IGD Indicator-Based Evolutionary Algorithm for Many-Objective Optimization Problems. IEEE Transactions on Evolutionary Computation[J], 2019,23 ( 2) : 173-187. [CrossRef]
- Steever Z, Karwan M, Murray C. Dynamic courier routing for a food delivery service[J]. Computers & Operations Research, 2019, 107: 173-188. [CrossRef]
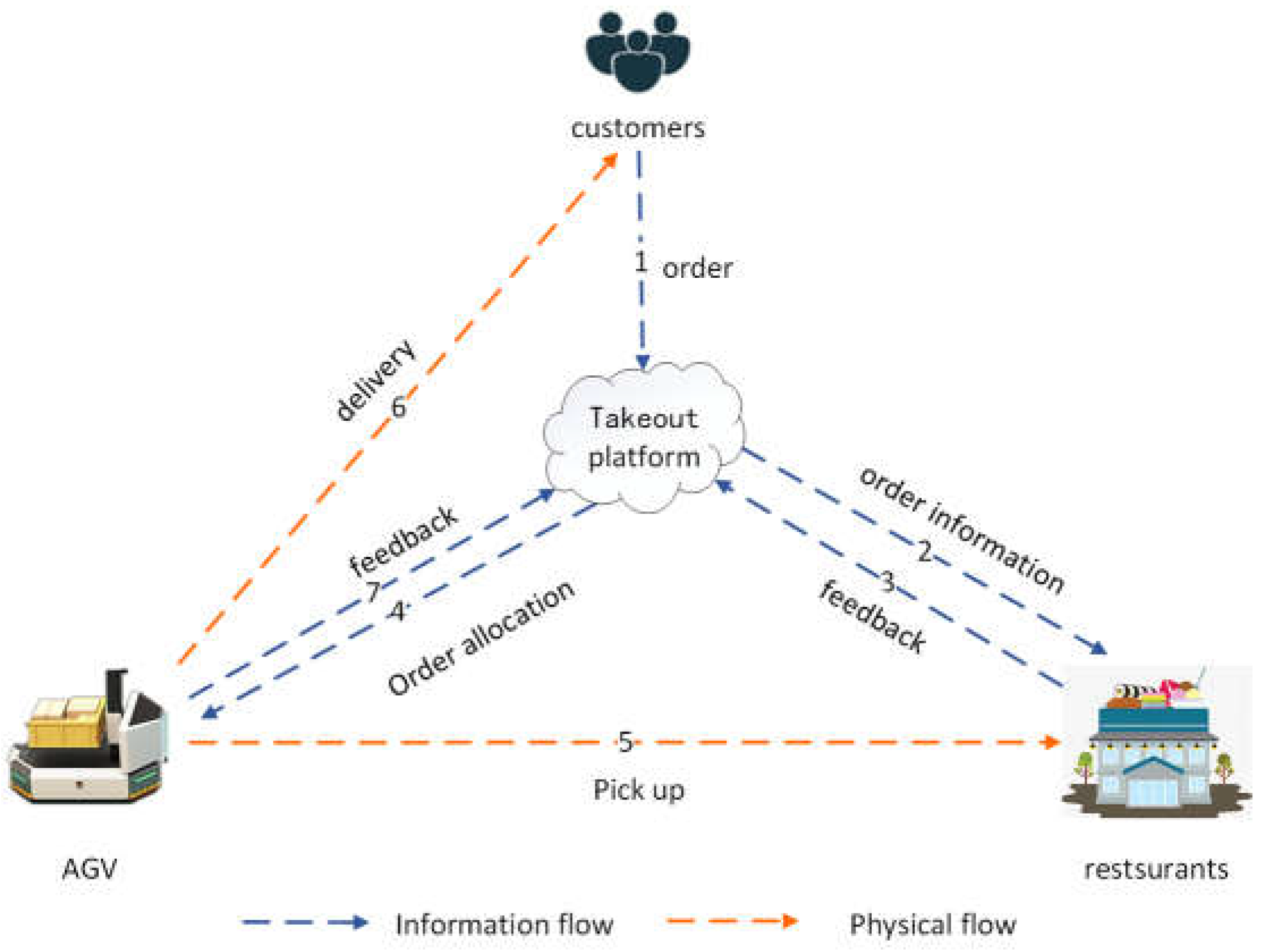
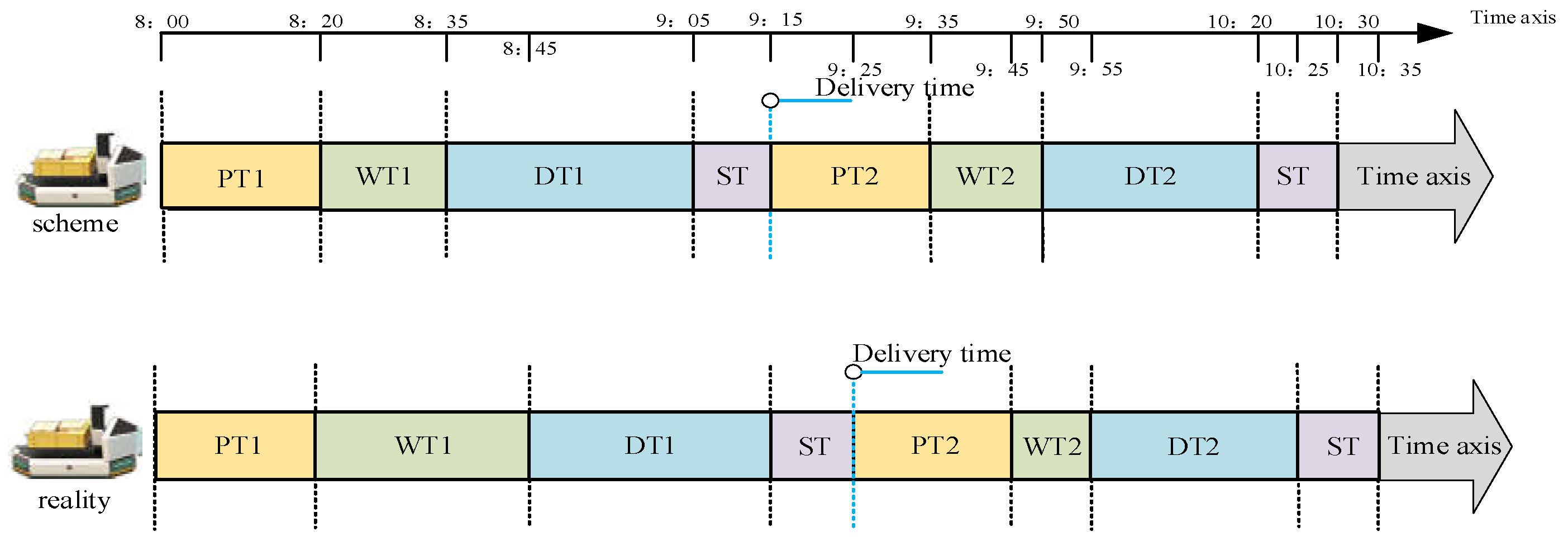
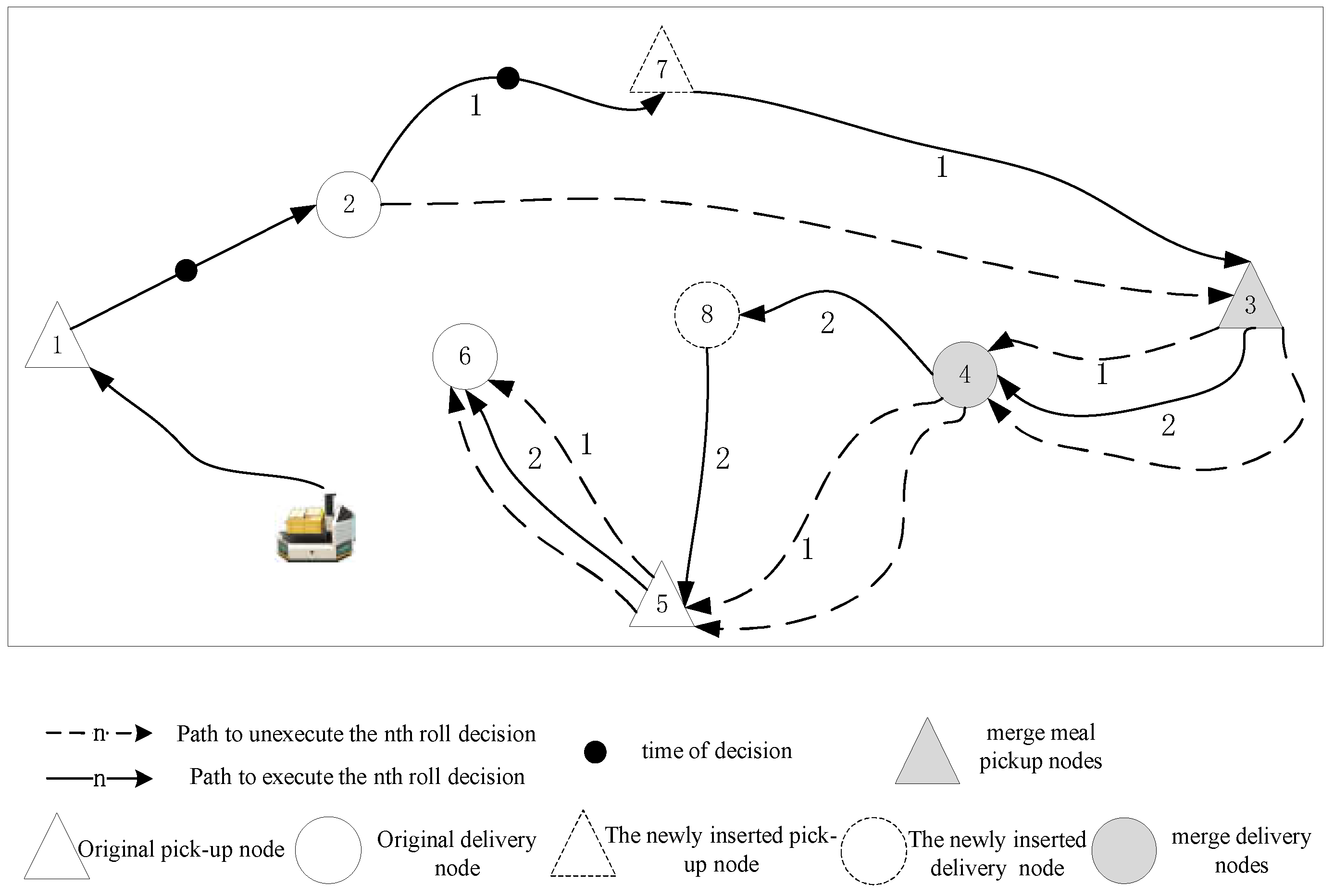
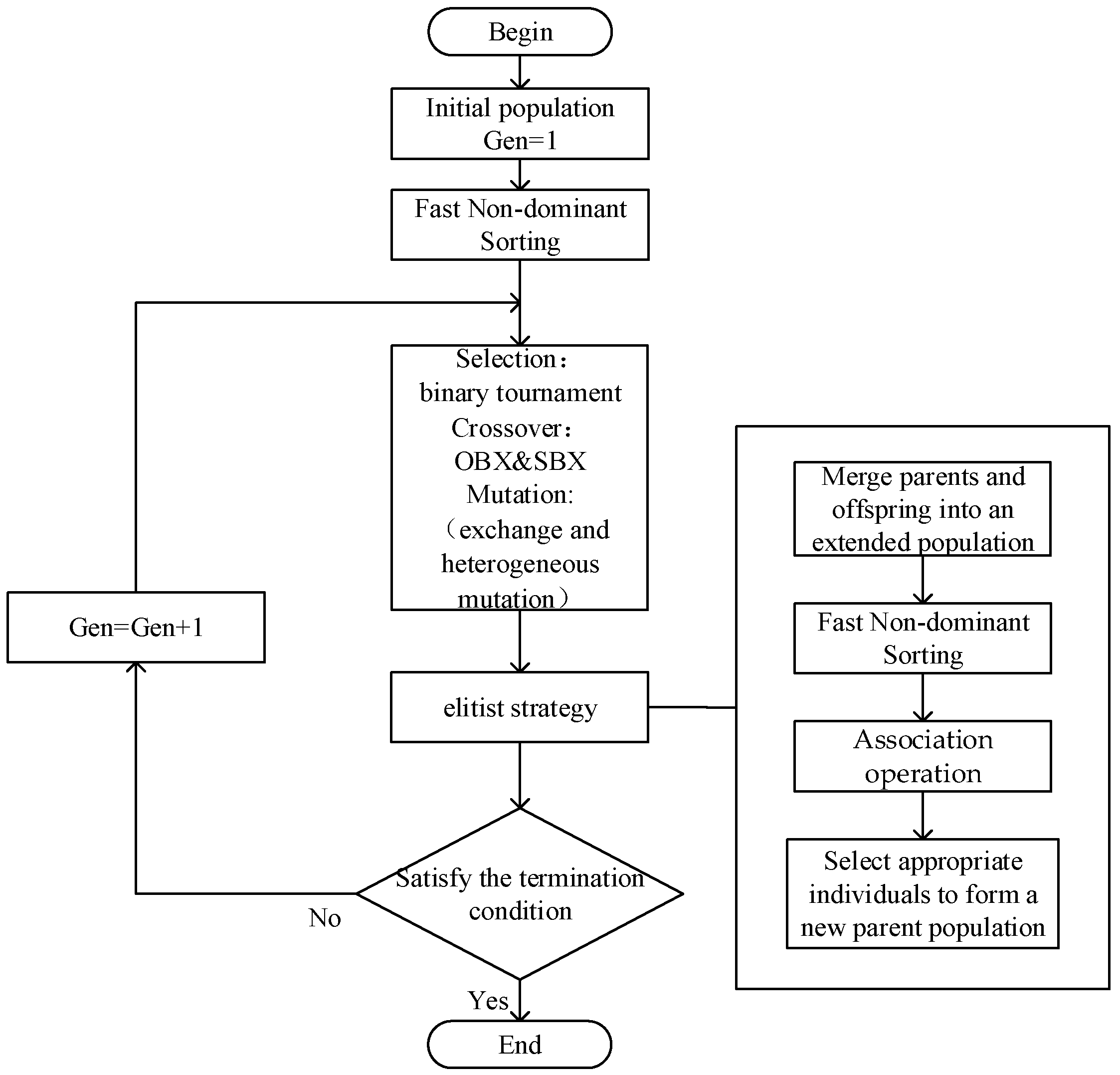
| Sets | description |
| the current set of orders that have been picked up but not delivered | |
| the current order set that has not been picked up | |
| set of orders involved in the current rolling period,, | |
| set of restaurant nodes, | |
| set of virtual restaurant nodes, | |
| set of customer nodes, | |
| set of virtual customer nodes, | |
| set of all nodes, | |
| set of restaurant nodes expansion, | |
| set of customer nodes expansion, | |
| set of all nodes expansion, | |
| virtual (actual) restaurant node i mapping of the actual restaurant node, | |
| virtual (actual) customer node j mapping of the actual customer node, | |
| the restaurant node number corresponding to the order ,if the restaurant node number corresponding to the order is ,then there is ,and there is an inverse mapping , , | |
| the customer node number corresponding to the order ,if the customer node number corresponding to the order is ,then there is ,and there is an inverse mapping , , | |
| parameters | |
| maximum capacity of delivery vehicle | |
| travel time from node to node , , | |
| number of the initial node | |
| the ready time of the AGV | |
| order time for order , | |
| the latest delivery time for order , | |
| the volume occupied by commodities for order , | |
| meal preparation time for order ,it follows the Gaussian distribution, , | |
| customer service time for order , | |
| Decision variable | |
| if the deliverer travels from node to node , the decision variable is equal to 1, otherwise, is equal to 0, | |
| Other variable | |
| the number of the th node to be visited, if the sequence of the node in the path is , ,and there is an inverse mapping , , | |
| if the th node and the next node merge to pick-up food, is equal to 1,otherwise , is equal to 0, | |
| if the th node and the next node merge to deliver food, is equal to 1,otherwise, is equal to 0, | |
| time to arrive , | |
| take-out volume carried on arrival at , | |
| the number of unfinished orders before visit , | |
| the completion time of order , | |
| the timeout rate of the order | |
| parameters | value |
| 68.45 | |
| 11:00 | |
| 5min | |
| 10 | |
| 0.8 | |
| 0.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




