Submitted:
25 August 2025
Posted:
19 September 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
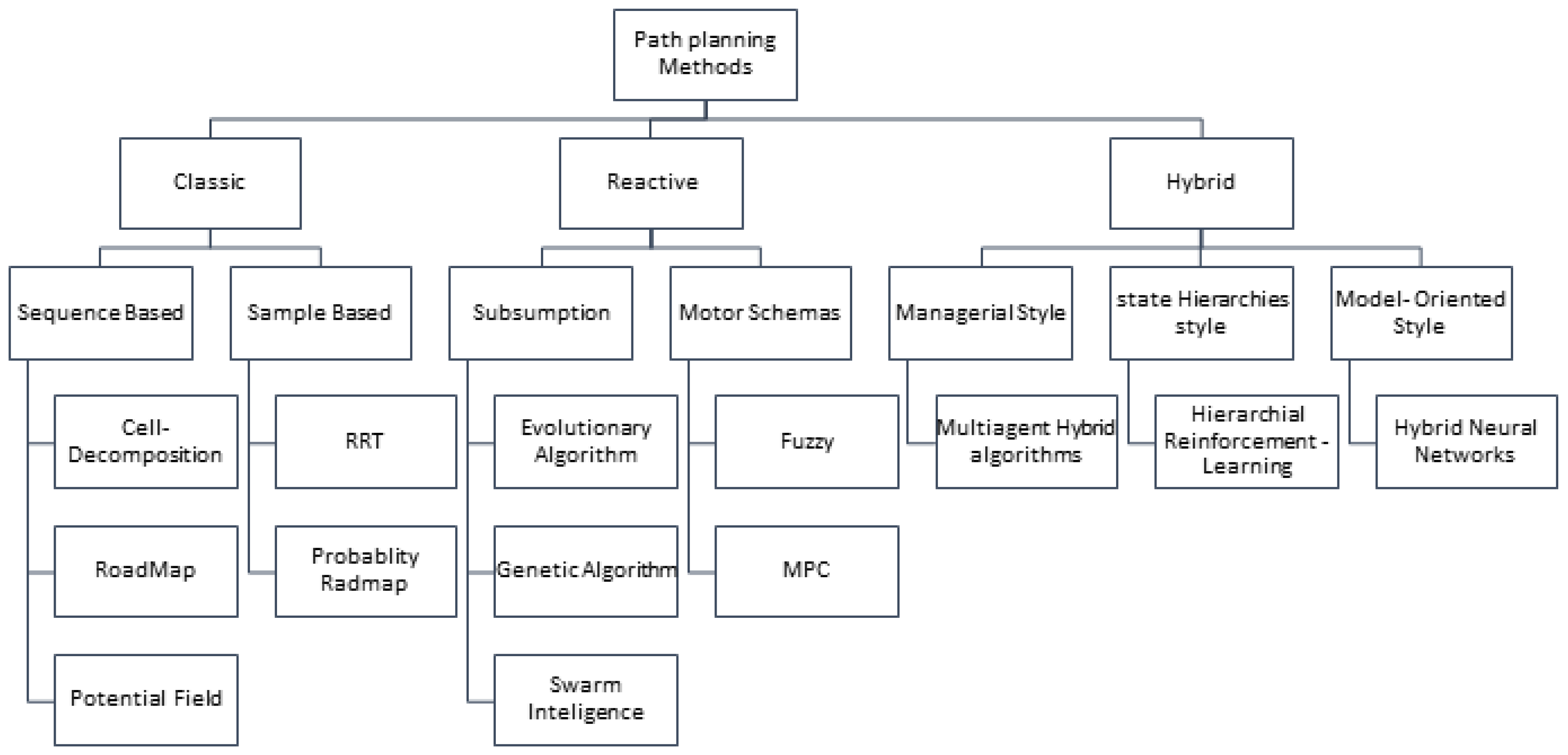
2. Navigation Methods
2.1. Classical Path Planning Methods
-
Roadmap Methods: These methods create a graph representation of the environment, connecting obstacles and the target point. Examples include:
-
Cell Decomposition: This approach divides the workspace into smaller cells, enabling the robot to navigate through collision-free regions. Notable examples include:
- –
- Lozano-Perez’s C-Space Decomposition (1983): Treats the robot as a C-shaped object and subdivides the environment into cells to identify feasible paths [10].
- –
- Grid-Based Methods: Popularized by Hachour (2008), this technique discretizes the environment into a grid, simplifying path planning through cell-by-cell exploration [11].
- Potential Field Method: Models the robot as a particle influenced by artificial potential fields. Attractive potentials guide the robot toward the goal, while repulsive potentials push it away from obstacles. This method ensures smooth navigation but can suffer from local minima issues [12].
- Mathematical Programming: Formulates path planning as an optimization problem, treating obstacle avoidance as a set of inequalities. The goal is to minimize a scalar quantity (e.g., path length or energy consumption) while finding a feasible curve between the start and target points [8].
2.2. Reactive Path Planning Methods
- Subsumption Architecture: Organizes robot behaviors into hierarchical layers, with higher-level actions overriding lower-level ones. This structure enables quick responses to environmental changes but may lack global optimization [13].
- Motor Schemas: Generates output vectors for distinct behaviors (e.g., obstacle avoidance, goal seeking), which are combined through vector summation to determine the robot’s overall response. This approach allows for flexible and adaptive navigation [14].
2.3. Hybrid Path Planning Methods
- Managerial Approaches: Use a high-level planner to generate global paths while employing reactive strategies for local obstacle avoidance [17].
- State Hierarchies: Organize navigation tasks into hierarchical states, enabling seamless transitions between global and local planning [18].
- Model-Oriented Styles: Incorporate environmental models to enhance decision-making, balancing long-term planning with real-time adjustments [19].
3. Optimization Criteria in Geometric Trajectory Planning
3.1. Key Optimization Criteria
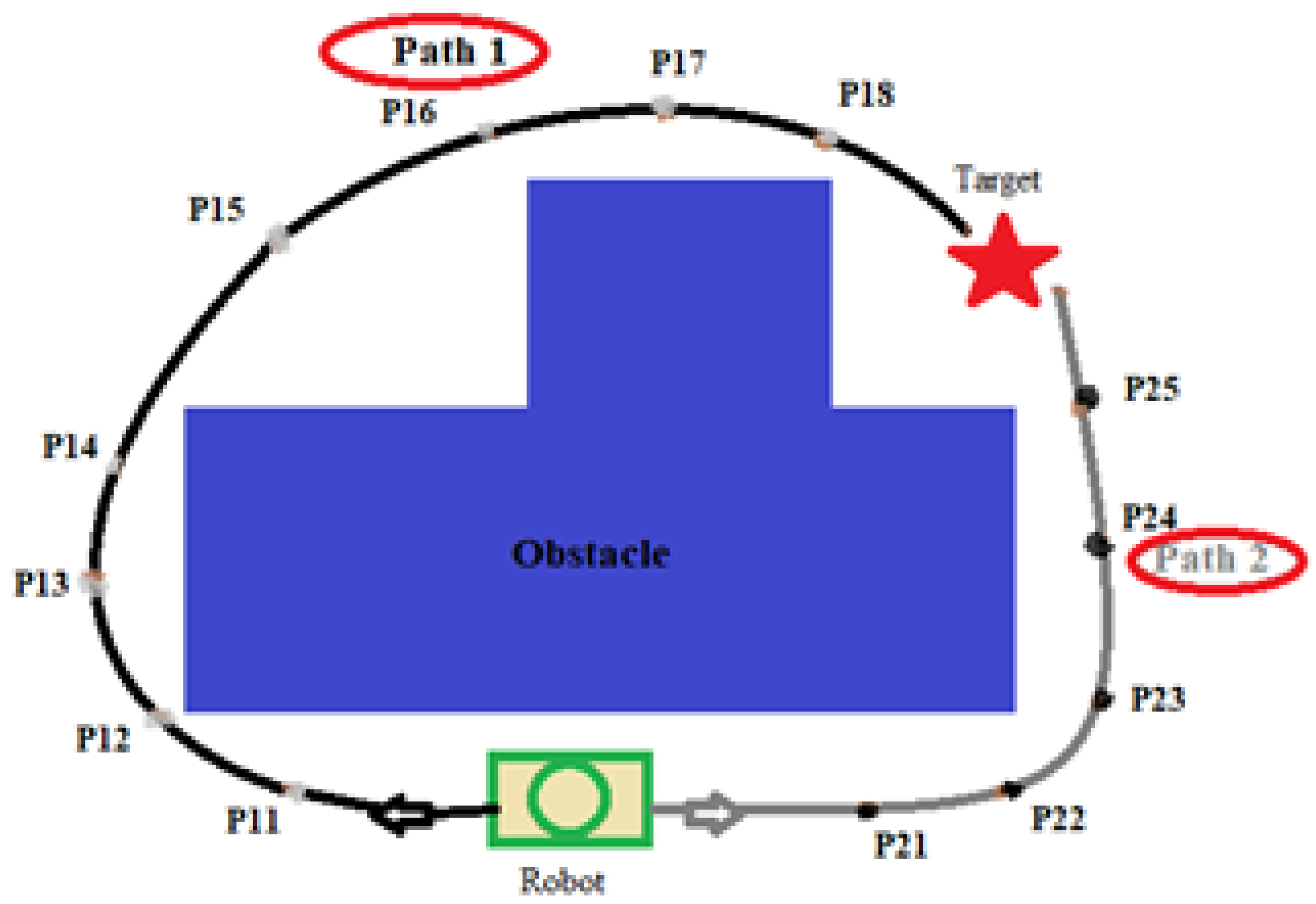
- Trajectory Length: Minimizing the path length is often the primary objective, as it directly impacts the robot’s efficiency and resource utilization. Shorter trajectories reduce travel time and energy consumption, making them ideal for many applications [8].
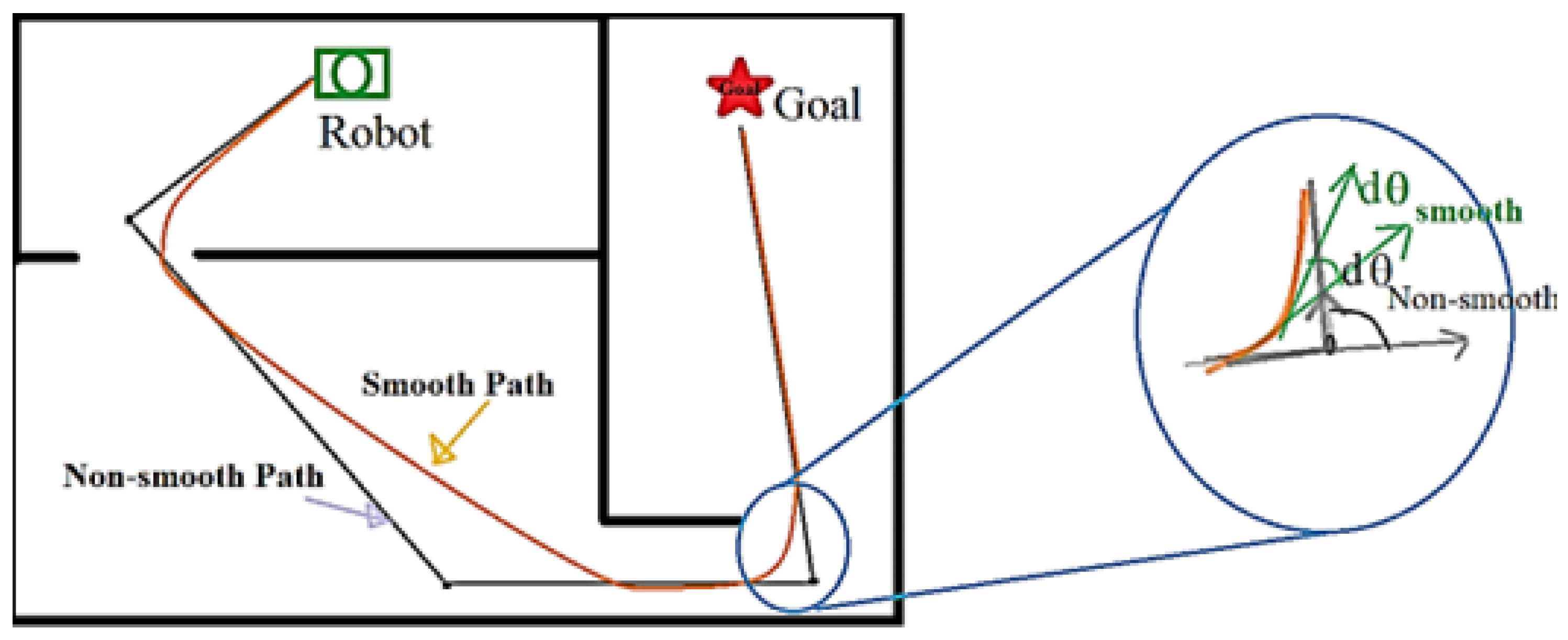
- Trajectory Smoothness: Smooth trajectories are crucial for ensuring stable and efficient robot motion. Abrupt changes in direction or velocity can lead to mechanical stress, increased energy consumption, and reduced accuracy. Smoothness is often quantified using curvature and jerk metrics [20].
- Time Efficiency: Time-optimal trajectories are critical in applications where speed is a priority, such as in industrial automation or search-and-rescue operations. Time efficiency is closely tied to the robot’s velocity profile and acceleration limits [21].
- Energy Consumption: Energy-efficient trajectories are vital for battery-powered robots or systems operating in energy-constrained environments. Optimizing energy usage involves minimizing unnecessary acceleration, deceleration, and idling [22].
- Collision Avoidance: Ensuring collision-free trajectories is a fundamental requirement in any navigation task. This involves not only avoiding static obstacles but also dynamically adapting to moving obstacles in real-time [12].
- Environmental Factors: External conditions such as wind resistance, terrain roughness, or fluid dynamics (in underwater or aerial robots) can significantly impact trajectory planning. These factors must be modeled and accounted for to ensure robust performance [23].
3.2. Path Length as an Optimization Criterion
3.3. Path Smoothness in Robotic Navigation
- Curvature Continuity: Ensuring that the curvature of the path is continuous, which is critical for high-speed navigation and dynamic environments [35].
- Jerk Minimization: Minimizing the rate of change of acceleration (jerk) to ensure smoother motion and reduce wear on the robot’s actuators [36].
- Energy-Efficient Smoothing: Optimizing paths to minimize energy consumption, which is particularly important for battery-operated robots [37].
- Adaptive Smoothing: Dynamically adjusting the smoothness of the path based on environmental changes and obstacle movements [38].
3.4. Time Cost in Robotic Navigation
- is the state space of the robot dynamics,
- x is the state vector, consisting of position, velocity, and possibly acceleration,
- u is the control input that may depend on voltage, torque, or other functions of control manipulators,
- T is the total execution time.
- is the robot motion acceleration, which is a function of the control input at the k-th time sample,
- N is the final time step when the robot reaches the goal,
- is the k-th collision-free waypoint.
- is the velocity of the robot,
- is the control input,
- is a weighting factor that balances the trade-off between velocity and control effort.
- is a penalty function that increases the cost when the robot approaches obstacles or violates environmental constraints,
- is a weighting factor for the control effort.
- M is the number of robots,
- is a penalty function that ensures collision avoidance between robots j and k.
- Reward Function: Designed to penalize time consumption and deviations from the desired trajectory.
- State-Action Space: Encodes the robot’s dynamics and environmental constraints.
- Training Efficiency: Measured by the convergence rate and computational resources required.
- Horizon Length: Determines the number of future steps considered in the optimization.
- Constraint Handling: Ensures feasibility of the trajectory under dynamic and environmental constraints.
- Computational Complexity: Measured by the time required to solve the optimization problem at each time step.
- Pareto Front: Represents the trade-off between competing objectives.
- Weighting Factors: Used to prioritize time-optimality over other objectives.
- Scalability: Evaluated based on the ability to handle high-dimensional state spaces.
- Replanning Frequency: Determines how often the trajectory is updated.
- Convergence Speed: Measures the time required to adapt to new environmental conditions.
- Robustness: Evaluated based on the ability to handle uncertainties and disturbances.
- Autonomous vehicles,
- Industrial robotics,
- Aerial drones.
3.5. Energy Cost in Robotic Navigation
- Kinetic Energy (Ek): Energy associated with the robot’s motion.
- Traction Resistance Energy (Ef): Energy dissipated in overcoming traction resistances.
- Motor Heating Energy (Ee): Energy lost as heat in the motors.
- Mechanical Friction Energy (Em): Energy dissipated in overcoming friction torque.
- Idle Energy (Eidle): Energy consumed by idling motors and onboard electric devices.
- is the total power consumption and loss at time t,
- T is the total execution time.
- is the power consumed during motion,
- is the power consumed during idle states.
- is the efficiency of the regenerative braking system,
- is the power generated during braking.
3.6. Risk Cost in Robotic Navigation
- Collision Risk: Probability of collisions with environmental elements or individuals.
- Robot Malfunction: Probability of robot failure or abrupt movements.
- Environmental Hazards: Probability of natural events such as rain or wind increasing the risk of slipping or crashing.
- is the probability of a risk event at time t,
- is the cost associated with the event.
- is the neural network function,
- represents the network parameters.
- is the membership function for the i-th risk factor,
- is the cost associated with the i-th risk factor.
3.7. Integration of Optimization Criteria
4. Approaches to Solving Optimal Navigation Problems
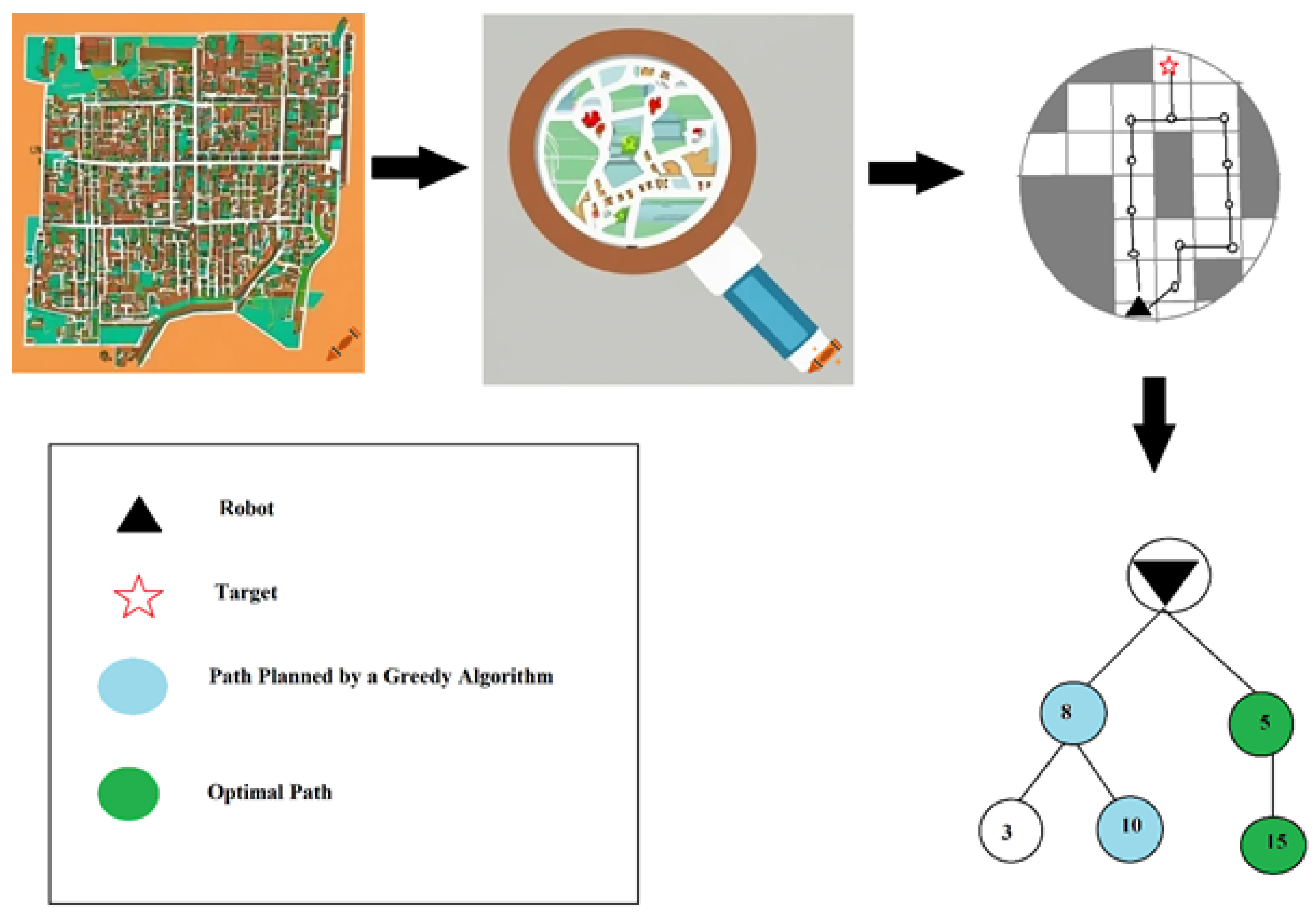
4.1. Greedy Algorithms
4.2. Dynamic Programming (DP)
4.3. Evolutionary Algorithms (EAs)
| Approach/Algorithm | Application Area | Main Advantages/Findings | Citation |
|---|---|---|---|
| Twin-Reinforced Chimp Optimization + Evolutionary Programming | Robot path planning | Outperforms other meta-heuristics in path length, consistency, time complexity, and success rate | (Zhang & Zhang, 2024) |
| Improved PSO with Evolutionary Operators (IPSO-EOPs) | Multi-robot navigation | Superior to DE and standard PSO in arrival time, safety, and energy use | (Das & Jena, 2020) |
| Many-Objective EAs (HypE, GrEA, KnEA, NSGA-III) | Agricultural robot route planning | HypE delivers best performance for minimizing navigation cost and turning angle | (Zhang et al., 2022) |
| Decomposition-based Multi-Objective EA (M2M-DW) | UAV path planning | Effectively handles constraints and infeasible solutions, reliable in complex scenarios | (Peng & Qiu, 2022; Jiang et al., 2024) |
| Multi-Objective Evolutionary PSO (MOEPSO) | Mobile robot path planning | Finds shortest, smoothest, and safest paths in static and dynamic environments | (Thammachantuek & Ketcham, 2022) |
| Bi-level Co-evolutionary Genetic Algorithm (IGA-CPP) | Coverage path planning | Efficient for irregular regions, fast convergence, optimized path length | (Chen et al., 2025) |
| NSGA-II and Multi-Objective EAs | Mobile robot navigation | NSGA-II excels in balancing path time and smoothness across diverse environments | (Jiménez-Domínguez et al., 2024) |
| Distributed Multi-Population EA | Maritime navigation | Multi-population approach improves solution quality over single-population EAs | (Smierzchalski et al., 2013) |
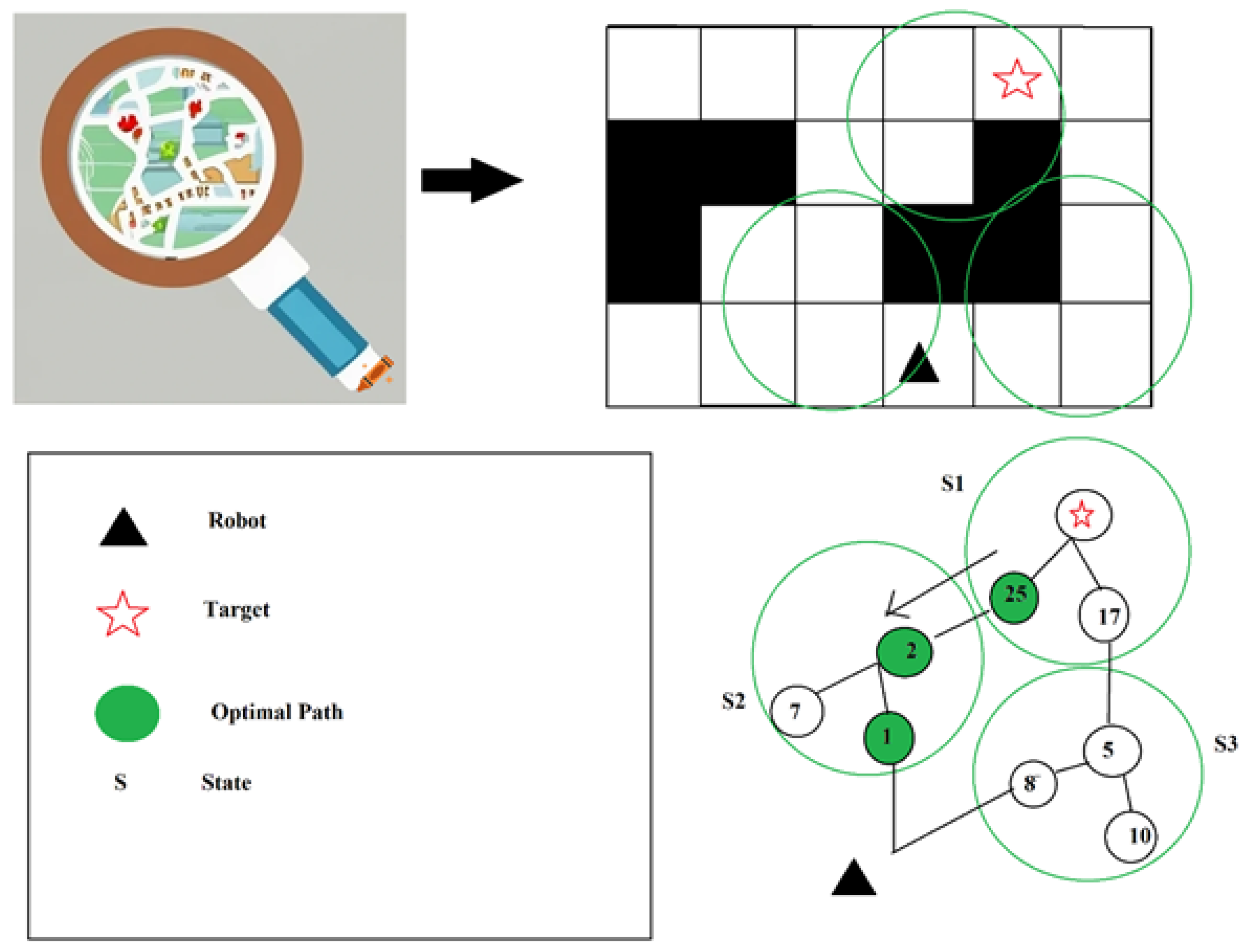
4.4. Sampling-Based Algorithms
| Method | Formula | Parameter Definitions |
|---|---|---|
| Adaptive RRT* | ||
|
: new node : nearest node : random sample : adaptive step size : smoothing factor : environment feature function |
||
| Deep Sampling-Based |
: learned sampling distribution : sampled state |
|
| Reward-Adaptive Sampling |
: distance metric : adaptive exponent : reward factor |
|
| NAMR-RRT | Neural network predicts guiding regions and risk-aware expansion | |
| Uses neural heuristics for sampling bias Incorporates dynamic obstacle risk metrics |
||
4.5. Recent Advances in Optimal Navigation
- Deep Reinforcement Learning (DRL): DRL-based approaches have been employed to learn optimal navigation policies in complex environments [66].
- Model Predictive Control (MPC): MPC frameworks have been extended to incorporate dynamic constraints, enabling real-time navigation optimization [67].
- Multi-Objective Optimization: Recent studies have combined navigation objectives, such as time-optimality and energy efficiency, using Pareto optimization techniques [68].
- Adaptive Navigation: Adaptive methods dynamically adjust navigation strategies based on environmental changes, ensuring robustness in dynamic settings [69].
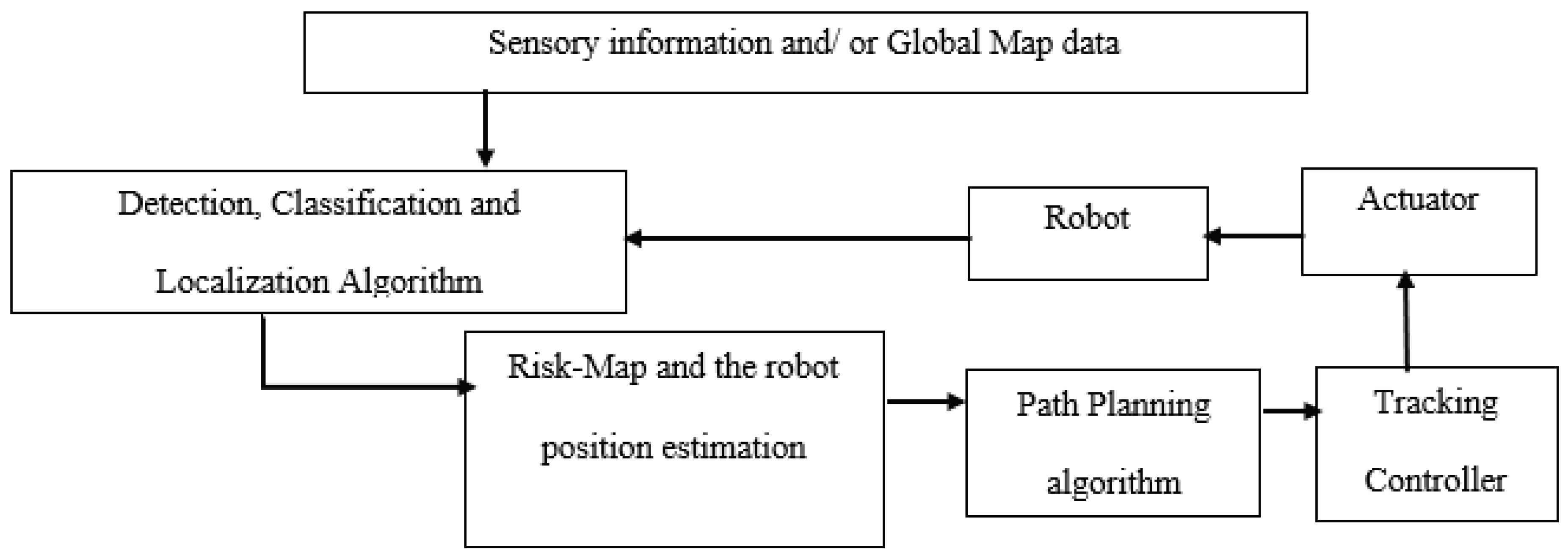
5. Overview of Collision-Free Path Planning Strategy
5.1. Hybrid Path Planning
- is the hybrid path,
- is the globally optimal path,
- is the locally adjusted path,
- is a weighting factor that balances global and local planning.
5.2. Real-Time Adaptation
- is the robot’s state at time t,
- is the reference trajectory,
- is the control input,
- T is the prediction horizon.
5.3. Recent Advancements in Collision-Free Path Planning
- Deep Reinforcement Learning (DRL): DRL-based approaches have been employed to learn collision-free navigation policies in complex environments [73].
- Multi-Agent Path Planning: Techniques for coordinating multiple robots to avoid collisions while achieving individual goals [74].
- Uncertainty-Aware Planning: Methods that account for uncertainties in sensor data and environmental dynamics [75].
- Energy-Efficient Path Planning: Energy-efficient path planning combines optimization of energy consumption with collision avoidance, employing various algorithmic strategies tailored to different robotic systems and environments. These approaches address challenges like terrain roughness, multi-agent coordination, and dynamic obstacles while minimizing motion costs [76].
6. Challenges in Geometric Optimal Navigation
6.1. Scalability in High-Dimensional Spaces
6.1.1. Dimensionality Reduction Techniques
- is the high-dimensional data matrix,
- is the transformation matrix,
- is the low-dimensional representation.
6.1.2. Machine Learning Approaches
6.2. Real-Time Computation for Dynamic Environments
- Parallelizing computationally intensive steps (sampling, collision checking, graph search)
- Adaptive spatial and temporal resolution to reduce unnecessary computation
- Decomposing the problem into hierarchical or modular subproblems
- Leveraging learned models to prune search space or estimate costs rapidly
6.3. Parallel Optimization for Real-Time Trajectory Planning
| Algorithm 1 Real-Time Parallel Trajectory Optimization |
|
6.4. Strategies for Real-Time Scalability
-
GPU-Accelerated Evaluation: Modern GPUs allow hundreds to thousands of trajectory knot gradients to be evaluated simultaneously, enabling speed-ups by orders of magnitude compared to serial CPUs. This parallelism dramatically reduces iteration times for gradient computation and constraint checking, empowering planners to meet real-time deadlines even in high-dimensional state spaces [81,82,83].Recent work by Rastgar [82] proposes novel GPU-parallel optimization algorithms that adapt constraint formulations to fully leverage GPU architectures, markedly enhancing scalability and robustness in dynamic scenarios. Similarly, Yu et al. [83] introduce TOP, a trajectory optimization via parallel consensus ADMM that achieves near-constant time complexity per iteration by decomposing long trajectories into parallelizable segments, enabling large-scale real-time path planning on GPUs.
-
Warm Starting: Utilizing the previously computed optimal trajectory as an initial guess accelerates convergence of iterative solvers. This approach is especially effective in dynamic environments where consecutive plans differ only slightly [82,84].By reusing prior solutions, planners reduce redundant computation while improving continuity and smoothness of resulting trajectories. This practical technique aligns with state-of-the-art GPU-accelerated approaches that integrate warm-starting for real-time feasibility.
-
Receding Horizon Execution: Instead of optimizing over the entire trajectory horizon, planners focus on a shorter, fixed-duration segment. Only the initial portion of the plan is executed before replanning occurs, maintaining continual responsiveness to environmental changes and dynamic obstacles [82,85].This limited horizon approach bounds computational demands, facilitates faster replanning, and supports adaptive trajectory refinement, key for scalable navigation in cluttered or rapidly changing environments.
-
Adaptive Termination and Step Sizing: Optimization algorithms dynamically adjust their step sizes and employ early stopping criteria once trajectories reach a suitable quality level within the operational time budget. This balances the trade-off between latency and solution optimality.For example, algorithms may terminate as soon as collision-free smooth paths are found, even if not perfectly optimal, ensuring timely availability of actionable plans without compromising safety [83].
-
Integrated Recent Advances:Incorporating the above core principles, recent methods extend scalability and robustness in real-time planning:
- –
- Semantic-Aware Optimization: He et al. [86] develop a spatio-temporal semantic graph optimizer tailored for urban autonomous driving. Their approach handles dynamic obstacle semantics through sparse graph formulations, enabling real-time feasible trajectories that intelligently incorporate semantic understanding of traffic participants and road elements.
- –
- Hybrid Sampling and Rewiring: Silveira et al. [87] propose RT-FMT, a hybrid of Fast Marching Tree and RT-RRT*, that combines incremental rewiring and local-to-global tree reuse for faster execution and improved path quality in dynamic environments. By efficiently reusing prior tree structures and limiting expansion scope, RT-FMT exemplifies algorithmic decomposition enabling scalability.
- –
- Piecewise Parallel Optimization: Yu et al. [83] introduce the TOP framework which decomposes long trajectories into smaller segments solved in parallel while ensuring high-order continuity through consensus constraints. Deploying this method on GPUs supports extremely large-scale and long-horizon real-time trajectory optimization, pushing the frontier of computational performance in robotics.
- –
- Constraint Reformulation for Parallelism: Rastgar’s thesis [82] innovates by remodeling kinematic and collision constraints to be more amenable to parallel GPU computation, thereby enhancing planner scalability and resulting in more reliable real-time performance.
6.5. Integration of Perception Systems
6.5.1. Deep Learning for Perception
6.6. Ethical and Safety Concerns in Human-Robot Interactions
- Transparency: Robots should clearly communicate intentions and behaviors to enhance human trust.
- Accountability: Developers and operators must be accountable for system behavior, particularly in high-stakes contexts.
- Fairness: Systems should actively mitigate bias and promote equitable treatment across user demographics.
- Collision Avoidance: Sensor fusion and predictive models allow robots to anticipate and avoid human contact.
- Emergency Stop Mechanisms: Systems must be capable of halting immediately under risk conditions.
- Human-in-the-Loop Control: Dynamic shared autonomy enables humans to intervene in uncertain or dangerous scenarios.
6.7. Toward Human-Centric Design and Learning
- Integration Complexity: Embedding ethical and safety modules into fast, real-time planners on resource-constrained platforms remains difficult.
- Standardization Gaps: Harmonization of international safety and ethics standards (e.g., ISO 12100, ISO/TS 15066) with learning-based models is ongoing [93].
- Human Perception: Models often neglect psychological dimensions such as perceived safety and emotional response.
7. Conclusion
Key Takeaways for Future Research
- Transformer-Based Planning: Future systems should explore integrating spatial-temporal attention mechanisms into planning pipelines to improve generalization and context-aware navigation, especially in multi-agent and partially observable environments.
- Real-Time and Embedded Efficiency: Further innovation is needed to support GPU and neuromorphic execution on power-constrained platforms, ensuring autonomy is feasible for small-scale robots and edge devices.
- Scalable Multi-Agent Coordination: Scalability remains a bottleneck. Approaches that combine decentralized optimization, learning-based approximations, and adaptive communication protocols are promising.
- Safe and Ethical Optimization: New planning frameworks should incorporate constraints and verification layers that explicitly account for safety, fairness, and human preferences, particularly when operating alongside humans.
- Standardization and Benchmarking: To assess progress meaningfully, standardized evaluation frameworks and real-world benchmarks—particularly those involving uncertainty, real-time constraints, and ethical dilemmas—must be developed.
Author Contributions
Funding
References
- Licardo, J.T.; Domjan, M.; Orehovački, T. Intelligent robotics—A systematic review of emerging technologies and trends. Electronics 2024, 13, 542. [Google Scholar] [CrossRef]
- Kamuni, N.; Dodda, S.; Vuppalapati, V.S.M.; Arlagadda, J.S.; Vemasani, P. Advancements in Reinforcement Learning Techniques for Robotics. Journal of Basic Science and Engineering 19, 101–111.
- Zhang, Y.; Zhao, W.; Wang, J.; Yuan, Y. Recent progress, challenges and future prospects of applied deep reinforcement learning: A practical perspective in path planning. Neurocomputing 2024, 608, 128423. [Google Scholar] [CrossRef]
- Kanakis, G.S.; Rovithakis, G.A. Motion Planning in Topologically Complex Environments Via Hybrid Feedback. IEEE Transactions on Automatic Control 2024. [Google Scholar] [CrossRef]
- Alqobali, R.; Alshmrani, M.; Alnasser, R.; Rashidi, A.; Alhmiedat, T.; Alia, O.M. A survey on robot semantic navigation systems for indoor environments. Applied Sciences 2023, 14, 89. [Google Scholar] [CrossRef]
- Zhao, Z.; Cheng, S.; Ding, Y.; Zhou, Z.; Zhang, S.; Xu, D.; Zhao, Y. A survey of optimization-based task and motion planning: From classical to learning approaches. IEEE/ASME Transactions on Mechatronics 2024. [Google Scholar] [CrossRef]
- Sutikno, T. The future of artificial intelligence-driven robotics: Applications and implications. IAES Int. J. Robot. Autom 2024, 13, 361–372. [Google Scholar] [CrossRef]
- LaValle, S.M. Planning Algorithms; Cambridge University Press, 2006.
- Choset, H.; Lynch, K.M.; Hutchinson, S.; Kantor, G.; Burgard, W.; Kavraki, L.E.; Thrun, S. Principles of Robot Motion: Theory, Algorithms, and Implementations; MIT Press, 2005.
- Lozano-Perez, T. Spatial Planning: A Configuration Space Approach. IEEE Transactions on Computers 1983, 32, 108–120. [Google Scholar] [CrossRef]
- Sánchez-Ibáñez, J.R.; Pérez-del Pulgar, C.J.; García-Cerezo, A. Path planning for autonomous mobile robots: A review. Sensors 2021, 21, 7898. [Google Scholar] [CrossRef] [PubMed]
- Khatib, O. Real-Time Obstacle Avoidance for Manipulators and Mobile Robots. The International Journal of Robotics Research 1986, 5, 90–98. [Google Scholar] [CrossRef]
- Brooks, R.A. A Robust Layered Control System for a Mobile Robot. IEEE Journal on Robotics and Automation 1986, 2, 14–23. [Google Scholar] [CrossRef]
- Burgess-Limerick, B.; Haviland, J.; Lehnert, C.; Corke, P. Reactive base control for on-the-move mobile manipulation in dynamic environments. IEEE Robotics and Automation Letters 2024, 9, 2048–2055. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, W.; Wang, J.; Yuan, Y. Recent progress, challenges and future prospects of applied deep reinforcement learning: A practical perspective in path planning. Neurocomputing 2024, 608, 128423. [Google Scholar] [CrossRef]
- Mohanan, M.; Salgoankar, A. A survey of robotic motion planning in dynamic environments. Robotics and Autonomous Systems 2018, 100, 171–185. [Google Scholar] [CrossRef]
- Amar, L.B.; Jasim, W.M. Hybrid metaheuristic approach for robot path planning in dynamic environment. Bulletin of Electrical Engineering and Informatics 2021, 10, 2152–2162. [Google Scholar] [CrossRef]
- He, H.; Shi, P.; Zhao, Y. Adaptive connected hierarchical optimization algorithm for minimum energy spacecraft attitude maneuver path planning. Astrodynamics 2023, 7, 197–209. [Google Scholar] [CrossRef]
- Wang, N.; Jin, Z.; Wang, T.; Xiao, J.; Zhang, Z.; Wang, H.; Zhang, M.; Li, H. Hybrid path planning methods for complete coverage in harvesting operation scenarios. Computers and Electronics in Agriculture 2025, 231, 109946. [Google Scholar] [CrossRef]
- Ben-Messaoud, W.; Basset, M.; Lauffenburger, J.P.; Orjuela, R. Smooth obstacle avoidance path planning for autonomous vehicles 2018. pp. 1–6.
- Betts, J.T. Practical Methods for Optimal Control and Estimation Using Nonlinear Programming; SIAM, 2010.
- Zhang, H.; Zhang, Y.; Yang, T. A survey of energy-efficient motion planning for wheeled mobile robots. Industrial Robot: the international journal of robotics research and application 2020, 47, 607–621. [Google Scholar] [CrossRef]
- Liu, J.; Yan, Y.; Yang, Y.; Li, J. An improved artificial potential field UAV path planning algorithm guided by RRT under environment-aware modeling: Theory and simulation. IEEE Access 2024, 12, 12080–12097. [Google Scholar] [CrossRef]
- Karur, K.; Sharma, N.; Dharmatti, C.; Siegel, J.E. A survey of path planning algorithms for mobile robots. Vehicles 2021, 3, 448–468. [Google Scholar] [CrossRef]
- Sun, S.; Yu, D.; Wang, C.; Xie, C. A smooth tool path generation and real-time interpolation algorithm based on B-spline curves. Advances in Mechanical Engineering 2018, 10, 1687814017750281. [Google Scholar] [CrossRef]
- Sun, S.; Yu, D.; Wang, C.; Xie, C. A smooth tool path generation and real-time interpolation algorithm based on B-spline curves. Advances in Mechanical Engineering 2018, 10, 1687814017750281. [Google Scholar] [CrossRef]
- Simba, K.R.; Uchiyama, N.; Sano, S. Real-time smooth trajectory generation for nonholonomic mobile robots using Bézier curves. Robotics and Computer-Integrated Manufacturing 2016, 41, 31–42. [Google Scholar] [CrossRef]
- Zafar, M.N.; Mohanta, J. Methodology for path planning and optimization of mobile robots: A review. Procedia computer science 2018, 133, 141–152. [Google Scholar] [CrossRef]
- Niu, H.; Lu, Y.; Savvaris, A.; Tsourdos, A. An energy-efficient path planning algorithm for unmanned surface vehicles. Ocean Engineering 2018, 161, 308–321. [Google Scholar] [CrossRef]
- Belanger, N. External fake constraints interpolation: The end of Runge phenomenon with high degree polynomials relying on equispaced nodes Application to aerial robotics motion planning. indicator 2017, 2, 1–9. [Google Scholar]
- Villagra, J.; Milanés, V.; Rastelli, J.P.; Godoy, J.; Onieva, E. Path and speed planning for smooth autonomous navigation 2012.
- Wang, H.; Ren, G.; Chen, J.; Ding, G.; Yang, Y. Unmanned aerial vehicle-aided communications: Joint transmit power and trajectory optimization. IEEE Wireless Communications Letters 2018, 7, 522–525. [Google Scholar] [CrossRef]
- Liu, J.; Anavatti, S.; Garratt, M.; Abbass, H.A. Modified continuous ant colony optimisation for multiple unmanned ground vehicle path planning. Expert Systems with Applications 2022, 196, 116605. [Google Scholar] [CrossRef]
- Ma, C.; Zhao, M.; Liu, Y. Vehicle navigation path optimization based on complex networks. Physica A: Statistical Mechanics and its Applications 2025, 665, 130509. [Google Scholar]
- Wang, X.; Jiang, P.; Li, D.; Sun, T. Curvature continuous and bounded path planning for fixed-wing UAVs. Sensors 2017, 17, 2155. [Google Scholar] [CrossRef]
- Dai, C.; Lefebvre, S.; Yu, K.M.; Geraedts, J.M.; Wang, C.C. Planning jerk-optimized trajectory with discrete time constraints for redundant robots. IEEE Transactions on Automation Science and Engineering 2020, 17, 1711–1724. [Google Scholar]
- Datouo, R.; Motto, F.B.; Zobo, B.E.; Melingui, A.; Bensekrane, I.; Merzouki, R. Optimal motion planning for minimizing energy consumption of wheeled mobile robots 2017. pp. 2179–2184.
- Liu, X.; Li, Y.; Zhang, J.; Zheng, J.; Yang, C. Self-adaptive dynamic obstacle avoidance and path planning for USV under complex maritime environment. Ieee Access 2019, 7, 114945–114954. [Google Scholar] [CrossRef]
- .
- Shen, P.; Zhang, X.; Fang, Y. Complete and time-optimal path-constrained trajectory planning with torque and velocity constraints: Theory and applications. IEEE/ASME Transactions on Mechatronics 2018, 23, 735–746. [Google Scholar] [CrossRef]
- Xu, Z.; Han, X.; Shen, H.; Jin, H.; Shimada, K. Navrl: Learning safe flight in dynamic environments. IEEE Robotics and Automation Letters 2025. [Google Scholar]
- Choudhury, S.; Gupta, J.K.; Kochenderfer, M.J.; Sadigh, D.; Bohg, J. Dynamic multi-robot task allocation under uncertainty and temporal constraints. Autonomous Robots 2022, 46, 231–247. [Google Scholar]
- Saeedinia, S.A.; Tale Masouleh, M. The synergy of the multi-modal MPC and Q-learning approach for the navigation of a three-wheeled omnidirectional robot based on the dynamic model with obstacle collision avoidance purposes. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science 2022, 236, 9716–9729. [Google Scholar] [CrossRef]
- Mohaghegh, M.; Saeedinia, S.A.; Roozbehi, Z. Optimal predictive neuro-navigator design for mobile robot navigation with moving obstacles. Frontiers in Robotics and AI 2023, 10, 1226028. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Wang, Y.; Zhao, X.; Zhao, P.; He, L. Time-optimal trajectory planning of serial manipulator based on adaptive cuckoo search algorithm. Journal of Mechanical Science and Technology 2021, 35, 3171–3181. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Yang, T. A survey of energy-efficient motion planning for wheeled mobile robots. Industrial Robot: the international journal of robotics research and application 2020, 47, 607–621. [Google Scholar] [CrossRef]
- Parasuraman, R.; Kershaw, K.; Pagala, P.; Ferre, M. Model based on-line energy prediction system for semi-autonomous mobile robots 2014. pp. 411–416.
- Palomba, I.; Wehrle, E.; Carabin, G.; Vidoni, R. Minimization of the energy consumption in industrial robots through regenerative drives and optimally designed compliant elements. Applied Sciences 2020, 10, 7475. [Google Scholar] [CrossRef]
- Shamsfakhr, F.; Bigham, B.S. A neural network approach to navigation of a mobile robot and obstacle avoidance in dynamic and unknown environments. Turkish Journal of Electrical Engineering and Computer Sciences 2017, 25, 1629–1642. [Google Scholar] [CrossRef]
- Jacob, I.J. Fuzzy Logic Decision Model for Robust Risk Management in ubiquitous environment-A Review. Journal of Ubiquitous Computing and Communication Technologies 2024, 5, 399–411. [Google Scholar]
- Zhang, X.; Shi, G. Multi-objective optimal trajectory planning for manipulators in the presence of obstacles. Robotica 2022, 40, 888–906. [Google Scholar] [CrossRef]
- Mellouk, A.; Benmachiche, A. A survey on navigation systems in dynamic environments 2020. pp. 1–7.
- Xiao, B.; Zhang, Z.; Wang, Q.; Zhang, B.; Zheng, S. TSP-based depth-first search algorithms for enhanced path planning in laser-based directed energy. Precision Engineering 2025, 93, 224–236. [Google Scholar] [CrossRef]
- Sundarraj, S.; Reddy, R.V.K.; Basam, M.B.; Lokesh, G.H.; Flammini, F.; Natarajan, R. Route planning for an autonomous robotic vehicle employing a weight-controlled particle swarm-optimized Dijkstra algorithm. IEEE Access 2023, 11, 92433–92442. [Google Scholar]
- Korkmaz, M.; Durdu, A. Comparison of optimal path planning algorithms 2018. pp. 255–258.
- Halder, U.; Das, S.; Maity, D. A cluster-based differential evolution algorithm with external archive for optimization in dynamic environments. IEEE transactions on cybernetics 2013, 43, 881–897. [Google Scholar]
- Saeedi, S.; Bodin, B.; Wagstaff, H.; Nisbet, A.; Nardi, L.; Mawer, J.; Melot, N.; Palomar, O.; Vespa, E.; Spink, T.; et al. Navigating the landscape for real-time localization and mapping for robotics and virtual and augmented reality. Proceedings of the IEEE 2018, 106, 2020–2039. [Google Scholar] [CrossRef]
- Mohaghegh, M.; Jafarpourdavatgar, H.; Saeedinia, S.A. New design of smooth PSO-IPF navigator with kinematic constraints. IEEE Access 2024. [Google Scholar] [CrossRef]
- Miao, C.; Chen, G.; Yan, C.; Wu, Y. Path planning optimization of indoor mobile robot based on adaptive ant colony algorithm. Computers & Industrial Engineering 2021, 156, 107230. [Google Scholar] [CrossRef]
- Bao, C.; Gao, D.; Gu, W.; Xu, L.; Goodman, E.D. A new adaptive decomposition-based evolutionary algorithm for multi-and many-objective optimization. Expert Systems with Applications 2023, 213, 119080. [Google Scholar] [CrossRef]
- Hu, Y.; Yang, X.; Zhou, K.; Liu, Q.; Ding, K.; Gao, H.; Zhu, P.; Liu, C. SwarmPRM: Probabilistic Roadmap Motion Planning for Large-Scale Swarm Robotic Systems 2024. pp. 10222–10228.
- Zhang, Z.; Qiao, B.; Zhao, W.; Chen, X. A predictive path planning algorithm for mobile robot in dynamic environments based on rapidly exploring random tree. Arabian Journal for Science and Engineering 2021, 46, 8223–8232. [Google Scholar] [CrossRef]
- Wang, J.; Chi, W.; Li, C.; Wang, C.; Meng, M.Q.H. Neural RRT*: Learning-based optimal path planning. IEEE Transactions on Automation Science and Engineering 2020, 17, 1748–1758. [Google Scholar] [CrossRef]
- Sun, Z.; Xia, B.; Xie, P.; Li, X.; Wang, J. NAMR-RRT: Neural Adaptive Motion Planning for Mobile Robots in Dynamic Environments. IEEE Transactions on Automation Science and Engineering 2025. [Google Scholar] [CrossRef]
- Wang, J.; Jia, X.; Zhang, T.; Ma, N.; Meng, M.Q.H. Deep neural network enhanced sampling-based path planning in 3D space. IEEE Transactions on Automation Science and Engineering 2021, 19, 3434–3443. [Google Scholar] [CrossRef]
- Zhu, K.; Zhang, T. Deep reinforcement learning based mobile robot navigation: A review. Tsinghua Science and Technology 2021, 26, 674–691. [Google Scholar] [CrossRef]
- Han, J.R.; Thomas, H.; Zhang, J.; Rhinehart, N.; Barfoot, T.D. DR-MPC: Deep Residual Model Predictive Control for Real-World Social Navigation. IEEE Robotics and Automation Letters 2025. [Google Scholar] [CrossRef]
- Sellers, T.; Lei, T.; Jan, G.E.; Wang, Y.; Luo, C. Multi-objective optimization robot navigation through a graph-driven PSO mechanism 2022. pp. 66–77.
- Zeng, J.; Qin, L.; Hu, Y.; Yin, Q.; Hu, C. Integrating a path planner and an adaptive motion controller for navigation in dynamic environments. Applied Sciences 2019, 9, 1384. [Google Scholar] [CrossRef]
- Hsueh, H.Y.; Toma, A.I.; Ali Jaafar, H.; Stow, E.; Murai, R.; Kelly, P.H.; Saeedi, S. Systematic comparison of path planning algorithms using PathBench. Advanced Robotics 2022, 36, 566–581. [Google Scholar] [CrossRef]
- Zhong, X.; Tian, J.; Hu, H.; Peng, X. Hybrid path planning based on safe A* algorithm and adaptive window approach for mobile robot in large-scale dynamic environment. Journal of Intelligent & Robotic Systems 2020, 99, 65–77. [Google Scholar] [CrossRef]
- Wang, J.; Swartz, C.L.; Huang, K. Deep learning-based model predictive control for real-time supply chain optimization. Journal of Process Control 2023, 129, 103049. [Google Scholar] [CrossRef]
- Wang, H.; Qiu, Y.; Hou, Y.; Shi, Q.; Huang, H.W.; Huang, Q.; Fukuda, T. Deep Reinforcement Learning-Based Collision-Free Navigation for Magnetic Helical Microrobots in Dynamic Environments. IEEE Transactions on Automation Science and Engineering 2024. [Google Scholar] [CrossRef]
- Murano, A.; Perelli, G.; Rubin, S. Multi-agent path planning in known dynamic environments 2015. pp. 218–231.
- Nardi, L.; Stachniss, C. Uncertainty-aware path planning for navigation on road networks using augmented MDPs 2019. pp. 5780–5786.
- Gouda, K.C.; Thakur, R. Energy-efficient clustering and path planning for UAV-assisted D2D cellular networks. Ad Hoc Networks 2025, 170, 103757. [Google Scholar] [CrossRef]
- Yu, H.; Lu, W.; Han, Y.; Liu, D.; Zhang, M. Heterogeneous dimensionality reduction for efficient motion planning in high-dimensional spaces. IEEE Access 2020, 8, 42619–42632. [Google Scholar] [CrossRef]
- Khalilullah, K.I.; Jindai, M.; Ota, S.; Yasuda, T. Fast road detection methods on a large scale dataset for assisting robot navigation using kernel principal component analysis and deep learning 2018. pp. 798–803.
- Hu, K.; O’Connor, P. Learning a representation map for robot navigation using deep variational autoencoder. arXiv 2018, arXiv:1807.02401. [Google Scholar] [CrossRef]
- Williams, S.; Indelman, V.; Kaess, M.; Roberts, R.; Leonard, J.J.; Dellaert, F. Concurrent filtering and smoothing: A parallel architecture for real-time navigation and full smoothing. The International Journal of Robotics Research 2014, 33, 1544–1568. [Google Scholar] [CrossRef]
- .
- Rastgar, F. Towards Reliable Real-Time Trajectory Optimization. PhD thesis, University of Tartu, 2024.
- Yu, J.; Chen, N.; Liu, G.; Xu, C.; Gao, F.; Cao, Y. TOP: Trajectory Optimization via Parallel Optimization towards Constant Time Complexity 2025. Available online: https://arxiv.org/abs/2507.10290.
- Dastider, A.; Ray, A. Retro-trajectory optimization: A memory-efficient warm-start approach. IEEE Transactions on Robotics 2023, 39, 1105–1117. [Google Scholar]
- Williams, G.; et al. Model predictive path integral control: From theory to parallel computation. In Proceedings of the IEEE ICRA, 2017.
- He, S.; Ma, Y.; Song, T.; Jiang, Y.; Wu, X. A Real-Time Spatio-Temporal Trajectory Planner for Autonomous Vehicles With Semantic Graph Optimization. IEEE Robotics and Automation Letters 2024. [Google Scholar] [CrossRef]
- Silveira, J.; Cabral, K.; Givigi, S.; Marshall, J. Real-Time Fast Marching Tree for Mobile Robot Motion Planning in Dynamic Environments. arXiv 2025, arXiv:2502.09556. [Google Scholar]
- Guo, X.; Jiang, F.; Chen, Q.; Wang, Y.; Sha, K.; Chen, J. Deep learning-enhanced environment perception for autonomous driving: MDNet with CSP-DarkNet53. Pattern Recognition 2025, 160, 111174. [Google Scholar] [CrossRef]
- Papachristos, C.; Mascarich, F.; Khattak, S.; Dang, T.; Alexis, K. Localization uncertainty-aware autonomous exploration and mapping with aerial robots using receding horizon path-planning. Autonomous Robots 2019, 43, 2131–2161. [Google Scholar] [CrossRef]
- Parasuraman, R.; Cosenzo, K.A.; De Visser, E.J. Integrating automation, human factors and ethics for effective human–robot interaction in military settings. Military Psychology 2010, 22, 1–10. [Google Scholar]
- Eder, K.; Harper, R.; Leonards, U. Towards ethical robots: A survey of existing paradigms. In Proceedings of the IEEE International Conference on Advanced Robotics, 2014, pp. 1–6.
- Martinetti, A.; van Wingerden, J.W.; et al. Redefining safety in human-robot interaction: From physical protection to social understanding. Frontiers in Robotics and AI 2021, 8. [Google Scholar]
- Valori, A.; Mendes, A. Validating robot safety protocols with international ISO standards: Challenges and best practices. In Proceedings of the IEEE Int. Conf. on Human-Robot Interaction (HRI), 2021.
- Shuming, L.; Cho, Y. Safety-Aware Learning for Human-Robot Teams in Real-Time Interaction. IEEE Transactions on Robotics 2024. [Google Scholar]
- Achiam, J.; Held, D.; Tian, A.; Abbeel, P. Constrained policy optimization. In Proceedings of the International Conference on Machine Learning, 2017, pp. 22–31.
- Ramviyas, A.; Mataric, M. Integrating physical and psychological safety in human-robot collaboration: A unified model. Robotics and Autonomous Systems 2010. [Google Scholar]
| Method | Mathematical Definition | Parameters and Description |
|---|---|---|
| Bézier Curve [24,27] | Parameters: , (control points), n (degree). | |
| Description: Smooth curve defined by control points, parameterized by t. | ||
| Elastic Stretching [39] | Parameters: (curvature), s (arc length). | |
| Description: Minimizes total squared curvature for smooth paths. | ||
| Minimum Angle Difference [24] | Parameters: (angle at waypoint i). | |
| Description: Minimizes angular difference for smooth turns. | ||
| Curvature Continuity [35] | Parameters: (curvature derivative). | |
| Description: Ensures continuous curvature along the path. | ||
| Jerk Minimization [36] | Parameters: (jerk at time t). | |
| Description: Minimizes jerk for smoother motion. | ||
| Energy-Efficient Smoothing [37] | Parameters: (force/energy as a function of velocity). | |
| Description: Optimizes energy consumption. | ||
| Adaptive Smoothing [38] | Parameters: (curvature at arc length s and time t). | |
| Description: Dynamically adjusts smoothness based on environment. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





