Differential Diagnosis of Prostate Cancer Grade to Augment Clinical Diagnosis Based on Classifier Models With Tuned Hyperparameters

1. Introduction

Prostate cancer is the second most common male tumor globally, with 1,276,106 new cases and 358,989 deaths in 2018 [1,2]. That is 7.1% of new cases and 3.8% of all male cancer mortality in 2018 [3]. Globally, the median age for detection of prostate cancer is 66 years old, and both the recurrence and fatality rates rise with age [4,5]. Early detection of tumors increases the chances of being cured because treatment works even if the cancer is localized.

Multiparametric magnetic resonance imaging (mp-MRI) has been used extensively in prostate cancer (PCa) scanning, identification, and grading throughout the last few decades [6,7]. It is possible to obtain high-resolution anatomical and functional images using the mp-MRI imaging technique [8]. T₁ weighted images (T₁WI) and T₂ weighted images (T₂WI) are anatomic sequences used in multiparametric prostate MRI. For example, the zonal structure and tumor foci cannot be identified using T₁WI. It is possible to employ T₁WI to discover biopsy-associated haemorrhage, which can interfere with the capacity of other PCa MRI techniques to provide accurate diagnoses. T₂WI provides the best soft-tissue imaging for malignancies, zonal morphology, seminal vesicle (SV), anterior fibromuscular stroma (AFS), neurovascular bundles, and the capsule [9]. Diffusion-weighted imaging (DWI), Magnetic resonance spectroscopic imaging (MRSI), and Dynamic contrast-enhanced (DCE) are functional MRI sequences [10]. The DWI technique was developed and implemented to detect an acute cerebrovascular stroke. DWI compares water diffusion in soft tissues and free solution to produce image contrast. When a PCa grows, there is a growth in cellularity and degradation of ductal architecture, which limits fluid flow through the prostate [11]. The b-value and Apparent Diffusion Coefficient (ADC) are the two types of images used for analysis in DWI. Tumor diagnostic outcome is improved by utilizing b-values between 1,400 and 2,000 [12,13,14]. Clinical interpretation from DWI is subjective; nevertheless, water molecules’ limitations may be measured quantitatively. Interpretation is performed with ADC maps and ADC measurements (mm²/s). and ADC levels and Gleason scores are proportionally related [15,16]. By using a machine learning approach with clinically relevant radiomics metrics as inputs we aim to improve the interpretation and augment clinical diagnosis.

Radiomics improves image analysis by generating (200+) statistical variables from medical images automatically. Patients can significantly vary in shape and texture depending on the imaging technique used [17] and by utilizing automated or semi-automated radiomics we could improve diagnostic accuracy via statistically analyzing medical images. Textural analysis has been used to extract tissue information from medical images since the 1980s [18,19]. It recognizes that intratumor heterogeneity has significant implications for cancer research, which could be represented by tumors’ texture [20]. Radiomics relies heavily on texture analysis, a necessary part of the process [21]. Radiomics is the technique used to collect essential and extensive data from clinical images and give variables that can be used to assist in detection, prognostic, and treatment response [22]. It aids in the classification of benign and malignant tumors and predicts outcomes in practically every tissue [23,24,25,26,27]. Furthermore, when developing a radiomics model, selecting the best ML model is significant. Different ML approaches may perform differently when applied to different tissues [27,28,29,30,31].

Training is used to derive many of the algorithm parameters used by machine learning, and most contemporary ML algorithms must tune parameters to improve feature identification referred to as Hyperparameters [28,29,30]. The hyperparameters are fine-tuned to optimize an algorithm for a specific learning task [32]. Hyperparameter optimization usually employs Grid and Random Search techniques [33]. Grid Search is a method using all possible permutations of hyperparameters. The training data and the number of layers can be adjusted in a grid search as hyperparameters [34]. In contrast to a grid search, randomized search does not perform a comprehensive investigation of the hyperparameter space. Nonetheless, it permits us to investigate a wider variety of hyperparameter value settings more effectively and affordably. Weerts et al. [35] stated that an increased tuning risk and relative tuning risk were observed from the random forest’s max features and SVM’s gamma and C, suggesting that it is essential to tune these hyperparameters. In the domain of prostate cancer classification and grading, many prior studies have applied machine learning techniques with default hyperparameters, often without extensive hyperparameter optimization. In contrast, our research distinguishes itself by prioritizing hyperparameter tuning. This deliberate optimization process enhances the precision and reliability of our machine-learning models, contributing to more accurate and clinically relevant results. Our work aims to advance the field by systematically refining the parameters that underpin the diagnosis of prostate cancer.

The study aimed to use different classifiers (with tuned hyperparameters) and two feature selection methods (i.e., to find the best for classification and prediction). Multiparametric MRI-derived radiomics features were used (including T₂WI and ADC map images). First, to quantify tumor heterogeneity between significant versus non-tumor regions. Second, to predict Gleason scores (i.e., G2 = 3 + 4; G3 = 4 + 3; and G4, Gleason primary pattern of 4 + 4 = 8 G4, 3+5 = 8 (G4), 9 (G5) or 10 (G5)) for significant prostate cancer.

2. Materials and method

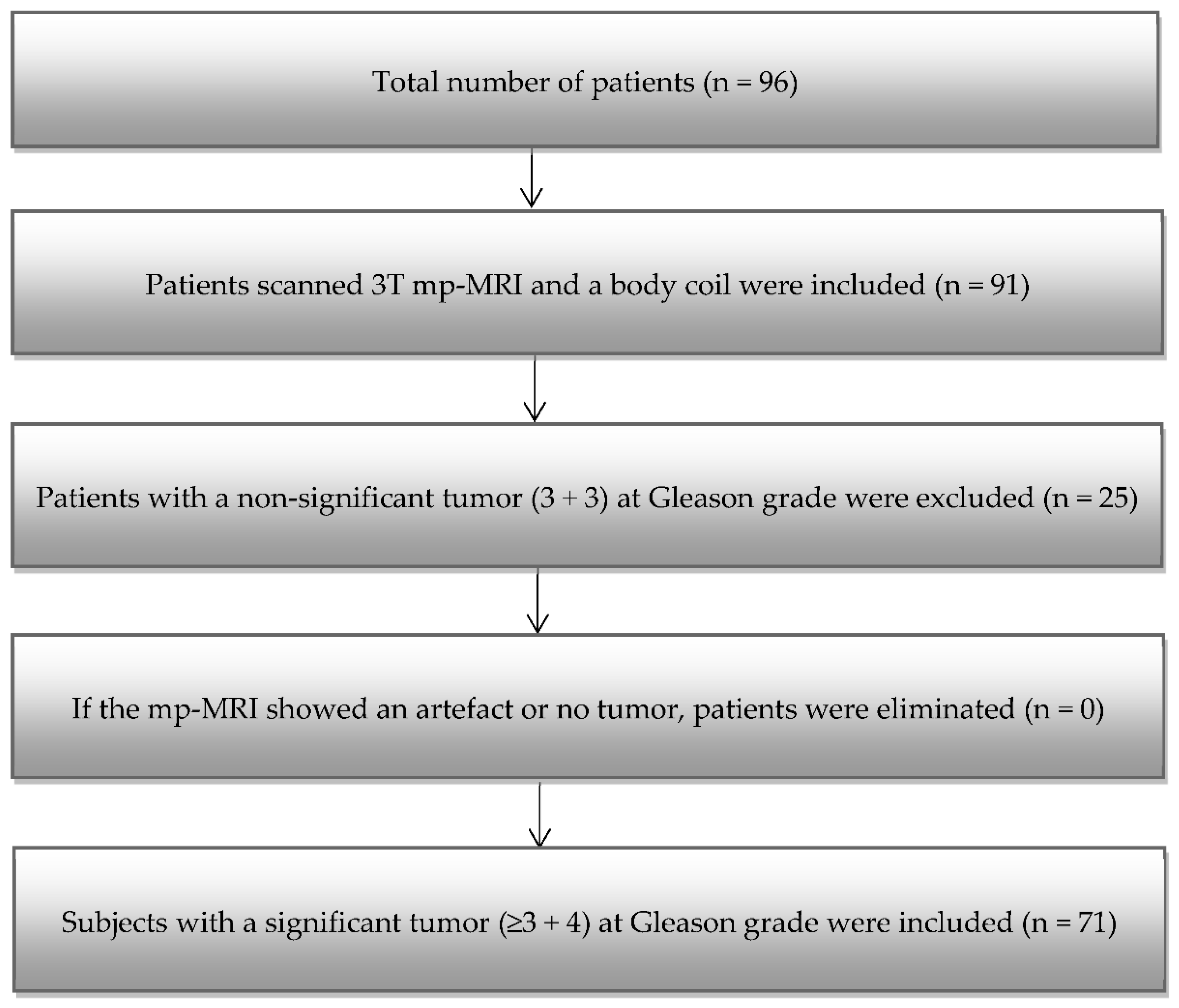
2.1. Patient Group

This study used a dataset from The Cancer Imaging Archive (TCIA) funded through the SPIE, NCI/NIH, AAPM, and Radboud University. The population set used in this work consists of 96 patients, including T₂WI and ADC map series from the open-source, freely released SPIE-AAPM-NCI PROSTATEx-2 [34].

Figure 1 illustrates the exclusion and inclusion criteria: (a) the total number of patients (n = 96); (b) patients scanned 3T mp-MRI, and a body coil included (n = 96); (c) patients with a non-significant tumor at (3 + 3) Gleason grade excluded (n = 25); (d) If the mp-MRI showed an artefact or tumour, patients were eliminated (n = 0); and (e) subjects with a significant tumor (≥3 + 4) at Gleason grade included (n = 71).

2.2. Multiparametric Magnetic Resonance Imaging

The images were acquired by Siemens 3T MRI techniques (MAGNETOM Skyra, Siemens Healthcare, Erlangen, Germany) utilising a pelvic phased-array coil. The axial T₂WI and ADC maps were employed for imaging assessment. The current clinical agreement is that T₂WI, including at least one or two functional approaches, should be used to identify prostate cancer (from DWI, DCE, and spectroscopic imaging) [5,35,36]. For precise localization, all biopsies were done under MR monitoring. A pathologist then rated biopsy specimens, which served as the ground truth. T₂WI was obtained using a turbo spin echo sequence with 0.5 mm resolution and 3.6 mm slice thickness. The DWI images were obtained using a single-shot echo-planar imaging procedure utilizing 2 mm in-plane resolution, 3.6 mm slice thickness, and three-dimensional diffusion encoding gradients. The scanner program generated the ADC map from three b-values (50, 400, and 800 s/mm²). Table 1 contains a description of the mp-MRI acquisition settings. The images were collected with no endorectal coil, According to PI-RADS recommendations regarding prostate MRI images [39].

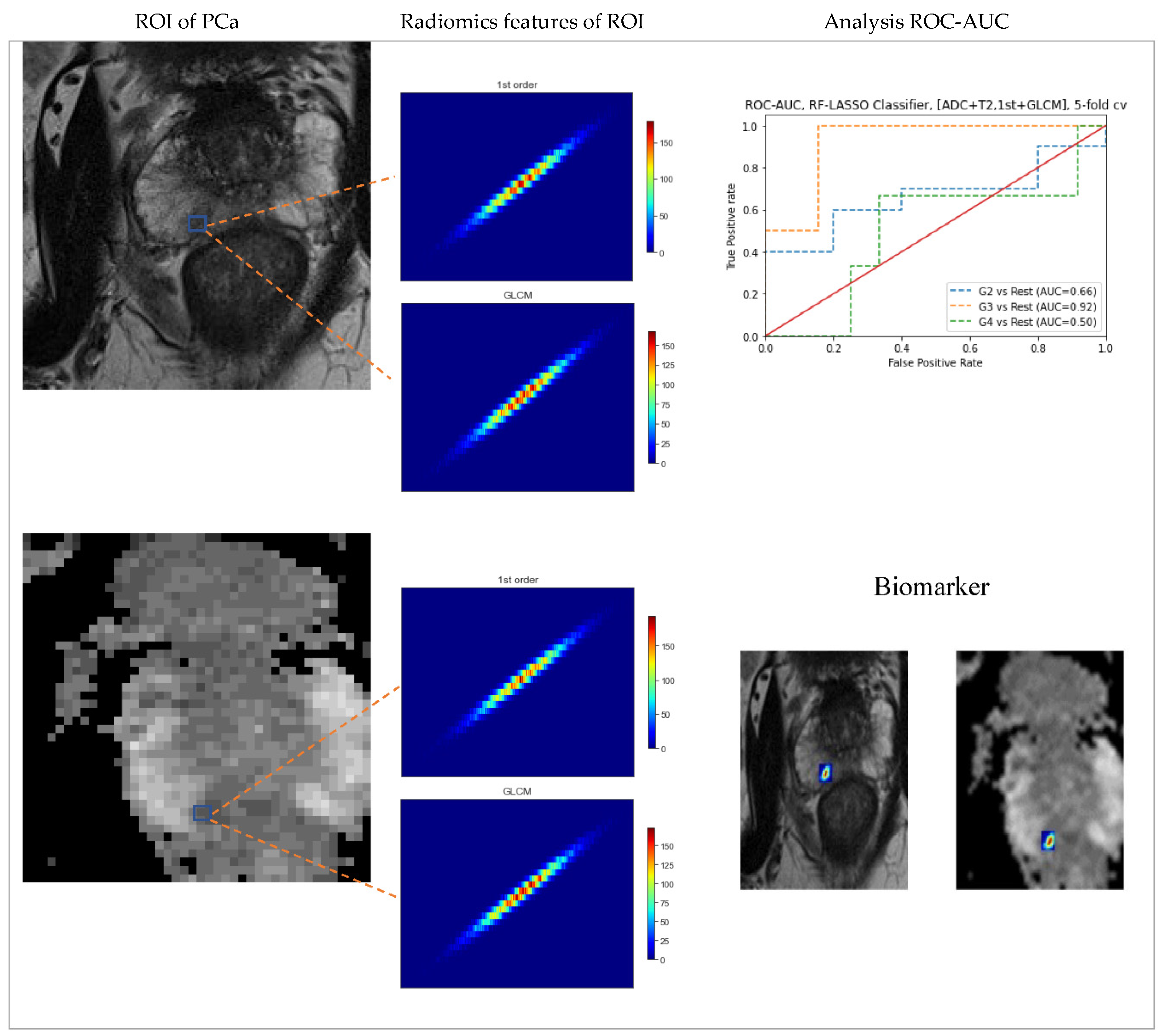
2.3. Segmentation

ROIs for significant cancer were segmented manually from T₂WI, and ADC images predefined ROIs from PROSTATEx-2 Challenge that is available on TCIA [37]. The LIFEx package was used for the segmentation process [16]. Non-tumor regions cancers segmented depending on the same region for significant cancer (in different regions) assessed for every subject’s lesion. Figure 2 illustrates a typical malignancy cancer segmentation on mp-MRI.

2.4. Feature extraction

Pre-processing, including intensity normalization and spatial resampling, was conducted for all mp-MRI images using LIFEx to derive radiomics features. The dimensions were rescaled to 0.5 × 0.5 × 3 mm, preserving the dataset’s in-plane and inter-plane resolutions. The radiomics features uniformity achieved using grey-level discretization defined between 1 and 128 bits/pixel. Absolute resampling between the minimum and maximum fixed bounds for all ROIs used for intensity resizing parameters [20]. Figure 2 demonstrates the analysis procedures. For each ROI, (a) 5 features were computed from the histogram, and (b) Six features were computed from grey-level features co-occurrence, leading to 11 features per ROI for each patient.

2.5. Feature selection

Feature selection refers to the process of selecting essential features in predictive models. Irrelevant features can degrade the prediction model by contributing little to it [6]. Model overfitting challenges arise when there are too numerous features in the algorithm. A significant feature containing fewer numbers, but high precision can be minimised by determining the size of the feature set through the feature selection approach [42]. It is popular to use recursive feature elimination [29,43,44,45,46] and LASSO to select the best features from the dataset. Recursive feature elimination (RFE) and the least absolute shrinkage and selection operator (LASSO) were employed in this study for feature selection due to their high performance and widespread use. The Python environment with scikit-learn (version 1.0.2) was used to implement these feature selection algorithms.

2.5.1. Classification and Prediction

Both SVM with hyperparameter tuning via grid search [43,46,47,48] and RF with hyperparameter tuning via a randomized search [28,49] were used to achieve optimal and robust classification performance for significant cancer versus non-tumor regions and tuning hyper using the scikit-learn library from Python (1.0.2). These classification techniques were selected and assessed because they have been extensively used to identify different organs, as mentioned in previous studies [26,43,45,50]. To differentiate between regions with significant cancer and those without tumors, we employed radiomics parameters. These parameters included statistical features from both the 1st and 2nd order, extracted from the Gray-Level Co-occurrence Matrix (GLCM). Our approach involved utilizing two machine learning classifiers: the Random Forest (RF) classifier and the Support Vector Machine (SVM) classifier. For the RF model, we conducted a randomized search to fine-tune its hyperparameters, which encompassed factors such as the number of estimators, criterion, max depth, and max features. In contrast, for the SVM model, we engaged in a grid search method to optimize hyperparameters such as C, gamma, and the choice of kernel function.

To evaluate the performance and reliability of these models, we conducted a K-fold cross-validation process with K set to 5. This rigorous validation procedure ensured that our models could effectively distinguish between regions with significant cancer and non-tumor regions based on radiomics data.

For prediction among GS cohorts, radiomics parameters, including 1st and 2nd orders looking at GLCM, were entered into an RF classifier via randomized search and an SVM classifier with hyperparameter tuning via grid search to prove their significance. The RF model with a randomized search trained with different hyperparameter settings (including number estimators, criterion, max depth, and max features). The SVM model with grid search trained with different hyperparameter settings (including c, gamma, and kernel). Then the models were computed using starfield K-fold cross-validation (k=5). The RF and SVM-based tuning hyperparameter classifiers were interpreted using a binary classification method, with G2 vs rest, G3 versus rest, and G4 versus rest employed to illustrate the AUC-ROC. Because of class imbalance, a classifier’s performance may suffer if all of the datasets are assigned to the majority class, leading to high accuracy in classification but low specificity or sensitivity. Several ways to deal with this issue are through oversampling [51] and sample weighting [52,53]. G2 was classified from G3 and G4 using ROC-AUC. The G3 and G4 areas under curves were calculated utilizing the same approach (one vs rest). This study used Python’s scikit-learn (1.0.2) library to verify model validity using a five-fold cross-validation approach.

2.6. Statistical analysis

Each radiomics parameter was tested for significance using the Kruskal-Wallis technique. Radiomic features and PCa patients’ significant cancer versus non-tumor regions were correlated using Spearman correlation. Statistical significance was determined using the Holm-Bonferroni method at a p-value of ˂0.05 [54].

Using the Kruskal-Wallis test, each radiomics feature was looked at again to see if it was significant in the GS cohorts. The value of the correlation between radiomics characteristics and the GS groups for prostate cancer subjects was determined using the Spearman correlation, which was employed to measure the correlation value. Statistical significance was determined using the Holm-Bonferroni method at a p-value of ˂0.05 [54].

3. Result

3.1. Patients

This study used 71 prostate cancer subjects from the SPIE, NCI/NIH, and AAPM PROSTATEx-2 Cancer Imaging Archive (TCIA). Epstein et al. [52] identified pathology Gleason Grade Group (GG) numbers for cancer tumors. To better represent clinical management, the patients redefined by GGG: 39 subjects, G2 = 3 + 4; 18 subjects, G3 = 4 + 3; and G4, 14 subjects, Gleason primary pattern of 4+4 = 8, 3+5 = 8, 9 (G5), or 10 (G5).

3.2. Association between radiomic attributes and significant versus non-tumor regions

Each prostate cancer patient’s T₂WI and ADC map images were used to extract radiomics features. The Kruskal-Wallis approach was used to ascertain if any feature from radiomics had statistical significance to make a comparison between significant tumor versus non-tumor regions. The radiomics features correlated with significant cancer versus nontumor regions using Spearman correlation.

In the Kruskal-Wallis significance test, eleven features were statistically significant: skewness, kurtosis, entropylog10, entropylog2, uniformity, jointentropylog10, jointentropylog2, correlation, contrast, dissimilarity, and angular second moment after applying the Holm-Bonferroni correction (Table 2). Spearman correlation among radiomics attributes and significant cancer versus non-tumor regions reflects significant strong correlation values of 0.31, 0.30, -0.33, -0.23, 0.37, 0.46, 0.56, 0.56, -0.25, 0.27, 0.26, 0.76, 0.80, and 0.37 for skewness, kurtosis, entropylog10, entropylog2, uniformity, jointentropylog10, jointentropylog2, angular second moment, contrast, dissimilarity, and correlation, respectively (Table 3).

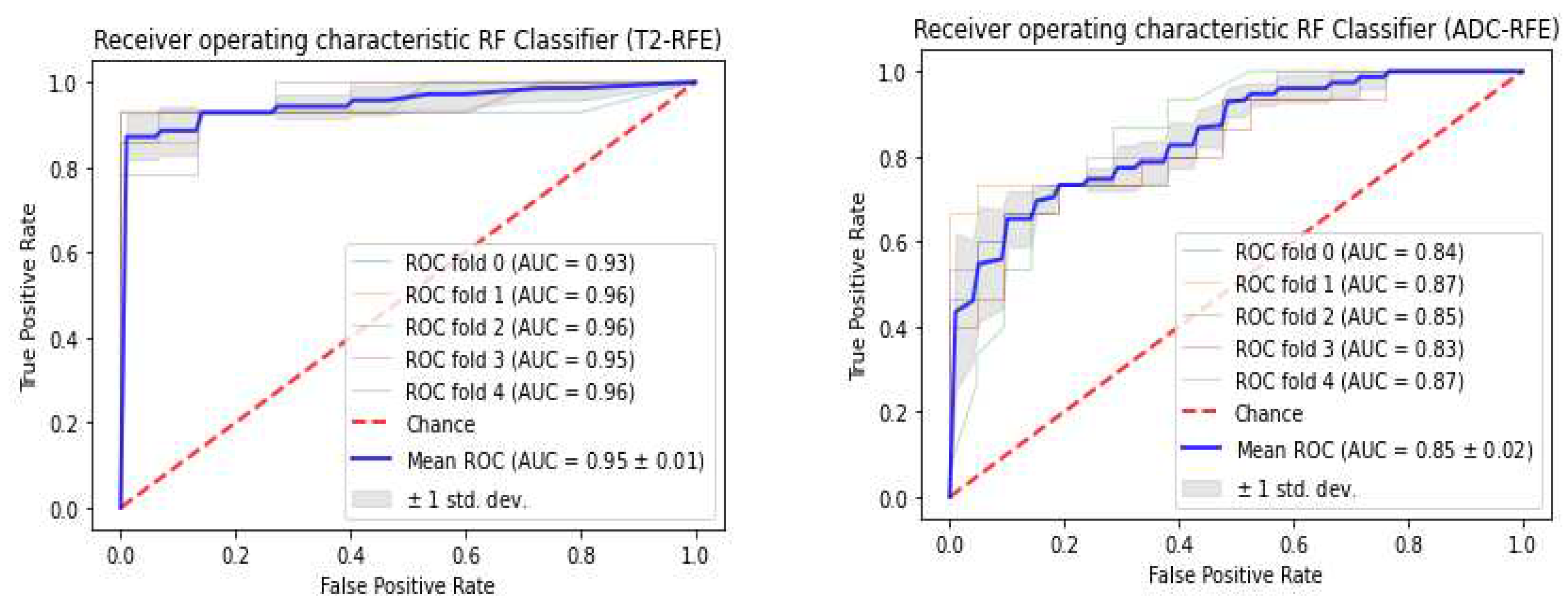
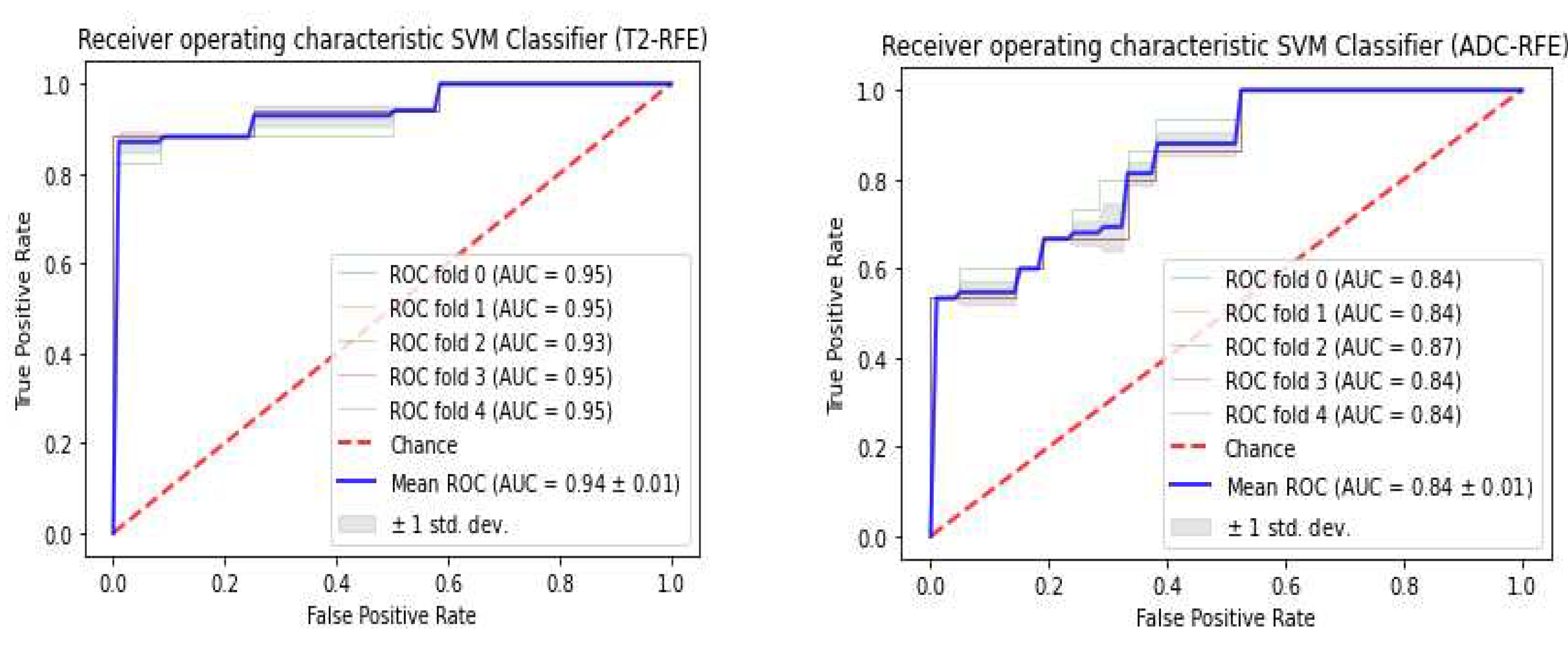
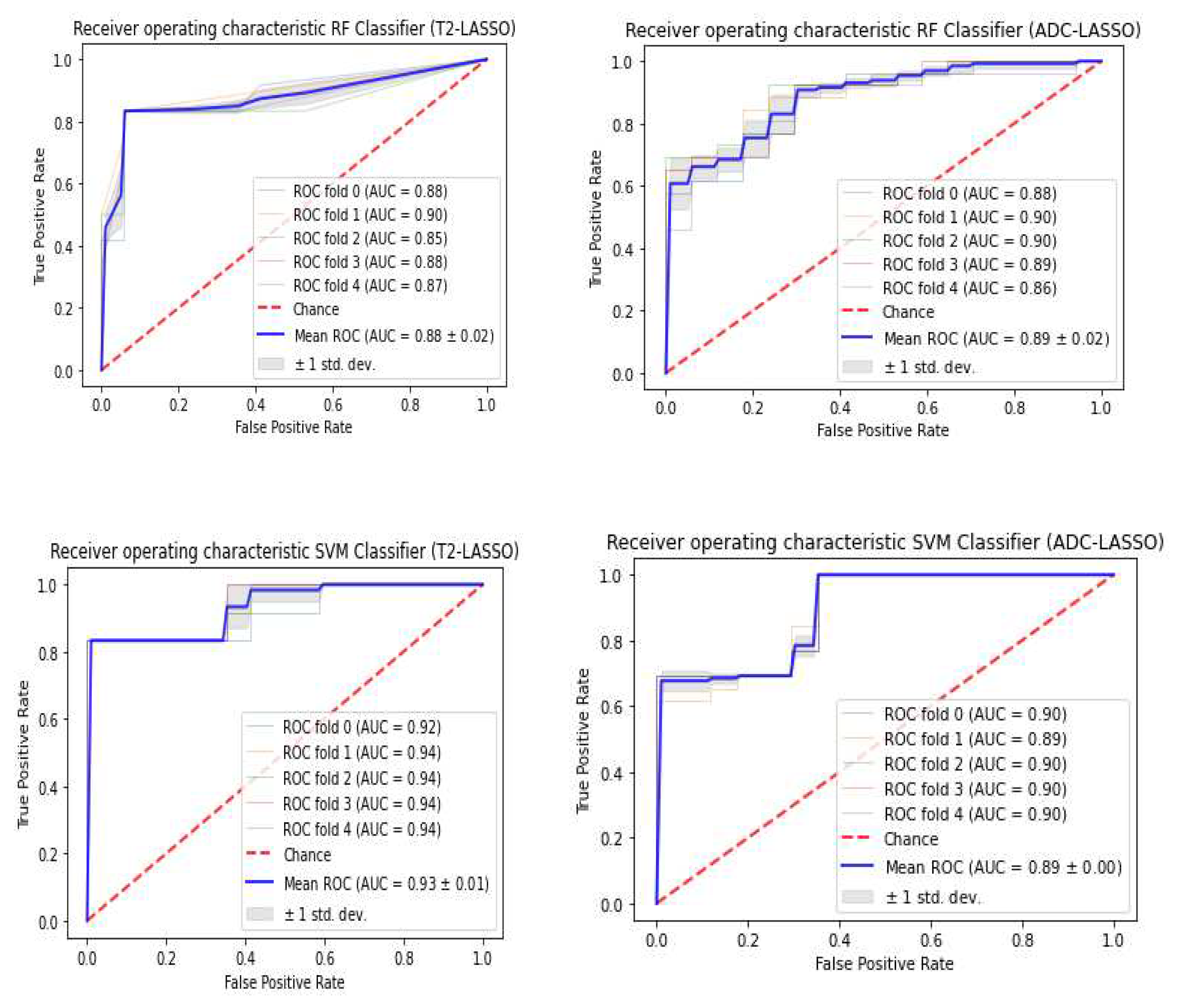
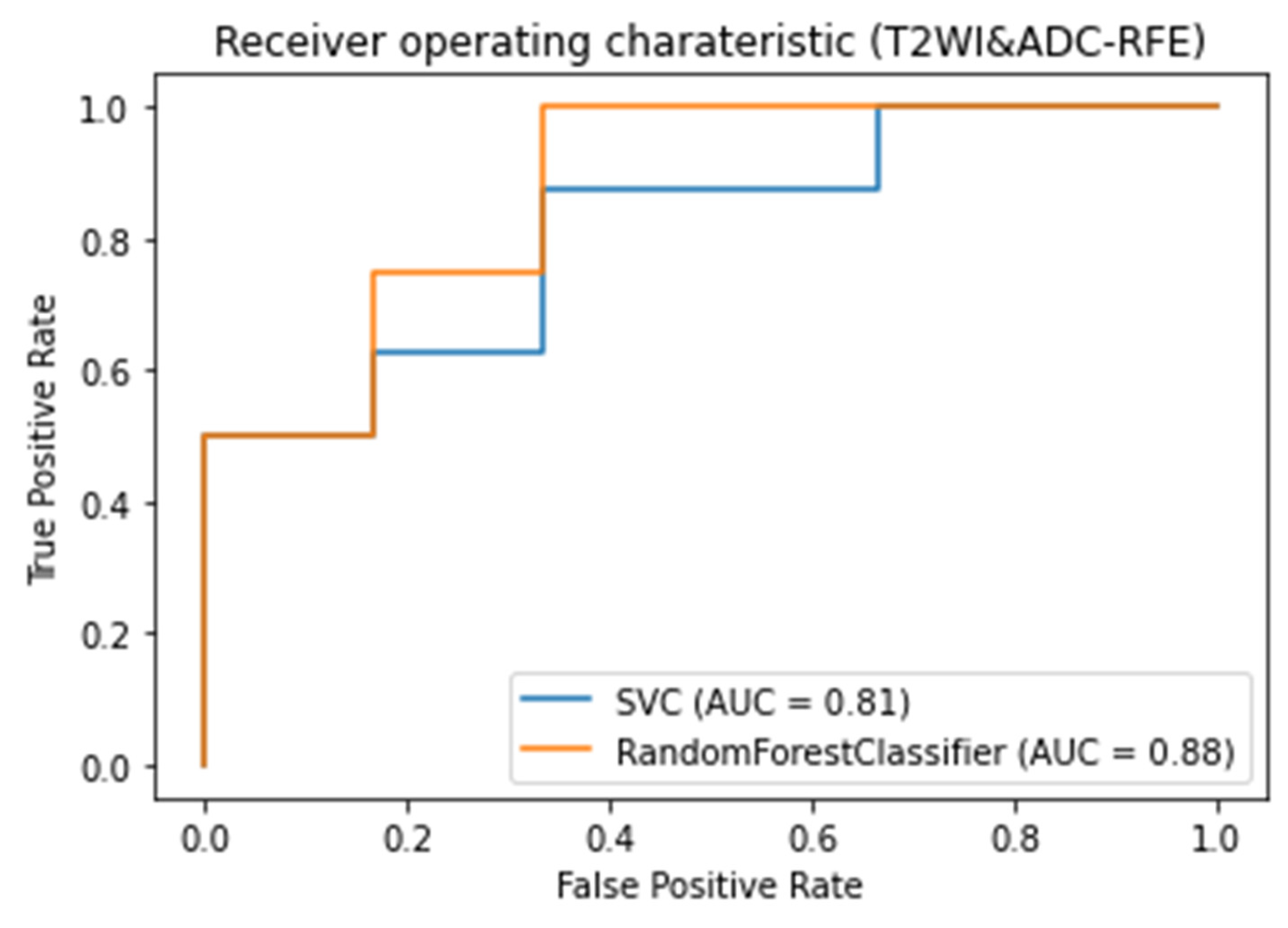
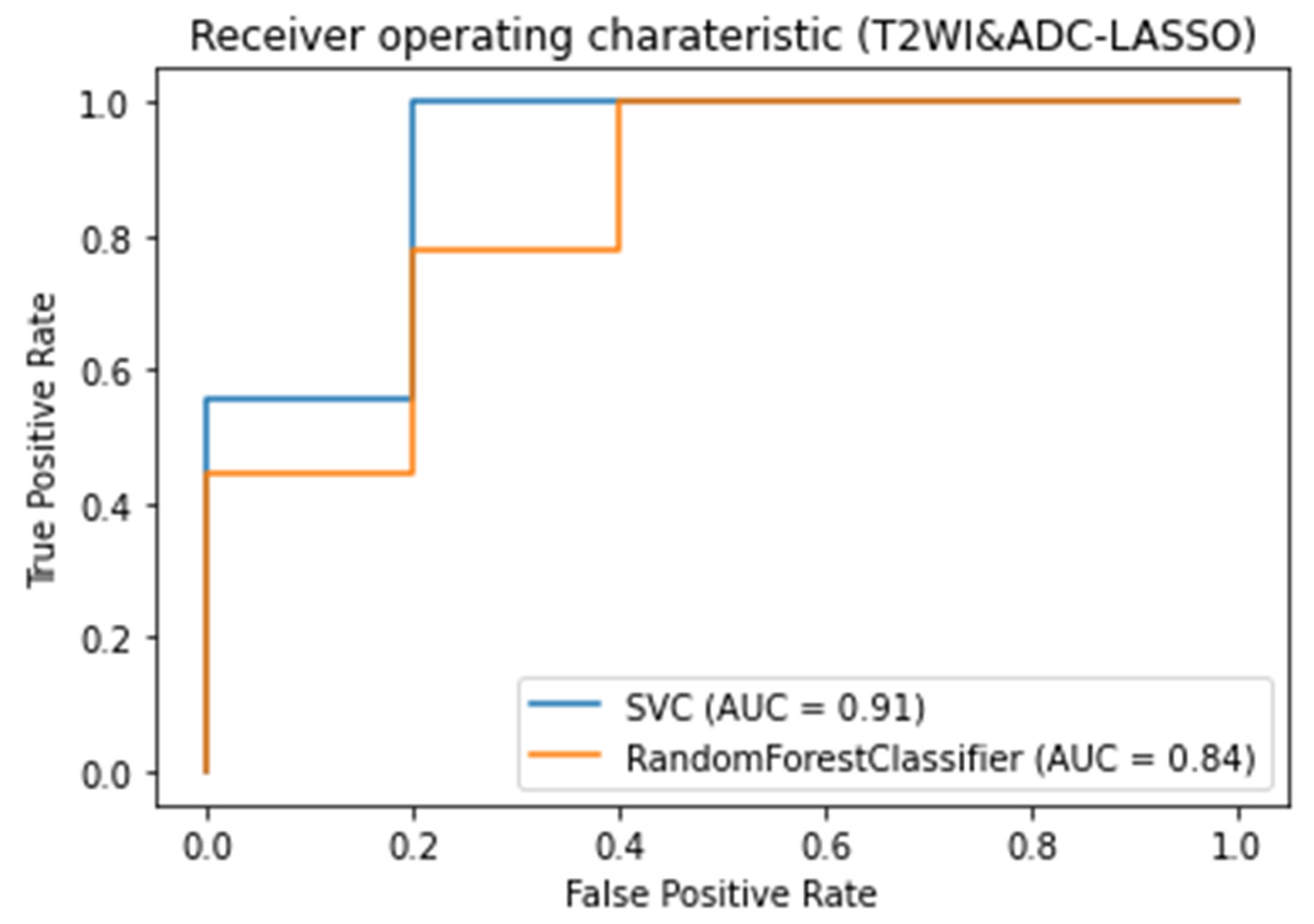
3.3. Classifiers and Feature Selection Performance

The radiomics features were fed into a model that used RF and SVM classifiers with tuned hyperparameters to distinguish between significant cancer versus non-tumor regions in 71 PCa patients. For T₂WI images, the RFE combined RF Classification algorithm obtained the maximum AUC of 0.95 ± 0.01 (with 5-fold CV). Furthermore, the RFE with the SVM classification algorithm obtained the second maximum AUC of 0.94 ± 0.01 (with 5-fold cross-validation). Nevertheless, the selection technique LASSO with support vector machine classifier obtained the highest AUC of 0.93 ± 0.01 (with 5-fold cross-validation). Furthermore, the selection technique LASSO with random forest obtained the second-highest AUC of 0.88 ± 0.02 (with 5-fold CV). The LASSO combined SVM Classification algorithm obtained the maximum AUC of 0.89 ± 0.00 (with 5-fold CV) for ADC images.

The selection method LASSO with RF classification algorithm also obtained the second highest AUC of 0.89 ± 0.02 (with 5-fold CV). Nevertheless, the selection approach recursive feature elimination with random forest classification algorithm obtained the highest AUC of 0.85 ± 0.02 (with 5-fold cross-validation). Furthermore, the RFE combined SVM selection technique obtained the second maximum AUC of 0.84 ± 0.01 (with 5-fold CV). In conclusion, we selected the most appropriate feature selection technique and classification algorithm for each sequence. Figure 3 and Figure 4 depict the receiver operating characteristic area under curves (ROC-AUC) for T₂WI and ADC map images, respectively.

For combined sequences (T₂WI and ADC map images), the LASSO combined SVM Classification algorithm obtained the maximum AUC of 0.91. Furthermore, the RFE with the RF classification algorithm obtained the second maximum AUC of 0.88 (Figure 5 and Figure 6). For combined sequences (T₂WI and ADC map images), the RFE combined SVM Classification algorithm obtained an AUC of 0.81 (Figure 5). Furthermore, the LASSO with RF classification algorithm obtained an AUC of 0.84 (Figure 6).

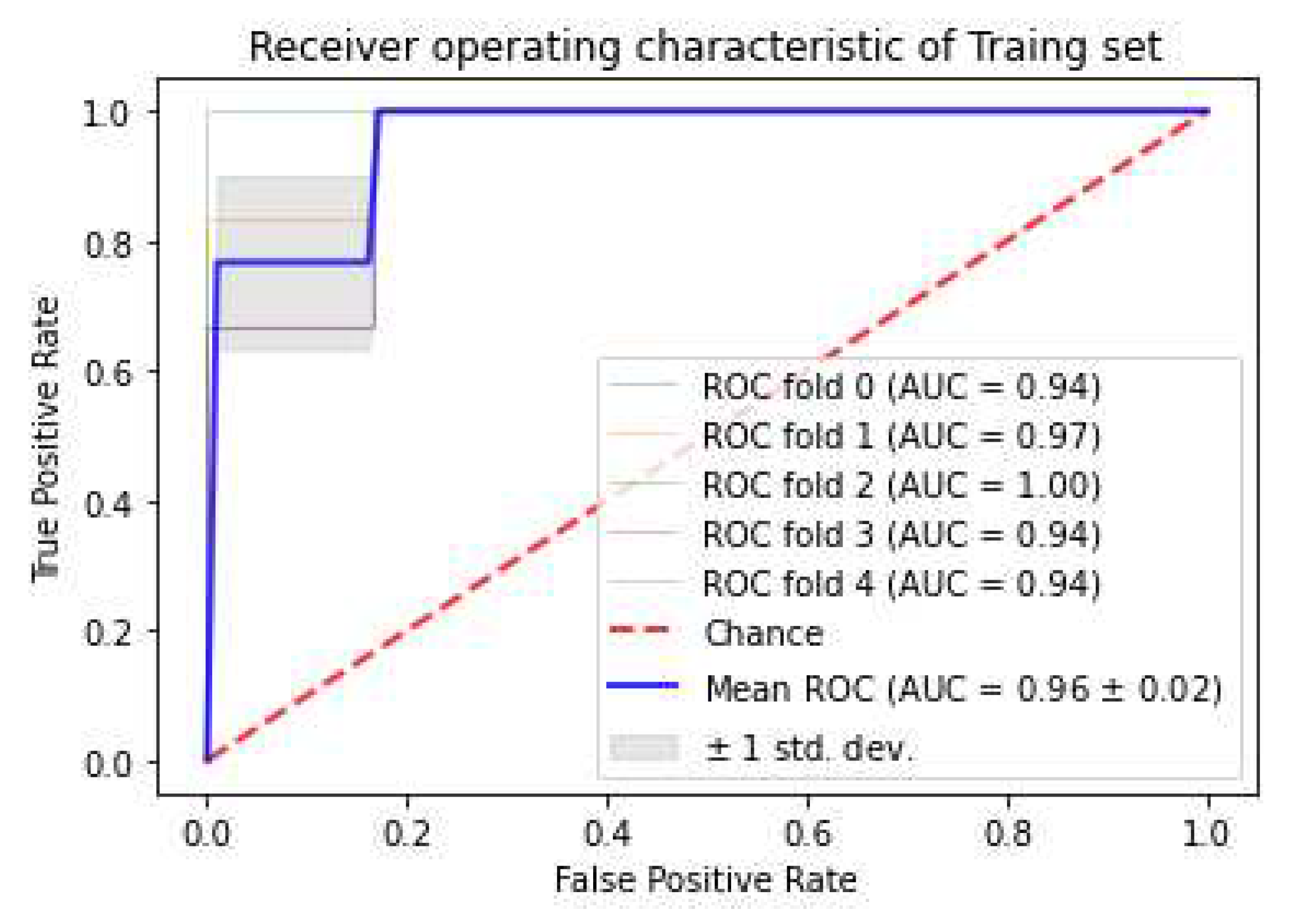
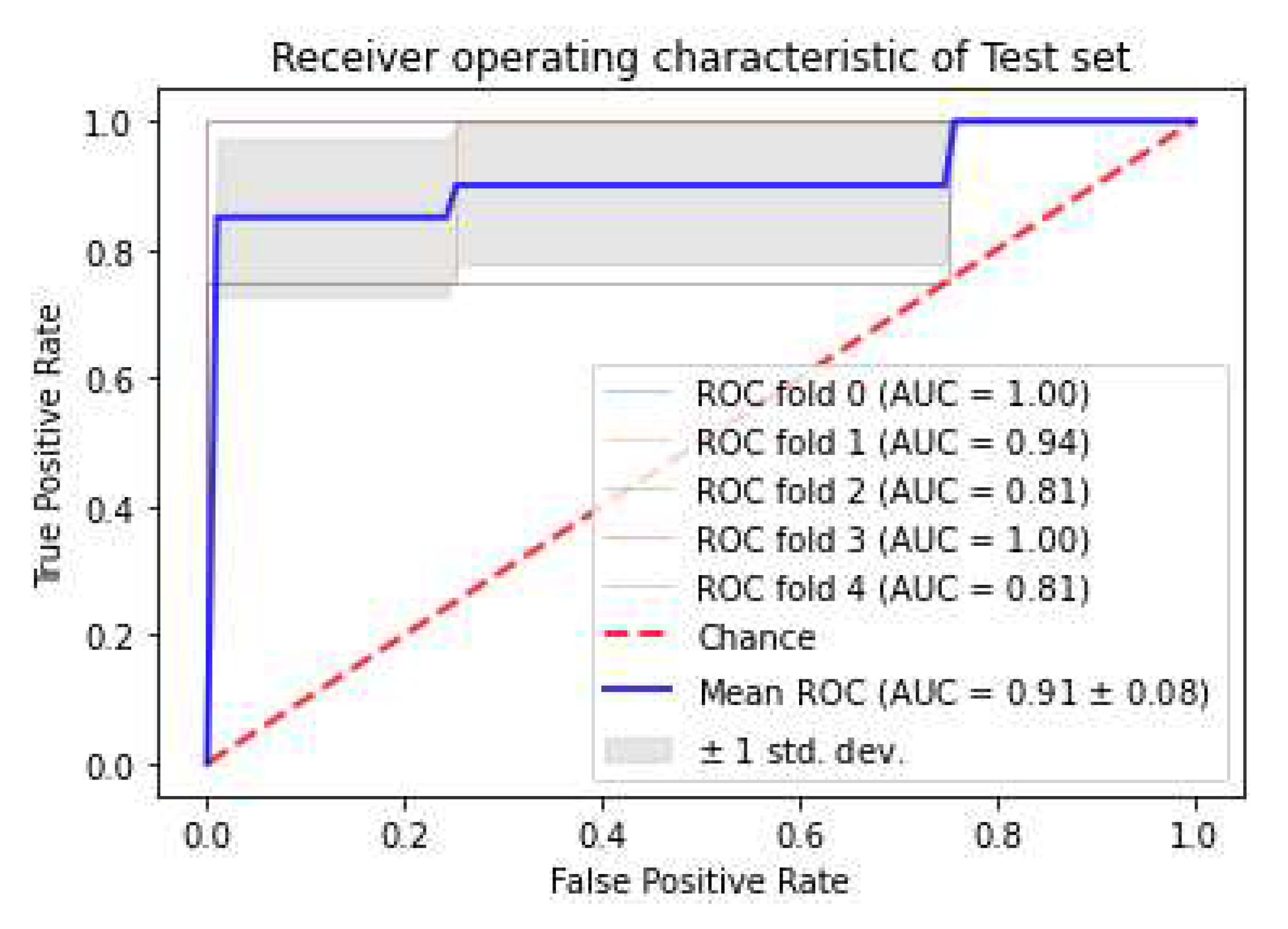
3.4. Model strength and performance variations

Model strength and performance variations were presented in this section to demonstrate how the model performs in different data sets. As illustrated in Figure 7 and Figure 8, the training and test sets performed effectively. Figure 7, illustrates that the AUC for each of the five folds in the training set is 0.94, 0.97, 1.00, 0.94, and 0.94, respectively. The mean AUC is 0.96 ± 0.02 (precision 82%; accuracy 82%; recall 82%; f1-score 82%). Figure 8 shows the receiver operator characteristic area under a curve in the test dataset for the five folds: 1.00, 0.94, 0.81, 1.00, and 0.81, respectively. The mean AUC is 0.91 ± 0.08 (precision 90%; accuracy 87.5.%; recall 88%; f1-score 87%). The model’s performance was tested using the test sets’ mean performance with five-fold cross-validation.

3.5. Association between GS and Radiomics Attributes

The Kruskal-Wallis approach was used to ascertain if any feature from the radiomics aspect had statistical significance to make comparisons between the GS groups after retrieving radiomics features from T₂WI and ADC map images of every prostate cancer subject. The radiomics features and GS cohorts were correlated using Spearman’s correlation.

The Kruskal-Wallis test showed that the three GS cohorts (G2, G3, and G4) were statistically different in uniformity (Table 4). After applying the Holm-Bonferroni correction, no other characteristics were significantly different between GS groups. The correlation coefficients for entropylog2, entropylog10, uniformity and the angular second moment are 0.23, 0.23, -0.24, and -0.26. These numbers have a low correlation (Table 5).

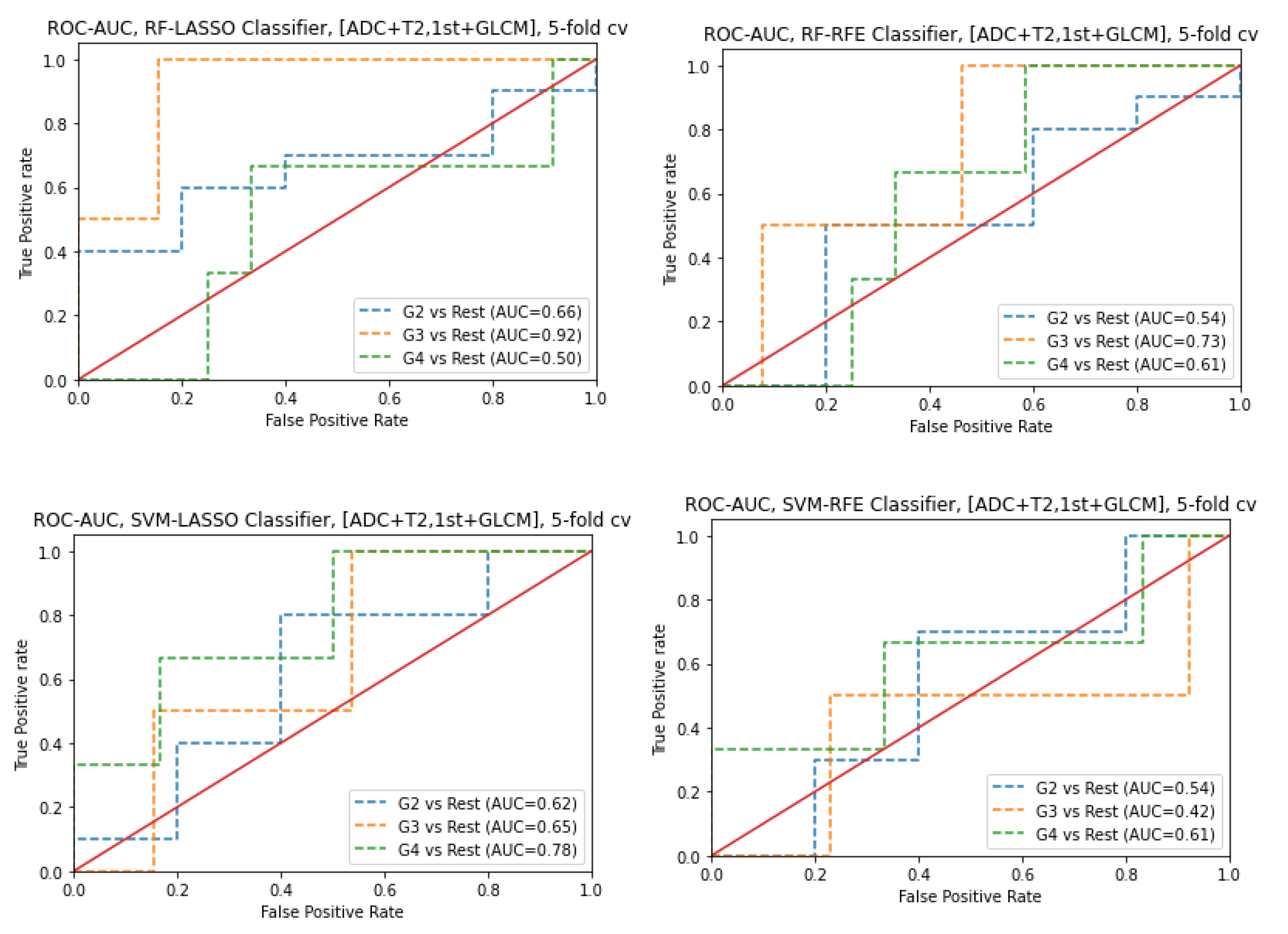
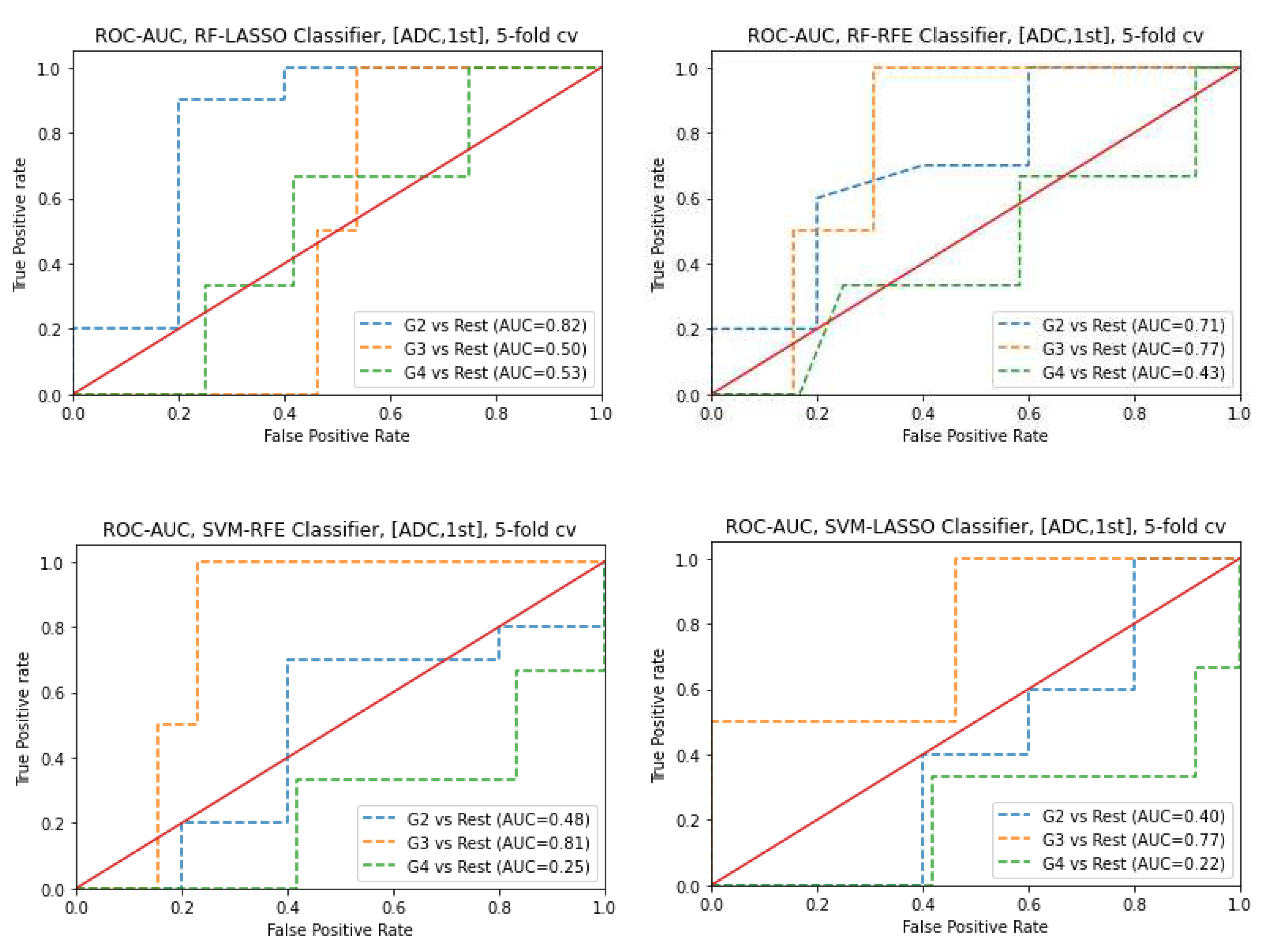
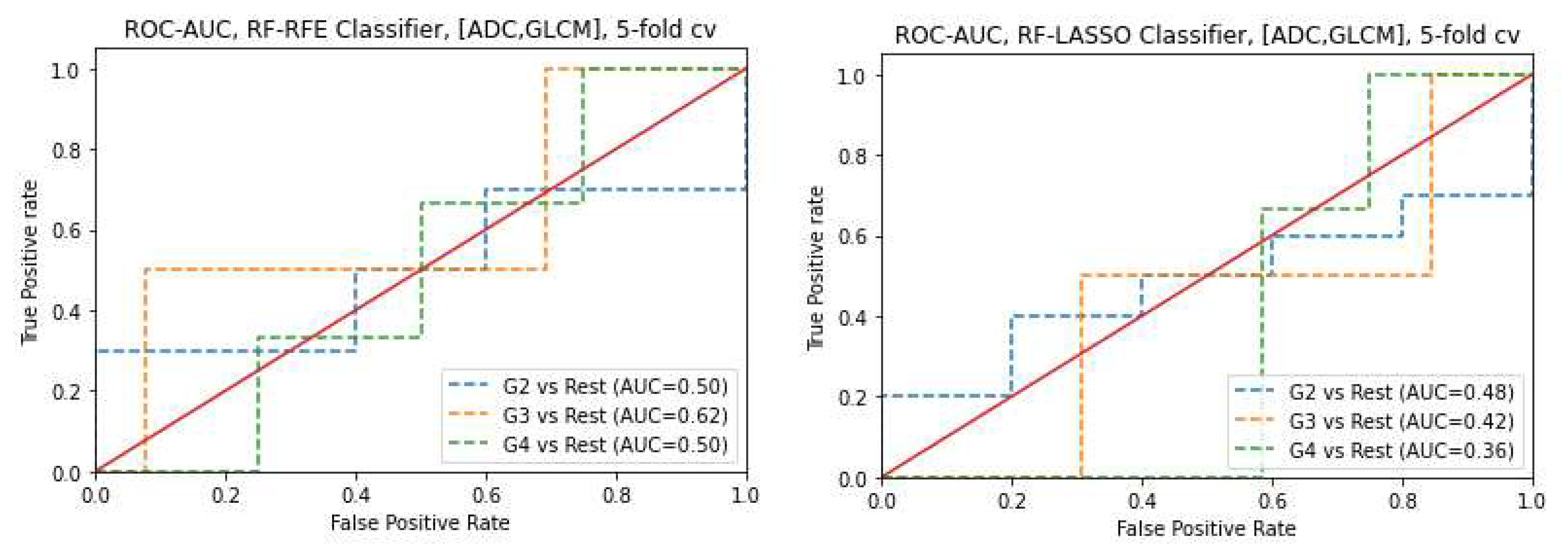
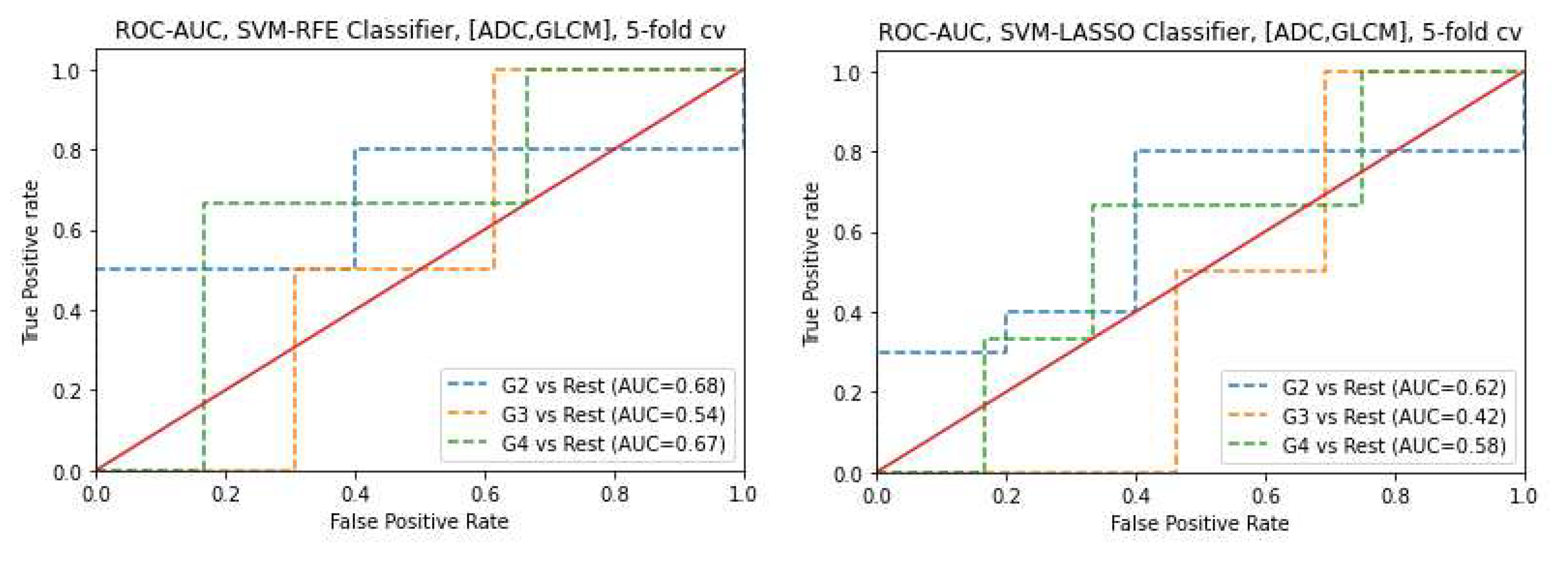
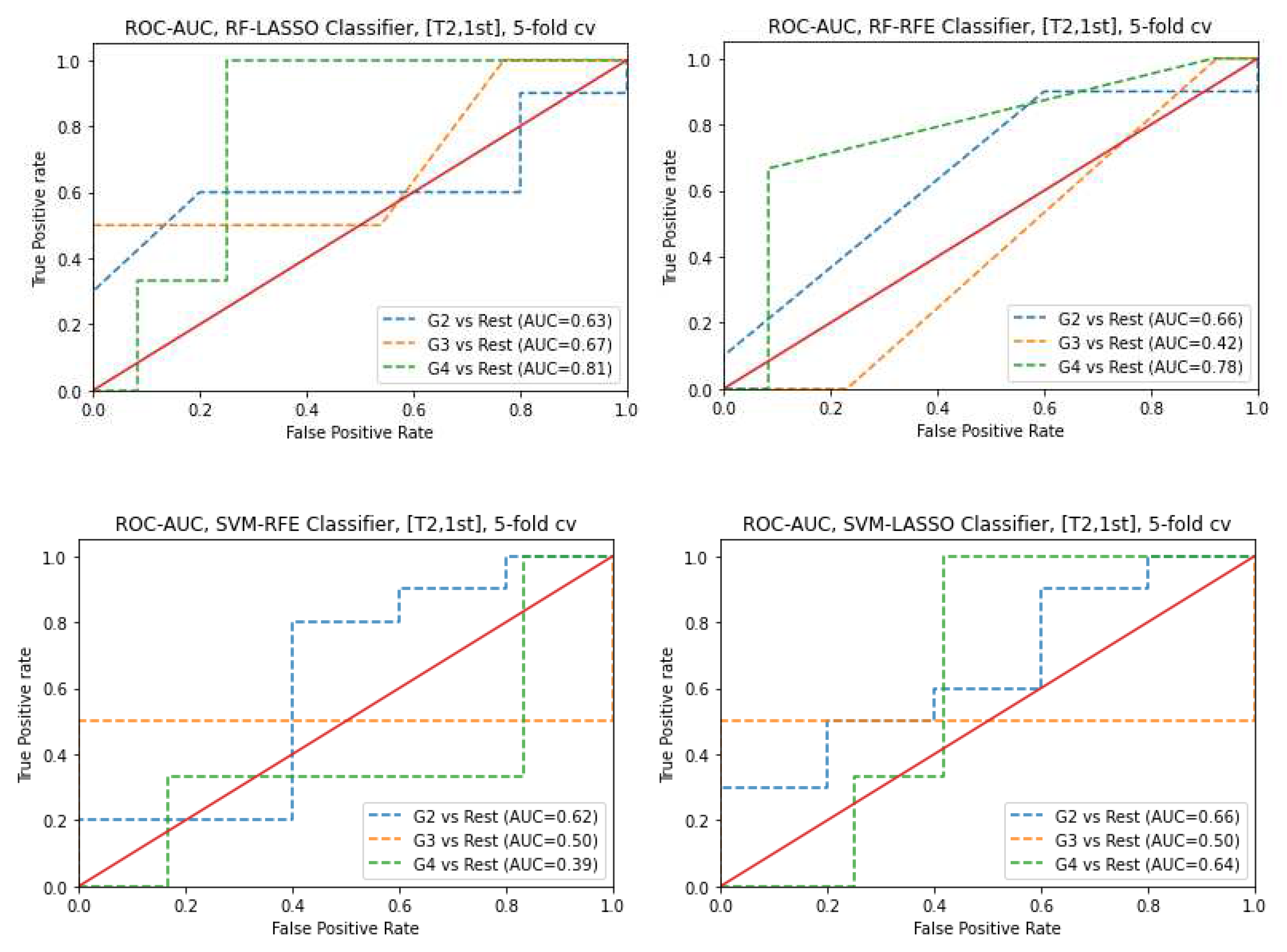
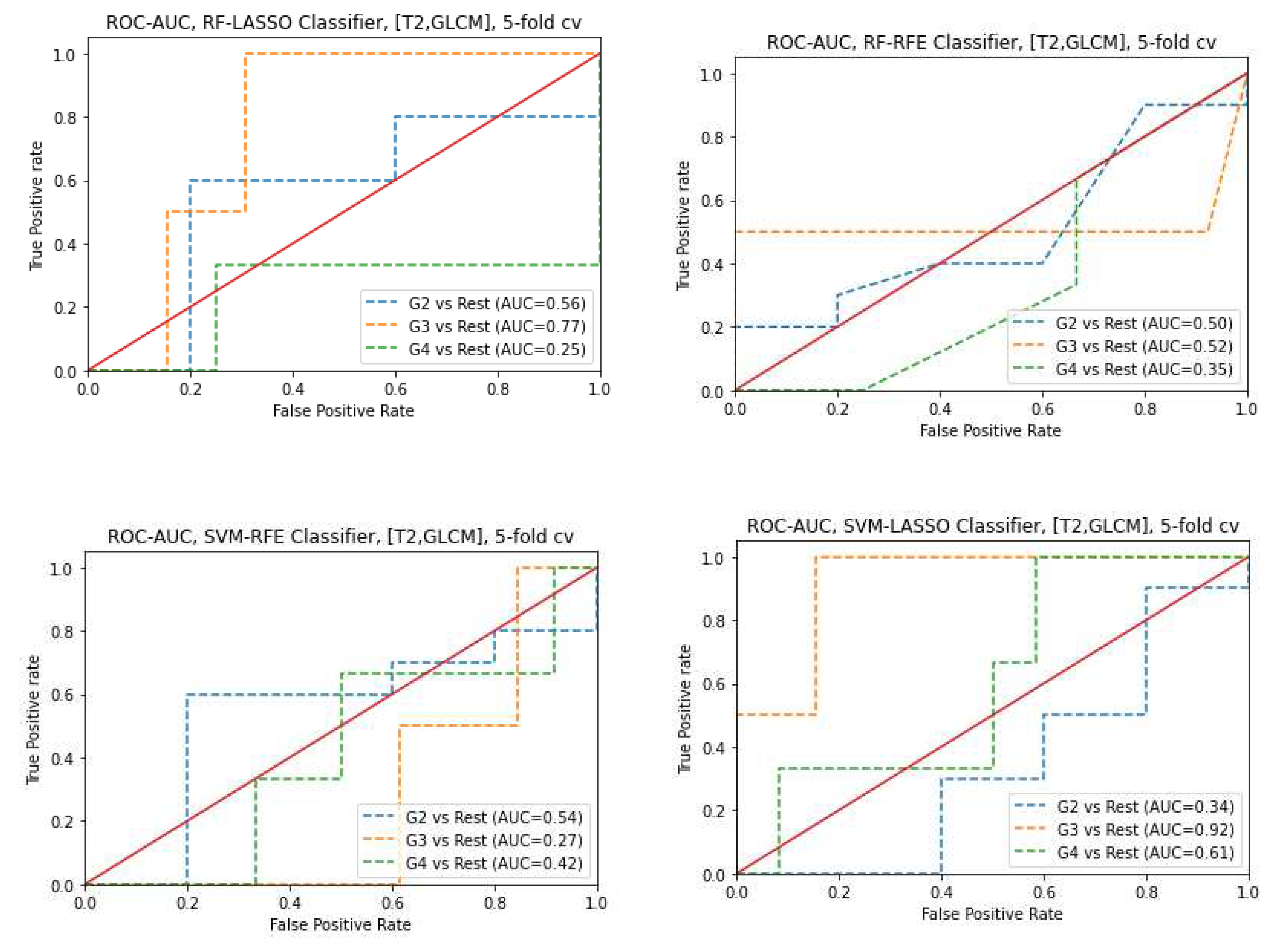
3.6. Prediction of Gleason score

The RF and SVM classifiers with tuning hyperparameters model predicted the GS groups of 71 prostate cancer subjects using all radiomics features. For combined sequences (T₂WI and ADC map images) and features (1st order and GLCM), the LASSO combined RF Classification algorithm had an AUC of 0.92 for G3 subjects and 0.66 for G2 and 0.50 for G4 subjects. For combined sequences (T₂WI and ADC map images) and features (1st order and GLCM), the RFE combined RF Classification algorithm was AUC of 0.73 for G3 subjects and 0.61 for G4 subjects, respectively and 0.54 for G2 subjects. For combined sequences (T₂WI and ADC map images) and features (1st order and GLCM), the LASSO combined SVM classification algorithm was an AUC of 0.78 for G4 subjects, 0.65 for G3, and 0.62 for G2 subjects. For combined sequences (T₂WI and ADC map images) and features (1st order and GLCM), the RFE combined SVM Classification algorithm had an AUC of 0.61 for G4 subjects, 0.54 for G2, and 0.42 for G3 subjects. For combined sequences (T₂WI and ADC map images), the LASSO with RF classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G4 (SVM-LASSO, AUC = 0,78) and G2 (RF-LASSO, AUC = 0.66) (Figure 9).

For ADC map images, using 1st-order features, the LASSO combined RF Classification algorithm was an AUC of 0.82 for G2 subjects, 0.53 for G4 subjects, and 0.50 for G3 subjects. The RFE combined RF Classification algorithm was an AUC of 0.77 for G3 subjects, 0.71 for G3 subjects, and 0.43 for G4 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.81 for G3 subjects, 0.48 for G2 subjects, and 0.25 for G4 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.77 for G4 subjects, 0.40 for G2 subjects, and 0.22 for G4 subjects. For ADC map images, using 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.82 to predict G2 compared to G3 (SVM-RFE, AUC = 0,81) and G4 (SVM-LASSO, AUC = 0.53) (Figure 10).

However, For ADC map images and GLCM features, the LASSO combined RF Classification algorithm was an AUC of 0.48 for G2 subjects, 0.42 for G3 subjects, and 0.36 for G4 subjects. The RFE combined RF Classification algorithm was an AUC of 0.62 for G3 subjects, 0.50 for G4 subjects, and 0.50 for G2 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.68 for G2 subjects, 0.67 for G4 subjects, and 0.54 for G3 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.62 for G2 subjects, 0.58 for G4 subjects, and 0.42 for G3 subjects. For ADC map images, using GLCM features, the RFE with SVM classification algorithm obtained the highest AUC of 0.68 to predict G2 compared to G4 (SVM-RFE, AUC = 0,67) and G3 (RF-RFE, AUC = 0.62) (Figure 11).

………………………………………………………………………………………………………………………………………………………………………………

For T₂WI images, using 1st-order features, the LASSO combined RF Classification algorithm was an AUC of 0.81 for G4 subjects, 0.67 for G3 subjects, and 0.63 for G2 subjects. The RFE combined RF Classification algorithm was an AUC of 0.78 for G4 subjects, 0.66 for G2 subjects, and 0.42 for G3 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.62 for G2 subjects, 0.50 for G3 subjects, and 0.39 for G4 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.66 for G2 subjects, 0.64 for G4 subjects, and 0.50 for G3 subjects. For T₂WI images, using 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.81 to predict G4 compared to G2 (SVM-LASSO and RF-RFE, AUC = 0,66, and 0.66 respectively) and G4 (RF-RFE, AUC = 0.78) (Figure 12).

For T₂WI images, using GLCM features, the LASSO combined RF Classification algorithm was an AUC of 0.77 for G3 subjects, 0.56 for G2 subjects, and 0.25 for G4 subjects. The RFE combined RF Classification algorithm was an AUC of 0.52 for G3 subjects, 0.50 for G2 subjects, and 0.34 for G4 subjects. The RFE combined SVM Classification algorithm was an AUC of 0.54 for G2 subjects, 0.42 for G4 subjects, and 0.27 for G3 subjects. The LASSO combined SVM Classification algorithm was an AUC of 0.92 for G3 subjects, 0.61 for G4 subjects, and 0.34 for G2 subjects. For T₂WI images, using GLCM features, the LASSO with SVM classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G2 (RF-LASSO, AUC = 0,56) and G4 (SVM-LASSO, AUC = 0.61) (Figure 13).

4. Discussion

In PCa assessment, mp-MRI has been demonstrated to be a superior technique, allowing for greater accuracy when detecting cancerous growths. That is the only imaging approach with enough spatial resolution and soft tissue contrast to identify prostate cancer effectively [8] without using ionising radiation. Prostate tumor aggressiveness can be evaluated using artificial intelligence, such as radiomics [56]. Consequently, radiomics could be an innovative and effective method for extracting further clinically relevant data [17]. Radiomics can diagnose prostate cancer early, grade it according to Gleason, determine therapy response, and anticipate biochemical recurrence [56].

Different clinical settings may require different ML techniques for discriminating between sacral chordoma and sacral giant cell malignancies; LASSO using a generalised linear model (GLM) significantly outperformed [27]. However, when it came to scoring colon microarray gene expression and identifying meningioma, random forest and eXtreme Gradient Boosting (XGBoost) classification methods achieved the best performance [28,29,30,57]. Wang et al. revealed that the ML approach of recursive elimination features using a support vector machine is better than other feature selection and classification methods [46]. As a result, it is essential and recommended to discover appropriate machine learning approaches in various clinical implementations in future studies. In the context of prostate cancer classification and grading, our research stands out due to its focus on hyperparameter tuning. While many prior studies have applied machine learning techniques with default hyperparameters, we have systematically optimized these parameters to enhance the precision and robustness of our models. This approach has demonstrated its potential to contribute to more accurate and clinically relevant diagnoses, highlighting the critical role of hyperparameter optimization in medical applications of machine learning.

• Significant cancer versus non-tumor regions

The Kruskal-Wallis test was utilised to examine radiomics characteristics’ relevance in differentiating significant cancer versus non-tumor regions. Then, Spearman correlation was performed to determine the association between radiomics attributes and significant cancer versus non-tumor regions. Two feature selection methods (REF and LASSO) and two classifiers (RF and SVM) with tuned hyperparameters (randomised search and grid search) were used to create an effective ML algorithm. The analysis between radiomics features and the significant versus non-tumor regions revealed eleven radiomics features that are statistically significant (i.e., skewness, kurtosis, entropylog1o, entropylog2, uniformity, jointEntropyLog2, jointEntropyLog10, correlation, contrast, dissimilarity, and angular second moment) with the capacity to discriminate between the significant and non-tumor regions.

Prostate cancer discrimination employing multiparametric MRI radiomics was designed and tested in this study, and the technique consistently performed well in the present study. As this study reveals, classification accuracy varies between ML techniques. For T₂WI, RF and SVM classifiers were observed to be very useful when used with REF (AUC = 0.95 ± 0.01, and 0.94 ± 0.01, respectively). The second-best result was observed using LASSO selection with SVM and RF classifiers (AUC = 0.93 ± 0.01 for T₂WI, and 0.89 ± 0.00 for ADC map, respectively). That is following previous findings have shown that this system is adequate to other feature selection techniques and classifiers in various organs [29,30,43,53,56,58,59]. With support vector machines and random forests classifiers, the AUC for the T₂WI sequence was highest with the selection approach using the REF. Radiomic features can be used to identify the T1-2 and T3-4 stages using an unsupervised clustering algorithm and the supervised LASSO technique, according to Sun et al. [60]. This finding might link to the fact that morphological T₂WI depends on the tumor signal for its assessment. The second-highest AUC was achieved using the selection approach of LASSO with SVM and RF. Wang et al. achieved the best result when combining a support vector machine with recursive feature reduction [46].

Nevertheless, the T₂WI model performed better than the ADC model (AUCs of 0.95 vs 0.89, respectively). We observed that the AUC of the classification algorithm generated from T₂WI images using RF classifiers using the feature selection technique (RFE) was the highest AUC of 0.95 ± 0.01. In addition, the RFE with the SVM classification algorithm obtained the second maximum AUC of 0.94 ± 0.01 (with 5-fold cross-validation). Additionally, T₂WI could perform a non-invasive analysis of PCa biological growth, which might assist in classifying patients for adequate treatment. It also provides morphologic data for cancer diagnosis, localisation, and staging [61]. SVM and RF classifiers with LASSO (For LASSO, AUC of 0.89 ± 0.00, 0.89 ± 0.02 for SVM, and RF classifiers, respectively) and RFE (for RFE, AUC of 00.84 ± 0.01, 0.85 ± 0.02 for SVM, and RF classifiers, respectively) for classification between significant cancer versus non-tumor from ADC map images were lower when compared to T₂WI images. For combined sequences (T₂WI and ADC map images), the LASSO with SVM classification algorithms had an AUC of 0.91. The second-highest AUC was 0.88 for the RFE with the RF classification algorithm. Features from several sequences achieved lower performance compared to single sequence features.

• GS prediction

The Kruskal-Wallis test assessed radiomics features’ ability to predict GS in prostate cancer patients. Radiomics attributes and GS cohorts were then correlated using Spearman correlation. The ML algorithm was developed using feature selection methods (REF and LASSO) and classifiers (RF and SVM) with tuned hyperparameters (randomised search and grid search). ADC map images revealed one radiomics feature from the uniformity that could distinguish GS cohorts.

For combined sequences (T₂WI and ADC map images), the LASSO with RF classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G4 (SVM-LASSO, AUC = 0,78) and G2 (RF-LASSO, AUC = 0.66). In addition, for T₂WI images, using GLCM features, the LASSO with SVM classification algorithm obtained the highest AUC of 0.92 to predict G3 compared to G2 (RF-LASSO, AUC = 0,56) and G4 (SVM-LASSO, AUC = 0.61). Furthermore, for ADC map images, using the 1st order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.82 to predict G2 compared to G3 (SVM-RFE, AUC = 0,81) and G4 (SVM-LASSO, AUC = 0.53). Additionally, for T₂WI images, using First-order features, the LASSO with RF classification algorithm obtained the highest AUC of 0.81 to predict G4 compared to G2 (SVM-LASSO and RF-RFE, AUC = 0,66, and 0.66 respectively) and G4 (RF-RFE, AUC = 0.78).

The results we obtained agree with those of several other studies using texture analysis. It was shown that GLCM texture features are helpful for both PCa detection and GS evaluation [62,63]. Texture features, such as those of the first and second order derived from ADC and T₂WI, and sample augmentation, were demonstrated to effectively achieve reasonably accurate classification of Gleason patterns [53]. Our findings align with employing the Gleason score as the primary criterion for differentiating benign from significant prostate tumors.

There were a few limitations identified in this research. As a starting point, we included only 71 patients and additional validation of these findings in a more significant subject cohort is required. Moreover, validation in multiple clinical settings is required to obtain high-level confirmation for its medical use. We agree that there are limitations to this work and that in clinical settings there are compromises made on mismatched resolutions. Ideally all our data and all clinical data would be at the same resolution field strength etc. providing uniformity in data acquisition and this step could be avoided. Due to the nature of clinical MRI time and the time requirement of different sequences employed this mismatch of resolutions will persist for the near future…

5. Conclusion

Within the scope of this study, the classification of prostate cancer and prediction of GS groups using multiparametric MRI-based radiomics has been proposed. This study presents two types of feature selection and two classifier algorithms with tuning hyperparameters. Our study presents a distinct approach to the classification and grading of prostate cancer. By prioritizing hyperparameter tuning, we have significantly improved the precision and reliability of our machine-learning models. This work underscores the importance of meticulous parameter optimization in enhancing the accuracy of medical diagnoses.

Radiomics analysis based on multiparametric MRI showed excellent results in discriminating non-tumor regions from significant prostate cancer results obtained. Findings suggest that recursive feature elimination as a feature selection method with SVM and RF is the best method for classifying significant cancer from non-tumor regions. The second approach we found for classification is LASSO, which combines feature selection methods with SVM and RF. Compared to features taken from a single sequence, the performance of features taken from multiple sequences was lower.

The results of the radiomics analysis, which depended on the multiparametric MRI, demonstrated superior outcomes in predicting between GS groups. This study used combined sequences (ADC and T₂WI) and radiomics features to classify three groups of GS utilising RF and SVM classifiers with tuned parameters. When combining sequences (T₂WI and ADC map images) and radiomics features (1st and GLCM), LASSO with RF had the highest AUC of 0.92, which enabled it to predict G3. When GLCM features were used, LASSO with SVM achieved the highest AUC (0.92 to predict G3) for single sequence analysis (T₂WI images).

Our approach suggests that using multiple features and classifiers with tuning hyperparameters provided a more clinically dependable method of identifying clinically relevant features. It is essential to perform additional prospective studies to verify and establish the significance of our findings.