Submitted:
05 November 2023
Posted:
07 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Inner Edge of a Neutron Star Inner Crust
3. Determination of the EoS
4. Regression Analysis
4.1. The Regression Function
4.2. The Consistency Assumption for Considered Models
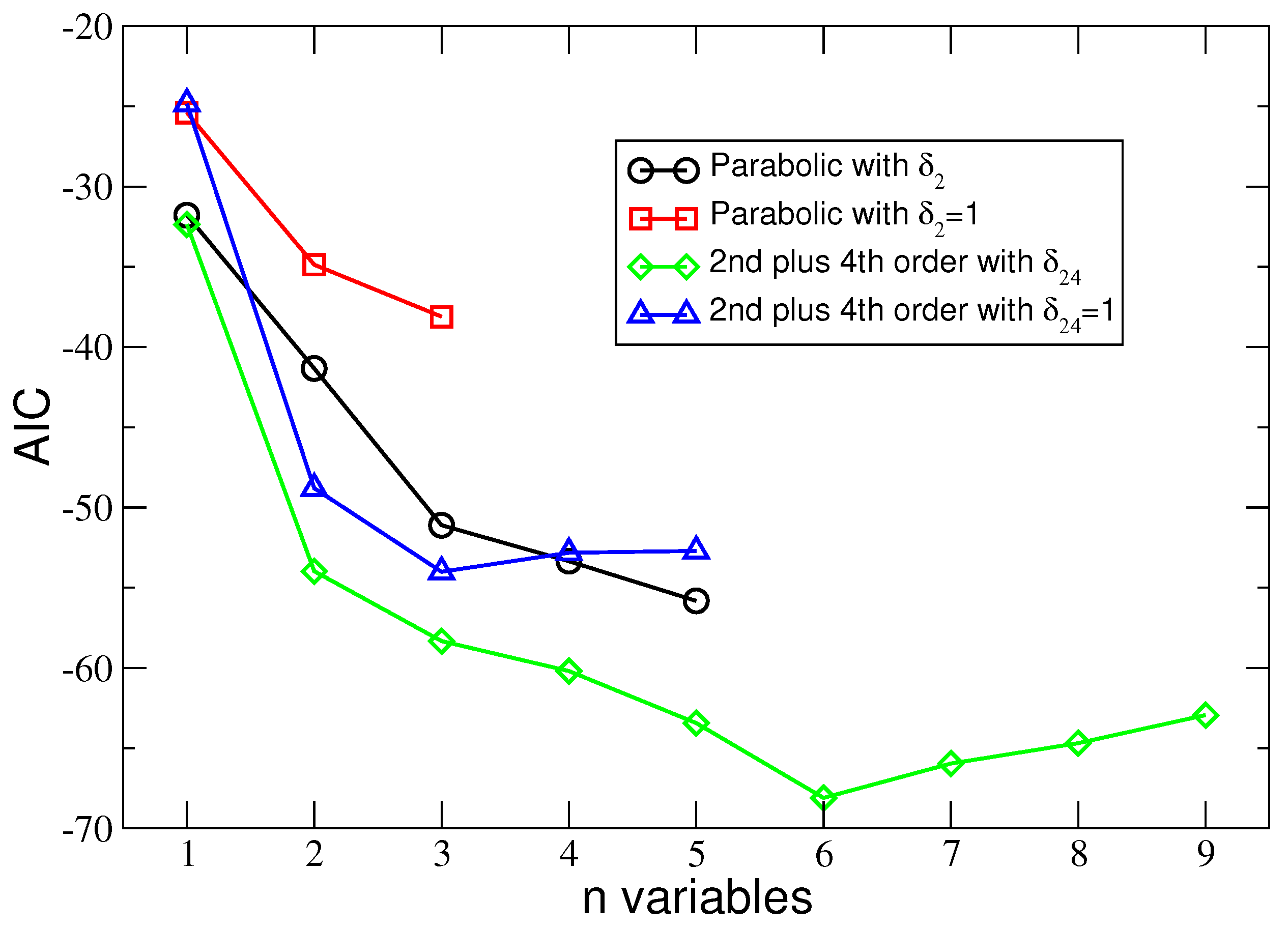
4.3. The Akaike Information Criterion Analysis
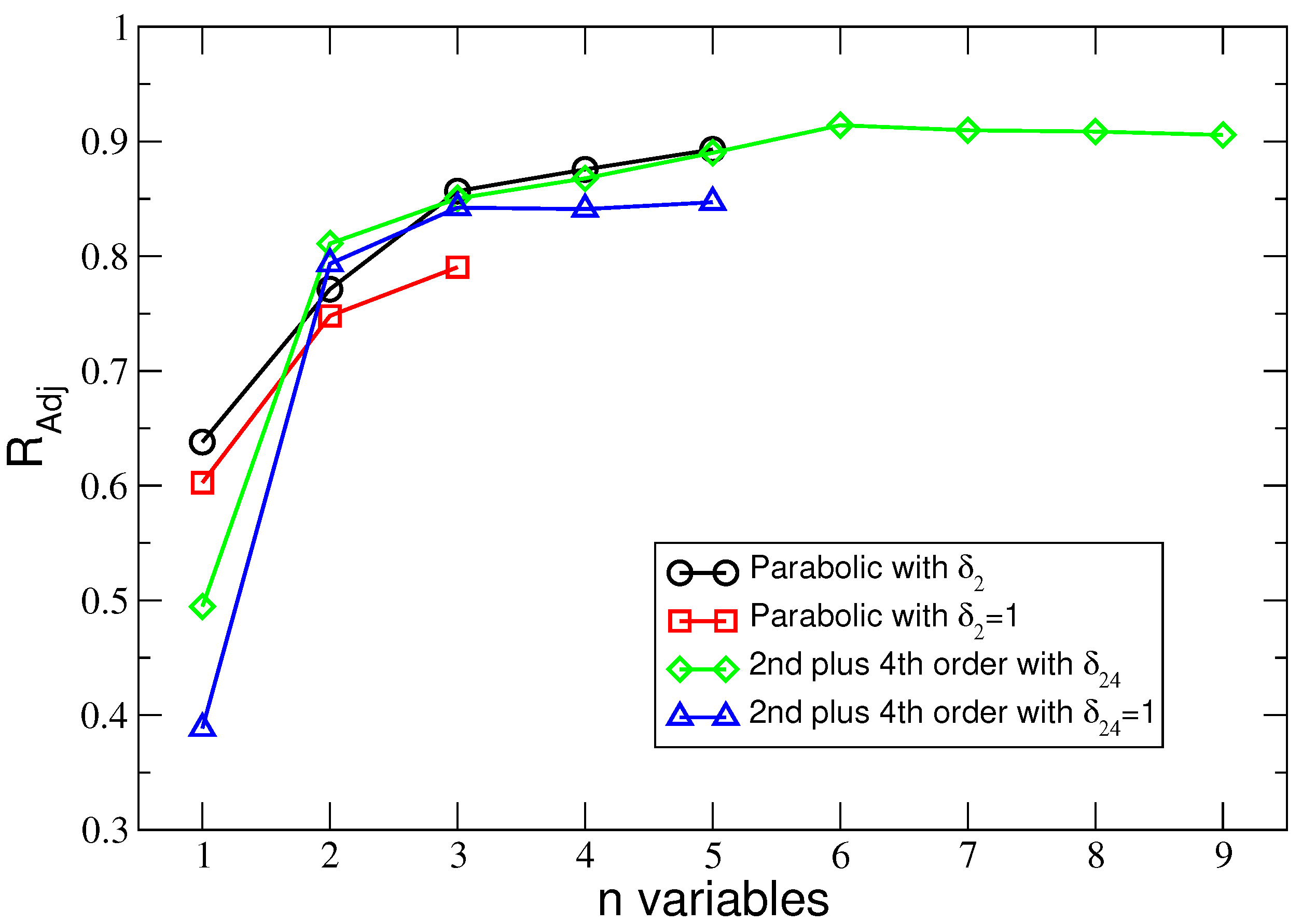
4.4. The Characteristics of the Regressions. Coefficient of Determination and adjusted
4.5. The Backward Selection Method
4.5.1. Statistics
4.5.2. Backward Elimination Method
5. Discussion
5.1. The Results of the Selection of the Regression Models
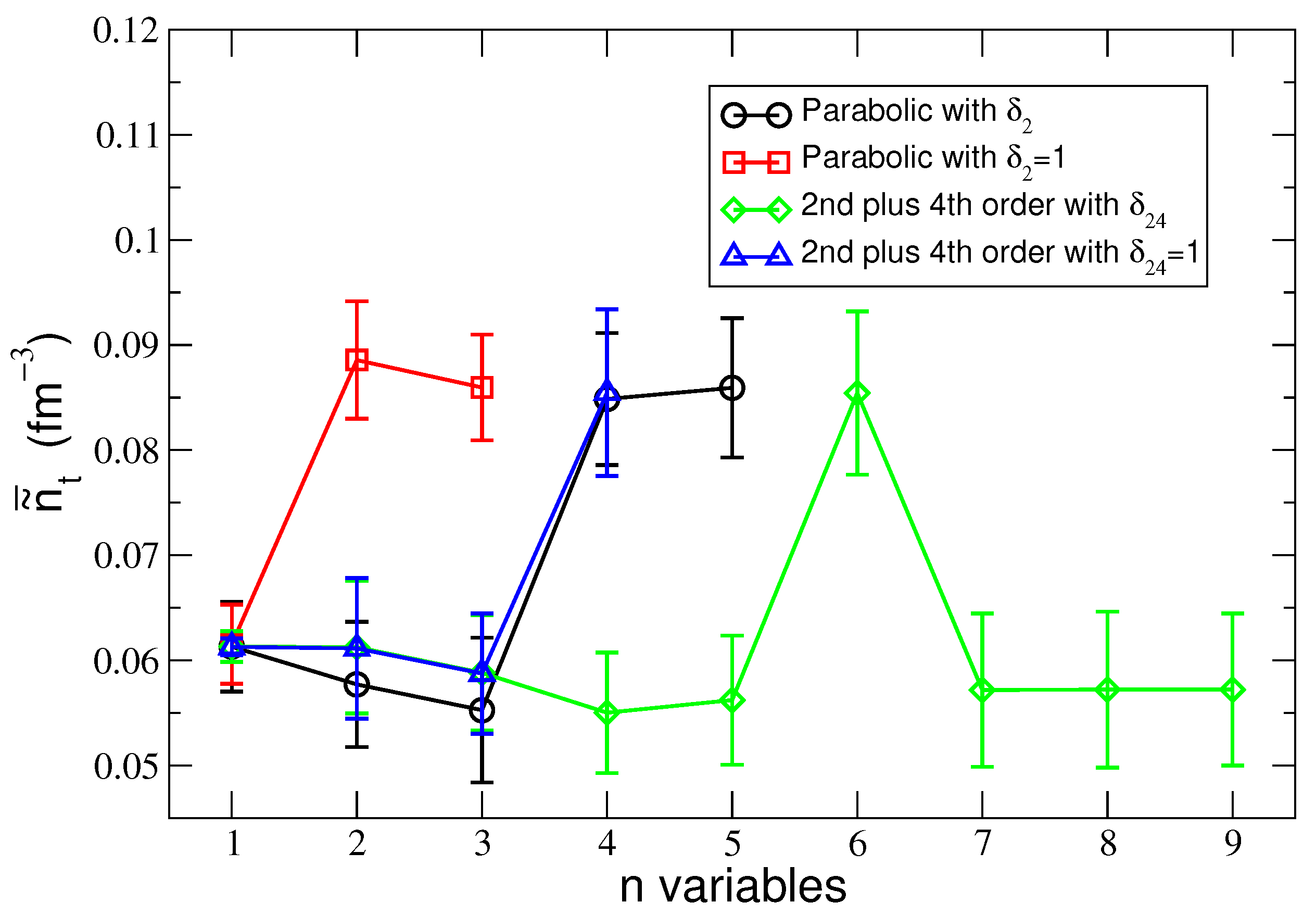
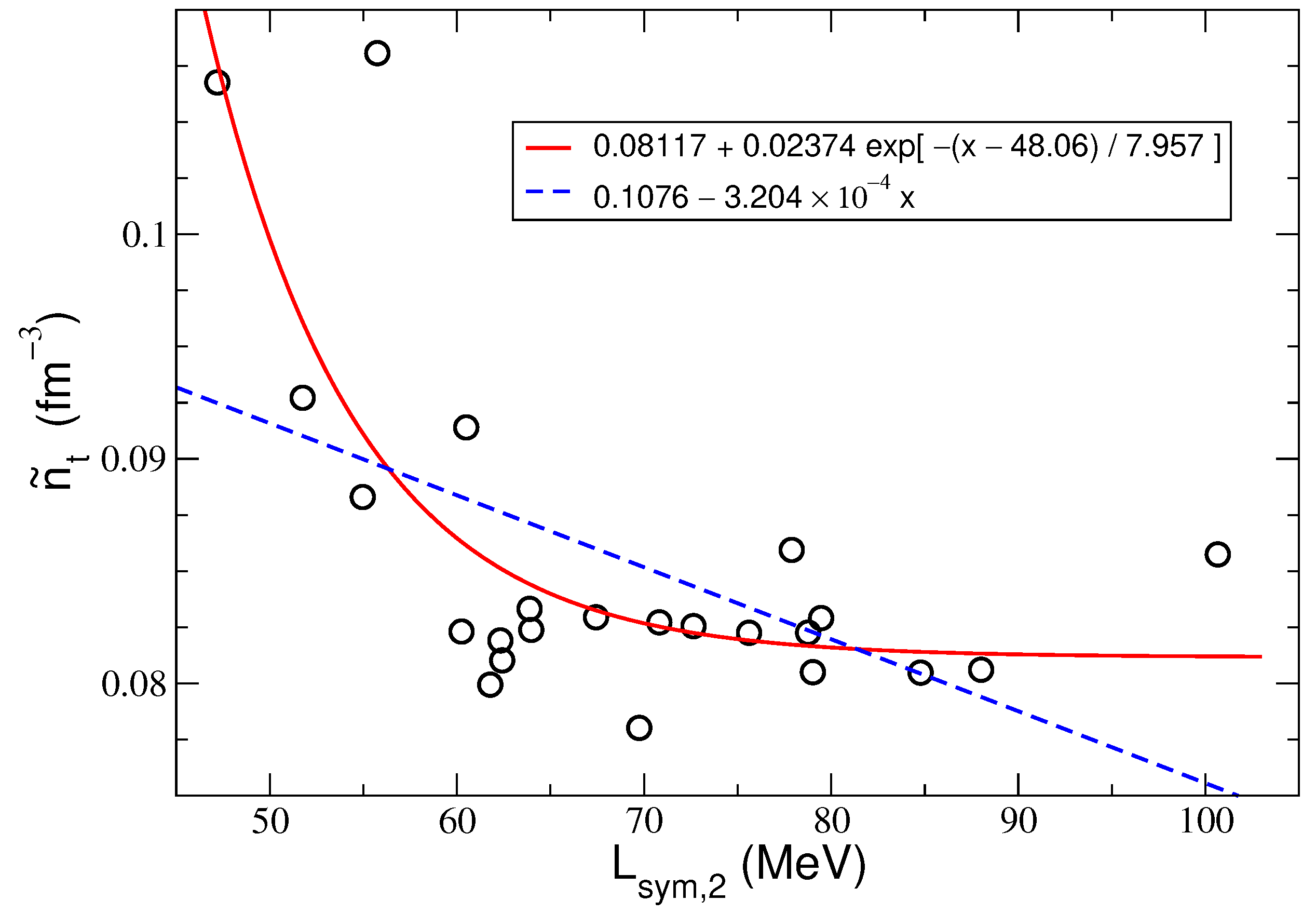
5.2. The Most Probable Value of the Transition Density
6. Conclusions
References
- Ravenhall, D. G.; Pethick, C. J.; Wilson, J. R. Structure of Matter below Nuclear Saturation Density. Phys. Rev. Lett. 1983, 50, 2066–2069. [Google Scholar] [CrossRef]
- Hashimoto, M.; Seki, H.; Yamada, M. Shape of Nuclei in the Crust of Neutron Star. Prog. Theor. Phys. 1984, 1984 71, 320–326. [Google Scholar] [CrossRef]
- Horowitz, C. J.; Pérez-García, M. A.; Piekarewicz, J. Neutrino-“pasta” scattering: The opacity of nonuniform neutron-rich matter. Phys. Rev. C 2004, 69, 045804. [Google Scholar] [CrossRef]
- Steiner, A. W. Neutron star inner crust: Nuclear physics input. Phys. Rev. C 2008, 77, 035805. [Google Scholar] [CrossRef]
- Avancini, S. S.; Menezes, D. P.; Alloy, M. D.; Marinelli, J. R.; Moraes, M. M. W.; Providência, C. Warm and cold pasta phase in relativistic mean field theory. Phys. Rev. C 2008, 78, 015802. [Google Scholar] [CrossRef]
- Devore, J.L.; Berk, K.N. Modern Mathematical Statistics with Applications, 2nd ed., Springer: New York, USA, 2012; pp.352–377.
- Akaike, H. Information Theory and an Extension of the Maximum Likelihood Principle. In Selected Papers of Hirotugu Akaike, 1st ed.; Parzen, E., Tanabe, K., Kitagawa, G., Eds.; Springer: New York, NY, USA, 1998; pp. 199–214. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification, IEEE Transactions on Automatic Control, 1974, 19, 716–723.
- Pawitan, Y. all likelihood: Statistical modeling and inference using likelihood, 1st ed.; Oxford Univ. Press: New York, USA, 2007; pp. 375–382. [Google Scholar]
- Kleinbaum, D.G. Kupper, L.L. Muller, K.E. Nizam, A. Applied Regression Analysis and Other Multivariable Methods, 3rd ed.; Duxbury Press: Pacific Grove, CA, USA, 1998; pp. 172–174. [Google Scholar]
- Ezekiel, M. Methods of Correlation Analysis, 1st ed.; John Wiley & Sons: New York, USA, 1930; pp. 208–211. [Google Scholar]
- Kutner, M.; Nachtsheim, Ch.; Neter, J.; Li, W. Applied Linear Statistical Models, 5th ed.; McGraw-Hill: New York, USA, 2005; pp. 511–537. [Google Scholar]
- Kubis, S. The diffusive instability of kaon condensate in neutron stars. Phys. Rev. C 2004, 70, 065804. [Google Scholar] [CrossRef]
- Kubis, S. Nuclear symmetry energy and stability of matter in neutron stars. Phys. Rev. C 2007, 76, 025801. [Google Scholar] [CrossRef]
- Lattimer, J. M.; Prakash, M. Neutron star observations: Prognosis for equation of state constraints Phys. Rep. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Xu, J.; Chen, L. W.; Li, B.A.; Ma, H.R. Nuclear constraints on properties of neutron star crust. ApJ 2009, 697, 1549–1568. [Google Scholar] [CrossRef]
- Mueller, H.; Serot, B.D. Relativistic Mean-Field Theory and the High-Density Nuclear Equation of State. Nucl. Phys.A 1996, 606, 508–537. [Google Scholar] [CrossRef]
- Todd-Rutel B., G.; Piekarewicz, J. Neutron-Rich Nuclei and Neutron Stars: A New Accurately Calibrated Interaction for the Study of Neutron-Rich Matter. Phys. Rev. Lett. 2005, 95, 122501. [Google Scholar] [CrossRef] [PubMed]
- Serot, B.D.; Walecka, J.D. Relativistic Nuclear Many-Body Theory. Adv. Nucl. Phys. 1986, 16, 1–327. [Google Scholar]
- Serot, B.D.; Walecka, J.D. Recent Progress in Quantum Hadrodynamics. Int. J. Mod. Phys. E 1997, 6, 515–631. [Google Scholar] [CrossRef]
- Boguta, J.; Bodmer, A.R. Relativistic calculation of nuclear matter and the nuclear surface. Nucl. Phys. A 1977, 292, 413–428. [Google Scholar] [CrossRef]
- Bednarek, I.; Manka, R.; Pienkos, M. The Influence of the Enhanced Vector Meson Sector on the Properties of the Matter of Neutron Stars. PLoS ONE 2014 9, e106368. [CrossRef]
- Dutra, M.; Lourenço, O.; Avancini, S.S.; Carlson, B.V.; Delfino, A.; Menezes, D.P.; Providência, C.; Typel, S.; Stone, J.R. Relativistic mean-field hadronic models under nuclear matter constraints. Phys. Rev. C 2014, 90, 055203. [Google Scholar] [CrossRef]
- Dutra, M.; Lourenço, O.; Hen, O.; Piasetzky, E.; Menezes, D.P. The symmetry energy γ parameter of relativistic mean-field models. Chinese Phys. C 2018, 42, 064105. [Google Scholar] [CrossRef]
- Stone, J.R.; Stone, N.J.; Moszkowski, S.A. Incompressibility in finite nuclei and nuclear matter. Phys. Rev. C 2014, 89, 044316. [Google Scholar] [CrossRef]
- Khan, E.; J. Margueron, J.; Vidaña, I. Constraining the Nuclear Equation of State at Subsaturation Densities. Phys. Rev. Lett. 2012, 109, 092501.
- Khan, E.; Margueron, J. Determination of the density dependence of the nuclear incompressibility. Phys. Rev. C 2013, 88, 034319. [Google Scholar] [CrossRef]
- M. Farine, J. M. Pearson, and F. Tondeur, Nuclear-matter incompressibility from fits of generalized Skyrme force to breathing-mode energies. Nucl. Phys. A 1997, 615, 135–161.
- Lynch, W.G.; Tsang, M.B.; Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Steiner, A.W. Probing the symmetry energy with heavy ions. Prog. Part. Nucl. Phys. 2009, 62, 427–432. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef]
- Tsang, M. B; Zhang, Y.; Danielewicz, P.; Famiano, M.; Li, Z.; Lynch, W.G.; Steiner, A.W. Constraints on the Density Dependence of the Symmetry Energy. Phys. Rev. Lett. 2009, 102, 122701. [Google Scholar] [CrossRef] [PubMed]
- Stone, J.R.; Reinhard, P.G. The Skyrme interaction in finite nuclei and nuclear matter. Prog. Part. Nucl. Phys. 2007, 58, 587–657. [Google Scholar] [CrossRef]
- Tsang, M.B.; Stone, J.R.; Camera, F.; Danielewicz, P.; Gandolfi, S.; Hebeler, K.; Horowitz, C.J.; Lee, J.; Lynch, W.G.; Kohley, Z.; Lemmon, R.; Moller, P.; Murakami, T.; Riordan, S.; Roca-Maza, X.; Sammarruca, F.; Steiner, A.W.; Vidaña, Yennello, S.J. Constraints on the symmetry energy and neutron skins from experiments and theory. Phys. Rev. C 2012 86, 015803.
- Li B.-A.; et al. Imprints of nuclear symmetry energy on properties of neutron stars. J. Phys.: Conf. Ser. 2011, 312, 042006.
- Centelles, M.; Roca-Maza, X.; Viñas, X.; Warda, M. Nuclear Symmetry Energy Probed by Neutron Skin Thickness of Nuclei. Phys. Rev. Lett. 2009, 102, 122502. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Gang, U.; Liu, Y.; Marks, R.; Nayak, B.K.: P. V. Madhusudhana Rao, P.V.; Fujiwara, M.; Hashimoto, H.; Kawase, K.; Nakanishi, K.; Okumura, S.; Yosoi, M.; Itoh, M.; Ichikawa, M.; Matsuo, R.; Terazono, T.; Uchida, M.; Kawabata, T.; Akimune, H.; Iwao, Y.; Murakami, T.; Sakaguchi, H.; Terashima, S.; Yasuda, Y.; Zenihiro, J.; Harakeh, M.N. Isotopic Dependence of the Giant Monopole Resonance in the Even-A112-124 Sn Isotopes and the Asymmetry Term in Nuclear Incompressibility. Phys. Rev. Lett. 2007, 99, 162503.
- Danielewicz, P. Surface symmetry energy. Nucl. Phys. A 2003, 727, 233–268. [Google Scholar] [CrossRef]
- Dhiman, S.K.; R. Kumar; Agrawal, B.K. Nonrotating and rotating neutron stars in the extended field theoretical model. Phys. Rev. C 2007, 76, 045801.
- Kumar, R.; Agrawal, B.K.; Dhiman, S.K. Effects of omega meson self-coupling on the properties of finite nuclei and neutron stars. Phys. Rev. C 2006, 74, 034323–034345. [Google Scholar] [CrossRef]
- Agrawal, B.K. Asymmetric nuclear matter and neutron skin in an extended relativistic mean-field model. Phys. Rev. C 2010, 81, 034323. [Google Scholar] [CrossRef]
- Furnstahl, R.J; Serot, B.D.; Tang, H.-B. A chiral effective lagrangian for nuclei. Nucl. Phys. A 1997, 615, 441–482.
- Sulaksono, A.; Mart, T. Low density instability in relativistic mean field models. Phys. Rev. C 2006, 74, 045806. [Google Scholar] [CrossRef]
- Piekarewicz, J.; Weppner, S.P. Insensitivity of the elastic proton-nucleus reaction to the neutron radius of 208Pb. Nucl. Phys.A 2006, 778, 10–21. [Google Scholar] [CrossRef]
- Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J.; Shen, G. Relativistic effective interaction for nuclei, giant resonances, and neutron stars. Phys. Rev. C 2010, 82, 055803. [Google Scholar] [CrossRef]
- Sugahara, Y.; Toki, H. Relativistic mean-field theory for unstable nuclei with non-linear σ and ω terms. Nucl. Phys. A 1994, 579, 557–572. [Google Scholar] [CrossRef]
- Bednarek, I.; Olchawa, W.; Sładkowski, J.; Syska, J. Regression analysis of the nuclear symmetry energy for relativistic mean-field models. Phys. Rev. C 2022, 106, 055805. [Google Scholar] [CrossRef]
- Bednarek, I.; Olchawa, W.; Sładkowski, J.; Syska, J. Statistical analysis of the effect of the symmetry energy on the crust-core transition density and pressure in neutron stars. Phys. Rev. C 2023, 108, 055801. [Google Scholar] [CrossRef]
| Variables | AIC | |||
|---|---|---|---|---|
| 0.7629 | 0.7516 | -40.4399 | ||
| 0.6544 | 0.6380 | -31.7806 | 0.06131 ± 0.00427 | |
| 0.1782 | 0.1391 | -11.8554 | ||
| 0.0197 | -.0270 | -7.7978 | ||
| 0.0001 | -.0475 | -7.3445 | ||
| ( ) | 0.8224 | 0.8046 | -44.9683 | |
| ( ) | 0.7920 | 0.7712 | -41.3372 | 0.05772 ± 0.00596 |
| ( ) | 0.8763 | 0.8567 | -51.1033 | 0.05527 ± 0.00688 |
| ( ) | 0.8624 | 0.8407 | -48.6563 | |
| ( ) | 0.8982 | 0.8756 | -53.3467 | 0.08487 ± 0.00628 |
| ( ) | 0.8932 | 0.8694 | -52.2390 | |
| ( ) | 0.9173 | 0.8930 | -55.8201 | 0.08593± 0.00663 |
| Variables | AIC | |||
|---|---|---|---|---|
| 0.6637 | 0.6477 | -40.6499 | ||
| 0.5177 | 0.4947 | -32.3577 | 0.06131 ± 0.00146 | |
| 0.2235 | 0.1865 | -21.4046 | ||
| 0.0848 | 0.0413 | -17.6258 | ||
| 0.0129 | -.0341 | -15.8845 | ||
| 0.0090 | -.0382 | -15.7954 | ||
| 0.0025 | -.0450 | -15.6451 | ||
| 0.0015 | -.0460 | -15.6214 | ||
| 0.0014 | -.0461 | -15.6199 | ||
| ( ) | 0.8282 | 0.8110 | -53.9753 | 0.06125 ± 0.0063 |
| ( ) | 0.7554 | 0.7310 | -45.8542 | |
| ( ) | 0.8707 | 0.8503 | -58.3342 | 0.05882 ± 0.0055 |
| ( ) | 0.8636 | 0.8421 | -57.1077 | |
| ( ) | 0.8918 | 0.8678 | -60.1982 | 0.05503 ± 0.00573 |
| ( ) | 0.8906 | 0.8663 | -59.9435 | |
| ( ) | 0.9150 | 0.8901 | -63.4363 | 0.05623 ± 0.00614 |
| ( ) | 0.9087 | 0.8819 | -61.7911 | |
| ( ) | 0.9375 | 0.9141 | -68.1043 | 0.08543± 0.00776 |
| ( ) | 0.9267 | 0.8992 | -64.4407 | |
| ( ) | 0.9384 | 0.9097 | -65.9606 | 0.05718 ± 0.0073 |
| ( ) | 0.9377 | 0.9086 | -65.6782 | |
| ( ) | 0.9418 | 0.9086 | -64.6885 | 0.05723 ± 0.00742 |
| ( ) | 0.9384 | 0.9033 | -63.3813 | |
| ( ) | 0.9442 | 0.9056 | -62.9401 | 0.05723 ± 0.00723 |
| Variables | AIC | |||
|---|---|---|---|---|
| 0.6206 | 0.6026 | -25.3983 | 0.06154 ± 0.00377 | |
| 0.2024 | 0.1644 | -8.3058 | ||
| 0.0018 | -0.0457 | -3.1471 | ||
| ( ) | 0.7709 | 0.7480 | -34.8749 | 0.08857 ± 0.00559 |
| ( ) | 0.7558 | 0.7314 | -33.4109 | |
| ( ) | 0.2186 | 0.1405 | -6.6566 | |
| ( ) | 0.8190 | 0.7904 | -38.1132 | 0.08596 ± 0.00503 |
| Variables | AIC | |||
|---|---|---|---|---|
| 0.4163 | 0.3885 | -24.8389 | 0.06129 ± 0.00081 | |
| 0.2614 | 0.2262 | -19.4268 | ||
| 0.0406 | -.0051 | -13.411 | ||
| 0.0080 | -.0393 | - 12.6422 | ||
| 0.0040 | -.0434 | -12.5512 | ||
| ( ) | 0.8122 | 0.7934 | -48.8023 | 0.06115 ± 0.00668 |
| ( ) | 0.6648 | 0.6313 | -35.4791 | |
| ( ) | 0.8638 | 0.8423 | -54.004 | 0.05876± 0.00572 |
| ( ) | 0.8320 | 0.8055 | -49.1883 | |
| ( ) | 0.8699 | 0.8410 | -52.8228 | 0.08547 ± 0.00793 |
| ( ) | 0.8657 | 0.8359 | -52.0968 | |
| ( ) | 0.8818 | 0.8470 | -52.7082 | 0.05447 ± 0.00657 |
| order | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 2-nd | 0.7276 | 0.001335 | 0.9738 | 0.01369 | 0.573 | 0.0009326 | 0.06771 | 0.7514 | 0.003983 | |
| 2-nd + 4-th | 0.8433 | 0.001034 | 1.9201 | 0.01683 | 0.8438 | 0.000839 | 15.7805 | 0.03577 | 0.5369 | 0.002236 |
| Model | for | for | for | for |
|---|---|---|---|---|
| BSR8 | 0.299938 | 0.343839 | 0.292153 | 0.334073 |
| BSR9 | 0.342497 | 0.385733 | 0.339439 | 0.382146 |
| BSR10 | 0.428416 | 0.473291 | 0.439006 | 0.487483 |
| BSR11 | 0.534352 | 0.583563 | 0.567858 | 0.627902 |
| BSR12 | 0.675834 | 0.751728 | 0.721884 | 0.814746 |
| BSR15 | 0.278423 | 0.316262 | 0.272518 | 0.308937 |
| BSR16 | 0.306975 | 0.348112 | 0.303324 | 0.343495 |
| BSR17 | 0.392911 | 0.437461 | 0.401624 | 0.448741 |
| BSR18 | 0.510366 | 0.564637 | 0.536236 | 0.5984 |
| BSR19 | 0.643445 | 0.708704 | 0.695239 | 0.778184 |
| BSR20 | 0.698844 | 0.759885 | 0.777745 | 0.866059 |
| FSUGoldGZ03 | 0.345584 | 0.388768 | 0.343134 | 0.385933 |
| FSUGoldGZ06 | 0.310274 | 0.351434 | 0.307171 | 0.34749 |
| BKA20 | 0.470379 | 0.519487 | 0.494073 | 0.549805 |
| BKA22 | 0.468696 | 0.507039 | 0.495763 | 0.542082 |
| BKA24 | 0.574315 | 0.617998 | 0.623478 | 0.682634 |
| 0.800376 | 0.851973 | 0.925128 | 1.01912 | |
| 0.438749 | 0.471592 | 0.46765 | 0.507 | |
| FSUGold | 0.55059 | 0.654896 | 0.528628 | 0.618851 |
| FSUGold4 | 0.312472 | 0.391891 | 0.272145 | 0.330303 |
| IU FSUGold | 0.31685 | 0.404539 | 0.257654 | 0.315325 |
| XS | 0.206939 | 0.262488 | 0.18285 | 0.225486 |
| TM1 | 0.674766 | 0.822694 | 0.645515 | 0.772463 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





