1. Introduction
The nuclear reactions mediated by weak interactions play crucial role in presupernova evolution of massive stars [
2]. The
decay, electron and positron capture are the fundamental weak interaction processes that occur during the presupernova phases. The
-decay and electron capture are transformations which produce (anti)neutrinos. A change of lepton-to-baryon fraction (
) of the core matter effects the dynamics of collapse and subsequent explosion of the massive stars [
3,
4]. The sensitivity of core-collapse dynamics depends on time rate of
and entropy of the core material [
5]. The weak interaction mediated rates play an important role in stellar processes including hydrostatic burning, pre-supernova evolution in massive stars and nucleosynthesis (
s-,
p-, and
r-) processes [
6,
7]. The
r-process synthesizes half of the elements heavier than iron [
7]. The site of
r-process remains uncertain to-date [
8,
9,
10]. Pre-requisites include high neutron densities and core temperatures. The study of stellar weak interaction rates is a key area for investigation due to its significant contribution in understanding of pre-supernova evolution of massive stars. The core-collapse simulation depends on reliable computation of ground- and excited-states Gamow-Teller (GT) strength functions [
5]. A substantial species of unstable nuclei are present in the core with varying abundances. Weak interactions of these nuclei in stellar matter may contribute to a better understanding of the complex dynamics of core-collapse. In the recent years, much experimental work has been conducted to study the nuclear properties of exotic nuclei. Since the majority of these nuclei cannot be created under lab conditions, microscopic calculations of stellar weak-decay properties have gained importance in our quest to comprehend stellar processes. Numerous computations have focused on the mechanisms underlying stellar development and nucleosynthesis (e.g.,[
11,
12,
13,
14,
15,
16]). Once an iron core develops in a giant star’s later stages of evolution, there is no more fuel available to start a new burning cycle. Lepton capture and photo-disintegration processes lead to core’s increasing instability and eventual collapse. The number of electrons available for pressure support is reduced by electron capture process, whereas degeneracy pressure is enhanced during
decays [
17].
With the advancement of computing and new technologies, calculation of ground and excited states GT strength distributions have gained attention of many researchers. The charge-changing reaction rates in stellar environment were estimated using several nuclear models. Fuller, Fowler, and Newman made the first substantial effort to compute the astrophysical rates using the independent particle model (IPM) [
18]. To enhance the reliability of their calculation, they took into account the measurable data that was available at the time. Later many other sophisticated nuclear models were used to calculate reduced transition probabilities of GT transitions. Few noticeable mentions include shell model Monte Carlo technique (e.g., [
19]), thermal quasi-particle random-phase approximation, QRPA (e.g., [
19,
20,
21]), large-scale shell model (e.g., [
3]), Gross theory (e.g., [
13]), density functional theory (e.g., [
14]), Hartree-Fock-Bogoliubov method (e.g., [
15]) and shell model (e.g., [
16]).
The current study investigates the effect of pairing gaps on calculated GT strength functions and the associated
decay rates under terrestrial and stellar conditions. The
-decay properties were studied using the quasiparticle random phase approximation model with a separable multi-shell schematic and separable interaction on top of axially symmetric-deformed mean-field calculation. Previously a similar investigation was performed separately for
- [
22] and
-shell nuclei [
23,
24]. Recently a list of the top 50 electron capturing and
decay nuclei, possessing the largest effect on
for conditions after silicon core burning, was published [
1]. This investigation led to the determination of most important weak interaction nuclei in the presupernova evolution of massive stars. To achieve this goal, an ensemble containing 728 nuclei in the mass range of
A = (1–100) was considered. The idea was to sort nuclei having the largest effect on
post silicon core burning, by averaging the contribution from each nucleus to
(time-rate of change of lepton fraction) over the entire chosen stellar trajectory. In the current project, we specifically focus on the top-ranked 50
decay nuclei, as per the findings of Ref. [
1], and study the effect of pairing gaps on
-decay properties of these nuclei.
Pairing gaps are one of the most important parameters in the pn-QRPA model. It is to be noted that the present investigation includes neutron-neutron and proton-proton pairing correlations, which have only isovector contribution. For the isoscalar part, one has to include the neutron-proton (
) pairing correlations, not considered in the present manuscript. The current pn-QRPA model has the limitation of ignoring the
pairing effect and incorporation of
pairing may be taken as a future assignment. Such kind of calculations were performed earlier by author in Ref. [
25], albeit only for N=Z+2 nuclei. The conclusions of their study stated that isoscalar interaction behaves in a fashion similar to the tensor force interaction. The calculations of author [
25] showed that the tensor force shifts the GT peak to low excitation energies. Incorporation of tension force may result in lower centroid values of calculated GT strength distributions and could lead to higher values of calculated
decay rates. In order to compensate, the same effect of shifting calculated
strength to lower excitation energies in the current pn-QRPA model was achieved by incorporation of particle-particle forces (see
Section 2 of Ref. [
26]). The pairing energy of identical nucleons in even-even isotopes can be estimated using a variety of methods based on the masses of neighboring nuclei, but despite the extensive study of the issue, the issue of which relation most closely approximates the pairing interaction is still open for debate [
27,
28,
29,
30]. We chose to employ three different recipes for calculation of pairing gaps in our investigation. Details follow in the next section.
The paper is organized as follows: The theoretical framework used for calculations, is described in
Section 2.
Section 3 presents the discussion on our investigation. Finally, the summary and concluding remarks of the present work are presented in
Section 4.
2. Formalism
The Hamiltonian of the current pn-QRPA model is given as
where
,
,
and
denote the single-particle Hamiltonian, pairing forces for BCS calculation, particle-hole (
) and particle-particle (
) interactions for GT strength, respectively. The single-particle eigenfunctions and eigenvalues were computed using the Nilsson model [
31]. Other parameters essential for calculation of weak-interaction rates are nuclear deformation, the Nilsson potential parameters (NPP), the Q-values and the pairing gaps. Nuclear deformation parameter (
) was determined using the formula
where
is the electric quadrupole moment taken from [
32]. The NPP were chosen from [
33]. Nilsson oscillator constant was taken as
in units of MeV, similar for neutrons and protons. Q-values were determined using the recent mass compilation [
34].
The pairing gaps between nucleons were chosen using three different formulae. The first formula is most often used in literature [
26,
35,
36]. It has the same value for neutron-neutron and proton-proton pairing. It is given by
This is the traditionally used formula for calculation of pairing gaps. The second formula contains three terms and is based on separation energies of neutrons and protons. It is given by
The third recipe contains 5 terms and is a function of the binding energies of the nucleons. It is given by
The values of binding energies were taken from Ref. [
37]. Henceforth in this text, we will refer to the first formula of pairing gaps as TF (one-term or traditional formula), the second as 3TF (three-term formula) and the last formula as 5TF (five-term formula).
In our pn-QRPA model, charge-changing transitions were defined by phonon creation operators. The pn-QRPA phonons were given as
The summation was taken on all the p-n pairs having
=(
m-m) = 0, ±1, where
m (
m) represents the third component of angular momentum of neutron (proton). The
a is the creation operator of a quasi-particle (q.p) state of neutron (proton).
represents the time reversed state of
p. The ground level of the theory with respect to the QRPA phonons was considered as the vacuum, A
= 0. The excitation energies (
) and amplitudes (
X) of phonon operator were obtained by solving the RPA equation. Detailed solution of RPA matrix equation can be seen from Refs. [
38,
39]. The stellar
decay rates from the
nth parent state to
mth daughter level was calculated using
The term
is linked to the reduced transition probabilities (
) of Fermi and GT transitions
where
The constant
D value was chosen as 6143 s [
40] and
was taken as -1.254. The reduced Fermi and GT transition probabilities were explicitly determined using
where
and
denote the spin and the isospin lowering operators, respectively. For the construction of daughter and parent excited states and calculation of nuclear matrix elements, we refer to [
41]. For details on solution of Equation
1 we refer to [
26,
39,
41]. The phase space integrals (
) over total energy was calculated using
where we used natural units (
). The Fermi functions,
, were estimated as per the prescription given in Ref. [
42].
is the total
-decay energy given by
where
and
, represent parent and daughter excitation energies, respectively. If the electron emission total energy (
) value was larger than -1, then
= 1, and if
≤ 1, then
.
is the electron distribution function
where
E = (
w - 1),
denote the kinetic and Fermi energy of the electrons, respectively.
k is the Boltzmann constant. As the stellar core temperature rises, there is always a finite chance of occupation of parent excited levels. The total
decay rates were calculated using
where
is the occupation probability of parent excited state following the normal Boltzmann distribution. In Equation
17, the summation was applied on all final and initial states until reasonable convergence in
-decay rates was obtained.
The
decay partial half-lives
from parent ground state were calculated using the relation
where
E = (
Q -
). The integrals of the available phase space for axial vector and vector transitions are denoted as
and
, respectively. The total
-decay half-lives were computed, including all transition probabilities to the states in the daughter within the
Q window.
3. Results and Discussion
The aim of the current study is to re-examine the effect of pairing gaps on charge-changing transitions and associated
-decay rates of 50 top-ranked nuclei bearing astrophysical significance. The nuclei were selected from a recent study by Nabi et al. [
1] where a total of 728 nuclei were ranked on the basis of ranking parameter,
, defined by
such that the nuclei having highest
value will contribute most to the time-rate of change of lepton fraction (
). As discussed earlier, three different sets of empirically calculated pairing gaps were used in our analysis to investigate the
-decay properties of these nuclei.
The pairing gaps arise from the pairing interaction between nucleons. They have a direct impact on the occupation probabilities of different single-particle states in the nucleus. These probabilities bear consequences for the charge-changing transitions. In general, a larger pairing gap leads to smaller number of nucleons occupying states near the Fermi level. This can contribute to lowering the chances for transitions and may result in redistribution of GT strength to higher excitation energies.
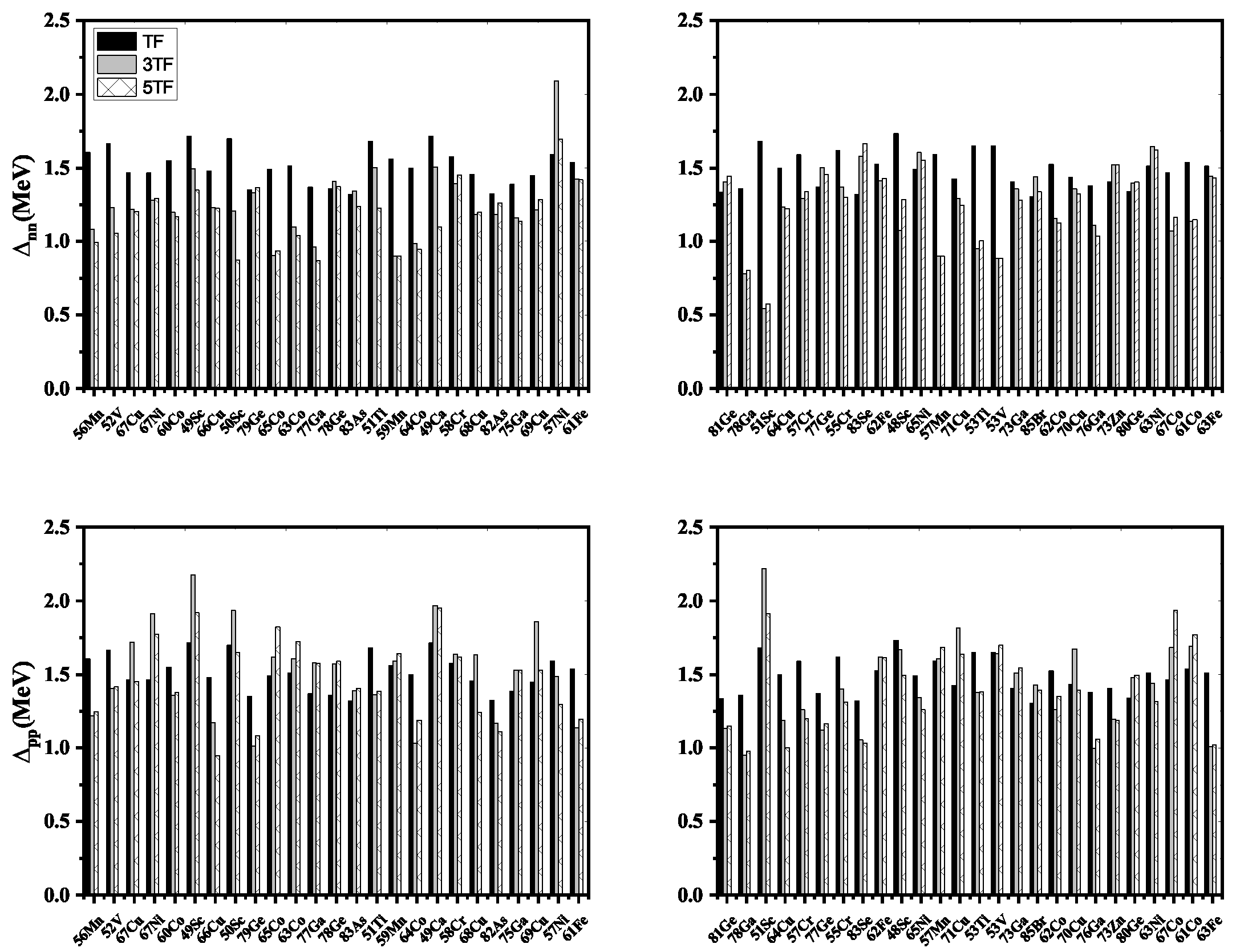
We first display the computed pairing gaps in
Figure 1 for the selected 50 nuclei. The upper panels show the neutron-neutron pairing gaps. The proton-proton pairing gaps are displayed in the lower panels. The TF formula (Eq.
3) is only a function of the mass number of the parent nucleus. Nuclear properties of parent and neighbouring nuclei are considered in 3TF formulae (Eq.
4 and Eq.
5). In the 5TF formulae (Eq.
6 and Eq.
7), nuclear properties of two nearest neighbouring nuclei are considered. Difference of more than 0.5 MeV in
values is noted, between the TF and 3TF schemes, for
Sc and
Fe. A difference of similar magnitude is noted for
between TF and 5TF schemes for the case of
Cu. The differences between
values exceed even more reaching to 0.7 MeV for
Mn and more than 1 MeV for
Sc.
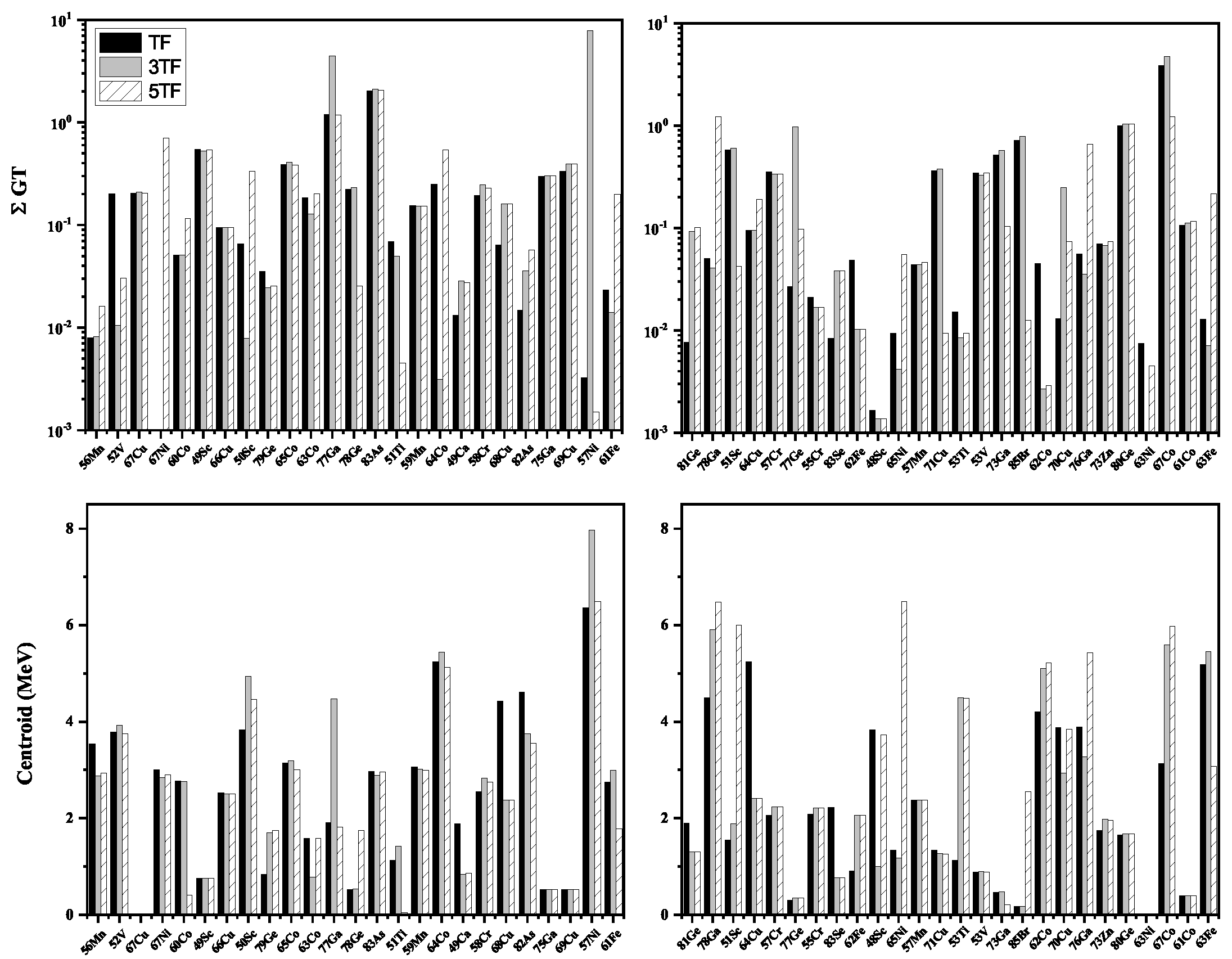
The total strength and centroid values of the calculated GT strength distributions are shown in
Figure 2 as a function of pairing gap values. The upper panels show the calculated total GT strength whereas the bottom panels show the computed centroids of the resulting distributions. It is noted from
Figure 2 that the total strength and centroid values are sensitive function of the pairing gaps. Orders of magnitude differences are noted for the total GT strength as pairing gap value changes. The effect is more pronounced when the
N or
Z of the nucleus is a magic number. This includes the nuclei
Ni,
Br. This was expected as changing pairing gap values would create a bigger impact for closed shell nuclei. It may also be noted that for the case of
Ni (3TF) and
Ni (TF), the total GT strength are smaller than 10
and therefore not shown in
Figure 2. The average total GT strength calculated by TF, 3TF and 5TF schemes are 0.30, 0.56 and 0.28, respectively. It was concluded that, overall, the 3TF scheme calculated the largest strength values. The placement of centroids changes by an order of magnitude or more as we switch from TF to 3TF schemes. The 5TF has a tendency to move the centroid to higher excitation energies whereas the 3TF places the centroid at much lower energies. The average of all centroids computed by TF, 3TF and 5TF are 2.44 MeV, 2.47 MeV and 2.62 MeV, respectively. More than an order of magnitude difference in the placement of centroid is noted for the case of
Ti and
Br (bottom panels of
Figure 2). For the case of
Ti, only one GT transition was calculated by TF and 3TF schemes at energies 1.1 MeV and 1.4 MeV, respectively. The 5TF schemes calculated more fragmentation of the total strength and at low energies (< 0.1 MeV). This explains the placement of centroids at much higher energies for
Ti employing the pairing gap parameter from TF and 3TF schemes. For the case of
Br, the 5TF scheme resulted in high-lying GT transitions (between (2-3) MeV). On the other hand, the TF scheme calculated one GT transition at 2.7 Mev, albeit of magnitude 0.00007. All remaining transitions were within 0.5 MeV in daughter states. The 3TF scheme also computed GT transitions within 0.5 MeV in daughter. Consequently, both TF and 3TF placed the centroid at 0.17 MeV in daughter.
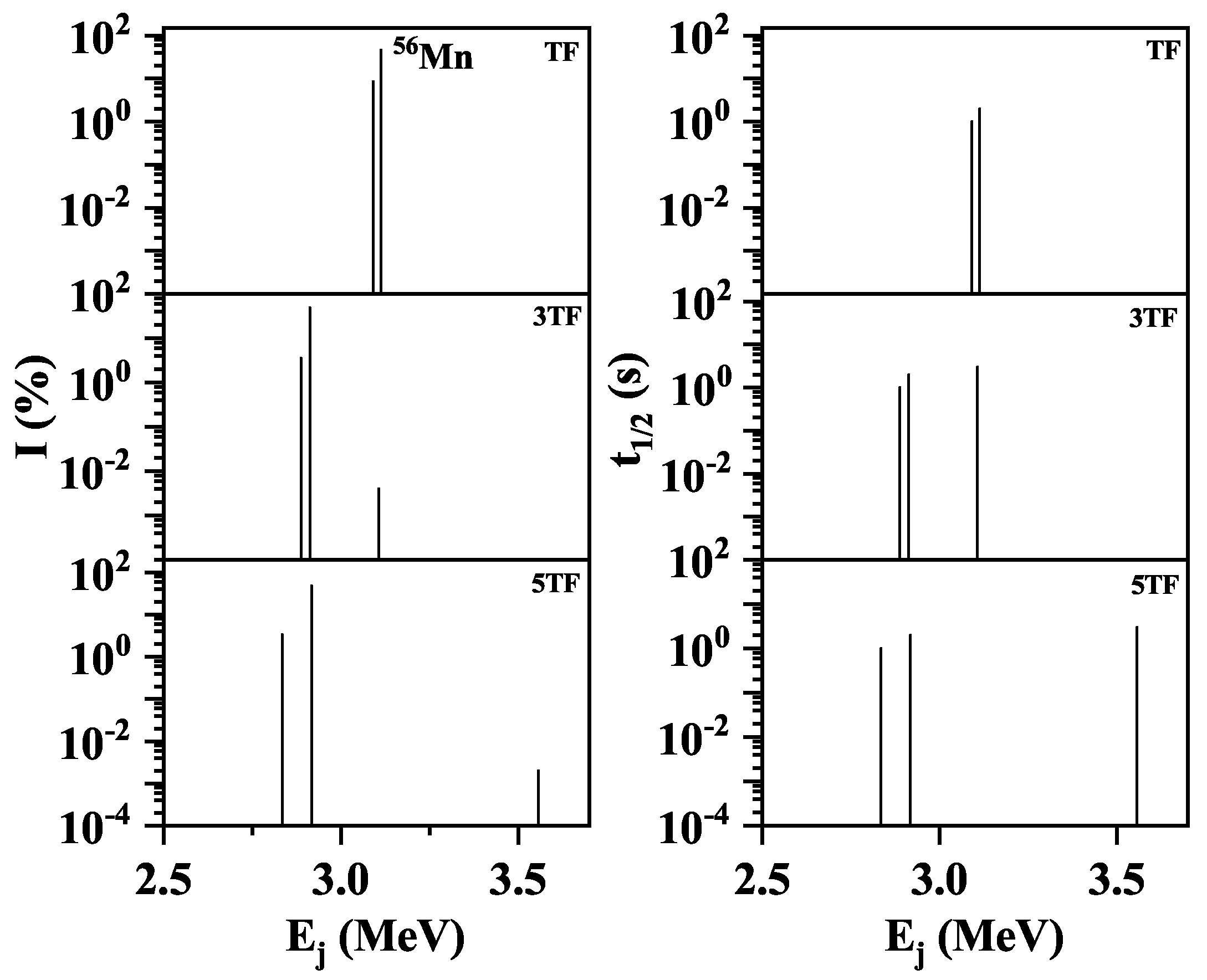
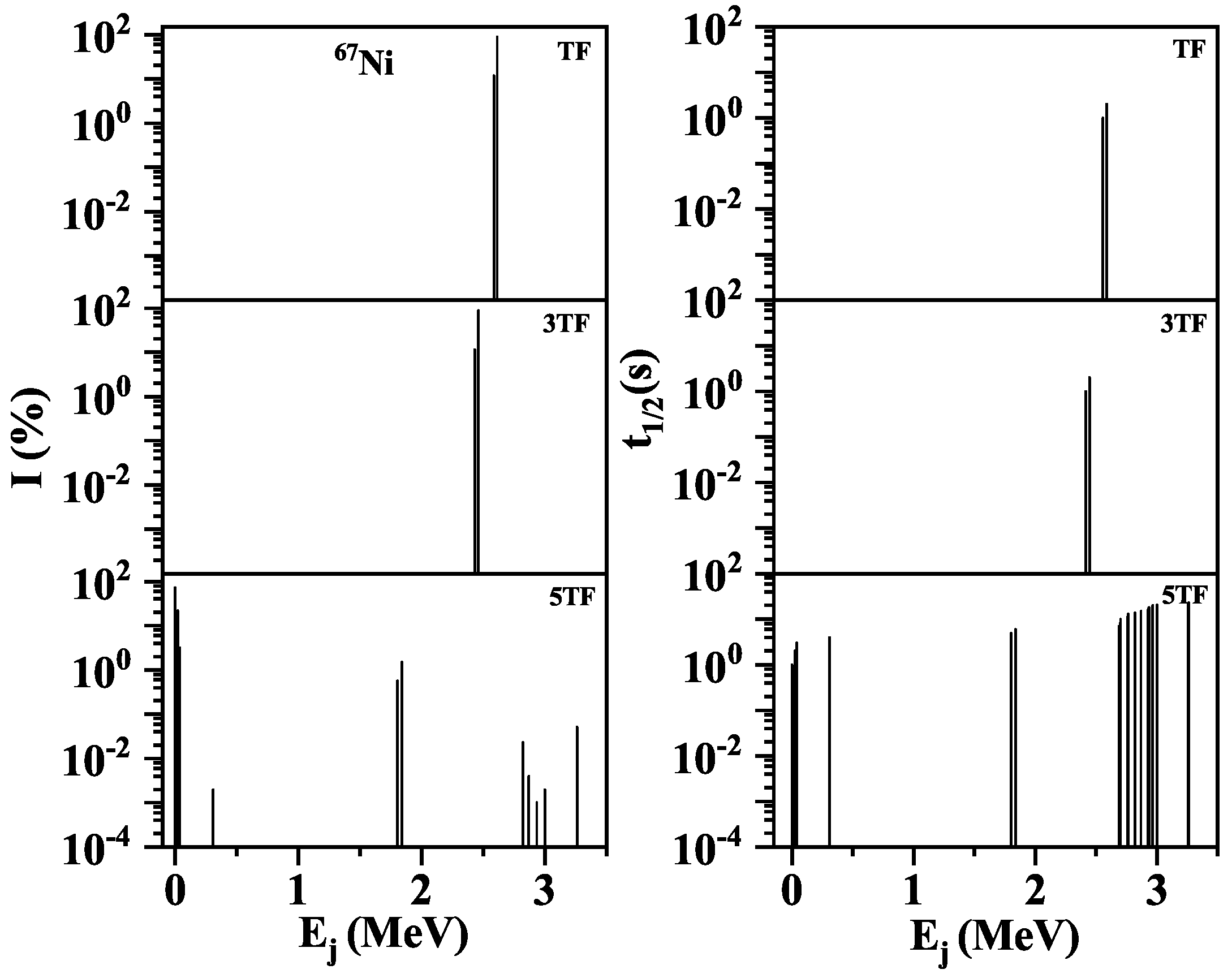
Branching ratios (I) of charge-changing transitions in daughter was calculated using the equation
Figure 3,
Figure 4,
Figure 5 and
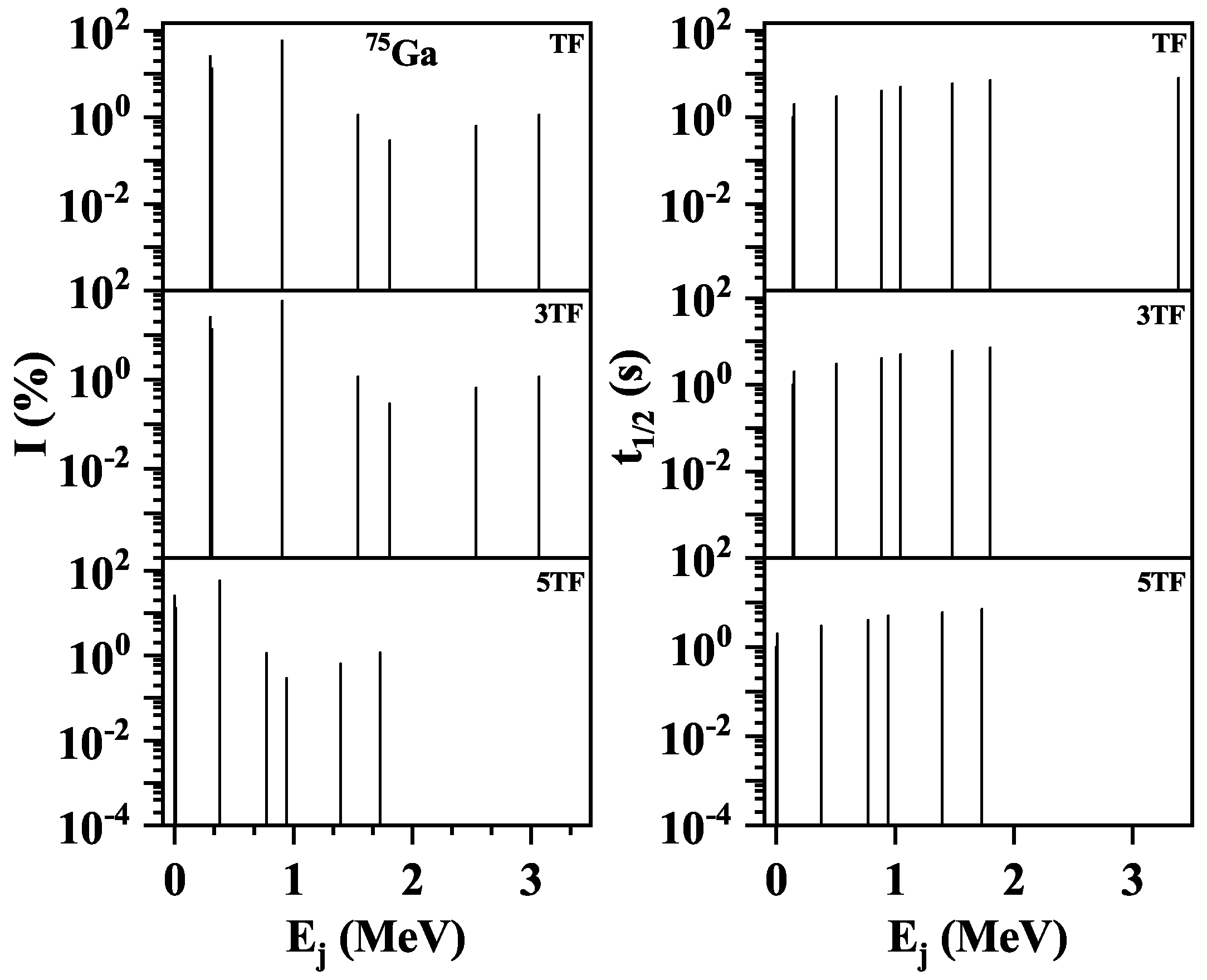
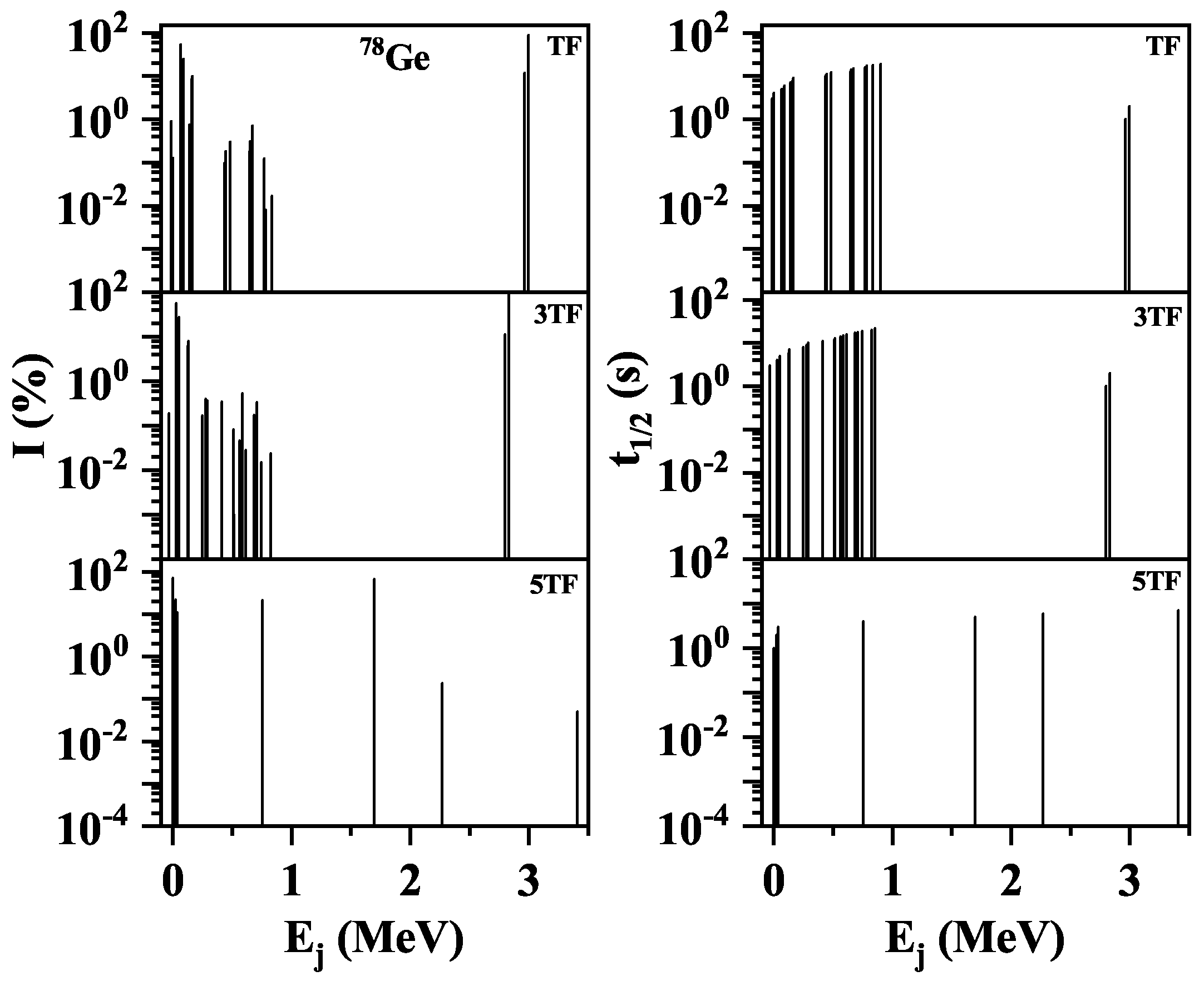
Figure 6 show the computed branching ratios and partial half-lives as a function of daughter excitation energy for the three selected pairing gaps (TF, 3TF and 5TF) for
Mn,
Ni,
Ga, and
Ge respectively. These nuclei were selected belonging to odd-odd, even-odd, odd-even and even-even categories from the top-ranked 50 nuclei for the analysis of branching ratios and partial half-lives. Fragmentation of the total GT strength (
Figure 2) to low-lying states is altered by changing pairing gap values. The effect is different for different classes of nuclei. For odd-odd cases,
Figure 3 shows that low-lying transitions with more fragmentation are produced with 3TF and 5TF schemes. For the magic number nucleus
Ni,
Figure 4 shows that the 5TF scheme result in considerable enhancement of the fragmentation of the GT strength when compared with the other two schemes. The 5TF scheme resulted in low lying transition also for the odd-even nucleus
Ga as exhibited in
Figure 5. For even-even nucleus
Ge,
Figure 6 reveals that the 5TF scheme resulted in lesser fragmentation and high-lying transitions when compared with the TF and 3TF schemes.
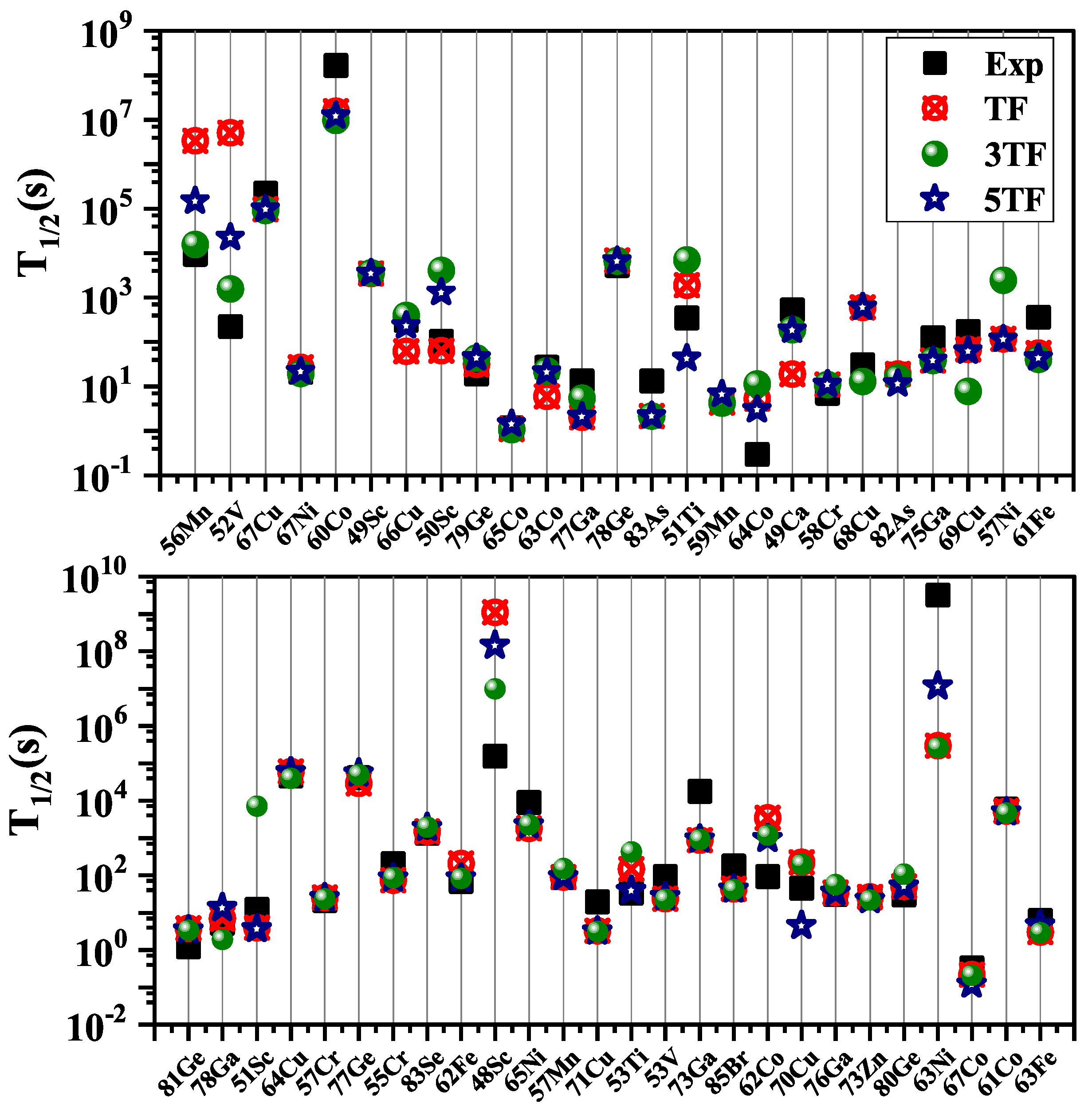
The comparison of calculated and measured half-lives for selected top-ranked 50 nuclei is presented in
Figure 7. The terrestrial half-lives were calculated using the pn-QRPA model with TF, 3TF and 5TF pairing gap values. The calculated half-life depends on the total strength and distribution of the GT transitions in the daughter states. These two quantities were shown earlier in
Figure 2 as a function of the pairing gaps. Three orders of magnitude or more differences in calculated half-life values may be noted from
Figure 7. Higher total GT strength values and lower placement of GT centroid result in smaller calculated half-lives.
Table 1 shows the accuracy of the current nuclear model using different pairing gap values as one of the input parameters. We defined the ratios of calculated to measured half-lives using the variable
In
Table 1,
n is the number of half-lives (out of a total of 50 cases) reproduced under the condition given in the first column. The average deviation (
) was calculated using
Table 1 shows that the current model with 3TF pairing gap reproduces
(
) of measured half-lives values within a factor of 10 (2) with an average deviation of 2.42 (1.22). We conclude that the 3TF pairing gap results in calculation of bigger total GT strength and best prediction of half-live values for these top-ranked 50 nuclei.
Because of the crucial importance of these nuclei in stellar environment, we decided to calculate
-decay rates of the selected 50 nuclei as a function of pairing gaps in stellar matter. In general, larger pairing gaps tend to shift the GT centroid to higher excitation energies in daughter. This in turn decreases the
-decay rates. A larger pairing gap leads to smaller number of nucleons occupying states near the Fermi level. This may result in redistribution of GT strength to higher excitation energies.
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 show the
decay rates of top-ranked 50 nuclei at selected densities [
= (10, 10
,
) g cm
] and temperature [T = (0.1, 1, 5, 10, 15, 30) GK]. In these tables entries written as < 10
means that the calculated
-decay rates were less than 10
.
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 display that
decay rates increase as the core temperature increases and decrease as
increases. The decay rates, for a predetermined density, increase due to accessibility of a large phase space with increasing core temperature. Soaring core temperatures increase the occupation probabilities of parent excited levels, thereby leading to a larger contribution of partial rates from parent excited states to the total rates. As the stellar core became denser, the electron Fermi energy increases leading to a substantial decrease in the
-decay rates at high stellar density values. Specially at high density (
=
g cm
), because of choking of the phase space, the
-decay rates tend to zero. It is concluded from
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 that the 3TF scheme leads to calculation of biggest stellar
-decay rates. This has a direct correlation with calculation of bigger total GT strength using the 3TF scheme.
Table 7 shows the average values of the calculated stellar
-decay rates using different pairing gap values under predetermined physical conditions.
4. Conclusions and Summary
In this study, we re-examined the influence of pairing gaps on charge-changing transitions, partial half-lives, branching ratios and -decay rates, for top-ranked 50 nuclei having astrophysical significance. Pairing gaps are one of the most important model parameters in the pn-QRPA approach for calculation of -decay rates. In order to investigate the effect of pairing gaps on calculated GT strength distributions and half-lives, we used three different empirically calculated values (referred to as TF, 3TF and 5TF). Changing pairing gap values led to significant alterations in the total GT strength and -decay rates. It was concluded that the 3TF pairing gaps resulted in the best prediction of -decay half-lives. Following main conclusions are drawn form the current investigation:
⊙ The available empirical formulae for pairing gaps give values of differing by 0.5 MeV or more. The difference in is more than 1 MeV.
⊙ The total GT strength changes by orders of magnitude and the placement of GT centroid by up to an order of magnitude or more as the pairing gap values change. The 3TF pairing gap leads to lower placement of GT centroid and higher total GT strength.
⊙ The 3TF scheme gives the best predictive power to the current pn-QRPA model.
⊙ The 3TF pairing gaps result in biggest stellar -decay rates for the selected top-50 ranked nuclei.