Analogical Visuospatial Matrix Reasoning, Verbal Relational Reasoning, Verbal IQ and Memory Relationships with Maths and Science: A Behavioural and fMRI Study

1. Introduction and Aims of the Study

An analogy denotes a partial similarity, or resemblance of a logical homologue connection between two physical objects, or two concepts, events or phenomena in general (https://www.merriam-webster.com/dictionary/analogy). Polya (1957) suggests that analogies are the foundational building blocks of reasoning to construct new logical arguments and new coherent conceptual models. Analogical reasoning (AR) is a mental leap, underpinning problem solving and effective communication of concepts in science, mathematics, politics, economics and generally in education because it provides a clearer way to convey complicated new concepts through existing and well-known empirical examples (Holyoak & Thagard, 1995). AR is the cognitive process of using existing knowledge, skills, and experiences to identify new meaningfully logical patterns from seemingly unrelated events, to solve problems and create new understanding (Krawczyk, 2012; 2018).

AR is a cognitive scaffolding process which connects existing knowledge with new concepts via analogical representations of a priori well understood examples (Holyoak and Thagard 1995). The degree of corresponding similarities, either visuospatial or verbal semantic attributes determine the degree of analogical representation (Krawczyk, 2018). AR processing is a complex multifaceted function, involving a number of brain networks. During AR processing, the executive function network selects which pieces of information are relevant and salient as opposed to irrelevant in any learning task (Downar, Crawley, Mikulis, & Davis, 2002). The executive control network (ECN) is associated with formation of new conceptual frameworks, manipulating abstract concepts, working memory, fluid intelligence, inhibiting irrelevant information and sustaining attentional focus (Bunge, Wendelken, Badre, & Wagner, 2005; Begolli et al., 2018; Dumontheil, 2014; Green et al., 2006). In addition, the semantic information processing network is considered relevant during the assessment and construction of relevant abstract analogical concepts (Binder, Desai, Graves & Conant, 2009) as well as visuospatial information processing (Wendelken, Chung & Bunge, 2012).

The aim of the present study is to investigate the putative interactions between the IVs of executive control brain networks’ activation during AR, with the DVs of maths and science performance for adolescents aged 11-15 years old. More specifically, the research reviews and examines the relationships between verbal relational AR, visuospatial AR, working memory, verbal IQ and maths and science performance. The paper’s analysis objective is to use structural equation modelling (SEM, Warp Partial Least Squares, 7.0 software), to test empirically all hypothesised simultaneous multiple relationships of interactive direct, indirect, and mediating effects, between IVs and DVs; including the hypothesised activated four brain regions which are engaged during AR processing of maths and science tasks. The structure of the paper follows a logical sequence by defining AR, reviewing the foundational theoretical perspectives on AR; identifying the relevant relationships previous researchers found between the current study’s IVs and DVs and develop a new set of hypotheses and overall testable research models; analyse and test all the hypotheses postulated in the new models, and discuss the findings and implications for educational practitioners.

2. Definitions of AR and review of theoretical perspectives

Analogies vary according to the degree of similarity between visuospatial characteristics of objects or related semantic concepts. Some analogies are more obvious if they contain large amounts of similar attributes as opposed to others which have very few similar attributes and therefore are more obtuse and harder to discern any embedded similarity. There is a gradation of analogical correspondence and according to Goswami (1992) people of all ages can identify degrees of pattern similarity through analogical reasoning. Discerning new conceptual relational patterns is an essential cognitive process for making sense of new phenomena which have multifaceted applications in academic learning, e.g., maths, science, artificial intelligence, languages, engineering, medicine, etc. (Trey & Khan, 2008; DeWolf, Bassok, & Holyoak, 2015; Ehri, Satlow, & Gaskins, 2009).

AR is considered an important cognitive process affecting multiple cognitive processes, and therefore neuroscientists are interested in understanding how the brain processes analogical relational reasoning, from a structural and functional perspective, aiming to improve its application for educational, occupational and health related outcomes (Dumas, Alexander, & Grossnickle, 2013; Krawczyk, 2012; Kumar, Cervesato, & Gonzalez, 2014). For example, targeted training of young people can improve AR skills to detect relational visuospatial patterns and understanding of ideational semantic correspondence in abstract concepts encountered in many educational and occupational problem-solving activities (Guerra-Carrillo, & Bunge, 2018).

There are two competing theories of AR, the structure-mapping theory by Gentner (1983) and the multiconstraint theory by Holyoak & Thagard (1997). According to Gentner’s (1983) theory of structure-mapping, two seemingly unrelated elements are cognitively mapped out to identify differences and similarities. Analogical reasoning is based on two implicit constraints, structural consistency of direct correspondence for each element between two apparently similar phenomena or objects; and systematic comparison of the corresponding conceptual relations which have varying degrees of similarity (Gentner, & Markman, 1997). AR enables the extrapolation of logically coherent semantic inferences based on degrees of similarity, rather than irrelevant comparisons of haphazard elements without any logical similarities. Structure-mapping theory provides a framework for delineating different kinds of similarities: relational similarity (i.e., conceptual analogy), surface structural similarity, and literal similarity (identikit) (Falkenhainer, Forbus, & Gentner, 1989).

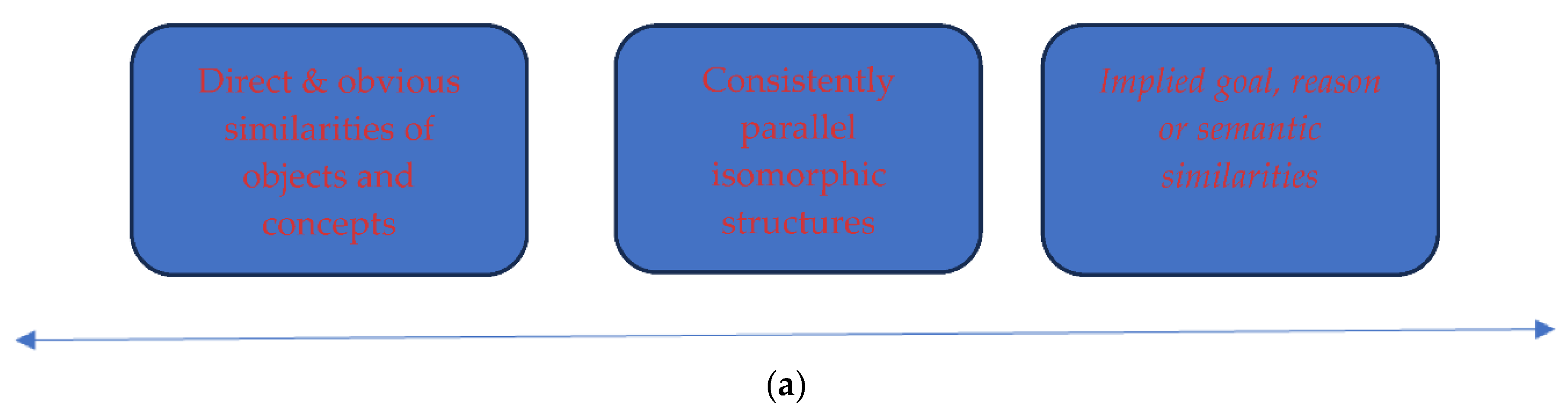
Analogies can be positioned in a graded continuum of incremental scaffolding from the simple to the more complex semantic relational and object-based AR (Gentner, 1983). Similarities which are identical or literal are at the first rank of the continuum. The middle rank consists of metaphors and conceptual relational analogies, with few concrete object attribute similarities, containing mainly implicit relational abstract semantic similarities. At the third rank of the continuum are semantically distant and obtuse abstract semantic similarities, which are found in creative AR and new generalised scientific theories, laws, and models. The following continuum (figure 1a) describes the graded differences from literal/complete similarities, to analogies with relational metaphors, to creative relationships underpinning new scientific generalised AR (Green et al., 2006; 2010; 2012).

Analogical abstractions can be based on language exemplars, which contain coherent logical comparisons and relational analogies (Gentner et al., 2011). Therefore, language learning often facilitates acquisition of various metaphorical and semantic analogies, which are used as scaffolding blocks to create new knowledge structures and generate new abstract ideas or new scientific models and discoveries (e.g., maths and science new insights and theories). Analogical learning enables learners to transfer knowledge through conceptual mapping from maths to science related issues, which is portable to solve new problems and make sense of new phenomena. Therefore, AR helps to align existing physical object similarities and semantic relational evidence to other related phenomena (e.g., music, construction, engineering applications), thus increasing the range and quality of understanding. AR facilitates incremental cross situational learning of new physical and abstract scientific categories which can be used in future learning scaffolding to construct new comparative physical and abstract scientific schemas (Gentner, 1983; Gick & Holyoak, 1983).

The second, multiconstraint theory (Holyoak & Thagard, 1997), proposes that there are three broad parameters or conditions which underpin AR. The first parameter, is that analogies contain direct and obvious similarities at any level of conceptual abstraction between the analogy source and target analogy outcome. For example, an analogy concerning visuospatial attributes of objects, events or attitudinal intentions should be directly and obviously compared with equivalent target objects, events or attitudinal analogies. The second analogical parameter, is the consistent isomorphic structural parallels between the relations of the source and the target analogue. For example, the isomorphic mapping between the visuospatial source analogy should be compared with homologue visuospatial analogies to generate direct and empirically coherent inferences, based on one-to-one correspondences to ensure consistent interpretation of the relational analogies. The third parameter, is the type of implied goal or reason and semantic meaning between the source and target analogue. For example, if the source analogue is an abstract goal or intention or personality trait, the implied target analogue outcome should be able to map out and show a similar relational connection, which corresponds logically to the source analogue (see Figure 1b). The multiconstraint theory suggests that relational reasoning can be part of visuospatial analogies, as opposed to the structure-mapping theory which suggests that relational reasoning is contained in both object and semantic conceptual analogies.

The major difference between the two theories is that Gentner (1983) extends and includes AR into the creative insights, ideas and concepts that are not easily apparent similarities. Fluid intelligence is normally associated AR and the generation of novel creative thinking and innovative solutions (Green et al., 2006). According to Green et al. (2006) AR is associated with fluid intelligence and it is a form of relational conceptual reasoning, which analyses different types and degrees of similarities to make new logically sound inferences to create new knowledge and new conceptual maps. A priori knowledge of abstract and empirically concrete types of knowledge are used to create new schemas of relational analogies and reasoning about all types of new relationships (Goswami, 1992; 1996). This relational process of a priori and posteriori knowledge can be achieved by the usage of semantic memory. AR can be achieved if there is sufficient and relevant experiential knowledge in the working memory to produce new analogies and conceptual maps (Halford, 1993).

The definitions of AR include relational similarities of both physical/structural visuospatial objects and events, as well as relational similarities of abstract semantic constructs. Analogies according to Gentner & Markman (1997) are based on perceived abstract relations of objects or/and semantic meanings coalescing to generate logical mapping of concepts which correspond to systematic rules of similarity above and beyond the physical and structural object attributes. Analogies convey implicitly systematic connections of logically coherent similarities between abstract relations as well as obvious similarities of factual visuo-spatial attributes, which may or may not contain emotional or conceptual comparisons. Therefore, abstract relational analogies are conceptual maps of higher order predicates, which are qualitatively different from the lower levels of analogies of factual object attributes. The research focus of this paper is on the relational analogies that young adolescents mentally construct during visuospatial and verbal semantic tasks while performing maths and science tasks, which require AR of similarities for both visuo-spatial and semantic conceptual relations.

2.1. Review of age and developmental stages of AR

Analogical thinking is age related and developmental changes are due to increasing educational knowledge and experiential learning over the years (Gentner & Rattermann, 1991). AR development in children is an incremental process dependent on both educational accretion and physical brain maturation. The brain’s ability to process incrementally more complex analogical relational problems increases as the relevant brain networks develop with age and training. Several researchers suggest that analogical relational reasoning evolves from simple visuospatial similarities during early childhood to more abstract semantic relational analogies during adolescence and early adulthood (Gentner, 2010; Childers et al., 2016). Analogical reasoning in 3-years old children starts with detecting similarities and understanding simple object attributes matching-to-sample task analogies, in a specific domain, and gradually progress to a relational shift by focusing on more abstract relational similarities (Gentner & Rattermann, 1991). Analogical reasoning for children of more than 5 years old, which have been exposed to more educational experiences, improves incrementally to more than one relational analogy and are able to process higher levels of semantic abstract relational match- to-sample task analogies, deciphering metaphors and causal analogies (Rattermann & Gentner, 1998; Halford, et al., 1998). Anderson et al. (2018) found that 3 months old children can discriminate between “same-different” attributes of stimuli, therefore, language is not a prerequisite to making simple structure-mapping relational comparisons, but language acquisition does help in the gradual developmental shift for processing more abstract relational matching-to-task analogical reasoning (Hespos, Anderson, Gentner, 2020).

The experimental stimuli, researchers have used with children, vary from simple action type of comparisons depicted in cartoons and word pairs, which can assess analogical reasoning based on physical features and conceptual relations of function, e.g., bread: slice of bread :: orange:? and/or using cartoon stimuli that contain a similarity to select between three options, e.g., slice of orange, slice of cake, or orange balloon (Ferrer et al., 2009). Analogical reasoning in young children is possible if they have relevant domain specific knowledge and therefore, can remember certain events, meanings, and object characteristics to use during analogical processing tasks and being able to control or inhibit irrelevant information (Morrison et al., 2011).

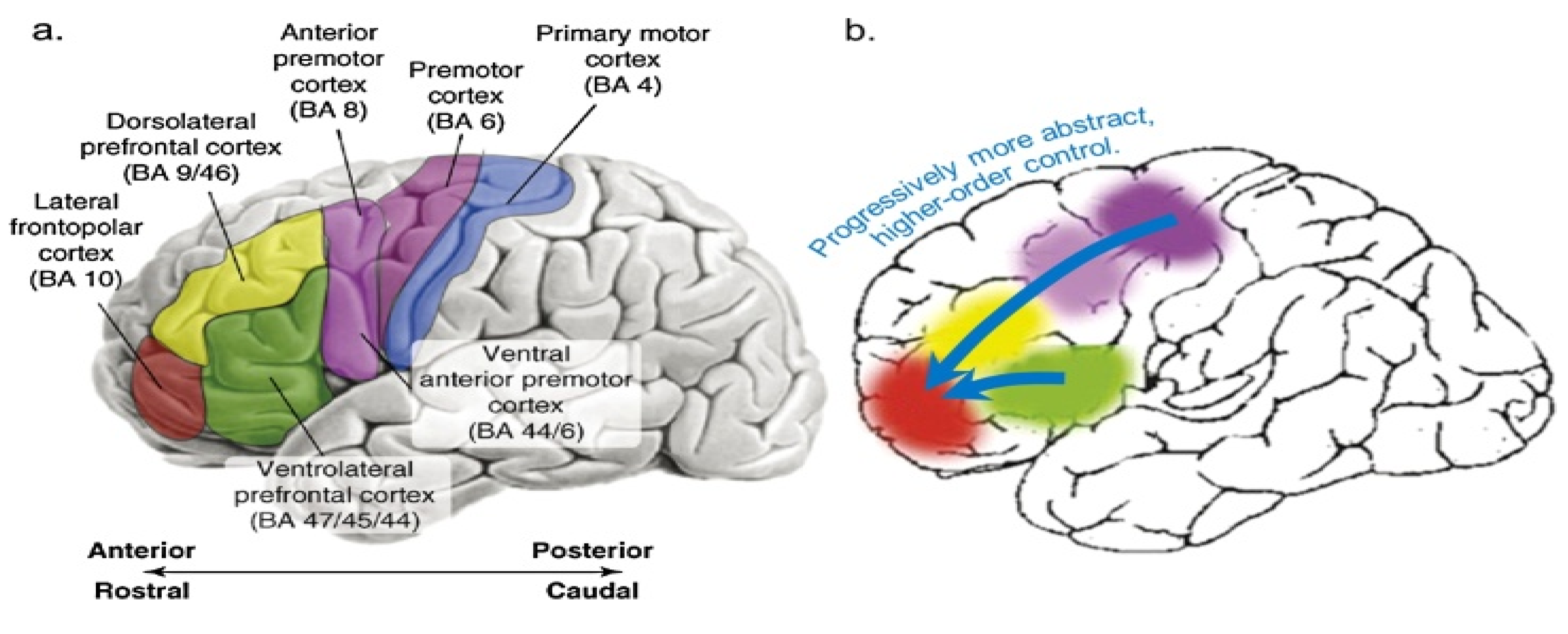
Brain development is dependent on biological age and therefore as children and adolescents grow, their brain’s ability to process more complex analogies increases (Dumas, Hummel & Sandhofer, 2008; Thibaut, French & Vesneva, 2010). Age related brain development facilitates incrementally better functionality of brain regions such as BA10 or corresponding to the Rostro Lateral Prefrontal Cortex (RLPFC), which is associated with higher level of cognition, prospective memory, working memory, multitasking and task switching (Crone et al., 2009). Children’s ability to process complex relational information is affected by their executive functional ability to inhibit irrelevant and distracting information (Morrison, Doumas, & Richland, 2011). The dorsal prefrontal cortex (DPFC) and the executive network (EN) are associated with integrating relational analogies, theory of mind, processing of abstract information (Christoff et al, 2004; Mason et al., 2007), and selective attention of stimulus-independent information (Burges et al., 2005; Burges, Dumontheil & Gilbert, 2007).

The hypothesis that during adolescence brain processing of abstract ideas and abstract thoughts is a non-linear development, associated with brain structure and grey matter volumes, which influence behavioural outcomes in a variety of tests, was tested using a multimethod approach using behavioral and functional MRI data (Dumontheil, Houlton, Christoff & Blakemore, 2010a). Using reliable relational AR stimuli, a sample of female participants N=178, age 7-27 years old for the behavioural study; and N=37, age 11-30 years old for the fMRI study, found that the biggest significant improvements were observed by the 7- 9 and 14-17 years old. However, the 9-11 performed at adult age levels, but performance accuracy dropped for the 11-14-years old. When the researchers investigated the combined effects of reaction time in relation to response accuracy (a ratio of speed over accuracy) for 2-relational, vs. 1-relation tasks, the data suggested a linear performance improvement during late childhood and mid-adolescence, with a significant improvement between 7–9 and 14–17 years old age groups.

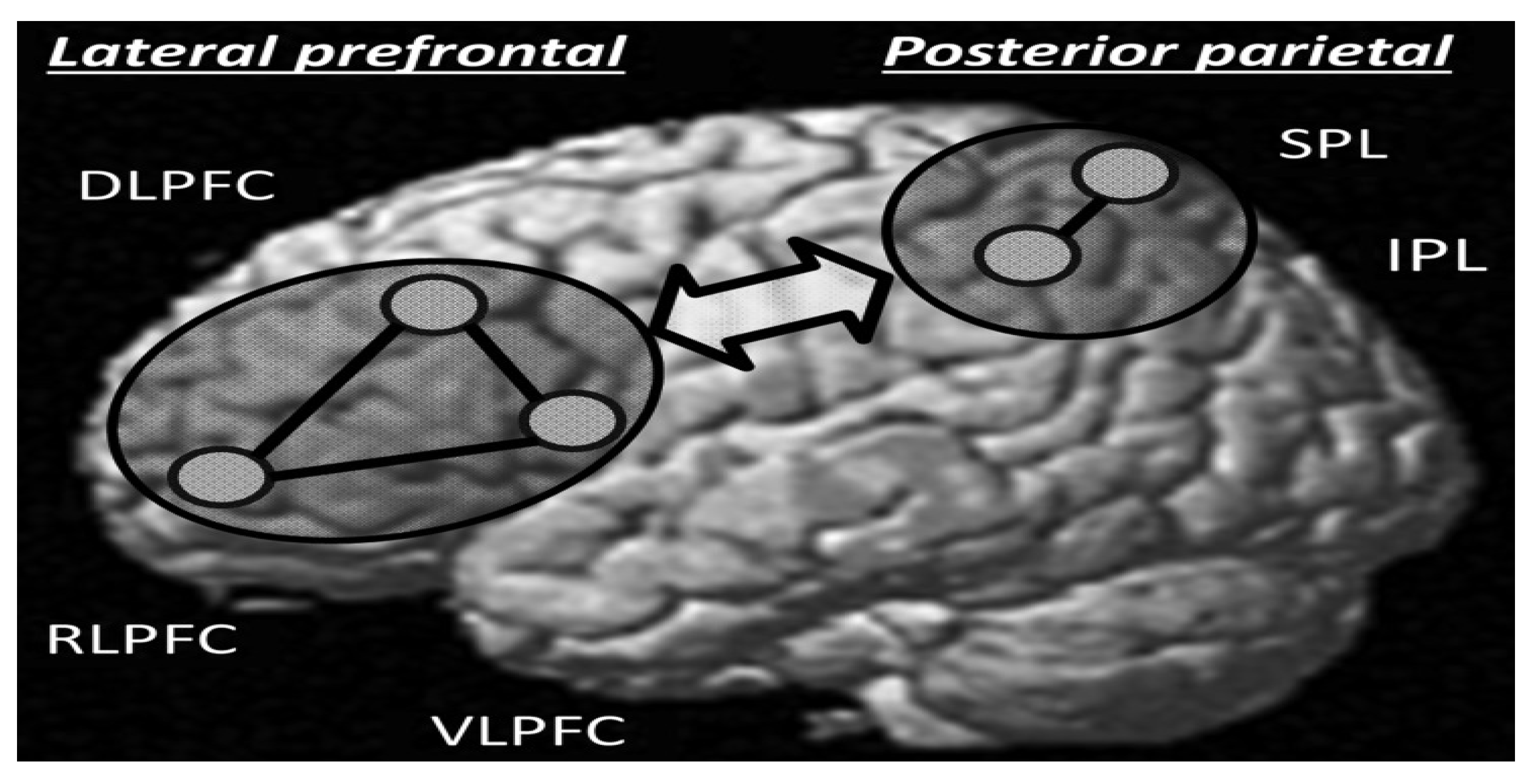
Overall relational reasoning for processing 2-relational vs 1-relational reasoning tasks improved with age until maturity (Dumontheil, et al., 2010a). They found confirmatory evidence of complex age related linear and non-linear changes in processing accuracy especially during mid-adolescence age groups. Age related structural brain changes in RLPFC, and medial superior frontal gyrus are posited to influence behavioural outcomes for mid-adolescence and adulthood. But they also suggest that educational input, working memory (WM), and cognitive maturation skills may play a mediating role in influencing behavioural outcomes. Dumontheil, Hassan, Gilbert, & Blakemore (2010b) fMRI study found that age is related to the ability for processing self and other/stimuli-generated thoughts, and therefore relational reasoning is associated with brain developmental changes, partly involving the dorso lateral prefrontal cortex (DLPFC) during adolescence. Their fMRI data analysis produced positive correlations between age and specific brain region activations including the DLPFC (see Figure 2).

The proposition that reasoning is contingent to age and brain development stages was recently tested with a large sample (N=132) of children and adolescents ranging from 6-18 years old (Wendelken, et al., 2018). They hypothesised that two major brain network connectivities are associated with reasoning abilities, namely the lateral fronto-parietal network (LFPN) (Wendelken, et al., 2018). Their results suggest that for the 6-8 years-old children’s LFPN connectivity was not associated with reasoning, but the actual speed of processing mediated the children’s reasoning ability. For 9-11 years old, LFPN connectivity between left and right RLPFC was mediated by working memory (WM). The 12-18 years-old reasoning abilities were associated with strong connectivity between the left RLPFC and inferior parietal lobule (IPL). More specifically, the left anterior prefrontal cortex (LAPFC, BA 47/45), which is activated during controlled semantic retrieval, was found to be positively correlated with participants’ age. The research supports the hypothesis that improved performance during middle childhood and early adolescence on AR tasks is driven largely by improvements in their ability to selectively retrieve task-relevant semantic relationships (Wendelken, et al., 2018). Therefore, age and development stages of reasoning ability are associated with different degrees of connectivity in the RLPFC-IPL network and that development of reasoning is strongly associated with late childhood and early adolescence (Whitaker, Vendetti, Wendelken, & Bunge, 2018) (see Figure 3).

A comprehensive meta-analysis of 27 experiments attempted to identify the statistically significant activation networks for AR using semantic and visuospatial tasks (Hobeika et al., 2016). The researchers suggest that AR activates a number of cortical (frontal and parietal cortices) and subcortical basal ganglia (BG) structures and provides evidence that analogical and deductive reasoning are sensitive to the types of stimuli used. The data suggest that bilateral posterior parietal cortex (PPC) and right middle frontal gyrus (MFG) are relevant for relational arguments; left inferior frontal gyrus (IFG) and BG for categorical arguments; and left precentral gyrus (PG) for propositional arguments. Urbanski et al. (2016) show that the left RLPFC is a critical node in the analogical reasoning processing network and suggest that the consistently common brain area activated during all studies was the left RLPFC. The semantic and visuospatial types of stimuli activate differentially domain specific brain areas (inferior and middle frontal gyri) from general brain regions (left RLPFC). Similarly, differences in brain activation were found between visuospatial and matrix types of stimuli analogies, with distinct regions in the left and right networks of the left RLPFC. Different types of analogical tasks produce different brain anatomical activations and therefore accurate prediction of brain activation depends on the fine differences between the types of stimuli which afford more nuanced and accurate understanding of AR. Other meta-analyses and voxel-based morphometry studies found that the left RLPFC is consistently correlated with AR (Vartanian, 2012; Aichelburg et al., 2014). The implication of a left RLPFC can be explained by the verbal semantic type of stimuli being processed and the right RLPFC for processing more visuospatial types of information stimuli (Cho et al., 2010; Hampshire et al., 2011). A transcranial direct current stimulation (tDCS) experiment found that, the anodal stimulation tests produced strong positive correlations between tDCS stimulation and improvement in memory source retrieval at the RLPFC, but no significant change occurred in AR and visuospatial perception task performance (Westphal et al., 2019). Therefore, the RLPFC is consistently engaged in multiple activities and is positively associated with WM activation during abstract conceptual and AR processing.

2.2. Working Memory, Executive Network, and IQ relationships with AR

Researchers suggest that WM and IQ are positively associated with educational success (Cowan & Alloway, 2008; Alloway & Alloway, 2010; Donati, Meaburn & Dumontheil, 2018). However, there are contrasting views on the specific relationship between WM and IQ. Some researchers view the two constructs as identical (Colom et al., 2004); but others recognise the similarities and shared attributes, but they consider them as two different brain functions (Alloway et al., 2004; Conway et al., 2002). A meta-analysis found that WM and IQ are not identical but highly correlated and have a shared variance of approximately 20%, but both account for learning success (Ackerman, Beier, & Boyle, 2005). Therefore, it is difficult to clearly delineate precisely IQ’s and WM’s contributions towards learning, but the research evidence suggests that although they are dissociable, they are highly related at different stages of cognitive processing (Alloway & Alloway, 2010; Morris, Farran, & Dumontheil, 2019).

An extensive review found that several neuroimaging studies support the idea that during adolescence the RLPFC is strongly associated with processing abstract logical thinking, relational analogical integration, and episodic memory retrieval (Dumontheil, 2014). According to Barker and Warburton (2020), associative recognition memory, used during AR, combines different types of information representation in specific contexts of time and space. Associative memory integration depends on widespread cooperation of brain networks and multiple overlapping brain subnetworks are co-activated to perform specific behavioural and cognitive memory retrieval tasks. For example, the hippocampal-prefrontal networks process object spatial and temporal memories, but other networks process experiential and behavioural representations (Barker & Warburton, 2020). However, these findings are based on correlational studies but not causal research evidence, because, the left frontopolar cortex is also activated during inductive types of relational reasoning, and WM brain regions were more active during deductive reasoning tasks than inductive processing (Goel, 2014; Goel et al., 1997). In addition, similar activations in the frontopolar cortex during abstract relational integration and during AR of relational categorization, was not related to WM activation (Green et al., 2006). Strong activation occurred in the parieto-frontal network during processing and analysis of both AR and category relational processing tasks for semantic categorisation (Green et al., 2006, Green, et al., 2012). These researchers suggest that WM mediates analogical reasoning, which underpins mapping out logically relational criteria used for categorisation and making mental leaps.

Memory and AR tasks are associated with activation in the left RLPFC, while the right RLPFC is activated during reasoning tasks only, and serves an auxiliary role to the RLPFC, which is responsible for domain general reasoning processing (Westphal, Reggente, Ito, & Rissman, 2016). These fMRI findings provide supporting evidence that the RLPFC processes domain general and specific representations during evaluation and integration of relevant analogical information, and that episodic memory is engaged during correct information retrieval and monitoring of different types of computations (Westphal et al., 2016). These researchers suggest that the reason for memory engagement in the left RLPFC may be due to the verbal types of stimuli used, which is consistent with the findings by Bunge, et al. (2005) and Green et al. (2010). Westphal et al. (2016) suggest that the multiple cognitive processes carried out by the RLPFC interact flexibly with the default mode network (DMN), the memory retrieval network (MRN) and the semantic network (SN) as well as with many posterior networks involved in problem solving, fluid intelligence and behavioural decisions.

AR is often associated with the executive control function (EF), which is responsible for coordinating WM, goal integration, motivational intentions and inhibiting irrelevant information (Kruger et al., 2002; Reynolds et al., 2006; Hobeika et al., 2016). Several brain networks are involved during AR problem solving, such as EF, WM, the salient system (Downar et al., 2002), and the semantic control system (Binder et al., 2009; Lambon et al., 2017) which activate the DLPFC as well as the parietal and anterior cingulate cortex (ACC) (Bartley et al., 2019). Relational reasoning is therefore associated with EF which includes WM, attentional control for individual tasks and new task switching (Miyake et al., 2000; Ferrer, O’Hare & Bunge, 2009). Research with patients with clinical damage to the EF network, impairs analogical relational reasoning processing, which is evident in several studies with various populations, varied clinical contexts and types of assessments (Krawczyk et al., 2008; Morrison, Doumas, & Richland, 2011; Frausel, Simms, & Richland, 2018).

2.3. AR association with maths and science performance

Understanding maths and science is essential for success in education and virtually all aspects of life because they assist in discovering and analysing patterns and relationships embedded within concepts and visuospatial physical phenomena (Bressan, 2018; Project 2061, 2009). Making sense of the relationships between numbers is the basis for developing arithmetic and mathematical reasoning skills useful for students at all levels of education including science subjects (Dehaene, 1997). Several longitudinal research studies in the UK (Bynner & Parsons, 1997; 2006) and globally (OECD, 2016) found that poor skills in maths can negatively impact employment opportunities, health outcomes, social-civic involvement, and overall quality of life. Educational progress for all age groups is affected by the ability to process effectively mathematical concepts such as counting, ranking and proportional comparisons, often represented as percentages or ratios (Schwartz, et al., 2018; 2020). Processing numbers and maths skills are fundamentally important because they are domain general abilities, which utilise relational reasoning and therefore rely on many brain regions to carry out different types of computations (Dehaene, 2011; Dehaene, Bossini, & Giraux, 1993). Several researchers found that there is a natural educationally supportive relationship between maths and science and the two are by necessity integrated and mutually beneficial for learning new concepts (Czerniak, Weber, Sandmann, & Ahern, 1999; Goldstrom, 2004; Lonning, & DeFranco, 1997).

Processing numerical concepts necessitates semantic comprehension of numerical symbols, manipulation and remembering relevant processes to apply for solving maths and science problems (Prado, Chadha, & Booth, 2011)). Researchers suggest that WM is essential function for processing numerical concepts and the PFC is positively associated with generic abstract cognitive functions of computing, monitoring, and integrating mathematical concepts (Christoff & Gabrieli, 2000). The amount of memory resources required for complex maths computations are greater than for simple tasks (Fehr et al., 2007; Kong et al., 2005), and a number of cognitive models have been suggested regarding how the brain processes numbers. One of the most cited models is the ‘triple code’ model by Dehaene & Cohen (1995; 1997), which predicts that numerical calculations are processed in three formats: a) visual processing for Arabic symbolic numerals, processed bilaterally by the inferior ventral occipital-temporal brain areas; b) assessing quantity magnitudes and analogical relationships, processed by the inferior parietal regions; c) and verbal semantic processing of words describing mathematical relationships, activating the left perisylvian areas (Dehaene, 1992; Dehaene & Cohen, 1997).

A meta-analysis conducted by Arsalidou & Taylor (2011) proposes a more comprehensive model of additional brain networks regarding mental arithmetic processing, by adding the inferior parietal cortex, temporal cortex, verbal system, basal ganglia, thalamus, cingulate gyri, the insula, the cerebellum, and the mediating role WM plays in assisting the prefrontal cortices (DLPFC (BA 9, BA 46) and frontopolar (BA 10). A recent meta-analysis, with children 14 years and younger, found strong positive activation in the parietal area (e.g., inferior parietal lobule and precuneus) and frontal cortices (e.g., superior, and medial frontal gyri) for processing mental-arithmetic; and the insula and claustrum, which are involved during maths problem solving (Arsalidou, Pawliw-Levac, Sadeghi, & Pascual-Leone, 2018). Understanding science and using scientific reasoning procedures to solve various problems, is often associated with scientific literacy competence, deemed to be essential for multiple educational and professional applications. During cognitive processing of novel tasks, e.g., maths and science problem solving, or aiming to discover novel patterns without any obvious order or sequence, brain activation increases in the left premotor area, left anterior cingulate, and right ventral striatum, but decreases in the right DLPFC and parietal areas (Berns, Cohen, & Mintun, 1997). According to Nenciovici, Allaire-Duquette & Masson (2019) there are three main types of scientific reasoning tasks: overcoming misconceptions, causal reasoning, and hypothesis generation and testing. Their meta-analysis suggests that there are similar brain activations for all three types of scientific reasoning processing which are: the lateral prefrontal regions, which are also related to EF, and the middle temporal regions which are associated with declarative memory.

A mixed methods study, combining behavioural survey and fMRI data to investigate the complex interactions between analogical relational reasoning and performance in maths and science tasks, suggests that verbal AR with WM and verbal IQ are strong predictors of science and maths accuracy (Brookman-Byrne, Mareschal, Tolmie, & Dumontheil, 2019). In addition, they found that matrix non-verbal relational AR, was positively associated with science accuracy and multiple brain regions were activated, including the occipital cortex, superior and inferior parietal gyri, precuneus, pre-supplemental motor area (PSMA), posterior parts of superior and middle frontal gyri, anterior insula, posterior parts of the inferior and middle temporal gyri. On the other hand, maths processing was positively associated with verbal AR, the anterior temporal cortex, and negatively associated with nonverbal matrix AR and the middle temporal gyrus. Matrix non-verbal relational reasoning tasks produced positive correlations with parietal, frontal, and temporal cortex clusters, as well as in the cerebellum, the left superior parietal lobule (SPL) and the left middle temporal gyrus (MTG). The literature review supports and leads to the proposition of the following hypotheses to test empirically with behavioural and fMRI neuroscience research protocols.

2.4. Hypotheses to be tested for both the behavioural and fMRI data

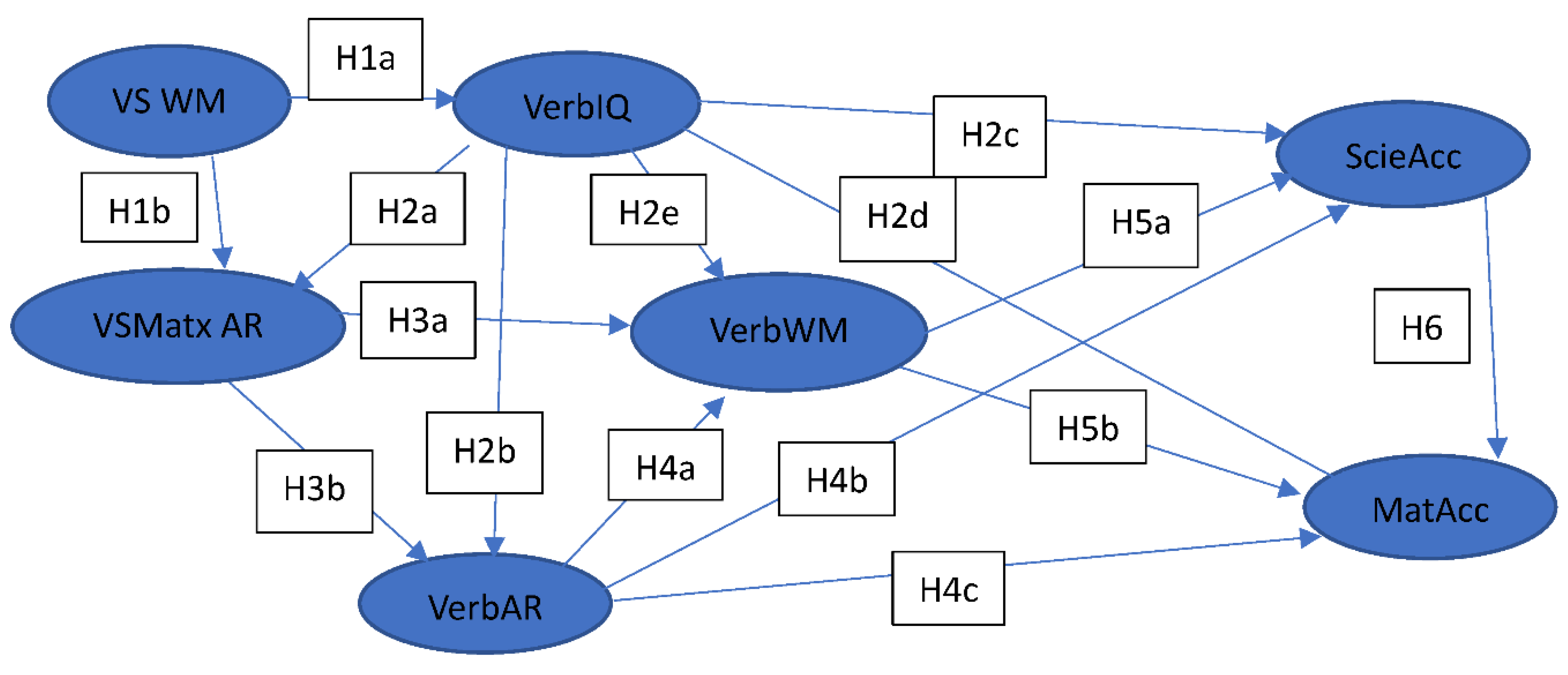
Hypothesis 1: WM (verbal & Visuospatial WM) are positively related to Verbal IQ (H1a) and Visuospatial Matrix AR (H1b).

Hypothesis 2: Verbal IQ is positively related to Visuospatial Matrix AR (H2a), verbal AR (H2b), Verbal WM (H2c), with maths (H2d) and science (H2e) performance.

Hypothesis 3: Visuospatial Matrix AR is positively related to Verbal WM (H3a), and Verbal AR (H3b).

Hypothesis 4: Verbal AR is positively related to Verbal WM (H4a), Science (H4b) and Maths (H4c).

Hypothesis 5: Verbal WM, mediates the relationship between IQ, Verbal AR and Visuospatial Matrix (VS) AR, and is positively related to science (H5a) and maths (H5b) performance.

Hypothesis 6: Science is positively related to Maths (H6a for behavioural data).

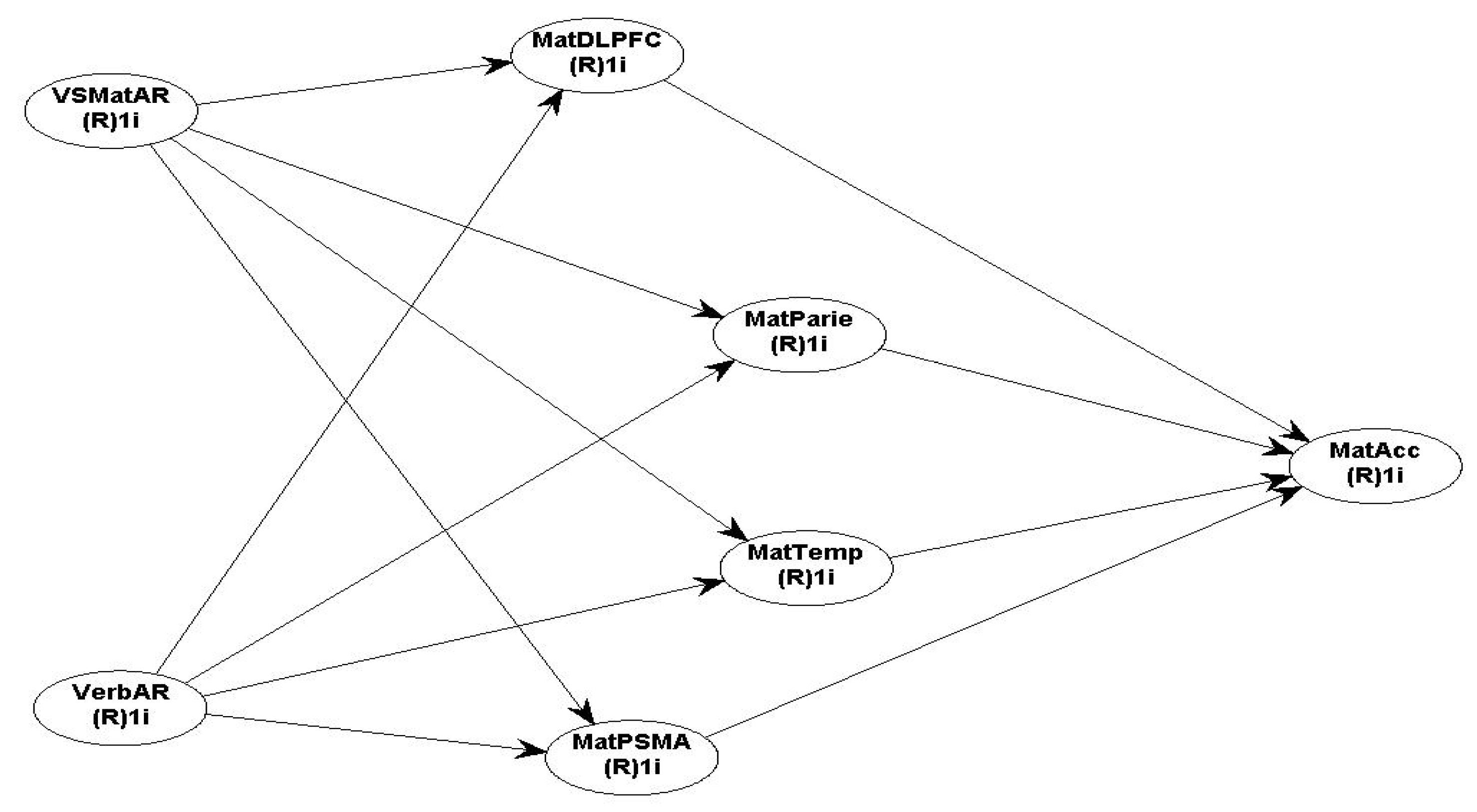
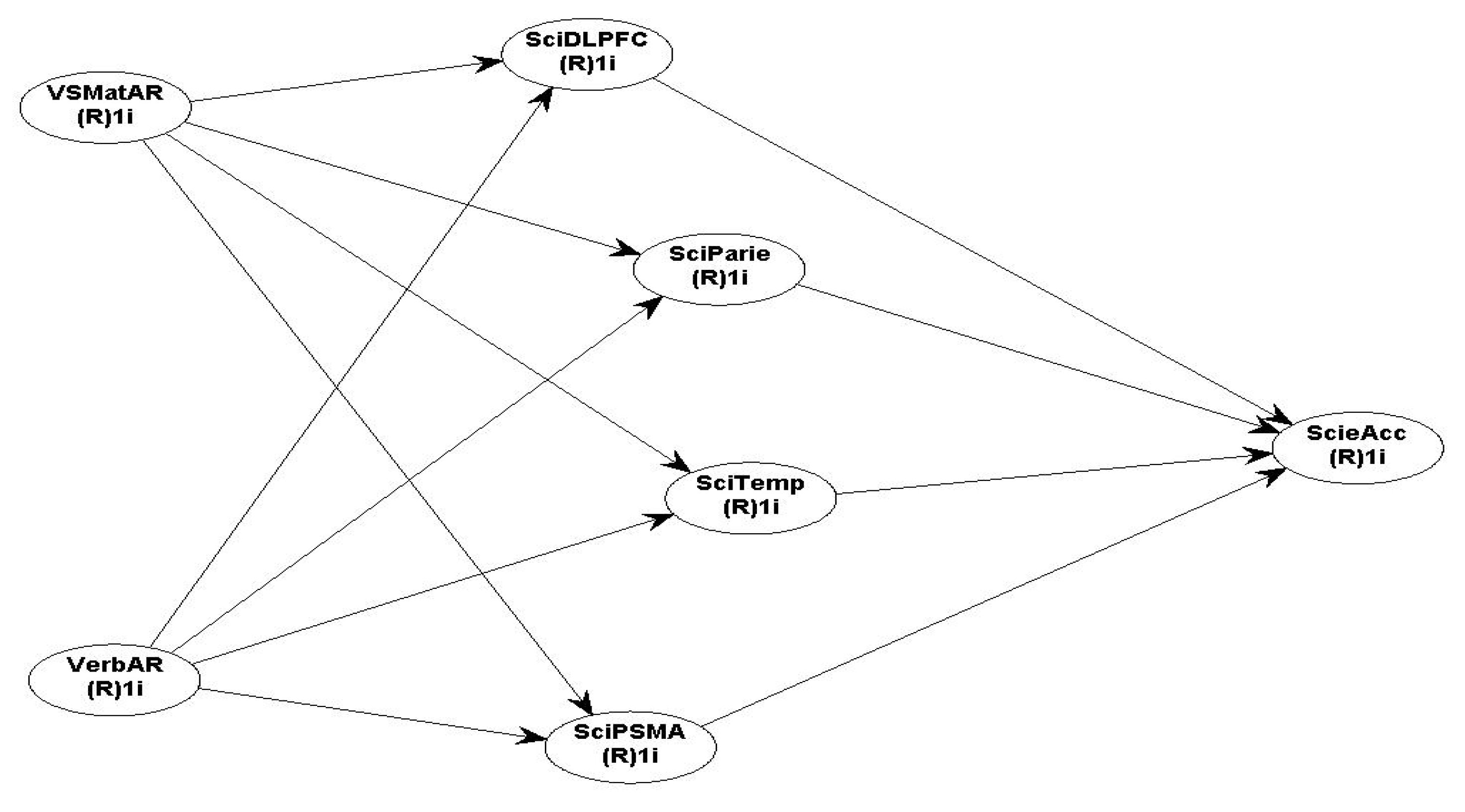
Hypothesis 7: For the neuroscience fMRI data; there is a positive relationship between Verbal AR and Visuospatial Matrix AR with activation in the frontoparietal network (H7 a, b, c, d, e), which includes the DLPFC & RLPFC, Parietal, temporal, and PSMA. In turn, all four brain regions of interest are positively related to Maths and Science accuracy (DVs).

3. Materials and Methods

To test the proposed hypotheses derived from the literature review, behavioural and fMRI data were collected as part of a much larger research project, testing a wide range and different sets of hypotheses than the present study. Some aspects of the broader research project findings have been published in a journal paper (Brookman-Byrne et al., 2019). However, this paper presents a new separate set of hypotheses, with a different focused literature review supporting a new research model, which posits that Verbal WM is a mediator between the independent variable of VS Matrix AR, VSWM, Verbal AR and Verbal IQ. The second major difference from any other published paper is that the authors use Warp PLS Structural Equation Modelling (SEM) to test multiple relationships, analysing simultaneously multiple non-linear interactions which is unique in this field of research. Warp PLS SEM is a more informative analysis than a simple linear hierarchical regression and is appropriate for interval non-normally distributed data. A description of the participants, tasks and data collection follows below to support the analysis plan and interpretation of the study’s results.

3.1. Participants

Participants were recruited from a range of schools in London UK to achieve a mixture of socio-economic backgrounds. The initial sample consisted of N=38 students, aged 11-15 years old, 20 girls and 18 boys. One participant was excluded from the final analysis because of low accuracy scores in the maths and science tasks; and three other participants were excluded because of excessive head movement during the fMRI scanning tests. The final sample consisted of N=34 participants (aged 137-185 months, mean= 161 months, and SD=16), consisting of an equal number of girls and boys. The original study data collection and the secondary data analyses carried out for this research were approved by the university of London research ethics committee. Written parental and participant consent were obtained before participation in the non-invasive fMRI study. All participants received £20 for participation and additional reimbursement for all travel expenses.

3.2. Experimental design and research instruments

All participants completed the science and maths problem solving tasks in the fMRI scanner, as well as tests of vocabulary IQ and visuospatial relational reasoning, verbal analogical reasoning, and verbal and visuospatial WM. Participants completed two additional tasks in the fMRI scanner, which measured inhibitory control, but they are part of a wider project and not included in this study.

The science and maths tasks were adapted from a prior behavioural study by Brookman-Byrne et al. (2018). The experimental design chosen was event-related paradigm (Chee et al., 2003). Participants carried out two scanning runs of the maths problems, two scanning runs of science problems, which alternated, and each run comprised 24 problems. Half of the problems focused on a counterintuitive concept, while the other half targeted a similar topic where the intuitive response was correct. The science and maths problems contained a range of questions on topics covered by the standard school curriculum in England. The tests required a selection of one choice out of four (true, false, probably true, probably false) by pressing the corresponding button. Each trial lasted 16 seconds. Stimuli were a mixture of text and pictures and were presented until a response was given or 12s had passed; a fixation cross was then presented on one third of the trial, or participants carried out an active baseline task until the trial ended. The science and maths tasks took approximately 30 minutes to complete. The science and maths tasks’ construct internal reliability were previously tested and the Cronbach alpha was a=.66, and a=.83 (Brookman-Byrne et al., 2019), which are broadly acceptable but not if they are below a=.70 (Cronbach, 1951). The maths and science testing assessed the degree of accuracy and response times (speed of responses) of responses.

The fMRI data were acquired on a 1.5 Tesla Siemens Avanto MRI scanner, with whole-brain coverage and a voxel-size of 3 x 3 x 3 mm³. MRI data were pre-processed and analysed using SPM12 (www.fil.ion.ucl.ac.uk/ spm/software/ spm12/). Functional images were realigned to correct for movement, and co-registered to the structural MRI image which were segmented based on Montreal Neurological Institute (MNI) registered International Consortium for Brain Mapping tissue probability maps. Normalisation parameters were applied to the functional images, maintaining the voxel-size, and images were finally smoothed with an 8 mm full-width at the half-maximum Gaussian Kernel. Framewise displacement (FD) was calculated and volumes with an FD greater than 0.9 mm were censored by including a regressor of no interest in the first-level general linear model (GLM) analyses. Science and maths trials of each run were modelled using boxcar regressors of reaction time duration for a given trial. The baseline task blocks were modelled in a similar manner. All regressors were convolved with the canonical hemodynamic response function. Contrasts at the first level were carried out to identify changes in BOLD signal during science problem solving and maths problem-solving, collapsing across intuitive and counter-intuitive trials. These were entered in second-level group analyses and 10 mm spheres around peak of activation were drawn to identify regions of interest. Data were extracted for each ROI and averaged between hemispheres, leading to five ROIs for maths and five for science, corresponding to the DLPFC (Brodmann area (BA) 44, 2 spheres), pre-supplementary motor area (PSMA)/middle cingulate cortex (BA 6/32, 1 sphere), inferior parietal lobule (IPL)/postcentral gyrus (BA 40/3) and inferior/superior parietal lobules (BA 7) (4 spheres), and temporal cortex (BA 37, 2 spheres). These are the brain regions of interest to be tested in the SEM modelling for fMRI research data.

The Wechsler Abbreviated Scale of Intelligence (WASI-II) was used to assess the participants levels of performance on vocabulary and matrix reasoning tests (Wechsler, 2011). The WASI vocabulary sub-scale required to explain the meaning of words and therefore assess the understanding of the semantic relational reasoning (VerbAR) ability levels which was used as a proxy for verbal IQ. For the matrix reasoning tests, a measure of non-verbal relational reasoning of visuospatial matrix AR (VSMatAR), the participants were asked to identify similarities and differences and therefore choose the most relationally appropriate visuospatial option which fits the pattern. Visuospatial working memory (VSWM) was assessed using an adaptation of the Dot Matrix test of the Automated Working Memory Assessment (Alloway, 2007), and verbal working memory (VerbWM) was assessed by using the backwards digit span memory test. The WM tests increased in difficulty in blocks of four trials, and when participants committed two or more errors at a particular level, testing stopped. The total number of correct trials identified the overall score for each task. All tests were scored as per the manual instructions and the raw scores were used for the behavioural and fMRI analysis.

3.3. Analysis plan

The analysis plan consists of two steps: first, the analysis of the behavioural data findings, and second, the fMRI data analysis. Both analyses include descriptive and inferential tests. The descriptive analysis of both data sets includes Pearson Correlations of all relevant IVs & DVs; and the inferential analysis carries out SEM multiple regressions simultaneously testing all hypothesised relationships between the IVs with DVs (maths and science accuracy performance). Given the small sample size (N=34), the most appropriate analytical tool to test multiple model relationships between IVs and DVs, is Warp Partial Least Squares (WarpPLS, 7.0), which is a SEM software capable of testing all hypothesised non-linear direct and indirect moderating and mediating relationships. The PLS regression approach using WarpPLS 7.0 software program (Kock, 2020) is the most appropriate to estimate all model parameters simultaneously with small sample sizes, identifying the degree of covariance between all hypothesised relationships. WarpPLS uses a bootstrapping approach that reduces the variations of data variability distribution properties to estimate all hypothesised relations (Kock, 2014, Kock & Hadara, 2018). WarpPLS is designed to identify all types of non-linear or ‘warped’ relationships, including moderating and mediating relationships simultaneously and adjusts the values of path coefficients accordingly. WarpPLS assumes that psychological and behavioural constructs are complex and have iterative non-linear complex relationships which need to be represented as such and estimated simultaneously rather than in isolation as separate inert entities. It is capable of measuring ‘real empirical’ relationships between independent and dependent variables, represented in a SEM (Kock, 2011; 2014; 2020).

While PLS models do not have an equal range of goodness of fit (GoF) measures used in covariance-based procedures, like LISREL and AMOS, the GoF is sufficient and reliable measure of robustness of the model findings. The GoF is calculated as the square root of the average variance extracted score for the model’s constructs and the average R-squared for all the endogenous constructs. Several researchers suggest that the GoF value of 0.36 implies there would be large effect sizes within the model and therefore the model performs well (Tenenhaus et al., 2005; Wetzels et al., 2009; Chin, Marcolin, & Newsted, 2003; Koch & Hadaya, 2018).

3.4. The hypothesised research models for behavioural and Neuroscience fMRI data

The literature review underpins the hypothesised relationships in the behavioural research between the IVs of visuospatial WM, VS Matrix AR, Verbal IQ, verbal AR and verbal WM, with maths and science accuracy (MatAcc, SciAcc) performance. More specifically the proposed behavioural research model presents visually all the hypotheses in Figure 4.

The proposed research models for the Neuroscience fMRI data with all the assumed hypotheses for Maths and Science performance are presented in Figure 5 (maths) & Figure 6 (science).

Hypothesis H7 (for maths & science): Verbal AR and VSMatrix AR are positively related to brain activation in the frontal cortices (DLPFC & RLPFC), Parietal, Temporal and PSMA; and activation in the DLPFC, Parietal, Temporal and PSMA is positively related to maths and science accuracy performance.

4. Results from behavioural and fMRI data analysis

4.1. Behavioural data analysis results

The first step of the analysis focuses on the behavioural data (descriptive and inferential analysis) to test the direct and indirect relationships between the five IVs of Verbal IQ (VerbIQ), Verbal analogical reasoning (VerbAR), Visuospatial Matrix analogical reasoning (VSMatAR), Verbal WM (VerbWM), and Visuospatial WM (VSWM), with the two DVs of Maths accuracy (MathsAcc) and Science accuracy (ScieAcc). Based on prior research studies the construct of Verbal WM is hypothesised to mediate VSMatrix AR and VerbAR (Green et al., 2006); VSWM is hypothesised to influence/relate to VSMatAR and VerbIQ because it contains relevant prior knowledge used during VSMatAR and VerbIQ processing. The descriptive data in Tables 1, and the correlations in Table 2, present the SD and correlations between IVs and DVs.

4.1.1. Test results of Behavioural Model 1: Full hypothesised relationships between DVs (Science & Maths accuracy) with all IVs (VerbIQ, VerbWM, VerbAR, VSMatAR, VSWM)

Testing the full hypothesised behavioural research model 1 with all the predicted relationships, the overall model quality fit indices (see Table 3a,b) are acceptable and therefore the model fits the data well. However, five predicted relationships are not statistically significant, namely, VerbAR -> VerbWM (β=0.13, P=0.21), VerbWM->ScieAcc (β=0.20 P=0.10), VerbWM-MatAcc (β=0.22, P=0.08), VerbIQ -> MatAcc (β=0.18, P=0.13) and VerbAR->MatAcc (β=0.05, P=0.39). The literature suggested that there is a strong relationship between maths and science (Goldstrom, 2004; Lonning, & DeFranco,1997) and our data support this hypothesis (β=0.48, P<.01).

Model 1:. All hypothesised behavioural model 1 relationships tested with WarpPLS. 

Model 1:. All hypothesised behavioural model 1 relationships tested with WarpPLS. 

All fit indices (Table 3a) are acceptable, and the GoF=0.64 confirms that the model fits the data. The Sympson’s paradox ratio is acceptable, confirming that the results are valid and not a happenstance.

However, if we eliminate the two non-significant relationships, i.e., VerbAR -> VerbWM and VerbWM-> ScieAcc, as well as the independent association between ScieAcc-> MathsAcc, the next model 2 performs better.

4.1.2. Behavioural Model 2 testing results

All path coefficients are positive and statistically significant. Maths accuracy is weakly predicted by VerbWM ->MatAcc (β =0.32 P=0.02), VerbIQ-> MatAcc (β =0.28 P=0.04) and strongly by VerbAR -> MatAcc (β =0.36 P<.01). Science accuracy is strongly predicted by VerbAR->SciAcc (β =0.57 P<.01) and VerbIQ (β =0.40 P<.01).

Behavioural Model 2:. Maths & Science accuracy predicted by all IVs and mediating VerbWM. 

Behavioural Model 2:. Maths & Science accuracy predicted by all IVs and mediating VerbWM. 

Overall, all fit and quality indices for model 2 are all positive (see Table 4a and 4b) which indicates that the data fit the model very well, and all the predicted relationships are valid and reliable. All SEM path coefficients are positive and statistically significant (Table 4b) and the results support all hypotheses, except the relationships between VerbAR-> VerbWM and VerbWM -> ScieAcc.

The overall findings of behavioural research model 2, whereby all hypothesised relationships were tested simultaneously, are robust and fit the data very well. The GoF as the key criterion that determines the overall model 2 fit is very acceptable and the data support all the hypothesised relationships. The GoF index is well within the recommended level (GoF=0.62, large if >= 0.36); and the Sympson’s paradox ratio (SPR)=1.000, (is acceptable if >= 0.7). The Nonlinear bivariate causality direction ratio (NLBCDR=0.964) is above the recommended level of >=0.7 and therefore the assumed nonlinear relationships between all hypothesised paths are acceptable and valid.

4.2. Neuroscience fMRI data analysis results

The analysis plan for the neuroscience fMRI data aims to first, interrogate the descriptive data (testing Means, SD), and bivariate Pearson correlations (see Table 5, Table 6 and Table 7); secondly, using SEM WarpPLS) to test all direct and indirect relationships simultaneously between the IVs (VerbAR and VSMatAR) with the DVs of brain regions of interest (ROI) and with maths and science accuracy.

The maths bivariate correlations (table 6) with all IVs, indicate strong relationships between VerbAR with MatAcc, the DLPFC and PSMA. The DLPFC is strongly correlated with Parietal, Temporal and PSMA; and the Parietal is also strongly associated with the Temporal and PSMA brain regions.

The science bivariate correlations (table 7) indicate strong and significant relationships exist between the IVs of VSMatAR and VerbAR, VSMatAR with P-SMA and VerbAR with SciAcc. In addition, there are strong and significant associations between the four brain ROI namely: DLPFC with Parietal, Temporal and PSMA, Parietal with Temporal and PSMA; and Temporal with PSMA.

4.2.1. Maths Accuracy fMRI data analysis and SEM modelling using WarpPLS software

Using Warp PLS, the hypothesised fMRI SEM model 3 (SEM), tests MatAcc as the DV and the predictor IVs are: VSMatAR, VerbAR, the bilateral DLPFC, bilateral Parietal, bilateral Temporal, and the Pre-Supplementary motor area (PSMA) (model 3, presents all the direct path β coefficient associations and P values).

Neuroscience Maths SEM fMRI Model 3:. VerbAR and VSMatrix AR with four brain ROI. 

Neuroscience Maths SEM fMRI Model 3:. VerbAR and VSMatrix AR with four brain ROI. 

The interesting finding in the maths model 3 is that only two brain ROI are statistically significant with maths, namely bilateral Parietal (β =-0.38, P<.01) and PSMA (β=0.49, P<.01) (see Table 8 with all path coefficients and P values). However, the Parietal -> maths path coefficient is negative and significant (β= - 0.38, P<.01). In contrast, the PSMA -> maths path coefficient is positive and significant (β=0.49, P<.01). The relationship between the DLPFC and Maths is very small but non-significant (β =0.04, P=0.40); and Temporal ->Maths path coefficient is negative and non-significant (β =-0.10, P=0.27).

The path coefficients between VSMatAR and two brain ROI are negative and statistically significant, namely: VSMatAR -> DLPFC (β =-0.47, P<.01), and VSMatAR -> parietal (β =-0.32, P=0.02). The VSMatAR -> temporal (β =-0.22, P=0.08) is negative and non-significant. However, VSMatAR -> PSMA path coefficient is positive but non-significant (β = 0.09, P=0.29).

The results between VerbAR and brain ROI are mixed. VerbAR -> PSMA is positive and significant (β=0.47 (P<.01); VerbAR with Temporal is positive, not significant (β =0.22, P=0.08); with Parietal is negative, non-significant (β = -0.24, P=0.07); and DLPFC it is positive but non-significant (β = 0.20, P=0.10). The only significant positive predictor of Maths accuracy is PSMA->MatAcc (β =0.49, P<.01).

All the Maths Model 3 fit and quality indices are overall acceptable (see Table 8), and the model fits the data well. However, as mentioned above, some path coefficients are not significant and therefore do not contribute much to the overall model robustness (see Table 9).

To improve the overall model 3 fit and quality indices, the path coefficients that are statistically significant will remain and the non-significant can be eliminated. By excluding the non-significant path coefficients, the overall fit indices for model 4 have improved and consequently model 4 works very well with the data. The strongest predictors of maths accuracy performance are activation in the parietal cortex and PSMA, which are related to VSMatAR and VerbAR. VSMatAR is negatively related to the bilateral DLPFC (β = - 0.48, P<.01), and parietal cortex (β = - 0.40, P<.01), which suggests that there is strong deactivation when maths accuracy processing takes place. The most plausible reason for the deactivation in the DLPFC and parietal regions is because developmentally the adolescent brain has not yet completely evolved to be fully functional for processing these cognitive tasks, like adult brains do (Spanoudis, & Demetriou, 2020). The hypothesised relationship between VSMatAR and VerbAR (β=0.59, P<.01) is supported by the literature (Dehaene, et al., 2003), because visualising maths formulas and numerical relationships aids verbal relational reasoning processing.

Maths Model 4:. MathAcc predicted by bilateral Parietal, PSMA & VerbAR. 

Maths Model 4:. MathAcc predicted by bilateral Parietal, PSMA & VerbAR. 

The maths Model 4 fit and quality indices have improved in comparison to model 3, and all path coefficients are statistically significant and therefore overall, the model predictions are robust and reliable (see Table 10 fit indices and 11 all path coefficients and P values) supporting the hypotheses.

The actual model 4 path β coefficients and the significance P values are presented in Table 11.

Overall, the predicted positive relationships between VSMatAR with DLPFC, and Parietal are in fact negative and therefore not supported. The predicted positive relationships between VSMatAR with Temporal, and PSMA are non-statistically significant and therefore not supported. The predicted positive relationships between VerbAR with DLPF, Parietal and Temporal are non-statistically significant and therefore not supported. However, the VerbAR->PSMA relationship is supported. The predicted positive relationships between DLPFC and Temporal with MatAcc are positive but non-statistically significant; but, the relationships of Parietal and PSMA -> MathAcc are positive and significant and therefore supported.

4.2.2. Science Accuracy fMRI data analysis and SEM using WarpPLS software

The descriptive and bivariate correlation between all the IVs and DVs for the Science accuracy model are presented in Table 5, Table 6 & Table 7. It is interesting to note that the bivariate correlations are strong and highly significant between all brain ROI themselves. The Science SEM hypothesised research model 5 fits the data well and tests all relationships between VSMatAR and VerbAR with bilateral DLPFC, Parietal, Temporal and PSMA, which are in turn related to science accuracy outcomes.

Scheme 5. all independent and dependent variables (brain ROI and Science accuracy).

Scheme 5. all independent and dependent variables (brain ROI and Science accuracy).

The following Table 13 presents all the model 5 path β coefficients and the P significance. Overall, all the relationships between the four brain ROI and Science performance are not significant. The relationships between the VSMatAR and brain ROI are mixed, e.g., VSMatAR -> DLPFC is negative but significant (β = - 0.40, P<.01); VSMatAR -> Parietal is non-significant (β = 0.14, P=0.20); VSMatAR -> Temporal is non-significant (β=0.14, P=0.19); but, VSMatAR -> PSMA is significant (β=0.30, P=0.03). In contrast, VerbAR produced significant relationships with all four brain ROI, i.e., VerbAR with DLPFC (β=0.27, P=0.04), VerbAR with Parietal (β=0.31, P=0.02); VerbAR with Temporal (β=0.34, P=0.01); and VerbAR with PSMA is negative but significant (β=- 0.39, P<.01). Overall, there are no significant relationships between DLPFC, Parietal, Temporal and PSMA with MatAcc.

By removing the non-significant paths, the adjusted and simplified Science model 6 produces different β coefficients and different model fit and quality indices (see model 6, Table 14).

Scheme 6. SciAcc with DLPF, Parietal, Temporal and PSMA and VSMatAR and VerbAR.

Scheme 6. SciAcc with DLPF, Parietal, Temporal and PSMA and VSMatAR and VerbAR.

The model 6 fit and quality indices overall suggest a reasonable GoF with the data, but Sympson’s paradox ratio is below the acceptable level (see Table 14). Therefore, the elimination of the non-significant path coefficients made model 6 weaker than model 5. The path coefficients between the IVs (VerbAR and VSMatAR) are all acceptable and have statistically significant P values; but, two path coefficients between DLPFC, and Parietal -> SciAcc are negative and non-significant. The relationship of Temporal -> SciAcc (β=0.18, P=0.13) and PSMA->SciAcc (β=0.20, P=0.11) are positive but non-significant (see Table 15). Interestingly, the VerbAR relationships with all 4 ROI are statistically significant but VerbAR-PSMA is negative (β=-0.39, P<.01). VSMatAR -> DLPFC is negative but statistically significant (β=-0.40, P<.01), but VSMatAR->PSMA is positive (β= 0.30, P<.01).

Overall, the SEM science model 5 has a better fit with the data than model 6. The predicted positive hypotheses between the DLPFC, Parietal, Temporal and PSMA with ScieAcc are not supported. The predicted positive hypotheses between VSMatAR with DLPFC, Parietal and Temporal are also not supported; but VSMatAR -> PSMA is positive and significant and therefore supported. The predicted positive hypotheses between VerbAR with DLPFC, Parietal and Temporal are supported, but rejected the relationship between VerbAR with PSMA because the relationship is negative and significant.

5. Discussion of Behavioural and Neuroscientific fMRI Research findings

5.1. Discussion of Behavioural data results

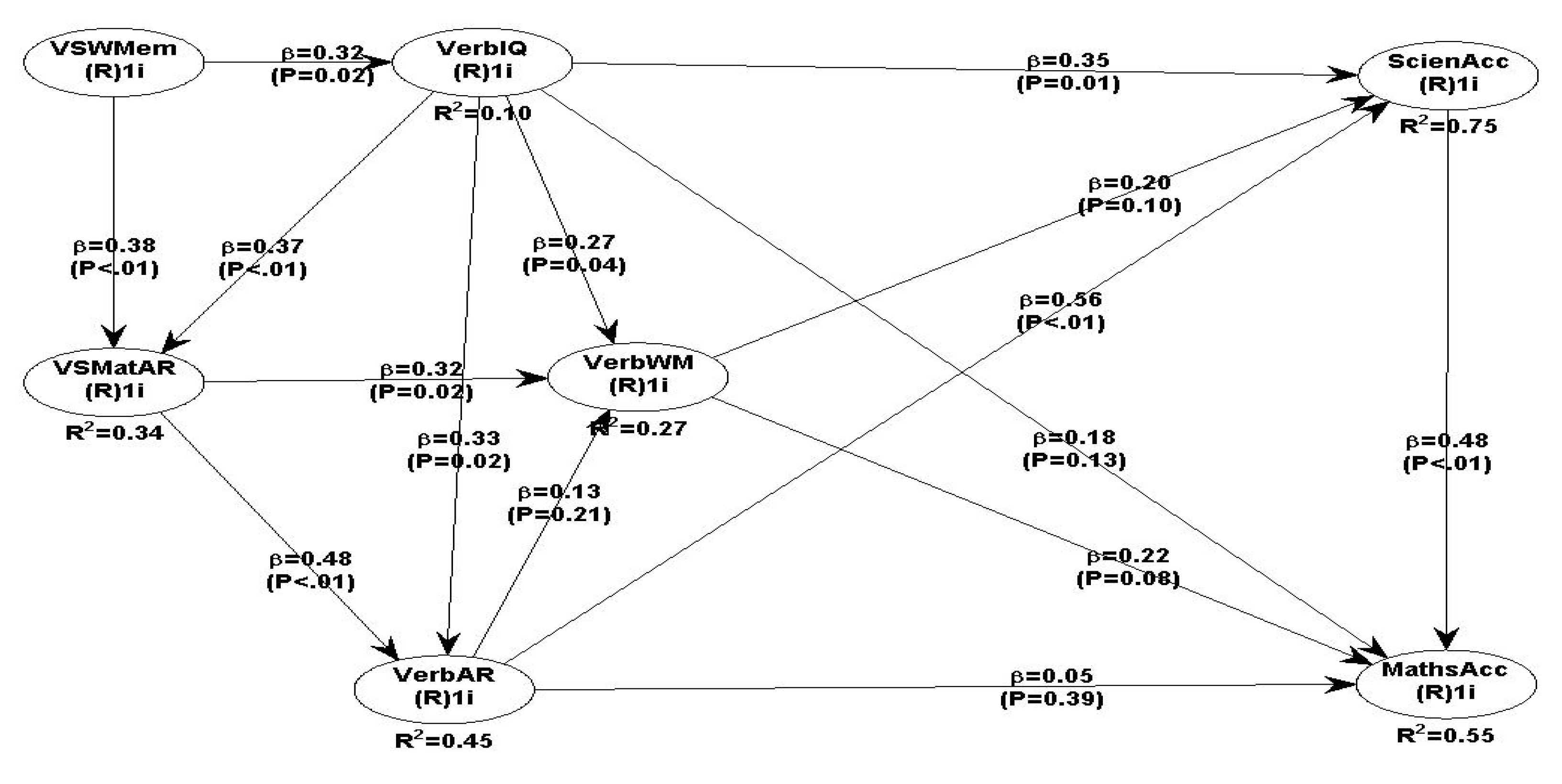
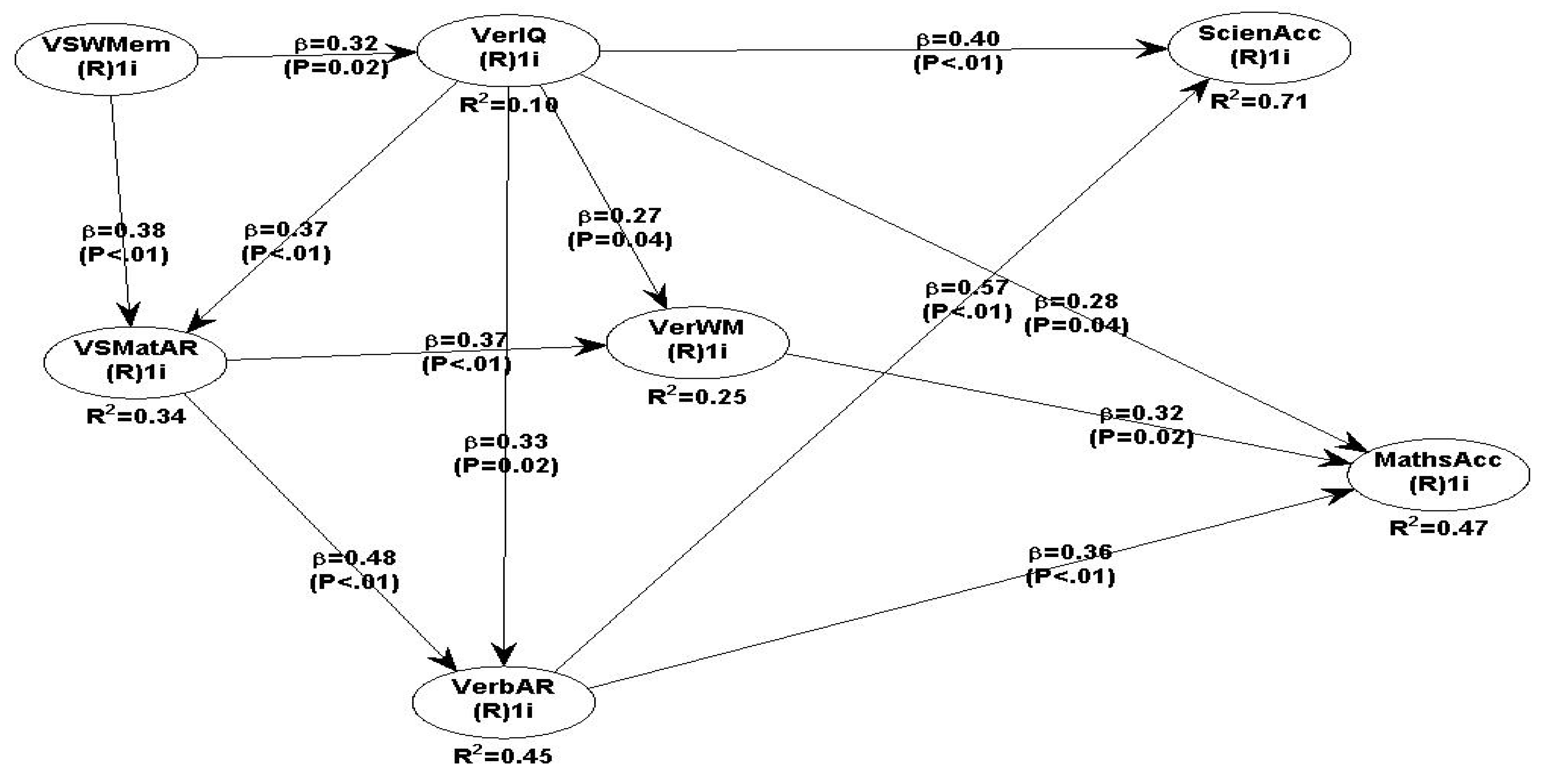
This discussion evaluates first the behavioural and secondly the neuroscience fMRI results. Overall, the behavioural data results support most of the hypotheses made except two, namely the VerbAR->VerbWM (β = 0.13, P=0.21) and VerbWM->ScieAcc (β = 0.20, P=0.10). However, several interesting findings emerged, which are useful to academics and educational practitioners. The behavioral SEM data modelling suggests that verbal IQ is an important influence for maths (β = 0.28, P=0.04) and science accuracy performance (β = 0.40, P<.01). In addition, verbal IQ is positively related to a number of IVs, namely, VerbWM (β = 0.27, P=0.04), with verbal AR (β = 0.33, P=0.02), with VSMatrix AR (β = 0.37, P<.01) and with VSWM (β = 0.32, P=0.02). No other study has tested simultaneously with SEM the combined effects of verbal IQ on maths and science accuracy combined with verbal and VS matrix AR. Verbal IQ appears to be a driving influence for multiple cognitive processes including memory for verbal and matrix visuospatial information, as well as VerbAR and VS matrix AR. In fact, verbal AR ->science (β = 0.57, P<.01) and verbal IQ->science (β = 40, P<.01) are the two strongest predictors of science accuracy and therefore, educationalists need to consider the multiple learning benefits by developing strong verbal analogical reasoning skills and integrate relevant scientific semantic knowledge to improve teaching and outcomes in maths and science. Verbal WM is strongly associated with VS matrix AR (β = 0.37, P<.01), and also as a mediator with maths accuracy (β = 0.32, P=0.02), which suggests that overall verbal IQ combined with Verbal AR skills and VerbWM are the strongest and most significant predictors for science and maths performance for adolescent students.

The strong relationship between VSMatrix AR->verbal AR (β = 0.48, P<.01) suggests a positive contribution to the overall association with maths accuracy (β = 0.36, P<.01). The vital role that VSWM plays with VS matrix AR (β = 0.38, P<.01), and VSWM with VerbIQ (β = 0.32, P=0.02) suggests that students need both visuospatial empirical experiences and skills, because they are strongly associated with Verbal WM, Verbal IQ and in turn with Verbal AR. In combination, VSWM and VerbWM contribute indirectly to the accretion of knowledge and understanding of procedural methods for Visuospatial and Verbal AR tasks, which in turn are relevant resources for more efficient visualising processing of maths and science relationships and conceptualising new analogical relationships, thus creating new ideas and better thinking models.

A second major finding is that, science performance is strongly predicted by two factors, primarily by verbal AR (β = 0.57, P<.01) and secondly, by Verbal IQ (β = 0.40, P<.01), as well as with an indirect contribution by VSWM-> VerbIQ (β = 0.32, P=0.02) and VSMatAR -> VerbAR. The positive association between maths and science accuracy shown in model 1 (β =0.48, P<.01), suggests that the two subjects share a substantial common body of knowledge and skills and supports the previous findings that effective studying of science needs certain amount of maths knowledge to conduct meaningful calculations and measurements of scientific phenomena (Goldstrom, 2004; Lonning, & DeFranco, 1997). Educational practitioners need to design curricula that combine relevant vocabulary and conceptual knowledge of both maths and science to integrate science and maths literacy with rigorous and clear semantic understanding of relevant conceptual relationships. Relational analogical reasoning appears to improve maths and science performance and therefore students need to understand the foundational meanings and relationships embedded in both maths and science theories. Language teaching should aim to make analogical connections between general as well as domain specific knowledge of maths and science curricula (Nenciovici, Allaire-Duquette & Masson, 2019; Dündar-Coecke, & Tolmie (2020).

5.2. Discussion of the fMRI Results

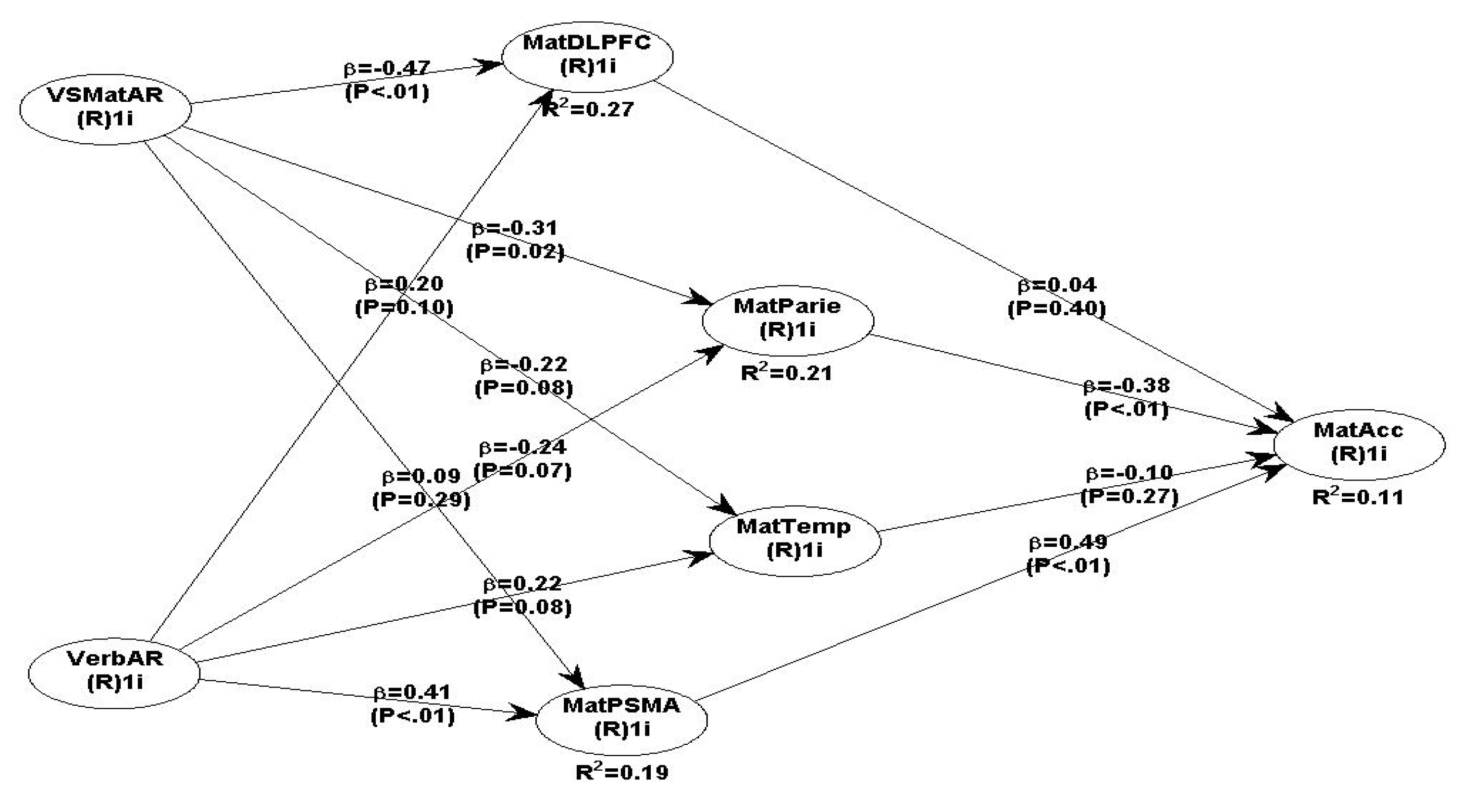
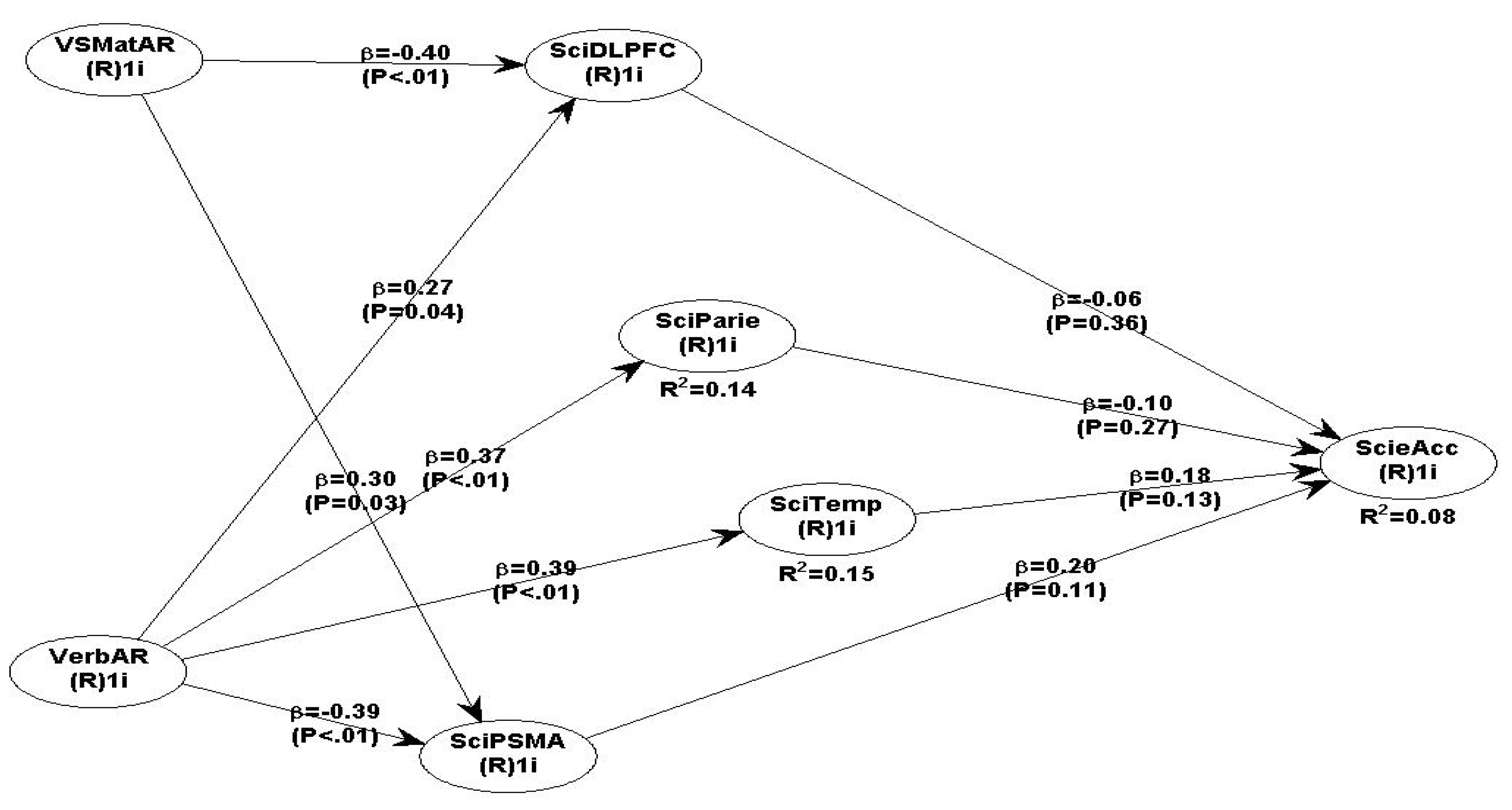
The fMRI maths model 3 produced a mixture of positive and negative relationships between VerbAR and VSMatrix AR with all four brain ROI, which in turn were related to Maths and Science accuracy. The hypothesis that all four brain regions (bilateral DLPFC, Parietal, Temporal and PSMA) would be positively related to Maths accuracy performance is not supported by the actual data results. The only positive and significant path coefficients are between Verbal AR and PSMA (β =0.41, P<.01), and PSMA with Maths accuracy (β =0.49, P<.01). The three statistically significant but negative path coefficients are between VSMatAR -> DLPFC (β = - 0.47, P<.01), VSMatAR -> Parietal (β = - 0.31, P=0.02) and Parietal->Maths (β = - 0.38, P<.01). These three negative path coefficients are possible deactivations due to the lower age developmental stages of the adolescent brains indicating non engagement yet for maths processing (Dumontheil et al., 2010b; Wendelken, Chung & Bunge, 2012). The five statistically non-significant path coefficients between the two IVs with brain ROI indicate that there is no activation during the maths processing, e.g., VSMatAR->Temporal (β = 0.22, P=0.08), VSMatAR ->PSMA (β = 0.09, P=0.29); and VerbAR->DLPFC (β = 0.20, P=0.10), VerbAR->Parietal (β = 0.24, P=0.07), and VerbAR->Temporal (β = 0.22, P=0.08). A plausible explanation is that the fronto-parietal brain networks including the EF and semantic network are not yet fully developed in the adolescent brains and therefore there is no activation during maths and science problem solving (Wendelken et al., 2016; Whitaker et al., 2018; Nenciovici et al., 2019).

The two non-significant path coefficients between the three brain ROI indicate that they are disengaged during the maths processing tasks, namely, DLPFC ->Maths accuracy is very weak and (β= 0.04, P=0.40), and, Temporal ->Maths (β = 0.04, P=0.04). These relationships require further investigation to ascertain if they are caused or influenced by the VS Matrix AR or/and the Verbal AR or both, or if they are due to young adolescent brains’ underdevelopment of relevant networks (Hobeika et al., 2016; Nenciovici et al., 2019). The overall maths model 3 fit and quality indices are within the acceptable levels and therefore the model fits the data well despite the presence of several negative or non-significant path coefficients. The main model fit index, GoF=0.393 is large enough and the Sympson’s paradox ration (SPR=0.750) is close to the ideal level required and therefore all relationships are valid and reliable.

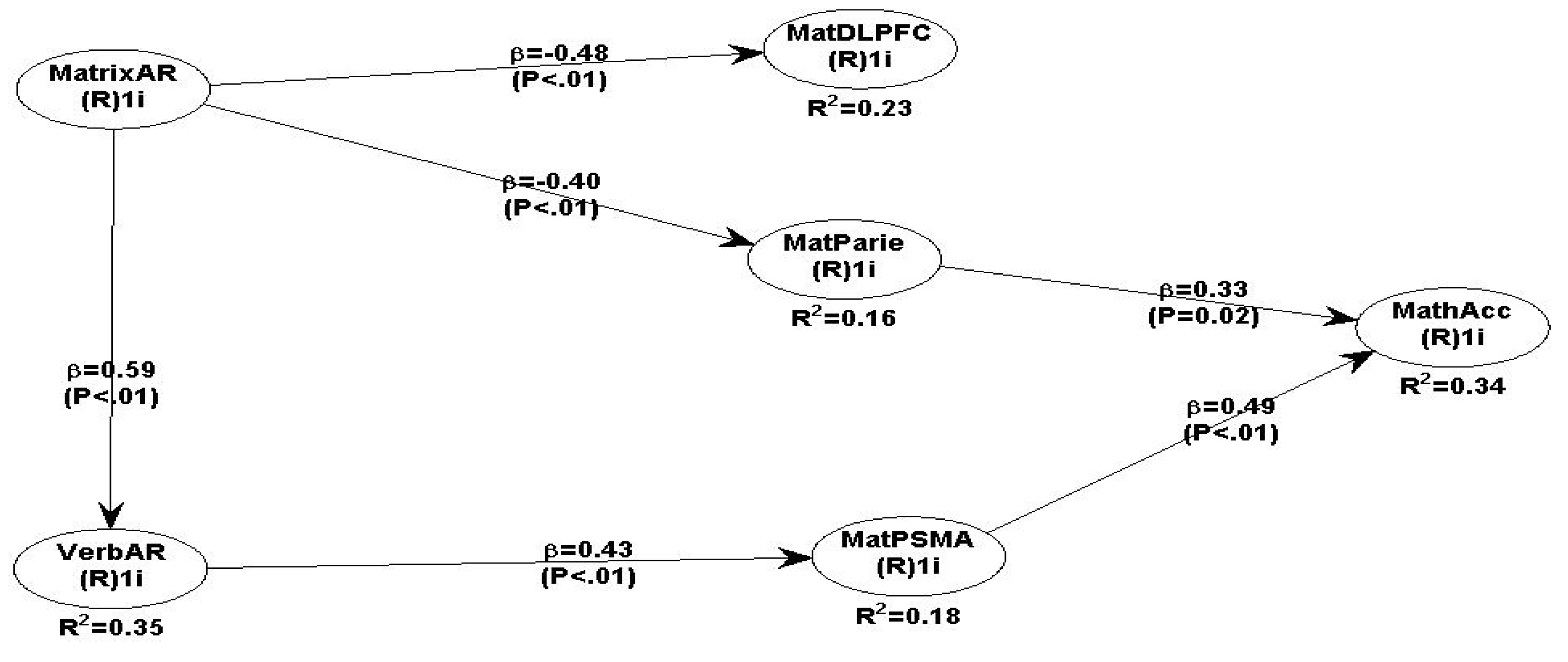
The more parsimonious maths model 4 incudes only the statistically significant path coefficients and the model fit indices have improved even more thus producing a very good fit with the data. The negative relationships between VS Matrix AR -> DLPFC (β = -0.48, P<.01) does not have any further connection with MathAcc performance and therefore it suggests that for adolescents it is deactivated, thus strongly indicating that it may be due to younger age-related brain development (Ferrer et al., 2009; Dumas et al., 2008; Dumontheil et al., 2010b). VSMatAR is also negatively related with Parietal but it is very significant (β = - 0.40, P<.01). However, the best predictors of maths accuracy are Verbal AR, which is related to PSMA (β = 0.43, P<.01), and PSMA which is related to Maths (β = 0.49, P<.01); and Parietal -> MatAcc (β = 0.33, P=0.02). The positive relationship between maths accuracy and the parietal cortex is strongly supported by other researchers who found similar relationships (Arsalidou et al., 2011; 2018; Dehaene, 2011; Dehaene et al., 2003). The strong positive relationships between PSMA and Parietal with math accuracy indicate that these two brain regions are important during the maths conceptualisation and choosing which method of analysis to utilise. Maths model 4 fit indices are all acceptable, with all path coefficients are statistically significant, robust and fitting the data very well.

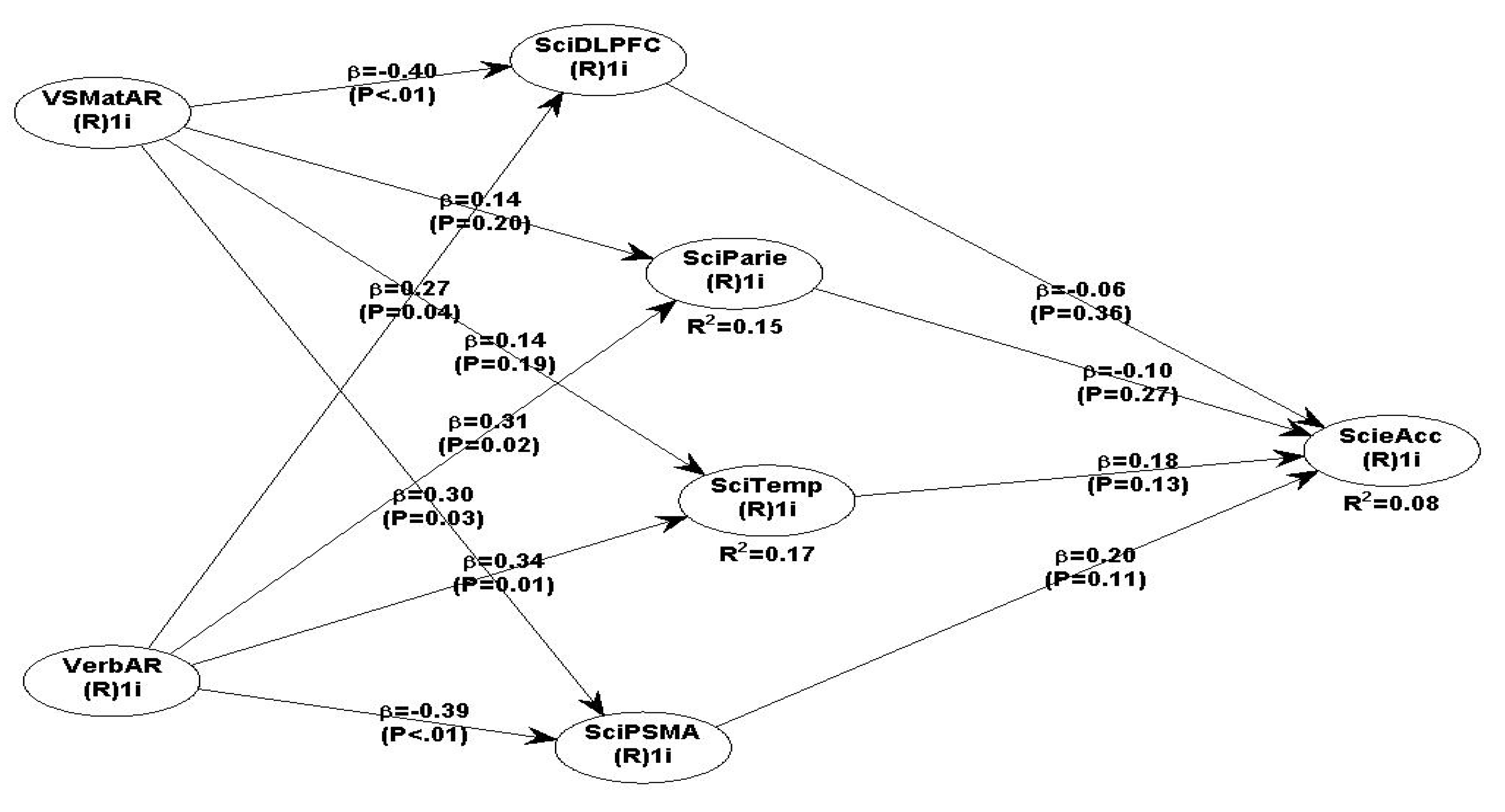
Regarding the SEM model 5 for science accuracy, testing all the hypothesised brain region activations by the IVs of VS Matrix AR and Verbal AR produced mixed results. There are a few non-significant path coefficients, e.g., VSMatAR -> Parietal (β =0.14, P=0.20) and VSMatAR ->Temporal (β = 0.14, P=0.19). All brain ROI path coefficients with science are non-significant, e.g., DLPFC-> science (β =0.06, P=0.36), Parietal -> science (β = - 0.10, P=0.27), Temporal -> science (β =0.18, P=0.13) and PSMA-science (β =0.20, P=0.11). The interpretation as mentioned above, is that age related brain network development is not yet complete and therefore during science tasks they are inactive (Whitaker et al., 2018).

Interestingly, all VerbAR path coefficients with all brain ROI are statistically significant, e.g., VerbAR->DLPFC (β =0.27, P=0.04), VerbAR-> Parietal (β =0.31, P=0.02), VerbAR -> Temporal (β =0.34, P=0.01); but VerbAR -->PSMA is negative and significant (β = - 0.39, P<.01), indicating disengagement during the action of actual science task processing. Like the maths model, the relationship of science VSMatAR -> DLPFC is negative but significant (β = - 0.40, P<.01) which can be interpreted as disengagement due to lack of age-related development of the frontal brain regions (Brookman-Byrne et al., 2019; Suarez-Pellicioni, Berteletti, & Booth, 2020; Wang et al., 2020). Normally, the DLPFC is the last part of the brain regions that becomes fully developed by the age of late adolescence and early maturity (Dumontheil, 2014; Dumontheil, Houlton, Christoff & Blakemore, 2010a; Geake & Hansen, 2005; Wendelken et al., 2016). Abstract thinking about maths and science involves several brain regions including the parietal and temporal cortex and the current research findings partially support prior similar findings (Wang et al., 2020; Belkacem et al., 2020).

Fluid intelligence is also related to the DLPFC and therefore the adolescents lack of full development implies less availability of brain network connectivity indexed by lower or negative BOLD activation during maths and science thinking and novel problem solving (Heidekum, Vogel, & Grabner, 2020; Wright et al., 2007; Yuan, Voelkle & Raz, 2018). However, the general model 5 fit indices of GoF=0.413 and Symonds paradox ratio =0.846 are very good. The experimental and more parsimonious science model 6 produced slightly better path coefficients but overall, it does not provide any new insights.

In summary, the fMRI research data support some of the hypothesised science model relationships. Overall VerbAR is positively related to DLPFC, Parietal and Temporal, but negatively with PSMA. The VSMatAR is positively related to PSMA, but negatively related to DLPFC. Surprisingly, none of the four brain ROI are activated during science tasks. Regarding the maths hypothesised relationships, the findings support one hypothesis, e.g., a strong positive and significant relationship between VerbAR and PSMA, but VSMatAR is negatively related to both DLPFC and Parietal. Only two brain regions, Parietal and PSMA are positively and statistically significantly related to maths accuracy.

6. Conclusions, implications for educational practitioners and limitations

Regarding educational practice applications, it is important to note that overall verbal IQ and therefore knowledge and understanding of maths and science concepts is very important. In addition, scientific literacy and understanding of maths/science language expressions and semantics of formulas, aids conceptual thinking and contributes to developing relevant verbal and visuospatial memory resources. Science and maths concepts cannot be entirely separated from linguistic knowledge as well as abstract analogical thinking and making sense of verbal and visuo-spatial representations of scientific phenomena and scientific theories (Fuchs, et al., 2016). Educationalists need to develop students’ all rounded knowledge of relevant language representations of symbolic mathematical and scientific concepts and commensurate analytical skills to enable adolescent students to achieve good results and progress intellectually, to become competent abstract and concrete empirical thinkers. Making explicit analogical relational connections between well-known phenomena with new ones is an essential scaffolding skill that needs to be incrementally developed rigorously by teachers.

One of the key findings, that VerbAR is associated with the parietal and temporal cortex, suggests that adolescent learners need to have the required linguistic knowledge and verbal semantic understanding of the scientific terminology, to enable analogical links and conceptual leaps to be made with new conceptual meanings embedded in their scientific tasks and experiments (Downer, et al., 2002). Adolescent students need to be engaged with actual physical real-life activities to be able to identify clear empirical relationships and correlations with other similar new phenomena.

Analogical relational reasoning should be used extensively and systematically to clarify various relationships taught during science visuospatial Matrix AR tasks and to expand incrementally existing connections with new phenomena and general mathematical theories. Semantic processing skills are essential to build a series of interconnecting and comprehensive mental maps between source (base line knowledge) with target relational analogues (new relational contexts), thus connecting abstract mathematical constructs with empirical scientific realities. The importance of the EF system involving many of the brain regions tested in this research suggests that teachers need to focus on developing the student’s overall attention, emotional control, cognitive evaluation skills and cognitive integration of novel stimuli with other related subjects (Spagna, et al., 2020). Effective learning of maths and science concepts depends can be achieved if multiple brain regions are sufficiently evolved and biologically developed, including the multiple demand network (Duncan, 2003; 2013), EF, frontal and posterior networks, semantic processing and decision making, (Shashidhara et al., 2019; Wu et al., 2019; Aben et al., 2020). In addition, Dündar-Coecke, & Tolmie (2020) suggest that higher levels of scientific causal reasoning abilities for 5-10-year-olds are predicted by nonverbal imagery and knowledge of scientific terminology as opposed to generic language skills (Zhang, et al., 2019). They suggest that educational curriculum needs to consider new teaching methods to develop abstract nonverbal imagery types of thinking for improving the conceptual understanding of the relevant scientific vocabulary for maths and science.

6.1. Limitations of research and future directions

The research design, combining behavioural and fMRI data, has several strengths because it combines verbal IQ with all the core analogical constructs which are relevant for solving novel problems but requiring sufficient fluid intelligence (IQ) and verbal conceptual working memory. However, there are a few limitations which are unavoidable because of the necessary constraints of testing young students for too long with multiple psychometric and behavioural tests. The small sample size (N=34) is considered adequate for the usage of Warp PLS but, larger samples are far better to test more specific differences regarding age groups within the 11-15 category as well as the possible gender differences between males and females. Taylor et al. (2020) conducted a magneto encephalography (MEG) study with neurotypically developing adolescent participants aged 10-16 years old, found robust and distinct sex differences in brain networks processing abstract reasoning tasks. They claim that age and gender are associated with increased theta brain activity in the occipital, cerebellar and frontoparietal regions during fluid reasoning tasks. Their research results support the notion that male and female adolescents use different neurocognitive processes across different age-related developmental stages to achieve similar behavioural goals.

Language skills development is affected by biological age, family structure, quality of educational experiences and socio-cultural and economic conditions. The complex genetic and epigenetic interactions variously fine-tune individual differences which are impossible to investigate within the current sample, but it is an opportunity for future researchers to explore. The brain network activity through can be explored by tractography and diffusion tensor research tools, which could provide new and useful evidence of possible causal relationships between the IVs and all brain areas identified in the SEM models. Configuring the mode of network connectivity and dynamic interactions between different brain regions would improve understanding of the actual brain processes that take place. Diffusion tensor research would also be able to identify more precisely ongoing brain regions’ activations during processing of visual, verbal, and non-relational reasoning measures. The EF’s contribution is not yet fully understood in relation to the creation and usage of scientific and mathematical knowledge and the types of educational training needed to improve flexible conceptual manipulation, and therefore more research is needed (Vosniadou, Pnevmatikos, & Makris, 2018). The genetic influence of individual maths and science abilities is another relevant and important research line to explore (Skeide et al., 2020), because some researchers claim that these abilities are heritable and can be linked to several gene expressing proteins in certain brain regions. However, the links between phenotype and genotype influences are not fully understood yet and more research would be able to shed light in the interpretation of the current behaviour-neuroscience data findings.