Submitted:
07 October 2023
Posted:
09 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Experiment and Mechanism of Fatigue Delamination
2.1. Delamination Test
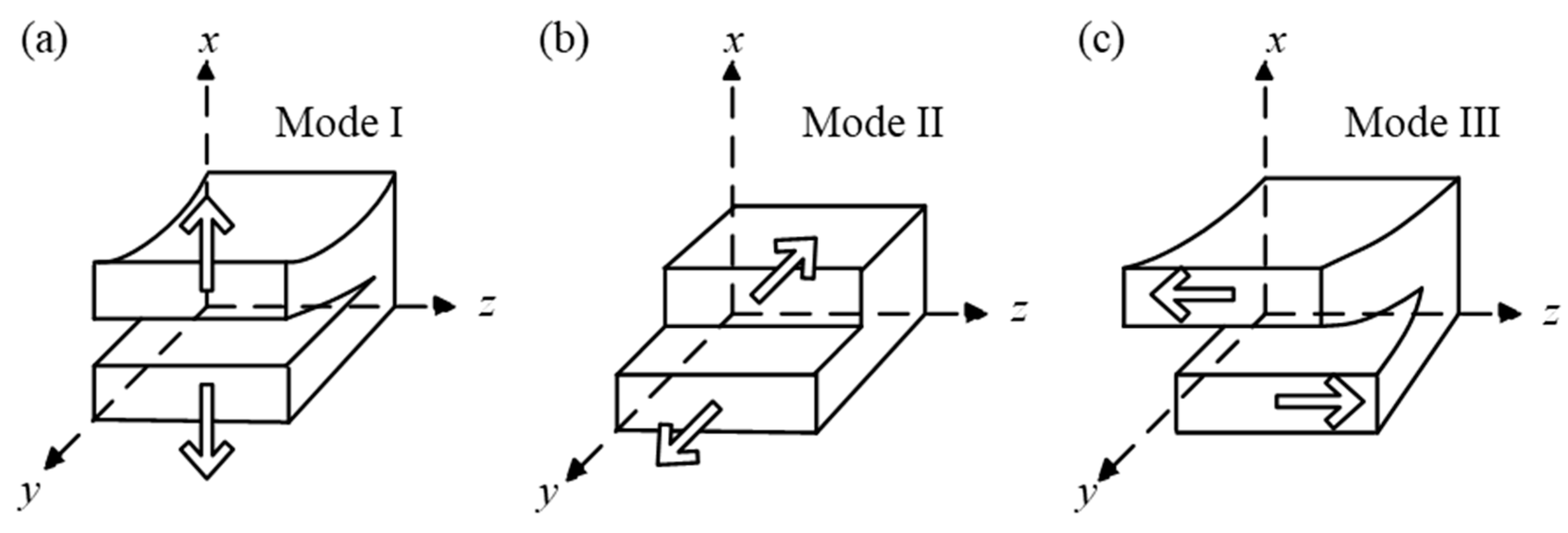
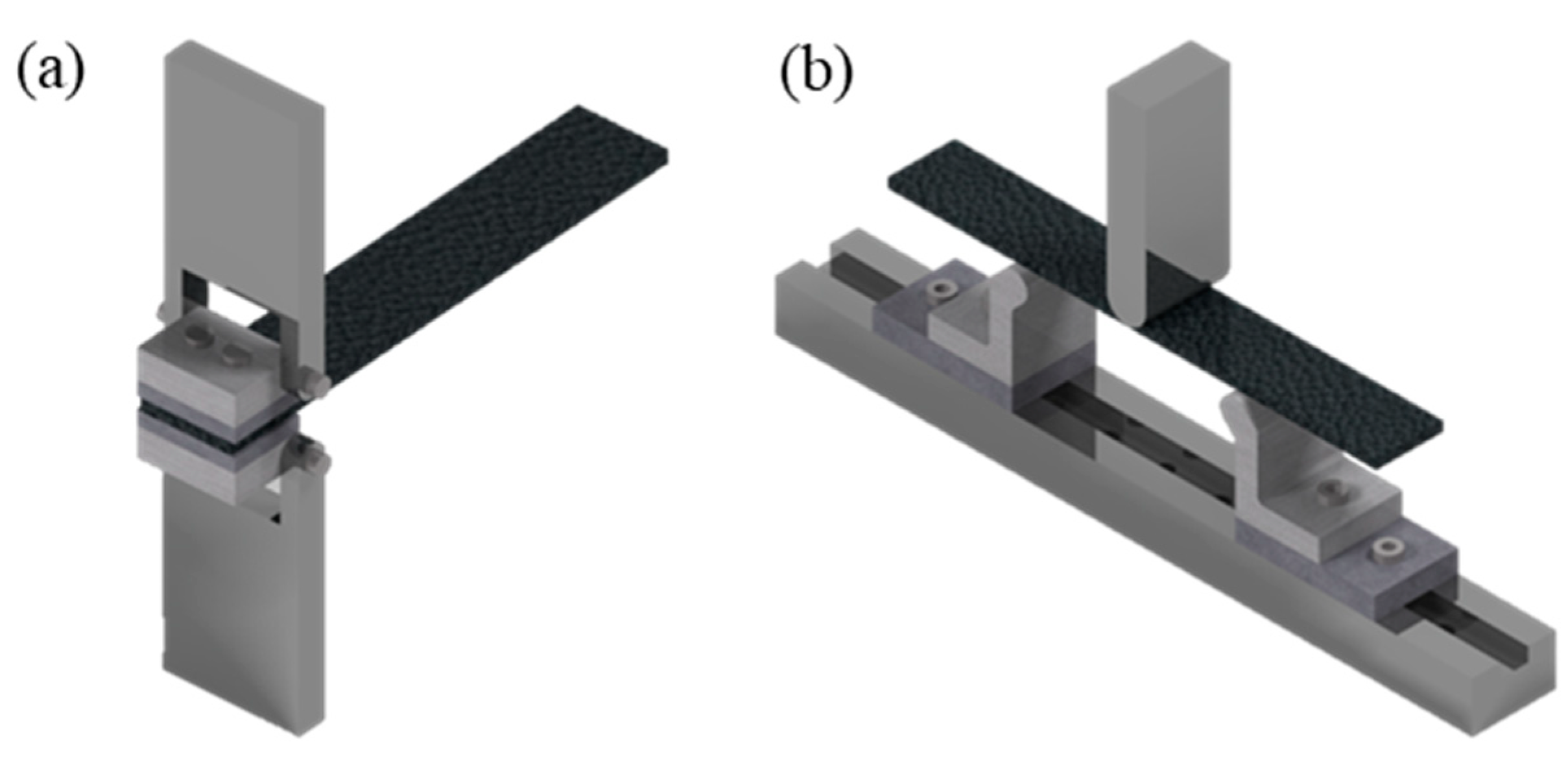
2.1.1. Pure Mode Delamination Test
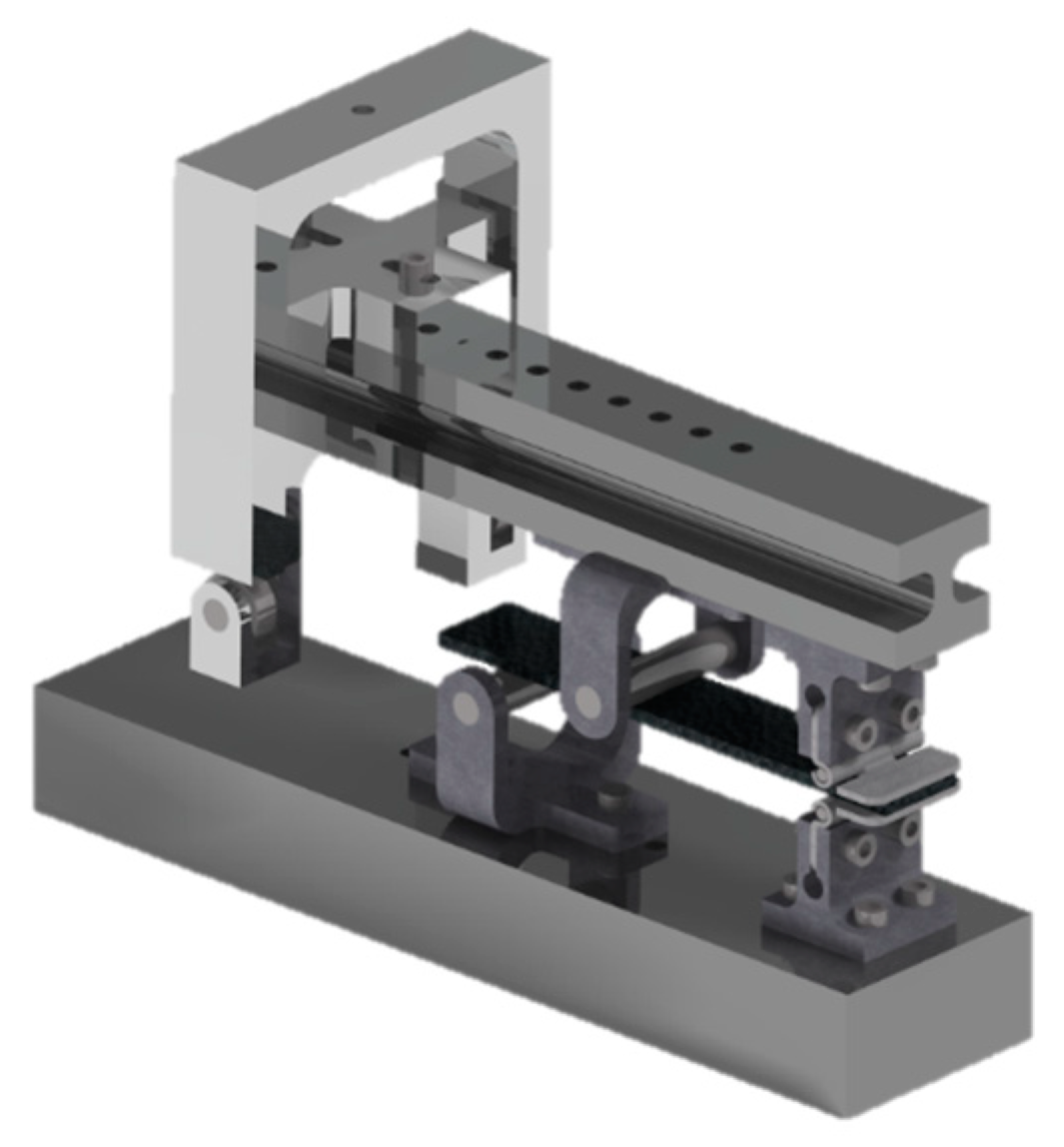
2.1.2. Mixed-mode Delamination Test
2.1.3. Other Delamination Test
2.2. Characterization for Fatigue Delamination
2.2.1. Fatigue Delamination Onset
2.2.2. Fatigue Delamination Propagation
2.3. Influencing Factors of Fatigue Delamination
2.3.1. Mixed-Mode Ratio
2.3.2. Fiber Bridging effect
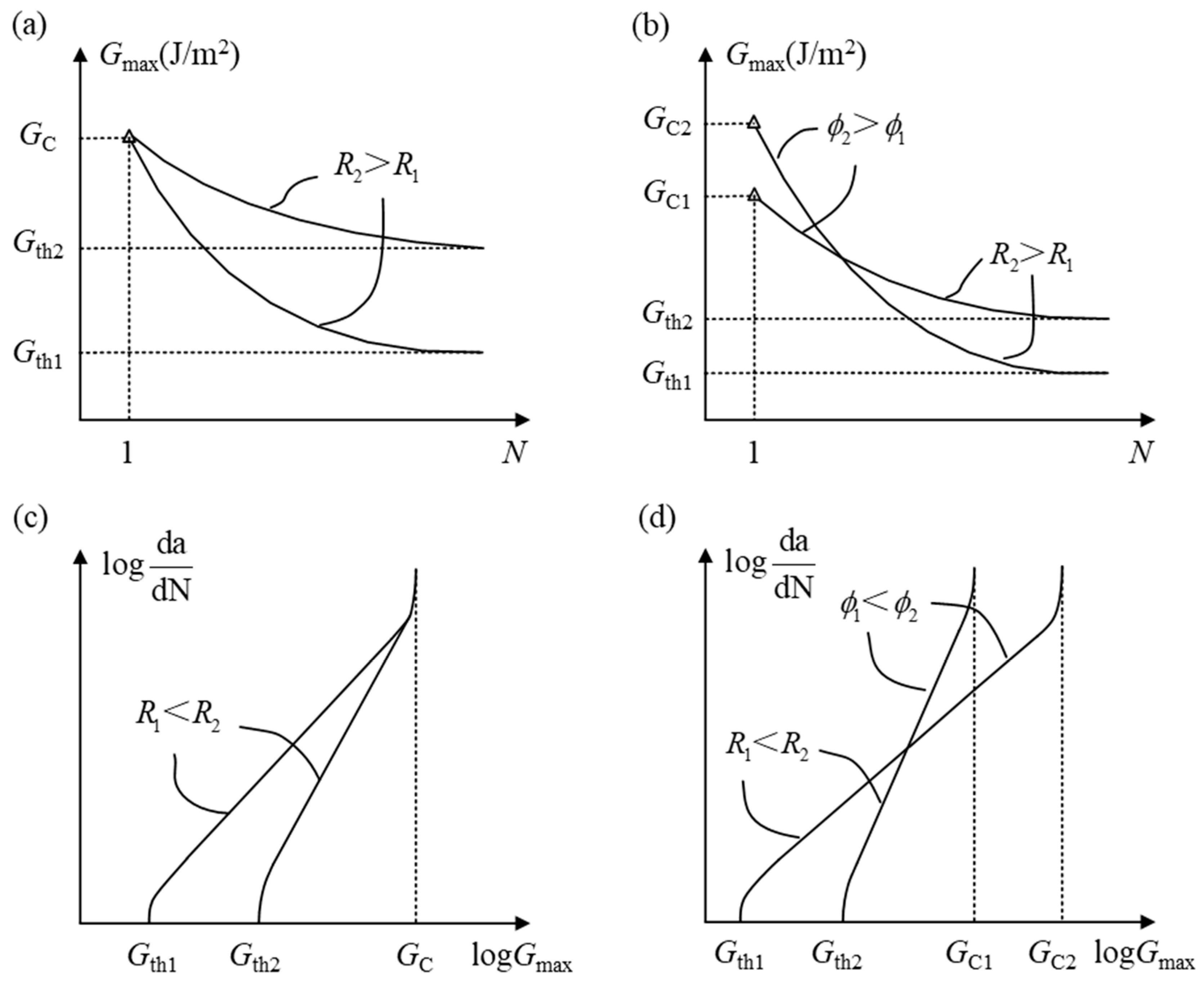
2.3.3. Loading Ratio
2.3.4. Other Major Factors
2.3.4. Other Secondary Factors
3. Phenomenological Model of Fatigue Delamination
3.1. Calculation of SERR
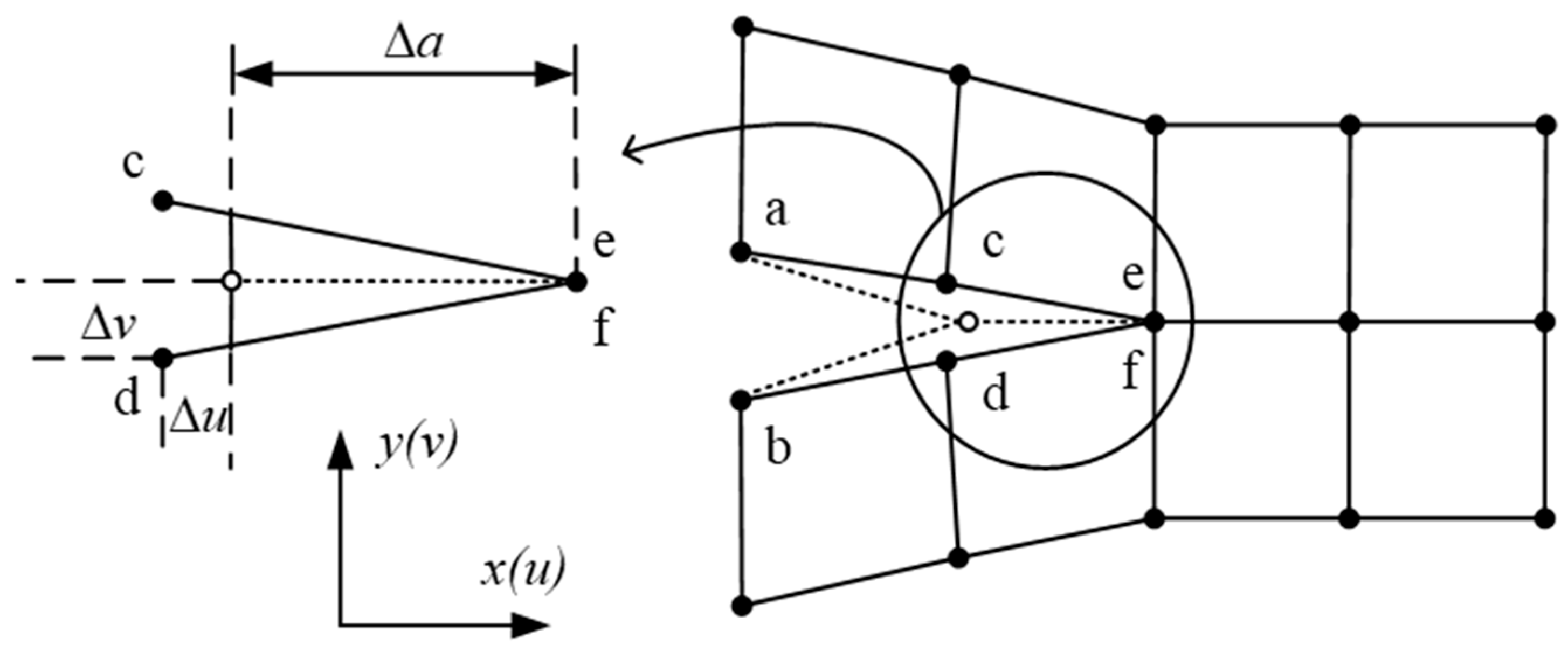
3.1.1. VCCT
3.1.2. J-Integral
3.2. Delamination Onset Phenomenological Model
3.3. Delamination Propagation Phenomenological Model
3.3.1. Mixed-Mode Ratio Modified Model
3.3.2. Fiber Bridge Modified Model
3.3.3. Loading Ratio Modified Model
3.3.4. Temperature Modified Model
3.3.5. Other Modified Models
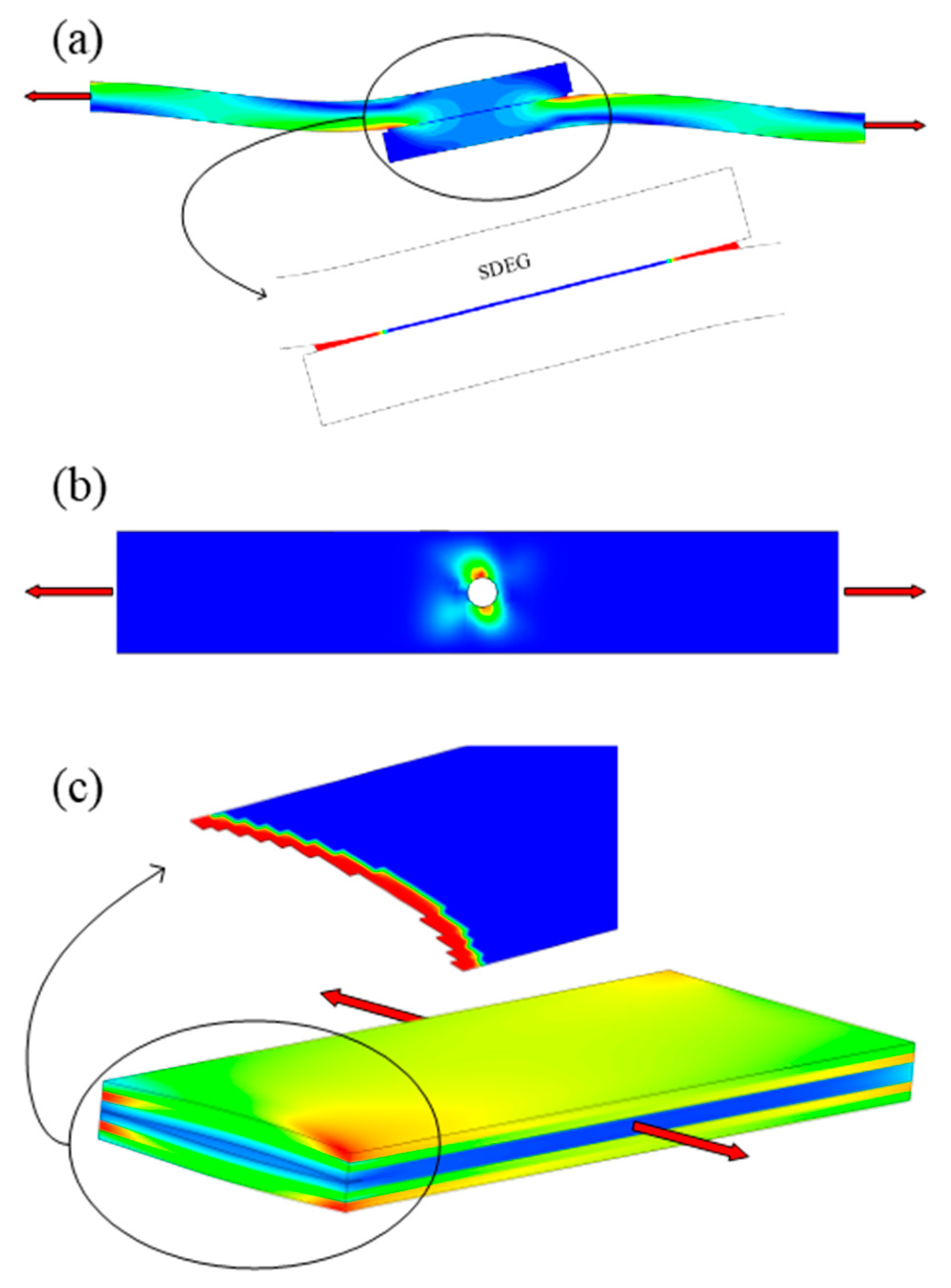
4. Finite Element Simulation of Delamination Fatigue
4.1. Strength Model
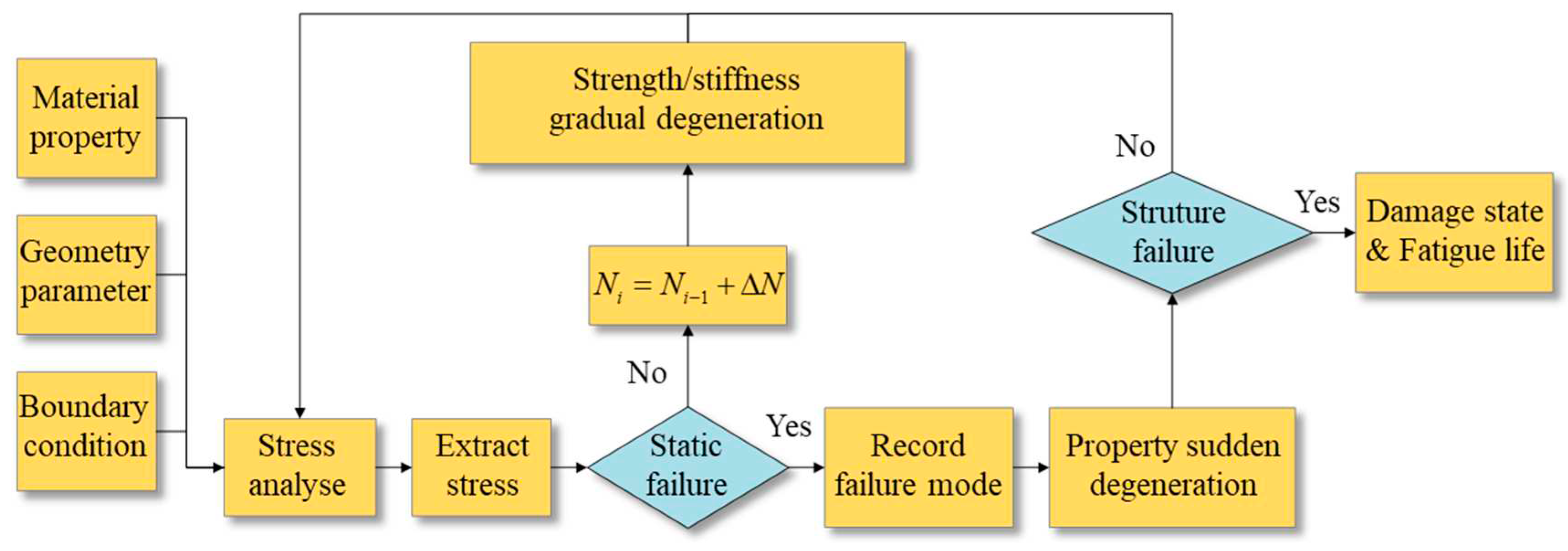
4.2. Fracture Mechanics Model
- Artificial pre-cracks are added to laminated composite structures. Set the growth path of crack propagation and adapt displacement loading mode.
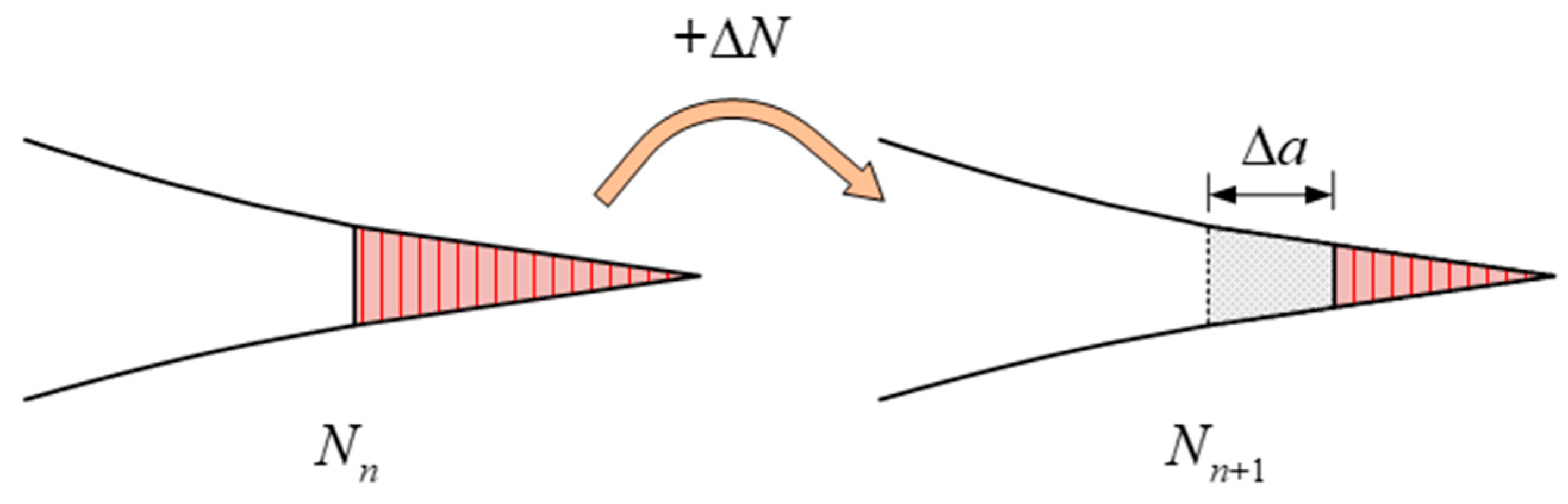
- When structure is applied cyclic loading, it is assumed that f (K or G) is constant during the increasement of fatigue crack length ∆a. The general Paris Law is converted into incremental form as shown in Eq.(21).
- 3.
- By means of VCCT or J-integral method in FEM, f (K or G)n near the crack tip of delamination in current increment step is calculated.
- 4.
- (∆N)n is acquired by substituting known coefficients of Paris Law C and m, ∆a and f (K or G)n which are obtained in previous step into Eq.(21). It should be noticed that C and m can be material constants or functions of parameters such as fatigue crack length a.
- 5.
- Update cycles of fatigue loading Nn+1 by Eq(22). The stiffness of structure declines because of delamination damage. Go back to step (2) and calculate delamination propagation of next incremental step until it stops when f (K or G) ≤ f (K or G)th. Record final fatigue crack length a and cycles of fatigue loading N. f (K or G)th is inherent properties of material which is obtained in test of fatigue crack growth rate.
4.3. Damage Mechanics Model
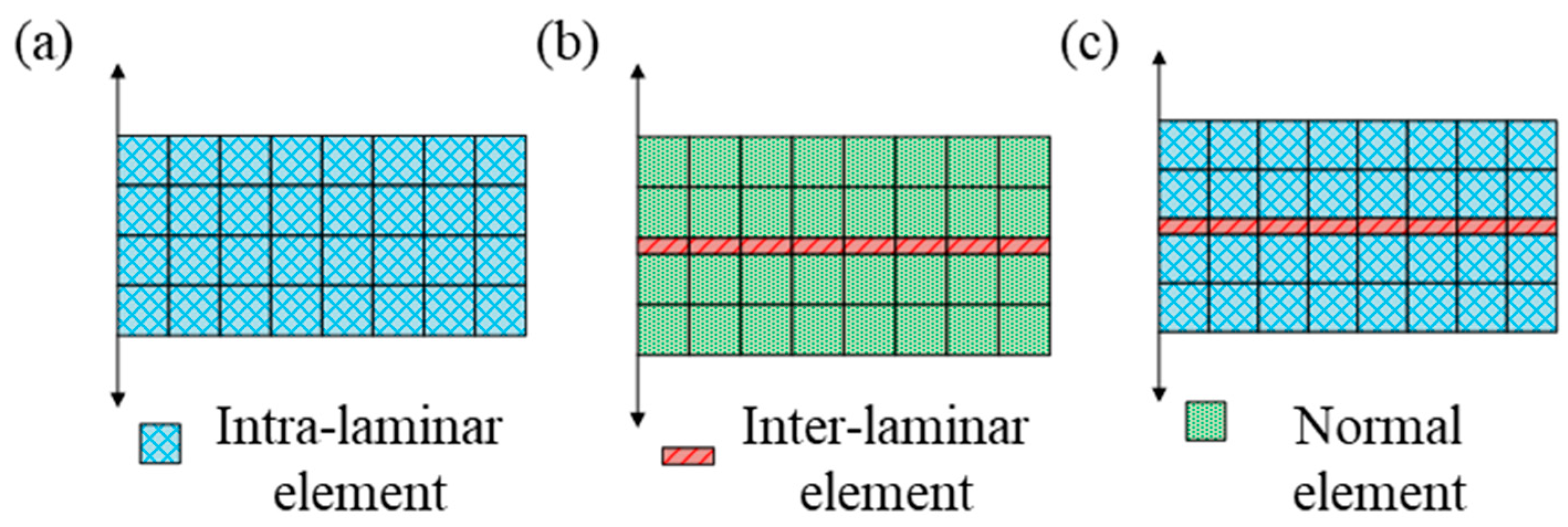
4.3.1. Intra-laminar Element Model
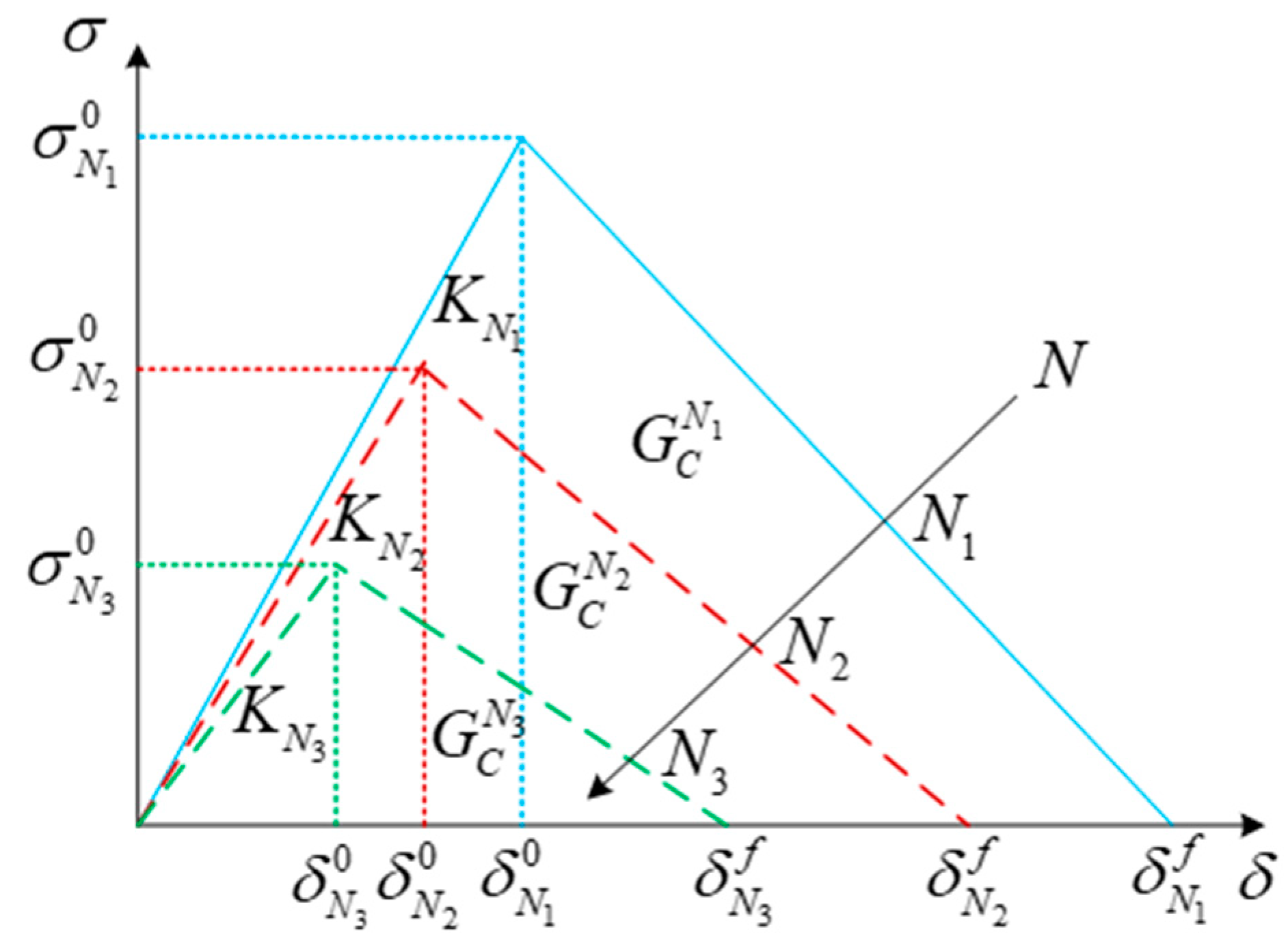
4.3.2. Inter-laminar Element Model
- (1)
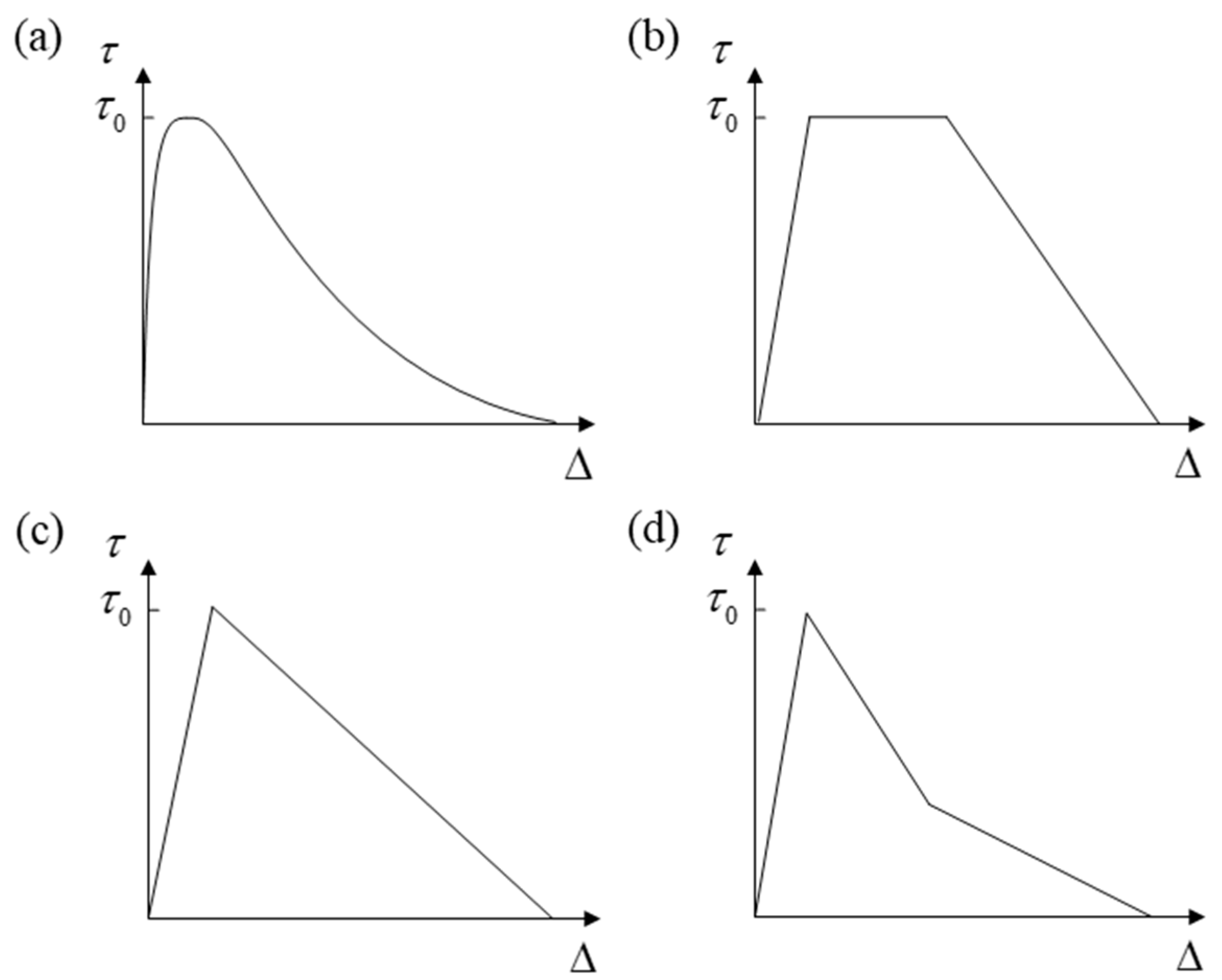
- Derive the stiffness matrix and the constitutive equation (that is cohesive law) of cohesive element.
- (2)
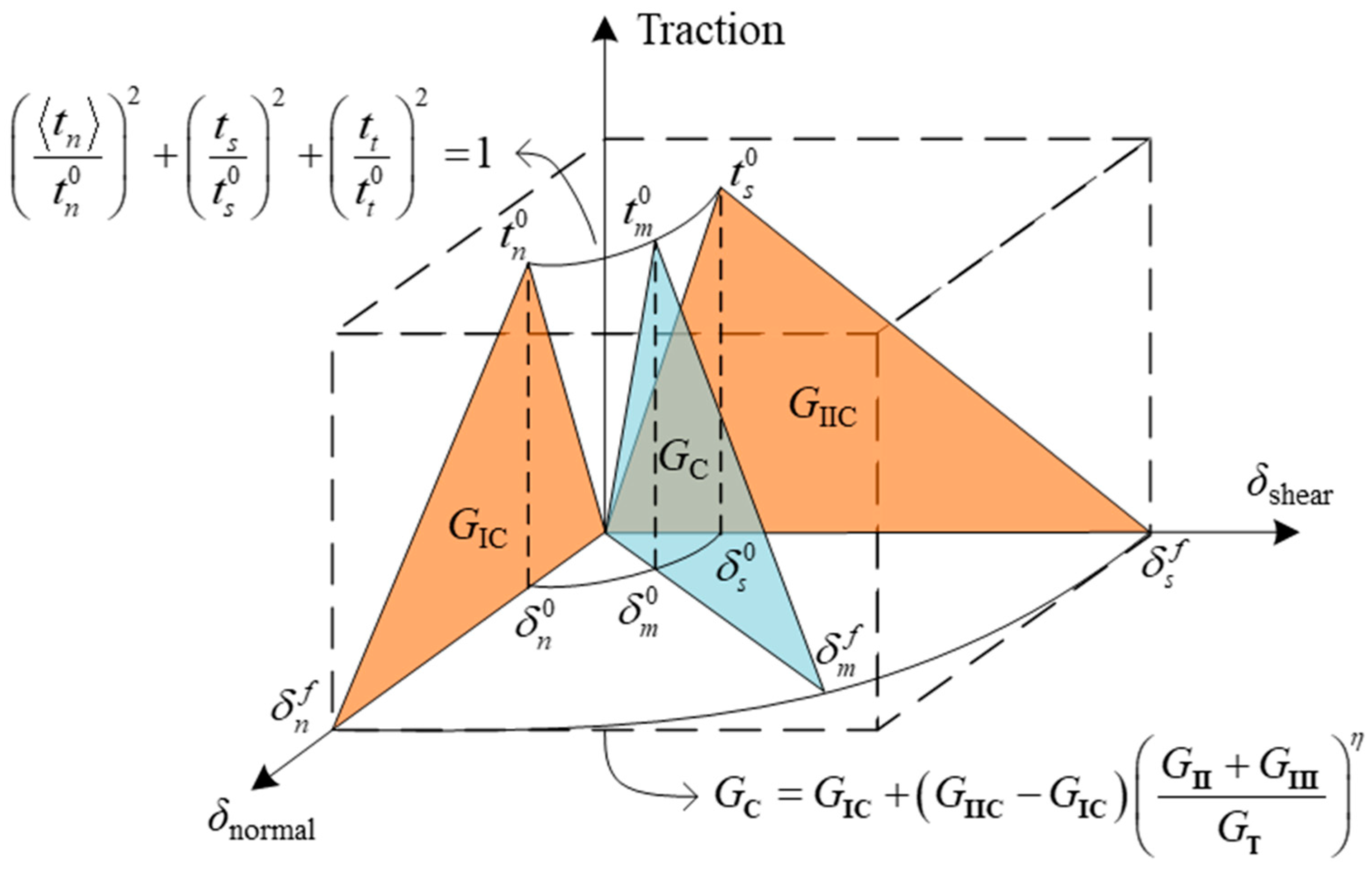
- Determine the damage initiation and evolution criterion of mixed-mode fatigue delamination.
- (3)
- (4)
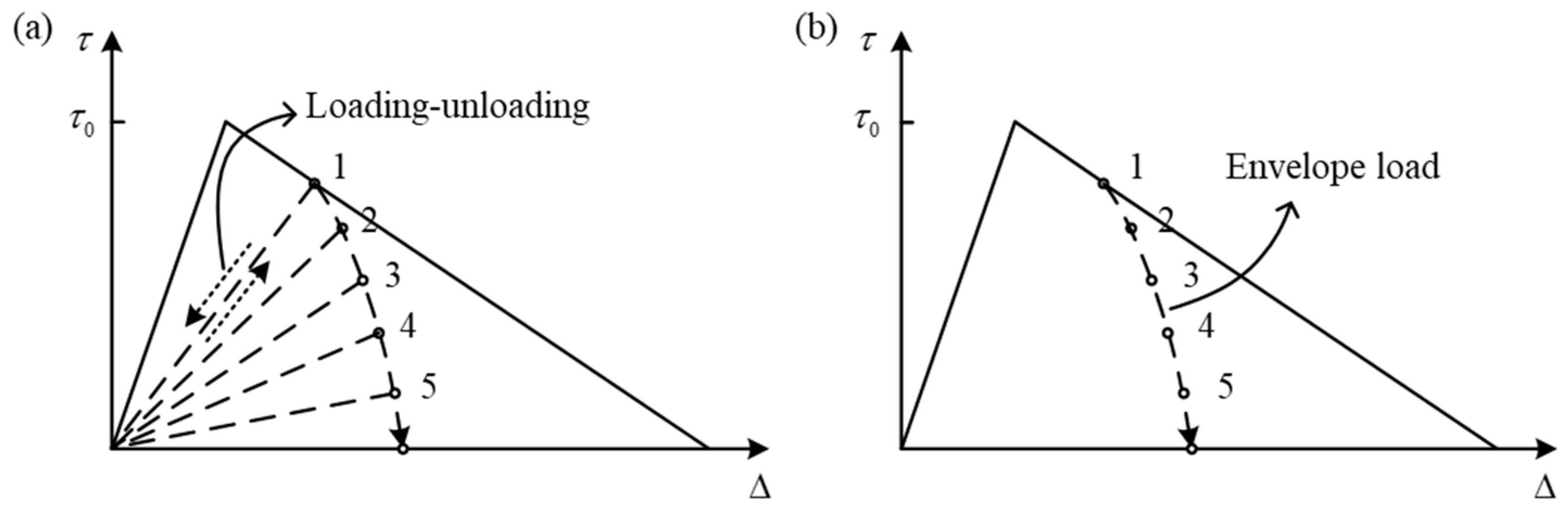
- Establish the differential relationship between damage variables and the number of loading cycles. Furthermore, the reasonable formula of fatigue delamination damage rate can be obtained.
- (5)
- Select the inter-laminar parameters of fatigue delamination damage that need to be degraded. Then, establish the functional relationship between degradation parameters and damage variables.
- (6)
- Realize loading/unloading cycles of FDDMs by FEM software and formulate the standard of integral structure failure. Finally, fatigue life of delamination under specific loading can be calculated.
4.3.3. Mixed Intra-laminar/Inter-laminar Element Model
4.4. Hybrid Model
5. Summary and Prospect
Acknowledgments
References
- Bak, B.L.V.; Sarrado, C.; Turon, A.; Costa, J. Delamination Under Fatigue Loads in Composite Laminates: A Review on the Observed Phenomenology and Computational Methods. Appl. Mech. Rev. 2014, 66, 060803. [Google Scholar] [CrossRef]
- Daneshjoo, Z.; Amaral, L.; Alderliesten, R.; Shokrieh, M.; Fakoor, M. Development of a physics-based theory for mixed mode I/II delamination onset in orthotropic laminates. Theor. Appl. Fract. Mech. 2019, 103, 102303. [Google Scholar] [CrossRef]
- Carraro, P.A.; Maragoni, L.; Quaresimin, M. Characterisation and analysis of transverse crack-induced delamination in cross-ply composite laminates under fatigue loadings. Int. J. Fatigue 2019, 129, 105217. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N.; Zhang, C. An insight into three approaches for determining fatigue delamination resistance in DCB tests on composite laminates. Compos. Part B: Eng. 2019, 176. [Google Scholar] [CrossRef]
- Bak, B.; Turon, A.; Lindgaard, E.; Lund, E. A benchmark study of simulation methods for high-cycle fatigue-driven delamination based on cohesive zone models. Compos. Struct. 2017, 164, 198–206. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Bernasconi, A.; Beretta, S.; Moroni, F.; Pirondi, A. Local Stress Analysis of the Fatigue Behaviour of Adhesively Bonded Thick Composite Laminates. J. Adhes. 2010, 86, 480–500. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Y.; Fu, K.; Wu, X. Progressive fatigue damage modelling of fibre-reinforced composite based on fatigue master curves. Thin-Walled Struct. 2020, 158, 107173. [Google Scholar] [CrossRef]
- De Carvalho, N.; Mabson, G.; Krueger, R.; Deobald, L. A new approach to model delamination growth in fatigue using the Virtual Crack Closure Technique without re-meshing. Eng. Fract. Mech. 2019, 222, 106614. [Google Scholar] [CrossRef]
- Gong, Y.; Zhao, L.; Zhang, J.; Hu, N. Crack closure in the fatigue delamination of composite multidirectional DCB laminates with large-scale fiber bridging. Compos. Struct. 2020, 244, 112220. [Google Scholar] [CrossRef]
- Mazaheri, F.; Hosseini-Toudeshky, H. Low-cycle fatigue delamination initiation and propagation in fibre metal laminates. Fatigue Fract. Eng. Mater. Struct. 2014, 38, 641–660. [Google Scholar] [CrossRef]
- Amiri-Rad, A.; Mashayekhi, M.; van der Meer, F.P. Cohesive zone and level set method for simulation of high cycle fatigue delamination in composite materials. Compos. Struct. 2017, 160, 61–69. [Google Scholar] [CrossRef]
- Al-Azzawi, A.S.; Kawashita, L.; Featherston, C. A modified cohesive zone model for fatigue delamination in adhesive joints: Numerical and experimental investigations. Compos. Struct. 2019, 225. [Google Scholar] [CrossRef]
- Turon, A.; Costa, J.; Camanho, P.; Dávila, C. Simulation of delamination in composites under high-cycle fatigue. Compos. Part A: Appl. Sci. Manuf. 2007, 38, 2270–2282. [Google Scholar] [CrossRef]
- Wang, C.; Xu, X. Cohesive element analysis of fatigue delamination propagation in composite materials with improved crack tip tracking algorism. Compos. Struct. 2015, 134, 176–184. [Google Scholar] [CrossRef]
- Dávila, C. From S-N to the Paris law with a new mixed-mode cohesive fatigue model for delamination in composites. Theor. Appl. Fract. Mech. 2020, 106, 102499. [Google Scholar] [CrossRef]
- Liang, Y.-J.; Dávila, C.G.; Iarve, E.V. A reduced-input cohesive zone model with regularized extended finite element method for fatigue analysis of laminated composites in Abaqus. Compos. Struct. 2021, 275, 114494. [Google Scholar] [CrossRef]
- Gomez M, Anderson W. A Rational Analytic Theory of Fatigue. The trend in engineering. 1961;13(1):9-14.
- Blanco, N.; Gamstedt, E.; Asp, L.; Costa, J. Mixed-mode delamination growth in carbon–fibre composite laminates under cyclic loading. Int. J. Solids Struct. 2004, 41, 4219–4235. [Google Scholar] [CrossRef]
- Kenane, M.; Benmedakhene, S.; Azari, Z. Fracture and fatigue study of unidirectional glass/epoxy laminate under different mode of loading. Fatigue Fract. Eng. Mater. Struct. 2010, 33, 284–293. [Google Scholar] [CrossRef]
- Jin, K.; Chen, K.; Luo, X.; Tao, J. Fatigue crack growth and delamination mechanisms of Ti/CFRP fibre metal laminates at high temperatures. Fatigue Fract. Eng. Mater. Struct. 2020, 43, 1115–1125. [Google Scholar] [CrossRef]
- Giuliese, G.; Pirondi, A.; Moroni, F. A Cohesive Zone Model for Three-dimensional Fatigue Debonding/Delamination. Procedia Mater. Sci. 2014, 3, 1473–1478. [Google Scholar] [CrossRef]
- Carreras, L.; Renart, J.; Turon, A.; Costa, J.; Bak, B.; Lindgaard, E.; de la Escalera, F.M.; Essa, Y. A benchmark test for validating 3D simulation methods for delamination growth under quasi-static and fatigue loading. Compos. Struct. 2019, 210, 932–941. [Google Scholar] [CrossRef]
- Aoki, R.; Higuchi, R.; Yokozeki, T. Fatigue simulation for progressive damage in CFRP laminates using intra-laminar and inter-laminar fatigue damage models. Int. J. Fatigue 2020, 143, 106015. [Google Scholar] [CrossRef]
- Siddique, A.; Abid, S.; Shafiq, F.; Nawab, Y.; Wang, H.; Shi, B.; Saleemi, S.; Sun, B. Mode I fracture toughness of fiber-reinforced polymer composites: A review. J. Ind. Text. 2019, 50, 1165–1192. [Google Scholar] [CrossRef]
- ASTM Standard D5528-13. Standard Test Method for Mode I Interlaminar fracture toughness of unidirectional fiber reinforced polymer matrix composites. American Society for Testing and Materials, West Conshohocken, PA. 2013.
- ASTM Standard D7905/D7905M-14. Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites American Society for Testing and Materials, West Conshohocken, PA. 2014.
- Nwosu, S.N.; Hui, D.; Dutta, P.K. Dynamic mode II delamination fracture of unidirectional graphite/epoxy composites. Compos. Part B: Eng. 2003, 34, 303–316. [Google Scholar] [CrossRef]
- Szekrényes, A.; Uj, J. Mode-II Fracture in E-glass-polyester Composite. J. Compos. Mater. 2005, 39, 1747–1768. [Google Scholar] [CrossRef]
- Fan, C.; Benjar, P.; Rogercheng, J. A unified approach to quantify the role of friction in beam-type specimens for the measurement of mode II delamination resistance of fibre-reinforced polymers. Compos. Sci. Technol. 2007, 67, 989–995. [Google Scholar] [CrossRef]
- Wang, W.-X.; Nakata, M.; Takao, Y.; Matsubara, T. Experimental investigation on test methods for mode II interlaminar fracture testing of carbon fiber reinforced composites. Compos. Part A: Appl. Sci. Manuf. 2009, 40, 1447–1455. [Google Scholar] [CrossRef]
- Audd, C.; Davidson, B.D.; Ratcliffe, J.G.; Czabaj, M.W. Reexamination of the edge crack torsion test for determining the mode III delamination toughness of laminated composites. Eng. Fract. Mech. 2019, 215, 138–150. [Google Scholar] [CrossRef]
- Rizov, V.; Shindo, Y.; Horiguchi, K.; Narita, F. Mode III Interlaminar Fracture Behavior of Glass Fiber Reinforced Polymer Woven Laminates at 293 to 4 K. Appl. Compos. Mater. 2006, 13, 287–304. [Google Scholar] [CrossRef]
- de Moura MFSF, Gonçalves JPM. Cohesive zone model for high-cycle fatigue of adhesively bonded joints under mode I loading. International Journal of Solids and Structures. 2014;51(5):1123-1131. [CrossRef]
- Bai R, Wang L, Lei Z, Chen H. Experimental and numerical analysis of interfacial fracture in piezoelectric composites. Optoelectronics and Advanced Materials-Rapid Communications. 2011;5(12):1328-1335.
- Tserpes, K.; Peikert, G.; Floros, I. Crack stopping in composite adhesively bonded joints through corrugation. Theor. Appl. Fract. Mech. 2016, 83, 152–157. [Google Scholar] [CrossRef]
- Mollón, V.; Bonhomme, J.; Viña, J.; Argüelles, A.; Fernández-Canteli, A. Influence of the principal tensile stresses on delamination fracture mechanisms and their associated morphology for different loading modes in carbon/epoxy composites. Compos. Part B: Eng. 2012, 43, 1676–1680. [Google Scholar] [CrossRef]
- Reeder, J.R.; Crews, J.H., Jr. Mixed-mode bending method for delamination testing. AIAA J. 1990, 28, 1270–1276. [Google Scholar] [CrossRef]
- ASTM Standard D6671-01. Standard Test Method for Mixed Mode I-Mode II Interlaminar Fracture Toughness of Unidirectional Fiber Reinforced Polymer Matrix Composites. American Society for Testing and Materials, West Conshohocken, PA. 2001.
- Mariam, M.; Afendi, M.; Majid, M.A.; Ridzuan, M.; Azmi, A.; Sultan, M. Influence of hydrothermal ageing on the mechanical properties of an adhesively bonded joint with different adherends. Compos. Part B: Eng. 2019, 165, 572–585. [Google Scholar] [CrossRef]
- Chuang, W.-Y.; Tsai, J.-L. Investigating the performances of stepwise patched double lap joint. Int. J. Adhes. Adhes. 2013, 42, 44–50. [Google Scholar] [CrossRef]
- Du, D.; Hu, Y.; Li, H.; Liu, C.; Tao, J. Open-hole tensile progressive damage and failure prediction of carbon fiber-reinforced PEEK–titanium laminates. Compos. Part B: Eng. 2016, 91, 65–74. [Google Scholar] [CrossRef]
- Bogenfeld, R.; Schmiedel, P.; Kuruvadi, N.; Wille, T.; Kreikemeier, J. An experimental study of the damage growth in composite laminates under tension–fatigue after impact. Compos. Sci. Technol. 2020, 191, 108082. [Google Scholar] [CrossRef]
- ASTM Standard D6115-19. Standard Test Method for Mode I Fatigue Delamination Growth Onset of Unidirectional Fiber-Reinforced Polymer Matrix Composites. American Society for Testing and Materials, West Conshohocken, PA. 2019.
- ASTM Standard E647-05. Standard test method for measurement of fatigue crack growth rates. American Society for Testing and Materials, West Conshohocken, PA. 2005.
- Harris, B. Fatigue in Composites. Woodhead Publishing; 2003.
- Hojo M, Tanaka K, Gustafson C, Hayashi R. Effect of stress ratio on near-threshold propagation of delamination fatigue cracks in unidirectional CFRP. Composites Science and Technology. 1988;19(4):329-330. [CrossRef]
- Hojo, M.; Matsuda, S.; Fiedler, B.; Kawada, T.; Moriya, K.; Ochiai, S.; Aoyama, H. Mode I and II delamination fatigue crack growth behavior of alumina fiber/epoxy laminates in liquid nitrogen. Int. J. Fatigue 2002, 24, 109–118. [Google Scholar] [CrossRef]
- Van Paepegem, W.; Degrieck, J. Effects of Load Sequence and Block Loading on the Fatigue Response of Fiber-Reinforced Composites. Mech. Adv. Mater. Struct. 2002, 9, 19–35. [Google Scholar] [CrossRef]
- Zhang, J.; Peng, L.; Zhao, L.; Fei, B. Fatigue delamination growth rates and thresholds of composite laminates under mixed mode loading. Int. J. Fatigue 2012, 40, 7–15. [Google Scholar] [CrossRef]
- Yao, L.; Alderliesten, R.; Zhao, M.; Benedictus, R. Discussion on the use of the strain energy release rate for fatigue delamination characterization. Compos. Part A: Appl. Sci. Manuf. 2014, 66, 65–72. [Google Scholar] [CrossRef]
- Yao, L.; Cui, H.; Guo, L.; Sun, Y. A novel total fatigue life model for delamination growth in composite laminates under generic loading. Compos. Struct. 2020, 258, 113402. [Google Scholar] [CrossRef]
- O’Brien, TK. Fatigue delamination behaviour of PEEK thermoplastic composite laminates. Composites. 1989;20(3):341-359. [CrossRef]
- Armanios, E.; Bucinell, R.; Wilson, D.; Asp, L.; Sjögren, A.; Greenhalgh, E. Delamination Growth and Thresholds in a Carbon/Epoxy Composite Under Fatigue Loading. J. Compos. Technol. Res. 2001, 23, 55. [Google Scholar] [CrossRef]
- Sjögren, A.; E Asp, L. Effects of temperature on delamination growth in a carbon/epoxy composite under fatigue loading. Int. J. Fatigue 2002, 24, 179–184. [Google Scholar] [CrossRef]
- Liu, W.; Chen, P. Theoretical analysis and experimental investigation of the occurrence of fiber bridging in unidirectional laminates under Mode I loading. Compos. Struct. 2020, 257, 113383. [Google Scholar] [CrossRef]
- Catalanotti, G.; Arteiro, A.; Hayati, M.; Camanho, P. Determination of the mode I crack resistance curve of polymer composites using the size-effect law. Eng. Fract. Mech. 2013, 118, 49–65. [Google Scholar] [CrossRef]
- Wang, H.-W.; Wu, Z.-M.; Wang, Y.-J.; Yu, R.C. An analytical method for predicting mode-I crack propagation process and resistance curve of rock and concrete materials. Theor. Appl. Fract. Mech. 2019, 100, 328–341. [Google Scholar] [CrossRef]
- Teimouri, F.; Heidari-Rarani, M.; Aboutalebi, F.H. Finite element modeling of mode I fatigue delamination growth in composites under large-scale fiber bridging. Compos. Struct. 2021, 263, 113716. [Google Scholar] [CrossRef]
- Yao, L.; Sun, Y.; Guo, L.; Zhao, M.; Jia, L.; Alderliesten, R.; Benedictus, R. A modified Paris relation for fatigue delamination with fibre bridging in composite laminates. Compos. Struct. 2017, 176, 556–564. [Google Scholar] [CrossRef]
- Matsubara, G.; Ono, H.; Tanaka, K. Mode II fatigue crack growth from delamination in unidirectional tape and satin-woven fabric laminates of high strength GFRP. Int. J. Fatigue 2006, 28, 1177–1186. [Google Scholar] [CrossRef]
- Allegri, G.; Wisnom, M.; Hallett, S. A new semi-empirical law for variable stress-ratio and mixed-mode fatigue delamination growth. Compos. Part A: Appl. Sci. Manuf. 2013, 48, 192–200. [Google Scholar] [CrossRef]
- Springer, M.; Turon, A.; Pettermann, H. A thermo–mechanical cyclic cohesive zone model for variable amplitude loading and mixed–mode behavior. Int. J. Solids Struct. 2018, 159, 257–271. [Google Scholar] [CrossRef]
- Ramírez, F.M.G.; Garpelli, F.P.; Sales, R.d.C.M.; Cândido, G.M.; Arbelo, M.A.; Shiino, M.Y.; Donadon, M.V. Hygrothermal effects on the fatigue delamination growth onset in interlayer toughened CFRP joints. Int. J. Fatigue 2020, 138, 105729. [Google Scholar] [CrossRef]
- Li, L. Interfacial Debonding and Slipping of Carbon Fiber-Reinforced Ceramic-Matrix Composites Subjected to Different Fatigue Loading Sequences. Journal of Aerospace Engineering. 2016;29(5):04016029. [CrossRef]
- Yao, L.; Alderliesten, R.; Benedictus, R. The effect of fibre bridging on the Paris relation for mode I fatigue delamination growth in composites. Compos. Struct. 2016, 140, 125–135. [Google Scholar] [CrossRef]
- Yao, L.; Sun, Y.; Alderliesten, R.; Benedictus, R.; Zhao, M. Fibre bridging effect on the Paris relation for mode I fatigue delamination growth in composites with consideration of interface configuration. Compos. Struct. 2017, 159, 471–478. [Google Scholar] [CrossRef]
- Gong, Y.; Li, W.; Liu, H.; Yuan, S.; Wu, Z.; Zhang, C. A novel understanding of the normalized fatigue delamination model for composite multidirectional laminates. Compos. Struct. 2019, 229, 111395. [Google Scholar] [CrossRef]
- Duragkar, M.S.; Paretkar, R.K.; Peshwe, D.R.; Paranjpe, S.A. Investigation of the load sequence effects in fatigue of damaged composite laminate & characterization of fatigue damage. Trans. Indian Inst. Met. 2010, 63, 565–569. [Google Scholar] [CrossRef]
- Ekhtiyari, A.; Alderliesten, R.; Shokrieh, M.M. Loading rate dependency of strain energy release rate in mode I delamination of composite laminates. Theor. Appl. Fract. Mech. 2021, 112, 102894. [Google Scholar] [CrossRef]
- Hashemi, S.; Kinloch, A.J.; Williams, J.G.; Hashemi, S.; Kinloch, A.J.; Williams, J.G.; Hashemi, S.; Kinloch, A.J.; Williams, J.G. Corrections needed in double-cantilever beam tests for assessing the interlaminar failure of fibre-composites. J. Mater. Sci. Lett. 1989, 8, 125–129. [Google Scholar] [CrossRef]
- Airoldi, A.; Dávila, C.G. Identification of material parameters for modelling delamination in the presence of fibre bridging. Compos. Struct. 2012, 94, 3240–3249. [Google Scholar] [CrossRef]
- Rybicki, E.; Kanninen, M. A finite element calculation of stress intensity factors by a modified crack closure integral. Eng. Fract. Mech. 1977, 9, 931–938. [Google Scholar] [CrossRef]
- Teimouri, F.; Heidari-Rarani, M.; Aboutalebi, F.H. An XFEM-VCCT coupled approach for modeling mode I fatigue delamination in composite laminates under high cycle loading. Eng. Fract. Mech. 2021, 249, 107760. [Google Scholar] [CrossRef]
- Rice JR, Rosengren GF. Plane strain deformation near a crack tip in a power-law hardening material. Journal of the Mechanics and Physics of Solids. 1968;16(1):1-12. [CrossRef]
- Jagannathan, N.; Chandra, A.R.A.; Manjunatha, C.M. Onset-of-growth behavior of mode II delamination in a carbon fiber composite under spectrum fatigue loads. Compos. Struct. 2015, 132, 477–483. [Google Scholar] [CrossRef]
- Ramkumar R, Whitcomb J. Characterization of Mode I and mixed-mode delamination growth in T300/5208 graphite/epoxy. Delamination and Debonding of Materials. 1985;876:315-335.
- Gustafson, C.-G.; Hojo, M. Delamination Fatigue Crack Growth in Unidirectional Graphite/Epoxy Laminates. J. Reinf. Plast. Compos. 1987, 6, 36–52. [Google Scholar] [CrossRef]
- Dahlen, C.; Springer, G.S. Delamination Growth in Composites under Cyclic Loads. J. Compos. Mater. 1994, 28, 732–781. [Google Scholar] [CrossRef]
- Rocha, A.V.; Akhavan-Safar, A.; Carbas, R.; Marques, E.; Goyal, R.; El-Zein, M.; Da Silva, L.F. Fatigue crack growth analysis of different adhesive systems: Effects of mode mixity and load level. Fatigue Fract. Eng. Mater. Struct. 2019, 43, 330–341. [Google Scholar] [CrossRef]
- Kardomateas, G.; Pelegri, A.; Malik, B. Growth of internal delaminations under cyclic compression in composite plates. J. Mech. Phys. Solids 1995, 43, 847–866. [Google Scholar] [CrossRef]
- Kenane, M.; Benzeggagh, M. Mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites under fatigue loading. Compos. Sci. Technol. 1997, 57, 597–605. [Google Scholar] [CrossRef]
- Shivakumar, K.; Chen, H.; Abali, F.; Le, D.; Davis, C. A total fatigue life model for mode I delaminated composite laminates. Int. J. Fatigue 2006, 28, 33–42. [Google Scholar] [CrossRef]
- Jones, R.; Kinloch, A.; Hu, W. Cyclic-fatigue crack growth in composite and adhesively-bonded structures: The FAA slow crack growth approach to certification and the problem of similitude. Int. J. Fatigue 2016, 88, 10–18. [Google Scholar] [CrossRef]
- Yao, L.; Sun, Y.; Guo, L.; Jia, L.; Zhao, M. A validation of a modified Paris relation for fatigue delamination growth in unidirectional composite laminates. Compos. Part B: Eng. 2018, 132, 97–106. [Google Scholar] [CrossRef]
- Atodaria, D.R.; Putatunda, S.K.; Mallick, P.K. Delamination Growth Behavior of a Fabric Reinforced Laminated Composite Under Mode I Fatigue. J. Eng. Mater. Technol. 1999, 121, 381–385. [Google Scholar] [CrossRef]
- Ishiyama, S.; Eto, M.; Oku, T. Effect of Stress Ratio on Crack Extension Rate of Fine-Grained Isotropic Nuclear Graphite. J. Nucl. Sci. Technol. 1987, 24, 719–723. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, Y.; Gong, Y.; Li, W.; Ren, S.; Liu, H. A new model characterizing the fatigue delamination growth in DCB laminates with combined effects of fiber bridging and stress ratio. Compos. Struct. 2021, 268. [Google Scholar] [CrossRef]
- Miura, M.; Shindo, Y.; Takeda, T.; Narita, F. Mixed-mode I/III fatigue delamination growth in woven glass/epoxy composite laminates at cryogenic temperatures. J. Compos. Mater. 2013, 48, 1251–1259. [Google Scholar] [CrossRef]
- Zhong, Z.; Gu, Y.; Osada, T.; Yuan, Y.; Cui, C.; Yokokawa, T.; Tetsui, T.; Harada, H. Fatigue crack growth characteristics of a new Ni–Co-base superalloy TMW-4M3: effects of temperature and load ratio. J. Mater. Sci. 2011, 46, 7573–7581. [Google Scholar] [CrossRef]
- Li, L. Effect of multiple loading sequence on in-phase thermomechanical fatigue hysteresis of silicon carbide fiber-reinforced ceramic-matrix composites. Journal of Ceramic Science and Technology. 2018;9(2):163-174.
- Jia, J.; Davalos, J.F. Loading variable effects on mode—I fatigue of wood–FRP composite bonded interface. Compos. Sci. Technol. 2004, 64, 99–107. [Google Scholar] [CrossRef]
- Degrieck and J, Van Paepegem W. Fatigue damage modeling of fibre-reinforced composite materials: Review. Applied Mechanics Reviews. 2001;54(4):279-300. [CrossRef]
- Hashin, Z. Fatigue Failure Criteria for Unidirectional Fiber Composites. J. Appl. Mech. 1981, 48, 846–852. [Google Scholar] [CrossRef]
- Chang, K.-Y.; Llu, S.; Chang, F.-K. Damage Tolerance of Laminated Composites Containing an Open Hole and Subjected to Tensile Loadings. J. Compos. Mater. 1991, 25, 274–301. [Google Scholar] [CrossRef]
- Hou, J.P.; Petrinic, N.; Ruiz, C.; Hallett, S.R. Prediction of impact damage in composite plates. Compos. Sci. Technol. 2000, 60, 273–281. [Google Scholar] [CrossRef]
- Zou Z, Reid SR, Li S, Soden PD. Application of a delamination model to laminated composite structures. Composite Structures. 2002;56(4):375-389. [CrossRef]
- Camanho, P.P.; Dávila, C.G.; Pinho, S.T.; Iannucci, L.; Robinson, P. Prediction of in situ strengths and matrix cracking in composites under transverse tension and in-plane shear. Compos. Part A: Appl. Sci. Manuf. 2006, 37, 165–176. [Google Scholar] [CrossRef]
- Tserpes, K.; Papanikos, P.; Labeas, G.; Pantelakis, S. Fatigue damage accumulation and residual strength assessment of CFRP laminates. Compos. Struct. 2004, 63, 219–230. [Google Scholar] [CrossRef]
- Jia, J.; Davalos, J.F. Study of Load Ratio for Mode-I Fatigue Fracture of Wood-FRP-Bonded Interfaces. J. Compos. Mater. 2004, 38, 1211–1230. [Google Scholar] [CrossRef]
- Wimmer, G.; Schuecker, C.; Pettermann, H. Numerical simulation of delamination in laminated composite components – A combination of a strength criterion and fracture mechanics. Compos. Part B: Eng. 2009, 40, 158–165. [Google Scholar] [CrossRef]
- Turon, A.; Camanho, P.; Costa, J.; Renart, J. Accurate simulation of delamination growth under mixed-mode loading using cohesive elements: Definition of interlaminar strengths and elastic stiffness. Compos. Struct. 2010, 92, 1857–1864. [Google Scholar] [CrossRef]
- Irwin, G.R. Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Pradhan, S.; Tay, T. Three-dimensional finite element modelling of delamination growth in notched composite laminates under compression loading. Eng. Fract. Mech. 1998, 60, 157–171. [Google Scholar] [CrossRef]
- Krueger, R. Development of benchmark examples for static delamination propagation and fatigue growth predictions. Proceedings of The American Society for Composites. 2011;4:2593-2616.
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Llobet, J.; Maimí, P.; Turon, A.; Bak, B.; Lindgaard, E.; Carreras, L.; Essa, Y.; de la Escalera, F.M. A continuum damage model for composite laminates: Part IV- Experimental and numerical tests. Mech. Mater. 2020, 154, 103686. [Google Scholar] [CrossRef]
- Ramtekkar, G.S.; Desai, Y.M.; Shah, A.H. Mixed Finite-Element Model for Thick Composite Laminated Plates. Mech. Adv. Mater. Struct. 2002, 9, 133–156. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.; Mayugo, J.; Dávila, C. A continuum damage model for composite laminates: Part I – Constitutive model. Mech. Mater. 2007, 39, 897–908. [Google Scholar] [CrossRef]
- Lapczyk, I.; Hurtado, J.A. Progressive damage modeling in fiber-reinforced materials. Compos. Part A: Appl. Sci. Manuf. 2007, 38, 2333–2341. [Google Scholar] [CrossRef]
- Linde P, Pleitner J, Boer H, Carmone C. Modelling and Simulation of Fibre Metal Laminates. ABAQUS Users’ Conference. 2004.
- Dugdale, DS. Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids. 1960;8(2):100-104. [CrossRef]
- Barenblatt, G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture. Adv. Appl. Mech. 1962, 7, 55–129. [Google Scholar]
- Jiang, W.; Hallett, S.R.; Green, B.G.; Wisnom, M.R. A concise interface constitutive law for analysis of delamination and splitting in composite materials and its application to scaled notched tensile specimens. Int. J. Numer. Methods Eng. 2006, 69, 1982–1995. [Google Scholar] [CrossRef]
- Needleman, A. A Continuum Model for Void Nucleation by Inclusion Debonding. J. Appl. Mech. 1987, 54, 525–531. [Google Scholar] [CrossRef]
- Tvergaard, V.; Hutchinson, J.W. The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. J. Mech. Phys. Solids 1992, 40, 1377–1397. [Google Scholar] [CrossRef]
- Mi, Y.; Crisfield, M.A.; Davies, G.A.O.; Hellweg, H.B. Progressive Delamination Using Interface Elements. J. Compos. Mater. 1998, 32, 1246–1272. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Shokrieh, M.; Camanho, P. Finite element modeling of mode I delamination growth in laminated DCB specimens with R-curve effects. Compos. Part B: Eng. 2012, 45, 897–903. [Google Scholar] [CrossRef]
- Alfano, G. On the influence of the shape of the interface law on the application of cohesive-zone models. Compos. Sci. Technol. 2006, 66, 723–730. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]
- Reeder, JR. 3D mixed mode delamination fracture criteria - an experimentalist’s perspective. Proceedings of American Society for Composites, 21st Annual Technical Conference, Dearborn, MI, USA, 17-20 September 2006. [Google Scholar]
- Turon, A.; Camanho, P.P.; Costa, J.; Dávila, C.G. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mech. Mater. 2006, 38, 1072–1089. [Google Scholar] [CrossRef]
- Yang, B.; Mall, S. Cohesive-Shear-Lag Model for Cycling Stress-Strain Behavior of Unidirectional Ceramic Matrix Composites. Int. J. Damage Mech. 2003, 12, 45–64. [Google Scholar] [CrossRef]
- Amiri-Rad, A.; Mashayekhi, M.; van der Meer, F.P.; Hadavinia, H. A two-scale damage model for high cycle fatigue delamination in laminated composites. Compos. Sci. Technol. 2015, 120, 32–38. [Google Scholar] [CrossRef]
- Rafiee, R.; Sotoudeh, S. A cohesive zone model for predicting the initiation of Mode II delamination in composites under cyclic loading. J. Reinf. Plast. Compos. 2020, 40, 179–192. [Google Scholar] [CrossRef]
- Hosseini-Toudeshky, H.; Sheibanian, F.; Ovesy, H.R.; Goodarzi, M.S. Prediction of interlaminar fatigue damages in adhesively bonded joints using mixed-mode strain based cohesive zone modeling. Theor. Appl. Fract. Mech. 2020, 106, 102480. [Google Scholar] [CrossRef]
- Raimondo, A.; Bisagni, C. Analysis of Local Stress Ratio for Delamination in Composites Under Fatigue Loads. AIAA Science and Technology Forum and Exposition (AIAA SciTech) / AIAA Guidance, Navigation, and Control Conference. LOCATION OF CONFERENCE, COUNTRYDATE OF CONFERENCE; pp. 455–463.
- Peerlings RHJ, Brekelmans WAM, Borst RD, Geers MGD. Gradient-enhanced damage modelling of high-cycle fatigue. International Journal for Numerical Methods in Engineering. 2000;49(12):1547-1569. [CrossRef]
- Zhang, B.; Kawashita, L.F.; Hallett, S.R. Composites fatigue delamination prediction using double load envelopes and twin cohesive models. Compos. Part A: Appl. Sci. Manuf. 2019, 129, 105711. [Google Scholar] [CrossRef]
- Khoramishad, H.; Crocombe, A.; Katnam, K.; Ashcroft, I. Predicting fatigue damage in adhesively bonded joints using a cohesive zone model. Int. J. Fatigue 2010, 32, 1146–1158. [Google Scholar] [CrossRef]
- Kawashita, L.F.; Hallett, S.R. A crack tip tracking algorithm for cohesive interface element analysis of fatigue delamination propagation in composite materials. Int. J. Solids Struct. 2012, 49, 2898–2913. [Google Scholar] [CrossRef]
- Tumino, D.; Cappello, F. Simulation of Fatigue Delamination Growth in Composites with Different Mode Mixtures. J. Compos. Mater. 2007, 41, 2415–2441. [Google Scholar] [CrossRef]
- Muñoz, J.; Galvanetto, U.; Robinson, P. On the numerical simulation of fatigue driven delamination with interface elements. Int. J. Fatigue 2006, 28, 1136–1146. [Google Scholar] [CrossRef]
- Beaurepaire, P.; Schuëller, G. Modeling of the variability of fatigue crack growth using cohesive zone elements. Eng. Fract. Mech. 2011, 78, 2399–2413. [Google Scholar] [CrossRef] [PubMed]
- Skvortsov, Y.; Chernyakin, S.; Glushkov, S.; Perov, S. Simulation of fatigue delamination growth in composite laminates under mode I loading. Appl. Math. Model. 2016, 40, 7216–7224. [Google Scholar] [CrossRef]
- Koloor, S.; Abdullah, M.; Tamin, M.; Ayatollahi, M. Fatigue damage of cohesive interfaces in fiber-reinforced polymer composite laminates. Compos. Sci. Technol. 2019, 183. [Google Scholar] [CrossRef]
- Chen, J.-F.; Morozov, E.V.; Shankar, K. Progressive failure analysis of perforated aluminium/CFRP fibre metal laminates using a combined elastoplastic damage model and including delamination effects. Compos. Struct. 2014, 114, 64–79. [Google Scholar] [CrossRef]
- Roe, K.; Siegmund, T. An irreversible cohesive zone model for interface fatigue crack growth simulation. Eng. Fract. Mech. 2003, 70, 209–232. [Google Scholar] [CrossRef]
- Gustafson, P.A.; Waas, A.M. The influence of adhesive constitutive parameters in cohesive zone finite element models of adhesively bonded joints. Int. J. Solids Struct. 2009, 46, 2201–2215. [Google Scholar] [CrossRef]
- Turon, A.; González, E.; Sarrado, C.; Guillamet, G.; Maimí, P. Accurate simulation of delamination under mixed-mode loading using a cohesive model with a mode-dependent penalty stiffness. Compos. Struct. 2018, 184, 506–511. [Google Scholar] [CrossRef]
- Tarfaoui, M.; El Moumen, A.; Lafdi, K. Progressive damage modeling in carbon fibers/carbon nanotubes reinforced polymer composites. Compos. Part B: Eng. 2017, 112, 185–195. [Google Scholar] [CrossRef]
- Pirondi, A.; Moroni, F. A Progressive Damage Model for the Prediction of Fatigue Crack Growth in Bonded Joints. J. Adhes. 2010, 86, 501–521. [Google Scholar] [CrossRef]
- Harper, P.W.; Hallett, S.R. A fatigue degradation law for cohesive interface elements – Development and application to composite materials. Int. J. Fatigue 2010, 32, 1774–1787. [Google Scholar] [CrossRef]
- Nixon-Pearson OJ, Hallett SR, Harper PW, Kawashita LF. Damage development in open-hole composite specimens in fatigue. Part 2: Numerical modelling. Composite Structures. 2013;106:890-898. [CrossRef]
- Tao, C.; Qiu, J.; Yao, W.; Ji, H. A novel method for fatigue delamination simulation in composite laminates. Compos. Sci. Technol. 2016, 128, 104–115. [Google Scholar] [CrossRef]
- Ebadi-Rajoli, J.; Akhavan-Safar, A.; Hosseini-Toudeshky, H.; da Silva, L. Progressive damage modeling of composite materials subjected to mixed mode cyclic loading using cohesive zone model. Mech. Mater. 2020, 143, 103322. [Google Scholar] [CrossRef]

| Criterions | expression of |
|---|---|
| Hashin | |
| Chang-Change | |
| Hou | |
| Zou | |
| LaRC |
| Initiation criteria | expression | Evolution law | expression |
|---|---|---|---|
| Maximum principal stress/strain criterion | Power law | ||
| Maximum nominal stress/strain criterion |
B-K law | ||
| Quadratic nominal stress/strain criterion | Reeder law |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




