Submitted:
26 September 2023
Posted:
27 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
Nomenclatures
|
, ∆: Total strain tensor, increment of total strain tensor , : Viscoelasticity strain tensor, viscoplasticity strain tensor , ∆, : Stress tensor, increment of stress tensor, deviatoric stress tensor , : Hydrostatic stress, second order identity tensor , : Damage variable, critical damage variable , : Entropy generation, final fracture entropy : Nonlinear coefficient , : Time : Dissipated energy : Damage parameters : Relaxation tensor : Viscosity matrix : Constant matrix , , v: Stiffness matrix, initial Young’s modulus, Poisson’s ratio η: Viscoelasticity properties of Maxwell elements , : Equivalent stress, equivalent viscoplastic strain , , α, β, : Viscoplasticity coefficients , : Generalized thermodynamic force and internal flow vectors , : Temperature, heat flux vector |
2. Numerical methodology
2.1. Entropy-based failure criterion
2.2. Finite element modeling
3. Results and discussions
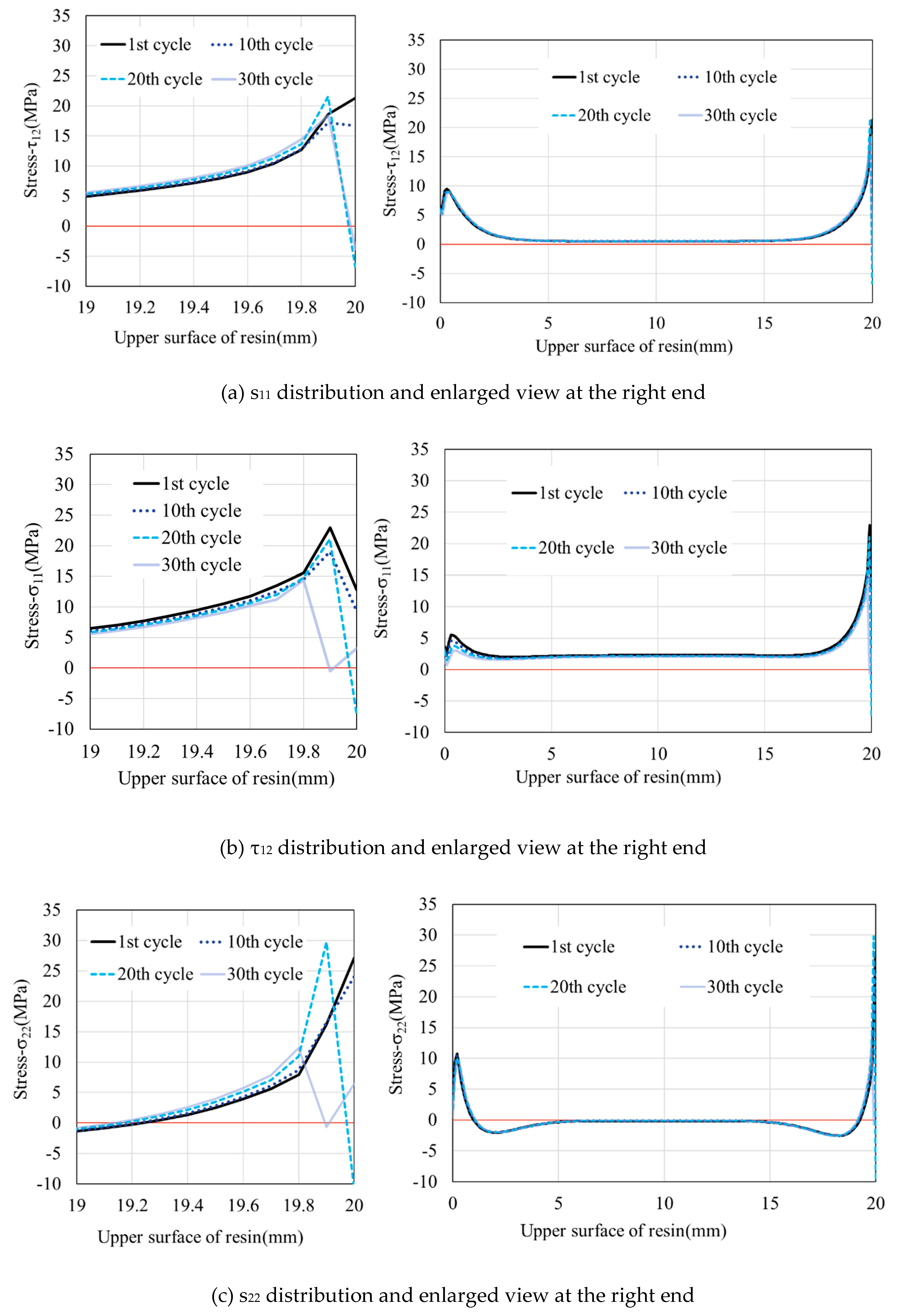
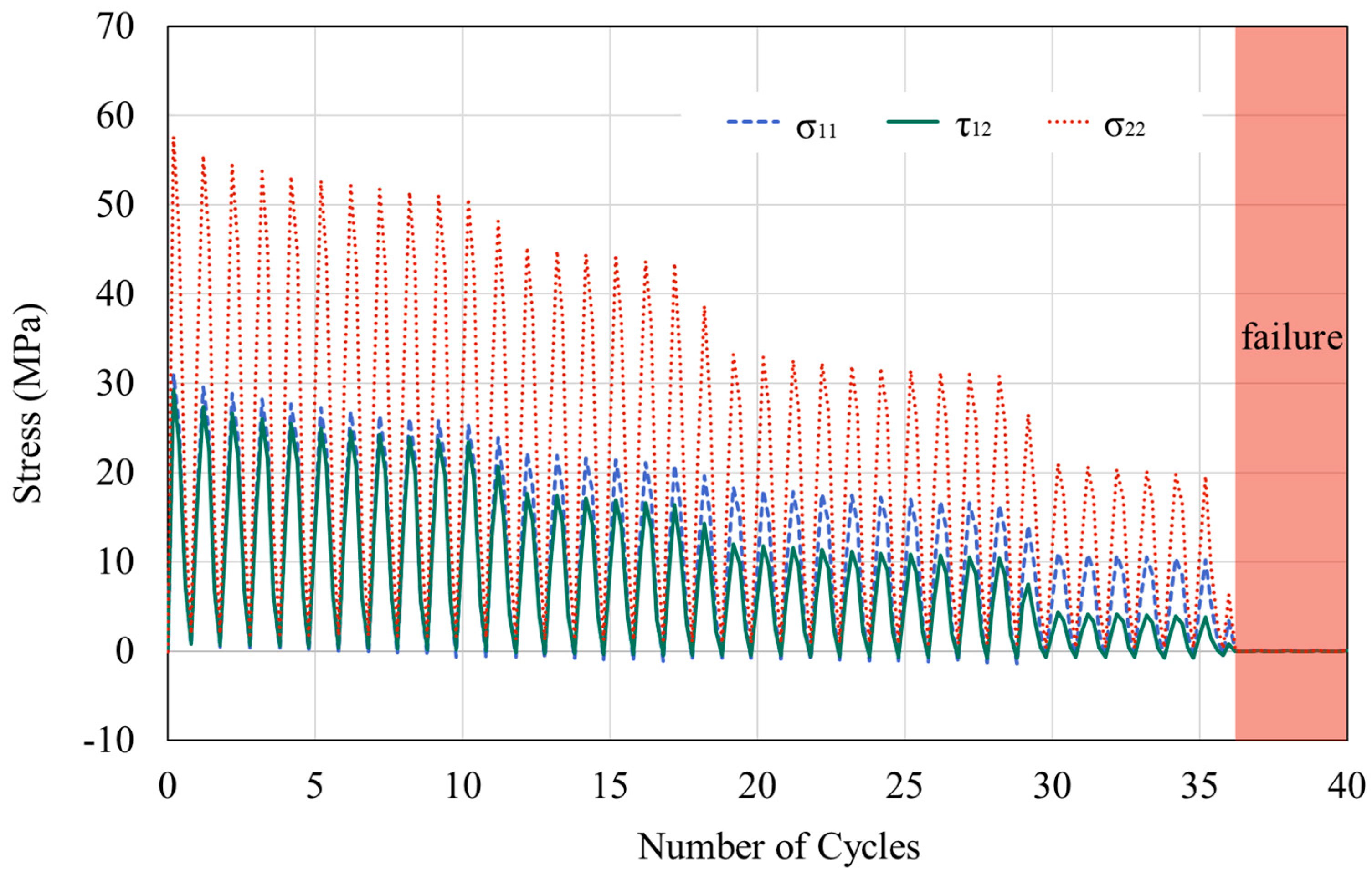
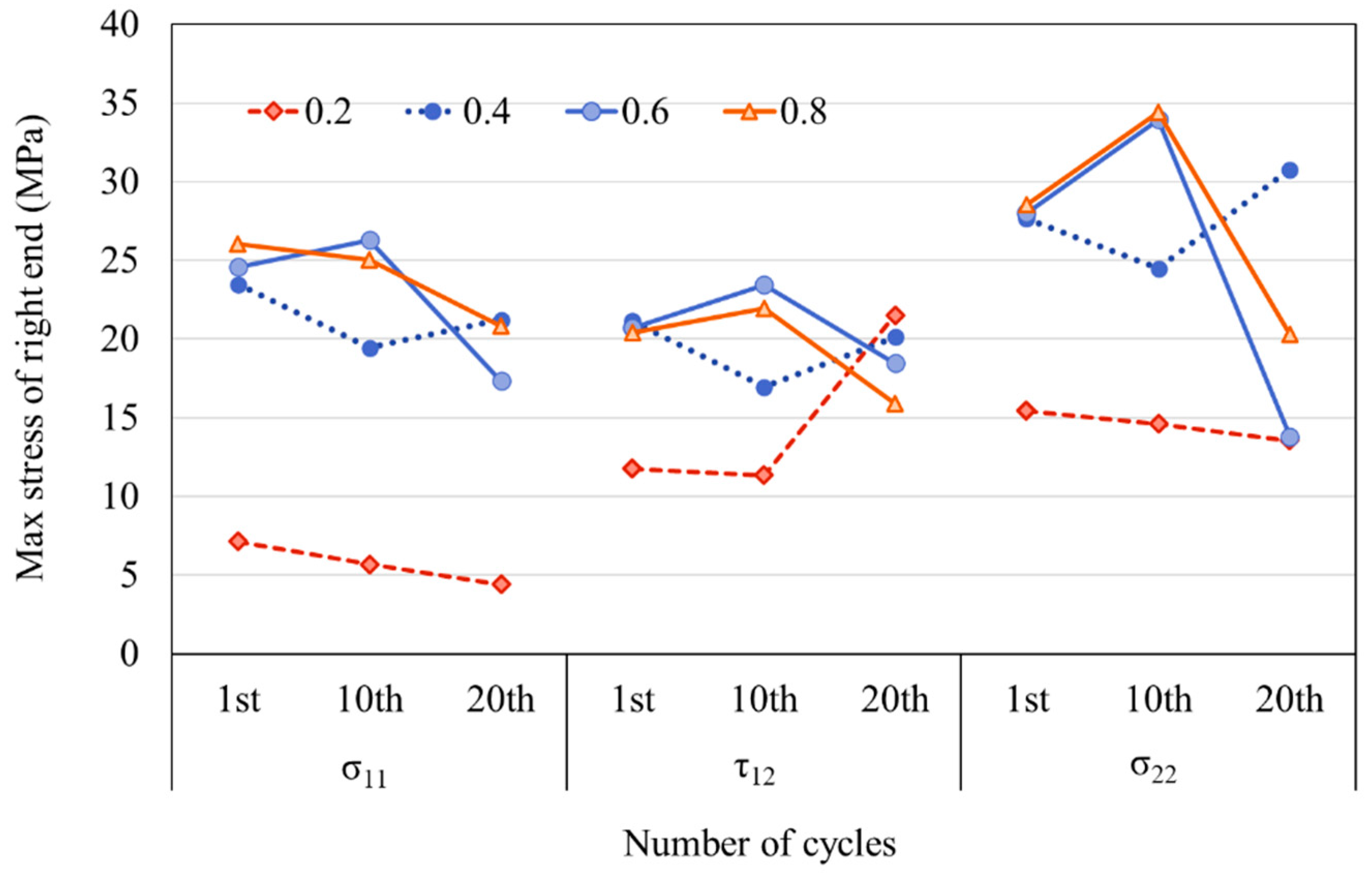
3.1. Evolution of stress along the interface versus cyclic loadings
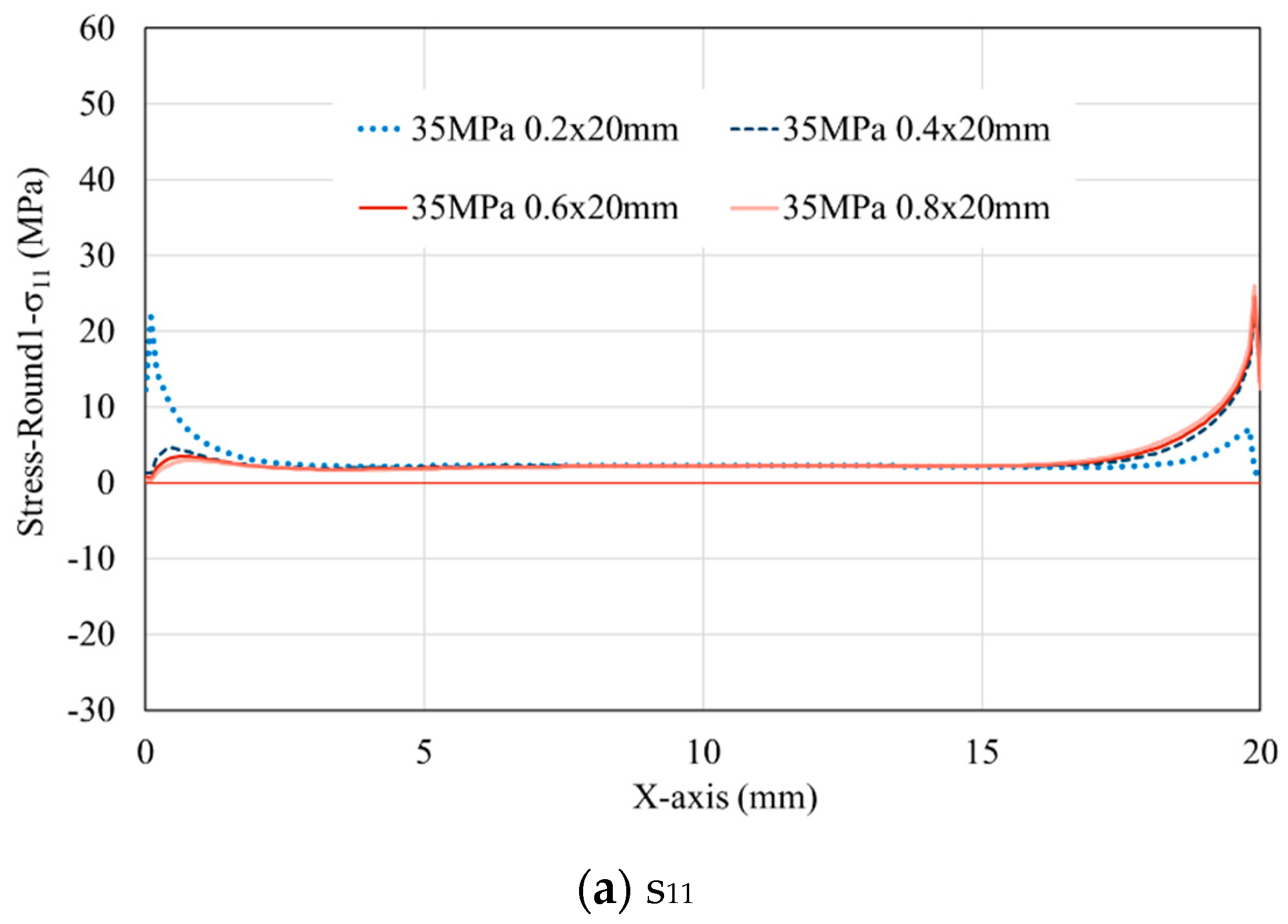
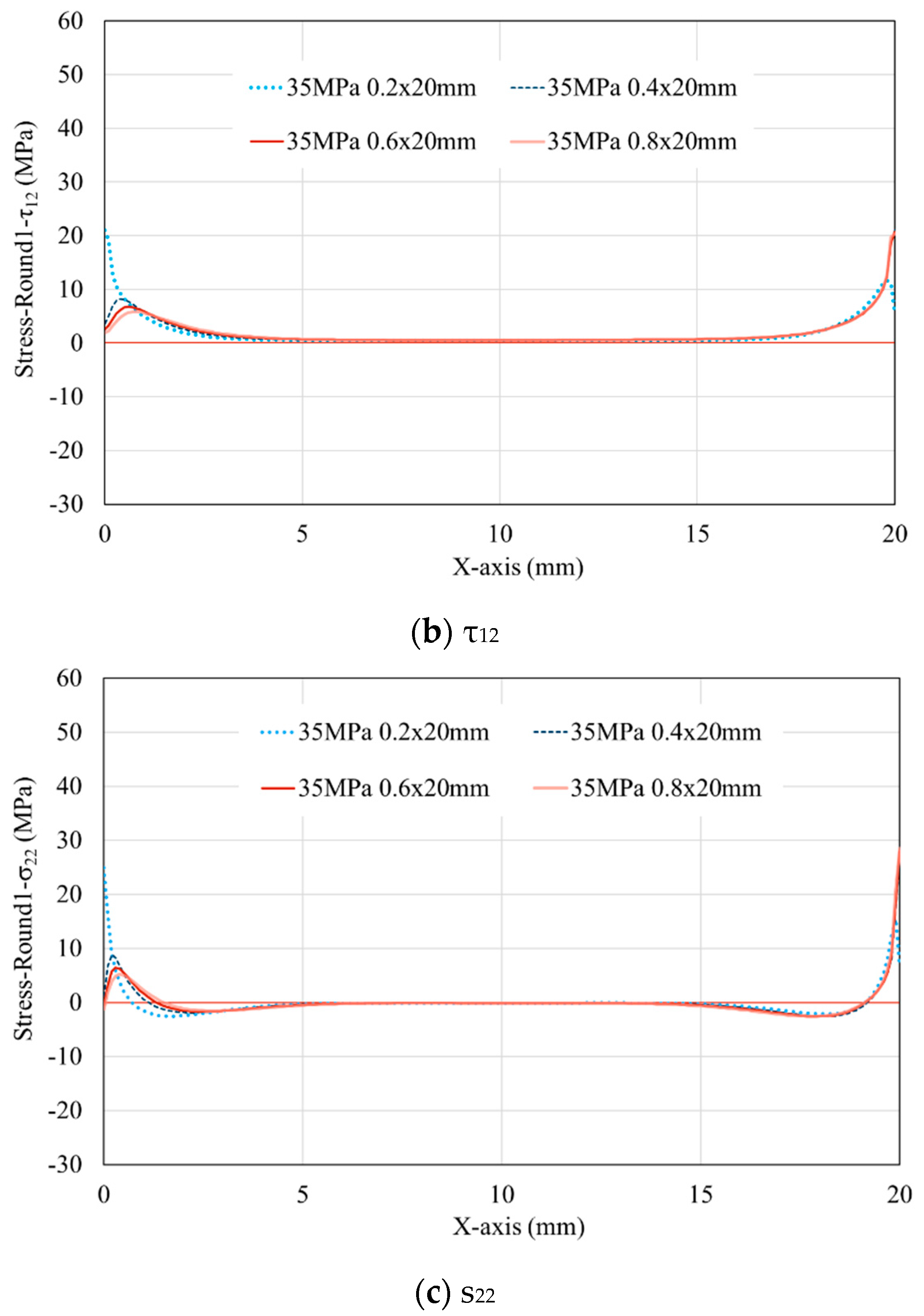
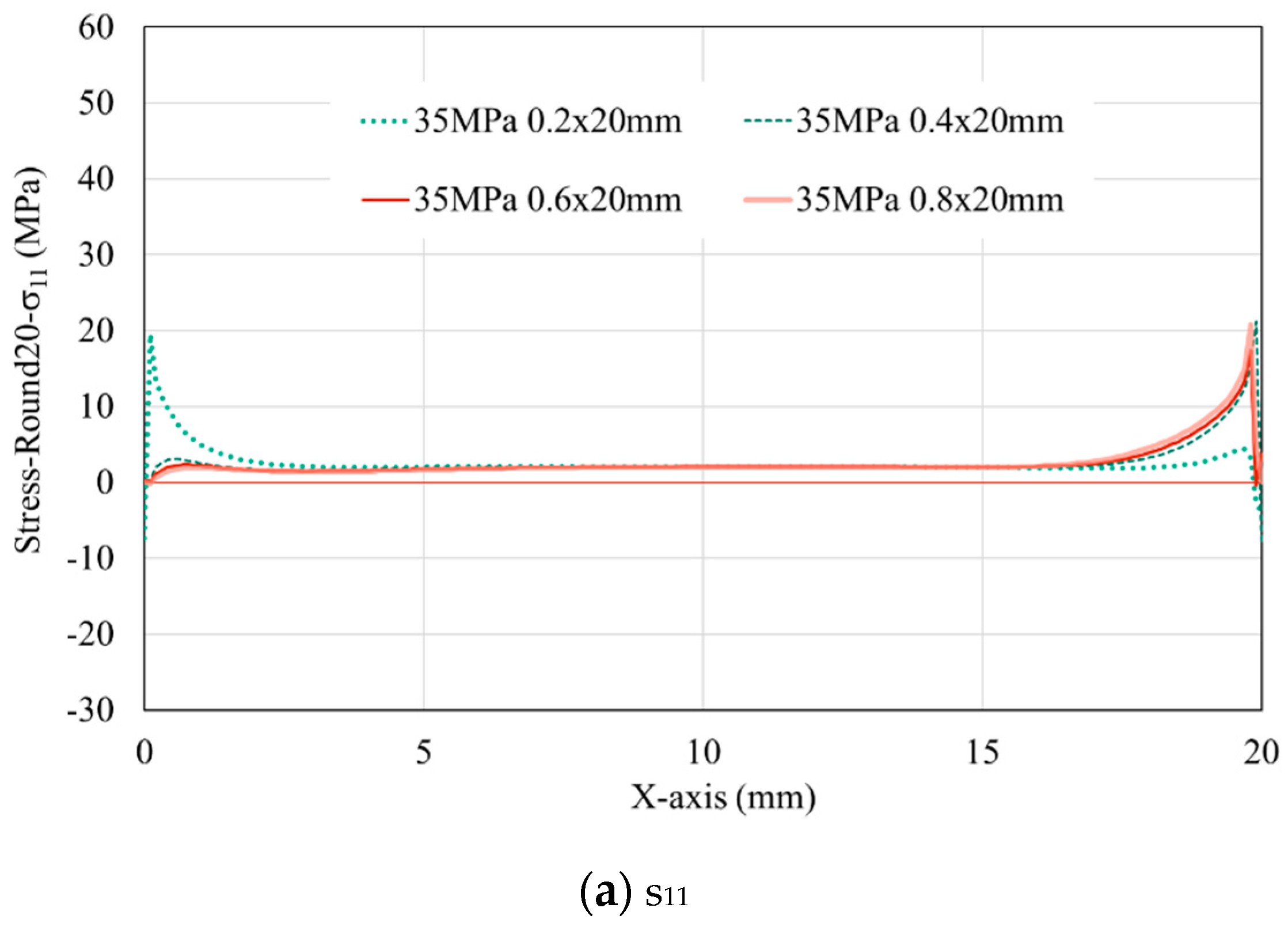
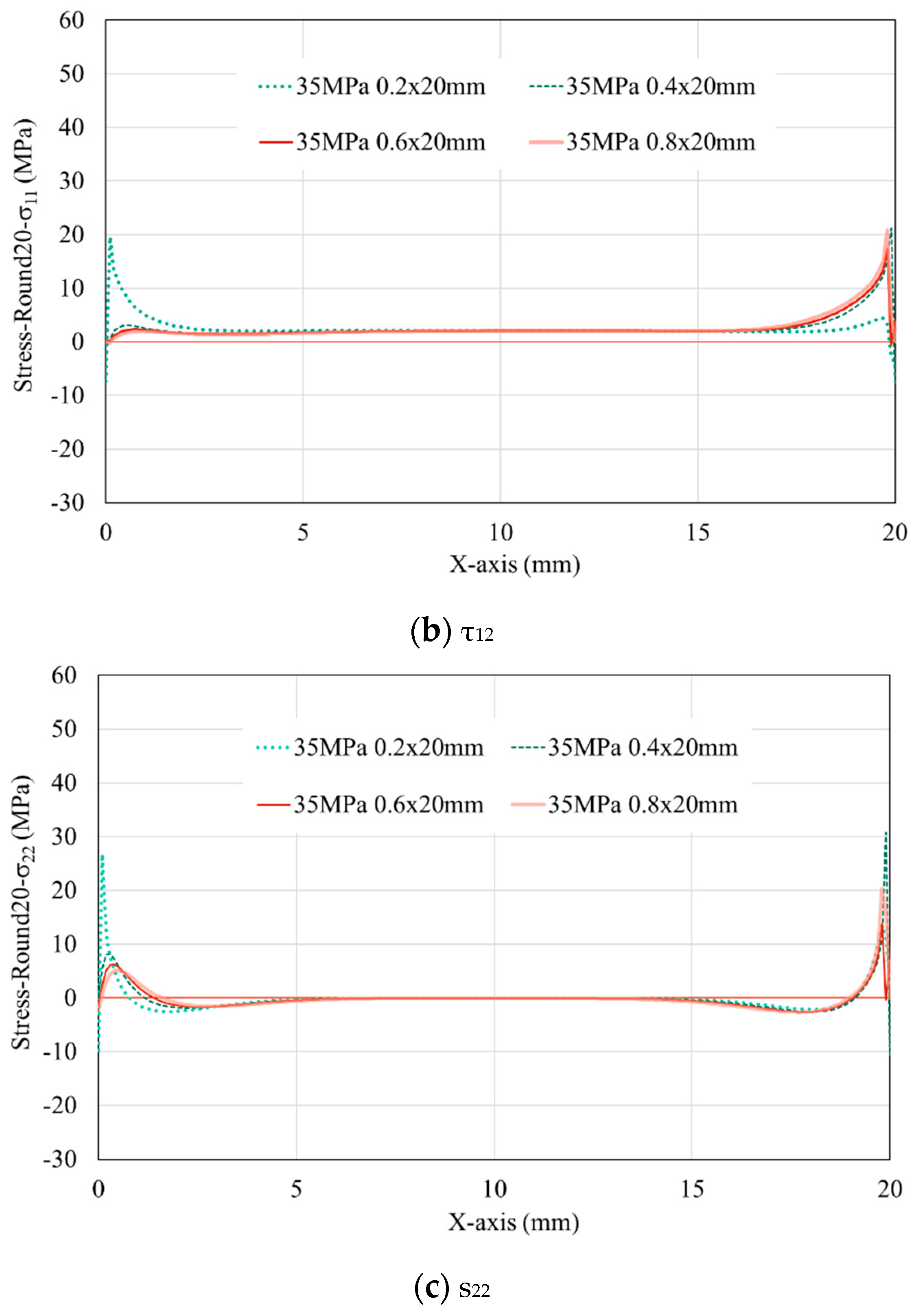
3.2. Effect of adhesive thickness on the evolution of stress along the interface
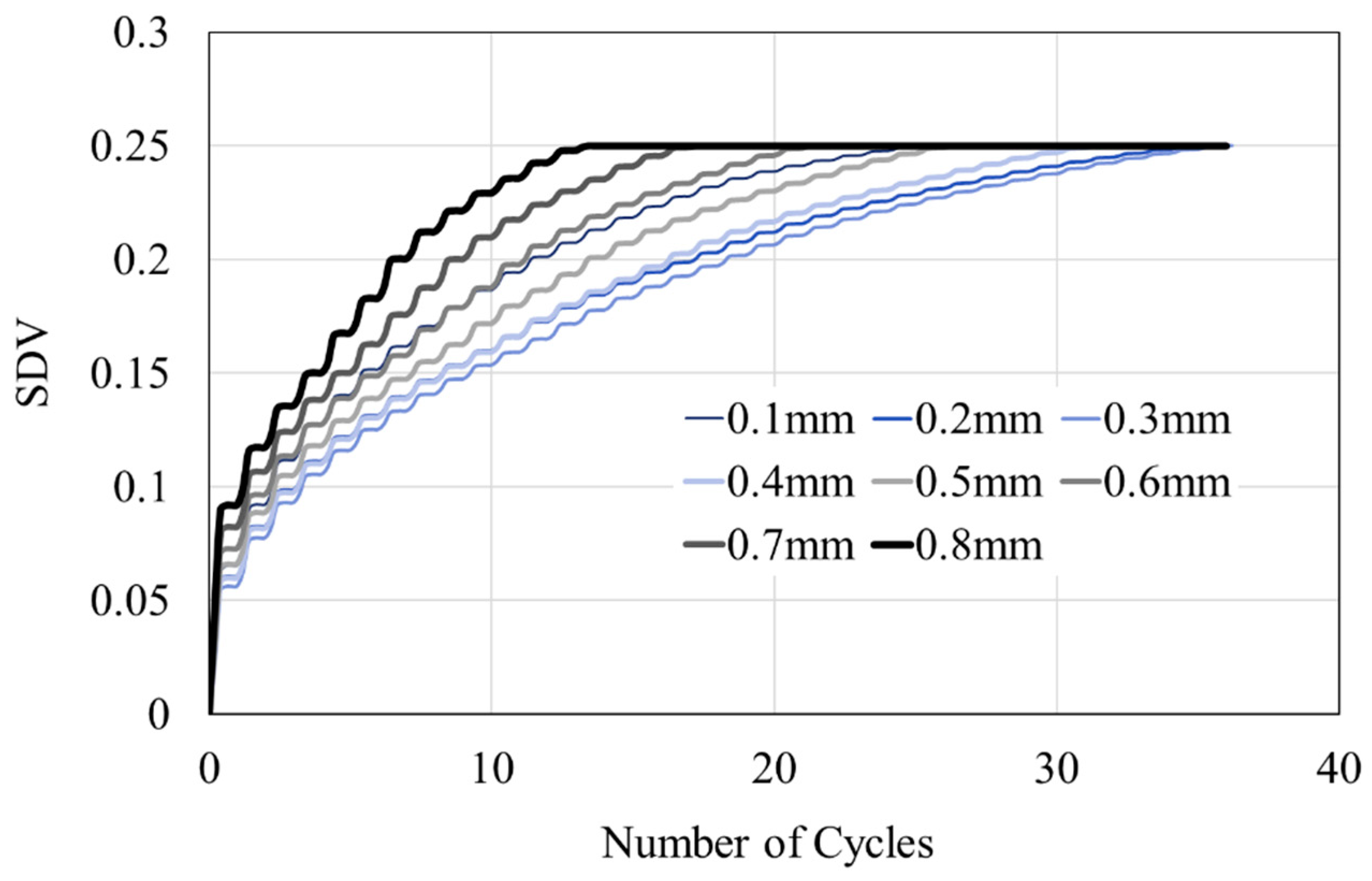
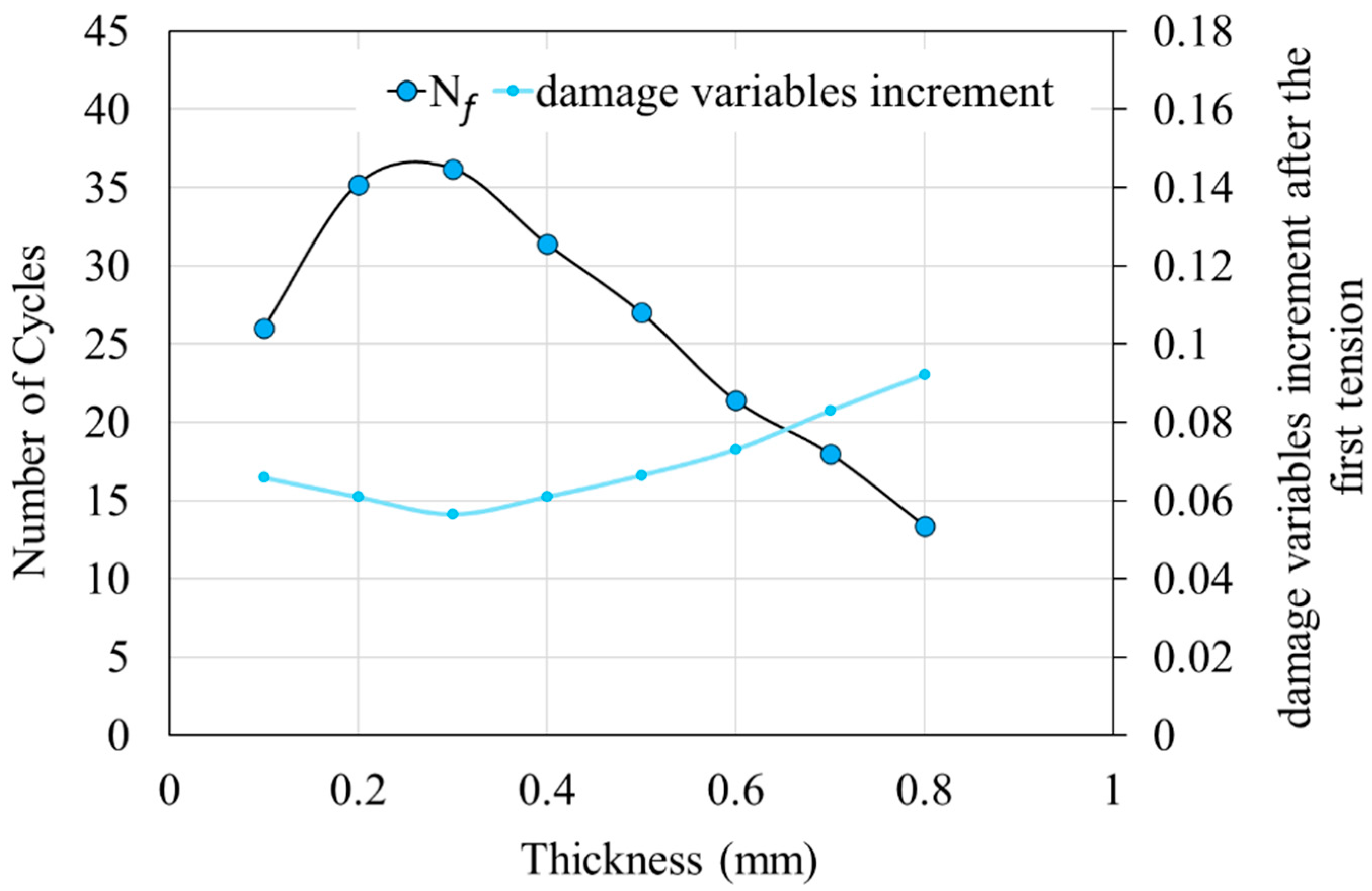
3.3. Relationship between number of cycles to failure (Nf) and thickness
4. Conclusions
Acknowledgments
References
- A. Akhavan-Safar, F. Ramezani, F. Delzendehrooy, M.R. Ayatollahi, L.F.M. da Silva, A review on bi-adhesive joints: Benefits and challenges, Int J Adhes Adhes. 114 (2022) 103098. https://doi.org/10.1016/j.ijadhadh.2022.103098. [CrossRef]
- L.D.C. Ramalho, I.J. Sánchez-Arce, D.C. Gonçalves, J. Belinha, R.D.S.G. Campilho, Numerical analysis of the dynamic behaviour of adhesive joints: A review, Int J Adhes Adhes. 118 (2022) 103219. https://doi.org/10.1016/j.ijadhadh.2022.103219. [CrossRef]
- S. Ebnesajjad, A.H. Landrock, Adhesives Technology Handbook, Third, Elsevier Inc., Oxford, 2014. https://doi.org/10.1115/1.3225943. [CrossRef]
- S. Bhowmik, H.W. Bonin, V.T. Bui, R.D. Weir, Durability of adhesive bonding of titanium in radiation and aerospace environments, Int J Adhes Adhes. 26 (2006) 400–405. https://doi.org/10.1016/j.ijadhadh.2005.05.004. [CrossRef]
- C. V. Katsiropoulos, A.N. Chamos, K.I. Tserpes, S.G. Pantelakis, Fracture toughness and shear behavior of composite bonded joints based on a novel aerospace adhesive, Compos B Eng. 43 (2012) 240–248. https://doi.org/10.1016/j.compositesb.2011.07.010. [CrossRef]
- E.A.S. Marques, L.F.M. Da Silva, M. Flaviani, Testing and simulation of mixed adhesive joints for aerospace applications, Compos B Eng. 74 (2015) 123–130. https://doi.org/10.1016/j.compositesb.2015.01.005. [CrossRef]
- D. Quan, J.L. Urdániz, C. Rouge, A. Ivanković, The enhancement of adhesively-bonded aerospace-grade composite joints using steel fibres, Compos Struct. 198 (2018) 11–18. https://doi.org/10.1016/j.compstruct.2018.04.071. [CrossRef]
- J. Kupski, S. Teixeira de Freitas, Design of adhesively bonded lap joints with laminated CFRP adherends: Review, challenges and new opportunities for aerospace structures, Compos Struct. 268 (2021) 113923. https://doi.org/10.1016/j.compstruct.2021.113923. [CrossRef]
- S. Wang, Y. Kitamura, N. Hiraishi, S. Taira, A. Tsuge, T. Kaneko, D. Kaneko, Preparation of mussel-inspired biopolyester adhesive and comparative study of effects of meta- or para-hydroxyphenylpropionic acid segments on their properties, Polymer (Guildf). 165 (2019) 152–162. https://doi.org/10.1016/j.polymer.2019.01.012. [CrossRef]
- C. Xu, T. Siegmund, K. Ramani, Rate-dependent crack growth in adhesives: II. Experiments and analysis, Int J Adhes Adhes. 23 (2003) 15–22. https://doi.org/10.1016/S0143-7496(02)00063-5. [CrossRef]
- X.-Y. Miao, X. Chen, R. Lu, M.A. Eder, Multi-site crack initiation in local details of composite adhesive joints, Compos B Eng. 242 (2022) 110055. https://doi.org/10.1016/j.compositesb.2022.110055. [CrossRef]
- V. Dumont, G. Stamoulis, C. Badulescu, A. Lefèvre, D. Thévenet, Investigation of the influence of the temperature on the fracture properties of adhesive joints using the Arcan device, Eng Fract Mech. 269 (2022) 108524. https://doi.org/10.1016/j.engfracmech.2022.108524. [CrossRef]
- K. Ishii, M. Imanaka, H. Nakayama, H. Kodama, Fatigue failure criterion of adhesively bonded CFRP/metal joints under multiaxial stress conditions, Compos Part A Appl Sci Manuf. 29 (1998) 415–422. https://doi.org/10.1016/S1359-835X(97)00096-1. [CrossRef]
- K. Ishii, M. Imanaka, H. Nakayama, H. Kodama, Evaluation of the fatigue strength of adhesively bonded CFRP/metal single and single-step double-lap joints, Compos Sci Technol. 59 (1999) 1675–1683. https://doi.org/10.1016/S0266-3538(99)00028-7. [CrossRef]
- J.A.M. Ferreira, P.N. Reis, J.D.M. Costa, M.O.W. Richardson, Fatigue behaviour of composite adhesive lap joints, Compos Sci Technol. 62 (2002) 1373–1379. https://doi.org/10.1016/S0266-3538(02)00082-9. [CrossRef]
- Y. Zhang, A.P. Vassilopoulos, T. Keller, Environmental effects on fatigue behavior of adhesively-bonded pultruded structural joints, Compos Sci Technol. 69 (2009) 1022–1028. https://doi.org/10.1016/j.compscitech.2009.01.024. [CrossRef]
- J.H. Tang, I. Sridhar, N. Srikanth, Static and fatigue failure analysis of adhesively bonded thick composite single lap joints, Compos Sci Technol. 86 (2013) 18–25. https://doi.org/10.1016/j.compscitech.2013.06.018. [CrossRef]
- P.N.B. Reis, J.F.R. Monteiro, A.M. Pereira, J.A.M. Ferreira, J.D.M. Costa, Fatigue behaviour of epoxy-steel single lap joints under variable frequency, Int J Adhes Adhes. 63 (2015) 66–73. https://doi.org/10.1016/j.ijadhadh.2015.08.008. [CrossRef]
- B. Schneider, V.C. Beber, M. Brede, Estimation of the lifetime of bonded joints under cyclic loads at different temperatures, J Adhes. 92 (2016) 795–817. https://doi.org/10.1080/00218464.2015.1114928. [CrossRef]
- H. Khoramishad, A.D. Crocombe, K.B. Katnam, I.A. Ashcroft, Predicting fatigue damage in adhesively bonded joints using a cohesive zone model, Int J Fatigue. 32 (2010) 1146–1158. https://doi.org/10.1016/j.ijfatigue.2009.12.013. [CrossRef]
- S. Jimenez, R. Duddu, On the parametric sensitivity of cohesive zone models for high-cycle fatigue delamination of composites, Int J Solids Struct. 82 (2016) 111–124. https://doi.org/10.1016/j.ijsolstr.2015.10.015. [CrossRef]
- L. Ben Fekih, O. Verlinden, G. Kouroussis, Derivation of a fatigue damage law for an adhesive from in-situ bending tests, Eng Fract Mech. 245 (2021) 107587. https://doi.org/10.1016/j.engfracmech.2021.107587. [CrossRef]
- J. Schijve, Fatigue of structures and materials, 2009. https://doi.org/10.1007/978-1-4020-6808-9. [CrossRef]
- C. Basaran, S. Nie, An irreversible thermodynamics theory for damage mechanics of solids, International Journal of Damage Mechanics. 13 (2004) 205–223. https://doi.org/10.1177/1056789504041058. [CrossRef]
- M. Naderi, M. Amiri, M.M. Khonsari, On the thermodynamic entropy of fatigue fracture, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 466 (2010) 423–438. https://doi.org/10.1098/rspa.2009.0348. [CrossRef]
- M. Amiri, M.M. Khonsari, Life prediction of metals undergoing fatigue load based on temperature evolution, Materials Science and Engineering A. 527 (2010) 1555–1559. https://doi.org/10.1016/j.msea.2009.10.025. [CrossRef]
- G. Meneghetti, Analysis of the fatigue strength of a stainless steel based on the energy dissipation, Int J Fatigue. 29 (2007) 81–94. https://doi.org/10.1016/j.ijfatigue.2006.02.043. [CrossRef]
- A. Mahmoudi, M.M. Khonsari, Investigation of metal fatigue using a coupled entropy-kinetic model, Int J Fatigue. 161 (2022) 106907. https://doi.org/10.1016/j.ijfatigue.2022.106907. [CrossRef]
- P. Ribeiro, J. Petit, L. Gallimard, Experimental determination of entropy and exergy in low cycle fatigue, Int J Fatigue. 136 (2020) 105333. https://doi.org/10.1016/j.ijfatigue.2019.105333. [CrossRef]
- J. Huang, C. Li, W. Liu, Investigation of internal friction and fracture fatigue entropy of CFRP laminates with various stacking sequences subjected to fatigue loading, Thin-Walled Structures. 155 (2020) 106978. https://doi.org/10.1016/j.tws.2020.106978. [CrossRef]
- J. Huang, H. Yang, W. Liu, K. Zhang, A. Huang, Confidence level and reliability analysis of the fatigue life of CFRP laminates predicted based on fracture fatigue entropy, Int J Fatigue. 156 (2022) 106659. https://doi.org/10.1016/j.ijfatigue.2021.106659. [CrossRef]
- H.W. Lee, C. Basaran, H. Egner, A. Lipski, M. Piotrowski, S. Mroziński, N. Bin Jamal M, C. Lakshmana Rao, Modeling ultrasonic vibration fatigue with unified mechanics theory, Int J Solids Struct. 236–237 (2022). https://doi.org/10.1016/j.ijsolstr.2021.111313. [CrossRef]
- J. Huang, C. Li, W. Liu, Investigation of internal friction and fracture fatigue entropy of CFRP laminates with various stacking sequences subjected to fatigue loading, Thin-Walled Structures. 155 (2020) 106978. https://doi.org/10.1016/j.tws.2020.106978. [CrossRef]
- J. Koyanagi, A. Mochizuki, R. Higuchi, V.B.C. Tan, T.E. Tay, Finite element model for simulating entropy-based strength-degradation of carbon-fiber-reinforced plastics subjected to cyclic loadings, Int J Fatigue. 165 (2022) 107204. https://doi.org/10.1016/j.ijfatigue.2022.107204. [CrossRef]
- M. Sato, K. Hasegawa, J. Koyanagi, R. Higuchi, Y. Ishida, Residual strength prediction for unidirectional CFRP using a nonlinear viscoelastic constitutive equation considering entropy damage, Compos Part A Appl Sci Manuf. 141 (2021) 106178. https://doi.org/10.1016/j.compositesa.2020.106178. [CrossRef]
- N. Takase, J. Koyanagi, K. Mori, T. Sakai, Molecular Dynamics Simulation for Evaluating Fracture Entropy of a Polymer Material under Various Combined Stress States, Materials. 14 (2021) 1884. https://doi.org/10.3390/ma14081884. [CrossRef]
- T. Sakai, N. Takase, Y. Oya, J. Koyanagi, A Possibility for Quantitative Detection of Mechanically-Induced Invisible Damage by Thermal Property Measurement via Entropy Generation for a Polymer Material, Materials. 15 (2022) 737. https://doi.org/10.3390/ma15030737. [CrossRef]
- H. Deng, K. Toda, M. Sato, J. Koyanagi, Micro-Scale Numerical Simulation of Fatigue Failure for CFRP Subjected to Multiple-Amplitude Cyclic Loadings Based on Entropy Damage Criterion, Materials. 16 (2023) 6120. https://doi.org/10.3390/ma16186120. [CrossRef]
- C. Basaran, S. Nie, An irreversible thermodynamics theory for damage mechanics of solids, International Journal of Damage Mechanics. 13 (2004) 205–223. https://doi.org/10.1177/1056789504041058. [CrossRef]
- H. Kagawa, Y. Umezu, K. Sakaue, J. Koyanagi, Numerical simulation for the tensile failure of randomly oriented short fiber reinforced plastics based on a viscoelastic entropy damage criterion, Composites Part C: Open Access. 10 (2023) 100342. https://doi.org/10.1016/j.jcomc.2022.100342. [CrossRef]
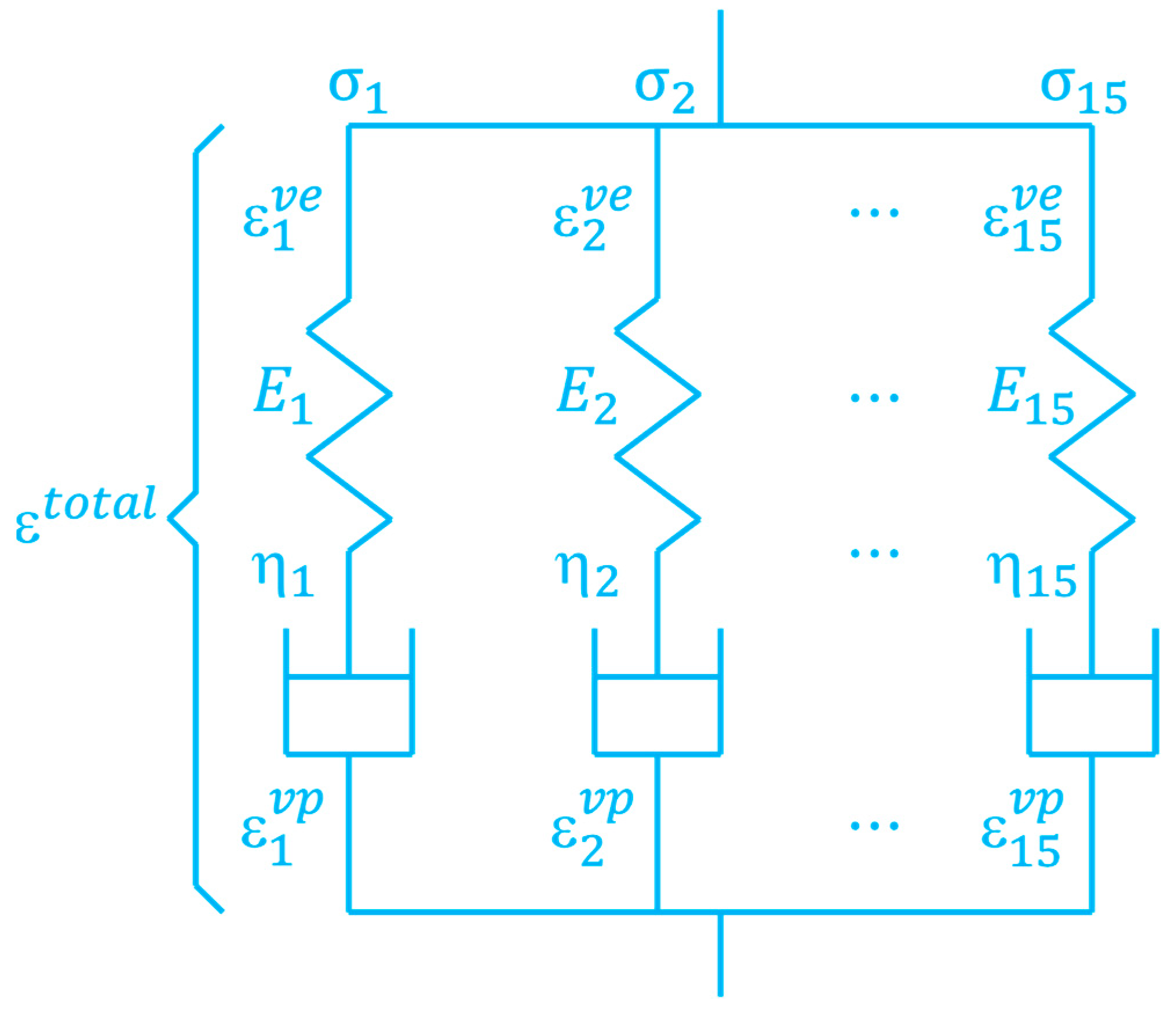
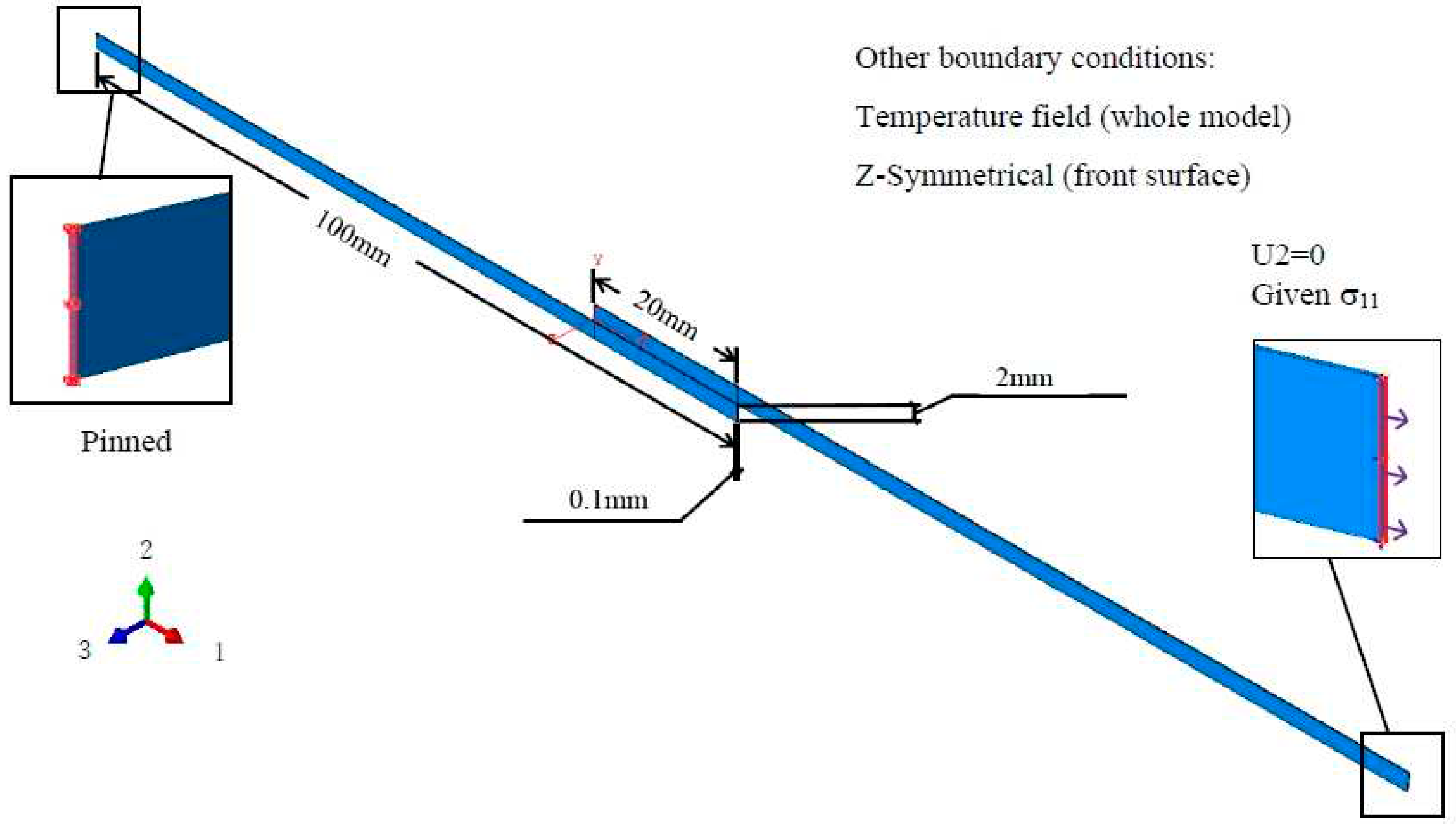
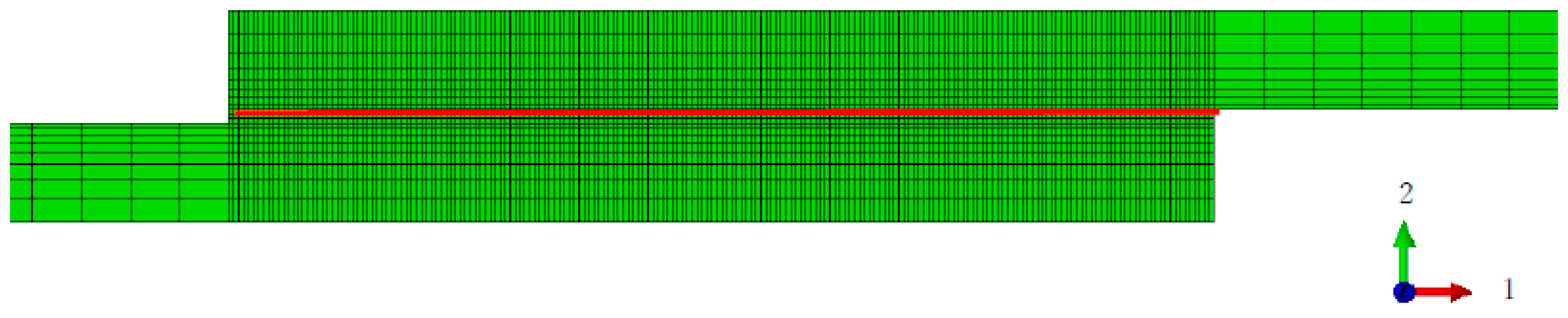
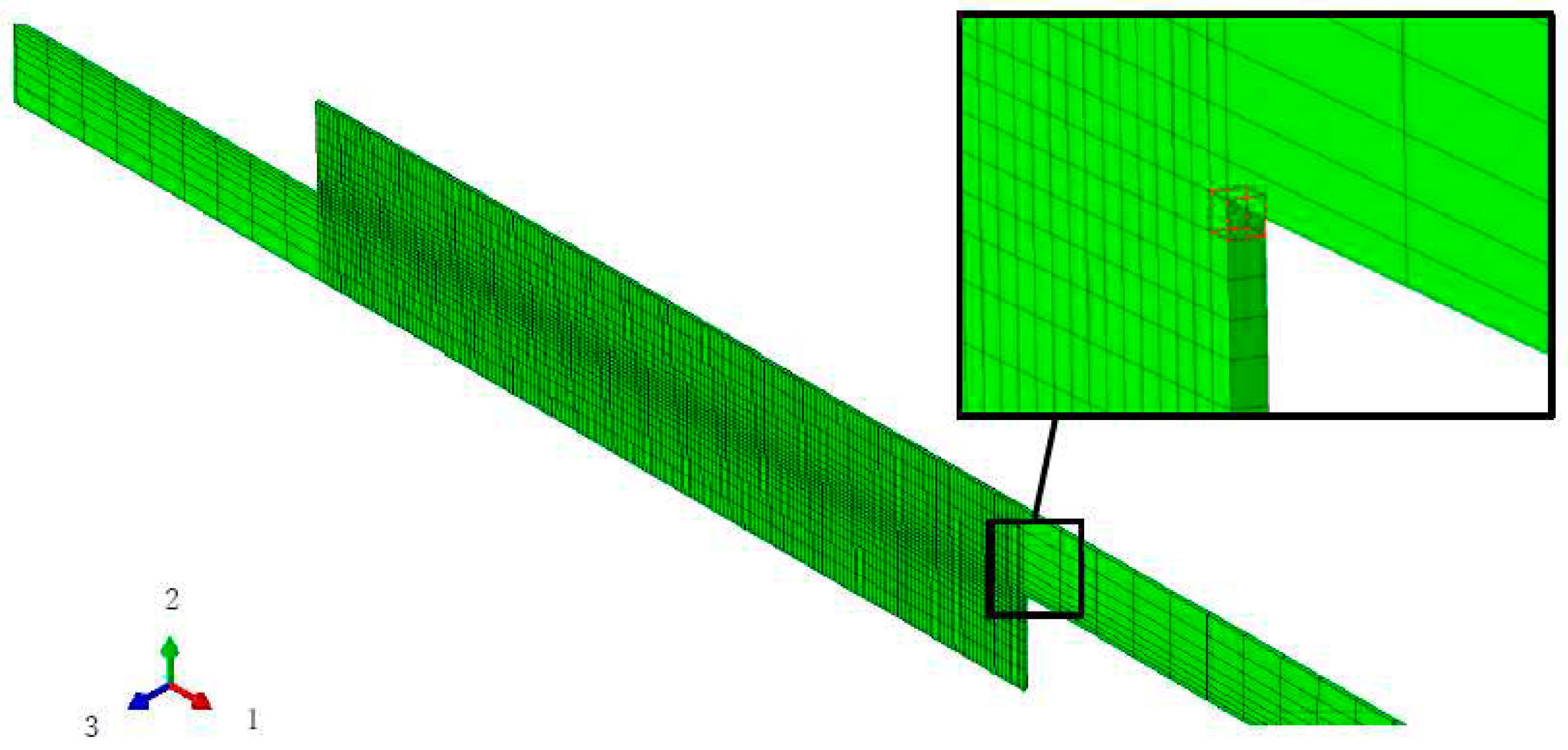
| E1 | E2 | E3 | Nu12 | Nu13 | Nu23 | G12 | G13 | G23 |
| 15000 | 15000 | 294000 | 0.3 | 0.02 | 0.02 | 6000 | 18000 | 18000 |
| n | s | Elasticity | ||
| 1 | 284 | 4.5×102 | 4260 | |
| 2 | 284 | 3.3×103 | v | 0.3 |
| 3 | 284 | 1.2×105 | Nonlinearity | |
| 4 | 284 | 1.9×106 | 70 | |
| 5 | 284 | 1.8×107 | α | 2 |
| 6 | 284 | 1.4×108 | m | 7 |
| 7 | 284 | 8.5×108 | Viscoplastic strain | |
| 8 | 284 | 5.0×109 | 1.0×1023 | |
| 9 | 284 | 3.0×1010 | 0 | |
| 10 | 284 | 1.9×1011 | 0 | |
| 11 | 284 | 1.4×1016 | 0 | |
| 12 | 284 | 1.3×1019 | χ | 0 |
| 13 | 284 | 2.1×1022 | ||
| 14 | 284 | 1.3×1026 | Damage variables | |
| 15 | 284 | 2.5×1029 | 4 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





