Modified CPL Models for Dark Energy and Observational Constraints

1. Introduction

Several independent observations, namely Type Ia supernovae (SN Ia) [1,2], cosmic microwave background (CMB) [3,4,5,6], Baryonic Acoustic Oscillation [7,8], Wilkinson Microwave Anisotropy Probe (WMAP) [9] established for the last two decades that our universe is going through an accelerating expansion phase in the present time. This acceleration started at recent past $z\approx 0.7$ [10,11] and this phase is known as late-time acceleration in cosmology. However, the cause of this acceleration is unknown. In order to address this issue, cosmologists trying to search in two distinct paths. Firstly, Modifying the gravity theory [12,13,14,15,16,17,18,19], and secondly, introducing some unknown kind of exotic matter, namely, dark energy, which have large negative pressure [20,21,22,23,24,25]. However, after the incredible success of Einstein gravity theory through the gravity wave detection [26,27], cosmologists are more inclined to the second option.

If one assumes our universe is filled with barotropic fluid, then the accelerating phase indicates the equation of state for dark energy is ${\omega }_{fld}\equiv p/\rho <-1/3$. The $\Lambda$CDM model (${\omega }_{fld}=-1$) is the best simplest model which supports the observation. However, it has potential drawback which is known as cosmological constant problem [28,29,30,31]. There are also several studies where the equation of state for the dark energy is considered as a function of redshift parameter z, for example, phantom fields [32,33,34], tachyons [35], quintessence[36,37,38], k-essence model [39,40], etc.

If the equation of state for the dark energy is considered to be an arbitrary function of redshift parameter z, then one needs infinite number of datasets to constrain the model parameter as an unknown function can be expand in terms of infinite Taylor (or, Laurent) series, which is practically impossible. Therefore, cosmologists attempt with considering finite number of parameters in the equation of state for the dark energy. One of the popular models is Chevallier-Polarski-Linder (CPL) model which has two parameters in the equation state having explicit form as [41,42]

$$\omega ={\omega }_0+{\omega }_1\left(\frac{z}{1+z}\right)$$

(1)

where ${\omega }_0$ and ${\omega }_1$ are constant. The notable feature for the model is that it is a well behaved and bounded function at high redshift and linear in z at low redshift.

In the present work, we shall choose two possible modifications of this CPL equation of state and examined them from the observational view point. The plan of the paper is as follows: In Section 2, basic equations of non-interacting DM and DE Friedmann-Lemaitre-Robertson-Walker (FLRW) cosmology has been presented and two specific equation of state of DE has been introduced. Section 3, deals with the numerical investigation of these models with the observational data, while Section 4, a comparison study of these models has been shown on the basis of Akaike, Bayesian Information criteria and Bayesian evidence. The paper ends with a conclusion in Section 5.

2. Friedmann-Lemaitre-Robertson-Walker Cosmology

Now, considering the spatially flat Friedmann-Lemaitre-Robertson-Walker (FLRW) space-time having the line element

$$d{s}^2=-d{t}^2+a{\left(t\right)}^2(d{x}^2+d{y}^2+d{z}^2)$$

(2)

the Friedmann equations take the form

$$\begin{array}{ccc}\hfill 3H^2& =& \kappa ({\rho }_m+{\rho }_{de})\hfill \\ \hfill 2\dot{H}+3H^2& =& -\kappa (p_m+p_{de})\hfill \end{array}$$

(3)

where $a\left(t\right)$ is the scale factor, $\kappa =8\pi G$ and $H=\frac{\dot{a}}{a}$ is the Hubble parameter. The energy conservation equations of individual component can be expressed as

$$\begin{array}{c}\hfill {\dot{\rho }}_m+3H({\rho }_m+p_m)=0\\ \hfill {\dot{\rho }}_{de}+3H({\rho }_{de}+p_{de})=0.\end{array}$$

(4)

If one assumes the equation of state for matter component is $p_m=\omega {\rho }_m$, the energy density of the matter component can be obtained as

$${\rho }_m={\rho }_{m0}{a}^{-3(1+\omega )}$$

(5)

Here, we have considered matter component as dust particle $i.e.,\omega =0$, so ${\rho }_m={\rho }_{m0}{a}^{-3}$. For the dark energy part, we have assumed equation of state parameter ${\omega }_{fld}$ varies with the redshift parameter z, then the energy density can be expressed as

$${\rho }_{de}={\rho }_{de0}{e}^{-3{\int }_{a_0}^a(1+{\omega }_{fld})d{a}^{\prime }/a^{\prime }},$$

(6)

where $a_0$ is the present value of the scale factor and it is considered to be $a_0=1$ and ${\rho }_{m0},{\rho }_{de0}$ are integration constant. Thus the Hubble parameter H cane expressed as

$$H\left(a\right)=H_0{\left[{\Omega }_{m0}{a}^{-3}+{\Omega }_{de0}{e}^{-3{\int }_{a_0}^a(1+{\omega }_{fld})d{a}^{\prime }/a^{\prime }}\right]}^{1/2}$$

(7)

where $H_0,{\Omega }_{m0}=\frac{\kappa {\rho }_{m0}}{3H_0^2}$ and ${\Omega }_{de0}=\frac{\kappa {\rho }_{de0}}{3H_0^2}$ are the present value of the Hubble parameter $H\left(a\right)$, matter density ${\Omega }_m\left(a\right)$ and the dark energy density ${\Omega }_{de}\left(a\right)$, respectively. Therefore, ${\Omega }_{m0}+{\Omega }_{de0}=1$.

For the dark energy sector, we have considered here two variable of equation of state which are following:

2.1. Model I: ${\omega }_{fld}={\omega }_0+{\omega }_1{\left(\frac{z}{1+z}\right)}^p$

2.2. Model II: ${\omega }_{fld}={\omega }_0+{\omega }_1\frac{1}{1+z}{\left(log(1+z)\right)}^p$

where ${\omega }_0$ and ${\omega }_1$ are constants. We may emphasize here that the model I is nothing but a generalized form of the CPL model. For $p=1$, it reduces to CPL model. At low redshift both the models are linear in z. However, at high redshift, ${\omega }_{fld}={\omega }_0+{\omega }_1$ for model I, whereas for model II, ${\omega }_{fld}={\omega }_0$.

3. Numerical Analysis and Observational constraints

In this section, our goal here is to constrain the cosmological parameters analyzing the observational data sets. In oder to include the dark energy sector as a fluid, we have modified the public version of the CLASS Boltzmann code. The MCMC code Montepython3.5 [43] has been used to estimate the relevant cosmological model parameters.

For the statistical inference, we use the cosmological datasets (Pantheon+ [44], BAO (BOSS DR12 [7], SMALLZ - 2014 [8]) with the latest BAO dataset which spanning the redshift range $0.122\le z\le 2.334$ [45,46,47,48,49] and HST [50]) and a PLANCK18 [51] prior has been imposed. We have made the choice of flat priors on the base cosmological parameters as follows: the baryon density $100{\omega }_b=100{\Omega }_b{h}^2=[1.9,2.5]$; cold dark matter density ${\omega }_{cdm}={\Omega }_{cdm}{h}^2=[0.0,0.145]$; Hubble parameter $H0=[60,80]km{s}^{-1}Mp{c}^{-1}$, where $h=H_0{100}^{-1}$. A wide range of flat prior has been chosen for ${\omega }_0=[-2.0,2.0]$, ${\omega }_1=[-5.0,5.0]$, $p=[-3.0,3.0]$ and M is the nuisance parameter.

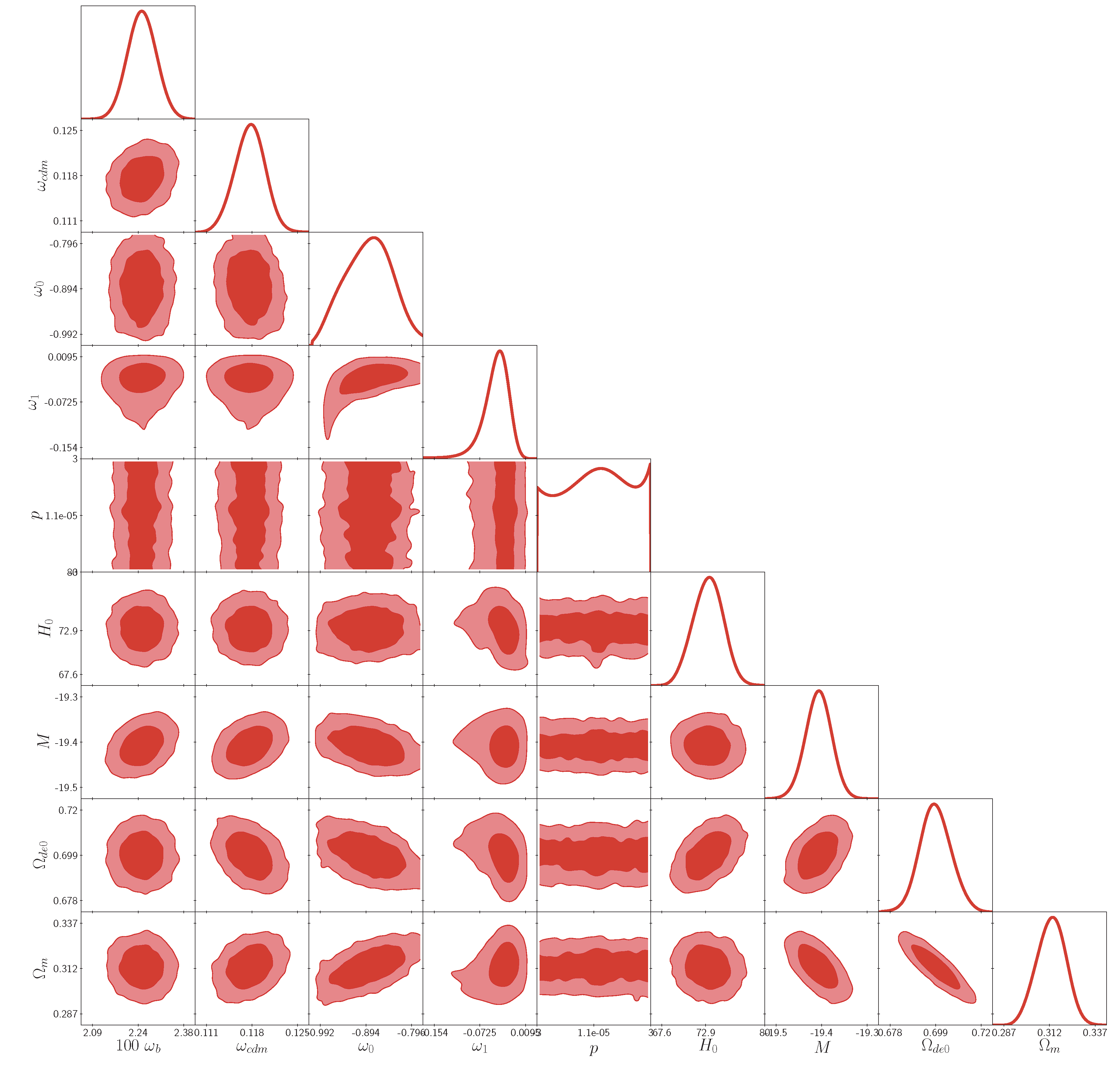
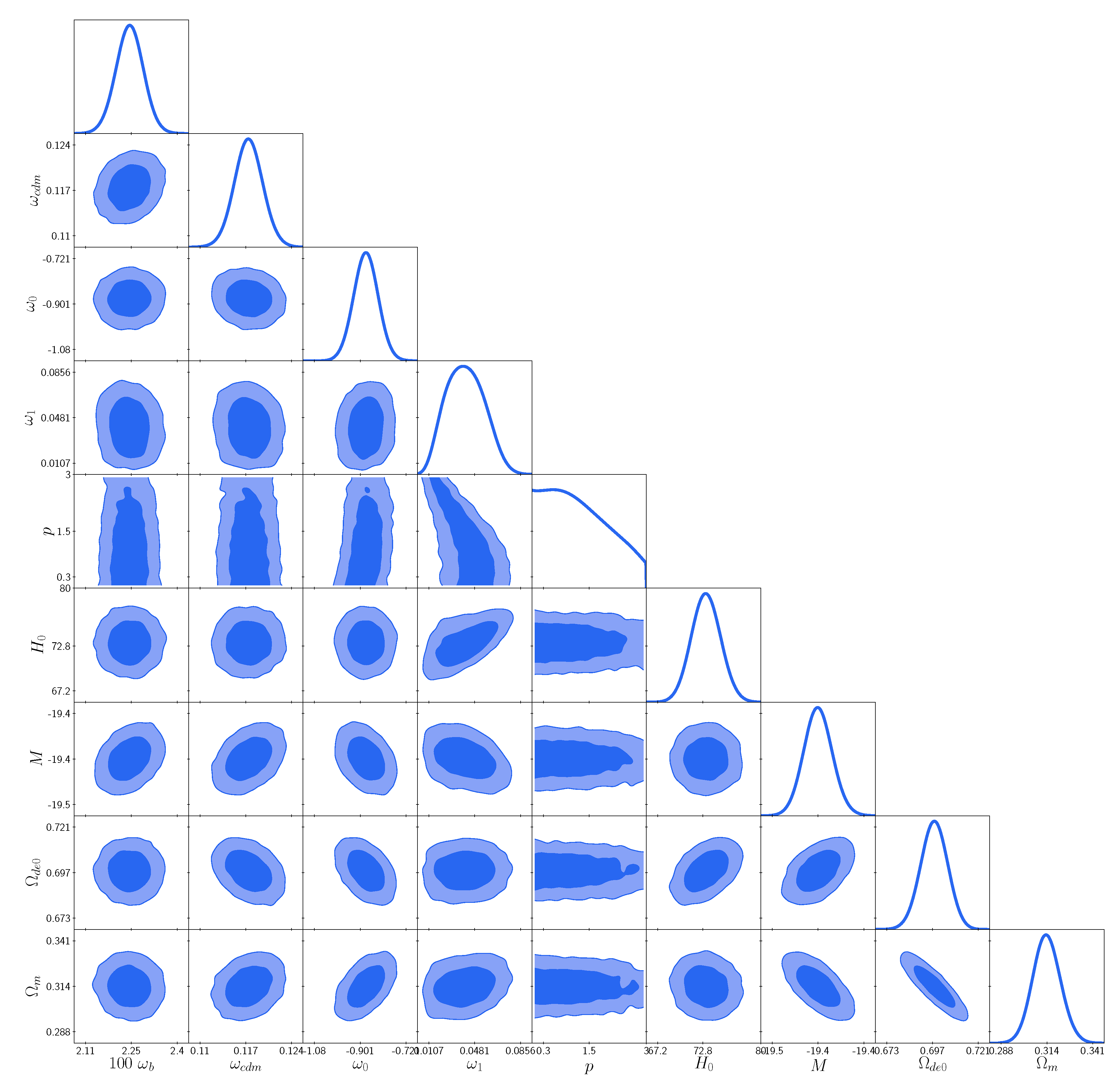
Using the cosmological data sets, we run MCMC until the Gelman- Rubin convergence criterion $R-1<0.05$ is reached and we have plotted the posterior distribution for the model I and model II in the Figure 1 and Figure 2, respectively. The corresponding best-fit and mean values are enlisted in Table 1. One can see here that for both models, the best-fit value of ${\omega }_0$ is almost same ${\omega }_0\approx -0.86$, $i.e.,$ the present value of the equation of state converges almost at same point. One can also observed that ${\omega }_1$ is close to zero for both the models. It means the variation of equation of state for the dark energy with respect to the redshift parameter z is small as shown in the sub-Figure-(a) of Figure 3. We also note that the parameter p can not be constrained for Model I. However, for Model II, it can be constrained and there is also a lower bound on p. In order to understand which model is more preferable, we discuss Akaike, Bayesian Information Criterion (BIC) and Bayesian Evidence in the next section.

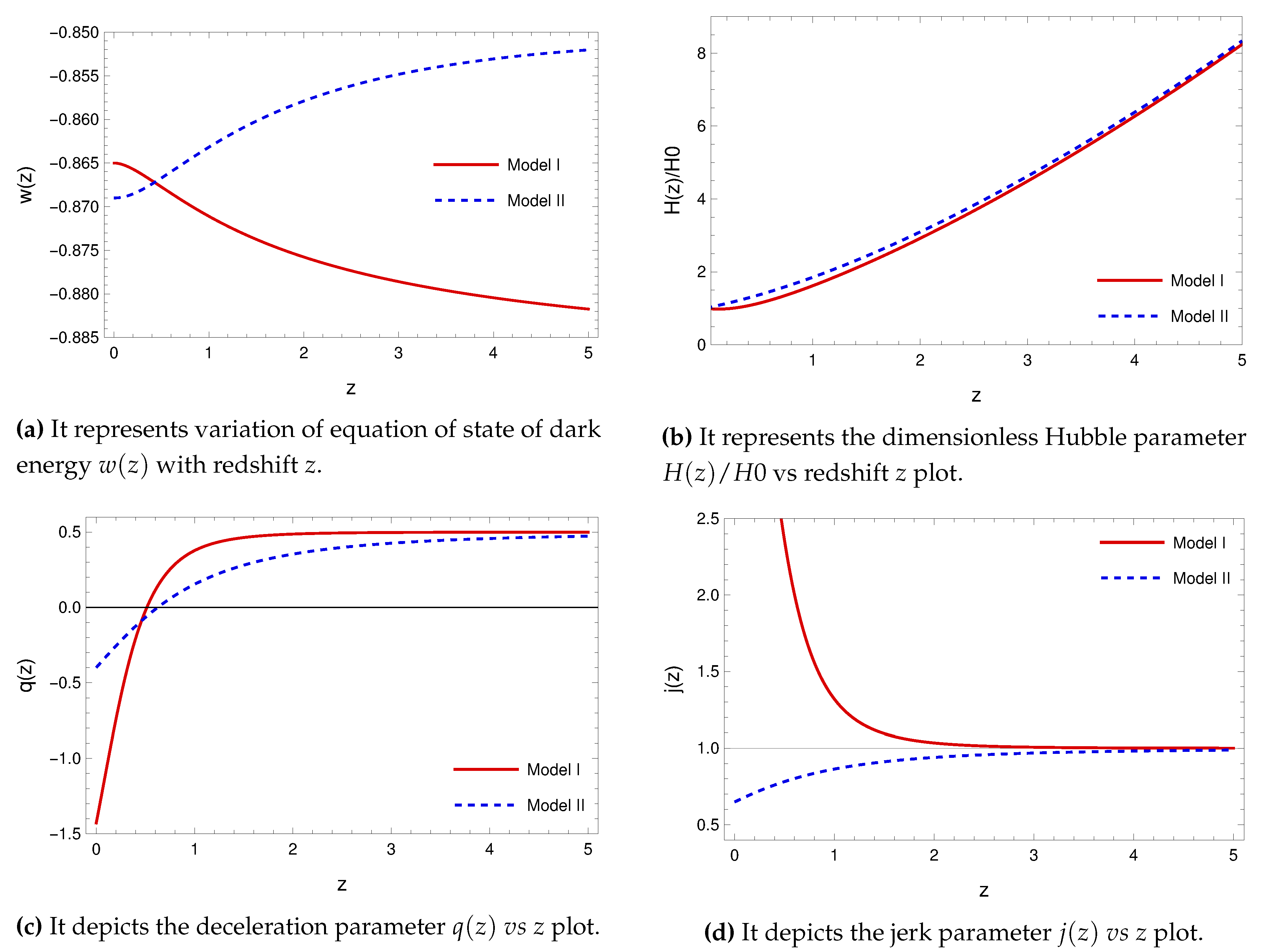
One can understand the cosmological models from the different variables like Hubble parameter $H\left(z\right)$, deceleration parameter $q\left(z\right)$, jerk parameter $j\left(z\right)$ which are all derived from the derivatives of the scale factor. Using the best fit value of the cosmological parameters of the different models inferred from the cosmological datasets, we have plotted the Hubble parameter $H\left(z\right)$ with respect the redshift z in sub-Figure (b) of Figure 3. One can see here that $H\left(z\right)$ is monotonically increasing with z and it is almost same for both the models. We also plotted the deceleration parameter $q\left(z\right)$ in the sub-Figure (c) of Figure 3, which is defined as [52]

$$q\left(z\right)=-\frac{\ddot{a}a}{{\dot{a}}^2}=-\left(1+\frac{\dot{H}}{H^2}\right)$$

(8)

Here it is observed that the Model I has gone through from deceleration to acceleration phase at $z\approx 0.514$ whereas Model II at $z\approx 0.625$. However, the present value of deceleration parameter $q\left(z\right)$ is quite distinct, namely $q(z=0)=-1.42$ for Model I that implies (from Eq. 8) that $\dot{H}{|}_{z=0}>0$ which does not support observation but $q(z=0)=-0.398$ for Model II which supports the observation. We have also plotted the jerk parameter $j\left(z\right)$ in the sub-Figure (d) of Figure 3, which is defined as [53,54]

$$\begin{array}{ccc}\hfill j\left(a\right)& =& \frac{\stackrel{⃛}{a}}{a{H}^3}\hfill \\ \hfill & =& q(2q+1)+(1+z)\frac{dq}{dz}\hfill \end{array}$$

(9)

Here, one can see that at higher z it converges to $j\left(z\right)=1$ for both models.

4. Information Criteria and Model Comparison

In order to make a comparison between the models, here we apply the well known Akaike Information Criterion (AIC) [55] and the Bayesian Information Criterion (BIC) [56]. This allows us to analyze which model best fits the observational data. Based on the information theory, AIC is an estimator of the Kullback-Leibler information with the property of asymptotically unbiasedness. Under the standard Gaussian error assumptions, the expression of AIC reads as [57,58,59]

$$AIC=-2ln\left({\mathcal{L}}_{max}\right)+2k+\frac{2k(k-1)}{N_{tot}-k-1},$$

(10)

where ${\mathcal{L}}_{max}$ is the maximum likelihood of the datasets, $N_{tot}$ is the total data points and k is the number of parameters of the model. For large number of data points $N_{tot}$, it reduces to $AIC\approx -2ln\left({\mathcal{L}}_{max}\right)+2k$. The AIC gives goodness of fit through the maximum likelihood. However, the additional term of the AIC acts as a penalty for models which have a large number of parameters. Whereas, the BIC is defined as [60,61]

$$BIC=-2ln\left({\mathcal{L}}_{max}\right)+kln\left(N_{tot}\right).$$

(11)

It is clearly seen that the penalty for BIC is higher than that of AIC. In general, the model having lower values of AIC and BIC corresponds to the model that best fits the data.

4.1. The Bayesian Evidence

For the given dataset D, the posterior probability distribution $p(\theta ,\mathcal{M}|D)$ of a model $\mathcal{M}$ is related by the Likelihood function $\mathcal{L}\left(D\right|\theta ,\mathcal{M})$ and prior $\pi (\theta ,M)$ is related by Bayes’ theorem

$$p(\theta ,\mathcal{M}|D)=\frac{\mathcal{L}\left(D\right|\theta ,\mathcal{M}\left)\pi \right(\theta ,M)}{E\left(D\right|\mathcal{M})}$$

(12)

where $\theta$ is the parameter of the model $\mathcal{M}$ and the normalization constant E is called the Bayesian evidence which is given by

$$E\left(D\right|\mathcal{M})={\int }_{\Omega }d\theta \mathcal{L}\left(D\right|\theta ,\mathcal{M})\pi (\theta ,M)$$

(13)

where $\Omega$ is the parameter space under the model $\mathcal{M}$. The ratio of the Bayesian evidences for the two competing models is given by

$${\mathcal{B}}_{ij}=\frac{E\left(D\right|{\mathcal{M}}_i)}{E\left(D\right|{\mathcal{M}}_j)}$$

(14)

which is known as the Bayes factor. In order to determine the preference for one model over another, we used Jeffrey’s scale. According to it the decisive condition is summarized in the Table 3 [62].

We have computed Bayesian evidence using the publicly available code MCEvidence [63] and the results are enlisted in the Table 2. From the table, it is seen that in the context of AIC and BIC, both models are very close to each other and from the Bayesian Evidence, the value $\left|ln\right({\mathcal{B}}_{ij}\left)\right|<1$. Therefore, on the basis of these statistical analysis we can not make any comment on which model is more preferable.

5. Conclusion

A detailed study has been done for the two modified CPL models where the dark energy is considered as a perfect fluid and the equation of state is chosen as the generalized form of CPL model(Model I) and logarithmic form (Model II). The parameters involved in these two models are estimated from the observation data data sets (Pantheon+ [44], BAO [7,8,45,46,47,48,49] and HST [50]) with prior from PLANCK18 data set [51].

From the observational analysis using the data set I, it is found that the parameter p can not be constrained for the model I. However, for model II it can be constrained and there is a lower bound on it. For both the models, the parameter ${\omega }_0$ converges at ${\omega }_0\approx -0.86$ and ${\omega }_1$ is close to zero for both models which indicates that the equation of state ${\omega }_{fld}$ varies very slowly. We also notice that the Hubble parameter $H_0$ is very close to each other.

We have also plotted the deceleration parameter $q\left(z\right)$ which goes from deceleration to acceleartion phase near $z=0.514$ for the model I and near $z=0.625$ for model II. We have also plotted jerk parameter $j\left(z\right)$ where one can see that at higher z it converges to $j\left(z\right)=1$ for both models. Finally, we have compared the models analyzing AIC, BIC and Bayesian Evidence. Here we have seen that the value of AIC and BIC are almost same and $\left|ln\right({\mathcal{B}}_{12}\left)\right|<1$. Therefore, it is very hard to find the best model between them. Though both the CPL modified paramatrization models are identical from the observed dataset considered in the paper but all the parameters in model II can be constrained but it is not possible for model I. Moreover, the present value of deceleration parameter ${q\left(z\right)|}_{z=0}<-1$ for Model I which does not support observation. Therefore, we may conclude that Model II is better compared to the Model I.