Submitted:
15 August 2023
Posted:
16 August 2023
Read the latest preprint version here
Abstract
Keywords:
1. Background and Introduction
2. Materials and Method
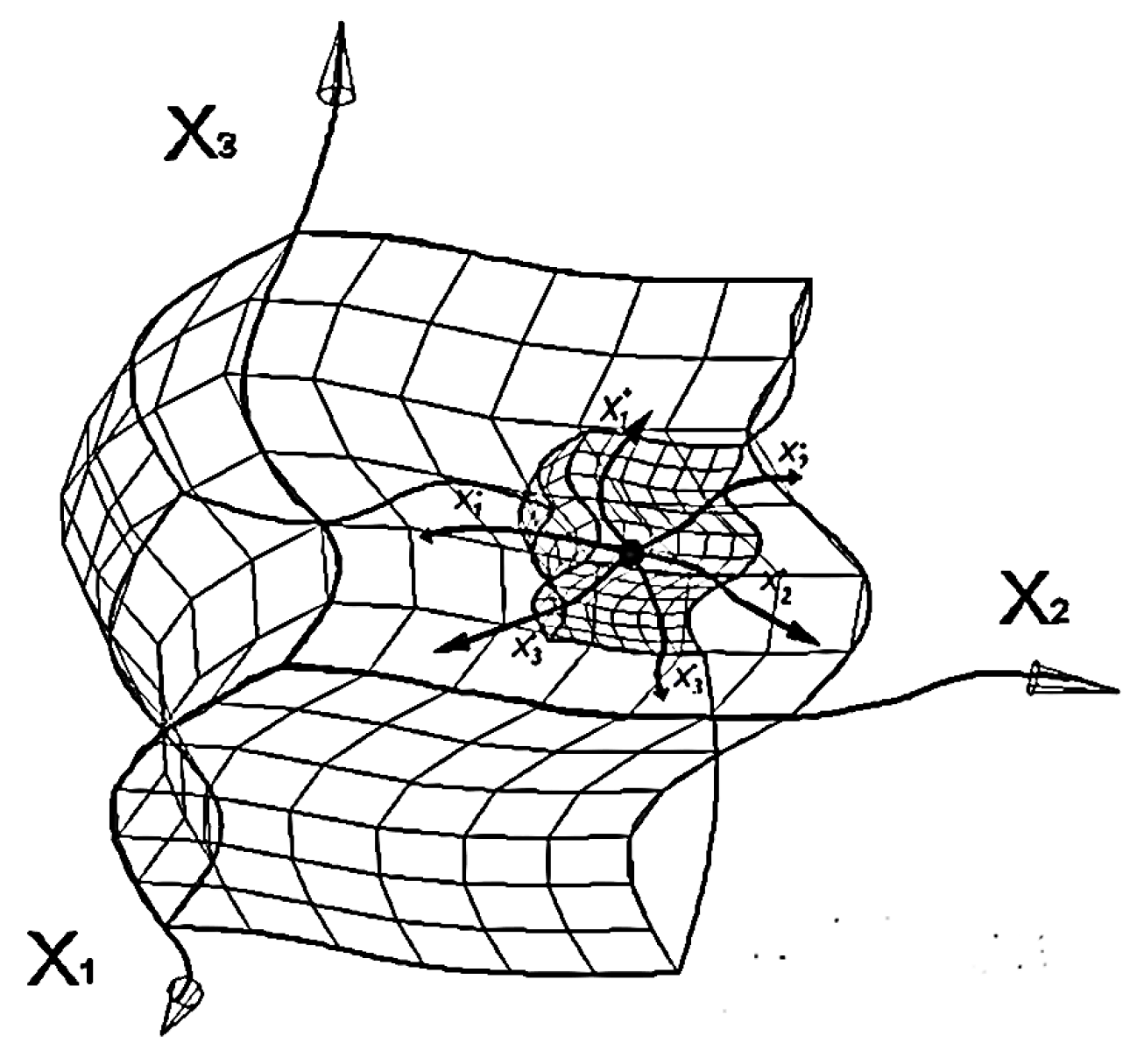
2.1. Curved area of λm,n-vacuum
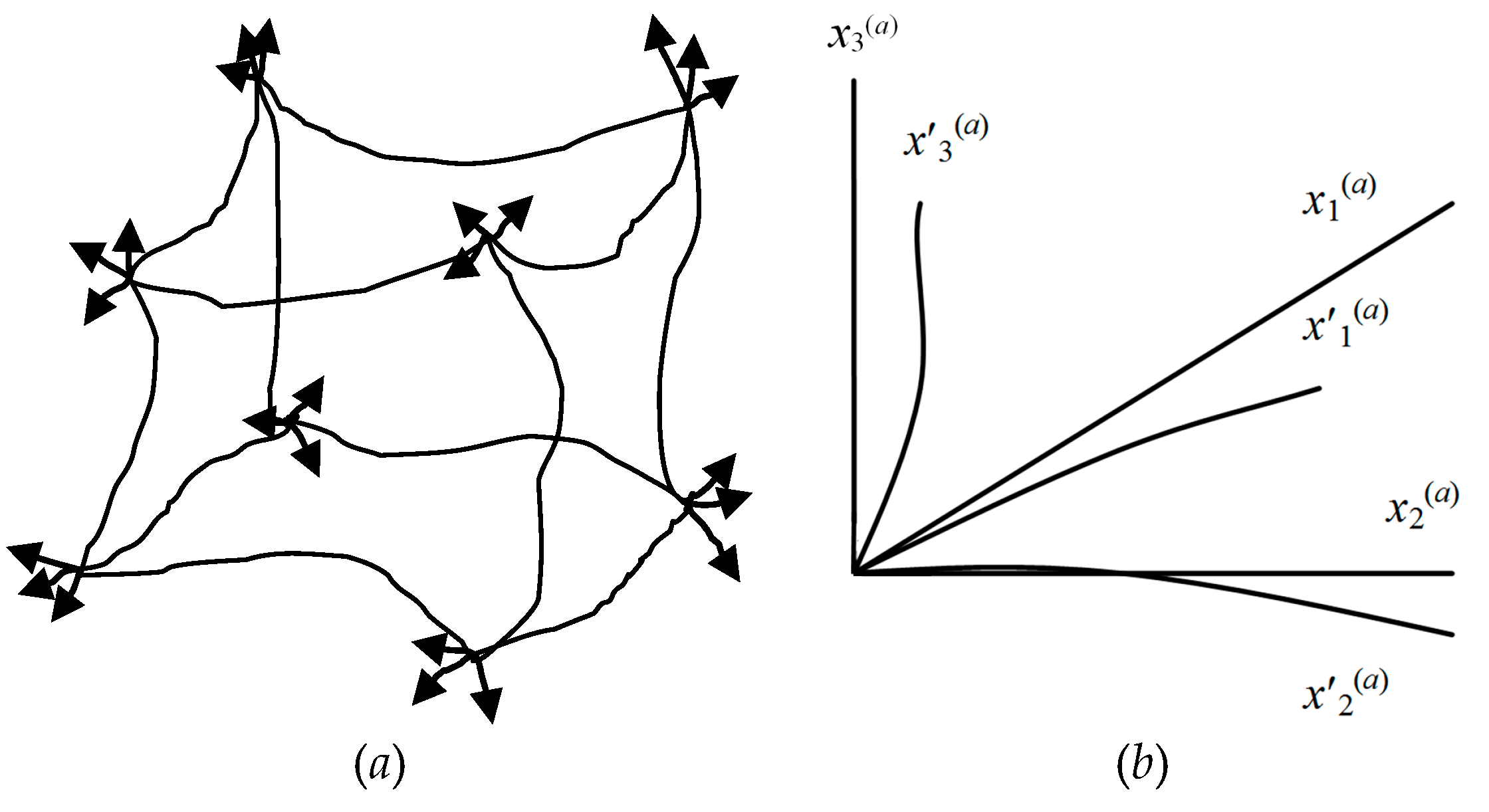
x′1(а) = α10(а)x0(а) + α11(а)x1(а) + α12(а)x2(а) + α13(а)x3(а);
x′2(а) = α20(а)x0(а) + α21(а)x1(а) + α22(а)x2(а) + α23(а)x3(а);
x′3 (а) = α30(а)x0(а) + α31(а)x1(а) + α32(а)x2(а) + α33(а)x3(а),
e′1(a) = β10(a) e0(a) + β11(a) e1(a) + β12(a) e2(a) + β13(a) e3(a);
e′2(a) = β20(a) e0(a) + β21(a) e1(a) + β22(a) e2(a) + β23(a) e3(a);
e′3(a) = β30(a) e0(a) + β31(a) e1(a) + β32(a) e2(a) + β03(a) e3(a),
2.2. Curved metric 4-spaces
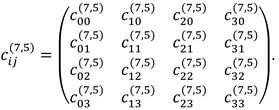
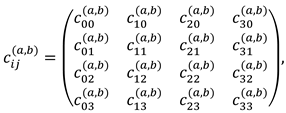
2.3. The first stage of compactification of curved measurements

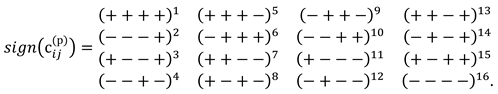
<ds(– – + –)2> <ds(+ + – –)2> <ds(– + – –)2> <ds(+ – + –)2>
<ds(– + + +)2> <ds(– – – – )2> <ds(+ + + –)2> <ds (– + + –)2>
<ds(+ + – +)2> <ds(– – + +)2> <ds(+ – + +)2> <ds(– + – +)2>,
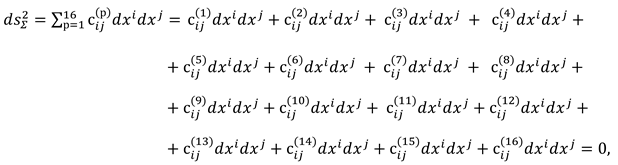
Recall that the “vacuum balance condition” was formulated in the introduction of the article [1], and this is the basic statement that, in particular, no matter what convex-concave curvatures (fluctuations) occur with the local area of the λm,n-vacuum, on average over the entire area they are equal to zero.
2.4. The second stage of compactification of curved mathematical measurements
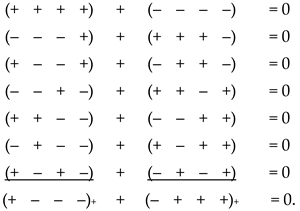
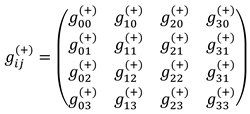
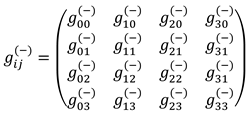
Recall that the two-sided model of λm,n-vacuum, that is, the result of averaging complex metric-dynamic fluctuations of λm,n-vacuum to a two-sided level of consideration, is called in §2.7 in [2] “23- λm,n-vacuum”, because in this case, only 4 + 4 = 8 = 23 mathematical measurements remain within the framework of consideration.
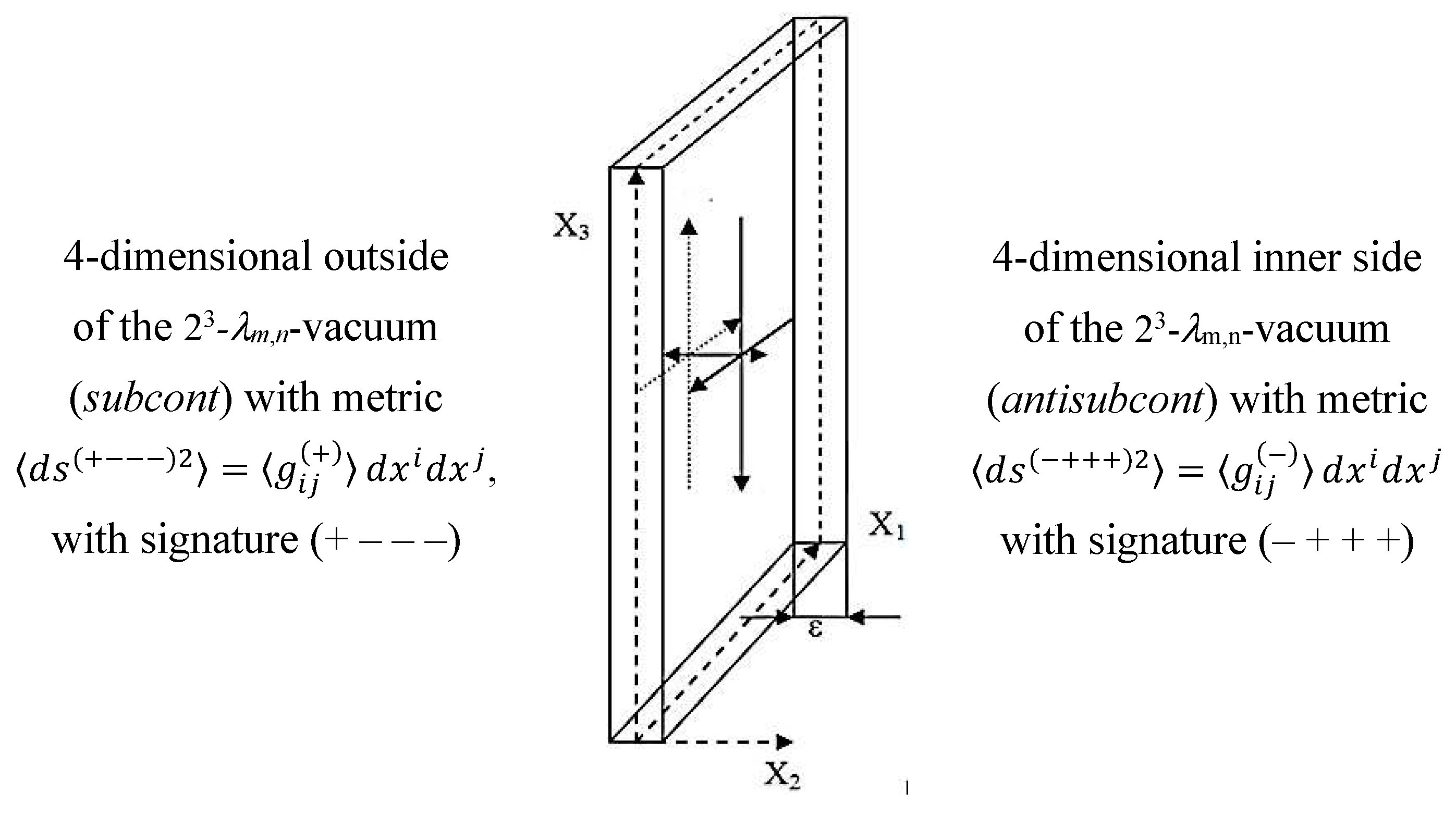
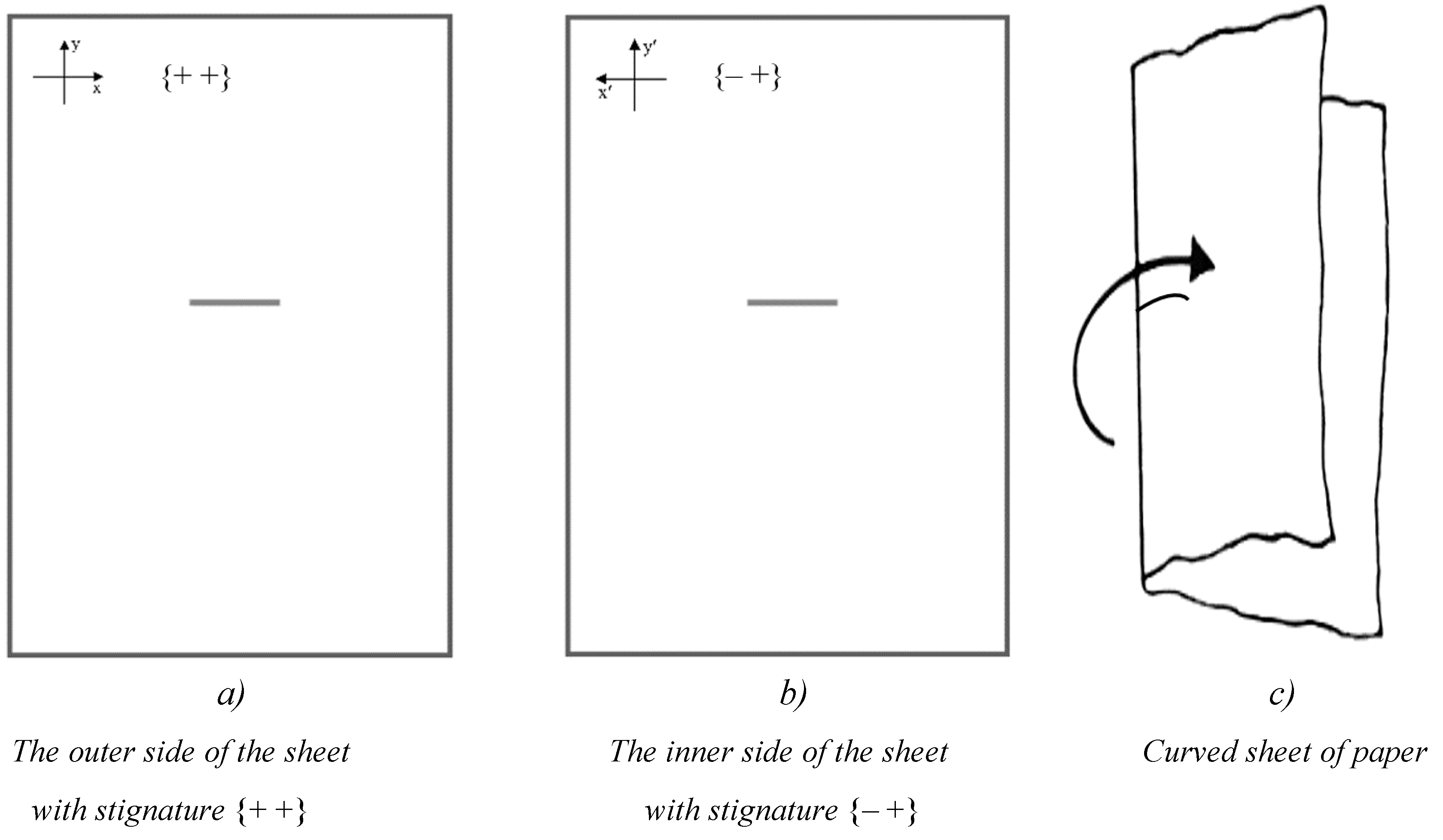
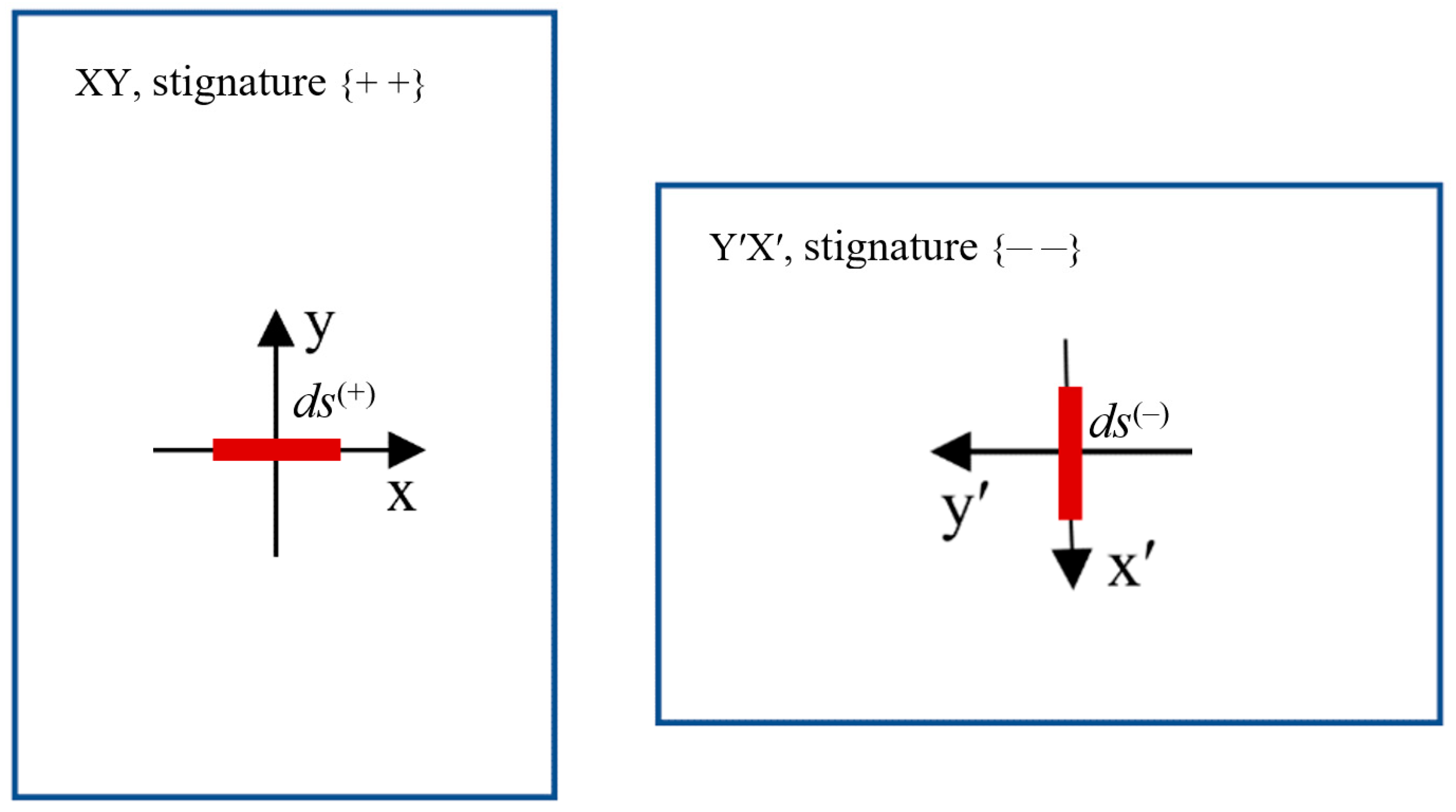
Reference systems ХУ or Х′У′ on two opposite sides of a sheet of paper have different stignatures, respectively {+ +} and {+ –}. To understand this, take a sheet of paper and draw on it the XY reference system (as in Figure 8a). Then turn the sheet over, and on its reverse side depict the Х′У′ reference system in the same way in the same place. If you compare these reference systems, you will find that the X and X′ axes are directed in different directions, so their stignatures are different.
2.5. Four-strain tensor of 23-λm,n-vacuum in the case of a simplified two-sided consideration
2.5.1. Four-strain tensors of two sides of 23-λm,n-vacuum

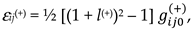
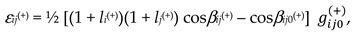
- βij0(+) is the angle between the axes xi and xj of the reference system, “frozen” into the initial uncurved state of the subcont section under study;
- βij(+) is the angle between the axes xi′and xj′ of the distorted reference system “frozen” into the distorted state of the same section of the subcont.
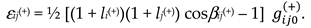
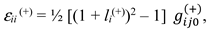
2.5.2. The 4-strain tensor of 23-λm,n-vacuum in the case of two-sided consideration
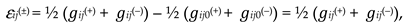
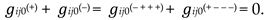
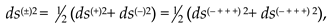
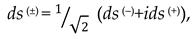
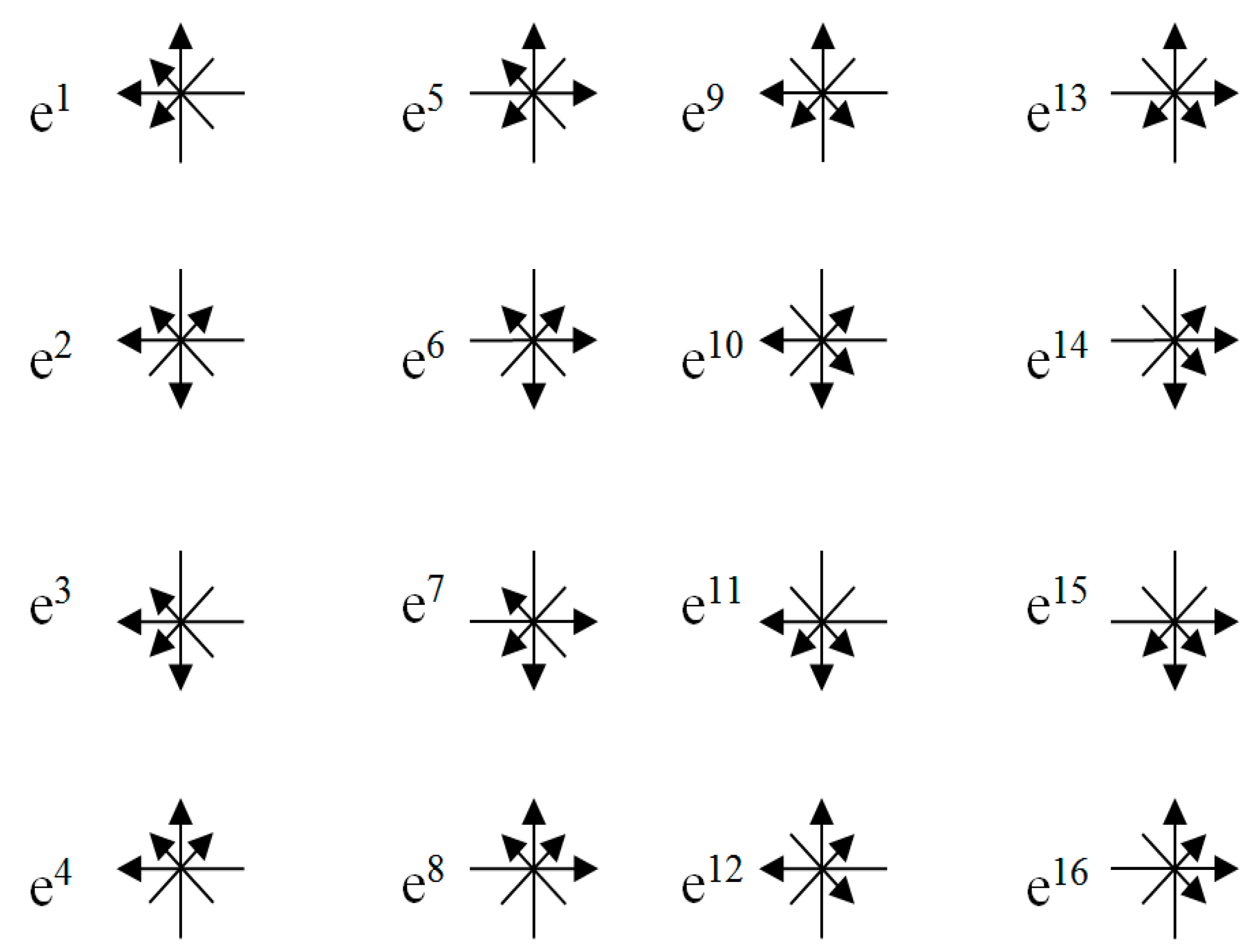
Below, a k-braid is the result of averaging metrics with different signatures (where k is the number of averaged metrics, i.e., the number of “threads” in the “braid”). For example, the averaged metric (61) is called a 2-braid, since it is “twisted” from 2 lines : ds(+) = ds (+ – – –) and ds(–) = ds(– + + +).

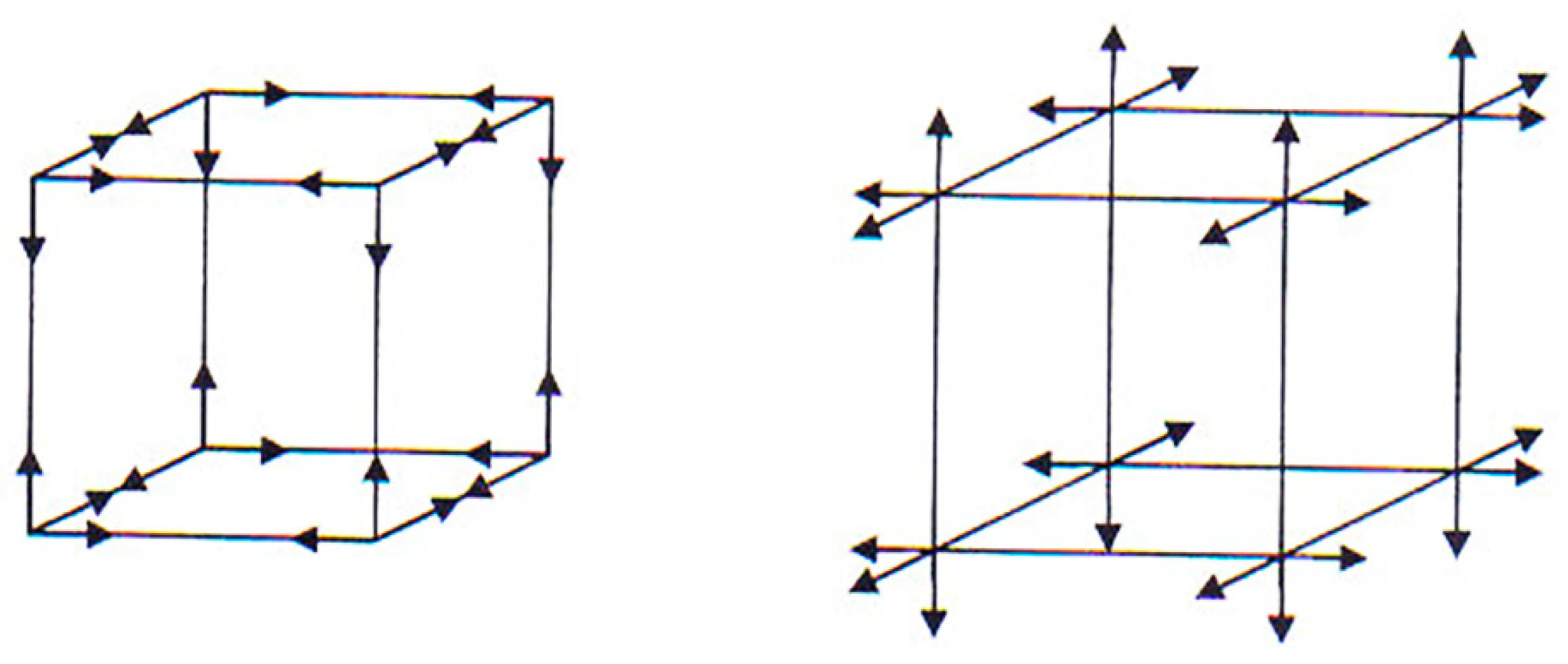
2.5.3. The 4-strain tensor of a curved 26-λm,n-vacuum in the case of sixteen-sided consideration
+ ds(– – + –)2 + ds(+ + – –)2 + ds(– + – –)2 + ds(+ – + –)2 +
+ ds(– + + +)2 + ds(– – – – )2 + ds(+ + + –)2 + ds(– + + –)2 +
+ ds(+ + – +)2 + ds(– – + +)2 + ds(+ – + +)2 + ds(– + – +)2).
- сij0(p) is the metric tensor of the non-curved region of the p-th 4-space with the corresponding signature;
- сij(p) is the metric tensor of the same but curved region of the p-th 4-space with the same signature.
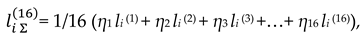
+ η5 ds(– – + –) + η6 ds(+ + – –) + η7 ds(– + – –) + η8 ds(+ – + –) +
+ η9 ds(– + + +) + η10 ds(– – – –) + η11 ds(+ + + –) + η12 ds (– + + –) +
+ η13 ds(+ + – +) + η14 ds(– – + +) + η15 ds(+ – + +) + η16 ds(– + – +).
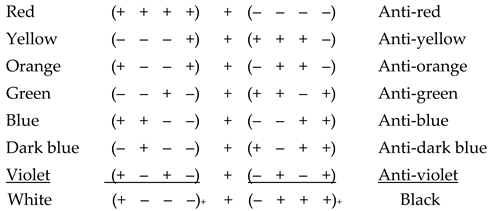

6. Physical meaning of the components of the metric tensor
6.1. Nonzero components of the metric tensor
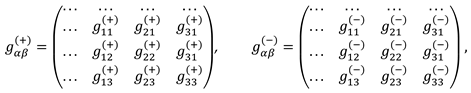
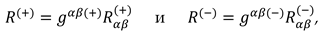
2.6.2. Zero components of the metric tensor
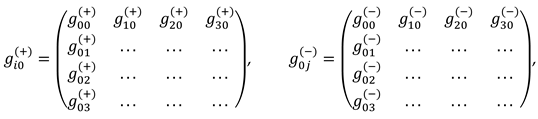
Under the kinematics of vacuum layers is meant such a section of geometrized vacuum physics based on the Algebra of Signatures (Alsigna), in which the displacements (movements) of different sides of the λm,n-vacuum are considered independently of their deformations. With a more consistent approach, i.e. during the development of the dynamics of vacuum layers in subsequent articles of this cycle, it turns out that any displacement of the local region of one layer of λm,n-vacuum is inevitably accompanied by its curvature. This, in turn, sets in motion the curvature of other adjacent layers of the λm,n-vacuum. At the same time, and vice versa, the curvature of the local region of one layer of the λm,n-vacuum is necessarily accompanied by its displacement (i.e., flow), which leads to a disturbance of all adjacent layers. In what follows, interconnected flows and curvatures of local sections of different layers of the λm,n-vacuum are considered as multidimensional 4-deformations using the mathematical apparatus of the general theory of relativity.
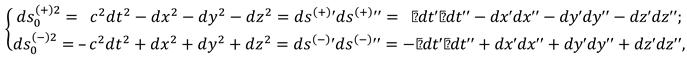
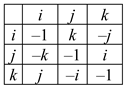
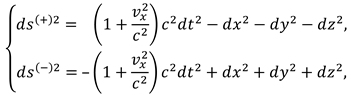
t′′ = t, x′′ = x cosΩ t – y sinΩ t, z′′ = z, y′′ = x sinΩ t + y cosΩ t.
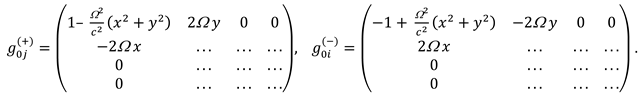
2.7. Predictions of the kinetics of vacuum layers
2.7.1. The limiting speed of movement of 23-λm,n-vacuum layers
2.7.2. Inert properties of layers of 23-λm,n-vacuum
- ax(+) is the actual acceleration section of the mask of the subcont, taking into account its inert properties;
- аx(+)' is the ideal acceleration of the same section of the mask of the subcont, without taking into account its inert properties.
2.7.3. Kinematics of the rupture of the local section of the 23-λm,n-vacuum
| “For in much wisdom is much vexation, and he |
| who increases knowledge increases sorrow.” |
| Kohelet (Ecclesiastes 1:18) |
3. Conclusions
| “Whoever fights monsters, you yourself do not become a monster. And when you gaze long |
| into an Abyss, the Abyss also gazes into you.” |
| Friedrich W. Nietzsche |
| “Jenseits Gut und böse” (Beyond Good and evil) |
Acknowledgments
References
- Batanov-Gaukhman, M. (2023) “Geometrized vacuum physics. Part I. Algebra of Stignatures”. [CrossRef]
- Batanov-Gaukhman, M. (2023) “Geometrized vacuum physics. Part II. Algebra of Signatures”. [CrossRef]
- Sedov, L.I. (1994) “Continuum mechanics. T1”, – Moscow: Nauka, [in Russian]. (Available in English “A course in continuum mechanics”, translation from the Russian, ed. by J. R. M. Radok).
- Shipov, G. (1998) “A Theory of Physical Vacuum”, – Moscow ST-Center, Russia ISBN 5 7273-0011-8. (available in English).
- Gaukhman, M.Kh. (2007) “Algebra of Signatures “Void” (yellow Alsigna), – Moscow: URSS, p. 308, ISBN 978-5-382-00580-5, (available at www.alsigna.ru).
- Gaukhman, M.Kh. (2017) “Algebra of Signatures “Massless physics” (purple Alsigna). – Moscow: Filin, ISBN 978-5-9216-0104-8 (available in English http://metraphysics.ru/).
- Landau, L.D. & Lifshits, E.M. (1988) “Field theory”. Vol. 2. – Moscow: Nauka, p. 509, ISBN 5-02-014420-7 [in Russian]. (available in English “The Classical theory of fields”, Vol. 2. fourth English edition).
- Logunov, A.A. (1987) “Lectures on the theory of relativity and gravity”, – Moscow: Nauka, p. 271 [in Russian].
- Gaukhman, M.Kh. (2007) “Algebra of Signatures “NAMES” (orange Alsigna), – Moscow: LKI, p.228, ISBN 978-5-382-00077-0 (available on site www.alsigna.ru) [in Russian].

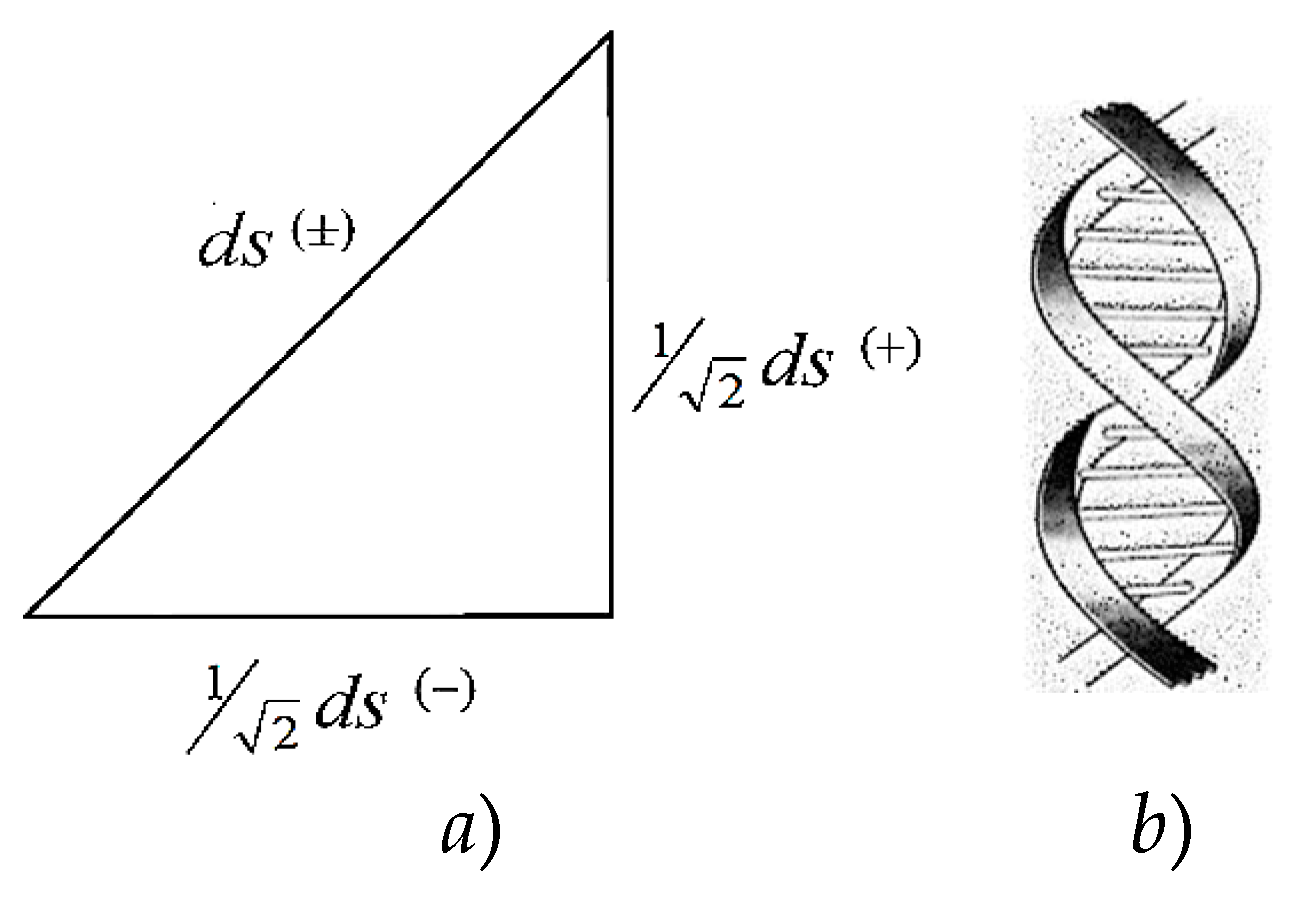

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).