Submitted:
30 July 2023
Posted:
02 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Modeling of Milling Forces
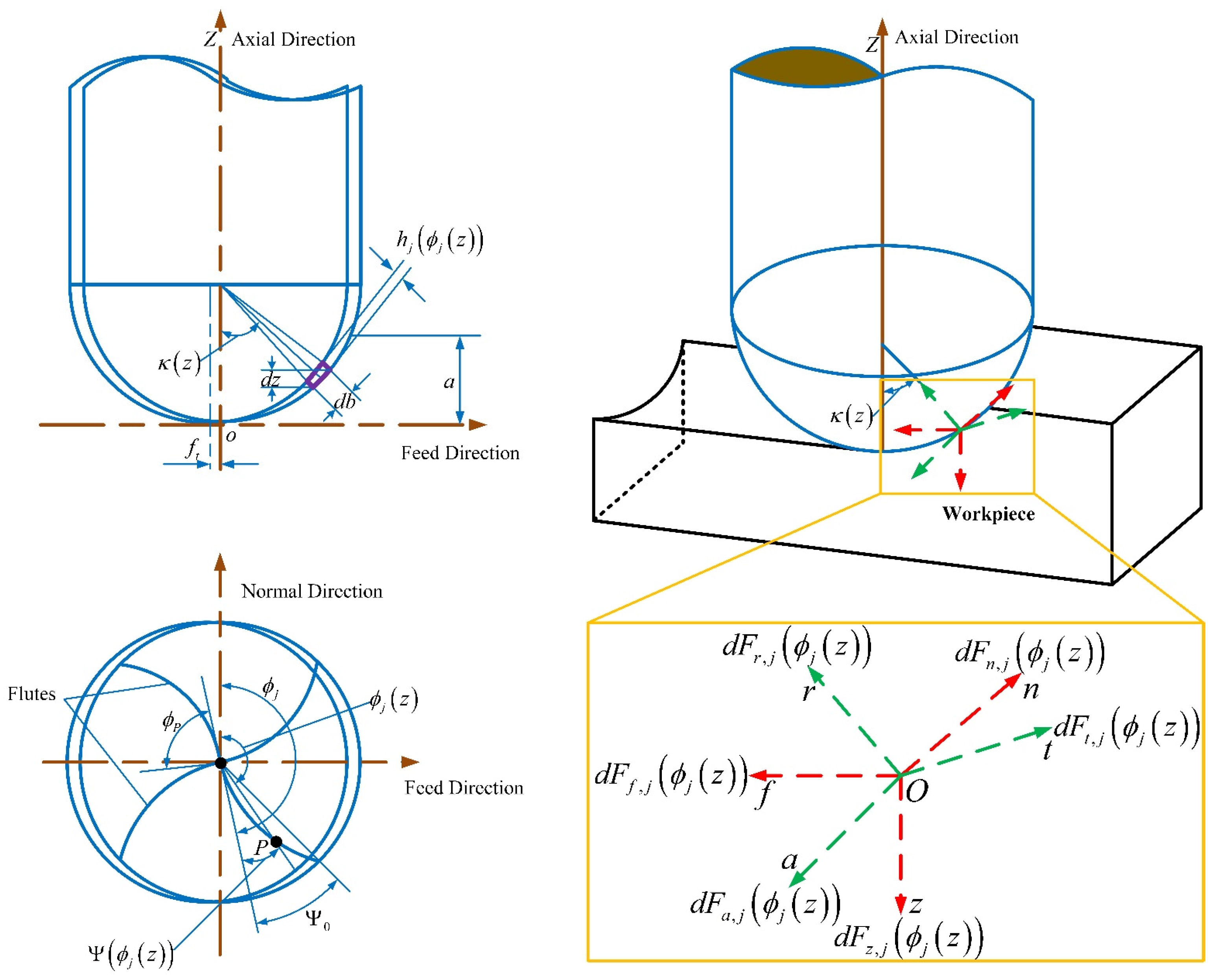
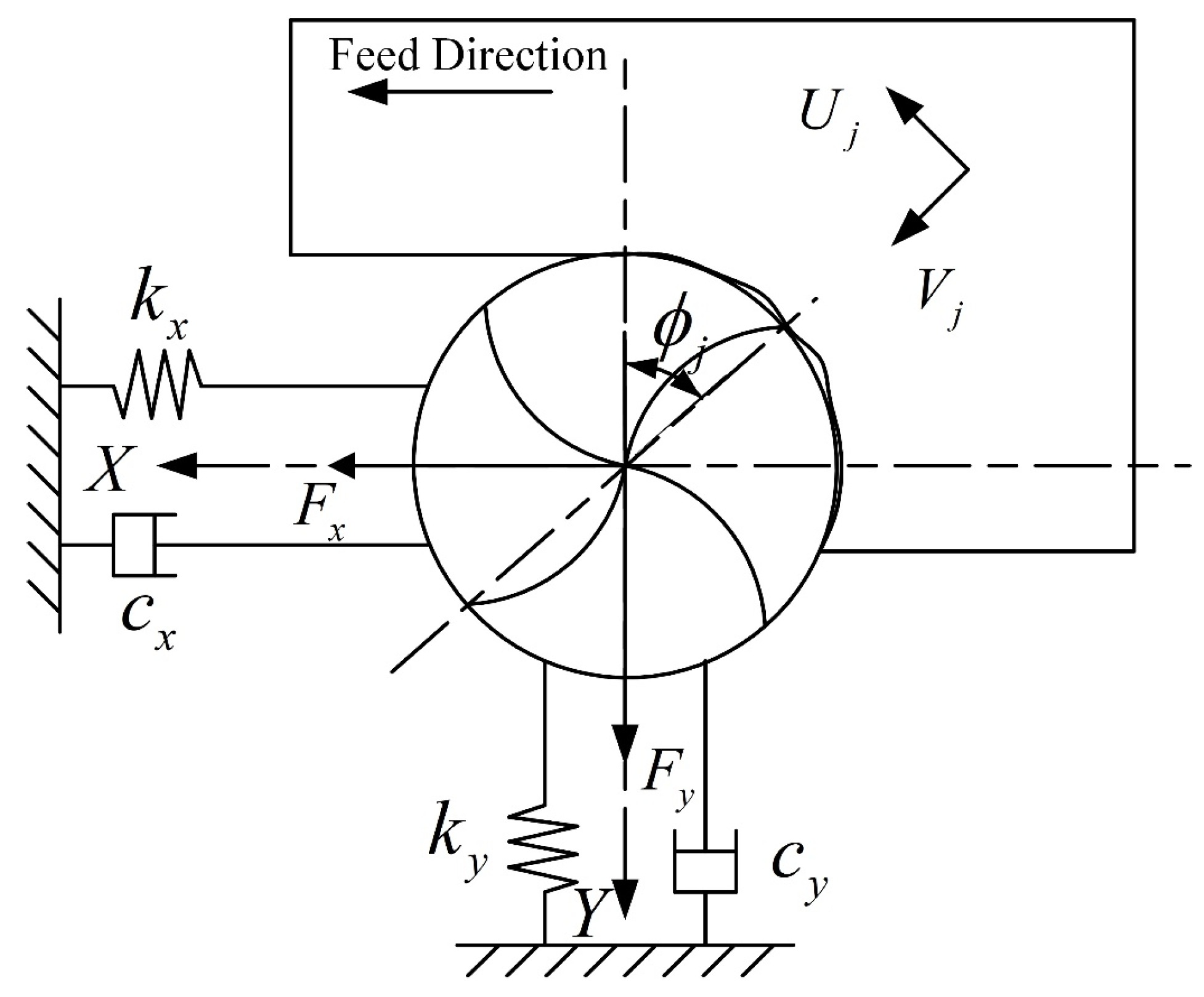
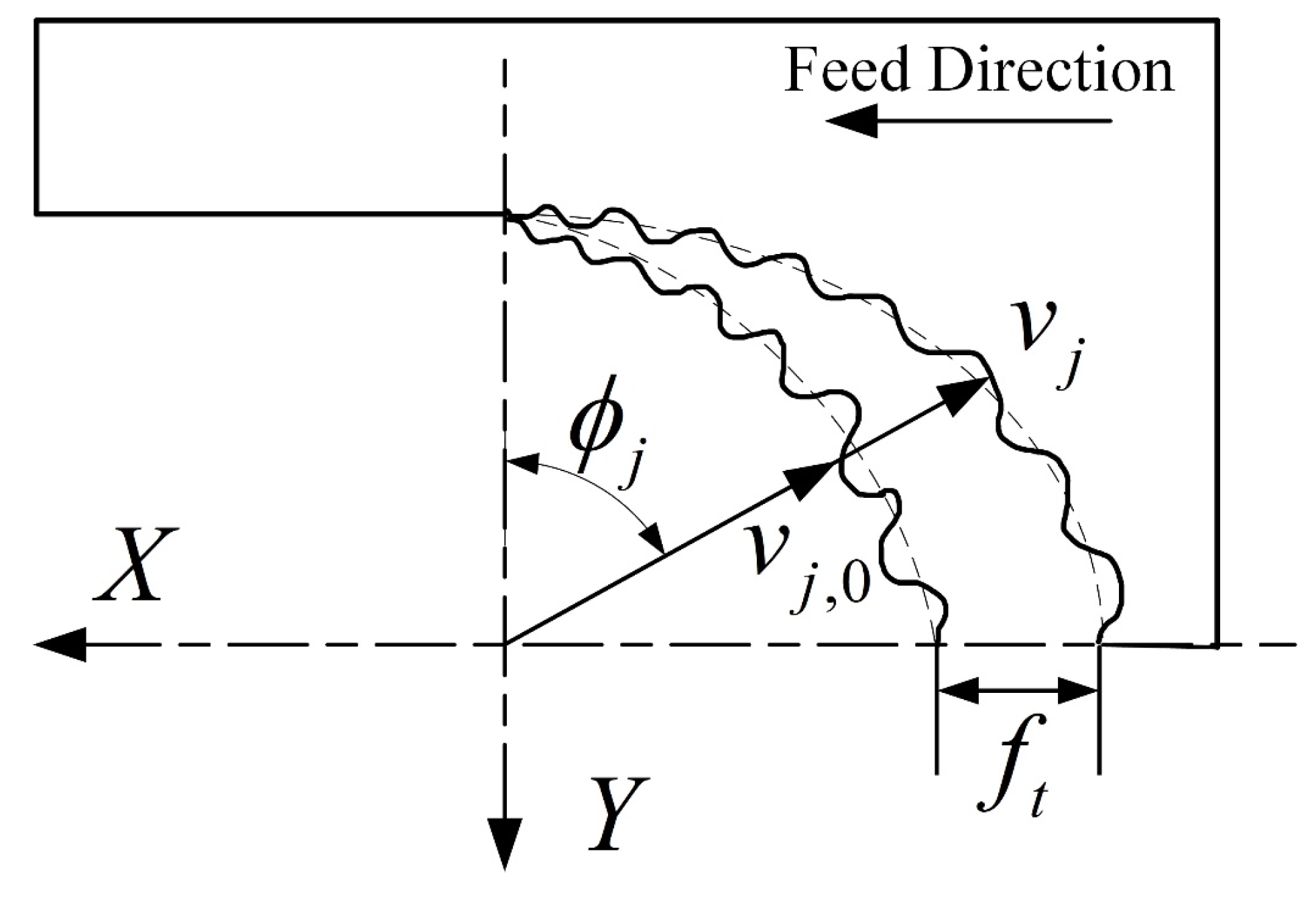
2.1 Modeling of Milling Forces of Ball-End Milling Cutter
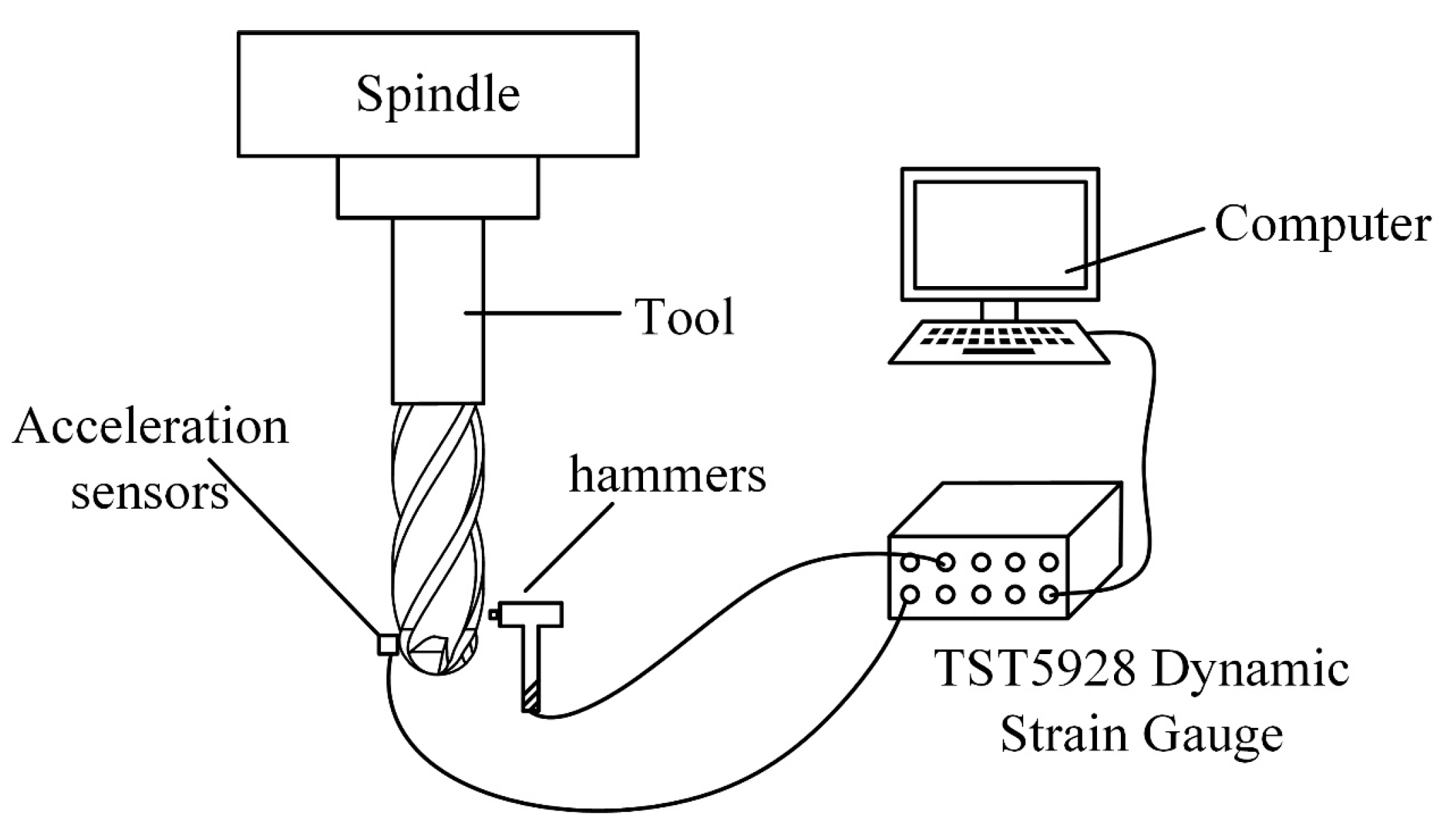
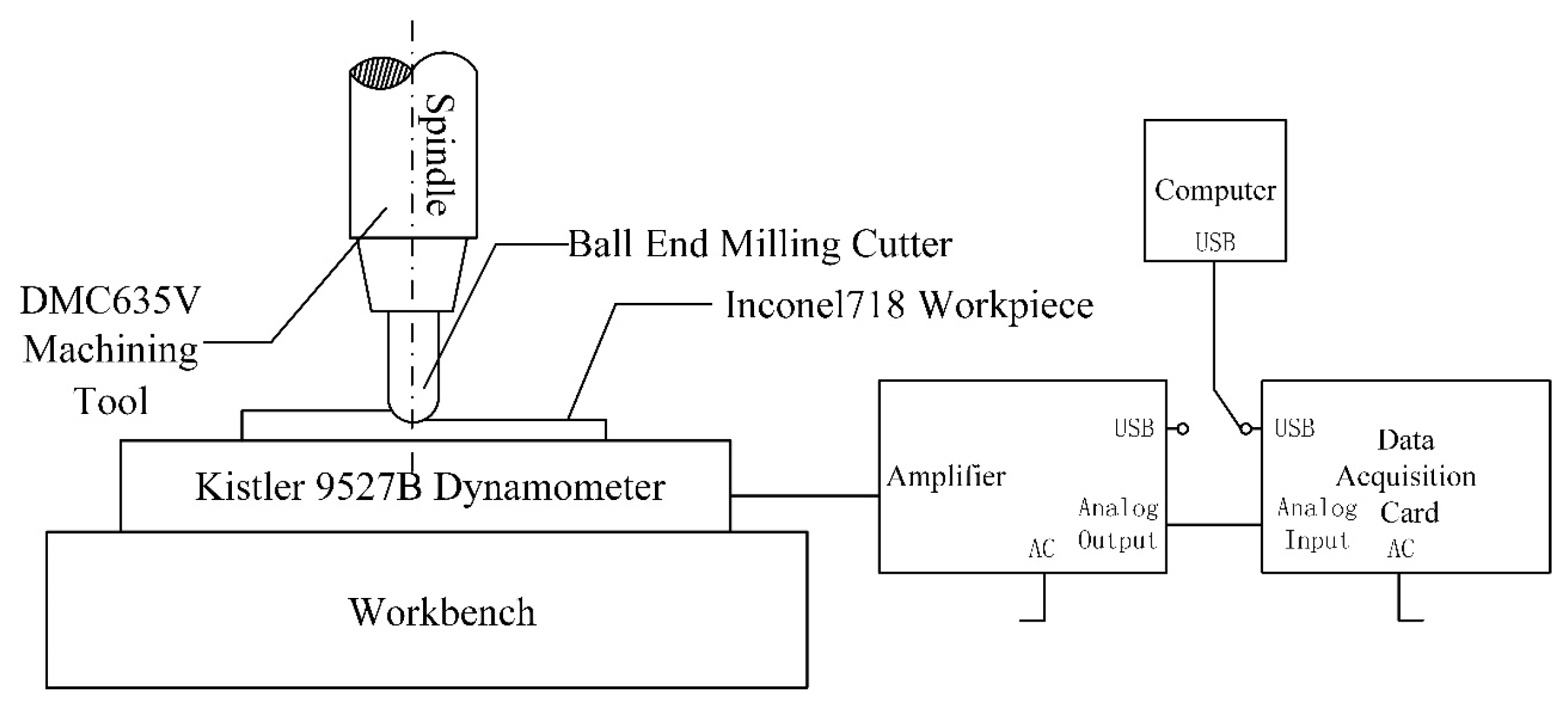
2.2 Recognition Experiment of Milling Force Coefficients
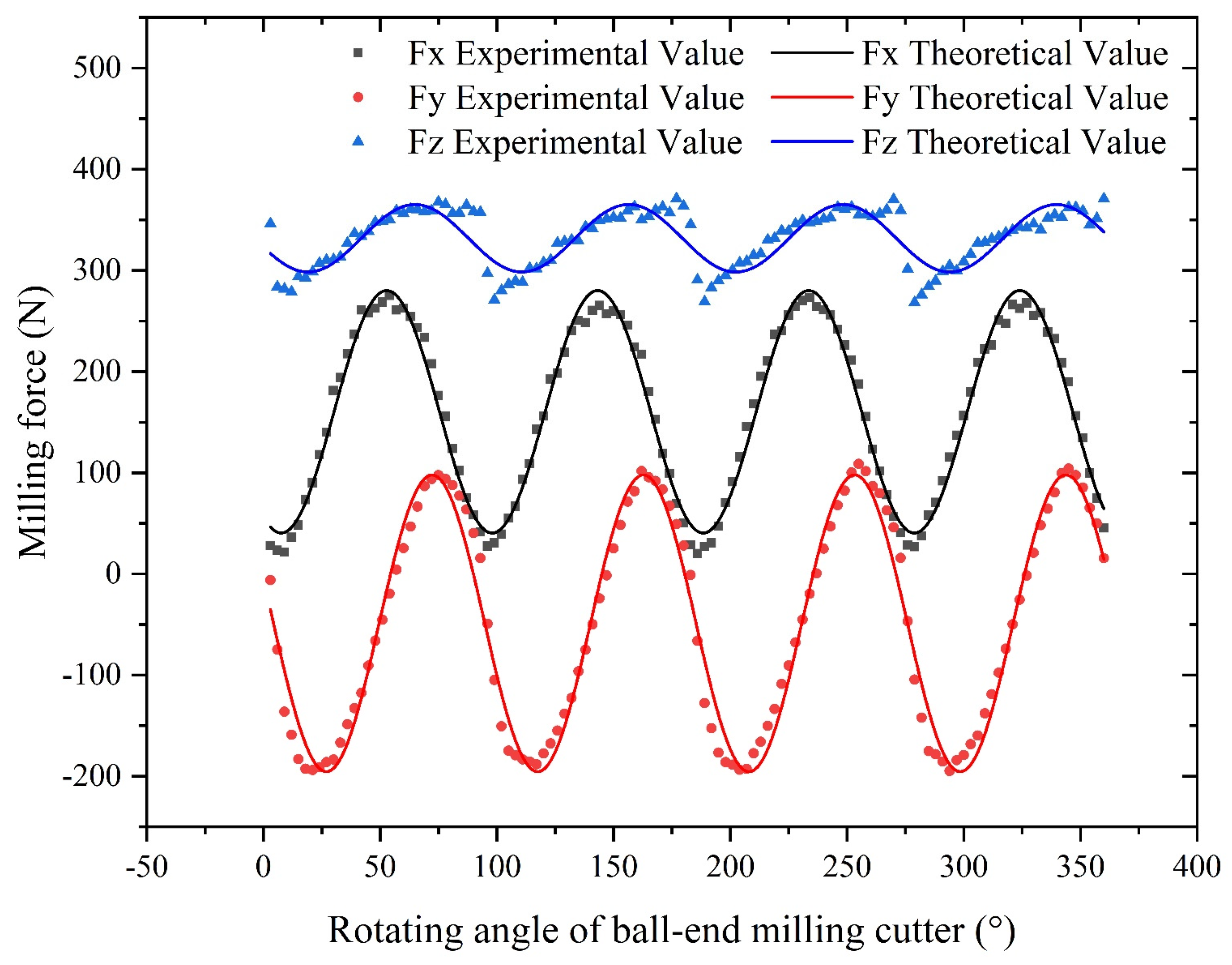
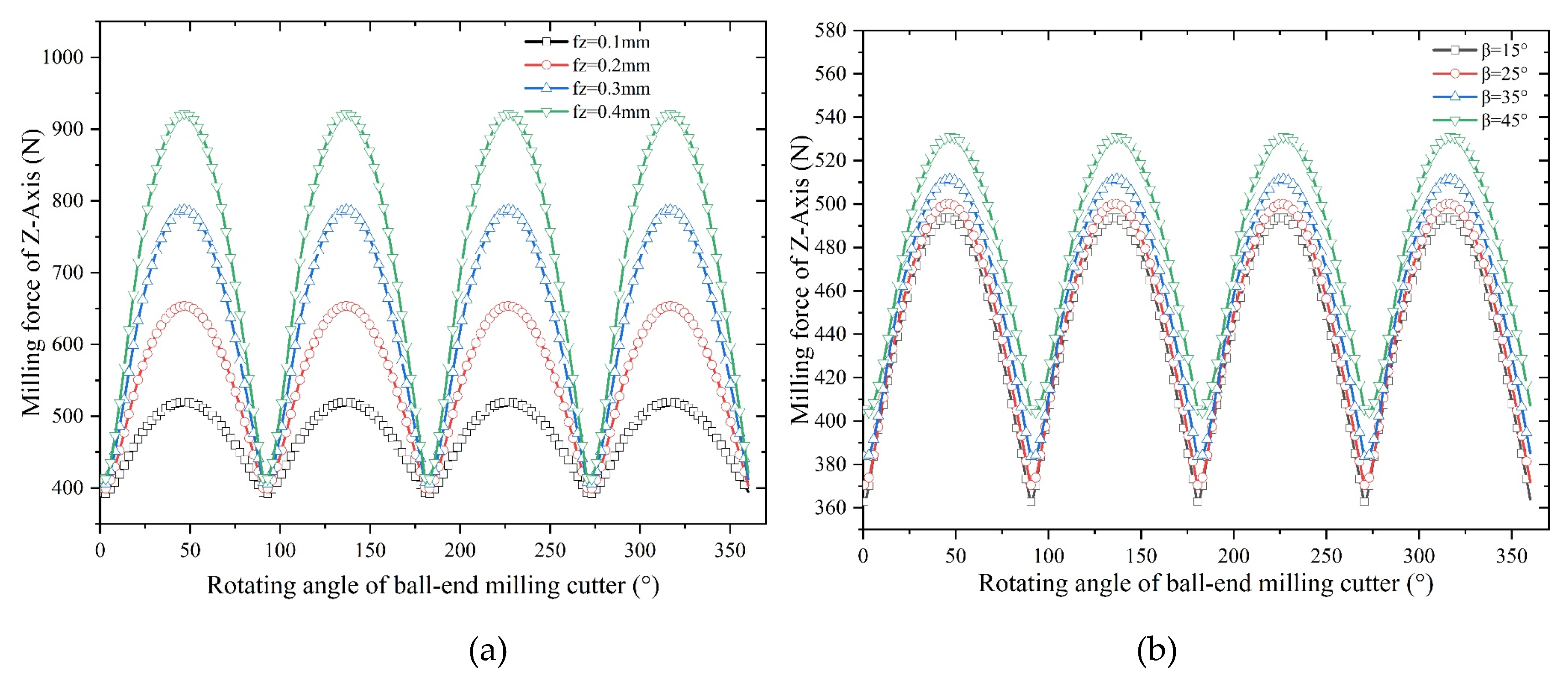
2.3 Validation of Milling Force Model for Ball-End Milling Cutter and Results Analysis
3. Finite Element Analysis of Milling of Inconel718
3.1. The Constitutive Model of Inconel718
3.2 The Result of Finite Element Analysis
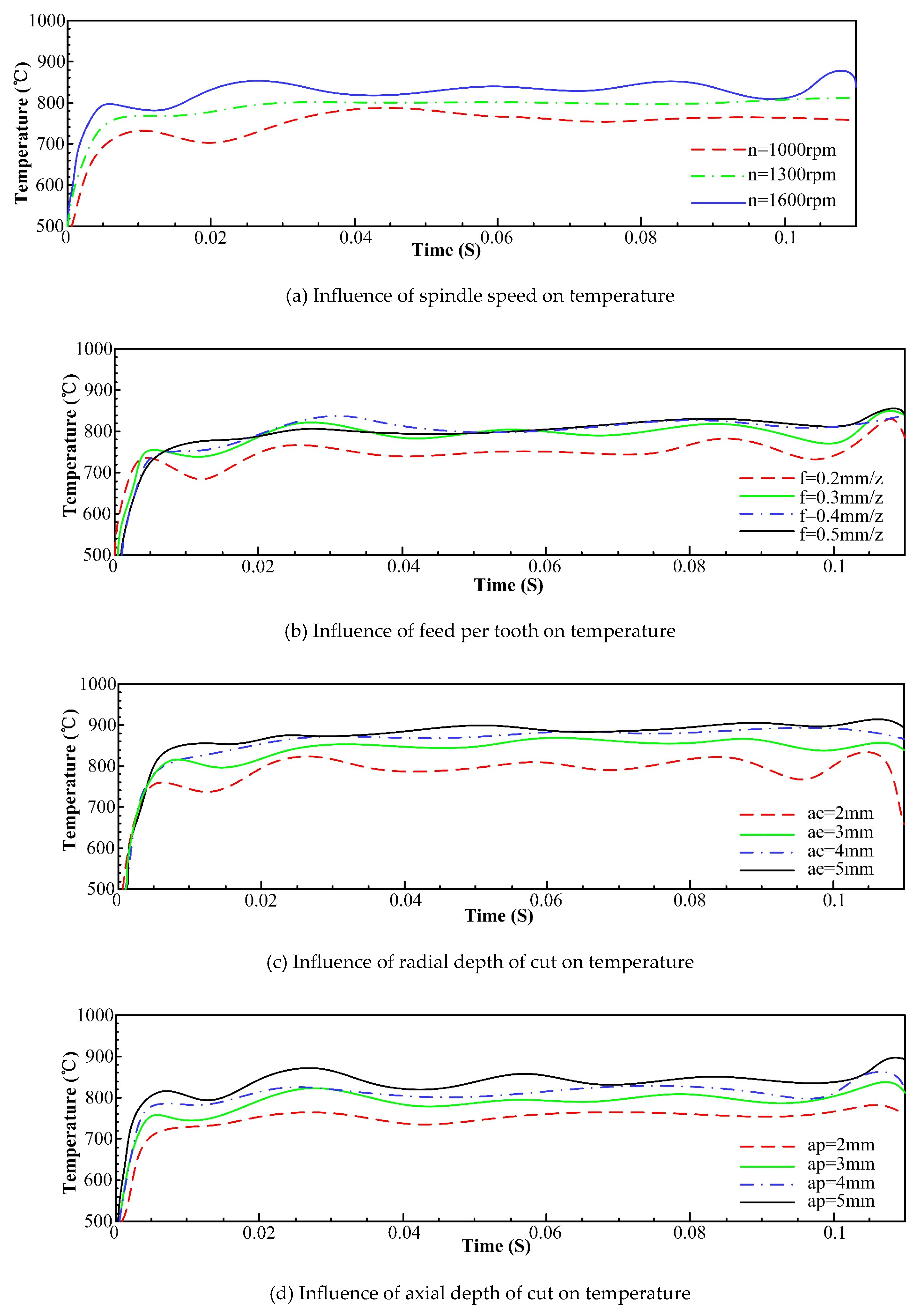
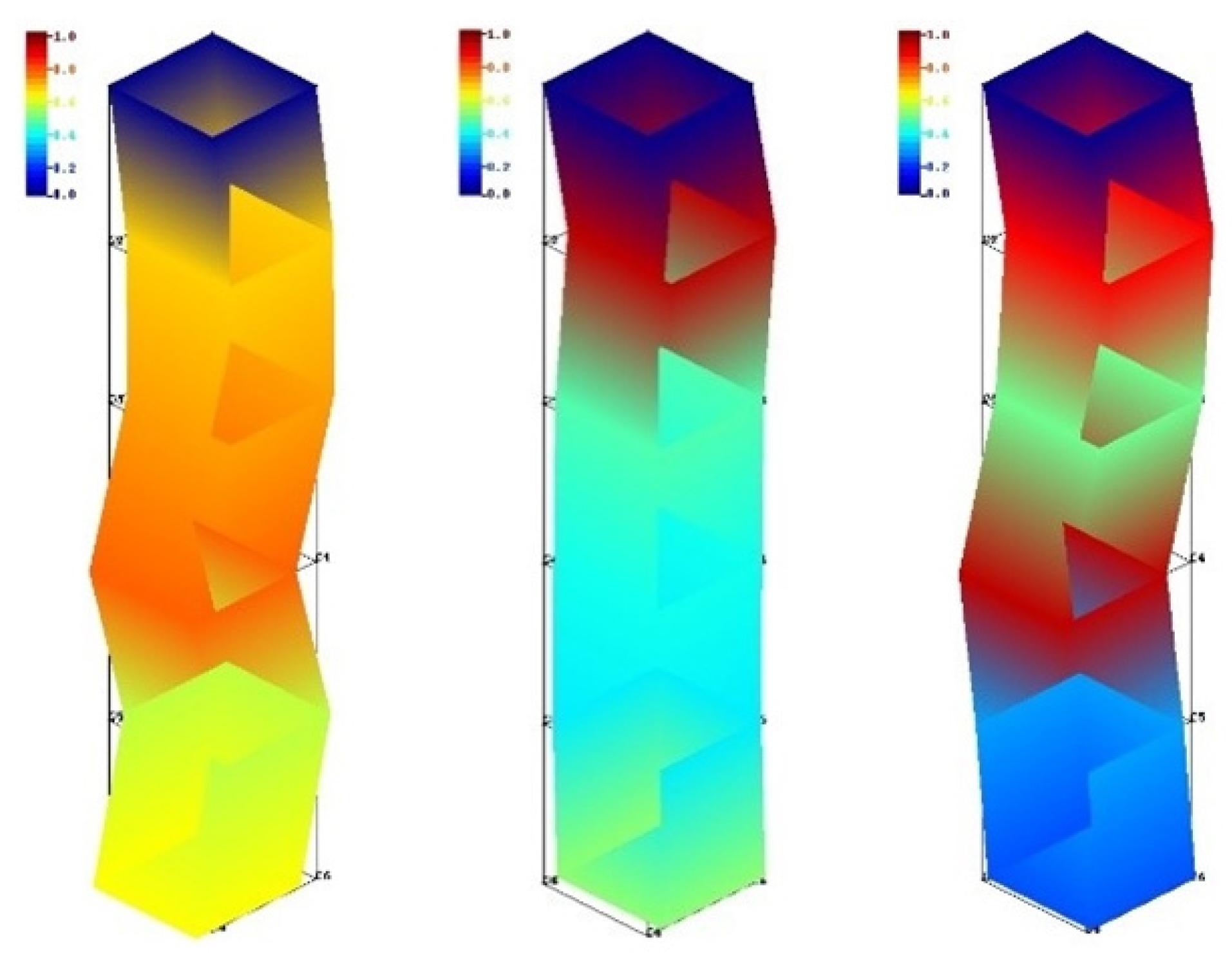
3.2.1 Temperature Field Analysis of Milling Process
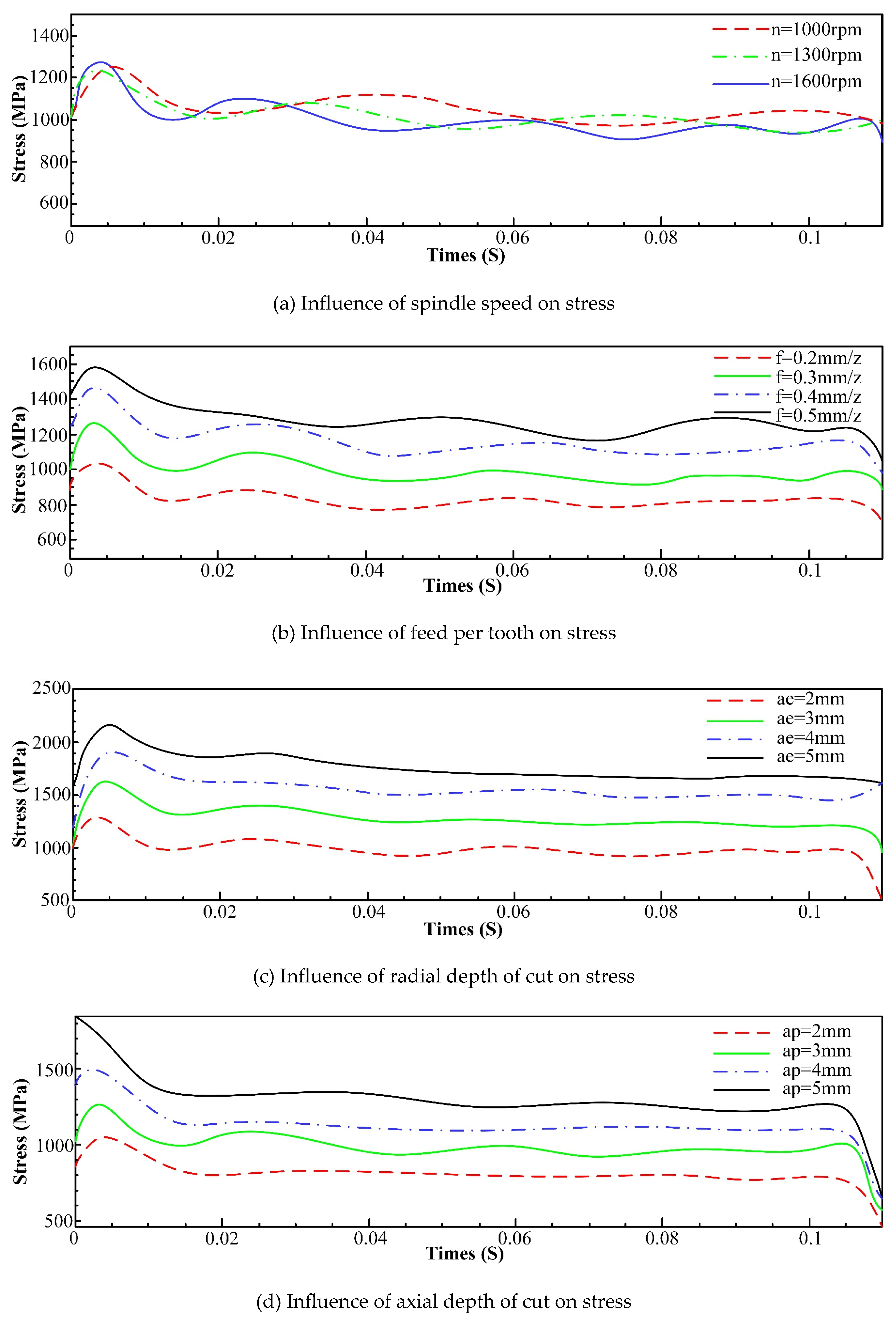
3.2.2 Stress Field Analysis of Milling Process
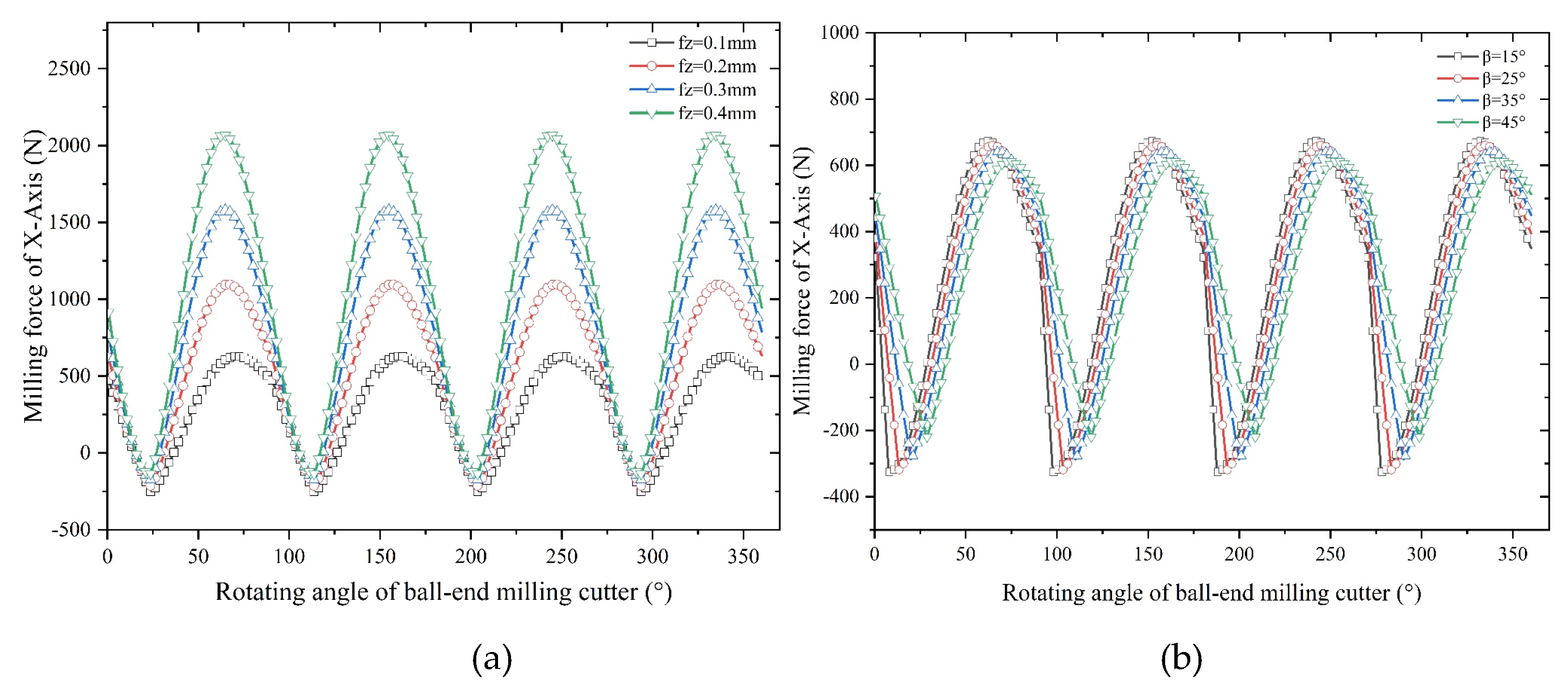
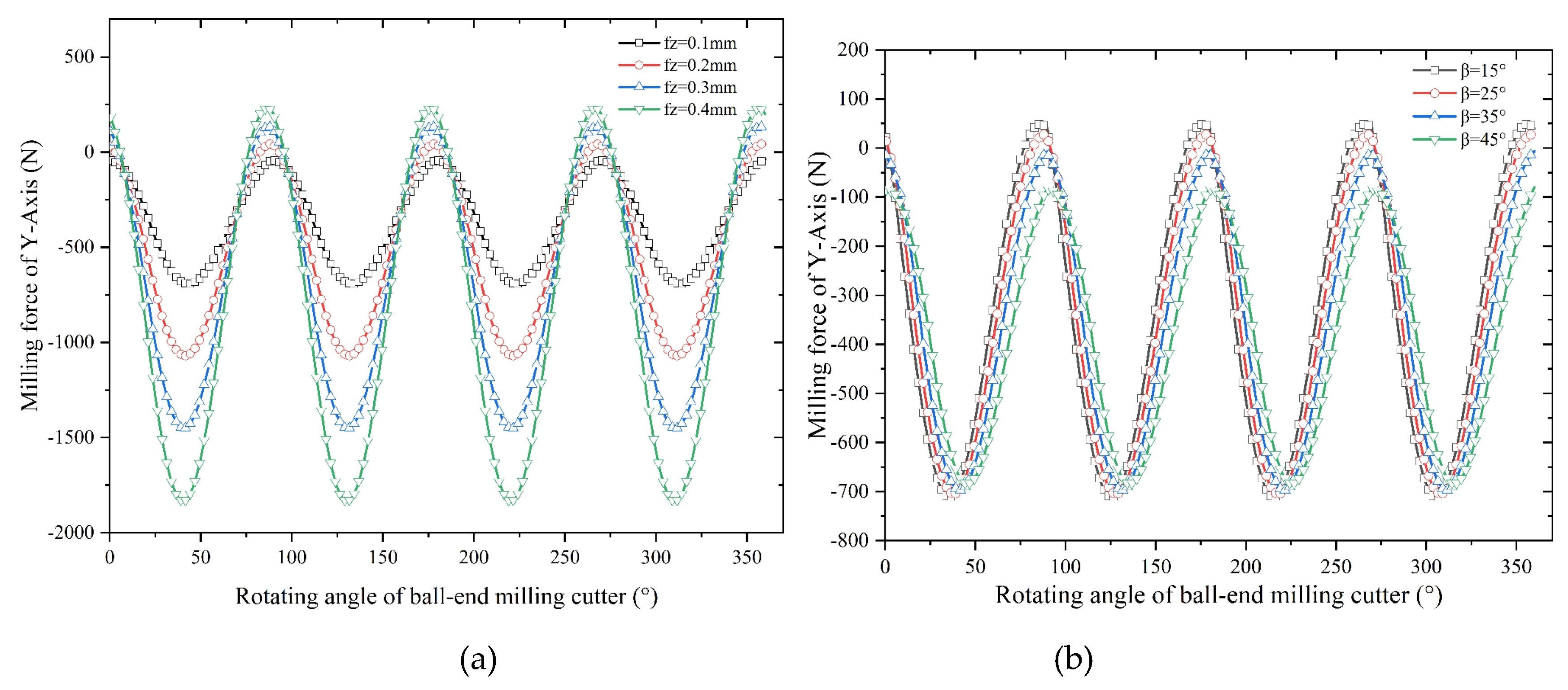
3.2.3 Force Analysis of Milling Process
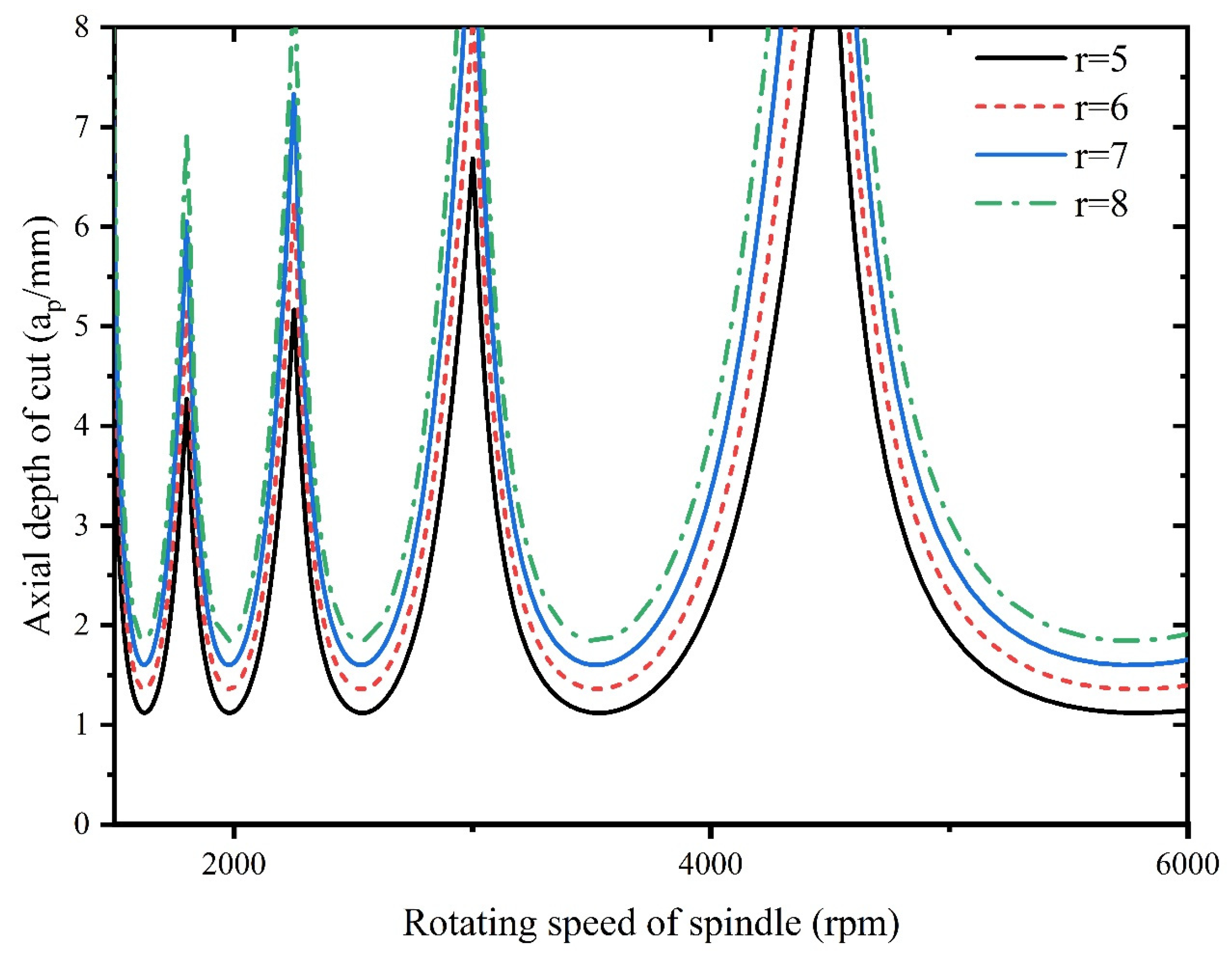
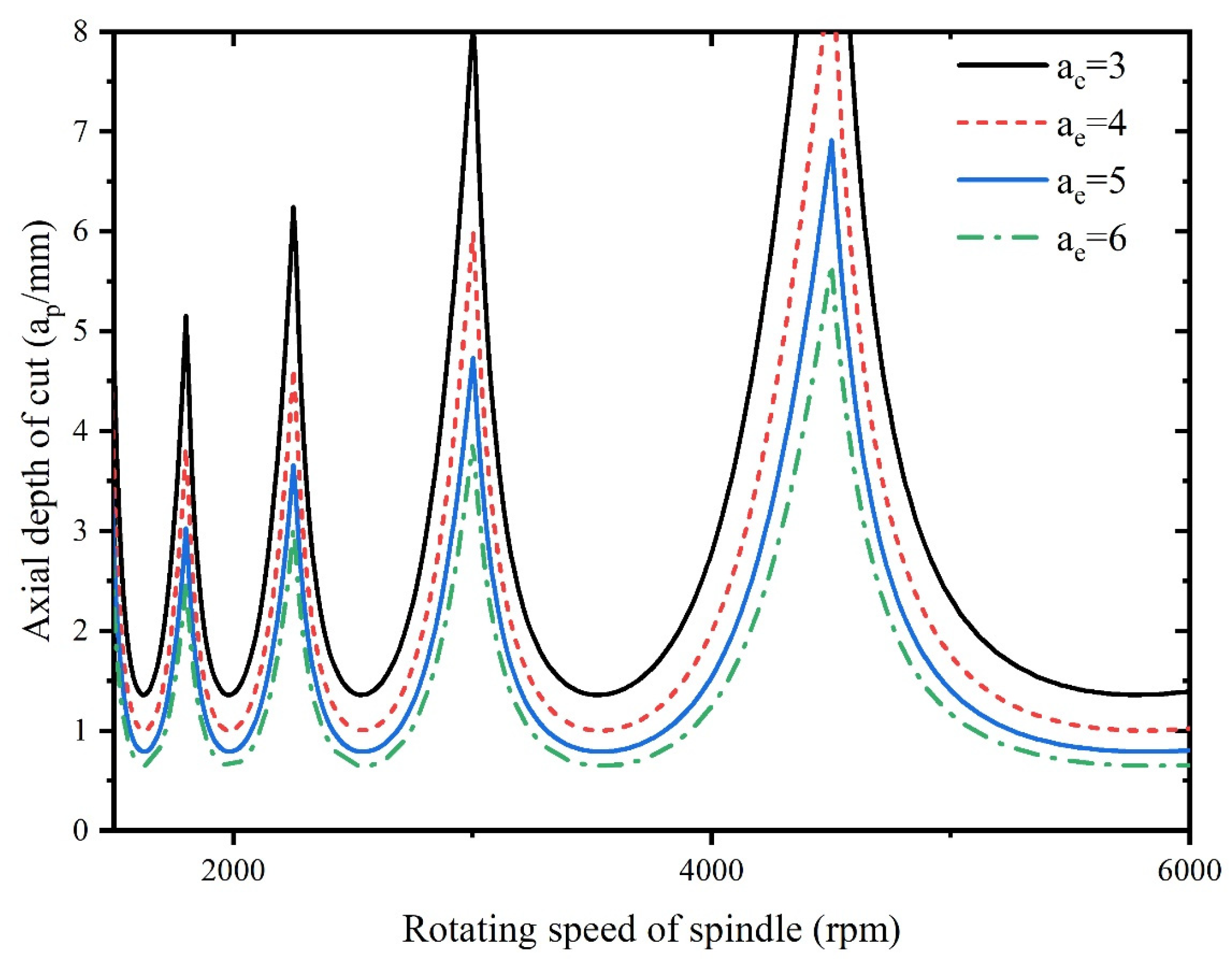
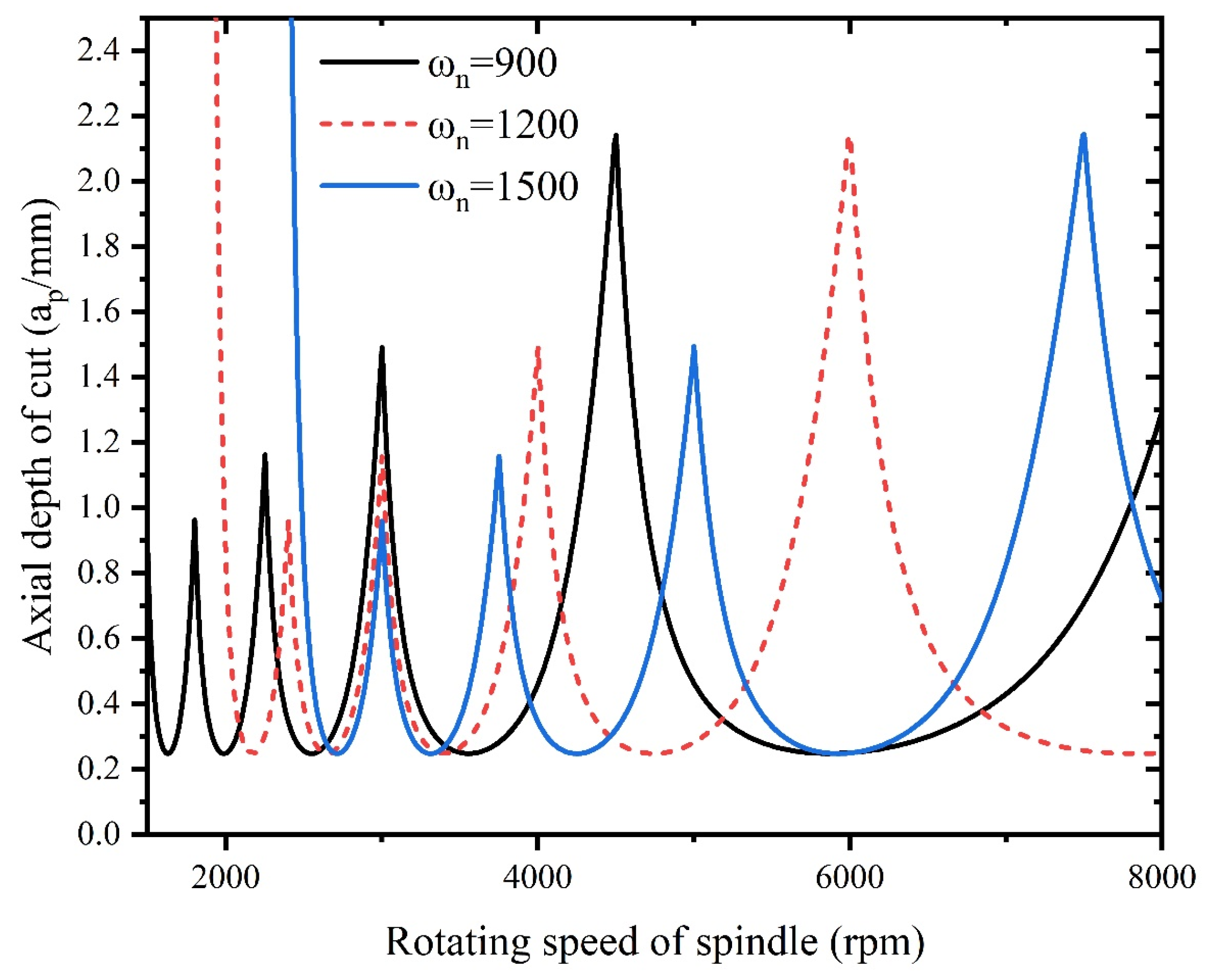
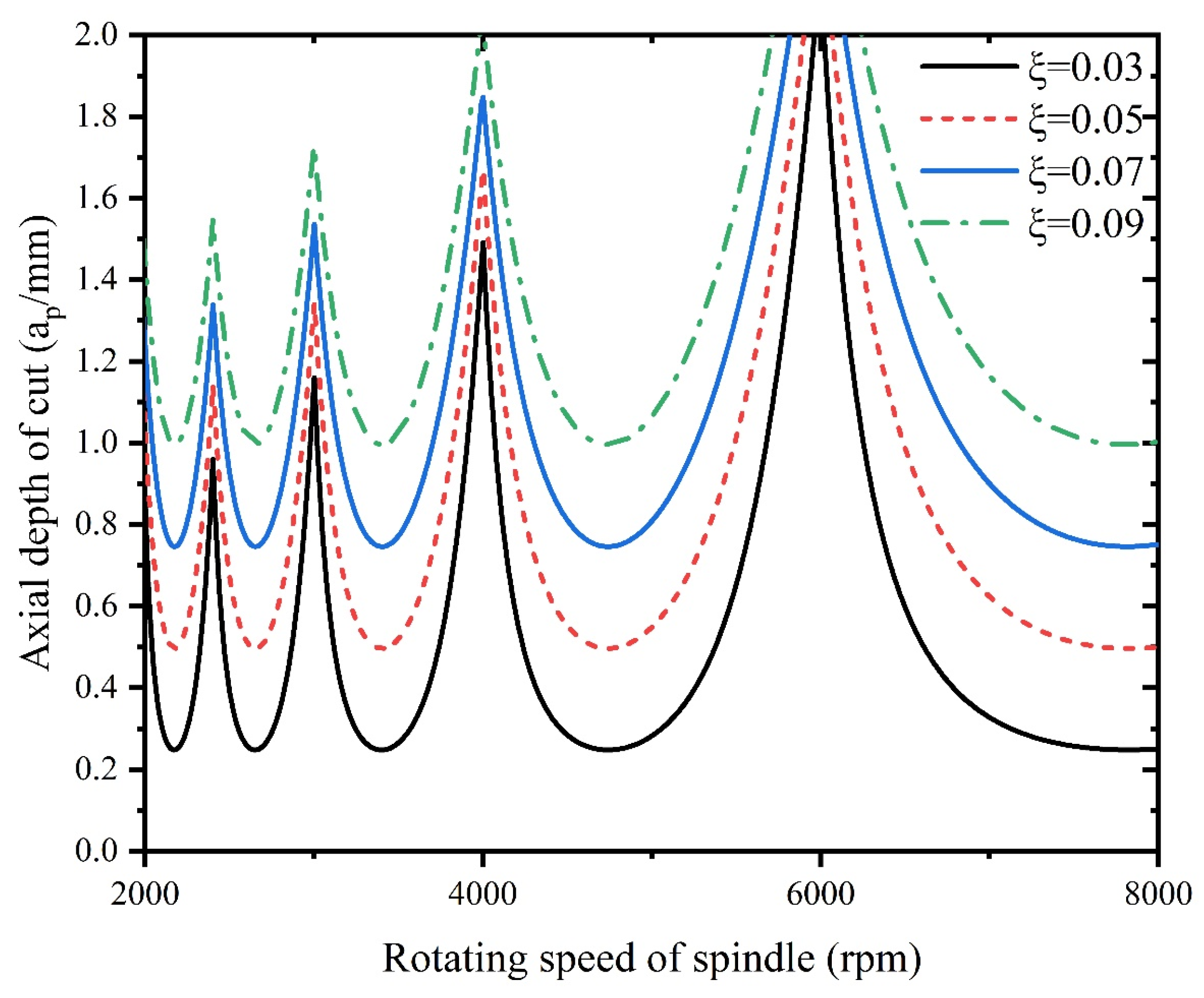
4. Analysis of Milling Stability
5. Milling Experiment of Inconel718 and Parameter Optimization
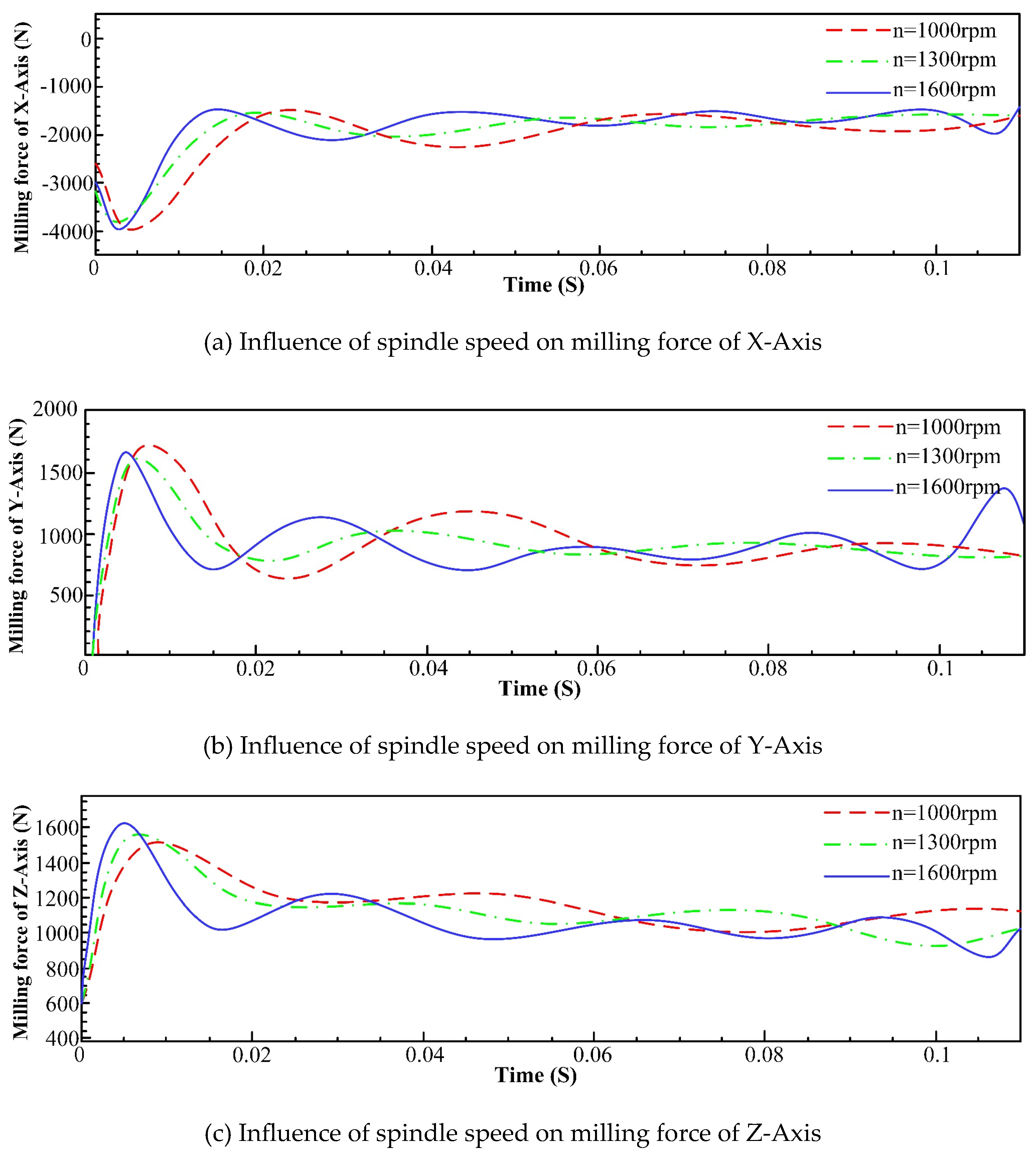
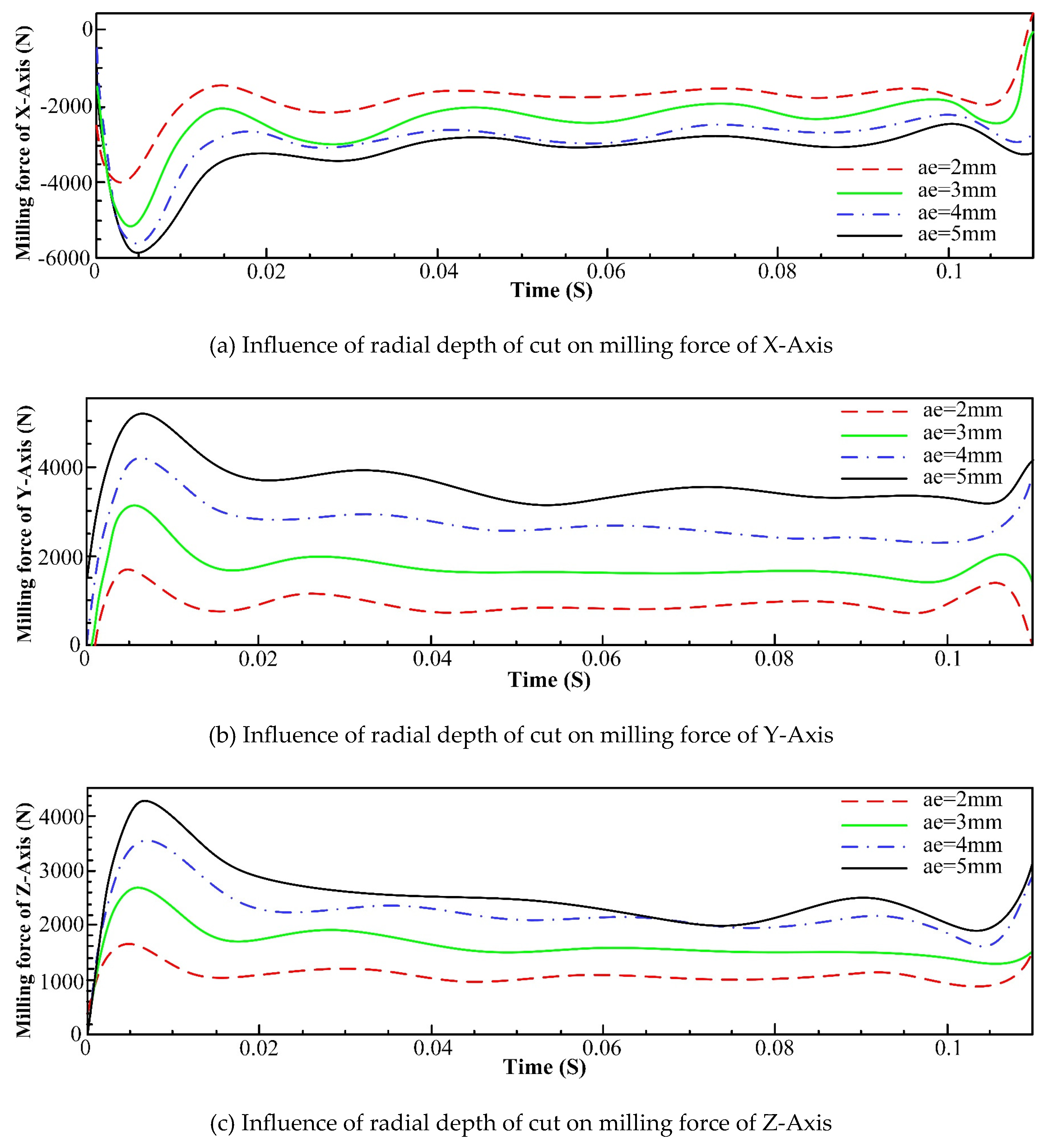
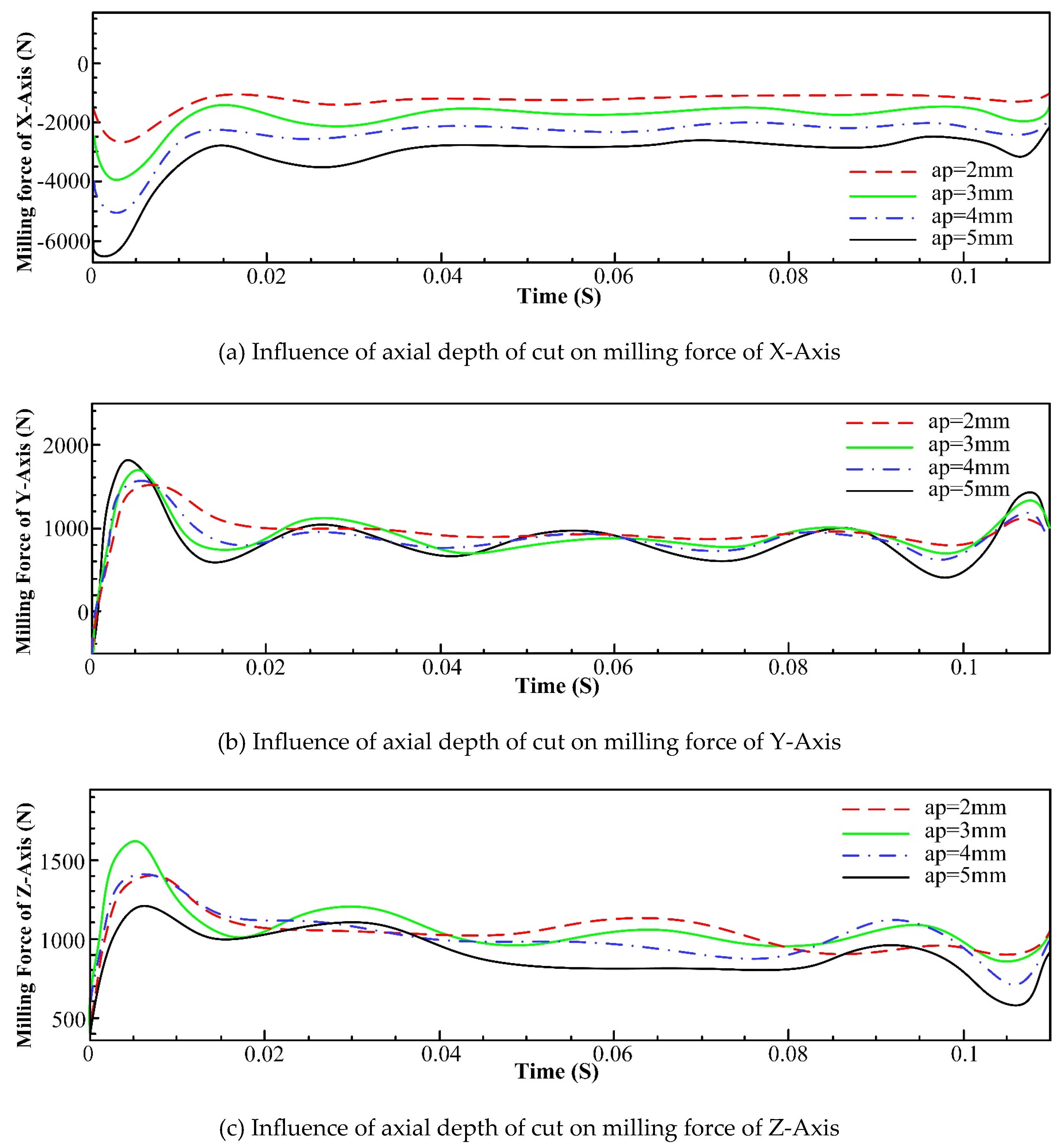
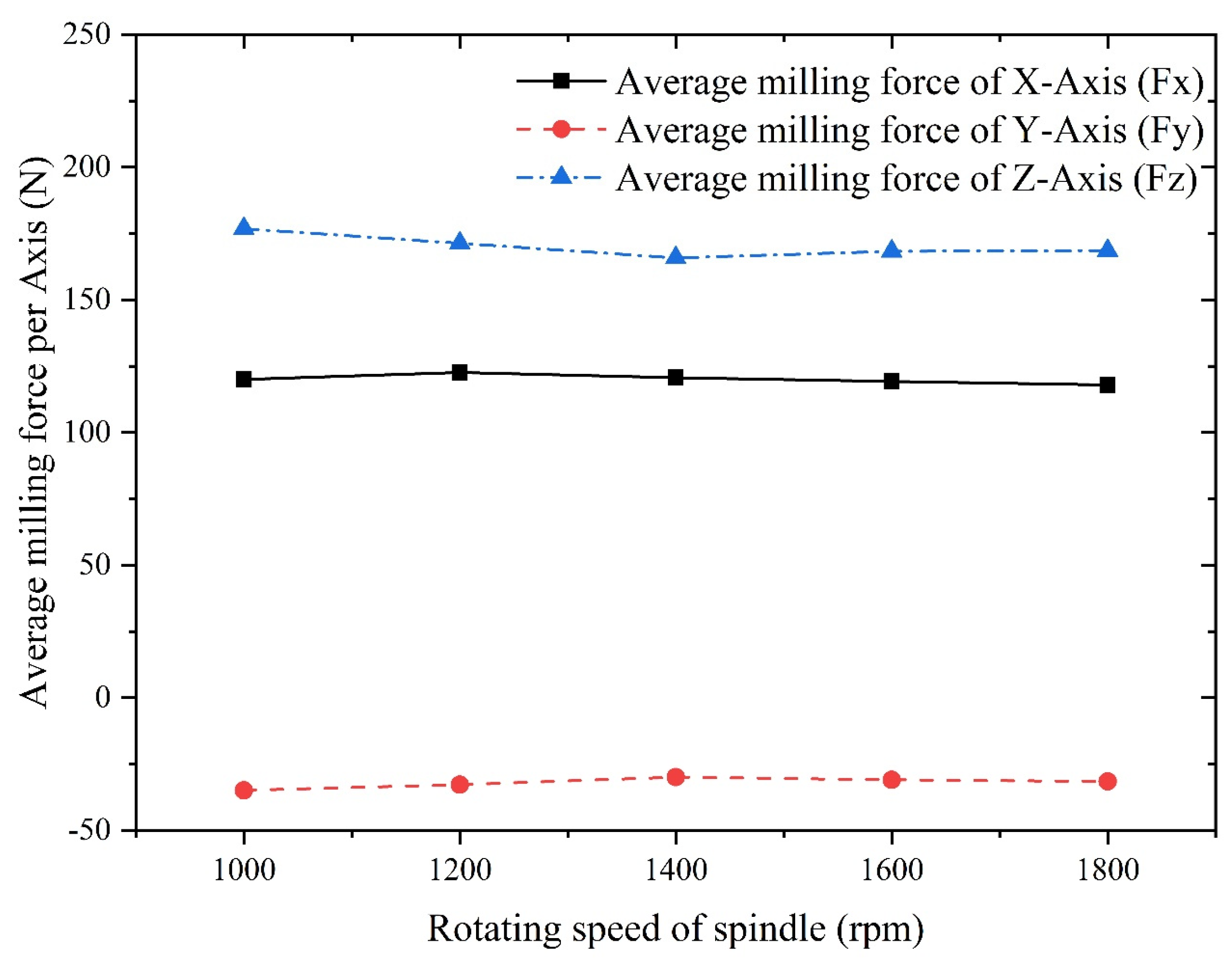
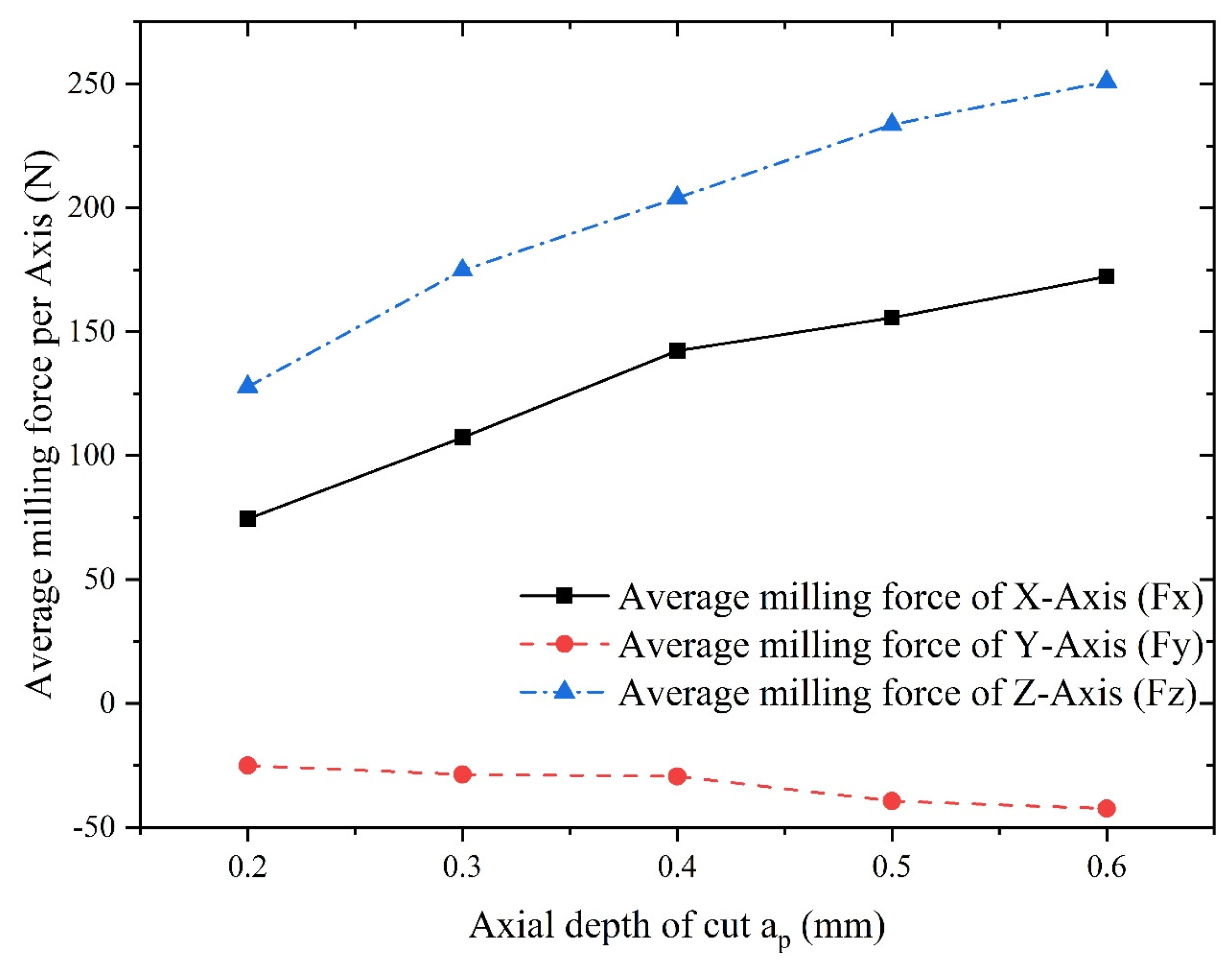
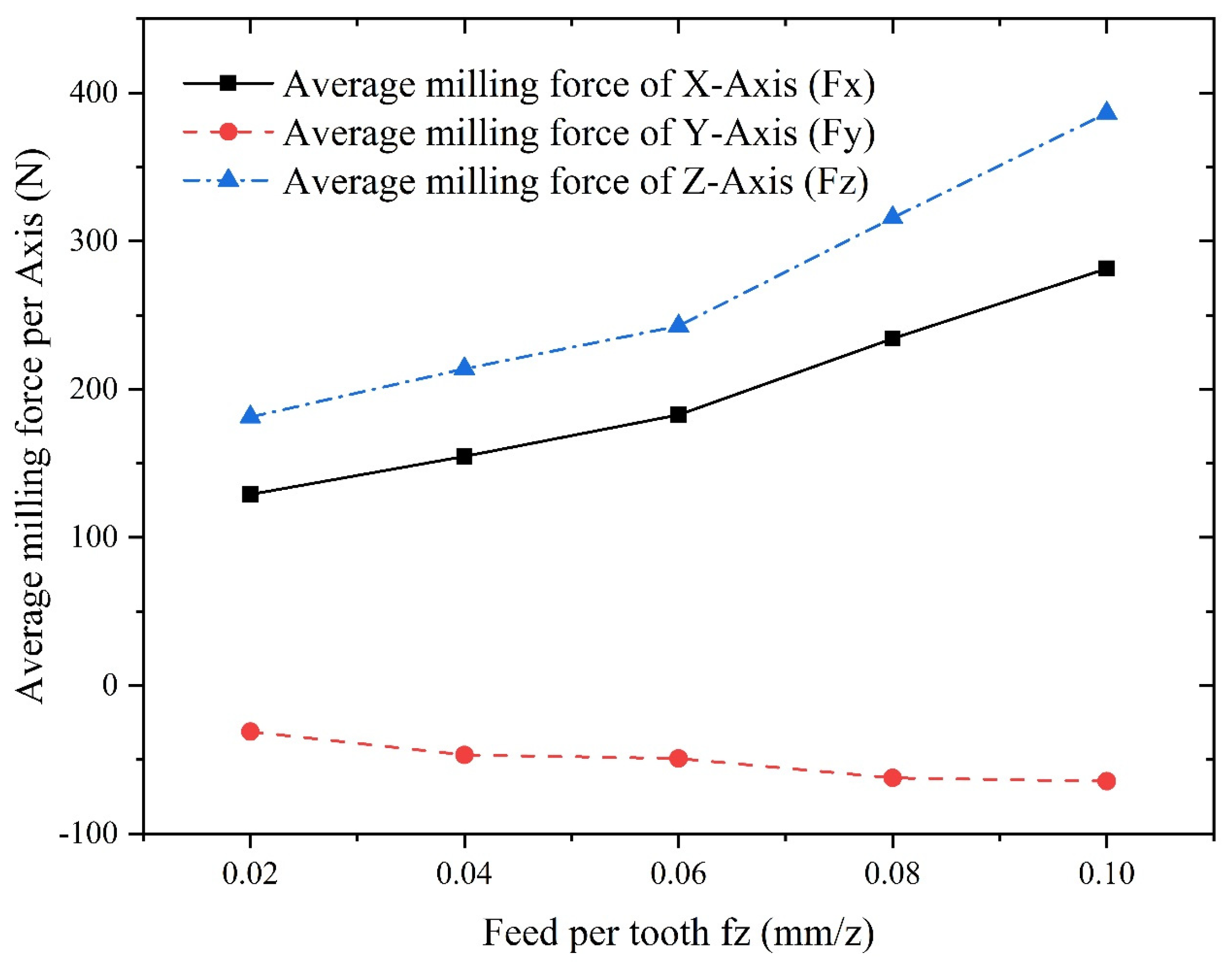
5.1 Results Analysis of Single Factor Experiment
5.2 Results Analysis of Orthogonal Experiments
- Axial depth of cut is the most influential factor on the average milling force in X-axis, followed by feed per tooth and spindle speed.
- Feed per tooth is the most influential factor on the average milling force in Y-axis, followed by axial depth of cut and spindle speed.
- Axial depth of cut is the most influential factor on the average milling force in Z-axis, followed by the feed per tooth and spindle speed.
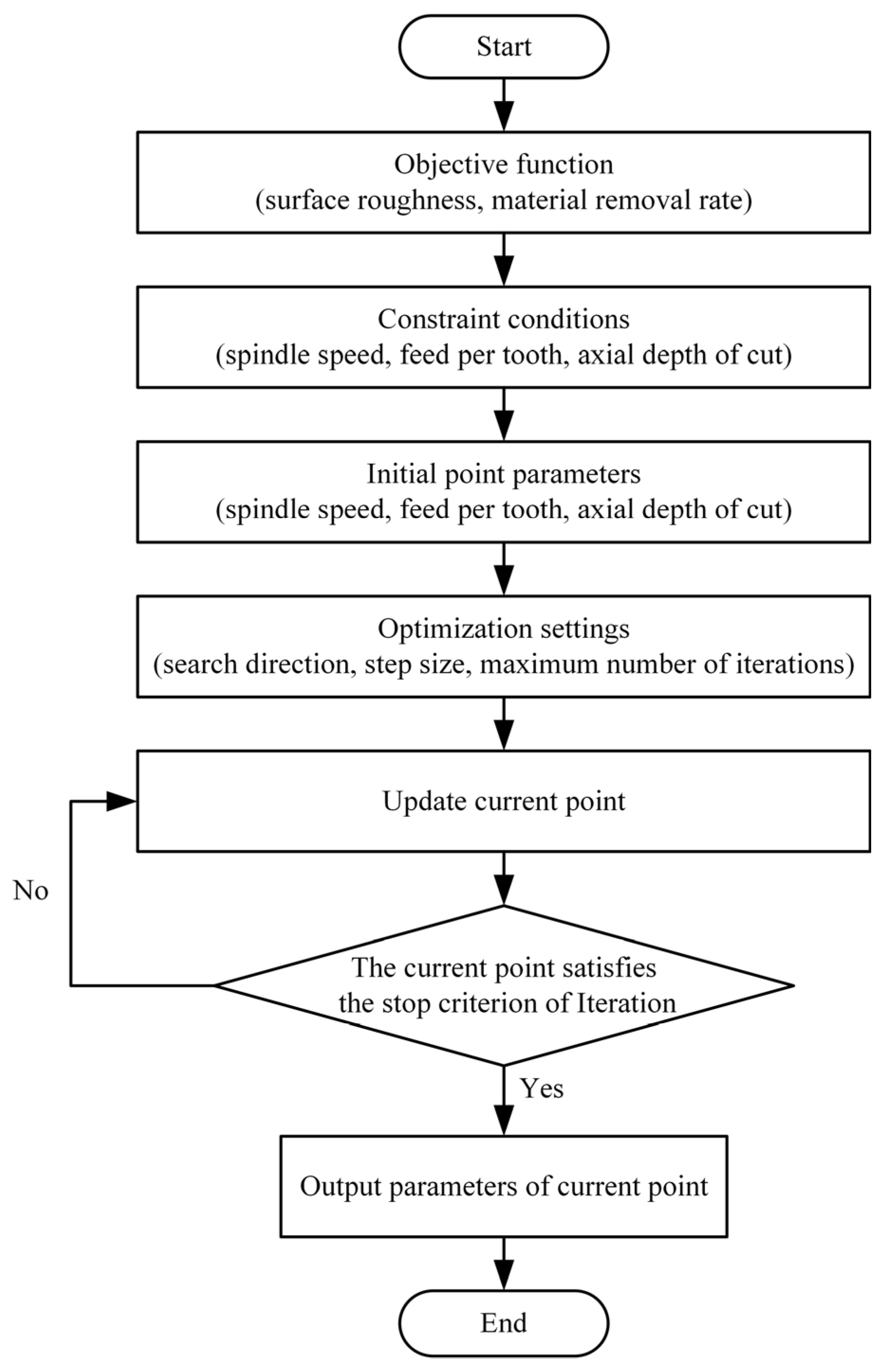
5.3 Establishment of Optimization Objective Function
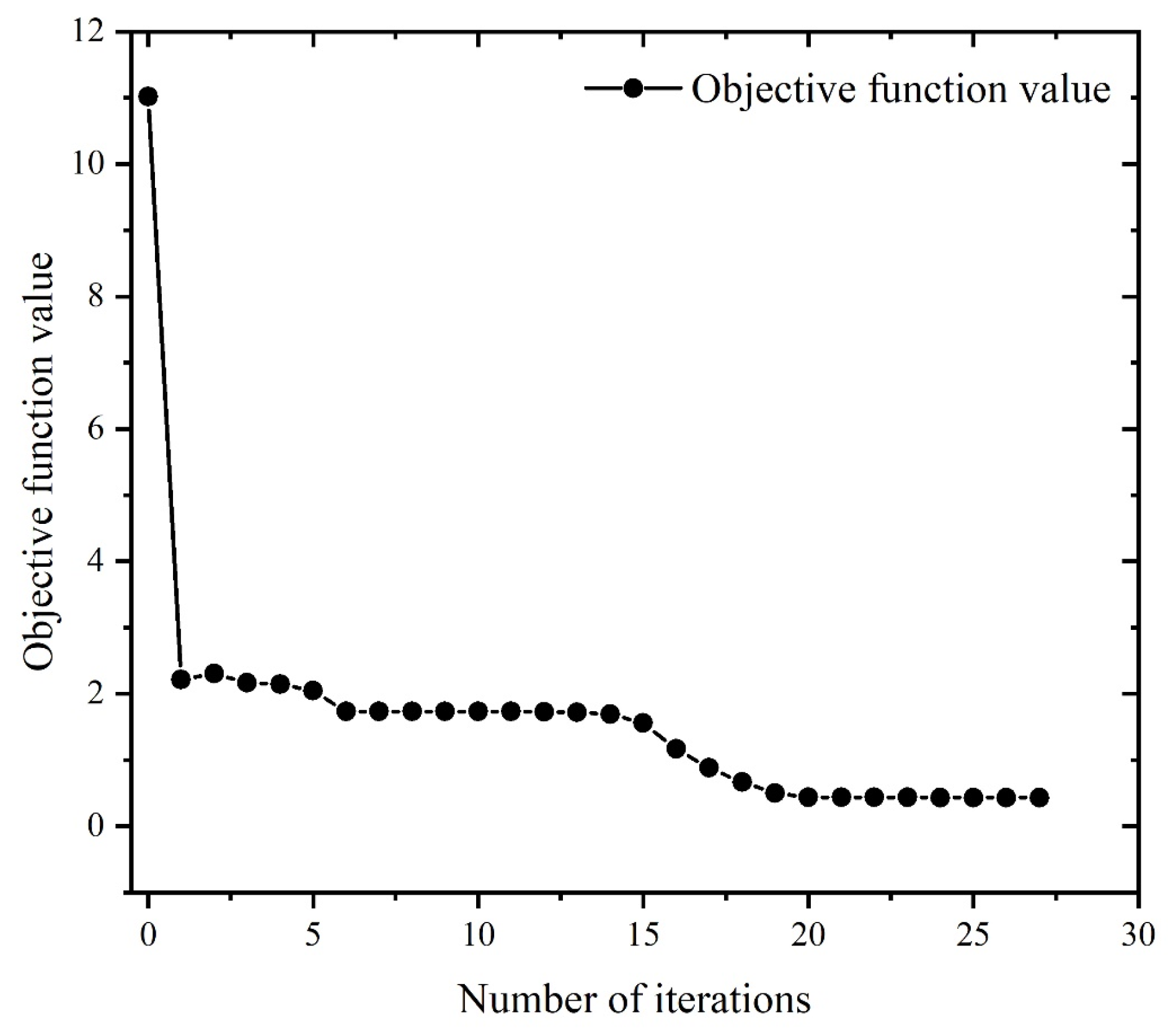
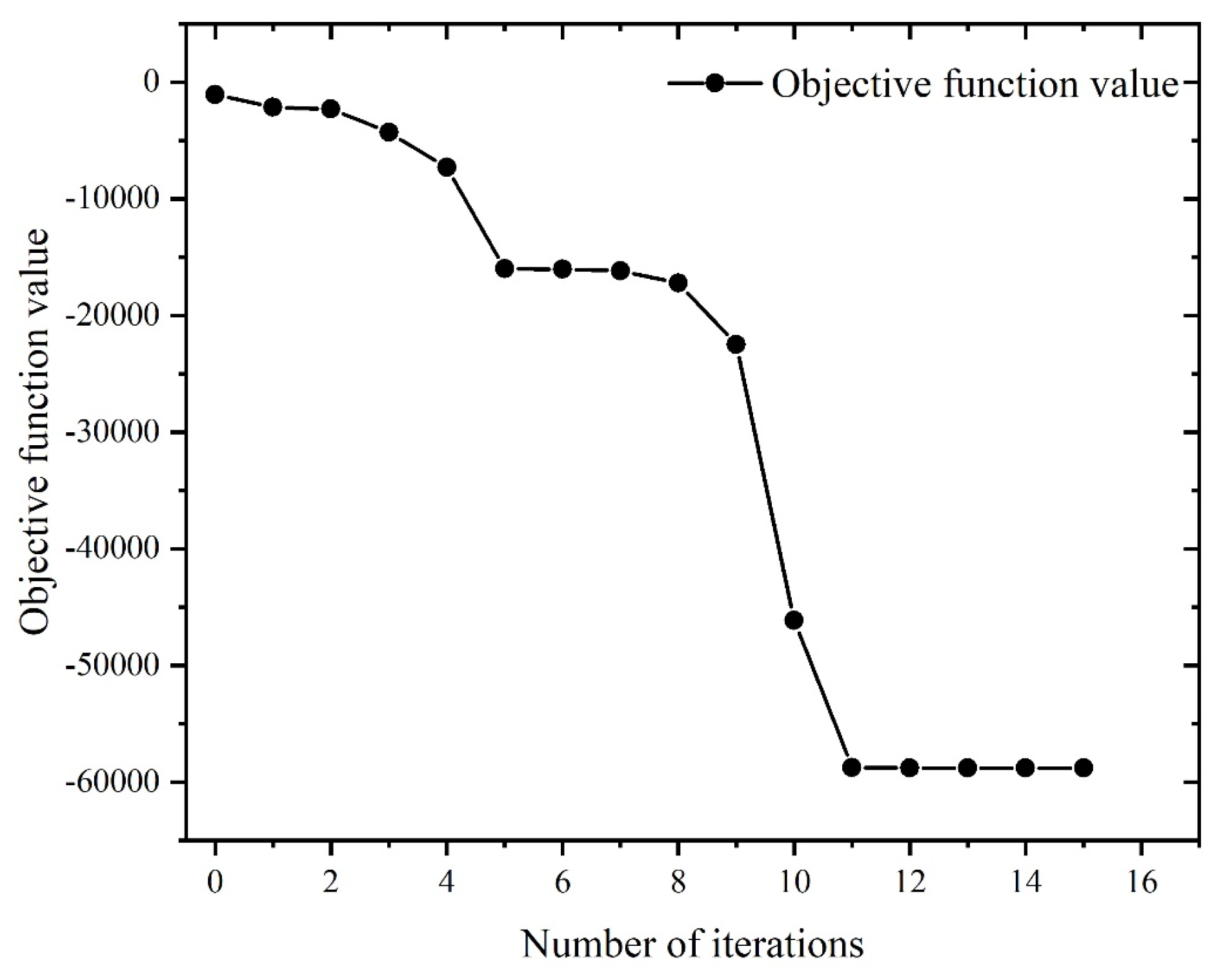
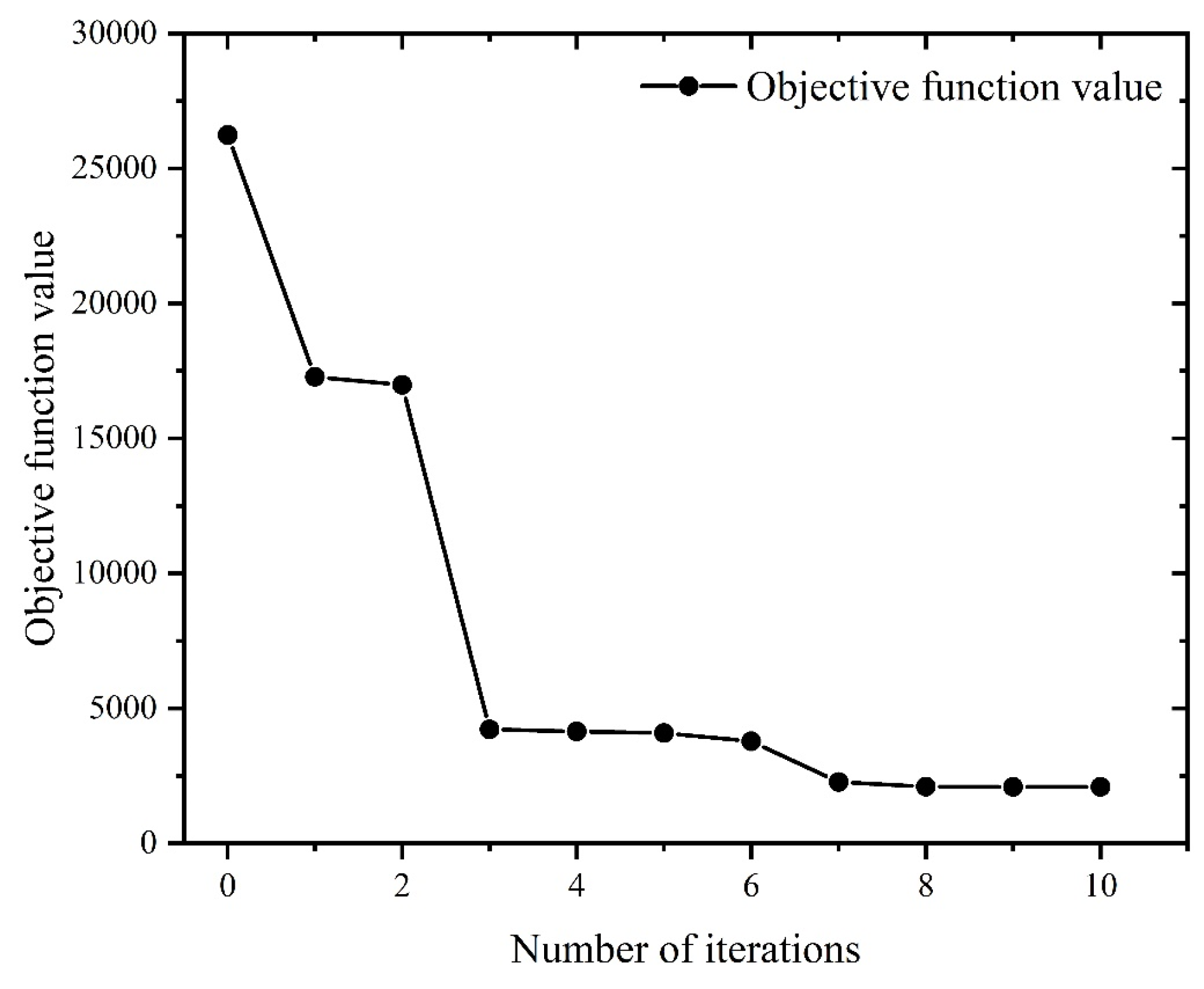
5.4 Optimization Results Analysis
6. Conclusion
- An increase in feed and tool helix angle leads to an increase in milling force, and the results of finite element analysis indicate that with the increase of the spindle speed, radial depth of cut, axial depth of cut and feed per tooth, the increase of temperature in the machining area becomes more conspicuous. However, with the increase of spindle speed, the change of tool stress is not obvious, but with the increase of feed per tooth, radial depth of cut and axial depth of cut, the tool stress increases significantly. The spindle speed does not have a significant effect on the milling force in each axis. With the increase of feed per tooth and radial depth of cut, the milling force in X-, Y- and Z-Axis increases significantly, herein, the axial depth of cut has a greater effect on milling force of X-Axis and a smaller effect on milling forces of both Y- and Z-Axis.
- An increase in tool radius improves stability of milling system, however, an increase in radial depth of cut is detrimental to the stability. With increase of natural frequency, the critical depth of cut of milling remains unchanged, however, increase in damping ratio improves the system stability.
- The order of influence on the average milling force in X-axis is: axial depth of cut > feed per tooth > spindle speed, and the order of influence on the average milling force in Y-axis is: spindle speed > feed per tooth > axial depth of cut.
- Using the fmincon algorithm, if the minimum surface roughness is considered as the optimization objective, the optimal machining parameters are: spindle speed 3999.63rpm, feed rate 80.01mm/min, axial depth of cut 0.25mm, at this time, the optimal value of surface roughness is 0.43 μm. If the maximum material removal rate is considered as the optimization objective, the optimal machining parameters are: spindle speed 4000rpm, feed speed 700mm/min, axial depth of cut 2.54mm, at this time, the optimal value of material removal rate is 58788.32mm3/min. If both the minimum surface roughness and maximum material removal rate are considered as the optimization objective, the optimal processing parameters are: spindle speed 3199.2rpm, feed speed 80mm/min, axial depth of cut 0.25mm. At this time, the value of surface roughness is 3.5 μm, and the value of material removal rate is 4199.2mm3/min.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| The differential tangential cutting force[N] | |
| The differential radial cutting force[N] | |
| The differential axial cutting force[N] | |
| Tangential shearing force coefficient[N/mm2] | |
| Radial shearing force coefficient[N/mm2] | |
| Axial shearing force coefficient[N/mm2] | |
| Tangential edge force coefficient[N/mm] | |
| Radial edge force coefficient[N/mm] | |
| Axial edge force coefficient[N/mm] | |
| The instantaneous chip thickness at immersion angle[mm] | |
| The instantaneous edge length of the cutting segment[mm] | |
| The instantaneous chip width[mm] | |
| The cutting force in feed direction[N] | |
| The cutting force in normal direction[N] | |
| The cutting force in axial direction[N] | |
| The average cutting force in the feed direction[N] | |
| The average cutting force in the normal direction[N] | |
| The average cutting force in the axial direction[N] | |
| , | The components of linear model force in the feed direction[N] |
| , | The components of linear model force in the normal direction[N] |
| , | The components of linear model force in the axial direction[N] |
| Workpiece material flow stress | |
| Strain enhancement function | |
| Strain rate effect function | |
| Thermal softening function | |
| Strain rate | |
| Temperature | |
| Initial yield stress | |
| Plastic strain | |
| Reference plastic strain | |
| Cut-off strain value | |
| Contingency strengthening index | |
| Instantaneous strain increment | |
| Material failure strain | |
| , | Mass of machine-tool system in X and Y direction |
| , | Damping of machine-tool system in X and Y direction |
| , | Stiffness of machine-tool system in X and Y direction |
| , | Cutting force components acting on the tooth in X and Y direction |
| Dynamic displacement of the cutter in the previous cycle | |
| Dynamic displacement of the cutter in the current cycle | |
| Unit step function | |
| Direct transfer function in X direction | |
| Direct transfer function in Y direction | |
| Cross-transfer function in X direction | |
| Cross-transfer function in Y direction | |
| Speed of milling process | |
| Rotating speed of spindle | |
| Feed per tooth | |
| Radial depth of cut | |
| Axial depth of cut |
Appendix B
References
- Zhou, Y.; Ma, L.; Gong, Y.; Zhang, L.; Yin, G.; Sun, Y.J.T.I.J.o.A.M.T. Study on the mechanism of chip forming and the microhardness of micro-grinding nickel-based single-crystal superalloy. 2019, 103, 281–295. [Google Scholar] [CrossRef]
- Thellaputta, G.R.; Chandra, P.S.; Rao, C.S.P. Machinability of Nickel Based Superalloys: A Review. Materials Today: Proceedings 2017, 4, 3712–3721. [Google Scholar] [CrossRef]
- Miller, S. Advanced materials mean advanced engines. Interdisciplinary Science Reviews 1996, 21, 117–129. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Wang, Z.M.; Machado, A.R. The machinability of nickel-based alloys: a review. Journal of Materials Processing Technology 1999, 86, 1–16. [Google Scholar] [CrossRef]
- Ge, Y.; Zhu, Z.; Wang, D. Electrochemical Dissolution Behavior of the Nickel-Based Cast Superalloy K423A in NaNO3 Solution. Electrochimica Acta 2017, 253, 379–389. [Google Scholar] [CrossRef]
- Alabort, E.; Reed, R.C.; Barba, D. Combined modelling and miniaturised characterisation of high-temperature forging in a nickel-based superalloy. Materials & Design 2018, 160, 683–697. [Google Scholar] [CrossRef]
- Xu, D.; Liao, Z.; Axinte, D.; Sarasua, J.A.; M'Saoubi, R.; Wretland, A. Investigation of surface integrity in laser-assisted machining of nickel based superalloy. Materials & Design 2020, 194, 108851. [Google Scholar] [CrossRef]
- Sharma, P.; Kishore, K.; Sinha, M.K.; Singh, V. Electrical discharge machining of nickel-based superalloys: a comprehensive review. International Journal of Materials Engineering Innovation 2022, 13, 157–190. [Google Scholar] [CrossRef]
- Ezugwu, E.O.; Bonney, J.; Yamane, Y. An overview of the machinability of aeroengine alloys. Journal of Materials Processing Technology 2003, 134, 233–253. [Google Scholar] [CrossRef]
- Ding, T.; Zhang, S.; Wang, Y.; Zhu, X.J.T.I.J.o.A.M.T. Empirical models and optimal cutting parameters for cutting forces and surface roughness in hard milling of AISI H13 steel. 2010, 51, 45–55.
- Zhao, C.; Fu, T.; Liu, Y.; Guo, Y.J.I.J.I.T. Different Impact on the Stability Limits Caused by the Selection of Milling Force Coefficient under the State of High-Speed Milling. 2015, 8, 153–160. [Google Scholar] [CrossRef]
- Shi, L.; Liu, E.F.; Zhang, Y.; Chen, P.; Li, Z.B. The simulation of cutting force of free-form surface machining with ball-end milling cutter. In Proceedings of the 2009 IEEE International Conference on Industrial Engineering and Engineering Management; 2009; pp. 2314–2318. [Google Scholar]
- Bergmann, J.A.; Wöste, F.; Wiederkehr, P. An analysis of the sensitivity of cutting force coefficients and their influence on the variability of stability diagrams. Production Engineering 2023, 17, 407–414. [Google Scholar] [CrossRef]
- Zhao, M.; Zhu, J.; Song, S.; Xue, B.; Zhao, B. Influence of machining parameters in longitudinal-torsional ultrasonic vibration milling titanium alloy for milling force. The International Journal of Advanced Manufacturing Technology 2022, 123, 3587–3597. [Google Scholar] [CrossRef]
- Newby, G.; Venkatachalam, S.; Liang, S.Y. Empirical analysis of cutting force constants in micro-end-milling operations. Journal of Materials Processing Technology 2007, 192-193, 41–47. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Miao, L.; Zhang, W. Deformation Analysis of Continuous Milling of Inconel718 Nickel-Based Superalloy. Micromachines 2022, 13. [Google Scholar] [CrossRef] [PubMed]
- Jiang, F.; Zhang, T.; Yan, L. Analytical model of milling forces based on time-variant sculptured shear surface. International Journal of Mechanical Sciences 2016, 115-116, 190–201. [Google Scholar] [CrossRef]
- Madajewski, M.; Wojciechowski, S.; Znojkiewicz, N.; Twardowski, P. Hybrid Numerical-Analytical Approach for Force Prediction in End Milling of 42CrMo4 Steel. In Proceedings of the Advances in Manufacturing II, Cham, 2019; 2019//; pp. 223–232. [Google Scholar]
- Huang, W.; Li, X.; Wang, B.; Chen, J.; Zhou, J. An analytical index relating cutting force to axial depth of cut for cylindrical end mills. International Journal of Machine Tools and Manufacture 2016, 111, 63–67. [Google Scholar] [CrossRef]
- Kao, Y.-C.; Nguyen, N.-T.; Chen, M.-S.; Huang, S.-C. A combination method of the theory and experiment in determination of cutting force coefficients in ball-end mill processes. Journal of Computational Design and Engineering 2015, 2, 233–247. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, H.J.T.I.J.o.A.M.T. Full life-cycle cutting force prediction in ball helical milling based on oblique cutting analysis. 2023, 124, 1623–1638. [Google Scholar] [CrossRef]
- Kaneko, K.; Nishida, I.; Sato, R.; Shirase, K.J.P.C. Virtual milling force monitoring method based on in-process milling force prediction model to eliminate predetermination of cutting coefficients. 2018, 77, 22–25. [Google Scholar] [CrossRef]
- Li, S.-J.; Zhou, Y.-F.; Jin, R.-C.; Ji, Z. Dynamic Force Modelling for a Ball-End Milling Cutter Based on the Merchant Oblique Cutting Theory. The International Journal of Advanced Manufacturing Technology 2001, 17, 477–483. [Google Scholar] [CrossRef]
- Falta, J.; Sulitka, M.; Zeman, P.J.T.I.J.o.A.M.T. An analytical formulation of ZOA-based machining stability for complex tool geometries: application to 5-axis ball-end milling. 2022, 123, 1499–1519. [Google Scholar] [CrossRef]
- Yongheng, D.; Shujuan, L.; Xiantao, H.; Pengyang, L.; Yan, L.; Qi, L.J.C.J.M.E. Modeling on the milling force of ball-end milling cutter based on Z-MAP method. 2019, 55, 201–212. [Google Scholar] [CrossRef]
- Huang, S.; Liu, Y.; Jiao, K.; Li, J. Three-dimensional finite element simulation analysis of milling deformation of SiCp/Al composites thin-walled parts. International Journal of Machining and Machinability of Materials 2017, 19, 408–425. [Google Scholar] [CrossRef]
- Yu, J.; Shi, Y.X.; Yang, G.W. Finite Element Analysis and Experimental of Milling Force for Aeronautical Thin-Walled Workpiece. Advanced Materials Research 2011, 328-330, 685–689. [Google Scholar] [CrossRef]
- Haijun, H.; Yazhou, S.; Zesheng, L. Simulation and experiment of cutting force in ultrasonic torsional vibration assisted micro-milling. In Proceedings of the Proc.SPIE; 2010; p. 76570. [Google Scholar]
- Pratap, T.; Patra, K.; Dyakonov, A.A.J.P.E. Modeling cutting force in micro-milling of Ti-6Al-4V titanium alloy. 2015, 129, 134–139. [Google Scholar] [CrossRef]
- Li, M.-Y.; Ding, W.-B.; Yu, H.-B.; Huang, J.-G. RESEARCH ON DEFORMATION CHARACTERISTICS OF RULED SURFACE BLADES IN MILLING PROCESSES. In Material Engineering and Mechanical Engineering: Proceedings of Material Engineering and Mechanical Engineering (MEES2015); pp. 2016910–919.
- Altintaş, Y.; Budak, E.J.C.a. Analytical prediction of stability lobes in milling. 1995, 44, 357–362. [Google Scholar] [CrossRef]
- Merdol, S.; Altintas, Y.J.J.M.S.E. Multi frequency solution of chatter stability for low immersion milling. 2004, 126, 459–466. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H. Second-order full-discretization method for milling stability prediction. International Journal of Machine Tools and Manufacture 2010, 50, 926–932. [Google Scholar] [CrossRef]
- Ding, Y.; Zhu, L.; Zhang, X.; Ding, H.J.I.J.o.M.T. ; Manufacture. A full-discretization method for prediction of milling stability. 2010, 50, 502–509. [Google Scholar]
- Insperger, T.; Stépán, G.; Turi, J.J.J.o.S. ; Vibration. On the higher-order semi-discretizations for periodic delayed systems. 2008, 313, 334–341. [Google Scholar]
- Insperger, T.; Stépán, G.J.I.J.f.n.m.i.e. Semi-discretization method for delayed systems. 2002, 55, 503–518. [Google Scholar] [CrossRef]
- Insperger, T.; Stépán, G.J.I.j.f.n.m.i.e. Updated semi-discretization method for periodic delay-differential equations with discrete delay. 2004, 61, 117–141. 2004, 61, 117–141. [Google Scholar]
- Sun, L.; Zheng, K.; Liao, W. Chatter suppression and stability analysis of rotary ultrasonic milling titanium alloy thin-walled workpiece. The International Journal of Advanced Manufacturing Technology 2022, 118, 2193–2204. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, J.F.; Feng, P.F.; Yu, D.W.; Wu, Z.J. Determination of Constitutive Equation Parameters for Face Milling 3-D Simulation via Pressure Bar and Orthogonal Cutting Tests. Materials Science Forum 2012, 723, 136–142. [Google Scholar] [CrossRef]
- Li, B.; Hu, Y.; Wang, X.; Li, C.; Li, X. AN ANALYTICAL MODEL OF OBLIQUE CUTTING WITH APPLICATION TO END MILLING. Machining Science and Technology 2011, 15, 453–484. [Google Scholar] [CrossRef]
- Tao, F. The Experiment of Cutting Performance of Polished Cemented Carbide Insert in Cutting Nickel-Based Superalloy. Xiangtan University, 2017.

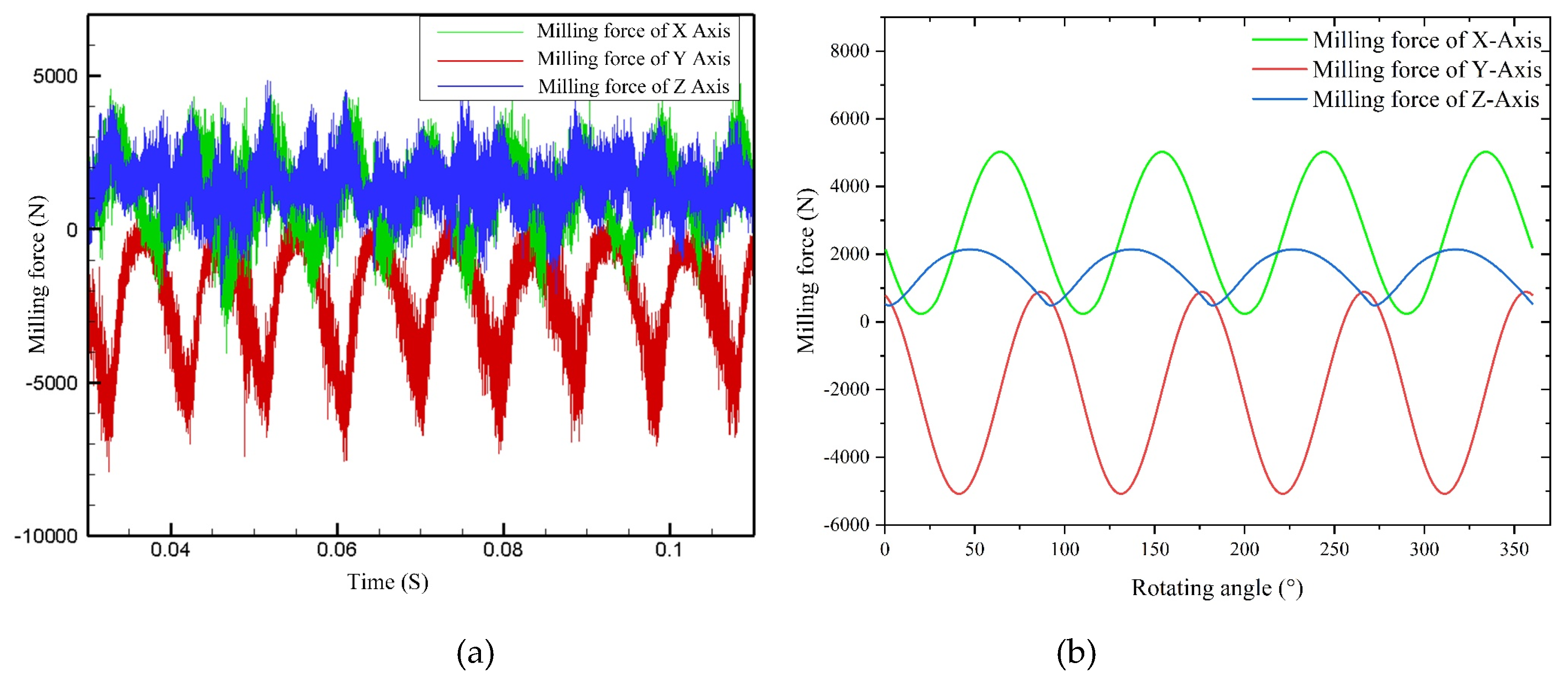



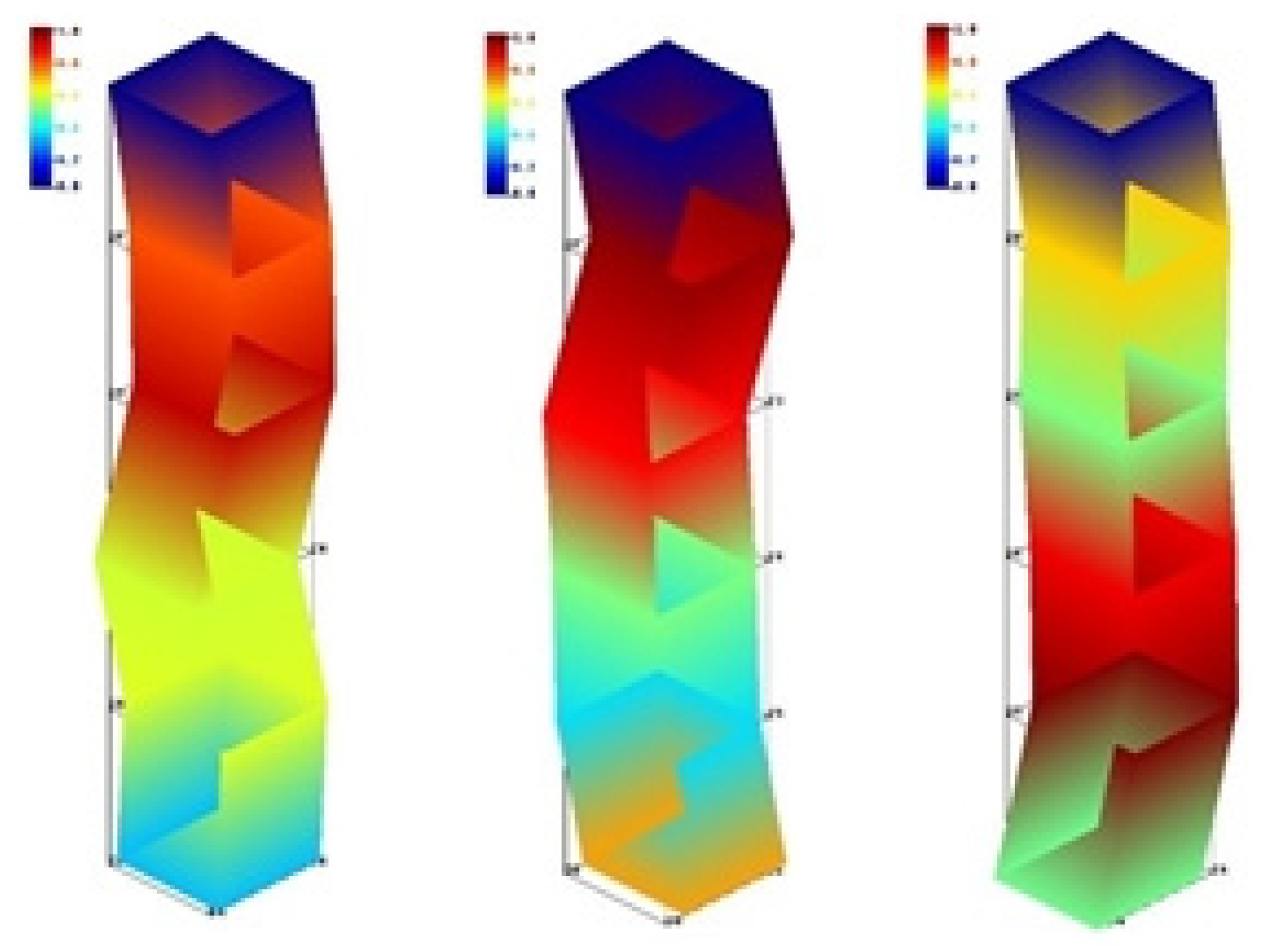

| Experiment No. | (mm/z) | Feed speed (mm/min) | |||
| 1 | 0.02 | 80 | 76.88 | -59.25 | 11.97 |
| 2 | 0.04 | 160 | 174.5 | -210.7 | 44.67 |
| 3 | 0.06 | 240 | 251.7 | -378.8 | 133.1 |
| 4 | 0.08 | 320 | 314.1 | -572.0 | 265.2 |
| 5 | 0.10 | 400 | 353.4 | -720.6 | 430.1 |
| 6 | 0.12 | 480 | 421.6 | -830.1 | 552.3 |
| Shearing force coefficient (N/mm2) | Value | Edge force coefficient (N/mm2) | Value |
| -15934.72 | 149.15 | ||
| -6636.28 | -51.95 | ||
| 8949.06 | -159.45 |
| Initial yield stress | Reference plastic strain | Cut-off strain | Strain enhancement index n |
| 3.6 MPa | 0.3 | 9.55 |
| Ambient Temperature | Linear cut-off temperature | Melting Temperature | ||||||
| 0.998 |
| Low strain rate sensitivity factor | High strain rate sensitivity factor | Reference plastic strain rate | Strain rate critical value |
| 25.5 | 25.5 | 1 sec-1 | 1×107 sec-1 |
| Rotating speed of spindle n(rpm) | Feed per tooth (mm/z) | Radial depth of cut (mm) | Axial depth of cut (mm) |
| 1000 | 0.2 | 2 | 2 |
| 1300 | 0.3 | 3 | 3 |
| 1600 | 0.4 | 4 | 4 |
| - | 0.5 | 5 | 5 |
| Modal order | Natural frequency (Hz) | Damping ratio (%) |
| First order of X direction | 935.06 | 0.049 |
| Second order of X direction | 1235.96 | 0.036 |
| Third order of X direction | 1567.99 | 0.093 |
| First order of Y direction | 911.87 | 0.045 |
| Second order of Y direction | 1233.52 | 0.059 |
| Third order of Y direction | 1539.92 | 0.050 |
| Experiment No. | Rotating speed of spindle n(r/min) |
Feed per tooth (mm/z) |
Axial depth of cut (mm) |
| 1 | 1000/1200/1400/1600/1800 | 0.02 | 0.4 |
| 2 | 1000 | 0.02/0.04/0.06/0.08/0.10 | 0.4 |
| 3 | 1000 | 0.02 | 0.2/0.3/0.4/0.5/0.6 |
| Experiment No. |
Rotating speed of spindle n(rpm) |
Feed per tooth (mm/z) |
Axial depth of cut (mm) |
| 1 | 800 | 0.015 | 0.1 |
| 2 | 800 | 0.03 | 0.2 |
| 3 | 800 | 0.045 | 0.3 |
| 4 | 800 | 0.06 | 0.4 |
| 5 | 1000 | 0.015 | 0.2 |
| 6 | 1000 | 0.03 | 0.1 |
| 7 | 1000 | 0.045 | 0.4 |
| 8 | 1000 | 0.06 | 0.3 |
| 9 | 1200 | 0.015 | 0.3 |
| 10 | 1200 | 0.03 | 0.4 |
| 11 | 1200 | 0.045 | 0.1 |
| 12 | 1200 | 0.06 | 0.2 |
| 13 | 1400 | 0.015 | 0.4 |
| 14 | 1400 | 0.03 | 0.3 |
| 15 | 1400 | 0.045 | 0.2 |
| 16 | 1400 | 0.06 | 0.1 |
| Experiment No. |
Parameters of experiment | Result of experiment(N) | |||||
| Rotating speed of spindle n(rpm) |
Feed per tooth (mm/z) |
Axial depth of cut (mm) |
|||||
| 1 | 800 | 0.015 | 0.1 | 15.81 | 8.410 | 25.53 | 31.18 |
| 2 | 800 | 0.03 | 0.2 | 49.01 | -7.847 | 68.23 | 84.37 |
| 3 | 800 | 0.045 | 0.3 | 85.91 | -18.33 | 107.4 | 138.75 |
| 4 | 800 | 0.06 | 0.4 | 131.0 | -28.87 | 137.0 | 191.74 |
| 5 | 1000 | 0.015 | 0.2 | 57.65 | -15.96 | 87.60 | 106.08 |
| 6 | 1000 | 0.03 | 0.1 | 39.64 | -8.765 | 65.59 | 77.14 |
| 7 | 1000 | 0.045 | 0.4 | 58.2 | 42.99 | 70.62 | 101.11 |
| 8 | 1000 | 0.06 | 0.3 | 118.4 | -13.09 | 148.7 | 190.53 |
| 9 | 1200 | 0.015 | 0.3 | 79.75 | -16.09 | 117.9 | 143.25 |
| 10 | 1200 | 0.03 | 0.4 | 121.9 | -24.2 | 157.3 | 200.47 |
| 11 | 1200 | 0.045 | 0.1 | 38.06 | -9.168 | 66.27 | 76.97 |
| 12 | 1200 | 0.06 | 0.2 | 53.36 | 35.24 | 69.54 | 94.47 |
| 13 | 1400 | 0.015 | 0.4 | 86.23 | 2.896 | 120.7 | 148.37 |
| 14 | 1400 | 0.03 | 0.3 | 54.12 | 40.37 | 82.35 | 106.49 |
| 15 | 1400 | 0.045 | 0.2 | 87.04 | -23.66 | 134.8 | 162.19 |
| 16 | 1400 | 0.06 | 0.1 | 66.65 | -12.69 | 101.1 | 121.76 |
| Experiment No. |
Milling force | Theoretical result (N) | Experimental result (N) | Relative error (%) |
| 1 | 17.86 | 15.81 | 12.97 | |
| 9.46 | 8.41 | 12.49 | ||
| 27.74 | 25.53 | 8.66 | ||
| 2 | 55.68 | 49.01 | 13.61 | |
| 8.64 | 7.847 | 10.11 | ||
| 59.96 | 68.23 | 12.12 | ||
| 3 | 80.36 | 85.91 | 6.46 | |
| 19.99 | 18.33 | 9.06 | ||
| 97.27 | 107.4 | 9.43 | ||
| 4 | 144.22 | 131 | 10.09 | |
| 30.74 | 28.87 | 6.48 | ||
| 123.98 | 137 | 9.50 |
| Experiment No. |
Milling force | FEA result (N) | Experimental result (N) | Relative error (%) |
| 1 | 13.63 | 15.81 | 13.80 | |
| 7.25 | 8.41 | 13.79 | ||
| 23.28 | 25.53 | 8.81 | ||
| 2 | 46.93 | 49.01 | 4.24 | |
| 8.63 | 7.847 | 9.98 | ||
| 75.02 | 68.23 | 9.95 | ||
| 3 | 91.02 | 85.91 | 5.95 | |
| 16.97 | 18.33 | 7.42 | ||
| 121.34 | 107.4 | 12.98 | ||
| 4 | 119.35 | 131 | 8.89 | |
| 32.76 | 28.87 | 13.47 | ||
| 149.8 | 137 | 9.34 |
| Spindle speed (rpm) | Feed speed (mm/min) | Axial depth of cut (mm) | Surface roughness R() | |
| Initial Value | 1000 | 100 | 1.2 | 11 |
| Optimized Value | 3999.63 | 80.01 | 0.25 | 0.43 |
| Spindle speed (rpm) |
Feed speed (mm/min) | Axial depth of cut (mm) | Material removal rate (mm3/min) | |
| Initial Value | 1000 | 100 | 1.2 | 1049.79 |
| Optimized Value | 4000 | 700 | 2.54 | 58788.32 |
| Spindle speed (rpm) | Feed per tooth (mm/z) | Axial depth of cut (mm) | Material removal rate (mm3/min) | ) | |
| Initial Value | 1000 | 100 | 1.2 | 10498 | 11 |
| Optimized Value | 3199.2 | 80 | 0.25 | 4199.2 | 3.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





