Prerpints.org logo
Preprint
Article

Energy Renormalization in a Berry Geometrical Phase: Low-Energy Perturbations of the Strong Interaction and the QCD Mass Gap

This version is not peer-reviewed.

Submitted:

17 April 2024

Posted:

18 April 2024

Read the latest preprint version here

Abstract
A Berry geometrical phase is identified in a strongly metastable system containing dynamically responsive clathrate hydrate structures within a crystal-fluid material. High energy degeneracy in the associated chemistry produces local stability and false vacuum conditions that lead to non-extensive and non-additive contributions in the fundamental thermodynamic relation. Application of Ginzburg-Landau theory and the scaling laws reveals a coherence length and a penetration depth for a macro-scale dual superconductor. The coherence length determines non-extensive volume changes whilst its inverse gives the Higgs mass. The penetration depth determines the extent of QCD vacuum suppression whilst its inverse gives the vector boson mass together with indirect manifestation as non-additive hyperbolic curvature. Simultaneous emergence of the Ginzburg-Landau superconducting phase transition is consistent with gauge-invariant coupling of the scalar field to the Yang-Mills action in QCD. The discovery of an energy gap in the gradient energy term of the system Lagrangian is associated with a critical correlation length revealed in the transition from a gapped to a gapless superconducting state. Together with the emergence and absorption of the Higgs-like scalar field, a mechanism for describing a renormalized QCD mass gap arises.
Keywords: 
Berry geometrical phase
;  
dual superconductivity
;  
scale- and gauge-invariance
;  
hyperbolic curvature
;  
strong gravity
;  
renormalization
;  
QCD mass gap
Subject: 
Physical Sciences  -   Particle and Field Physics

1. Introduction

Gravity-mediated entanglement has been advanced as a phenomenon that, if detected, would support the quantum nature of gravity [1]. It is claimed that such experimental evidence would substantiate most tentative quantum gravity theories, for example, perturbative quantum general relativity, loop quantum gravity and string theory. Here, it is postulated that gravity-mediated entanglement arises naturally from application of many fundamental theories and concepts within modern physics to recent experimental results [2]. The most pertinent of these theories and concepts are: thermodynamics, electromagnetism, scaling relations, geometry, symmetry and topology, special and general relativity, Noether’s theorem, the Ginzburg-Landau theory of superconductors, Yang-Mills theory, and confinement in quantum chromodynamics (QCD). In fact, nearly all Carroll’s Biggest Ideas in the Universe [3] are applied in some degree to realize a coherent and accurate interpretation of the experimental data. It is remarkable that application of so many fundamental theories and concepts to relatively simple experimental investigations can reveal new insights into some extant and intractable problems within contemporary physics. The current work is focused on the QCD mass gap problem.
The experimental investigation on which the current exposition is based has been previously reported [2]. This earlier work identifies the emergence of spontaneous diamagnetism and paramagnetism in the behaviour of nanoscale clathrate hydrate structures (or water ice cages) as critical phenomena responsible for work output in a kinetic system. The accompanying analysis centres upon a superconducting phase transition where scaling laws reveal the emergence of a critical correlation length ξ. The Ginzburg-Landau parameter κ (defined in Appendix A) is also uncovered together with topological ordering. It is shown [2] that relativistic length expansion and time contraction on a Lorentz manifold describe the critical correlation length ξ. It is also noted that the Ginzburg-Landau theory of superconductors invokes gauge-invariant coupling of a scalar field Φ to the Yang-Mills action in QCD. These relativistic and quantum aspects of the findings are examined here in further detail within the context of the Berry geometrical phase, complex energy band gaps and the QCD mass gap.
Situations can arise in thermodynamics whereby a physical system is prevented from attaining its lowest energy and highest entropy state through the existence of an energy barrier. False vacuum conditions can result from such metastability in the extreme so that on short timescales a positive, non-minimum energy density cannot be raised or lowered in response to external interactions. Where an energy barrier is maintained through dynamic inhomogeneities, a system can be isolated from external interactions through local stability conditions, as characterized by a non-concave entropy function [4]. The process of thermodynamic isolation is also described by the characteristic of asymptotic freedom in particle physics [5]. Opposition to dynamical change is established through complex reorganization of individual system components, i.e., degenerate hydrogen bonding in dissipative condensed matter systems [2]; gluon splitting and recombining in the case of colour confinement; and gluon exchange in quark confinement [5,6]. The experimental results reported in [2] reveal that water ice cages under negative pressure can give rise to false vacuum behaviour as a result of which non-extensive and non-additive interactions generate work in a constant energy Hamiltonian oscillator.
The low-energy system reported encompasses both a crystal-fluid material and its embedding vacuum manifold whereby variable volume V and hyperbolic curvature K of the embedding manifold rather than any fluid mechanical response determine the work performed by the system. The chemical and physical properties associated with water ice cage structures are also shown to elicit magnetic and superconducting behaviours that facilitate the Berry phase whilst the material maintains almost constant density.
The crystal-fluid is composed of dissipative, reorganizing, water ice cage structures suspended within a polar dielectric inhibitor solvent. The formulation results in false vacuum behaviour [7] such that the material part of the system is effectively isolated from any external thermodynamic interactions. However, despite the presence of strong local stability conditions, it is possible to perturb the system through an external pressure interaction to induce a ‘rolling’ critical response [8]. This, in turn, imposes a hyperbolic curvature action on the vacuum manifold that combines with a mutually emergent coupling energy to deliver a symmetry-related net energy gain, i.e., an additional source of energy enters the system.
Hyperbolic Gaussian curvature K originates in the negative potential of the false vacuum established by the variable effective radius (i.e., variable inertia) of the highly degenerate system. Conservation of angular momentum requires that a reducing effective radius results from an acceleration whilst an increasing effective radius results from a deceleration. Since the crystal-fluid retains constant total energy, acceleration acts to reduce the Gaussian radius of hyperbolic curvature Rg of the embedding manifold whilst deceleration increases Rg. Quantum interactions leading to non-additivity can be identified in both instances. The associated changes in swept volume V arising from the condensation of magnetic charges are non-extensive.
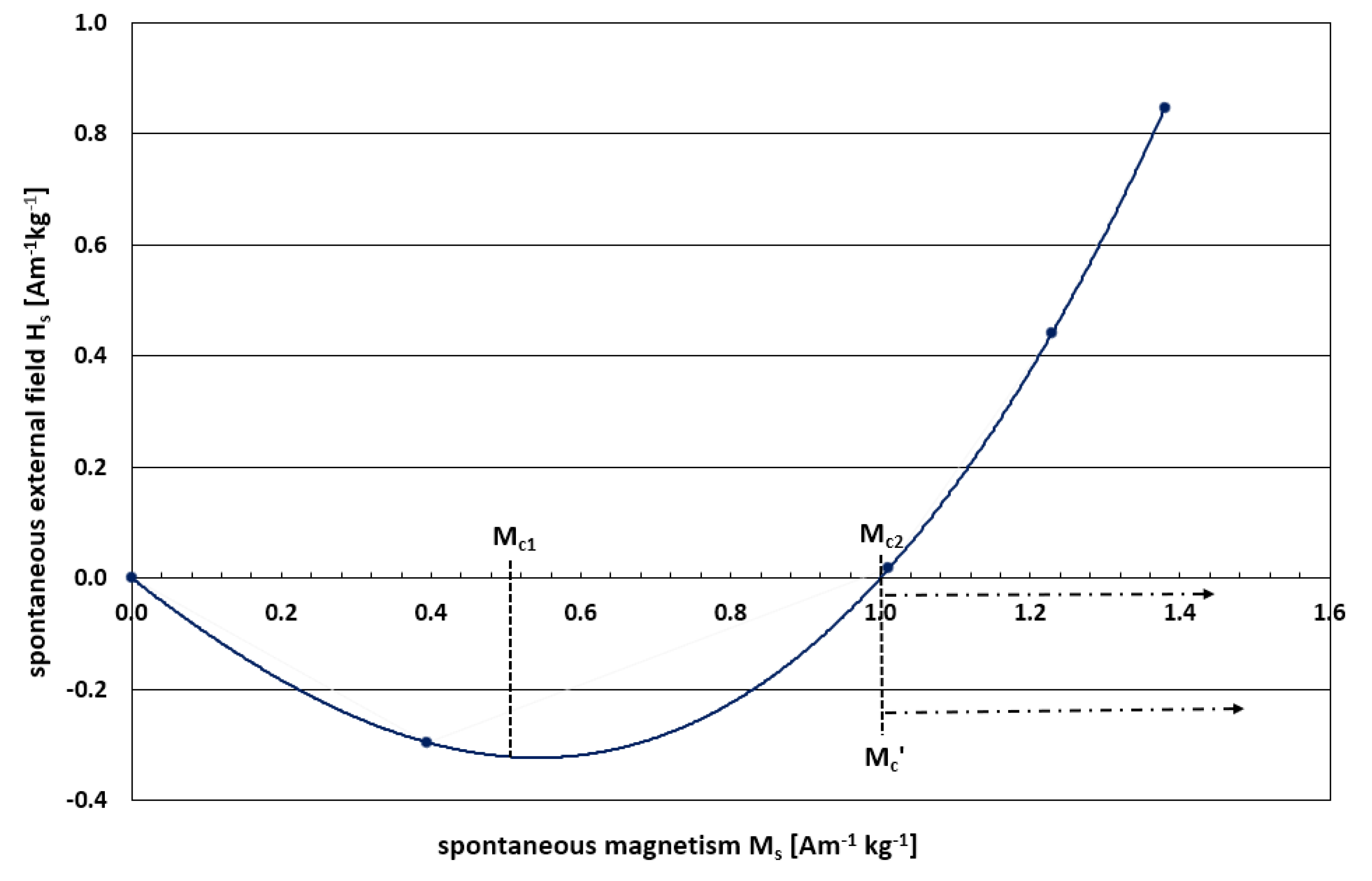
During the ‘rolling’ critical response, the magnetic and superconducting behaviours are quantified by a distinctive universality class of critical exponents [2]. Formation of a magnetic condensate induces a phase transition from Type-II superconductivity to a dual of Type-I superconductivity where the spontaneous magnetic field Hs, as an ‘auxiliary’ order parameter, reduces to zero [9]. Following this, ordering is attributed to an emergent complex parameter field, similar to the topological ordering of spin ices as described by Castelnovo et al. [10].
A definitive theory of quark confinement remains elusive despite experimental and lattice gauge theory/ computer simulation successes. The QCD large lattice technique is based upon strong coupling conditions so that perturbative techniques are deemed impractical. From a mathematical perspective, the confinement problem is known as the mass gap problem. A promising solution originally proposed by t’Hooft [11] and Mandelstam [12] claims that the ground-state of QCD is a dual superconductor in which quarks are confined by chromoelectric vortices. These vortices are analogous to the Abrikosov vortices seen in Type-II superconductors. In the current exposition QCD descriptions are also relevant to the macro-scale dual superconductor uncovered.
In a dual superconductor, the roles of the electric and magnetic fields are exchanged so that in this case the electric field is excluded. The significance of dual superconductivity in furthering an understanding of the strong interaction is examined in comprehensive reviews by Ripka [13] and Kondo et al. [14]. The superconducting phase transition established is consistent with Ginzburg-Landau theory suggesting gauge-invariant coupling of a scalar field Φ to the Yang-Mills action in QCD [14]. The emergent gauge field is associated with an apparent broken symmetry with gradient energy expressed on the hyperbolic surface of the system where the electric field is excluded. However, gauge symmetry is revealed not to be broken but rather decomposed and synchronized to become more capacious in extent.
A model for the emergent gauge symmetry is presented here to account for the net energy gain initiated by the ‘rolling’ critical behaviour (and subsequent geometrical action of the vacuum manifold) in terms of Noether-conserved quantities, i.e., energy and angular momentum for the case being considered. Since a topological phase factor, or Berry phase, reveals gauge structure in quantum mechanics [15], the existence of a parity-time (PT) symmetry may account for quantum mechanical interactions manifesting as real energy [16] in the gradient energy term of the Lagrangian describing the dual superconducting phase [2].
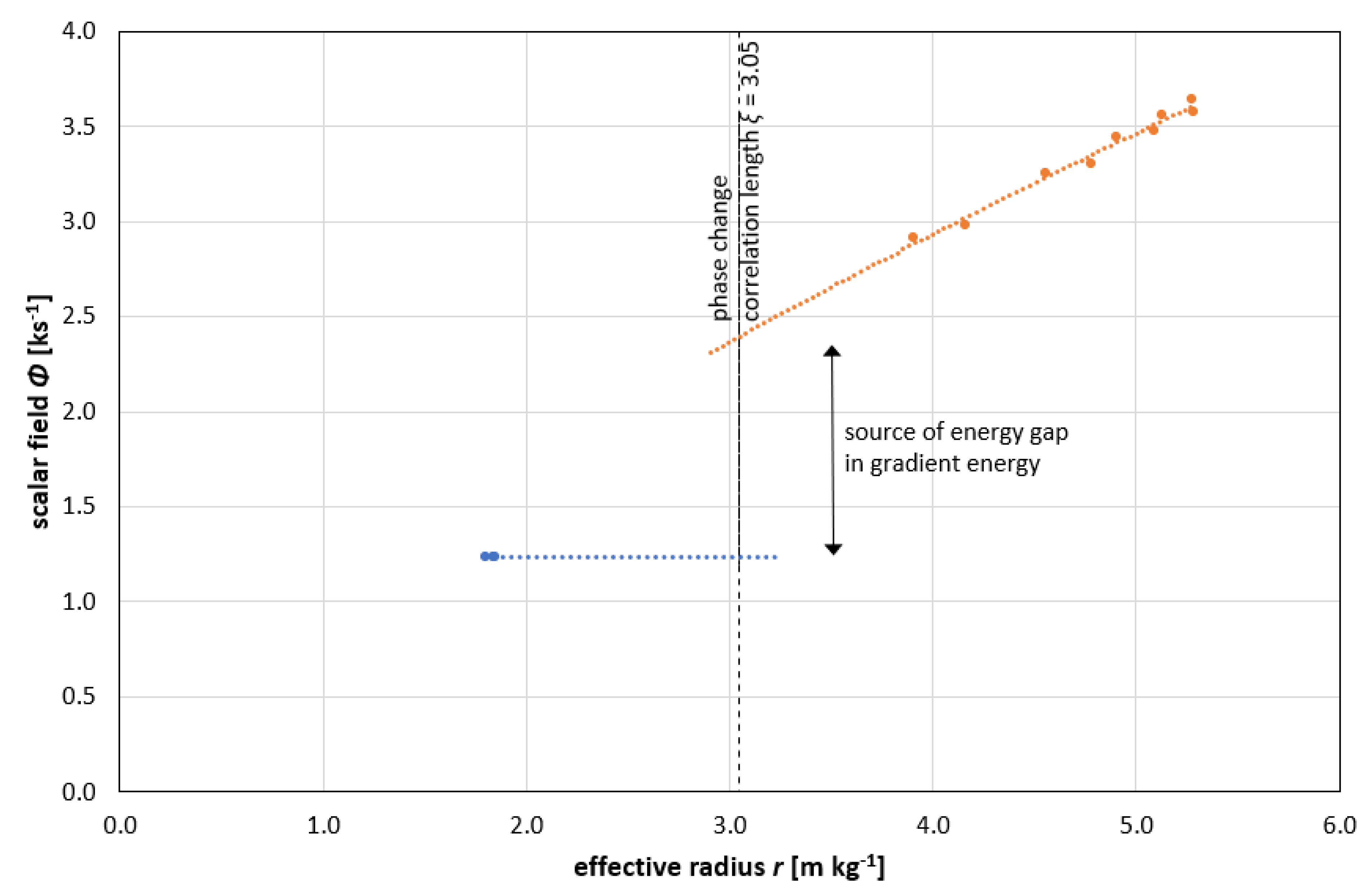
Emergence of the gauge field corresponds to a critical correlation length ξ that represents long-range ordering of magnetic spins, i.e., a magnetic condensate. This divergence is responsible for an energy gap in the gradient energy term analogous to complex energy band gaps reported in non-Hermitian PT symmetric systems [17]. Also, the existence of a mass gap in QCD is necessary to explain why the strong interaction is strong but only short-ranged. Confirmation of a mass gap would account for the fact that quantum particles have positive masses even though classical waves travel at the speed of light [18]. Evidence of a Berry phase and the Ginzburg-Landau parameter κ [2] thus enables insights into the Yang-Mills action and the mass gap phenomenon in QCD.
Experimental evidence and background material
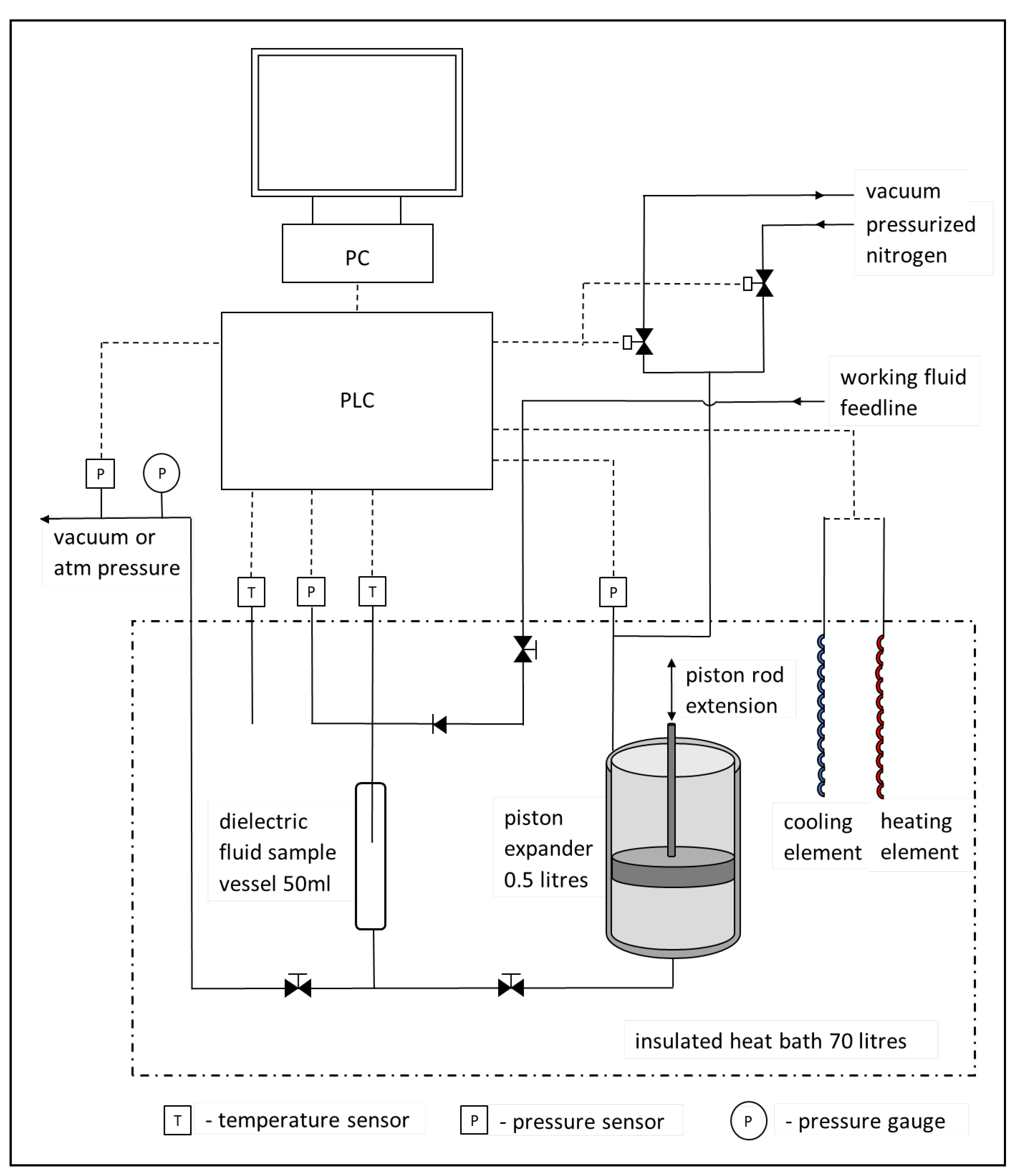
The temperature and pressure of the crystal-fluid are measured at five-second intervals with sensors that have direct contact with the crystal-fluid and recorded by a PLC/ PC monitoring system. All values for energy and thermodynamic potentials are derived from the pressure and temperature measurements by the NIST REFPROP program/database [19]. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0) [20]. The piston expander is completely immersed in a heat bath with a temperature of 270K, approx. The schematic arrangement provided in Figure 1 is reproduced from [2].
A negative pressure fluid is established by the Berthelot method [21]. Approx. 3.5 grams of crystal-fluid are transferred into a previously evacuated stainless-steel sample vessel (50ml). A low-energy, negative pressure regime results in the formation of water ice cages hosting methane molecules. The sample vessel is completely immersed in a relatively large heat bath (70 litres) where the temperature of the bath is controlled with an electric element and a refrigeration dip cooler. Once the desired temperature is obtained, the sample is released into the fluid-side of the 0.5 litre retracted piston expander, also completely immersed in the heat bath, which displaces the piston vertically upwards to the fully-extended position. The gas-side of the piston is open to atmospheric pressure during the extension. This action reduces the energy of the system further and is intended to transfer the guest methane molecules from the host water ice cages to similar structures within the inhibitor solvent. Negative and positive piston displacements are then induced through pressurized nitrogen perturbations to produce negative and positive work outputs where displacement ratios are 1:100 and 100:1, approx.
From completion of the Berthelot mixing process through subsequent positive and negative displacements of the piston expander, REFPROP determines that the crystal-fluid material remains in a subcooled liquid phase, as recorded in Appendix A of [2]. It is both astonishing and remarkable that 3.5 grams of material does not transition to a vapour or gas, nor produce any methane outgassing, when contained within the initial sample volume of 50 ml. More remarkable still is that an additional work-generating positive piston displacement of 0.5 litre also has no effect upon the integrity of the subcooled liquid phase. Notwithstanding, a conventional interpretation in terms of fluid mechanics would locate all the crystal-fluid material in the lowest section of stainless-steel tubing connecting the sample vessel to the piston expander (excluding any capillary action) due to ordinary gravity and the generation of work would be inconceivable. This perplexing and counterintuitive outcome is examined in more detail below together with supporting mathematical expressions.
In addition to the temperature and pressure measurements, only the piston position and mass of the material components are required to calculate all the thermodynamic properties, critical exponents and scaling relations shown in Appendix A of [2]. Whilst validity of the REFPROP calculations may be reasonably challenged, it has been demonstrated successfully that the program/ database is very sensitive to outgassing and re-absorption events associated with phase transitions in similar materials when performing quasi-thermodynamic cycles [7]. In such circumstances methane outgassing accompanies the formation of low-energy, guest-free water ice cages and is consistent with the fluctuation-dissipation theorem. With these phase-change processes, long-range interactions are also established whereby non-additivity in the fundamental thermodynamic relation is revealed.
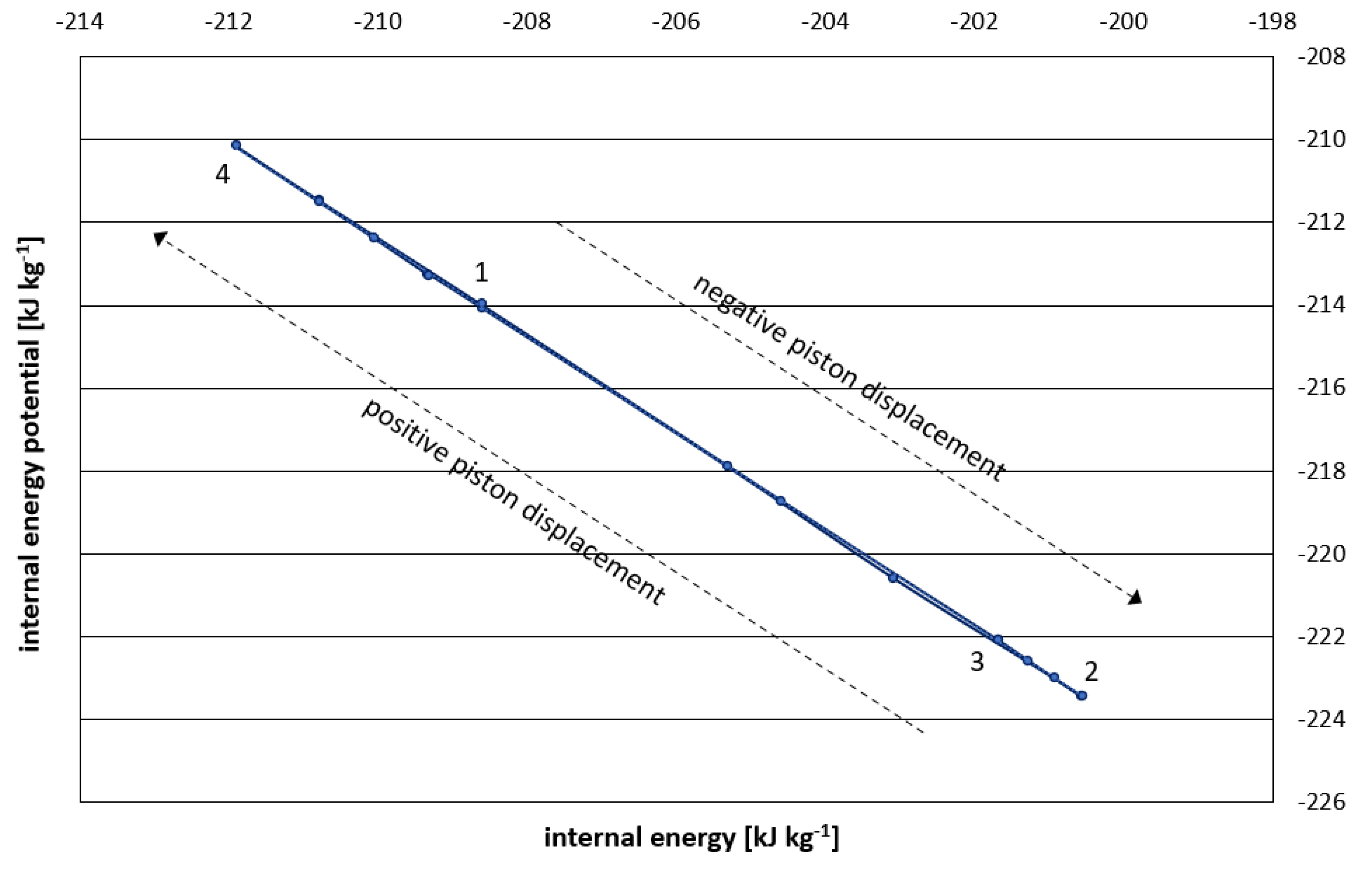
Figure 2 is reproduced (with some additional annotation) from the recent experimental results reported in [2] where Points 1-4 identify particular stages of the work cycle in a low-energy system; Stage 1-2 corresponds to negative displacement of the 0.5 litre piston expander and Stage 3-4 corresponds to positive displacement.
Changes in negative potential energy and internal energy vary in a 1:1 relationship after discounting the Pv work term associated with the walls of the vessel. Thus, a linear oscillator or constant energy Hamiltonian function is determined. The associated affine non-concave entropy function represents local stability conditions achieved through dynamically responsive inhomogeneities, i.e., the complex reorganization of dissipative structures composed of water ice cages, such that energy cannot be minimized and entropy cannot be maximized [4]. Specific volume and internal energy are shown to be highly constrained intensive parameters.
Loss of homogeneity is characteristic of phase transitions that give rise to critical phenomena. The discovery of a distinctive universality class of critical exponents that obey the scaling laws of Fisher, Rushbrooke, Widom and Josephson [22] reveals spontaneous magnetic and superconducting properties for the crystal-fluid material investigated. A phase transition from Type-II superconductivity to dual Type-I superconductivity is identified through the Ginzburg-Landau parameter κ where the spontaneous magnetic field Hs transitions from negative to positive [2] and a complex order parameter field Ψ(r) emerges. Spontaneous magnetism Ms can either increase or decrease dependent upon the change in magnitude of hyperbolic curvature K. Positive piston displacement results from a reduction in K to give increasing values of Ms. Negative piston displacement results from an increase in K to give reducing values of Ms.
Derivation of the Gaussian hyperbolic curvature K also gives the Gaussian radius Rg as its inverse, as shown below. This enables the hyperbolic surface area of a hollow, walled sphere having effective radius R to be determined (A = 4πsinh2(R/2)) [2]. The hyperbolic surface area maps almost exactly to the negative inverse of the gradient energy where topological defects are introduced. The external pressure perturbations may be interrupted at any point such that both the swept volume V and the hyperbolic curvature K become fixed and stable. This suggests that the non-equilibrium gradient energy is captured and confined within the hydrogen bonding interactions of the water ice cages and inhibitor solvent as the system relaxes into a non-critical, stable state.
Inequalities in the associated Maxwell relations together with calculations of the hyperbolic geometry reveal non-additivity and non-extensivity in the fundamental thermodynamic relation. Additivity can be restored through hyperbolic curvature (i.e., surface area A) whilst extensivity can be restored through gradient energy/ coupling energy (i.e., volume V) [23]. The coupling energy is related to the critical correlation length exponent v in 3-dimensions combined with values of a scalar field Φ as derived from the gradient energy term -½(∇Φ)2 of the Lagrangian such that:
c o u p l i n g   e n e r g y ∝ e Φ 3 v
The critical correlation length ξ associated with the universality class is linked to volume V through Lorentz boosts, i.e., relativistic velocity and the reference frames associated with acceleration and deceleration [2]. The critical correlation length ξ is revealed to be a Lorentz length expansion; a relativistic phenomenon coinciding with the formation of a magnetic condensate [14]. The relativistic time contraction conjugate to the critical correlation length is also revealed in Figure 3 where the y-axis representing scalar field values has units of s-1, i.e., the reciprocal of time.
Again, the correlation length ξ is associated with a superconducting phase transition and related to a Lorentz boost in 3-dimesional space [2]. Its value reveals the presence of self-organized criticality responsible for a ‘rolling’ critical response in accordance with:
ξ ~ │ T − T c │ − v
where T is the system temperature and Tc is the critical temperature. Both temperatures are dynamic under external pressure perturbation to reveal sustained anisotropy in the water ice cage structures in either direction. ξ corresponds to a gap in gradient energy and increasing values of the gauge field Φ are associated with relativistic length expansion and time contraction [2].
The gradient energy term -½(∇Φ)2 equates with PV work (i.e., it is described by the least action principle of the Lagrangian) whilst the hyperbolic surface area is a function of the Gaussian radius of hyperbolic curvature Rg. Both properties are calculated from experimental results [2]. In order for the gradient energy to be fully expressed on the surface of the system, it is necessary to introduce topological defects at the superconducting phase transition where the spontaneous magnetic field Hs moves from negative to positive through zero.
Application of the scaling laws to the experimental results [2] reveals that pressure perturbation induces low susceptibility χ leading to spontaneous magnetism Ms with associated spontaneous magnetic field Hs. For positive Hs, ordering is attributed to the emergence of the complex parameter field Ψ(r) and the topology associated with magnetic frustration and charge fractionalization. Condensation of fractionalized magnetic charges into a monopole condensate [13,14] would act to exclude magnetic current from the embedding vacuum manifold resulting in the spontaneous magnetism that also excludes the electric field E to establish dual superconducting behaviour.

2. Analysis and Discussion

2.1. Gauge Symmetry

The exponential function for the coupling energy e3vΦ, as derived from experiment (1), represents a capturing of the magnetic condensate wavefunction through the energy degeneracy of the water ice cage structures such that it becomes real and observable. It also expresses the scale-invariant and gauge-invariant properties of the critical system. Conservation of angular momentum requires the existence of a sink/ source for the associated changes in inertia (variable effective radius) together with a corresponding symmetry relation.
Scale-invariance is attributed to the hyperbolic curvature of Lorentz boosts that impose a conformal symmetry on the embedding vacuum manifold [24]. Conformal symmetry is able to describe the tetrahedral, hydrogen bonded, 3-dimensional spatial geometry of the crystal-fluid under non-extensive volume changes whilst its variable hyperbolic surface area maps to the gradient energy term of the Lagrangian (see below). Since a universality class of topologically invariant critical exponents has been determined for the continuous (second order) phase transition, the system can be modelled through conformal field theory in 4-spacetime dimensions, i.e., it is describable by a renormalizable quantum field theory in which the non-perturbative conformal bootstrap is irrelevant [25].
Yang-Mills theory is a strongly coupled quantum field theory [18], i.e., a gauge theory in which the low-energy dynamics are far removed from any classical description [26]. It is represented through the mathematical structure of Lie groups that provide for intricate topologies. The compact, simple Lie group SU(3) describes the strong interaction in QCD, i.e., the binding of quarks and gluons through confinement mechanisms. The mechanical action of the piston expander can be described by the emergence of a gauge field Φ and the critical length exponent v (as equation (4) below). In QCD such gauge fields are collectively known as gluon fields. The field strength, or curvature Fμν, has the general form:
F μ ν   = ∂ μ A ν − ∂ ν A μ − i A μ , A ν
where Aν provides for Lorentz invariance and Aμ is the gauge connection.
The gauge connection depends upon a complex scaling symmetry that is exact but not directly observable [27]. In the quantum state Ψ → eiθΨ, which could be interpreted as a potential sink/ source for the ‘hidden’ inertia of the false vacuum system (although later this is revealed not to be the case). It also represents the complex order parameter field of the Ginzburg-Landau superconducting phase transition included in equation (7) below.
Experimental results lead to a relativistic manifestation of length expansion and time contraction arising from false vacuum behaviour in a thermodynamically constrained condensed matter system. The local stability conditions maintained through dynamically responsive inhomogeneities in this soft matter are deemed equivalent to the property of asymptotic freedom, or antiscreening, which accounts for the mechanism of colour confinement in particle physics, i.e., scale-invariance is effective across the micro- and macro-scales of the system. In QCD it is the emergence of clouds of virtual gluons that establish the antiscreening phenomenon [5]. In both mechanisms, increasing kinetic energy is mirrored by an increasing negative energy potential such that total energy remains constant.
Whilst the crystal-fluid material displays high stability in total energy and density, the embedding manifold always remains on the threshold of instability. Small positive or negative pressure perturbations produce divergent critical behaviour manifesting as large variations in swept volume V. However, this is not the specific volume of the material system (density remaining almost constant) but rather the non-extensive volume change associated with the condensation of magnetic charges and simultaneous emergence of a gradient energy term.
The ‘rolling’ critical response initiated by anisotropy in water ice cage structures facilitates net energy gain for the duration of external pressure perturbations, either positive or negative, in a display of self-organized criticality [28]. The angular momentum of the material is transferred to or from the embedding vacuum manifold through self-organizing behaviour and high energy degeneracy of the water ice cage structures. However, this brief statement does not provide a full description and a more detailed hypothesis follows.
Work derived from the piston expander can be expressed in terms of an electromagnetic pseudo-scalar gauge-invariantly coupled to the gauge field Φ and the critical length exponent v. The relationship is in agreement with the cosmological inflation model proposed by Ratra [29]:
∫ P d V = 1 2   F μ ν F μ ν e 3 v Φ
where the covariant vector Fμν and contravariant gradient potential Fμν combine to produce Lorentz invariance for the pseudo-scalar field when rotated on a hyperbolic manifold, i.e., the electromagnetic field pseudo-scalar enables a non-additive energy contribution to enter the non-equilibrium system in the form of hyperbolic curvature.
In the quasi-micro-canonical ensemble [2], the electromagnetic field pseudo-scalar is involved in the coupling mechanism but contributes no work in itself. It expresses the Berry curvature of the vacuum manifold whilst hosting the magnetic exchange pathways that facilitate energy transfers either to or from the vacuum manifold. The inner-product of the E and B fields remains the same viewed in all relativistic frames [30] with the pseudo-scalar field remaining Lorentz invariant such that:
1 2   F μ ν F μ ν = B 2 − E 2 c 2 = c o n s t a n t
where c is the speed of light.
Ginzburg-Landau theory states that the free energy of a superconductor near a phase transition can be expressed in terms of a complex order parameter field [31]:
Ψ r = Ψ ( r ) e i Φ ( r )
Then a complex rendering of the coupling energy term e3vΦ maps to a complex wavefunction of the Berry phase:
e i Φ 3 v → Ψ ( r ) e i Φ ( r ) 3 v
where the quantity |Ψ(r)|2 reflects the density of superconducting charge carriers; electrons for Type-II and the magnetic counterpart arising from gauge monopole charges for dual Type-I [13]. Appendix A provides a summary of the Ginzburg-Landau theory of superconductors.
In the dual superconductor model of confinement [11,12], the Yang–Mills vacuum is based on the condensate of a magnetically charged Higgs field. In this situation, the critical correlation length ξ also represents the coherence length ξ’ of the magnetic monopole condensate [14] which diverges to encompass total hyperbolic volume V of the system at the superconducting phase transition [31]. In this case the coherence length ξ’ becomes exceptionally large under relativistic Lorentz rotation [2]. ξ’ also gives the distance over which the dual superconductor can be represented by a wavefunction.
Since the coherence length ξ’ and maximum value for the Ginzburg-Landau parameter κ for the Type-I dual superconductor are known [2], the London penetration depth λ can be derived (see Appendix A). ξ’ and λ are equal to the inverse Higgs mass mH and inverse vector boson mass mV, respectively [13]. In normal metallic superconductors λ is the distance within which an externally applied magnetic field disappears inside the superconductor. However, for the dual superconductor λ represents a distance beyond the developing QCD flux tubes within which the magnetic current and electric field are expelled as a result of the dual Meissner effect.
So, mH determines the extent of QCD vacuum, which manifests in the embedding vacuum manifold volume V
and mV determines the Gaussian hyperbolic curvature K of the embedding vacuum manifold.
Appendix A includes supporting quantitative analysis.
The complex form of the coupling energy term resembles a quantum mechanical wavefunction in which the energy spectrum is made entirely real and observable through dissipative structuring of water ice cages. Ψ0(r) corresponds to the emergence of the gauge field Φ at the Type-II to dual Type-I superconducting phase transition. Dissipation of either the scalar field or the critical correlation length ξ would represent a collapse in the wavefunction.
Application of de Moivre’s formula and isomorphic mapping of the complex field to hyperbolic rotational matrix form gives:
e i Φ 3 v = cosh ⁡ 3 v Φ + i sinh ⁡ 3 v Φ →   cosh ⁡ 3 v Φ i   sinh ⁡ 3 v Φ   − i   sinh ⁡ 3 v Φ cosh ⁡ 3 v Φ ≕ V
and similarly expressing electromagnetic duality as rotations in the 2-dimensional hyperbolic plane:
1 2   F μ ν F μ ν →   cosh ⁡ 3 v Φ − i   sinh ⁡ 3 v Φ i   sinh ⁡ 3 v Φ cosh ⁡ 3 v Φ ≕ V H
The conjugate transpose of (8) is (9) and the determinant of VVH = 1 suggesting that PV work of the piston expander is contingent upon the decomposition of a Hermitian unitary matrix A into two 2 x 2 non-Hermitian unitary matrices (i.e., two complex matrices V and VH containing both real and imaginary components such that VH ≠ V) [32]. The gauge field and the electromagnetic pseudo-scalar are thereby coupled through a marginal interaction in the hyperbolic plane.
Although this interpretation appears at odds with the expression for PV work stated in (4), in fact any 2 x 2 complex symmetric matrix A can be eigendecomposed into a diagonal matrix D sandwiched between two complex unitary matrices, i.e., VDVH in this case. Minkowski spacetime vectors can be represented by 2 x 2 orthogonally diagonalizable matrices and incorporated into the extended physical VDVH decomposition to reveal the coupling energy source:
D ≔ e Φ 3 v 0   0 e Φ − 3 v
These Hermitian matrices exhibit basic 3-dimensional rotation as well as 4-dimensional Lorentz transformation properties consistent with the relativistic length expansion and time contraction associated with the non-extensive element of PV work, as revealed through the experimental results [2]. Thus, the 2 x 2 unitary matrix A as a member of the U(2) symmetry group is decomposed into factors identifiable as both Hermitian and non-Hermitian.
When represented in terms of gauge symmetry groups [32], the U(1) group of electromagnetism (via its mapping to SO(2) in the 2-dimensional real plane) and the SU(2) group of the complex order parameter Ψ(r), are in fact subgroups of the U(2) group such that:
U 1 ⊗ S U 2 /   Z 2 →   U ( 2 )
which describes a mapping to a Yang-Mills electroweak symmetry group [33] where ℤ2 represents the topology associated with the condensation of gauge monopoles [34]. Formation of the U(2) group is accompanied by critical behaviour and emergence of the gauge field Φ as predicted by the Yang-Mills theory.
The dual superconductor model has several interpretations that require condensation of gauge monopoles, just as normal superconductivity results from the condensation of electric charges (or Cooper pairs – see Appendix A) [13,14]. Theoretical frameworks for the condensation of gauge monopoles have been structured in terms of Abelian gauge-invariance (the SU(2) gauge symmetry group) or non-Abelian gauge-invariance (the SU(3) gauge symmetry group). Recent efforts [14] have sought to extract the Abelian component responsible for gauge-independent quark confinement from non-Abelian gauge-invariance required for gauge monopole condensation without losing the essential characteristic of asymptotic freedom. From the experimental findings [2] such a solution emerges out of an electroweak interaction that preserves asymptotic freedom, as described below.
In the vacuum of a dual superconductor, the dual Meissner effect compresses the chromoelectric flux between a quark and antiquark into a thin flux tube to form the hadronic string [13,35]. As the distance between quark and antiquark increases, the flux tube becomes longer whilst maintaining a minimal thickness. This geometry ensures that the energy increases linearly with length to create a linear confining potential between the quark and antiquark that bears a similarity to the linear oscillating Hamiltonian of the system. The flux tube determines the extent of QCD vacuum suppression, i.e., positions where the colour-electric field is maximally expelled to leave a residual dual superconductivity [36].
Yang-Mills theory requires the existence of both chromomagnetic monopole condensation (given by a coherence length) and the dual Meissner effect (given by a penetration depth) [13,14]. The force carrying gauge bosons of QCD are gluons which perform a similar role to photons in electromagnetism. Since the gluon field represents a local expulsion of the QCD vacuum, the absorption of physical gluon emissions into the QCD vacuum would tend to reduce local ‘space density’ and effective magnetic permeability μ0. The net effect is to increase the hyperbolic curvature K of the embedding manifold, i.e., a quantum mechanical process manifests as ‘strong gravity’ [37].

2.2. Berry Phase and Parity-Time (PT) Symmetry

The foundations of Berry phase physics lie in the adiabatic theorem of quantum mechanics [38] which provides a formal description for a system coupled to a slowly changing environment. If the system Hamiltonian H(t) varies adiabatically and │Ψ(t)⟩ is an associated eigenstate then, following cyclic evolution of the environmental parameters where H(T) = H(0), the state returns to itself but gains an additional phase factor [38,39]:
│ Ψ T ⟩ = e i α │ Ψ 0 ⟩
where α represents the angular momentum of the wavefunction. For a dual superconductor, it originates from the exclusion of momentum resulting from chromomagnetic monopole condensation which is effectively stored in the electromagnetic field pseudo-scalar [24].
The adiabatic theorem is based upon a single, non-degenerate eigenstate to which the system ‘clings’ as the environment is slowly changed [40]. However, for the pressure-perturbed system being examined, asymptotic freedom constrains innumerable, degenerate and excited eigenstates to a singular value of total energy in the oscillating Hamiltonian function. External pressure perturbations applied to the crystal-fluid material see changes in kinetic/ internal energy mirrored by changes in negative energy potential such that total energy remains constant. When perturbations cease, the negative energy potential dissipates but internal energy becomes fixed close to the final resting value. So, in this case, a positive or negative perturbation of any duration is responsible for a single linear oscillation, or cycle, that is imposed upon a linear, sliding-scale of discrete values. Integration of the scalar potential ∇Φ over a Hamiltonian cycle reveals the gradient energy term -½(∇Φ)2 that becomes observable in the PV work extracted from the piston expander (see equation (22) below).
The transient negative energy potential responsible for the phase factor Ψ(T) exists only for the duration of the pressure perturbation. Whilst the Hamiltonian remains constant under perturbation (as Figure 2), it resolves to a different, stable value once the perturbation ceases. The final value of internal energy is then ‘propped’ and stabilized through dissipative structuring of water ice cages, subject to limited dielectric relaxation, as quantified by Stage 2-3 and Stage 4-1 (Figure 2).
For acceleration (Stage 1-2) the effective radius decreases, and for deceleration (Stage 3-4) the effective radius increases. However, the resulting ‘hidden’ inertia is deemed not to be directly responsible for the Berry curvature term within the geometrical phase (7) since the externally-induced momentum manifests entirely in non-additivity of the hyperbolic curvature K. Instead, the Berry curvature is linked to the condensation of magnetic charges whereby the resulting exclusion of charge momentum manifests in the energy potential of the electromagnetic field pseudo-scalar (5). The Berry curvature is subsequently captured to be made real and observable in the variable hyperbolic volume V of the embedding vacuum manifold. Again, this hyperbolic volume is stabilized by the dissipative structuring of water ice cages within the crystal-fluid material so that the complex Berry phase is transformed into real work done.
For a classical thermodynamic system, changes in inertia ½mr2 represent changes in kinetic/ internal energy. However, since both internal energy and specific volume are highly constrained parameters within a false vacuum system, the energy of acceleration/ deceleration is prevented from manifesting in the crystal-fluid material. Thus, Pv work is limited to interactions with the walls of the vessel. For the synchronized U(2) symmetry group identified below, angular momentum is instead conserved in the acceleration/ deceleration of quarks that results in the emission/ absorption of gluons, i.e., changes in negative energy potential. Gluons emitted by quarks are absorbed by the QCD vacuum manifold whilst the gluons absorbed by quarks emerge from the QCD manifold, thereby tending to effect local ‘space density’ and effective permeability μ0.
Pv is insignificant in comparison to PV such that it represents the negative energy potential of the crystal-fluid material only. Therefore, for a constant Hamiltonian oscillator of constant mass m, ½r2 ∝ 1/Pv, as described in Appendix B of [2]. The average 1-dimensional radius rx of the stable, pre-critical system is then found:
r x   ∝   2 P v
The Gaussian curvature K for the 2-dimensional, hyperbolic surface of the pre-critical system (i.e., with no topological defects) for the principal curvature relationship of rx = - ry , can then be determined:
K = 1 r x r y
or
K   ∝ − P v 2
Then, the average Gaussian radius of hyperbolic curvature (1/K or Rg) is given by:
R g = 2 P v
Gaussian curvature K has units of m2 s-2 that map directly to the vector boson mass mV as the inverse of the penetration depth λ (as described in Appendix A). Through this mechanism, the negative energy potential of gluons is conserved through indirect hyperbolic curvature quantifiable by the non-equilibrium values of pressure P and specific volume v. Thereby, a quantum mechanical action is tuned thermodynamically under false vacuum conditions.
Decomposition of the complex gauge connection (eiΦ)3ν in equations (8) and (9) suggests that complex Berry curvature is necessary for emergence of real coupling energy (1). It also determines the phase of electromagnetic duality, which in the extreme leads to dual superconducting behaviour, i.e., condensation of magnetic charges resulting in the exclusion of magnetic current and the electric field. The cyclic evolution of the gauge connection results from the effective adiabatic property of the constrained false vacuum system (as revealed in the constant Hamiltonian oscillator of Figure 2) to establish a novel form of the Berry phase [38], one responsible for topological ordering in the dual Type-I superconductor [10]. As with the conventional ground-state Berry phase, this ‘excited-states’ variant exposes the gauge structure in quantum mechanics [15,41].
In addition to describing the emergence of a gauge field Φ, the gradient energy term -½(∇Φ)2 of the Lagrangian also maps to the complex order parameter field Ψ(r) in accordance with Ginzburg-Landau theory. The PV work generated in the piston expander suggests that the associated quantum mechanical wavefunction is made real and observable, a phenomenon recently uncovered by Gu et al. [15]. More precisely, the VDVH decomposition reveals that the wavefunction becomes entirely real as the coupling energy is exposed through the diagonal matrix D in the VDVH decomposition (10).
Since the system can be described through a combination of Hermitian and non-Hermitian matrices, it resembles a PT symmetric system [16]. Such systems are characterized as not being isolated from the environment (i.e., non-adiabatic) but subject to highly constrained interactions. This description is consistent with the false vacuum behaviour of the crystal-fluid material where both specific volume and internal energy are highly constrained. Energy and entropy gains and losses to the environment (including the embedding vacuum manifold in this case) are exactly balanced, i.e., a renormalized, scale-invariant interaction between condensed matter and quantum wavefunction becomes evident in the constant energy Hamiltonian.
PT symmetry requires both space reflection and time reversal symmetries. The upside-down potential of the quartic term as identified by Bender [16] is consistent with the marginal interaction and negative gradient energy term derived from experiment [2]. However, the results presented here reveal the symmetry of Lorentz boosts, i.e., symmetries in the expansion and contraction of both space and time, which may represent a more generalized form of PT symmetry.

2.3. Symmetry Synchronization and Conserved Quantities

Quark acceleration produces gluon emissions since a lower binding potential is necessary to maintain the momentum and energy of any given quark colour configuration [42]. This results from a gluon recombination process whereby a quark and antiquark pair are annihilated. The emergence and absorption of physical gluons represents an exchange between the non-Abelian gauge symmetry of QCD and the Abelian gauge symmetry of the vacuum manifold, i.e., an electroweak interaction.
The following non-Abelian Faddeev-Niemi decomposition is considered [43]:
S U N + 1 →   S U N ⊗ U ( 1 ) Z N   ~   U ( N )
This decomposition is a restricted one since splitting and recombining gluons in SU(3) represents a limited interaction with a U(2) spacetime manifold rather than full symmetry breaking to SU(2). The requirement for a Higgs-type scalar field is satisfied by the emergent gauge field Φ [14]. So:
S U 3 →   S U 2 ⊗ U ( 1 ) Z 2   ~   U 2   ~   S U 2 ⊗ U ( 1 ) Z 2   →   S U 3
Asymptotic freedom is thereby maintained through the dominant SU(3) group. Again, U(2) appears as an electroweak symmetry group [33] with ℤ2 representing a topology consistent with the condensation of gauge monopoles [34].
A U(2) gauge symmetry that provides for the condensation of gauge monopoles has so far been identified in both the condensed matter system and the underlying QCD particle physics. However, it is also possible to determine a U(2) gauge symmetry for the vacuum manifold of local spacetime through which hyperbolic curvature and scalar field potential are effected. That is, where the splitting and recombining of force-carrying gluons are associated with fictitious forces in non-inertial reference frames.
The Lorentz group SO(4) provides for the conservation of energy and angular momentum in 4-dimensions (ℝ4) through two continuous symmetries; rotations in 3-dimensional Euclidean space and Lorentz boosts which influence both space and time [44]. The 4 x 4 orthogonal matrix representation of the metric tensor can also be cast in terms of a 2 x 2 unitary matrix operating on a complex 2-component spinor. The complete unitary 2 x 2 transformation matrix for spinor rotations and boosts can be expressed as:
U = e 1 2 i σ . θ − 1 2 σ . φ
or
U = e 1 2 i σ . θ + 1 2 σ . φ
where θ is the Lorentz rotation angle, σ is the Pauli spin matrix, and ϕ is the angle associated with the Lorentz boost (or rapidity) [45]. Equation (19) represents a ‘right-handed’ spinor ϕR and (20) represents a ‘left-handed’ spinor ϕL, i.e., the Weyl spinors. Later insights by Dirac led to the concept of the bispinor which, unlike (19) and (20), preserves parity of the wavefunction under the sign reversal operation Ψ(x,t) → Ψ(-x,t) thereby maintaining a positive gauge field and positive energy (whilst also predicting the existence of antimatter). However, retaining the 2 x 2 unitary matrix whilst acknowledging parity preservation requirements produces the following spacetime group representation [46]:
S O 4 → S U 2 ⊕ S U ( 2 )
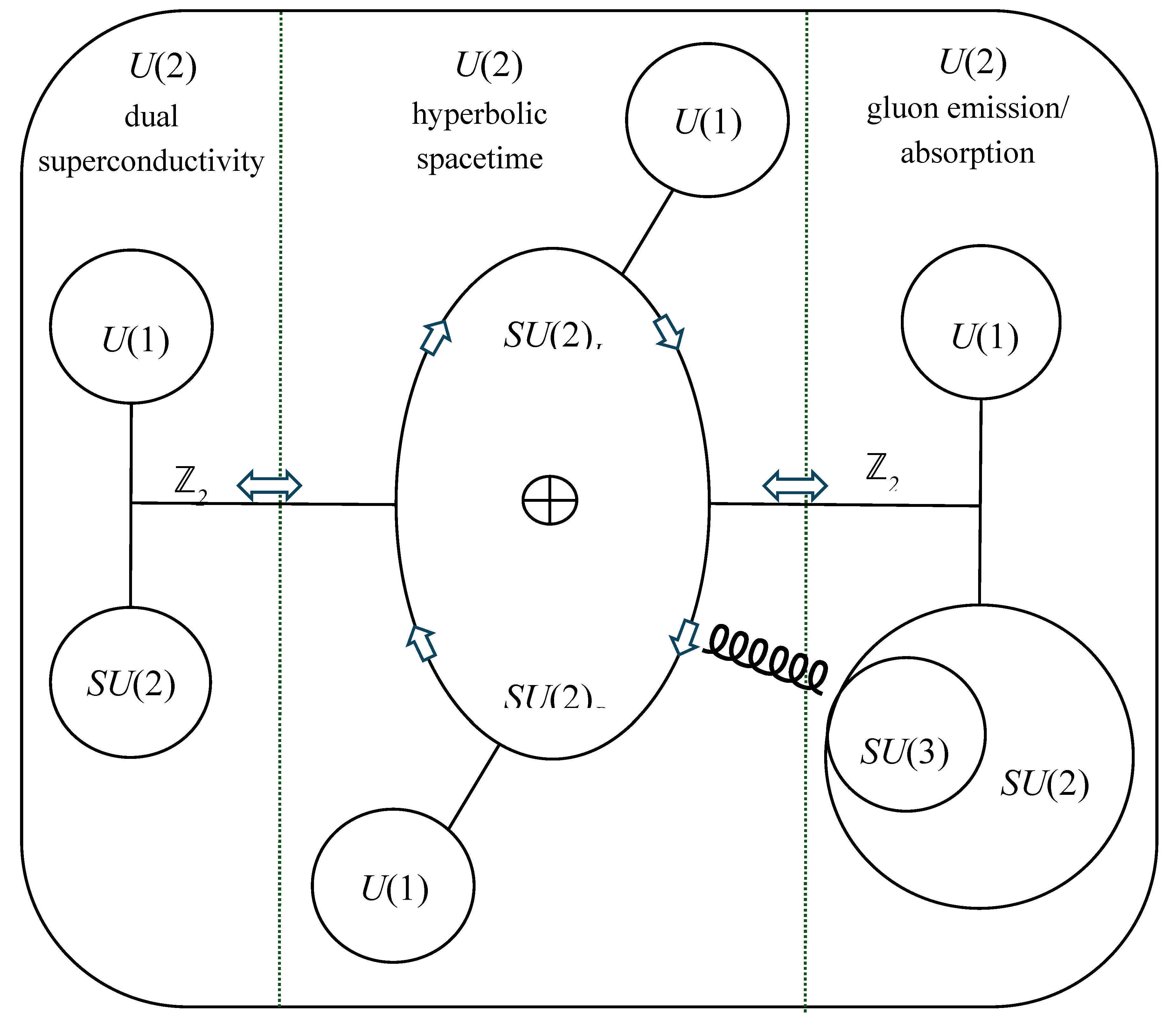
The symmetry group decompositions in (11), (18) and (21) are then amalgamated to describe a consolidated ‘symmetry synchronization’ that establishes common scale- and gauge-invariance in U(2), as shown schematically in Figure 4:
When a symmetry is broken, a corresponding order parameter that diminishes to zero can often be identified. However, in this case the complex order parameter Ψ(r) emerges where symmetry is synchronized.
Both energy and angular momentum are conserved within the common U(2) group to reveal the time and space symmetries of a Lorentz boost in agreement with Noether’s theorem (see below). Since there is a gluon field for each colour charge, it follows that each gluon field can be composed of a time-like component and three space-like components. These components relate to the electric potential and the magnetic potential, respectively, and will interact with the vacuum manifold to determine the values of effective permittivity ε0 and effective permeability μ0.
Variations in effective μ0 require that a spontaneous magnetic flux Ms, with associated spontaneous magnetic field Hs, emerges to conserve magnetic charge. Fractionalized magnetic charges arising from the geometrically frustrated crystal-fluid material can be interpreted as condensing into a gauge monopole topology that excludes magnetic current to provide magnetic exchange pathways. The correlation length ξ of the magnetic monopole condensate produces divergent critical behaviour that is shown to have a distinctive universality class of critical exponents. The gauge monopole topological defects act as both convergent sinks (under acceleration) and divergent sources (under deceleration) of the magnetic flux Ms [10]. The nature of these defects is speculated in Appendix A.
Similar principles apply to variations in vacuum energy determined by the local ‘space density’ (which determines the embedding manifold curvature). Conservation of energy requires that negative PV work is performed under false vacuum acceleration (energy is transferred to the vacuum manifold) whilst positive PV work is performed under deceleration (energy is transferred from the vacuum manifold). Work is related to the gauge/ scalar field Φ as follows [2]:
∫ P d V = − 1 2 ∇ Φ 2
The right-side of equation (22) represents the gradient energy term of the Lagrangian function resulting from the scalar potential ∇Φ developed across the gauge monopole topology to give the integral of the scalar potential ∇Φ. The Lagrangian action of the left-side, i.e., mechanical work, is also related to the critical response function revealed in the coupling relationship (1) to confirm energy renormalization in the synchronized U(2) group complex parameter field Ψ(r). That is, energy equivalence between the long-range dissipative structuring of water ice cages and the short-range confinement mechanisms of sub-atomic particles, as illustrated in Figure 4. This outcome aligns with Anderson’s speculative prediction [47]:
‘Physics in the 20th century solved the problems of constructing hierarchical levels which obeyed clear-cut generalizations within themselves […]. In the 21st century one revolution which can take place is the construction of generalizations which jump and jumble the hierarchies, or generalizations which allow scale-free or scale transcending phenomena. The paradigm for the first is broken symmetry, for the second self-organized criticality.’
With U(2) scale- and gauge-invariance spanning the asymptotically-free behaviour of both the macro-scale dual superconducting system and the quark-gluon system via interactions with the embedding vacuum manifold, a physical correspondence between non-equilibrium thermodynamics and quantum mechanics is established. Since the superconducting phase transition is represented by Ginzburg-Landau theory (i.e., gauge-invariant coupling of a scalar field to the Yang-Mills action is predicted) it seems reasonable to link the gradient energy gap of Figure 3 to the mass gap problem in QCD.

2.4. Gapped and Gapless Topologies

The results in Figure 3 show emergence of the gauge field Φ as a gap between Type-II superconductivity on the left and dual Type-I superconductivity on the right. This represents a transition between the gapped state of the magnetically ordered Type-II superconductor and gapless state of the topologically ordered dual Type-I superconductor. At this point, the gauge monopole charges condense and the electric field E is excluded to be confined on the surface of the system (prior to the emergence of topological defects that penetrate the magnetic condensate). That is, a gapless surface is established so that the Berry phase manifests as a non-trivial topological insulator [38].
The gapless surface may be protected from external perturbations tending to re-open the gap through non-Abelian topology, as represented by the ℤ2 Chern number in the symmetry group decompositions of (11) and (18). In a review of topological superconductors [48], Sato and Ando explore the connection between ℤ2 and time reversal symmetry that is consistent with the symmetry of Lorentz boosts described above. The ℤ2 Chern number can be interpreted as a U(2) group that fibres over a circle as a 3-sphere bundle, i.e., a Hopf fibration results [49].
Typically, a topological insulator is characterized by a non-robust, non-degenerate ground-state in which energy bands coincide and exceptional, or ‘diabolical’, points occur. However, the Berry phase variant identified above displays the following features: asymptotic behaviour (robustness against perturbations); a critical correlation length ξ (long-range entanglement); conformal geometry (describable through quantum field theory); and degeneracy in non-trivial topology on a hyperbolic manifold [49]. Thus, the system also appears to be topologically ordered and so describable by an effective, low-energy topological quantum field theory (TQFT) in which many-body states would typically have topological ground-state degeneracy [50]. In TQFT the critical correlation length ξ is topologically invariant and therefore insensitive to the geometry of the embedding manifold, i.e., the critical exponents within the universality class remain constant under Lorentz boosts.
Within the research field of topological phases of matter, as investigated to date, all the topologically ordered states realized experimentally or investigated theoretically are established through strong electron-electron interactions. The coinciding valence bands of gapless ‘diabolical’ points allow for degenerate electron movements between the bands. In a crystal structure, the electronic band structures are described by Bloch’s theorem as expressed by:
Ψ r = e i k . r u ( r )
where Ψ is the wavefunction, r is position, u is a periodic function, and k is the crystal momentum vector.
However, the original formulation of the Berry phase was not specifically related to Bloch electrons. Instead, it was based on the general idea that quantum adiabatic transport of particles in slowly varying fields (e.g., electric, magnetic, or strain) could in principle modify the wavefunction by terms other than just the dynamical phase. So, equation (23) is seen to map to the experimentally derived equation (7) where variable electromagnetic duality of the pseudo-scalar field gives the periodic function u(r) and (eiΦ(r))3v represents the angular momentum of magnetic charges that becomes effectively stored in the pseudo-scalar field as the magnetic monopole condensate forms [26].
Since the degeneracy associated with the crystal-fluid material occurs in metastable excited-states (with non-zero temperatures), the gapless degeneracy of the crystal-fluid material cannot be attributed to Bloch electrons. So, whilst the gapless surface of the dual superconductor is protected through ℤ2 topology, an additional mechanism is necessary to supress excited-state fluctuations such that Bloch-wave behaviour can emerge.
A potential solution is presented in Figure 4 where the synchronized continuous symmetry group U(2) leads to descriptions of asymptotic freedom in both quantum and condensed matter systems. As conservation of angular momentum extends into the microscopic quantum realm, so confinement mechanisms extend out into the macroscopic condensed matter of the dual superconductor under a renormalized Noether symmetry. The non-Abelian SU(3) group of QCD remains dominant so that excited-state fluctuations due to changes in momentum are suppressed through confinement mechanisms and the constant Hamiltonian function is preserved. Topological defects may represent the penetration of the dual superconductor by the excluded electric field in the form of chromoelectric flux tubes, so enabling the formation of quark-antiquark pairs together with an inherent confinement mechanism.
Acceleration and deceleration of the crystal-fluid material thereby become confined interactions responsible for the splitting and recombining of gluons. Gluons are either absorbed by or emerge from the QCD vacuum manifold. The Higgs-like gauge field Φ also emerges in the transition from gapped Type-II superconductivity to gapless dual Type-I superconductivity to establish a reciprocal gap in the gradient energy, as revealed in Figure 3. For the gapless state, the spin-1 vector gluons are the force-carrying SU(3) gauge bosons/ quasiparticles that generate the Bloch-wave description in the magnetic condensate [51]. Gluon interactions with the embedding QCD vacuum manifold enable fictitious forces to emerge in non-inertial reference frames that lead to PV work in the piston expander.
Whilst the massless gluons either emitted or absorbed by accelerating or decelerating quarks act as gauge particles, gauge invariance is only established where the associated gauge field can emerge under U(2) ‘symmetry synchronization’ above a critical correlation length ξ in the low-energy system. That is, gauge monopole charges are required to condense so that the scalar field potential induces a flow of magnetic charge such that ∇. Bs = 0, where Bs is the spontaneous magnetic flux density.
By extension, the lower bound of the QCD mass gap can be attributed to a symmetry-breaking of U(2) and the evaporation of a gauge monopole condensate from below in the low-energy, infrared limit. In this event, the conservation pathway between the condensed matter and quantum systems no longer exists since the systems are effectively isolated except for weak residual gravitational interactions, i.e., the systems are decoupled. With this spontaneous breaking of U(2) gauge symmetry into isolated sub-groups, and the collapse of any critical magnetic correlation length ξ, there is no mechanism through which non-equilibrium angular momentum can be conserved through gluon interactions and the corresponding curvature imposed on the embedding manifold, i.e., conservation of energy and momentum becomes limited to the individual symmetry groups and the condensed matter system becomes describable by classical thermodynamics and discontinuous (first order) phase transitions. Thus, in this interpretation of broken gauge symmetry, a strong gravitational interaction [37] is replaced by a far weaker one essentially limited to gluon interactions arising from quantum fluctuations and other irrelevant interactions. In other words, it decoheres and becomes non-renormalizable.

2.5. Cosmological Analogy

The same principle may be applied to the high-energy bound of the QCD mass gap from above. Guth’s model of cosmological inflation [52,53] is also founded upon false vacuum and negative pressure conditions. The associated deceleration of inflationary expansion within a false vacuum would result in gluon splitting where conservation of energy and momentum are mediated by a synchronized order parameter field/ symmetry group together with the corresponding cosmic monopole condensate necessary to facilitate a critical coherence length and penetration depth. The splitting of gluons and the emergence of quark-antiquark pairs act to increase the strong interaction through confinement mechanisms.
The non-extensive inflationary volume expansion model is [2]:
V r = T − T c − 3 v
where Vr is the reduced volume │(V – Vc)/ Vc│ at the critical temperature Tc with a correlation length exponent v in 3-dimensions. Critical volume Vc and critical temperature Tc are not absolute values but rather ‘rolling’ dynamical values determined by structural anisotropy and dissipative false vacuum restructuring of elementary particles under non-equilibrium conditions. At the collapse of critical behaviour, Vr = 1 and non-extensive inflationary volume expansion ceases.
The critical length exponent v represents the dimensionless group parameter of rapidity such that its emergence on a Lorentz hyperbolic manifold (i.e., a Lorentz boost) is associated with a relativistic length expansion to describe non-extensive inflationary volume expansion [2]. Deceleration increases the effective radius of structural elements under false vacuum conditions such that angular momentum is removed from the sub-atomic quarks. The counteracting emergence of quark- antiquark pairs qq̄ plus gluons from the QCD vacuum, the associated gluon splitting, together with subsequent integration of the emergent particles into complex binding arrangements, establishes the colour and quark confinement mechanisms. 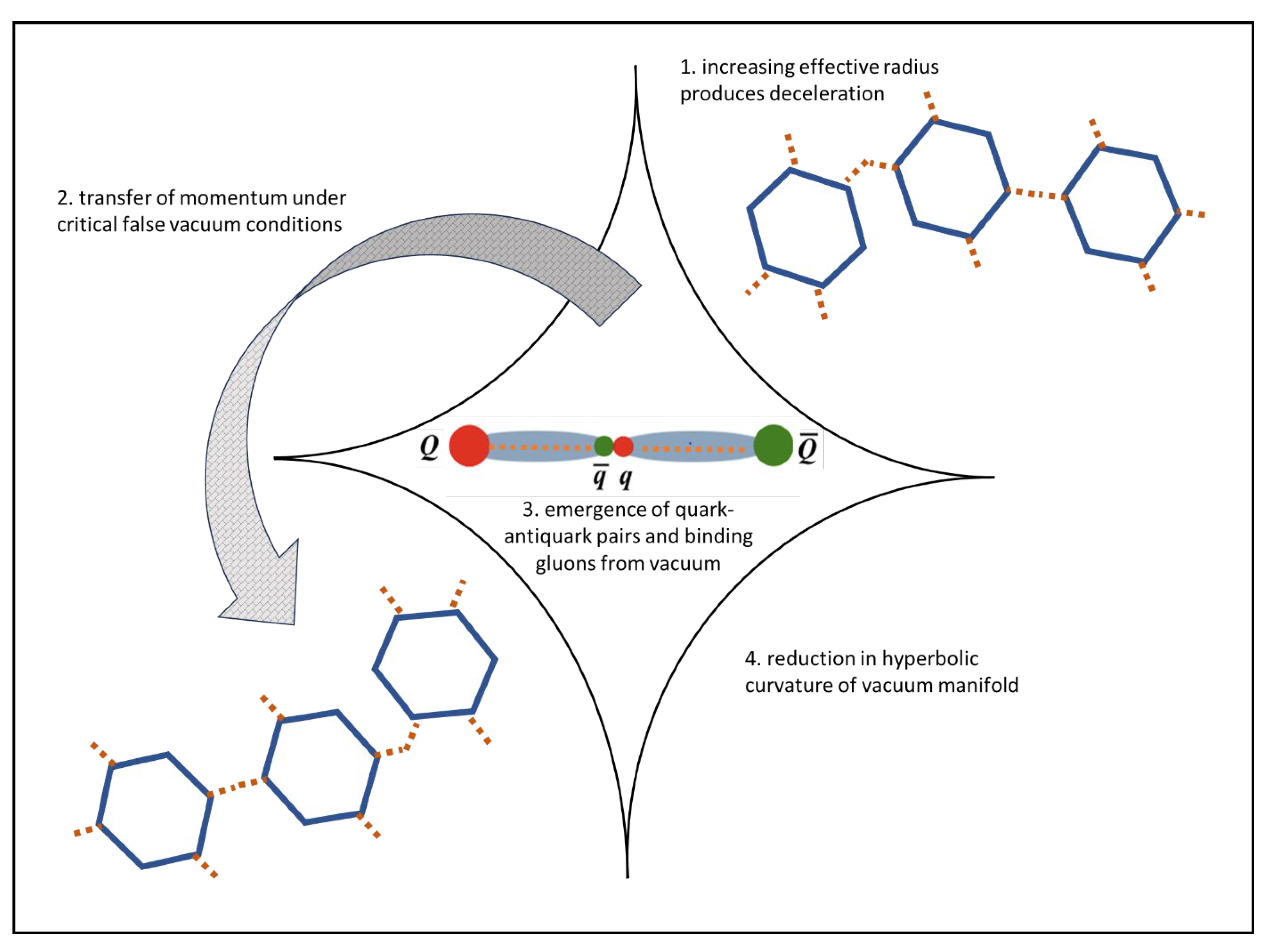These tend to increase local ‘space density’ and effective magnetic permeability μ0. The resultant effect sees hyperbolic curvature K of the embedding vacuum manifold reduce leading to inflationary expansion work. The process is shown as an analogue of the experimental findings in Figure 5.
At the collapse of critical behaviour, the synchronized gauge symmetry is broken, the cosmic monopole condensate with associated topology evaporates, and critical correlation length is destroyed. Absorption of the gauge field into the QCD colour field attributes mass to the emergent quark and antiquark pairs qq̄ of the confinement process under a Higgs-like mechanism associated with an electroweak interaction, whilst volume and internal energy are ‘propped’ and stabilized by reorganizing dissipative structural elements. Again, under such an interpretation, classical thermodynamics essentially separates, or decoheres, from quantum mechanics to leave only weak residual gravitational interactions, i.e., the strong interaction becomes short-ranged. The energy and mass of the strong interaction are thereby effectively fixed at the point where the common symmetry group associated with cosmological inflation is broken, the cosmic monopole condensate evaporates, and the critical correlation length is destroyed.

3. Conclusions

The complex reorganization of systems with high energy degeneracy is responsible for asymptotic freedom, as characterized by the emergence of variable negative potential that maintains constant total energy. In these systems, the excess negative potential imposes variable hyperbolic curvature on the embedding manifold to create strong local gravitational effects that combine with the mutually emergent coupling energy to produce mechanical work. This ‘strong gravity’ emerges only when quantum interactions are coupled to non-equilibrium thermodynamics through a critical correlation length.
Experimental investigations based upon external pressure perturbations uncover a macro-scale dual superconductor linked to the emergence of a gauge field and the associated synchronization of a common U(2) symmetry group that encompasses the dual superconductivity, Minkowski spacetime and quantum interactions. Combining Ginzburg-Landau theory with the scaling laws reveals a coherence length and a penetration depth that describe the macro-scale dual superconductor. The coherence length determines non-extensive volume changes whilst its inverse gives the Higgs mass. The penetration depth determines the extent of QCD vacuum suppression whilst its inverse gives the vector boson mass and resulting indirect hyperbolic curvature. In addition, the dual superconductor signifies long-range entanglement within a magnetic condensate displaying relativistic effects, whilst hyperbolic curvature of the vacuum manifold is attributed to quantum interactions. Gravity-mediated entanglement within the laboratory is thereby deduced.
Conservation of energy and angular momentum across the condensed matter and quantum domains is linked to time and rotational space symmetries in agreement with Noether’s theorem. It has been widely conjectured that gauge monopoles are associated with the U(2) group and ℤ2 topology, which enables a critical correlation length to be established. For the synchronized U(2) group, the gauge vector bosons are represented by the quark emission/ vacuum absorption of gluons from acceleration, and vacuum emission/ quark absorption of gluons from deceleration.
The emergent gauge structure combines with the effective adiabatic property of the constrained false vacuum system to establish an ‘excited-states’, degenerate Berry phase. This geometrical phase is responsible for topological ordering in the dual Type-I superconductor. The excluded electric field represents the gapless surface of a topological insulator that is protected from external perturbations through ℤ2 topology.
In complex form the gradient energy term of the Lagrangian strongly resembles a quantum mechanical wavefunction in which the energy spectrum becomes entirely real and observable. Such behaviour is also found in PT symmetric systems that are not isolated from the environment (i.e., non-adiabatic) but subject to highly constrained interactions. Conservation of energy and momentum are determined through the symmetry of Lorentz boosts, i.e., symmetries in both time and space, in a system containing both Hermitian and non-Hermitian elements. A net energy gain results from changing symmetry relations and the emergence of the Higgs mass associated with changes in quantum confinement energies.
The complex parameter field is revealed as the order parameter that emerges to signify a superconducting phase transition from Type-II to a dual of Type-I. The phase transition is consistent with Ginzburg-Landau theory that describes gauge-invariant coupling of a scalar field to the Yang-Mills action in QCD. The Higgs-like gauge field emerges out of the transition from gapped Type-II superconductivity to gapless dual Type-I superconductivity to establish a reciprocal gap in the gradient energy. The point at which the critical coherence length and penetration depth emerge in the macro-scale dual superconductor is postulated as the low-energy, infrared bound of the QCD mass gap.

Funding

No funding was received to assist with the preparation of this manuscript.

Conflicts of Interest

There are no competing interests relating to the work.

Appendix A. Ginzburg-Landau Theory

The Ginzburg-Landau (GL) theory of superconductors is founded upon a general approach to continuous phase transitions that are accompanied by a change in symmetry [54]. Landau proposed that these phase transitions are characterized by an order parameter that is zero in the disordered state above Tc but obtains a non-zero value below Tc. For the relatively simple case of a magnet, its magnetization M(r) provides a suitable order parameter.
For a superconducting system, GL postulates the existence of a complex order parameter Ψ, assumed to be an unspecified physical quantity that characterizes the state of the system. For the normal metallic state above the superconductor Tc it is zero, whilst for the superconducting state below Tc it is non-zero, such that:
Ψ =   0   T > T c   Ψ T ≠ 0   T < T c
However, for the non-metallic dual superconducting state observed experimentally, the system is instead characterized by:
Ψ =   0     T − T c   ≠ 0   0 < M s < 1   Ψ T ≠ 0     T − T c   ≠ 0   M s > 1
where Ms is the spontaneous magnetism and Ψ represents the complex form of the coupling energy (eiΦ)3v. For 0 < Ms < 1 the system is characterized by an ‘auxiliary’ order parameter Hs, the spontaneous magnetic field.
GL assumes that the real free energy of the superconductor varies smoothly and can only depend upon the complex value of |Ψ| so that the free energy density is given by:
f s T = f n T + α T | Ψ | 2 + β T | Ψ | 4 + …
where:
fs(T) and fn(T) are the superconducting state and normal state free energy densities, respectively
and
α(T) and β(T) are generally phenomenological, temperature dependent parameters.
The order parameter Ψ(r) is found by minimizing the free energy of the system which, through further mathematical manipulation, yields an effective non-linear Schrödinger equation:
− ℏ 2 2 m * ∇ 2   Ψ r + α + β Ψ r 2   Ψ r = 0
where:
ℏ is the reduced Planck’s constant,
and
m* determines the energy cost associated with gradients in the order parameter Ψ(r) to define an effective mass for the quantum system where m* = 2me and me is the bare electron mass in the normal metallic state.
The non-linearity introduced by the second term in the bracket of (28) ensures that the quantum mechanical principle of superposition does not apply, i.e., it cannot be normalized to zero.
GL theory is developed further to incorporate: inhomogeneous systems introducing a gradient into the order parameter; the effect of external perturbations; and the effect of a magnetic field. The free energy density of the superconductor then takes the form [54]:
f s T = f n T + ℏ i   ∇ + 2 e A Ψ 2 + ℏ 2 2 m * + α | Ψ | 2 + β 2 | Ψ | 4
where:
2e is the net charge for a Cooper pair of electrons with positive sign convention
and
A is the electromagnetic vector potential
The full GL equations (not included here) are obtained by minimizing the free energy with respect to fluctuations in the order parameter and the vector potential A. These equations predict the existence of two characteristic lengths in a superconductor [54]:
the coherence length ξ’(T):
ξ ' ( T ) = ℏ 2 2 m *   | α ( T ) |
(the distinction between coherence length ξ’(T) and correlation length ξ(T) is explained in [31])
and the London penetration depth λ(T):
λ ( T ) = m e β 2 μ 0 e 2 α ˙ T − T c
where:
α(T) = ά|T – Tc|
Both lengths diverge as Tc → T.
The ratio κ = λ(T)/ξ’(T) is known as the Ginzburg-Landau parameter where κ > 1/√2 identifies a Type-II superconductor whilst κ < 1/√2 identifies a Type-I superconductor. The ratio is dimensionless and independent of temperature within GL theory.
The transition from Type-II to Type-I and the effect of Abrikosov vortices is related to the experimental results described in [2] from which Figure 6 is updated to reflect the latest findings:
Preprints 104232 g006
Figure 6. Critical exponents reveal a magnetic phase transition and superconductor-like behaviour for a negative pressure perturbation. The initial response between 0 < Ms < 0.5 appears as diamagnetism (Hs < 0) and peaks at a lower critical field point Mc1, a result of high susceptibility χ such that Ms >> Bs. Diamagnetism is then completely destroyed at Ms = 1, which represents an upper critical field point Mc2. For Ms > 1 both Mc1 and Mc’ become ‘rolling’ critical values.
Figure 6. Critical exponents reveal a magnetic phase transition and superconductor-like behaviour for a negative pressure perturbation. The initial response between 0 < Ms < 0.5 appears as diamagnetism (Hs < 0) and peaks at a lower critical field point Mc1, a result of high susceptibility χ such that Ms >> Bs. Diamagnetism is then completely destroyed at Ms = 1, which represents an upper critical field point Mc2. For Ms > 1 both Mc1 and Mc’ become ‘rolling’ critical values.
Preprints 104232 g006
For Hs < 0, the profile resembles Type-II superconductor behaviour, although it is large rather than negative values of susceptibility χ that are held responsible for the diamagnetic effect. The diamagnetism peaks at Mc1, the lower critical field, corresponding to minimal magnetic flux density Bs. Moving beyond Mc1 towards Mc2 the upper critical field, Bs increases until all superconducting behaviour is destroyed at Ms = 1, Hs = 0. For 0 < Ms < 1, the Ginzburg-Landau parameter κ is determined:
κ = M c 2 2 M c 1   to   give   κ > 1 2  
i.e., a Type-II superconductor classification.
For Ms > 1, Hs takes positive values as the susceptibility χ falls below unity. A new value for the critical field Mc’ is deemed to be established at or to the right of the Mc2 value. Both Mc2 and Mc’ become ‘rolling’ critical values such that 0.9 ≤ Mc2/ Mc’ ≤ 1.0 as determined by calculations of κ below. For this region κ < 1/√2 which is consistent with Type-I superconducting behaviour. Here, large values of excluded Bs coincide with exclusion of the electric field E to establish dual superconducting behaviour.
If Mc’ has a minimum value of 1.0 Am-1kg-1 then at the positive displacement phase transition κ = 0.707.
Since ξ’(T) is equal to 3.05 m, the penetration depth λ(T) = 2.2 m to give the vector boson mass mV (1/ λ(T)) ≤ 0.46 kg in the constant energy Hamiltonian, kg ∝ m-2s2 as derived through dimensional analysis with E = mc2 so that mV can be expressed in units of Gaussian curvature m2s-2 then comparing to the Gaussian curvature calculations using equation (14):
K ∝ - Pv/2 which at Point 3 gives - (610 x 0.0015)/ 2 = - 0.46 m2s-2 [2] and at Point 1 gives - (290 x 0.0015)/ 2 = - 0.22 m2s-2 [2]
∴ 0.22 m2s-2 ≤ mV ≤ 0.46 m2s-2
and 0.65 ≤ κ ≤ 0.707
The Higgs mass mH (1/ ξ’(T)) = 0.33 kg
which determines the non-extensive volume V (mH/ ρ)
where ρ is the density of the crystal-fluid material with an approximate value of 664 kg m-3 [2] to give V = 0.33/ 664 x 10-3 = 0.5 litre, i.e., the swept volume of the piston expander.
Also, mH is approximately 100 times greater than the mass of the crystal-fluid (3.5 grams, approx.), supporting the hypothesis that mH quantifies changes in quantum confinement energies resulting from the conservation of angular momentum under critical false vacuum conditions (see Figure 5).
For spontaneous diamagnetism seen where Hs < 0, and below the critical correlation length ξ in Figure 3, the system appears to be in a gapped superconducting state with Hs acting as an ‘auxiliary’ order parameter. The effects of topological defects in the dual superconductor seem to reflect those of magnetic impurity states that fill-in the energy gap in conventional superconductors. Topological defects may represent the penetration of the dual superconductor by the excluded electric field in the form of chromoelectric flux tubes that enable the formation of quark-antiquark pairs and the confinement mechanism. Where Hs > 0, and above the critical correlation length ξ, the system can be described as being in a protected gapless superconducting state with Ψ(r) as the complex order parameter. Similarly, it has been shown [55,56] that the transition between the gapped and gapless superconducting states in the Abrikosov-Gor’kov theory of a superconducting alloy with paramagnetic impurities is of the Lifshitz type, ie a topological phase transition where the number of the components of topological connectivity on the Fermi surface undergoes changes under the influence of different factors; pressure, magnetic field, doping, etc.

References

  1. M. Christodoulou, et al., Locally Mediated Entanglement in Linearized Quantum Gravity, Phys. Rev. Lett., 130, 100202 (2023). [CrossRef]
  2. M. Gibbons, Superconducting phase transition reveals an electromagnetic coupling to a scalar field potential that generates mechanical work, J. Phys. D: Appl. Phys., 56, 054001 (2022), doi: 10.1088/1361-6463/acab0d. [CrossRef]
  3. S. M. Carroll, The Biggest Ideas in the Universe, Series of online presentations: https://www.youtube.com/playlist?list=PLrxfgDEc2NxZJcWcrxH3jyjUUrJlnoyzX The Biggest Ideas in the Universe 1: Space, Time and Motion (Oneworld Publications, London, 2023) The Biggest Ideas in the Universe 2: Quanta and Fields (Oneworld Publications, London, 2024).
  4. H. Callen, Thermodynamics and an Introduction to Thermostatistics (Wiley, New York, 1985), Chap. 8,10.
  5. F. Wilczek, Nobel Lecture: Asymptotic freedom: From paradox to paradigm, Rev. Mod. Phys., 77, 3, 857 (2005). [CrossRef]
  6. J. Greensite, An Introduction to the Confinement Problem (Springer, Cham, 2020), Chap. 1,2,3). [CrossRef]
  7. M. Gibbons, A condensed-matter analogue of the false vacuum, J. Phys. Commun., 5, 065005 (2021). [CrossRef]
  8. F. Pázmándi, G. Zaránd and G. T. Zimányi, Self-Organized Criticality in the Hysteresis of the Sherrington-Kirkpatrick Model, Phys. Rev. Lett., 83, 1034-1037 (1999). [CrossRef]
  9. S. V. G. Menon, Renormalization Group Theory of Critical Phenomena (Wiley, New Delhi, 1995), Chap. 1,2,3.
  10. C. Castelnovo, R. Moessner and S. L. Sondhi, Magnetic monopoles in spin ice, Nature, 451, 42-45, (2008). [CrossRef]
  11. G. t’Hooft, Topology of the gauge condition and new confinement phases in non-abelian gauge theories, Nuclear Physics B, 190, 3, 455-478 (1981). [CrossRef]
  12. S. Mandelstam, Vortices and quark confinement in non-Abelian gauge theories, Physics Reports, 23, 3, 245-249 (1976). [CrossRef]
  13. G. Ripka, Dual superconductor models of color confinement, Lecture Notes in Physics (2004), Chap. 1,3,5. [CrossRef]
  14. K. Kondo, et al., Quark confinement: Dual superconductor picture based on a non-Abelian Stokes theorem and reformulations of Yang–Mills theory, Phys. Rep., 579, 1-266 (2015). [CrossRef]
  15. Y. Gu, X. Hao and J. Liang, Generalized Gauge Transformation with PT-Symmetric Non-Unitary Operator and Classical Correspondence of Non-Hermitian Hamiltonian for a Periodically Driven System, Ann. Phys., 6, 534, 2200069 (2022). [CrossRef]
  16. C. M. Bender, PT-symmetric quantum theory, J. Phys.: Conf. Ser., 631, 012002 (2015). [CrossRef]
  17. Fan, G-Y. Huang and S-D Liang, Complex Berry curvature pair and quantum Hall admittance in non-Hermitian systems, J. Phys. Commun., 4, 115006 (2020). [CrossRef]
  18. Jaffe, E. Witten, Quantum Yang-Mills Theory https://www.claymath.org/wp-content/uploads/2022/06/yangmills.pdf.
  19. E. W. Lemmon, L. H. Huber, M.O. McLinden, and I. Bell, Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) (Boulder, Colorado, 2020). https://www.nist.gov/programs-projects/reference-fluid-thermodynamic-and-transport-properties-database-refprop.
  20. Kunz and W. Wagner, Journal of Chemical & Engineering Data, 57, 11, 3032-3091 (2012). [CrossRef]
  21. Imre, K. Martinás and L. P. N. Rebelo, Thermodynamics of negative pressure in liquids, Non-Equilibrium Thermodynamics, 23, 4 (1998). [CrossRef]
  22. Cowan, Topics in Statistical Mechanics (World Scientific, London, 2022), Chap. 4.
  23. H. Callen, Thermodynamics and an Introduction to Thermostatistics (Wiley, New York, 1985), Chap. 3,7.
  24. P. Herzog, Supersymmetry and Conformal Field Theory (CMMS40), Lecture Notes, Spring Term 2021. https://www.nms.kcl.ac.uk/christopher.herzog/SUSYCFTnotes.pdf.
  25. W. Zhu, Uncovering Conformal Symmetry in the 3D Ising Transition: State-Operator Correspondence from a Quantum Fuzzy Sphere Regularization, Phys. Rev. X, 13, 021009 (2023). [CrossRef]
  26. Tong, University of Cambridge, Lectures on Gauge Theory, 2018. http://www.damtp.cam.ac.uk/user/tong/gaugetheory/gt.pdf.
  27. R. Penrose, The Road to Reality (Vintage, London, 2005), Chap. 19.
  28. P. Bak and K. Chen, The physics of fractals, Physica D, 38, 1-3, 5-12 (1989). [CrossRef]
  29. Ratra, Cosmological ‘seed’ magnetic field from inflation, ApJL, 391, L1-L4, (1992), https://adsabs.harvard.edu/full/1992ApJ...391L...1R.pdf.
  30. Tong, University of Cambridge, Lectures on Electromagnetism, Chap. 4, 2023 https://www.damtp.cam.ac.uk/user/tong/em/el4.pdf.
  31. S. Huber, ETH Zürich, Experimental and Theoretical Aspects of Quantum Gases lecture notes, Chapter 7, 2023 https://ethz.ch/content/dam/ethz/special-interest/phys/theoretical-physics/cmtm-dam/documents/qg/Chapter_07.pdf.
  32. Zee, Group Theory in a Nutshell for Physicists (Princeton University Press, Princeton, 2016), Preface and Parts 1, 2.
  33. R. Penrose, The Road to Reality (Vintage, London, 2005), Chap. 13, 25.
  34. I.G. Halliday and A. Schwimmer, Z(2) monopoles in lattice gauge theories, Physics Letters B, 102, 5, 337-340 (1981). [CrossRef]
  35. Bissey, A. I. Signal, and D. B. Leinweber, Comparison of gluon flux-tube distributions for quark-diquark and quark-antiquark hadrons, Phys. Rev. D, 80, 114506 (2009). [CrossRef]
  36. H. Suganuma, S. Sasaki and H. Toki, Color confinement, quark pair creation and dynamical chiral-symmetry breaking in the dual Ginzburg-Landau theory, Nuclear Physics B, 435, 1–2, 207-240 (1995). [CrossRef]
  37. Salam and C. Sivaram, Strong gravity approach to QCD and confinement, Mod. Phys. Lett., 8, 4, 321–326 (1993). [CrossRef]
  38. Andrei Bernevig, Topological Insulators and Topological Superconductors (Princeton University Press, Princeton, 2013), Chap. 1-4, 9-10.
  39. J. W. Zwanziger, M. Koenig and A. Pines, Berry’s Phase, Annu. Rev. Phys. Chem., 41, 601-46 (1990). [CrossRef]
  40. Tong, University of Cambridge, Lectures on the Quantum Hall Effect, Chap. 1, 2016 https://www.damtp.cam.ac.uk/user/tong/qhe/qhe.pdf.
  41. M. V. Berry, Quantal phase factors accompanying adiabatic changes, R. Soc. London, 392, 45–57 (1984). [CrossRef]
  42. L. M. Lederman and C. T. Hill, Symmetry and the Beautiful Universe (Prometheus Books, New York, 2004), Chap. 12.
  43. J. Evslin, et al., Nonabelian Faddeev-Niemi decomposition of the SU(3) Yang-Mills theory, J. High Energ. Phys. 94 (2011). [CrossRef]
  44. M. E. Peskin and D. V. Schroeder, An Introduction to Quantum Field Theory (CRC Press, Boca Raton, 1995), Chap. 3.
  45. J-M. Lévy-Leblond, J-P. Provost, Additivity, rapidity, relativity, Am. J. Phys., 47, 12, 1045-1049 (1979). [CrossRef]
  46. N. Mukunda and S. Chaturvedi, Continuous Groups for Physicists (Cambridge University Press, Cambridge, 2022), Chap. 10.
  47. P. W. Anderson, More And Different: Notes From A Thoughtful Curmudgeon (World Scientific, New Jersey, 2011), Chap. II.
  48. M. Sato and Y. Ando, Topological superconductors: a review, Rep. Prog. Phys., 80, 076501 (2017). [CrossRef]
  49. J. Cayssol and J. N. Fuchs, Topological and geometrical aspects of band theory, J. Phys. Mater., 4, 034007 (2021). [CrossRef]
  50. X-G. Wen, Colloquium: Zoo of quantum-topological phases of matter, Rev. Mod. Phys., 89, 041004 (2017). [CrossRef]
  51. S. D. Bass, Emergent gauge symmetries: making symmetry as well as breaking it, Phil. Trans. R. Soc. A, 380, 20210059 (2022). [CrossRef]
  52. H. Guth, Inflation, Proc. Natl. Acad. Sci. USA, 90, 4871-4877 (1993). [CrossRef]
  53. H. Guth, The Beamline, 27, 14 (1997), The Inflationary Universe. ned.ipac.caltech.edu/level5/Guth/Guth3.html.
  54. J. A. Annett, Superconductivity, Superfluids and Condensates (Oxford University Press, Oxford, 2004), Chap. 2,3,4.
  55. Y. Yerin, C. Petrillo and A. A. Varlamov, The Lifshitz nature of the transition between the gap and gapless states of a superconductor, SciPost Phys, Core 5, 009 (2022). [CrossRef]
  56. Y. Yerin, A. A. Varlamov and C. Petrillo, Topological nature of the transition between the gap and the gapless superconducting states, EPL, 138, 1 (2022). [CrossRef]
Preprints 104232 g001
Figure 1. Schematic arrangement of the experimental apparatus in which a negative pressure material is formulated and manipulated. Dissipative structuring of the crystal-fluid material is controlled with a view to establishing a power cycle in the piston expander through non-equilibrium, non-extensive volume displacements.
Figure 1. Schematic arrangement of the experimental apparatus in which a negative pressure material is formulated and manipulated. Dissipative structuring of the crystal-fluid material is controlled with a view to establishing a power cycle in the piston expander through non-equilibrium, non-extensive volume displacements.
Preprints 104232 g001
Preprints 104232 g002
Figure 2. Excess internal energy potential resulting from excess thermodynamic potentials during external pressure perturbations. All values for energy, work and thermodynamic potentials are derived by the NIST REFPROP program/database based only upon temperature, pressure and mass measurements together with the piston position. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0). The piston expander is completely immersed in a heat bath with a temperature of 270K, approx.
Figure 2. Excess internal energy potential resulting from excess thermodynamic potentials during external pressure perturbations. All values for energy, work and thermodynamic potentials are derived by the NIST REFPROP program/database based only upon temperature, pressure and mass measurements together with the piston position. The calculations are in accordance with GERG-2008 modified by the Kunz and Wagner Model 0 (KW0). The piston expander is completely immersed in a heat bath with a temperature of 270K, approx.
Preprints 104232 g002
Preprints 104232 g003
Figure 3. Effect of the critical correlation length ξ on the magnitude of the scalar field Φ. A gradient energy term -½(∇Φ)2, as derived from the non-equilibrium Lagrangian function, is equivalent in magnitude to the coupling energy. From this, scalar field Φ values associated with the critical response are determined. Values of negative gradient energy and positive coupling energy are both equivalent in magnitude to PV work done by the piston expander which can be either negative or positive.
Figure 3. Effect of the critical correlation length ξ on the magnitude of the scalar field Φ. A gradient energy term -½(∇Φ)2, as derived from the non-equilibrium Lagrangian function, is equivalent in magnitude to the coupling energy. From this, scalar field Φ values associated with the critical response are determined. Values of negative gradient energy and positive coupling energy are both equivalent in magnitude to PV work done by the piston expander which can be either negative or positive.
Preprints 104232 g003
Preprints 104232 g004
Figure 4. Decomposition of symmetry groups to establish common U(2) scale- and gauge-invariance. This model of invariance provides a mechanism through which the pressure-induced ‘rolling’ critical response results in PV work that is either positive or negative. The complex reorganization of water ice cages produces variable inertia which, through the conservation of angular momentum, is responsible for either an acceleration or deceleration of quarks. In the case of acceleration, this leads to the emission of physical gluons that are absorbed into the QCD vacuum manifold. A corresponding tendency to reduce local ‘space density’ and effective magnetic permeability μ0 manifests as increased hyperbolic curvature K.
Figure 4. Decomposition of symmetry groups to establish common U(2) scale- and gauge-invariance. This model of invariance provides a mechanism through which the pressure-induced ‘rolling’ critical response results in PV work that is either positive or negative. The complex reorganization of water ice cages produces variable inertia which, through the conservation of angular momentum, is responsible for either an acceleration or deceleration of quarks. In the case of acceleration, this leads to the emission of physical gluons that are absorbed into the QCD vacuum manifold. A corresponding tendency to reduce local ‘space density’ and effective magnetic permeability μ0 manifests as increased hyperbolic curvature K.
Preprints 104232 g004
Preprints 104232 g005
Figure 5. Deceleration of dissipative water ice cage structures under critical false vacuum conditions results in the transfer of momentum away from sub-atomic quarks. The processes of colour and quark confinement see compensating quark-antiquark pairs qq̄ and gluons emerge from the quantum vacuum to enable gluon splitting. The energy of confinement is revealed in the Higgs mass. A corresponding tendency to increase local ‘space density’ reduces the hyperbolic curvature of the vacuum manifold to facilitate positive expansion work. The external pressure perturbations may be interrupted at any point such that gradient energy is captured and confined through water ice cage structuring where the system relaxes into a non-critical, stable state.
Figure 5. Deceleration of dissipative water ice cage structures under critical false vacuum conditions results in the transfer of momentum away from sub-atomic quarks. The processes of colour and quark confinement see compensating quark-antiquark pairs qq̄ and gluons emerge from the quantum vacuum to enable gluon splitting. The energy of confinement is revealed in the Higgs mass. A corresponding tendency to increase local ‘space density’ reduces the hyperbolic curvature of the vacuum manifold to facilitate positive expansion work. The external pressure perturbations may be interrupted at any point such that gradient energy is captured and confined through water ice cage structuring where the system relaxes into a non-critical, stable state.
Preprints 104232 g005
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

762

Views

540

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated