Submitted:
13 August 2023
Posted:
14 August 2023
Read the latest preprint version here
Abstract

Keywords:
1. Introduction
2. Experimental Evidence and Background Material
3. Analysis and Discussion
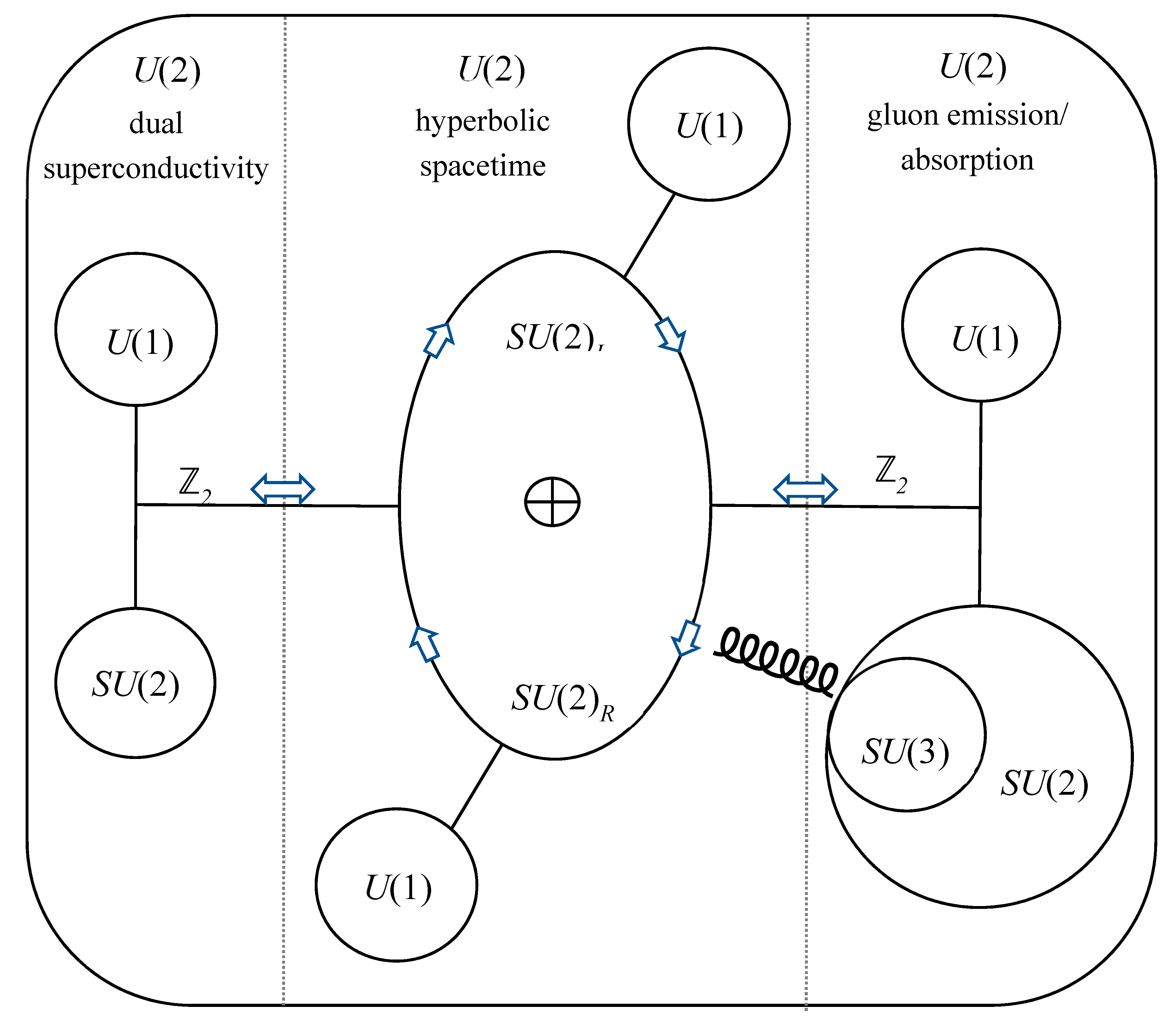
3.1. Gauge Symmetry
3.2. Berry Phase and Parity-Time (PT) Symmetry
3.3. Symmetry Synchronization and Conserved Quantities
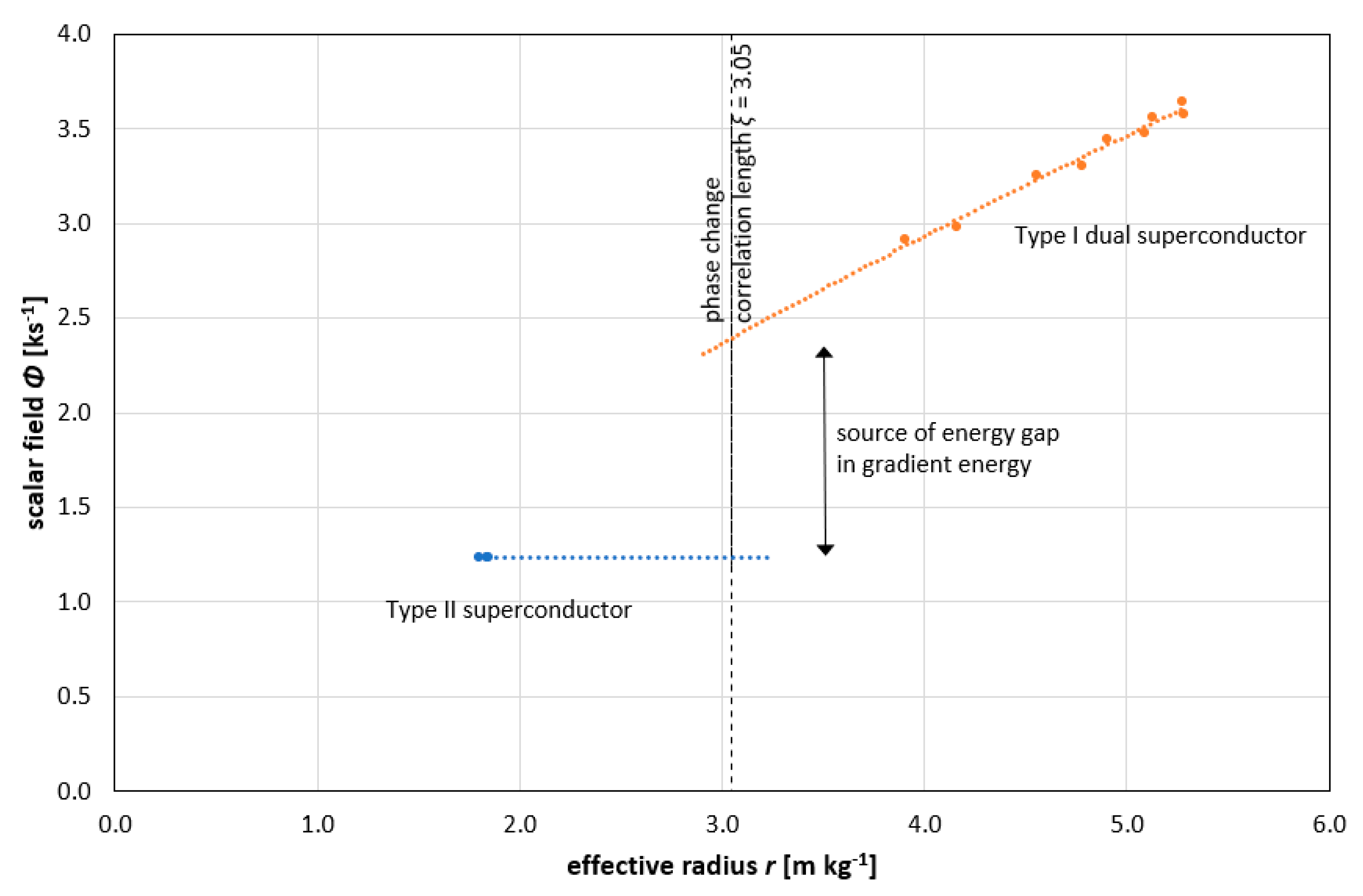
3.4. Energy Band Gaps
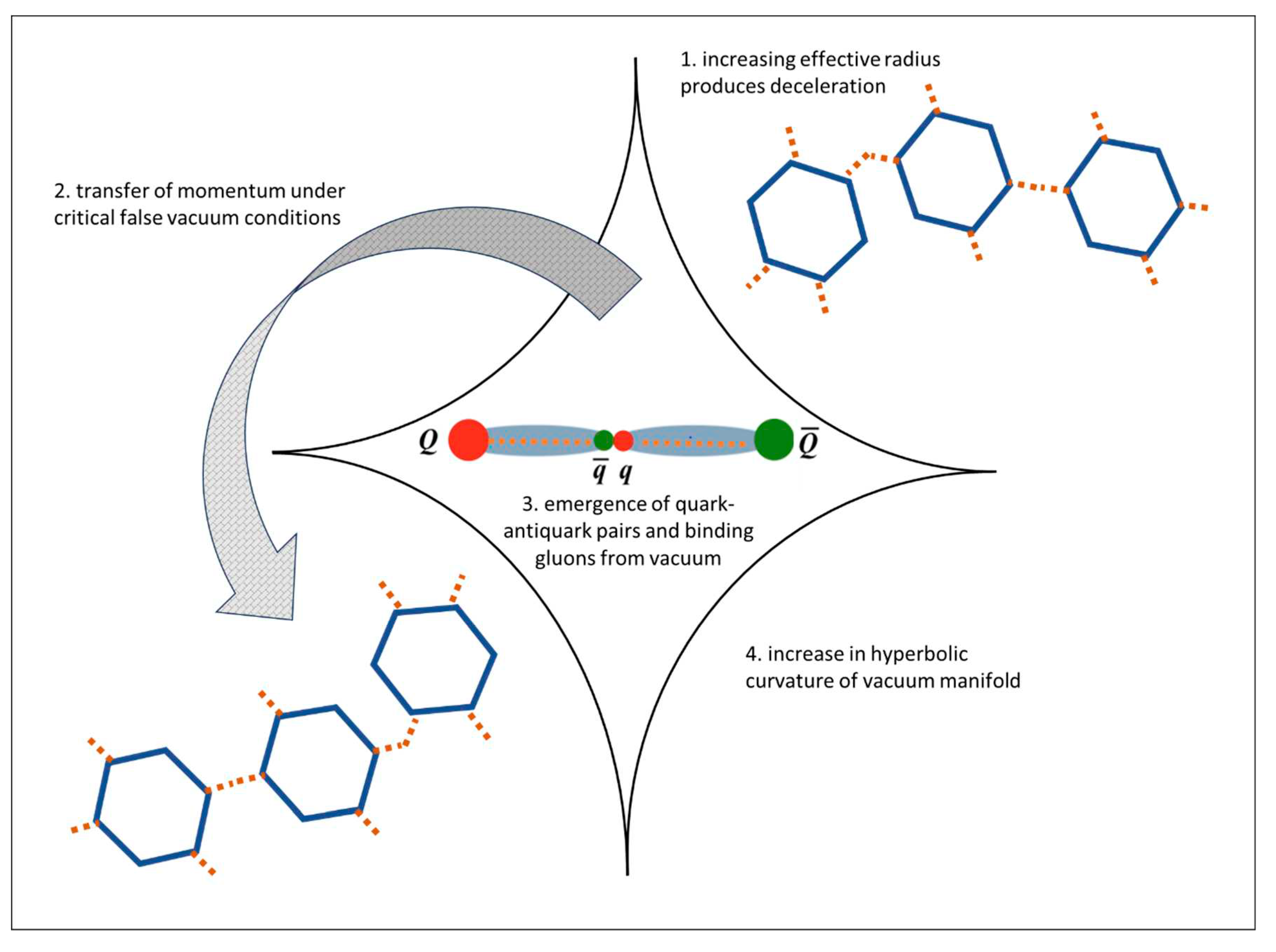
3.5. Cosmological Analogy
4. Conclusions
Appendix A. Ginzburg-Landau Theory
References
- Gibbons, M. Superconducting phase transition reveals an electromagnetic coupling to a scalar field potential that generates mechanical work. J. Phys. D: Appl. Phys. 2023, 56, 054001. [Google Scholar] [CrossRef]
- Callen, C. Thermodynamics and an Introduction to Thermostatistics; Chap. 8,10; Wiley: New York, 1985. [Google Scholar]
- Wilczek, F. Nobel Lecture: Asymptotic freedom: From paradox to paradigm. Rev. Mod. Phys. 2005, 77, 857–870. [Google Scholar] [CrossRef]
- Greensite, J. An Introduction to the Confinement Problem. 2020. [CrossRef]
- Gibbons, M. A condensed-matter analogue of the false vacuum. J. Phys. Commun. 2021, 5, 065005. [Google Scholar] [CrossRef]
- Pázmándi, F.; Zaránd, G.; Zimányi, G.T. Self-Organized Criticality in the Hysteresis of the Sherrington-Kirkpatrick Model. Phys. Rev. Lett. 1999, 83, 1034–1037. [Google Scholar] [CrossRef]
- Menon, S.V. G. Renormalization Group Theory of Critical Phenomena; New Delhi,; Wiley: New Delhi, 1995. [Google Scholar]
- Castelnovo, C.; Moessner, R.; Sondhi, S.L. Magnetic monopoles in spin ice. Nature 2008, 451, 42–45. [Google Scholar] [CrossRef] [PubMed]
- Hooft, G. Topology of the gauge condition and new confinement phases in non-abelian gauge theories. Nucl. Phys. B 1981, 190, 455–478. [Google Scholar] [CrossRef]
- Mandelstam, S. II. Vortices and quark confinement in non-Abelian gauge theories. Phys. Rep. 1976, 23, 245–249. [Google Scholar] [CrossRef]
- Dual Superconductor Models of Color Confinement. 2004. [CrossRef]
- Kondo, K.-I.; Kato, S.; Shibata, A.; Shinohara, T. Quark confinement: Dual superconductor picture based on a non-Abelian Stokes theorem and reformulations of Yang–Mills theory. Phys. Rep. 2015, 579, 1–226. [Google Scholar] [CrossRef]
- Gu, Y.; Hao, X.; Liang, J. Generalized Gauge Transformation with PT -Symmetric Non-Unitary Operator and Classical Correspondence of Non-Hermitian Hamiltonian for a Periodically Driven System (Ann. Phys. 6/2022). Ann. der Phys. 2022, 534. [Google Scholar] [CrossRef]
- Bender, C.M. PT-symmetric quantum theory. J. Physics: Conf. Ser. 2015, 631, 012002. [Google Scholar] [CrossRef]
- Fan, A.; Huang, G.-Y.; Liang, S.-D. Complex Berry curvature pair and quantum Hall admittance in non-Hermitian systems. J. Phys. Commun. 2020, 4, 115006. [Google Scholar] [CrossRef]
- Jaffe, A.; Witten, E. 2000 Quantum Yang-Mills Theory. Available online: www.claymath.org/millennium/Yang-MillsTheory/yangmills.pdf.
- Lemmon, E.W.; Huber, L.H.; McLinden, M.O.; Bell, I. Reference Fluid Thermodynamic and Transport Properties Database (REFPROP) (Boulder, Colorado, 2020). Available online: https://www.nist.gov/programs-projects/reference-fluid-thermodynamic-and-transport-properties-database-refprop.
- Kunz, O.; Wagner, W. The GERG-2008 Wide-Range Equation of State for Natural Gases and Other Mixtures: An Expansion of GERG-2004. J. Chem. Eng. Data 2012, 57, 3032–3091. [Google Scholar] [CrossRef]
- Imre, A.; Martinás, K.; Rebelo, L.P.N. Thermodynamics of Negative Pressures in Liquids. J. Non-Equilibrium Thermodyn. 1998, 23, 351–375. [Google Scholar] [CrossRef]
- Cowan, B. Topics in Statistical Mechanics; World Scientific: London, UK, 2022. [Google Scholar]
- Callen, H. Thermodynamics and an Introduction to Thermostatistics; Wiley: New York, 1985. [Google Scholar]
- Bak, P.; Chen, K. The physics of fractals. Phys. D: Nonlinear Phenom. 1989, 38, 5–12. [Google Scholar] [CrossRef]
- Ratra, B. Cosmological 'seed' magnetic field from inflation. Astrophys. J. 1992, 391, L1–L4. [Google Scholar] [CrossRef]
- Tong, D. University of Cambridge, Lectures on Electromagnetism, Chap. 4, 2023. https://www.damtp.cam.ac.uk/user/tong/em/el4.pdf.
- Huber, S. ETH Zürich, Experimental and Theoretical Aspects of Quantum Gases lecture notes, Chapter 7, 2023. Available online: https://ethz.ch/content/dam/ethz/special-interest/phys/theoretical-physics/cmtm-dam/documents/qg/Chapter_07.
- Cayssol, J.; Fuchs, J.-N. Topological and geometrical aspects of band theory. J. Physics: Mater. 2021, 4, 034007. [Google Scholar] [CrossRef]
- Zee, A. Group Theory in a Nutshell for Physicists; Princeton University Press: Princeton, 2016. [Google Scholar]
- Penrose, R. The Road to Reality; Vintage: London, 2005. [Google Scholar]
- Halliday, I.; Schwimmer, A. Z(2) monopoles in lattice gauge theories. Phys. Lett. B 1981, 102, 337–340. [Google Scholar] [CrossRef]
- Bissey, F.; Signal, A.I.; Leinweber, D.B. Comparison of gluon flux-tube distributions for quark-diquark and quark-antiquark hadrons. Phys. Rev. D 2009, 80, 114506. [Google Scholar] [CrossRef]
- Suganuma, H.; Sasaki, S.; Toki, H. Color confinement, quark pair creation and dynamical chiral-symmetry breaking in the dual Ginzburg-Landau theory. Nucl. Phys. B 1995, 435, 207–240. [Google Scholar] [CrossRef]
- Salam, A.; Sivaram, C. ; Strong gravity approach to QCD and confinement. Mod. Phys. Lett. A 1993, 8, 321–326. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. London. Ser. A, Math. Phys. Sci. 1984, 392, 45–57. [Google Scholar] [CrossRef]
- Lederman, L.M.; Hill, C.T. Symmetry and the Beautiful Universe; Prometheus Books: New York, 2004. [Google Scholar]
- Evslin, J.; Giacomelli, S.; Konishi, K.; Michelini, A. Nonabelian Faddeev-Niemi decomposition of the SU(3) Yang-Mills theory. J. High Energy Phys. 2011, 2011, 1–25. [Google Scholar] [CrossRef]
- Peskin, M.E.; Schroeder, D.V. An Introduction to Quantum Field Theory; Chap. 3; CRC Press: Boca Raton, 1995. [Google Scholar]
- Lévy-Leblond, J.-M.; Provost, J.-P. Additivity, rapidity, relativity. Am. J. Phys. 1979, 47, 1045–1049. [Google Scholar] [CrossRef]
- Mukunda, N.; Chaturvedi, S. Continuous Groups for Physicists; Cambridge University Press: Cambridge, 2022. [Google Scholar]
- Anderson, P.W. More And Different: Notes From A Thoughtful Curmudgeon; World Scientific: New Jersey, 2011. [Google Scholar]
- Guth, A.H. Inflation. Proc. Natl. Acad. Sci. 1993, 90, 4871–4877. [Google Scholar] [CrossRef] [PubMed]
- Guth, A.H. The Beamline, 27, 14 (1997), The Inflationary Universe. Available online: ned.ipac.caltech.edu/level5/Guth/Guth3.
- Annett, J.A. Superconductivity, Superfluids and Condensates; Chap. 2,3,4; (Oxford University Press,: Oxford, 2004. [Google Scholar]
- Yerin, Y.; Petrillo, C.; Varlamov, A.A. Topological phase transition between the gap and the gapless superconductors. SciPost Phys. Core 2022, 5, 009. [Google Scholar] [CrossRef]
- Yerin, Y.; Varlamov, A.A.; Petrillo, C. Topological nature of the transition between the gap and the gapless superconducting states. EPL (Europhysics Lett. 2022, 138, 16005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




