1. Introduction
A growing number of solar photovoltaic systems are being integrated with electric utilities due to their outstanding environmental, economic, and technical characteristics [
1]. The availability of solar radiation in most regions of the world makes solar energy generation and storage systems an attractive option for customers looking for a quick and efficient method of upgrading their electrical systems. In PV systems, solar energy is converted into electricity. In addition to solar radiation and temperature, several other factors affect the capacity of solar energy to generate electricity. As a result, it is essential to analyze how PV systems perform in real time so that they are capable of being optimized, managed, and modeled [
2]. Single-diode model (SDM), double-diode model (DDM), and PV module model (PVMM) are typically used despite the existence of many mathematical models for PV nonlinearity. These models must include parameters that can change with environmental changes, faults, and aging [
3]. Thus, regardless of the model used, it is essential to accurately determine unknown parameters as early as possible by using a robust optimization algorithm. Therefore, developing an optimization algorithm capable of accurately estimating the properties of PV models using the current-voltage measurements of the PV cell and module is imperative [
4].
An optimization problem can be established to extract PV cell and module parameters, which involves the formulation of an objective function and the establishment of a set of constraints. There is noise in the measured current-voltage data. There are, therefore, several local optima in the search space, resulting in a nonlinear and multimodal search space [
5], [
6]. Deterministic and metaheuristic algorithms are commonly used to solve this challenging optimization problem. The former method makes use of gradient information, as well as initial points. As a result, classical techniques are ineffective in identifying the parameters of photovoltaic models due to their non-linear and non-convex nature [
7]–[
9]. There is a consensus that metaheuristic algorithms are more modern and easier to use than deterministic algorithms. Since then, there has been an increase in interest in metaheuristic algorithms for optimizing PV systems more efficiently and flexibly.
The field of study has been subjected to extensive research in recent years. Various metaheuristic and analytical methods have been employed by researchers in order to estimate the parameters of the solar cell/module. They are performance-guided JAYA (PGJAYA) algorithm [
6], differential evolution (DE) [
10], genetic algorithms (GA) [
11], particle swarm optimization (PSO) [
12], war strategy optimization (WSO) algorithm [
13], SEDE [
14], an efficient salp swarm-inspired algorithm (SSA) [
15], improved JAYA (IJAYA) [
16], RAO [
17], modified artificial bee colony (MABC) [
18], improved mosth-flame optimization (IMFO) [
19], Shuffled frog leaping algorithm (SFLA) [
20], triple-phase teaching-learning-based optimization (TPTLBO) [
21], improved chaotic whale optimization (ICWO) algorithm [
22], Sine-cosine algorithm (SCA) [
23], a new hybrid algorithm based on grey wolf optimizer and cuckoo search (GWO-CS) [
24], Coyote optimization algorithm (COA) [
25], Marine predators algorithm (MPA) [
26], adaptive genetic algorithm (AGA) based multi-objective optimization [
27], an improved equilibrium optimizer (IEO) [
28], new stochastic slime mould algorithm (SMA) [
29], and orthogonally adapted Harris hawks optimization (OAHHO) [
30], An overview of some of these research papers is presented in
Table 1.
Although researchers are developing and modifying meta-heuristic algorithms in light of the “No Free Lunch” theorem [
31] to determine the parameters of PV models. According to the authors’ knowledge, past algorithms have not provided a satisfactory balance between accuracy and reliability while maintaining a reasonable computing time. To improve the performance of metaheuristic algorithms, new ideas must be developed to produce simple and efficient methods for dealing with practical optimization problems.
Recently, Akbari et. al., [
32] introduced a new and powerful algorithm namely the CO algorithm, which is inspired by the behavior of cheetahs during the hunting process. However, it is necessary to test the performance of this algorithm on different optimization problems so that its strengths are known more, and its weaknesses are also identified and resolved. In this article, this algorithm is utilized for the first time to identify PV parameters. Based on the experiences of the authors, this algorithm has a relatively high computational volume, and its complexity needs to be simplified to be used in optimization problems.
The purpose of this article is to introduce a simplified and improved version of CO, namely ICO, that can improve the features of CO while requiring significantly less computational effort. As part of the ICO algorithm, the search phase is controlled according to the position of the leader, and its step length is also adjusted following the sorted population. This new operator also aids the algorithm’s global search in addition to the local search. In addition, the interaction factor in the attack phase is adjusted based on the prey position, and the turning factor is controlled by a random value. It is believed that the proposed attack operator will improve the behavior of the algorithm in the global search as well as its convergence speed. When it comes to estimating optimal parameters for PV cells and models, the CO and proposed ICO are compared to two recently well-established algorithms for parameter extraction of PV models, i.e., PGJAYA [
6] and SEDE [
14], and eight well-known original algorithms, i.e., DE [33], PSO [34], GA [35], TLBO [36], JAYA [37], SSA [38], WSO [
13], GWO [39].
Following is a summary of an overview of the remainder of the paper. In section 2, we describe in detail the SDM, DDM, and PVMM. The proposed ICO algorithm is presented in section 3. A simulation and evaluation of the results of the experiment are presented in
Section 4. Finally, section 5 makes some closing remarks.
2. PV Modeling and Problem Formulation
In the literature, many PV models are presented to describe the characteristics of solar cells and PV module models. Among these models are SDM, DDM, and PVMM. This section describes the mathematical model used to formulate the optimization problem of determining the optimal parameters for these models.
2.1. The Model of a Solar Cell
2.1.1. SDM
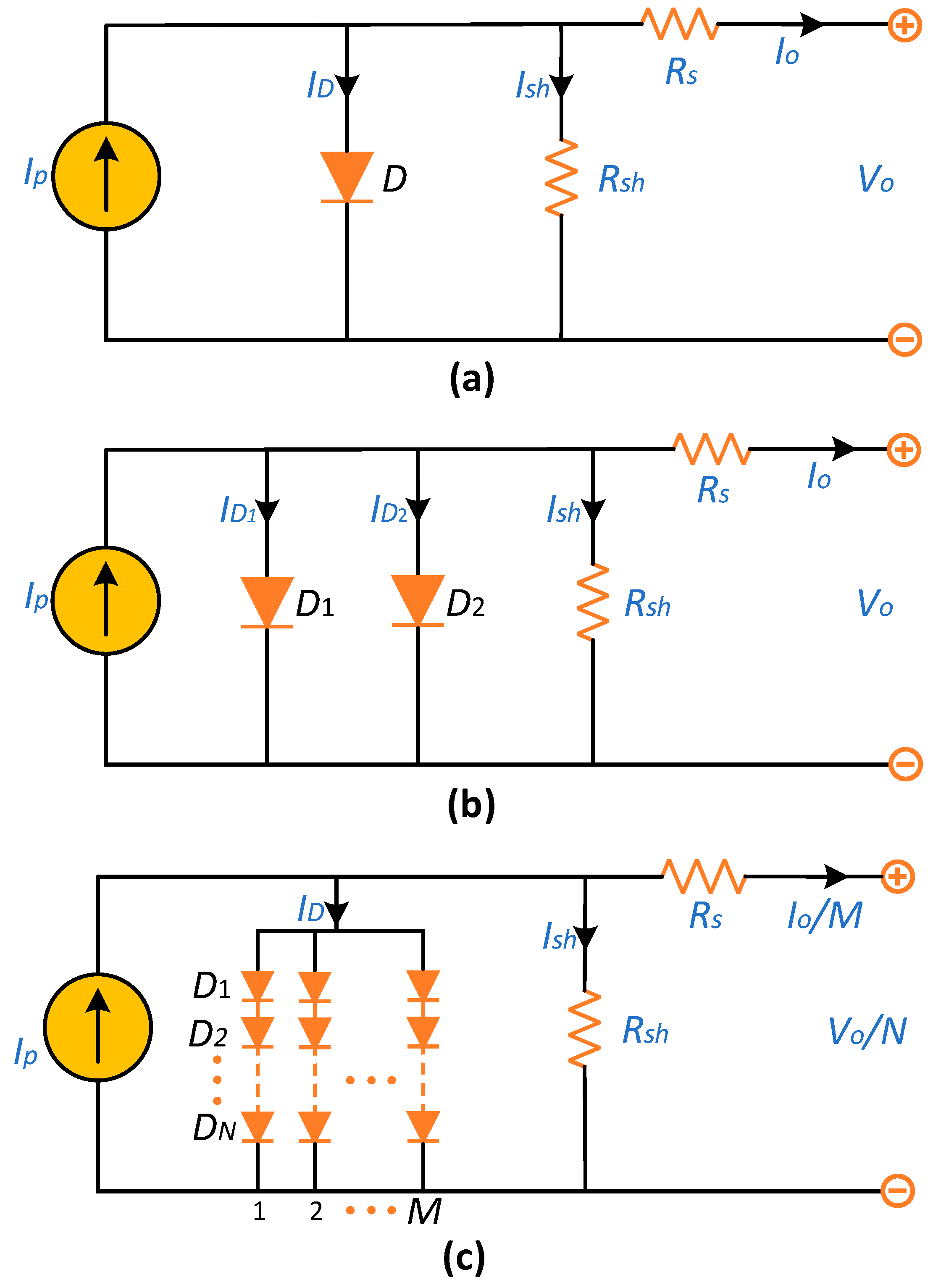
For demonstrating the real-time characteristics of PV systems, their mathematical modeling is required by practical considerations. A PV array can be modeled using the cell as its basic unit. SDMs are widely used due to their simplicity and ease of implementation. According to
Figure 1(a), the equivalent circuit for the SDM consists of a parallel resistor, a series resistor, a diode, and a current source. Calculating the output current can be accomplished using the following formula [
22]:
Where, , , and are, respectively, the photogenerated, shunt resistor, and diode currents.
Calculating
and
can be accomplished using Kirchhoff’s Voltage Law (KVL) and Shockley’s equation as follows:
here,
represents the non-physical diode ideality factor, whereas
represents the diode reverse saturation current;
represents cell output voltage;
represent shunt resistance; and
represents the series resistance.
The junction thermal voltage can be calculated using the electron charge,
(
C), the junction temperature,
, and Boltzmann’s constant,
(
J/K), as follows:
Combining Equations (3) to (6) will result in the cell output current (
) for SDM as follows:
2.1.2. DDM
Although it is widely employed to simulate PV cells, SDM ignores recombination current in the depletion region. As shown in
Figure 1(b), by combining the photo-generated current source, the shunt resistance, two rectifying diodes, and the series resistance, DDM can solve the problem.
Using KCL, one can calculate the output current in DDM as follows:
Current flows through the first and second diodes (i.e.,
and
) as described by the Shockley diode equations in (9) and (10). Diodes also have two ideality factors known as
and
. Diffusion and saturation currents are
and
. Thus, substituting (5), (9) and (10), (8) can be rewritten as follows:
2.2. PVMM
A photovoltaic module may be designed to increase voltage and current by arranging several PV cells in parallel or series (see
Figure 1(c)). Using the PVMM, the output current can be calculated as follows:
Here, a parallel arrangement consists of M solar cells, and a series arrangement consists of N solar cells.
2.3. Problem Formulation
The goal of the proposed optimization problem is to determine unknown parameters of PV cells and module accurately. An optimization algorithm is commonly employed to minimize the differences between the estimated and experimental I-V data obtained from the PV systems. Hence, as a rule, it is common to consider that the minimization of root mean square error (RMSE) is an objective function that should be considered when determining an estimate of current.
S is the number of experimental paired sample data. and are the s-th measured sample, and the determined value of PV output current, respectively. Constraints (14) indicate the upper () and lower () bounds on the PV parameters (decision variables). For the SDM and PVMM five unknown parameters are , and seven decision variables, i.e., should be defined for the DDM using an optimization technique. Finally, the calculated PV output current in each sample s, , can be expressed using (15), (16), and (17) for SDM, DDM, and PVMM, respectively.
Figure 1.
Equivalent representation of the (a) SDM, (b) DDM, and (c) PVMM.
Figure 1.
Equivalent representation of the (a) SDM, (b) DDM, and (c) PVMM.
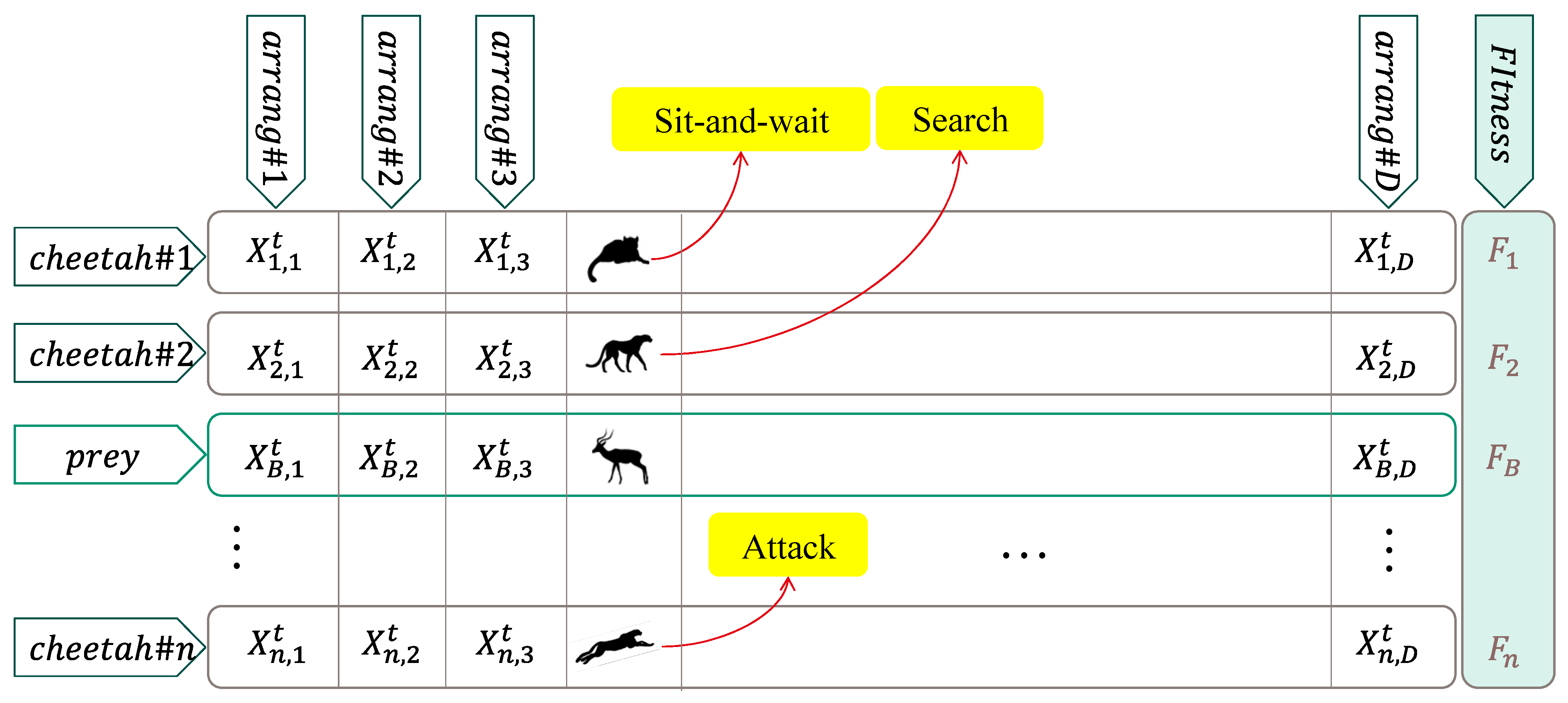
Figure 2.
Representation of the CO algorithm.
Figure 2.
Representation of the CO algorithm.
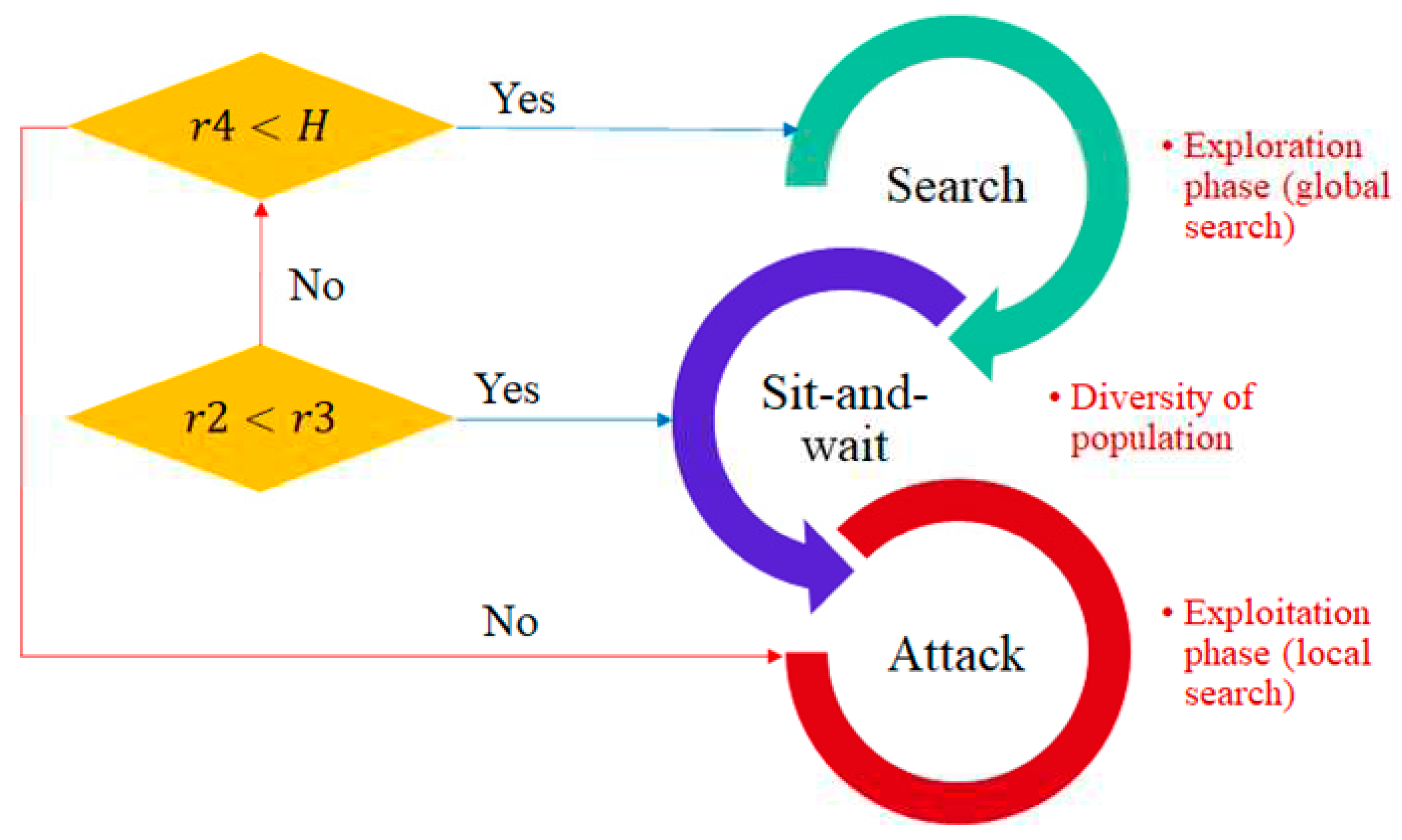
Figure 3.
An overview of the strategy selection mechanism in the CO algorithm.
Figure 3.
An overview of the strategy selection mechanism in the CO algorithm.
Figure 4.
Average ranks of the utilized population sizes in three models.
Figure 4.
Average ranks of the utilized population sizes in three models.
Figure 5.
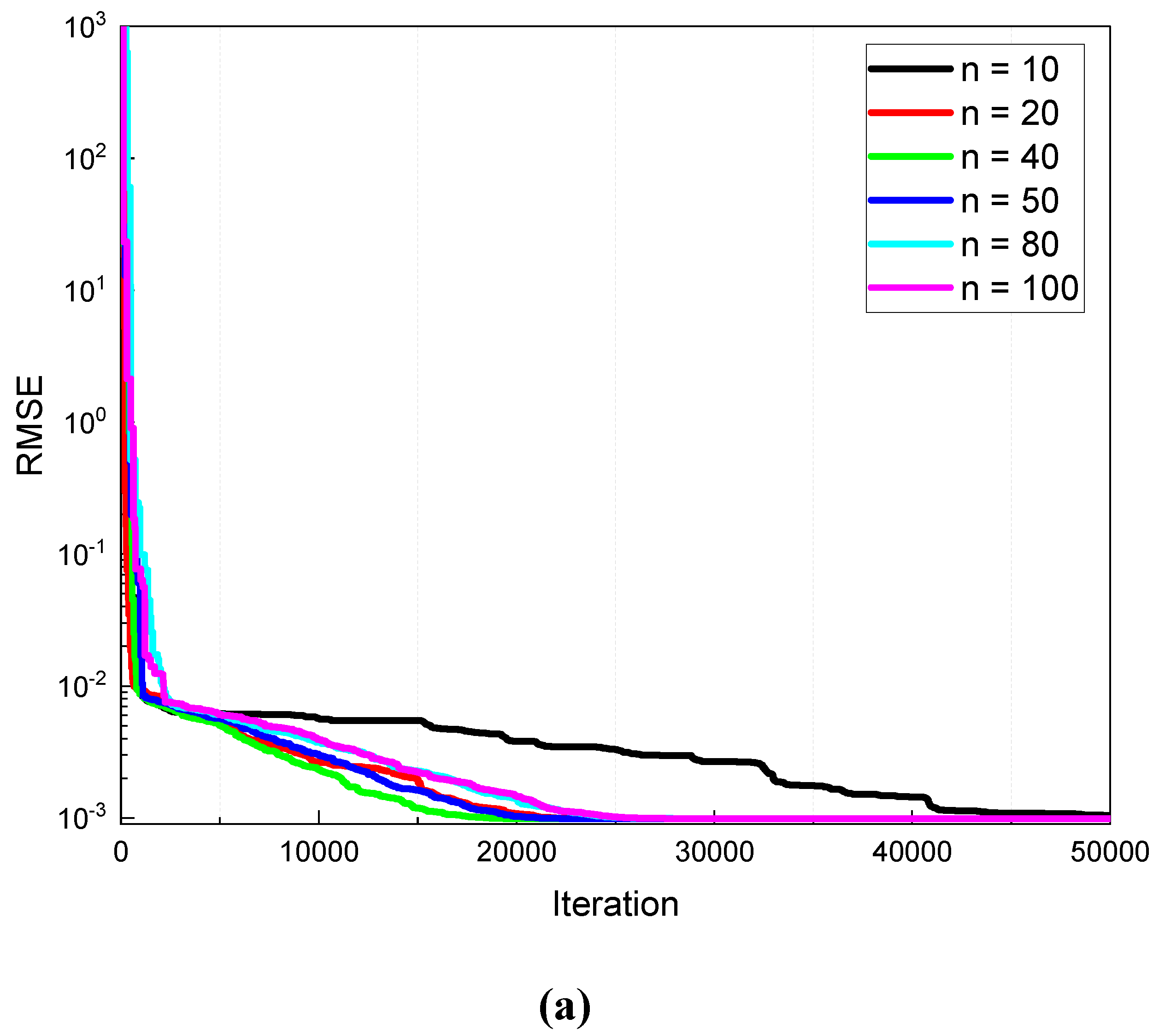
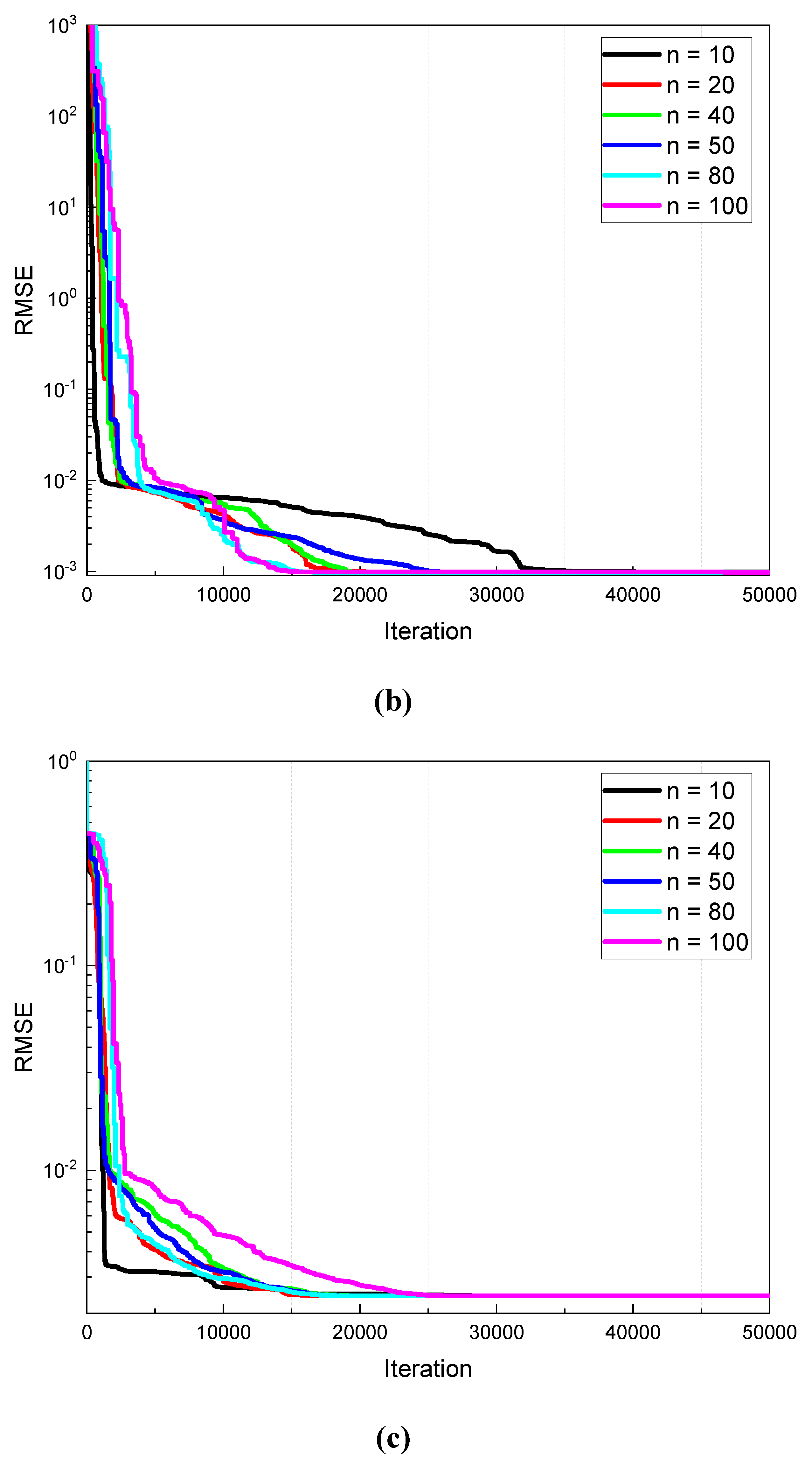
Convergence curves of ICO with different population sizes in solving (a) SDM, (b) DDM, and (c) PVMM.
Figure 5.
Convergence curves of ICO with different population sizes in solving (a) SDM, (b) DDM, and (c) PVMM.
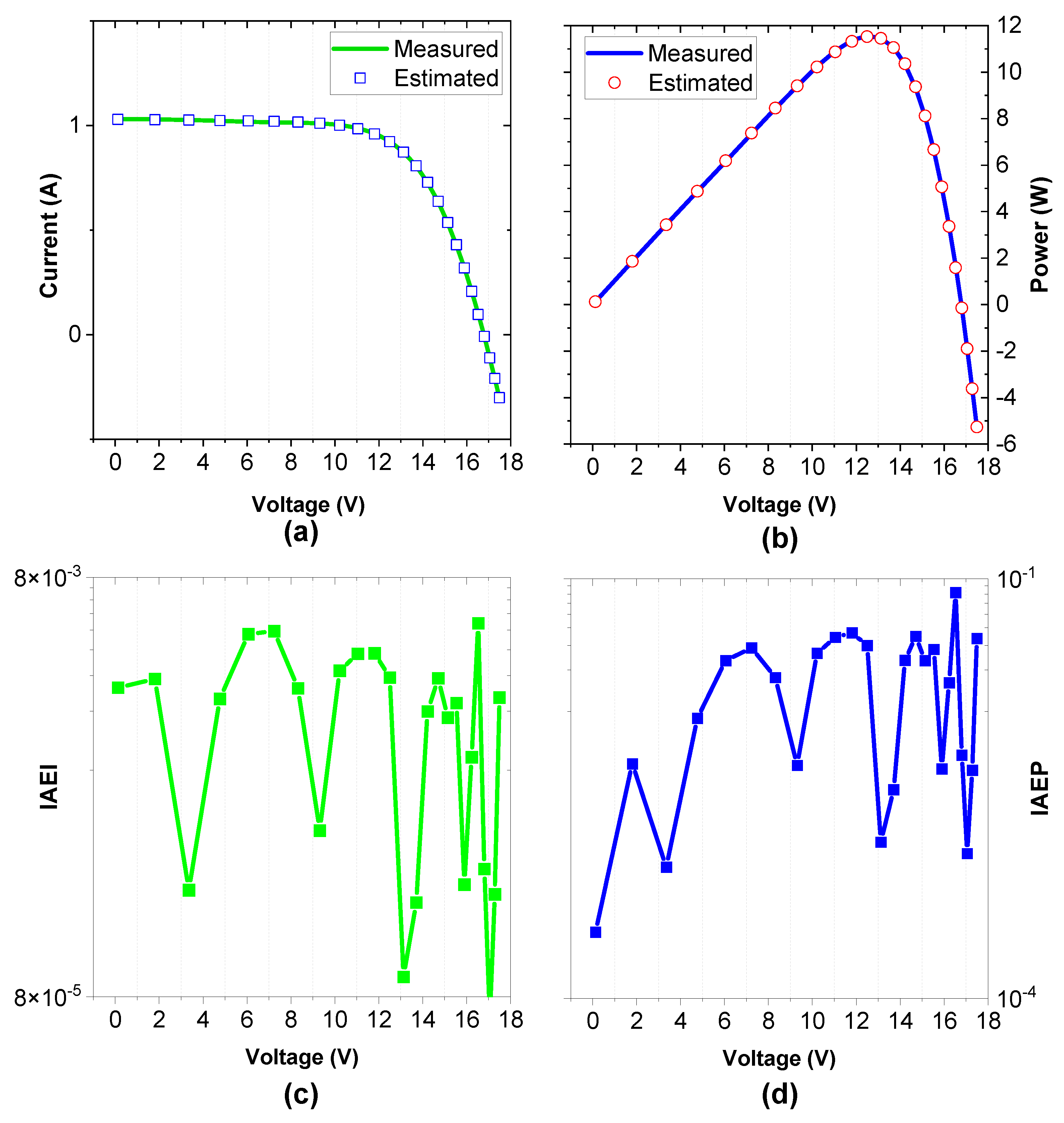
Figure 6.
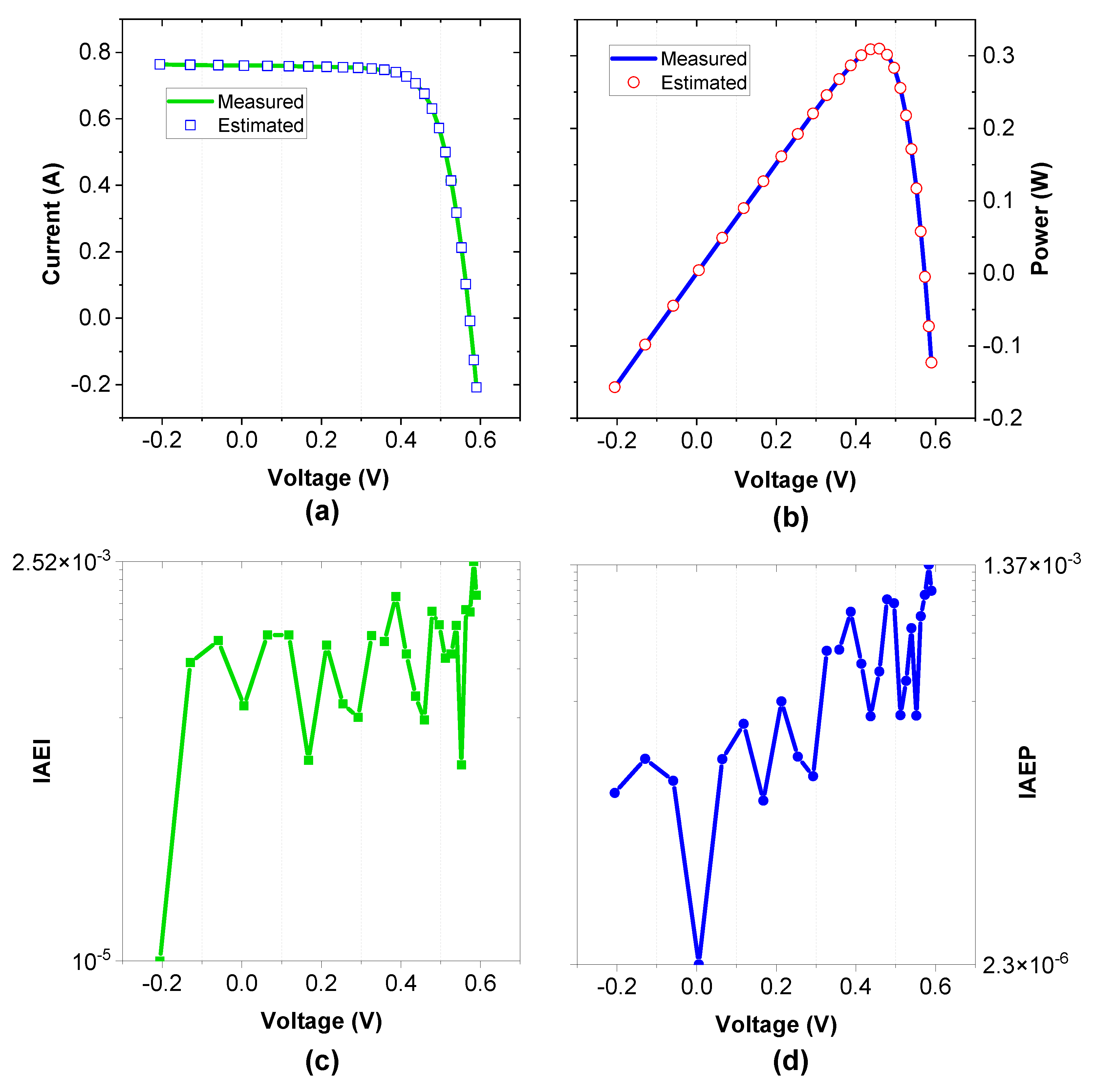
Estimated and measured data of the RTC France silicon solar cell based on the SDM by ICO; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
Figure 6.
Estimated and measured data of the RTC France silicon solar cell based on the SDM by ICO; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
Figure 7.
Estimated and measured data of the RTC France silicon solar cell based on DDM by ICO; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
Figure 7.
Estimated and measured data of the RTC France silicon solar cell based on DDM by ICO; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
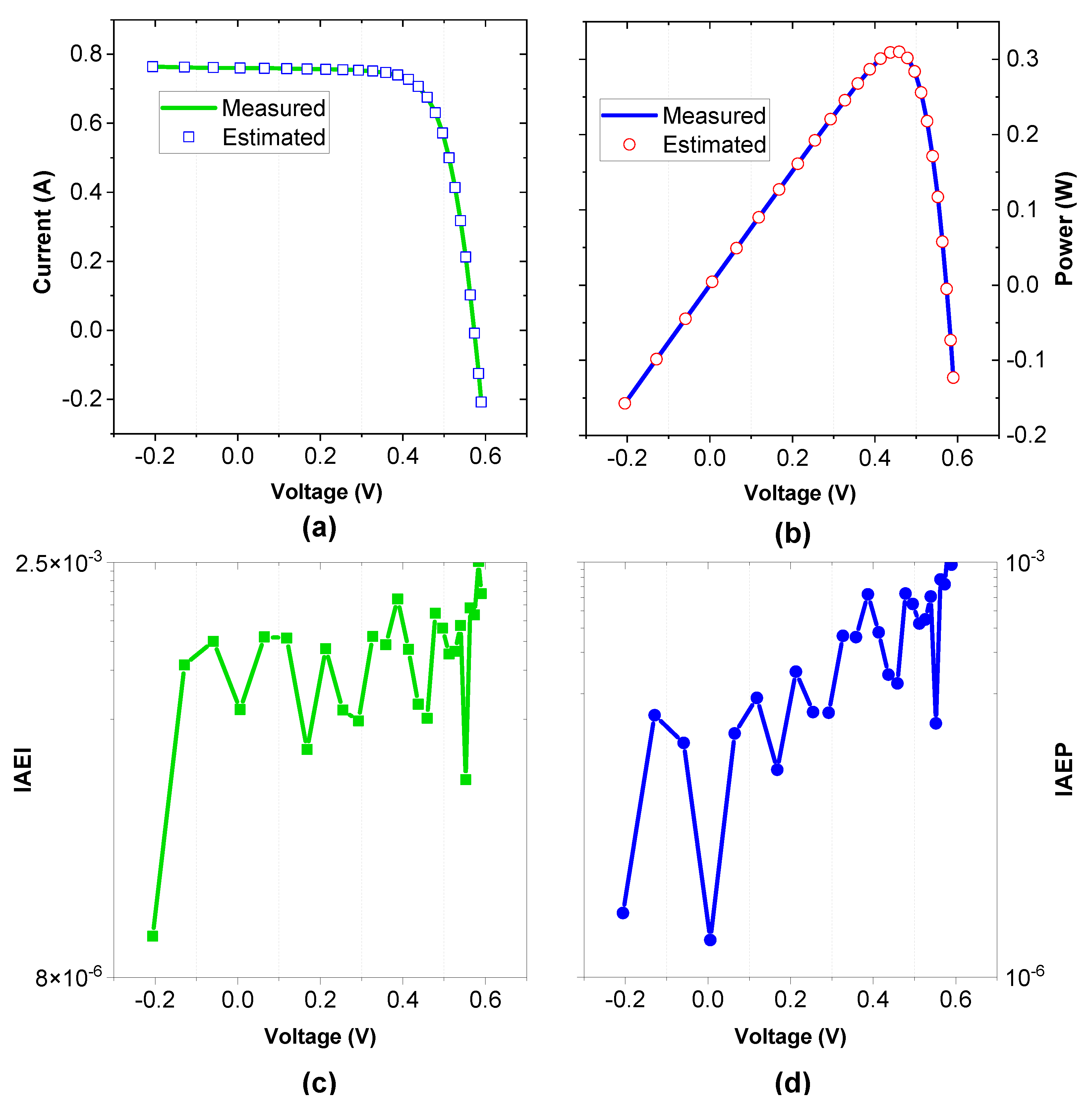
Figure 8.
Estimated and measured data yielded by ICO for the PV module model based on Photo Watt-PWP 201; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
Figure 8.
Estimated and measured data yielded by ICO for the PV module model based on Photo Watt-PWP 201; (a) I–V, (b) P–V, (c) IAEI, and (d) IAEP.
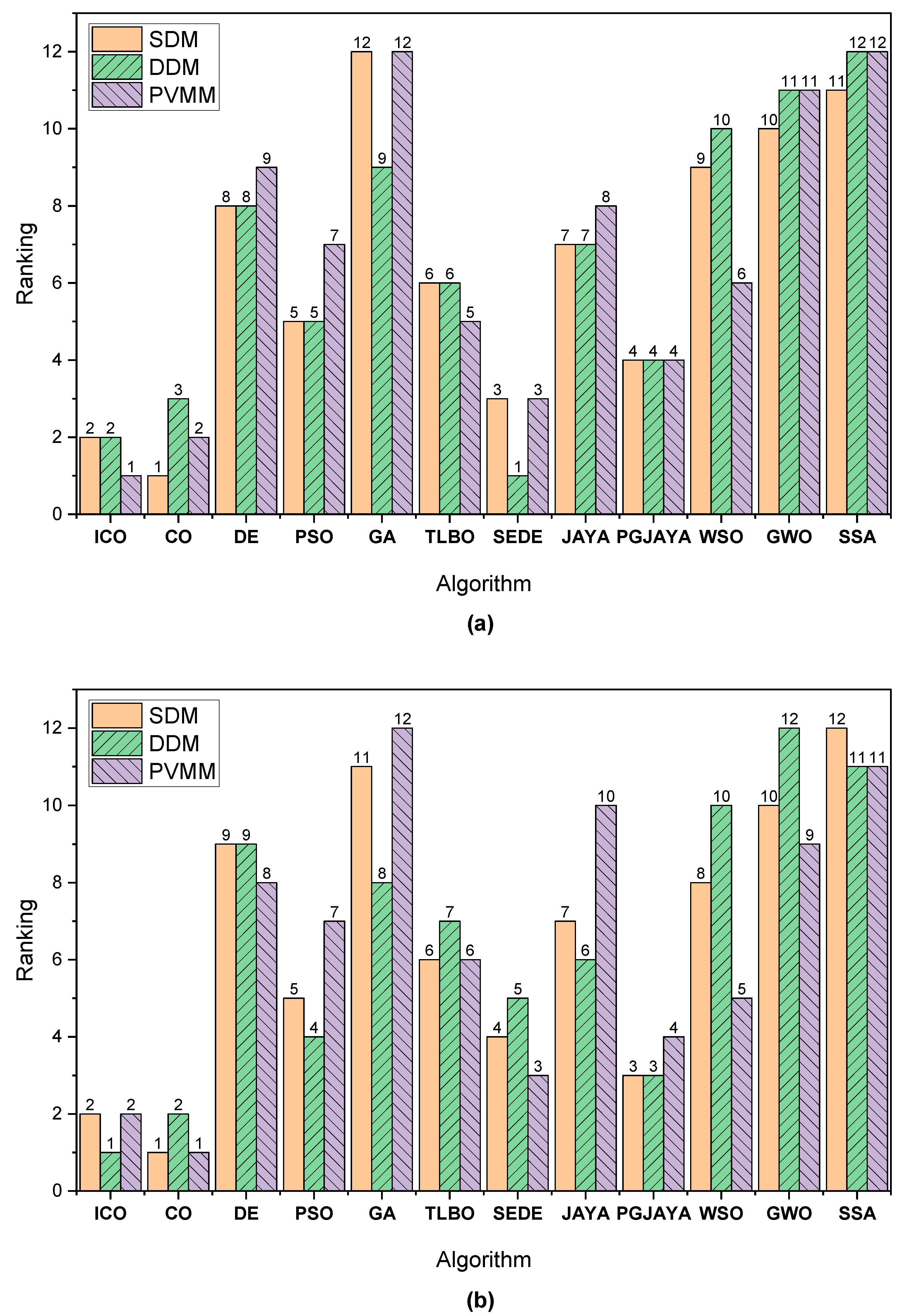
Figure 9.
Final ranking of applied algorithms for three models based on the Friedman test: (a) n = 40, and (b) n = 80.
Figure 9.
Final ranking of applied algorithms for three models based on the Friedman test: (a) n = 40, and (b) n = 80.
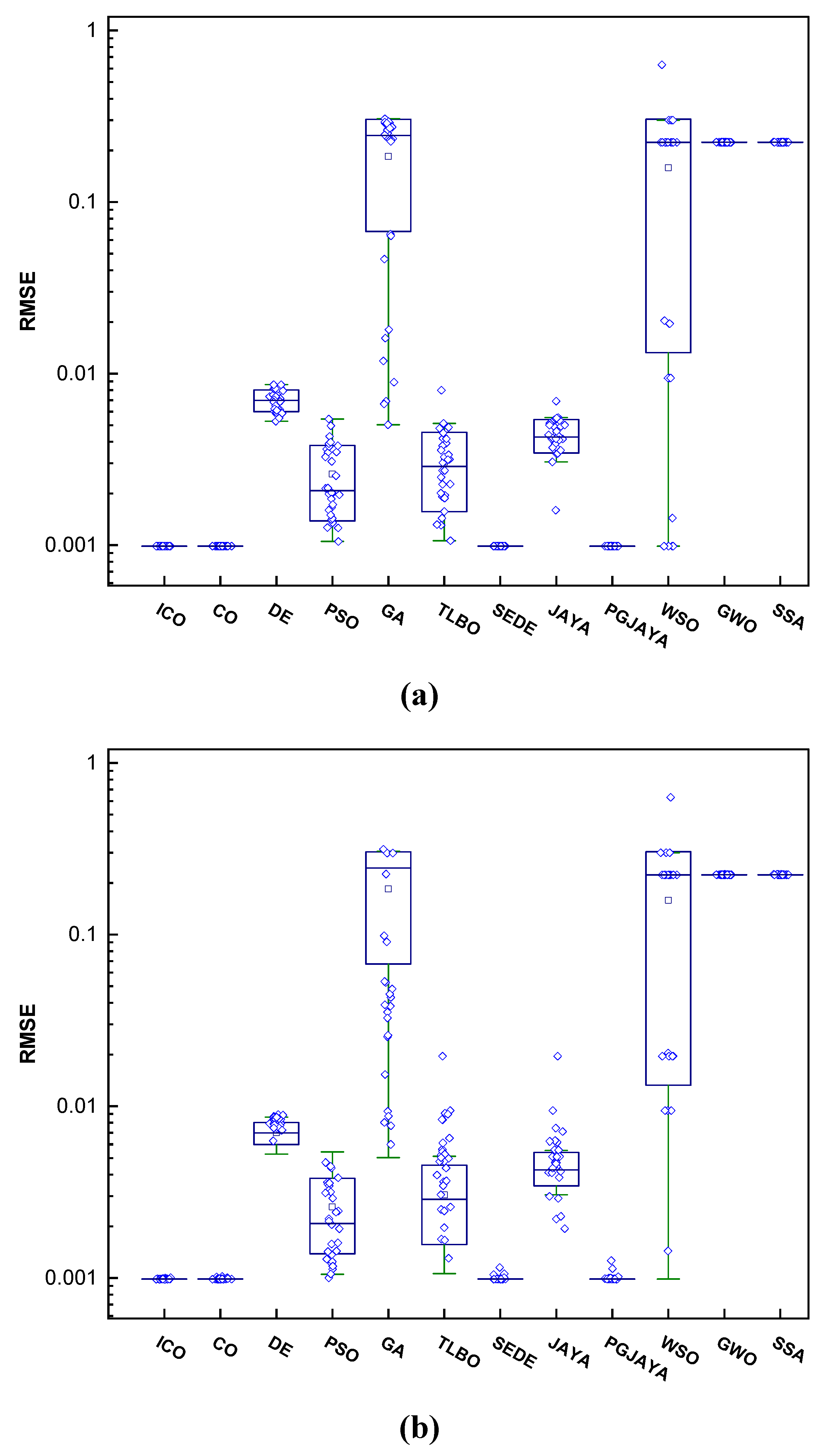
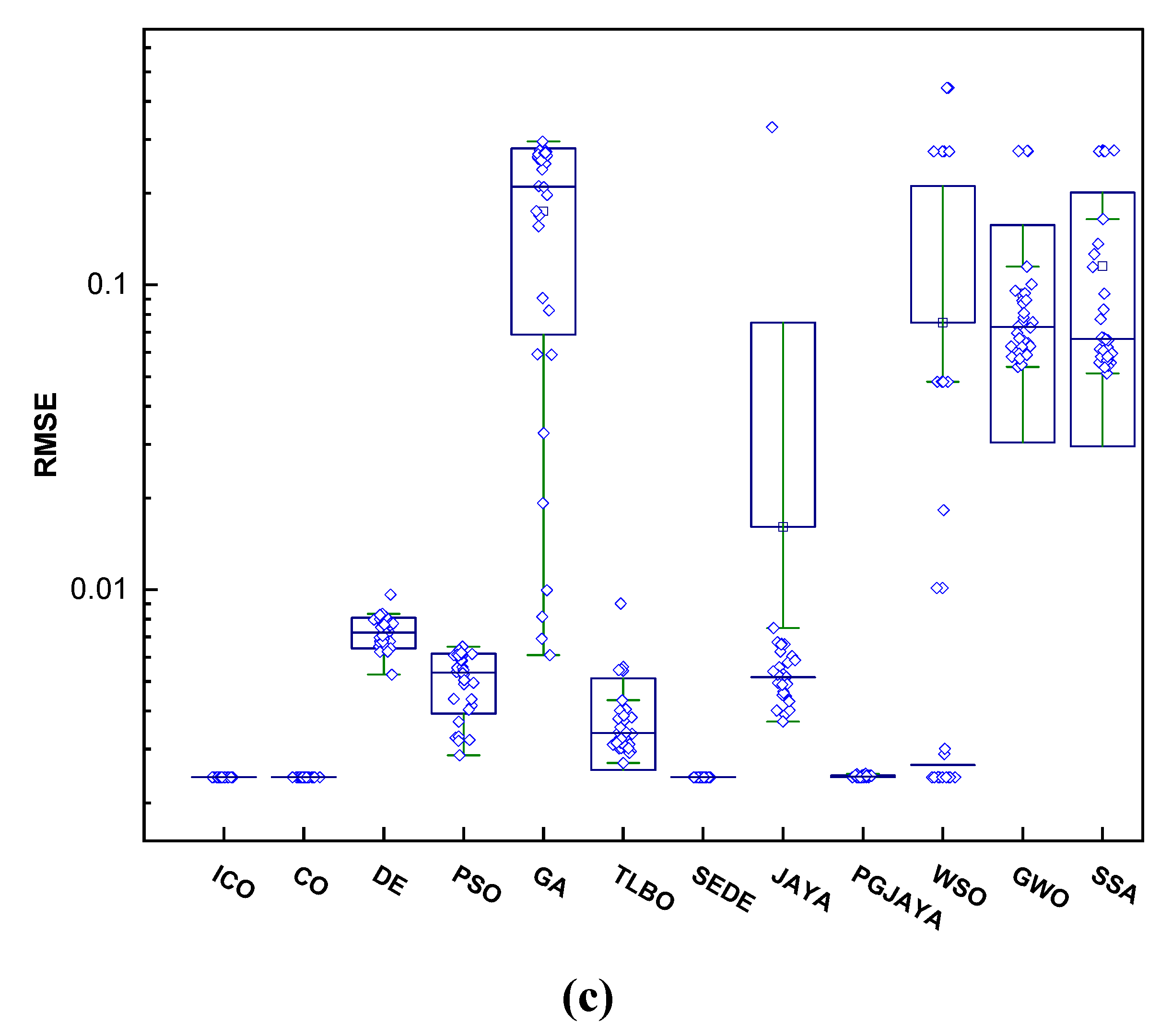
Figure 10.
Boxplot of best RMSE in 30 runs for n = 40: (a) SDM, (b) DDM, and (c) PVMM.
Figure 10.
Boxplot of best RMSE in 30 runs for n = 40: (a) SDM, (b) DDM, and (c) PVMM.
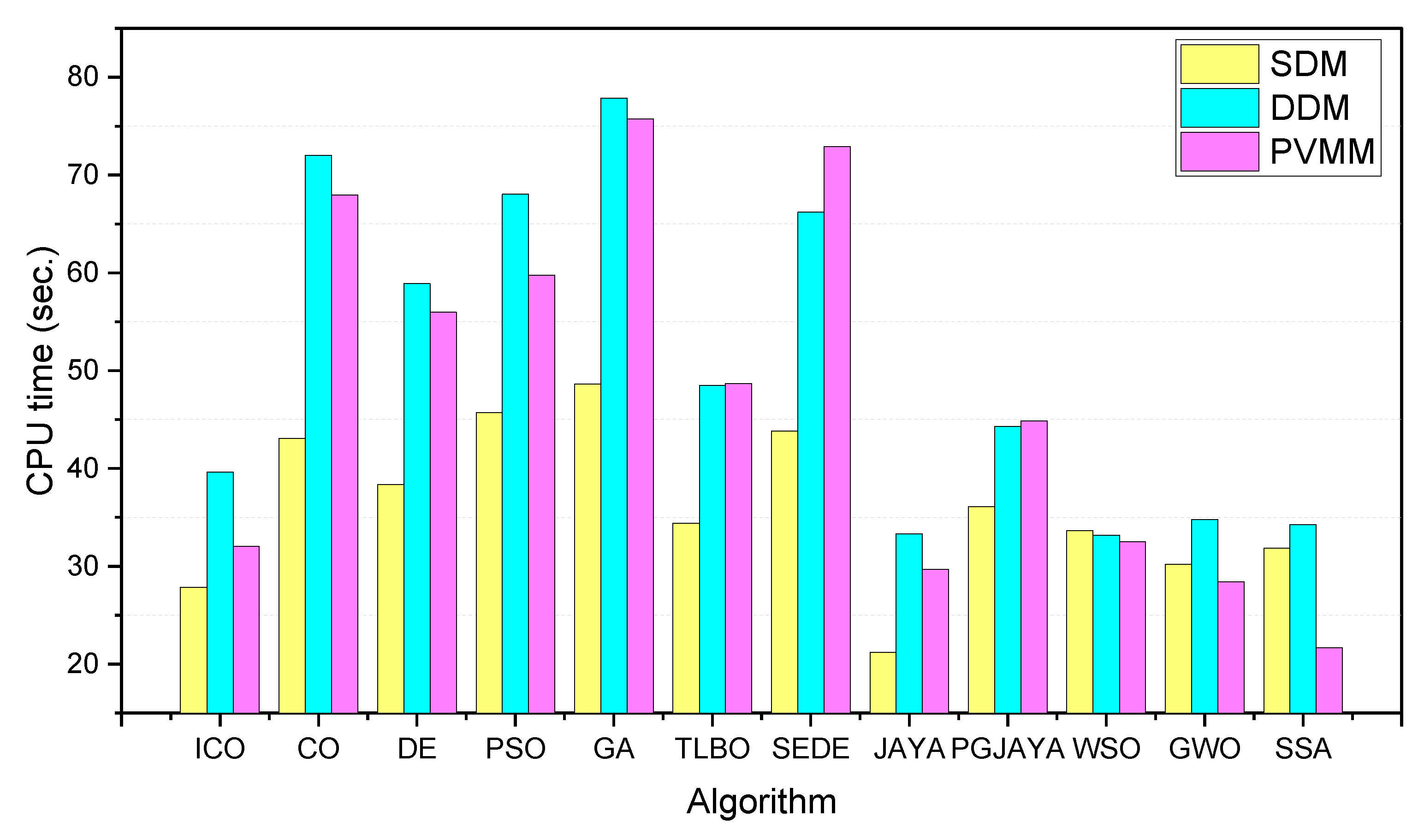
Figure 11.
CPU time over 30 runs by different algorithms with n = 40 for SDM, DDM, and PVMM.
Figure 11.
CPU time over 30 runs by different algorithms with n = 40 for SDM, DDM, and PVMM.
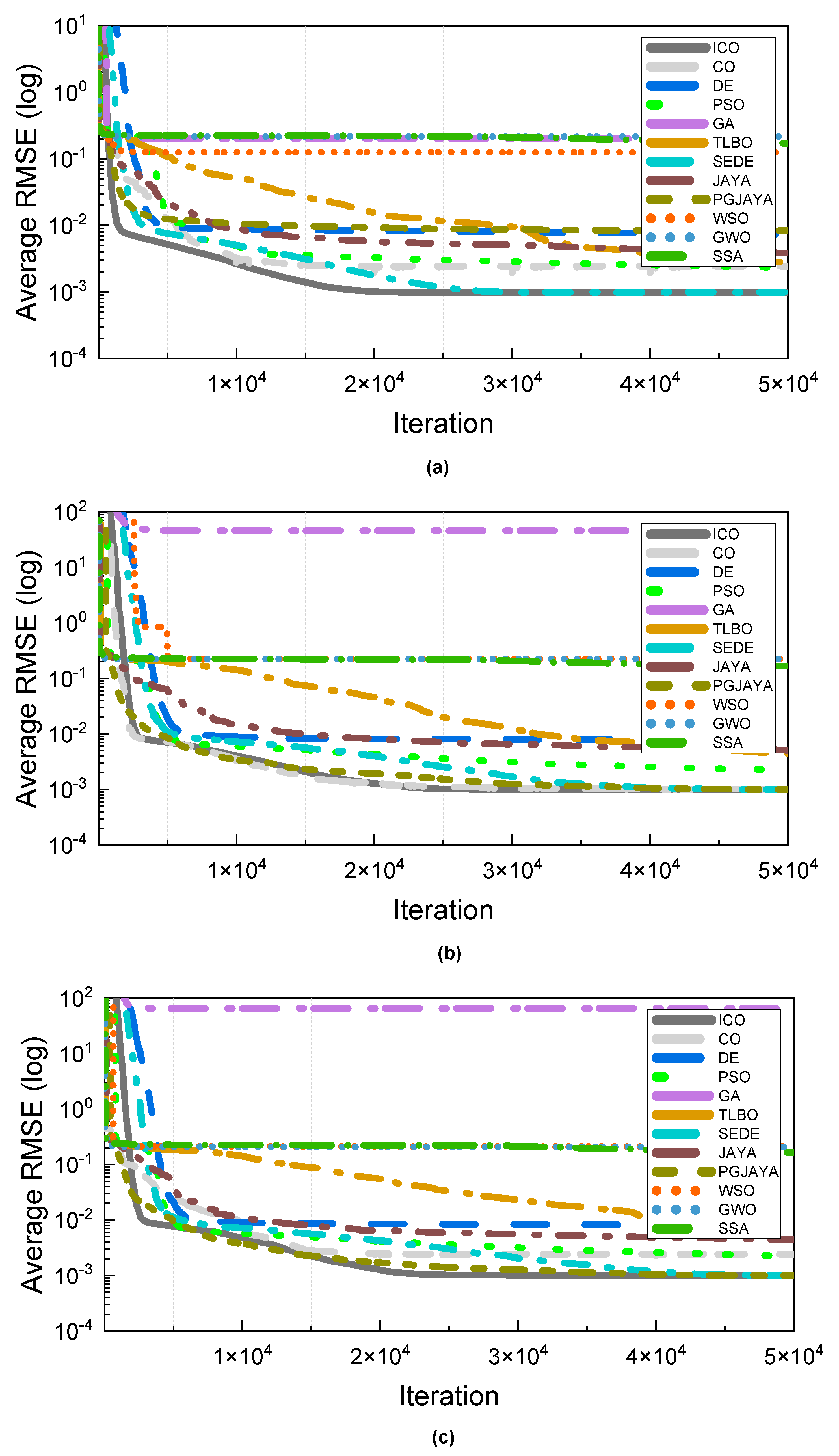
Figure 12.
Convergence curves of comparative algorithms with n = 40 for three models; (a) SDM, (b) DDM, and (c) PVMM.
Figure 12.
Convergence curves of comparative algorithms with n = 40 for three models; (a) SDM, (b) DDM, and (c) PVMM.
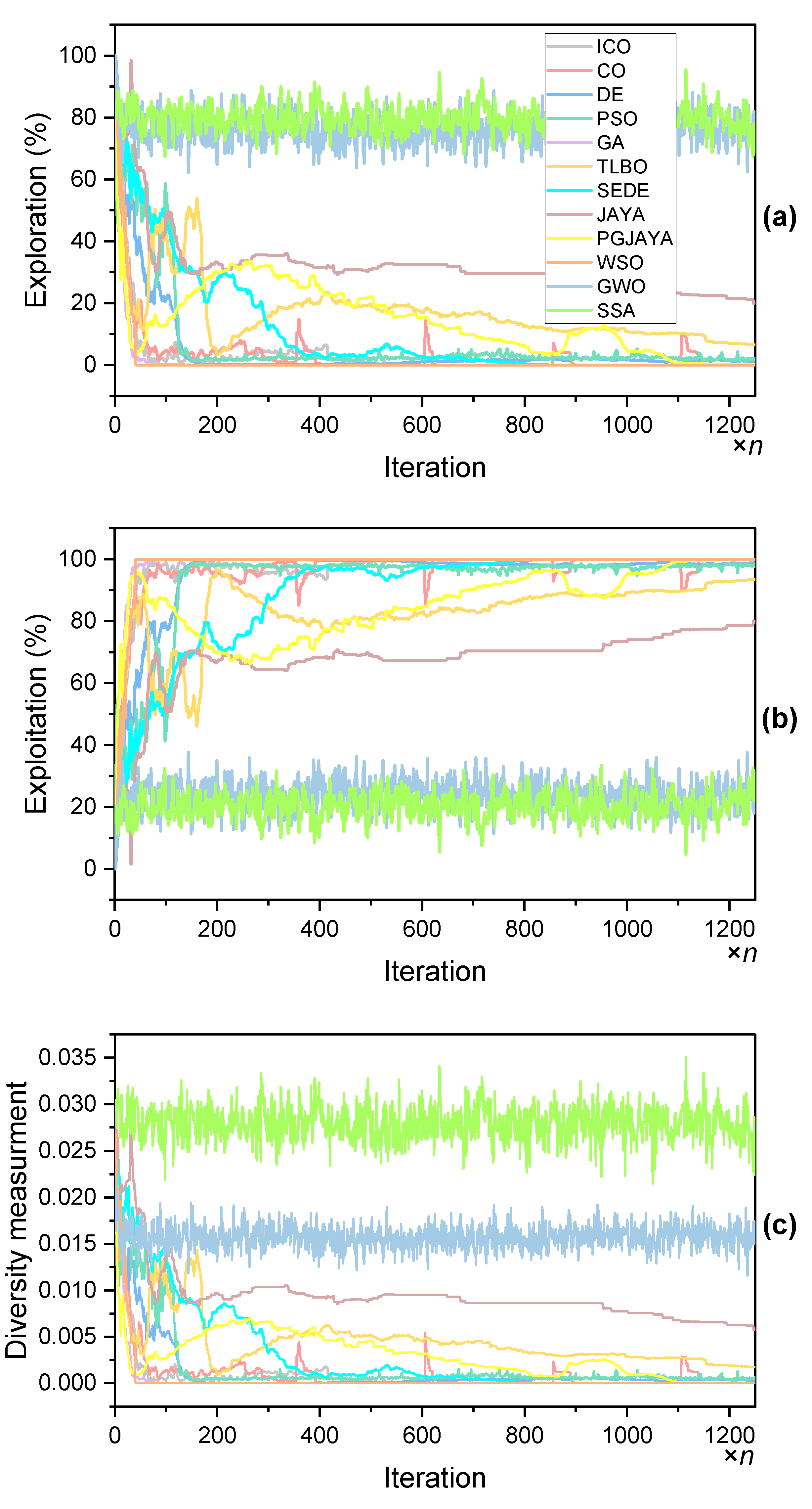
Figure 13.
Exploration-exploration and diversity of comparative algorithms on SDM.
Figure 13.
Exploration-exploration and diversity of comparative algorithms on SDM.
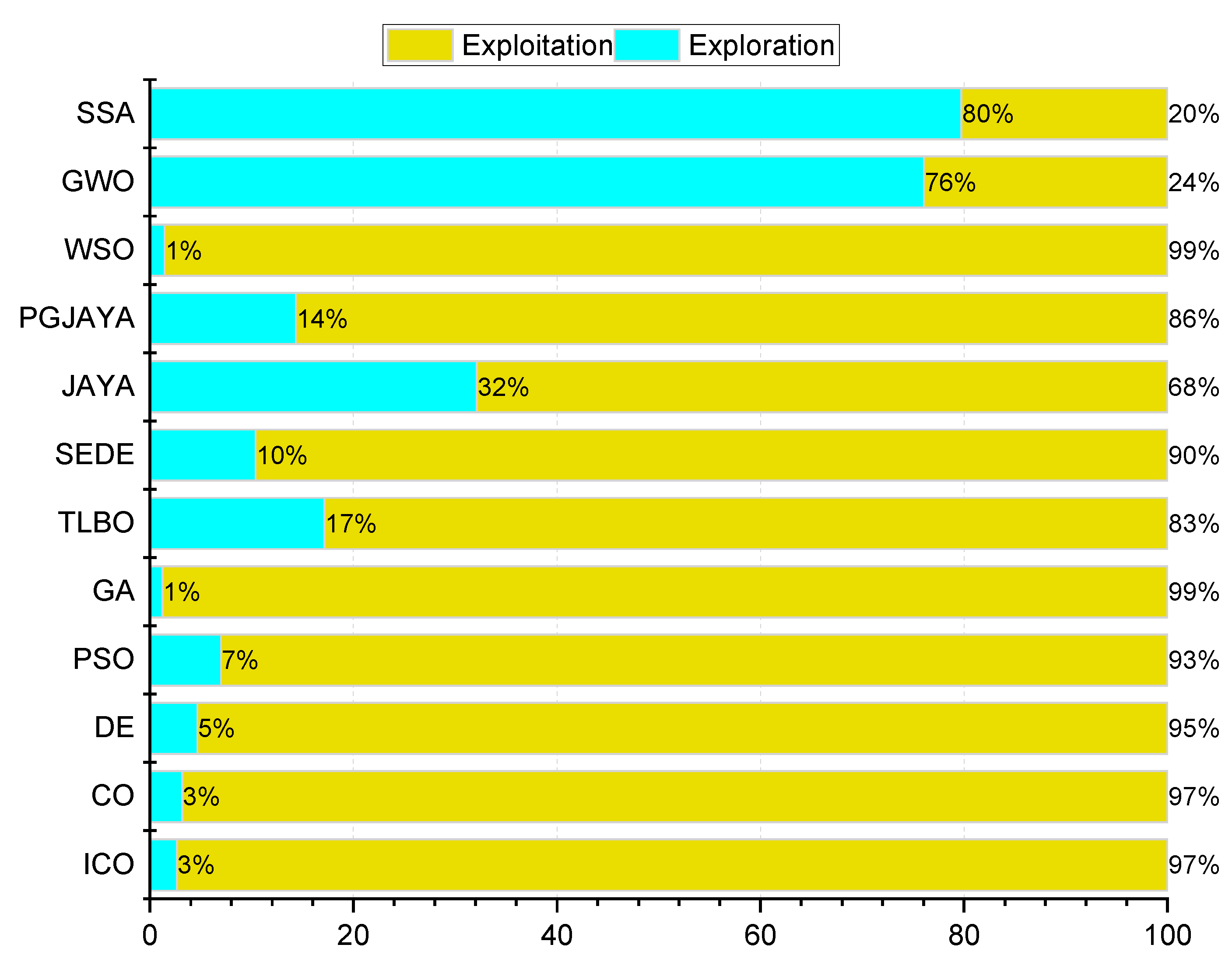
Figure 14.
Mean Exploration-exploitation of comparative algorithms on SDM.
Figure 14.
Mean Exploration-exploitation of comparative algorithms on SDM.
Table 1.
A review of the solar PV parameter extraction methods.
Table 1.
A review of the solar PV parameter extraction methods.
| Algorithm |
PV Type |
PV Model |
Disadvantage |
Advantage |
| PGJAYA [1] |
RTC France Si cell and PhotoWatt-PWP201 |
SDM, DDM, PVMM |
Insufficient reliability |
Acceptable accuracy |
| DE [2] |
SM55 Module |
SDM |
The parameters need to be adjusted, insufficient capability for exploitation. |
Accurate performance under a variety of operating conditionsPossessing good exploration capabilities |
| PSO [3] |
Not specified |
SDM, DDM |
Stuck in local minima, convergence at the beginning |
High level of accuracy in the solutionEase of implementationRobustness |
| SEDE [4] |
RTC France Si cell and PhotoWatt-PWP201 |
SDM, DDM, PVMM |
High computation time |
High accuracy and robustness |
| WSO [5] |
RTC France silicon solar cell, Photo watt-PWP 201, and STM6-40/36 PV modules |
SDM, DDM, PVMM |
Insufficient robustness |
New optimization algorithm for parameter extraction of PV cells and modules, low CPU time |
| SSA [6] |
TITAN-12-50 |
DDM |
Caught within local minimums, convergence occurs early in the process |
Low computational time |
| IJAYA [7] |
RTC France Si cell |
SDM, DDM |
Caught by local minima, Inaccurate solution |
A simpler and more efficient algorithmConvergence and robustness are high |
| Rao [8] |
RTC France Si cell and PhotoWatt-PWP201 |
SDM, DDM |
Stuck in local minima, commercial modules haven’t been tested |
Ease of implementationThe ability to explore well |
| MABC [9] |
RTC France Si cell |
SDM, DDM |
Excessive computation timeParameters need to be adjusted frequently, achieving convergence early |
High accuracy and robustnessInsensitive to noise |
| IMFO [10] |
Q6-1380 solar cell and CS6P-240P module |
SDM, DDM |
It takes a long time to compute, commercial modules have not been tested |
Convergence speed is high, it is simpler |
| SFLA [11] |
KC200GT and MSX-60 |
SDM |
Not accurateA lot of control parameters |
Fast convergence |
| TPTLBO [12] |
RTC France Si cell |
SDM, DDM |
High computational costsUncertainty about the solution |
Ease of implementationFewer control parametersFast convergence |
| ICWO [13] |
KC200GT |
SDM, DDM |
Inability to explore, caught within local minimums, convergence occurs early in the process |
Easily implemented, a lower cost of computationCapacity for fair exploitation |
| SCA [14] |
KC200GT |
SDM |
KC200GT module only tested, a local minimum trap |
Easy to implement and simple to use, a fair degree of accuracy |
| GWO-CS [15] |
KC200GT |
SDM |
The convergence speed is very slow |
A robust designReduced possibility of local optima trappingThe accuracy of the solution is high |
| COA [16] |
RTC France Si cell, PhotoWatt-PWP201, KC200GT, ST40, and SM55 |
SDM, DDM |
Insufficient ability to exploit, convergence at an early stage |
The quality of the solution is high, high convergence speed |
| MPA [17] |
KC200GT and MSX-60 |
DDM |
Convergence at an early stageStuck in local minima |
A high degree of accuracy in the solutionExcel exploratory skills |
| AGA [18] |
RTC France Si cell |
SDM |
Caught in the trap of local minima, a lack of local search capability |
A reasonable degree of accuracyIdentify promising search areas to find solutions |
| IEO [19] |
RTC France Si cell, PhotoWatt-PWP201, ST40, and SM55 |
SDM, DDM |
Long computation times |
High level of accuracyA good ability to explore and exploit |
| SMA [20] |
RTC France Si cell and PhotoWatt-PWP201 |
SDM, DDM |
It takes a long time to compute |
A high degree of accuracy, a good ability to explore and exploit |
| OAHHO [21] |
RTC France Si cell, PhotoWatt-PWP201, PVM 752 GaAs, ST40, and SM55 |
SDM, DDM |
Not specified |
Rapid convergence ratesAvoiding local optimum situationsHigh-quality solutions |
Table 2.
Parameters’ bounds for three models.
Table 2.
Parameters’ bounds for three models.
| Model |
|
|
|
|
|
|
|
|
|
|
| |
Min |
Max |
|
Min |
Max |
|
Min |
Max |
|
Min |
Max |
|
Min |
Max |
| SDM |
|
0 |
1 |
|
0 |
1 |
|
1 |
2 |
|
0 |
0.5 |
|
0 |
100 |
| DDM |
|
0 |
1 |
|
0 |
1 |
|
1 |
2 |
|
0 |
0.5 |
|
0 |
100 |
| PV module |
|
0 |
2 |
|
0 |
50 |
|
1 |
50 |
|
0 |
2 |
|
0 |
2000 |
Table 3.
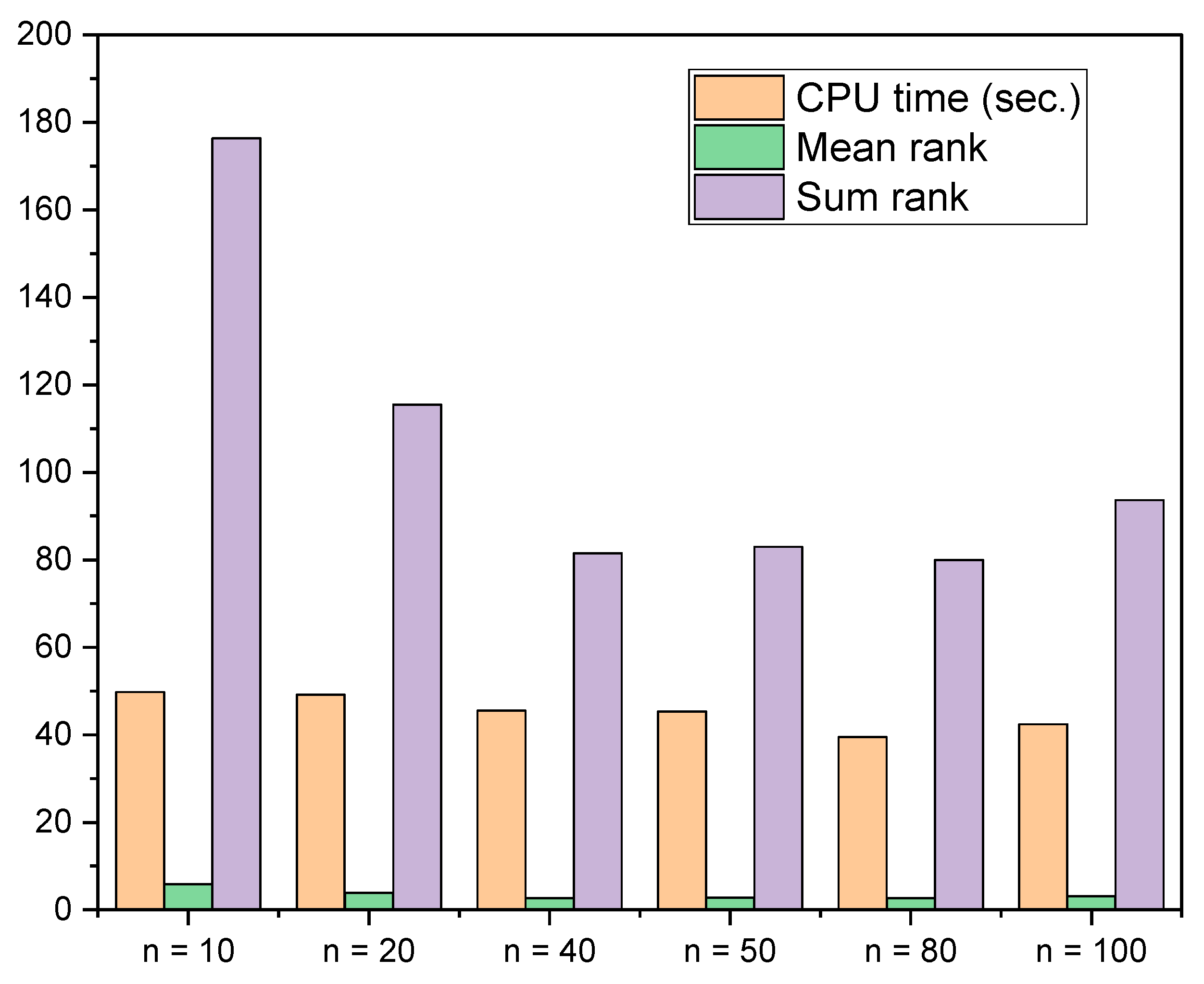
An analysis of the effect of population size on ICO performance for different PV models.
Table 3.
An analysis of the effect of population size on ICO performance for different PV models.
| Model |
n |
Min |
Mean |
Max |
SD |
CPU time (sec.) |
Mean rank in the Freidman test |
Sum rank in the Freidman test |
| SD |
10 |
9.860219E-04 |
1.006557E-03 |
1.268819E-03 |
5.47E-05 |
48.59 |
6.0 |
180 |
| 20 |
9.860219E-04 |
9.860219E-04 |
9.860219E-04 |
8.17E-17 |
48.02 |
3.6 |
106.5 |
| 40 |
9.860219E-04 |
9.860219E-04 |
9.860219E-04 |
6.30E-17 |
37.42 |
2.6 |
76.5 |
| 50 |
9.860219E-04 |
9.860219E-04 |
9.860219E-04 |
3.24E-17 |
40.23 |
2.5 |
74.5 |
| 80 |
9.860219E-04 |
9.860219E-04 |
9.860219E-04 |
4.85E-17 |
41.11 |
2.9 |
87 |
| 100 |
9.860219E-04 |
9.860219E-04 |
9.860219E-04 |
4.66E-17 |
50.89 |
3.5 |
105.5 |
| DD |
10 |
9.849747E-04 |
1.046876E-03 |
1.199696E-03 |
5.90E-05 |
52.52 |
5.6 |
169 |
| 20 |
9.832470E-04 |
9.909079E-04 |
1.016172E-03 |
8.43E-06 |
55.21 |
3.9 |
116 |
| 40 |
9.824888E-04 |
9.869534E-04 |
1.002805E-03 |
4.35E-06 |
53.12 |
2.9 |
87 |
| 50 |
9.825601E-04 |
9.861925E-04 |
9.948859E-04 |
2.43E-06 |
50.93 |
3.0 |
90 |
| 80 |
9.824849E-04 |
9.860955E-04 |
9.895027E-04 |
1.43E-06 |
38.32 |
2.6 |
78 |
| 100 |
9.836909E-04 |
9.878873E-04 |
1.014303E-03 |
6.14E-06 |
36.53 |
3.0 |
90 |
| PVM |
10 |
2.425075E-03 |
2.435752E-03 |
2.498069E-03 |
1.99E-05 |
48.36 |
6.0 |
180 |
| 20 |
2.425075E-03 |
2.425075E-03 |
2.425075E-03 |
2.14E-16 |
44.27 |
4.1 |
124 |
| 40 |
2.425075E-03 |
2.425075E-03 |
2.425075E-03 |
1.24E-16 |
46.07 |
2.7 |
81 |
| 50 |
2.425075E-03 |
2.425075E-03 |
2.425075E-03 |
3.65E-17 |
44.76 |
2.8 |
84.5 |
| 80 |
2.425075E-03 |
2.425075E-03 |
2.425075E-03 |
2.65E-17 |
39.16 |
2.5 |
75 |
| 100 |
2.425075E-03 |
2.425075E-03 |
2.425075E-03 |
3.17E-17 |
39.84 |
2.9 |
85.5 |
Table 4.
Optimal parameters of SDM obtained by different algorithms with n = 40.
Table 4.
Optimal parameters of SDM obtained by different algorithms with n = 40.
| n |
Algorithm |
|
|
|
|
|
RMSE |
| 40 |
ICO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778914E-04 |
| CO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778914E-04 |
| DE |
0.763 |
3.18E-06 |
100.000 |
0.0243 |
1.7547 |
5.274028415510E-03 |
| PSO |
0.761 |
2.67E-07 |
48.768 |
0.0371 |
1.4623 |
1.049908843005E-03 |
| GA |
0.764 |
2.63E-06 |
70.532 |
0.0257 |
1.7285 |
5.028715197625E-03 |
| TLBO |
0.761 |
3.77E-07 |
63.546 |
0.0358 |
1.4967 |
1.061394487359E-03 |
| SEDE |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778915E-04 |
| JAYA |
0.761 |
6.08E-07 |
70.138 |
0.0337 |
1.5478 |
1.596303286167E-03 |
| PGJAYA |
0.761 |
3.23E-07 |
53.713 |
0.0364 |
1.4812 |
9.860219332331E-04 |
| WSO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778915E-04 |
| GWO |
0.838 |
0.00E+00 |
1.139 |
0.0000 |
2.0000 |
2.228699161204E-01 |
| SSA |
0.835 |
0.00E+00 |
1.162 |
0.0000 |
1.0000 |
2.228762271791E-01 |
| 80 |
ICO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778914E-04 |
| CO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778914E-04 |
| DE |
0.763 |
1.54E-06 |
99.600 |
0.0296 |
1.6569 |
3.541687987531E-03 |
| PSO |
0.761 |
3.54E-07 |
56.556 |
0.0360 |
1.4903 |
1.001530647734E-03 |
| GA |
0.759 |
1.29E-07 |
46.427 |
0.0399 |
1.3938 |
2.248309383635E-03 |
| TLBO |
0.761 |
3.40E-07 |
55.608 |
0.0362 |
1.4865 |
9.917684200620E-04 |
| SEDE |
0.761 |
3.36E-07 |
54.054 |
0.0362 |
1.4852 |
9.902825250634E-04 |
| JAYA |
0.762 |
9.73E-07 |
88.523 |
0.0312 |
1.6013 |
2.589835639165E-03 |
| PGJAYA |
0.761 |
3.23E-07 |
53.722 |
0.0364 |
1.4812 |
9.860220454267E-04 |
| WSO |
0.761 |
3.23E-07 |
53.719 |
0.0364 |
1.4812 |
9.860218778915E-04 |
| GWO |
0.769 |
4.43E-06 |
24.455 |
0.0200 |
1.8059 |
9.281563258264E-03 |
| SSA |
1.000 |
8.72E-07 |
1.098 |
0.0007 |
1.6512 |
1.525312427660E-01 |
Table 5.
Optimal parameters for DDM obtained by different algorithms with n = 40.
Table 5.
Optimal parameters for DDM obtained by different algorithms with n = 40.
| n |
Algorithm |
|
|
|
|
|
|
|
RMSE |
| 40 |
ICO |
0.760781 |
7.46E-07 |
2.26E-07 |
0.036740 |
55.456 |
2.000 |
1.4511 |
9.82486099138E-04 |
| CO |
0.760781 |
7.50E-07 |
2.26E-07 |
0.036741 |
55.486 |
2.000 |
1.4510 |
9.82484882272E-04 |
| DE |
0.764966 |
2.55E-06 |
2.40E-06 |
0.022457 |
100.000 |
1.752 |
1.9806 |
6.28139269321E-03 |
| PSO |
0.760733 |
1.71E-07 |
1.46E-06 |
0.036757 |
61.054 |
1.429 |
2.0000 |
1.00247341473E-03 |
| GA |
0.763271 |
0.00E+00 |
4.23E-06 |
0.022775 |
97.844 |
1.670 |
1.7963 |
5.99279194424E-03 |
| TLBO |
0.760090 |
9.73E-08 |
2.76E-06 |
0.036975 |
100.000 |
1.387 |
1.9994 |
1.30300020067E-03 |
| SEDE |
0.760769 |
2.14E-07 |
8.07E-07 |
0.036790 |
55.795 |
1.447 |
1.9869 |
9.82753663536E-04 |
| JAYA |
0.759873 |
5.29E-07 |
4.02E-11 |
0.034438 |
70.729 |
1.532 |
1.8894 |
1.93867560984E-03 |
| PGJAYA |
0.760782 |
2.45E-07 |
2.90E-07 |
0.036477 |
54.289 |
1.999 |
1.4720 |
9.84193519571E-04 |
| WSO |
0.759500 |
4.52E-07 |
0.00E+00 |
0.035285 |
100.000 |
1.516 |
2.0000 |
1.43847589737E-03 |
| GWO |
1.000000 |
0.00E+00 |
1.16E-05 |
0.000000 |
2.179 |
1.000 |
2.0000 |
1.54903625180E-01 |
| SSA |
0.834308 |
0.00E+00 |
0.00E+00 |
0.000000 |
1.152 |
1.000 |
1.0000 |
2.22868413284E-01 |
| 80 |
ICO |
0.760780 |
6.63E-07 |
2.36E-07 |
0.036695 |
55.257 |
2.000 |
1.4547 |
9.82538943274E-04 |
| CO |
0.760781 |
2.22E-07 |
7.72E-07 |
0.036757 |
55.539 |
1.450 |
1.9969 |
9.82528425982E-04 |
| DE |
0.763865 |
5.19E-08 |
9.13E-06 |
0.023974 |
99.963 |
1.407 |
1.9937 |
6.73013079580E-03 |
| PSO |
0.760797 |
6.03E-07 |
2.03E-07 |
0.036852 |
54.797 |
1.900 |
1.4430 |
9.84648707354E-04 |
| GA |
0.760727 |
0.00E+00 |
9.74E-07 |
0.031507 |
100.000 |
1.681 |
1.6015 |
2.39573932360E-03 |
| TLBO |
0.760754 |
3.22E-07 |
5.04E-17 |
0.036453 |
55.423 |
1.481 |
1.0230 |
9.95677091382E-04 |
| SEDE |
0.760178 |
8.63E-07 |
2.07E-07 |
0.034961 |
82.980 |
1.806 |
1.4577 |
1.47037750973E-03 |
| JAYA |
0.761997 |
1.39E-06 |
0.00E+00 |
0.028824 |
100.000 |
1.644 |
2.0000 |
3.57709882707E-03 |
| PGJAYA |
0.760851 |
5.18E-07 |
2.30E-07 |
0.036667 |
54.633 |
1.917 |
1.4533 |
9.84200147988E-04 |
| WSO |
0.760776 |
0.00E+00 |
3.23E-07 |
0.036377 |
53.719 |
2.000 |
1.4812 |
9.86021877892E-04 |
| GWO |
0.999003 |
0.00E+00 |
5.29E-06 |
0.000514 |
1.373 |
2.000 |
1.8772 |
1.38743574369E-01 |
| SSA |
0.836762 |
1.17E-09 |
0.00E+00 |
0.000071 |
1.149 |
1.121 |
1.4507 |
1.57126305055E-01 |
Table 6.
Optimal parameters for PVMM by different algorithms with n = 40 and n = 80.
Table 6.
Optimal parameters for PVMM by different algorithms with n = 40 and n = 80.
| n |
Algorithm |
|
|
|
|
|
RMSE |
| 40 |
ICO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868095030E-03 |
| CO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868094980E-03 |
| DE |
1.02991 |
1.49E-05 |
1065.617 |
0.0284 |
1.5261 |
5.266650305240960E-03 |
| PSO |
1.02677 |
5.98E-06 |
88.261 |
0.0318 |
1.4111 |
2.864391667859010E-03 |
| GA |
1.02370 |
1.52E-05 |
1944.805 |
0.0278 |
1.5294 |
6.099240455880790E-03 |
| TLBO |
1.02611 |
4.78E-06 |
75.270 |
0.0325 |
1.3855 |
2.700403640152360E-03 |
| SEDE |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868095090E-03 |
| JAYA |
1.02742 |
8.89E-06 |
911.208 |
0.0305 |
1.4586 |
3.697656950234140E-03 |
| PGJAYA |
1.03052 |
3.48E-06 |
27.250 |
0.0334 |
1.3511 |
2.425077305006140E-03 |
| WSO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868095050E-03 |
| GWO |
1.04843 |
5.00E-05 |
3.016 |
0.0000 |
1.7509 |
5.383466416567090E-02 |
| SSA |
1.15116 |
5.00E-05 |
2.191 |
0.0129 |
1.7224 |
5.130174319081860E-02 |
| 80 |
ICO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868095010E-03 |
| CO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868094990E-03 |
| DE |
1.02868 |
2.27E-05 |
1968.622 |
0.0264 |
1.5866 |
6.921126739647050E-03 |
| PSO |
1.02664 |
6.66E-06 |
115.721 |
0.0314 |
1.4238 |
3.029451135597340E-03 |
| GA |
1.03138 |
2.87E-05 |
2000.000 |
0.0252 |
1.6215 |
7.712963596737400E-03 |
| TLBO |
1.02522 |
5.63E-06 |
881.405 |
0.0321 |
1.4034 |
3.244452302450550E-03 |
| SEDE |
1.03013 |
3.56E-06 |
28.820 |
0.0333 |
1.3536 |
2.427164258722220E-03 |
| JAYA |
1.02758 |
1.51E-05 |
1713.306 |
0.0277 |
1.5278 |
5.590302366807740E-03 |
| PGJAYA |
1.02922 |
4.29E-06 |
33.745 |
0.0327 |
1.3739 |
2.518017787843970E-03 |
| WSO |
1.03051 |
3.48E-06 |
27.277 |
0.0334 |
1.3512 |
2.425074868095060E-03 |
| GWO |
1.07157 |
5.00E-05 |
5.528 |
0.0187 |
1.7213 |
2.019064583084870E-02 |
| SSA |
1.06056 |
4.31E-05 |
12.652 |
0.0238 |
1.6888 |
1.554532543514840E-02 |
Table 7.
Statistical results of different algorithms with n = 40 and n = 80 for SDM.
Table 7.
Statistical results of different algorithms with n = 40 and n = 80 for SDM.
| n |
Algorithm |
Min |
Mean |
Max |
SD |
Mean rank |
Sum rank |
Significance |
| 40 |
ICO |
9.86021877891E-04 |
9.86021877892E-04 |
9.86021877892E-04 |
3.091E-17 |
1.633 |
49 |
|
| CO |
9.86021877891E-04 |
9.86021877892E-04 |
9.86021877893E-04 |
2.299E-16 |
1.600 |
48 |
|
| DE |
5.27402841551E-03 |
7.00472269280E-03 |
8.61400240318E-03 |
1.008E-03 |
8.200 |
246 |
|
| PSO |
1.04990884301E-03 |
2.59824261345E-03 |
5.43861383375E-03 |
1.215E-03 |
5.700 |
171 |
|
| GA |
5.02871519763E-03 |
1.85106717646E-01 |
3.05981702986E-01 |
1.178E-01 |
10.933 |
328 |
|
| TLBO |
1.06139448736E-03 |
3.05558085709E-03 |
7.98832352445E-03 |
1.489E-03 |
5.867 |
176 |
|
| SEDE |
9.86021877891E-04 |
9.86021877892E-04 |
9.86021877892E-04 |
4.368E-17 |
2.867 |
86 |
|
| JAYA |
1.59630328617E-03 |
4.42292722271E-03 |
6.90548939964E-03 |
9.777E-04 |
6.933 |
208 |
|
| PGJAYA |
9.86021933233E-04 |
9.86276195755E-04 |
9.89060476576E-04 |
6.385E-07 |
4.133 |
124 |
|
| WSO |
9.86021877892E-04 |
1.58438200609E-01 |
6.30741696212E-01 |
1.452E-01 |
8.733 |
262 |
|
| GWO |
2.22869916120E-01 |
2.23053219785E-01 |
2.23414777753E-01 |
1.541E-04 |
10.600 |
318 |
|
| SSA |
2.22876227179E-01 |
2.23093108473E-01 |
2.23798438512E-01 |
1.976E-04 |
10.800 |
324 |
|
| 80 |
ICO |
9.86021877891E-04 |
9.86021877892E-04 |
9.86021877892E-04 |
5.21E-17 |
1.933 |
58 |
|
| CO |
9.86021877891E-04 |
9.86021877891E-04 |
9.86021877892E-04 |
1.02E-16 |
1.267 |
38 |
|
| DE |
3.54168798753E-03 |
7.44468352091E-03 |
8.66642059402E-03 |
8.63E-04 |
8.233 |
247 |
|
| PSO |
1.00153064773E-03 |
2.60127712828E-03 |
4.82228315158E-03 |
1.30E-03 |
5.633 |
169 |
|
| GA |
2.24830938364E-03 |
1.73964495048E-01 |
2.97093810571E-01 |
9.96E-02 |
10.767 |
323 |
|
| TLBO |
9.91768420062E-04 |
5.34155103461E-03 |
1.97944235719E-02 |
4.83E-03 |
6.600 |
198 |
|
| SEDE |
9.90282525063E-04 |
1.01400153629E-03 |
1.09363977975E-03 |
2.20E-05 |
4.033 |
121 |
|
| JAYA |
2.58983563916E-03 |
5.68192621557E-03 |
9.00499477318E-03 |
1.14E-03 |
7.067 |
212 |
|
| PGJAYA |
9.86022045427E-04 |
1.01574698584E-03 |
1.18949290801E-03 |
4.93E-05 |
3.767 |
113 |
|
| WSO |
9.86021877892E-04 |
3.86485383212E-02 |
2.99953326338E-01 |
8.23E-02 |
7.233 |
217 |
|
| GWO |
9.28156325826E-03 |
2.08662190383E-01 |
2.22887009586E-01 |
5.41E-02 |
10.650 |
319.5 |
|
| SSA |
1.52531242766E-01 |
1.76192424924E-01 |
2.22861399093E-01 |
2.22E-02 |
10.817 |
324.5 |
|
Table 8.
Statistical results of different algorithms with n = 40 and n = 80 for DDM.
Table 8.
Statistical results of different algorithms with n = 40 and n = 80 for DDM.
| n |
Algorithm |
Min |
Mean |
Max |
SD |
Mean rank |
Sum rank |
Sign. |
| 40 |
ICO |
9.82486099138221E-04 |
9.87266271841069E-04 |
1.00565345910251E-03 |
5.0E-06 |
2.400 |
72 |
|
| CO |
9.82484882272263E-04 |
9.90014277022917E-04 |
1.02092378170200E-03 |
9.2E-06 |
2.667 |
80 |
|
| DE |
6.28139269320691E-03 |
8.08813241671442E-03 |
8.93742409284825E-03 |
5.8E-04 |
7.867 |
236 |
|
| PSO |
1.00247341473318E-03 |
2.42462675866429E-03 |
4.70972999662043E-03 |
1.2E-03 |
5.233 |
157 |
|
| GA |
5.99279194423828E-03 |
9.40346251766308E-02 |
3.14531449266952E-01 |
9.2E-02 |
9.533 |
286 |
|
| TLBO |
1.30300020066498E-03 |
5.31395638216597E-03 |
1.95451852804007E-02 |
3.5E-03 |
6.533 |
196 |
|
| SEDE |
9.82753663536365E-04 |
9.96916197397831E-04 |
1.15176160603947E-03 |
3.4E-05 |
2.133 |
64 |
|
| JAYA |
1.93867560984064E-03 |
5.30491570084624E-03 |
1.95452348011886E-02 |
3.1E-03 |
6.567 |
197 |
|
| PGJAYA |
9.84193519571165E-04 |
1.00336927015568E-03 |
1.26370280495224E-03 |
5.6E-05 |
2.867 |
86 |
|
| WSO |
1.43847589736749E-03 |
1.86584575264940E-01 |
6.30741696211904E-01 |
1.5E-01 |
9.967 |
299 |
|
| GWO |
1.54903625179668E-01 |
2.21100841293962E-01 |
2.24562995128955E-01 |
1.3E-02 |
11.067 |
332 |
|
| SSA |
2.22868413284217E-01 |
2.23443763002107E-01 |
2.24750772827690E-01 |
5.3E-04 |
11.167 |
335 |
|
| 80 |
ICO |
9.8253894327E-04 |
9.8641995737E-04 |
9.9981923040E-04 |
3.134E-06 |
1.633 |
49 |
|
| CO |
9.8252842598E-04 |
9.9825780367E-04 |
1.0827441957E-03 |
2.432E-05 |
1.900 |
57 |
|
| DE |
6.7301307958E-03 |
8.0618449324E-03 |
8.8108931833E-03 |
6.169E-04 |
7.933 |
238 |
|
| PSO |
9.8464870735E-04 |
2.3813391278E-03 |
5.5055357165E-03 |
1.184E-03 |
4.533 |
136 |
|
| GA |
2.3957393236E-03 |
2.2114853037E-02 |
1.1924927342E-01 |
3.269E-02 |
7.800 |
234 |
|
| TLBO |
9.9567709138E-04 |
1.8966303725E-02 |
6.2679374194E-02 |
1.887E-02 |
7.700 |
231 |
|
| SEDE |
1.4703775097E-03 |
2.6141249460E-03 |
4.0397037616E-03 |
8.191E-04 |
4.833 |
145 |
|
| JAYA |
3.5770988271E-03 |
6.7480847825E-03 |
9.7931015684E-03 |
1.726E-03 |
7.067 |
212 |
|
| PGJAYA |
9.8420014799E-04 |
1.0315913230E-03 |
1.3731176270E-03 |
7.747E-05 |
2.700 |
81 |
|
| WSO |
9.8602187789E-04 |
1.1327669684E-01 |
2.9995332634E-01 |
1.185E-01 |
9.700 |
291 |
|
| GWO |
1.3874357437E-01 |
1.6797247572E-01 |
2.2219565068E-01 |
1.317E-02 |
11.167 |
335 |
|
| SSA |
1.5712630505E-01 |
1.6563118085E-01 |
1.7878158052E-01 |
5.962E-03 |
11.033 |
331 |
|
Table 9.
Statistical results of different algorithms with n = 40 and n = 80 for PVMM.
Table 9.
Statistical results of different algorithms with n = 40 and n = 80 for PVMM.
| n |
Algorithm |
Min |
Mean |
Max |
SD |
Mean rank |
Sum rank |
Sign. |
| 40 |
ICO |
2.4250748680950E-03 |
2.4250748680950E-03 |
2.4250748680950E-03 |
4.998E-17 |
1.917 |
57.5 |
|
| CO |
2.4250748680950E-03 |
2.4250748680950E-03 |
2.4250748680950E-03 |
1.105E-16 |
1.983 |
59.5 |
|
| DE |
5.2666503052410E-03 |
7.2566226992670E-03 |
9.6379708296680E-03 |
8.375E-04 |
8.433 |
253 |
|
| PSO |
2.8643916678590E-03 |
5.0462723254080E-03 |
6.5034717549490E-03 |
1.123E-03 |
6.800 |
204 |
|
| GA |
6.0992404558810E-03 |
1.7462237365350E-01 |
2.9547389242870E-01 |
1.059E-01 |
11.000 |
330 |
|
| TLBO |
2.7004036401520E-03 |
3.8363781147850E-03 |
9.0053151975850E-03 |
1.277E-03 |
5.933 |
178 |
|
| SEDE |
2.4250748680950E-03 |
2.4250748680950E-03 |
2.4250748680950E-03 |
2.319E-17 |
2.833 |
85 |
|
| JAYA |
3.6976569502340E-03 |
1.6079498126920E-02 |
3.2966678818700E-01 |
5.923E-02 |
7.333 |
220 |
|
| PGJAYA |
2.4250773050060E-03 |
2.4419751596470E-03 |
2.4895343685670E-03 |
1.780E-05 |
4.467 |
134 |
|
| WSO |
2.4250748680950E-03 |
7.5247794485460E-02 |
4.4356045864950E-01 |
1.357E-01 |
6.100 |
183 |
|
| GWO |
5.3834664165670E-02 |
9.3745614784530E-02 |
2.7590077173170E-01 |
6.334E-02 |
10.633 |
319 |
|
| SSA |
5.1301743190820E-02 |
1.1525567589300E-01 |
2.7696629442010E-01 |
8.570E-02 |
10.567 |
317 |
|
| 80 |
ICO |
2.4250748680950E-03 |
2.4250748680951E-03 |
2.4250748680952E-03 |
3.193E-17 |
2.083 |
62.5 |
|
| CO |
2.4250748680950E-03 |
2.4250748680950E-03 |
2.4250748680952E-03 |
4.371E-17 |
1.300 |
39 |
|
| DE |
6.9211267396471E-03 |
8.2205499846706E-03 |
9.1644830901135E-03 |
5.053E-04 |
7.733 |
232 |
|
| PSO |
3.0294511355973E-03 |
5.6849600297253E-03 |
7.4169012983030E-03 |
1.083E-03 |
6.267 |
188 |
|
| GA |
7.7129635967374E-03 |
1.8430319719111E-01 |
4.0758844972356E-01 |
1.287E-01 |
10.533 |
316 |
|
| TLBO |
3.2444523024506E-03 |
5.3311216098958E-03 |
9.2734827389708E-03 |
1.343E-03 |
6.033 |
181 |
|
| SEDE |
2.4271642587222E-03 |
2.4987409190963E-03 |
2.6543169613205E-03 |
5.638E-05 |
3.533 |
106 |
|
| JAYA |
5.5903023668077E-03 |
6.1914139863795E-02 |
1.2797477931005E-01 |
3.926E-02 |
9.800 |
294 |
|
| PGJAYA |
2.5180177878440E-03 |
2.8115756633088E-03 |
3.0907794548476E-03 |
1.572E-04 |
4.533 |
136 |
|
| WSO |
2.4250748680951E-03 |
9.1707088610467E-02 |
4.4400407477152E-01 |
1.376E-01 |
5.983 |
179.5 |
|
| GWO |
2.0190645830849E-02 |
8.4207804663943E-02 |
2.7422933458200E-01 |
9.724E-02 |
9.767 |
293 |
|
| SSA |
1.5545325435148E-02 |
1.4408325701658E-01 |
2.7424833297126E-01 |
1.240E-01 |
10.433 |
313 |
|