HyperZ: Hyper Z-Tree Topology

1. Introduction

The next generation of supercomputers will face more challenges to tackle far more complex and larger programming problems and open new horizons in the scientific, engineering and business disciplines [1–3]. However, an increase in the computational speed of processors can lead to extreme power constrains [4].  Interconnecting a larger number of chips, while keeping the overall cost under budget and delivering the required performance, is a trade-off.  A need to interconnect those high-speed processing elements in the best manner possible is a challenging task [5].  While the technology for higher speed processors keeps advancing, the search for resilient interconnection networks of high performance computing lags behind and shows trifling contributions [6].

Fat tree topologies [7], with their simplistic properties and ability to scale, are deemed to be the most popular solution for computing clusters, data centers and HPC [8–10]. They can be seen as universal networks that emulate any other topology deploying the same amount of resources with slight reduction in the power consumption.  The high path diversity in fat trees, with its fault tolerant property, plays a critical role in the overall performance of the communication networks.  One interesting approach is hybrid networks which involve the incorporation of fat tree design as building blocks within large scale parallel systems. This is the inspiration of the research presented in this paper.  There are several hybrid interconnections that use different topologies at each level as in BlueGene IBM [11–13], Dragonfly [14,15], X-Mesh [16] and Torus [17].  Furthermore, newer technologies on optical networks and photonic switches are emerging.  These technologies have shown potential to attain higher bandwidth and effective power consumption.  The papers [18,19] show the possibility to interconnect fat tree topologies by photonic routers. Although issues such as crosstalk that limit the scalability of these systems can be an obstacle. Current research is advancing in this direction to provide effective solutions. Our proposed architecture takes advantage of photonic switches of any radix. Fat trees can also be considered a candidate for wireless networks in HPC environments.  Initial work has been done in this direction [20] to execute parallel tasks on wireless nodes with up to 8 transceivers acting as nodes’ degree.  The major constraints of on-chip radio devices are the limitation of the transmission rate and high-power consumption which make them less favorable for modern parallel platforms. However, with the new 802.11ac and beyond, the speed of the WiFi is reaching the 7Gbps and over.

  This paper considers hosting the Z-tree [21] as nodes for a generalized hypercube network (GHC) [22].  The choice of a GHC is procured based on the scalability of the architecture and its small radius. Its high degree per node is compensated for by the provision of the side links (global links) offered by the switch of the Z-Tree. This approach has already been adopted by HyperX topology [23,24].  However, HyperX offers a single switch of high radix per node.  This makes, as this paper proves later on, HyperZ a generalized version of HyperX. The proposed approach outperforms the HyperX and allows a larger design space to select optimal topologies that answer the demands of parallel applications.

This paper contributes by developing a new multi-level direct network based on a Z-tree as a computational node for a GHC interconnect.  The topology is viewed as an extension to HyperX. It accommodates far more processors with smaller switch radix compared to the HyperX of the same size.  This design relying on the number of levels of the Z-Tree offers high bisection bandwidth, lower latency, and multiple concurrent communications between nodes of the GHC. To take advantage of this structure, two adaptive routing algorithms which are more efficient and fault tolerant than HyperX are suggested.  The algorithm exploits the path diversities constructed from the Hyper Z-Tree.

2. Related Work

Symmetric Tori connected Torus Network (STTN) [26] is a hierarchical interconnection network of 2D Torus hosting iterative nodes formed from other tori.  STTN architecture is a good solution for moderate and small high performance systems due to its scalable nature as the node degree is always fixed.  However, for large scale networks, the diameter is inevitably large which leads to higher latencies, with large bisection bandwidth. Torus embedded hypercube interconnect proposed by Kini [27] is a network architecture that can offer scalability in parallel computation. However, for this solution to work, the size of hypercube is required to stay constant at all times to avoid node degree changes. But for large scale systems this will not be the case, and the diameter has to increase to fit the size of the network. The hierarchical network (HTN) consists of 3D-tori modules connected together by a 2D torus network. The Pruned HTN version [28] removes links along the dimensions to reduce complexity, and it achieves better results than the original HTN in terms of power consumption, latency and bandwidth. The dimension order routing is adopted to route messages.  However, the dimension routing algorithm is not adaptive and it does not exploit all the paths within the network, hence putting a limit on the performance for large-scale parallel systems.  Hyper nodes torus is an architecture that extends torus interconnection by replacing each node in the torus with a ring [29].  A distributed environment is laid down as each node can be either a memory or a processor. An optimal version of the XY-routing was proposed to take into consideration the routing within the ring. The results presented show the hyper node torus achieves lower latency than the hypercube and torus for 16, and 64 nodes.  There is no evidence that the proposed system will work for large-scale networks, as the size of the ring has to be kept to a minimum, which is not always the case with higher number of processors.

Recently, a lot of interest has been devoted to multi-level direct networks as promising scalable topology for high performance computing such as PETCS [30], Dragonfly [14,15] and Cray [30]. These networks built from high-radix switches give the impression of an all-to-all interconnection. PERCS high performance interconnect aims to improve the bisection bandwidth for high performance supercomputers challenge.  The hub chip comes with a large number of local and remote links fully equipped with routing components, so it requires no external switches or routers.  Similarly, to Dragonfly and Cray, PERCS implements 2-level direct-connect.  Unlike PERCS, Cray and the Dragonfly networks offers the possibility to emulate  any topologies within the groups.  The full connectivity at level 1 and 2 of the supernodes in PERCS brands it as non-scalable for large size networks. PERCS also uses 3 hopes routing for inter and intra supernodes communications for normal traffic conditions.  For hot-spot traffic, the routing algorithm deviates the path to a random supernode and then routes to the destination making a path of 5 hopes.  The dragonfly is a hierarchical topology that reduces the network diameter and the number of long cables. It includes multiple groups that are connected by all-to-all links.  Each groups can have different internal topology, and connects fully to other groups via global long optical channels, when it is possible.  

HyperZ, presented in this paper, and HyperX belong to these classes of networks but using hypercube (GHC) rather than all-to-all interconnections to maximise the bisection bandwidth, and minimise the diameter and the latency, at the expense of more cables.  The cost of the external cabling can be justified by the usage of optical connections.  HyperZ, like others, is driven by the technology evolution in active optical cables and the increase in pin-bandwidth that is high radix switches with large number of narrow ports.  HyperZ uses Z-tree as a computing node. The levels or height of the Z-tree add extra global cables but create parallel layers that segregate traffic and achieve higher bandwidth and lower latencies.  The HyperX has only 1 level, and therefore a single layer.

3. Hyper Z Construction

The HyperZ is a generalized hypercube interconnection whose processing nodes are fat trees. The fat trees have the specifications of the Z-tree [21].  A regular Z-node has equal number of routing nodes (switches) of equal radix at all levels of the tree.   Unlike HyperX which can be viewed as flattened butterfly or hypercube with nodes containing single switches with several processing elements, our proposed architecture is more general and includes also HyperX configuration in its space when the height of the Z-node is 1.  A group of Z-nodes in the k^th-dimension is refere to as a super node, S-node, where k is 1≤k≤d with d representing the number of dimensions in the GHC topology.

The definition of the HyperZ of dimension d and height h can be written as  

H_d,h (s₁, …,s_d ; Q₁, …,Q_d) (Z_h)

(1)

The specification of (Z_h) is defined in [21], as Z_h (z₁, …,z_h ; r₁, …,r_h;  g₁, …g_h),  where h is the number of levels (height), z_i of zones, r_i switches, and g_i of internal links in the Z-tree at level i.  The vector Q_k = (q_1k, … q_ik, …, q_hk) is the set of external or side connections in the k^th-dimension of GHC, 1≤k≤d, where q_ikis the number of links between two z-nodes along the dimension k, at level i of the Z-Tree,  1≤i≤h.  The vector (s₁, …, s_d) symbolizes the number of S-Nodes in each dimension, 1 to d. For convenience, when all the links at each level of the Z-nodes are equal, the parameter, Q_{k, is}replaced byq_k.  The HyperX topology has only one level, a height of h=1, and a single switch per Z-node.  As shown in Figure 1, at level 2, the HyperZ can be seen as 2-parallel layers of HyperX. This configuration will increase the bandwidth and accommodate far more processing nodes while reducing the connectivity – ports numbers - per routing nodes.

In general, the total number of nodes (processing, i=0 or routing, i≥1, nodes) in the Z-node, R_i, and HyperZ, N_i, can be expressed as

$$\begin{gathered} R_i=r_i{\prod }_{j=i+1}^{h+1}{z}_j \\ {N}_i=R_i{\prod }_{k=1}^d{s}_k \end{gathered}$$

(2)

Figure 1. HyperZ of dimension, d=1, and height, h=3, H_1,3(2;2)(Z₂) with Z₂ (4,2;1,2;1,2). There are (q₁=2) external links per level per switch.

Figure 1. HyperZ of dimension, d=1, and height, h=3, H_1,3(2;2)(Z₂) with Z₂ (4,2;1,2;1,2). There are (q₁=2) external links per level per switch.

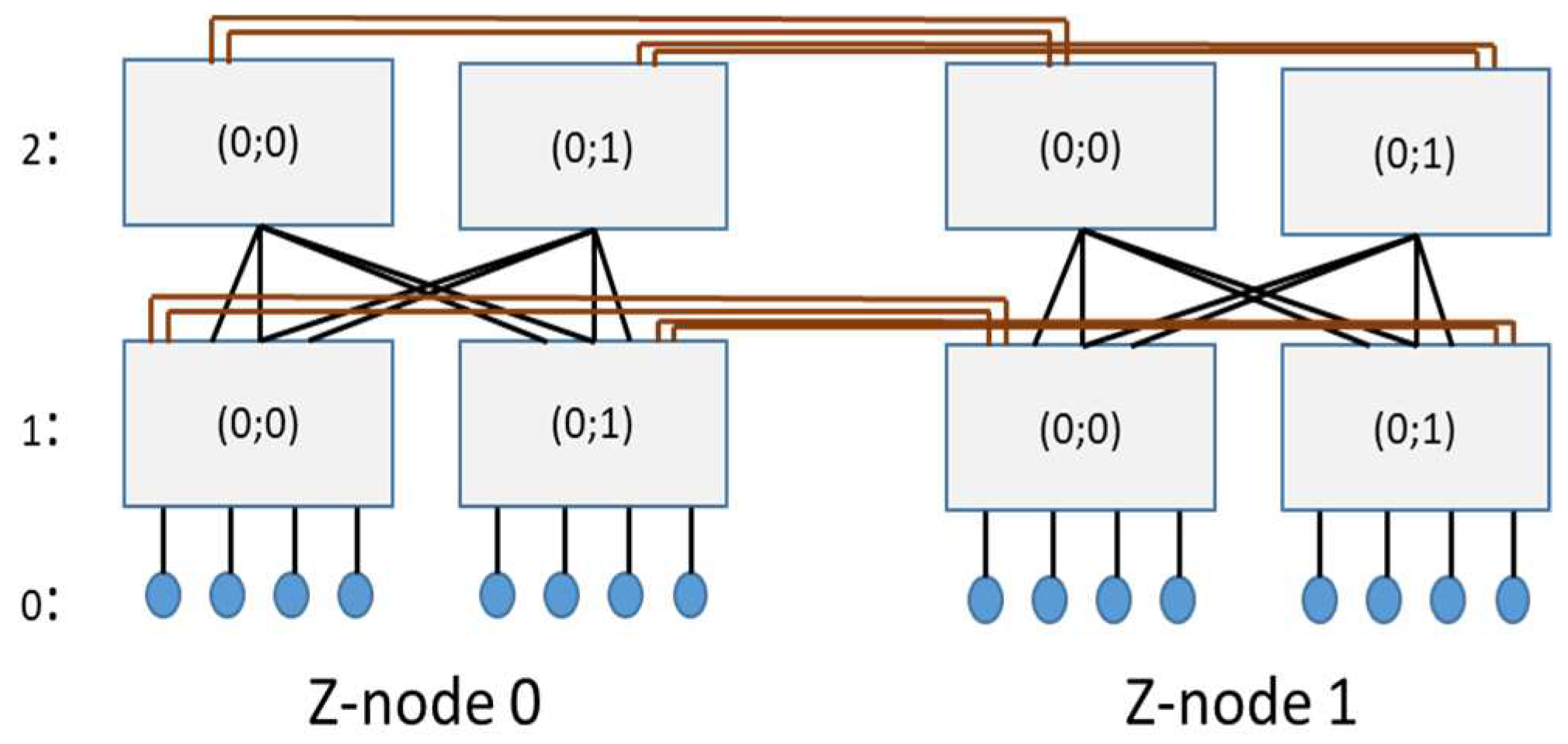
3.1.Hyper Z-Fat Tree Connectivity Rules

Each node at level i, 0 ≤i ≤ h, within the Z-node, can be represented by a flat address, X_i, where X_i ϵ {0, 1, …, $R_i$-1}. On the other hand, each node in the HyperZ can be extended by the tuple (a_d, a_d-1, …, a₁; X_i) where a_k ϵ {0, 1, …, s_k -1} for 1≤k≤d. The hierarchical address (a_d, a_d-1, …, a₁) is also an abstract address of a Z-node in the HyperZ. For instance, in Figure 1, at level 2 there are 2 routing nodes, R₂=2, in the Z-node 0 and Z-node 1. Thus, the tuple (a₁, X₂) has the flat address X₂ ϵ {0, 1}, and the hierarchical address a₁ ϵ {0, 1} since s₁ = 2, giving the tuples (0; 0), (0; 1) for the Z-node 0 and the tuples (1; 0), (0; 1) for the Z-node 1 at level 2.

The levels offer the traffic several paths from each Z-node to the others across the network.  Thus, the communications take place concurrently though the layers. In Figure 2, there are 2 layers corresponding to 2 levels of the Z-node. Each layer has several paths emerging from the links of each routing node, switch.

The Z-tree bidirectional connectivity can be established by first instantiating all the nodes (processing node i=0 and routing nodes i>0), assigning them unique flat address X_i and then linking them internally according to the rule of the Z-tree connections [21].  The inter-connections of the Z-nodes in the GHC network along each dimension can be established as stated below.

A node A of tuple (a_d, a_d-1, …, a₁; X_i) connects by bidirectional links to a node B of tuple (b_d, b_d-1, …, b₁; Y_i), if and only if:

• They have the same flat address within their Z-nodes X_i =Y_i ,
• The vector connectivity degree Q_k = (q_1k, q_2k,…, q_ik …,q_hk) in the k^th-dimension has at least one element q_ik≠0,
• They differ in exactly one value in the k^th dimension, a_k ≠ b_kfor all 1≤k≤d.

In Figure 2 illustrates an example on how Z-nodes are connected in a HyperZ topology define as H_3,h(4,3,4;1,1,1)(Z_h).  In this example, a Z-node is an abstract computational node, (Z_h), of any height and internal structure.  In the dimension 1, 2 and 3, there are 4, 3 and 4 S-nodes, s₁ =4, s₂=3 and s₃=4, respectively.  All the connections between the Z-nodes in all the dimensions at all levels are equal to 1, q_k= 1. Dimension 0 is the Z-node itself, shown as a filled triangle.  In dimension 1, there are four S-nodes, labeled 0, 1, 2, and 3, each containing 1 single Z-node.  In dimension 2, there are three S-nodes, labelled 0, 1, and 2, each containing four Z-nodes making a total of twelve Z-nodes.  Finally, in dimension 3, there are four S-nodes, labelled 0, 1, 2, and 3, each accommodating twelve Z-nodes.  The Z-node (0, 0, 0) connects to Z-nodes (0, 0, 1), (0, 0, 2) and (0, 0, 3) for all levels i as they differ in dimension 1.  It also connects to Z-nodes (0, 1, 0) and (0, 2, 0), which differs in dimension 2, and finally connects to Z-nodes (1, 0, 0), (2, 0, 0) and (3, 0, 0) by differing in dimension 3. 

Figure 2. Hyper Z-Tree, H_3,h (3, 4;1, 1_, 1) (Z_h) , the degree of connectivity vector is 1 in all levels of Z-tree. Only the connections from Znode (0, 0, 0) to all others are shown.

Figure 2. Hyper Z-Tree, H_3,h (3, 4;1, 1_, 1) (Z_h) , the degree of connectivity vector is 1 in all levels of Z-tree. Only the connections from Znode (0, 0, 0) to all others are shown.

3.2. Topology Features

This section describes the extent of the topology and its design space to accommodate large number of processors.

Definition 3.1

A regular HyperZ is a topology with z_i = z for all 1 ≤ i ≤ h and s_k = s and q_k=q for all 1 ≤ k ≤ d.

This means that the regular HyperZ is constituted from Regular Z-nodes. Furthermore, if the number of zones in the Z-nodes is equal to the number of S-nodes at any levels and dimensions, a fully regular HyperZ is constructed.

Definition 3.2

A fully regular HyperZ is a topology with z_i = s_k = s and q_k=q for all 1 ≤ i ≤ h and 1 ≤ k ≤ d.

For a fully regular HyperZ to accommodate$N_0$ processors, there should be at least R₀ processors per regular Z-node, with each switch radix limited to,  $2z+dq\left(z-1\right)\le L_{max}$, where L_max is a given technology dependent switch radix, q the number of side links between Z-nodes and z is the number of zones within the Z-node, yielding 2z ports per switch. Thus, the number of S-nodes (s=z) required in all dimensions is bounded by the radix available

$$z\le \frac{dk+L_{min}}{dk+2}$$

(3)

A lower bound to the minimum number of processors accommodated by the HyperZ can therefore be expressed as  $z^h{s}^d\ge R_{0min}$ , refer to Eq. 2, since z=s for a fully regular hyperZ, one can write

$$z\ge {\left(R_{0min}\right)}^{1/(h+d)}$$

(4)

The equations (3) and (4) establish both an upper and lower bound for each possible network configuration.  It is apparent from Figure 3 that topologies with lower height such as HyperX, to maintain fixed number of ports per routing node, they required higher dimensions, and therefore higher diameter leading to higher latencies. HyperZ with higher height comparable to h=3 and 8 S-nodes would interconnect a minimum number of processors ranging from 131072, with yet smaller number of ports per routing node in the order of 32, with GHC of 3 dimensions, see Figure 3.  This is an important result to minimise complexities of switches and thus reduce power consumption.

Figure 3. HyperZ design space for $R_{0min}=$131072 processors.

Figure 3. HyperZ design space for $R_{0min}=$131072 processors.

4. Adaptive Routing in HyperZ

The routing in the HyperZ is considered within the Z-node travelling through the levels and outside the Z-node travelling through the dimensions. In the up direction, the messages travel to one of the common levels before making their way down to the destination processor if it destination is within the same Z-node.  If the destination of the message is another Z-node, the message crosses the dimensions of the GHC connections, by following the offset dimensions though the aligned routing nodes belonging to the shortest path, until the destination, Z-node, is reached. Finally, the message will make it way down the tree to the destination processor.

Definition 4.1

Given two Z-nodes (a_d, …, a₂, a₁; q)(Z_h)and (b_d, …, b_2,; q)(Z_h)where a_k, b_k ϵ {0, 1, …, s_k-1} for all 1≤k≤d, the ordered set of shortest paths for a dimension d between the two nodes can be writte as ^(d)= {x_k | x_k = 1 if a_k=b_k ∨ x_k = 0 if a_k≠b_k, ∀ 1≤k≤d}.

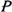For instance, refer to Figure 2, the set of short paths between the Z-nodes (0, 0, 0) and (3, 0, 1) is ⁽³⁾ = {1, 0, 1} meaning the routes have to go through dimension 3 and then dimension 1, or dimension 1 followed by dimension 3.  There is no route through dimension 2.  This is a well-known concept of GHC topology.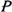

Definition 4.2

A set of offset dimensions is a subset of ^(d) where all the elements are equal to 1 referring to routable or offset dimensions, 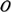⊆ 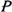^(d)= {x_k≠0, ∀ 1≤k≤d}.

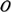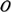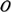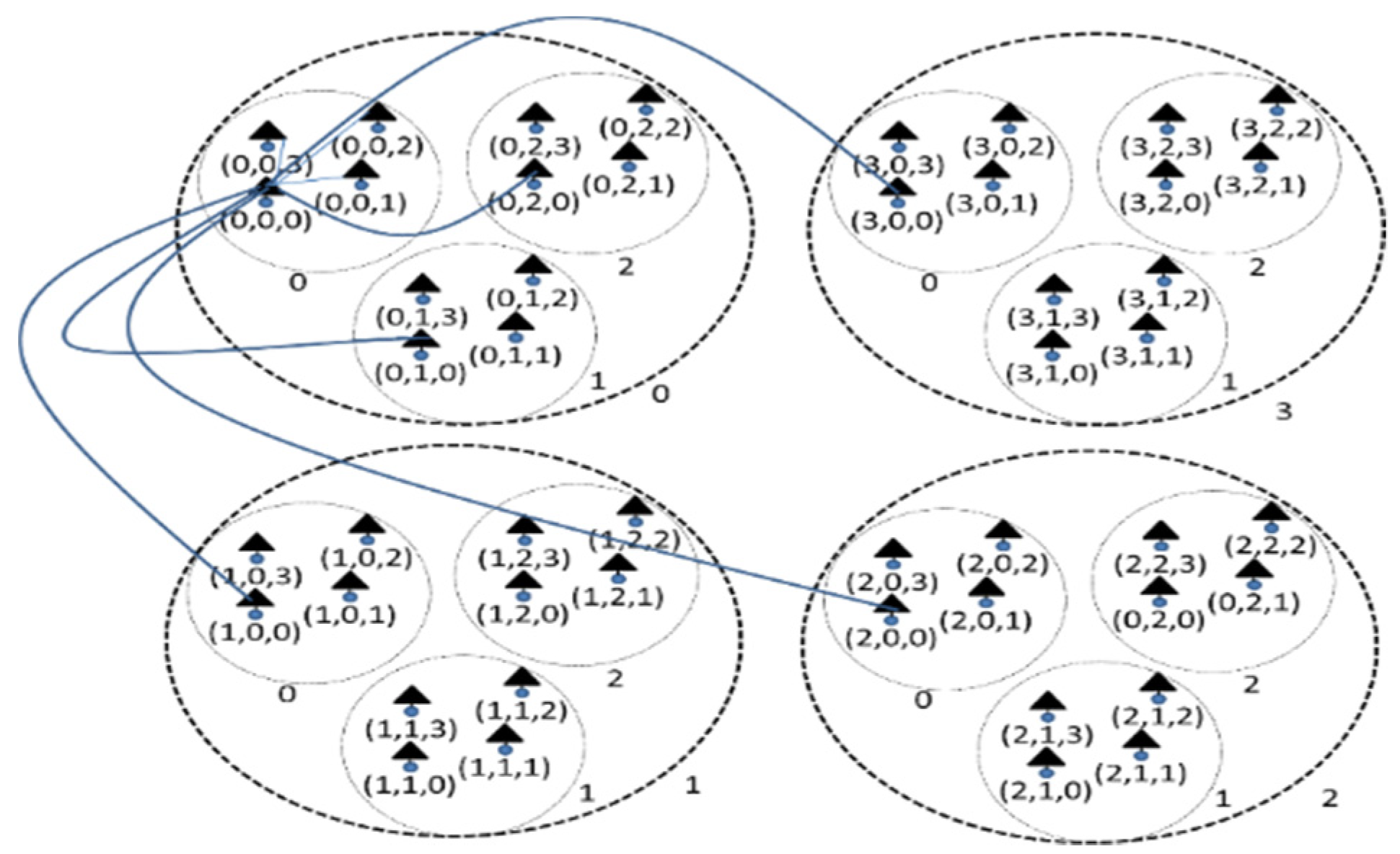
The cardinality, ||, of the set, , determines the number of hops to reach the destination and the factorial of the cardinality, ||! defines the number of possible shortest paths between two Z-nodes.  Again in Figure 3, the ordered set of short paths between the Z-nodes (0, 0, 0) and (3, 0, 1) is 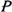⁽³⁾= {1, 0, 1}, and the set, 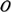{1, 1}, ||! = 2! = 2, indicates that there are 2 shortest paths of 2 hops each.

4.1 CLIOD and ALIOD Algorithms

In general, adaptive routing performs better than deterministic and oblivious routing both for benign and adversary traffics.  Several adaptive routings have been proposed for Generalized Hyper Cube networks [22].

These routing algorithms can be classified as minimal and non-minimal routing.  The minimal routing uses adaptively the shortest path between any source and destination pairs.  Non-minimal avoids the traffic by taken longer routes.  Valiant routing [32] initially routes to a randomly chosen destination and then performs minimal routing to the destination.  Other non-minimal routing use information about the network at the source to decide if it is wise to route minimally or no minimally to adapt to the benign and adversary traffics. Universal Globally-Adaptive Load-Balanced algorithm [33] choses between minimal and Valiant routing on a packet-by-packet basis based on the queue lengths.  One can argue the decision to route minimally or not at the source loses the ability to adapt to the traffic ahead that is dynamically changing, and in some other instance, it introduces dimensional asymmetry. This section proposes two minimal routing algorithms that use local information of the queues to randomly adapt to the traffic.  Virtual channels are also deployed to prevent deadlock.

Any Level Idle Offset Dimension (ALIOD) routing algorithm, as shown in Figure 4, alternates between up and side directions until the least common level in the Z-node is reached, then alternate between down and side directions until the destination is reached while changing layers to adapt to the traffic.  When no idle offset dimensions are found, the ordered dimension routing is chosen in the side directions.  The alternation is adopted to avoid heavily loaded links (large queues).  On the other hand, the Common Level Idle offset dimensions (CLIOD) reaches the least common level (LCL) first in the source Z-node adaptively, and then searches for idle offset dimensions or use ordered dimension routing and then routes down within the destination Z-node.  This paper shows that ALIOD performs better than CLIOD in all traffic patterns. CLIOD is an extension to the routing algorithm described for HyperX.  ALIOD is described below.

Figure 4. ALIOD and CLIOD routing paths in the Hyper Z, with the LCL least common level.

Figure 4. ALIOD and CLIOD routing paths in the Hyper Z, with the LCL least common level.

Table 1. ALIOD Algorithm.

Table 1. ALIOD Algorithm.

The algorithm is deadlock free. When an idle offset dimension is found, the messages cross it and move one hop closer to the destination, without queuing delay.  When no idle dimension is found, the message will use dimension-order routing, ODim, which is known to be deadlock free. It dynamically exploits a higher path diversity to avoid saturated links. 

5. Performance Evaluation

This section describes the simulation models and parameters used to evaluate our proposed Z-Fat tree with the routing suggested in this paper, and provides the explanation of the obtained results.

5.1. Simulation Model

The simulation environment is based on a tool developed in C++ at the University of Portsmouth in the School of Computing.

The topology consists 1024 processors transmitting at an effective link rate of 10Gbits/s.  All the links in the network have 1-bit propagation delay (.1ηsec).  The simulator generates 100000 messages with an average processing time derived from an exponential distribution. The processing time, uniformly distributed between 640-3200 ηsec, is the time taken by the processor to perform some computations before a communication takes place.  The communication used a single Virtual Cut Through (VCT) buffer with virtual channels to avoid deadlock in each routing node.  The average processing time normalizes the message transmission time to produce different offered loads per processing node.  The payload of the messages is chosen to be 3200bits on average. The normalized delay (average delay/transmission time of a complete message) is recorded against the offered load, that is a fraction of the total capacity of the system. The adaptive routing dimension order (ODim), common level idle offset dimension (CLIOD), any level idle offset dimension (ALIOD) and the deterministic routing based on DRR are compared in this simulation.

Standard traffic patterns were used.  They are commonly found in computational intensive scientific applications, namely the transpose, the bit-reversal and the complement patterns.

5.2 Results of the simulation

Figure 5 (a)(b) and (c) illustrate comparisons of normalized delays for a 2-dimensional HyperZ with levels 1, 2 and 3 respectively.  Notice that level, h=1, represents the HyperX topology.  The ALIOD routing performs better that all the others and manage to use the levels of the Z-node to avoid traffic built in the queues of the routing nodes. It outperforms HyperX based on the CLIOD.  For higher load, with higher level, ALIOD achieves a delay of less than 3 times the packet length. For h=1, the deterministic (Deter) dimension-order routing and (ODim) are identical.  For level h>1, ODim improves slightly by using the adaptive up direction of the Z-node, based on the tree routing.

Similar patterns can be observed for transport traffic in Figure 6 (a)(b)(c).  However, CLIOD and ODim saturate at 40% of offered load.  Level 2 shows better performance. The deterministic is less tolerant to transport traffics and saturates at an offered load less than 10%, for higher levels.

Figure 5. Normalized delay for 1024 processors with random pattern.

Figure 5. Normalized delay for 1024 processors with random pattern.

Figure 6. Normalized delay for 1024 processors with Transpose Traffic.

Figure 6. Normalized delay for 1024 processors with Transpose Traffic.

For bit Reverse traffic shown on Figure 7. (a)(b) at level 2 and 3 respectively for 2-dimensional (OHG), ALIOD achieves a normalized delay between 2.5 to 3 times the packet length at an offered load of 60%.

As illustrated in Figure 8, with complement traffic, both CLIOD and ODim saturate at an offered load of 30%.  ALIOD makes use of the up, and side links to divert the traffic. The deterministic is less tolerant to complement traffics and saturates at an offered load less than 10%, which is not shown in the graph.  Results obtained in [23] have shown that the HyperX with the DAL which is similar to CLIOD and ALIOD, when the level of the computational node, Z-node, is 1, performs well compare to Valiant [32], ordered dimension, referred to in this paper by ODim, and the fat tree based on folded Closed–fat tree.

Figure 7. Normalized delay for 1024 processors with bit-reverse Traffic.

Figure 7. Normalized delay for 1024 processors with bit-reverse Traffic.

Figure 8. Normalized delay for 1024 processors with Complement Traffic.

Figure 8. Normalized delay for 1024 processors with Complement Traffic.

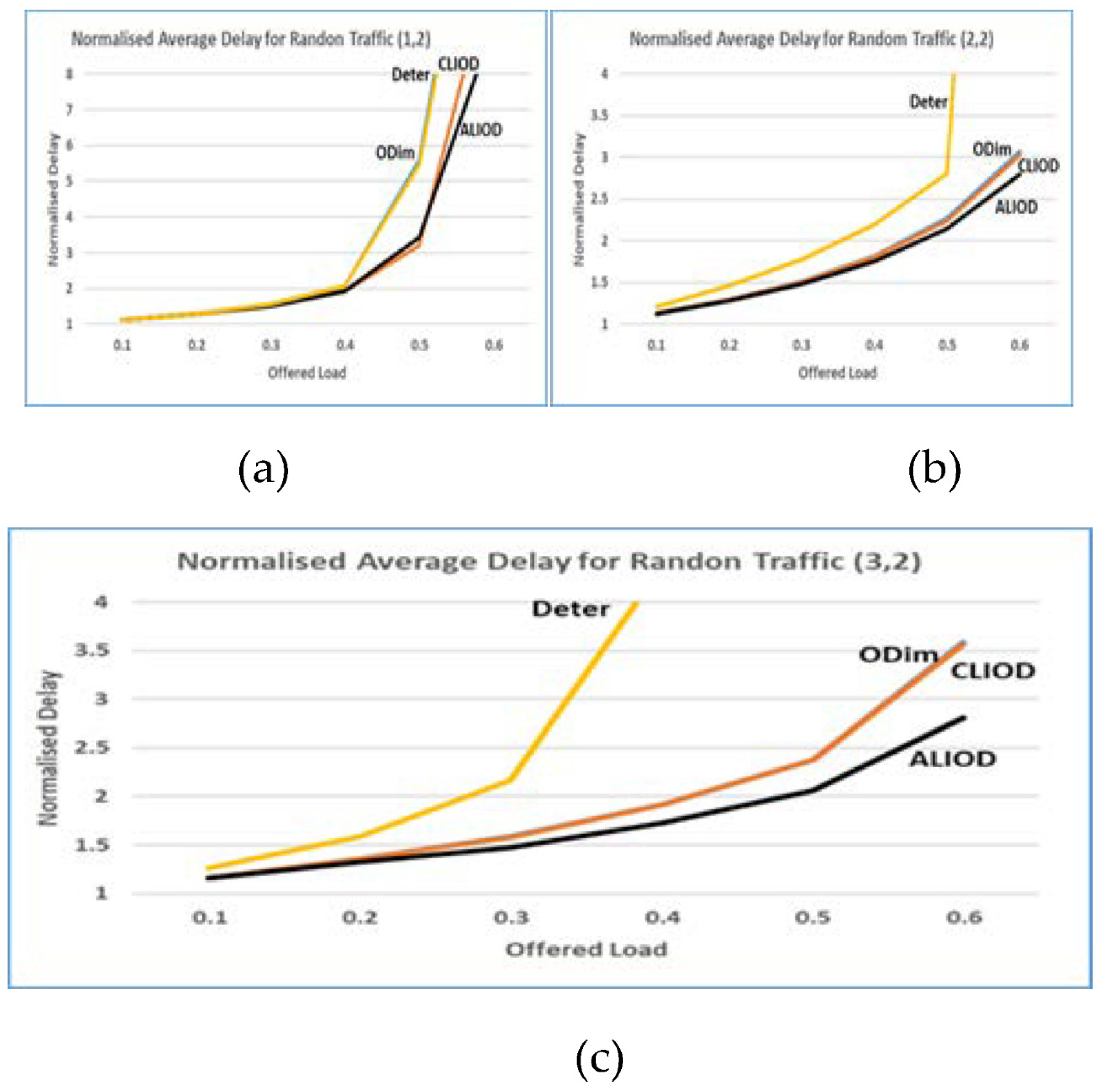
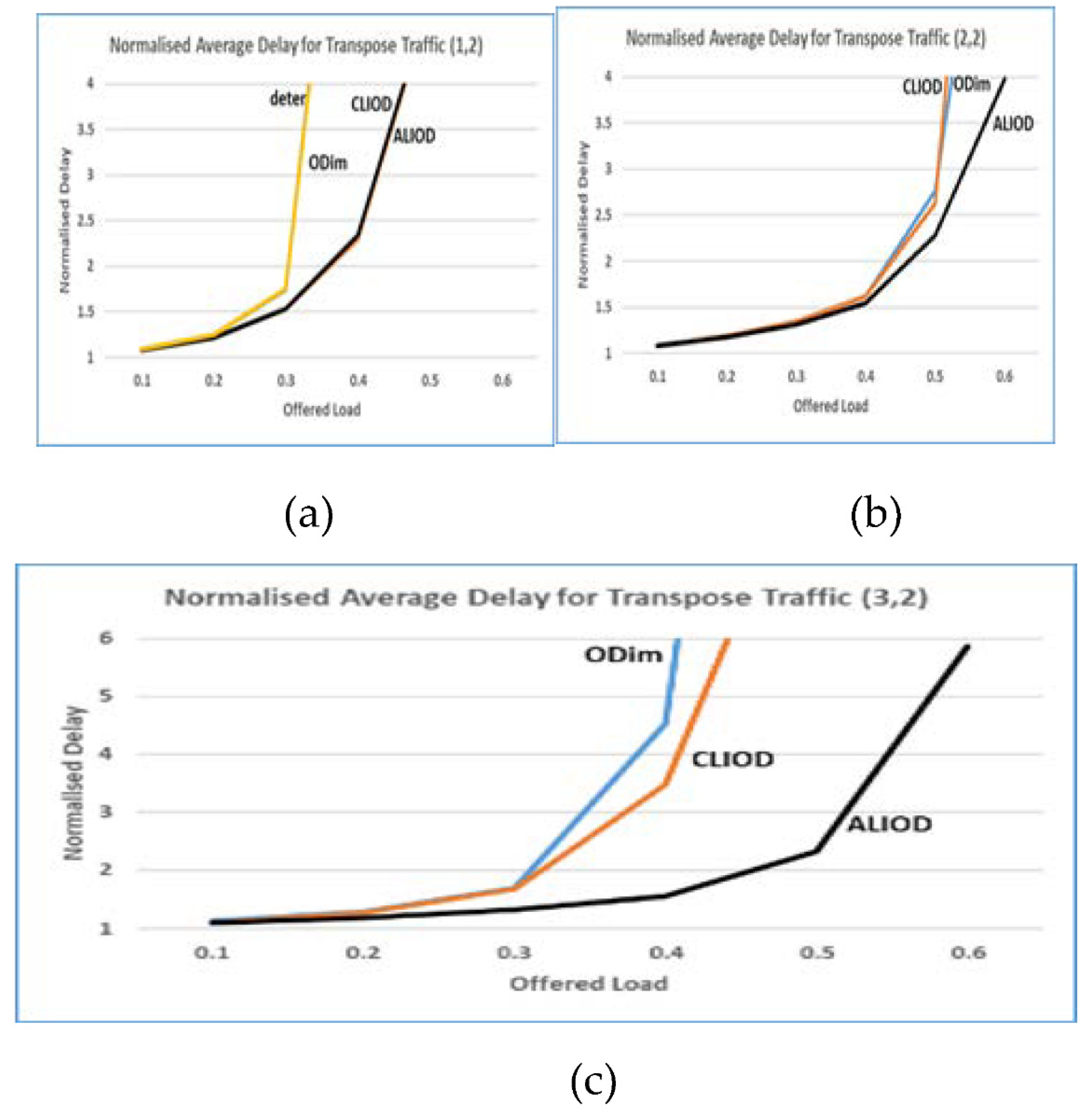
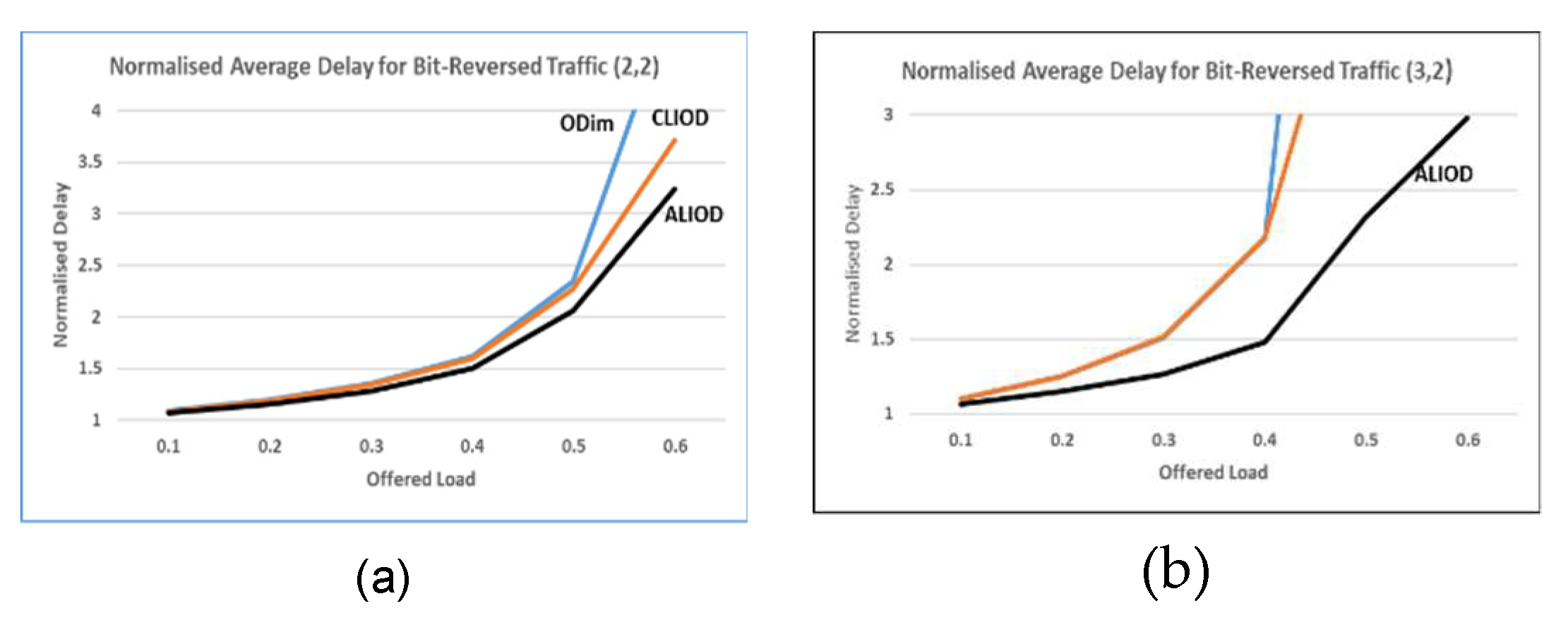
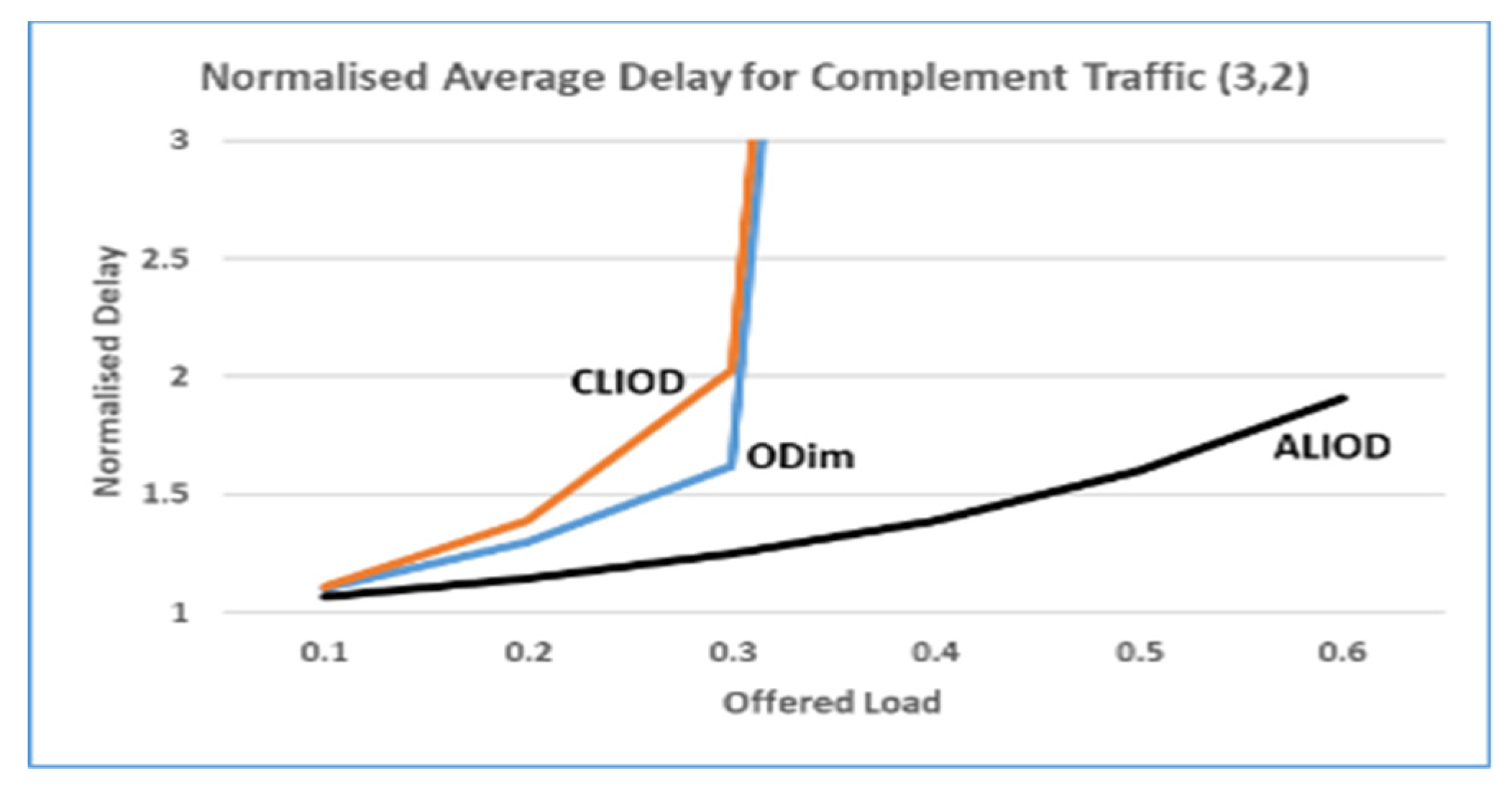
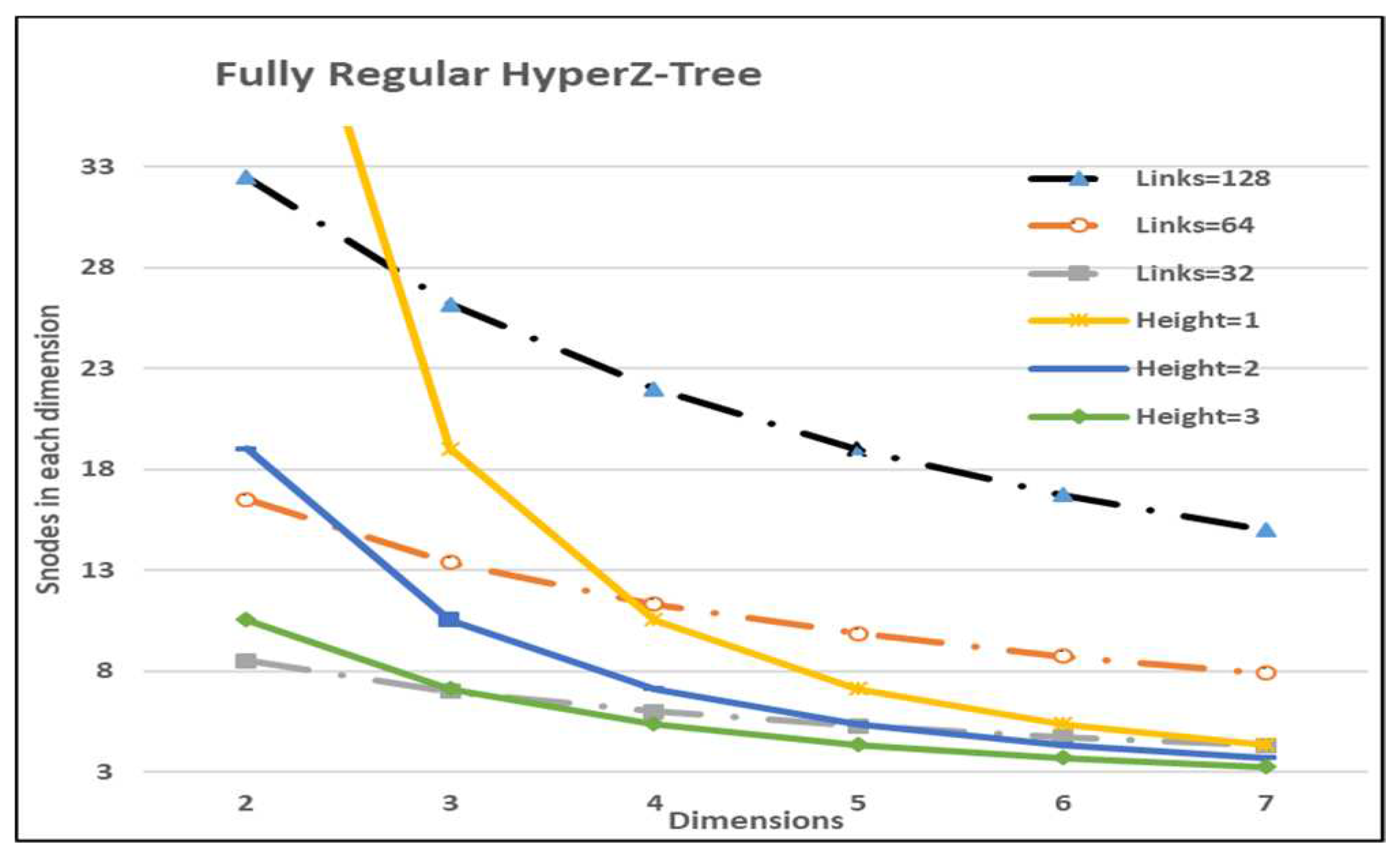
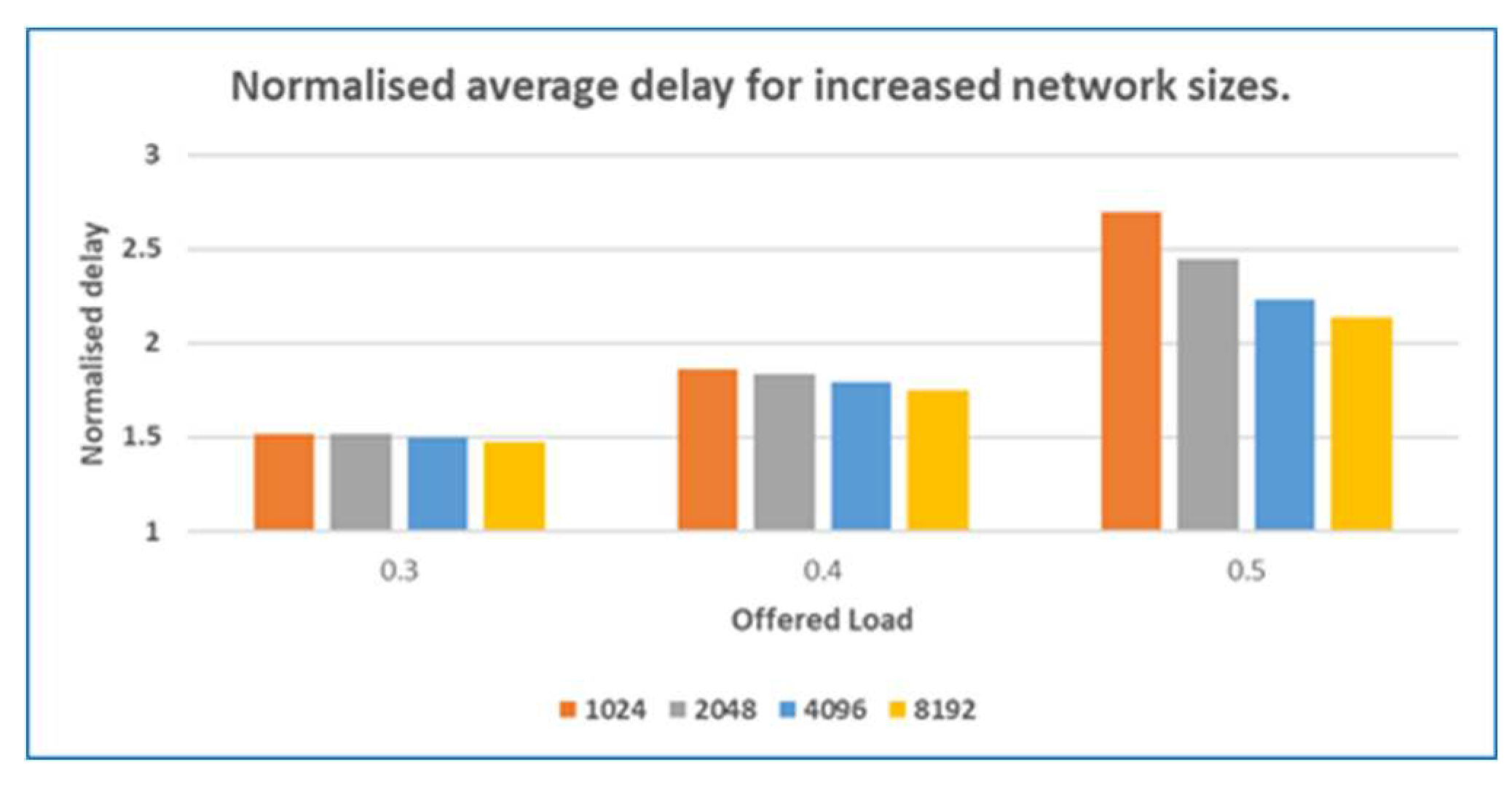
5.3. Scalability

It is possible to build a network with any size, while maintaining the regularity and the symmetry of hyper Z-Tree. One way to do it is to create an optimal Z-node with its components - links and switches - set to some maximum radix that is available in the market.  The Z-node can then be replicated across the dimensions to meet the extended network requirements.

An optimal Z-node, Z₂(8,4,8; 1,4,8; 1,2,2), connecting 256 processors is replicated into several H_2,2(s₁, s₂)(Z₂) through the dimensions 1 and 2 giving 1024, 2048, 4096 and 8192 processors with (s₁, s₂) = (2, 2), (4, 2), (4, 4) and (8, 4) respectively. For instance, 1024 = s₁*s₂*256 = 2*2*256.  Each network requires switches of equal radix 18, 20, 22, and 26 ports. The radix of the switch is chosen as 32, which is the maximum value, and unused ports are switched off. Larger size networks can be obtained with higher radix switch, or with higher dimensions. The graph in Figure 9 shows clearly that as the network size increases by replicating the Z₂ node across the first and second dimensions, the normalized average delay is bounded between 1.5 and 3 times the message size.

Figure 9. Normalized delay for different network sizes with 1024, 2048, 4096 and 8192 processors, level h =2 and dimension d=2, with random pattern, at offered loads 30%, 40% and 50%.

Figure 9. Normalized delay for different network sizes with 1024, 2048, 4096 and 8192 processors, level h =2 and dimension d=2, with random pattern, at offered loads 30%, 40% and 50%.

5.4. Fault Tolerance

In larger scale networks of millions of connections, the dominant failures come from the links’ failures. The massive path diversity of the HyperZ defined by equation (4) creates many opportunities for fault tolerance. In [22] we have addressed fault tolerance within the Z-node. We proposed a recoiling algorithm to determine the paths of unfaulty links, and hence selected the uplinks that will avoid meeting faulty downlinks. ALIOD is more tolerant to faults than DAL routing. For ALIOD routing, there are h parallel links from one dimension to another, defined by the vector Q_k = (q_1k, q_2k, …, q_hk) giving a maximum of $l_{max}=\sum _{i=1}^h{q}_{ik}$ links in an offset dimension k. For a message to be blocked due to a link failure, there should be only one remaining offset dimension with all the parallel links, $l_{max}$, failing. If the number of failed links is less than $l_{max}$, additional rerouting in the up and then down directions within the Z-node is required to locate the level of non-faulty links. This approach is already adopted within the Z-node, [22]. If all the $l_{max}$ links fail, one has to reroute through the side links. This scheme is adopted by DAL.

6. Conclusions

This paper introduces a multi-level direct network called HyperZ which is an extension to HyperX. The main feature of this architecture is the inclusion of the Z-Tree as a computing node in a GHC interconnection. This topology is driven by the high-radix switches and low diameter. The organization based on a Z-Tree node offers tree-levels that make parallel layers and hence increases the bisection bandwidth, reduce the latency and provide a resilient fault tolerant network. As shown in the resuts, the computing nodes with multi-levels performs better than a single level. This is achieved by the ALIOD routing algorithm which makes better use of the link diversities and the parallel layers. The topology scales with the size of the network by adding more Z-nodes in the first and second dimension; while maintaining the radius constant and for a low (GHC) dimension, the latency can be kept bounded to less than 3 times the message size.