Minimal Length Deformation of Spacetime Curvature

1. Introduction

Nearly every physical phenomenon in the world can be explained using either general relativity or quantum mechanics, two fundamental theoretical frameworks. These conceptual frameworks contain the ideas and models that describe matter and its fundamental interactions and are capable of predicting a wide range of empirically observed events. Quantum mechanics (QM) and special theory of relativity (SR) describe interactions between atoms, molecules, elementary particles like electrons, muons, photons, and quarks and their anti-particles at very small scales, of the order of ${10}^{-10}$ to ${10}^{-19}$ m, in the physical framework of the standard model of particle physics (SM) and the mathematical disguise of quantum field theory (QFT).

In the context of SM, QM primarily describes interactions involving the electromagnetic, weak nuclear, and strong nuclear forces, three of the four basic forces. The General Relativity (GR) paradigm explains how matter responds to the gravitational force, which is the fourth basic force of nature. When compared to classical physics, including GR and its consequences, QM uses a conceptual framework that is significantly different. The conceptual distinction between classical and quantum physics is largely based on the Heisenberg uncertainty principle (HUP). HUP asserts that, in sharp contrast to classical mechanics, it is impossible to have a particle for which a pair of canonically conjugate quantities, such as position and momentum, are precisely defined to any arbitrary limit even if all other conditions are satisfied.

Despite its many accomplishments, the Standard Model of Particles (SM) and Quantum Field Theory (QM) cannot be viewed as the whole theory of the visible world. This is due to a several weaknesses, especially the inability of these theories to explain how basic particles behave in the presence of gravitational interactions, the last of the four fundamental interactions. This results from interpreting spacetime as an unchanging, flat background, which General Relativity (GR) demonstrates is not the case in the following.

On the other hand, the general theory of relativity (GR), which is the dominant explanation of gravity, postulates that the apparent gravitational force between masses is brought about by the bending of spacetime that these masses have on space. The gravitational field is therefore geometric in character. Flat spacetime appears to be bent by mass and energy into a four-dimensional Riemannian manifold with an affine (linear) link and a symmetric metric tensor. The latter may be calculated in terms of the metric tensor itself since it is torsion-free and metric compatible.

General relativity (GR) has been successfully tested using high-precision astronomical and cosmic data like as the perihelion precession of Mercury’s orbit, gravitational lensing, gravitational red shift of light, the rapid expansion of our universe, and gravitational waves.

In reality, gravitational interactions are the only ones that matter at astronomically large distances and/or matter densities, and when combined with the so-called dark matter and dark energy, they provide an almost complete account of the composition and development of the universe from its inception to its ultimate end.

Even on a curved space-time background, the special theory of relativity appears to be completely consistent with quantum mechanics. However, it appears that there are still lingering discrepancies between QM and classical GR that prevent their reconciliation. Such incompatibilities include, in addition to the well-known renormalizability issue, which may have been resolved in a few Quantum Gravity theories like String Theory and Loop Quantum Gravity. Due to the fuzziness (uncertainty) of position and velocity in quantum mechanics, it is still unknown how to estimate the gravitational field of a quantum particle. Additionally, time has a distinct meaning in quantum mechanics and classical general relativity.

In contrast to QM’s conception of spacetime as a flat, static background, general relativity (GR) sees it as a dynamic object that interacts with matter and energy. On the other hand, GR disregards the probabilityistic nature of the observables described by QM. In order to reproduce QM and GR in their respective disciplines, a new theory must be created. Unfortunately, the simple approach of applying QFT principles to GR doesn’t work as expected based on prior experience. this is due to the fact that no finite measurable result is obtained when perturbatively quantized gravity is subjected to renormalization procedures intended to tame divergences. As a result, it might be assumed that a new approach is essential to tackle QG in a unique way. The phrase "theories of quantum gravity" (QG) designates a range of models and/or theories that have been created to tackle the problem of quantizing gravity. These QG class of theories/models, for instance, include Doubly Special Relativity (DSR), Loop Quantum Gravity (LQG), and String Theory (ST). These are only a handful of the initiatives that have been made to address the problem, all of which have varied degrees of success. There are several long-standing problems with quantum gravity theories and methodologies and a comprehensive overview may be found in Reference [1].

The so-called Generalised Uncertainty Principle (GUP) is one of many approaches to a consistent theory of Quantum Gravity (QG), particularly those class of models attempting to modify the classical GR using quantum arguments [2,3,4,5,6,7,8,9,10,11,12,13,14]. The GUP predicts a deformed canonical commutator as a modified Heisenberg uncertainty relation. Surprisingly, GUP can result in certain phenomenological quantum gravity models that can, a priori, be investigated at low energies [15,16].

A fundamental physical minimum length and/or a generalized uncertainty principle (GUP) near the Planck scale are suggested by string theory, loop quantum gravity, doubly special relativity, and black hole thermodynamics, to name a few. For an extensive account, see for example [17]. Moreover, in [16,18], the three primary techniques for a GUP are motivated. Using arguments from Quantum Gravity and String Theory [8], as well as from other, more specialised quantum mechanical and group theoretical arguments [19], a GUP recipe has been developed that characterises the minimal length as a minimal uncertainty in position measurements. This recipe is the one we’ll use in the current work.

The general relativity (GR) theory is well described by curved spacetime, in which the dynamical variable is the spacetime curvature; the gravity [20]. The general theory of relativity assumes that the gravitational field has a geometrical nature. This is a four–dimensional Riemannian manifold having a symmetric metric tensor and an affine (linear) connection. The latter is torsion–free and metric compatible and thus can be determined in terms of the metric tensor, itself. The deformed affine connection can be defined by the deformed metric tensor [21]. The deformed affine connection ${\tilde{\mathsf{\Gamma }}}_{\beta \mu }^{\gamma }$ is symmetric under interchange of its lower indices like the classical affine connection.

The present script introduces a minimal length approach, in which the inherent uncertainties emerging in detecting a quantum state are constrained in noncommutative operators as governed by Heisenberg uncertainty principle (HUP), which limits these to simultaneous measurements but obviously doesn’t incorporate the impacts of the gravitational fields. The extended version of HUP known as generalized uncertainty principle (GUP) is also predicted in string theory, loop quantum gravity, doubly special relativity, and various gedanken experiments [18,22]. GUP could be seen as an approach emerging from the gravitational impacts on the quantum measurements. The latter are essential components of the underlying quantum theory. In other words, GUP helps explaining the origin of the gravitational field and how a particle behaves in it [23,24].

Riemann curvature tensor, Ricci tensor, Ricci scalar, and Einstein tensor are the geometric entities that describe the curvature of space-time manifold. The Riemann tensor is a (1,3) rank tensor and its components represent the change of a vector after the parallel transport of it around a loop.

The possible contraction of the Riemann tensor gives a second rank tensor called Ricci tensor. The contraction of Ricci tensor gives a zero tank tensor (scalar) called Ricci scalar. Based on a combination of Ricci tensor and Ricci scalar, the Einstein tensor has been constructed.

The present script is organized as follows. A short review of minimal measurable length, Section 2. The deformed line element and deformed affine connection is discussed in Section 3. The deformation of Riemann manifold based on the deformed affine connection Section 4. The minimal length deformation of the Ricci curvature tensor and Ricci scalar are derived in Section 5 and Section 6, respectively. The construction of the deformed Einstein tensor and its covariant derivative are discussed in Section 7. Section 8 is devoted to the summary and conclusion.

2. Minimal measurable length

The loop quantum gravity, doubly–special relativity, and string theory, for instance, predicted an existence of a minimum measurable length. In quantum mechanics, this can be translated to nonvanishing position uncertainty due to the impacts of finite gravitational field on the Heisenberg uncertainty principle, the fundamental theory of quantum mechanics [25],

$$\begin{array}{c}\hfill \Delta x\Delta p\ge \frac{\hslash }{2}\left[1+\beta {\left(\Delta p\right)}^2+\beta {\langle p\rangle }^2\right],\end{array}$$

(1)

where $\langle p\rangle$ is the momentum expectation value and $\Delta x$ and $\Delta p$ represents the length and momentum uncertainties, respectively. The GUP parameter $\beta ={\beta }_{0}G/(c^3\hslash )={\beta }_0{({\ell }_{\mathtt{p}}/\hslash )}^2$ with ${\beta }_0$ a dimensionless numerical coefficient to be determined from table–top laboratory experiments [26] or recent cosmological observations [27,28] introduces the consequences of gravity to the uncertainty principle, where G is the gravitational constant, c is the speed of light, ℏ is the reduced Planck constant, and ${\ell }_{\mathtt{p}}$ is the Planck length. The commutation relation of position and momentum operators can be given as

$$\begin{array}{ccc}\hfill \left[\widehat{x},\widehat{p}\right]& =& i\hslash \left(1+\beta {\widehat{p}}^2\right).\hfill \end{array}$$

(2)

The GUP approach, Eq. (2), has been successfully applied to various physical problems [29,30] and quantum mechanical corrections [31,32,33,34,35].

The minimum uncertainty of position $\Delta x_{min}$ for all values of expectation values of momentum $\langle p\rangle$ will be

$$\begin{array}{c}\hfill \Delta x_{min}\left(\langle p\rangle \right)=\hslash \sqrt{\beta }\sqrt{1+\beta {\langle p\rangle }^2},\end{array}$$

(3)

then the absolute minimum uncertainty of position is at ${\langle p\rangle }^2=0$,

$$\begin{array}{c}\hfill \Delta x_0=\hslash \sqrt{\beta }\end{array}$$

(4)

The value of $\Delta x_0$ can be considered as the possible minimal length according to the GUP, which represents the effect of gravitational field on the QM, then the minimal length is emerging as follows

$$\begin{array}{c}\hfill L=\hslash \sqrt{\beta }.\end{array}$$

(5)

Another approach for the existence of minimal length may be assumed as a fundamental physical quantity obtained from a combination of fundamental physical quantities, gravitational constant (G) from gravity, reduced Planck constant (ℏ) from quantum mechanics, and speed of light (c) from spacial relativity [36]. The minimal length will be

$$\begin{array}{cc}\hfill L& =l_p\hfill \\ & =\sqrt{{\displaystyle \frac{\hslash G}{c^3}}},\hfill \end{array}$$

(6)

where $l_p$ is called Planck length. The minimal length according to that approach is a universal constant like ℏ, G, and c.

The existence of maximal acceleration can be related to the existence of minimal length as a combination of fundamental physical quantities [37],

$$\begin{array}{cc}\hfill A_{max}& ={\displaystyle \frac{c^2}{l_p}}\hfill \\ & =\sqrt{{\displaystyle \frac{c^7}{\hslash G}}}\hfill \end{array}$$

(7)

According to the GUP definition of minimal length stated in Eq. (5), the maximal acceleration can be defined as the following,

$$\begin{array}{cc}\hfill A_{max}& ={\displaystyle \frac{c^2}{L}}\hfill \\ & =\sqrt{{\displaystyle \frac{c^4}{{\hslash }^2\beta }}}\hfill \end{array}$$

(8)

3. The deformed line element and deformed affine connection

Caianiello suggested that curvature in relativistic eight–dimensional manifold $M_8$ is conjectured to mimic deformation of the four–dimensional spacetime manifold $M_4$; Riemannian manifold [38,39,40,41]. The eight dimensions $x^A$ can be expressed as

$$\begin{array}{c}\hfill x^A=(x^{\mu },(L/c){\dot{x}}^{\mu }),\end{array}$$

(9)

where $x^{\mu }$ is the four spacetime dimensions, ${\dot{x}}^{\mu }={\displaystyle \frac{d{x}^{\mu }}{ds}}$ is the four velocity, $ds$ is the classical line element, $A=0,...,7$, $\mu =0,...,3$, L is the minimal length. L may be defined according to GUP as a minimal uncertainty of positions $L=\hslash \sqrt{\beta }$[25] or one can consider the value of minimal length to be the Planck length $L=l_p=\sqrt{(\hslash G/c^3)}$.

With minimal length-induced corrections, the line element on eight–dimensional manifold $M_8$ [42,43] reads,

$$\begin{array}{ccc}\hfill d{\tilde{s}}^2& =& g_{AB}d{x}^{A}d{x}^B,\hfill \end{array}$$

(10)

where $g_{AB}$ is a result of outer product; $g_{AB}=g_{\mu \nu }\otimes g_{\mu \nu }$, where $g_{\mu \nu }$ is the classical metric tensor. Substitutes for $d{x}^A$ and $d{x}^B$ from Eq.(9) into Eq.(10), to get

$$\begin{array}{c}\hfill d{\tilde{s}}^2=\left(1+L{g}_{\mu \nu }{\displaystyle \frac{d{x}^{\mu }}{ds}}{\displaystyle \frac{d{\dot{x}}^{\nu }}{ds}}+L{g}_{\mu \nu }{\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}{\displaystyle \frac{d{x}^{\nu }}{ds}}+L^2{g}_{\mu \nu }{\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}{\displaystyle \frac{d{\dot{x}}^{\nu }}{ds}}\right)d{s}^2,\end{array}$$

(11)

where $c=1$, $d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$ is the classical line element,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=d{s}^2+L^2{g}_{\mu \nu }{\ddot{x}}^{\mu }{\ddot{x}}^{\nu }d{s}^2,\end{array}$$

(12)

where ${\ddot{x}}^{\mu }={\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}$ is the acceleration, $\mu$, $\nu$ are dummy indices, and $\overrightarrow{\dot{x}}.\overrightarrow{\dot{x}}=-1$, then $\overrightarrow{\dot{x}}.\overrightarrow{\ddot{x}}=0$,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=(1+L^2{\ddot{x}}^2)d{s}^2,\end{array}$$

(13)

where ${\ddot{x}}^2=g_{\mu \nu }{\ddot{x}}^{\mu }{\ddot{x}}^{\nu }$. The deformed line element in four dimensions spacetime, as a projection from eight dimensions onto four dimensions, will be

$$\begin{array}{c}\hfill d{\tilde{s}}^2={\tilde{g}}_{\mu \nu }d{x}^{\mu }d{x}^{\nu },\end{array}$$

(14)

where ${\tilde{g}}_{\mu \nu }$ is assumed deformed metric tensor, which will be calculated by equating Eqs.(13), and (14),

$$\begin{array}{c}\hfill {\tilde{g}}_{\mu \nu }=(1+L^2{\ddot{x}}^2)g_{\mu \nu },\end{array}$$

(15)

where ${\ddot{x}}^2=g_{\alpha \beta }{\ddot{x}}^{\alpha }{\ddot{x}}^{\beta }$, $\beta$, $\alpha$ are dummy indices, $\mu$, and $\nu$ are free indices.

The entire contribution of the existence of minimal length according to GUP is summarized in the term

$$\begin{array}{c}\hfill L^2{\ddot{x}}^2{g}_{\mu \nu }=\beta {\hslash }^2{\ddot{x}}^2{g}_{\mu \nu },\end{array}$$

(16)

and the definition of minimal length based on the combination of fundamental physical quantities will be

$$\begin{array}{cc}\hfill L^2{\ddot{x}}^2{g}_{\mu \nu }& =l_p^2{\ddot{x}}^2{g}_{\mu \nu }\hfill \\ & =\hslash G{\ddot{x}}^2{g}_{\mu \nu },\hfill \end{array}$$

(17)

where $c=1$.

For flat spacetime,

$$\begin{array}{c}\hfill {\tilde{\eta }}_{\mu \nu }=(1+L^2{\ddot{x}}^2){\eta }_{\mu \nu },\end{array}$$

(18)

where ${\eta }_{\mu \nu }$ is the classical metric tensor in flat spacetime.

The correction factor of deformed metric tensor can be redefined by the maximal acceleration $A_{max}$, where $A_{max}=(c^2/L)=\sqrt{(c^7/\hslash G)}$ [37], the deformed metric tensor will be

$$\begin{array}{c}\hfill {\tilde{g}}_{\mu \nu }=\left(1+{\displaystyle \frac{1}{A_{max}^2}}{\ddot{x}}^2\right)g_{\mu \nu },\end{array}$$

(19)

where $c=1$.

The symmetry property, and the compatibility of deformed metric tensor is discussed in [21], where the deformed metric tensor is symmetric and compatible as the classical metric tensor. The deformed affine connection ${\tilde{\mathsf{\Gamma }}}_{\beta \mu }^{\gamma }$ has been derived in [21], and found to be

$$\begin{array}{c}\hfill {\tilde{\mathsf{\Gamma }}}_{\beta \mu }^{\gamma }={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\beta \mu }^{\gamma },\end{array}$$

(20)

where ${\mathsf{\Gamma }}_{\beta \mu }^{\gamma }$ is the classical affine connection. The deformed affine connection where proven to be symmetric in its lower indices [21].

4. Deformed Riemann curvature tensor

In GR, the components of the Riemann curvature tensor $R_{\beta \mu \nu }^{\gamma }$ can be constructed from the affine connection [44,45,46],

$$\begin{array}{ccc}\hfill R_{\beta \mu \nu }^{\gamma }& =& {\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }-{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }+{\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\hfill \end{array}$$

(21)

This expression holds for all connections regardless of their metric compatibility or torsion-freedom property [44]. Accordingly, the deformed Riemann tensor can be expressed in terms of the deformed affine connections and their derivatives as follows

$$\begin{array}{ccc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }& =& {\tilde{\mathsf{\Gamma }}}_{\beta \nu ,\mu }^{\gamma }-{\tilde{\mathsf{\Gamma }}}_{\beta \mu ,\nu }^{\gamma }+{\tilde{\mathsf{\Gamma }}}_{\sigma \mu }^{\gamma }{\tilde{\mathsf{\Gamma }}}_{\beta \nu }^{\sigma }-{\tilde{\mathsf{\Gamma }}}_{\sigma \nu }^{\gamma }{\tilde{\mathsf{\Gamma }}}_{\beta \mu }^{\sigma }\hfill \end{array}$$

(22)

We can substitute from Eq. (20) into Eq. (22) for the deformed affine connection in terms of the classical one,

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\sigma \mu }^{\gamma }& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\gamma \alpha }}{2}\left(g_{\mu \alpha ,\sigma }+g_{\sigma \alpha ,\mu }-g_{\sigma \mu ,\alpha }\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\sigma \mu }^{\gamma },\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\sigma \nu }^{\gamma }& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\gamma \alpha }}{2}\left(g_{\nu \alpha ,\sigma }+g_{\sigma \alpha ,\nu }-g_{\sigma \nu ,\alpha }\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma },\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\beta \mu }^{\sigma }& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\sigma \alpha }}{2}\left(g_{\mu \alpha ,\beta }+g_{\beta \alpha ,\mu }-g_{\beta \mu ,\alpha }\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\beta \mu }^{\sigma },\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\beta \nu }^{\sigma }& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\frac{g^{\sigma \alpha }}{2}\left(g_{\nu \alpha ,\beta }+g_{\beta \alpha ,\nu }-g_{\beta \nu ,\alpha }\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }\hfill \end{array}$$

(26)

Thus, we can straightforwardly derive the derivative of the deformed affine connection to be

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\beta \mu ,\nu }^{\gamma }& =& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left[\frac{g_{,\nu }^{\gamma \alpha }}{2}\left(g_{\mu \alpha ,\beta }+g_{\beta \alpha ,\mu }-g_{\beta \mu ,\alpha }\right)+\frac{g^{\gamma \alpha }}{2}\left(g_{\mu \alpha ,\beta ,\nu }+g_{\beta \alpha ,\mu ,\nu }-g_{\beta \mu ,\alpha ,\nu }\right)\right]\hfill \\ & +& \frac{2\left(1+L^2{\ddot{x}}^2\right)-\left(1+2L^2{\ddot{x}}^2\right)}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{L}^2{\left(g_{\xi \zeta }{\ddot{x}}^{\xi }{\ddot{x}}^{\zeta }\right)}_{,\nu }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\hfill \\ & =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }+\frac{L^2{g}_{\xi \zeta ,\nu }{\ddot{x}}^{\xi }{\ddot{x}}^{\zeta }}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\mathsf{\Gamma }}_{\beta \mu }^{\gamma },\hfill \end{array}$$

(27)

where $\xi$, $\zeta$ are dummy indices, ${\ddot{x}}_{,\nu }^{\xi }=0$, and ${\ddot{x}}_{,\nu }^{\zeta }=0$, as elaborated in Appendix A. Similarly,

$$\begin{array}{ccc}\hfill {\tilde{\mathsf{\Gamma }}}_{\beta \nu ,\mu }^{\gamma }& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}\left[\frac{g_{,\mu }^{\gamma \alpha }}{2}\left(g_{\nu \alpha ,\beta }+g_{\beta \alpha ,\nu }-g_{\beta \nu ,\alpha }\right)+\frac{g^{\gamma \alpha }}{2}\left(g_{\nu \alpha ,\beta ,\mu }+g_{\beta \alpha ,\nu ,\mu }-g_{\beta \nu ,\alpha ,\mu }\right)\right]\hfill \\ & +& \frac{2\left(1+L^2{\ddot{x}}^2\right)-\left(1+2L^2{\ddot{x}}^2\right)}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{L}^2{\left(g_{\xi \zeta }{\ddot{x}}^{\xi }{\ddot{x}}^{\zeta }\right)}_{,\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }\hfill \\ & =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }+\frac{L^2{g}_{\xi \zeta ,\mu }{\ddot{x}}^{\xi }{\ddot{x}}^{\zeta }}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }.\hfill \end{array}$$

(28)

With $g_{\xi \zeta }{g}^{\xi \zeta }=1$, we will replece $g_{\xi \zeta ,\nu }{\ddot{x}}^{\xi }{\ddot{x}}^{\zeta }$ by ${\ddot{x}}^2{g}_{\xi \zeta ,\nu }{g}^{\xi \zeta }$ in equations (27), and (28). By substituting into Eq. (22), the minimal length-induced correction to the Riemann curvature tensor are

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }& ={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }+{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}_{\eta \zeta ,\mu }{g}^{\eta \zeta }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }\hfill \end{array}$$

$$\begin{array}{c}\hfill -{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}_{\eta \zeta ,\nu }{g}^{\eta \zeta }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }+{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma },\end{array}$$

(29)

Taking common factors , and rearranging, we obtain

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }& ={\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }-{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left(g_{\eta \zeta ,\mu }{g}^{\eta \zeta }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-g_{\eta \zeta ,\nu }{g}^{\eta \zeta }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right)\end{array}$$

(30)

In Eq. (30), the partial derivatives of all metric tensors $g_{\eta \zeta ,\mu }$, and $g_{\eta \zeta ,\nu }$ can respectively be replaced by metric tensors and affine connections as follows

$$\begin{array}{ccc}\hfill g_{\xi \zeta ,\mu }& =& g_{\zeta \lambda }{\mathsf{\Gamma }}_{\xi \mu }^{\lambda }+g_{\xi \lambda }{\mathsf{\Gamma }}_{\zeta \mu }^{\lambda },\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill g_{\xi \zeta ,\nu }& =& g_{\zeta \lambda }{\mathsf{\Gamma }}_{\xi \nu }^{\lambda }+g_{\xi \lambda }{\mathsf{\Gamma }}_{\zeta \nu }^{\lambda },\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }& ={\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }-{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[\left({\delta }_{\lambda }^{\xi }{\mathsf{\Gamma }}_{\xi \mu }^{\lambda }+{\delta }_{\lambda }^{\zeta }{\mathsf{\Gamma }}_{\zeta \mu }^{\lambda }\right){\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-\left({\delta }_{\lambda }^{\xi }{\mathsf{\Gamma }}_{\xi \nu }^{\lambda }+{\delta }_{\lambda }^{\zeta }{\mathsf{\Gamma }}_{\zeta \nu }^{\lambda }\right){\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right]\end{array}$$

(33)

By using delta tensor to transform the dummy indices, Eq. (33) could be reexpressed as,

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }=& {\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left({\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }-{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right],\end{array}$$

(34)

substitute by Eq. (21) into Eq. (34) for $\left({\mathsf{\Gamma }}_{\beta \nu ,\mu }^{\gamma }-{\mathsf{\Gamma }}_{\beta \mu ,\nu }^{\gamma }\right)$,

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }=& {\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\left(R_{\beta \mu \nu }^{\gamma }+{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right],\end{array}$$

(35)

and take $\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)$ as a common factor,

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }=& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{R}_{\beta \mu \nu }^{\gamma }+{\displaystyle \frac{{(1+2L^2{\ddot{x}}^2)}^2-(1+L^2{\ddot{x}}^2)(1+2L^2{\ddot{x}}^2)}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)\hfill \end{array}$$

$$\begin{array}{c}\hfill +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right],\end{array}$$

(36)

and simplify the second term of Eq. (36),

$$\begin{array}{cc}\hfill {\tilde{R}}_{\beta \mu \nu }^{\gamma }=& {\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{R}_{\beta \mu \nu }^{\gamma }+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\gamma }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\gamma }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\gamma }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\gamma }\right]\hfill \end{array}$$

(37)

Equation (37) generalizes the Riemann curvature tensor by introducing the effect of minimal length. At vanishing $L^2$ and/or ${\ddot{x}}^2$, the undeformed Riemann curvature tensor $R_{\beta \mu \nu }^{\gamma }$ could entirely be retrieved.

The eminent ingredients added by the correction $L^2{\ddot{x}}^2$ can be illustrated in an example of a sphere surface (two-dimensional manifold) with radius $r=1$. The complementary geometric structure likely reveals supplementary insights to be discovered. The Cartesian coordinates could be expressed by polar coordinates; radius r, inclination $u^1$, and azimuth $u^2$ as $x=cos\left(u^2\right)sin\left(u^1\right)$, $y=sin\left(u^2\right)sin\left(u^1\right)$, and $z=cos\left(u^1\right)$. As shown in Eqs. (15), (23)–(), the minimal length induced corrections originated in $L^2{\ddot{x}}^2$ are combined in the deformed metric tensor and connection. Therefore, we just need to determine the components of the classical metric tensor

$$\begin{array}{ccc}\hfill g_{ij}& =& \left[\begin{array}{cc}\hfill cc1& 0\\ \hfill 0& {(sin\left(u^1\right))}^2\end{array}\right],\hfill \end{array}$$

and coefficients of the classical connections

$$\begin{array}{ccc}\hfill {\mathsf{\Gamma }}_{11}^1=0,& & {\mathsf{\Gamma }}_{11}^2=0,\hfill \\ \hfill {\mathsf{\Gamma }}_{12}^1=0,& & {\mathsf{\Gamma }}_{12}^2=cot\left(u^1\right),\hfill \\ \hfill {\mathsf{\Gamma }}_{21}^1=0,& & {\mathsf{\Gamma }}_{21}^2=cot\left(u^1\right),\hfill \\ \hfill {\mathsf{\Gamma }}_{22}^1=\frac{1}{2}sin\left(2u^1\right),& & {\mathsf{\Gamma }}_{22}^2=0.\hfill \end{array}$$

Then, the corresponding coefficients of deformed Riemann curvature tensor are given as

$$\begin{array}{ccc}\hfill {\tilde{R}}_{212}^1& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\left[sin\left(u^1\right)\right]}^2+\frac{\left(2L^2{\ddot{x}}^2-1\right)L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}{\left[cos\left(u^1\right)\right]}^2,\hfill \end{array}$$

(38)

which means that at the poles, where $u^1=\{0,\pi \}$, ${\tilde{R}}_{212}^1=(2L^2{\ddot{x}}^2-1)L^2{\ddot{x}}^2/{(1+L^2{\ddot{x}}^2)}^2$, i.e., finite, as well as at the equator, where $u^1=\pi /2$, ${\tilde{R}}_{212}^1=(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$, i.e., finite as well. These two examples highlight the significance of the minimal length contributions encoded in $L^2{\ddot{x}}^2$. In the classical limit, i.e., vanishing $L^2$ and/or ${\ddot{x}}^2$, only finite $R_{212}^1$ signals curved spaces, as this exclusively depends on the inclination. For instance, at the poles, the space is flat! with this correction, this isn’t necessarily the case everywhere. The only exception might be ${\ddot{x}}^2=0.5$ in units of $1/L^2$. Here, both classical and deformed coefficients $R_{212}^1$ indeed vanish, at $u^1=\{0,\pi \}$, while their values, at $u^1=\pi /2$, are also coincident and positive.

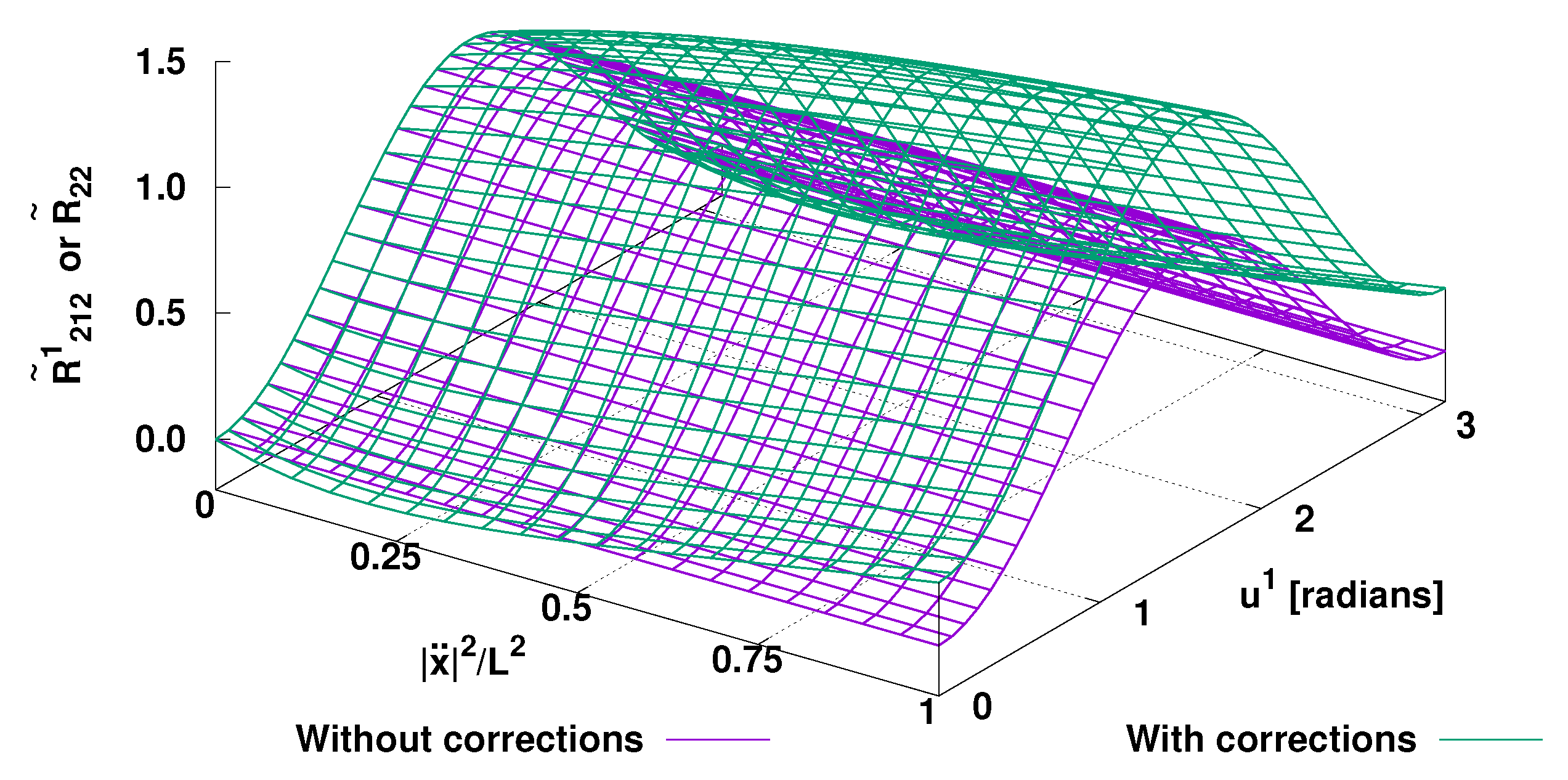
Figure 1 shows the coefficients of Riemann and Ricci curvature tensors in a sphere surface (two-dimensional manifold) with radius $r=1$, Eq. (38). For the sake of simplicity, we assume that the squared spacelike acceleration ${\ddot{x}}^2$ is given in units of $1/L^2$. This assures correct dimensions and sets upper bound on ${\ddot{x}}^2$ in units of $1/L^2$.

The Figure 1 depicts the dependence of ${\tilde{R}}_{212}^1$ and ${\tilde{R}}_{22}$ on both $u^1$ and ${\ddot{x}}^2$. It is apparent that the minimal length contributions are significant everywhere. It seems that the second term in Eq. (38), which is the same for Riemann and Ricci tensors, reveal additional geometrical structures and curvatures. Their nature shall be subject of a future study.

5. Deformed Ricci curvature tensor

The Ricci curvature tensor is the only possible contraction of Riemann curvature tensor. Ricci tensor represents the changing of the volume along geodesics due to the changing of curvature in space-time, and its definition from Riemann tensor contraction is

$$\begin{array}{ccc}\hfill g_{\gamma }^{\mu }{R}_{\beta \mu \nu }^{\gamma }& =& R_{\beta \mu \nu }^{\mu }=R_{\beta \nu }\hfill \end{array}$$

(39)

The deformed Ricci tensor according to Eq. (39),

$$\begin{array}{c}\hfill {\tilde{R}}_{\beta \nu }={\tilde{R}}_{\beta \mu \nu }^{\mu }.\end{array}$$

(40)

Substitute ${\tilde{R}}_{\beta \mu \nu }^{\mu }$ from Eq. (37) in Eq. (40),

$$\begin{array}{ccc}\hfill {\tilde{R}}_{\beta \nu }& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{R}_{\beta \nu }\hfill \\ & +& \frac{\left(1+2L^2{\ddot{x}}^2\right)L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\mu }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+\frac{2L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\mu }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\mu }\right]\hfill \end{array}$$

(41)

Similar to the deformed Riemann curvature tensor, the classical Ricci curvature tensor $R_{\beta \nu }$ can be fully restored, at vanishing $L^2$ and/or ${\ddot{x}}^2$. Eq. (41) is a generalization of $R_{\beta \nu }$, i.e, the minimal length deformation version of $R_{\beta \nu }$ is suggested.

For a sphere surface with a unity radius, the same expression as in Eq. (38) can be obtained for ${\tilde{R}}_{22}$. Thus, the results in Figure 1 and the corresponding conclusions are also valid for ${\tilde{R}}_{22}$.

6. Deformed Ricci scalar

The Ricci scalar gives how the volume in curved space deviates from its equivalent flat–space size and can be contracted from Ricci curvature tensor,

$$\begin{array}{ccc}\hfill g^{\beta \nu }{g}^{\gamma \mu }{R}_{\gamma \beta \mu \nu }& =& g^{\beta \nu }{R}_{\beta \nu }=R_{\nu }^{\nu }=R\hfill \end{array}$$

(42)

Therefore, the deformed Ricci scalar apparently reads

$$\begin{array}{ccc}\hfill \tilde{R}& =& {\tilde{g}}^{\beta \nu }{\tilde{R}}_{\beta \nu }.\hfill \end{array}$$

(43)

Substituting ${\tilde{R}}_{\beta \nu }$ from Eq. (41) in Eq. (43), we get

$$\begin{array}{ccc}\hfill \tilde{R}& =& \frac{1+2L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}R\hfill \\ & +& \frac{\left(1+2L^2{\ddot{x}}^2\right)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^3}{g}^{\beta \nu }\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\mu }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+\frac{2L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^3}{g}^{\beta \nu }\left[{\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\mu }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\mu }\right],\hfill \end{array}$$

(44)

where ${\tilde{g}}^{\beta \nu }={(1+L^2{\ddot{x}}^2)}^{-1}{g}^{\beta \nu }$. At vanishing $L^2$ and/or ${\ddot{x}}^2$, the undeformed Ricci scalar R can be straightforwardly obtained.

For a sphere surface (two-dimensional manifold) with radius $r=1$, the deformed Ricci scalar is evaluated as

$$\begin{array}{ccc}\hfill \tilde{R}& =& \frac{2(1+2L^2{\ddot{x}}^2)}{{\left(1+L^2{\ddot{x}}^2\right)}^2}\hfill \\ & +& \frac{2\left(1+2L^2{\ddot{x}}^2\right)L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^2}\left\{{\left[cot\left(u^1\right)\right]}^2-cot\left(u^1\right)\right\}-\frac{4L^2{\ddot{x}}^2}{{\left(1+L^2{\ddot{x}}^2\right)}^3}{\left[cot\left(u^1\right)\right]}^2,\hfill \end{array}$$

(45)

this equation with minimal length contributions including additional curvatures and geometrical structures. They are graphically depicted in Figure 2. It shows the dependence of $\tilde{R}$ on inclination $u^1$ and $|\ddot{x}{|}^2$. The latter is normalized to $1/L^2$. At vanishing $L^2$ and/or ${\ddot{x}}^2$, as in Einstein’s classical GR, there is no dependence on the inclination $u^1$.

The entire dependence of $\tilde{R}$ on $u^1$ and ${\ddot{x}}^2$ is depicted in Figure 2. Near the equator, the value of $\tilde{R}$ comes closer to the value of classical Ricci scalar R. One can roughly estimate that while minimal length correction is positive, at ${\ddot{x}}^2\gtrsim 0.5$, it’s negative, at ${\ddot{x}}^2\lesssim 0.5$. This rich structure is to be discovered in future studies.

7. Deformed Einstein tensor

The Einstein tensor is constructed as

$$\begin{array}{ccc}\hfill G_{\beta \nu }& =& R_{\beta \nu }-\frac{1}{2}{g}_{\beta \nu }R,\hfill \end{array}$$

(46)

and the deformed Einstein tensor will be

$$\begin{array}{ccc}\hfill {\tilde{G}}_{\beta \nu }& =& {\tilde{R}}_{\beta \nu }-\frac{1}{2}{\tilde{g}}_{\beta \nu }\tilde{R}.\hfill \end{array}$$

(47)

By substituting ${\tilde{R}}_{\beta \nu }$, ${\tilde{g}}_{\beta \nu }$, and $\tilde{R}$ as given in Eqs. (41), (15), and (44), respectively, into Eq. (47), we get

$$\begin{array}{cc}\hfill {\tilde{G}}_{\beta \nu }& ={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{R}_{\beta \nu }+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\mu }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\mu }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\mu })\hfill \\ & -g_{\beta \nu }[{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{2(1+L^2{\ddot{x}}^2)}}R+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{2{(1+L^2{\ddot{x}}^2)}^2}}{g}^{\alpha \rho }\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\alpha \rho }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \rho }^{\mu }{\mathsf{\Gamma }}_{\alpha \mu }^{\sigma }\right)\hfill \\ & +{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}^{\alpha \rho }\left({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\alpha \rho }^{\mu }-{\mathsf{\Gamma }}_{\lambda \rho }^{\lambda }{\mathsf{\Gamma }}_{\alpha \mu }^{\mu }\right)],\hfill \end{array}$$

(48)

where the indices $\beta$ and $\nu$ of Ricci scalar have replaced by dummy indices $\alpha$ and $\rho$, respectively, and take ${\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}$ as a common factor,

$$\begin{array}{cc}\hfill {\tilde{G}}_{\beta \nu }& ={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{G}_{\beta \nu }+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\mu }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)+{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\mu }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\mu })\hfill \end{array}$$

$$\begin{array}{c}\hfill -g_{\beta \nu }\left[{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{2{(1+L^2{\ddot{x}}^2)}^2}}{g}^{\alpha \rho }\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\alpha \rho }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \rho }^{\mu }{\mathsf{\Gamma }}_{\alpha \mu }^{\sigma }\right)+{\displaystyle \frac{L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}{g}^{\alpha \rho }\left({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\alpha \rho }^{\mu }-{\mathsf{\Gamma }}_{\lambda \rho }^{\lambda }{\mathsf{\Gamma }}_{\alpha \mu }^{\mu }\right)\right],\end{array}$$

(49)

where $G_{\beta \nu }=R_{\beta \nu }-{\displaystyle \frac{1}{2}}{g}_{\beta \nu }R$, take ${\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}$ and ${\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}$ as common factors,

$$\begin{array}{cc}\hfill {\tilde{G}}_{\beta \nu }& ={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{G}_{\beta \nu }+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\beta \nu }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \nu }^{\mu }{\mathsf{\Gamma }}_{\beta \mu }^{\sigma }\right)-{\displaystyle \frac{1}{2}}{g}_{\beta \nu }{g}^{\alpha \rho }\left({\mathsf{\Gamma }}_{\sigma \mu }^{\mu }{\mathsf{\Gamma }}_{\alpha \rho }^{\sigma }-{\mathsf{\Gamma }}_{\sigma \rho }^{\mu }{\mathsf{\Gamma }}_{\alpha \mu }^{\sigma }\right)\right]\hfill \\ & +{\displaystyle \frac{2L^2{\ddot{x}}^2}{{(1+L^2{\ddot{x}}^2)}^2}}\left[({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\beta \nu }^{\mu }-{\mathsf{\Gamma }}_{\lambda \nu }^{\lambda }{\mathsf{\Gamma }}_{\beta \mu }^{\mu })-{\displaystyle \frac{1}{2}}{g}_{\beta \nu }{g}^{\alpha \rho }({\mathsf{\Gamma }}_{\lambda \mu }^{\lambda }{\mathsf{\Gamma }}_{\alpha \rho }^{\mu }-{\mathsf{\Gamma }}_{\lambda \rho }^{\lambda }{\mathsf{\Gamma }}_{\alpha \mu }^{\mu })\right]\hfill \end{array}$$

(50)

At $L^2{\ddot{x}}^2=0$, the undeformed $G_{\beta \nu }$ is obviously fully retrieved from Eq. (50). At finite $L^2{\ddot{x}}^2$, the resulting spacetime curvature seems to have more structures than that of the Einstein’s classical tensor $G_{\beta \nu }$. Accordingly, additional sources of gravity are likely emerging. Their nature shall be characterized elsewhere.

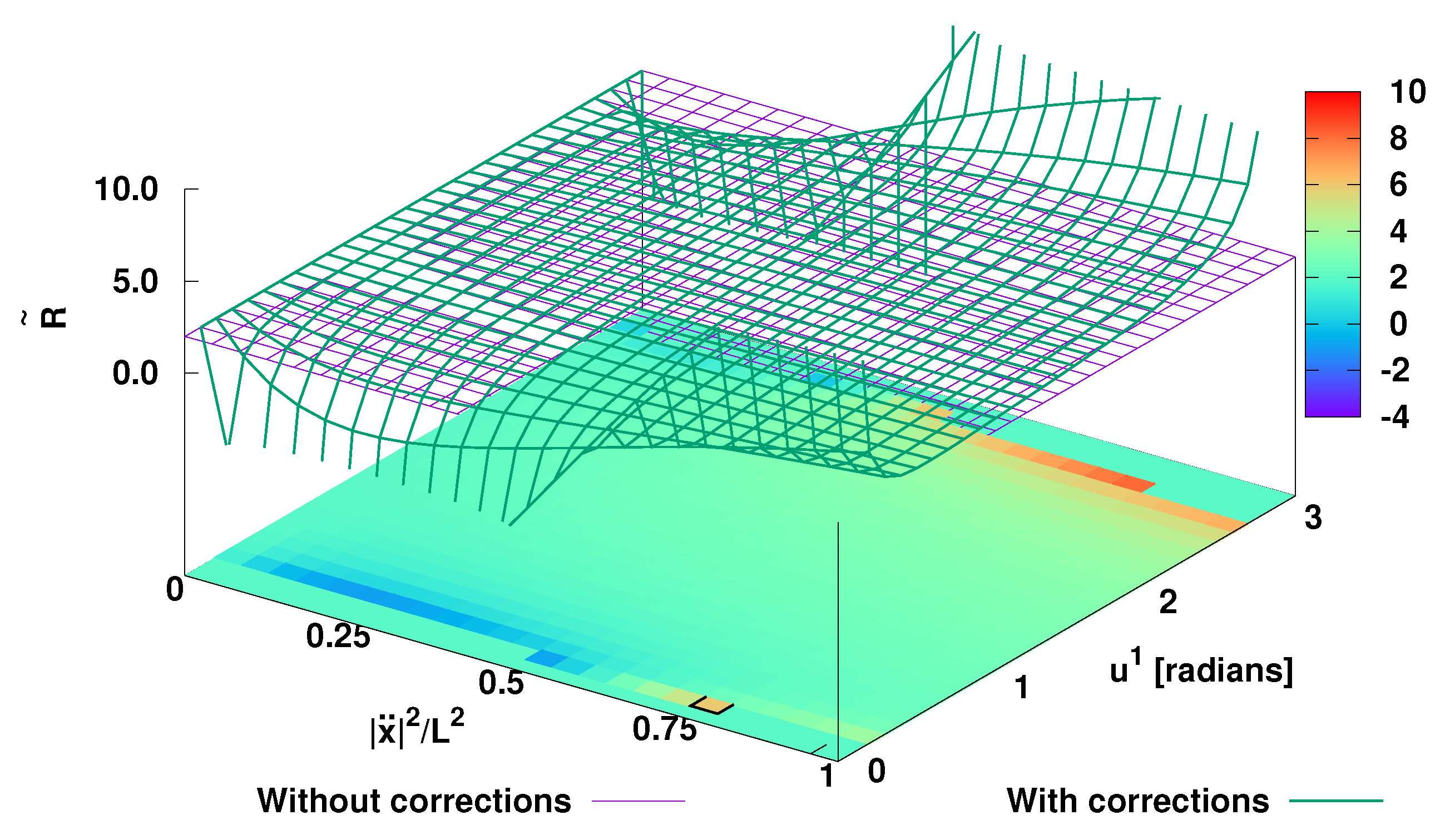
For a sphere surface (two-dimensional manifold) with radius $r=1$, Eq. (50) gives

$$\begin{array}{ccc}\hfill {\tilde{G}}_{22}& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{sin}^2\left(u^1\right)-\frac{\left(1-2L^2{\ddot{x}}^2\right)L^2{\ddot{x}}^2}{{\left(1+2L^2{\ddot{x}}^2\right)}^2}{cos}^2\left(u^1\right)-\frac{1+2L^2{\ddot{x}}^2}{{\left(1+2L^2{\ddot{x}}^2\right)}^2}{sin}^2\left(u^1\right)\hfill \\ & -& \frac{\left(1+2L^2{\ddot{x}}^2\right)L^2{\ddot{x}}^2}{{\left(1+2L^2{\ddot{x}}^2\right)}^3}\left[{cos}^2\left(u^1\right)-cos\left(u^1\right)sin\left(u^1\right)\right]+\frac{2L^2{\ddot{x}}^2}{{\left(1+2L^2{\ddot{x}}^2\right)}^3}{cos}^2\left(u^1\right).\hfill \end{array}$$

(51)

Accordingly, a comparison between $G_{22}$ and ${\tilde{G}}_{22}$ is depicted in Figure 3. a sphere surface with radius $r=1$.

In freely falling frames, in which the covariant derivative of tensor is the same for all observers, and the affine connection is vanishing so that the covariant derivative of deformed Einstein tensor Eq. (50) will be

$$\begin{array}{cc}\hfill {\nabla }^{\beta }{\tilde{G}}_{\beta \nu }& ={\nabla }^{\beta }\left[{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{G}_{\beta \nu }\right]\hfill \end{array}$$

(52)

$$\begin{array}{c}\hfill ={\nabla }^{\beta }\left({\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\right)G_{\beta \nu }+{\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\nabla }^{\beta }{G}_{\beta \nu }\end{array}$$

(53)

$$\begin{array}{c}\hfill ={\nabla }^{\beta }\left({\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}\right)G_{\beta \nu },\end{array}$$

(54)

where ${\nabla }^{\beta }{G}_{\beta \nu }=0$ in general relativity. In the flat space-time, the covariant derivative is a partial derivative, then Eq. (54) becomes

$$\begin{array}{cc}\hfill {\nabla }^{\beta }{\tilde{G}}_{\beta \nu }& ={\partial }^{\beta }\left({\displaystyle \frac{1+2\mathcal{T}{\ddot{x}}^2}{1+\mathcal{T}{\ddot{x}}^2}}\right)G_{\beta \nu }\hfill \end{array}$$

(55)

$$\begin{array}{c}\hfill =\mathcal{T}{\left({\ddot{x}}^2\right)}_{,\beta }{\displaystyle \frac{2(1+\mathcal{T}{\ddot{x}}^2)-(1+2\mathcal{T}{\ddot{x}}^2)}{{(1+\mathcal{T}{\ddot{x}}^2)}^2}}{G}_{\beta \nu }\end{array}$$

(56)

$$\begin{array}{c}\hfill =\mathcal{T}{g}_{\eta \zeta ,\beta }{\ddot{x}}^{\eta }{\ddot{x}}^{\zeta }{\displaystyle \frac{2(1+\mathcal{T}{\ddot{x}}^2)-(1+2\mathcal{T}{\ddot{x}}^2)}{{(1+\mathcal{T}{\ddot{x}}^2)}^2}}{G}_{\beta \nu },\end{array}$$

(57)

where ${\left({\ddot{x}}^2\right)}_{,\beta }=g_{\eta \zeta ,\beta }{\ddot{x}}^{\eta }{\ddot{x}}^{\zeta }$ see Appendix A. In free falling frame, $g_{\eta \zeta }={\eta }_{\eta \zeta }$, then

$$\begin{array}{cc}\hfill {\nabla }^{\beta }{\tilde{G}}_{\beta \nu }& =\mathcal{T}{\eta }_{\eta \zeta ,\beta }{\ddot{x}}^{\eta }{\ddot{x}}^{\zeta }{\displaystyle \frac{2(1+\mathcal{T}{\ddot{x}}^2)-(1+2\mathcal{T}{\ddot{x}}^2)}{{(1+\mathcal{T}{\ddot{x}}^2)}^2}}{G}_{\beta \nu }\hfill \end{array}$$

(58)

$$\begin{array}{c}\hfill =0,\end{array}$$

(59)

where ${\eta }_{\eta \zeta ,\beta }=0$. Eq. (59) is valid for flat or curved space-time therefore, the divergence of deformed Einstein tensor is vanishing.

The central assumption of general relativity is that the divergence of $G_{\beta \nu }$ vanishes as that of the energy–momentum tensor $T_{\beta \nu }$, that is ${\nabla }^{\beta }{G}_{\beta \nu }=0$ and ${\nabla }^{\beta }{T}_{\beta \nu }=0$. This means that extending the spacetime curvature preserves the central assumption of GR.

8. Summary and Conclusion

As prescribed in loop quantum gravity, doubly–special relativity, string theory, and noncommutative geometry, gravitational impacts could be embedded in the generalized noncommutative Heisenberg algebra. The minimal length correction to the metric tensor could be determined by the extended coordinates ($x^{\mu },L{\dot{x}}^{\mu })$. By equating the line element in the eight-dimensional manifold $M_8$ and the deformed line element in the four-dimensional manifold $M_4$, the minimal length-induced correction to the metric tensor ${\tilde{g}}_{\mu \nu }$ is determined. With this extension of manifold and minimal length correction, we have been able to extend the affine connection on the Riemann manifold and thereby suggesting minimal length-induced corrections to the Riemann and Ricci curvature tensors and Ricci scalar. Accordingly, we have constructed a deformed version of the Einstein tensor.

In differential geometry, the covariant derivative of Einstein tensor used to describes the spacetime curvature due to the presence of the energy–momentum tensor $T_{\beta \nu }$, the physical quantity expressing density and flux of energy and momentum in curved spacetime, vanishes. We have proved that the covariant derivative of the Einstein tensor with minimal length–induced corrections vanishes, as well. Thus, the deformed spacetime curvature presented in the present script seems to fulfil the entire assumptions of the Einstein’s theory of general relativity, on one hand. On the other hand, the deformation of the spacetime curvature adds additional curvatures and geometric structures and thereby might suggest a generalization of the energy–momentum tensor $T_{\beta \nu }$, which will be discussed in a future research.