On Possible Minimal Length Deformation of Metric Tensor and Affine Connection

1. Introduction

Quantum mechanics and general relativity, two fundamental theoretical frameworks, can both be used to explain nearly every physical occurrence in the universe. These conceptual frameworks include the theories and models that explain matter and its basic interactions and can foretell a large number of experimentally observed outcomes. In the physical framework of the standard model (SM), and the mathematical disguise of Quantum Field Theory (QFT), Quantum Mechanics (QM) in partnership with the special theory of relativity (SR) describe the interactions between atoms, molecules, elementary particles such as electrons, muons, photons, quarks and their anti-particles at very small scales, of the order of ${10}^{-10}$ to ${10}^{-19}$ m.

QM within the framework of SM mainly describe interactions involving three of the four fundamental forces, namely the electromagnetic, weak nuclear, and strong nuclear forces. The behavior of matter under the influence of the fourth fundamental force of nature, namely the gravitational force, is described by the theory of General Relativity (GR). The conceptual framework employed by QM differs drastically from that of classical physics including GR and its implications. Heisenberg uncertainty principle (HUP) is one major aspect of the conceptual difference between classical and quantum physics. In stark contrast to classical mechanics, HUP states that it is impossible to have a particle for which a pair of canonically conjugate quantities, such as position and momentum, are accurately defined to arbitrary limit even if all initial conditions are known. HUP obviously arises from the wave-particle duality, which tells us that there is a fuzziness in nature at a fundamental level.

Despite its great achievements, QM and its extensions, such as the Standard Model of Particles (SM), cannot be regarded as the whole theory of the observable universe. This is because of a few flaws, specifically the fact that they are unable to explain how elementary particles behave when gravitational interactions, the final of the four fundamental interactions, are present. This is a consequence of treating spacetime as a constant, flat background, which General Relativity (GR) shows us is not the case, as demonstrated in what follows.

On the other hand, the mainstream theory of gravity; The general theory of relativity (GR) assumes that the apparent gravitational pull between masses is caused by the bending of spacetime caused by those masses. Thus, the gravitational field has a geometrical nature. Mass and energy seem to curve flat spacetime into a four-dimensional Riemannian manifold having a symmetric metric tensor and an affine (linear) connection. The latter is torsion-free and metric compatible and thus can be determined in terms of the metric tensor, itself.

High-precision astronomical and cosmological observations, such as the perihelion precession of Mercury’s orbit, gravitational lensing, gravitational red shift of light, the accelerated expansion of our Universe, and gravitational waves, have been successfully used to test general relativity (GR).

In reality, gravitational interactions are the only ones that matter at astronomically large distances and/or matter density, and when combined with the so called dark matter and dark energy, they offer an almost complete account of the composition and development of the universe from its inception to its ultimate end.

Although the special theory of relativity seems to be fully concordant with quantum mechanics even in a curved space-time background. It seems, however, that there are some persistent inconsistencies between QM and classical GR that impedes their reconciliation. Apart from the famous problem of renormalizability, which could have been sorted out in few Quantum Gravity approaches such as String Theory and Loop Quantum Gravity, such incompatibilities include: First, QM becomes incompatible with classical GR near singularities; Second, it’s not yet known how to determine the gravitational field of a quantum particle given the fuzziness (uncertainty) of location and velocity in QM; Third, time has a different meaning in QM and classical GR.

As was noted earlier, GR views spacetime as a dynamic object that interacts with matter and energy, as opposed to QM’s view of it as a flat immobile background. The probabilistic aspect of the observables represented by QM, on the other hand, is not taken into consideration by GR. Therefore, a new theory must be developed that will give rise to QM and GR in their respective domains. Unfortunately, the minimalist approach of implementing the techniques of Quantum Field Theory (QFT) to GR doesn’t work as anticipated based on previous experience. this is because when perturbatively quantized gravity is subjected to renormalization techniques sought to tame divergences, no finite measurable result is produced. Consequently, it can be inferred that there is a need to approach QG differently. The term "theories of quantum gravity" (QG) refers to a variety of models and/or theories that have been developed to address the challenge of quantizing gravity. String Theory (ST), Loop Quantum Gravity (LQG), and Doubly Special Relativity (DSR), are a few examples. These theories are only a few attempts at solving the issue, all of which have had varying degrees of success. There are a number of issues with quantum gravity theories and approaches that have remained unresolved for a long time (a survey can be found in Reference [1]).

Among the variety of attempts to approach a consistent theory of Quantum Gravity (QG), particularly those class of (models) endeavoring to modify the classical GR using quantum arguments, is the so called Generalized Uncertainty Principle (GUP)[2,3,4,5,6,7,8,9,10,11,12,13,14], which has been used extensively in attempts to incorporate the effects of gravity in quantum physics.

GUP is a modified Heisenberg uncertainty relation that predicts a deformed canonical commutator. Interestingly enough, GUP can lead to some phenomenological quantum gravitational models that can, in principle, be probed at relatively low energies [15,16].

String Theory, Loop Quantum Gravity, Doubly Special Relativity as well as Black Hole thermodynamics suggest the inevitability of the existance of a fundamnetal physical minimum length and/or a modification of the Heisenberg’s Uncertainty Principle near the Planck scale to a so-called Generalized Uncertainty Principle (GUP)[17]. There are three main approaches to a GUP, which are motivated here [16,18]. A generalised uncertainty relation that characterizes the minimal length as a minimal uncertainty in position measurements have been constructed using Quantum Gravity and String Theory arguments [8] and independently from special other quantum mechanical and group theoretical arguments [19]. This approach is the one we are going to adopt in the present work.

The present script introduces a minimal length approach, in which the inherent uncertainties emerging in detecting a quantum state are constrained in noncommutative operators as governed by Heisenberg uncertainty principle (HUP), which limits these to simultaneous measurements but obviously doesn’t incorporate the impacts of the gravitational fields. The extended version of HUP known as generalized uncertainty principle (GUP) is also predicted in string theory, loop quantum gravity, doubly special relativity, and various gedanken experiments [18,20].

GUP could be seen as an approach emerging from the gravitational impacts on the quantum measurements. The latter are essential components of the underlying quantum theory. In other words, GUP helps explaining the origin of the gravitational field and how a particle behaves in it [21,22]. Recently, the effects of the minimal length approach on the line element, the metric tensor, and the geodesics have been evaluated [21,22]. While in line element and metric tensor an additional term of the GUP parameter and squared spacelike four–acceleration appears in each quantity, multiple terms with higher–order derivatives appear in the geodesics [21].

An affine connection is defined as a geometric object on a smooth manifold connecting nearby tangent spaces. The tangent vector fields are covariant derivatives on that manifold. An affine connection dictates how to perform parallel transport of tangent vectors on manifold. In general relativity, the connection plays the role of the gravitational force field, where the metric tensor is the corresponding gravitational potential. Spacetime geometry cannot be considered in isolation from other branches of physics; its concepts and laws are inseparably mixed with those of mechanics, electrodynamics etc. Extrapolating this line of argument, there got to be some imprint of geometry on quantum mechanics and, intuitively, vice-versa.

In Section 2, a short review of the minimal measurable length is outlined. Extending the four–dimensional manifold M to an eight-dimentional spacetime tangent bundle $TM$, the possible deformation of the metric tensor is derived in Section 3. The possible deformation of the affine connection on Riemannian manifold is discussed in Section 4. The parallel transport of a vector on Riemannian manifold is elaborated in Section 5. The symmetry properties of the deformed metric tensor and affine connection are discussed in Section 6. Section 7 is devoted to the summary and conclusion.

2. Minimal Measurable Length

The minimal length L emerged from the assumption that a minimal length uncertainty that was predicted in various theories of quantum gravity, string theory, for instance, as a consequence of the gravitational fields on the uncertainty principle suggests that [7],

$$\begin{array}{c}\hfill \Delta x\Delta p\ge \frac{\hslash }{2}\left[1+\beta {\left(\Delta p\right)}^2+\beta {\langle p\rangle }^2\right],\end{array}$$

(1)

where $\langle p\rangle$ is the momentum expectation value, $\Delta x$ and $\Delta p$, respectively, represent the length and momentum uncertainties. The GUP parameter, $\beta ={\beta }_{0}G/(c^3\hslash )$, with ${\beta }_0$ is a dimensionless parameter to be determined from recent cosmological observations [23,24] introduces the consequences of gravity to the uncertainty principle, the fundamental theory of quantum mechanics. The commutation relation between length and momentum operators,

$$\begin{array}{ccc}\hfill \left[\widehat{x},\widehat{p}\right]& =& i\hslash \left(1+\beta {\widehat{p}}^2\right).\hfill \end{array}$$

(2)

The minimum uncertainty of position $\Delta x_{min}$ for all values of expectation values of momentum $\langle p\rangle$ will be

$$\begin{array}{c}\hfill \Delta x_{min}\left(\langle p\rangle \right)=\hslash \sqrt{\beta }\sqrt{1+\beta {\langle p\rangle }^2}\end{array}$$

(3)

then the absolute minimum uncertainty of position is at ${\langle p\rangle }^2=0$,

$$\begin{array}{c}\hfill \Delta x_0=\hslash \sqrt{\beta }\end{array}$$

(4)

One can consider the value of $\Delta x_0$ as the possible minimal length according to the GUP, which represents the effect of gravitational field on the QM, then the minimal length will be

$$\begin{array}{c}\hfill L=\hslash \sqrt{\beta }\end{array}$$

(5)

The minimal length may be assumed as a fundamental physical quantity obtained from a combination of fundamental physical quantities, gravitational constant (G) from gravity, reduced Planck constant (ℏ) from quantum mechanics, and speed of light (c) from spacial relativity [25]. The minimal length will be

$$\begin{array}{cc}\hfill L& =l_p\hfill \\ & =\sqrt{{\displaystyle \frac{\hslash G}{c^3}}}\hfill \end{array}$$

(6)

where $l_p$ is called Planck length.

The existence of maximal acceleration can be assumed by the existence of minimal length as a combination of fundamental physical quantities [26],

$$\begin{array}{cc}\hfill A_{max}& ={\displaystyle \frac{c^2}{l_p}}\hfill \\ & =\sqrt{{\displaystyle \frac{c^7}{\hslash G}}}\hfill \end{array}$$

(7)

According to the GUP definition of minimal length stated in Eq. (5), the maximal acceleration will be

$$\begin{array}{cc}\hfill A_{max}& ={\displaystyle \frac{c^2}{L}}\hfill \\ & =\sqrt{{\displaystyle \frac{c^4}{{\hslash }^2\beta }}}\hfill \end{array}$$

(8)

3. The Deformation of Metric Tensor

Caianiello suggested that the deformed GR can be described by the four dimensional spacetime embedded as a hypersurface in the eight dimensions manifold $M_8$[27,28,29]. The eight dimensions $x^A$ is

$$\begin{array}{c}\hfill x^A=(x^{\mu },(L/c){\dot{x}}^{\mu })\end{array}$$

(9)

where $x^{\mu }$ is the four spacetime dimensions, ${\dot{x}}^{\mu }={\displaystyle \frac{d{x}^{\mu }}{ds}}$ is the four velocity, $A=0,...,7$, $\mu =0,...,3$, L is the minimal length. L may be defined according to GUP as a minimal uncertainty of position; $L=\hslash \sqrt{\beta }$[7] or one can consider the value of minimal length to be the Planck length $L=\sqrt{(\hslash G/c^3)}$.

The deformed line element in eight dimensions manifold $M_8$ [30,31] is,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=g_{AB}d{x}^{A}d{x}^B\end{array}$$

(10)

where $g_{AB}$ is a result of outer product as the following $g_{AB}=g_{\mu \nu }\otimes g_{\mu \nu }$. In Eq.(10), substitute $d{x}^A$, and $d{x}^B$ by Eq.(9),

$$\begin{array}{c}\hfill d{\tilde{s}}^2=\left(1+L{g}_{\mu \nu }{\displaystyle \frac{d{x}^{\mu }}{ds}}{\displaystyle \frac{d{\dot{x}}^{\nu }}{ds}}+L{g}_{\mu \nu }{\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}{\displaystyle \frac{d{x}^{\nu }}{ds}}+L^2{g}_{\mu \nu }{\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}{\displaystyle \frac{d{\dot{x}}^{\nu }}{ds}}\right)d{s}^2\end{array}$$

(11)

where $c=1$, $d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$ is the classical line element,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=d{s}^2+L^2{g}_{\mu \nu }{\ddot{x}}^{\mu }{\ddot{x}}^{\nu }d{s}^2\end{array}$$

(12)

where ${\ddot{x}}^{\mu }={\displaystyle \frac{d{\dot{x}}^{\mu }}{ds}}$ is the acceleration, $\mu$, $\nu$ are dummy indices, and $\overrightarrow{\dot{x}}.\overrightarrow{\dot{x}}=-1$, then $\overrightarrow{\dot{x}}.\overrightarrow{\ddot{x}}=0$,

$$\begin{array}{c}\hfill d{\tilde{s}}^2=(1+L^2{\ddot{x}}^2)d{s}^2\end{array}$$

(13)

where ${\ddot{x}}^2=g_{\mu \nu }{\ddot{x}}^{\mu }{\ddot{x}}^{\nu }$. The deformed line element in four dimensions spacetime, as a projection from eight dimensions into four dimensions, will be

$$\begin{array}{c}\hfill d{\tilde{s}}^2={\tilde{g}}_{\mu \nu }d{x}^{\mu }d{x}^{\nu }\end{array}$$

(14)

where ${\tilde{g}}_{\mu \nu }$ is an assumed deformed metric tensor, which will be calculated by equating Eqs.(13), and (14),

$$\begin{array}{c}\hfill {\tilde{g}}_{\mu \nu }=(1+L^2{\ddot{x}}^2)g_{\mu \nu }\end{array}$$

(15)

where ${\ddot{x}}^2=g_{\alpha \beta }{\ddot{x}}^{\alpha }{\ddot{x}}^{\beta }$, $\beta$, $\alpha$ are dummy indices, $\mu$, and $\nu$ are free indices.

For flat spacetime,

$$\begin{array}{c}\hfill {\tilde{\eta }}_{\mu \nu }=(1+L^2{\ddot{x}}^2){\eta }_{\mu \nu }\end{array}$$

(16)

The correction factor of deformed metric tensor can be redefined by the maximal acceleration $A_{max}$, where $A_{max}=(c^2/L)=\sqrt{(c^7/\hslash G)}$ [26], the deformed metric tensor will be

$$\begin{array}{c}\hfill {\tilde{g}}_{\mu \nu }=\left(1+{\displaystyle \frac{1}{A_{max}^2}}{\ddot{x}}^2\right)g_{\mu \nu }\end{array}$$

(17)

where $c=1$.

4. The Deformation of Affine Connection in Riemannian Manifold

The minimal length approach, suggests deformation of the metric tensor as follows

• For curved space,

  $$\begin{array}{ccc}\hfill {\tilde{g}}_{\mu \nu }& =& g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu }=g_{\mu \nu }+q_{\mu \nu }.\hfill \end{array}$$

  (18)
  With Eq. (5), the $q_{\mu \nu }$ can be suggested as GUP contributed part, which reads

  $$\begin{array}{ccc}\hfill q_{\mu \nu }& =& \beta {\hslash }^2{\ddot{x}}^2{g}_{\mu \nu }\hfill \end{array}$$

  (19)
• For flat space,

  $$\begin{array}{ccc}\hfill {\tilde{\eta }}_{\mu \nu }& =& {\eta }_{\mu \nu }+\beta {\hslash }^2{\ddot{x}}^2{\eta }_{\mu \nu }={\eta }_{\mu \nu }+h_{\mu \nu },\hfill \end{array}$$

  (20)

  where $h_{\mu \nu }=\beta {\hslash }^2{\ddot{x}}^2{\eta }_{\mu \nu }$.

Both $g_{\mu \nu }$ and ${\tilde{g}}_{\mu \nu }$ share common properties. They turn the covariant tensor into contravariant tensor and vice versa. The symmetry property of deformed metric tensor is

$${\tilde{g}}_{\mu \nu }={\displaystyle \frac{1}{2}}({\tilde{g}}_{\mu \nu }+{\tilde{g}}_{\nu \mu }),$$

(21)

the L.H.S of Eq. (21) will be

$${\tilde{g}}_{\mu \nu }=g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu },$$

(22)

and the R.H.S of Eq. (21) is

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mu \nu }+{\tilde{g}}_{\nu \mu })={\displaystyle \frac{1}{2}}(g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu }+g_{\nu \mu }+L^2{\ddot{x}}^2{g}_{\nu \mu })$$

(23)

we know that $g_{\mu \nu }$ in classical GR is symmetric in its indices, then we will replace $g_{\nu \mu }$ in third and fourth terms by $g_{\mu \nu }$,

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mu \nu }+{\tilde{g}}_{\nu \mu })={\displaystyle \frac{1}{2}}(g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu }+g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu })$$

(24)

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mu \nu }+{\tilde{g}}_{\nu \mu })={\displaystyle \frac{1}{2}}(2g_{\mu \nu }+2L^2{\ddot{x}}^2{g}_{\mu \nu })$$

(25)

$${\displaystyle \frac{1}{2}}({\tilde{g}}_{\mu \nu }+{\tilde{g}}_{\nu \mu })=g_{\mu \nu }+L^2{\ddot{x}}^2{g}_{\mu \nu }$$

(26)

we find that Eq. (22) and Eq. (26) are equal, then R.H.S = L.H.S of Eq. (21). The deformed metric tensor is symmetric under interchange of its indices $\mu$ and $\nu$.

For the deformed affine connection, we replace $g_{\mu \nu }$ in Eq. (A3) with the deformed metric tensor ${\tilde{g}}_{\mu \nu }$ Eq. (18), where the partial derivatives are obviously commutative, as well. The deformed metric tensor is compatible, see appendix B. Thus, the deformation of the affine connection, Eq. (A3), can be expressed as

$${\tilde{\Gamma }}_{\beta \mu }^{\gamma }={\displaystyle \frac{1}{2}}{\tilde{g}}^{\alpha \gamma }({\tilde{g}}_{\alpha \beta ,\mu }+{\tilde{g}}_{\alpha \mu ,\beta }-{\tilde{g}}_{\beta \mu ,\alpha }).$$

(27)

For curved space, by substituting Eqs. (18), and (A12) into Eq. (27), we get

$$\begin{array}{ccc}\hfill {\tilde{\Gamma }}_{\beta \mu }^{\gamma }& =& \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}\frac{1}{2}{g}^{\alpha \gamma }\left(g_{\alpha \beta ,\mu }+g_{\alpha \mu ,\beta }-g_{\beta \mu ,\alpha }\right)={\displaystyle \frac{1+2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\beta \mu }^{\gamma }.\hfill \end{array}$$

(28)

where ${\tilde{g}}^{\alpha \gamma }={\displaystyle \frac{g^{\alpha \gamma }}{(1+L^2{\ddot{x}}^2)}}$.

It is obvious that vanishing $L^2{\ddot{x}}^2$ straightforwardly retrieves the undeformed affine connection ${\Gamma }_{\beta \mu }^{\gamma }$. This is also the case, at vanishing $L^2$, no minimal length uncertainty, and/or at vanishing ${\ddot{x}}^2$, cancellation of the GUP effect on GR. We have shown in Eq. (18) that both deformation ingredients are interdependent. The parameterization of the four–coordinates on M in eight–coordinates on $TM$ emerges spacelike four-acceleration ${\ddot{x}}^2$ and creates additional geometric structure. Eq. (28) reveals that the deformation of the affine connection is exclusively localized in its coefficient: while undeformed ${\Gamma }_{\beta \mu }^{\gamma }$ possesses unity as a coefficient, its deformed version gets the coefficient $(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$. This means that the affine (linear) connection preserves, on one hand, its geometric nature as in GR, for instance. On the other hand, the deformation via additional curvature on higher–dimensional manifold, especially at the energy scale, in which $L^2{\ddot{x}}^2$ becomes significant.

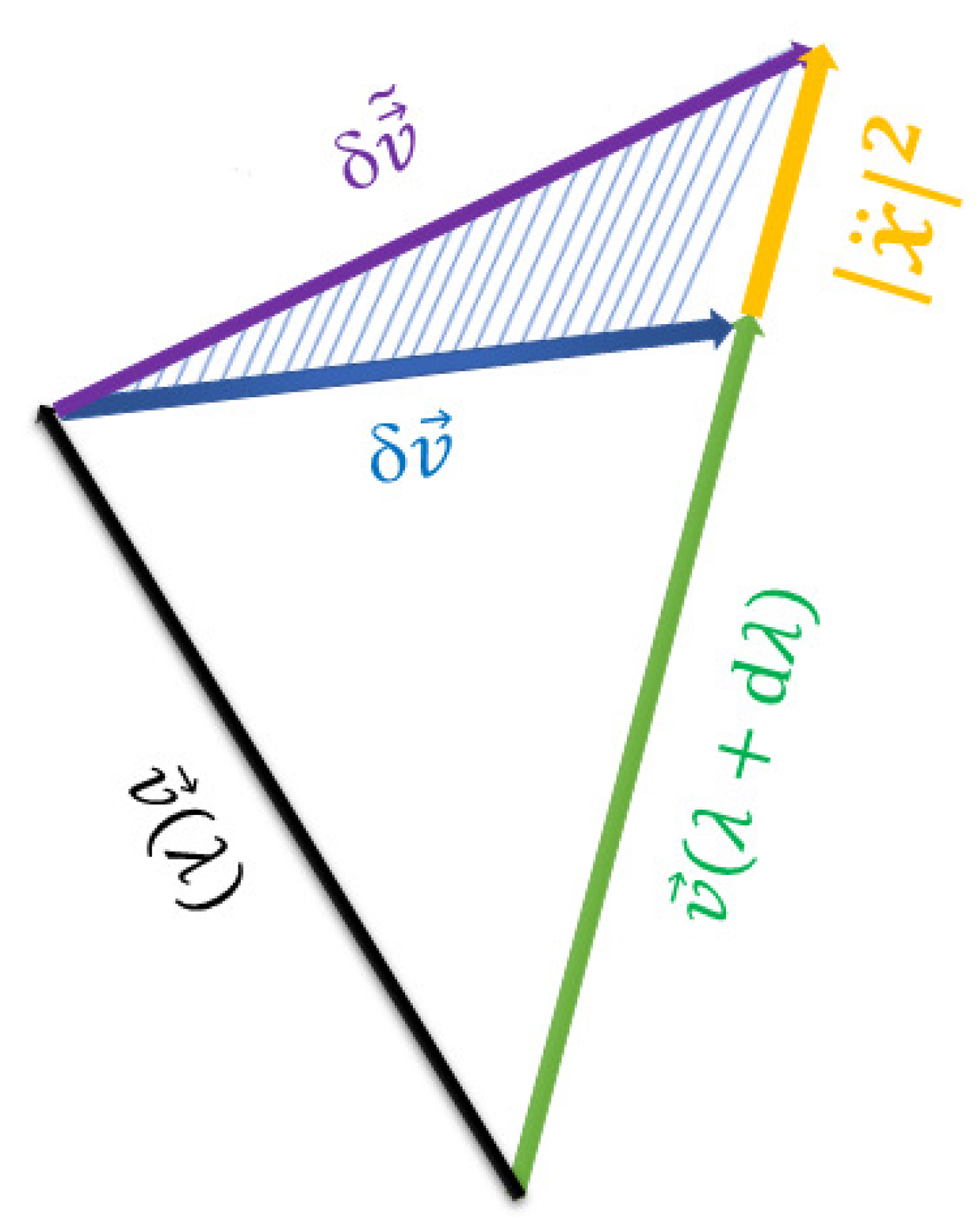
5. Parallel Transport on Riemannian Manifold

In flat space, the covariant derivatives, where the vector components and the basis vectors are also differentiated, are just the ordinary derivatives. In curved space, the differentiation of the basis vectors can be expressed by the Christoffel symbols. In both flat and curved spaces, the covariant derivatives can be defined as the rates of change of the tangent vector fields (ordinary derivatives, for instance) with the normal component subtracted, i.e., parallel transport. Vanishing covariant derivatives of a vector $\overrightarrow{v}=v^{\alpha }{e}_{\alpha }$ means that $\overrightarrow{v}$ is parallel transported, i.e., keeping $\overrightarrow{v}$ as constant as possible,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\lambda }}{v}^{\alpha }+{\Gamma }_{\sigma \rho }^{\alpha }{\displaystyle \frac{d{x}^{\sigma }}{d\lambda }}{v}^{\rho }=0,\end{array}$$

(29)

where the dependence of the parallel transport on the connection ${\Gamma }_{\sigma \rho }^{\alpha }$ is obvious. With the deformation, ${\Gamma }_{\sigma \rho }^{\alpha }$ is to be replaced by ${\tilde{\Gamma }}_{\sigma \rho }^{\alpha }$, Eq. (28), i.e., Eq. (29) can then be rewritten as

$${\displaystyle \frac{d}{d\lambda }}{v}^{\alpha }+{\displaystyle \frac{(1+2L^2{\ddot{x}}^2)}{(1+L^2{\ddot{x}}^2)}}{\Gamma }_{\sigma \rho }^{\alpha }{\displaystyle \frac{d{x}^{\sigma }}{d\lambda }}{v}^{\rho }=0$$

(30)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{d}{d\lambda }}{v}^{\alpha }& =& -{\displaystyle \frac{1}{1+L^2{\ddot{x}}^2}}{\Gamma }_{\sigma \rho }^{\alpha }{\displaystyle \frac{d{x}^{\sigma }}{d\lambda }}{v}^{\rho }-\frac{2L^2{\ddot{x}}^2}{1+L^2{\ddot{x}}^2}{\Gamma }_{\sigma \rho }^{\alpha }{\displaystyle \frac{d{x}^{\sigma }}{d\lambda }}{v}^{\rho }.\hfill \end{array}$$

(31)

The Fig. Figure 1 draws the affine connection between the vector $\overrightarrow{v}$ parameterized in $\lambda$; $\overrightarrow{v}\left(\lambda \right)$ and its parallel transported counterpart, at $\lambda +d\lambda$; $\overrightarrow{v}(\lambda +d\lambda )$.

The parallel transport can define the curvature of a manifold by take the parallel transport of a vector over a closed loop then it will give the definition of curvature tensor [32,33]. The equation of parallel transport of the vector $v^{\alpha }$ around a loop with the deformed connection will be

$$\delta v^{\alpha }=\delta a\delta b[{\tilde{\Gamma }}_{\mu \sigma ,\lambda }^{\alpha }-{\tilde{\Gamma }}_{\mu \lambda ,\sigma }^{\alpha }+{\tilde{\Gamma }}_{\nu \lambda }^{\alpha }{\tilde{\Gamma }}_{\mu \sigma }^{\nu }-{\tilde{\Gamma }}_{\nu \sigma }^{\alpha }{\tilde{\Gamma }}_{\mu \lambda }^{\nu }]v^{\mu }$$

(32)

where $\delta v^{\alpha }$ is the changing of $v^{\alpha }$ by the transport around the loop and $\delta a\delta b$ is the area of the loop. According to Eq. (32), the deformed curvature tensor is

$${\tilde{R}}_{\mu \lambda \sigma }^{\alpha }={\tilde{\Gamma }}_{\mu \sigma ,\lambda }^{\alpha }-{\tilde{\Gamma }}_{\mu \lambda ,\sigma }^{\alpha }+{\tilde{\Gamma }}_{\nu \lambda }^{\alpha }{\tilde{\Gamma }}_{\mu \sigma }^{\nu }-{\tilde{\Gamma }}_{\nu \sigma }^{\alpha }{\tilde{\Gamma }}_{\mu \lambda }^{\nu }.$$

(33)

More investigation and discussion of deformed curvature tensor Eq. (33) will be conducted in future research.

6. Symmetry Properties of Deformed Affine Connection

The symmetry property of the affine connection depends on a) the symmetry property of the metric tensor, and b) the commutation of the partial derivatives. The deformed affine connection, Eq. (28), fulfills both conditions:

• In any coordinates, the deformed affine connection can be expressed in the deformed metric tensor and its derivatives,

  $${\tilde{\Gamma }}_{\beta \mu }^{\gamma }={\displaystyle \frac{1}{2}}{\tilde{g}}^{\alpha \gamma }({\tilde{g}}_{\alpha \beta ,\mu }+{\tilde{g}}_{\alpha \mu ,\beta }-{\tilde{g}}_{\beta \mu ,\alpha }),$$

  (34)

  where the deformed metric tensor is symmetric, then the deformed affine connection is symmetric, as well.
• The affine connection can be expressed as [34]

  $${\tilde{\Gamma }}_{\beta \mu }^{\gamma }={\displaystyle \frac{\partial x^{\gamma }}{\partial X^{\alpha }}}{\displaystyle \frac{{\partial }^2{X}^{\alpha }}{\partial x^{\beta }\partial x^{\mu }}},$$

  (35)

  where $x^{\lambda }$ and $X^{\alpha }$ represent different coordinates in curved space, the commutation of the partial derivatives is still satisfied in the deformed affine connection, Eq. (28). This is also valid even when $X^{\alpha }$ is deformed to encounter the existence of a minimal length uncertainty.

Therefore, we conclude that the deformed affine connection is symmetric in its lower indices ${\tilde{\Gamma }}_{\left(\beta \mu \right)}^{\gamma }$, so that

$${\tilde{\Gamma }}_{\left(\beta \mu \right)}^{\gamma }={\tilde{\Gamma }}_{\beta \mu }^{\gamma }={\tilde{\Gamma }}_{\mu \beta }^{\gamma }.$$

(36)

Also, because the deformed affine connection on Riemannian manifold is torsion–free, then

$$T_{\beta \mu }^{\gamma }={\tilde{\Gamma }}_{\beta \mu }^{\gamma }-{\tilde{\Gamma }}_{\mu \beta }^{\gamma }=2{\tilde{\Gamma }}_{\left[\beta \mu \right]}^{\gamma }=0,$$

(37)

where ${\tilde{\Gamma }}_{\left[\beta \mu \right]}^{\gamma }=0$.

7. Summary and Conclusion

The minimal length approach emerging from noncommutative Heisenberg algebra, generalized uncertainty principle (GUP), is conjectured to integrate gravity in quantum mechanics through generalizing Heisenberg uncertainty principle to encounter impacts of gravitational fields [18,20]. When applying this recipe to general relativity, the metric tensor becomes deformed, by gaining an additional term, which is related to the GUP parameter, undeformed metric tensor, and squared four–acceleration ${\ddot{x}}^2$.

To achieve the deformation on spacetime monifold M, we have followed the same recipe for the curvature in relativistic eight–dimentional spacetime tangent bundle $TM$ in the Riemannian manifold. The local coordinates $x^{\mu }$ on M are combined with the tangent vectors ${\dot{x}}^{\mu }=d{x}^{\mu }/ds$ on $TM$.

The present script focuses on the possible deformation of the affine connection, which can exclusively be expressed in the metric tensor and its derivatives. We have also discussed its symmetry property and evaluated the dependence of a normalized parallel transported vector on the spacelike four–acceleration. This observation manifests that the minimal length uncertainty and the deformation recipe are significant, especially at the energy scale in which $L^2{\ddot{x}}^2$ becomes finite.

We conclude that the correction of the affine connection is exclusively factorized in the coefficient $(1+2L^2{\ddot{x}}^2)/(1+L^2{\ddot{x}}^2)$, which combines minimal length uncertainty (GUP effect), geometric structural, noncommutative algebraic, and gravitational ingredients. On one hand, this means that the affine connection preserves all properties of its undeformed counterpart, such as torsion-freedom and metric compatibility. On the other hand, its geometric nature as connecting nearby tangent spaces on a smooth manifold is also preserved on discrete spaces. The deformation via additional curvature on higher–dimensional manifold likely reveals fine geometric structure, similar to radiation beam in classical and quantum mechanics.

Finally, we have studied how the deformed affine connection performs parallel transport of a tangent vector on Riemannian manifold.