A Novel Framework for Production Planning and Class-Based Storage Location Assignment: Multi-Criteria Classification Approach

1. Introduction

Warehouse administrators are interested in finding the most economical direction of order to be met to meet customer demands with the shortest cycle time when the order arrives. Therefore, for effective warehouse management, various criteria should be taken into consideration in terms of inventory management, storage/unloading/transport, transportation distance, usage area, delivery-waiting times, and minimizing the costs that may arise from them [1].

One of the main operations in the warehouse is order picking. Order picking operation is the process of preparing the order by picking related products from the shelf in the warehouse according to the order received from the customer and it is among the most important operations. Since thousands of order picking processes are carried out during the day, warehouse design and operation criteria must be determined from the very beginning to increase order picking performance and reduce costs. For these reasons, a large part of the studies on warehouse management includes the studies carried out in the field of order picking. Order picking process, respectively; includes the processes of determining the orders, picking the products, classifying the collected products according to the orders and sending them to the customer by packaging.

Warehouse administrators play a crucial role in optimizing the responsiveness of their systems through various controls such as capacity management in picking-classification operations and storage policies. The selection of an order picking method or policy is a strategic decision that significantly impacts warehouse design and operations compared to other decisions. Within warehouse operations management, storage location assignment emerges as a critical decision problem. This problem entails determining the optimal utilization of shelves by assigning storage locations based on specific criteria. The primary objectives of solving SLAP are to minimize transportation time or distance during the storage process and reduce required space. It is important to highlight the interplay between the storage location assignment rule and the routing approach since products need to be appropriately placed in storage locations prior to being picked for fulfilling customer orders. The storage location assignment process comprises a set of rules employed for allocating products to specific storage locations, thus establishing the framework for determining which pick activities will occur within the storage system [2].

The literature has revealed that the importance of SLAP and order picking policy selected in order picking systems. Class-based policy, which is one of these policies, has allowed for evaluations on the place of other policies, the method of creating classes based on various criteria and its suitability for real-life use. Many methods are used for class formation and allocation in warehouse storage systems where multiple criteria are important. One of these methods is the COI technique, which is widely used in the literature. In the COI technique, two criteria are taken into account, namely space and demand. The COI technique is especially used in warehouses where the space usage is not identical and the rack columns are parallel to the input-output point. However, this situation changes in warehouses where different criteria are taken into account as well as criteria such as space, size, cost, weight and demand. These criteria can conflict with each other and the selection of the best products becomes a difficult problem. In this case, SLAP is considered a Multi-Criteria Decision Making (MCDM) problem [3].

In this study, a mixed-integer nonlinear mathematical model is proposed for the integrated production planning and multi-criteria SLAP. In this model, the TOPSIS class-based policy is used. To create a class according to multiple criteria, the ideal distance values of each product have been calculated with the TOPSIS method. These values have been added to the proposed model as priority constraints. In order to test the effectiveness of the model, a solution has been made using randomly generated data sets. In addition, a decision support system flow has been proposed that takes into account the single criterion, multiple criteria and COI index criteria of the developed model and provides its integration with different order picking policies. Detailed literature research; It has been revealed that the proposed mathematical model and decision support system flow have the feature of applying an existing field of science to a new problem.

2. Lıterature Research

The existing literature encompasses a wide range of studies examining warehousing, order picking, warehouse operations, and storage location assignment. These studies emphasize the significance of optimizing various performance measures within real-world industrial contexts. As the field of warehouse management continually evolves and novel technologies are introduced, there is a growing demand for research that addresses the distinct challenges and opportunities presented in this domain. One specific area of focus is SLAP, which has attracted considerable attention in recent research efforts aimed at optimizing factors such as travel time and space cost [4].

Different storage location assignment policies can be implemented in an order picking system. Turner [5] defines seven storage location assignment policies: Class-based, turnover-based, volume-based, dedicated, random, shared storage, and duration of stay policy. Class-based policy, which is one of these policies, has allowed for evaluations on the place of other policies, the method of creating classes based on various criteria and its suitability for real-life use. In this study, the literature review was conducted under two headings: Studies on class-based storage location assignment and studies on storage location assignment using the MCDM method.

2.1. Studies on Class-Based Storage Location Assignment

Hausman et al. [6] conducted a study focusing on pallet assignment in a warehouse with the objective of minimizing crane transportation time in automatic storage systems. Their research demonstrated the superiority of the class-based storage location assignment policy over percentage-based and random storage policies. Berg [7] addressed the problem of class-based storage location assignment in single command storage and unloading systems. He proposed an efficient dynamic programming algorithm to minimize the average single command cycle time by optimizing class assignment. Le-Duc and De Koster [8] proposed a class-based probabilistic model to estimate the average transport distance of a picking tour. Muppani and Adil [9] employed the COI technique to form product classes for storage location assignment and presented a nonlinear integer programming model that considered transportation costs, storage activities, and space utilization. Li et al. [10] developed a multi-objective mathematical model for SLAP, incorporating order frequency and shelf balance in their classification strategy. Meghelli and Sari [11] proposed a demand-based class-based storage location assignment method for warehouse layout design. Kovacs [4] developed a mathematical mixed-integer programming model for class-based storage location assignment in a warehouse with planned routes, multiple routes, and a multi-command milk-run system. Ene and Öztürk [12] aimed to optimize storage location assignment and order picking system design using stochastic optimization and mathematical modeling techniques. They proposed a class-based integer linear programming model to minimize transport distance. Yang and Nguyen [13] introduced a novel approach based on constrained clustering. Their method takes into account the specific constraints and requirements of the stuck operation. By considering these factors, the proposed approach offers a tailored solution for effectively grouping stuck items in a class-based warehouse. Deng et al. [14] studied the performance of shuttle-based compact storage systems under different storage policies. They used a probability and queueing-based approach to analyze the systems and found that a class-based storage policy with a steep ABC curve and skewed demand rate distribution provided the best performance.

2.2. Studies on Integrated Storage Location Assignment and Production Planning (or Inventory Model)

Wilson’s [15] pioneering academic study integrated the optimization of reorder points and storage location assignment in a mathematical model. The objective was to minimize order picking costs and inventory costs by considering various cost factors such as production, inventory, setup, and transportation costs. Daellenbach [16] focused specifically on SLAP and incorporated inventory planning and renewal policies into the analysis. Hodgson and Lowe [17] addressed the challenge of integrated product assignment and reorder point determination. Malmborg and Deutsch [18] formulated a cost model that captured the relationship between inventory costs and order picking costs, taking transportation costs into account as well. Their contributions advanced the understanding and optimization of storage systems. Malmborg [19] developed a successful model for evaluating alternative storage location assignment policies based on order picking costs, considering total space allocation and storage location. Kültürel et al. [20] combined SLAP with the continuous review inventory control model (Q, r). Hassini [21] focused on storage assignment and renewal times, particularly in situations where the number of products is lower than the number of available storage areas. Zhang et al. [22] proposed an integrated strategy that merged SLAP with the capacitated lot size problem commonly found in the literature. They developed a mixed-integer linear programming model to minimize the overall cost of production and warehouse operations by considering the multi-product capacitated lot size problem and the dynamic SLAP. The study conducted by Yerlikaya and Arıkan [23], the problem of class-based storage location assignment and production planning was addressed using a Mixed Integer Nonlinear Program (MINLP) formulation to obtain the optimal solution. The results of the study demonstrate that the proposed model outperforms the existing solutions in the literature, leading to cost reduction, location savings, and improvements.

2.3. Studies On Storage Location Assignment Using the Multi-Criteria Decision Making Method

MCDM methods have proven to be effective and valuable in addressing the complexities of storage systems that involve conflicting criteria. Fontana and Calvante [24] utilized the ELECTRE TRI method to evaluate and rank products based on stock strategies and product characteristics in warehouses. Their aim was to assign products to suitable storage locations using a class-based policy, considering the preferences of the decision maker. Similarly, Fontana and Cavalcante [1] employed the PROMETHEE method to solve the SLAP (Storage Location Assignment Problem) based on a class-based policy and decision maker’s preferences. In a different approach, Da Silva et al. [25] proposed the SMARTER & lexicographic method as an alternative to COI for product sorting in dedicated policies. Fontana and Nepomuceno [26] developed a multi-criteria decision model specifically designed for classifying products in high-level storage systems, such as multi-layer warehouses. Their model aimed to address the SLAP by considering various criteria. To deal with uncertainty, Micale et al. [27] proposed a combined approach using the ELECTRE TRI and TOPSIS methods. They utilized the ELECTRE TRI method to assign Stock Keeping Units (SKUs) to rack levels, and then applied the TOPSIS method to identify specific storage locations within each level for placing the SKUs. The study conducted by Yerlikaya [28] proposes the utilization of the fuzzy PROMETHEE (F-PROMETHEE) method for ranking products and assigning them to the most suitable storage locations in warehouse systems with uncertain demands. This approach allowed for more robust decision-making in the face of uncertainty. These studies highlight the versatility and applicability of MCDM methods in addressing the complexities of storage location assignment problems, offering insights into different methodologies and approaches to optimize storage systems.

In the literature, there are very few studies that deal with SLAP using MCDM methods. However, these studies did not take production planning into account and made product assignment according to the MCDM method, which they discussed directly, without using a mathematical model. In this study, an integrated mathematical model is proposed, which includes the assignment of products to storage areas and production planning, using the class based policy-creating class with TOPSIS method for storage systems where multiple criteria are important.

2.4. Contribution of the Proposed Model

When the literature studies on storage location assignment problems are examined, the methods used for problem solving are typically; order quantity, order frequency and the relationship between demands. In these studies, it was aimed to minimize 5 basic criteria, namely space, distance, picking time, order picking effort and the costs arising from these, while locationing the products in the storage. In this study, products have been evaluated by considering multiple criteria and have been used in the proposed model as a priority constraint for classification. TOPSIS method, one of the MCDM methods that allows the products to be evaluated according to multiple criteria, has been used. The second important point about the proposed product assignment approach is to propose a decision support system flow that will guide the decision maker, as well as approaches that consider one or two criteria such as cost, demand, space, cycle rate, COI, which are frequently used in the literature for class formation.

The most critical point about the proposed approach is; in real systems, there will be many benefits that will increase the efficiency of the system in terms of assigning products to warehouse areas, taking into account multiple criteria according to their differing characteristics, in terms of order picking and efficient use of warehouse space. Therefore, the class-based policy used in the proposed model differs from other policies in that it aims to classify products by considering multiple criteria and assign these classes to warehouse locations.

3. Problem Definition and Formulation

The primary challenge in practical storage systems arises when the available space in the warehouse proves insufficient during the transfer of products from the production area. The problem at hand revolves around the layout, handling, storage, and production processes within the warehouse. In this scenario, products produced in the production area undergo classification, placement in suitable storage locations, and subsequent transportation to the assigned delivery point for customer orders. The objective is to assign product classes to the most appropriate storage locations, thereby minimizing costs associated with transportation, storage, production, inventory, and setup. The product flow process within the warehouse can be outlined as follows:

• Manufactured products originate from the production area.
• These products are gathered from the production area and conveyed to automatic pallets, where they are placed.
• Forklift trucks are utilized to collect the products from these pallets and assign them to their respective storage locations.
• Subsequently, forklift trucks transport the products from these locations to the I/O point.

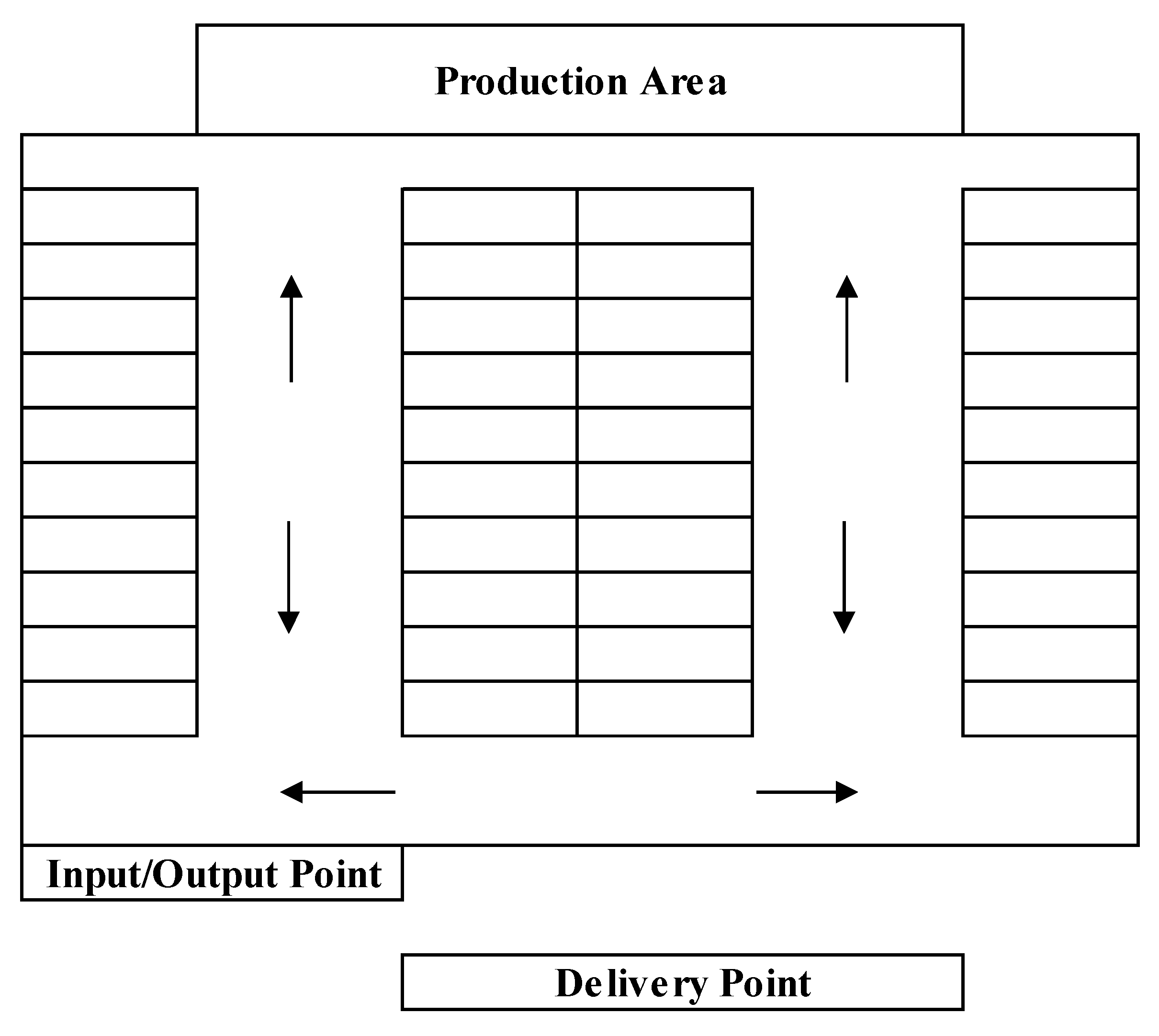
A sample warehouse layout for the problem is given in Figure 1. The warehouse system discussed in the sample consists of the production area, delivery point to the customer, pallet racks, and an output-input door (I/O).

The costs related to the transportation of products from the production area to the storage locations and from the storage locations to the I/O point were determined according to the operator movement. The cost of moving to two different points in warehouses with a single I/O point is not the same due to the difference in distance.

The problem is based on the following assumptions:

• A class-based storage location assignment policy is employed.
• All products are transported and stored on pallets.
• Pallets vary in size and weight, but their impact on transportation costs is disregarded.
• A specific number of storage locations are utilized.
• Products are moved from the production area to storage locations and from storage locations to the delivery point using a forklift with single command capability.
• The system includes an input/output (I/O) point and a production area where products originate.
• Costs associated with placing and retrieving products are directly proportional to the distance traveled.
• Demand is known, and stockouts are not permitted.
• Each product has a defined shelf life, and expired products are transported from storage locations to the I/O point.
• Setup costs are determined by the time required for manufacturing a product within the production area.

In the domain of storage location assignment, various methods are employed for class formation and allocation in systems where multiple criteria are crucial. One of the widely adopted techniques in the literature is the COI technique. In the COI technique, two criteria are taken into account, namely space and demand. However, this situation changes in storage systems where different criteria are taken into account as well as criteria such as space, cost and demand. For example, when a product’s shelf life is over, it is collected regardless of whether there is demand or not. Therefore, such products can be collected not only when there is demand, but also in different situations. In this study, a nonlinear mathematical model has been developed for the integrated production planning and multi-criteria SLAP, and the TOPSIS method, which allows the evaluation and classification of products according to multiple criteria has been preferred. The reason why TOPSIS method is preferred is that products (alternatives) cannot be substituted for each other in the warehouse system of the proposed model. In other words, alternative products are not close to each other and the criteria taken into account are different. TOPSIS ideal distance values have been a constraint input to the mathematical model.

The application steps of the proposed mathematical model are as follows:

• Determining the criteria for the products to be classified (If the criteria are space and demand, the COI index is used),
• Creation of the decision matrix,
• Weighting the criteria,
• Determining the ideal distance values for each product with the TOPSIS method,
• Adding the ideal distance values to the proposed base model as a class formation priority constraint,
• Solution of the mathematical model.

3.1. Decision Support System Flow

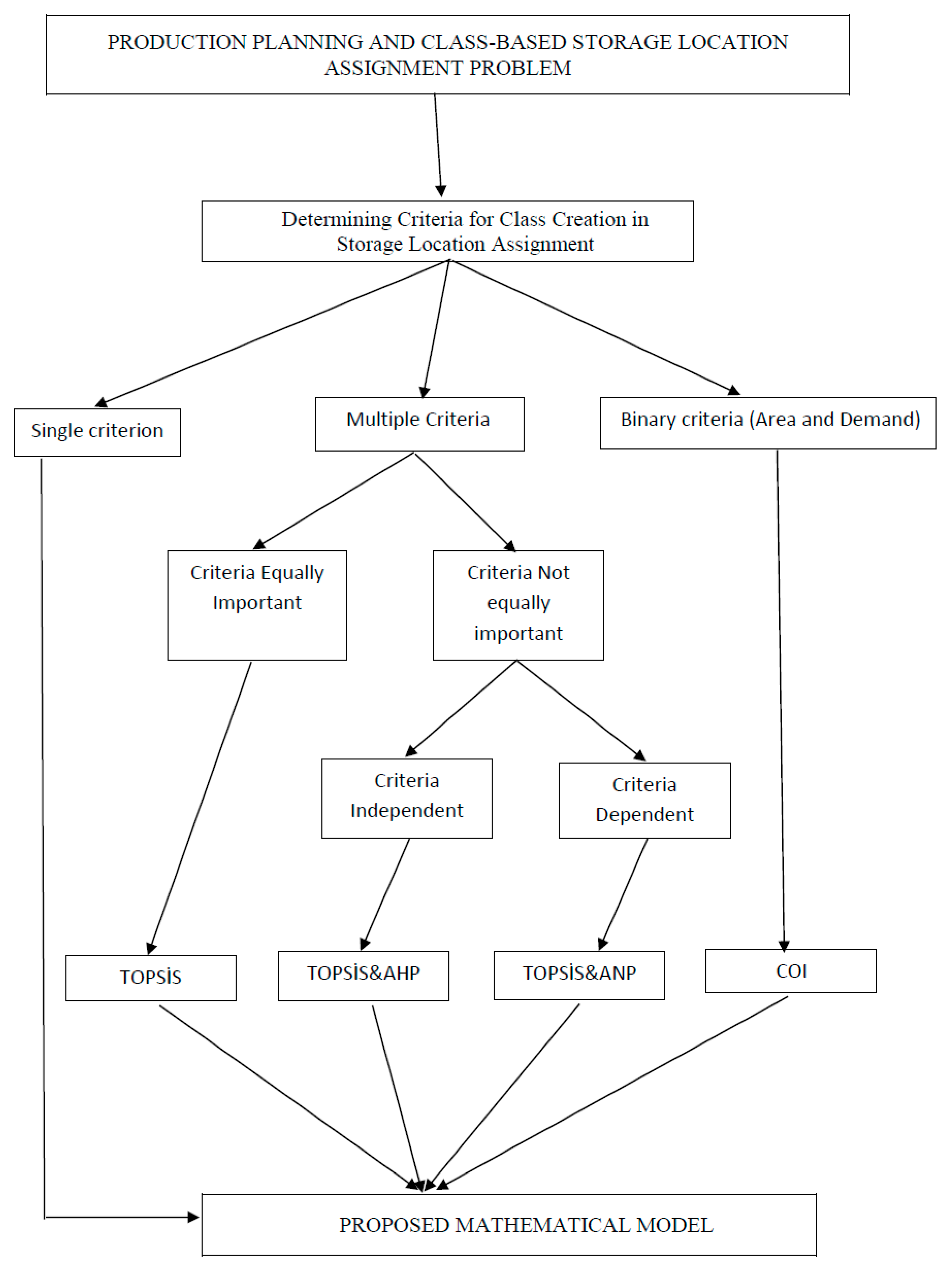
In the proposed model, there are different types of class formation methods according to the repository structure. Therefore, a decision support system flow that guides the decision maker in storage systems where one (Demand or space) or two criteria (COI) as well as multiple criteria (TOPSIS), is important to create a class is given in Figure 2.

In the decision support system flow, if the creation of the product class depends on a single criterion, the basic mathematical model that does not contain any prioritization constraints is solved and the products are classified according to the assignments that minimize the order picking cost. The only criterion here is the cost defined by the objective function. If the creation of the product class depends on more than one criterion, the ideal distance values are determined for each product with the TOPSIS method, these ideal distance values are added to the basic mathematical model as a class formation priority constraint and solved as a new variation of the proposed basic mathematical model with priority constraints added. In the mathematical model adapted for the case that considers multiple criteria in the creation of product classes, if the criteria are not equally important, the criteria weights are; It is determined with the help of ANP method according to the dependency status of AHP or criteria. Obtained criterion weights are used as input to the TOPSIS method. The most frequently used COI in the literature for creating product classes, by definition, takes into account two criteria, space and demand, and is more preferred in warehouse systems where space usage is critical. In cases where COI is preferred for the creation of the product class in accordance with the needs of the system of interest, the COI value can be determined for each product, and these values can be added to the mathematical model as a class formation priority constraint and solved as a variation of the proposed mathematical model for the case that considers multiple criteria in the creation of product classes.

3.2. TOPSIS Method

For storage assignment, many methods are used for class formation and allocation in storage systems where multiple criteria are important. One of these methods is the most widely used COI technique. The COI technique is especially used in warehouses where the space usage is not identical and the rack columns are parallel to the entry-exit point. However, this situation changes in storage systems where different criteria are taken into account as well as criteria such as space, cost and demand. In this study, the TOPSIS method, which allows the evaluation and classification of products according to multiple criteria, and which has not been used for storage assignment in the literature before, was preferred. The ideal distance values obtained as a result of the TOPSIS method solution are included in the proposed mathematical model as class formation and allocation constraints.

The TOPSIS method solution process consists of 6 steps [29]:

1)

Formulating the Decision Matrix (A_ij): The decision matrix consists of alternatives represented in the rows and the decisive criteria for decision-making represented in the columns.

$$A_{ij}=\left[\begin{array}{cccc}{a}_{11}& a_{12}& \mathrm{...}& a_{1n}\\ a_{21}& a_{22}& \mathrm{...}& a_{2n}\\ .& & & .\\ .& & & .\\ .& & & .\\ a_{m1}& a_{m2}& \mathrm{...}& a_{mn}\end{array}\right]$$

(1)

2)

Constructing the Normalized Decision Matrix (R_ij): The normalized decision matrix is obtained by normalizing the values in the decision matrix.

$$r_{ij}=\frac{a_{ij}}{\sqrt{{\displaystyle \sum _{k=1}^m{a}_{kj}^2}}}$$

(2)

3)

Determining the Weighted Normalized Decision Matrix (v_ij): Each element of the normalized decision matrix is multiplied by the corresponding weight value (w_i) assigned to the criterion, resulting in a weighted normalized decision matrix. In this study, equal weights are assigned to all criteria.

4)

Establishing the Positive Ideal Solution (V⁺) and Negative Ideal Solution (V^-): TOPSIS methodology aims to identify the alternatives that are closest to the positive ideal solution and furthest from the negative ideal solution using Euclidean distance. By calculating the relative proximity of each alternative, the positive ideal and negative ideal solutions are determined.

$$V^{+}=\left\{\underset{i}{(\max }{v}_{ij}|j\in J),(\underset{i}{\min }{v}_{ij}|j\in J^{\text{'}}\right\}$$

(3)

5)

Computing Discrimination Measures: The TOPSIS method employs dimensional Euclidean measurement to quantify the deviations of each alternative’s criterion values from the positive ideal (S_i⁺) and negative ideal (S_i^-) solution sets, thereby determining their discrimination measures.

$$S_i^{+}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{+})}^2}}$$

(4)

$$S_i^{-}=\sqrt{{\displaystyle \sum _{j=1}^n{(v_{ij}-v_j^{-})}^2}}$$

(5)

6)

Calculation of Relative Proximity to Ideal Solution (C_i^*): The relative proximity (C_i^*) of each alternative to the ideal solution is determined by evaluating the separation measures between the positive ideal and negative ideal solutions. C_i^* represents the ratio of the discrimination measure related to the negative ideal solution to the total discrimination measure. The value of C_i^* ranges from 0 to 1, where C_i^*= 1 indicates the alternative’s absolute proximity to the positive ideal solution, while C_i^* = 0 implies its proximity to the negative ideal solution. This section exhibits similarities to existing literature and can be revised accordingly.

$$C_i^{*}=\frac{S_i^{-}}{S_i^{-}+S_i^{+}}$$

(6)

3.3. Notations

The proposed model encompasses various parameters including the number of storage locations, products, forecasted demand, planning horizon, and costs associated with production, travel, storage, setup, and reservation. The notations used in the model are defined as follows:

• Indices:

i: Index representing a specific product (i = 1, 2, ..., N)

c: Index representing a class (c = 1, 2, ..., C = N)

t: Index representing a period within the planning horizon (t = 1, 2, ..., T)

l: Index representing a storage location (l = 1, 2, ..., L)

• Variables:

x_it : Quantity of product i produced during period t.

s_it : Inventory level for product i at the end of period t.

y_it : Binary variable (1 if product i is produced during period t, 0 otherwise).

q_ic : Binary variable (1 if product i is assigned to class c, 0 otherwise).

z_lc : Binary variable (1 if class c is assigned to location l for the planning horizon, 0 otherwise).

• Parameters:

Z: Objective value in terms of currency ($)

P_l: Unit cost of moving a column of any product from the production area to storage location l

O_l: Unit cost of moving a column of any product from storage location l to the output point

R_l: Unit cost of reserving storage location l

h_it: Unit inventory cost for product i in period t

c_it: Unit production cost for product i in period t

u_it: Unit setup cost for product i in period t

d_it: Demand quantity for product i in period t

v_it: Capacity for product i in period t

f_t: Key resource constraint on production (Production area setup time capacity)

M: A large scalar value representing an important limiting factor in production

C_i^*: TOPSIS value (Relative Proximity to Ideal Solution)

3.4. Model

The proposed integrated problem is formulated as a mixed-integer nonlinear programming (MINLP) model, which aims to minimize the objective function and optimize the decision variables. By incorporating both integer and nonlinear components, the MINLP model provides a comprehensive framework for addressing the complex nature of the problem at hand.

Objective function:

$$\begin{array}{l}{Z}_{\min }={\displaystyle \sum _c{\displaystyle \sum _l{R}_l.z_{lc}}}+{\displaystyle \sum _c{\displaystyle \sum _t(\{\frac{{\displaystyle \sum _l{P}_l.z_{lc}}}{{\displaystyle \sum _l{z}_{lc}}}\}.{\displaystyle \sum _i{x}_{it}.q_{ic})}}}+{\displaystyle \sum _c{\displaystyle \sum _t(\{\frac{{\displaystyle \sum _l{O}_l.z_{lc}}}{{\displaystyle \sum _l{z}_{lc}}}\}.{\displaystyle \sum _i{d}_{it}.q_{ic})}}}+\\ {\displaystyle \sum _i{\displaystyle \sum _t(c_{it}.x_{it}+u_{it}.}}{y}_{it}+h_{it}.s_{it})\end{array}$$

(7)

Constraints:

$${\displaystyle \sum _c{z}_{lc}}\le 1\forall l,$$

(8)

$${\displaystyle \sum _c{q}_{ic}}=1$$

(9)

$$d_{it}\le x_{it}+s_{it-1}\forall it,$$

(10)

$$s_{it}=x_{it}-d_{it}+s_{it-1}\forall it,$$

(11)

$${\displaystyle \sum _i(x_{it}}+s_{it-1}).q_{ic}\le {\displaystyle \sum _l{z}_{lc}}\forall ct,$$

(12)

$$x_{it}\le y_{it}.M\forall it,$$

(13)

$${\displaystyle \sum _i^{}{x}_{it}.v_{it}}\le f_t\forall t,$$

(14)

$$C_i^{*}.q_{ic}\ge C_{i\text{'}}^{*}.q_{i\text{'}c\text{'}}\forall p\ne p\text{'},\forall c<c\text{'}$$

(15)

$$\frac{{\displaystyle \sum _l(P_l+O_l).z_{lc}}}{{\displaystyle \sum _l{z}_{lc}}}\le \frac{{\displaystyle \sum _{l^{ı}}(P_{l\text{'}}+O_{l\text{'}}).z_{l\text{'}c\text{'}}}}{{\displaystyle \sum _{l^{ı}}{z}_{l\text{'}c\text{'}}}}\forall l\ne l\text{'}\mathrm{ve}\forall c<c\text{'},$$

(16)

$$z_{lc}\in \{0,1\}\forall lc,$$

(17)

$$q_{ic}\in \{0,1\}\forall ic,$$

(18)

$$x_{it}\ge 0\forall it,$$

(19)

$$s_{it}\ge 0\forall it,$$

(20)

$$y_{it}\ge 0\forall it,$$

(21)

The objective function (7) of the proposed MINLP model encompasses four cost terms, including the cost of reserving locations for product classes, travel costs from the production area to storage locations, transportation costs from storage locations to the I/O, and production planning costs. The objective is to assign product classes to optimal locations and optimize production planning to minimize the total cost. Constraint (8) ensures that each location is assigned to at most one class, while constraint (9) ensures that each product is assigned to a single class. Classes are determined based on production and demand flow to minimize space and transportation costs. Constraint (10) guarantees that the sum of production quantities and inventory levels meets the demand for each product. Constraint (11) represents the inventory balance, and constraint (12) restricts the sum of production quantities and inventory levels for products assigned to a class to be within the reserved locations for that class. Constraint (13) accounts for the setup constraint, limiting production during each period. The fixed number ‘M’ in constraint (14) represents the production capacity restriction. Constraints (15)–(16) prioritize the assignment of products with high TOPSIS values to class ‘c’ and those with low TOPSIS values to class ‘c’, considering lower-cost locations for class ‘c’. Constraints (17)–(18) are binary integer and variable constraints, while constraints (19)–(21) enforce positive variable constraints.

4. Solution Approach

In this section, a solution was presented using GAMS/BARON optimization software to test the validity and solvability of the proposed mathematical model. First of all, the ideal distance values of each product were obtained with the TOPSIS method for the classification of products according to multiple criteria and they were utilized as a set of a constraints’ input in the proposed mathematical model. The TOPSIS method solution was obtained by the Microsoft Excel program. For the mathematical model solution, a random data set (10-product, 3-period, 30-location) produced by the Microsoft Excel program were used.

4.1. Prioritizing Products with TOPSIS Method

The proposed model is for the warehouse of a food company producing dry food, and 4 criteria have been determined for this. These criteria for ranking the products are equally important and are as follows:

• COI: The COI method, introduced by Hesket [30], is utilized to determine the ratio between the maximum space required per SKU and the order frequency for product positioning or class formation (Equation (22)). In this equation, D_i represents the total demand for product i during period t, f_i denotes the space required to stock product i, and I^t_i represents the stock level of product i in period t.

$$CO{I}_i=\frac{f_i*\left[Maks{I}^t{}_i\right]}{D_i}$$

(22)

• Weight (kg): It is the weight of the product.
• Shelf life (year): It is the period during which a product can be stored before the product becomes suitable for consumption or sale, or the period during which a product with a certain expiry date can remain on sale.

The 10-item decision matrix created according to these data is given in Table 1. After applying the TOPSIS method process steps to this decision matrix, the ideal distance values (Ci*) values for each product were formed in Table 2. According to these values, the products that should be positioned closest to the entry-exit point are respectively; they are product3 and product5. Ideal distance values for each product have been a constraint input to the integrated production planning and product assignment model that creates a class according to multiple criteria.

4.2. Solution of the Mathematical Model

The parameters of the sample problem, which involves 10 products, 3 periods, and 30 locations, are summarized in Table 3. Optimal results were obtained for the mathematical model using GAMS/BARON optimization software. The solutions determine the production quantities for each product, the number of production setups based on different batch sizes, the assignment of products to suitable locations based on demand and classification, and the retrieval of products from locations categorized by classes within specific time intervals.

Table 4 illustrates the production quantities of different products for the months of January, February, and March. Each product exhibits variable production quantities. For instance, Product 1 had a production of 3 units in January, 2 units in February, and 2 units in March. The production quantities for other products were determined similarly. Table 5 demonstrates the allocation of products to different classes. Each product is assigned to a specific class. For example, Product 1 belongs to Class 2, Product 2 belongs to Class 2, Product 3 belongs to Class 1, and Product 4 belongs to Class 4. The class assignments for other products are also indicated in the table. Table 6 displays the arrangement of storage locations according to different classes. Each class is associated with specific locations. For instance, Class 1 products are stored in Location 3, Location 9, and Location 20. The location assignments for other classes are provided in the table. Table 7 presents the numerical results obtained from the optimization of the sample problem. The “Object Value” column represents the value of the optimized objective function, which reflects the problem’s objective. The “GAP (%)” column indicates the percentage deviation of the optimized value from the target value. The “Time (s)” column denotes the time taken to find the solution.

Based on the conducted analysis, it can be concluded that the sample problem was successfully optimized under the given constraints, yielding the best solution. This solution demonstrates the optimal determination of production quantities, class assignments, and storage locations based on the provided tables.

5. Conclusions

In this study, the focus was on integrating the classification of multi-criteria storage systems using the TOPSIS method into a mathematical model and considering class-based production planning. The results of this approach demonstrate the optimization of class-based production planning and product positioning. The utilization of the mathematical model aims to increase warehouse efficiency and reduce costs. This study highlights the importance of integrating classifications using the TOPSIS method into the model instead of COI for food companies and provides a foundation that can guide the solution of similar problems. Additionally, a decision support system flow was proposed to support the use of the suggested mathematical model. The decision support system flow considers different methods of class creation depending on the warehouse structure and the importance of multiple criteria, providing guidance to decision-makers and generating solutions. The findings of this study demonstrate that the suggested mathematical model and decision support system flow are effective strategies for using the TOPSIS method instead of COI in multi-criteria storage systems. The application of this approach enhances warehouse efficiency, reduces costs, and enables more effective class-based production planning.

In conclusion, this study recommends that food companies integrate the classification of multi-criteria storage systems using the TOPSIS method into the mathematical model and consider class-based production planning. This approach provides a more optimized strategy for warehouse management and offers guidance for solving similar problems. In the future, the following studies can be carried out regarding the proposed method:

• Comparison of Classification Methods: Comparing the performance of different classification methods can be an important research area. The utilization of various multi-criteria approaches and analyzing their impact on warehouse efficiency, costs, and production planning can contribute to a more comprehensive decision-making process.
• Real-Time Application and Investigation of Dynamic Variables: Focusing on studies that incorporate real-time data and consider dynamic variables can be beneficial. Exploring how the mathematical model and decision support system flow can be adapted to dynamic conditions can lead to more realistic and applicable solutions.

These suggestions can provide valuable insights for advancing class-based production planning and multi-criteria warehouse systems to a higher level of optimization.