Decaying Turbulence as a Fractal Curve

Preprint

Article

Decaying Turbulence as a Fractal Curve

Altmetrics

Downloads

329

Views

Comments

Alexander Migdal^*

This version is not peer-reviewed

Submitted:

05 July 2023

Posted:

06 July 2023

You are already at the latest version

Alerts

Abstract

We develop a quantitative microscopic theory of decaying Turbulence by studying the dimensional reduction of the Navier-Stokes loop equation for the velocity circulation. We have found an infinite dimensional manifold of solutions of the Navier-Stokes loop equation\cite{M93, M23PR} for the Wilson loop in decaying Turbulence in arbitrary dimension $d >2$. This family of solutions corresponds to a fractal curve in complex space $\mathbb C^d$, described by an algebraic equation between consecutive positions plus a nonlinear periodicity condition. We derive the constrained SDE for the evolution of the fractal curve at a fixed moment of physical time as a function of an auxiliary stochastic time. We expect this stochastic process to cover our fixed manifold of the solutions of the decaying Turbulence. The energy density of the fluid decays as $\mathcal E_0/t$, where $\mathcal E_0$ is an initial dissipation rate. Presumably, we have found a new phase of extreme Turbulence yet to be observed in real or numerical experiments.

Keywords:

Subject: Computer Science and Mathematics - Analysis

1. Introduction

A while ago, we derived [1,3] a functional equation for the so-called loop average [4,5] or Wilson loop in Turbulence. The path to an exact solution by a dimensional reduction in this equation was proposed in the ’93 paper [1] but has just been explored.

At the time, we could not compare a theory with anything but crude measurements in physical and numerical experiments at modest Reynolds numbers. All these experiments agreed with the K41 scaling, so the exotic equation based on unjustified methods of quantum field theory was premature.

The specific prediction of the Loop equation, namely the Area law [1], could not be verified in DNS at the time with existing computer power.

The situation has changed over the last decades. No alternative microscopic theory based on the Navier-Stokes equation emerged, but our understanding of the strong turbulence phenomena grew significantly.

On the other hand, the loop equations technology in the gauge theory also advanced over the last decades. The correspondence between the loop space functionals and the original vector fields was better understood, and various solutions to the gauge loop equations were found.

In particular, the momentum loop equation was developed, similar to our momentum loop used below [6,7,8]. Recently, some numerical methods were found to solve loop equations beyond perturbation theory [9,10].

The loop dynamics was extended to quantum gravity, where it was used to study nonperturbative phenomena [11,12].

All these old and new developments made loop equations a major nonperturbative approach to gauge field theory.

So, it is time to revive the hibernating theory of the loop equations in Turbulence, where these equations are much simpler.

The latest DNS [13,14,15,16] with Reynolds numbers of tens of thousands revealed and quantified violations of the K41 scaling laws. These numerical experiments are in agreement with so-called multifractal scaling laws [17].

However, as we argued in [2,18], at those Reynolds numbers, the DNS cannot yet distinguish between pure scaling laws with anomalous dimension

ζ (n)

and some algebraic function of the logarithm of scale

ζ (n, log r)

modifying the K41 scaling.

Theoretically, we studied the loop equation in the confinement region (large circulation over large loop C), and we have justified the Area law, suggested back in ’93 on heuristic arguments [1].

This law says that the tails of velocity circulation PDF in the confinement region are functions of the minimal area inside this loop.

It was verified in DNS four years ago [13] which triggered the further development of the geometric theory of turbulence[2,14,15,16,18,19,20,21,22,23,24,25,26,27,28,29,30].

In particular, the Area law was justified for flat and quadratic minimal surfaces [22], and an exact scaling law in confinement region

Γ \propto \sqrt{A r e a}

was derived [21]. The area law was verified with better precision in [14].

It was later conjectured in [18] that the dominant field configurations in extreme Turbulence are so-called Kelvinons, which were shown to solve stationary Navier-Stokes equations assuming the sparse distribution of vorticity structures.

These topological solitons of the Euler theory are built around a vortex sheet bounded by a singular vortex line. This vortex line is locally equivalent to the cylindrical Burgers vortex [31], with infinitesimal thickness in the limit of a large Reynolds number.

As we argued in [2,18], the Kelvinon has an anomalous dissipation, surviving the strong turbulent limit. This dissipation is proportional to the square of constant circulation of the Burgers vortex times a line integral of the tangent component of the strain along the loop.

The Kelvinon minimizes the energy functional, with anomalous terms coming from the Burgers core of the vortex line. There is also a constant scale factor Z in the representation of the Kelvinon vorticity in terms of spherical Clebsch variables:

\begin{matrix} \vec{ω} = \frac{1}{2} Z e_{a b c} S_{a} \vec{\nabla} S_{b} \times \vec{\nabla} S_{c} = \vec{\nabla} ϕ_{1} \times \vec{\nabla} ϕ_{2}; \end{matrix}

(1)

\begin{matrix} S_{1}^{2} + S_{2}^{2} + S_{3}^{2} = 1; \end{matrix}

(2)

\begin{matrix} ϕ_{2} = arg (S_{1} + ı S_{2}); ϕ_{1} = Z S_{3}; \end{matrix}

(3)

In that paper, the constant Z was related to the Kolmogorov energy dissipation density and the boundary value of the

S_{3}

variable at the loop C.

The anomalous Hamiltonian [2,18] explicitly violated the K41 scaling by the logarithmic terms

log Z / ν

in the region of small loops C. This region resembles the asymptotically free QCD. The logarithmic terms were summed up by RG equation with running coupling constant logarithmically small in this region.

These exciting developments explain and quantitatively describe many interesting phenomena [2] but do not provide a complete microscopic theory covering the full inertial range of Turbulence without simplifying assumptions of the sparsity of vortex structures.

Moreover, while the Kelvinon (presumably) solves the stationary Navier-Stokes equations, it does not solve the loop equations for the following reason.

The loop equation assumes that the velocity field is independent of the loop C. In this case, the circulation

\oint_{C} v_{α} d r_{α}

variations in the loop functional by the shape C of the loop can be reduced to the Navier-Stokes equation.

Otherwise, the variation would also involve the variation of the velocity field

\oint_{C} δ v_{α} d r_{α}

This problem does not invalidate the Kelvinon theory as an ideal gas of random vortex rings sparsely distributed in a turbulent flow.

The loop functional is not needed for that statistical theory, and the stationary solution of the Navier-Stokes equation is sufficient. The shape of the loop and the vortex sheet inside would become random variables influenced by a background strain like in the pure vortex sheet solutions [2].

These objections, however, prevent the Kelvinon gas model from being a complete theory of strong isotropic Turbulence. This model is merely an approximation of the full theory.

In the present work, we develop the theory free of these assumptions by exactly solving the loop equations for decaying Turbulence.

2. Loop equation

2.1. Loop operators

We introduced the loop equation in Lecture Series at Cargese and Chernogolovka Summer Schools [1].

Here is a summary for the new generation.

We write the Navier-Stokes equation as follows

\begin{matrix} \partial_{t} v_{α} = ν \partial_{β} ω_{β α} - v_{β} ω_{β α} - \partial_{α} (p + \frac{v_{β}^{2}}{2}); \end{matrix}

(4)

\begin{matrix} \partial_{α} v_{α} = 0; \end{matrix}

(5)

The Wilson loop average for the Turbulence

\begin{matrix} Ψ [γ, C] = 〈exp (\frac{ı γ}{ν} \oint_{C} v_{α} d r_{α})〉 \end{matrix}

(6)

treated as a function of time and a functional of the periodic function

C : r_{α} = C_{α} (θ); θ \in (0, 2 π)

(not necessarily a single closed loop), satisfies the following functional equation

\begin{matrix} ı ν \partial_{t} Ψ = H_{C} Ψ; \end{matrix}

(7a)

\begin{matrix} H_{C} = H_{C}^{(1)} + H_{C}^{(2)} \end{matrix}

(7b)

\begin{matrix} H_{C}^{(1)} = ν γ \oint_{C} d r_{α} \partial_{β} {\hat{ω}}_{α β} (r); \end{matrix}

(7c)

\begin{matrix} H_{C}^{(2)} = γ \oint_{C} d r_{α} {\hat{ω}}_{α β} (r) {\hat{v}}_{β} (r); \end{matrix}

(7d)

\begin{matrix} {\hat{ω}}_{α β} \equiv - ı \frac{ν}{γ} \frac{δ}{δ σ_{α β}} \end{matrix}

(7e)

\begin{matrix} {\hat{v}}_{β} (r) = \frac{1}{\partial_{μ}^{2}} \partial_{α} {\hat{ω}}_{β α} (r) \end{matrix}

(7f)

We added a dimensionless factor

γ

in the exponential compared to some previous definitions as an extra parameter of the Wilson loop. Without loss of generality, we shall assume that

γ > 0

. The negative

γ

corresponds to a complex conjugation of the Wilson loop.

In Abelian gauge theory, this would be the continuous electric charge. In turbulence theory, the Fourier transform of the Wilson loop by

γ

would produce the PDF for velocity circulation.

The statistical averaging

〈\dots〉

corresponds to initial randomized data, to be specified later.

The area derivative

\frac{δ}{δ σ_{α β}}

is related to the variation of the functional when the little closed loop

δ C

is added

\begin{matrix} Σ_{α β} (δ C) \frac{δ F [C]}{δ σ_{α β} (r)} = F [C + δ C] - F [C]; \end{matrix}

(8)

\begin{matrix} Σ_{α β} (δ C) = \frac{1}{2} \oint_{δ C} r_{α} d r_{β} \end{matrix}

(9)

In the review, [1,2], we present the explicit limiting procedure needed to define these functional derivatives in terms of finite variations of the loop while keeping it closed.

All the operators

\partial_{μ}, {\hat{ω}}_{α β}, {\hat{v}}_{α}

are expressed in terms of the spike operator

D_{α} (θ, ϵ) = \int_{- ϵ}^{+ ϵ} d ξ (1 - \frac{| ξ |}{ϵ}) \frac{δ}{δ C_{α} (θ + ξ)}

(10)

The area derivative operator can be regularized as

\begin{matrix} Ω_{α β} (θ, ϵ) = - ı \frac{ν}{γ} \frac{δ}{δ C_{α}^{'} (θ)} \int_{- ϵ}^{ϵ} d ξ \frac{δ}{δ C_{β} (θ + ξ)} - {α \leftrightarrow β}; \end{matrix}

(11)

and velocity operator (with

δ, ϵ \to 0^{+}

)

V_{α} (θ, ϵ, δ) = \frac{1}{D_{μ}^{2} (θ, ϵ)} D_{β} (θ, ϵ) Ω_{β α} (θ, δ);

(12)

In addition to the loop equation, every valid loop functional

F [C]

must satisfy the Bianchi constraint [4,5]

\begin{matrix} \partial_{α} \frac{δ F [C]}{δ σ_{β γ} (r)} + cyclic = 0 \end{matrix}

(13)

In three dimensions, it follows from identity

\vec{\nabla} \cdot \vec{ω} = 0

; in general dimension

d > 3

, the dual vorticity

\tilde{ω}

is an antisymmetric tensor with

d - 2

components. The divergence of this tensor equals zero identically.

However, for the loop functional, this restriction is not an identity; it reflects that this functional is a function of a circulation of some vector field, averaged by some set of parameters.

This constraint was analyzed in [2] in the confinement region of large loops, where it was used to predict the Area law. The area derivative of the area of some smooth surface inside a large loop reduces to a local normal vector. The Bianchi constraint is equivalent to the Plateau equation for a minimal surface (mean external curvature equals zero).

In the Navier-Stokes equation, we did NOT add artificial random forces, choosing instead to randomize the initial data for the velocity field.

These ad hoc random forces would lead to the potential term [2] in the loop Hamiltonian

H_{C}

, breaking certain symmetries needed for the dimensional reduction we study below.

With random initial data instead of time-dependent delta-correlated random forcing, we no longer describe the steady state (i.e., statistical equilibrium) but decaying Turbulence, which is also an interesting process, manifesting the same critical phenomena.

The energy is pumped in at the initial moment

t = 0

and slowly dissipates over time, provided the viscosity is small enough, corresponding to the large Reynolds number we are studying.

2.2. Dimensional reduction

The crucial observation in [1] was that the right side of the Loop equation, without random forcing, dramatically simplifies in functional Fourier space. The dynamics of the loop field can be reproduced in an Ansatz

Ψ [γ, C] = 〈exp (\frac{ı γ}{ν} \oint d C_{α} (θ) P_{α} (θ))〉

(14)

The difference with the original definition of

Ψ [γ, C]

is that our new function

P_{α} (θ)

depends directly on

θ

rather then through the function

v_{α} (r)

taken at

r_{α} = C_{α} (θ)

This transformation is the dimensional reduction

d \Rightarrow 1

we mentioned above. From the point of view of the loop functional, there is no need to deal with field

v (r)

; one could take a shortcut.

The reduced dynamics must be equivalent to the Navier-Stokes dynamics of the original field. With the loop calculus developed above, we have all the necessary tools to build these reduced dynamics.

Let us stress an important point: the function

\vec{P} (θ, t)

is independent of the loop C. As we shall see later, it is a random variable with a universal distribution in functional space.

This independence removes our objection in the Introduction to the Kelvinon theory and any other Navier-Stokes stationary solutions with a singularity at fixed loop C in space.

The functional derivative, acting on the exponential in ((14)) could be replaced by the derivative

P^{'}

as follows

\frac{δ}{δ C_{α} (θ)} \leftrightarrow - \frac{ı γ}{ν} P_{α}^{'} (θ)

(15)

The equation for

P (θ)

as a function of

θ

and also a function of time, reads:

\partial_{t} P_{α} = (ν D_{β} - V_{β}) Ω_{β α}

(16)

where the operators

V, D, Ω

should be regarded as ordinary numbers, with the following definitions.

The spike derivative D in the above equation

\begin{matrix} D_{α} (θ, ϵ) = - \frac{ı γ}{ν} \int_{- 1}^{1} d μ s g n (μ) P_{α} (θ + ϵ μ) \end{matrix}

(17)

The vorticity (11) and velocity (12) also become singular functionals of the trajectory

P (θ)

The first observation about this equation is that the viscosity factor cancels after the substitution (17).

As we shall see, the viscosity enters initial data so that at any finite time t, the solution for P still depends on viscosity.

Another observation is that the spike derivative

D (θ, ϵ)

turns to the discontinuity

Δ P (θ) = P (θ^{+}) - P (θ^{-})

in the limit

ϵ \to 0^{+}

\begin{matrix} D (θ, 0^{+}) = - \frac{ı γ}{ν} Δ P (θ) \end{matrix}

(18)

The relation of the operators in the QCD loop equation to the discontinuities of the momentum loop was noticed, justified, and investigated in [7,8].

In the Navier-Stokes theory, this relation provides the key to the exact solution.

In the same way, we find the limit for vorticity

\begin{matrix} Ω_{α β} (θ, 0^{+}) = \frac{- ı γ}{ν} P_{α β} (θ); \end{matrix}

(19)

\begin{matrix} P_{α β} (θ) = Δ P_{α} (θ) P_{β} (θ) - {α \leftrightarrow β}; \end{matrix}

(20)

\begin{matrix} P_{α} (θ) \equiv \frac{P_{α} (θ^{+}) + P_{α} (θ^{-})}{2} \end{matrix}

(21)

and velocity (skipping the common argument

θ

)

\begin{matrix} V_{α} = \frac{Δ P_{β}}{Δ P_{μ}^{2}} P_{β α} = P_{α} - \frac{Δ P_{α} Δ P_{β} P_{β}}{Δ P^{2}} \end{matrix}

(22)

The Bianchi constraint is identically satisfied as it should

\begin{matrix} Δ P_{α} (Δ P_{β} P_{γ} - {β \leftrightarrow γ}) + cyclic = 0 \end{matrix}

(23)

We arrive at a singular loop equation for

P_{α} (θ)

\begin{matrix} \frac{ν}{γ} \partial_{t} \vec{P} = - γ^{2} {(Δ \vec{P})}^{2} \vec{P} + \\ Δ \vec{P} (γ^{2} \vec{P} \cdot Δ \vec{P} + ı γ (\frac{{(\vec{P} \cdot Δ \vec{P})}^{2}}{Δ {\vec{P}}^{2}} - {\vec{P}}^{2})); \end{matrix}

(24)

This equation is complex due to the irreversible dissipation effects in the Navier-Stokes equation.

The viscosity dropped from the right side of this equation; it can be absorbed in units of time. Viscosity also enters the initial data, as we shall see in the next Section on the example of the random rotation.

However, the large-time asymptotic behavior of the solution would be universal, as it should be in the Turbulent flow.

We are looking for a degenerate fixed point [2], a fixed manifold with some internal degrees of freedom. The spontaneous stochastization corresponds to random values of these hidden internal parameters.

Starting with different initial data, the trajectory

\vec{P} (θ, t)

would approach this fixed manifold at some arbitrary point and then keep moving around it, covering it with some probability measure.

The Turbulence problem is to find this manifold and determine this probability measure.

2.3. Random global rotation

Possible initial data for the reduced dynamics were suggested in the original papers [1,2]. The initial velocity field’s simplest meaningful distribution is the Gaussian one, with energy concentrated in the macroscopic motions. The corresponding loop field reads (we set

γ = 1

for simplicity in this section)

\begin{matrix} Ψ_{0} [C] = exp (- \frac{1}{2 ν^{2}} \int_{C} d \vec{C} (θ) \cdot d \vec{C} (θ^{'}) f (\vec{C} (θ) - \vec{C} (θ^{'}))) \end{matrix}

(25)

where

f (\vec{r})

is the velocity correlation function

〈v_{α} (r) v_{β} (r^{'})〉 = (δ_{α β} - \partial_{α} \partial_{β} \partial_{μ}^{- 2}) f (r - r^{'})

(26)

The potential part drops out in the closed loop integral.

The correlation function varies at the macroscopic scale, which means that we could expand it in the Taylor series

f (r - r^{'}) \to f_{0} - f_{1} {(r - r^{'})}^{2} + \dots

(27)

The first term

f_{0}

is proportional to initial energy density,

\frac{1}{2} 〈v_{α}^{2}〉 = \frac{d - 1}{2} f_{0}

(28)

and the second one is proportional to initial energy dissipation rate

E_{0}

f_{1} = \frac{E_{0}}{2 d (d - 1) ν}

(29)

where

d = 3

is the dimension of space.

The constant term in (27) as well as

r^{2} + r^{' 2}

terms drop from the closed loop integral, so we are left with the cross-term

r r^{'}

, which reduces to a full square

\begin{matrix} Ψ_{0} [C] \to exp (- \frac{f_{1}}{ν^{2}} {(\oint d C_{α} (θ) C_{β} (θ))}^{2}) \end{matrix}

(30)

This distribution is almost Gaussian: it reduces to Gaussian one by extra integration

\begin{matrix} Ψ_{0} [C] \to const \int (d ϕ) exp (- ϕ_{α β}^{2}) \\ exp (2 ı \frac{\sqrt{f_{1}}}{ν} ϕ_{μ ν} \oint d C_{μ} (θ) C_{ν} (θ)) \end{matrix}

(31)

The integration here involves all

\frac{d (d - 1)}{2} = 3

independent

α < β

components of the antisymmetric tensor

ϕ_{α β}

. Note that this is ordinary integration, not the functional one.

The physical meaning of this

ϕ

is the random uniform vorticity

\hat{ω} = \sqrt{f_{1}} \hat{ϕ}

at the initial moment.

However, as we see it now, this initial data represents a spurious fixed point unrelated to the turbulence problem.

It was discussed in our review paper [2]. The uniform global rotation represents a fixed point of the Navier-Stokes equation for arbitrary uniform vorticity tensor.

Gaussian integration by

ϕ

keeps it as a fixed point of the Loop equation.

The right side of the Navier-Stokes equation vanishes at this special initial data so that the exact solution of the loop equation with this initial data equals its initial value (30).

Naturally, the time derivative of the momentum loop with the corresponding initial data will vanish as well.

It is instructive to look at the momentum trajectory

P_{α} (θ)

for this fixed point.

The functional Fourier transform [1,2] leads to the following simple result for the initial values of

P_{α} (θ)

In terms of Fourier harmonics, this initial data read

\begin{matrix} P_{α} (θ) = \sum_{n = 1}^{\infty} P_{α, n} exp (ı n θ) + {\bar{P}}_{α, n} exp (- ı n θ); \end{matrix}

(32)

\begin{matrix} P_{α, n} = N (0, 1) \forall α, n > 0; \end{matrix}

(33)

\begin{matrix} {\bar{P}}_{α, n} = \frac{4 \sqrt{f_{1}}}{n ν} ϕ_{α β} P_{β, n}; \forall β, n > 0; \end{matrix}

(34)

\begin{matrix} ϕ_{α β} = - ϕ_{β α}; \end{matrix}

(35)

\begin{matrix} ϕ_{α β} = N (0, 1) \forall α < β; \end{matrix}

(36)

As for the constant part

P_{α, 0}

P_{α} (θ)

, it is not defined, but it drops from equations by translational invariance.

Note that this initial data is not real, as

{\bar{P}}_{α, n} \neq P_{α, n}^{★}

. Positive and negative harmonics are real but unequal, leading to a complex Fourier transform. At fixed tensor

ϕ

the correlations are

\begin{matrix} {〈P_{α, n} P_{β, m}〉}_{t = 0} = \frac{4 \sqrt{f_{1}}}{m ν} δ_{- n m} ϕ_{α β}; \end{matrix}

(37)

\begin{matrix} {〈P_{α} (θ) P_{β} (θ^{'})〉}_{t = 0} = 2 ı \frac{\sqrt{f_{1}}}{ν} ϕ_{α β} sign (θ^{'} - θ); \end{matrix}

(38)

This correlation function immediately leads to the uniform expectation value of the vorticity

〈P_{α} (θ) Δ P_{β} (θ)〉 = 4 ı \sqrt{f_{1}} ϕ_{α β}; \forall θ

(39)

The uniform constant vorticity kills the linear term of the Navier-Stokes equation in the original loop space, involving

\partial_{α} {\hat{Ω}}_{α β} = 0

The nonlinear term

{\hat{V}}_{α} {\hat{Ω}}_{α β}

vanishes in the coordinate loop space only after integration around the loop.

Here are the steps involved

\begin{matrix} {\hat{V}}_{β} = \frac{1}{2} {\hat{Ω}}_{α β} C_{β}; \end{matrix}

(40)

\begin{matrix} \oint {\hat{Ω}}_{α β} C_{β} {\hat{Ω}}_{β γ} d C_{α} \propto {\hat{Ω}}_{α β} {\hat{Ω}}_{β γ} Σ_{α β} (C); \end{matrix}

(41)

Here the tensor area

Σ

was defined in (). It is an antisymmetric tensor; therefore its trace with a symmetric tensor

{\hat{Ω}}_{α β} {\hat{Ω}}_{β γ}

vanishes.

This calculation demonstrates how an arbitrary uniform vorticity tensor satisfies the loop equation in coordinate loop space.

We expect the turbulent solution of the loop equation to be more general, with the local vorticity tensor at the loop becoming a random variable with some distribution for every point on the loop.

2.4. Decay or fixed point

The absolute value of loop average

Ψ [γ, C]

stays below 1 at any time, which leaves two possible scenarios for its behavior at a large time.

\begin{matrix} Decay : & \vec{P} \to 0; Ψ [γ, C] \to 1; \end{matrix}

(42)

\begin{matrix} Fixed Point : & \vec{P} \to {\vec{P}}_{\infty}; Ψ [γ, C] \to Ψ_{\infty} [C]; \end{matrix}

(43)

The Decay scenario in the nonlinear ODE (24) corresponds to the

1 / \sqrt{t}

decrease of

\vec{P}

Omitting the common argument

θ

, we get the following exact time-dependent solution (not just asymptotically, at

t \to + \infty

\begin{matrix} \vec{P} = \sqrt{\frac{ν}{2 (t + t_{0})}} \frac{\vec{F}}{γ}; \\ ({(Δ \vec{F})}^{2} - 1) \vec{F} = \end{matrix}

(44)

\begin{matrix} Δ \vec{F} (\vec{F} \cdot Δ \vec{F} + \frac{ı}{γ} (\frac{{(\vec{F} \cdot Δ \vec{F})}^{2}}{{(Δ \vec{F})}^{2}} - {\vec{F}}^{2})); \end{matrix}

(45)

The Fixed Point would correspond to the vanishing right side of the momentum loop equation (24). Multiplying by

{(Δ \vec{P})}^{2}

and reducing the terms, we find a singular algebraic equation

\begin{matrix} γ^{2} {(Δ \vec{P})}^{2} ({(Δ \vec{P})}^{2} \vec{P} - (\vec{P} \cdot Δ \vec{P}) Δ \vec{P}) = \\ ı γ Δ \vec{P} \cdot ({(\vec{P} \cdot Δ \vec{P})}^{2} - {\vec{P}}^{2} {(Δ \vec{P})}^{2}); \end{matrix}

(46)

The fixed point could mean self-sustained Turbulence, which would be too good to be true, violating the second law of Thermodynamics. Indeed, it is easy to see that this fixed point cannot exist.

The fixed point equation (46) is a linear relation between two vectors

\vec{P}, Δ \vec{P}

with coefficients depending on various scalar products. The generic solution is simply

\begin{matrix} Δ \vec{P} = λ \vec{P}; \end{matrix}

(47)

with the complex parameter

λ

to be determined from the equation (46).

This solution is degenerate: the fixed point equation is satisfied for arbitrary complex

λ

The discontinuity vector

Δ \vec{P}

aligned with the principal value

\vec{P}

corresponds to vanishing vorticity in (19), leading to a trivial solution of the loop equation

Ψ [γ, C] = 1

We are left with the decaying turbulence scenario () as the only remaining physical solution.

3. Fractal curve in complex space

3.1. Random walk

One may try the solution where the discontinuity vector is proportional to the principal value. However, in this case, such a solution does not exist.

\begin{matrix} Δ \vec{F} \overset{?}{=} λ \vec{F}; \end{matrix}

(48)

\begin{matrix} λ^{2} {\vec{F}}^{2} - 1 \overset{?}{=} λ^{2} {\vec{F}}^{2}; \end{matrix}

(49)

There is, however, another solution where the vectors

Δ \vec{F}, \vec{F}

are not aligned. This solution requires the following relations

\begin{matrix} {(Δ \vec{F})}^{2} = 1; \end{matrix}

(50a)

\begin{matrix} {(2 \vec{F} \cdot Δ \vec{F} - ı γ)}^{2} + γ^{2} = 4 {\vec{F}}^{2} \end{matrix}

(50b)

These relations are very interesting. The complex numbers reflect irreversibility and lack of alignment leads to vorticity distributed along the loop.

Also, note that this complex vector

\vec{F} (θ)

is dimensionless, and the fixed point equation (Section 3.1) is completely universal, up to a single dimensionless parameter

γ

One can build this solution as a Markov process by the following method. Start with a complex vector

\vec{F} (θ = 0) = {\vec{F}}_{0}

We compute the next values

{\vec{F}}_{k} = \vec{F} (\frac{2 π k}{N})

from the following discrete version of the discontinuity equations (Section 3.1).

\begin{matrix} {({\vec{F}}_{k + 1} - {\vec{F}}_{k})}^{2} = 1; \end{matrix}

(51a)

\begin{matrix} {({\vec{F}}_{k + 1}^{2} - {\vec{F}}_{k}^{2} - ı γ)}^{2} + γ^{2} = {({\vec{F}}_{k + 1} + {\vec{F}}_{k})}^{2} \end{matrix}

(51b)

3.2. Constraints imposed on a random step

A solution to these equations can be represented using a complex vector

{\vec{q}}_{k}

subject to two complex constraints

\begin{matrix} {\vec{q}}_{k}^{2} = 1; \end{matrix}

(52a)

\begin{matrix} {(2 {\vec{F}}_{k} \cdot {\vec{q}}_{k} - ı γ)}^{2} = 4 {\vec{F}}_{k}^{2} + γ (2 ı - γ) \end{matrix}

(52b)

after which we can find the next value

\begin{matrix} {\vec{F}}_{k + 1} = {\vec{F}}_{k} + {\vec{q}}_{k}; \end{matrix}

(53)

We assume N steps, each with the angle shift

Δ θ = \frac{2 π}{N}

This recurrent sequence is a Markov process because each step only depends on the current position

{\vec{F}}_{k}

. On top of this Markov process, there is a closure requirement

{\vec{F}}_{N} = {\vec{F}}_{0}

This requirement represents a nonlinear restriction on all the variables

{\vec{F}}_{k}

, which we discuss below.

With this discretization, the circulation can be expressed in terms of these steps

\begin{matrix} \oint \vec{F} (θ) \cdot d \vec{C} (θ) = - \oint \vec{C} (θ) \cdot d \vec{F} (θ) \Rightarrow - \sum_{k = 0}^{N - 1} \frac{{\vec{C}}_{k + 1} + {\vec{C}}_{k}}{2} \cdot {\vec{q}}_{k} \end{matrix}

(54)

Note that the complex unit vector is not defined with the Euclidean metric in six dimensions

〈\vec{A}, \vec{B}〉 = Re \vec{A} \cdot Re \vec{B} + Im \vec{A} \cdot Im \vec{B}

. Instead, we have a complex condition

\begin{matrix} {\vec{q}}^{2} = 1 \end{matrix}

(55)

which leads to two conditions between real and imaginary parts

\begin{matrix} {(Re \vec{q})}^{2} = 1 + {(Im \vec{q})}^{2}; \end{matrix}

(56)

\begin{matrix} Re \vec{q} \cdot Im \vec{q} = 0; \end{matrix}

(57)

In d dimensions, there are

d - 1

complex parameters of the unit vector; with an extra linear constraint in (52a), there are now

d - 2

free complex parameters at every step of our iteration, plus the discrete choice of the sign of the root in the solution of the quadratic equation.

3.3. Closure condition

At the last step,

k = N - 1

, we need to get a closed loop

{\vec{F}}_{N} = {\vec{F}}_{0}

. This is one more constraint on the complex vectors

{\vec{q}}_{0}, \dots {\vec{q}}_{N - 1}

\begin{matrix} \sum_{0}^{N - 1} {\vec{q}}_{k} = 0; \end{matrix}

(58)

We use this complex vector constraint to fix the arbitrary initial complex vector

{\vec{F}}_{0}

as a function of all remaining parameters.

Looking ahead into the rest of our investigation, it turns out that the closure conditions fix only half of the

2 d

real parameters in the initial point

{\vec{F}}_{0}

. The remaining parameters are free zero modes of our fixed manifold.

Due to the closure of the space loop

\vec{C} (θ)

, the global translation of the momentum loop

\vec{P} (θ)

leaves invariant the Wilson loop; therefore, the translational zero modes of the momentum loop do not lead to ambiguities.

However, the missing d out of

2 d

parameters in

{\vec{F}}_{0}

mean that some other d parameters should be adjusted to provide the momentum loop closure.

We discuss this issue in the next Section, where we derive the SDE for the closed momentum loop in three dimensions. This SDE has explicit terms, which we computed in Appendix B and coded in Mathematica^®in [32].

The adjustment of parameters we mentioned earlier yields three constraints on the Wiener process we derived.

3.4. Mirror pairs of solutions

Return to the general study of the discrete loop equations (Section 3.2).

There is a trivial solution to these equations at any even N

\begin{matrix} {\vec{f}}_{k} = \frac{{(- 1)}^{k} \vec{q}}{2}; \end{matrix}

(59)

\begin{matrix} {\vec{q}}^{2} = 1; \end{matrix}

(60)

We reject this solution as unphysical: the corresponding vorticity equals zero, as all the vectors

{\vec{f}}_{k}

are aligned.

Our set of equations has certain mirror reflection symmetry

\begin{matrix} {\vec{F}}_{k} \leftrightarrow {\vec{F}}_{N - k}^{*} \end{matrix}

(61)

Thus, the complex solutions come in mirror pairs

{\vec{F}}_{k}, {\vec{F}}_{N - k}^{*}

. The real solutions are only a particular case of the above trivial solution with real

\vec{q}

Each nontrivial solution represents a periodic random walk in complex vector space

C^{d}

. The complex unit step

{\vec{q}}_{k} \in C^{d}

depends on the current position

{\vec{F}}_{k} \in C^{d}

, or, equivalently, on the initial position

{\vec{F}}_{0}

plus the sum of the preceding steps.

We are interested in the limit of infinitely many steps

N \to \infty

, corresponding to a closed fractal curve with a discontinuity at every point.

3.5. The degenerate fixed point and its statistical meaning

This solution’s degeneracy (fewer restrictions than the number of free parameters) is a welcome feature. One would expect this from a fixed point of the Hopf equation for the probability distribution.

In the best-known example, the microcanonical Gibbs distribution covers the energy surface with a uniform measure (ergodic hypothesis, widely accepted in Physics).

The parameters describing a point on this energy surface are not specified– in the case of an ideal Maxwell gas, these are arbitrary velocities of particles.

Likewise, the fixed manifold, corresponding to our fractal curve, is parametrized by N arbitrary local rotations, as discussed in the next Section.

This rich internal random structure of our fixed manifold, combined with its rotation and translation invariance in loop space C, makes it an acceptable candidate for extreme isotropic Turbulence.

4. The structure of turbulent manifold

The simplest case where these equations have nontrivial solutions is the three-dimensional space. For smaller dimensions of space, there is only a degenerate solution with zero vorticity (a vanishing cross product

\hat{Ω} \propto \vec{P} \times Δ \vec{P}

). Thus, we only consider

d > 2

in the rest of the paper.

4.1. Canonical form of a single step

The complex unit vector in d dimensions can be parametrized by rotation matrix and a unit real vector in

d - 2

dimensions

\begin{matrix} \vec{q} = \hat{O} \cdot \vec{u} (α_{1}, α_{2}, \vec{w}, β); \end{matrix}

(62a)

\begin{matrix} \vec{u} (α_{1}, α_{2}, \vec{w}, β) = {α_{1}, α_{2} \vec{w}, ı β}; \end{matrix}

(62b)

\begin{matrix} {\vec{w}}^{2} = 1; \end{matrix}

(62c)

\begin{matrix} α_{1}^{2} + α_{2}^{2} = 1 + β^{2}; \end{matrix}

(62d)

The following steps lead to this canonical form. Take a general complex d-vector

\vec{q}

and choose the rotation

\hat{O} \in O (d)

to direct its imaginary part at the last axis d.

The imaginary part of the condition

{\vec{q}}^{2} = 1

implies the real part of this vector has zero component d. This real vector in

d - 1

dimensions can be parametrized as

{α_{1}, α_{2} \vec{w}}

with the unit vector

\vec{w} \in S_{d - 3}

and arbitrary real parameters

α_{1}, α_{2}

There is a multiple counting of the same unit vector with this parametrization: the rotation matrix space

O (d)

must be factored by rotations

O (d - 3)

of the unit vector

\vec{w}

\begin{matrix} \hat{O} \in (^{O (d)} /_{O (d - 3)}) \end{matrix}

(63)

Also, the sign change of

α_{2}

is equivalent to the reflection of the vector

\vec{w}

, so we have to factor out such reflections and keep an arbitrary sign of

α_{2}

\begin{matrix} \vec{w} \in (^{S^{d - 3}} /_{Z^{2}}); \end{matrix}

(64)

\begin{matrix} {α_{1}, α_{2}} \in R_{2} \end{matrix}

(65)

The complex constraint for

{\vec{F}}_{k} \cdot {\vec{q}}_{k}

can be used to fix these

α_{1}, α_{2}

as a linear function of

β

given a complex vector

\begin{matrix} {\vec{f}}_{k} = {\hat{O}}_{k}^{T} \cdot {\vec{F}}_{k}; \end{matrix}

(66)

as follows:

\begin{matrix} {α_{1}, α_{2}} = {\hat{M}}^{- 1} . {Re (R) - β Im (c), β Re (c) + Im (R)}; \end{matrix}

(67)

\begin{matrix} R = \frac{1}{2} (ı γ \pm \sqrt{4 {\vec{f}}_{k}^{2} + γ (2 ı - γ)}) \end{matrix}

(68)

where

{\vec{f}}_{k} = {a, \vec{b}, c}

and

\hat{M} = (\begin{matrix} Re (a) & Re (\vec{b} \cdot \vec{w}) \\ Im (a) & Im (\vec{b} \cdot \vec{w}) \end{matrix})

(69)

After that,

α_{1}^{2} + α_{2}^{2} = 1 + β^{2}

yields a quadratic equation for

β

Note in passing that

\vec{u}

belongs to De Sitter space

d S_{d - 1}

. However, this is where an analogy with the ADS/CFT duality ends.

There are, in general, four solutions for

β

: two signs for R in () and two more signs in a solution of the quadratic equation for

β

(62a).

We have to choose a particular real solution for

β

. A universal option is to choose the step with the smallest Euclidean distance

{(Re \vec{q})}^{2} + {(Im \vec{q})}^{2}

. We used this choice in our initial simulations [32], but later we switched to another method, using the SDE we describe later in this work. The SDE guarantees the closure condition, unlike the naive random walk approach.

4.2. Partition function

We arrive at the invariant distribution for our fractal curve. At a fixed N, the partition function (in terms of statistical mechanics)

\begin{matrix} Z = \int d Ω_{d} (N) = \int \prod_{k = 0}^{N - 1} \frac{(d {\hat{O}}_{k}) (d {\vec{w}}_{k})}{2 |O (d - 3)|} \int d^{2 d} {\vec{F}}_{0} δ^{2 d} (\vec{Q}); \end{matrix}

(70a)

\begin{matrix} \vec{Q} = {\vec{F}}_{N} - {\vec{F}}_{0} = \sum_{k = 0}^{N - 1} {\vec{q}}_{k}; \end{matrix}

(70b)

\begin{matrix} {\vec{F}}_{k + 1} = {\vec{F}}_{k} + {\vec{q}}_{k}; \forall k = 0, \dots N - 1; \end{matrix}

(70c)

where

{\vec{q}}_{k}

are complex vectors, parametrized by

{\hat{O}}_{0}, \dots {\hat{O}}_{N - 1}, {\vec{w}}_{0}, \dots {\vec{w}}_{N - 1}

via recurrent equations (Section 4.1),(67).

The complex vector’s integration and delta function is understood as a product of its real and imaginary parts.

We conclude that the fixed manifold

T_{d} (N)

of the decaying Turbulence is a subset of the tensor product of rotational and spherical spaces.

\begin{matrix} T_{d} (N) \in {((^{O (d)} /_{O (d - 3)}) \otimes (^{S^{d - 3}} /_{Z^{2}}))}^{\otimes N} \end{matrix}

(71)

This subset is selected by imposing the closure condition

\sum_{k} {\vec{q}}_{k} = 0

, which in general provides

2 d

nonlinear relations between all parameters:

\vec{λ}, {\hat{O}}_{k}, {\vec{w}}_{k}

for each choice of the real solutions for

β

on each step.

This closure condition is sufficient by parameter count to eliminate a complex vector

{\vec{F}}_{0}

; however, we discovered in 3D that half of the parameters in complex vector

{\vec{F}}_{0}

are left undetermined, leading instead to three real constraints on the parameters of the rotation matrices.

We cannot resolve the global closure conditions. Still, we found a way to achieve the same goal by an SDE describing the evolution of our curve from the exact symmetric solution (72) we have found; this method preserves the closure condition at each infinitesimal step of the stochastic process.

4.3. Symmetric fixed point

The above formal definition of the probability measure does not offer a practical simulation method for covering this manifold.

We attempted to simulate a random walk

{\vec{F}}_{k} \Rightarrow {\vec{F}}_{k + 1}

step by step, taking random rotation matrices. Unfortunately, there was a rapidly diminishing probability of the return to the vicinity of the initial point

{\vec{F}}_{N} = {\vec{F}}_{0}

after N steps.

We could not numerically solve the resulting transcendental equation for the initial position

{\vec{F}}_{0}

at large N, neither by analytical nor by Monte Carlo methods.

Instead, we have found an alternative algorithm for covering this manifold, preserving the closed curve.

First, we have found a symmetric family of solutions [32] of our recurrent equation (Section 3.1) for arbitrary N

\begin{matrix} {\vec{Φ}}_{k} = \frac{1}{2} csc (\frac{β}{2}) \{cos (α_{k}), sin (α_{k}) \vec{w}, i cos (\frac{β}{2})\}; \end{matrix}

(72)

Here

\vec{w} \in S^{d - 3}

is a unit vector.

The angles

α_{k}

must satisfy recurrent relation

\begin{matrix} α_{k + 1} = α_{k} + σ_{k} β; \end{matrix}

(73)

\begin{matrix} α_{N} = α_{0} = 0; \end{matrix}

(74)

\begin{matrix} σ_{k}^{2} = 1 \end{matrix}

(75)

This sequence with arbitrary signs

σ_{k}

solves recurrent equation (Section 3.1) independently of

γ

For the curve to be closed, the angle

β

must be a rational multiple of

2 π

\begin{matrix} β = \frac{2 π p}{q} \end{matrix}

(76)

In this case, the closure condition

\begin{matrix} β \sum_{0}^{N - 1} σ_{k} = 2 π n p, n \neq 0 . \end{matrix}

(77)

will always have a solution for the discrete variables

σ_{k} = \pm 1

. All that is needed is a relation between the net numbers

N_{\pm}

of positive and negative

σ_{k}

\begin{matrix} N_{+} - N_{-} = n q, n \neq 0 . \end{matrix}

(78)

There are

(\binom{N}{N_{-}})

different states

σ_{0} = \pm 1, \dots σ_{N - 1} = \pm 1

satisfying the closing condition, provided

N > 2 N_{-} + q

The variables

σ_{k}

can otherwise be random, like the spin variables in the Ising model. This distribution is less trivial than the Ising model because the angles

α_{k}

are related to all the preceding

σ

variables, not just the local one

σ_{k}

This solution describes a closed random walk on a circle. It is characterized by an integer N and a rational number

\frac{p}{q}

with

q \leq N

As we pointed out in Section 3, a reflected sequence

{\vec{Φ}}_{N - k}^{*}

also represents a solution to the recurrent equations (Section 3.1).

At first glance, this simple formula seems a valid solution for the loop equations for decaying turbulence.

Unfortunately, it does not have any energy dissipation. The vorticity vector is finite

\begin{matrix} {\vec{ω}}_{k} = ı {\vec{Φ}}_{k} \times {\vec{Φ}}_{k + 1} = \frac{σ_{k}}{2} cot (\frac{β}{2}) \{cos (\frac{β σ_{k}}{2} + α_{k}), sin (\frac{β σ_{k}}{2} + α_{k}), i\} \end{matrix}

(79)

However, the square of this complex 3-vector is identically zero.

\begin{matrix} {\vec{ω}}_{k}^{2} \equiv 0 \end{matrix}

(80)

This solution can serve as initial data for the Brownian motion over the turbulence manifold, but the energy dissipation appears only after averaging over this motion.

This square of the complex vector, in the general case, can be related to the square of the vertex

{\vec{F}}_{k}

by the recurrent equations (Section 3.2):

\begin{matrix} {({\vec{F}}_{k} \times {\vec{F}}_{k + 1})}^{2} = \frac{1}{2} γ (γ + i (- 1 \pm \sqrt{4 {\vec{F}}_{k} \cdot {\vec{F}}_{k} - γ (γ - 2 i)})) \end{matrix}

(81)

Our symmetric solution corresponds to

{\vec{F}}_{k} \cdot {\vec{F}}_{k} = \frac{1}{4}

, and

\pm = 1

, where this expression vanishes identically at arbitrary

γ

The random walk step

{\vec{q}}_{k} = {\vec{Φ}}_{k + 1} - {\vec{Φ}}_{k}

is a real unit vector in this case

\begin{matrix} {\vec{q}}_{k} = σ_{k} {- sin δ_{k}, \vec{w} cos δ_{k}, 0}; \end{matrix}

(82)

\begin{matrix} δ_{k} = α_{k} + \frac{β σ_{k}}{2} \end{matrix}

(83)

The direction of this vector is not random, though; in addition to the random sign

σ_{k}

and random unit vector

\vec{w}

d > 3

dimensions, its direction depends on the previous position

α_{k}

on a circle.

So, this is a perfect example of a Markov chain, with the closure condition analytically solved by quantizing the angular step to a rational number

β = \frac{2 π p}{q}

This solution corresponds to the real value of velocity circulation on each of these two solutions; however, the reflection changes the circulation.

Thus, the arithmetic average of two Wilson loops with two reflected solutions is reflection-symmetric, but it is still a complex number.

Our covering algorithm will use a symmetric fixed point with a random choice of sign variables

σ_{k}

or its reflection as a starting element.

The imaginary parts of the steps

{\vec{q}}_{k}

are zero vectors at the start. Still, the evolution below will involve complex infinitesimal rotations

δ {\vec{q}}_{k} = {\vec{μ}}_{k} \times {\vec{q}}_{k}

so that the imaginary parts appear later in the evolution.

Due to the global

O (d)

symmetry, the rotated curve

{\hat{O} \cdot {\vec{Φ}}_{0}, \dots \hat{O} \cdot {\vec{Φ}}_{N - 1}}

with arbitrary orthogonal matrix

\hat{O}

is also a solution. In our simulations, we integrate the Wilson loop by this global rotation after finding a particular numerical solution for the momentum loop

\vec{F} (θ)

. The corresponding

O (3)

group Fourier integral is computed in Appendix A.

4.4. Infinitesimal complex rotations in 3D

Let us assume we already know a particular solution

{\vec{F}}_{0}, {\vec{q}}_{0}, \dots {\vec{q}}_{N - 1}

of the recurrent equations (Section 3.2) in

d = 3

and perturb it by an infinitesimal transformation of the complex vectors

{\vec{q}}_{k}

, preserving their square.

We also shift the initial point

{\vec{F}}_{0}

to keep the loop closed after infinitesimal transformations of all the steps

{\vec{q}}_{k}

\begin{matrix} δ {\vec{q}}_{k} = {\vec{μ}}_{k} \times {\vec{q}}_{k}; \end{matrix}

(84)

\begin{matrix} δ {\vec{F}}_{0} = \vec{λ}; \end{matrix}

(85)

Here

{\vec{μ}}_{k}, \vec{λ}

are infinitesimal complex 3D vectors.

The real part

Re {\vec{μ}}_{k} \in R^{3}

comes from the infinitesimal group transformation

δ_{L}

of rotation matrices in our canonical form (Section 4.1)

\begin{matrix} δ_{L} {\hat{O}}_{k} = {\hat{Ω}}_{k} \cdot {\hat{O}}_{k}; \end{matrix}

(86)

\begin{matrix} {\hat{Ω}}_{k}^{α β} = e^{α β γ} Ω_{k}^{γ}; \end{matrix}

(87)

\begin{matrix} {\vec{Ω}}_{k} = - Re {\vec{μ}}_{k}; \end{matrix}

(88)

\begin{matrix} δ_{L} {\vec{q}}_{k} = Re {\vec{μ}}_{k} \times {\vec{q}}_{k}; \end{matrix}

(89)

The imaginary part

Im {\vec{μ}}_{k}

leads to the infinitesimal transformation of parameters

α_{1}, α_{2}, β

in two-dimensional de Sitter space

d S_{2}

; therefore, there are only two independent components of

Im {\vec{μ}}_{k}

We do not need an explicit split of the parameters of

{\vec{μ}}_{k}

into these two transformations; it is sufficient to know that cross product

{\vec{μ}}_{k} \times {\vec{q}}_{k}

with any complex vector

{\vec{μ}}_{k}

is orthogonal to

{\vec{q}}_{k}

, as we need it in our random walk with

{\vec{q}}_{k}^{2} = 1

Below, we will parameterize

Im {\vec{μ}}_{k}

by two scalar parameters.

There are two contributions to the variation of each position

{\vec{F}}_{k}

. One variation comes from the rotation of the step from the previous position, and another comes from the variation of the previous position.

\begin{matrix} δ {\vec{F}}_{k} = δ {\vec{F}}_{k - 1} + {\vec{μ}}_{k - 1} \times {\vec{q}}_{k - 1} = λ + \sum_{0}^{k - 1} {\vec{μ}}_{l} \times {\vec{q}}_{l}; \end{matrix}

(90)

By variation of the second of the constraints in (Section 3.2), we find the following set of relations between infinitesimal

{\vec{μ}}_{k}, \vec{λ}

\begin{matrix} (G_{k} {\vec{q}}_{k} \times {\vec{F}}_{k}) \cdot {\vec{μ}}_{k} = - {\vec{V}}_{k} \cdot (\vec{λ} + \sum_{0}^{k - 1} {\vec{μ}}_{l} \times {\vec{q}}_{l}); \end{matrix}

(91a)

\begin{matrix} G_{k} = (2 {\vec{F}}_{k} \cdot {\vec{q}}_{k} - ı γ); \end{matrix}

(91b)

\begin{matrix} {\vec{V}}_{k} = G_{k} {\vec{q}}_{k} - 2 {\vec{F}}_{k}; \end{matrix}

(91c)

Some constraints are left in the solution for the vectors

{\vec{q}}_{k}

even after the complex rotations. Three scalar constraints on the imaginary parts of the complex rotation vectors

{\vec{μ}}_{k}

remain in three dimensions.

These constraints are needed to provide the closure condition. There are only three scalar constraints among N real vectors, which leads to a nontrivial

3 N - 3

dimensional quotient space.

4.5. The closure equation

We treat it as a recurrent system of equations for

Im {\vec{μ}}_{k}

, assuming known values of

Re μ_{l}, \vec{λ}

After solving that system, the complex vector

\vec{λ}

is supposed to be determined from the closure equation

\begin{matrix} \sum_{l = 0}^{N - 1} {\vec{μ}}_{l} \times {\vec{q}}_{l} = 0 \end{matrix}

(92)

assuming all

{\vec{μ}}_{l}

expressed as linear combinations of

Re \vec{λ}, Im \vec{λ}, Re {\vec{μ}}_{i}

As we found in [32] in three dimensions, this system of equations for

\vec{λ}

is degenerate: three parameters in

\vec{λ}

are left undetermined.

The solution for

\vec{λ}

exists only if N vectors

{Re {\vec{μ}}_{0}, \dots Re {\vec{μ}}_{N - 1}}

obey three scalar constraints.

In other words, the complex vector equation (92) reduces to three constraints for

\vec{λ}

and another three constraints for

Re {\vec{μ}}_{k}

. The complex vector

\vec{λ}

is left with three free components, and the vectors

{Re {\vec{μ}}_{0}, \dots Re μ_{N - 1}}

are left with

3 N - 3

free components out of

3 N

The solution of these equations, which we find in Appendix B, has the form

\begin{matrix} \vec{λ} = \sum_{l = 0}^{N - 1} {\hat{Λ}}_{l} \cdot Re {\vec{μ}}_{l}; \end{matrix}

(93)

\begin{matrix} Im {\vec{μ}}_{k} = \sum_{l = 0}^{N - 1} {\hat{S}}_{k l} \cdot Re {\vec{μ}}_{l} \end{matrix}

(94)

with real

3 \times 3

matrices

{\hat{S}}_{k l}

, and complex

3 \times 3

matrices

{\hat{Λ}}_{l}

; these matrices depend on the current values of all the vectors

{\vec{F}}_{k}

4.6. Linear constraints and zero modes

In addition, we have found three linear constraints on

Re {\vec{μ}}_{l}

, related to three complex null vectors of a block matrix

\hat{H}

involved in the equation for

\vec{λ}

The vector

\vec{λ}

is defined modulo superposition of elements of these three zero modes

\begin{matrix} \vec{λ} \Rightarrow \vec{λ} + \sum_{i = 1}^{3} c_{i} {\vec{ψ}}_{i} \end{matrix}

(95)

Due to the closure of the original loop

C \in R_{d}

, the translation of

\vec{λ}

by arbitrary complex vector does not change the circulation in (54). This translation of

\vec{λ}

leads to the global translation of our momentum curve

\vec{P} (θ)

, preserving the circulation over the closed loop in space.

We resolved this ambiguity of

\vec{λ}

by choosing the pseudo-inverse of the degenerate matrix

\hat{H}

when computing the coefficients

{\hat{Λ}}_{l}

The three constraints on infinitesimal rotations have a form (A36). These constraints define a subspace

S

of the whole space

R_{3}^{\otimes N}

of our rotation vectors

Re {\vec{μ}}_{k}

(dual to elements of Lie algebra on each

S O (3)

)

\begin{matrix} S : \sum_{k} {\vec{Θ}}_{i k} \cdot Re {\vec{μ}}_{k} = 0; i = 1, 2, 3; \end{matrix}

(96)

\begin{matrix} {\vec{Θ}}_{i k} = Re ({\vec{ψ}}_{i}^{*} {\hat{W}}_{k}); \end{matrix}

(97)

The rotation vectors

Re {\vec{μ}}_{k}

vary in the quotient space

\begin{matrix} F = (^{R_{3}^{\otimes N}} /_{S}) \end{matrix}

(98)

The null-vectors

{\vec{ψ}}_{i}

and coefficients

{\hat{W}}_{k}

, depending on the current positions

{\vec{F}}_{k}

are computed using recurrent equations in [32].

We get numerical results on a laptop for arbitrary

N < 100

. Larger values of N would require a supercomputer.

4.7. Brownian motion on turbulent manifold

Now, we are ready to write down the SDE for the evolution of our complex curve using the stochastic process

d {\vec{ξ}}_{l} = Re {\vec{μ}}_{l}

\begin{matrix} d {\vec{q}}_{k} = \sum_{l = 0}^{N - 1} {\hat{T}}_{k l} \cdot d {\vec{ξ}}_{l}; \end{matrix}

(99a)

\begin{matrix} {\hat{T}}_{k l} = δ_{k l} {\hat{q}}_{k} + ı {\hat{q}}_{k} \cdot {\hat{S}}_{k l}; \end{matrix}

(99b)

\begin{matrix} d {\vec{F}}_{0} = \sum_{l = 0}^{N - 1} {\hat{Λ}}_{l} \cdot d {\vec{ξ}}_{l}; \end{matrix}

(99c)

\begin{matrix} {\vec{F}}_{k} = {\vec{F}}_{0} + \sum_{l = 0}^{k - 1} {\vec{q}}_{l}; \end{matrix}

(99d)

\begin{matrix} \sum_{k = 0}^{N - 1} {\vec{Θ}}_{i k} \cdot d {\vec{ξ}}_{k} = 0; i = 1, 2, 3; \end{matrix}

(99e)

These constrained stochastic differential equations describe the evolution of the point on our fixed manifold

T_{3} (N)

of closed complex curves subject to the loop equations (Section 3.1), starting with one of the symmetric fixed points (72)

\begin{matrix} {{\vec{F}}_{k}|}_{τ = 0} = {\vec{Φ}}_{k} or {\vec{Φ}}_{N - k}^{*} \end{matrix}

(100)

The constrained SDE were studied in the mathematical literature [33].

We use a standard method of the projection of the Brownian motion to a quotient space. Let us introduce new stochastic real vector variables

d \hat{η} = {d {\vec{η}}_{0}, \dots d {\vec{η}}_{N - 1}} \in R_{3}^{\otimes N}

and project out the constraints as follows (in matrix notations)

\begin{matrix} d \hat{ξ} = d \hat{η} - P \cdot d \hat{η}; \end{matrix}

(101)

\begin{matrix} P = {\hat{Θ}}^{†} \cdot {(\hat{Θ} \cdot {\hat{Θ}}^{†})}^{- 1} \cdot \hat{Θ}; \end{matrix}

(102)

The variables

d \hat{η}

are assumed to be delta correlated (in proper units of stochastic time)

\begin{matrix} 〈\frac{d \hat{η}}{d τ} \otimes \frac{d \hat{η}}{d τ^{'}}〉 = \hat{I} δ (τ - τ^{'}) \end{matrix}

(103)

Here

\hat{I}

is a unit matrix in

3 N

dimensions.

It is straightforward to check that

d ξ

satisfies the constraints for arbitrary

d \hat{η}

\begin{matrix} \hat{Θ} \cdot d \hat{ξ} = 0 \end{matrix}

(104)

The variables

d \hat{ξ}

do not change when variables

d \hat{η}

are shifted by superposition of transposed constraints

\begin{matrix} δ d \hat{η} = {\hat{Θ}}^{†} \cdot d \vec{w}; \end{matrix}

(105)

\begin{matrix} δ d \hat{ξ} = 0 \end{matrix}

(106)

So, our stochastic process

d \hat{η}

has some redundant (gauge) degrees of freedom

d \vec{w}

The variables

d \hat{ξ}

evolve in the quotient space

F

, covering it with an

O (3)

invariant measure. This invariance is easy to check by noticing that all the matrices

\hat{Θ}, \hat{Λ}, \hat{S}, \hat{T}

in our equations are made of rotation-covariant parameters in the linearized recurrent equations. These parameters are direct products of vectors times some dot products of other vectors.

In mathematical terms,

d \hat{η}

is a Wiener process in

R_{3}^{\otimes N}

with a unit variance matrix, and

d \hat{ξ}

is a Brownian motion in the quotient space

F

. This quotient space evolves with stochastic time, as the constraint matrix

\hat{Θ}

depends on current values of all vectors

{\vec{F}}_{.}

The projection can be used to redefine the matrices

\begin{matrix} T = \hat{T} - P \cdot \hat{T}; \end{matrix}

(107)

\begin{matrix} L = \hat{Λ} - P \cdot \hat{Λ}; \end{matrix}

(108)

after which our SDE takes a usual form

\begin{matrix} d {\vec{q}}_{k} = \sum_{l = 0}^{N - 1} T_{k l} \cdot d {\vec{η}}_{l}; \end{matrix}

(109)

\begin{matrix} d {\vec{F}}_{0} = \sum_{l = 0}^{N - 1} L_{l} \cdot d {\vec{η}}_{l}; \end{matrix}

(110)

\begin{matrix} {\vec{F}}_{k} = {\vec{F}}_{0} + \sum_{l = 0}^{k - 1} {\vec{q}}_{l}; \end{matrix}

(111)

We propose this stochastic process in a limit $N \to \infty$ as a mathematical definition of the fixed manifold of decaying Turbulence.

The proof of this conjecture and extension to higher dimensions is left for a detailed mathematical study, which is beyond the scope of this work.

We coded these SDE in [32] using Mathematica^®. This code may be useful for theoretical development, but the optimized computations should be translated into Python and C++ and run on a supercomputer or a Tensorflow cluster.

Before even attempting such a computation, the random walk algorithm must be optimized. Its computational complexity grows as

N^{4}

per time step. These issues will be addressed in a subsequent publication, where we modify the random walk to reduce the

N^{4}

complexity to a linear one and optimize it for massively parallel execution on a supercomputer cluster.

Once we fix the initial value at one of the two mirror fixed points

{\vec{Φ}}_{k}, {\vec{Φ}}_{N - k}^{*}

, the evolution is unambiguous, unlike the global description of the manifold in Section 4, where we had to choose between four solutions of two quadratic equations for the point

{α_{1}, α_{2}, β}

in de Sitter space

d S_{2}

We are still left with a choice of one of the two mirror solutions or, in the general case, the coefficients of their linear superposition in the Wilson loop.

Such linear superposition will still solve the loop equation (7a), as this equation is linear in loop space. This superposition is found in the next Section.

4.8. Mirror symmetry and inequality for the Wilson loop

There is an obvious problem with the solution we have found. The loop equation for

\vec{P} (θ)

is complex, and so is the solution, particularly the vorticity in (19). Since the equation for

\vec{P}

is nonlinear, we cannot take a real part of

\vec{P}

The negative imaginary part of the circulation in momentum space may lead to violation of inequality

|Ψ [γ, C]| \leq 1

Here is how we suggest to solve this problem.

In the previous Sections, we described two mirror solutions, originating in (72) and evolving by an SDE (99a).

For any particular loop, we have to choose the solution with the positive imaginary part of the circulation

\begin{matrix} Ψ [γ, C] = 〈exp (\frac{ı γ Γ}{ν}) Θ (Im Γ)〉 + {\vec{P} (θ) \Leftrightarrow {\vec{P}}^{*} (2 π - θ)}; \end{matrix}

(112a)

\begin{matrix} Γ = \oint d \vec{C} (θ) \cdot \vec{P} (θ); \end{matrix}

(112b)

The averaging

〈\dots〉

corresponds to averaging over the stochastic process or, equivalently, over the stochastic time

τ

. On top of that, there is averaging over global rotation

{\vec{F}}_{k} \Rightarrow \hat{O} \cdot {\vec{F}}_{k}

over the group measure for

\hat{O} \in S O (d)

At any moment of stochastic time, the inequality restricts the loop C, but not the momentum loop

\vec{P}

: for some loops C, the circulation

Γ

has a positive imaginary part; for other loops, the reflected circulation

\tilde{Γ}

does.

This choice is like selecting a decaying wave function for the bound state in the Schrödinger equation for a quantum potential problem.

The theta functions in this solution represent certain boundary conditions for the loop functional in the areas (if they exist) where

Im Γ = 0

Im \tilde{Γ} = 0

Let us study this constraint in more detail. The general solution of the loop equation involves above-mentioned averaging over the global rotation of the whole momentum loop

\vec{P} (θ)

We can write the solution as follows (in three dimensions)

\begin{matrix} Ψ [γ, C] = 〈\int_{O (3)} \frac{d Ω}{| O (3) |} exp (\frac{ı γ}{ν} Γ_{Ω}) Θ (Im Γ_{Ω}) + {\vec{P} (θ) \Leftrightarrow {\vec{P}}^{*} (2 π - θ)}〉; \end{matrix}

(113)

\begin{matrix} Γ_{Ω} = \oint d θ {\vec{C}}^{'} (θ) \cdot \hat{Ω} \cdot \vec{P} (θ) \end{matrix}

(114)

We use the quaternionic representation for the group measure in Appendix A to elaborate this group integral, including extra requirements of the positive imaginary part of the circulation.

The reflected solution is treated the same way, with

\begin{matrix} {\tilde{Γ}}_{Ω} = \oint d θ {\vec{C}}^{'} (θ) \cdot \hat{Ω} \cdot {\vec{P}}^{*} (2 π - θ) \end{matrix}

(115)

After the addition of the reflected solution, the Wilson loop acquires the reflection symmetry

\begin{matrix} Ψ [γ, \vec{C} (2 π - θ)] = Ψ^{*} [γ, \vec{C} (θ)] \end{matrix}

(116)

which symmetry has to be obeyed by a Wilson loop for any real velocity field.

Each of the two complementary terms in

Ψ [γ, C]

is bounded by

\frac{1}{2}

, which provides desired inequality

|Ψ [γ, C]| < 1

after the addition of the reflection.

Verifying the normalization condition

Ψ [0] = 1

for the loop reduced to a point

C = 0

is straightforward.

4.9. Vorticity distribution and energy dissipation

The simplest quantity to compute in our theory is the local vorticity distribution.

As we shall see, it determines the energy dissipation rate.

The local vorticity for our decaying solution of the loop equation

\begin{matrix} \vec{ω} = \frac{- ı \vec{F} (θ) \times Δ \vec{F} (\vec{θ})}{2 (t + t_{0})}; \end{matrix}

(117)

Here

θ

is an arbitrary point at the loop, which makes this expression a random variable.

Note that viscosity is canceled here, as it should be by dimensional counting (vorticity has the dimension of

1 / t

In our random walk representation, the complex vorticity operator

\begin{matrix} {\vec{ω}}_{k} = \frac{- ı {\vec{G}}_{k}}{2 (t + t_{0})}; \end{matrix}

(118)

\begin{matrix} {\vec{G}}_{k} = {\vec{F}}_{k} \times {\vec{F}}_{k + 1} = {\vec{F}}_{k} \times {\vec{q}}_{k}; \end{matrix}

(119)

The time derivative of energy density in our theory is

\begin{matrix} E^{'} (t) = - \frac{ν κ}{4 {(t_{0} + t)}^{2}}; \end{matrix}

(120)

\begin{matrix} κ = - \frac{1}{N} \sum \frac{{\vec{G}}_{k}^{2} + {({\vec{G}}_{N - k}^{*})}^{2}}{2} = - \frac{1}{N} \sum Re {\vec{G}}_{k}^{2}; \end{matrix}

(121)

Solving this equation with boundary value

E (t = \infty) = 0

we relate

t_{0}

to mean initial energy

\begin{matrix} 〈E (t)〉 = \frac{ν 〈κ〉}{4 (t_{0} + t)}; \end{matrix}

(122)

\begin{matrix} t_{0} = \frac{ν 〈κ〉}{4 〈E_{0}〉} \end{matrix}

(123)

The probability distribution of

κ

and its mean value

〈κ〉

can be computed using our random walk. For the anomalous dissipation, we need the mean enstrophy to diverge [2,18] so that viscosity is compensated in the extreme turbulent limit.

\begin{matrix} 〈κ〉 = + \infty \end{matrix}

(124)

As we shall see later, in Section 5, this happens in our numerical simulations.

The microscopic picture of this infinite enstrophy differs from the singular vortex line.

In the Euler theory, divergence came from the singularity of the classical field. However, in our dual theory, it comes from the large fluctuation of the fractal curve in momentum space.

4.10. The Group average of the Wilson loop and manifest inequality

We can now write down our result for the Wilson loop in decaying Turbulence as a functional of the contour C. We limit ourselves to the three-dimensional case:

\begin{matrix} Ψ {[γ, C]}_{t \to \infty} = {〈exp (\frac{- ı \oint d θ \vec{C} (θ) \cdot {\vec{F}}^{'} (θ)}{\sqrt{2 ν (t + t_{0})}}) Θ (Γ)〉}_{F} + reflected; \end{matrix}

(125)

The finite steps approximation we considered above

\begin{matrix} 〈exp (- \frac{ı \oint d θ \vec{C} (θ) \cdot {\vec{F}}^{'} (θ)}{\sqrt{2 ν (t + t_{0})}})〉 = \end{matrix}

\begin{matrix} lim_{N \to \infty} 〈exp (- \frac{ı}{2} \frac{\sum_{k = 0}^{N - 1} ({\vec{C}}_{k + 1} + {\vec{C}}_{k}) \cdot {\vec{q}}_{k}}{2 \sqrt{2 ν (t + t_{0})}})〉; \end{matrix}

(126)

\begin{matrix} {\vec{C}}_{k} = \vec{C} (\frac{2 π k π}{N}); \end{matrix}

(127)

For the simplest circular loop in an

x y

plane, we have

\begin{matrix} \vec{C} (\vec{θ}) = r {cos θ, sin θ, 0}; \end{matrix}

(128)

\begin{matrix} \frac{{\vec{C}}_{k} + {\vec{C}}_{k + 1}}{2} = R cos (\frac{π}{N}) \{cos (\frac{π (2 k + 1)}{N}), sin (\frac{π (2 k + 1)}{N}), 0\} \end{matrix}

(129)

We observe that even at the large time

t ≫ t_{0}

when the asymptotic fractal curve is already in place, there is a region of parameters

\begin{matrix} r \sim \sqrt{ν t} \end{matrix}

(130)

where the Wilson loop is a nontrivial universal function of a single variable. We compute these group integrals in Appendix A

\begin{matrix} Ψ [γ, C] \to W (\hat{R}) + reflected; \end{matrix}

(131)

\begin{matrix} R_{α β} = \frac{r}{4 \sqrt{2 ν t}} (T_{i j}^{α β} + T_{i j}^{β α}) X_{i j}; \end{matrix}

(132)

\begin{matrix} T_{i j}^{α β} = tr σ_{i} σ_{j} τ_{α} τ_{β}^{†}; \end{matrix}

(133)

\begin{matrix} τ_{α} = {1, ı \vec{σ}}; α = (0, 1, 2, 3); \end{matrix}

(134)

\begin{matrix} \hat{X} = cos (\frac{π}{N}) \sum_{k = 0}^{N - 1} {\vec{q}}_{k} \otimes \{cos (\frac{π (2 k + 1)}{N}), sin (\frac{π (2 k + 1)}{N}), 0\}; \end{matrix}

(135)

The function

W (\hat{R})

only depends on invariants. For our complex symmetric matrix, these invariants can be chosen as four eigenvalues

τ_{i}

of its imaginary part, plus ten independent components

r_{i j} = r_{j i}

of the real part in the basis of the imaginary part

\begin{matrix} Im \hat{R} \cdot {\vec{n}}_{i} = τ_{i} {\vec{n}}_{i}; i = 1 \dots 4; \end{matrix}

(136)

\begin{matrix} r_{i j} = {\vec{n}}_{i} \cdot Re \hat{R} \cdot {\vec{n}}_{j} \end{matrix}

(137)

The reflected term involves the complex conjugate fractal curve

{\vec{q}}_{N - k}^{*}

. However, this reflected term is not a complex conjugate of the first one.

Thus, the Wilson loop is a complex function despite its reflection invariance. In other words, the dissipative effects are present in a big way in our solution.

We can compute our prediction for this function by numerically simulating the SDE for our vectors

{\vec{F}}_{k}

and wait for the results with physical or numerical experiments in conventional three-dimensional decaying Turbulence.

4.11. Correlation functions

The simplest observable quantities we can extract from the loop functional are the vorticity correlation functions [2], corresponding to the loop C backtracking between two points in space

{\vec{r}}_{1} = 0, {\vec{r}}_{2} = \vec{r}

, see Figure 1. The vorticity operators are inserted at these two points.

The correlation function reduces to a random walk with a complex weight

\begin{matrix} 〈\vec{ω} (\vec{0}) \otimes \vec{ω} (\vec{r})〉 = \frac{1}{4 {(t + t_{0})}^{2}} \end{matrix}

\begin{matrix} \sum_{n, m} 〈\frac{{\vec{F}}_{m} \times {\vec{F}}_{m + 1} \otimes {\vec{F}}_{n} \times {\vec{F}}_{n + 1}}{N^{2}} exp (\frac{ı \vec{r} \cdot ({\vec{S}}_{n, m} - {\vec{S}}_{m, n})}{2 \sqrt{ν (t + t_{0})}})〉 + reflected; \end{matrix}

(138)

\begin{matrix} {\vec{S}}_{m, n} = \frac{\sum_{m}^{n} {\vec{F}}_{k}}{n - m (mod N)}; \end{matrix}

(139)

The averaging

〈\dots〉

in these formulas involves group integration

\int_{O (3)} d Ω

with

{\vec{F}}_{k} \Rightarrow \vec{Ω} \cdot {\vec{F}}_{k}

The positivity restrictions are inserted here as a theta function of the positive imaginary part of the circulation, in our case,

\begin{matrix} \vec{r} \cdot (Im {\vec{S}}_{n, m} - Im {\vec{S}}_{m, n}) > 0 \end{matrix}

(140)

With these restrictions, the absolute value of the Wilson loop is bounded by 1 from above.

We present these computations in Appendix A.

Presumably, the vorticity vectors

{\vec{G}}_{m} = {\vec{F}}_{m} \times {\vec{F}}_{m + 1}

as well as the vectors

{\vec{S}}_{m, n}

are distributed by some power laws in our random walk on a fixed manifold; this would lead to scaling laws with some fractal dimensions.

The numerical simulation of this correlation function would require significant computer resources.

Still, these resources are much more modest than those for full d dimensional simulations of the Navier-Stokes equation.

In our theory, the dimension of space enters as the number of components of the one-dimensional fluctuating field

\vec{F} (θ)

rather than the number of variables

\vec{r} \in R_{d}

in the fluctuating velocity field

\vec{v} (\vec{r})

Also, note that our quantum problem of the complex random walk naturally fits quantum computer architecture. Thus, in the future, when large quantum computers would become available for researchers, we can expect a real breakthrough in numerical simulations of the loop equation.

5. Open loop computations

We wrote a Mathematica^®program [34] generating our random walk, starting with a random complex vector

{\vec{F}}_{0}

and using random orthogonal

S O (3)

matrix

O_{k}

at every step. If there is more than one real solution for

β

, we have chosen the shortest step in Euclidean metric

{|\vec{q}|}^{2} = 1 + 2 β^{2}

, i.e., the one with minimal

| β |

We have chosen the simplest circular coordinate loop C in (128) and imposed the inequality

Im Γ > 0

on the last step.

For 1000 steps, it takes a few seconds on a laptop to compute the whole path. We generate a parallel table of 100000 paths, each with 1000 steps, with various random initial vectors

{\vec{F}}_{0}

with a random set of rotation matrices for each step.

The path’s closure requires a numerical solution of the SDE (99a), which we plan to implement later on a supercomputer. This open path simulation only covers the big space of the direct product of rotation matrices at every step; the true turbulent fixed point corresponds to the projection of this space onto the closure condition. We cannot do it at the global level, only at the level of the SDE described in the previous Section.

Thus, this open-path simulation cannot be used for predictions of fractal dimensions in the scaling laws; this has to wait until the SDE simulation is performed at the supercomputer.

With these comments in mind, let us analyze the open curves’ fractal properties, discarding the closure conditions.

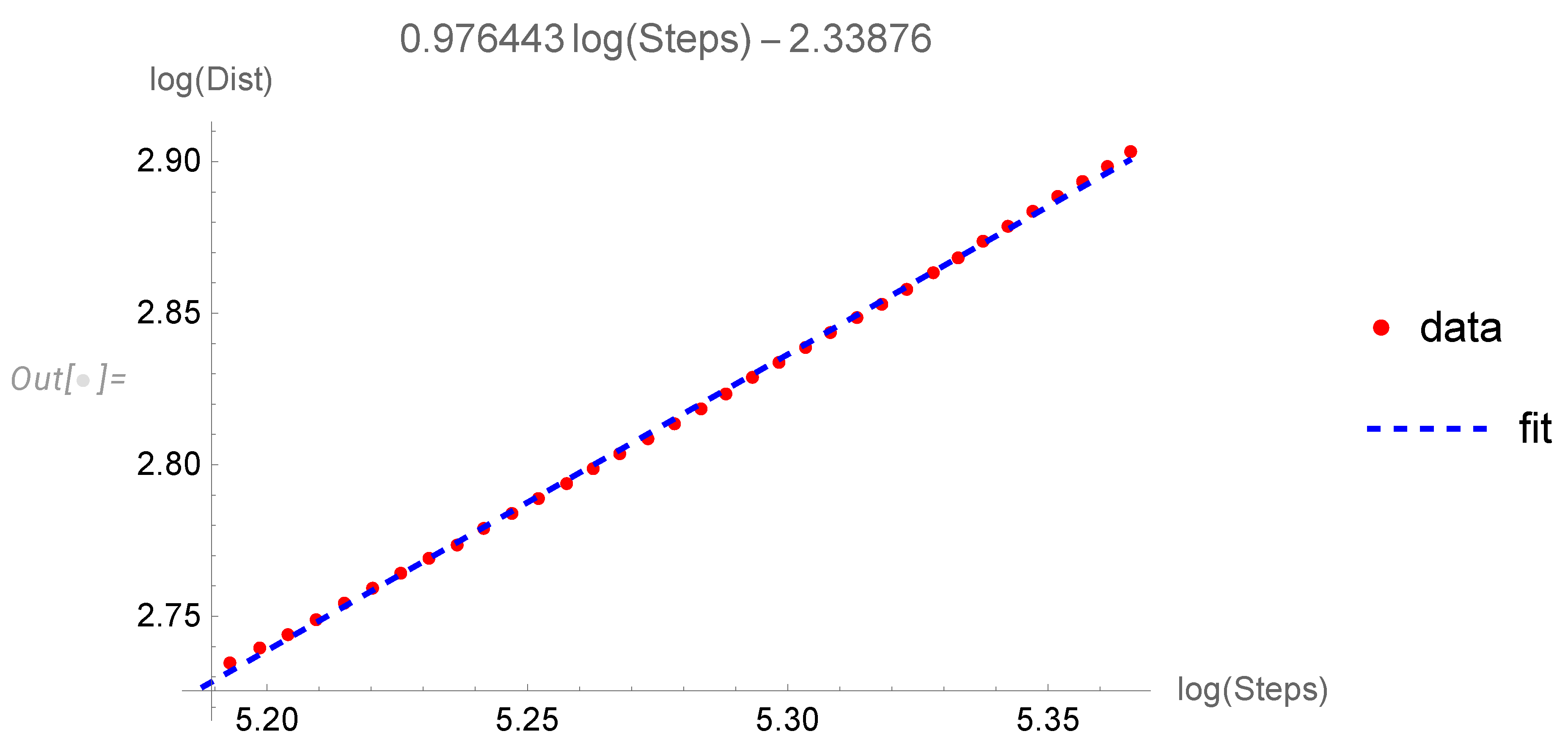
The simplest quantity to compute is a fractal dimension

d_{f}

of this random walk, defined as

\begin{matrix} \frac{1}{d_{f}} = lim_{N \to \infty} \frac{d log |{\vec{F}}_{N} - {\vec{F}}_{0}|}{d log N} \end{matrix}

(141)

The ordinary Brownian motion (linear random walk) has

d_{f} = 2

, but our random walk is very different, mainly because the Euclidean distance of an elementary step

|{\vec{F}}_{k + 1} - {\vec{F}}_{k}|

in De Sitter space is unlimited from above (though it is limited by 1 from below).

Here is the plot of

log |{\vec{F}}_{N} - {\vec{F}}_{0}|

log N

(Figure 2).

The statistical data for parameters

\begin{matrix} Estimate & Standard Error & t - Statistic & P - Value \\ 1 & - 2.33876 & 0.0241623 & - 96.7941 & 4.3388931215906555 \overset{`}{} *^{\land} - 42 \\ ξ & 0.976443 & 0.00457433 & 213.461 & 2.1004008453460444 \overset{`}{} *^{\land} - 53 \end{matrix}

(142)

This data is compatible with

d_{f} = 1.02412 \pm 0.005

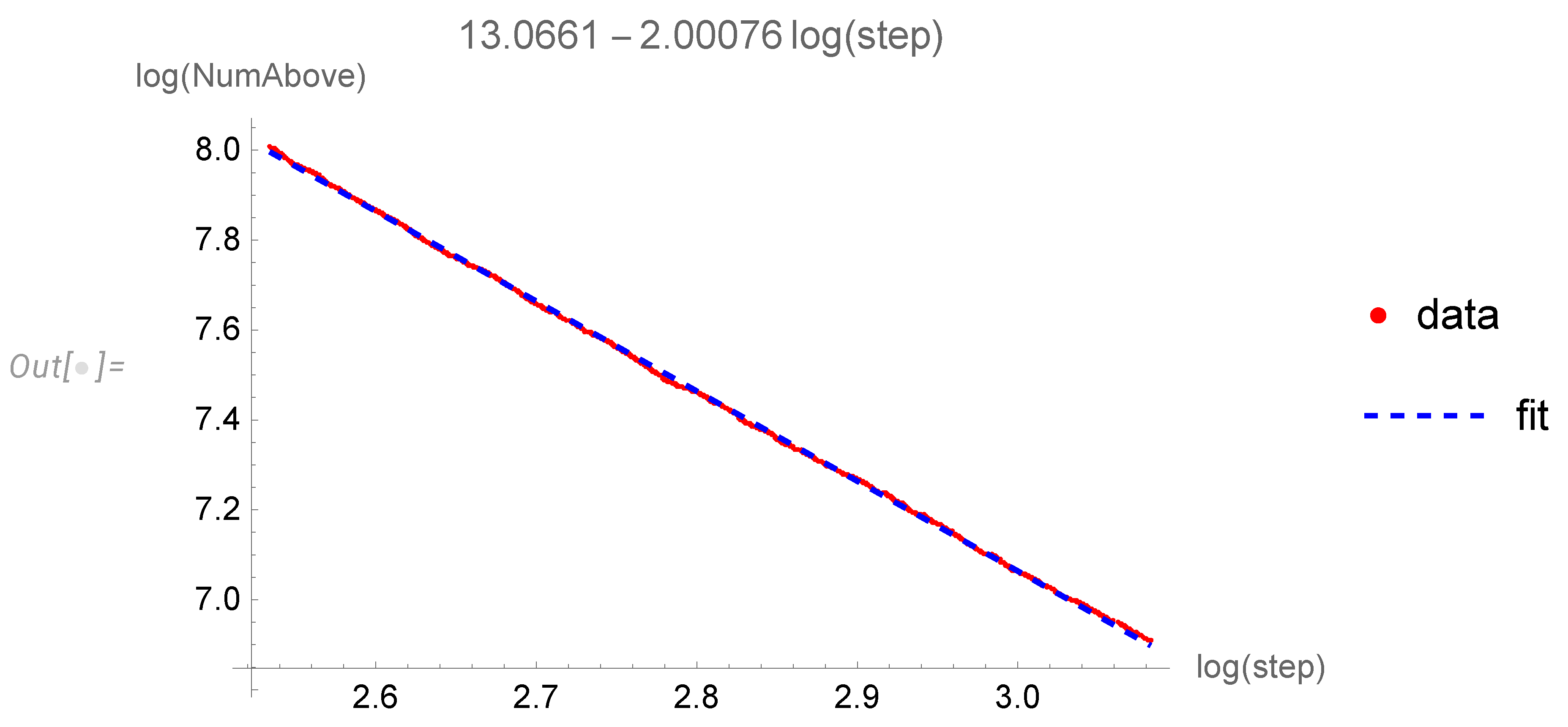
The distribution of the Euclidean length of each step

|{\vec{F}}_{k + 1} - {\vec{F}}_{k}|

(Figure 3).

The statistical table for the parameters of this fit

\begin{matrix} Estimate & Standard Error & t - Statistic & P - Value \\ 1 & 13.0661 & 0.00203512 & 6420.3 & 0 . \\ log (step) & - 2.00076 & 0.000737843 & - 2711.64 & 0 . \end{matrix}

(143)

The mean is finite,

〈s t e p〉 = 1.07056

, but the variance of the step is divergent.

Such a slow decay of the step distribution undermines the concept of a finite fractal dimension as defined in (141). The linear fit is inadequate for such large statistics.

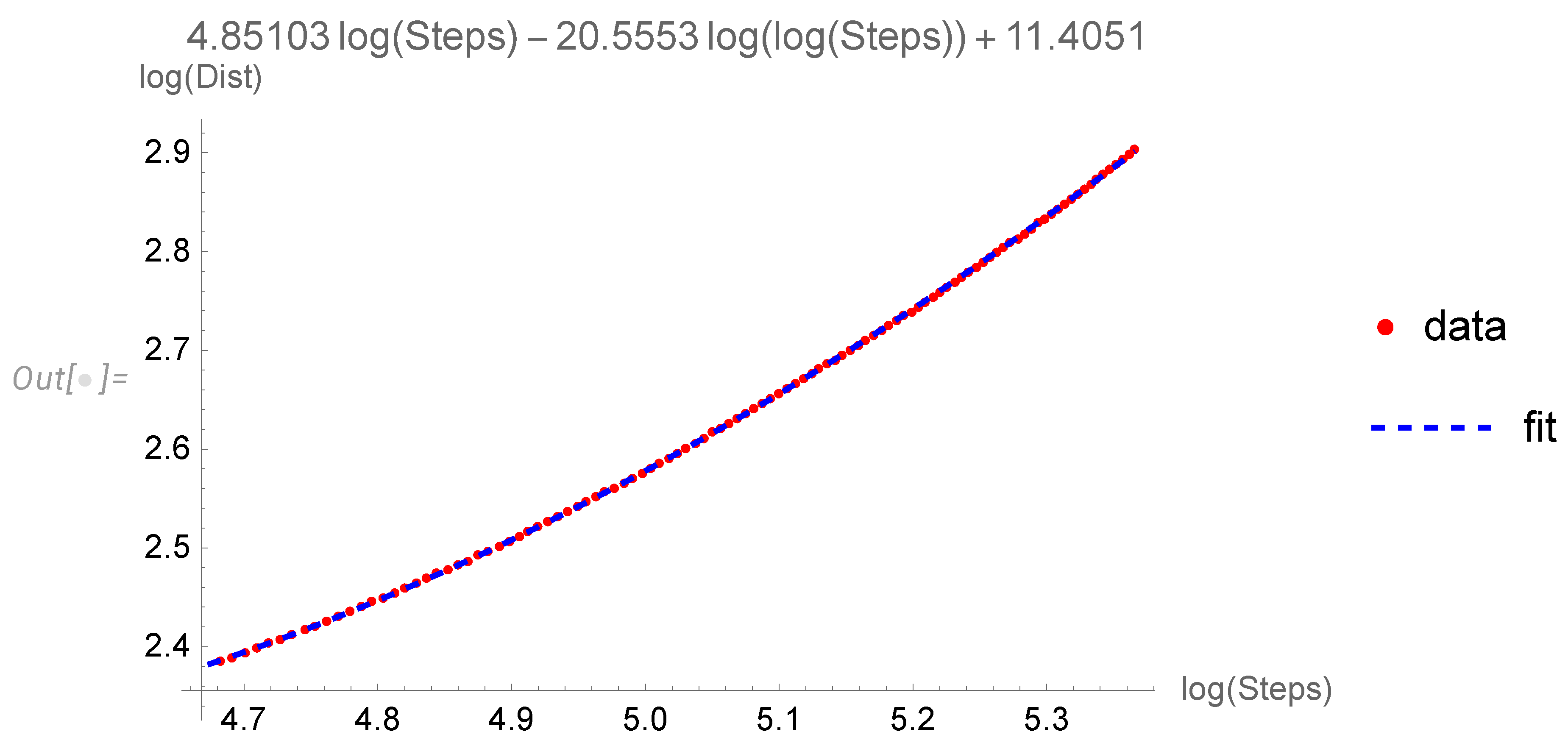
With large statistics, one can reach a perfect fit by adding the next correction to the linear log-log law

\begin{matrix} log |{\vec{F}}_{N} - {\vec{F}}_{0}| \approx a + b log N + c log log N \end{matrix}

(144)

The fit at larger interval of N becomes perfect, with a very different coefficient b in front of

log N

\begin{matrix} \begin{matrix} Estimate & Standard Error & t - Statistic & P - Value \\ 1 & 11.4051 & 0.067611 & 168.688 & 1.201777144099837 \overset{`}{} *^{\land} - 128 \\ ξ & 4.85103 & 0.0218164 & 222.357 & 4.3433787030416533 \overset{`}{} *^{\land} - 141 \\ log (ξ) & - 20.5553 & 0.109809 & - 187.192 & 2.4775697694919745 \overset{`}{} *^{\land} - 133 \end{matrix} \end{matrix}

(145)

This data fit is shown at Figure 4.

Our random walk with unbounded step size differs from an ordinary fractal curve. The fractal dimension does not properly describe this random object as the distance grows by a more complex law than a pure power of the number of steps.

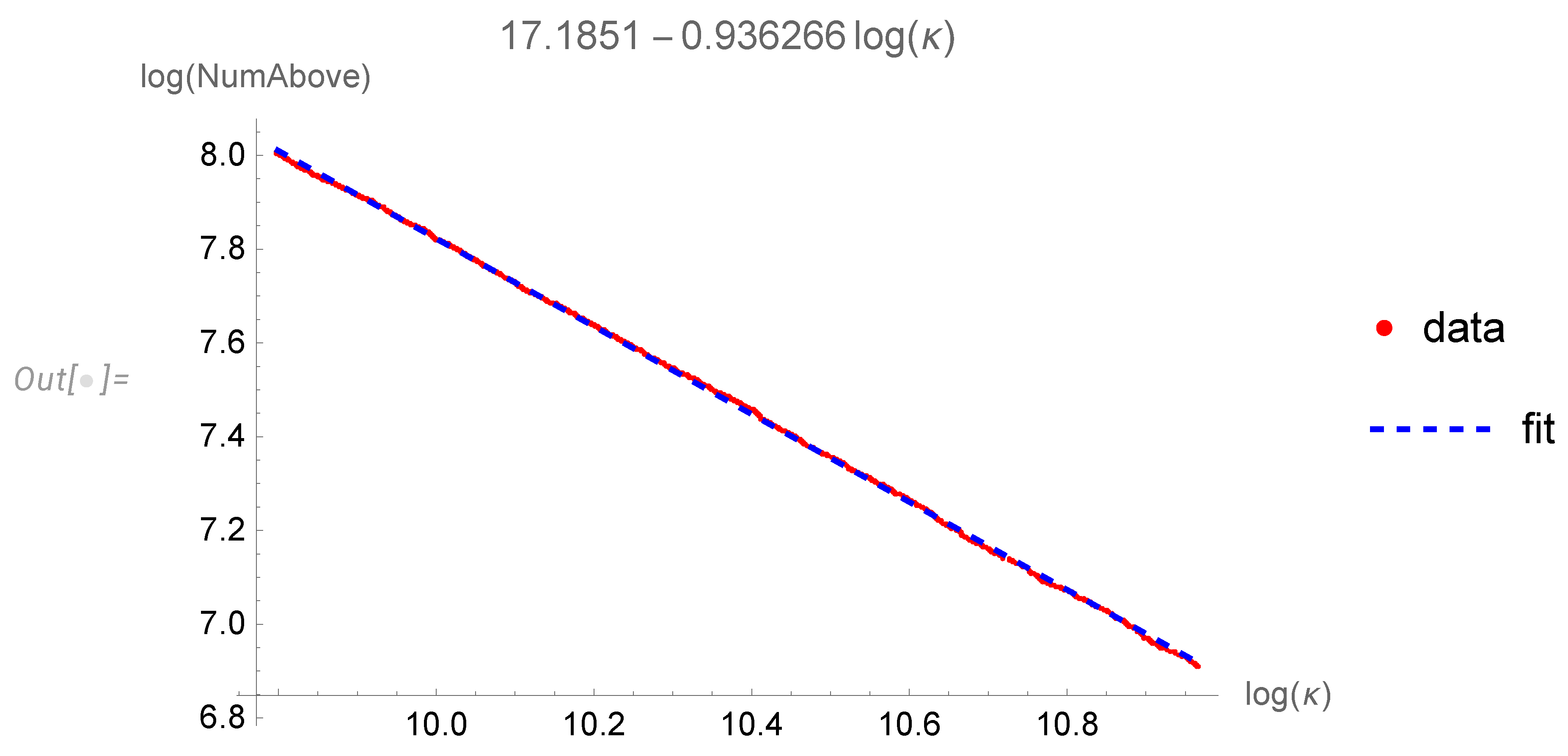
Another interesting distribution is the enstrophy density

κ

in (120).

The CDF is shown in Figure 5. The tail is compatible with

κ^{- 0.936266}

decay, corresponding to the

κ^{- 1.936266}

decay of the PDF. The mean value and all higher moments diverge, leading to anomalous dissipation.

The statistical table for the parameters of this fit

\begin{matrix} Estimate & Standard Error & t - Statistic & P - Value \\ 1 & 17.1851 & 0.00330287 & 5203.09 & 0 . \\ log (κ) & - 0.936266 & 0.000320989 & - 2916.81 & 0 . \end{matrix}

(146)

The computation of the Wilson loop and related correlation functions of vorticity needs an ensemble of closed fractal loops with various sets of random matrices.

The closure condition for the loop would require some computational effort because the probability of the random curve with fractal dimension

d_{f} \sim 1 .

returning to an initial point goes to zero with the increased number of steps.

An alternative approach of starting with a large closed loop

{\vec{F}}_{k}; {\vec{F}}_{N} = {\vec{F}}_{0}

and randomizing it point by point while preserving its closure.

This approach would replace an SDE (99a) with a Monte-Carlo process in a closed polygon space. Each step would correspond to a small shift of a few subsequent vertices

{\vec{F}}_{k + 1} \dots {\vec{F}}_{k + L}

of the polygon preserving the sequence’s first and last vertex

{\vec{F}}_{k}, {\vec{F}}_{k + L + 1}

. This small shift must also preserve the recurrent equations (Section 3.2) involving this sequence.

The first approximation to this shift would be our solution in Appendix B of the linearized equations. Then, a Newton iteration will finalize this shift to fulfill the quadratic relations (Section 3.1).

These extra layers of computational complexity would require a supercomputer, which we plan to do later.

6. Discussion

6.1. The Duality of Turbulence

We have presented an analytical solution of the Navier-Stokes loop equations for the Wilson loop in decaying Turbulence as a functional of the shape and size of the loop in arbitrary dimension

d > 2

The solution expresses the probability distribution and expected value for the Wilson loop at any given moment t in terms of a nonlinear SDE for the dual loop in complex momentum space as a function of auxiliary time

τ

. The loop is approximated as a polygon with

N \to \infty

sides.

Our solution also depends on the arbitrary dimensionless positive constant

γ

, corresponding to the frequency of the Fourier transforms from the Wilson loop to the PDF of circulation. This parameter explicitly enters our reduced loop equations for a momentum-space fractal curve.

Compared to the original Navier-Stokes equation, this is the reduction of

d \Rightarrow 1

of the dimension of space. This SDE is straightforward to simulate by a Monte Carlo method.

The equivalence of a strong coupling phase of the fluctuating vector field to quantum geometry is a well-known phenomenon in gauge theory (the ADS/CFT duality), ringing a bell to the modern theoretical physicist.

In our case, this is a much simpler quantum geometry: a fractal curve in complex space.

An expert in the traditional approach to Turbulence may wonder why the Loop equation’s solutions have any relation to the velocity field’s statistics in a decaying turbulent flow.

Such questions were raised and answered in the last few decades in the gauge theories, including QCD[6,8,9,10] where the loop equations were derived first [4,5].

Extra complications in the gauge theory are the short-distance singularities related to the infinite number of fluctuating degrees of freedom in quantum field theory. The Wilson loop functionals in coordinate space are singular in the gauge field theory and cannot be multiplicatively renormalized.

Fortunately, there is no short-distance divergence in the Navier-Stokes equations nor the Navier-Stokes loop dynamics. The Euler equations represent the singular limit, which, as we argued, should be resolved using singular topological solitons regularized by the Burgers vortex.

In the present theory, we keep viscosity constant and do not encounter any short-distance singularities. The anomalous dissipation is achieved in our solution via a completely different mechanism.

The loop equation describes the gauge invariant sector of the gauge field theory. Therefore, the gauge degrees of freedom are lost in the loop functional. However, the gauge-invariant correlations of the field strength are recoverable from the solutions of the loop equation[4,5].

6.2. Stokes-type functionals and vorticity correlations

There is no gauge invariance regarding the velocity field in fluid dynamics (though there is such invariance in the Clebsch variables [2]). The longitudinal, i.e., a potential part of the velocity, has a physical meaning – it is responsible for pressure and energy pumping. This part is lost in the loop functional, but is recoverable from the rotational part (the vorticity) using the Biot-Savart integral.

In the Fourier space, the correlation functions of the velocity field are algebraically related to those of vorticity

{\vec{v}}_{k} = \frac{ı \vec{k} \times {\vec{ω}}_{k}}{{\vec{k}}^{2}}

. Thus, the general solution for the Wilson loop functional

Ψ [γ, C]

allows computing both vorticity and velocity correlation functions.

The solution of the loop equation with finite area derivative, satisfying Bianchi constraint, belongs to the so-called Stokes-type functionals [4], the same as the Wilson loop for Gauge theory and fluid dynamics.

As we discussed in detail in [2,4,5], any Stokes-type functional

Ψ [γ, C]

satisfying boundary condition at shrunk loop

Ψ [0] = 1

, and solving the loop equation can be iterated in the nonlinear term in the Navier-Stokes equations (which would apply at large viscosity).

The resulting expansion in inverse powers of viscosity (weak Turbulence) exactly coincides with the ordinary perturbation expansion of the Navier-Stokes equations for the velocity field, averaged over the distribution of initial data or boundary conditions at infinity.

We have demonstrated in [1,2] (and also here, in Section 2.3) how the velocity distribution for the random uniform vorticity in the fluid was reproduced by a singular momentum loop

\vec{P} (θ)

The solution for

\vec{P} (θ)

in this special fixed point of the loop equation was random complex and had slowly decreasing Fourier coefficients, leading to a discontinuity

sign (θ - θ^{'})

in a pair correlation function (37). The corresponding Wilson loop was equal to the Stokes-type functional (30).

Our general Anzatz (14) satisfies the loop equation and boundary condition at

Ψ [C = 0] = 1

. It has a finite area derivative, which obeys the Bianchi constraint, making it a Stokes-type functional.

The exact solution for

\vec{P} (θ)

in decaying Turbulence which we have found in this paper, leads to the Stokes functional

Ψ [γ, C]

satisfying the boundary value

Ψ [0] = 1

at the shrunk loop.

Therefore, it represents a statistical distribution in a turbulent Navier-Stokes flow, corresponding to the degenerate fixed point of the Hopf equation for velocity circulation. It sums up all the Wylde diagrams in the limit of vanishing random forces plus nonperturbative effects, which are missed in the Wylde functional integral. Whether this exact solution is realized in Nature remains to be seen.

6.3. Random walk around the Turbulent manifold

The fixed point we have found is infinitely more complex than the randomly rotated fluid; our curve

\vec{P} (θ)

has a discontinuity at every

θ

, corresponding to a distributed random vorticity.

This solution is described by a fractal curve in complex d dimensional space, a limit of a random walk with nonlinear algebraic relations between the previous position

{\vec{F}}_{k}

and the next one

{\vec{F}}_{k + 1}

. These relations are degenerate: each step

{\vec{q}}_{k} = {\vec{F}}_{k + 1} - {\vec{F}}_{k}

is characterized by an arbitrary element

{\hat{O}}_{k} \in (^{O (d)} /_{O (d - 3)})

and an arbitrary element

{\vec{w}}_{k} \in (^{S^{d - 3}} /_{Z^{2}})

. This step also depends upon the previous position

{\vec{F}}_{k}

, making this process a Markov chain.

The periodicity condition

{\vec{F}}_{N} = {\vec{F}}_{0}

provides a nonlinear equation for an initial position

{\vec{F}}_{0}

as a function of the above free parameters

{\hat{O}}_{k}, {\vec{w}}_{k}

This periodicity condition presents a hard problem, particularly in the limit

N \to \infty

, when the probability of our random walk returning to the initial point afterN steps rapidly diminishes with N.

We found a way around this problem by utilizing an exact periodic solution (72) to the momentum loop equations (Section 3.1). This analytical solution for arbitrary N is equivalent to a periodic Ising chain or a random walk on a circle with constant angular steps or random signs. This sequence of

{\vec{F}}_{k}

can serve as initial data for the SDE, which preserves the periodicity. In Appendix B, we constructed this SDE for

d = 3

, leaving the generalizations to mathematicians.

This SDE describes the Brownian motion of the rotation matrices

{\hat{O}}_{k} \in S O (3)

in our canonical representation (Section 4.1) of the solution to the discrete loop equations (Section 3.2). Each matrix moves independently, while the remaining parameters

{α_{1}, α_{2}, β}

move around de Sitter space

d S_{2}

to satisfy the loop equation (Section 3.2).

The closure condition further restricts the set of N infinitesimal rotations

δ {\vec{q}}_{k} = δ {\vec{θ}}_{k} \times {\vec{q}}_{k}

: there are three linear relations between N vector parameters

δ {\vec{θ}}_{k}

of these rotations. We found the projection matrix required to project the whole array of vector rotations

δ {\vec{θ}}_{k}

onto the quotient space, satisfying the closure condition.

After this projection, we obtain the motion in the quotient space, where the closure condition is satisfied at every step. We have found the tangent space to our discreet loop equations and factored out the normal directions (i.e., the null space of linearized equations) like it is done with Brownian motion on a sphere.

Presumably, this SDE uniformly covers our fixed manifold

T_{3} (N)

for arbitrary N. The limit

N \to \infty

presents a computational challenge, and we are planning to address this challenge in the next publication using a supercomputer.

6.4. Simplified version of numerical Simulation

We simulated the open random walk (without the closure condition) in three dimensions and studied its statistical properties. We have chosen

γ = 1

at this early stage of our studies; later, we investigate the

γ

dependence.

The distribution of lengths of steps in Euclidean six-dimensional space

Re \vec{F}, Im \vec{F}

has a long tail

PDF \propto x^{- 2}

The fractal dimension is not an adequate characteristic for a random walk with such an intermittent step size, unbounded from above. The linear log-log fit as in (141) yields

d_{f} \approx 1.20

, but this fit is imperfect with our large statistics.

As for the distribution of an enstrophy density, it has a power tail

x^{- 1.9}

corresponding to an infinite mean value and all higher moments. This infinity is how anomalous dissipation manifests in our solution.

These numerical simulations must be repeated on a supercomputer with better statistics and more steps. There are many things to do next with this conjectured solution to the decaying turbulence problem; the first is to look for unnoticed inconsistencies.

One important step is yet to be made: the MC simulation of the SDE (99a). Let us assume that the qualitative properties and fractal dimensions we have found for the open fractal curves will stay the same or at least close.

6.5. Preliminary comparison with experiments

As a first test of this hypothesis, let us compare it with various experimental data and those from DNS [35].

There is no agreement between these data, they vary in Reynolds number, and they have other differences related to the experimental setup. No value n for the decay power

t^{- n}

would fit all that data. However, a consensus seems to be around

n \approx 1.2 - 1.4

, which means faster decay than we have.

We are skeptical about these data. As we recently learned [36], there is a regime change at large Reynolds numbers; the numbers achievable in modern DNS may belong to such a transitional regime.

Besides, fitting powers is not a reliable method of deriving physical laws.

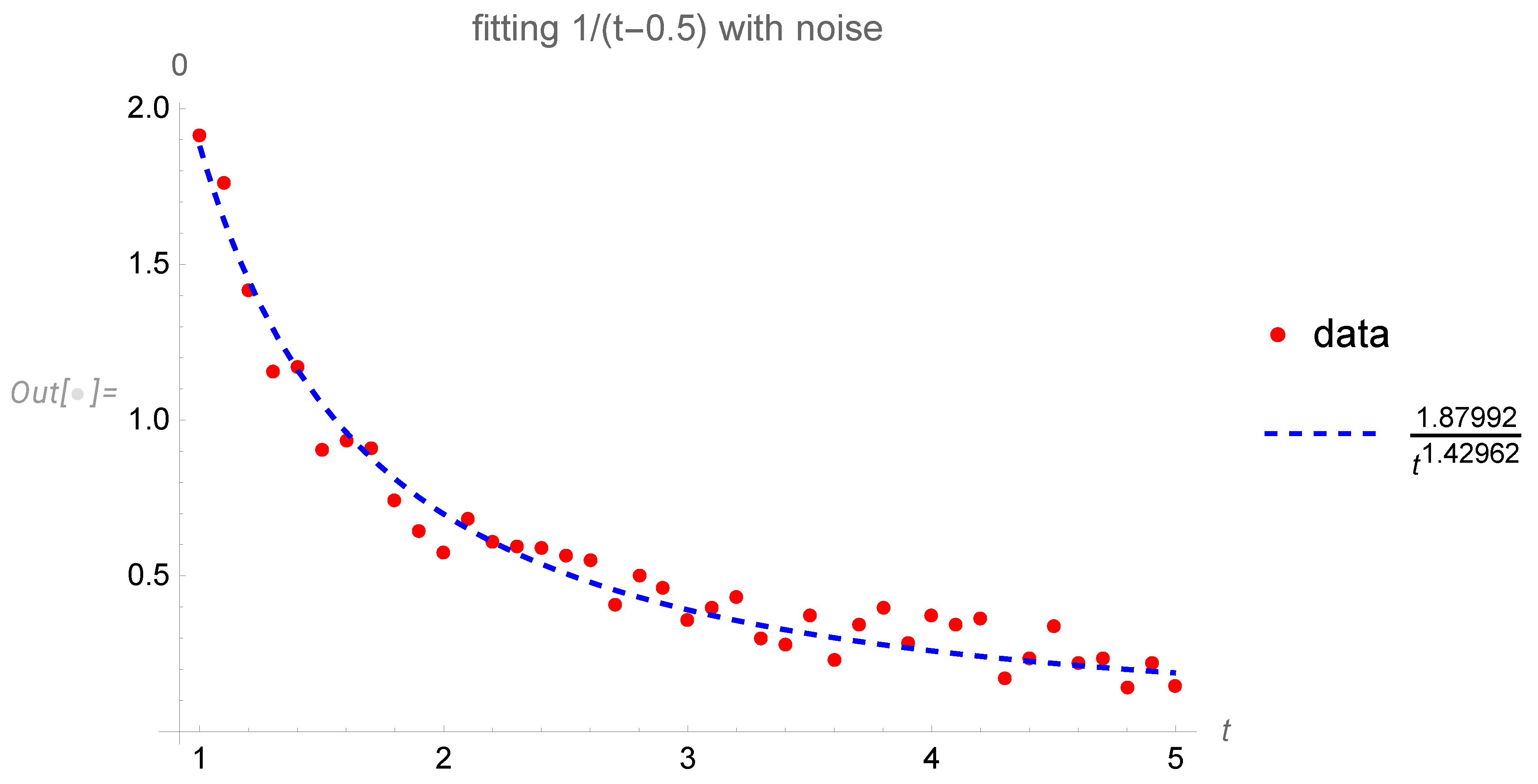
For example, we took a formula

1 / (t - 0.5)

, added random noise between

(- 0.1, 0.1)

and fitted this data to

b t^{- n}

. The best fit produced some fake power

n \approx 1.43

and some fake coefficient

b \approx 1.88

in front (see Figure 6)

Instead, one should compare a hypothetical theory with a null hypothesis by estimating the log-likelihood of both fits. In case the new theory is more likely as an explanation of the data, you may temporarily accept it until a better theory or better data will appear.

A good history lesson is fitting the power n in Newton’s gravity law to explain the astronomic data for the Mercury perihelion before the General Relativity theory. A small correction to

n = 1

"explained" the data, but this was useless without a theory.

Presumably, our fixed point corresponds to a true infinite Reynolds limit, as it is completely universal and does not depend on the Reynolds scales.

If you assume no hidden scales are left, our

E \propto ν / t

law follows from dimensional analysis. Observed or simulated data with

n > 1

all have the powers of some other dimensional parameters related to the Reynolds number. They rely on (multifractal versions of) K41 spectra and other intermediate turbulent phenomena.

We have an anomalous dissipation rate: the mean value of the vorticity square diverges, compensating for the viscosity factor in the energy decay in extreme turbulent limit.

This mechanism of anomalous dissipation differs from the one we studied in the Kelvinon [2,18]. In those fixed points, the viscosity canceled in the dissipation rate due to the singular vorticity configurations with the thin vortex line resolved as a core of a Burgers vortex.

Here, in the dual theory of fractal momentum loop, the large fluctuations of this momentum loop would lead to the divergent expectation value of the enstrophy.

6.6. Conclusion

Our solution is universal, rotational, and translational invariant. It has the expected properties of extreme isotropic Turbulence. Is it THE solution? Time will tell.

Data Availability Statement

We generated new data for the nonlinear complex random walk and the enstrophy distribution using the Mathematica^® code. This code, the data, and the three-dimensional plots are publicly available in Wolfram Cloud [32,34,37,38,39]. These notebooks also present analytical computations needed to verify our symmetric solution of the loop equation and linearized equations used in the SDE.

Acknowledgments

I benefited from discussions of this theory with Sasha Polyakov, K.R. Sreenivasan, Greg Eyink, Luca Moriconi, Vladimir Kazakov, and Kartik Iyer. This research was supported by a Simons Foundation award ID 686282 at NYU Abu Dhabi.

Appendix A The O(3) group average with and without restrictions

The correlation function (138) involves an integral over the

O (3)

group

\begin{matrix} Q {(\vec{r}, \vec{V})}_{i j; k l} = \int_{O (3)} \frac{d Ω}{| O (3) |} Ω_{i j} Ω_{k l} exp (ı \vec{r} \cdot \hat{Ω} \cdot \vec{V}); \end{matrix}

(A1)

with the vector

\vec{V}

related to our fractal curve

\vec{F} (θ)

at any given moment of stochastic time.

The vector

\vec{r}

is real, but generally, the vector

\vec{V}

can have complex components. We shall consider this problem below and start with real vector

\vec{V}

This integral is a particular case of a Harish-Chandra-Itzykson-Zuber integral formula [40],

\int_{U (n)} e^{tr (A U B U^{*})} d U = (\prod_{p = 1}^{n - 1} p!) \frac{det [e^{a_{i} b_{j}}]}{Δ (A) Δ (B)}

(A2)

where

Δ (A) = \prod_{i < j} (a_{j} - a_{i})

(A3)

is the Vandermonde determinant.

In our case,

O (3) = (^{S U (2)} /_{Z_{2}})

, so we use

n = 2

formula with

\begin{matrix} A = ı σ_{i} r_{i}, Δ (A) = 2 ı | \vec{r} | \end{matrix}

(A4)

\begin{matrix} B = σ_{j} V_{j}, Δ (B) = 2 | \vec{V} | \end{matrix}

(A5)

\begin{matrix} det [e^{a_{i} b_{j}}] = 2 ı sin (| \vec{r} | | \vec{V} |) \end{matrix}

(A6)

where

\vec{σ}

are Pauli matrices. With proper normalization to 1 at

\vec{r} = 0

, the HCIZ integral reads

\begin{matrix} \int_{O (3)} \frac{d Ω}{| O (3) |} exp (ı \vec{r} \cdot \hat{Ω} \cdot \vec{V}) = \frac{sin (| \vec{r} | | \vec{V} |)}{| \vec{r} | | \vec{V} |} \end{matrix}

(A7)

Next, let us consider the case of the complex vector V. In that case, there are separate invariants for real and imaginary parts, and the complex vector cannot be rotated to another one by an orthogonal transformation.

The HCIZ formula does not apply in this case: the result depends not just on the complex variable

\vec{V} \cdot \vec{V}

but in addition, there are three components of

Re \vec{V}

in the coordinate frame where

Im \vec{V}

points in the z direction (or the other way around).

We consider a more general integral with

tr \hat{X} \cdot \hat{Ω}

instead of

\vec{r} \cdot \hat{Ω} \cdot \vec{V}

. This integral does not reduce to the HCIZ integral and needs special treatment.

We use a quaternionic representation of

O (3)

and write this integral:

\begin{matrix} Q {(\vec{r}, \vec{V})}_{i j; k l} = T_{i j}^{α β} T_{k l}^{μ ν} H_{α β μ ν} (\hat{R}); \end{matrix}

(A8)

\begin{matrix} H_{α β μ ν} (\hat{R}) = \int_{S_{3}} \frac{(d q)}{| S_{3} |} q_{α} q_{β} q_{μ} q_{ν} exp (ı q_{λ} q_{ρ} R_{λ ρ}); \end{matrix}

(A9)

\begin{matrix} R_{λ ρ} = \frac{1}{2} (T_{i j}^{λ ρ} + T_{i j}^{ρ λ}) X_{i j}; \end{matrix}

(A10)

\begin{matrix} T_{i j}^{α β} = \frac{1}{2} tr σ_{i} τ_{α} σ_{j} τ_{β}^{†}; \end{matrix}

(A11)

\begin{matrix} τ_{α} = {1, ı \vec{σ}}; α = (0, 1, 2, 3) \end{matrix}

(A12)

In this representation, we have full

O (4)

symmetry of this integral over unit sphere

S_{3}

in four dimensions, plus there is a symmetry of the tensor

R_{α β} = R_{β α}

. There is, in fact, only one basic integral, with H related to its derivatives by the real parts of components of

Re R_{α β}

\begin{matrix} W (\hat{R}) = \int_{S_{3}} \frac{(d q)}{| S_{3} |} exp (ı q_{α} q_{β} R_{α β}); \end{matrix}

(A13)

\begin{matrix} H_{α β μ ν} (\hat{R}) = - \frac{\partial^{2} W (\hat{R})}{\partial Re R_{α β} \partial Re R_{μ ν}} \end{matrix}

(A14)

The integral can be reduced to a calculable one-dimensional integral using the following transformations.

\begin{matrix} W (\hat{R}) = \frac{1}{π^{2}} \int_{- \infty}^{+ \infty} \frac{d τ exp (ı τ)}{2 π} \int d^{4} q exp (- q_{α} q_{β} (ı τ δ_{α β} - ı R_{α β})) = \\ - \int_{- \infty}^{+ \infty} \frac{d τ exp (ı τ)}{2 π \sqrt{det (τ \hat{I} - \hat{R})}} \end{matrix}

(A15)

The normalization can be verified by tending

\hat{R} \to \pm ı ϵ \hat{I}

. The integral can be computed by taking residue in a double pole at the origin. If this limit is taken from the upper semiplane where the exponent decreases, the result equals 1; otherwise, from the lower semiplane, the integral yields zero.

In the general case of complex matrix

\hat{R}

, the integration path for

τ

should be shifted down to the lower semiplane to stay below all the roots of the determinant as a characteristic polynomial in

τ

Our algorithm finds these roots and shifts the path in the complex plane of

τ

twice farther than the lowest root with a negative imaginary part to avoid singularities in the line integral.

Figure A1. Mathematica^® code computing

S^{3}

Fourier integral for arbitrary tensor R

Figure A1. Mathematica^® code computing

S^{3}

Fourier integral for arbitrary tensor R

It can be computed numerically in a fraction of a second in Mathematica^® for arbitrary tensor

\hat{R}

by the following simple code Figure A1, see [39].

As for the derivatives of this generating function

W (R)

by each component of the tensor

R_{α β}

it is given by a well-known formula from perturbation theory

\begin{matrix} \frac{\partial W (\hat{R})}{\partial R_{α β}} = \sum_{k = 1}^{4} ψ_{k}^{α} ψ_{k}^{β} \frac{\partial W (\hat{R})}{\partial R_{k}} \end{matrix}

(A16)

Here the

ψ_{k}^{α}

is the eigenvector of

\hat{R}

corresponding to eigenvalue

R_{k}

. The second derivatives we would need for the product of two

Ω

matrices would require the differentiation of the eigenfunctions, given by the same perturbation theory, this time for the eigenfunction

\begin{matrix} \frac{\partial ψ_{i}}{\partial R_{k ℓ}} = \sum_{j \neq i} \frac{1}{R_{i} - R_{j}} (\frac{\partial \hat{R}}{\partial R_{k ℓ}} ψ_{i}, ψ_{j}) ψ_{j} . \end{matrix}

(A17)

So far, we ignored the requirement of a positive imaginary part of the circulation. This requirement amounts to the insertion of the theta function of this imaginary part.

We can use the

O (4)

transformations of the vector

q_{α}

to diagonalize the imaginary part of the tensor

\hat{R}

. Unfortunately, we cannot simultaneously diagonalize these two matrices by an orthogonal transformation.

Thus we are left with the following restricted integral over the sphere

S_{3}

, using the stereographic coordinates to avoid spurious singularities

\begin{matrix} W (\hat{R}) = \frac{4}{π^{2}} \int_{R_{3}} \frac{d^{3} V exp (ı q_{α} q_{β} Re R_{α β} - q_{i}^{2} Im R_{i})}{{(1 + \vec{V} \cdot \vec{V})}^{3}} Θ (q_{i}^{2} Im R_{i i}); \end{matrix}

(A18)

\begin{matrix} \vec{q} = \{2 \vec{V}, (1 - \vec{V} \cdot \vec{V})\} / (1 + \vec{V} \cdot \vec{V}); \end{matrix}

(A19)

The positivity condition in the stereographic coordinates reduces to a positive region of an algebraic surface in

R_{3}

\begin{matrix} 4 x^{2} Im R_{1} + 4 y^{2} Im R_{2} + 4 z^{2} Im R_{3} + {(1 - x^{2} - y^{2} - z^{2})}^{2} Im R_{4} > 0 \end{matrix}

(A20)

The positivity condition can be resolved analytically for one coordinate, say z, as an algebraic function of the remaining two.

Figure A2. The Mathematica^® code to compute the restricted

S^{3}

Fourier integral

Figure A2. The Mathematica^® code to compute the restricted

S^{3}

Fourier integral

Thus, the positivity inequality selects some calculable regions in

R_{3}

, which speeds up the computation. This representation of

\tilde{W} (\hat{R})

was implemented as a Mathematica^® algorithm [38], Figure A2. The three-dimensional convergent integral over

R_{3}

is still a numerical challenge, which takes a minute of Mathematica^® time.

We also implemented a Python version in the popular library SciPy, but the computations took too much CPU time to be useful.

Appendix B Linearized loop equations in 3D

Let us solve in 3D the linear set of recurrent equations derived in Section 4.4.

Only two independent real parameters exist in

Im {\vec{μ}}_{k}

. In the canonical form (Section 4.1) in 3D the two parameters were shifts of coordinates

α_{1}, α_{2}

with third coordinate

β

related to them by

α_{1}^{2} + α_{2}^{2} = 1 + β^{2}

We resolve this ambiguity by using the pseudo-inverse

2 \times 2

matrix. Here are the original complex equations.

\begin{matrix} Im {\vec{μ}}_{k} \cdot {\vec{U}}_{k} = ı B_{k}; \end{matrix}

(A21a)

\begin{matrix} B_{k} = (Re {\vec{μ}}_{k}) \cdot {\vec{U}}_{k} + {\vec{V}}_{k} \cdot (\vec{λ} + \sum_{0}^{k - 1} {\vec{μ}}_{l} \times {\vec{q}}_{l}); \end{matrix}

(A21b)

\begin{matrix} {\vec{U}}_{k} = G_{k} {\vec{q}}_{k} \times {\vec{F}}_{k}; \end{matrix}

(A21c)

\begin{matrix} {\vec{V}}_{k} = G_{k} {\vec{q}}_{k} - 2 {\vec{F}}_{k}; \end{matrix}

(A21d)

The solution of these three equations in [32] has the form

\begin{matrix} Im {\vec{μ}}_{k} = Re ({\vec{γ}}_{k} B_{k}) \end{matrix}

(A22a)

\begin{matrix} {\vec{γ}}_{k} = {\vec{Q}}_{k} \cdot {ı, 1} \end{matrix}

(A22b)

\begin{matrix} {\hat{Q}}_{k} = {({\hat{R}}_{k}^{†} \cdot {\hat{R}}_{k})}^{- 1} \cdot {\hat{R}}_{k}^{†} \end{matrix}

(A22c)

\begin{matrix} {\hat{R}}_{k} = {Re {\vec{U}}_{k}, Im {\vec{U}}_{k}} \end{matrix}

(A22d)

where the inverse

3 \times 3

matrix

{\hat{X}}^{- 1}

is understood as pseudo-inverse (dropping the null space part).

The complex number

B_{k}

is linearly related to

Re {\vec{μ}}_{k}

, the known previous vectors

{\vec{μ}}_{l < k}

and unknown

\vec{λ}

, which yields recurrent relations, which we are going to study below.

After solving these equations, the variation of the closure equation

\begin{matrix} \sum_{l = 0}^{N - 1} {\vec{μ}}_{l} \times {\vec{q}}_{l} = 0 \end{matrix}

(A23)

provides a linear set of six equations for

Re \vec{λ}, Im \vec{λ}

, relating these two vectors to all the rotation vectors

Re μ_{k}

Let us now proceed by assuming the following linear set of real vector relations (with some real

3 \times 3

matrices

{\hat{M}}_{k l}, {\hat{P}}_{k}, {\hat{Q}}_{k}

to be determined ):

\begin{matrix} Im {\vec{μ}}_{k} = \sum_{l = 0}^{k} {\hat{M}}_{k l} \cdot Re {\vec{μ}}_{l} + {\hat{P}}_{k} \cdot Re \vec{λ} + {\hat{Q}}_{k} \cdot Im \vec{λ}; \end{matrix}

(A24)

Let us compare it with the above relations (A22a), (A21a):

\begin{matrix} Im {\vec{μ}}_{k} = Re ({\vec{γ}}_{k} \otimes {\vec{U}}_{k} \cdot Re {\vec{μ}}_{k}) + Re ({\vec{γ}}_{k} \otimes (Σ_{k} + {\vec{V}}_{k} \cdot \vec{λ})); \end{matrix}

(A25)

\begin{matrix} Σ_{k} = \sum_{l = 0}^{k - 1} {\vec{q}}_{l} \times {\vec{V}}_{k} \cdot (Re {\vec{μ}}_{l} + ı Im {\vec{μ}}_{l}) \end{matrix}

(A26)

Comparing the terms, we obtain a set of recurrent equations for

\hat{M}, \hat{P}, \hat{Q}

\begin{matrix} {\hat{M}}_{k k} = Re ({\vec{γ}}_{k} \otimes {\vec{U}}_{k}); \end{matrix}

(A27a)

\begin{matrix} {\hat{M}}_{k > l} = Re ({\vec{γ}}_{k} \otimes {\vec{V}}_{k} \cdot {\hat{q}}_{l}) - \sum_{n = l}^{k - 1} Im ({\vec{γ}}_{k} \otimes {\vec{V}}_{k} \cdot {\hat{q}}_{n}) \cdot {\hat{M}}_{n l}; \end{matrix}

(A27b)

\begin{matrix} {\hat{P}}_{k} = Re ({\vec{γ}}_{k} \otimes {\vec{V}}_{k}) + \sum_{l = 0}^{k - 1} Im ({\vec{γ}}_{k} \otimes {\vec{V}}_{k} \cdot {\hat{q}}_{l}) \cdot {\hat{P}}_{l}; \end{matrix}

(A27c)

\begin{matrix} {\hat{Q}}_{k} = - Im ({\vec{γ}}_{k} \otimes {\vec{V}}_{k}) + \sum_{l = 0}^{k - 1} Im ({\vec{γ}}_{k} \otimes {\vec{V}}_{k} \cdot {\hat{q}}_{l}) \cdot {\hat{Q}}_{l}; \end{matrix}

(A27d)

where the dual tensor

\hat{X}

to the vector

\vec{X}

is defined as

{\hat{X}}_{α β} \equiv e_{α β γ} X_{γ};

(A28)

The last two equations can be combined into one complex recurrent equation for

{\hat{Γ}}_{k} = {\hat{P}}_{k} - ı {\hat{Q}}_{k}

\begin{matrix} Im {\vec{μ}}_{k} = \sum_{l = 0}^{k} {\hat{M}}_{k l} \cdot Re {\vec{μ}}_{l} + Re ({\hat{Γ}}_{k} \cdot \vec{λ}); \end{matrix}

(A29)

\begin{matrix} {\hat{Γ}}_{k} = {\vec{γ}}_{k} \otimes {\vec{V}}_{k} + \sum_{l = 0}^{k - 1} Im ({\vec{γ}}_{k} \otimes {\vec{V}}_{k} \cdot {\hat{q}}_{l}) \cdot {\hat{Γ}}_{l}^{*}; \end{matrix}

(A30)

Finally, the closure equation becomes

\begin{matrix} \sum_{k = 0}^{N - 1} (- ı {\hat{q}}_{k} \cdot Re {\vec{μ}}_{k} + \sum_{l = 0}^{k} {\hat{q}}_{k} \cdot {\hat{M}}_{k l} \cdot Re {\vec{μ}}_{l} + {\hat{q}}_{k} \cdot {\hat{P}}_{k} \cdot Re \vec{λ} + {\hat{q}}_{k} \cdot {\hat{Q}}_{k} \cdot Im \vec{λ}) = 0; \end{matrix}

(A31a)

This is a complex vector equation for two real vectors

Re \vec{λ}, Im \vec{λ}

\begin{matrix} \hat{P} \cdot Re \vec{λ} + \hat{Q} \cdot Im \vec{λ} = \vec{R}; \end{matrix}

(A32b)

\begin{matrix} \hat{P} = \sum_{k = 0}^{N - 1} {\hat{q}}_{k} \cdot {\hat{P}}_{k}; \end{matrix}

(A32c)

\begin{matrix} \hat{Q} = \sum_{k = 0}^{N - 1} {\hat{q}}_{k} \cdot {\hat{Q}}_{k}; \end{matrix}

(A32d)

\begin{matrix} \vec{R} = \sum_{n = 0}^{N - 1} (ı {\hat{q}}_{n} \cdot Re {\vec{μ}}_{n} - \sum_{l = 0}^{n} {\hat{q}}_{n} \cdot {\hat{M}}_{n l} \cdot Re {\vec{μ}}_{l}) \end{matrix}

(A32e)

The solution is expressed in terms of a block matrix

\begin{matrix} \hat{H} = \{\begin{matrix} Re \hat{P} & Re \hat{Q} \\ Im \hat{P} & Im \hat{Q} \end{matrix}\} \end{matrix}

(A33)

\{\begin{matrix} Re \vec{λ} \\ Im \vec{λ} \end{matrix}\} = {\hat{H}}^{- 1} \cdot \{\begin{matrix} Re \vec{R} \\ Im \vec{R} \end{matrix}\}

(A34)

There is a following complication [32]. The matrix

\hat{H}

viewed as

6 \times 6

dimensional real matrix has a null space of three real 6-dimensional eigenvectors. These eigenvectors can be combined in complex 3d vectors

ψ_{1}, ψ_{2}, ψ_{3}

corresponding to the block structure of

\hat{H}

\begin{matrix} \hat{H} \cdot \{\begin{matrix} Re {\vec{ψ}}_{i} \\ Im {\vec{ψ}}_{i} \end{matrix}\} = 0, i = 1, 2, 3; \end{matrix}

(A35)

Therefore, the complex 3D vector

\vec{λ}

is defined modulo superposition of these three complex eigenvectors.

A particular solution for

\vec{λ}

can be obtained using the pseudo-inverse.

In addition, there are three constraints on the angular variables

Re {\vec{μ}}_{k}

. These constraints have the following form [32]

\begin{matrix} \sum_{k} {\vec{Θ}}_{i k} \cdot Re {\vec{μ}}_{k} = 0; i = 1, 2, 3; \end{matrix}

(A36)

\begin{matrix} {\vec{Θ}}_{i k} = Re ({\vec{ψ}}_{i}^{*} \cdot {\hat{R}}_{k}); \end{matrix}

(A37)

The coefficients

{\vec{Θ}}_{i k}

of these constraints are nonlinear functions of the current positions

{\vec{F}}_{0}, \dots {\vec{F}}_{N - 1}

. These constraints lead to projections of the SDE to the quotient space, as we derive in the Section 4.7.

Here are the results for

\vec{λ}, Im {\vec{μ}}_{k}

in terms of rotation parameters

Re {\vec{μ}}_{k}

(with

\hat{I}

being

3 \times 3

unit matrix)

\begin{matrix} \vec{λ} = \sum_{l = 0}^{N - 1} {\hat{Λ}}_{l} \cdot Re {\vec{μ}}_{l}; \end{matrix}

(A38)

\begin{matrix} {\hat{Λ}}_{l} = \{\begin{matrix} \hat{I} & ı \hat{I} \end{matrix}\} \cdot {\hat{H}}^{- 1} \cdot \{\begin{matrix} Re {\hat{R}}_{l} \\ Im {\hat{R}}_{l} \end{matrix}\}; \end{matrix}

(A39)

\begin{matrix} {\hat{R}}_{l} = ı {\hat{q}}_{l} - \sum_{n = l}^{N - 1} {\hat{q}}_{n} \cdot {\hat{M}}_{n l}; \end{matrix}

(A40)

\begin{matrix} Im {\vec{μ}}_{k} = \sum_{l = 0}^{N - 1} {\hat{S}}_{k l} \cdot Re {\vec{μ}}_{l}; \end{matrix}

(A41)

\begin{matrix} {\hat{S}}_{k l} = {\hat{M}}_{k l} θ (k - l + 1 / 2) + Re ({\hat{Γ}}_{k} \cdot {\hat{Λ}}_{l}); \end{matrix}

(A42)

References

Migdal, A. Loop Equation and Area Law in Turbulence. In Quantum Field Theory and String Theory; Baulieu, L.; Dotsenko, V.; Kazakov, V.; Windey, P., Eds.; Springer US, 1995; pp. 193–231. [CrossRef]
Migdal, A. Statistical Equilibrium of Circulating Fluids. Physics Reports 2023, arXiv:physics.flu-dyn/2209.12312]1011C, 1–117. [Google Scholar] [CrossRef]
Migdal, A.A. Random Surfaces and Turbulence. In Proceedings of the Proceedings of the International Workshop on Plasma Theory and Nonlinear and Turbulent Processes in Physics, Kiev, April 1987; p. 1988460.
Makeenko, Y.; Migdal, A. Exact equation for the loop average in multicolor QCD. Physics Letters B 1979, 88, 135–137. [Google Scholar] [CrossRef]
Migdal, A. Loop equations and 1N expansion. Physics Reports 1983, 201. [Google Scholar] [CrossRef]
Migdal, A. Momentum loop dynamics and random surfaces in QCD. Nuclear Physics B 1986, 265, 594–614. [Google Scholar] [CrossRef]
Migdal, A. Second quantization of the Wilson loop. Nuclear Physics B - Proceedings Supplements 1995, 41, 151–183. [Google Scholar] [CrossRef]
Migdal, A.A. Hidden symmetries of large N QCD. Prog. Theor. Phys. Suppl. 1998, 131, 269–307. [Google Scholar] [CrossRef]
Anderson, P.D.; Kruczenski, M. Loop equations and bootstrap methods in the lattice. Nuclear Physics B 2017, 921, 702–726. [Google Scholar] [CrossRef]
Kazakov, V.; Zheng, Z. Bootstrap for lattice Yang-Mills theory. Phys. Rev. D 2023, arXiv:hep-th/2203.11360]107, L051501. [Google Scholar] [CrossRef]
Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244–2247. [Google Scholar] [CrossRef]
Rovelli, C.; Smolin, L. Knot Theory and Quantum Gravity. Phys. Rev. Lett. 1988, 61, 1155–1158. [Google Scholar] [CrossRef]
Iyer, K.P.; Sreenivasan, K.R.; Yeung, P.K. Circulation in High Reynolds Number Isotropic Turbulence is a Bifractal. Phys. Rev. X 2019, 9, 041006. [Google Scholar] [CrossRef]
Iyer, K.P.; Bharadwaj, S.S.; Sreenivasan, K.R. The area rule for circulation in three-dimensional turbulence. Proceedings of the National Academy of Sciences of the United States of America 2021, 118, e2114679118. [Google Scholar] [CrossRef] [PubMed]
Apolinario, G.; Moriconi, L.; Pereira, R.; valadão, V. Vortex Gas Modeling of Turbulent Circulation Statistics. PHYSICAL REVIEW E 2020, 102, 041102. [Google Scholar] [CrossRef] [PubMed]
Müller, N.P.; Polanco, J.I.; Krstulovic, G. Intermittency of Velocity Circulation in Quantum Turbulence. Phys. Rev. X 2021, 11, 011053. [Google Scholar] [CrossRef]
Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence Turbulence and Predictability. In Proceedings of the Geophysical Fluid Dynamics: Proc. Intl School of Physics E. Fermi; M Ghil, R.B.; Parisi, G., 1985, Eds. Amsterdam: North-Holland; pp. 84–88.
Migdal, A. Topological Vortexes, Asymptotic Freedom, and Multifractals. MDPI Fractals and Fractional, Special Issue 2023, [arXiv:physics.flu-dyn/2212.13356]. arXiv:physics.flu-dyn/2212.13356].
Migdal, A. Universal Area Law in Turbulence, 2019, [arXiv:1903.08613]. 2019; arXiv:1903.08613].
Migdal, A. Scaling Index α=12 In Turbulent Area Law, 2019, [arXiv:1904.00900v2]. arXiv:1904.00900v2].
Migdal, A. Exact Area Law for Planar Loops in Turbulence in Two and Three Dimensions, 2019, [arXiv:1904.05245v2]. arXiv:1904.05245v2].
Migdal, A. Analytic and Numerical Study of Navier-Stokes Loop Equation in Turbulence, 2019, [arXiv:1908.01422v1]. 2019; arXiv:1908.01422v1].
Migdal, A. Turbulence, String Theory and Ising Model, 2019, [arXiv:1912.00276v3]. arXiv:1912.00276v3].
Migdal, A. Towards Field Theory of Turbulence, 2020, [arXiv:hep-th/2005.01231]. arXiv:hep-th/2005.01231].
Migdal, A. Probability Distribution of Velocity Circulation in Three Dimensional Turbulence, 2020, [arXiv:hep-th/2006.12008]. arXiv:hep-th/2006.12008].
Migdal, A. Clebsch confinement and instantons in turbulence. International Journal of Modern Physics A 2020, arXiv:hep-th/2007.12468v7]35, 2030018. [Google Scholar] [CrossRef]
Migdal, A. Asymmetric vortex sheet. Physics of Fluids 2021, 33, 035127. [Google Scholar] [CrossRef]
Migdal, A. Vortex sheet turbulence as solvable string theory. International Journal of Modern Physics A 2021, 36, 2150062. [Google Scholar] [CrossRef]
Migdal, A. Confined Vortex Surface and Irreversibility. 1. Properties of Exact solution, 2021, [arXiv:physics.flu-dyn/2103.02065v10]. arXiv:physics.flu-dyn/2103.02065v10].
Migdal, A. Confined Vortex Surface and Irreversibility. 2. Hyperbolic Sheets and Turbulent statistics, 2021, [arXiv:physics.flu-dyn/2105.12719]. arXiv:physics.flu-dyn/2105.12719].
Wikipedia. Burgers vortex. https://en.wikipedia.org/wiki/Burgers_vortex, 2022. [Online; accessed 27-April-2022].
Migdal, A. Symmetric Fixed Point. https://www.wolframcloud.com/obj/sasha.migdal/Published/SymmetricFixedPoint.nb, 2023.
Briand, P.; Cardaliaguet, P.; Éric Chaudru de Raynal, P.; Hu, Y. Forward and backward stochastic differential equations with normal constraints in law. Stochastic Processes and their Applications 2020, 130, 7021–7097. [Google Scholar] [CrossRef]
Migdal, A. Complex Nonlinear Random Walk. https://www.wolframcloud.com/obj/sasha.migdal/Published/FQequation.nb, 2023.
Panickacheril John, J.; Donzis, D.A.; Sreenivasan, K.R. Laws of turbulence decay from direct numerical simulations. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2022, 380, 20210089. [Google Scholar] [CrossRef] [PubMed]
Sreenivasan, K.R.; Yakhot, V. The saturation of exponents and the asymptotic fourth state of turbulence, 2022. [CrossRef]
Migdal, A. Moving Four Vertices. https://www.wolframcloud.com/obj/sasha.migdal/Published/MovingFourVertices.nb, 2023.
Migdal, A. Restricted O(3) Fourier Integral. https://www.wolframcloud.com/obj/sasha.migdal/Published/SphericalThetaIntegral.nb, 2023.
Migdal, A. Matrix Fourier Transform in S3. https://www.wolframcloud.com/obj/sasha.migdal/Published/ThetaIntegral.nb, 2023.
McSwiggen, C. The Harish-Chandra integral: An introduction with examples, 2021, [arXiv:math-ph/1806.11155]. arXiv:math-ph/1806.11155].

Figure 1. Backtracking wires corresponding to vorticity correlation function.

Figure 2. Logarithm of Euclidean distance for our random walk in six-dimensional space

Re \vec{F}, Im \vec{F}

as a function of a logarithm of the number of steps. The linear fit corresponds to fractal dimension

d_{f} = 1.02412 \pm 0.005

Figure 2. Logarithm of Euclidean distance for our random walk in six-dimensional space

Re \vec{F}, Im \vec{F}

as a function of a logarithm of the number of steps. The linear fit corresponds to fractal dimension

d_{f} = 1.02412 \pm 0.005

Figure 3. The logarithmic plot of the CDF for the Euclidean length s of each step of our complex random walk. The tail of the CDF decays as

s^{- 2 .}

, indicating the probability distribution with power tail in PDF

\propto s^{- 3 .}

Figure 3. The logarithmic plot of the CDF for the Euclidean length s of each step of our complex random walk. The tail of the CDF decays as

s^{- 2 .}

, indicating the probability distribution with power tail in PDF

\propto s^{- 3 .}

Figure 4. Fitting the random walk distance as a power of number N of steps times a power of

log N

Figure 4. Fitting the random walk distance as a power of number N of steps times a power of

log N

Figure 5. The logarithmic plot of the CDF for the

κ

density. The tail of the CDF decays as

κ^{- 0.936266}

, compatible with the

κ^{- 1.936266}

power tail for PDF. The mean value of enstrophy and all higher moments diverge.

Figure 5. The logarithmic plot of the CDF for the

κ

density. The tail of the CDF decays as

κ^{- 0.936266}

, compatible with the

κ^{- 1.936266}

power tail for PDF. The mean value of enstrophy and all higher moments diverge.

Figure 6. Fitting noisy data for

1 / (t - 0.5)

(red dots) by a power law

b t^{- n}

. The best fit is a dashed blue line, corresponding to

{b \to 1.87992, n \to 1.42962}

. This simple example shows how wrong laws can be "derived" by fitting noisy data.

Figure 6. Fitting noisy data for

1 / (t - 0.5)

(red dots) by a power law

b t^{- n}

. The best fit is a dashed blue line, corresponding to

{b \to 1.87992, n \to 1.42962}

. This simple example shows how wrong laws can be "derived" by fitting noisy data.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Decaying Turbulence as a Fractal Curve

Abstract

1. Introduction

2. Loop equation

2.1. Loop operators

2.2. Dimensional reduction

2.3. Random global rotation

2.4. Decay or fixed point

3. Fractal curve in complex space

3.1. Random walk

3.2. Constraints imposed on a random step

3.3. Closure condition

3.4. Mirror pairs of solutions

3.5. The degenerate fixed point and its statistical meaning

4. The structure of turbulent manifold

4.1. Canonical form of a single step

4.2. Partition function

4.3. Symmetric fixed point

4.4. Infinitesimal complex rotations in 3D

4.5. The closure equation

4.6. Linear constraints and zero modes

4.7. Brownian motion on turbulent manifold

4.8. Mirror symmetry and inequality for the Wilson loop

4.9. Vorticity distribution and energy dissipation

4.10. The Group average of the Wilson loop and manifest inequality

4.11. Correlation functions

5. Open loop computations

6. Discussion

6.1. The Duality of Turbulence

6.2. Stokes-type functionals and vorticity correlations

6.3. Random walk around the Turbulent manifold

6.4. Simplified version of numerical Simulation

6.5. Preliminary comparison with experiments

6.6. Conclusion

Data Availability Statement

Acknowledgments

Appendix A The O(3) group average with and without restrictions

Appendix B Linearized loop equations in 3D

References

MDPI Initiatives

Important Links

Subscribe