0. Introduction
A while ago, we derived [
1,
3] a functional equation for the so-called loop average [
4,
5] or Wilson loop in Turbulence. The path to an exact solution by a dimensional reduction in this equation was proposed in the ’93 paper [
1], but we have only started exploring this path.
At the time, we could not compare a theory with anything but crude measurements in physical and numerical experiments at modest Reynolds numbers. All these experiments agreed with the K41 scaling, so the exotic equation based on unjustified methods of quantum field theory was premature.
The specific prediction of the Loop equation, namely the Area law [
1], could not be verified in DNS at the time with existing computer power.
The situation has changed over the last decades. No alternative microscopic theory based on the Navier-Stokes equation emerged, but our understanding of the strong turbulence phenomena grew significantly.
On the other hand, the loop equations technology in the gauge theory also advanced over the last decades. The correspondence between the loop space functionals and the original vector fields was better understood, and various solutions to the gauge loop equations were found.
In particular, the momentum loop equation was developed, similar to our momentum loop used below [
6,
7,
8]. Recently, some numerical methods were found to solve loop equations beyond perturbation theory [
9,
10].
The loop dynamics was extended to quantum gravity, where it was used to study nonperturbative phenomena [
11,
12].
All these old and new developments made loop equations a major nonperturbative approach to gauge field theory.
So, it is time to revive the hibernating theory of the loop equations in Turbulence, where these equations are much simpler.
The latest DNS [
13,
14,
15,
16] with Reynolds numbers of tens of thousands revealed and quantified violations of the K41 scaling laws. These numerical experiments are in agreement with so-called multifractal scaling laws [
17].
However, as we argued in [
2,
18], at those Reynolds numbers, the DNS cannot yet distinguish between pure scaling laws with anomalous dimension
and some algebraic function of the logarithm of scale
modifying the K41 scaling.
Theoretically, we studied the loop equation in the confinement region (large circulation over large loop
C), and we have justified the Area law, suggested back in ’93 on heuristic arguments [
1].
This law says that the PDF tails of velocity circulation PDF in the confinement region are functions of the minimal area inside this loop.
It was verified in DNS four years ago [
13] which triggered the further development of the geometric theory of turbulence [
2,
14,
15,
16,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27,
28,
29,
30].
In particular, the Area law was justified for flat and quadratic minimal surfaces [
22], and an exact scaling law in confinement region
was derived [
21]. The area law was verified with better precision in [
14].
It was later conjectured in [
18] that the dominant field configurations in extreme Turbulence are so-called Kelvinons, which were shown to solve stationary Navier-Stokes equations assuming the sparse distribution of vorticity structures.
These topological solitons of the Euler theory are built around a vortex sheet bounded by a singular vortex line. This vortex line is locally equivalent to the cylindrical Burgers vortex [
31], with infinitesimal thickness in the limit of a large Reynolds number.
As we argued in [
2,
18], the Kelvinon has an anomalous dissipation, surviving the strong turbulent limit. This dissipation is proportional to the square of constant circulation of the Burgers vortex times a line integral of the tangent component of the strain along the loop.
The Kelvinon minimizes the energy functional, with anomalous terms coming from the Burgers core of the vortex line. There is also a constant scale factor
Z in the representation of the Kelvinon vorticity in terms of spherical Clebsch variables:
In that paper, the constant Z was related to the Kolmogorov energy dissipation density and the boundary value of the variable at the loop C.
The anomalous Hamiltonian [
2,
18] explicitly violated the K41 scaling by the logarithmic terms
in the region of small loops
C. This region resembles the asymptotically free QCD. The logarithmic terms were summed up by RG equation with running coupling constant logarithmically small in this region.
These exciting developments explain and quantitatively describe many interesting phenomena [
2] but do not provide a complete microscopic theory covering the full inertial range of Turbulence without simplifying assumptions of the sparsity of vortex structures.
Moreover, while the Kelvinon (presumably) solves the stationary Navier-Stokes equations, it does not solve the loop equations for the following reason.
The loop equation assumes that the velocity field is independent of the loop C. In this case, the variations of the circulation in the loop functional with respect to the shape C of the loop can be reduced to the Navier-Stokes equation.
Otherwise, the variation would also involve the variation of the velocity field .
This problem does not invalidate the Kelvinon theory as an ideal gas of random vortex rings sparsely distributed in a turbulent flow.
The loop functional is not needed for that statistical theory, and the stationary solution of the Navier-Stokes equation is sufficient. The shape of the loop and the vortex sheet inside would become random variables influenced by a background strain like in the pure vortex sheet solutions [
2].
These objections, however, prevent the Kelvinon gas model from being a complete theory of strong isotropic Turbulence. This is merely an approximation of the full theory.
In the present work, we develop the theory free of these assumptions by exactly solving the loop equations for decaying turbulence. Our representation of velocity circulation does not run into the problems of the Kelvinon gas model; nor do we make any approximations in the loop equations we are solving.
1. Loop Equation
We introduced the loop equation in Lecture Series at Cargese and Chernogolovka Summer Schools [
1].
Here is a summary for the new generation.
We write the Navier-Stokes equation as follows
The Wilson loop average for the Turbulence
treated as a function of time and a functional of the periodic function
(not necessarily a single closed loop), satisfies the following functional equation
The statistical averaging corresponds to initial randomized data, to be specified later.
The area derivative
is related to the variation of the functional when the little closed loop
is added
In the review, [
1,
2], we present the explicit limiting procedure needed to define these functional derivatives in terms of finite variations of the loop while keeping it closed.
All the operators
are expressed in terms of the spike operator
The area derivative operator can be regularized as
and velocity operator (with
)
In addition to the loop equation, every valid loop functional
must satisfy the Bianchi constraint [
4,
5]
In three dimensions, it follows from identity ; in general dimension , the dual vorticity is an antisymmetric tensor with components. The divergence of this tensor equals zero identically.
However, for the loop functional, this restriction is not an identity; it reflects that this functional is a function of a circulation of some vector field, averaged by some set of parameters.
In the Navier-Stokes equation, we did NOT add customary Gaussian random forces, choosing instead to randomize the initial data for the velocity field.
These random forces would lead to the potential term [
2] in the loop Hamiltonian
, breaking certain symmetries needed for the dimensional reduction we study below.
With random initial data instead of time-dependent delta-correlated random forcing, we no longer describe the steady state (i.e., statistical equilibrium) but decaying Turbulence, which is also an interesting process, manifesting the same critical phenomena.
The energy is pumped in at the initial moment and slowly dissipates over time, provided the viscosity is small enough, corresponding to the large Reynolds number we are studying.
2. Dimensional Reduction
The crucial observation in [
1] was that the right side of the Loop equation, without random forcing, dramatically simplifies in functional Fourier space. The dynamics of the loop field can be reproduced in a simple Ansatz
The difference with the original definition of
is that our new function
depends directly on
rather then through the function
taken at
.
This transformation is the dimensional reduction we mentioned above. From the point of view of the loop functional, there is no need to deal with field ; one could take a shortcut.
The reduced dynamics must be fitted to the Navier-Stokes dynamics of the original field. With the loop calculus developed above, we have all the necessary tools to build these reduced dynamics.
Let us stress an important point: the function is independent of the loop C. As we shall see later, it is a random variable with a universal distribution in functional space.
This removes an objection we made in the Introduction to the Kelvinon theory as well as any other Navier-Stokes stationary solutions, with a singularity at fixed loop C in space.
The functional derivative, acting on the exponential in (
14) could be replaced by the derivative
as follows
The equation for
as a function of
and also a function of time, reads:
where the operators
should be regarded as ordinary numbers, with the following definitions.
This transformation yields the following formula for the spike derivative
D in the above equation
The vorticity operator (
11) and velocity (
12) become ordinary numbers, which are some singular functionals of the trajectory
.
The first observation about this equation is that the viscosity factor cancels after the substitution (
17).
As we shall see, the viscosity enters initial data so that at any finite time t, the solution for P still depends on viscosity.
Another observation is that the spike derivative
turns to the discontinuity
in the limit
The relation of the operators in the QCD loop equation to the discontinuities of the momentum loop was noticed, justified, and investigated in [
7,
8].
In the Navier-Stokes theory, this relation provides the key to the exact solution.
In the same way, we find the limit for vorticity
and velocity (skipping the common argument
)
The Bianchi constraint is satisfied identically as it should
We arrive at a singular loop equation for
This equation is complex due to the irreversible dissipation effects in the Navier-Stokes equation.
The viscosity dropped from the right side of this equation; it can be absorbed in units of time. Viscosity also enters the initial data, as we shall see in the next section on the example of the random rotation.
However, the large-time asymptotic behavior of the solution would be universal, as it should be in the Turbulent flow.
We are looking for a degenerate fixed point [
2], a fixed manifold with some internal degrees of freedom. The spontaneous stochastization corresponds to random values of these hidden internal parameters.
Starting with different initial data, the trajectory would approach this fixed manifold at some arbitrary point and then keep moving around it, covering it with some probability measure.
The Turbulence problem is to find this manifold and determine this probability measure.
3. Random Global Rotation
Possible initial data for the reduced dynamics were suggested in the original papers [
1,
2]. The initial velocity field’s simplest but still meaningful distribution is the Gaussian one, with energy concentrated in the macroscopic motions. The corresponding loop field reads
where
is the velocity correlation function
The potential part drops out in the closed loop integral.
The correlation function varies at the macroscopic scale, which means that we could expand it in the Taylor series
The first term
is proportional to initial energy density,
and the second one is proportional to initial energy dissipation rate
where
is the dimension of space.
The constant term in (
27) as well as
terms drop from the closed loop integral, so we are left with the cross-term
, which reduces to a full square
This distribution is almost Gaussian: it reduces to Gaussian one by extra integration
The integration here involves all
independent
components of the antisymmetric tensor
. Note that this is ordinary integration, not the functional one.
The physical meaning of this is the random uniform vorticity at the initial moment.
Unfortunately, as we see it now, this initial data represents a spurious fixed point unrelated to the turbulence problem.
It was discussed in our review paper [
2]. The uniform global rotation represents a fixed point of the Navier-Stokes equation for arbitrary uniform vorticity tensor.
Gaussian integration by keeps it as a fixed point of the Loop equation.
The time derivative at this special initial data vanishes so that the exact solution of the loop equation with this initial data equals its initial value (
30).
Naturally, the time derivative of the momentum loop with the corresponding initial data will vanish as well.
It is instructive to look at the momentum trajectory for this fixed point.
The functional Fourier transform [
1,
2] leads to the following simple result for the initial values of
.
In terms of Fourier harmonics, this initial data read
As for the constant part of , it is not defined, but it drops from equations by translational invariance.
Note that this initial data is not real, as
. Positive and negative harmonics are real but unequal, leading to a complex Fourier transform. At fixed tensor
the correlations are
4. Decay or Fixed Point
The absolute value of loop average
stays below 1 at any time, which leaves two possible scenarios for its behavior at a large time.
The
Decay scenario in the nonlinear ODE (
24) corresponds to the
decrease of
.
Omitting the common argument
, we get the following
exact time-dependent solution (not just asymptotically, at
).
The
Fixed Point would correspond to the vanishing right side of the momentum loop equation (
24). Multiplying by
and reducing the terms, we find a singular algebraic equation
The fixed point could mean self-sustained Turbulence, which would be too good to be true, violating the second law of Thermodynamics. Indeed, it is easy to see that this fixed point cannot exist.
The fixed point equation (
43) is a linear relation between two vectors
with coefficients depending on various scalar products. The generic solution is simply
with the complex parameter
to be determined from the equation (
43).
This solution is degenerate: the fixed point equation is satisfied for arbitrary complex .
The discontinuity vector
aligned with the principal value
corresponds to vanishing vorticity in (
19), leading to a trivial solution of the loop equation
.
We are left with the decaying turbulence scenario (
42) as the only remaining physical solution.
5. Random Walk in Complex space
One may try the solution where the discontinuity vector is proportional to the principal value. However, in this case, such a solution does not exist.
There is, however, another solution where the vectors
are not aligned. This solution requires the following relations
These relations are very interesting. The complex numbers indicate irreversibility and lack of alignment leads to vorticity distributed along the loop.
Also, note that this complex vector is dimensionless, and the fixed point equation (47) is completely universal!
One can iteratively build this solution as a fractal curve by the following method.
Start with a complex vector .
We compute the next values
from the following discrete version of the discontinuity equations (47).
A solution of these equations can be represented using a complex vector
subject to two complex constraints
after which we can find the next value
We assume
N steps, each with the angle shift
.
Note that the complex unit vector is
not defined with the Euclidean metric in six dimensions
. Instead, we have a complex condition
which leads to
two conditions between real and imaginary parts
In
d dimensions, there are
complex parameters of the unit vector; with an extra linear constraint in (
49), there are now
free complex parameters at every step of our iteration, plus the discrete choice of the sign of the root in the solution of the quadratic equation.
At the last step,
, we need to get a closed loop
. This is one more constraint on the complex vectors
We use this complex vector constraint to fix the arbitrary initial complex vector as a function of all remaining parameters.
We have here a nonlinear random walk in complex vector space . The complex unit step depends on the current position .
The initial position is adjusted to close the trajectory after N steps at given rotations.
We are interested in the limit of infinitely many steps , corresponding to a closed fractal curve with a discontinuity at every point.
This solution’s ambiguity (there are fewer restrictions than the number of free parameters) is a welcome feature. One would expect this from a fixed point of the Hopf equation for the probability distribution.
In the best-known example, the microcanonical Gibbs distribution covers the energy surface with a uniform measure (ergodic hypothesis, widely accepted in Physics).
The parameters describing a point on this energy surface are not specified– in the case of an ideal Maxwell gas, these are arbitrary velocities of particles.
Likewise, the fixed manifold, corresponding to the limit of our fractal curve, is parametrized by N arbitrary local rotations, as discussed in the next section.
This degeneracy of our fixed manifold, combined with its rotation and translation invariance in loop space C, makes it an acceptable candidate for extreme isotropic Turbulence.
6. The Probability measure
The simplest case where these equations have nontrivial solutions is in three-dimensional space. For smaller dimensions, there is only a degenerate solution with zero vorticity (a vanishing cross product ).
The complex unit vector in
d dimensions can be parametrized by rotation matrix and a unit real vector in
dimensions
There is a multiple counting of the same unit vector with this parametrization: the rotation matrix space
must be factored by rotations
of the unit vector
.
Also, the sign change of
is equivalent to the reflection of the vector
, so we have to factor out such reflections to keep the sign of
arbitrary
The complex constraint for
can be used to fix these
as a linear function of
given a complex vector
as follows:
where
and
After that,
yields a quadratic equation for
.
Note in passing that belongs to De Sitter space . However, this is where an analogy with the ADS/CFT duality ends.
There are, in general, four solutions for : two signs for R in (60) and two more signs in a solution of the quadratic equation for (55d). We have to choose one of these four solutions at each step, also selecting the real solution for .
For each particular loop
C, there is a choice of the solution for each step, guaranteeing inequality
, namely, the one which would provide a positive projection of
on the local tangent vector of the loop:
This restriction guarantees the convergence of the Wilson loop as an expectation value over our manifold of the fractal curves. The
ambiguity of choosing one of the two restricted solutions remains at every step. We resolve this ambiguity by choosing the step
with minimal Euclidean length
The reason for choosing the shortest step is to avoid potential instability with growing steps as the number of these steps increases.
We found that the mean Euclidean distance of unconstrained random walk grows approximately linearly with the number N of steps, not showing any sign of instabilities.
We conclude that the fixed manifold of the decaying Turbulence is a tensor product of rotational and spherical spaces
We arrive at the invariant distribution for our fractal curve. At a fixed number
N of steps
where
are complex vectors, parametrized by
via recurrent equations (55),(
59).
The complex vector’s integration and delta function is understood as a product of its real and imaginary parts. This integration leads to a Jacobian factor in the measure, depending on the relative angles between all rotations.
This closure condition is sufficient by parameter count to eliminate a complex vector ; however, doing this at an arbitrary number of rotation matrices is a nontrivial technical problem.
We will address this and other technical problems in three dimensions using Mathematica®.
The remarkable universality of this fractal curve in complex space makes these problems worth an effort.
As for the computation of the Jacobian in (
67), it is easier than it looks.
There is a recurrent equation (in matrix notations, with complex vector treated as 6 dimensional real vector)
Finally, using the chain rule, we compute the Jacobian (the orthogonal matrices
all cancel)
7. Reflected solution and real correlation functions
There is an obvious problem with the solution we have found. The loop equation for
is complex, and so is the solution, particularly the vorticity in (
19). Since the equation for
is nonlinear, we cannot take a real part of
.
How do we make the correlation functions of vorticity real?
Another solution of the loop equations (47) corresponds to solving the recurrent equations (47) in the opposite direction on the loop. In the continuum limit, it corresponds to the orientation reversal .
A discrete version corresponds to counting points in the opposite direction on a loop. In the equations (47), only the sign in front of the gap will change, equivalent to a complex conjugation of the equation. In other words, the solution with the opposite orientation is the complex conjugate of the original solution .
The loop equation being linear, the arithmetic average of these two loop functionals would also solve the loop equation
Note that this is not equivalent to taking the real part of the Wilson loop, because we have not changed the sign of the imaginary unit in front of the loop integral in exponential.
8. Vorticity Distribution and Energy dissipation
The simplest quantity to compute in our theory is the local vorticity distribution.
As we shall see, it determines the energy dissipation rate.
The local vorticity for our decaying solution of the loop equation
Here
is an arbitrary point at the loop, which makes this expression a random variable.
Note that viscosity is canceled here, as it should be by dimensional counting (vorticity has the dimension of ).
In our random walk representation, the complex vorticity operator
The time derivative of energy density in our theory is
Solving this equation with boundary value
we relate
to mean initial energy
The probability distribution of
and its mean value
can be computed using our random walk. For the anomalous dissipation, we need the mean enstrophy to diverge [
2,
18], so that viscosity is compensated in the extreme turbulent limit.
As we shall see later, in
Section 10, this is what happens in our numerical simulations.
The microscopic picture of this infinite enstrophy differs from the singular vortex line.
In the Euler theory, divergence came from the singularity of the classical field. However, in our dual theory, it comes from the large fluctuation of the fractal curve in momentum space.
We can now write down our result for the Wilson loop in decaying Turbulence as a functional of the contour
C. Let us start with a three-dimensional case
The finite steps approximation we considered above
For the simplest circular loop in an
plane, we have
Figure 1.
Backtracking wires corresponding to vorticity correlation function.
Figure 1.
Backtracking wires corresponding to vorticity correlation function.
We observe that even at the large time
when the asymptotic fractal curve is already in place, there is a region of parameters
where the Wilson loop is a nontrivial universal function of a single variable
We can compute our prediction for this function by numerically solving the recurrent equations for our vectors and wait for the results with physical or numerical experiments in conventional three-dimensional decaying Turbulence.
9. Correlation Functions
The simplest observable quantities we can extract from the loop functional are the vorticity correlation functions [
2], corresponding to the loop
C backtracking between two points in space
, see
Figure 1. The vorticity operators are inserted at these two points.
The correlation function reduces to a random walk with a complex weight
In Fourier space, this reduces to the restricted random walk:
The numerical simulation of this correlation function would require significant computer resources.
Still, these resources are much more modest than those for full d dimensional simulations of the Navier-Stokes equation.
In our theory, the dimension of space enters as the number of components of the one-dimensional fluctuating field rather than the number of variables in the fluctuating velocity field .
Also, note that our quantum problem of the complex random walk naturally fits quantum computer architecture. Thus, in the future, when large quantum computers would become available for researchers, we can expect a real breakthrough in numerical simulations of the loop equation.
10. Computations
We wrote a
Mathematica®program [
32] generating our random walk, starting with a random complex vector
and using random orthogonal
matrix
at every step.
We have chosen the simplest circular loop (
84) and imposed the inequality (
62). In case two solutions were satisfying this inequality we have chosen the shortest step in Euclidean metric
, i.e., the one with minimal
.
For 1000 steps, it takes a few seconds on a laptop to compute the whole path. We generate a parallel table of 100000 paths 1000 steps, each with various random initial vectors with random set of rotation matrices for each step.
The path’s closure requires special efforts, which we plan to implement later on a supercomputer.
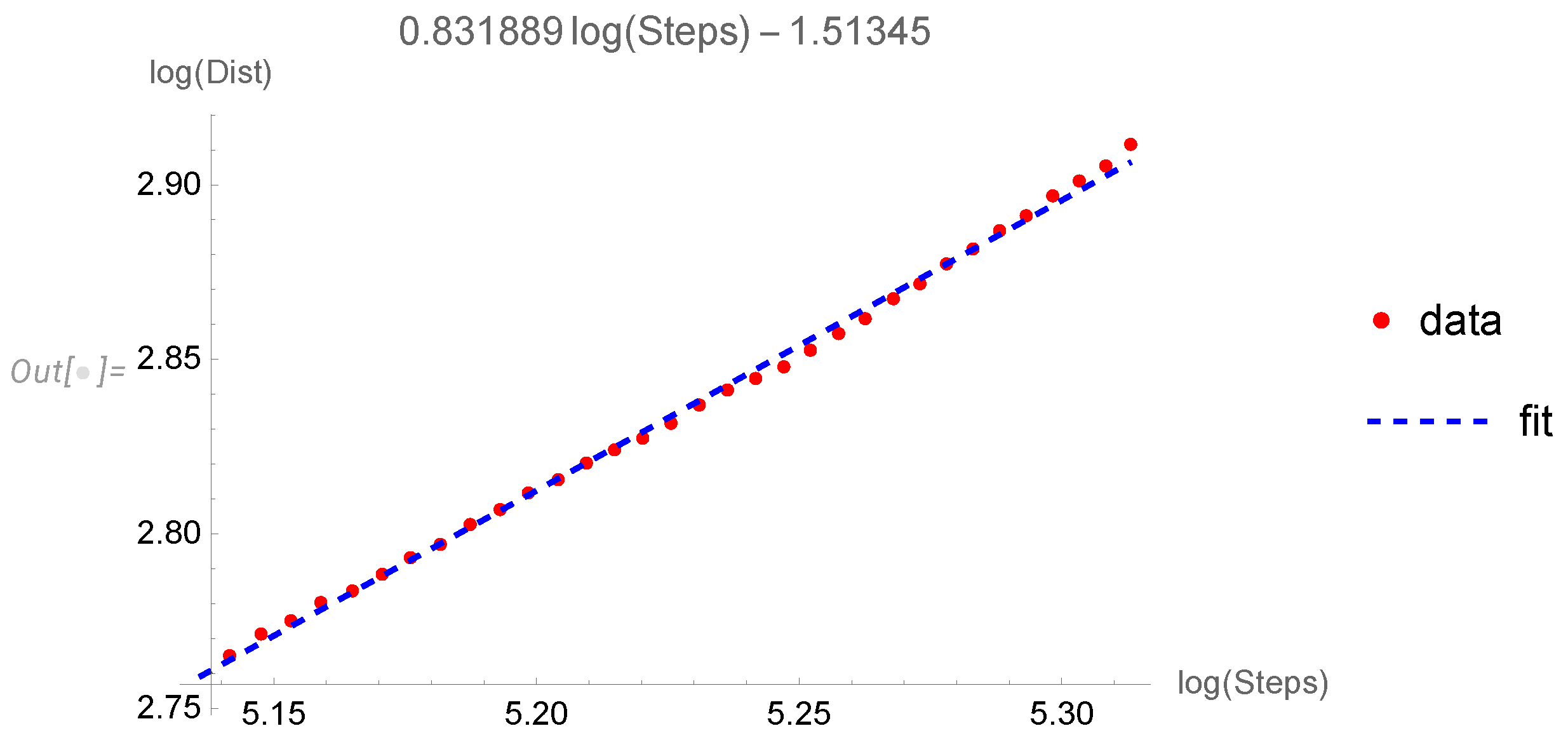
The simplest quantity to compute is a fractal dimension
of this random walk, defined as
The ordinary Brownian motion (linear random walk) has
, but our random walk is very different, mainly because the Euclidean distance of an elementary step
in De Sitter space is unlimited from above (though it is limited by 1 from below).
Here is the plot of
vs
(
Figure 2).
The statistical data for parameters
This data is compatible with
.
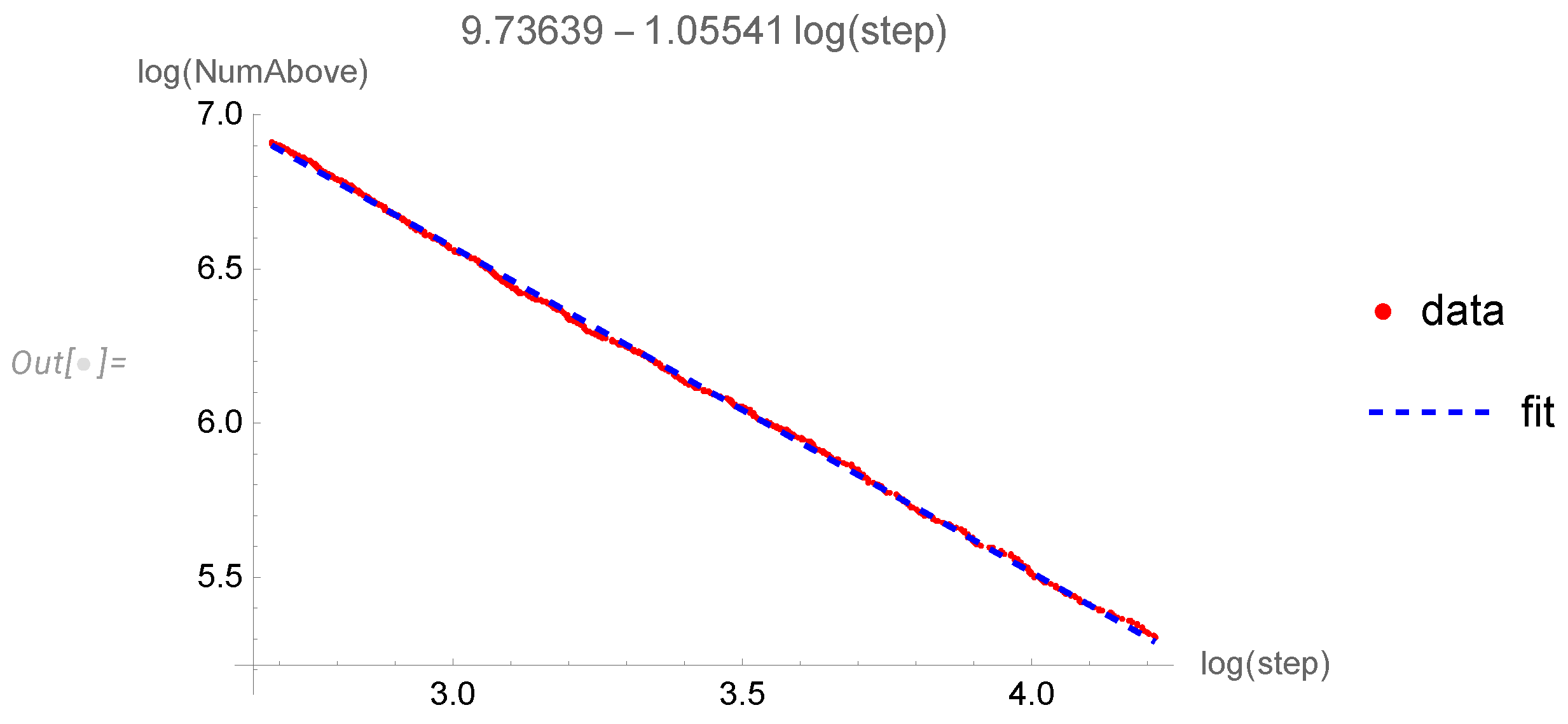
The distribution of the Euclidean length of each step
(
Figure 3).
The statistical table for the parameters of this fit
The mean value and error of a step are divergent.
Such a low decay of the step distribution undermines the concept of a finite fractal dimension as defined in (91). The linear fit is far from perfect for such a large statistics.
We conclude, that our random walk with unbounded step size is quite different from an ordinary fractal curve. The fractal dimension does not properly describe this random object.
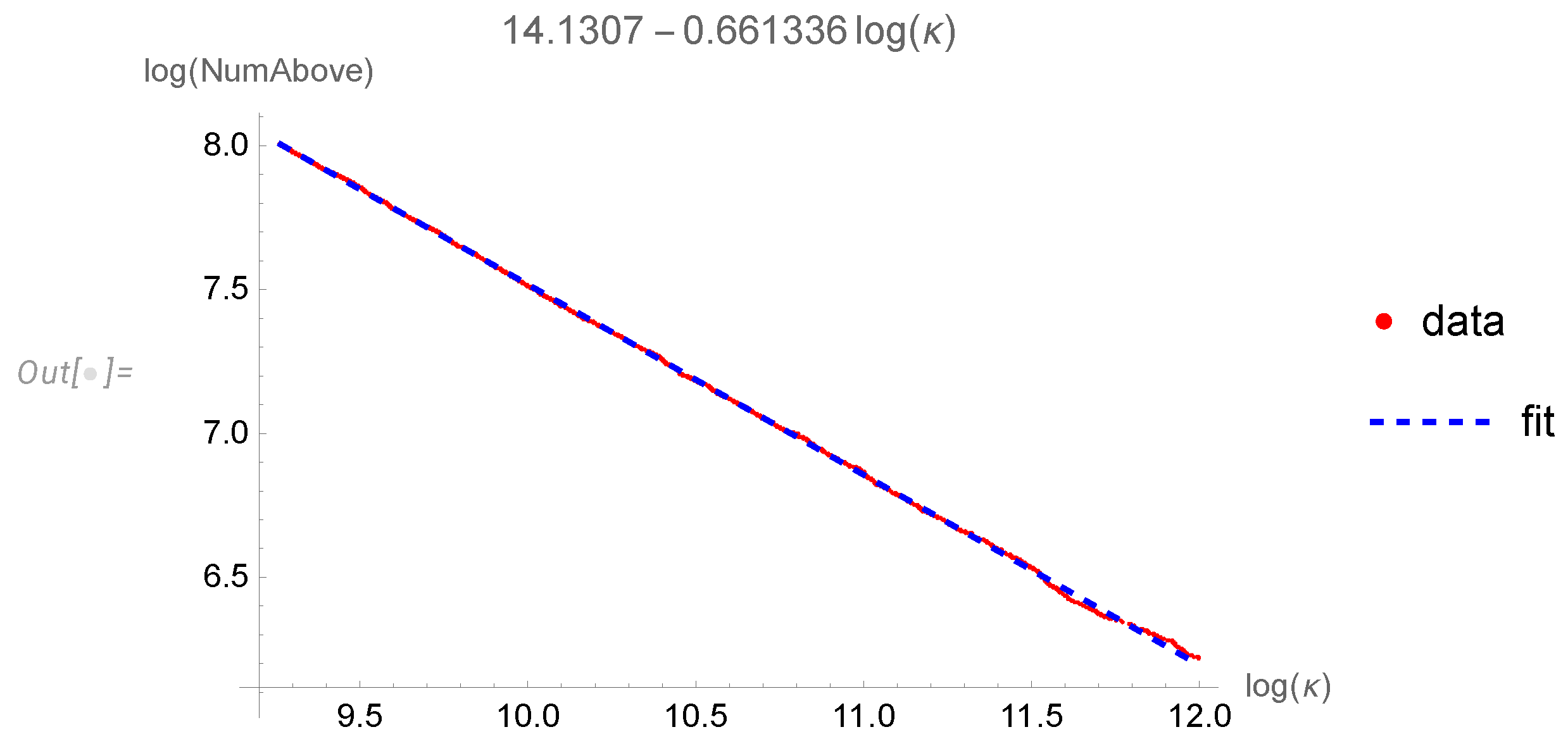
Another interesting distribution is
in (
75).
Figure 2.
Logarithm of Euclidean distance for our random walk in six-dimensional space as a function of a logarithm of the number of steps. The linear fit corresponds to fractal dimension .
Figure 2.
Logarithm of Euclidean distance for our random walk in six-dimensional space as a function of a logarithm of the number of steps. The linear fit corresponds to fractal dimension .
Figure 3.
The logarithmic plot of the CDF for the Euclidean length s of each step of our complex random walk. The tail of the CDF decays as , indicating the probability distribution with power tail in PDF .
Figure 3.
The logarithmic plot of the CDF for the Euclidean length s of each step of our complex random walk. The tail of the CDF decays as , indicating the probability distribution with power tail in PDF .
Figure 4.
The logarithmic plot of the CDF for the density. The tail of the CDF decays as , compatible with the power tail for PDF. The mean value of enstrophy and all higher moments diverge.
Figure 4.
The logarithmic plot of the CDF for the density. The tail of the CDF decays as , compatible with the power tail for PDF. The mean value of enstrophy and all higher moments diverge.
The CDF is shown in
Figure 4. The tail is compatible with
decay, corresponding to the
decay of the PDF. The mean value and all higher moments diverge, leading to anomalous dissipation.
The statistical table for the parameters of this fit
The computation of the Wilson loop and related correlation functions of vorticity needs an ensemble of closed fractal loops with various sets of random matrices.
The closure condition for the loop would require some computational effort because the probability of the random curve with fractal dimension returning to an initial point goes to zero with the increased number of steps.
An alternative approach of starting with a large closed loop and randomizing it point by point while preserving its closure.
These extra layers of computational complexity would require a supercomputer, which we plan to do later.
11. Discussion
We have presented an exact solution of the Navier-Stokes loop equations for the Wilson loop in decaying Turbulence as a functional of the shape and size of the loop in arbitrary dimension .
An expert in the traditional approach to Turbulence may wonder why the solutions of the Loop equation are relevant to the statistical distribution of the vorticity in a decaying turbulent flow.
Such questions were asked and answered in the gauge theories, including QCD [
6,
8,
9,
10] where the loop equations were derived first [
4,
5].
The solution of the loop equation with finite area derivative, satisfying Bianchi constraint, belongs to the so-called Stokes-type functionals [
4], the same as the Wilson loop for Gauge theory and fluid dynamics.
Extra complications in the gauge theory, which are fortunately absent in fluid dynamics, are the short-distance singularities related to the infinite number of fluctuating degrees of freedom in quantum field theory.
As we discussed in detail in [
2,
4,
5], any Stokes-type functional
satisfying boundary condition at shrunk loop
, and solving the loop equation can be iterated in the nonlinear term in the Navier-Stokes equations (which applies at large viscosity).
The resulting expansion in inverse powers of viscosity (weak Turbulence) exactly coincides with the ordinary perturbation expansion described by Wylde diagrams.
As we have seen, the Anzatz (
14) satisfies the loop equation and boundary condition at
. It has a finite area derivative, which obeys the Bianchi constraint, making it a Stokes-type functional.
We have demonstrated in [
1,
2] (and also here, in
Section 3) how the velocity distribution for the random uniform vorticity in the fluid was reproduced by a singular momentum loop
.
The solution for
in this special fixed point of the loop equation was random complex and had slowly decreasing Fourier coefficients, leading to a discontinuity
in a pair correlation function (38). The corresponding Wilson loop was equal to the Stokes-type functional (
30).
The exact solution for in decaying Turbulence which we have found in this paper, also leads to the Stokes functional satisfying the boundary value at the shrunk loop.
Therefore, it represents a statistical distribution in some Navier-Stokes flow, a degenerate fixed point of the Hopf equation for velocity circulation, summing up all the Wylde diagrams plus nonperturbative effects. Whether this exact solution is realized in Nature remains to be seen.
It is infinitely more complex than the randomly rotated fluid, as our curve has a discontinuity at every , corresponding to a distributed random vorticity.
This solution is described by a fractal curve in complex d dimensional space, a limit of a random walk with nonlinear algebraic relations between the previous position and the next one . These relations are degenerate: each step is characterized by an arbitrary element and an arbitrary element . This step also depends upon the previous position .
The periodicity condition provides a nonlinear equation for an initial position as a function of the above free parameters .
We simulated this random walk in three dimensions and studied its statistical properties. The distribution of lengths of steps in Euclidean six-dimensional space has a long tail .
The fractal dimension is not well defined for a random walk with such an intermittent step size, unbounded from above. The linear log-log fit as in (91) yields , but this fit is imperfect with our large statistics.
As for the distribution of an enstrophy density, it has a power tail corresponding to an infinite mean value and all higher moments. This infinity is how anomalous dissipation manifests in our solution.
These numerical simulations must be repeated on a supercomputer with better statistics and more steps. There are many things to do next with this conjectured solution to the decaying turbulence problem; the first is to look for unnoticed inconsistencies.
As a first test of this solution, let us compare it with various experimental data and those from DNS [
33].
There is no agreement between these data, they vary in Reynolds number, and they have other differences related to the experimental setup. No value n for the decay power would fit all that data. However, a consensus seems to be around , which means faster decay than we have.
We are skeptical about these data. As we recently learned [
34], there is a regime change at large Reynolds numbers; the numbers achievable in modern DNS are at such a transitional regime.
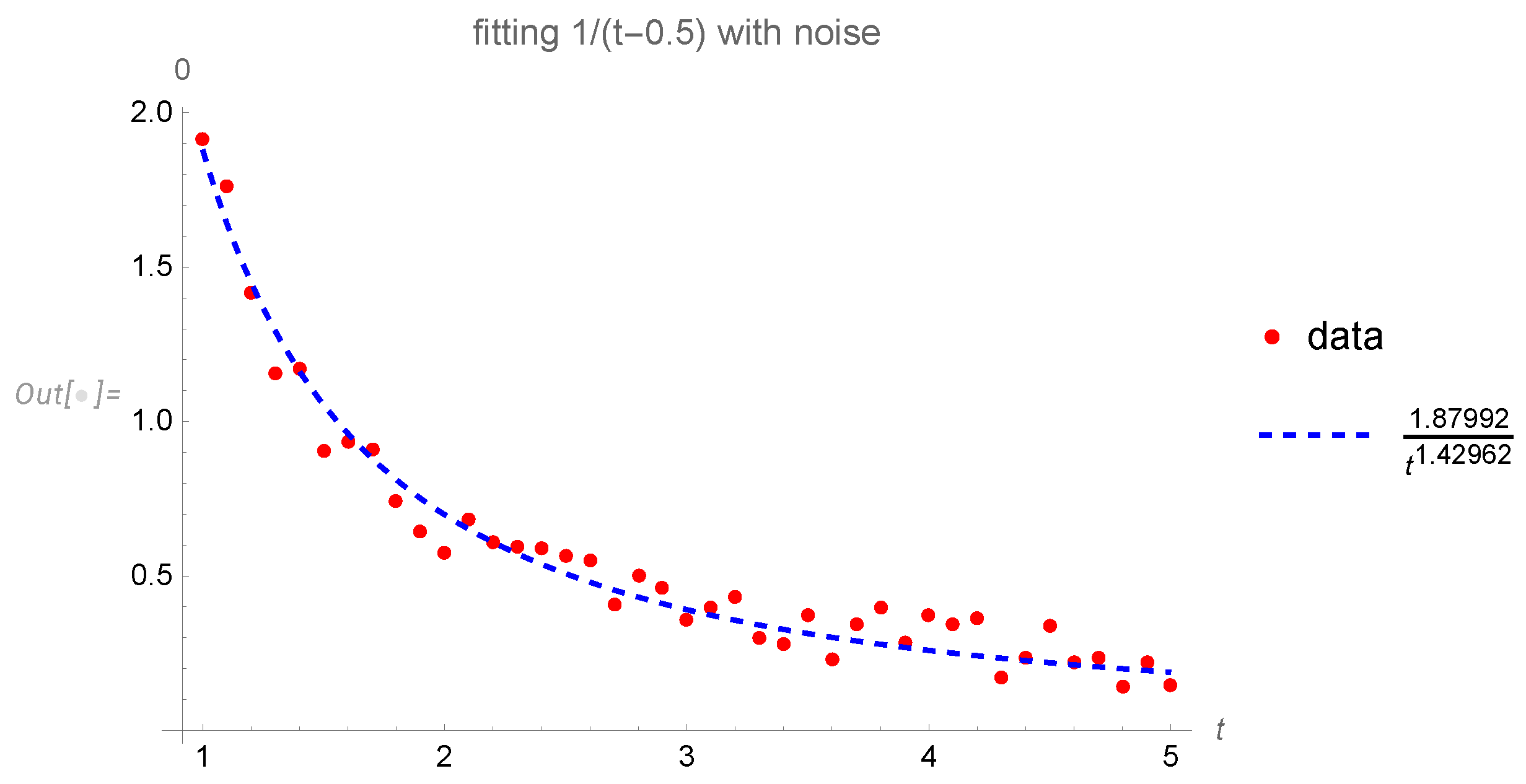
Besides, fitting powers is not a reliable method of deriving physical laws.
For example, we took a formula
, added random noise between
and fitted this data to
. The best fit produced some fake power
and some fake coefficient
in front (see
Figure 5)
Instead, one should compare a hypothetical theory with a null hypothesis by estimating the log-likelihood of both fits. In case the new theory is more likely as an explanation of the data, you may temporarily accept it until better data appears.
Presumably, our fixed point corresponds to a true infinite Reynolds limit, as it is completely universal and does not depend on the Reynolds scales.
If you assume no hidden scales are left, our law follows from dimensional analysis. Observed or simulated data with all have the powers of some other dimensional parameters related to the Reynolds number. They rely on (multifractal versions of) K41 spectra and other intermediate turbulent phenomena.
We have an anomalous dissipation rate: the mean value of the vorticity square diverges, compensating for the viscosity factor in the energy decay in extreme turbulent limit.
This mechanism of anomalous dissipation differs from the one we studied in the Kelvinon [
2,
18]. In those fixed points, the viscosity canceled in the dissipation rate due to the singular vorticity configurations with the thin vortex line resolved as a core of a Burgers vortex.
Here, in the dual theory of fractal momentum loop, the large fluctuations of this momentum loop lead to the divergent expectation value of the enstrophy.
Our solution is universal, rotational, and translational invariant. It has the expected properties of extreme isotropic Turbulence. Is it THE solution? Time will tell.
Data Availability Statement
We generated new data for the nonlinear complex random walk and the enstrophy distribution using the
Mathematica® code. This code, the data, and the three-dimensional plots are publicly available in Wolfram Cloud [
32].
Acknowledgments
I benefited from discussions of this theory with Sasha Polyakov, K.R. Sreenivasan, Greg Eyink, Luca Moriconi, Vladimir Kazakov, and Kartik Iyer. This research was supported by a Simons Foundation award ID 686282 at NYU Abu Dhabi.
References
- Migdal, A. Loop Equation and Area Law in Turbulence. In Quantum Field Theory and String Theory; Baulieu, L., Dotsenko, V., Kazakov, V., Windey, P., Eds.; Springer US, 1995; pp. 193–231. [Google Scholar] [CrossRef]
- Migdal, A. Statistical Equilibrium of Circulating Fluids. Physics Reports 2023, 1011C, 1–117. [Google Scholar] [CrossRef]
- Migdal, A.A. Random Surfaces and Turbulence. In Proceedings of the Proceedings of the International Workshop on Plasma Theory and Nonlinear and Turbulent Processes in Physics, Kiev, April 1987; Bar’yakhtar, V.G., Ed.; World Scientific, 1988; p. 460. [Google Scholar]
- Makeenko, Y.; Migdal, A. Exact equation for the loop average in multicolor QCD. Physics Letters B 1979, 88, 135–137. [Google Scholar] [CrossRef]
- Migdal, A. Loop equations and 1N expansion. Physics Reports 1983, 201. [Google Scholar]
- Migdal, A. Momentum loop dynamics and random surfaces in QCD. Nuclear Physics B 1986, 265, 594–614. [Google Scholar] [CrossRef]
- Migdal, A. Second quantization of the Wilson loop. Nuclear Physics B - Proceedings Supplements 1995, 41, 151–183. [Google Scholar] [CrossRef]
- Migdal, A.A. Hidden symmetries of large N QCD. Prog. Theor. Phys. Suppl. 1998, 131, 269–307. [Google Scholar] [CrossRef]
- Anderson, P.D.; Kruczenski, M. Loop equations and bootstrap methods in the lattice. Nuclear Physics B 2017, 921, 702–726. [Google Scholar] [CrossRef]
- Kazakov, V.; Zheng, Z. Bootstrap for lattice Yang-Mills theory. Phys. Rev. D 2023, 107, L051501. [Google Scholar] [CrossRef]
- Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244–2247. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Knot Theory and Quantum Gravity. Phys. Rev. Lett. 1988, 61, 1155–1158. [Google Scholar] [CrossRef]
- Iyer, K.P.; Sreenivasan, K.R.; Yeung, P.K. Circulation in High Reynolds Number Isotropic Turbulence is a Bifractal. Phys. Rev. X 2019, 9, 041006. [Google Scholar] [CrossRef]
- Iyer, K.P.; Bharadwaj, S.S.; Sreenivasan, K.R. The area rule for circulation in three-dimensional turbulence. Proceedings of the National Academy of Sciences of the United States of America 2021, 118, e2114679118. [Google Scholar] [CrossRef] [PubMed]
- Apolinario, G.; Moriconi, L.; Pereira, R.; valadão, V. Vortex Gas Modeling of Turbulent Circulation Statistics. PHYSICAL REVIEW E 2020, 102, 041102. [Google Scholar] [CrossRef] [PubMed]
- Müller, N.P.; Polanco, J.I.; Krstulovic, G. Intermittency of Velocity Circulation in Quantum Turbulence. Phys. Rev. X 2021, 11, 011053. [Google Scholar] [CrossRef]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence Turbulence and Predictability. In Proceedings of the Geophysical Fluid Dynamics: Proc. Intl School of Physics E. Fermi; M Ghil, R.B., Parisi, G., Eds.; North-Holland: Amsterdam, 1985; pp. 84–88. [Google Scholar]
- Migdal, A. Topological Vortexes, Asymptotic Freedom, and Multifractals. Fractal and Fractional 2023, 7, 351. [Google Scholar] [CrossRef]
- Migdal, A. Universal Area Law in Turbulence. arXiv 2019, arXiv:1903.08613. [Google Scholar]
- Migdal, A. Scaling Index In Turbulent Area Law. arXiv 2019, arXiv:1904.00900v2. [Google Scholar]
- Migdal, A. Exact Area Law for Planar Loops in Turbulence in Two and Three Dimensions. arXiv 2019, arXiv:1904.05245v2. [Google Scholar]
- Migdal, A. Analytic and Numerical Study of Navier-Stokes Loop Equation in Turbulence. arXiv 2019, arXiv:1908.01422v1. [Google Scholar]
- Migdal, A. Turbulence, String Theory and Ising Model. arXiv 2019, arXiv:1912.00276v3. [Google Scholar]
- Migdal, A. Towards Field Theory of Turbulence. arXiv 2020, arXiv:2005.01231. [Google Scholar]
- Migdal, A. Probability Distribution of Velocity Circulation in Three Dimensional Turbulence. arXiv 2020, arXiv:2006.12008. [Google Scholar]
- Migdal, A. Clebsch confinement and instantons in turbulence. International Journal of Modern Physics A 2020, 35, 2030018. [Google Scholar] [CrossRef]
- Migdal, A. Asymmetric vortex sheet. Physics of Fluids 2021, 33, 035127. [Google Scholar] [CrossRef]
- Migdal, A. Vortex sheet turbulence as solvable string theory. International Journal of Modern Physics A 2021, 36, 2150062. [Google Scholar] [CrossRef]
- Migdal, A. Confined Vortex Surface and Irreversibility. 1. Properties of Exact solution. arXiv 2021, arXiv:2103.02065v10. [Google Scholar] [CrossRef]
- Migdal, A. Confined Vortex Surface and Irreversibility. 2. Hyperbolic Sheets and Turbulent statistics. arXiv 2021, arXiv:2105.12719. [Google Scholar] [CrossRef]
- Wikipedia. Burgers vortex. 2022. https://en.wikipedia.org/wiki/Burgers_vortex (accessed on 27 April 2022).
- Migdal, A. Complex Nonlinear Random Walk. 2023. https://www.wolframcloud.com/obj/sasha.migdal/Published/FQequation.nb.
- Panickacheril John, J.; Donzis, D.A.; Sreenivasan, K.R. Laws of turbulence decay from direct numerical simulations. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2022, 380, 20210089. [Google Scholar] [CrossRef]
- Sreenivasan, K.R.; Yakhot, V. The saturation of exponents and the asymptotic fourth state of turbulence. arXiv 2022, arXiv:2208.09561. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).