Submitted:
10 May 2023
Posted:
11 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Related Work
- A subgraph node labeling method is provided, which can automatically learn graph structure features and input nodes of subgraphs into the full connection layer in a consistent order.
- A link prediction method (PLAS) based on subgraph is proposed, which can be applied to different network structures and is superior to other link prediction algorithms.
- Based on torch, the link prediction algorithm (PLAS) model based on subgraph is implemented and verified on seven real data sets. Experimental results show that PLAS algorithm is superior to other link prediction algorithms.
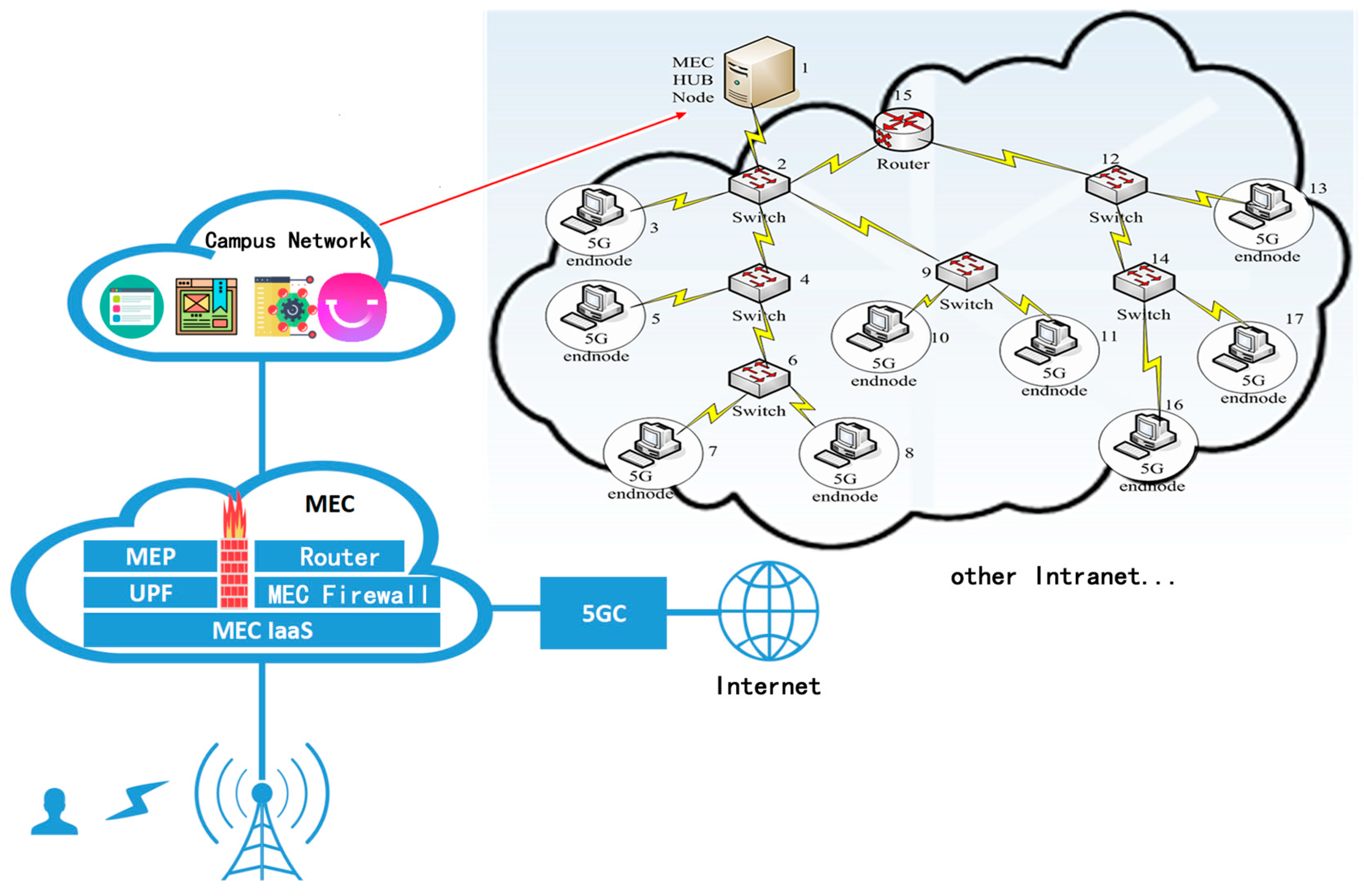
- The existing algorithm PLAS is improved by introducing graph attention network, and a link prediction algorithm (PLGAT) is proposed, which has been verified on seven real data sets and two 5G/6G space-air-ground communication networks. The experimental results show that PLGAT algorithm is superior to other link prediction algorithms. Furthermore, our proposed PLGAT algorithm for link prediction can precisely find out the new links on the Mobile MEC equipment network in 5G/6G to provide better QoS for data transportation.
3. PLAS model framework
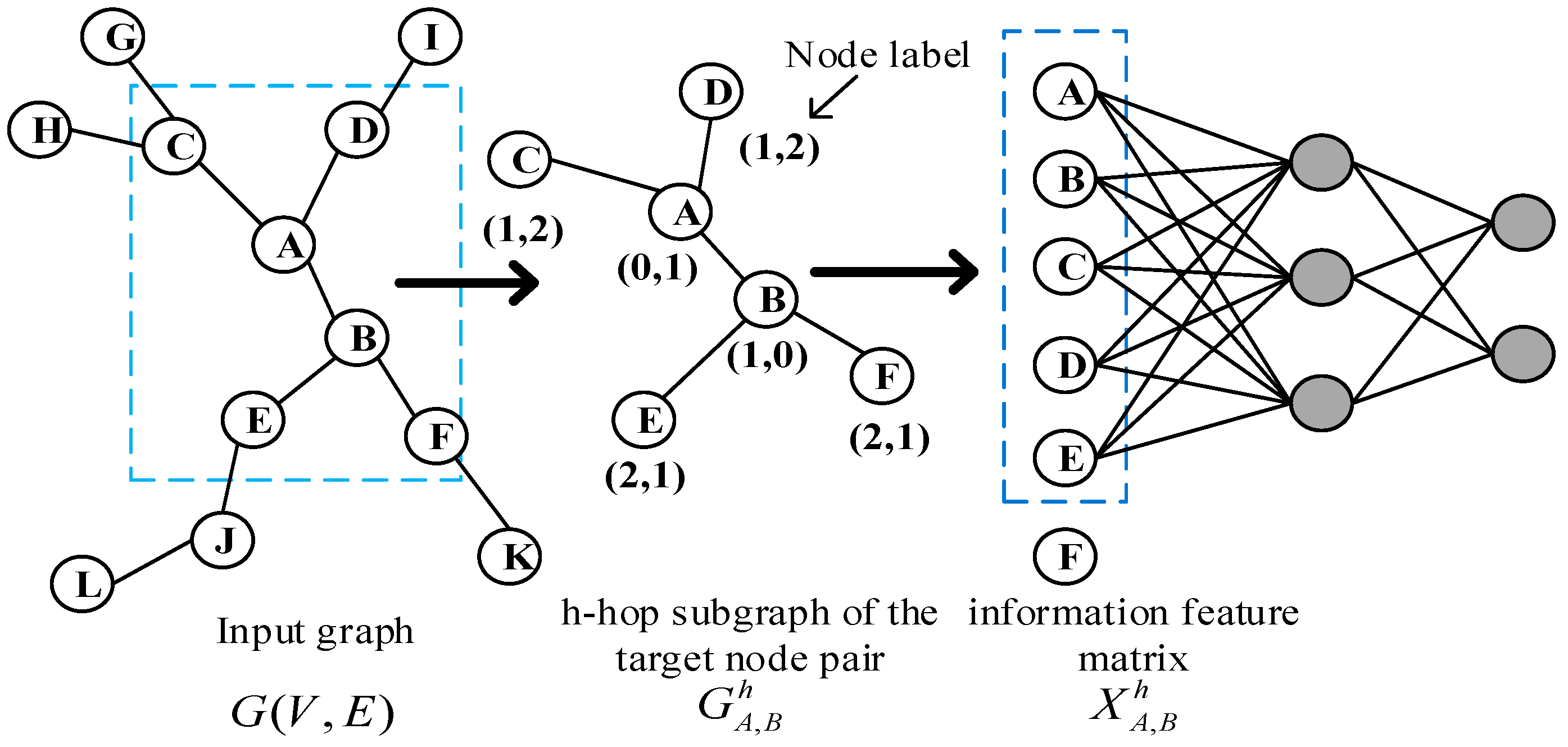
3.1. Extraction of subgraphs
| Algorithm: Subgraph extraction |
| Input: Target node pair , graph , h-hops neighbor nodes, threshold |
| Output: h-hops subgraph of target node pair |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
| 11: |
| 12: |
| 13: |
| 14: |
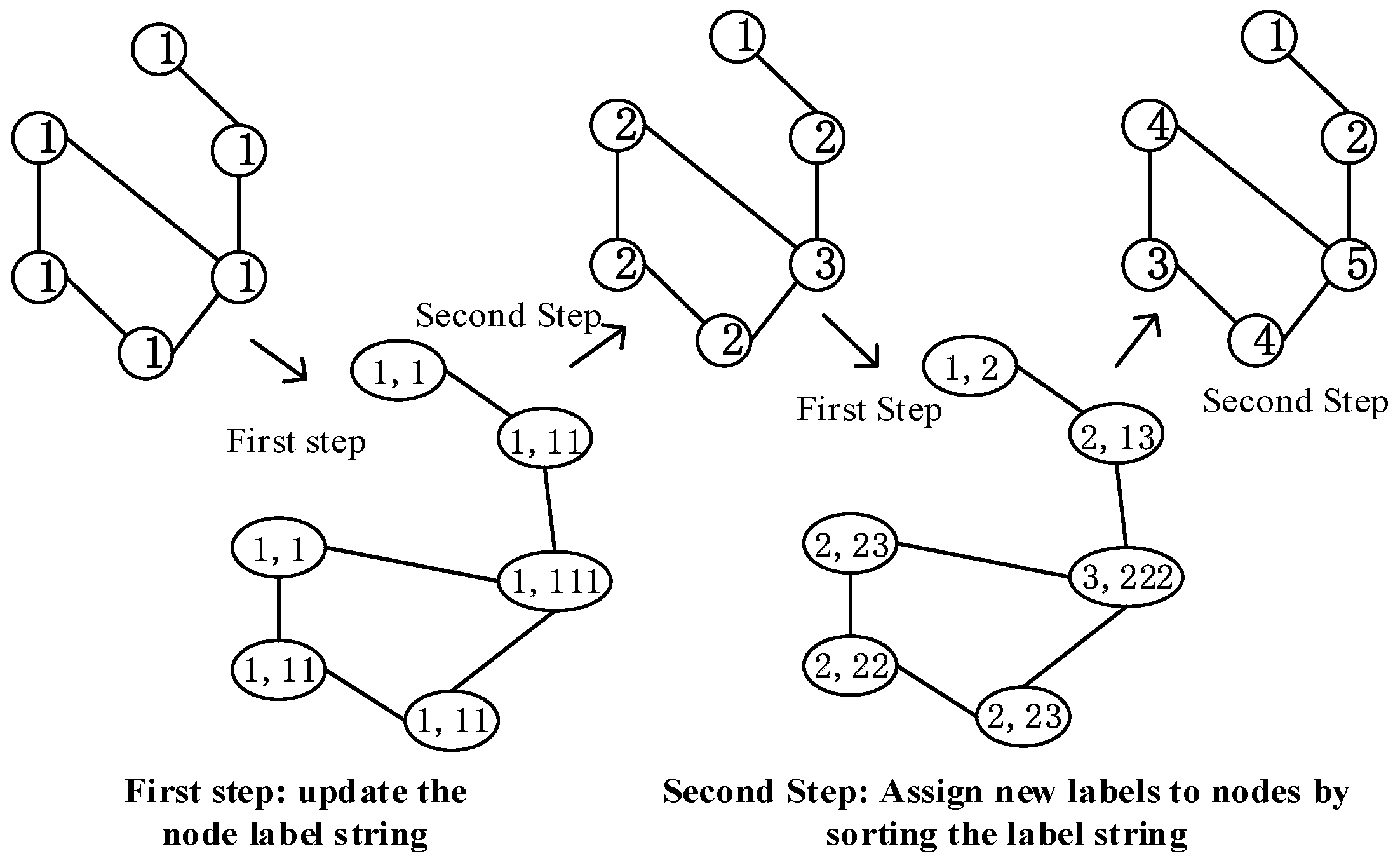
3.2. Graph labeling algorithm
- It initializes all nodes in the graph to the same label 1, and each node aggregates its label and the labels of neighbor nodes to construct a label string.
- The nodes in the graph are sorted in ascending order of label strings, and according to the sorting update to new labels 1, 2, 3, ... nodes with the same label string will get the same new label. For example, suppose that the label of node is 2, its neighbor label is {3,1,2}, the label of node is 2, and its neighbor label is {2,1,2}. The label strings of and are < 2123 > and < 2122 > respectively. Because < 2122 > is less than < 2123 > in the dictionary order, will be assigned a smaller label than in the next iteration.
- This process is repeated until the node label stops changing. Figure 2 shows updating the nodes' label from 1 to (1, ... 5).
| Algorithm: subgraph labeling |
| Input: Target node pair , subgraph node list , subgraph S |
| Output: Ordered list with labels |
| 1: |
| 2: |
| 3: |
| 4: |
| 5: |
| 6: |
| 7: |
| 8: |
| 9: |
| 10: |
3.3. Subgraph encoding
- It can represent that different nodes play different roles in the subgraph. The shorter the shortest path of other nodes in the subgraph relative to the target node pair, the greater its impact on whether the target node will generate links in the future, so it plays a more important role in the subgraph.
- Graph is an unordered data structure, which has no fixed order. Therefore, it is necessary to sort the nodes in the sub graph through labels, and then input them to the fully connection layer in a consistent order for learning.
- After extracting the h hop subgraph of the target link node pair (i,j), we calculate the shortest path from other nodes in the subgraph to the target node pair (i,j), and assign a label string to each node in the subgraph. When all node features in the subgraph are spliced and sent to the fully connection layer for learning, the fully connection layer will automatically learn the graph structure features suitable for the current network, including the discovered graph structure features or the undiscovered graph structure features. For example, CN algorithm is to calculate the number of common neighbor nodes of the target node pair. The full connection layer only needs to find the number of nodes with node label (1,1). By assigning a node label string to each node in the graph through the icon algorithm, our algorithm model can automatically learn the graph structure characteristics of the network, so it can be applied to different network structures. The later experimental results show that our algorithm is better in AUC than other link prediction algorithms.
3.4. Fully connected layer learning
4. Experiments Results
4.1. PLAS algorithm
4.2. PLGAT algorithm
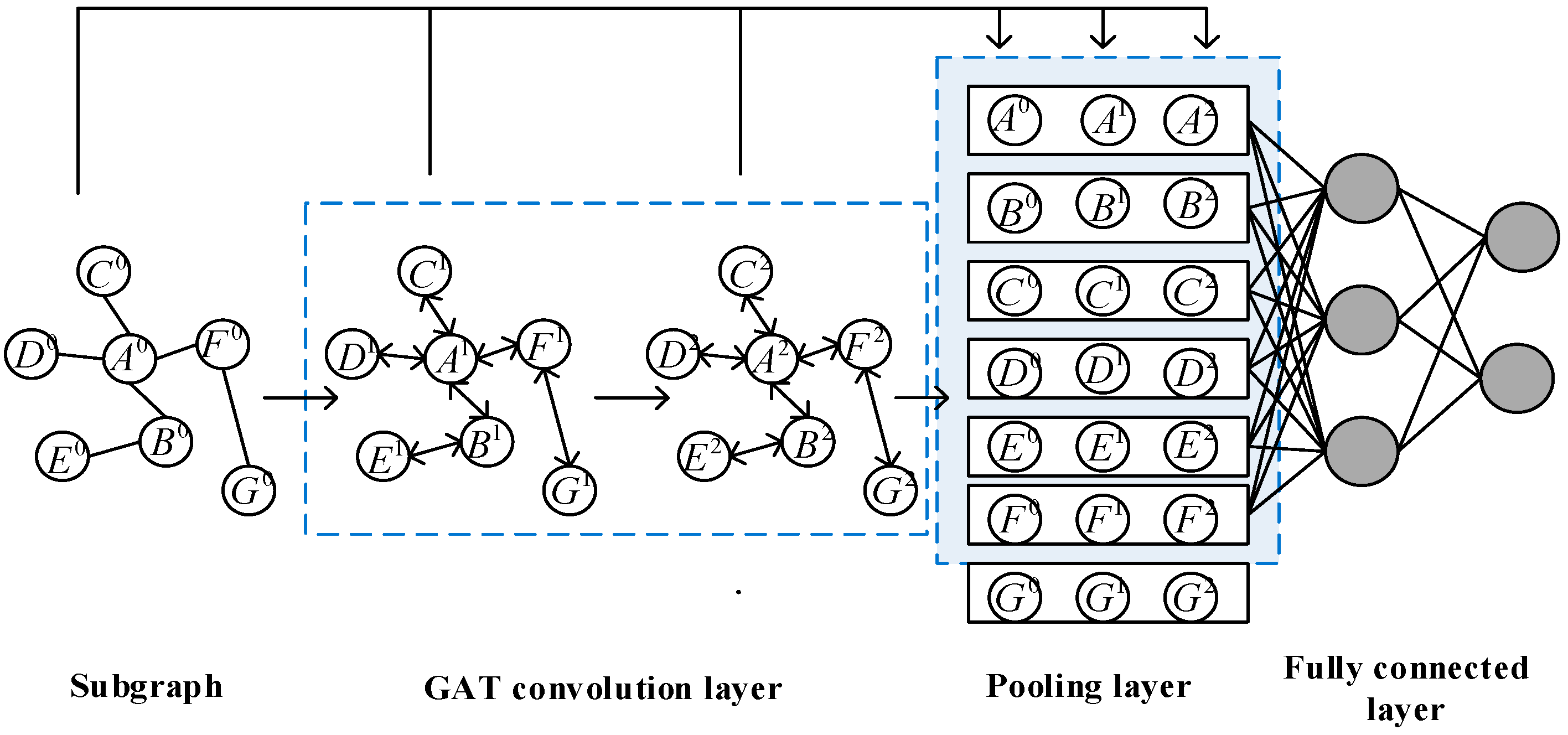
4.2.1. GAT convolution layer
4.2.2. Pooling layer
- The subgraph is centered on the target node pair and spreads out to the neighbor nodes on both sides, which has strong directionality.
- The number of neighbor hops in the subgraph is limited, resulting in the subgraph often being a small-scale graph.
- Because the shortest distance from other nodes in the subgraph to the target node pair , is greater than or equal to 1, the target node pair is always ranked in the first two elements, and the node closer to the target node in the subgraph will be ranked in the front, and the node farther away from the target node will be ranked in the back, which reflects the direction of the subgraph.
- Nodes in the subgraph will be sorted according to consistent rules. We only need to select the first nodes to represent the feature expression of the current subgraph, to unify the rules of node selection in the global pooling method. For the case that the number of nodes in the subgraph is greater than , only nodes after need to be truncated, and the discarded nodes will not lose all node information, because other nodes in the subgraph have learned the discarded node information through the two layers of GAT convolution layer. If the number of nodes in the subgraph is less than , simply add virtual nodes, where virtual nodes are represented by the zero vector.
4.3.3. Experimental dataset and settings
4.3.4. Experiment results analysis
5. Conclusions
Author Contributions
Acknowledgments
References
- Lü, L. Link Prediction on Complex Networks. Journal of University of Electronic Science and Technology of China 2010, 39, 651-661.
- Lü, L.; Zhou, T. Link Prediction, 1st ed.; Higher Education Press: Beijing, China, 2013.
- Adamic; Lada, A et al. Friends and neighbors on the Web. Social Networks 2003, 25, 211-230. [CrossRef]
- Chen, H.; Li, X.; Huang, Z. Link prediction approach to collaborative filtering. In Proceedings of the 5th ACM/IEEE-CS Joint Conference on Digital Libraries (JCDL'05), Denver CO, USA, 7-11 June 2005.
- Cannistraci, C.V.; Alanis-Lobato, G.; Ravasi, T. From link-prediction in brain connectomes and protein interactomes to the local-community-paradigm in complex networks. Scientific reports 2013, 3, 1-14. [CrossRef]
- Nickel, M.; Murphy, K.; Tresp, V.; Gabrilovich, E. A review of relational machine learning for knowledge graphs. Proceedings of the IEEE 2015, 104, 11-33. [CrossRef]
- LIU, W.; CHEN, L. Link prediction in complex networks. Information and Control 2020, 49, 1-23.
- Zhang, M.; Chen, Y. Link prediction based on graph neural networks. Advances in Neural Information Processing Systems 2018, 31, 5165-5175.
- Newman, M.E.J. Clustering and preferential attachment in growing networks. Physical review E 2001, 64, 025102. [CrossRef]
- Jaccard, P. Étude comparative de la distribution florale dans une portion des Alpes et des Jura. Bull Soc Vaudoise Sci Nat 1901, 37, 547-579.
- Zhou, T.; Lü, L.; Zhang, Y.C. Predicting missing links via local information. The European Physical Journal B 2009, 71, 623-630. [CrossRef]
- Kovács, I.A.; Luck, K.; Spirohn, K. et al. Network-based prediction of protein interactions. bioRxiv 2019, 10, 1240. [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining, San Francisco California, USA, 13-17 August 2016.
- Leman, A.A.; Weisfeiler, B. A reduction of a graph to a canonical form and an algebra arising during this reduction. Nauchno-Technicheskaya Informatsiya 1968, 2, 12-16.
- Batagelj, V; Mrvar, A. Pajek. datasets http://vlado. fmf. uni-lj. si/pub/networks/data/mix. USAir97. net, 2006.
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Physical review E 2006, 74, 036104. [CrossRef]
- Ackland, R. Mapping the US political blogosphere: Are conservative bloggers more prominent? In Proceedings of BlogTalk Downunder 2005 Conference, Sydney, Australia, 20-21 May 2005.
- Von Mering, C.; Krause, R.; Snel, B. et al. Comparative assessment of large-scale data sets of protein–protein interactions. Nature 2002, 417, 399-403. [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440-442. [CrossRef]
- Spring, N.; Mahajan, R.; Wetherall, D. Measuring ISP topologies with Rocketfuel. ACM SIGCOMM Computer Communication Review 2002, 32, 133-145.
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. science 1999, 286, 509-512. [CrossRef]
- Katz, L. A new status index derived from sociometric analysis. Psychometrika 1953, 18, 39-43. [CrossRef]
- Tang, J.; Qu, M.; Wang, M. et al. Line: Large-scale information network embedding. In Proceedings of the 24th international conference on world wide web, Florence, Italy, 18-22 May 2015.
- Kipf, T.N.; Welling, M. Variational graph auto-encoders. Computing Research Repository 2016, 1611, 07308.
- Ma, Y.; Wang, S.; Aggarwal, C.C. et al. Graph convolutional networks with eigenpooling. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage AK, USA, 4 – 8 August, 2019.
- Lee, J.; Lee, I.; Kang, J. Self-attention graph pooling. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, California, USA, 9-15 June 2019.
- Guoqiang, Z. An Algorithm for Internet AS Graph Betweenness Centrality Based on Backtrack. Journal of Computer Research and Development 2006, 43, 114-120.
- Petar, V.; Guillem, C.; Arantxa, C.; Adriana, R.; Pietro, L.; Yoshua, B. Graph Attention Networks. International Conference on Learning Representations, 2018.
- Hamad, A. A.; Abdulridha, M. M.; Kadhim, N. M.; Pushparaj, S.; Meenakshi, R.; Ibrahim, A. M. Learning methods of business intelligence and group related diagnostics on patient management by using artificial dynamic system. Journal of Nanomaterials 2022, 1-8. [CrossRef]
- Tao, W.; Hongyu, M.; Chao, W.; Shaojie, Q.; Liang, Z.; Shui, Y. Heterogeneous representation learning and matching for few-shot relation prediction. ACM Journal of Experimental Algorithmics, 2022, 131, 108830. [CrossRef]
- Xingping, X.; Tao, W.; Shaojie, Q.; Xi-Zhao, W.; Wei, W.; Yanbing, L. NetSRE: Link predictability measuring and regulating, Knowledge-based systems, 2020, 196, 105800. [CrossRef]
- Christos, F.; Kevin S., M.; Andrew, T. Fast discovery of connection subgraphs. ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2004, 118-127.
- Hasan, M. A.; Chaoji, V.; Salem, S.; Zaki, M. Link Prediction Using Supervised Learning. Proceedings of SDM'06 Workshop on Link Analysis, Counter terrorism and Security, 2006.
- David, L., & Jon M., K. The link-prediction problem for social networks. Journal of the Association for Information Science and Technology 2007, 58, 1019-1031. [CrossRef]
- Nesserine, B.; Rushed, K.; Celine, R. Supervised Machine Learning Applied to Link Prediction in Bipartite Social Networks. Advances in Social Networks Analysis and Mining, 2010, 326-330E-ISBN:978-0-7695-4138-9.
- Michael, F.; Lena, T.; Rami, P.; Ofrit, L.; Lior, R.; Yuval, E. Computationally efficient link prediction in a variety of social networks. ACM Transactions on Intelligent Systems and Technology 2014, 5, 1-25. [CrossRef]
- Yu, Z.; Ke-ning, G.; Ge, Y. Method of Link Prediction in Social Networks Using Node Attribute Information. Computer Science 2018, 45, 41-45.
- Haris, M.; Miroslav, M.; Sasho, G.; Igor, M. Multilayer Link Prediction In Online Social Networks. Telecommunications Forum. 2018, 823-826.
- Sanjay, K.; Abhishek, M.; B. S., P. Link prediction in complex networks using node centrality and light gradient boosting machine. World Wide Web 2022, 25, 2487-2513.
- Smriti, B.; Graham, C.; S.; M. Node Classification In Social Networks. Computing Research Repository 2011, 1101, 115-148. [CrossRef]
- Yu, R.; Wenbing, H.; Tingyang, X.; Junzhou, H. DropEdge: Towards Deep Graph Convolutional Networks on Node Classification. International Conference on Learning Representations, 2020.
- Muhan, Z.; Zhicheng, C.; Marion, N.; Yixin, C. An End-to-End Deep Learning Architecture for Graph Classification. AAAI Conference on Artificial Intelligence 2018, 4438-4445.
- John Boaz, L.; Ryan, R.; Xiangnan, K. Graph Classification using Structural Attention. ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2018, 1666-1674. [CrossRef]
- Víctor, M.; Fernando, B.; Juan Carlos Cubero, T. A Survey of Link Prediction in Complex Networks. ACM Computing Surveys 2017, 49, 69:1-69:33.
- Bryan, P.; Rami, A.; Steven, S. DeepWalk: online learning of social representations. ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2014, 1403, 701-710.
- DAIXIN, W.; Peng, C.; Wenwu, Z. Structural Deep Network Embedding. ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2016, 1225-1234.
- Shaosheng, C.; Wei, L.; Qiongkai, X. Deep Neural Networks for Learning Graph Representations. AAAI Conference on Artificial Intelligence 2016, 1145-1152.
- Thomas N., K.; Max, W. Semi-Supervised Classification with Graph Convolutional Networks. International Conference on Learning Representations 2017, 1609.02907.
- William L.; H.; Rex, Y.; Jure, L. Inductive Representation Learning on Large Graphs. Conference on Neural Information Processing Systems 2017, 30, 1024-1034.
- Haochen, C., Bryan, P., Yifan, H., & Steven, S. HARP: Hierarchical Representation Learning for Networks. AAAI Conference on Artificial Intelligence 2018, 1706, 2127-2134.
- Michael, S.; Thomas N.; K.; Peter, B.; Rianne van den, B.; Ivan, T.; Max, W. Modeling Relational Data with Graph Convolutional Networks. Extended Semantic Web Conference 2018, 1703.06103.
- Sam De, W.; Tim, D.; Sandra, M.; Bart, B.; Jochen De, W. Combining Temporal Aspects of Dynamic Networks with Node2Vec for a more Efficient Dynamic Link Prediction. Advances in Social Networks Analysis and Mining 2018, 1234-1241.
- Kai, L.; Meng, Q.; Bo, B.; Gong, Z.; Min, Y. GCN-GAN: A Non-linear Temporal Link Prediction Model for Weighted Dynamic Networks. IEEE International Conference Computer and Communications 2019, 1901, 388-396. [CrossRef]
- Muhan, Z.; Yixin, C. Weisfeiler-Lehman Neural Machine for Link Prediction. ACM SIGKDD Conference on Knowledge Discovery and Data Mining 2017, 575-583. [CrossRef]
- Newman M E, J. Fast algorithm for detecting community structure in networks. Physical Review E 2004, 69. [CrossRef]
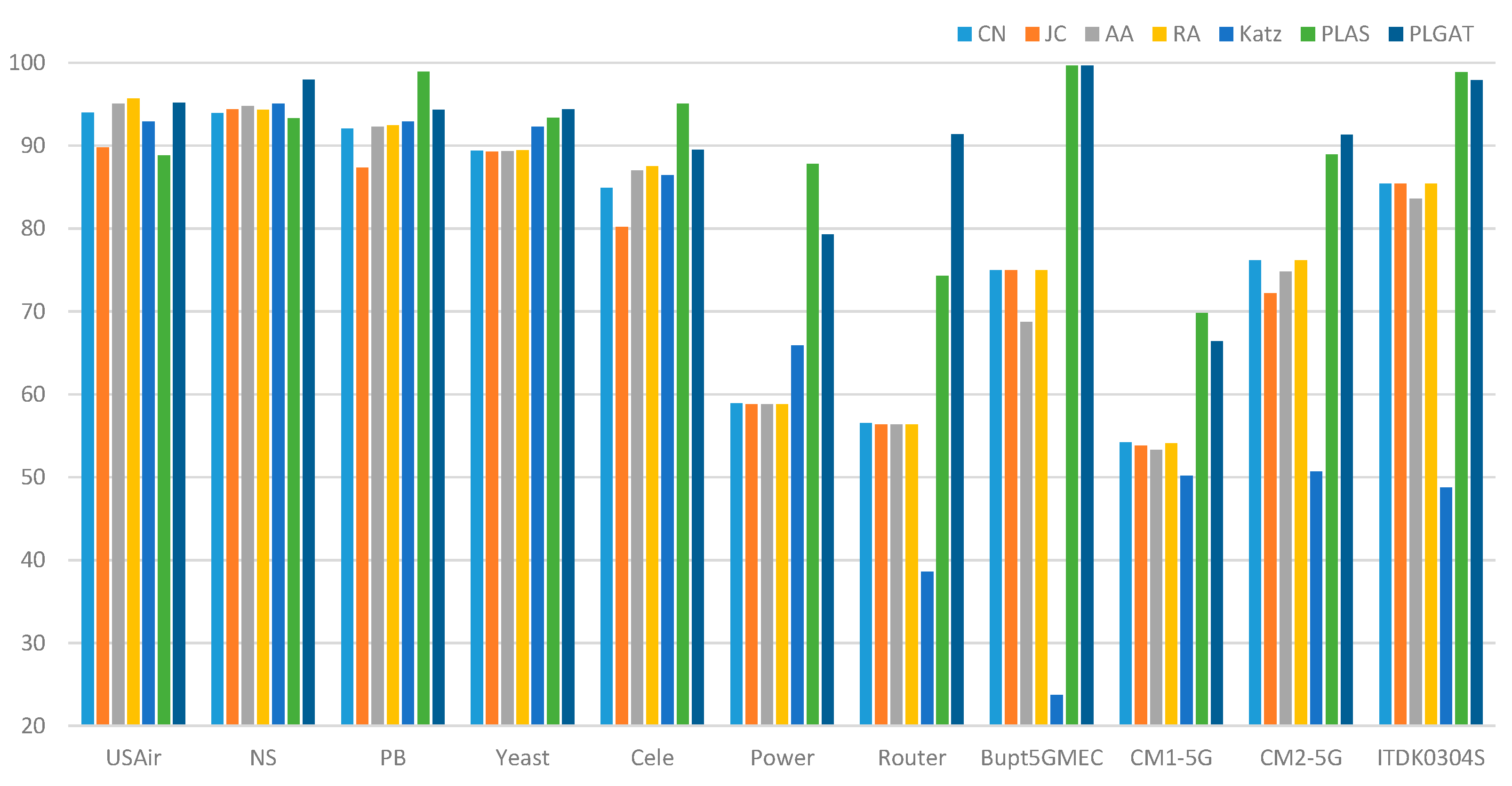
| DataSet | ||
|---|---|---|
| Router | 5022 | 6258 |
| USAir | 332 | 2126 |
| NS | 1589 | 2742 |
| PB | 1222 | 16714 |
| Yeast | 2375 | 11693 |
| Cele | 297 | 2148 |
| Power | 4941 | 6594 |
| Bupt5GMEC | 135 | 338 |
| CM1-5G | 1500 | 5990 |
| CM2-5G | 1499 | 4498 |
| ITDK0304S | 3780 | 10757 |
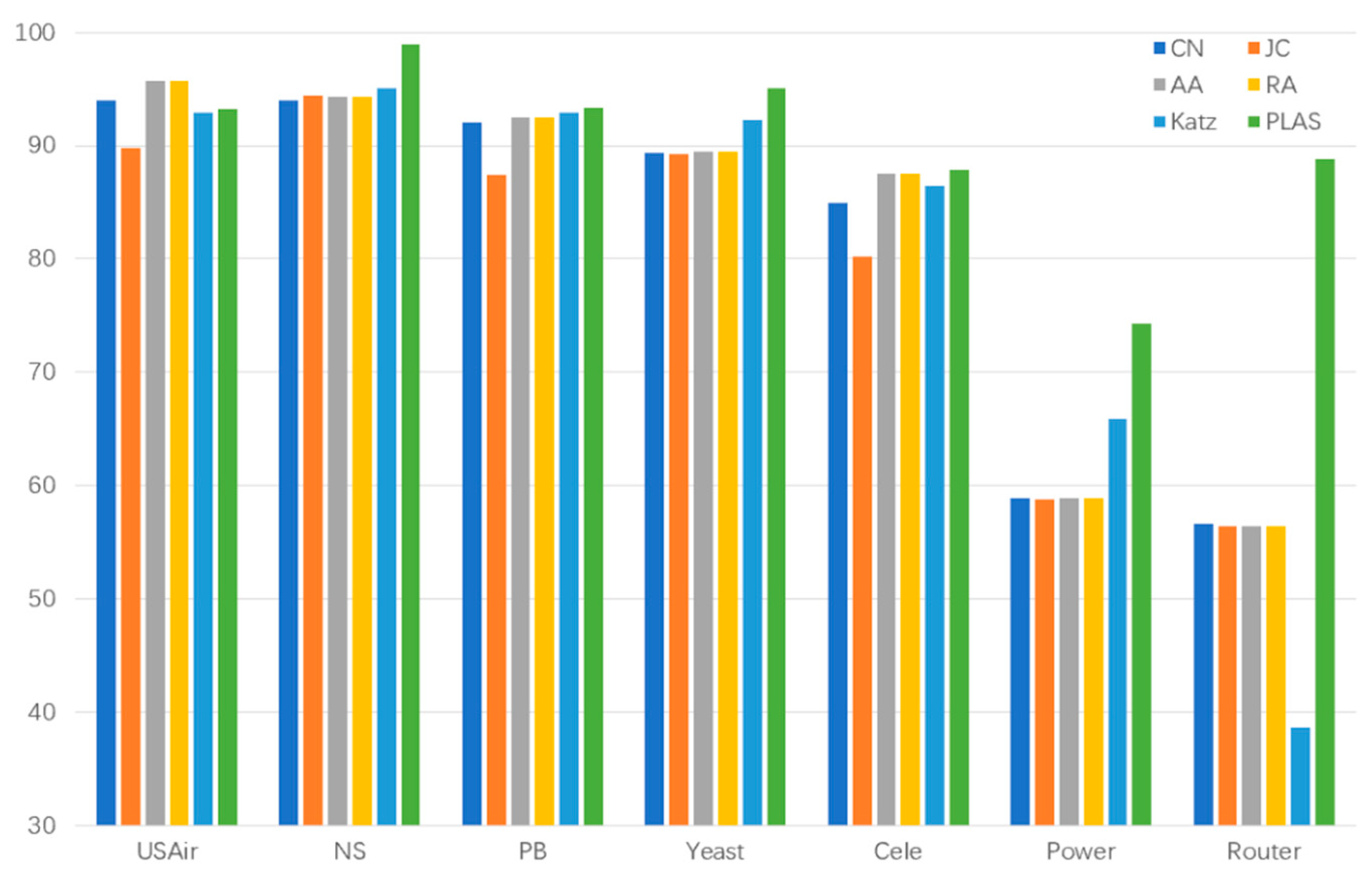
| DataSet | CN | JC | AA | RA | Katz | PLAS |
| Router | 56.57 | 56.38 | 56.40 | 56.38 | 38.62 | 88.81 |
| USAir | 94.02 | 89.81 | 95.08 | 95.67 | 92.90 | 93.28 |
| NS | 93.94 | 94.40 | 94.77 | 94.33 | 95.03 | 98.93 |
| PB | 92.07 | 87.39 | 92.31 | 92.45 | 92.89 | 93.37 |
| Yeast | 89.41 | 89.30 | 89.32 | 89.44 | 92.30 | 95.04 |
| Cele | 84.95 | 80.18 | 87.03 | 87.49 | 86.45 | 87.84 |
| Power | 58.90 | 58.80 | 58.83 | 58,83 | 65.90 | 74.27 |
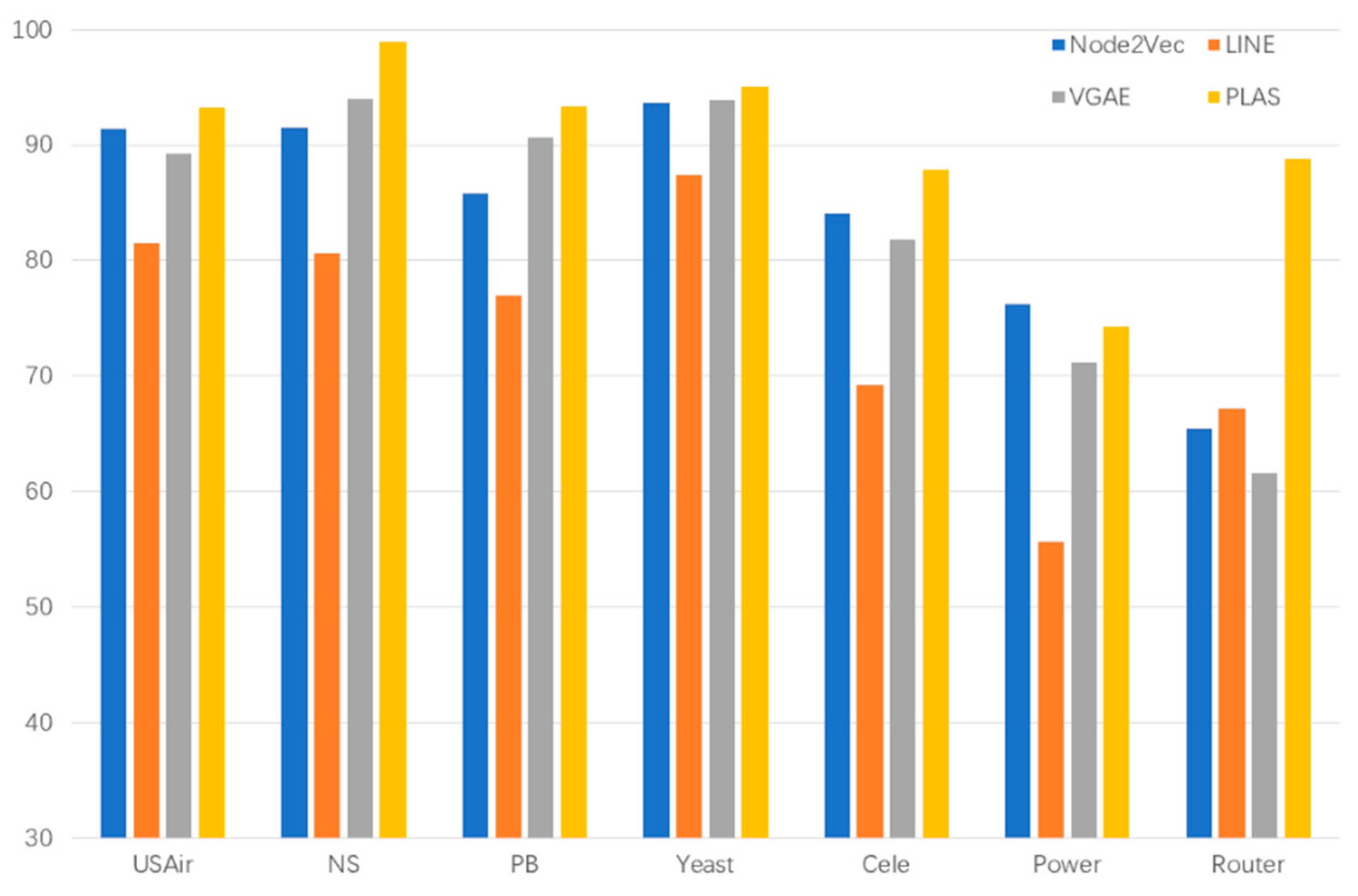
| Dataset | Node2Vec | LINE | VGAE | PLAS |
| Router | 65.46 | 67.17 | 61.53 | 88.81 |
| USAir | 91.40 | 81.47 | 89.30 | 93.28 |
| NS | 91.55 | 80.63 | 94.04 | 98.93 |
| PB | 85.79 | 76.94 | 90.70 | 93.37 |
| Yeast | 93.68 | 87.45 | 93.87 | 95.04 |
| Cele | 84.13 | 69.22 | 81.87 | 87.84 |
| Power | 76.23 | 55.64 | 71.20 | 74.27 |
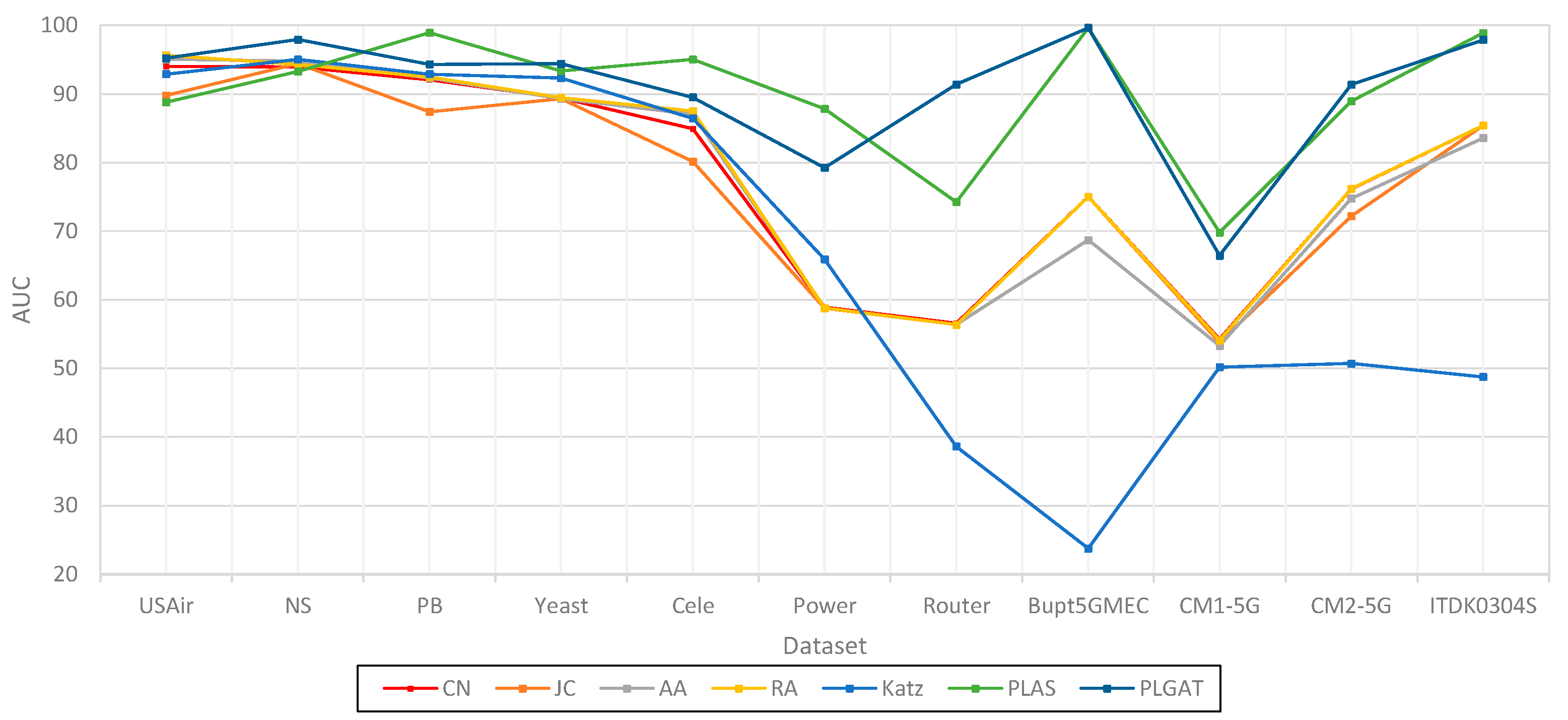
| Dataset | CN | JC | AA | RA | Katz | PLAS | PLGAT |
| USAir | 94.02 | 89.81 | 95.08 | 95.67 | 92.90 | 88.81 | 95.21 |
| NS | 93.94 | 94.40 | 94.77 | 94.33 | 95.03 | 93.28 | 97.96 |
| PB | 92.07 | 87.39 | 92.31 | 92.45 | 92.89 | 98.93 | 94.32 |
| Yeast | 89.41 | 89.30 | 89.32 | 89.44 | 92.30 | 93.37 | 94.41 |
| Cele | 84.95 | 80.18 | 87.03 | 87.49 | 86.45 | 95.04 | 89.52 |
| Power | 58.90 | 58.80 | 58.83 | 58,83 | 65.90 | 87.84 | 79.27 |
| Router | 56.57 | 56.38 | 56.40 | 56.38 | 38.62 | 74.27 | 91.42 |
| Bupt5GMEC | 75.01 | 75.02 | 68.75 | 75.02 | 23.78 | 99.67 | 99.67 |
| CM1-5G | 54.23 | 53.79 | 53.32 | 54.13 | 50.22 | 69.84 | 66.43 |
| CM2-5G ITDK0304S |
76.15 85.41 |
72.22 85.41 |
74.79 83.60 |
76.21 85.42 |
50.71 48.77 |
88.95 98.90 |
91.34 97.88 |
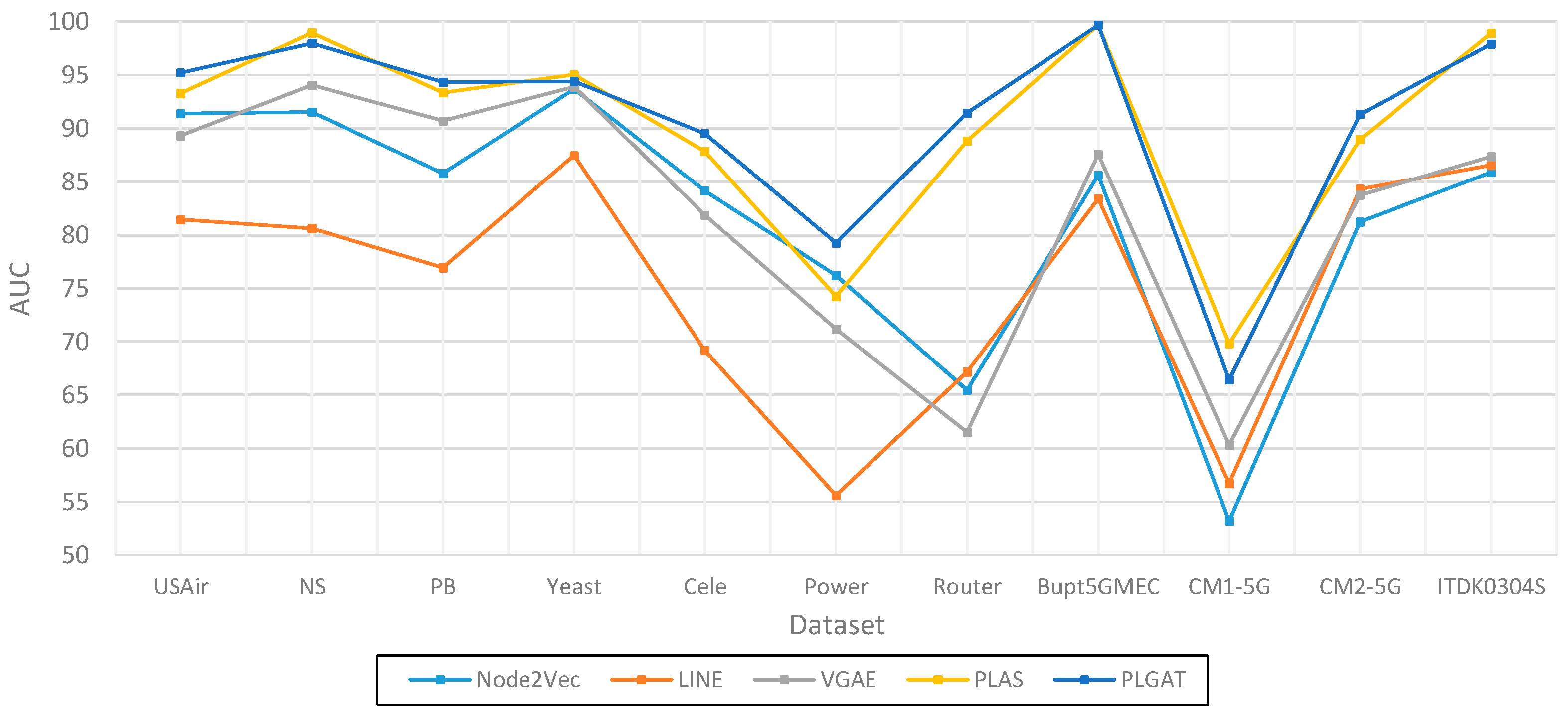
| Dataset | Node2Vec | LINE | VGAE | PLAS | PLGAT |
| USAir | 91.40 | 81.47 | 89.30 | 93.28 | 95.21 |
| NS | 91.55 | 80.63 | 94.04 | 98.93 | 97.96 |
| PB | 85.79 | 76.94 | 90.70 | 93.37 | 94.32 |
| Yeast | 93.68 | 87.45 | 93.87 | 95.04 | 94.41 |
| Cele | 84.13 | 69.22 | 81.87 | 87.84 | 89.52 |
| Power | 76.23 | 55.64 | 71.20 | 74.27 | 79.27 |
| Router | 65.46 | 67.17 | 61.53 | 88.81 | 91.42 |
| Bupt5GMEC | 85.61 | 83.42 | 87.56 | 99.67 | 99.67 |
| CM1-5G | 53.22 | 56.75 | 60.34 | 69.84 | 66.43 |
| CM2-5G | 81.24 | 84.31 | 83.76 | 88.95 | 91.34 |
| ITDK0304S | 85.87 | 86.56 | 87.35 | 98.90 | 97.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





