Introduction
Spin, first observed by Stern and Gerlach [
1], reveals two states of up and dn (dn = R(
)up). Spin is measured to be angular momentum of
magnitude, a vector quantity, and belongs to the SU(2) group. Spin is a fundamental property of Nature, purely quantum with no classical analogue. The mathematical basis for spin is the Dirac equation [
2]. Dirac’s analysis introduces his relativistic equation by linearizing the Klein-Gordon Equation while respecting conservation of mass and energy. He was led to his gamma matrices with four states rather than the two that are measured [
3]. He surmised that his equation described two spins rather than one. The second spin with negative energy and opposite sign was interpreted as the antimatter twin to the other spin [
2]. From this hole theory, antimatter production, and the sea of electron model followed [
4].
In this paper a small change is made whereby one of the gamma matrices is multiplied by the imaginary number
i and the effect is to change the symmetry from SU(2) to the quaternion group
. The gamma matrices still anti-commute, but the modified Dirac equation reveals a single spin has four states, rather than two: spin has structure under
, [
5,
6] rather than being the point particle that Dirac found. Quaternion spin carries two complementary properties: polarization and coherence. The former results from the usual magnetic moment of spin whereas the coherence is generated by a unit quaternion. This quaternion spins the spin axis in free flight making the intrinsic angular momentum of Dirac spin extrinsic. In addition, two mirror states, [
7] emerge from the Dirac field. Quaternion spin has two orthogonal polarization axes that are perpendicular to the axis of linear momentum.
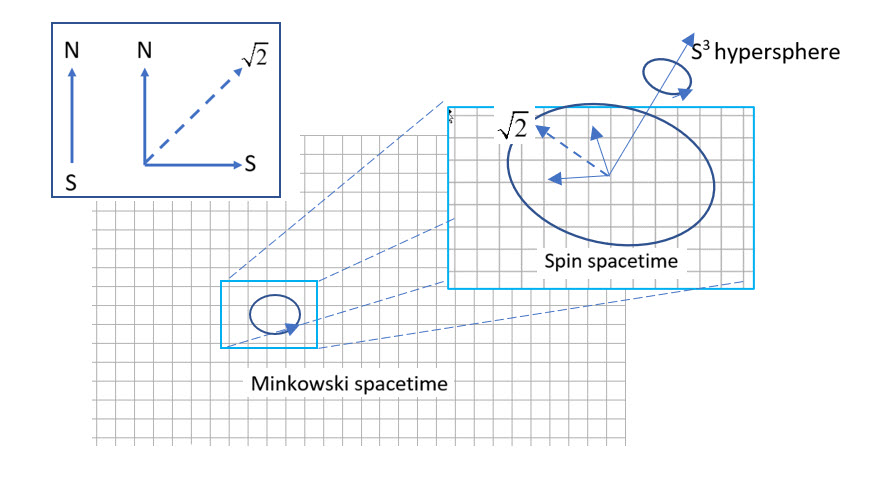
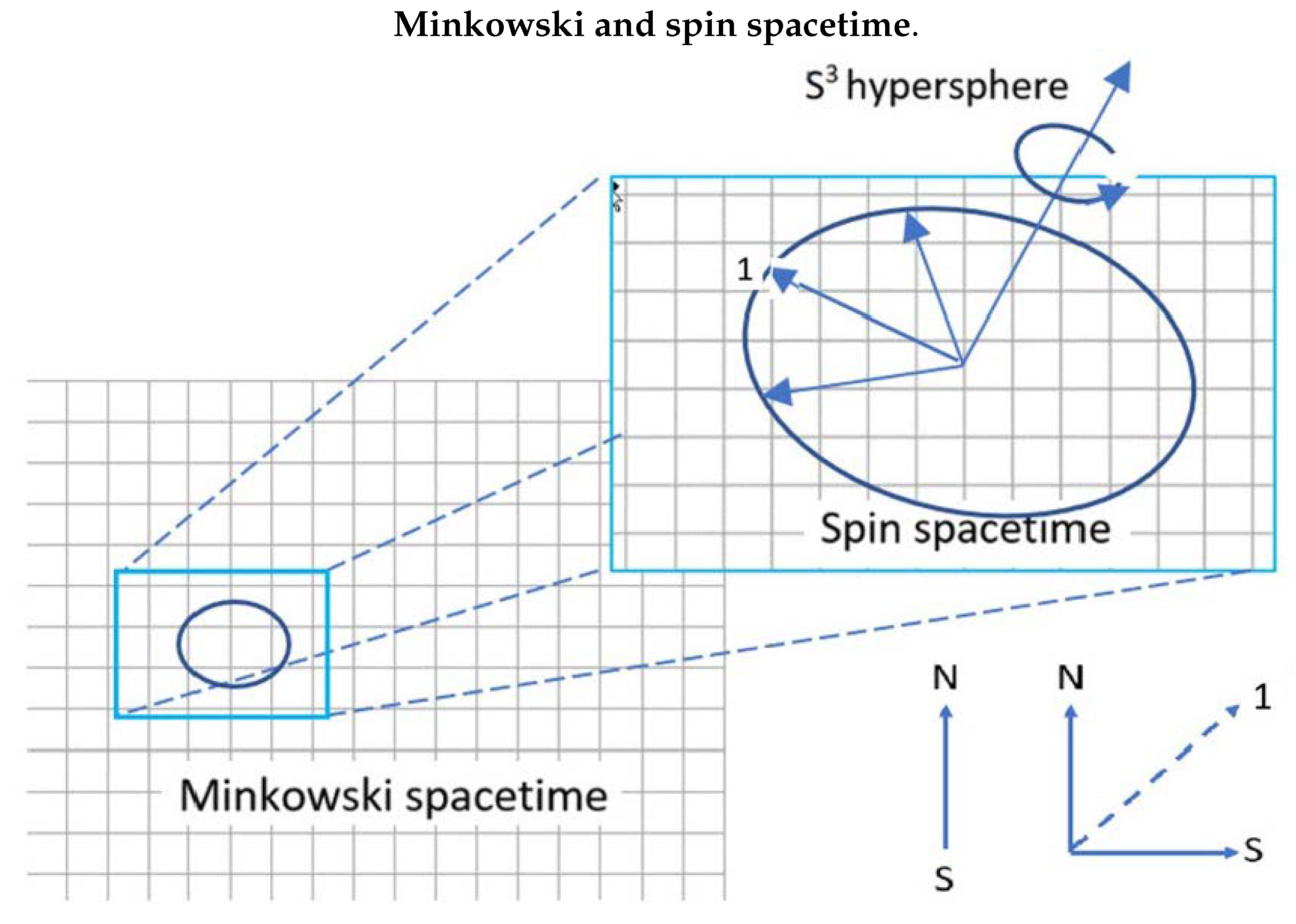
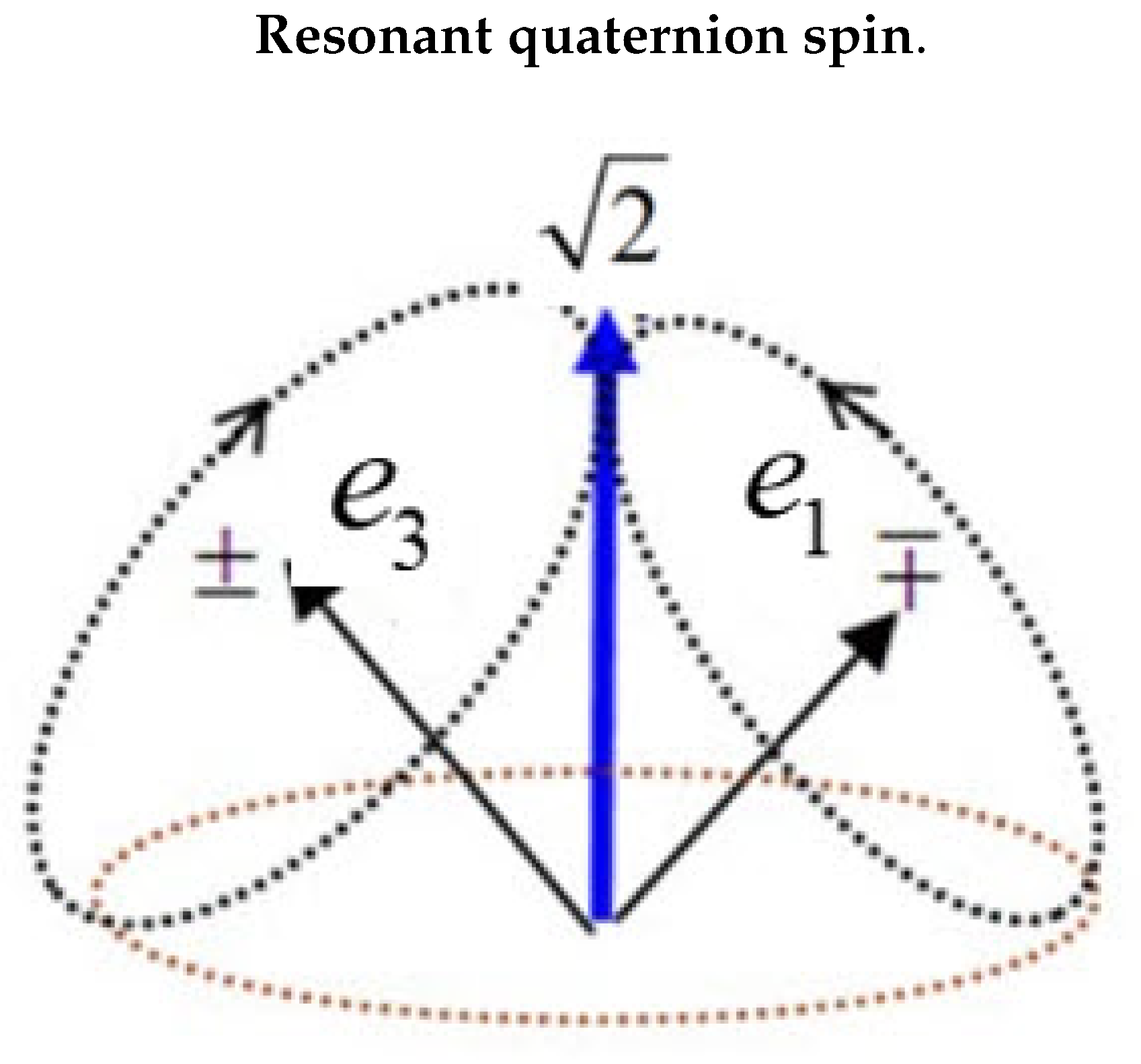
Figure 1 shows that a quaternion spin
is geometrically equivalent to that of a photon.
To motivate the discussion here, consider the well know equation for a dyadic of Pauli spin components,
Arising from Geometric Algebra, [
8,
9] the first term describes a symmetric component (the scalar product) that gives rise to polarization and measured Dirac spin. The second term, (the wedge product) is anti-symmetric and generates the helicity. In 3D Cartesian space the wedge product becomes the vector cross product. Dirac spin does not treat this component which requires a bivector,
. The only way to get the bivector is to change the spin symmmetry to the quaternion group. It is the purpose of this paper to include this term.
Spin coherence, expressed by a quaternion [
10], exists on the
hypersphere [
11,
12,
13] beyond Minkowski spacetime. It describes spin hyper-helicity as an additional property of spin from the second term in Equation (
1). The name hyper-helicity is used formally to distinguish it from the usual helicity found in particle physics [
14]. The two are entirely different, albeit both describe spinning the axis of linear momentum. Here hyper-helicity is in
hyper-space while particle helicity is constructed in Minkowski spacetime. Since we do not treat particle helicity, we call hyper-helicity simply the helicity.
This paper is the first of three in which the mathematical foundations of quaternion spin are presented. A second paper, “Spin with hyper-helicity” [
15] follows in which the ideas of this paper are used to study helicity applied to an EPR pair and which is responsible for the observed correlation without non-local connectivity. It shows the anti-symmetric part of a spin generates the spinning of the axis of linear momentum in free flight. The third paper, Ref. [
16] presents a computer simulation which shows that both polarization and coherent states are responsible for the apparent violation of Bell’s Inequalities.
In this work, there are no Local Hidden Variables (LHV) and consequently Bell’s theorem is either not applicable or is not violated.
We show the above symmetry change leads to a more detailed description of spin and there are compelling reasons to believe that quaternion spin is more fundamental that Dirac’s spin and should replace it in some applications.
Formally this four state spin is called quaternion spin to distinguish it from the usual Dirac spin. We show here that quaternion spin has the same mathematical foundation as usual point particle Dirac spin. An extended form of the Dirac equation is presented that admits both polarization and helicity. It describes spin as it exists in the absence of interactions including measurement, and therefore in free flight.
Spin Spacetime Algebra
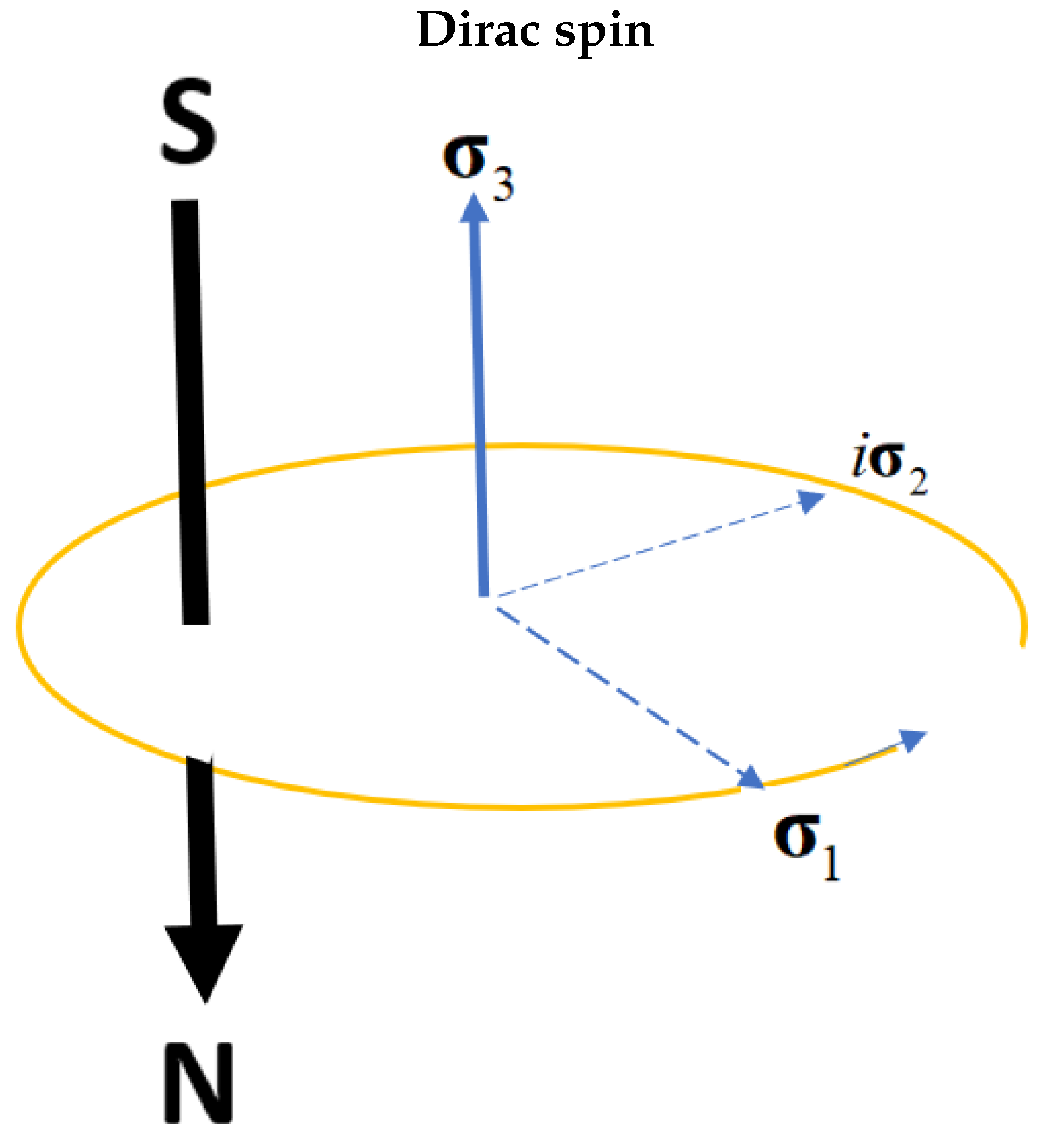
Dirac spin is measured in a direction
and has states with outcomes of
. These are expressed as usual by
. Quaternion spin, however, is more than a polarization vector and must include helicity with two states of
, expressed as a product,
This leads to the 4x4 space of the Dirac field. Quaternion spin describes one particle with two polarization axes and its chirality, (which is the same as handedness and helicity).
A point particle spin is described by the three Pauli spin components which along with the identity, gives the set (), which belongs to the SU(2) group. Simply by multiplying one gamma matrices by the imaginary number i, here chosen to be , changes the spin components to (), giving two spatial axes of polarization, and the needed bivector, . This set forms a normal subgroup of the quaternion group, , and gives spin structure. This requires defining a different Cartesian basis set , called the Body Fixed Frame, BFF, since every structured spin can have a different orientation relative to the Laboratory Fixed Frame of .
Take the spatial components of Minkowski spacetime as the LFF. In contrast, the BFF
refers to the coordinates of a particle in spin spacetime, see
Figure 2. The two spatial components,
denoted by
, are, up to a phase, simply a rotation away from Minkowski spacetime. This structure is shown in
Figure 2 in the top left insert which contrasts quaternion spin with the usual Dirac spin vector. Note that the two axes of quaternion spin couple to form a resonance component of length
which is a pure coherent state. The bivector,
, denoted by (2), orients the two dimensional plane formed from
axes by its normal component to the plane. We assume here that the particle propagates in the
direction. Whereas
with
is usual Minkowski spacetime, the set
is spin spacetime. The spin polarized structure can be expressed in Minkowski spacetime. The bivector cannot.
The bivector (2), is introduced by choosing to multiply
by the imaginary number
i,
rendering
Hermitian. Each Pauli component becomes a bivector. The set of gamma matrices in spin space, indicated by subscript
s,
, anticommute. They have a different signature from Minkowski spacetime,
The order of the components is and the term is not a spatial component but a frequency, Hermitian like the time variable, . This dimension is the origin of quantum coherence that leads to the formulation of helicity.
The commutation relations are changed from the usual three dimensional generator of rotations in Minkowski spacetime,
to ones that generate rotations in only two dimensions in spin spacetime
The former equation describes rotations in the 31 plane about the direction 2; whereas the imaginary term in the latter equation damps all rotation attempts out of the 31 plane.
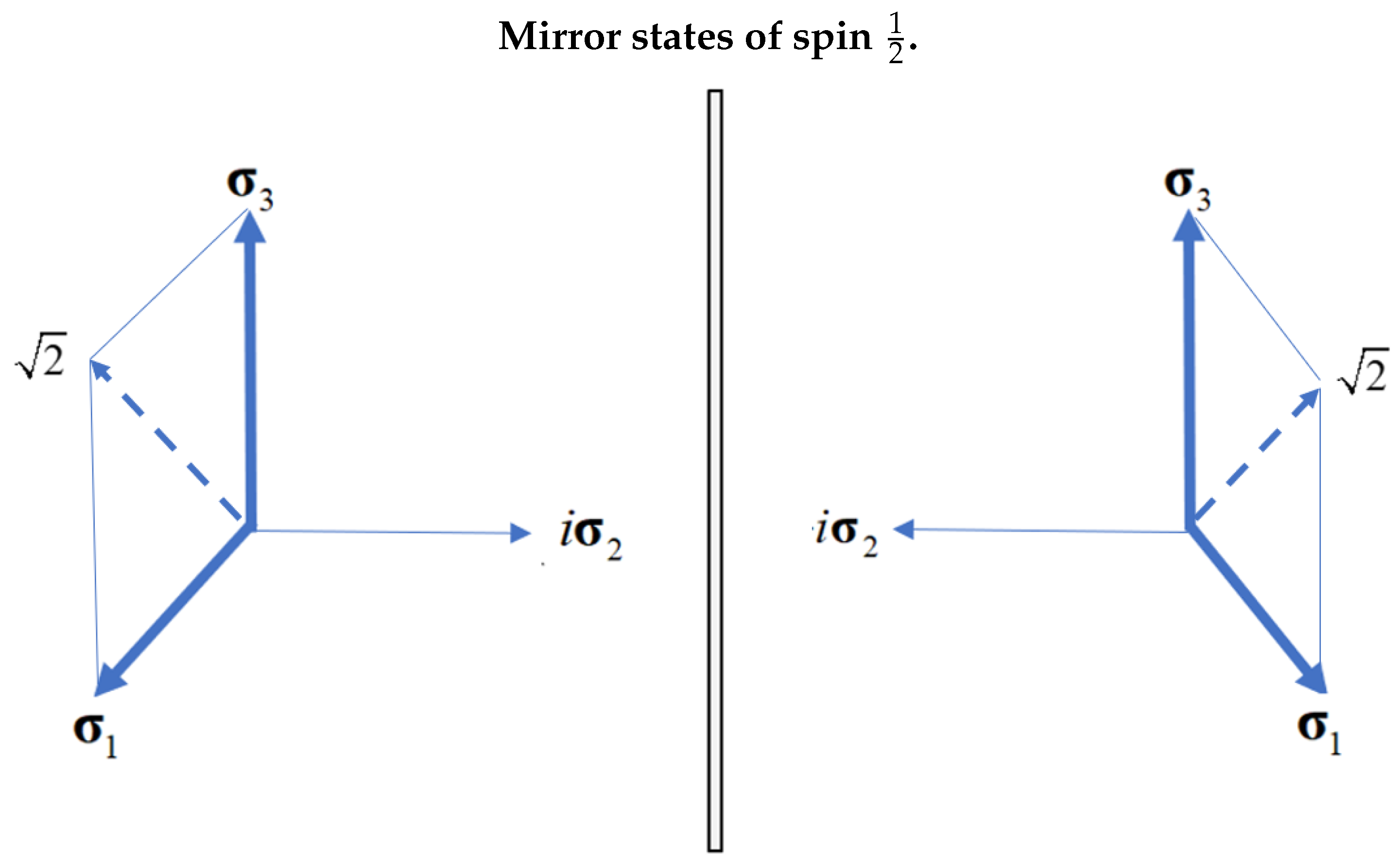
Mirror States and Parity
The new equation in spin-space follows from the gamma algebra as usual which gives a non-Hermitian equation by virtue of
,
and we suppress the subscript
s on the derivatives. By treating a spin in free-flight in an isotropic environment, the two axes
are indistinguishable. Therefore, permutation with the parity operator,
does not change the
dependence in Equation (
8), but the bivector,
is antisymmetric to 13 permutation. Therefore the above equations admits two solutions in left and right handed coordinate frames, which are mirror states, see
Figure 3,
, [
7,
17]. The anti-commutation of the
matrices ensures that energy is conserved and the Klein-Gordon equation is recovered.
The separation of the Dirac field into reflective states identifies each axis as carrying a spin such that each precesses in opposite direction. These two polarization axes each, with a magnetic moment
, constructively interfere producing a resonance which is a purely coherent spin, see
Figure 4.
Adding and subtracting the two equations in Equation (
8) leads to separation of the Hermitian part of the spin spacetime from the anti-Hermitian part,
where the two mirror states combine into those with odd and even parity,
with the definition,
We identify the even parity state with quaternion polarization. The odd parity state describes quaternion coherence.
Therefore spin spacetime separates into two distinct spaces: polarization spacetime,
, Equation (
9); and coherent space (not spacetime)
, Equation (
10). The Hermitian part, Equation (
9), is the same as the usual Dirac equation, but in two dimensions rather than three.
The bivector component,
, carries a massless Weyl spinor in coherent space, Equation (
10). Below it is shown that the spinning of the axis is generated by a unit quaternion, which has one real dimension,
and three imaginary axes. This describes the helicity in the 4th dimension hypersphere
. Within coherent space,
, time does not exist beyond the constant frequency of its spinning. Time and rest mass remain in polarization space.
Constructive interference of the two spin axes is expressed by their superposition leading to the addition of the two spin 1/2 vectors to give a total spin of 1 for the resonant spin,
An identical calculation as for a single spin,
, can be applied to quaternion spin showing it too is a Lorentz invariant [
3].
Hermitian space carries the polarizations, which support magnetic moments, charge, etc.; the anti-Hermitian space carries coherence, which support chirality, such as the helicity. Similar to the two complementary inverse spaces of position and momentume, here the Hermitian and anti-Hermitian spaces carry the two complementary properties of spin, polarization and coherence.
Re-define the spinor mirror states as and .
The Weyl Spinor
From Equation (
10) and using reference [
3], a Weyl spinor transforms under boosts and rotations as
Since time exists only in polarization space, Equation (
9), a boost of polarizations carries along the spinor. There are no boosts in coherent space; the left and right components are equal;
and the state is a unit quaternion which spins the axis of linear momentum in coherence space
by angle
, thereby generating the helicity.
The usual definition [
14] identifies helicity as the projection of the spin vector onto the axis of linear momentum in Minkowski space. Here helicity is defined only in coherence space where there is no momentum with which to contract. Helicity defined here, is represented by an anti-Hermitian, odd to parity, second rank helicity operator in coherent space,
Recall
, and the component,
, drives the quaternion in Equation (
16). Helicity no longer determines the
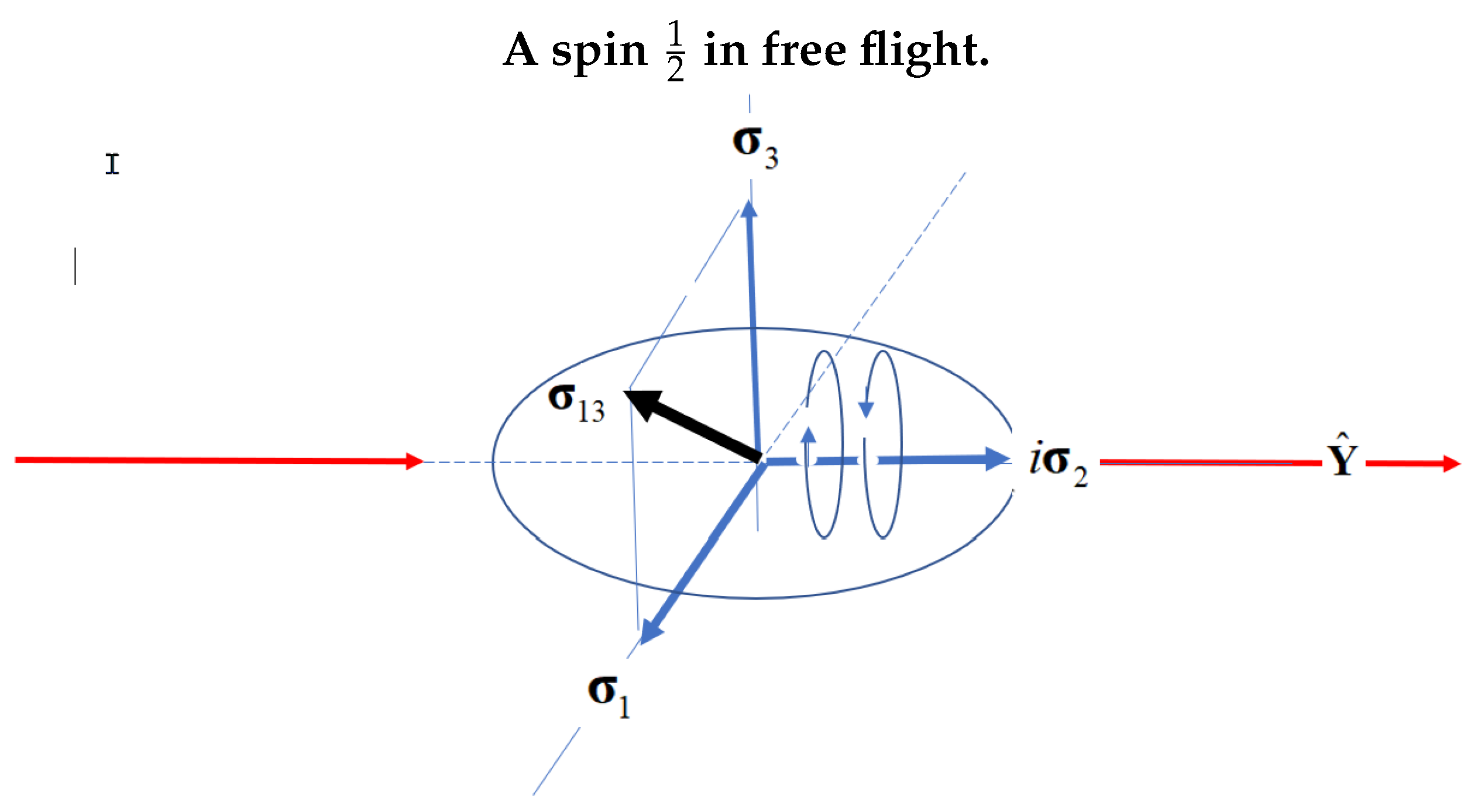
spin states along the direction of motion as usually defined. Rather hyper-helicity is a distinct element of reality and complementary to observed polarized spin. In free flight, helicity carries a quantum of energy in hyperspace, see
Figure 1.
The 2D Spin Equation
Turning to the 2D Hermitian part, Equation (
9), with states of even parity, we must first transform from the spin space to Minkowski spacetime,
giving a relationship independent of
,
Taking the linear momentum in the direction
requires setting
,
The polarization in spin spacetime is essentially the same as in Minkowski spacetime. This represents all that can appear of quaternion spin in Minkowski spacetime. The spinning from helicity is in coherent space and the effect in Minkowski spacetime is to spin the polarization. In free flight from our spacetime, a spin is a spinning plane, or worldsheet, [
18], with mass and energy only (along with any property the spinning polarizations generate). This changes when it encounters a measuring probe.
Define a momentum vector
and the 2D polarization equation becomes
where the even parity state is written as
. This leads to the same Klein-Gordon equation in Minkowski and spin spacetime,
with eigenvalues,
The relativistic energy from linear motion in the direction
Y is taken as
E. The helicity splits this giving, say, the + energy to R handed helicity and the − to the L handed helicity. Note that these carry relativistic energy, via
. Since there are no components of linear momentum in the
directions, these energies can only come from the relativistic precession of the
axes, see
Figure 1.
Further note that quaternion spin is naturally a 4x4 matrix due to the two spin axes, one L and the other R, Equation (
2). Expressing one spin axis as one of its polarization components,
, and taking the direct product with a helicity 2x2 matrix,
, naturally leads to the spatial gamma matrices,
with
. The states, Equation (
28) are elements of the Dirac field describing two axes carried on the same particle with helicity, contrary to the two separate particles that Dirac introduced, [
2].
The term
is normally used to project the R and L handed chiral states from a Dirac field. In contrast here, from Equation (
8), the odd and even parity states, Equation (
11) are projected from the mirror quaternion spin states in Equation (
8),
It appears energy is stored and transported in the helicity. A particle, for example, created through some decay with energy difference of , carries that energy in its hyperspace. This suggests how a quantum of energy is transported after emission.
Measured Spin
Quaternion spin, with elements of reality in both polarization and coherent spaces, projects only its polarization into our spacetime, Equation (
23). Whereas both the
and
axes are projected, measurement reveals only one vector component. From this, Dirac built his theory. Successful agreement with the Stern-Gerlach data confirmed its vector property.
Unaware of helicity and a second spin axis on a single particle, Dirac identified the 4x4 field as evidence for two distinct particles with spin: opposite from each other in every way,
the mirror states. He set
and called it the vacuum state and antimatter and hole theory resulted [
4]. At higher energies, however, it might be expected that quaternion spin would decay into a matter, antimatter pair. The antimatter particle would soon be annihilated, but the matter fragment would survive at these energies, as Dirac proposed. At lower energy, the quaternion spin would appear by re-combining with other matter particles. The energies at which this would occur are much higher than normal temperatures at which quaternion spin should be stable.
Dirac spin is obtained when the projected polarization, Equation (
23) is measured,
Figure 4. Whereas in free-flight quaternion spin displays no polarization, it being averaged by the helicity, when it encounters an anisotropic field, the two axes are no longer indistinguishable, quaternion spin is destroyed and the helicity stops. Measurement causes spin polarization to appear. If the measuring probe is closer to one of the two axes in
Figure 5, then that axis is pulled to align while the other randomizes. On the other hand, if the field lies along or close to the direction of the superposed spin axis, see again
Figure 4, then there is a competition as to which axis aligns. This is the source of the observed quantum coherence that gives an apparent violation of Bell’s inequalities, [
19]. Eventually, however, only one polarization axis lines up anti-parallel with the probe field,
Figure 4: this is Dirac spin. The alignment stabilizes that axis and lowers its energy, while the second unobserved axis, spins perpendicular to the probe field; has high energy; and its polarization is averaged to zero. It is this unobserved spin axis that Dirac attributed to antimatter production.
The quantization of the Dirac field for a measured spin is formally unchanged, [
3] although in two dimensions rather than three. However, the interpretation differs. Setting the vacuum state to zero and using the fermionic condition to fill the negative energy states needs re-assessment. Since the “second particle" with negative energy is here found to be the “second axis" of the same particle, its energy is not infinitely negative. We leave these questions for now.
All the internal energy from the 4th dimension helicity is transferred into our dimension upon measurement.
Discussion
Introducing the bivector into spin algebra significantly changes our view of a spin from a structureless point particle of intrinsic angular momentum in Minkowski spacetime to a four dimensional structured spin with extrinsic angular momentum in spin spacetime. Any structured particle can be expressed in its own coordinate frame and we find that the three spatial components of Minkowski spacetime become a 2D plane of spin polarization which is spun about its axis of linear momentum producing L or R handed helicity. The spinning 2D plane forms only in the isotropy of free-flight.
The bivector component supports a massless Weyl spinor which in turn is a unit quaternion and generates the helicity. Quaternions do not exist in polarization space, but rather in the 4th dimensional hypersphere of
[
11] which cannot be completely observed from any spacetime frame. Only the stereographic projection, [
10], is visible.
A Weyl spinor is considered not to be a Lorentz invariant for massive particles [
20]. In the usual treatment, helicity is defined in Minkowski spacetime and is, therefore, an observable. In contrast here, helicity exists only in hyperspace. Any observer in our dimension would see only a particle with kinetic energy (like in a bubble chamber). Neither the handedness of the spinor nor its internal quantum of energy are visible from any spacetime frame, and therefore cannot violate special relativity. A Weyl spinor is therefor a Lorentz Invariant for quaternion spin.
The question arises as to whether the quaternion spin exists and is more fundamental than measured spin. First the intrinsic angular momentum of the Dirac spin becomes extrinsic for quaternion spin. The axis actually spins. That the geometric structure of spin is equivalent to that of a photon,
Figure 1, is compelling. Other quantum observables come in complementary pairs, like position and momentum etc, in spaces that are the inverse of each other. It is therefore reasonable that spin also has two complementary properties, polarization in Hermitian space and coherence in anti-Hermitian space. Furthermore, spin is described by its Dirac gamma matrices, and there are only three algebras: (
); (
). (
) with the first giving Dirac SU(2) spin and the second and third belonging the quaternion group with respectively one and two axes of precession. Finally the experimental proof for the existence of quaternion spin is given by the apparent violation of BI . This is usually attributed as proof of non-locality. Quaternion spin, however, accounts for the violation locally as shown in the other papers, [
15,
16].
The measurement problem has a central premise that the act of observation perturbs the system. Quaternion spin makes a distinction between measurement (polarized) and free-flight (coherence). They epitomize the particle-wave duality.
EPR believed that QM is incomplete [
21] since it does not simultaneously describe two complementary elements of reality. In support of Einstein, both polarization and coherence are found to exist simultaneously on the same particle. On the other hand, supporting Bohr’s complementarity, in free flight only the coherence is present since the spinning axis averages out the polarization. Upon measurement, the helicity stops and only the polarization is realized. Although both properties exist simultaneously, only one is manifest at any instant. QM is, therefore, incomplete because it is a theory of measurement restricted to our space-time. QM does not include elements of reality that are anti-Hermitian on the
hypersphere.
These observation are confirmed in companion papers, [
15,
16]. The former describes an EPR pair and shows that the helicty introduces an antisymmetric component to spin which accounts for the apparent violation of BI, [
22,
23,
24]. To confirm this, the third paper gives a computer simulation that evaluates the two contributions to spin from the polarization, (CHSH=2) and from the coherence (CHSH=1), [
16] for a total of CHSH=3. Again we emphasize that there are no hidden variables, so Bell’s theorem [
25] is not applicable.
It was unforeseen that quaternion spin would give an alternate interpretation contrary to antimatter production. Although the existence of antimatter is not disputed, its manner of production is. The experimental evidence for antimatter appears to be scant and equivocal. Although high energy data interprets antimatter, there is perhaps another possibility. In the Standard Model, [
14] SU(3)SU(2)U(1) replace SU(2) by
. It is suggested that antimatter would not be needed to balance some of the lepton equations because the quarks would have an addition property of chirality, a conserved quantity, on decay.
Acknowledgments
The author is grateful to Hillary Sanctuary, PhD, EPFL Switzerland, for suggesting the name hyper-helicity to distinguish it from the usual definition of helicity.
References
- Gerlach, Walther, and Otto Stern. “Das magnetische moment des silberatoms." Zeitschrift für Physik 9.1 (1922): 353-355. [CrossRef]
- Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624. [CrossRef]
- Peskin, M. E. , Schroeder, D.V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder,CO.
- Dirac, P. A. M. (1930). “A Theory of Electrons and Protons". Proc. R. Soc. Lond. A. 3: 126 (801).
- Sanctuary, B. C. “Structure of a spin 12. arXiv:0908.3219 (2009). [CrossRef]
- Sanctuary, B. C. “The two dimensional spin and its resonance fringe. arXiv:0707.1763 (2007). [CrossRef]
- Okun, Lev B. "Mirror particles and mirror matter: 50 years of speculation and searching." Physics-Uspekhi 50.4 (2007): 380. [CrossRef]
- Doran, C. , Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press. [CrossRef]
- Muralidhar, K. "The spin bivector and zeropoint energy in geometric algebra." Adv. Studies Theor. Phys 6 (2012): 675-686.
- To visualize quaternions and its steriographic projection see 3 Blue 2 Brown: https://eater.net/quaternions.
- Peters, James F., and Arturo Tozzi. "Quantum entanglement on a hypersphere." International Journal of Theoretical Physics 55 (2016): 3689-3696. [CrossRef]
- Christian, Joy. "Bell’s theorem versus local realism in a quaternionic model of physical space." IEEE Access 7 (2019): 133388-133409. [CrossRef]
- Christian, Joy. "Symmetric Derivation of the Singlet Correlations within a Quaternionic 3-sphere. arXiv:2204.10288 (2022). [CrossRef]
- Schwartz, M. D. (2014). Quantum field theory and the standard model. Cambridge University Press. [CrossRef]
- Sanctuary, B. Spin with Hyper-helicity. . Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
- Sanctuary, B. Simulated Non-Local EPR Correlation: CHSH = 3. Preprints 2023, 2023010570. [Google Scholar] [CrossRef]
- Zhou, Ziheng, and Zhenhua Yu. "Interaction effects on the PT-symmetry-breaking transition in atomic gases." Physical Review A 99.4 (2019): 043412. [CrossRef]
- Maldacena, J. , Susskind, L. Cool horizons for entangled black holes. Fortschritte der Physik, 61(9), 781-811. [CrossRef]
- Bell, John S. “On the Einstein Podolsky Rosen paradox.” Physics Physique Fizika 1.3 (1964): 195. [CrossRef]
- Troha, T., D. Lukman, and N. S. Mankoč Borštnik. "Massless and massive representations in the spinor technique." International Journal of Modern Physics A 29.23 (2014): 1450124. [CrossRef]
- Einstein, A, Podolsky, B and Rosen, N, “Can quantum mechanical description of physical reality be considered complete?” Phys Rev 47, 777-780, (1935). [CrossRef]
- Clauser, J. F. , Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880. [CrossRef]
- Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 1: 14 (8), 15 October 1944. [CrossRef]
- Weihs, G. , Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039. [CrossRef]
- Bell, J. S. “Speakable and Unspeakable in Quantum Mechanics” (Cambridge University Press, 1987), 2004. See “Locality in quantum mechanics: reply to critics. Epistemological Letters”, Nov. 1975, pp 2–6.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).