Quaternion Spin

Bryan Sanctuary

doi:10.20944/preprints202302.0055.v4

Submitted:

18 May 2024

Posted:

20 May 2024

Read the latest preprint version here

Abstract

We present an analysis of the Dirac equation when the spin symmetry is changed from SU(2) to the quaternion group, $Q_8$, afforded by multiplying one of the $\gamma$-matrices by the imaginary number. The reason for doing this is to introduce a bivector into the spin algebra. This modifies the Dirac equation which separates into two distinct and complementary spaces: one describing polarization and the other coherence. The former describes a 2D structured spin and the latter its helicity, generated by a unit quaternion.

Keywords:

foundations of physics

;

Dirac equation

;

spin

;

quantum theory

;

non-locality

;

helicity

;

quaternion symmetry

;

Twistor theory

Subject:

Physical Sciences - Theoretical Physics

Introduction

Spin, first observed by Stern and Gerlach [1], reveals two states of up and down. Spin is measured to be angular momentum of

\frac{\sqrt{3}}{2} ℏ

magnitude, a vector quantity, belonging to the SU(2) group. Spin is a fundamental property of Nature, purely quantum with no classical analogue. The mathematical basis for spin is the Dirac equation [2]. Dirac’s analysis introduces his relativistic equation by linearizing the Klein-Gordon Equation while respecting conservation of mass and energy. He was led to his gamma matrices with four states rather than the two that are measured [3]. He surmised that his equation described two spins rather than one. The two are mirror image twins of each other, which Dirac interpreted as a matter-antimatter pair [2]. From this hole theory, antimatter production, and the sea of electron model followed [4].

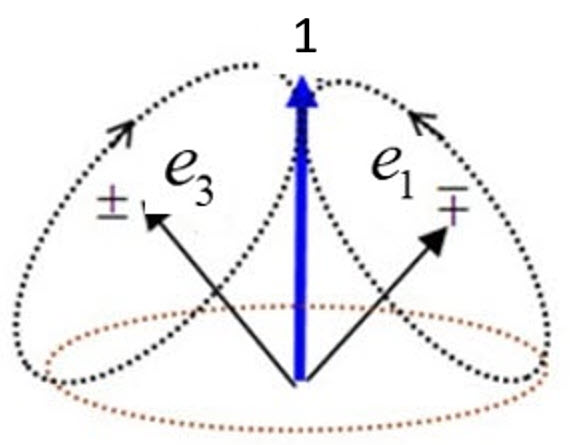
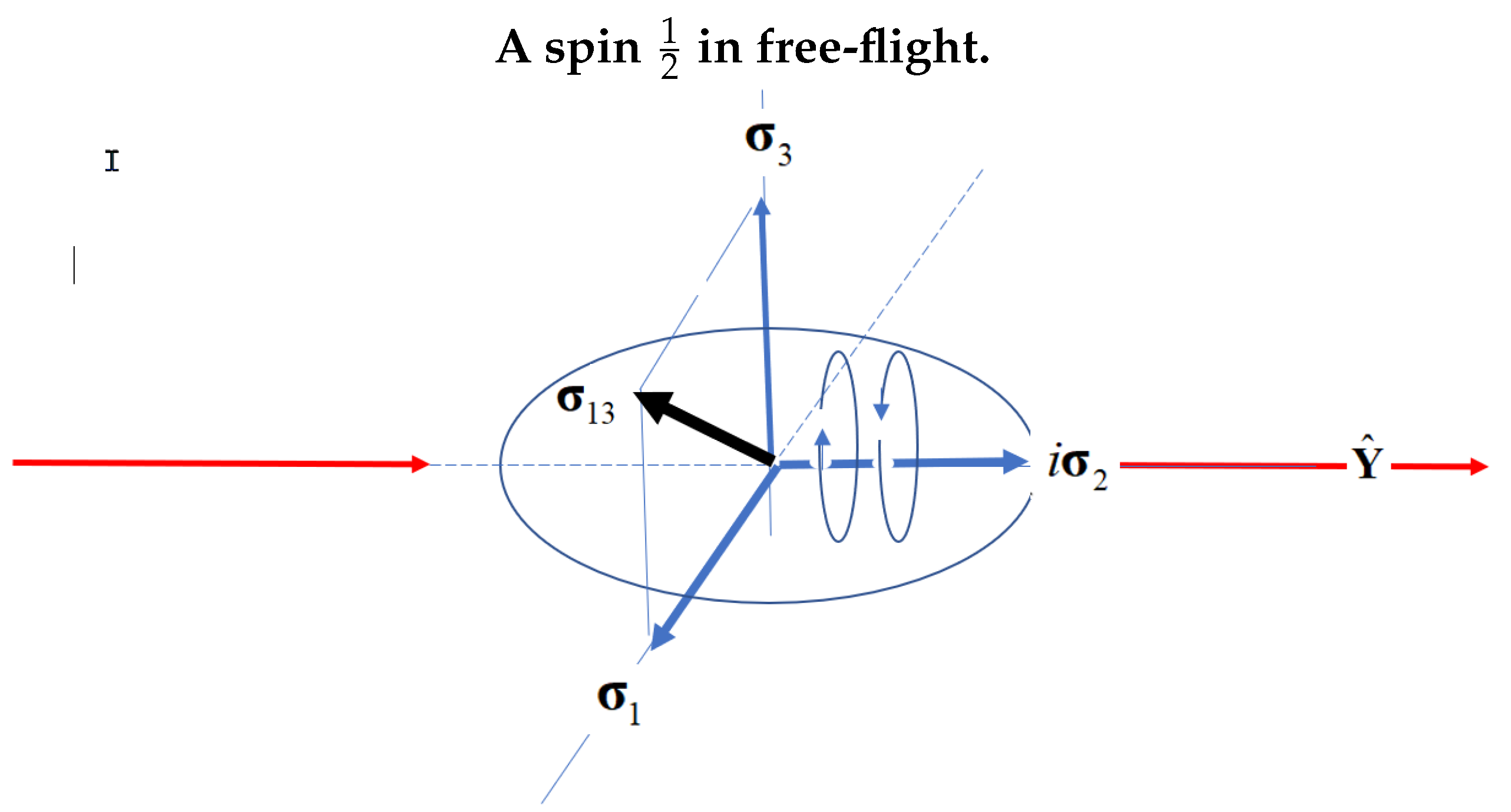
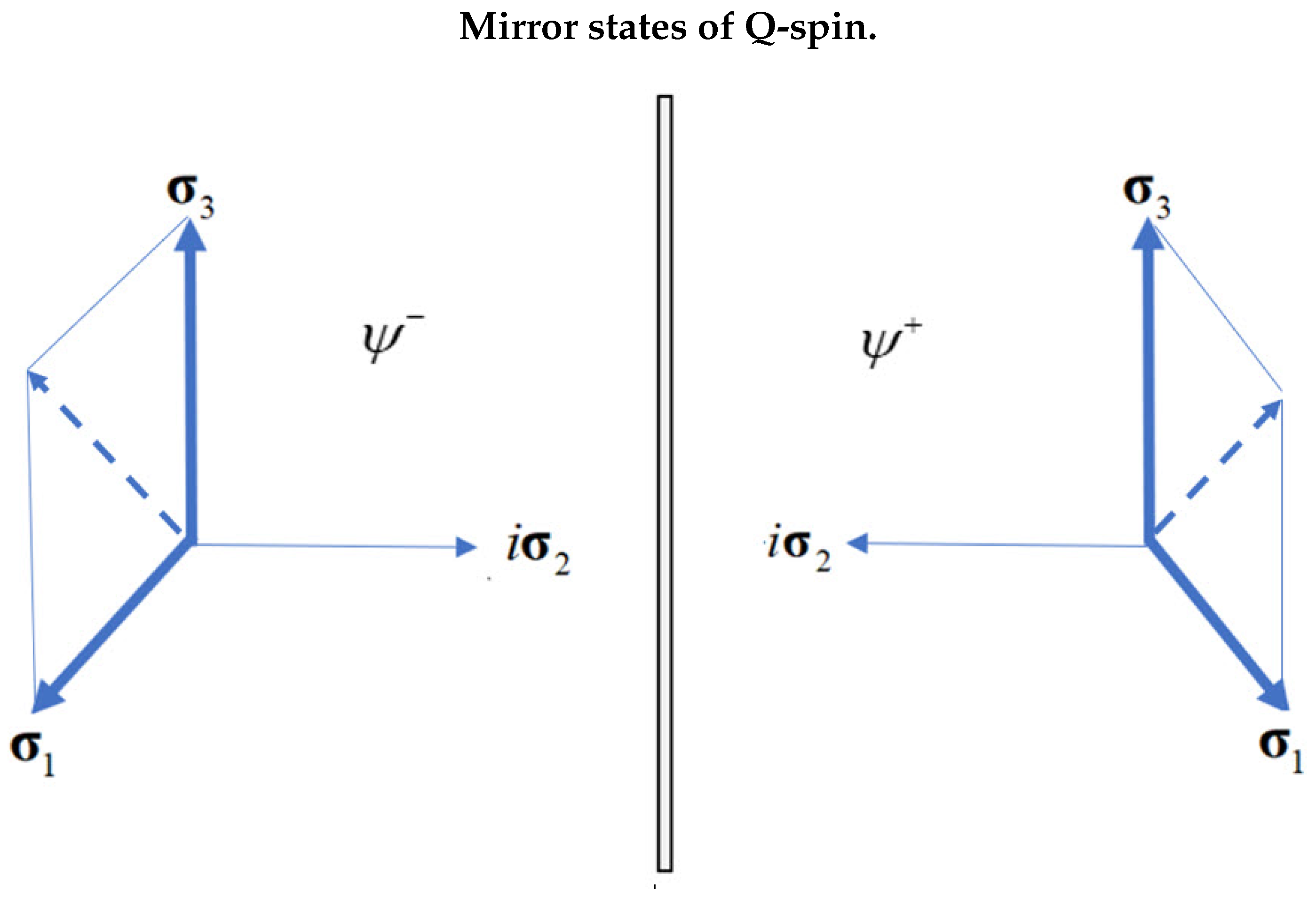
Under the quaternion group, the two point particles that Dirac found are replaced by one structured particle called quaternion spin, or Q-spin, that carries two complementary properties: polarization and coherence. The coherence is helicity which spins the axis of linear momentum in free-flight, (Figure 1), giving the two helicity states of L and R. In addition, two mirror states, [5] emerge which describe two orthogonal magnetic axes, each with magnetic moment of

μ

, that are perpendicular to the axis of linear momentum on the same particle. The figure shows that Q-spin is geometrically equivalent to a photon. The two magnetic fermionic axes,

e_{3}

and

e_{1}

each carry a spin

\frac{1}{2}

, which can couple to give a composite spin 1 boson,

e_{13}

. All three axes are orthogonal to

e_{2}

, see (Figure 1). Structured spin makes the intrinsic angular momentum of Dirac spin, extrinsic.

To motivate the discussion, consider the well know equation for the geometric product of Pauli spin components,

σ_{i} σ_{j} = δ_{i j} + ε_{i j k} i σ_{k}

(1)

Arising from Geometric Algebra, [6,7] the first term describes a symmetric component that gives rise to polarization and measured Dirac spin. The second term is anti-symmetric and depends upon a bivector,

i σ_{k}

and the Levi Civita third rank anti-symmetric tensor. Since i cannot simultaneously be equal and not-equal to j, the geometric product, Eq.(1), is complementary. There is, however, no bivector in the Dirac equation. We introduce a bivector by multiplying a gamma matrix by the imaginary number,

{\tilde{γ}}_{s}^{2} \equiv i γ_{s}^{2}

. This makes the Dirac field complex, which is origin of helicity. It is the purpose of this paper to include this anti-symmetric term as a property of spin, even though it is not measurable.

The procedure here has similarities to Penrose’s Twistor Theory, [8] [9]. Essentially Twistor Theory complexifies Minkowski space, a four dimensional real manifold M, into a complex Twistor space, T. As a complex space, it has two projections into helicity states of + and −, denoted by

P T^{\pm}

. The boundary between the two,

P N

, is real space of null vectors which are lightrays from the light cone. Different slices in T lead to different projections, groups and algebras.

Here we complexify the Dirac field in spin spacetime, and not Minkowski space. No additional parameters are introduced and the field is determined by a non-Hermitian Dirac equation. Under parity, this splits into complementary spaces. In the following, these ideas are formalized.

This paper is the first of several in which the properties and foundations of Q-spin are presented. A second paper, “Spin with helicity" [10] discusses the geometry and conservation of correlation. A third paper, [11], studies and simulates the correlation between a pair of spins. A general summary, [12] describes some consequences of this symmetry change..

Formally this four state spin is called Q-spin to distinguish it from the usual Dirac spin. A modified form of the Dirac equation is presented that admits both polarization and helicity, complementary elements of reality. It describes spin as it exists in the absence of interactions, and therefore in free-flight. Additionally, when measured, the boson spin decouples into a fermion of spin

\frac{1}{2}

. This is the measured spin Dirac formulated.

Q-spin is a boson of odd parity in free flight, a wave; and a fermion of even parity when measured, a particle.

Spin Spacetime Algebra

No bivector is found in the Dirac equation because his point-particle spin is defined in Minkowski space which is a four dimensional real manifold. In contrast, introducing a bivector gives spin structure, and since it can be oriented randomly relative to Minkowski space, we introduce spin spacetime,

(β_{s}, e_{1}, e_{2}, e_{3})

, which is the Body Fixed Frame, BFF of one spin. Minkowski space is the Laboratory Fixed Frame

(β, X, Y, Z)

, LFF.

Dirac’s gamma matrices,

(γ^{0}, γ^{1}, γ^{2}, γ^{3})

, represent the 4x4 Dirac field. Within this field there are two point particle spins of

\frac{1}{2}

: each described by the three Pauli spin components and the identity, (

I, σ_{X}, σ_{Y}, σ_{Z})

which belong to the SU(2) group; each is the mirror twin of the other: Dirac’s matter-antimatter pair.

Introducing

{\tilde{γ}}_{s}^{2} = i γ_{s}^{2}

complexifies, [8,9], spin spacetime (subscript s). Minkowski space obeys Clifford algebra

C ℓ_{1, 3}

. In contrast, the Clifford algebra of spin spacetime is

C ℓ_{2, 2}

. The immediate consequence of introducing the bivector is the Dirac equation becomes non-hermitian with two fields expressed by

(γ_{s}^{0}, γ_{s}^{1}, \pm {\tilde{γ}}_{s}^{2}, γ_{s}^{3})

, the solutions are mirror states,

ψ^{\pm}

with no parity. The ± division is complex conjugation.

The mirror states can be combined into odd and even parity states, and upon doing this, the field separates once more into two distinct spaces and the algebra changes from

C ℓ_{2, 2}

, to a 2D plane with algebra

C ℓ_{1, 2}

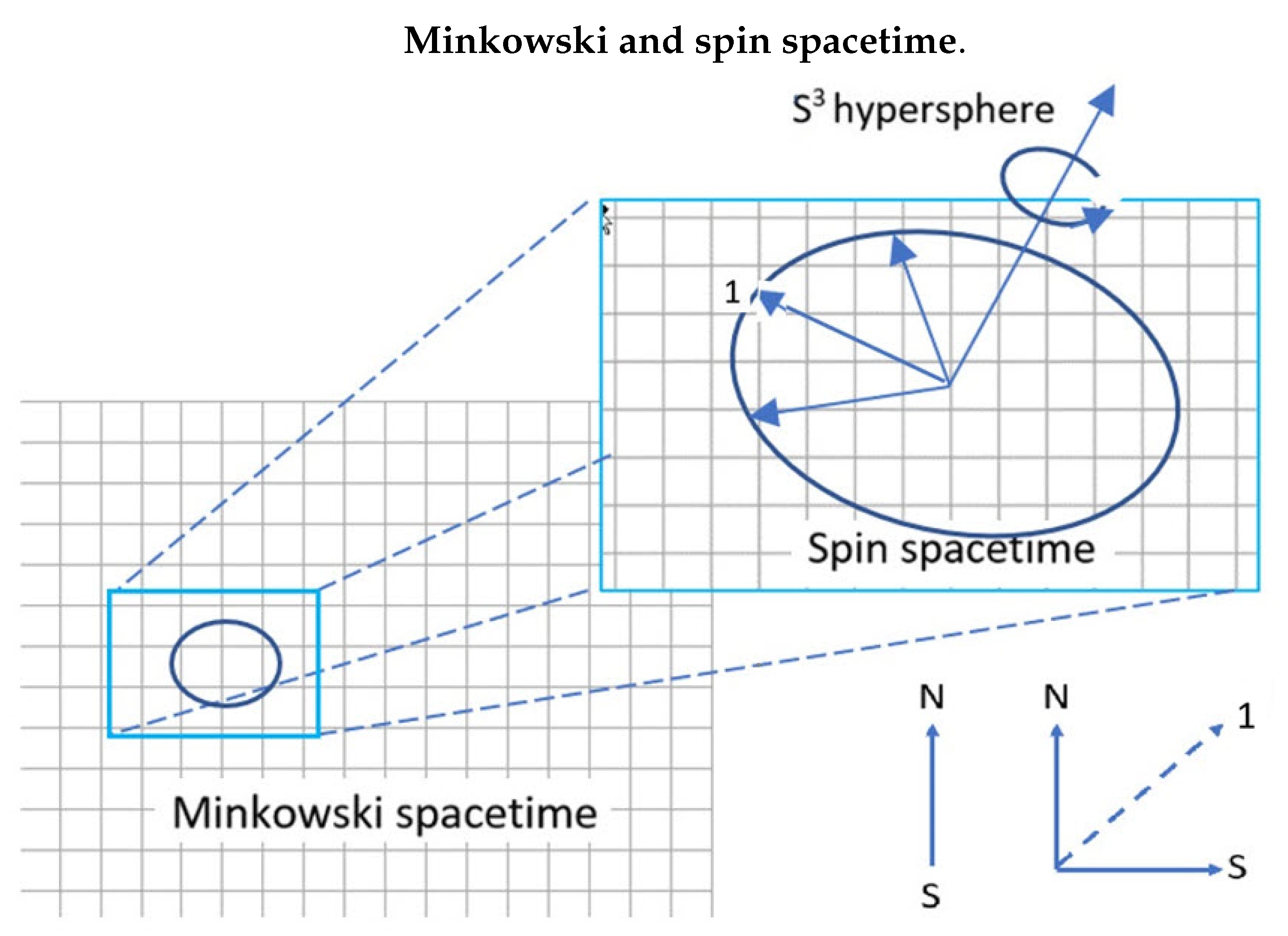
; and a connection to the S³ hypersphere via

{\tilde{γ}}_{s}^{2}

. Spin spacetime decomposes into two complementary spaces: polarization spacetime,(0,1,3) of even parity, and coherence space,(2),of odd parity. It has the structure of a 2D plane of polarization, see Figure 2.

The bivector,

i σ_{2}

, connects spin spacetime to the complementary space of the helicity states, generated by quaternions in the

S^{3}

hypersphere. This has four spatial dimensions, and cannot be measured. Its only role is to spin the axis of linear momentum,

Y = e_{2}

either L or R which are the two helicity states. Note that in free-flight the helicity generates its own

S^{3}

hyperspace. Otherwise it does not exist.

Q-spin is one particle with four states, not two particles with two states each. This is an entirely different interpretation from Dirac’s matter-antimatter pair. We do not deny antimatter is produced, but not under quaternion symmetry. We show, below, that Q-spin also solves the negative energy problem Dirac encountered.

When spin is measured the helicity stops and the usual two polarized states of up and down are observed in some direction,

|\pm, \hat{n}〉

. Away from polarizing fields, the spinning axis of linear momentum averages out the spin polarization. Only the helicity is then present.

The spin polarized structure can be expressed in Minkowski space. The bivector cannot.

Mirror states and parity

The spin space-time gamma matrices

(γ_{s}^{0}, γ_{s}^{1}, \pm {\tilde{γ}}_{s}^{2}, γ_{s}^{3})

, anticommute and have a different signature from Minkowski space,

{\tilde{η}}_{s}^{μ ν} = (\begin{matrix} + 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & + 1 & 0 \\ 0 & 0 & 0 & - 1 \end{matrix})

(2)

so the term

{\tilde{γ}}_{s}^{2}

is not a spatial component, but rather time-like and a frequency.

The commutation relations are changed from the usual three dimensional generator of rotations in Minkowski space,

S_{(3)}^{i j} = \frac{i}{4} [γ^{i}, γ^{j}] = \frac{1}{2} ε_{i j k} σ_{k} I_{4}

(3)

to ones that generate rotations in only two dimensions in spin spacetime

\begin{matrix} S_{(2)}^{i j} & = \frac{i}{4} [γ_{s}^{i}, γ_{s}^{j}] = \frac{i}{2} ε_{i 2 j} {\tilde{σ}}_{s 2} I_{4} \end{matrix}

(4)

\begin{matrix} S_{(2)}^{i 2} & = \frac{i}{4} [γ_{s}^{i}, {\tilde{γ}}_{s}^{2}] = \frac{i}{2} ε_{i 2 j} σ_{s j} I_{4} \end{matrix}

(5)

The former equation describes rotations in the 31 plane about the direction 2; whereas the imaginary term in the latter equation damps all rotation attempts out of the 31 plane.

Two new equations in spin spacetime follow from the gamma algebra which gives a non-Hermitian equation by virtue of

{\tilde{γ}}_{s}^{2}

,

(i γ_{s}^{0} \partial_{0} - i γ_{s}^{1} \partial_{1} \pm i {\tilde{γ}}_{s}^{2} \partial_{2} - i γ_{s}^{3} \partial_{3} - m) ψ^{\pm} = 0

(6)

and we suppress the subscript s on the derivatives.

By treating a spin in free-flight in an isotropic environment, the two axes

(1, 3)

are indistinguishable. Therefore, permutation with the parity operator,

P_{13}

does not change the

(1, 3)

dependence in Eq.(6), but the bivector,

i σ_{2} = σ_{3} σ_{1}

is anti-symmetric to 13 permutation. Therefore the above equations admits two solutions in left and right handed coordinate frames, which are mirror states, [5,13]

P_{13} ψ^{\pm} = ψ^{\mp}

(7)

see (Figure 3). The anti-commutation of the

γ_{s}^{μ}

matrices ensures that energy is conserved and the Klein-Gordon equation is recovered.

Adding and subtracting the two equations in Eq.(6) leads to their separation into a Hermitian part and an anti-Hermitian part,

\begin{matrix} (i γ_{s}^{' 0} \partial_{0} - i γ_{s}^{1} \partial_{1} - i γ_{s}^{3} \partial_{3} - m) Ψ^{+} & = 0 \end{matrix}

(8)

\begin{matrix} {\tilde{γ}}_{s}^{2} \partial_{2} Ψ^{-} & = 0 \end{matrix}

(9)

where the two mirror states combine into states with odd and even parity,

P_{13} Ψ^{\pm} = \pm Ψ^{\pm}

with the definition,

Ψ^{\pm} = \frac{1}{\sqrt{2}} (ψ^{+} \pm ψ^{-})

(10)

The even parity states describe polarization and the odd parity states describe its helicity.

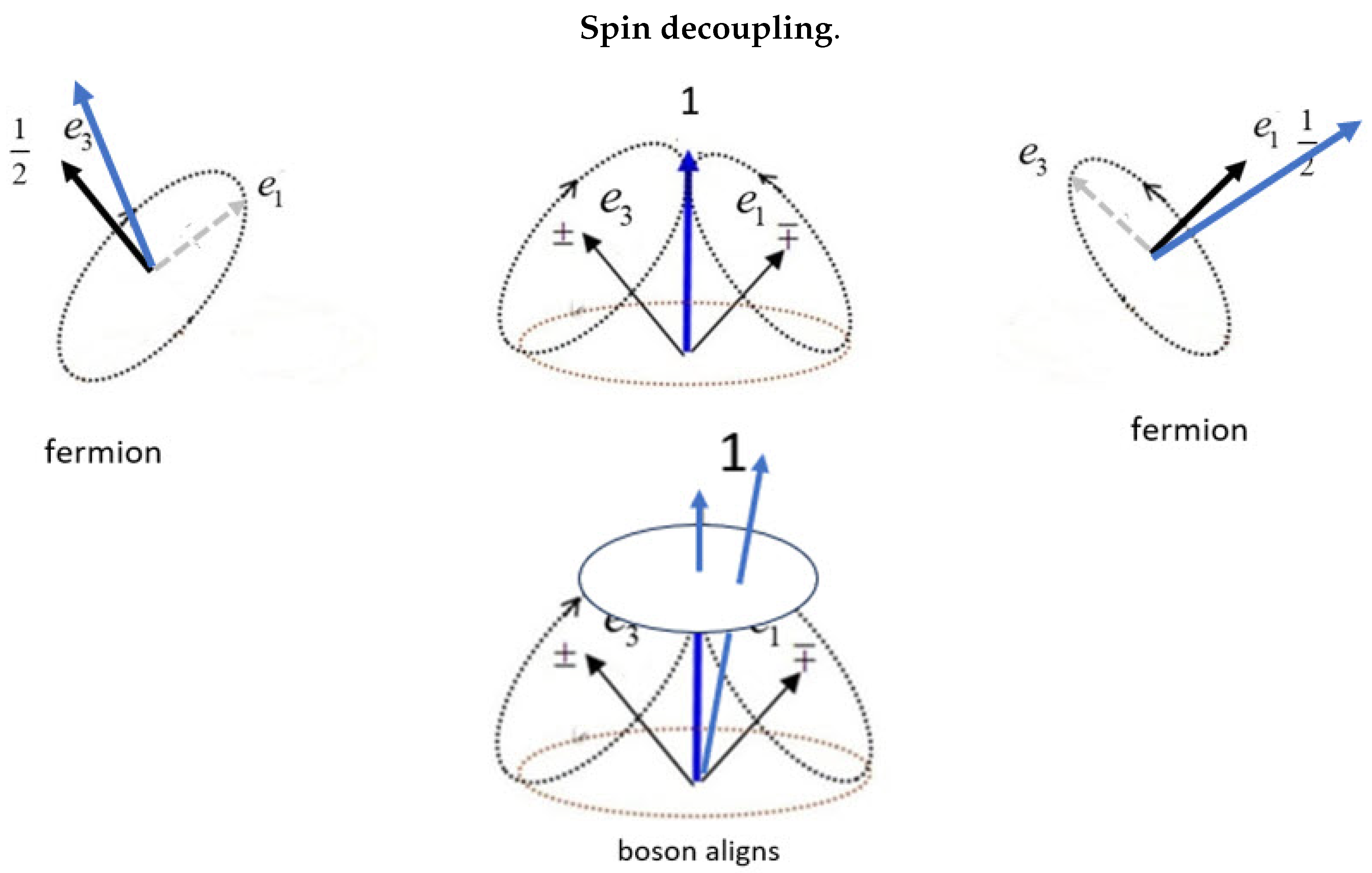
The separation of the Dirac field into reflective states means each axis precesses in the opposite direction. These two polarization axes, each with a magnetic moment

μ

, constructively interfere producing the resonance, and purely coherent spin, see (Figure 4), (middle upper). Such a resonance structure lowers the energy and stabilizes the 2D structure over that of two point particle spins.

The Hermitian part, Eq.(8), is the same as the usual Dirac equation, but in two dimensions rather than three. It describes a disk, as visualized in (Figure 1) and (Figure 2).

The bivector component,

(2)

, describes a massless Weyl spinor in coherent space, Eq.(9). Within this space, time does not exist beyond the constant frequency of its spinning. Time and rest mass remain in polarization space. Similar to the two complementary inverse spaces of position and momentum, here the two spin spaces carry the two complementary properties of polarization and coherence.

Redefine the spinor mirror states as

ψ^{+} \equiv ψ_{R}

and

ψ^{-} \equiv ψ_{L}

.

The Weyl spinor

From Eq.(9) and using reference [3,14] a Weyl spinor transforms under boosts and rotations as

\begin{matrix} ψ_{R} \to (1 - i χ \frac{σ_{2}}{2} + i β \frac{σ_{2}}{2}) ψ_{R} (0) \end{matrix}

(11)

\begin{matrix} ψ_{L} \to (1 - i χ \frac{σ_{2}}{2} - i β \frac{σ_{2}}{2}) ψ_{L} (0) \end{matrix}

(12)

Since time exists only in polarization space, Eq.(8), a boost of polarizations carries along the spinors. There are no boosts in coherent space; the left and right wave functions are equal;

ψ_{R} = ψ_{L}

(13)

and the state is a unit quaternion which spins the axis of linear momentum in coherence space

(2)

by angle

χ

, thereby generating the helicity,

ψ_{L} (χ) = exp (- i \frac{χ}{2} σ_{2}) ψ_{L} (0) = (cos \frac{χ}{2} - i σ_{2} sin \frac{χ}{2}) ψ_{L} (0)

(14)

The usual definition [15] identifies helicity as the projection of the spin vector onto the axis of linear momentum in Minkowski space. The helicity of the axis, L or R, gives spin state as

+ 1

or

- 1

. Spin and helicity are related and not independent. Q-spin is quite different .

Here helicity is defined only in quaternion space, the

S^{3}

hypersphere, [16,17,18] where there is no momentum with which to contract. Choosing

Y = e_{2}

connects Minkowski space to spin spacetime and finally to the

S^{3}

hypersphere, where the component

i σ_{2}

generates the quaternion in Eq.(14), and provides a mechanism for helicity.

Within the spinning disc in the (3,1) plane, the two ferminoic axes couple to give the composite boson of spin 1. However, the rapid spinning averages out the boson polarization in the disc, so only the helicity is present in free flight. That is, in free-flight an electron is a boson of odd parity,

e_{B}^{-}

.

Helicity is a distinct element of reality and complementary to observed polarized spin. All we observe of the helicity in our spacetime is its stereographic projection which is the spinning of the Y axis, giving a spinning disc of angular momentum in Minkowski space, Figure(Figure 2).

The 2D spin equation.

Transform from the BFF of the spin, to the LFF using,

\begin{matrix} e_{3} = cos θ Z + sin θ cos ϕ X + sin θ sin ϕ Y \\ e_{1} = - sin θ Z + cos θ cos ϕ X + cos θ sin ϕ Y \\ e_{0} = cos ϕ Y - sin ϕ X \end{matrix}

(15)

giving,

\begin{matrix} γ_{s}^{1} = (- sin θ γ^{3} + cos θ cos ϕ γ^{1} + cos θ sin ϕ γ^{2}) \\ γ_{s}^{3} = (cos θ γ^{3} + sin θ cos ϕ γ^{1} + sin θ sin ϕ γ^{2}) \\ p_{3} = p \cdot e_{3} = (cos θ p_{Z} + sin θ cos ϕ p_{X} + sin θ sin ϕ p_{Y}) \\ p_{1} = p \cdot e_{1} = (- sin θ p_{Z} + cos θ cos ϕ p_{X} + cos θ sin ϕ p_{Y}) \end{matrix}

(16)

and the following expression is independent of

θ

,

\begin{matrix} γ_{s}^{1} p_{1} + γ_{s}^{3} p_{3} = γ^{3} p_{Z} + (cos ϕ γ^{1} + sin ϕ γ^{2}) (cos ϕ p_{X} + sin ϕ p_{Y}) \end{matrix}

(17)

Taking the linear momentum in the direction

Y = e_{2}

requires setting

ϕ = 0

,

γ_{s}^{1} p_{1} + γ_{s}^{3} p_{3} = γ^{1} p_{X} + γ^{3} p_{Z}

(18)

The polarization in spin spacetime is projected onto Minkowski space. The spinning from helicity is in coherent space which spins the polarization in Minkowski space.

In contrast, the usual Dirac point particle, 2-state fermion spin is formed when

e_{B}^{-}

encounters a polarizing field. We denote this by

e_{F}^{-}

, which is even to parity. A fermion electron has two states of up and down. For boson electrons the two polarized states are suppressed, leaving the two helicity states of L and R.

Define a momentum vector

p = p_{3} e_{3} + p_{1} e_{1}

and the equation for 2D polarization becomes

(\begin{matrix} E - m & - p \cdot σ \\ + p \cdot σ & - (E + m) \end{matrix}) (\begin{matrix} u^{+} \\ v^{+} \end{matrix}) = 0

(19)

where the even parity state is written as

Ψ^{+} = (\begin{matrix} u^{+} \\ v^{+} \end{matrix})

. This leads to the same Klein-Gordon equation in Minkowski and spin spacetime,

\begin{matrix} (\partial_{0}^{2} - \partial_{Z}^{2} - \partial_{X}^{2} - m^{2}) ψ = 0 \end{matrix}

(20)

\begin{matrix} (\partial_{s} 0^{2} - \partial_{3}^{2} - \partial_{1}^{2} - m^{2}) ψ_{s} = 0 \end{matrix}

(21)

with eigenvalues for the latter of,

E = \pm \sqrt{m^{2} + p_{3}^{2} + p_{1}^{2}} .

(22)

We interpret the two energy states as internal energy which is absent for point particles. This is caused by the left and right spinning of the two spin axes on the same particle, see Figure(Figure 4). As mirror states, they are depicted as being in phase with equal, but opposite, energy. The two couple to give the resonance spin of 1. Precession as shown gives one component of, say,

m = + 1

. Reversing these precessions gives the

m = - 1

component. The

m = 0

component cannot form since it would violated the reflective symmetry between the mirror states. Note also a photon has no

m = 0

component.

The two axes form the resonance boson, (Figure 4). Rather than Dirac’s matter-antimatter pair, Q-spin resolves the negative energy problem Dirac encountered because the two axes must have equal energy, but spin oppositely.

Define the helicity matrix,

H_{g} = γ^{1} {\tilde{γ}}^{2} γ^{3}

, which give the spatial gamma matrices,

σ_{i} \otimes H_{g} = σ_{i} \otimes (\begin{matrix} 0 & + I \\ - I & 0 \end{matrix}) = γ^{i}

(23)

The gamma algebra of Q-spin is virtually the same as for Dirac spin.

Quaternion Spin

In this section we present more specific equations that describe the structure and some properties of Q-spin. Generally the equations are given that lead to the illustrations in (Figure 4).

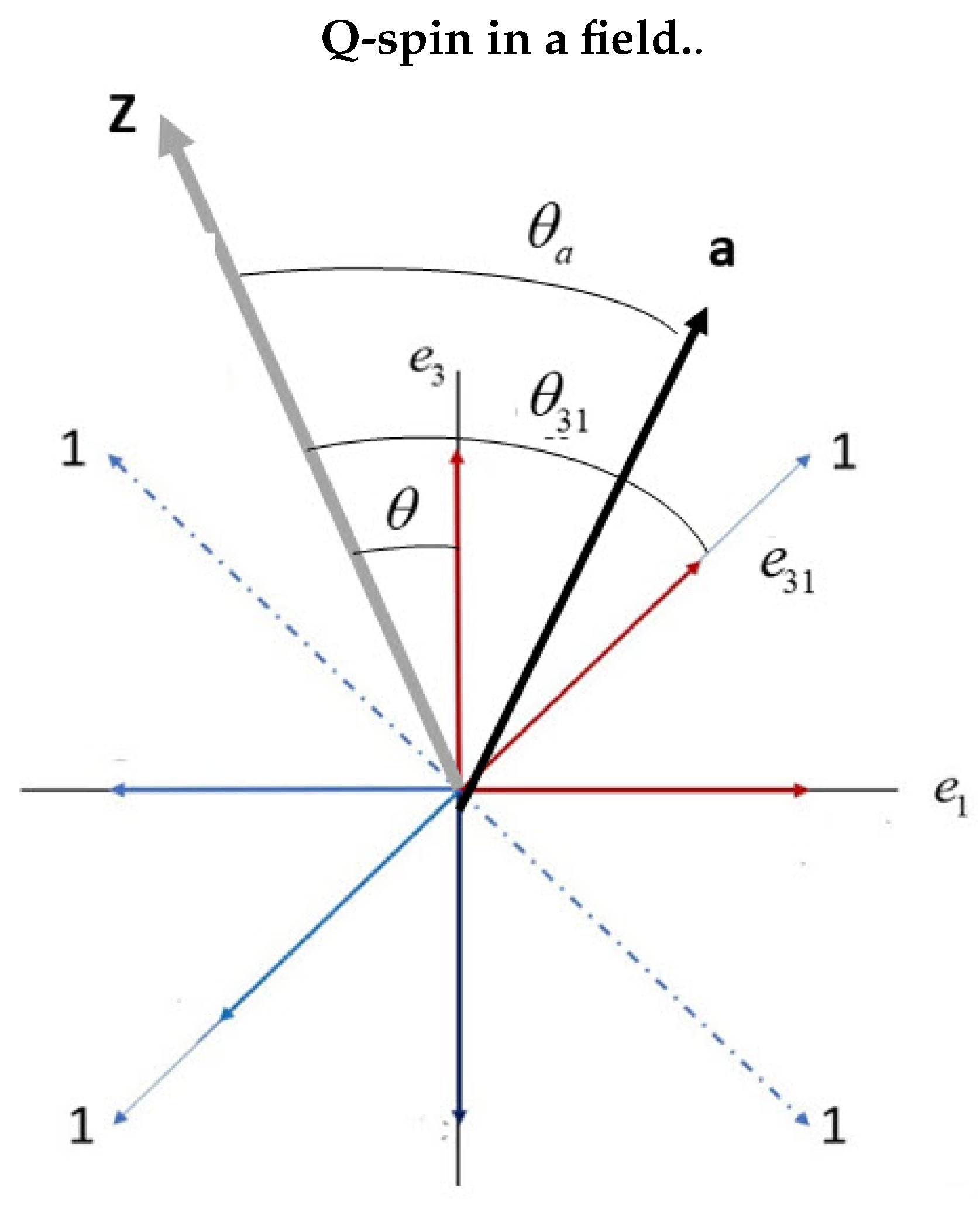
(Figure 5) shows the BFF with the Y axis perpendicular to the screen. The four bisectors are shown, and the first quadrant is labeled

e_{3} e_{1}

. Also shown is the long LFF Z axis oriented relative to the BFF by angle

θ

. The field axis,

a

, is oriented by angle

θ_{a}

from Z, and finally, the boson spin,

e_{31}

is at angle

θ_{13}

from the Z axis.

The spinning disc is orthogonal to the direction of motion, and therefore the polarizing filter and the disc are co-planar.

The complementary attributes of spin, polarization and coherence, simultaneously exist, but only one is manifest at any instant. Just as the geometric product, Eq.(1), is the sum of two complementary contributions, so we extend the usual definition of spin,

σ

, to define Q-spin,

Σ_{k}

, as possessing both these properties,

Σ_{k} = σ_{k} + {\underset{̲}{\underset{̲}{h}}}_{g}^{k} = σ_{k} + \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot i σ_{k} : (k = 1 or 3)

(24)

Motivated by the geometric product, Eq.(1), the geometric helicity operator,

{\underset{̲}{\underset{̲}{h}}}_{g} = \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot i σ, i s a n a n t i - s y m m e t r i c, a n t i - H e r m i t i a n, s e c o n d r a n k t e n s o r o f o d d p a r i t y,

[10].

T h e s t a t e o p e r a t o r, ρ, e x p r e s s e s t h e e x p e c t a t i o n v a l u e s f o r H e r m i t i a n o b s e r v a b l e s, A, o f a s y s t e m, a n d i s d e f i n e d b y t h e q u a n t u m t r a c e o v e r t h e o p e r a t o r s,

[19],

\begin{matrix} 〈A〉 = Tr (A ρ) \end{matrix}

(25)

Despite the helicity being an element of reality, it is not anobservable in Minkowskispace, where we observe. Therefore,we express the pure state operator of Q-spin in terms of the normalized sum of the two orthogonal axes giving,

\begin{matrix} ρ = \frac{1}{2} (I + \frac{1}{\sqrt{2}} (σ_{3}) + σ_{1}) = \frac{1}{2} (I + σ \cdot r) \end{matrix}

(26)

\begin{matrix} 〈Σ_{1}〉 = 〈σ_{1}〉 + \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot 〈i σ_{1}〉 = \frac{1}{\sqrt{2}} (e_{1} + i e_{3} Y) \\ 〈Σ_{3}〉 = 〈σ_{3}〉 + \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot 〈i σ_{3}〉 = \frac{1}{\sqrt{2}} (e_{3} - i e_{1} Y) \end{matrix}

(27)

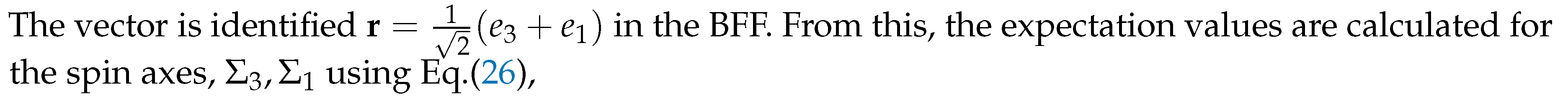
with

〈σ_{i}〉 = + \frac{1}{\sqrt{2}} e_{i}

, and the vector products,

\underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot 〈i σ_{1}〉 = + i \frac{1}{\sqrt{2}} e_{3} Y; \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot 〈i σ_{3}〉 = - i \frac{1}{\sqrt{2}} e_{1} Y

(28)

Permuting each axis in Eq.(27), shows the two fermionic axes are mirror states,

P_{13} 〈Σ_{1}〉 = {〈Σ_{3}〉}^{*}

. The first term in Eq.(27) is the usual spin polarization that is observed. The second shows the planes orthogonal to the axes:

e_{1}

is orthogonal to

e_{3} Y

, and

e_{3}

is orthogonal to

e_{1} Y

. These terms form the wedge, or vector product from GA, [6] leading to the formulation of helicity.

In free-flight the angular momentum of the two axes, Eqs.(27), constructively interfere to produce the resonance spin being a boson of magnitude 1,

\begin{matrix} Σ_{31} = Σ_{3} + Σ_{1} \end{matrix}

(29)

Substituting Eqs.(25) gives the free-flight boson in the BFF,

exp (\pm i \frac{π}{4} Y) = \frac{1}{\sqrt{2}} (1 \pm i Y)

,

〈Σ_{31}〉 = e_{1} exp (- i \frac{π}{4} Y) + e_{3} (+ i \frac{π}{4} Y)

(30)

This shows each axis multiplied by a unit quaternion that rotates around the Y axis. The

e_{1}

axis is rotated by

- \frac{π}{4}

, and

e_{3}

axis is rotated by

+ \frac{π}{4}

. Hence the two axes coincide and bisect the first quadrant and form the resonant boson spin labeled by

e_{31}

in (Figure 5). Bisectors of all the quadrants are found, corresponding to the boson resonance spins which can occupy any quadrant at any instant. Each quadrant gives the same results, so we use the first.

In (Figure 5), the axis of linear momentum, Y, is orthogonal to the

e_{1} e_{3}

plane, showing once again the geometric equivalence with a head-on view of a photon with the orthogonal magnetic and electric components oscillating out-of-phase.

Equation (30) couples the two fermionic axes which is depicted in the middle figure forming the spin 1. When the boson is influenced by a polarizing field, it decouples into a fermion.

Measured spin

Rotate Eq.(30) to the LFF using Eqs.(15) with

ϕ = 0

and contract with a polarizing field, oriented by angle

θ_{a}

,

a = cos θ_{a} Z + sin θ_{a} X

(31)

gives a unit quaternion,

\begin{matrix} a \cdot 〈Σ_{3}〉 & = cos (θ_{a} - θ) - i sin (θ_{a} - θ) Y \\ = exp (- i (θ_{a} - θ) Y) \end{matrix}

(32)

In a field, each orthogonal axis is described by a unit quaternion.

When a boson spin encounters a field

a

, the least action principle dictates the closer axis is influenced more than the further axis. This destroys the mirror property between the axes as one aligns with the field. The helicity stops as the second fermionic axis, orthogonal to the aligning axis, spins about the first, see the left and right panels of (Figure 4). In the presence of a field, the expectation value of the boson spin is

a \cdot 〈Σ_{31}〉 = a \cdot 〈Σ_{1}〉 + a \cdot 〈Σ_{3}〉

(33)

Competition between axes

Equation (30) shows Q-spin in its BFF. Transforming to the LFF and using Eq.(31) leads to,

a \cdot 〈Σ_{31}〉 = \frac{1}{\sqrt{2}} (cos (θ_{a} - θ) exp (+ i \frac{π}{4} Y) + sin (θ_{a} - θ) exp (- i \frac{π}{4} Y))

(34)

where the projections determine the contributions from each axis in the LFF,

\begin{matrix} a \cdot e_{3} = cos (θ_{a} - θ) \\ a \cdot e_{1} = sin (θ_{a} - θ) \end{matrix}

(35)

This expression shows the competition between the two axes. Equation (35), gives the projections of

e_{3}

and

e_{1}

onto the field direction,

Consider some angles which can be seen from (Figure 5), and using Eq.(35) shows that if

θ_{a} - θ = 0

or

\frac{π}{2}

, then the field is aligned with the

e_{3}

or

e_{1}

axis respectively. However, polarization along these axes is reduced from unity to

\frac{1}{\sqrt{2}}

, see Eq.(34). This is because the polarization of the orthogonal axis to the aligned axis is averaged out, and thereby reduces it. To get the full polarization, the angle must be aligned with the resonance boson spin. This occurs by choosing

θ_{a} - θ = \frac{π}{4}

. From (Figure 5), this value shows the field co-linear with the bisector, with equal contributions from both the

e_{3}

and the

e_{1}

axes, so the polarization has magnitude of 1. Choosing

θ_{a} - θ = - \frac{π}{4}

shows the field vector co-linear with the

- e_{31}

axis, orthogonal to

e_{31}

with zero value.

The boson projections

If the field is co-linear with the boson spin, then it precesses without uncoupling. This is illustrated in the lower middle part of (Figure 4), but as the field is oriented further from the bisector, the precession changes to nutation, wobbles and then decomposes as the field strength increases and moves further from the resonance spin and closer to one of the axes. From (Figure 5) the bisector lies 45^o from either

e_{3}

or

e_{1}

axes. We therefore assume, again motivated by the least action principle, the boson decouples directly, without nutation, when the field axis lies greater than

22 . 5^{o}

from the bisector. Within the 45^o wedge on either side of the bisector, we assume that the boson spin remains intact until the field strength overpowers the spin-spin coupling, and it decouples.

Depending of these orientation effects, Q-spin either persists as a boson, or rapidly decouples to a fermion.

Working in the first quadrant defined by

e_{1} e_{3}

, and, using Eq.(15) with

ϕ = 0

, then the relation between bisector in the the BFF and the LFF is,

\begin{matrix} (e_{3} + e_{1}) = (cos θ - sin θ) Z + (cos θ + sin θ) X \\ (e_{3} - e_{1}) = (cos θ + sin θ) Z + (sin θ - cos θ) X \end{matrix}

(36)

Alternately, Eq(35) projects

e_{1}

and

e_{3}

onto the field direction. First express Q-spin in its BFF, see Eq.(27),

〈Σ_{31}〉 = 〈Σ_{3}〉 + 〈Σ_{1}〉 = \frac{1}{\sqrt{2}} ((e_{3} + e_{1}) + i (e_{3} - e_{1}) Y)

(37)

Substitution of Eqs.(36) leads to,

\begin{matrix} a \cdot 〈Σ_{31}〉 & = \frac{1}{\sqrt{2}} ((cos θ - sin θ) e^{- i θ_{a} Y} + (cos θ + sin θ) e^{+ i (\frac{π}{2} - θ_{a}) Y}) \\ = \frac{1}{\sqrt{2}} ((cos θ_{a} + sin θ_{a}) e^{i θ Y} - (cos θ_{a} - sin θ_{a}) e^{- i (\frac{π}{2} - θ) Y}) \end{matrix}

(38)

In each equation, each axis is multiplied by a unit quaternion, and the two are orthogonal. From Eq.(36), and contracting with Z and X, shows the first term is the projection of the bisectors along the LFF Z axis, and the second term is the projection along X. These projections depend only on the spin’s orientation via

θ

,

\begin{matrix} (e_{3} + e_{1}) \cdot Z = (cos θ - sin θ) \\ (e_{3} + e_{1}) \cdot X = (cos θ + sin θ) \end{matrix}

(39)

A similar interpretation follows from the second line of Eq.(38). These can be compared to Eq.(34) which projects the axes

e_{3}

and

e_{1}

rather than their bisector, (Figure 5). Either equation can be used to determine the spin polarization.

Q-spin as quaternions

Equations (34) or (38) lead to a quaternion in terms of the angle differences

(θ_{31} - θ_{a})

which is independent of

θ

,

a \cdot 〈Σ_{31}〉 = exp (i (θ_{31} - θ_{a}) Y)

(40)

In the first quadrant the bisector is normalized to

e_{31} = \frac{1}{\sqrt{2}} (e_{3} + e_{1})

(41)

with the angle given by,

\begin{matrix} e_{31} \cdot Z = cos θ_{31} \\ e_{31} \cdot X = sin θ_{31} \end{matrix}

(42)

Clearly Eq.(40) shows that Q-spin aligns with the field when the angles are equal,

θ_{a} = θ_{13}

. When aligned, as discussed above, and when the field is off-set by a small amount, then the boson does not decouple but precesses as a spin 1 with magnetic moment of

2 μ

. This is shown in the middle lower panel of (Figure 4).

To determine which fermion axis will align, use Eq.(34) or (38)and determine which has the larger magnitude. The larger axis aligns, and its sign then determines if the aligned spin is up or down. Note that the two axes,

e_{3}

and

e_{1}

, have opposite spin components.

Consider further, Eq.(34), which can be written as,

\begin{matrix} a \cdot 〈Σ_{31}〉 & = exp (i (\frac{π}{4} - (θ_{a} - θ)) Y) \\ = e^{i \frac{π}{4} Y} e^{+ i θ Y} e^{- i θ_{a} Y} \end{matrix}

(43)

This shows that the Q-spin is determined by the product of three quaternions. The first is a phase, see Eq.(28), that rotates to the bisector of the (31) quadrant; the second is a geometric factor that orients the disc and is determined at the source; the third is a field quaternion that pulls the axis.

The EPR paradox

These features of Q-spin are crucial, [10], to understanding the extra correlation found in coincidence EPR experiments, [20,21,22] and which is more fully discussed in paper three, [10]. That is, the spin orientation relative to the field direction, and the strength of spin coupling relative to the field strength, provide two mechanistic pathways for the boson decoupling. The violation of Bell’s Inequalities, [23], is due to the transition from a free-flight boson to a measured fermion.

Despite the fact measurement reveals two real states, spin is a complex element of reality, and defined by Eq.(24). We have shown down to Eq.(43) that spin is governed by unit quaternions.

Consider the correlation between an EPR pair which, using Q-spin, is written as a product state between Alice and Bob,

\begin{matrix} E (a, b) = a \cdot \frac{1}{2} (〈Σ_{31}^{A}〉 {〈Σ_{31}^{B}〉}^{*} + {〈Σ_{31}^{A}〉}^{*} 〈Σ_{31}^{B}〉) \cdot b \\ = \frac{1}{2} exp (i (\frac{π}{2} - (θ_{a} - θ)) Y) exp (i (\frac{π}{2} + (θ_{b} - θ)) Y) + c . c . \\ = - cos (θ_{a} - θ_{b}) \end{matrix}

(44)

We have taken the angle

θ

to be

θ \pm \frac{π}{2}

for Alice and Bob so the two spins at the source have common orientation of

θ

that differs by

π

to maintain the two anti-parallel. Since we only measure in real space, then similar to light, the complex part can by removed by forming linear or circularly polarized components.

Discussion

In free-flight, the spinning disc is reminiscent of the worldsheet Susskind introduced, [25]. A 2D system is also an anyon, [26], which can be either a fermion or a boson. An important point about the boson in free-flight is the spinning axis averages out the boson polarization, Figure(Figure 1), so only the odd parity helicity remains. Upon measurement, a transition from a boson to a fermion occurs giving the usual two-state Dirac spin.

The motivation behind Twistor theory is that Nature is fundamentally complex, and we measure the real part. Q-spin supports this concept as seen from the discussion above on EPR. The coherence carried by the helicity accounts for the violation of Bell’s Inequalities, [11]. Dropping the complexity removes the quantum coherence, leaving only the classical correlation that obeys Bell’s Inqualities. Without helicity, we have Dirac’s two state spin, and no coherent properties.

Introducing the bivector into spin algebra significantly changes our view of a spin from a structureless point particle of intrinsic angular momentum in Minkowski space to a four dimensional structured spin with extrinsic angular momentum in spin spacetime. There are four axes that compose Q-spin. One is the axis of linear momentum spun by the quaternion. Two more are the magnetic axes which couple to give the fourth, being the boson spin, see Figure(Figure 1).

The question arises as to whether Q-spin exists and is more fundamental than point particle spin. That Q-spin and a photon have structure and properties in common, is compelling, Figure(Figure 1). Other quantum observables come in complementary pairs, like position and momentum

e t c .

, in spaces that are the inverse of each other. It is therefore reasonable that spin also has two complementary properties, real polarization in it’s spin spacetime, and imaginary coherence on the

S^{3}

hypersphere.

Measurement has a central premise that the act of observation perturbs the system. Q-spin makes a distinction between measurement of a Fermi electron,

e_{F}^{-}

(polarized, particle, fermion, even to parity) and free-flight of a Boson electron,

e_{B}^{-}

(coherence, wave, boson, odd to parity). They epitomize the particle-wave duality. An advantages of Q-spin lies in its expression in terms of quaternions. One can envisage a spin to be a stable qubit, where the two axes carry opposite spin. The evolution is calculated by products of quaternions, Eq.(43), and the coherence maintains correlation between gates.

The mathematical foundations of Q-spin are the same as usual Dirac spin. Changing symmetry from SU(2) to

Q_{8}

is our only modification to the Dirac field. The solution to the 2D Dirac equation and the spin spacetime gamma algebra carry over from the usual treatment without difficulty. One advantage of Q-spin is it gives alternate interpretations of some troubling properties: non-locality is repudiated, [11]; negative energies of the antimatter particle are resolved; and a number of other changes challenge our existing view off the microscopic, see [12].

Simply stated, Nature is complex and a free-flight electron is a boson of odd parity, and a measured electron is a fermion of even parity.

Acknowledgments

The author is grateful to Hillary Sanctuary, PhD, EPFL Switzerland, for useful and helpful discussions.

References

Gerlach, Walther, and Otto Stern. “Das magnetische moment des silberatoms." Zeitschrift für Physik 9.1 (1922): 353-355.
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624.
Peskin, M., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
Dirac, P. A. M. (1930). “A Theory of Electrons and Protons". Proc. R. Soc. Lond. A. 126 (801): 360–365.
Okun, Lev B. "Mirror particles and mirror matter: 50 years of speculation and searching." Physics-Uspekhi 50.4 (2007): 380.
Doran, C. , Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
Muralidhar, K. "The spin bivector and zeropoint energy in geometric algebra." Adv. Studies Theor. Phys 6 (2012): 675-686.
Penrose, Roger. "Twistor algebra." Journal of Mathematical physics 8.2 (1967): 345-366.
Penrose, Roger. "Solutions of the Zero-Rest-Mass Equations." Journal of mathematical Physics 10.1 (1969): 38-39.
Sanctuary, B. Spin with helicity. Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
Sanctuary, B. Non-local EPR Correlations Using Quaternion Spin. Preprints 2023, 2023010570. [Google Scholar] [CrossRef]
Sanctuary, B. Quaternion-Spin and Some Consequences. Preprints 2023, 2023121277. [Google Scholar] [CrossRef]
Zhou, Ziheng, and Zhenhua Yu. "Interaction effects on the PT-symmetry-breaking transition in atomic gases." Physical Review A 99.4 (2019): 043412.
Troha, T., D. Lukman, and N. S. Mankoč Borštnik. "Massless and massive representations in the spinor technique." International Journal of Modern Physics A 29.23 (2014): 1450124.
Griffiths, David (2009). Introduction to Elementary Particles. pp. 59–60. ISBN 978-3-527-40601-2.
Peters, James F., and Arturo Tozzi. "Quantum entanglement on a hypersphere." International Journal of Theoretical Physics 55 (2016): 3689-3696.
Christian, Joy. "Bell’s theorem versus local realism in a quaternionic model of physical space." IEEE Access 7 (2019): 133388-133409.
Christian, Joy. "Symmetric Derivation of the Singlet Correlations within a Quaternionic 3-sphere. arXiv:2204.10288 (2022).
Von Neumann, John. Mathematical foundations of quantum mechanics. Princeton university press, 1955.
Clauser, J. F. , Horne, M. A., Shimony, A., Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880.
Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951.
Weihs, G. , Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039.
Bell, John S. “On the Einstein Podolsky Rosen paradox.” Physics Physique Fizika 1.3 (1964): 195.
Bell, J. S. (2004). p. 139 or 147, Speakable and unspeakable in quantum mechanics: Collected papers on quantum philosophy. Cambridge university press.
Susskind, Leonard (1970). "Dual-symmetric theory of hadrons, I.". Nuovo Cimento A. 69 (1): 457–496.
Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Physical review letters, 49(14), 957.

Figure 1. Two properties of spin: two orthogonal spin

\frac{1}{2}

polarization vectors,

σ_{1}

and

σ_{3}

, perpendicular to the direction of linear momentum, Y. The helicity, generated by

i σ_{2}

, is in the direction of propagation,

e_{2} = Y

, and spins R or L. The two spin

\frac{1}{2}

vectors,

σ_{3}

and

σ_{1}

, couple to give a composite boson,

e_{13}

, of magnitude 1. These properties show spin is geometrically equivalent to that of a photon.

Figure 1. Two properties of spin: two orthogonal spin

\frac{1}{2}

polarization vectors,

σ_{1}

and

σ_{3}

, perpendicular to the direction of linear momentum, Y. The helicity, generated by

i σ_{2}

, is in the direction of propagation,

e_{2} = Y

, and spins R or L. The two spin

\frac{1}{2}

vectors,

σ_{3}

and

σ_{1}

, couple to give a composite boson,

e_{13}

, of magnitude 1. These properties show spin is geometrically equivalent to that of a photon.

Figure 2. A spin is oriented in spin spacetime by the BFF basis vectors

(e_{1}, e_{2}, e_{3})

which spins about the axis

e_{2}

so that in Minkowski space, with components

(X, Y, Z)

, only a smeared out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from the coupling of the (3,1) axes.

Figure 2. A spin is oriented in spin spacetime by the BFF basis vectors

(e_{1}, e_{2}, e_{3})

which spins about the axis

e_{2}

so that in Minkowski space, with components

(X, Y, Z)

, only a smeared out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from the coupling of the (3,1) axes.

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the right and

ψ^{-}

on the left. Note that adding these states is independent of

i σ_{2}

and subtracting them is independent of

σ_{1}

and

σ_{3}

.

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the right and

ψ^{-}

on the left. Note that adding these states is independent of

i σ_{2}

and subtracting them is independent of

σ_{1}

and

σ_{3}

.

Figure 4. The longer arrow denotes the direction of the polarizing field. The two polarization axes form Q-spin of even parity from the coupling of two mirror states. (middle top), The two mirror states in free flight,

e_{1}

and

e_{3}

couple to give the boson spin 1. (left and right) The axis closer to the field axis aligns. (middle lower) When the boson spin is close to the field, it precesses as a spin 1 before decoupling into its fermion components.

Figure 4. The longer arrow denotes the direction of the polarizing field. The two polarization axes form Q-spin of even parity from the coupling of two mirror states. (middle top), The two mirror states in free flight,

e_{1}

and

e_{3}

couple to give the boson spin 1. (left and right) The axis closer to the field axis aligns. (middle lower) When the boson spin is close to the field, it precesses as a spin 1 before decoupling into its fermion components.

Figure 5. The BFF showing the

e_{3} e_{1}

plane and the bisectors of the quadrants with boson spins of 1. The

e_{13}

boson is labeled. The plane is oriented in the LFF by the Z axis, and the angle

θ_{31}

is shown. Also

θ_{a}

orients the field vector

a

in the LFF. The angle

θ

is the orientation of a spin vector on the Bloch sphere.

Figure 5. The BFF showing the

e_{3} e_{1}

plane and the bisectors of the quadrants with boson spins of 1. The

e_{13}

boson is labeled. The plane is oriented in the LFF by the Z axis, and the angle

θ_{31}

is shown. Also

θ_{a}

orients the field vector

a

in the LFF. The angle

θ

is the orientation of a spin vector on the Bloch sphere.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Quaternion Spin

Abstract

Keywords:

Subject:

Introduction

Spin Spacetime Algebra

Mirror states and parity

The Weyl spinor

The 2D spin equation.

Quaternion Spin

Measured spin

Competition between axes

The boson projections

Q-spin as quaternions

The EPR paradox

Discussion

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe