Extrinsic Quaternion Spin

Bryan Sanctuary

doi:10.20944/preprints202302.0055.v2

Submitted:

31 March 2023

Posted:

03 April 2023

Read the latest preprint version here

Abstract

We present an analysis of the Dirac equation when the spin symmetry is changed from SU(2) to the quaternion group, $Q_8$, afforded by multiplying one of the $\gamma$-matrices by the imaginary number $i$. The reason for doing this is to introduce a bivector into the spin algebra. The resulting spin equation separates into distinct and complementary spaces, one describing polarization and the other coherence. The former describes a 2D structured spin and the latter its helicity, generated by a unit quaternion. We discuss some consequences.

Keywords:

foundations of physics

;

Dirac equation

;

spin

;

quantum theory

;

non-locality

;

helicity

Subject:

Physical Sciences - Theoretical Physics

Introduction

Spin, first observed by Stern and Gerlach [1], reveals two states of up and down. Spin is measured to be angular momentum of

\frac{\sqrt{3}}{2} ℏ

magnitude, a vector quantity, belonging to the SU(2) group. Spin is a fundamental property of Nature, purely quantum with no classical analogue. The mathematical basis for spin is the Dirac equation [2]. Dirac’s analysis introduces his relativistic equation by linearizing the Klein-Gordon Equation while respecting conservation of mass and energy. He was led to his gamma matrices with four states rather than the two that are measured [3]. He surmised that his equation described two spins rather than one. The second spin with negative energy and opposite sign is interpreted as the antimatter twin to the other spin [2]. From this hole theory, antimatter production, and the sea of electron model followed [4].

In this paper a small change is made whereby one of the gamma matrices is multiplied by the imaginary number i and the effect is to change the symmetry from SU(2) to the quaternion group

Q_{8}

. The gamma matrices still anti-commute, but the modified Dirac equation reveals a single spin has four states, rather than two: spin has structure under

Q_{8}

,5,6]. The two point particles that Dirac found are replaced by quaternion spin, or Q-spin, that carries two complementary properties: polarization and coherence. The former describe polarization, whereas the coherence is generated by a unit quaternion. This quaternion spins the spin axis in free-flight making the intrinsic angular momentum of Dirac spin extrinsic. In addition, two mirror states, [7] emerge from the Dirac field which describe two orthogonal polarization axes that are perpendicular to the axis of linear momentum. 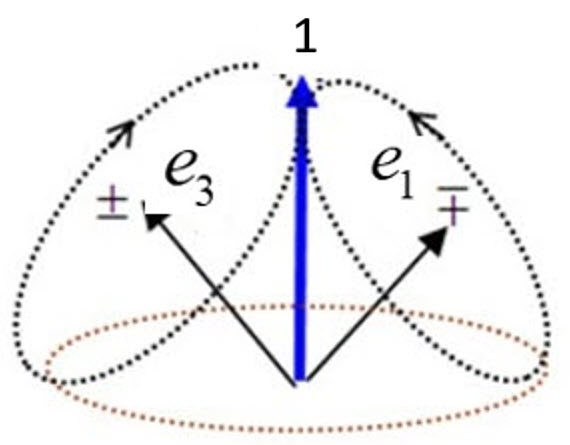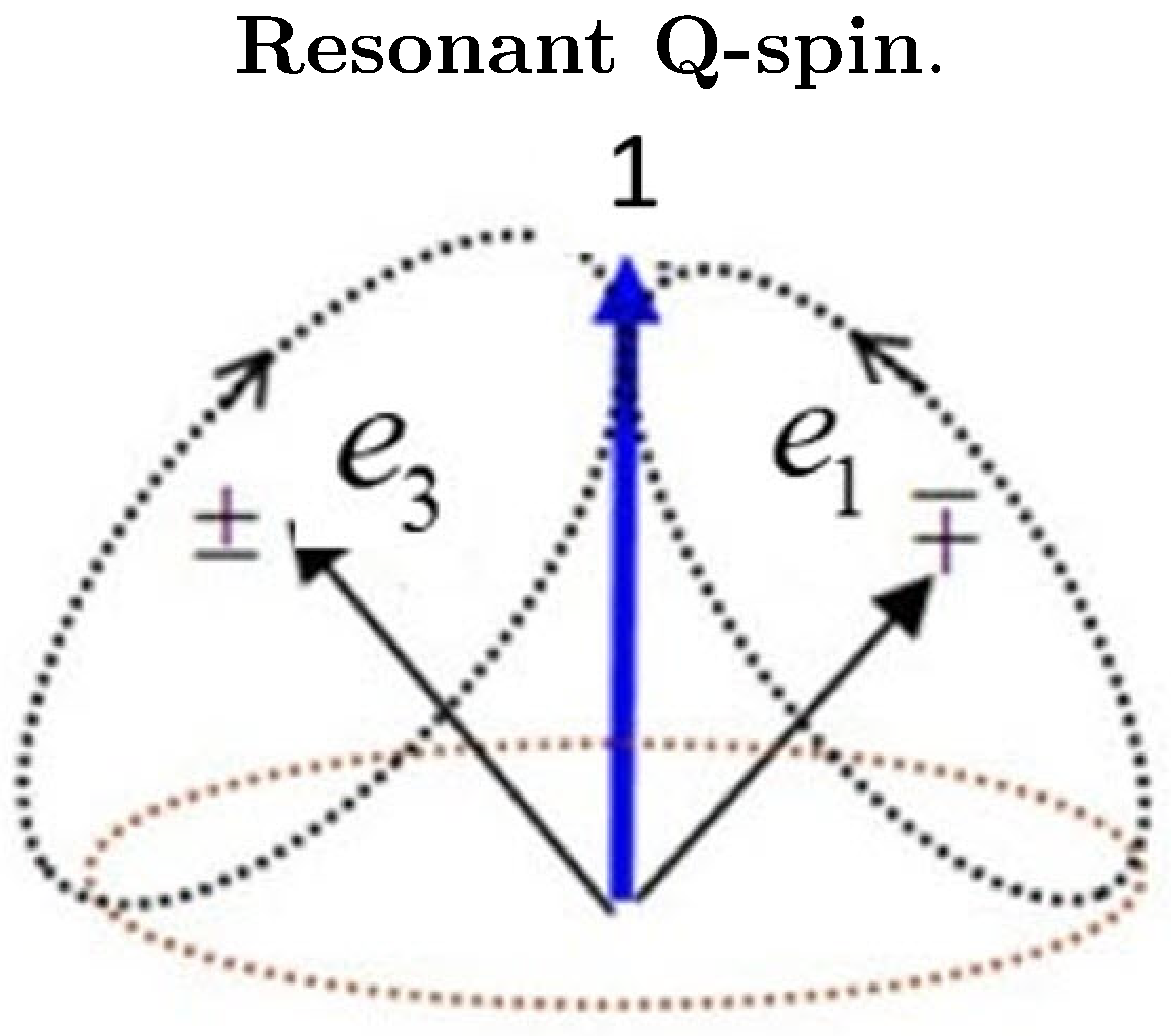Figure 1 shows that a Q-spin is geometrically equivalent to that of a photon.

To motivate the discussion here, consider the well know equation for a dyadic of Pauli spin components,

σ_{i} σ_{j} = δ_{i j} + ε_{i j k} i σ_{k}

(1)

Arising from Geometric Algebra, [8,9] the first term describes a symmetric component that gives rise to polarization and measured Dirac spin. The second term is anti-symmetric and depends upon a bivector,

i σ_{k}

and the Levi Civita third rank anti-symmetric tensor. This term describes coherence of a spin. Since i cannot be simultaneously equal and not-equal to j, the equation is complementary. Dirac spin does not treat the second component which requires a bivector,

i σ_{2} = σ_{3} σ_{1}

. The only way to get the bivector is to change the spin symmetry to the quaternion group. In this change, the helicity of a spin is formulated. It is the purpose of this paper to include this anti-symmetric term.

Spin coherence, expressed by a quaternion [10], exists on the

S^{3}

hypersphere [11,12,13] beyond Minkowski spacetime. It describes spin hyper-helicity as an additional property of spin. The name hyper-helicity is used formally to distinguish it from the usual helicity found in particle physics [14]. The two are formulated differently, albeit both describe spinning the axis of linear momentum. Here hyper-helicity is in

S^{3}

hyper-space while particle helicity is constructed in Minkowski spacetime. We generally call hyper-helicity simply the helicity.

The existence of a bivector allows us to formulate the two complementary attributes of spin that are consistent with Eq.(1). The focus of this paper is on characterizing Q-spin due to its structure which replaces the point particle spin that Dirac found.

This paper is the first of three in which the mathematical foundations of Q-spin are presented. A second paper, “Spin with hyper-helicity" [15] follows in which the ideas of this paper are used to study the geometry and conservation of correlation. Applied to an EPR pair, [16], it is responsible for the correlation that gives the observed violaton of Bell’s inequalities (BI) without non-local connectivity. The third paper, [17] presents a computer simulation which shows that both polarization and coherent states are responsible for the violation of BI.

Formally this four state spin is called Q-spin to distinguish it from the usual Dirac spin. A modified form of the Dirac equation is presented that admits both polarization and helicity. It describes spin as it exists in the absence of interactions including measurement, and therefore in free-flight.

Spin spacetime algebra

Dirac spin is measured in a direction

\hat{n}

and has states with outcomes of

\pm 1

. These are expressed as usual by

|\pm, \hat{n}〉

. Q-spin, however, is more than a polarization vector and must include helicity with additional two states of

h_{g} = \pm 1

. To repeat, this leads to the 4x4 space of the Dirac field that describes one particle with two axes rather than the matter-antimatter pair of two separate particles.

A point particle spin

\frac{1}{2}

is described by the three Pauli spin components which along with the identity, gives the set (

I, σ_{X}, σ_{Y}, σ_{Z}

), which belongs to the SU(2) group. Simply by multiplying one gamma matrices by the imaginary number i, here chosen to be

γ_{2}

, changes the spin components to (

I, σ_{1}, i σ_{2}, σ_{3}

), giving two spatial axes of polarization, and the needed bivector,

i σ_{2} = σ_{3} σ_{1}

. This set forms a normal subgroup of the quaternion group,

Q_{8}

. This requires defining a different Cartesian basis set

(e_{1}, e_{2}, e_{3})

, called the Body Fixed Frame, BFF, since every structured spin can have a different orientation relative to the Laboratory Fixed Frame of

(X, Y, Z)

, see see Figure 2.

The two spatial components,

(σ_{3}, σ_{1})

denoted by

(3, 1)

, are, up to a phase, simply a rotation away from Minkowski spacetime. This structure is shown in Figure 2 in the bottom right insert which contrasts Q-spin with the usual Dirac spin vector. Note that the two axes of Q-spin couple to form a resonance spin of magnitude 1 which is a pure coherent state. The bivector,

i σ_{2}

, denoted by (2), orients the two orthogonal spin axes, formed from

(3, 1)

, by its normal component to the plane. We assume here that the particle propagates in the

Y = e_{2}

direction. Whereas

(β, X, Y, Z)

with

β = c t

is usual Minkowski spacetime, the set

(β^{'}, e_{3}, e_{1}, e_{2})

is spin spacetime. The spin polarized structure can be expressed in Minkowski spacetime. The bivector cannot.

The bivector (2), is introduced by choosing to multiply

γ_{s}^{2}

by the imaginary number i,

{\tilde{γ}}_{s}^{2} \equiv i γ_{s}^{2} = (\begin{matrix} 0 & i σ_{s 2} \\ - i σ_{s 2} & 0 \end{matrix})

(2)

rendering

{\tilde{γ}}_{s}^{2}

Hermitian. The Pauli components become bivectors. The set of gamma matrices in spin space, indicated by subscript s,

(γ_{s}^{0}, γ_{s}^{3}, γ_{s}^{1}, {\tilde{γ}}_{s}^{2})

, anticommute. They have a different signature from Minkowski spacetime,

{\tilde{η}}_{s}^{μ ν} = (\begin{matrix} + 1 & 0 & 0 & 0 \\ 0 & - 1 & 0 & 0 \\ 0 & 0 & - 1 & 0 \\ 0 & 0 & 0 & + 1 \end{matrix})

(3)

The order of the components is

(0, 3, 1, 2)

and the term

{\tilde{γ}}_{s}^{2}

is not a spatial component but a frequency. This dimension is the origin of quantum coherence that leads to the formulation of helicity.

The commutation relations are changed from the usual three dimensional generator of rotations in Minkowski spacetime,

S_{(3)}^{i j} = \frac{i}{4} [γ^{i}, γ^{j}] = \frac{1}{2} ε_{i j k} σ_{k} I_{4}

(4)

to ones that generate rotations in only two dimensions in spin spacetime

\begin{matrix} S_{(2)}^{i j} & = \frac{i}{4} [γ_{s}^{i}, γ_{s}^{j}] = \frac{i}{2} ε_{i 2 j} {\tilde{σ}}_{s 2} I_{4} \end{matrix}

(5)

\begin{matrix} S_{(2)}^{i 2} & = \frac{i}{4} [γ_{s}^{i}, {\tilde{γ}}_{s}^{2}] = \frac{i}{2} ε_{i 2 j} σ_{s j} I_{4} \end{matrix}

(6)

The former equation describes rotations in the 31 plane about the direction 2; whereas the imaginary term in the latter equation damps all rotation attempts out of the 31 plane.

Mirror states and parity

The new equation in spin-space follows from the gamma algebra as usual which gives a non-Hermitian equation by virtue of

{\tilde{γ}}_{s}^{2}

,

(i γ_{s}^{0} \partial_{0} - i γ_{s}^{1} \partial_{1} \pm i {\tilde{γ}}_{s}^{2} \partial_{2} - i γ_{s}^{3} \partial_{3} - m) ψ^{\pm} = 0

(7)

and we suppress the subscript s on the derivatives. By treating a spin in free-flight in an isotropic environment, the two axes

(1, 3)

are indistinguishable. Therefore, permutation with the parity operator,

P_{13}

does not change the

(1, 3)

dependence in Eq.(7), but the bivector,

i σ_{2} = σ_{3} σ_{1}

is anti-symmetric to 13 permutation. Therefore the above equations admits two solutions in left and right handed coordinate frames, which are mirror states, see Figure 3,

P_{13} ψ^{\pm} = ψ^{\mp}

,7,18]. The anti-commutation of the

γ_{s}^{μ}

matrices ensures that energy is conserved and the Klein-Gordon equation is recovered.

The separation of the Dirac field into reflective states identifies each axis as carrying a spin such that they precesses in opposite directions. These two polarization axes, each with a magnetic moment

μ

, constructively interfere producing a resonance which is a purely coherent spin, see Figure 4.

Adding and subtracting the two equations in Eq.(7) leads to separation into a Hermitian part and an anti-Hermitian part,

\begin{matrix} (i γ_{s}^{' 0} \partial_{0} - i γ_{s}^{1} \partial_{1} - i γ_{s}^{3} \partial_{3} - m) Ψ^{+} & = 0 \end{matrix}

(8)

\begin{matrix} {\tilde{γ}}_{s}^{2} \partial_{2} Ψ^{-} & = 0 \end{matrix}

(9)

where the two mirror states combine into those with odd and even parity,

P_{13} Ψ^{\pm} = \pm Ψ^{\pm}

with the definition,

Ψ^{\pm} = \frac{1}{\sqrt{2}} (ψ^{+} \pm ψ^{-})

(10)

We identify the even parity state with 2D structured Q-spin. The odd parity state describes its helicity.

Therefore spin spacetime separates into two distinct spaces: polarization spacetime,

(0, 3, 1)

, Eq.(8); and coherent space (not spacetime)

(2)

, Eq.(). The Hermitian part, Eq.(8), is the same as the usual Dirac equation, but in two dimensions rather than three. This is depicted in Figure 2.

The bivector component,

(2)

, describes a massless Weyl spinor in coherent space, Eq.(9). Below it is shown that the spinning of the axis is generated by a unit quaternion, which has one real dimension,

(2)

and three imaginary axes. This describes the helicity in the 4th dimension hypersphere

S^{3}

. Within coherent space,

(2)

, time does not exist beyond the constant frequency of its spinning. Time and rest mass remain in polarization space.

Polarization spacetime reflects diagonal elements of the state operator,

|\pm〉 〈\pm|

which support magnetic moments, charge, etc.; coherent space reflects off-diagonal elements of the state operator,

|\pm〉 〈\mp|

which support chirality or helicity. Similar to the two complementary inverse spaces of position and momentum, here the two spin spaces carry the two complementary properties of spin, polarization and coherence.

Redefine the spinor mirror states as

ψ^{+} \equiv ψ_{R}

and

ψ^{-} \equiv ψ_{L}

.

The Weyl spinor

From Eq.(9) and using reference [3,19] a Weyl spinor transforms under boosts and rotations as

\begin{matrix} ψ_{R} \to (1 - i χ \frac{σ_{2}}{2} + i β \frac{σ_{2}}{2}) ψ_{R} (0) \end{matrix}

(11)

\begin{matrix} ψ_{L} \to (1 - i χ \frac{σ_{2}}{2} - i β \frac{σ_{2}}{2}) ψ_{L} (0) \end{matrix}

(12)

Since time exists only in polarization space, Eq.(8), a boost of polarizations carries along the spinor. There are no boosts in coherent space; the left and right components are equal;

ψ_{R} = ψ_{L}

(13)

and the state is a unit quaternion which spins the axis of linear momentum in coherence space

(2)

by angle

χ

, thereby generating the helicity.

ψ_{L} (χ) = exp (- i \frac{χ}{2} σ_{2}) ψ_{L} (0) = (cos \frac{χ}{2} - i σ_{2} sin \frac{χ}{2}) ψ_{L} (0)

(14)

The usual definition [14] identifies helicity as the projection of the spin vector onto the axis of linear momentum in Minkowski spacetime. Here helicity is defined only in quaternion space, the

S^{3}

hyper-sphere, where there is no momentum with which to contract. Choosing

Y = e_{2}

, then the component,

i σ_{2}

, drives the quaternion in Eq.(14), and spins the symmetry axis like usual helicity. Hyper-helicity is a distinct element of reality and complementary to observed polarized spin. All we observe of the hyper-helicity in our spacetime is its stereographic projection which is the spinning of the Y axis of a spin.

The 2D spin equation.

Transform from the BFF of the spin, the LFF giving,

\begin{matrix} γ_{s}^{1} = (- sin θ γ^{3} + cos θ cos ϕ γ^{1} + cos θ sin ϕ γ^{2}) \end{matrix}

(15)

\begin{matrix} γ_{s}^{3} = (cos θ γ^{3} + sin θ cos ϕ γ^{1} + sin θ sin ϕ γ^{2}) \end{matrix}

(16)

\begin{matrix} p_{3} = p \cdot e_{3} = (cos θ p_{Z} + sin θ cos ϕ p_{X} + sin θ sin ϕ p_{Y}) \end{matrix}

(17)

\begin{matrix} p_{1} = p \cdot e_{1} = (- sin θ p_{Z} + cos θ cos ϕ p_{X} + cos θ sin ϕ p_{Y}) \end{matrix}

(18)

which gives the following expression independent of

θ

,

\begin{matrix} γ_{s}^{1} p_{1} + γ_{s}^{3} p_{3} = γ^{3} p_{Z} + (cos ϕ γ^{1} + sin ϕ γ^{2}) (cos ϕ p_{X} + sin ϕ p_{Y}) \end{matrix}

(19)

Taking the linear momentum in the direction

Y = e_{2}

requires setting

ϕ = 0

,

γ_{s}^{1} p_{1} + γ_{s}^{3} p_{3} = γ^{1} p_{X} + γ^{3} p_{Z}

(20)

The polarization in spin spacetime is projected onto Minkowski spacetime, and is all that can be observed of Q-spin. The spinning from helicity is in coherent space and its effect in Minkowski spacetime is to spin the polarization. In free-flight from our spacetime, a spin is a spinning plane, or worldsheet, [20], with mass and energy only. This changes when it encounters a measuring probe.

Define a momentum vector

p = p_{Z} Z + p_{X} X = p_{3} e_{3} + p_{1} e_{1}

and the 2D polarization equation becomes

(\begin{matrix} E - m & - p \cdot σ \\ + p \cdot σ & - (E + m) \end{matrix}) (\begin{matrix} u^{+} \\ v^{+} \end{matrix}) = 0

(21)

where the even parity state is written as

Ψ^{+} = (\begin{matrix} u^{+} \\ v^{+} \end{matrix})

. This leads to the same Klein-Gordon equation in Minkowski and spin spacetime,

\begin{matrix} (\partial_{0}^{2} - \partial_{Z}^{2} - \partial_{X}^{2} - m^{2}) ψ = 0 \end{matrix}

(22)

\begin{matrix} ({\partial^{'}}_{0}^{2} - \partial_{3}^{2} - \partial_{1}^{2} - m^{2}) ψ^{'} = 0 \end{matrix}

(23)

with eigenvalues,

E = \pm \sqrt{m^{2} + p_{3}^{2} + p_{1}^{2}} .

(24)

We interpret the two energy states as the left and right spinning of the two spin axes on the same particle, see Figure 4. As mirror states, they are in phase giving the

m = + 1

component of this magnitude 1 Q-spin. Reversing these give the

m = - 1

component. The

m = 0

component cannot form since it would violated the reflective symmetry between the mirror states.

Quaternion spin

Quaternion spin with two axes and helicity covers the 4x4 Dirac field and is represented by the gamma matrices,

γ_{s}^{μ}

. Expressing one spin axis as one of its spatial components,

σ_{i}

, and taking the direct product with a helicity 2x2 matrix,

H_{g}

, leads to the spatial gamma matrices,

|\hat{n}, \pm〉 |h_{g}〉 \to σ_{i} H_{g} = γ_{s}^{i}

(25)

with

H_{g} = γ^{1} {\tilde{γ}}^{2} γ^{3} = (\begin{matrix} 0 & I \\ - I & 0 \end{matrix})

(26)

The term

γ^{5} = γ^{0} H_{g}

usually projects the R and L handed chiral states from a Dirac field. Here the odd and even parity states, Eq.(10) are projected from the mirror Q-spin states of Eq.(7),

Ψ^{\pm} = \pm \frac{1}{2} (I \pm γ_{0} H_{g}) (\begin{matrix} ψ^{+} \\ ψ^{-} \end{matrix})

(27)

The two spin axes on the same particle have equal but opposite energy, opposite magnetic moments, and constructively interfere to form the Q-spin.

This is substantially different from the matter-antimatter interpretation of Dirac. Without the bivector, spin has no structure so the second spin led Dirac to identify the 4x4 field as evidence for two distinct particles with spin: opposite from each other like the mirror states, one with positive energy and the other with negative energy. He defined the vacuum state and antimatter and hole theory resulted [4]. Whereas the infinite negative energy states are present in Dirac’s approach, here there is no problem since the two mirror axes carry the same, but opposite energy, Eq.(24).

The 2D Dirac equation gives a different view of spin from currently accepted. The 2D Hermitian part, Eq.(8), gives an even parity spin which is the sum of its two mirror states as seen in Figure 4. Now that a bivector is included in the Dirac field, we can define a quaternion spin by including the helicity given by an anti-symmetric, anti-Hermitian, odd to parity, second rank helicity operator,

{\underset{̲}{\underset{̲}{h}}}_{g} = \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot i σ

(28)

We define each mirror spin component of Q-spin,

Σ_{k}

, as possessing its two complementary attributes, Eq.(1). Each polarization axis carries both polarization and coherence, thereby defining a spin helicity carried by both twins,

Σ_{k} = σ^{k} + {\underset{̲}{\underset{̲}{h}}}_{g}^{k}

(29)

These superpose to give the Q-spin of magnitude 1,

Σ_{31}^{\pm} = \frac{1}{\sqrt{2}} (Σ_{3} \pm Σ_{1})

(30)

In spin calculations when approaching a filter, this leads directly to unit quaternions, [15] carried by each spin axis.

Measured spin

Quaternion spin, with elements of reality in both polarization and coherent spaces, projects only its stereographic image onto our spacetime, Eq.(20). Whereas both the

(1)

and

(3)

axes are projected as an intact Q-spin of magnitude 1, upon measurement only one of these two vector components is observed.

Dirac spin is obtained when the projected polarization, Eq.(20) is measured, Figure 5. Whereas in free-flight the polarization of Q-spin is averaged by the helicity, when it encounters an anisotropic field, the two axes are no longer indistinguishable under permutation by

P_{13}

. Q-spin then decouples into two spin 1/2 components, and the helicity stops. The spin polarization only appear upon measurement. Figure 5, shows the

e_{3}

axis aligned and its orthogonal components are randomized. Either spatial axis can align, and the one closer to the field is more strongly coupled and more easily aligned. If, however, the field is aligned with the Q-spin, then it does not readily decouple leading to it persisting as a spin of magnitude 1 as it moves towards the filter.

This feature of Q-spin is crucial, [15], to the understanding the extra correlation found in coincidence EPR experiments, [21,22,23], which depend upon the different orientations of the filters at Alice and Bob. When

(θ_{a} - θ_{b})

is odd multiples of

\frac{π}{4}

, both Alice and Bob simultaneously encounter the uncouple Q-spins, whereas at others, either Alice or Bob’s spin might be uncoupled. That is the orientation and the strength of the filter fields either decouples the Q-spin or leaves it intact. The former gives correlation from polarization and the latter from coherence. The complementarity shows a free-flight spin is a boson with spin 1, and when measured, it becomes a fermion of spin

\frac{1}{2}

.

Correlation between the Q-spin at Alice and Bob is the source of the quantum coherence that gives an observed violation of Bell’s inequalities, [24]. Eventually, however, only one polarization axis lines up with the probe field, Figure 5 and this is the two state measured Dirac spin. EPR coincidence experiments observe the transition from a boson to a fermion.

Discussion

Introducing the bivector into spin algebra significantly changes our view of a spin from a structureless point particle of intrinsic angular momentum in Minkowski spacetime to a four dimensional structured spin with extrinsic angular momentum in spin spacetime. Any structured particle can be expressed in its own coordinate frame and we find that the three spatial components of Minkowski spacetime become a 2D plane of spin polarization which is spun about its axis of linear momentum producing L or R handed helicity. The spinning 2D plane forms only in the isotropy of free-flight.

The bivector component leads to the massless Weyl spinor which in turn is a unit quaternion and generates the helicity. Quaternions do not exist in polarization space, but rather in the 4th dimensional hypersphere of

S^{3}

[11] which cannot be completely observed from any spacetime frame. Only the stereographic projection, [10], is visible.

The question arises as to whether the Q-spin exists and is more fundamental than measured spin. That the geometric structure of spin is equivalent to that of a photon, Figure 1; both with a spin of magnitude 1 with no zero component, is compelling. Other quantum observables come in complementary pairs, like position and momentum etc, in spaces that are the inverse of each other. It is therefore reasonable that spin also has two complementary properties, polarization in it spin spacetime, and coherence on the

S^{3}

hyper-sphere. Furthermore, spin is described by its Dirac gamma matrices, and we changed (

I, γ_{1}, γ_{2}, γ_{3}

); to (

I, γ_{1}, i γ_{2}, γ_{3}

), with the first giving Dirac SU(2) spin and the second leading to the quaternion group with two axes of precession. Finally the experimental proof for the existence of Q-spin is given by the violation of BI . This is usually attributed as proof of non-locality. Q-spin, however, accounts for the violation locally as shown in the other papers, [15] and [17].

Measurement has a central premise that the act of observation perturbs the system. Q-spin makes a distinction between measurement (polarized) and free-flight (coherence). They epitomize the particle-wave duality.

EPR believed that QM is incomplete [16] since it does not simultaneously describe two complementary elements of reality. In support of Einstein, both polarization and coherence are found to exist simultaneously on the same particle. On the other hand, supporting Bohr’s complementarity, in free-flight only the coherence is present since the spinning axis averages out the polarization. Upon measurement, the helicity stops and only the polarization is realized. Although both properties exist simultaneously, only one is manifest at any instant.

QM is, therefore, incomplete because it is a theory of measurement restricted to our space-time. QM does not include elements of reality that are anti-Hermitian on the

S^{3}

hypersphere.

These results are confirmed in companion papers, [15,17]. The former describes an EPR pair and shows that the helicity introduces an anti-symmetric component to spin which accounts for the apparent violation of BI, [21,22,23]. This is confirmed in the third paper which gives a computer simulation that evaluates the two contributions to spin from the polarization, (CHSH=2), [21], and from the coherence (CHSH=1), [17] for a total of CHSH=3. Neither polarization nor coherence violates Bell’s theorem [25].

It was unforeseen that Q-spin would give an alternate interpretation contrary to antimatter production. Although the existence of antimatter is not disputed, its manner of production is. In the Standard Model with symmetry, [14] SU(3)SU(2)U(1) this work suggests that SU(2) be replaced by

Q_{8}

. Perhaps then neutrinos, both matter and antimatter types would not be needed to balance some of the lepton equations because the quarks would have an addition property of chirality, a conserved quantity, on decay.

Acknowledgments

The author is grateful to Hillary Sanctuary, PhD, EPFL Switzerland, for suggesting the name hyper-helicity to distinguish it from the usual definition of helicity.

References

Gerlach, Walther, and Otto Stern. “Das magnetische moment des silberatoms." Zeitschrift für Physik 9.1 (1922): 353-355.
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624. [CrossRef]
Peskin, M., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
Dirac, P. A. M. (1930). “A Theory of Electrons and Protons". Proc. R. Soc. Lond. A. 126 (801): 360–365. [CrossRef]
Sanctuary, B. C. “Structure of a spin 12." arXiv preprint arXiv: 0908.3219 (2009).
Sanctuary, B. C. “The two dimensional spin and its resonance fringe." arXiv preprint arXiv:0707.1763 (2007).
Okun, Lev B. "Mirror particles and mirror matter: 50 years of speculation and searching." Physics-Uspekhi 50.4 (2007): 380.
Doran, C., Lasenby, J., (2003). Geometric algebra for physicists. Cambridge University Press.
Muralidhar, K. "The spin bivector and zeropoint energy in geometric algebra." Adv. Studies Theor. Phys 6 (2012): 675-686.
To visualize quaternions and its steriographic projection see 3 Blue 2 Brown: https://eater.net/quaternions.
Peters, James F., and Arturo Tozzi. "Quantum entanglement on a hypersphere." International Journal of Theoretical Physics 55 (2016): 3689-3696. [CrossRef]
Christian, Joy. "Bell’s theorem versus local realism in a quaternionic model of physical space." IEEE Access 7 (2019): 133388-133409. [CrossRef]
Christian, Joy. "Symmetric Derivation of the Singlet Correlations within a Quaternionic 3-sphere." arXiv preprint arXiv:2204.10288 (2022). arXiv:2204.10288 (2022).
Schwartz, M. D. (2014). Quantum field theory and the standard model. Cambridge University Press.
Sanctuary, B. Spin with Hyper-helicity.. Preprints 2023, 2023010571 (doi: 10.20944/preprints202301.0571.v1). [CrossRef]
Einstein, A, Podolsky, B and Rosen, N, “Can quantum mechanical description of physical reality be considered complete?” Phys Rev 47, 777-780, (1935). [CrossRef]
Sanctuary, B. Simulated Non-Local EPR Correlation: CHSH = 3. Preprints 2023, 2023010570 (doi: 10.20944/preprints202301.0570.v1). [CrossRef]
Zhou, Ziheng, and Zhenhua Yu. "Interaction effects on the PT-symmetry-breaking transition in atomic gases." Physical Review A 99.4 (2019): 043412. [CrossRef]
Troha, T., D. Lukman, and N. S. Mankoč Borštnik. "Massless and massive representations in the spinor technique." International Journal of Modern Physics A 29.23 (2014): 1450124. [CrossRef]
Maldacena, J., Susskind, L. (2013). Cool horizons for entangled black holes. Fortschritte der Physik, 61(9), 781-811. [CrossRef]
Clauser, J. F., Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880. [CrossRef]
Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804. Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951.
Bell, John S. “On the Einstein Podolsky Rosen paradox.” Physics Physique Fizika 1.3 (1964): 195.
Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039. [CrossRef]
Bell, J. S. “Speakable and Unspeakable in Quantum Mechanics” (Cambridge University Press, 1987), 2004. See “Locality in quantum mechanics: reply to critics. Epistemological Letters”, Nov. 1975, pp 2–6.”.

Figure 1. Two properties of spin: its polarization,

σ_{i}

, perpendicular to its helicity. The helicity is in the direction of propagation and spins R or L. The polarization carries a spin of magnitude 1 from the coupling of the two axes

σ_{3}

and

σ_{1}

. These properties show spin is geometrically equivalent to that of a photon.

Figure 1. Two properties of spin: its polarization,

σ_{i}

, perpendicular to its helicity. The helicity is in the direction of propagation and spins R or L. The polarization carries a spin of magnitude 1 from the coupling of the two axes

σ_{3}

and

σ_{1}

. These properties show spin is geometrically equivalent to that of a photon.

Figure 2. spin is oriented in spin spacetime by the BFF basis vectors

(e_{1}, e_{2}, e_{3})

which spins about the axis

e_{2}

so that in Minkowski spacetime, with components

(X, Y, Z)

, only a smeared out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from the coupling of the (3,1) axes.

Figure 2. spin is oriented in spin spacetime by the BFF basis vectors

(e_{1}, e_{2}, e_{3})

which spins about the axis

e_{2}

so that in Minkowski spacetime, with components

(X, Y, Z)

, only a smeared out image of the precessing spin is projected. The lower right insert contrasts Dirac spin and Q-spin, which is displayed as the resonance formed from the coupling of the (3,1) axes.

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the left and

ψ^{-}

on the right. Note that adding these states is independent of

e_{2}

and subtracting them is independent of

e_{1}

and

e_{3}

.

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the left and

ψ^{-}

on the right. Note that adding these states is independent of

e_{2}

and subtracting them is independent of

e_{1}

and

e_{3}

.

Figure 4. The two polarization axes form Q-spin of even parity from the coupling of two mirror states.

Figure 5. In the presence of a probe field, one polarization axis aligns with the field while the other axis and the helicity are averaged away. On the left and right sides, the Q-spin is decoupled by a field that is oriented either on the left or on the right. If the field is more aligned with the Q-spin, it spins without decoupling.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.