Submitted:
05 September 2023
Posted:
06 September 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Results and Discussion
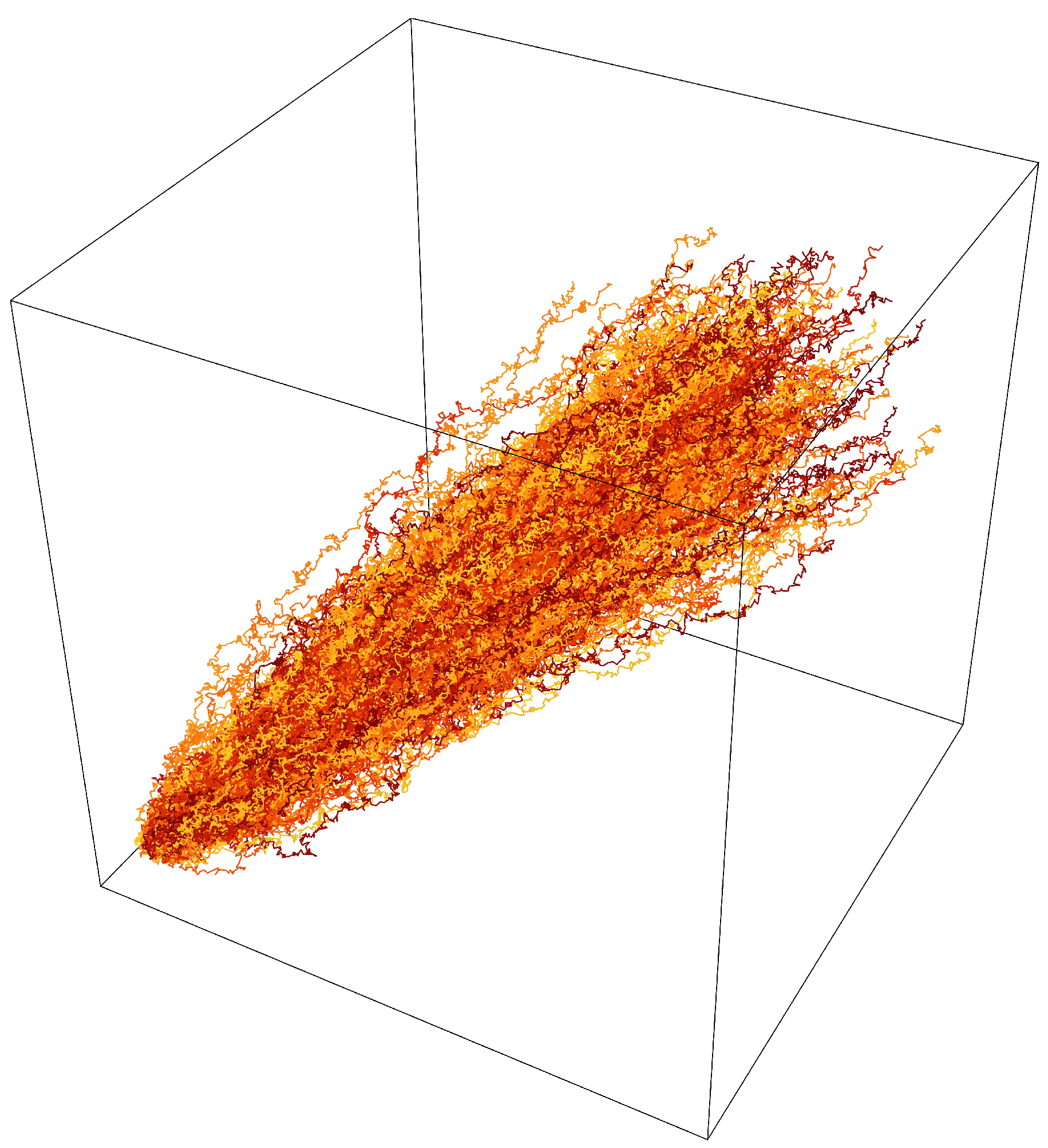
2.1. Biased Random Walk
2.2. Continuous Biased Random Process
2.3. Itô Equation of Biased Random Processes
3. Conclusions
Supplementary Materials
Data Availability Statement
Acknowledgments
References
- Tapiero, C.S.; Vallois, P. Run length statistics and the Hurst exponent in random and birth-death random walks. Chaos, Solitons & Fractals 1996, 7, 1333–1341. [Google Scholar]
- Guo, T. Study on the average speed of particles from a particle swarm derived from a stationary particle swarm. Scientific Reports 2021, 11, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Guo, T. Dynamics of stochastic-constrained particles. Scientific Reports 2023, 13, 2759. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.; Guo, T. The angular speed distribution of randomly moving-particle group. AIP Advances 2022, 12, 045005. [Google Scholar] [CrossRef]
- Codling, E.A.; Plank, M.J.; Benhamou, S. Random walk models in biology. Journal of the Royal society interface 2008, 5, 813–834. [Google Scholar] [CrossRef] [PubMed]
- Debbasch, F.; Chevalier, C. Relativistic stochastic processes. AIP Conference Proceedings. American Institute of Physics, 2007, Vol. 913, pp. 42–48.
- Dunkel, J.; Hänggi, P. Relativistic brownian motion. Physics Reports 2009, 471, 1–73. [Google Scholar] [CrossRef]
- Hakim, R. Relativistic stochastic processes. Journal of Mathematical Physics 1968, 9, 1805–1818. [Google Scholar] [CrossRef]
- Dunkel, J.; Talkner, P.; Hänggi, P. Relativistic diffusion processes and random walk models. Physical Review D 2007, 75, 043001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




