Submitted:
06 February 2023
Posted:
07 February 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Results and Discussion
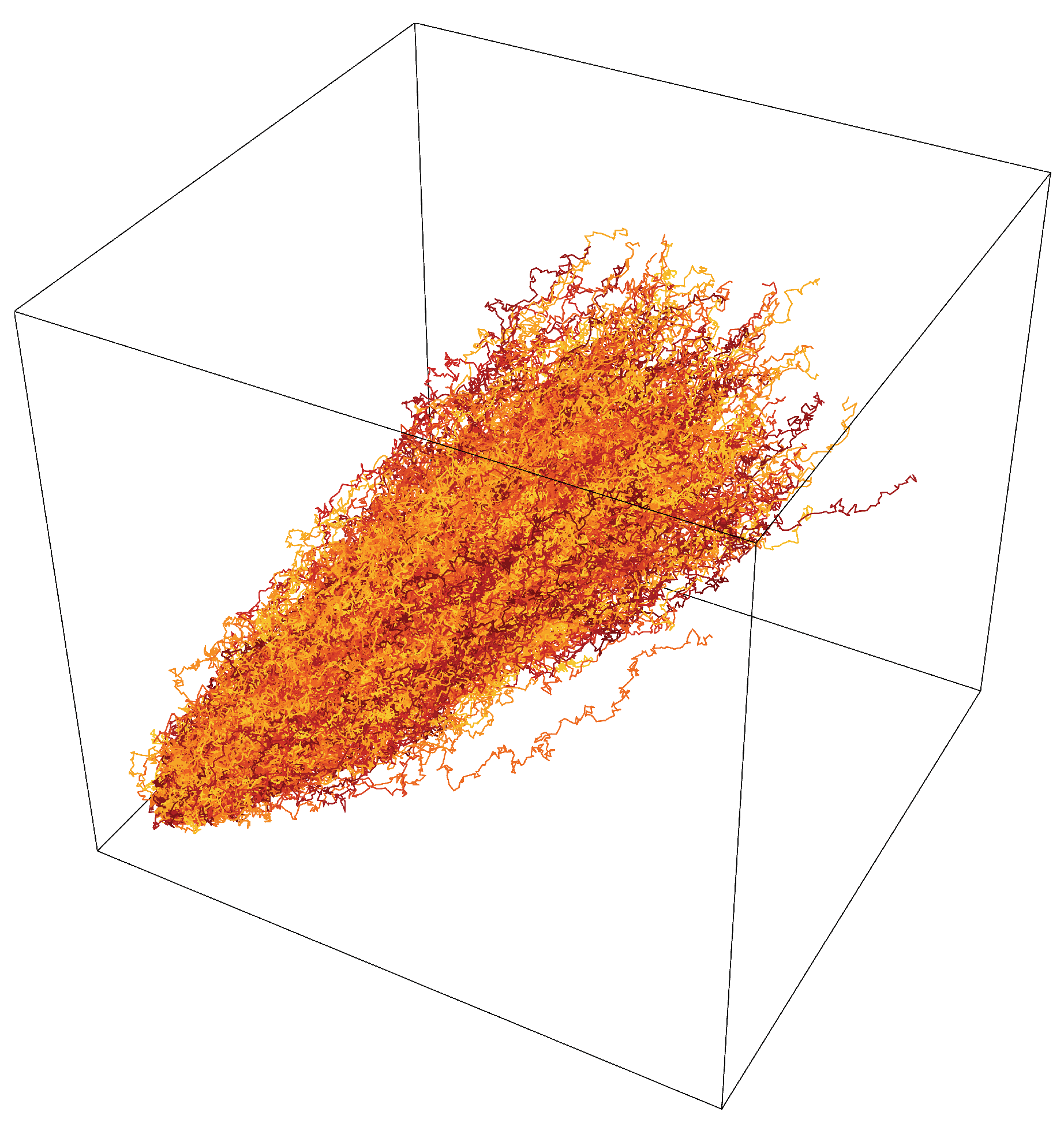
2.1. Biased Random Walk
2.2. Motion Law of the Stochastic Process of Randomly Moving Particles Following the Maxwell Distribution
2.3. Ito Equation of Biased Random Processes
3. Conclusions
Supplementary Materials
Data Availability Statement
Acknowledgments
References
- Tapiero, C.S.; Vallois, P. Run length statistics and the Hurst exponent in random and birth-death random walks. Chaos, Solitons & Fractals 1996, 7, 1333–1341. [CrossRef]
- Guo, T. Study on the average speed of particles from a particle swarm derived from a stationary particle swarm. Scientific Reports 2021, 11, 1–4. [CrossRef]
- Guo, T. Dynamics of Stochastic-constrained Particles 2022. [CrossRef]
- Yang, T.; Guo, T. The angular speed distribution of randomly moving-particle group. AIP Advances 2022, 12, 045005. [CrossRef]
- Codling, E.A.; Plank, M.J.; Benhamou, S. Random walk models in biology. Journal of the Royal society interface 2008, 5, 813–834. [CrossRef]
- Debbasch, F.; Chevalier, C. Relativistic stochastic processes. AIP Conference Proceedings. American Institute of Physics, 2007, Vol. 913, pp. 42–48. [CrossRef]
- Dunkel, J.; Hänggi, P. Relativistic brownian motion. Physics Reports 2009, 471, 1–73. [CrossRef]
- Hakim, R. Relativistic stochastic processes. Journal of Mathematical Physics 1968, 9, 1805–1818. [CrossRef]
- Dunkel, J.; Talkner, P.; Hänggi, P. Relativistic diffusion processes and random walk models. Physical Review D 2007, 75, 043001. [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




