A new theory of spacetime must either disprove SR/GR or else not conflict with SR/GR. Because of different concepts, ER does not conflict with SR/GR. However, ER tells us that the scope of SR/GR is limited: We must apply ER to objects that are very far away (such as high-redshift supernovae) or entangled (moving in opposite 4D directions at the speed ). In such extreme situations, the 4D vector “flow of proper time” of ER is crucial. ER raises questions: (1) Does ER predict the same relativistic effects as SR/GR? Yes, the Lorentz factor and gravitational time dilation are recovered in ER. (2) What are the benefits of ER? It solves mysteries of cosmology and quantum mechanics (QM). (3) Does ER also make quantitative predictions? Yes, it predicts the 10 percent deviation in the published values of
1. Introduction
Today’s concepts of space and time were coined by Albert Einstein. In SR, space and time are fused into a flat spacetime described by the Minkowski metric. SR is often presented in Minkowski space time [
3]. Predicting the lifetime of muons [
4] is one example that supports SR. In GR, a curved spacetime is described by the Einstein tensor. The deflection of starlight [
5] and the high accuracy of GPS [
6] are two examples that support GR. Quantum field theory [
7] unifies classical field theory, SR, and QM, but not GR.
In 1969, Newburgh and Phipps [
8] pioneered ER. Montanus [
9] added a constraint: A pure time interval must be a pure time interval for all observers. According to Montanus [
10], this constraint is required to avoid “distant collisions” (without physical contact) and a “character paradox” (confusion of photons, particles, and antiparticles). I show that the constraint is obsolete. There are no distant collisions once we take projections into account. There is no character paradox once we take the 4D vector “flow of proper time” (see
Sect. 3) into account. Not only can the proper time of an antiparticle flow backward with respect to an observer, but also the proper time of a particle or a galaxy (see
Sect. 5.15). Montanus calculated the precession of Mercury’s perihelion in ER [
10] and other effects [
11], but he failed to derive Maxwell’s equations because of a wrong sign [
10]. Montanus used coordinate time
t as the parameter. The correct parameter in ER is cosmic time
θ.
Almeida [
12] studied geodesics in ER. Gersten [
13] interpreted the Lorentz transformation as an SO(4) rotation. There is also an ER website:
https://euclideanrelativity.com/. Previous formulations of ER merely swap coordinate time
t with the parameter
τ. This is the first paper where we apply three steps to make ER work: (1) The new time coordinate is proper time
τ. (2) The new parameter is cosmic time
, where
is the Hubble parameter. (3) An observer’s reality is a projection from 4D Euclidean space (ES). Most physicists still reject ER because dark energy and non-locality make today’s cosmology and QM work, the SO(4) symmetry in ER seems to exclude waves, and there seem to be paradoxes in ER.
This paper marks a turning point. I show: Dark energy and non-locality are obsolete, SO(4) is compatible with waves, and projections avoid paradoxes.
The two postulates of ER: (1) All energy moves through ES at the speed of light
. (2) The laws of physics have the same form in each object’s reference frame. An object’s reference frame is spanned by its proper space and proper time. Unlike coordinate space and coordinate time in SR, proper space and proper time in ER are assembled to a Euclidean spacetime. My
first postulate is stronger than the second SR postulate:
is absolute and universal. My
second postulate is not limited to inertial frames. In addition, I reversed the order of the postulates. Absoluteness comes first. Relativity comes second.
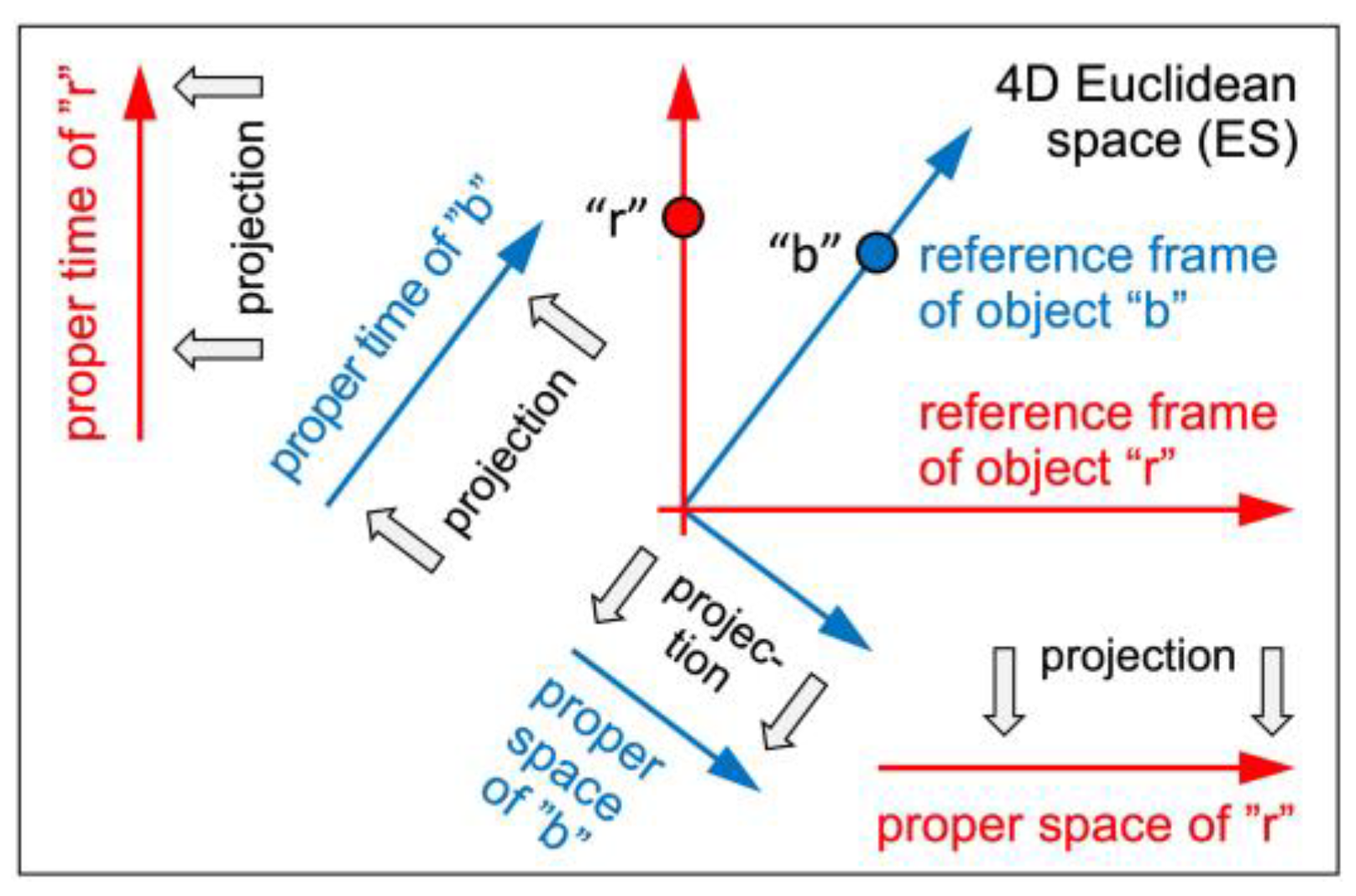
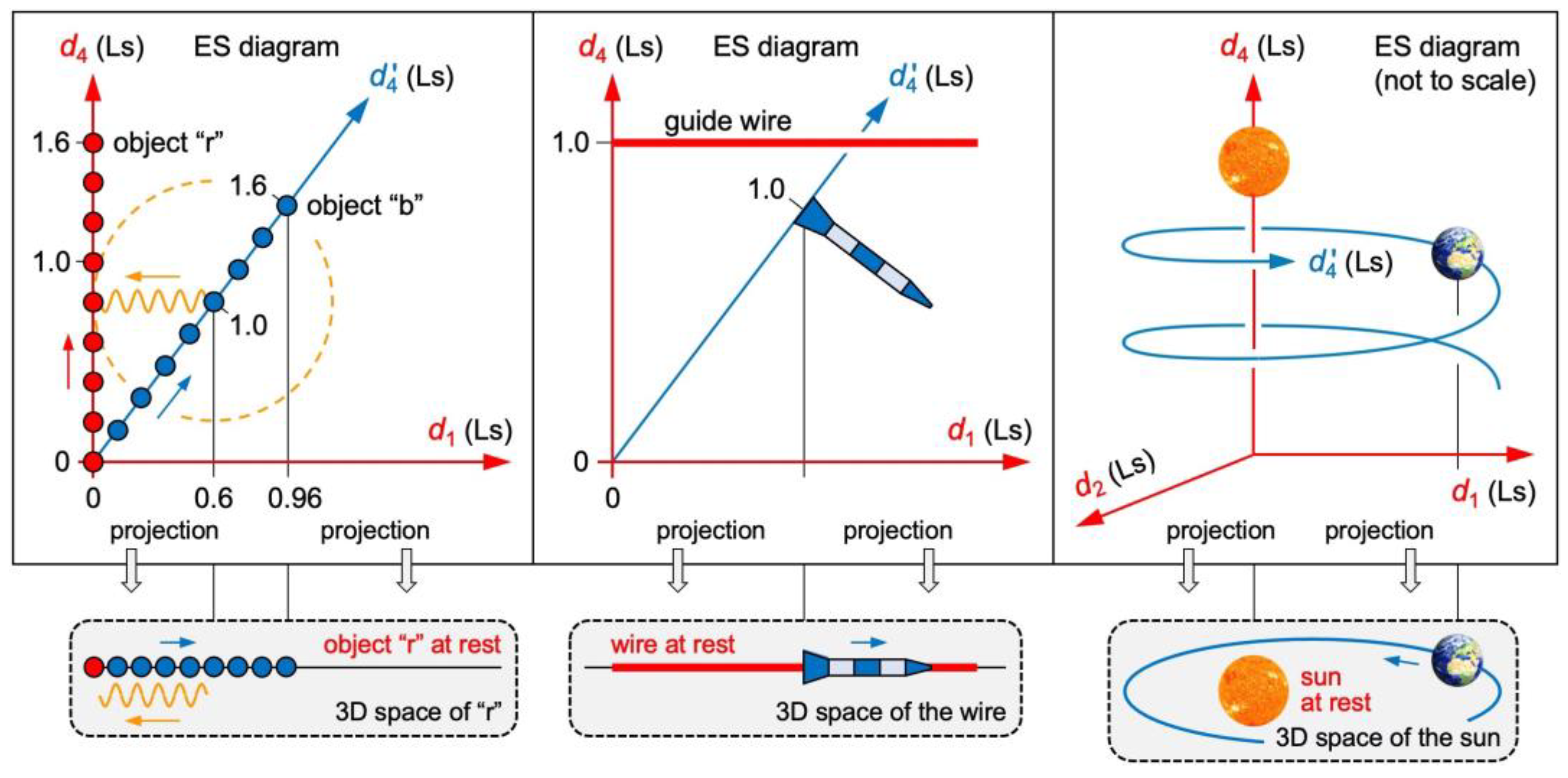
Fig. 1 illustrates the reference frames of two objects “r” and “b”. Each object experiences that axis in which it moves at the speed
as its proper time. It experiences the other three axes as its proper space. Proper space and proper time make up its “reality”. There are as many realities as there are objects. Mathematically, ES is 4D Euclidean space and an object’s proper space/proper time are two orthogonal projections from ES. Physically, three axes of ES are experienced as spatial, one axis as temporal, and projecting an object from ES to an observer’s reality is equivalent to measuring its coordinates.
Figure 1.
An object’s proper space and proper time are two orthogonal projections from ES.
Figure 1.
An object’s proper space and proper time are two orthogonal projections from ES.
It is instructive to contrast Newton’s physics, Einstein’s physics, and ER. In Newton’s physics, all energy moves through 3D Euclidean space as a function of independent time. There is no speed limit for matter. In Einstein’s physics, all energy moves through a non-Euclidean spacetime. The 3D speed of matter is
. In ER, all energy moves through ES. The 4D speed of all energy is
. Newton’s physics [
14] influenced many philosophers. I am convinced that ER will reform both physics and philosophy. For a better readability, I refer to an observer as “he”. To compensate, I refer to nature as “she”.
2. Identifying an Issue in Special and General Relativity
In SR, the fourth coordinate of spacetime is coordinate time
. In § 1 of SR, Einstein gives an instruction for synchronizing clocks at the points P and Q. At
, a light pulse is sent from P to Q. At
, it is reflected at Q. At
, it is back at P. The clocks synchronize if
In § 3 of SR, Einstein derives the Lorentz transformation. The coordinates
of an event in a system K are transformed to the coordinates
in K’ by
where K’ moves relative to K in
at the constant speed
and
is the Lorentz factor. Eqs. (
2a–c) transform the coordinates from K to K’. There are covariant equations that transform the coordinates from K’ to K. Mathematically, SR is correct. Physically, there is an issue in SR and also in GR:
The concepts of SR/GR fail to solve fundamental mysteries of physics. There are coordinate-free formulations of SR [
15] and also of GR [
16], but there is no absolute time in SR/GR and thus no “holistic view” (in a holistic view, the spacetime diagram is universal for all observers at once). The view in SR and GR is “multi-egocentric” (SR/GR work for each observer, but there is no universal spacetime diagram). All observers’ views taken together do not make a holistic view because they still do not provide absolute time. Without absolute time, observers will not always agree on what is past and what is future. Physics paid a high price for dismissing absolute time: ER restores absolute time and solves 15 mysteries (see
Sect. 5). Thus, the issue is real.
The issue in SR/GR is not about making wrong predictions. It has much in common with the issue in the geocentric model: Geocentrism is the egocentric view of mankind. In the old days, it was natural to believe that all celestial bodies would orbit Earth. Only the astronomers wondered about the retrograde loops of some planets and claimed that Earth orbits the sun. In modern times, engineers have improved the accuracy of rulers and clocks. Today, it is natural to believe that an observer’s rulers and clocks would be sufficient to describe nature. The reviewer of a top journal rejected ER because “modern physics is the discovery that absolute time plays no role in the phenomena that we observe”. The human brain is smart, but it often takes itself as the center/measure of everything.
The analogy of the geocentric model to SR/GR is not perfect: While heliocentrism and geocentrism exclude each other, ER does not conflict with SR/GR. Yet the analogy is close: (1) After taking another planet as the center of the Universe (or after a transformation in SR/GR), the view is still geocentric (or else egocentric). (2) Retrograde loops are obsolete in heliocentrism, but they make geocentrism work. Dark energy and non-locality are obsolete in ER, but they make today’s cosmology and QM work. (3) Heliocentrism overcomes the limitation of a geocentric view. ER overcomes the limitation of a multi-egocentric view. (4) The geocentric model was a dogma in the old days. SR and GR are dogmata nowadays. Have physicists not learned from history? Does history repeat itself?
3. The Physics of Euclidean Relativity
ER cannot be derived from measurement instructions because the proper coordinates of other objects cannot be measured. We start with the Minkowski metric of SR
where
is an infinitesimal distance in proper time
, whereas all
(
) and
are infinitesimal distances in an observer’s coordinate space
and coordinate time
. Coordinate spacetime
is a
man-made spacetime because its coordinates are constructs and thus not inherent in rulers and clocks. Rulers measure proper length. Clocks measure proper time. We introduce ER by the Euclidean metric
where
is an infinitesimal distance in the parameter
(to be given a meaning later on), whereas all
(
) are infinitesimal distances in 4D Euclidean space (ES). We prefer the indices 1–4 to 0–3 to stress the SO(4) symmetry. Each object (!) is free to label the axes of its reference frame in ES. Observers are objects too. We assume: Each object labels the axis of its
current 4D motion as
and the other three axes of ES as
. Because of my
first postulate, it thus always moves in the
axis at the speed
. The orientation of an object’s reference frame in ES can change: If it moves along a curved worldline, the orientation of its reference frame always adapts to this curvature. Because of length contraction at the speed
(see
Sect. 4), the
axis disappears for itself and is experienced as proper time. An object moving in
at the speed
experiences
as proper time. In ER,
is the length of a 4D Euclidean vector “flow of proper time”
.
where
is an object’s 4D velocity. In ER, speed is not defined as
(
), but as
(
). Thus, Eq. (
4) is nothing but my
first postulate
In other words: An object’s proper space and proper time span its reference frame in ES (). Absolute ES is experienced as a relative Euclidean spacetime (EST): Each object experiences its 4D motion through ES as its proper time and the other three axes as its proper space. In EST, the fourth coordinate is . The invariant parameter is . The metric tensor is the identity matrix. EST is a natural spacetime because its coordinates are measured by and thus inherent in rulers and clocks. Intrinsic rulers and clocks of all objects measure distances in EST and not in .
Montanus [
9,
10,
11] merely rearranged Eq. (
3) to enforce a Euclidean metric. He did not distinguish between
and
. He also rejected symmetric axes and promoted a spacetime, where a pure time interval always remains a pure time interval. I show: Whatever is proper time to me, it can be one axis of proper space (or a mix of proper space and proper time) for you. Do not confuse ER with a Wick rotation [
17], which keeps
invariant.
Because of
, there is no continuous transition between Eqs. (
3) and
(4) nor between SR/GR and ER. This fact underlines that ER provides a unique description of nature. SR describes nature in man-made spacetime
, where the parameter
is object-related. GR is locally equivalent to SR. ER describes nature in natural spacetime
, where
is what I call the “cosmic evolution parameter”. As I will demonstrate in
Sect. 5, the parameter
proves more powerful than the parameter
. Only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. In my
Conclusions, I will explain why this is fine.
It is instructive to contrast three concepts of time.
is a subjective measure of time: An observer uses his clock as the master clock.
is an objective measure of time: Clocks measure
independently of observers.
is the total distance covered in ES (length of a worldline) divided by
. As the invariant in Eq. (
4),
is a concept of absolute time. This is why I also call it “cosmic time”. In terms of cosmic time, there is no twin paradox. Twins share the same age in cosmic time
. By referring to
, observers always agree on what is past and what is future. Regarding causality, a finite
is incompatible with a coordinate “absolute time”, but compatible with a parameter “absolute time”.
We consider two identical clocks “r” (red clock) and “b” (blue clock). In SR, “r” moves in the
axis. Clock “b” starts at
and moves in the
axis at a constant speed of
.
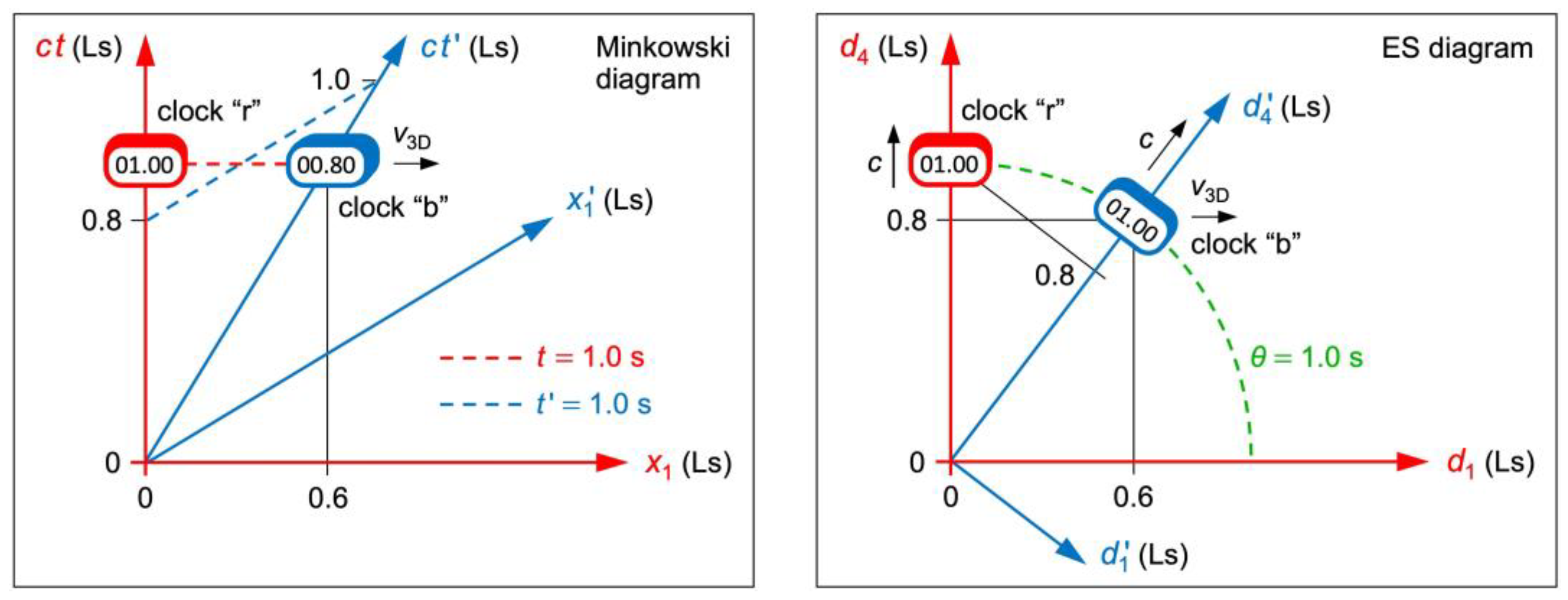
Fig. 2 left shows the instant when either clock moved 1.0 Ls (light seconds) in
. Clock “b” moved 0.6 Ls in
and 0.8 Ls in
. It displays “0.8”. In ER, “r” moves in the
axis.
Fig. 2 right shows the instant when either clock moved 1.0 s in its proper time. Both clocks display “1.0”. Since “r” remains at
and “b” remains at
, there is
for “r” and
for “b” according to Eq. (
4).
A uniformly moving clock always displays both its and . Yet
is not the invariant in ER. Thus,
of “r” is not equal to
of “b”. In ER,
is the invariant. Thus,
of “r” is equal to
of “b”.
We now assume that an observer R (or B) moves with clock “r” (or else “b”). In SR and only from the perspective of R, clock “b” is at
when “r” is at
(see
Fig. 2 left). Thus, “b” is slow with respect to “r” in
(of B). In ER and independently of observers, clock “b” is at
when “r” is at
(see
Fig. 2 right). Thus, “b” is slow with respect to “r” in
(of R). In SR and ER, “b” is slow with respect to “r”, but time dilation occurs in different axes. Experiments do not disclose that axis in which a clock is slow. Thus, both SR and ER describe time dilation correctly if ER yields the same Lorentz factor as SR. In
Sect. 4, I will show that this is the case.
“Relativity” has different connotations in SR and ER: In Minkowski spacetime, spatial and temporal distances are relative (they depend on an observer’s frame of reference). In ER, the orientation of an object’s frame of reference in ES is relative (it depends on the object’s 4D vector
). Absolute ES does not distinguish between spatial and temporal distances (the distances in all four axes are “pure distances”). Only in relative EST does an object experience
as spatial and
as temporal. There is also a great difference regarding clock synchronization: In SR, R can synchronize clock “b” to his clock “r” (same value of
in
Fig. 2 left). If he does, the clocks are not synchronized for B. In ER and independently of observers, clocks with the same
are naturally synchronized. Clocks with different
cannot be synchronized (different values of
in
Fig. 2 right).
But why does ER provide a holistic view? Eq. (
4) is symmetric in all
(
). R and B experience different axes as temporal. This is why
Fig. 2 left works for R, but not for B: A second Minkowski diagram is required, where
and
are orthogonal.
Here the view is multi-egocentric. Fig. 2 right works for R and for B at once (at the same cosmic time): Not only are
and
orthogonal, but also
and
. The ES diagram is independent of observers and thus universal.
Here the view is holistic. Note that the Michelson–Morley experiment [
18] refutes absolute 3D space (“ether”), but not absolute ES.
Regarding waves, I was misled by editors who insisted that the SO(4) symmetry of ES is incompatible with waves. SO(4) is incompatible with waves that propagate as a function of a coordinate time
, but compatible with waves that propagate as a function of the cosmic evolution parameter
. This is because Eq. (
4) can be rewritten as
which is of the same form as Eq. (
3). A great advantage of mathematics is that it remains the same when replacing variables. Maxwell’s equations thus have the same form in ER as in today’s physics except that
replaces
and that waves can propagate in one out of four axes. I claim:
All objects are “wavematters” (pure energy) that propagate through and oscillate in ES as a function of the parameter . In
Sect. 5.13, I will give evidence of my claim.
4. Geometric Effects in Euclidean Relativity
We consider two identical rockets “r” (red rocket) and “b” (blue rocket). Let observer R (or B) be in the rear end of “r” (or else “b”). The 3D space of R (or B) is spanned by
(or else
).
We use “3D space” as a synonym of proper space. The proper time of R (or B) relates to
(or else
) according to Eq. (
5). Both rockets start at the same point P and at the same cosmic time
. They move relative to each other at the constant speed
. R and B are free to label the axis of relative motion in 3D space. R (or B) labels it as
(or else
). The ES diagrams in
Fig. 3 must fulfill my
two postulates and the initial conditions (same P, same
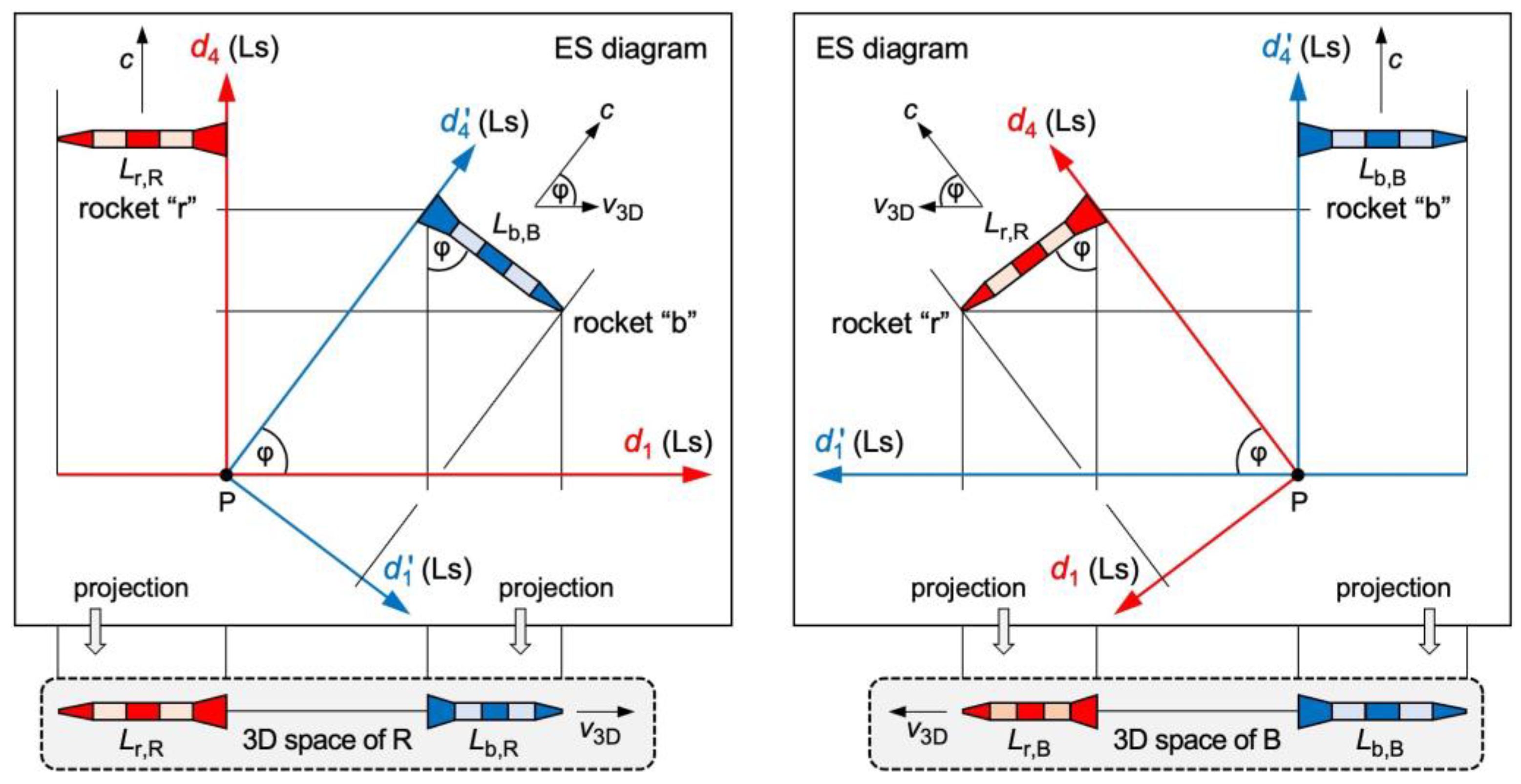
). This is achieved by rotating the red and the blue frame with respect to each other. Do not confuse ES diagrams with Minkowski diagrams.
In ES diagrams, objects maintain proper length and clocks display proper time. For a better readability, a rocket’s width is drawn in
(or
), although its width is in
(or else
).
Up next, we verify: Projecting distances in ES to the axes
and
of an observer causes length contraction and time dilation. Let
(or
) be the length of rocket “b” for observer R (or else B). In a first step, we project “b” in
Fig. 3 left to the
axis.
where
is the same Lorentz factor as in SR. For observer R, rocket “b” contracts to
. Despite the Euclidean metric, we calculate the same Lorentz factor as in SR. We now ask: Which distances will R observe in the
axis? We rotate rocket “b” until it serves as a ruler for R in the
axis. In his 3D space, this ruler contracts to zero length. In other words: The
axis disappears for R because of length contraction at the speed
. In a second step, we project “b” in
Fig. 3 left to the
axis.
where
(or
) is the distance that B moved in
(or else
). With
(R and B cover the same distance in ES, but in different 4D directions), we calculate
where
is the distance that R moved in
. Eqs. (
9) and (
12) tell us:
is recovered in ER once we project ES to the axes
and
of an observer.
Thus, ER predicts the same relativistic effects as SR. The two rockets only serve as an example. Other objects are projected the same way. For instance, the lifetime of a muon is recovered in ER when R is kept as the observer and the blue rocket is replaced by a muon. For orthogonal projections, the reader is referred to textbooks about geometry [
19,
20].
We now transform the proper coordinates of observer R (unprimed) to the ones of B (primed). R cannot measure the proper coordinates of B, and vice versa, but we can always calculate them from ES diagrams.
Fig. 3 right tells us how to calculate the 4D motion of R in the proper coordinates of B. The transformation is a 4D rotation by the angle
.
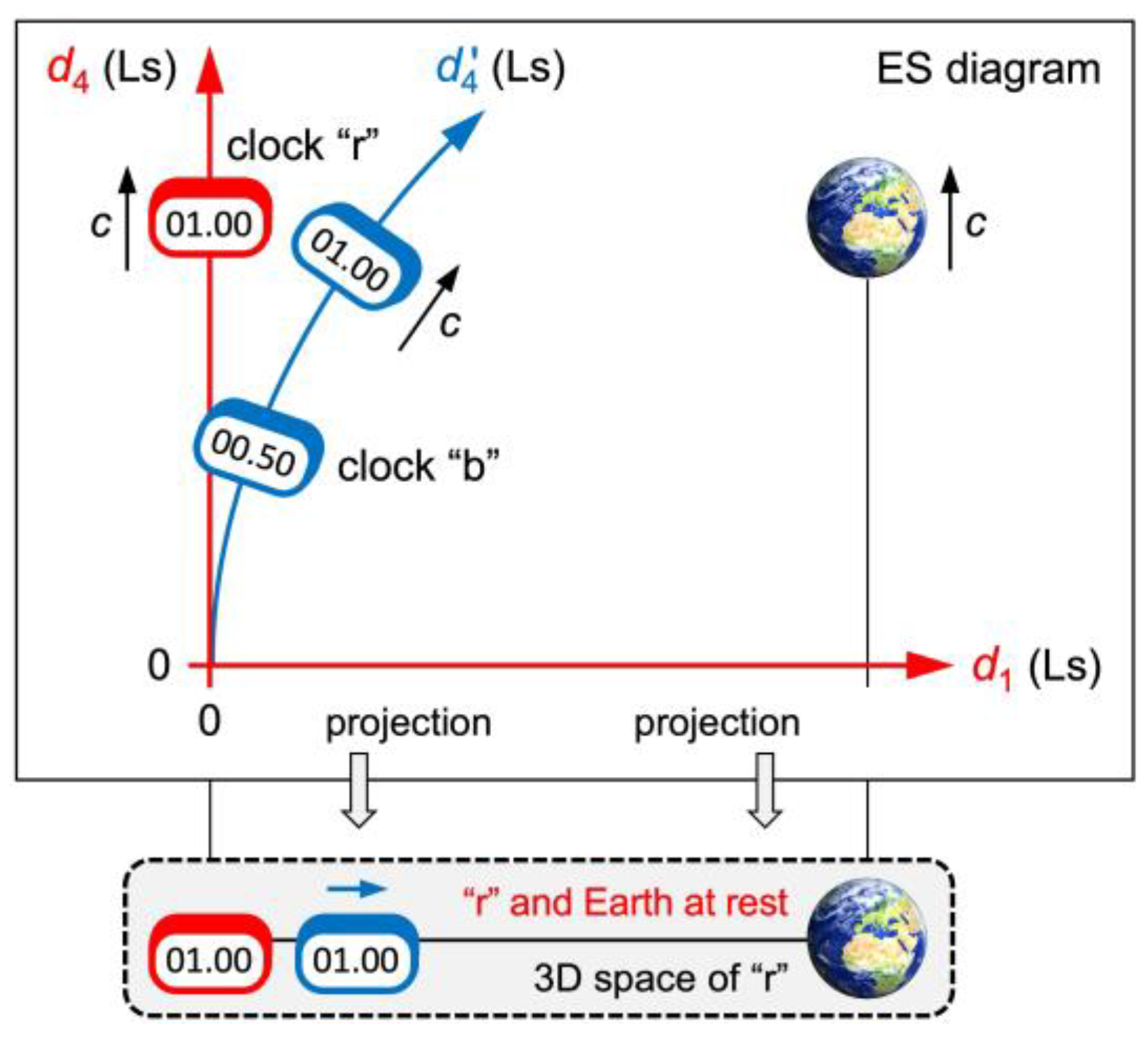
Up next, I show that not only the Lorentz factor is recovered in ER, but also gravitational time dilation. Initially, our two clocks “r” and “b” shall be very far away from Earth (see
Fig. 4). Eventually, “b” falls freely toward Earth and accelerates while maintaining the speed
in ES. Earth and “r” keep on moving in the
axis at the speed
.
Because of Eq. (
7), all accelerations in ES are transversal. The speed
of “b” in
increases at the expense of its speed
in
. Thus, “b” is slow with respect to “r” in
. In the gravitational field of Earth, the kinetic energy of “b” (mass
) in
is
where
is the gravitational constant,
is the mass of Earth, and
is the distance of “b” to the center of Earth in the 3D space of “r”. Eq. (
7) gives us
We now make use of differential geometry. With
(“b” moves in
at the speed
) and
(“r” moves in
at the speed
), we calculate
where
is the same dilation factor as in GR. Eq. (
17) tells us:
is recovered in ER once we project ES to the
axis of an observer.
Thus, ER predicts the same relativistic effects as GR. Yet there is a great difference: In GR, gravity is the curvature of spacetime. In ER, gravity makes its comeback as a force. Any acceleration rotates an object’s
and curves its worldline in ES. “Action at a distance” is not an issue if field variations propagate at the speed
and as a function of
. Since ES is projected (reduced) to an observer’s 3D space, the
law of gravity is maintained.
Clock “b” is slow with respect to “r” in
. Since “r” displays both its
and
, “b” is slow even with respect to absolute time
!
An accelerated clock displays its , but not . This is why clocks placed next to each other display different times after being exposed to different gravitational fields. Since
does not depend on
, “b” is slow with respect to
whether or not it stops moving relative to Earth. I invite theorists to show two things: (1) Gravitational waves [
21] are compatible with ER. (2) Variational principles [
22] are an alternative to derive ER. Here I showed:
and
are recovered in ER.
Summary of time dilation: In SR, a uniformly moving clock “b” is slow with respect to “r” in the time axis of “b”. In GR, an accelerated clock “b” or else a clock “b” in a more curved spacetime is slow with respect to “r” in the time axis of “b”. In ER, a clock “b” is slow with respect to “r” in the time axis of “r” (!) if the 4D vector
of “b” differs from the 4D vector
of “r”. Since both
and
are recovered in ER, the Hafele–Keating experiment [
23] supports ER too. GPS works in ER just as well as in SR/GR.
Fig. 5 illustrates how to read ES diagrams.
Problem 1: Two objects move through ES. “r” moves in
. “b” emits a radio signal at
. The signal recedes radially from “b” in all axes as a function of
, but cannot catch up with “r” in the
axis.
Can the signal and “r” collide in the 3D space of “r” if they do not collide in ES? Problem 2: A rocket moves along a guide wire. The wire moves in
. The rocket’s speed in
is less than
.
Doesn’t the wire escape from the rocket? Problem 3: Earth orbits the sun. The sun moves in
. Earth’s speed in
is less than
.
Doesn’t the sun escape from Earth’s orbit?
The last paragraph seems to reveal paradoxes in ER. The fallacy lies in the assumption that all four axes
would be spatial at once. This is not the case. Only three axes of ES are experienced as spatial and one as temporal. We solve all problems by projecting ES to the 3D space of that object which moves in
at the speed
. In its 3D space, it is always at rest. In
Fig. 5 left, the signal collides with “r” in the 3D space of “r” when their positions in
(not
) coincide. This is the case when
has elapsed since “r” and “b” started from the origin. The collision also takes place in the 3D space of the signal (not shown). In the 3D space of the signal, the 4D motion of “r” changes at
. Collisions in 3D space do not show up as collisions in ES. This is because events are a function of the parameter
, which is not an axis in ES diagrams.
ES diagrams do not show events, but each object’s flow of proper time. The sun does not spatially escape from Earth’s orbit. Rather, the sun and Earth are aging in different 4D directions.
6. Conclusions
Modern physics lacks two qualities of time: absolute and vectorial. On the one hand, there is the cosmic evolution parameter
(absolute time), which separates absolute past, present, and future. There is no absolute time in SR/GR. On the other hand,
is the length of a 4D Euclidean vector “flow of proper time”
. There is no
in SR/GR. While SR/GR work for all observers, the 15 mysteries solved in
Sect. 5 show that the scope of SR/GR is limited physically. The 4D vector
is crucial for objects that are very far away or entangled. Information hidden in
and in
is not available in SR/GR. It is very unlikely that 15 solutions in different (!) areas of physics are 15 coincidences. Some of the 15 mysteries had been solved without ER, but with concepts that now prove obsolete. ER declares cosmic inflation, expanding space, dark energy, and non-locality obsolete. They are all subject to Occam’s razor. Occam shaves off obsolete concepts. No exceptions.
It was a wise decision to award Einstein the Nobel Prize for his theory of the photoelectric effect [
47] and not for SR/GR. ER penetrates to a deeper level. Einstein, one of the most brilliant physicists ever, did not realize that the metric of nature is Euclidean. In fact, his instruction for synchronizing clocks blocks access to ER. He sacrificed absolute space and time. ER restores absolute time, but sacrifices the absolute nature of particles, matter waves, photons, and electromagnetic waves. In retrospect, two unfortunate practices of physicists delayed the formulation of ER: (1) Clocks measure
, but the construct
is more common in the equations of physics than natural
. (2) Cosmology is aware of the Hubble parameter
, but the parameter
is preferred to
in both SR and GR. For the first time ever, mankind now understands the nature of time: Cosmic time
is the total distance covered in ES divided by
. The human brain is able to imagine that we move at the speed
. With that said, conflicts of mankind become all so small.
Is ER a physical or a metaphysical theory? This is a very good question because only in proper coordinates can we access ES, but the proper coordinates of other objects cannot be measured. I now explain why this is fine: We can always calculate these proper coordinates from ES diagrams as I showed in Eqs. (
13a–c). Measuring is an observer’s source of knowledge, but ER tells us not to interpret too much into whatever we measure. Measurements are wedded to observers, whose concepts can be obsolete. I was often told that physics is all about observing. I disagree. We cannot observe quarks, can we? Regrettably, physicists have applied man-made concepts—which work well in everyday life—to the very distant and the very small. This is why cosmology and QM benefit the most from ER.
ER is a physical theory because it solves fundamental mysteries of physics.
Comments: (1) More studies on gravity are required, but this is no reason to reject ER. GR seems to solve gravity, but GR is incompatible with QM unless we add quantum gravity. Since ER solves mysteries of QM, quantum gravity is probably another obsolete concept. (2) In ES, there are no singularities and thus no black holes. Once again, this argument is no reason to reject ER. I can imagine that projecting several massive objects from ES onto a small region in an observer’s 3D space results in the formation of a supermassive object. (3) Mysteries often disappear if the symmetry is matched. The symmetry group of natural spacetime is SO(4). (4) Absolute time finally puts an end to discussions about time travel. Does any other theory explain time’s arrow as beautifully as ER? (5) Physics does not ask: Why is my reality a projection or a wave function? Projections are far less speculative than cosmic inflation plus expanding space plus dark energy plus non-locality.
It seems as if Plato had anticipated ER in his
Allegory of the Cave [
48]: Mankind experiences projections and cannot observe any reality beyond. I laid the groundwork for ER and showed how powerful it is. Paradoxes are only virtual. The pillars of physics are ER, SR/GR (for observers), and QM. Together they describe nature from the very distant down to the very small. The key question in science is this: How do we describe nature without adding highly speculative concepts? The answer leads to the truth. Introducing a holistic view to physics is the most significant contribution of this paper. SR/GR do not provide a holistic view. All observers’ views taken together do not make a holistic view because they still do not provide absolute time. Physics got stuck in its own concepts. Man-made concepts block our view of nature as a whole. Einstein described nature in a mix of man-made concepts (
) and natural concepts (
). ER describes nature exclusively in natural concepts (
,
).
Only in natural concepts does Mother Nature reveal her secrets. Everyone is welcome to solve even more mysteries by describing her in natural concepts.
Figure 2.
Minkowski diagram and ES diagram of two clocks “r” and “b”. Left: “b” is slow with respect to “r” in . Coordinate time is relative (“b” is at different positions in and ). Right: “b” is slow with respect to “r” in . Cosmic time is absolute (“r” and “b” are at the same position in ).
Figure 2.
Minkowski diagram and ES diagram of two clocks “r” and “b”. Left: “b” is slow with respect to “r” in . Coordinate time is relative (“b” is at different positions in and ). Right: “b” is slow with respect to “r” in . Cosmic time is absolute (“r” and “b” are at the same position in ).
Figure 3.
ES diagrams of two rockets “r” and “b”. Observer R (or B) is in the rear end of “r” (or else “b”). Left: “r” moves in the axis. “b” moves in the axis. In the 3D space of R, “b” contracts to . Right: The ES diagram has been rotated only. In the 3D space of B, “r” contracts to .
Figure 3.
ES diagrams of two rockets “r” and “b”. Observer R (or B) is in the rear end of “r” (or else “b”). Left: “r” moves in the axis. “b” moves in the axis. In the 3D space of R, “b” contracts to . Right: The ES diagram has been rotated only. In the 3D space of B, “r” contracts to .
Figure 4.
ES diagram of two clocks “r” and “b” and Earth. Clock “b” accelerates toward Earth. The axis is drawn curved because it indicates the current 4D motion of “b”.
Figure 4.
ES diagram of two clocks “r” and “b” and Earth. Clock “b” accelerates toward Earth. The axis is drawn curved because it indicates the current 4D motion of “b”.
Figure 5.
Three problems. Left: Objects “r” and “b” move through ES. The orange circle shows where a signal emitted by “b” at is at . In ES, the signal and “r” do not collide. In the 3D space of “r”, they do. Center: In ES, the wire escapes from the rocket. In the 3D space of the wire, it does not. Right: In ES, the sun escapes from Earth’s orbit. In the 3D space of the sun, it does not.
Figure 5.
Three problems. Left: Objects “r” and “b” move through ES. The orange circle shows where a signal emitted by “b” at is at . In ES, the signal and “r” do not collide. In the 3D space of “r”, they do. Center: In ES, the wire escapes from the rocket. In the 3D space of the wire, it does not. Right: In ES, the sun escapes from Earth’s orbit. In the 3D space of the sun, it does not.
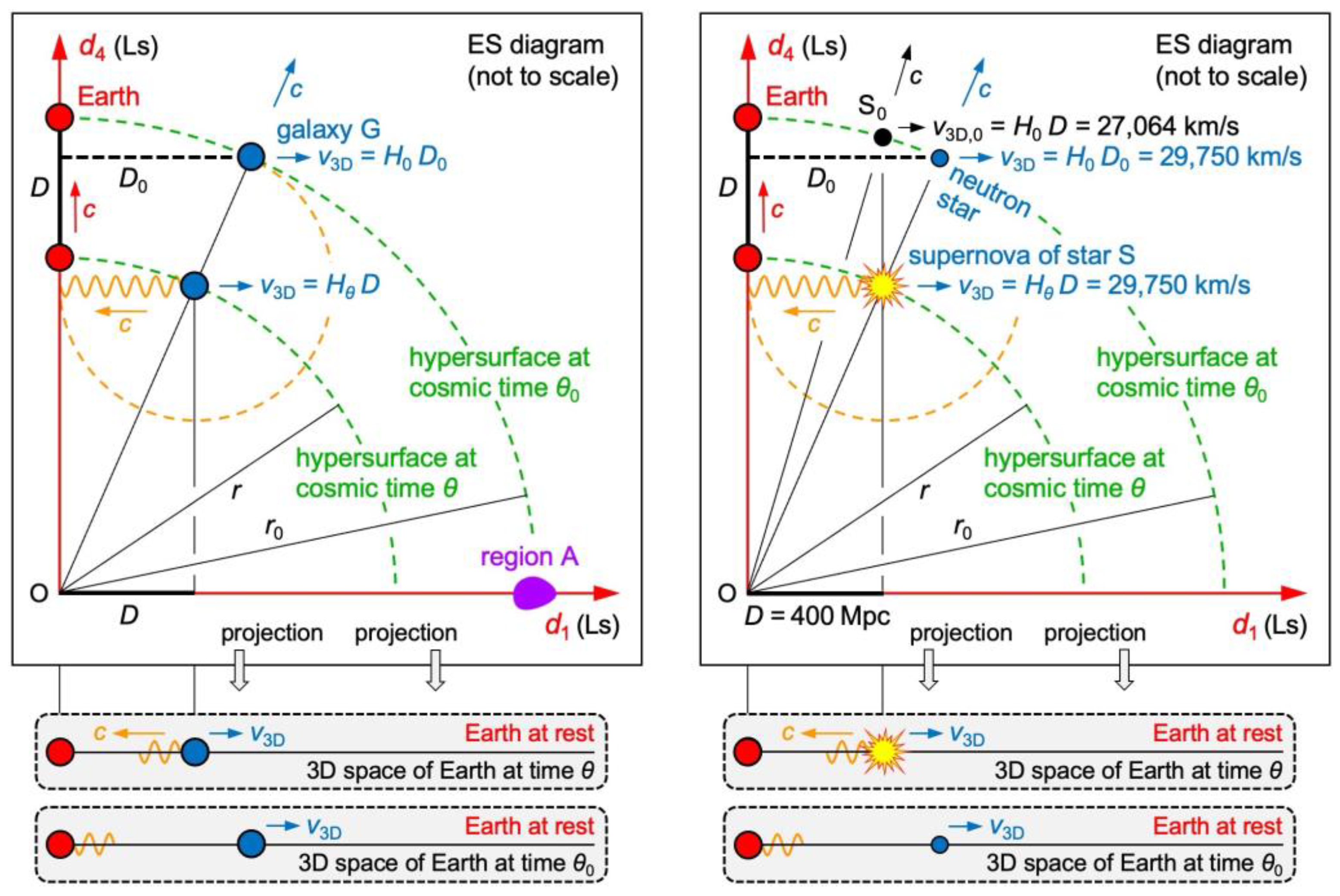
Figure 6.
ER-based model of cosmology. The green arcs show parts of a 3D hypersurface. The orange circles show where most of the energy emitted by G or S at the time is today. Left: G recedes from O at the speed and from the axis at the speed . Right: If a star happens to be at the same distance today at which the supernova of S occurred, recedes more slowly from than S.
Figure 6.
ER-based model of cosmology. The green arcs show parts of a 3D hypersurface. The orange circles show where most of the energy emitted by G or S at the time is today. Left: G recedes from O at the speed and from the axis at the speed . Right: If a star happens to be at the same distance today at which the supernova of S occurred, recedes more slowly from than S.
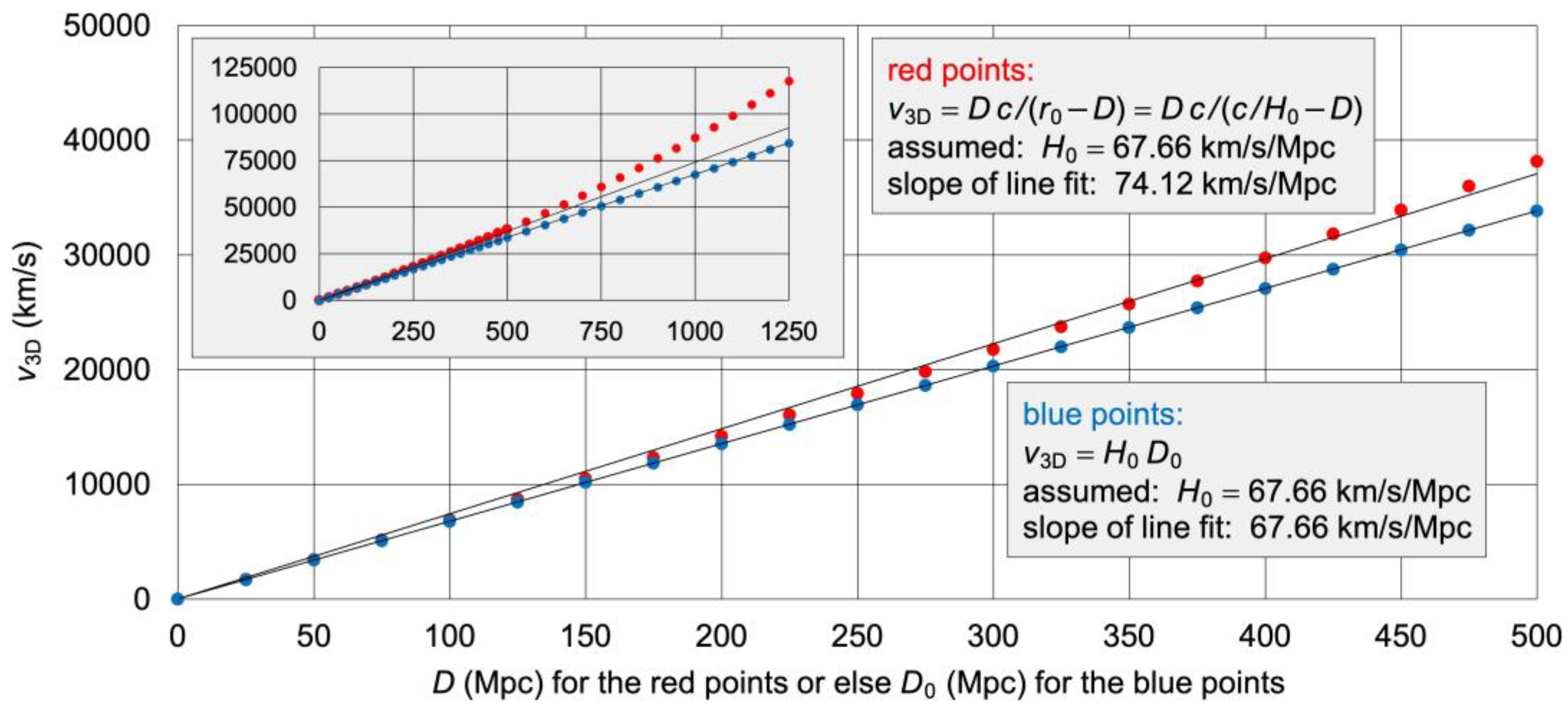
Figure 7.
Hubble diagram of simulated supernovae. The horizontal axis is
for the red points or else
for the blue points. The red points, calculated from Eq. (
20), do not yield a straight line because
is not a constant. The blue points, calculated from Eq. (
21), yield a straight line.
Figure 7.
Hubble diagram of simulated supernovae. The horizontal axis is
for the red points or else
for the blue points. The red points, calculated from Eq. (
20), do not yield a straight line because
is not a constant. The blue points, calculated from Eq. (
21), yield a straight line.
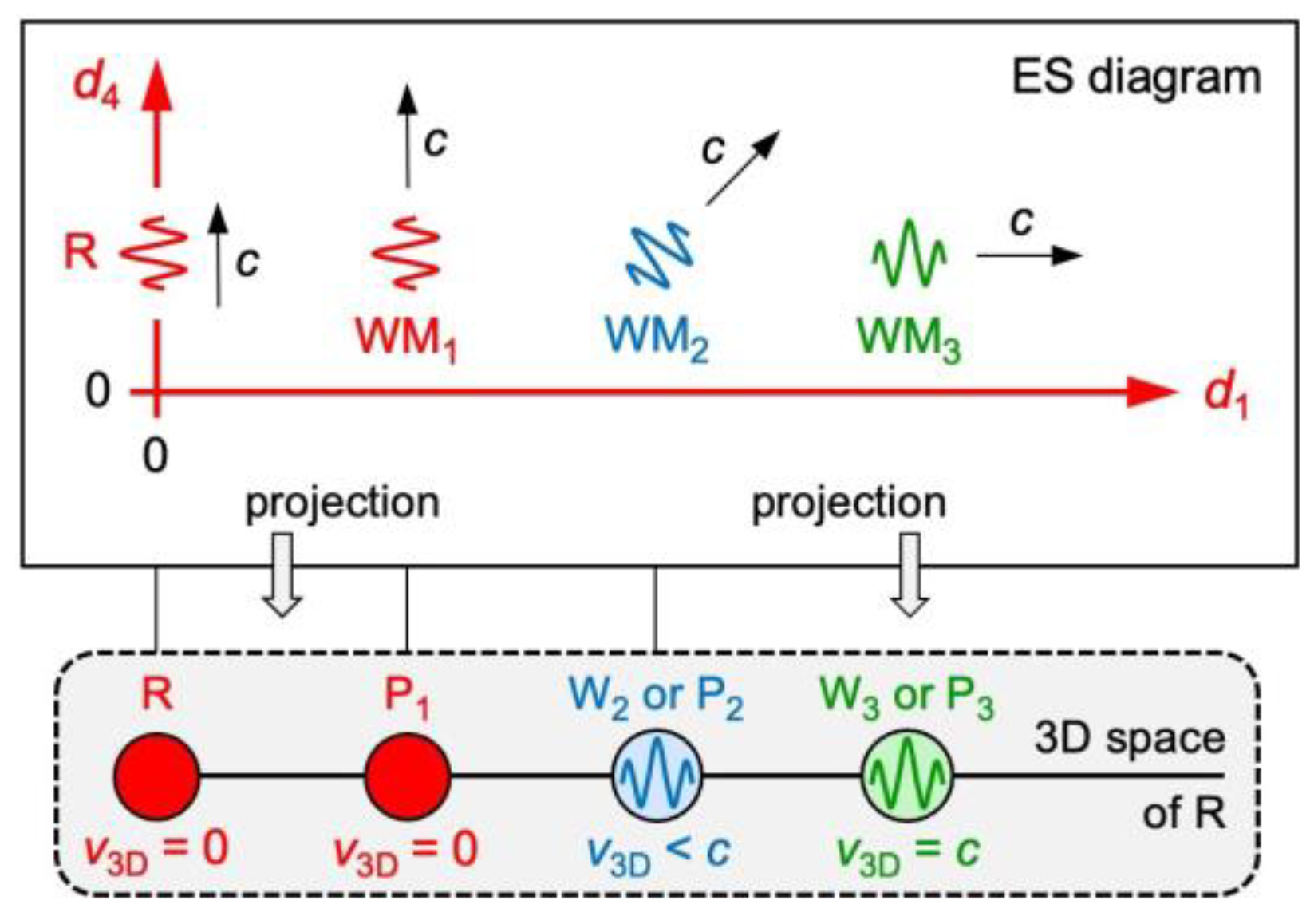
Figure 8.
Wavematters. Observer R moves in the axis. In his 3D space, and reduce to wave packets () if not tracked or else to particles () if tracked. : possibly an atom of R. : matter wave. : possibly a moving atom. : electromagnetic wave packet. : photon.
Figure 8.
Wavematters. Observer R moves in the axis. In his 3D space, and reduce to wave packets () if not tracked or else to particles () if tracked. : possibly an atom of R. : matter wave. : possibly a moving atom. : electromagnetic wave packet. : photon.
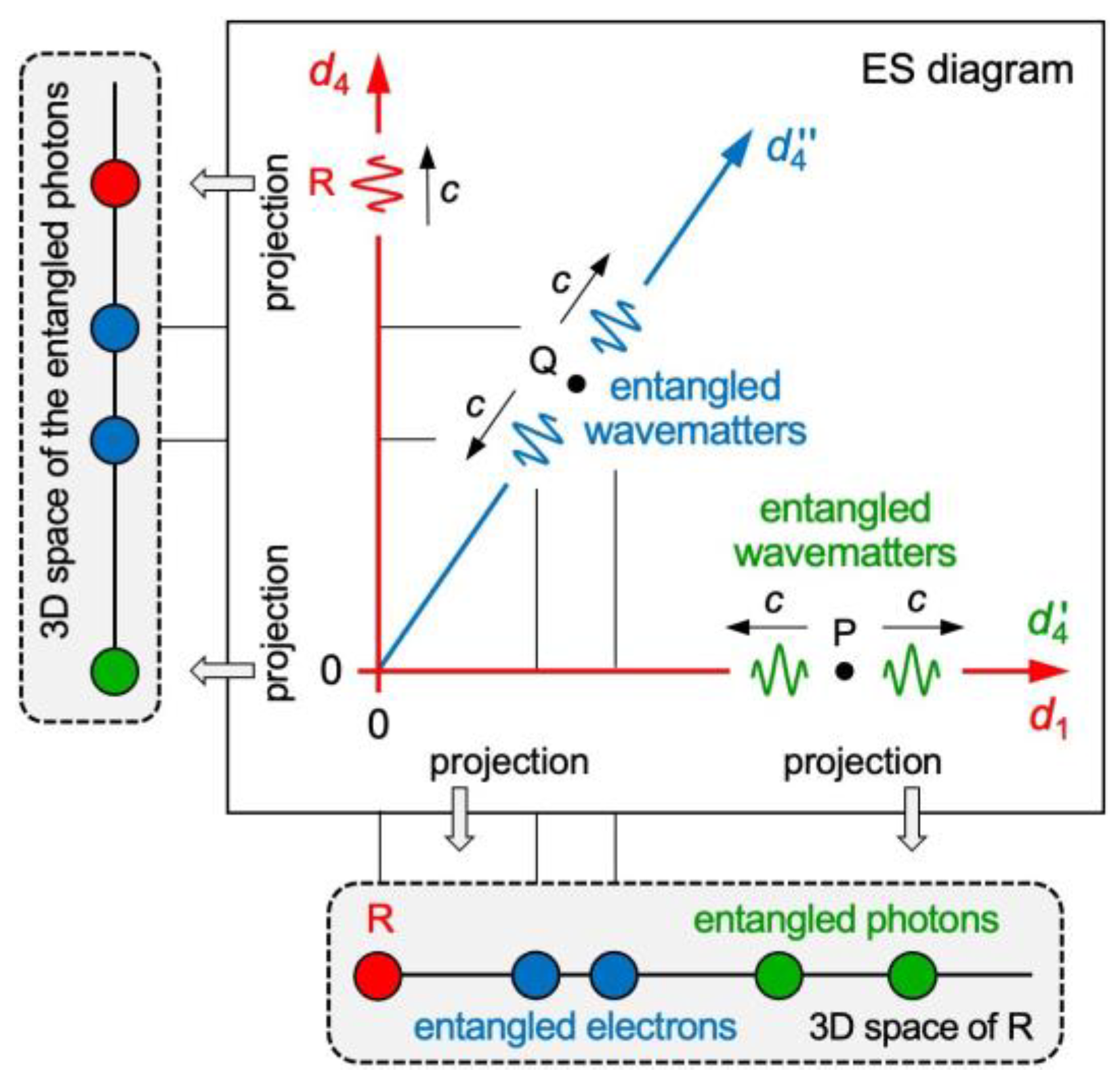
Figure 9.
Entanglement. Observer R moves in the axis. In the 3D space of R, one pair of wavematters reduces to entangled photons. The other pair reduces to entangled electrons. In the photons’ 3D space (or electrons’ 3D space, not shown), the photons (or else electrons) stay together.
Figure 9.
Entanglement. Observer R moves in the axis. In the 3D space of R, one pair of wavematters reduces to entangled photons. The other pair reduces to entangled electrons. In the photons’ 3D space (or electrons’ 3D space, not shown), the photons (or else electrons) stay together.
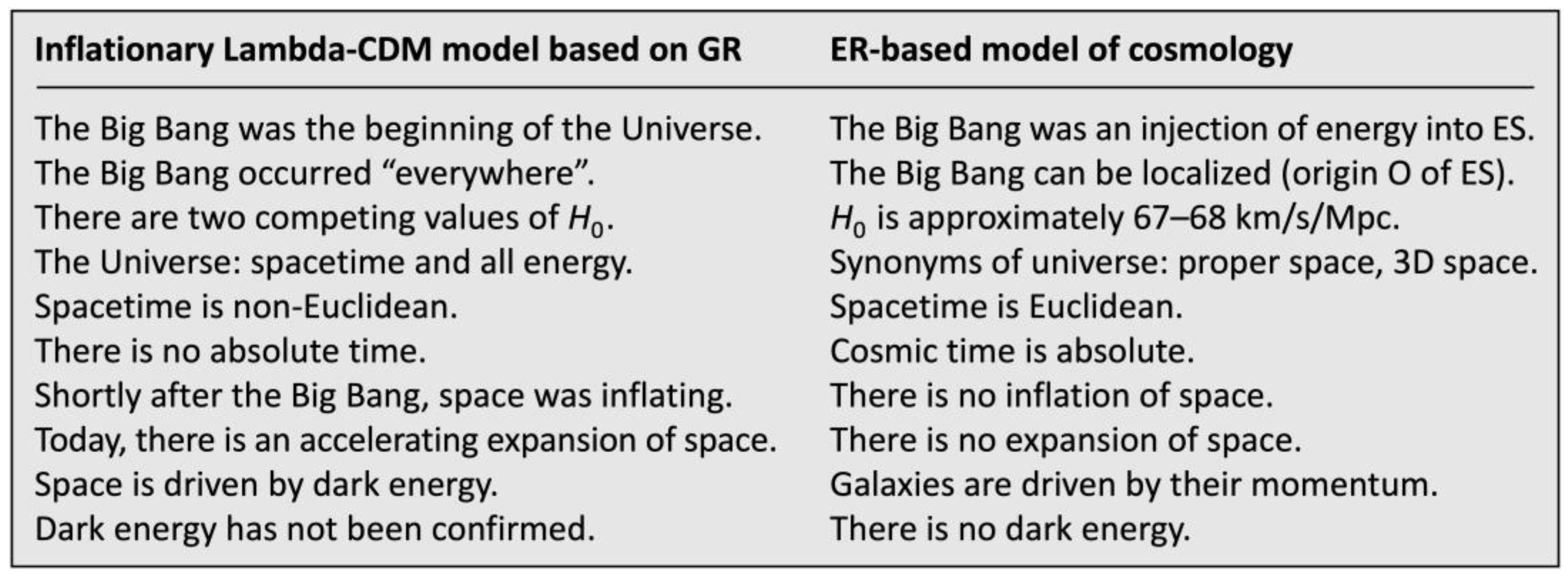
Table 1.
Comparing two models of cosmology
Table 1.
Comparing two models of cosmology