Is the Tendency to Maximise Energy Distribution an Optimal Collective Activity for Biological Purposes? A Proposal for a Global Principle of Biological Organization

1. Introducing the two problems

The investigation of the organization of the cellular collective activity associated with brain health and disease, and particularly with consciousness, is a foremost theme in current neuroscience. This paper addresses two problems. The biological problem concerns the search for the fundamental bases of the organization in the interactions among cells in the nervous system (or in any other organ for that matter) that give rise to conscious awareness and adaptability of the organism. The second problem is not so much biological but one of interpretation that sometimes makes the communication among scientists difficult: the nature of this organization of cellular activity as assessed by methods from thermodynamics (e.g. entropy and equilibrium) and concepts like order, disorder or complexity, terms that are ambiguous and sometimes hard to interpret when applied to open systems like all living processes are. Because we should not lose sight of the fact that order/disorder are relative terms, and therefore the notion of organization is ambiguous too, as the cybernetics pioneer W. Ross Ashby declared: “Organisation is partly in the eye of the beholder […] There is no property of an organisation that is good in any absolute sense; all are relative to some given environment” (Ashby, 1962). And herein lies the difficulty, to resolve the intertwined nature of the environment plus the body that contains a nervous system with a brain. The body, the (embodied) brain and the surroundings, and the relations among these three elements result in the neural organised activity leading to adaptive behaviours. By investigating with so much detail biological process and dividing them into pieces, the perspective that an organism is a functional whole immersed in a context —an environment— that imposes constraints, seems to have been somewhat lost. A complete understanding of nervous system dynamics necessitates consideration of the interaction with the environment because adaptive behaviours emerge from the dynamics of these interactions under the boundary conditions/constraints (Warren, 2006). As we will see later, it all depends on the context, the situation where the brain rests.

There are several theories of cognition/consciousness which, if their main essence is distilled, share some common aspects that already give us hints as to the principles of neural organization. And yet the question is, as can be found asked in recent papers —for instance in Perl et al. 2021— how the brain cell collective activities self-organise to fulfil the dynamic requirements of current consciousness theories. We will present a perspective based on the interactions among brain regions that, in our opinion, is the point of view from which the subject appears in its greatest simplicity (as J. W. Gibbs advised in a letter to the American Academy of Arts and Sciences in 1881: “One of the principal objects of theoretical research in any department of knowledge is to find the point of view from which the subject appears in its greatest simplicity”).

Let us now introduce the two problems with which we will deal. To better present the nature of the biological problem, with regards to nervous systems, we use Figure 1 to illustrate it.

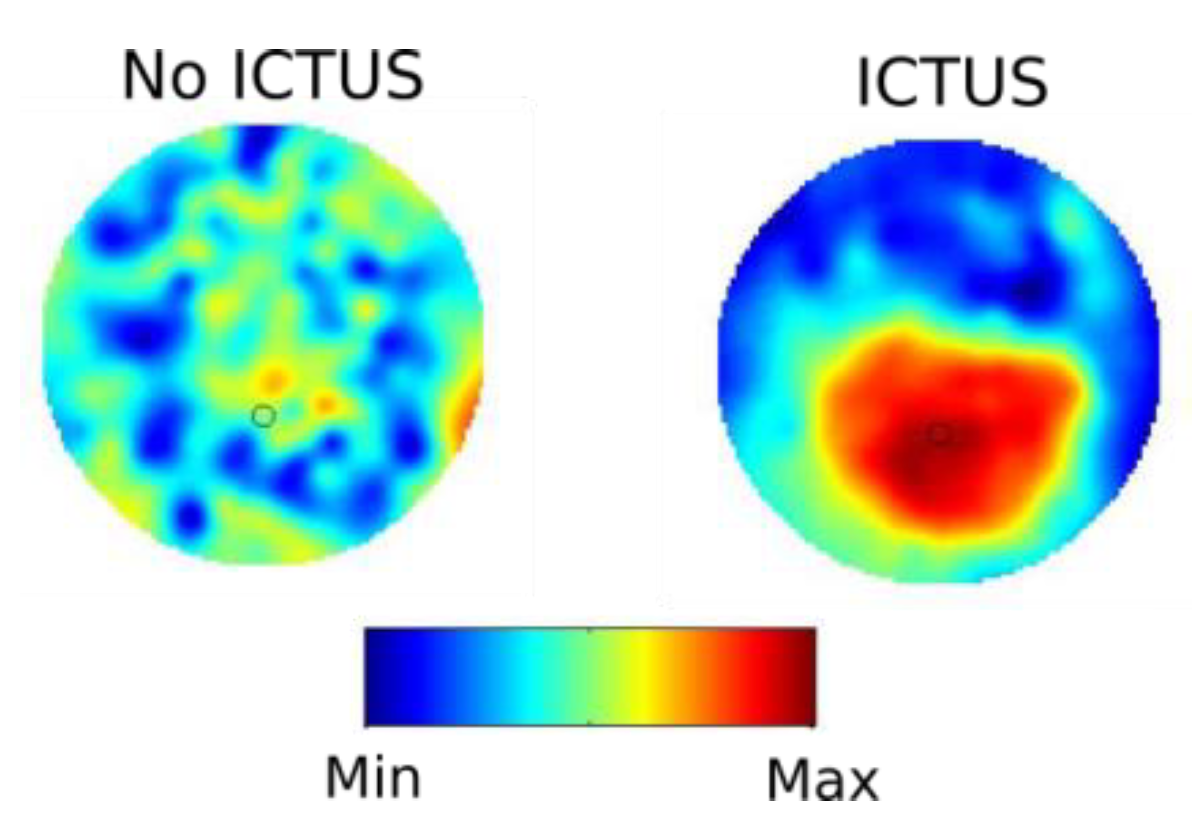
Without going into technical details (for details about the synchrony analysis please see Garcia Dominguez et al. 2005, 2008), Figure 1 shows schematically what happens with neuronal synchronization, specifically phase synchrony, during epileptic ictal events (seizures): the synchrony is higher and more uniform than that present at other times without seizures —in fact, the calculation of the spatial complexity of these synchrony patterns consistently showed lower spatial complexity during seizures, in that there were fewer fluctuations in synchrony (García Domínguez et al., 2008). And what happens to patients during seizures? They become unresponsive. A very brief note for those not too versed with epilepsy: there are different types of seizures, some are associated with convulsions, others with automatisms (unconscious behaviours out of context), and yet in other seizures there is no movement at all but the person remains unresponsive, and that is why these are called absence seizures. A common feature in most of these seizures is that patients become unresponsive —we use this term instead of “unconscious” so that we do not become entangled in the controversy, perhaps semantic to some extent, about being either unconscious or unresponsive during ictal events, which would lead us to the murky waters of the definition of consciousness (Perez Velazquez and Nenadovic, 2021).

In any event, this abnormal coordinated activity among brain cell networks during seizures does not allow these networks to properly interact, interactions leading to integration and segregation of information. Integration due to communication/connections in large ensembles of processing units —the brain cell networks in different regions that process diverse types of sensory inputs—, each of these units representing the segregation of information as each brain region is more or less specialised to process certain inputs. This combination of integration and segregation results in the accurate interpretation of the outer world and in the immense variety of sensorimotor transformations performed by the brain which lead to emergent phenomena, among these self-consciousness.

So, too much synchronised activity for an extended time period, as that shown in the second plot of the figure, is not appropriate for information processing (the patient was unresponsive at the time of the ictus, as normally occurs during seizures); neither, by the way, would be too little synchrony because a neuron normally needs a synchronous volley of synaptic potentials arriving from many other neurons to fire spikes and release the information to other neurons, hence a minimum synchrony should be always present if the nervous system is to work properly. A clarification: when talking about neural activity, the aforementioned “extended time period” means a few seconds to minutes, or even longer as occurs in patients during deep coma. Neural communication requires coupling among neuronal nets but also variability of these couplings. If the functional connections do not fluctuate enough, if the connectivity is too stable like during a seizure or in patients in coma, this is not optimal. Fluctuating patterns of coordinated activity in cell networks is a crucial aspect for healthy brain function that needs to process a myriad of sensorimotor transformations every minute of our lives. The foundations of ‘brain information’ processing lie in the interactions between cells: the activity of one cell acquires meaning as it relates to other cells’ activities. The existence of the flexible formation of neural activity patterns requires transient, fluctuating synchronization, thus the importance to examine the so-called “noise” in neural activity. Naturally, how much synchrony is too much or too little is not a trivial problem to address; this question and examples from normal and pathological brain activity has been explored at length in some texts (Perez Velazquez and Frantseva, 2011).

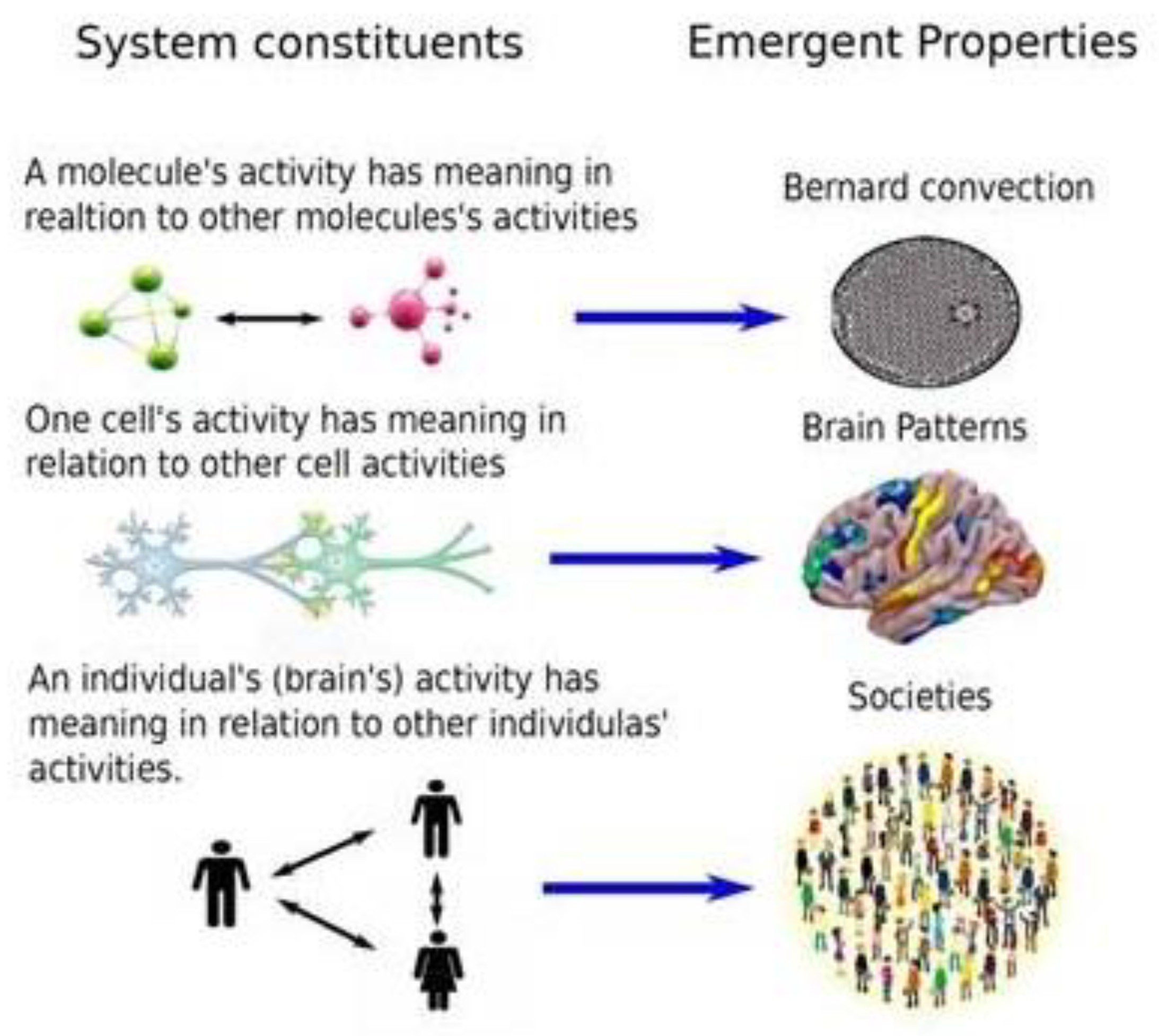
In fact, the perspective that consciousness relies on large-scale neuronal communication is common in several cognitive theories (Tagliazucchi, 2017). Not only nervous systems but in general almost all, if not all, living systems are characterized by the emergence of patterns due to the interplay between the short and long-range correlations among the system’s constituents. Always bearing in mind the aforesaid Gibb’s advice we will focus on a high level perspective of the coordinated activity of neuronal ensembles, if only because neural collective activity is fundamental —there are scores of studies suggesting the importance of correlated neural activity for sensorimotor integration. Some questions are best addressable in a global framework and this is the view we take here.

The second problem was already introduced in the first paragraph. It is about the ambiguity of the notions used to study neurodynamics and the difficulty with the interpretation of the results obtained in several studies using these high-level perspectives, especially thermodynamics and information theory, because, as explained below, one route to investigate the dynamics of nervous systems at macroscopic/mesoscopic levels passes through thermodynamic formalisms. Although nervous systems are not at strict equilibrium (but see comments on equilibrium and nonequilibrium in section 2.3), classical concepts in thermodynamics and statistical mechanics are being used to characterize neural activity; therefore there exist a plethora of studies using diverse, say, entropic measures applied to very different variables at completely distinct levels of description, such that reaching a global, unified view, is almost unfeasible, albeit if one is careful enough and understands all details of the study —or studies— of interest, then many of these complications evanesce. The challenging aspects about the ambiguity of some of these concepts will be addressed in the next section, and some solutions to overcome the relative nature of the concepts and methods will be proposed.

Having thus introduced the two problems that this paper addresses, we proceed to address initially the second problem in an attempt to expose and clarify some ambiguities that will facilitate the understanding of the descriptions of experimental results that follow while addressing the biological problem —the real one. Let us be clear and state that the intention is not to describe a detailed neural model but rather to examine the implications of certain perspectives about nervous system dynamics that may help unravel the necessary and sufficient conditions for cognition and consciousness to arise. Therefore, the paper is organised as follows. Section 2 describes problems associated with the interpretation of thermodynamic and information theory concepts to neuroscience and other biological phenomena. Section 3 proceeds with the description of experimental results to address the biological problem abovementioned. Section 4 and Section 5 are devoted to addressing some characteristics of the experimental results that may be somewhat ambiguous; specifically, a change in perspective from entropy results to energy gradients is described in section 5. Section 6 introduces a hypothesis that considers pathological states in physiology as reduced fluctuations in energy distribution. The paper concludes with final thoughts in section 7.

Because this paper is intended for a wide audience, some details (that those specialised in neuroscience most likely know) are explained briefly in footnotes and in the text.

2. Beware the ambiguity of thermodynamic concepts

Since thermodynamics characterises systems made up by enormous number of elements, it may seem well suited to address the study of the collective activity among brain cell ensembles. And indeed, it has been used in neuroscience if only because, paraphrasing Goldenfeld and Woese who said that “If we are to understand biology we need a statistical mechanics of genes” (Goldenfeld and Woese, 2011), one can claim that “if we are to understand the nervous system we need a statistical mechanics of nerve cell networks”. Hence, there have been efforts to characterise what can be called statistical neurodynamics, as in the early statistical neuro-dynamics of Amari et al. (1977) or the probabilistic framework of Buice and Cowan (2009), and others (Kirkaldy, 1965). These approaches are reasonable because it is the global pattern of the many cellular connections that is important and not so much the individual cell to cell connectivity, although it is obvious that the latter is required to have the former! Of importance for the study of nervous systems, which are systems that process information, is the connection of thermodynamics and information theory. Indeed, information theory is widely use in neuroscience, but the relation of thermodynamics and information theory is less well known to the neuroscience and biological communities; however, addressing this connection is beyond the scope of this paper. Let us briefly comment on the interpretations and misinterpretations of some of these concepts.

2.1. The elusive entropy

One concept widely applied in neuroscience is entropy. Entropic measures have been applied to the nervous system in many shapes and forms. Most of the measures of entropy used in neuroscience actually come from information theory, like Shannon entropy. So, from the Shannon entropy to spectral entropy, several measures of entropy have been applied to an assorted set of variables such as neuronal action potentials and functional magnetic resonance imaging data, with names like permutation entropy, wavelet entropy, von Newmann entropy, fuzzy entropy, differential entropy, relative entropy, multiscale entropy etc. (because this is not a review, we will not examine all those applications but there is a wide literature, e.g. Vakkur etal., 2004; Kannathal et al., 2005; Quian Quiroga et al., 2001; Saxe et al., 2018; Carhart-Harris et al., 2014).

Considering the almost ethereal nature of entropy (didn't von Neumann advise Shannon to call his measure entropy because “nobody knows what entropy really is?") these various applications to a number of observables (ions, neuronal connections, neurophysiological signals, etc.) pose the risk of confusion, of misleading the interpretations to understand nervous system function, and thus make it difficult the communication among neuroscientists. Hence, caution should be taken when comparing results from diverse applications of the concepts of entropy. And even when it is a similar type of entropy (say, Shannon entropy) that is applied to different variables —ions diffusing through membranes, network connectivity etc.— the results may not be comparable at all, each one will stand on its own and will have a specific interpretation. An example is a recent study where the authors used two types of entropy (fuzzy and distribution entropy) and found that one was reduced and the other increased in epileptic activity (Li et al., 2018). The ideal situation would be if a common essence could be extracted, distilled, from very different applications to a variety of observables. In the same manner we cannot use a man-made metric like weight measured by a balance to directly infer the volume occupied by that weight (ten kilograms of tomatoes occupy more volume than the same weight of iron), care should be exercised when directly inferring and comparing interpretations from entropy applied to a wide variety of observables.

The ambiguity of entropy has been known for a long time and expounded in several texts, e.g. Ottinger 2005. In fact, the controversy about entropy being subjective (epistemic) or objective (physical) has been present almost since the beginning of statistical mechanics. The term entropy had a clear physical connotation only when thermodynamics first appeared, in the notion proposed by Rudolf Clausius who coined the term, but the advent of statistical mechanics resulted in no little fuss about this concept, for instance E. T. Jaynes claiming that entropy is a subjective term quantifying lack of knowledge (Jaynes, 1983). And complications arise, as we will describe below, because it is the entropy notion from statistical mechanics and information theory that is being used in neuroscience. The classical thermodynamic entropy is not ambiguous: if you are equipped with a calorimeter and a thermometer you can measure the heat involved in a chemical reaction and the temperature, from where the thermodynamic entropy can be obtained as the heat divided by the temperature; simple and clear. But working with the entropy in the Boltzmann, Gibbs or Shannon sense is trickier, although in principle all these apparently widely diverse entropy notions are very closely related, as can be inspected in some textbooks, e.g. Le Bellac et al., 2004.

One pedagogical example that illustrates the relative nature of entropy (in the information theory sense) can be found in Ottinger 2005, where the case of the entropy of a messy room is nicely described. Very briefly (interested readers can consult the original explanation in pages 12-13 of that reference), the author explains how a children’s room is in an apparent disorganised state due to a great number of toys spread over the floor. The parents consider such a room a mess, and assign a high entropy because they apply entropy to the observable “toy density in the room”, whereas the children consider the toys well arranged for the purposes of their games and thus would assign a low entropy value, using the (for them) relevant variables “position and orientation” of the toys. As the author aptly asserts, entropy depends on the observable, or variable, of interest, and the room per se has no entropy, or at least none until one variable is chosen and a certain entropy measure is applied to it. Same can be said about a living organism, or about the brain: brains have no entropy until a variable is used. Later in section 3 some observations related to the entropy applied to the configuration of neural connections will be detailed, which revealed lower entropy during epileptic seizures as compared with normal conscious awareness; but if instead of the arrangements of neural connections another variable had been used, say the ions moving in and out of neurons, then the result would have been different, perhaps finding higher entropy during seizures due to the high neural activity caused by the seizure. It is fair to note that some scholars think that entropy is an objective quantity, on the same footing as energy or any other extensive quantities (Bennett, 1982; Zurek, 1989).

In fact it is an advantage there are several types of entropic measures, because while the thermodynamic entropy is difficult to estimate in living systems as it requires measures of heat (Martyushev, 2013), others are easier to obtain, like the Shannon entropy. In this case, an observable can be chosen to compute the probability of events and thus the information entropy can be calculated; for instance, in section 3.1 the observable consists of the combinations of connectivity among brain networks.

One thing that should be made clear is that entropy is not always a measure of disorder or chaos as commonly taught (Lambert, 2002) —even though in some specific contexts entropy is reflecting disorder—, indeed entropy should not be used to estimate the degree of disorder in self-organising systems (Martyushev, 2013). Entropy represents energy distribution. The issue of considering high entropy associated with disorder has its roots in some words used by scientists of the stature of Boltzmann and Gibbs, that became popularised by several authors and entered the collective culture to such an extent that this concept of entropy as a measure of order is taught everywhere to students. This is not the text to delve into this matter, suffice to say that already in the mid twentieth century, scholars warned against the perils of associating entropy with order/disorder, for instance in the words of E. T. Jaynes: “statements [..] that entropy measures randomness are [...] totally meaningless and present a serious barrier to any real understanding” (Jaynes, 1965); see as well comments on this issue of the association of disorder with entropy in Styer 2000, Lambert 2002, and Martyushev and Seleznev 2006. However, it is true that in some circumstances in classical physics the notion of disorder associated to entropy is a useful one, such as the cases when there is a clear connection between entropy and symmetry. For example, when a crystal melts its entropy increases whereas at the molecular level there is less symmetry in the crystal than in the liquid (crystals are normally symmetric only in certain directions). But this connection may be lost in more complicated situations, especially those of interest in this text, the complex biological systems.

One, perhaps psychological, reason why the growth of entropy is commonly associated with disorder is because an increase in entropy corresponds to an increased number of possibilities to realize the state of a system, so a macroscopic state with large entropy means there are many microscopic states compatible with that macrostate, and this is perceived by us as disorder. In section 3 we will describe results that indicate that the macroscopic brain state of neuronal network synchronization during conscious awareness is associated with many more microscopic states (of synchrony, or configurations of neural connections) than unconscious brain states like coma or epileptic seizures, and in this sense the patterns of neural connections during normal wakefulness can be associated with more disorder than the simple patterns of synchronization found during seizures, just because every time we sample the macrostate of “conscious synchrony patterns” the likelihood of finding the same pattern is low, but the “unconscious synchrony patterns” during coma or seizures are just a few so in our perception we attribute this macrostate as more “ordered” (see below for more detailed explanations on these results). To make matters worse, as described in the next section, the notions of order/disorder, organization, and randomness are ambiguous concepts that depend on perspective.

The preceding paragraphs are not meant to criticise the use of entropy in biology or neuroscience in particular, rather to point out that with several entropies and a great number of observables to which any of these entropies can be applied, the situation generates confusion; we emphasise again that it is fine that a study that uses one type of entropy applied to a particular variable reaches certain conclusions, but always having in mind that applied to another variable those conclusions may differ. The difficulty with entropy is a reflection of the difficulties afflicting almost all thermodynamic macroscopic variables, their interpretation oscillating between a subjective, or epistemic, and an objective, physical one (Shalizi and Moore, 2003). But this difficulty is not present only in the realm of thermodynamics; beyond thermodynamics, other concepts such as complexity and information are essentially subjective that can be defined by reference to observers. The notion of information does not escape this trouble either, and it is clear only in specific senses, such as when computing the Shannon information, but in the moment generalizations are attempted, other complicating concepts like meaning come into play and the issue of defining information in a global sense is far from settled (Capurro, 2009) —e.g., see the special issue of Entropy devoted to "Information and Self-Organization" for discussions on this matter (Haken and Portugali, 2017). A way out of these conundrums could be putting the classical thermodynamic entropy in connection with the Shannon entropy (and related entropies derived from information theory) through the Landauer limit, which makes entropy stand in a more solid, objective ground, but this is not the time to enter these technicalities other than the brief comment presented in section 5, as this theme will be a subject of a future, very technical, paper which we are developing.

Having thus considered the debate about the relative nature of entropy, one proposal we put forward is that the results of entropic measures are best understood from the perspective of energy rather than the more elusive entropy. The main advantage using the energy perspective is that it is less ambiguous than the possible arbitrariness of the entropic viewpoint, as explained in section 5.

2.2. The ambiguous order

Whereas many biological phenomena seem very regular, close inspection reveal irregularity, or variability, at all levels. Fluctuations in biological recordings are apparent from cardiac tissue to the brain; Figure 1 pictorially showed the association of fluctuations in neuronal synchrony with brain activity. It is therefore not surprising that the notion of “noise” in biological recordings, and particularly the nervous system, is an emergent research theme that is captivating great attention. But here what interests us are the accompanying notions of order/disorder in biological activity. In fact, a workshop on disorder in biology has recently taken place (Université Paris Saclay), illustrating the importance that biologists are giving to the question of how the apparent disorder affects biological processes.

Order, disorder and randomness, all close relatives of entropy, are ambiguous concepts too (Landsman, 2020; Lambert, 2002; Annila and Baverstock, 2016); as one can read in a recent publication, “Order, or disorder, are not well-defined concepts” (Struchtrup, 2020), which echoes the older statement by the mathematician Hans Freudenthal in 1969: “It may be taken for granted that any attempt at defining disorder in a formal way will lead to a contradiction. This does not mean that the notion of disorder is contradictory. It is so, however, as soon as I try to formalize it” (Terwijn, 2016). The relativity of this notion applied to studying self-organization was known long ago, to wit: “According to the thermodynamic criteria, any biological system is ordered no more than a lump of rock of the same weight” (Blumenfeld, 1981). That order/disorder and organization are ambiguous concepts which depend on perspective was exemplified in the previously mentioned messy room case, where children and parents have opposite views about the order of the toys within that room. It is tempting to paraphrase Einstein when he said that “Time and space are modes by which we think and not conditions in which we live”, and transform it into “Order and disorder are modes by which we think and not conditions in which we live”. It has been said too that “order and randomness are mere components in an ongoing process” (Crutchfield, 1994), and the process, we venture, is towards widespread distribution of energy —nothing more than the 2nd principle, the tendency towards more probable states/configurations.

As occurs in the case of entropy aforementioned, the term organization covers a multiplicity of meanings as it is used in various disciplines, particularly biology, physics, and chemistry. But it was J. Monod who probably hit the nail on the head when he declared that a crystal is more ordered than a living being, but of a different type of order. It is the same with the concept of equilibrium we will see in section 2.3, it is all a matter of different order and equilibria. The diversity of organisms offers examples of what “good”, or adaptive, organization is. As stated above, organization depends on context. Organization is a relative term related to the specific conditions and context where the phenomenon, or system, of interest takes place. In a similar fashion as randomness is a relative term that cannot be properly defined —as A. A. Tsonis reminded us: “defining true randomness has never been resolved and may never be to everybody’s satisfaction” (Tsonis, 2008), and for a quick demonstration of the relativity of this concept please see footnote 1 (Quick demonstration of the relativity of randomness. The number e (or equally ℼ) may be random or deterministic depending on how it is “measured”. Statistical tests applied to the sequence of digits will indicate randomness. But we know how to generate those digits using a formula, in case of e one formula is $e=\underset{\mathrm{n}\to \infty }{\lim }{\left(1+\frac{1}{\mathrm{n}}\right)}^{\mathrm{n}}$.

hence it is not random but totally determined by the mathematical expression. So, is e random or deterministic? It depends on the viewpoint. As well, a random sequence of digits has regularities, in that about 50% will be odd and the rest even numbers, so there are even laws to be found in randomness.)— perhaps the notions of order/disorder and organization are not possible to define in a global manner that satisfies every context. Intuitively we all know what organization means, however when we start to think deeply about how we determine something is organised or disorganised, we see that, just like beauty is in the eye of the beholder, organization too, recall W. R. Ashby words mentioned in section 1 where he very appropriately indicated that organization is relative to the context, to some given environment (Ashby, 1962). An illustration of this point is animal mimetism, when they perform mimicry of their environment in order to enhance their survival by looking similar to some environmental elements; these are examples of “well-organised” animals for their specific environment, but if they are placed in a different environment that organization is useless to them.

Same occurs with brain activity and nervous systems in general: the organization of the neural activity depends on context. As an example, the worm nervous system needs highly periodic, “organised” activity (mostly within its central pattern generators, the CPGs, that are primordial neural circuits which produce neural rhythms for motor behaviours without need of commands from higher centres) with little variability in order to crawl around, but a mammal needs high variability in the neuronal connections to process a myriad of sensorimotor transformations, many more than worms need to survive. Each situation/context will determine what is “good” or “bad” organization of neuronal connectivity. So, if one is sleeping, especially in the slow wave sleep (SWS) periods, the context does not demand sensory processing hence the brain activity looks more “organised”, more synchronous and uniform than during wakefulness when a large variety of network connections are needed to process the many sensorimotor transformations leading to adaptive behaviours.

And naturally, as an extension of organization, the concept of self-organization arose with impetus in the neurosciences too. Incidentally, Immanuel Kant already mentioned self-organization in his Critique of Judgment of 1790, so the notion has had its time to evolve… The main problem with biological systems is that these are open systems that are continuously exchanging energy and matter, thus the difficulty distinguishing from externally imposed organization or autonomous, self-organization: “Distinguishing self-organization from external organization in systems receiving structured input is tricky” (Shalizi et al., 2004). Of course, one can always assume that the external influences are not too specific, e.g. the temperature gradient is fundamental to develop the Rayleigh-Bénard instability (described below in section 2.1.1) although nothing in that gradient “forces” the hexagonal arrangement of the fluid molecules, this depending on a combination of factors including the properties of the molecules forming the fluid. Nevertheless, the interest has grown so much that a huge number of studies have addressed the related notions of criticality and self-organization in nervous systems. We will not go into the debate as to whether brains are critical (Gros, 2021), subcritical (Priesemann et al., 2014) or quasicritical (Fosque et al., 2010), suffice to say that the combination of driving external inputs with the recurrent, ongoing neural activity present all the time in brain circuitries leads to non-trivial activity that sometimes may be critical, other times not; therefore, as C. Gros suggests, perhaps it would be more fitting to use the term “self-regulation” instead of self-organization in some cases (Gros, 2021), as this notion entails the need of neural networks to regulate their activity as external inputs continuously arrive —a sort of combination of the forcing due to external influences and the intrinsic neural activity.

One aspect to note is that for physicists and chemists in general, organization is directly proportional to predictability, such that the organization, or order, normally denotes the complexity of prediction, so perhaps it could be less vague to equate organization with predictability (see for example Shalizi et al., 2004, where they quantify organization using optimal predictors). Incidentally, randomness too has been linked with (un)predictability (Eagle, 2005). In this sense, a direct link with dynamical system theory, e.g. chaotic dynamics, is established, with the benefit that instead of using relatively vague terms the discourse uses now aspects that are more feasible to be calculated and are less relative to the particular situations: talking about order or disorder in one system is, as we have seen, ambiguous, but talking about the system displaying, say, chaotic dynamics is better understood in general terms. Nevertheless, these are matters for discussion.

2.2.1. The deceptive organization: From microscopic disorder to macroscopic order and vice versa

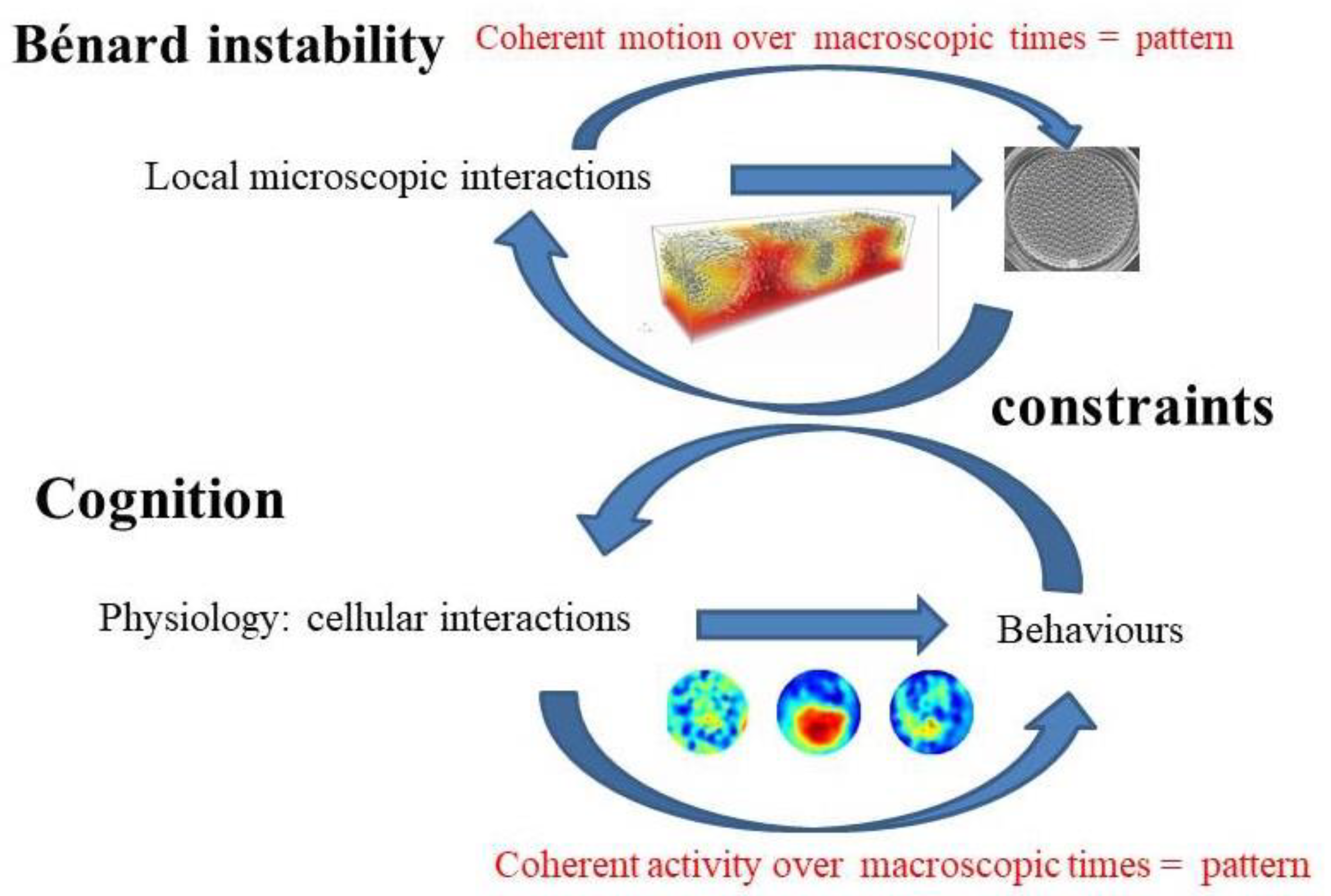
Lurking in the notions of order and (self-) organization are the local and global scales. In natural phenomena units exchange information (matter and energy) at local scales, giving rise to global patterns of organization. What at the microscopic, local scale may be “disorganised”, it becomes “organised” at the macroscopic, or global, scale. A typical example is the Rayleigh-Bénard instability —or convection, a paradigm to explain pattern formation, emergent properties and dynamical bifurcations. Most readers are probably familiar with this phenomenon, so we will only mention the very basics: the coherent motion of molecules emerges through small convective fluctuations that develop in the heated fluid; the molecules start moving randomly due to the heat but some of the fluctuations in the motion of many molecules become amplified and organised into a coherent motion of the majority of molecules (a dynamical bifurcation has taken place), originating a flow pattern that normally consists of hexagonal cells on the surface of the fluid. So from an apparent microscopic chaos results a macroscopic organised pattern, in other words, global regularity stems from local mess. This phenomenon can be studied from the synergetics perspective using the slaving principle invoking order and control parameters (Haken, 2006), but these are not matters for the current text where we focus on the basic features.

It can thus be stated that the striking final hexagonal pattern (the specific geometric pattern may depend on the liquid properties though) emerges from the dynamical repertoire of the fluid that is constrained by the range of microscopic molecular interactions and environmental perturbations, all of which determine the final dynamical evolution of the spatial arrangement. The environmental perturbations include the heat that sets up the temperature gradient between the top and bottom of the fluid layer, and the gravity which causes the up and down motions of myriad of molecules, whereas internal features include the physicochemical properties of the interacting molecules. The previous sentence can be translated to neuroscience, saying that the dynamical repertoire of brain networks is constrained by the range of neuronal interactions and environmental perturbations, all of which determine the final dynamical evolution of the nervous system that results in behaviours. Indeed in the case of brains we find too a multitude of internal and external factors —ion gradients, electrochemical interactions, hormonal influences, sensory stimuli and so on— that determine the final organised pattern of neural activity. The conceptual analogy between these two apparently distinct systems, liquids and brains, is graphically displayed in Figure 2.

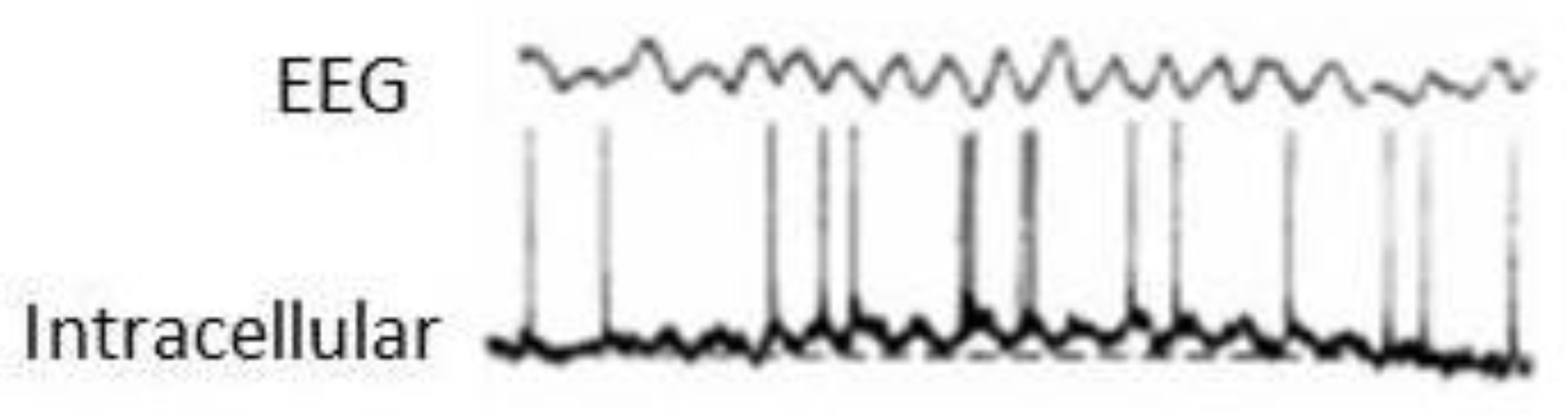
The term ‘macroscopic times’ appears in Figure 2 to emphasise that the microscopic or local level has distinct spatio-temporal scales and the emergent result (the hexagonal pattern in the fluid and the behaviour in humans) is observed for an extended, macroscopic scale in terms of duration and space. Depending on what constraints the environment imposes on the liquid or on the brain, one or another pattern (geometric arrangement of molecules or a determined behaviour) will emerge. A neural illustration of this local-global phenomenon is the cellular activity during slow wave sleep (SWS); if the electrophysiological recordings are taken in individual neurons, some cells will display a rhythmic pattern of bursting (bursts of action potentials, the spikes used by neurons to establish functional connection) with apparently random spikes dispersed among the bursts; but if the recordings are sampling the collective activity of thousands of cells, like in case of local field potentials or electroencephalograms (EEGs), then the activity will be nicely regular and rhythmic, where the typical slow waves between 0.5 and 1 Hz will be seen. Another similar example is found during theta wave activity, presented in Figure 3.

Now, the EEG recording shown in Figure 3 is nice and regular, but it is not always so. In fact, recordings taken during wakefulness are almost always seemingly “random”, noisy, and of low amplitude. If a power spectrum is calculated in these signals, the celebrated gamma activity will be found: low amplitude signals with frequencies ranging from 25 to over 100 Hz, all happening at the same time, thus the apparent randomness of the recordings. Why do we detect such messy activity? Because during wakefulness, as mentioned at the start of section 2.2,, brains need to process various sensorimotor transformations that need myriad of neuronal networks to exchange information, and from that myriad of microcircuits, when sampled at a global, collective level like the EEG does, we obtain a “chaotic” voltage time series (Perez Velazquez et al., 2019).

An example of this somewhat deceiving macroscopic perspective of neural activity is offered by the analysis of synchrony among surrogate signals. The generation of surrogate signals is commonplace in data analysis, especially in neuroscience, where random time series (surrogates) are derived from brain signals acquired with, for instance, electroencephalography —there are several manners to generate surrogates, we will not go into details now. If one computes a synchrony index, for example phase synchrony as in Mormann et al. (2000), from surrogate signals it will be found very similar to the index of the brain original signals taken during wakefulness (and with eyes open, this is important to note because on closing the eyes a prominent alpha rhythm appears in the brain cortex that will affect the values of the synchrony indices, at least in the frequencies close to the alpha waves between 8 and 12 Hz). The observation that the synchrony among normal brain signals do not differ much from that of random signals has been reported in various studies (e.g. Garcia Dominguez et al., 2005). Here we show a brief quantitative illustration: the average of the phase synchrony index in a montage of intracerebral EEG taken in a subject during normal waking consciousness was 0.399+-0.03, and that of the surrogate population was 0.394+-0.01; and in one of our close relatives, in monkey intracranial recordings the synchrony index average was 0.393+-0.02, and 0.391+-0.08 for the surrogates. But what does this mean, for brain function and cognition in general, to say that the synchronization between brain neural networks is the same as that of random signals? Is it that brain activity during normal wakefulness, at least in terms of synchronization, is equivalent to that of random activity?

Well, notwithstanding that the concept of randomness is ambiguous (recall the previous comments and footnote 1), the fact that surrogate signals provide similar synchrony as those during waking consciousness is a consequence of the signals measured, of the level of description; at the meso/macroscale level, those EEG signals (or equivalently if recording local field potentials or magnetoencephalograms) reflect the activity of very large cellular populations, and considering that the brain has to integrate and segregate numerous sensorimotor transformations simultaneously in order to adequately perceive and respond to incoming stimuli, then this combined neuronal activity at the microscale level is observed at higher levels as stochastic —the gamma waves aforementioned (in section 5 we will see that these electrophysiological recordings represent energy gradients). It does not mean a healthy brain displays random activity, rather it needs to support so many different configurations of micro-level connections that depending on the measurement it will appear as organised or as purely stochastic; if we were to follow the activity in specific microcircuits we would see organised activity, a precise arrangement of cellular activity that is needed to process information adequately, but when the recordings sample thousands of these organised microcircuits the result is a noisy, random-like time series. It is in this sense that it has been asserted that a noisy brain is a healthy brain (Protzner et al., 2010).

In sum, these are illustrations of the local and global scale of phenomena; fast time scales may be stochastic and yet an organised activity can be observed at slower and global scales, as exemplified in the abovementioned Bénard instability and brain recordings. An example of the local and global views on the complexity of brain activity will be offered in section 3.1 when discussing experimental results using the Shannon entropy and the Lempel-Ziv complexity —the former for the macroscopic scale and the latter for the microscopic— in conscious and unconscious states. Finally, to emphasise the main message of this section 2.2, when talking about the organization of nervous system activity one has to always consider and specify the context in which it occurs, because the only “bad” organization is the activity that, while being “good” for certain conditions, occurs in the wrong environment, when context does not require such activity but another; there is no absolute good or bad organization (with the exception of some pathologies, naturally).

2.3. The relative equilibrium

Later on, while discussing experimental results, some words about equilibrium in neural dynamics will appear, so let us try to clarify some points before that. As students we are taught that only death represents equilibrium, that living processes are far from equilibrium. Is this really true? Well, the body is, at the macroscopic level, very near equilibrium, it even has a name: homeostasis —constant temperature, blood pressure, etc. Death represents equilibrium too, perhaps a more “perfect” one since it happens at the micro and macro level. So we are talking about different types of equilibria, as above in section 2 we talked about different types of order in the organization of living organisms.

Particularly in the case of brains, the fact that a brain consumes ~20% of the body energy regardless of what it does, is already a hint of the stability that brain cellular networks need for proper function —and at the psychological level this stability results, among other things, in the stable sense of self we all possess in normal conditions (the extreme stability of the personal identity and its disruption in some pathologies are described in Perez Velazquez and Nenadovic, 2021). The fact is that brains need an internal “autonomous” dynamics colliding, so to speak, with arriving sensory information to generate phenomenal experience; that intrinsic brain dynamics should be relative stable, call it equilibrium or not (steady state, as will be discussed below, may be more appropriate).

And yet, the microscopic world of living bodies lives in non-equilibrium conditions: ions are maintained at different concentrations inside and outside cells, and so on —interested readers can consult several works on the non-equilibrium thermodynamics of living processes, from Prigogine’s initial efforts (Prigogine, 1961) to more recent ones (Lucia and Grisolia, 2022; Nicolis and De Decker, 2017). Therefore, is this another example of the local-global views of section 2.2? Microscopic non-equilibrium is seen as macroscopic near-equilibrium? As it happens, equilibrium is another relative, arbitrary notion that depends on context and the level of description. For starters, there are three classical opinions in statistical mechanics to identify equilibrium (Kuzemsky, 2014): the Boltzmann method (equilibrium as the most probable state), the Darwin-Fowler method (equilibrium as the average state) and the Gibbs ensemble method (postulating the canonical distribution).

As well, equilibrium is related to the observation time. Taking your body temperature or heart rate (at rest) every 10 minutes for a couple of hours will result in constant values, but now taking them twice a day every 12 hours, say at 3 in the morning and at 15 hours, larger variation than in the previous sampling in small time intervals will be found. Same impression you would have if the brain activity was recorded during wakefulness and later on during deep sleep at night, because during the day the recordings are those gamma waves of small amplitude whereas at night, particularly during SWS, your brain will show the slow, rhythmic high amplitude waves, little in common with the previous recordings of daytime; but taking the brain recordings at small intervals of, say, 10 minutes during daytime hours, all the neurophysiological traces recorded will look alike —that gamma activity—, hence you will think about equilibrium now. So, are we at equilibrium or not? It seems that depending on what frequency properties are measured, sometimes it will seem that the system is at equilibrium and sometimes it will not.

Not only to the observation time scale, but also equilibrium is connected to the spatial extension at which one observes the system: the atmospheric pressure at some nearby points will show constant values, hence equilibrium, now taking it at 1000 kilometres away you will most likely find a totally distinct value. Some didactic texts have devoted words to this matter of equilibrium being a relative notion (Callender, 2001); in fact H. B. Callen pointed out the circular character when attempting to define it: “In practice the criterion for equilibrium is circular. Operationally, a system is in an equilibrium state if its properties are consistently described by [equilibrium] thermodynamic theory!” (Callen, 1985).

And as it tends to occur in science, sometimes different ideas are sides (normally two!) of the same coin. For example, interpreting equilibrium as the constant values of variables, say gas pressure in a container, is translated at another, more micro, level as the gas molecules being more spread in the volume of the container (that is why the pressure is the same in any region of the container): there are more molecular microstates corresponding to the “equilibrium” macrostate, so this in accord with the notion of equilibrium as the macrostate made up of the largest number of microstates. As we will see below, this is what was found studying the configurations of brain network connections in wakefulness as opposed to unconscious states.

We have thus seen that phenomenological equilibrium is intimately tied to an observation time scale, to a spatial scale, and to the level of observation/description. It becomes then crucial, as in the case of entropy (or other measures like complexity), to be clear in each study about what notion of equilibrium is assumed and at what level the particular phenomenon is studied.

The essence of the notions of the approach to equilibrium —and perhaps the easiest manner to comprehend what this means— is to think about it as the approach to the most probable state, which normally consists of the macrostate represented by the largest number of microstates, one of the aforesaid concepts of equilibrium: “the physically realized states that nature chooses tend to correspond to the ones that maximize the number of possible particle rearrangements” (Shinbrot and Muzzio, 2001). This is also what the famous increase in entropy observed in natural phenomena represents, the tendency of natural phenomena to approach the most probable state. This state will be constrained by the environment, the context. As we will comment in sections 3.1 and 4, the brain will try to approach its most probable state, depending on the context. Perchance, too, rather than talking about this relative notion of equilibrium, it would be clearer to talk about steady states. Steady states need not be at thermodynamic equilibrium, for example the concentration of sodium ions in the intracellular and extracellular compartments is kept almost constant, so this steady state derives from a situation that is not a classical equilibrium where the sodium concentration should be equal in both compartments. Or, in dynamical system theory jargon, these steady states could be the attractors in a certain state space. Most of what we see in nature are transitions between attractors, so it is the approach to “equilibrium” that we observe, equilibrium that is only reached in very specific circumstances, such as in a test tube in a laboratory experiment studying a chemical reaction. The dynamical system perspective also considers the transitions as possible dynamical bifurcations.

These considerations about equilibrium will be needed in sections 3.1 and 4, where experimental results done on brain signals will be described and hopefully the matter with equilibrium, or the absence of, will be better understood.

3. A global perspective on fundamental characteristics of the brain networks’ collective activity that support cognition and consciousness

The previous sections attempted to clarify certain aspects that will be mentioned in the following paragraphs describing experimental results that may shed light in the search for the necessary and sufficient conditions for cognition and consciousness to arise. Therefore we now start dealing with the biological problem mentioned in the introduction, the fundamental features of the organization in the interactions among brain cells that give rise to conscious awareness and thus support the adaptability of the organism. We are particularly interested in studies that have investigated the coordinated activity of the collective neuronal ensembles, that is, the meso/macroscale, and will therefore discuss a few of those results that may shed light on this issue.

In the previous section it was pointed out the fact that brain accounts for 20% of the body's energy use regardless of the state, such that heavy mental effort adds only a tiny bit to that. It is not only the energy used, but also that the numbers of synaptic contacts devoted to process incoming external sensory inputs are much lower than those of the total number of synapses; a classical illustration is the visual system (Sillito and Jones, 2002). Hence it seems that brains are more concerned with themselves than with the external world. It is today recognised that brain functions are mostly intrinsic, its dynamics preparing it to collide with the information coming from the outside world and process it accordingly for the survival of the organism.

Let us see whether these observations can serve as a starting point in a line of reasoning. The almost constant energy consumption indicates that a sustained steady state of activity has to be maintained, to provide enough stability in brain cellular dynamics (we use ‘steady state’ rather than ‘equilibrium’ after the considerations of section 2.3). How can self-sustained activity be attained? The answer was found in the research for the origin of life; namely, the idea of catalytic closure was proposed, when chemicals started to autocatalyze themselves forming a closed web of chemical reactions (Kauffman, 1993). This closure resulted in self-sustaining networks of chemical reactions that create and are catalysed by components of the system itself. Going from self-sustaining biochemistry to self-sustaining neural activity may not be a great leap, in fact the idea of closure in nervous systems has been proposed (chapter 8 in von Foerster, 2003), and, as well, this notion is conceptually related to Maturana’s and Varela’s autopoiesis (Maturana and Varela, 1972). More specifically, instead of a closed web of chemical reactions we consider a closed web of connections among cell networks where one can reach any network in the brain starting from any other (Perez Velazquez, 2020) —it is known that in the brain, basically everything is connected to everything, directly or indirectly, due in part to the very abundant recurrent circuitries (Yuste, 2018). All nervous systems and brains in particular can be considered as a functionally closed, self-sustained system of cellular networks (note that this closure does not mean a closed system, the system is open, but presents closure).

Now, the central pattern generators, the CPGs mentioned in section 2.2, exhibit this type of closure but these primitive neural circuits do not have the complexity to endow that nervous system with certain “high order” features of consciousness; for sure “low order” features, so to speak, are achieved by animals whose nervous systems consist mostly of CPGs, in that they can sense and react to environmental inputs —in these words we have used the “definition” of consciousness as the enumeration of characteristics, as proposed in some works (Perez Velazquez, 2020). Let us not forget that the activity in that system has certain features that will depend on the context. Thus, those CPGs are fine for invertebrates to behave in their world, and for us too, as we use them for maintaining stable rhythms needed, for example, in respiration. But higher features of consciousness, like self-awareness and so on, require more complexity, that is, larger number of neurons with various intrinsic neurophysiological properties and extensive and varied anatomical connectivity. This anatomical connectivity will result in the so-called functional (and effective) connectivity between neural networks, that is, temporal relations between neural activity, for which, obviously, neuronal activity is needed; or in other words, a supply of energy is necessary.

Hence we have a necessary condition: neural activity, or its equivalent energy supply; but this is not sufficient. Quoting Shulman and colleagues: “high brain activity is not consciousness, rather it is a brain property that provides necessary, but not sufficient support of the conscious state” (Shulman et al., 2009). The activity needs certain coordination, it has to be somehow organised. Whereas the neurobiophysical details of that coordinated activity may be too complicated, perhaps some basic principles can be envisaged. It was mentioned in the introduction that several cognitive theories posit the perspective that consciousness relies on large-scale neuronal communication. A common theme in some of these theories is the proposal of a widespread distribution of information (that is, neural activity). For example, the global workspace theory (Baars, 1993), the information integrated theory (Tononi, 2004), the dynamic core hypothesis (Tononi and Edelman, 1998), and the metastability of brain states framework (Tognoli and Kelso, 2014) all have as an underlying idea the need for a substantial number of brain microstates —consciousness viewed as an integrated dynamic process capable of achieving a large number of configurations of neural network connections— in order to integrate information, to broadly broadcast activity to various brain regions and to avoid becoming trapped in one stable activity pattern. Is there experimental evidence supporting these claims? We will discuss some data in the following section.

3.1. Experimental evidence for the tendency to maximise configurations of neuronal connections

Let us consider a few studies that have indicated that consciousness is associated with high number of configurations of connectivity patterns among brain areas. We will focus on studies done at the meso/macroscale. The reason to emphasise the cellular collective dynamics to understand the integrative functions of nervous systems is exemplified in the words of the neurologist and polymath Oliver Sacks: “That the brain is minutely differentiated is clear: there are hundreds of tiny areas crucial for every aspect of perception and behavior... The miracle is how they all cooperate, are integrated together, in the creation of the world. This, indeed, is the problem, the ultimate question, in neuroscience..."(Sacks, 2012). It is therefore important to explore at a relatively high level of description the cooperation among brain cellular ensembles, for it is known that each neuron's activity is meaningful only with respect to other cells' actions; the foundation of neural information processing lies in the interaction between cells, and this is the reason why so many studies are devoted to the assessment of the patterns of neuronal organized activity using metrics like synchrony, coherence, correlations and similar methods.

Computational and theoretical studies endorse the main message of those theories aforementioned, indicating that the variability in the patterns of neural organised activity arising from the maximization of fluctuations in synchrony is fundamental for a healthy brain (Vuksanovic and Hovel, 2015; Garrett et al., 2013). Experimental studies have observed disrupted neural connectivity, reduced efficiency, and a more constrained repertoire of neurodynamic states during unconsciousness, therefore making difficult the integration of the information needed to support conscious awareness (reviewed in Mashour and Hudetz, 2018). More specifically, using resting state fMRI, it was found that at the optimal level of neural activation the diversity of state configurations was maximized in the conscious state, being reduced with states of diminished consciousness (Hudetz et al., 2014). This study found as well that during “equilibrium”, the diversity of large-scale brain states was maximum, compatible with maximum information capacity which is a presumed condition of consciousness, and the next study we will present employing the Shannon information entropy directly supports this idea.

Results derived from the estimation of the entropy associated with the number of possible configurations of pairwise brain network connectivity indicated that brain macrostates associated with conscious awareness possess more microstates (in terms of configurations of network connections) and thus higher entropy than unconscious states (Guevara et al, 2016; Mateos et al, 2017). These studies used invasive and non-invasive electrophysiological brain recordings in different states of consciousness (sleep, wakefulness, seizures and coma) and the phase synchrony between pairs of signals was evaluated. A threshold value of the synchronization index was used to determine when two signals were “connected" (see footnote 2 (The issue of whether measuring correlations between signals (as phase synchrony, coherence, cross-correlations etc.) reflect real connectivity is a matter that has been treated in numerous texts; suffice to say here that phase synchrony can be taken as an indication of connections because when two brain networks have synchronous activity this indicates that they are probably involved in processing the same input or performing same sensorimotor action. As this is not a review we will not plunge into the very extensive literature on anatomical and functional connectivity concepts and methods of evaluation.) for a brief comment on the notion of connection in this type of studies using brain recordings). Each state of consciousness studied was considered a macrostate of brain synchronization, composed of a number of microstates which are the several possible configurations of the connected signals. This notion of brain macrostate is, along the lines of the relativity of thermodynamic concepts, somewhat subjective: it depends on the observables one can measure. On this topic of the ambiguity about defining macrostates in general, please see Shalizi and Moore, 2003.

We clarify again that the states talked about here are the microstates of synchronised (or connected) brain regions that all together form the whole state, the macrostate, and that there is no assumption that a macrostate is associated with a particular mental state unless in simple cases like all-to-all connectivity where there is only one microstate forming the macrostate, which could represent a generalised epileptic seizure where almost all neural nets are synchronized. While no link is made with the psychological level of mental states, it is conceivable that the global mental macrostate during normal wakefulness corresponds to the combination of all that sensorimotor processing carried out by the different microstates. A limitation of these studies abovementioned is that pairwise interactions of signals were used, and the relevance of other high-order interactions has been demonstrated in theoretical neuroscience. Nonetheless, these results suggest, along the line of the previous comments, that it is not about how much energy is in the brain, but how that energy is distributed. The energy talked about here is the electrochemical energy neurons use to communicate: during conscious awareness the brain has the largest number of configurations of connected brain networks, or, from the energy perspective, more routes to disperse the electrochemical energy, and thus many more microstates to support cognition. In contrast, during unconscious states like seizures, coma or sleep, there are too many strongly connected neural networks resulting in fewer configurations, fewer microstates, fewer number of energy gradients (see section 5 on the energy gradient viewpoint).

Therefore we have a hint about a, perhaps, sufficient condition for cognition that we can add to the aforementioned necessary condition, it is how the energy is organized: the more ways brain networks can communicate, the better for the organism (especially vertebrates living in a complex world) processing a myriad of sensorimotor transformations. These results using synchrony in electrophysiological signals complement those mentioned above of Hudetz et al. (2014) that used signals of functional imaging, which are not as fast and represent an indirect measure of cellular activity: first, the diversity of state configurations was maximized in the conscious state; and second, their idea that the multiplicity of large-scale brain states is compatible with maximum information capacity is supported by the electrophysiological studies because the Shannon information entropy was computed from the number of configurations of connections between brain networks, and wakeful states were characterized by the greatest number of possible configurations, thus representing highest entropy values; therefore, the information content is larger in the macrostate associated to conscious states.

These studies furnish as well another example of the global and local perspectives in the apparent “complexity” of brain activity, recall the global and local views discussed in section 2.2.1. While the unconscious state of sleep during the SWS periods was found to be characterised by more global synchrony and lower number of configurations of connections than during wakefulness —that is, lower Shannon entropy—, inspection of the microscopic nature (fluctuations, or variability) of the configurations of connections using the joint Lempel-Ziv complexity (JLZC) revealed a complexity as high as during wakeful states (Mateos et al, 2017). In brief, the JLZC is a complexity measure that was used to evaluate the fluctuations in the connectivity pattern of the entire combination of networks (or, more precisely, the recorded signals) in very short time windows on the order of milliseconds, hence this represents a view at the local scale whereas the computation of the Shannon entropy represented the global, extended scale in time and space (because the whole set of signals were used here, this number depending on the electrophysiological montage used, such that magnetoencephalograms had about 144 sensors whereas electroencephalograms had fewer). That the fluctuations in connectivity patterns given by the JLZC did not show a decreased complexity during SWS —although it did show a decrease in pathological unconscious states like seizures and coma— is not paradoxical if we consider that substantial brain activity has been demonstrated using a variety of methods not only during rapid eye movement (REM) but also during non-REM sleep; in fact, electrophysiological recordings of oscillatory activity during non-REM phases were more complex than previously thought, and during SWS a re-organization of brain networks into localised modules was found (Spoormaker et al., 2012). It is known today that during sleep stages there are cognitive processes going on, e.g., brain activity during sleep is thought to be necessary for memory consolidation (Sejnowski and Destexhe, 2000). And there is also unconscious perception during sleep, this being the reason why the smallest cry of a baby awakens her mother while another loud noise (her partner’s snoring) not; this processing during sleep is unconscious because while the brain continues to receive sensory inputs from the outside world, the activations of neural networks do not extend beyond the primary sensory areas, as opposed to the awake state when the activity extends beyond these areas to association areas like the frontal and parietal cortex and therefore the sensory inputs enter awareness. In neurophysical terms, viewed from the Shannon entropy perspective, this entropy was reduced in sleep because the extension of the neural activations were not as varied as during wakefulness and thus generated fewer combinations of connections, although at the microscopic level there is still enough localised activity to be revealed using methods like the JLZC. To finish up this digression on sleep, let us listen again to W. Ross Ashby asking himself whether “Is it not good that a brain should have its parts in rich functional connection? I say, no —not in general; only when the environment is itself richly connected” (Ashby, 1962). These words emphasise again what has been mentioned many times in this text, that context dictates what is a “good”, or adaptive, behaviour and therefore brain activity: during sleep we do not perceive our world as “richly connected”, so there is no need for that “rich functional neural connectivity”.

Other works have observed too a decreased entropy associated with unconscious states, albeit the entropy in these studies was not applied to the number of configurations of connections as those discussed above. For instance, the entropy production evaluated from electrocorticography done in monkeys was lower in states of diminished awareness —sleep and anaesthesia (Perl et al., 2021). The entropy used in this study was calculated by associating to each brain state a matrix containing the probability of transition from one to another state, for which each recording was described as a sequence of states visited over time. Entropy production applied to synchrony measures also showed lower values during the unconscious states of coma and seizures (Perez Velazquez et al., 2019). Several other entropic measures have been used in various studies applied to time series of the neural recordings (e.g. Mammone, 2015). We will not review them as this is not a comprehensive review (there are several reviews that readers may consult, e.g. Keshmiri, 2020), but only comment that two of those entropies many times used, sample entropy and permutation entropy, measure the predictability of time series (the latter more concerned with the temporal ordering structure of the series), which in the end all reflect the variability in neural network connections from where the brain signals are recorded. This is so because the neurophysiological recordings used in these studies reflect the collective activity of many neurons, that is, the synaptic activity, in other words neuronal connections (for those not experienced with electroencephalography we will say that these recordings reflect mostly synaptic potentials due to the longer duration of these changes in neuronal voltage, whereas action potentials, or neuronal spikes, are very brief lasting only about 1-3 milliseconds and are not picked up as easily as the synaptic potentials).

Summing up, there seems to be experimental evidence supporting the aforesaid proposal for the sufficient condition for cognition (at least the high-level) to emerge, namely the multiplicity of configurations in which neural networks can communicate, or exchange information. In simple words: the more ways brain networks can communicate, the more “aware” an entity is.

4. A change of perspective: equilibrium as steady state

Let us recapitulate and pose a question. After all what was discussed in the previous section, was it found that there is more entropy, less order, in the brain during conscious awareness as opposed to unconsciousness? The answer is given by considering the arguments of section 2. Recall that in reality there is no such a thing as “brain entropy” per se (section 2.1). What those studies have found is that the neural degrees of freedom associated with the configurations of the connectivity among brain networks decrease in unconscious states, in that there are fewer (Guevara et al, 2016; Mateos et al, 2017); or that the signals in wakeful and unconscious states have different probabilities of transition between neural states in a certain configuration space (Perl et al., 2021). But we do not know what may happen to other degrees of freedom, other observables (e. g. ion concentrations) that could have been used to apply the Shannon, or another, entropy. It is just that our brains have more number of microstates (defined above in 3.1) when we are awake processing information.

So it is not a matter or more or less order, rather the key point is that the brain macrostate made up of the largest number of microstates —that is, the most probable macrostate— occurs during conscious awareness; in one of the studies this macrostate was referred to as near equilibrium (Guevara et al., 2016), because it corresponds to the aforesaid notion of equilibrium as the macrostate with largest number of microstates. But we also saw in section 2.3 how arbitrary this concept is. So, unsurprisingly, other studies have revealed the opposite, that is, nonequilibrium macroscopic brain dynamics during wakefulness (Perl et al., 2021). This was based on the idea that at equilibrium detailed balance is obeyed; specifically in that study this means that there are no net probability fluxes in the configuration space of the system, indicating reversible dynamics. And, as the authors pertinently declare: “This notion of equilibrium exists only in reference to a certain configuration space, which might reflect, in turn, a particular choice of spatiotemporal grain”, a sort of an acknowledgement of the relativity of the idea of equilibrium. So we see that depending on the perspective one takes, neurodynamics can be found near equilibrium or far from it.

In fact, we can be even more critical about one of those studies, in that instead of taking the perspective of equilibrium as the more probable macrostate we take now the viewpoint of the constancy of observables. So let us take as a variable the number of microstates that constitute every macrostate. If this number were to be evaluated in certain time intervals during the specific brain macrostates (sleep, coma, seizures, wakefulness), it would remain stable fluctuating about the mean —the difference would be that the number would be highest in the wake state. So, using this stance the, say, seizure or sleep macrostate is as much as equilibrium as the conscious state. One can see then the trouble with this type of studies, as they make a general interpretation very difficult. As repeated often in this text, only the specific interpretation is valid, therefore these studies should avoid making general statements.

Is there a way out of this conundrum, besides being very specific about what the different experiments study? One easy manner is to accept that there are many types of equilibria, like the pervious example of living homeostasis versus the death equilibrium. But perhaps the easier way out in order to facilitate the communication among scientists is to consider steady states or the concept of attractors instead of talking about equilibrium, as advised in section 2.3. As well, taking the perspective of systems (nervous system in particular) approaching the most probable steady state offers good insights to comprehend why the system is now in this or another state. Because these steady states depend on context, on the constraints imposed by the environment, and also on internal constraints derived from anatomical connectivity and so on. Thus, when the context determines a diminution of sensory inputs, such as when falling asleep, then there appears another most probable state that can be thought of as another steady state, this one determined by the specific features of thalamic and cortical neurons and their anatomical connections that cause the typical slow wave rhythms during deep sleep; this steady state lasts about 4 to 8 hours, depending on how much one likes to sleep (well, not really because there are dispersed REM and waking episodes at night).

Hence, depending on the context, the brain will try to approach its most likely state. It is the approach to steady states that we see in natural phenomena. Using the dynamical system language, transient dynamics rather than attractors is what is found in nature. In the case of the brain the constant bombardment by sensory information from the environment makes it difficult to attain a microscopic steady state, as the neural microcircuits are constantly processing information and therefore changing their connectivity, those aforesaid microstates or configurations of connections whose emergence and dissolution determines cognitive states (Mateos et al., 2017); but at the macroscopic scale, when the collective cellular activity is recorded, we find a relatively stable steady state.

5. Another change of perspective: entropy as energy distribution

We will consider now another change of view, going from entropy measures to energy dispersal. This has a similar advantage as the previously talked about using the concept of steady states instead of equilibrium, in that it may facilitate communication among scientists. From the perspective of what entropy really signifies, an index not so much of disorder but of energy distribution (recall section 2.1), the observations presented in previous sections of larger entropy found in conscious states as opposed to unconscious states, especially the entropy associated with the configurations of neuronal network connections, has a clear neurophysiological interpretation. It is not that brain activity is more disorganised or random during wakefulness, rather it means that energy (that is, cellular activity) is distributed in more ways. Voluntary motor actions or any mental event for that matter involve the coordinated activity of many neurons in many areas (organised activity after all), so for the sake of simplicity let us imagine there are 100 neuronal chains, each able to process one input of the many that an individual receives during the waking state. Each of those chains can be envisaged as an energy gradient, since electrochemical energy moves as action and synaptic potentials from the first to the last neuron in the chain: the source can be considered the first cell that emits a spike and the sink the last neuron in the chain.

Thus, establishing many energy gradients is an adequate brain organization for the adaptability of the organism to a changing environment: in our simple thought experiment of 100 neural chains, it can process 100 inputs simultaneously if we assume each chain can process one sensory input. We can further imagine this is what happens during wakeful states when many sensory inputs arrive at the brain. Now let us take one clear example of unconsciousness, or lack of responsiveness: absence seizures; in these cases the thalamus and the cortex are mutually entrained due to their recurrent anatomical connectivity, so it can be pictured as just one (very large) energy gradient from the thalamus to the cortex (and back). In our simple example assume that 50 chains are cortical and 50 thalamic, then during an absence seizure (almost) all cortical chains become entrained with the thalamic ones, forming in effect just one chain. One neuronal chain, one energy gradient, is not optimal to process a myriad of inputs, hence the unresponsive state of absence epilepsy ensues. Nervous systems work on the principle of mutual activations, where information/activity is passed from one cell network to another connected, and this activity depends on potential differences between the intracellular and extracellular compartments, differences that cause neurons to fire action potentials —the fundamental way neurons communicate. It is this spread of differences in potential that gives rise to the patterns of organised activity. Therefore, how the electrochemical energy is distributed seems to be a crucial aspect for cognition. In few words, our proposal is that cognition in organisms possessing brains, as a function of survival, depends on the capacity of neural electrochemical gradients and their distribution to capture the dynamics of fast-changing environments.

Neuronal activity in the neural chains —the energy gradients proposed here— are continuously produced and maintained in the nervous system not only by receiving external (or internal) sensory inputs but also by the self-sustained activity brought about by phenomena like recurrence (which goes under other names like re-entrance, bottom-up and top-down activity, or reverberating circuits), a most basic aspect of nervous system structure and function (Edelman and Gally, 2013) with fundamental physiological and psychological implications (Lamme and Roelfsema, 2000; Orpwood, 2017). In section 3 the notion of closure in brain cell circuitries was considered, which contributes to energy gradients being continuously maintained by self-sustaining activity afforded by that closure (Perez Velazquez, 2020). The intricate web of neuronal assemblies giving rise to a myriad of energy gradients supports information processing in the wake state, and when this wide and variable interconnectedness disappears transiently —for instance during epileptic seizures— the consequence is loss of conscious awareness.

Actually, the relation between energy and entropy (or information) has been the subject of study for many decades (Tribus and McIrvine, 1971). Indeed it was Clausius' original intention to relate energy and entropy —thermal entropy being part of the total energy content measuring how much of that energy becomes useless. Many scientists have further contributed fundamental notions on this relation, such as the Landauer's principle connecting the information theoretic notion of entropy to statistical mechanics; in simple words, this connection is given by the fact that erasing information leads to generation of heat, and therefore to an increase of entropy —we will not go into further details of Landauer’s theory which can be found in, e.g., the special issue of the journal Entropy on "The Landauer Principle: Meaning, Physical Roots and Applications" (Bormashenko, 2019).

But for our current purposes it is the aspect about energy distribution which is the fundamental aspect. The entropy applied to the distribution of cellular connectivity, neural synchronization and similar facets explained in section 3.1, are related to the characterization of cellular interactions, how the activity of cell networks is organised. But activity is after all energy, hence, the essence of the entropy applied to most of these variables detecting cellular activity is about energy distribution. The finding that the entropy associated with the number of the configurations of brain networks is largest during states of conscious awareness (Guevara Erra et al., 2016; Mateos et al., 2017) is an indication that energy is maximally distributed among those networks in these behavioural states. By energy distribution or dispersal we mean the number of ways that energy (that is, cellular activity) is distributed.

Therefore, to say that pathological cases like coma or seizures have fewer configurations of network connectivity means that there are fewer ways (less variability) to disperse or distribute the electrochemical energy. Of course during those pathological states energy is dispersed as well, but as there is almost no variability in neural connectivity then the number of paths to distribute that energy becomes much reduced. It is therefore in this sense we talk about “energy dispersal being healthy", basically as a shorthand for “greater variability in connectivity that is helpful for brains to operate". Figure 4 depicts graphically these ideas. It represents the main concept summarising the experimental results aforementioned where conscious awareness was associated with the largest number of configurations of connections among cell networks or brain areas; that is, there are more possible paths energy can be dispersed as the number of connectivity configurations increases, and the maximum of paths occurs at the top of the inverted U. Near the top of that curve, as can be seen in the figures of the original publications, is where the conscious states lie, and interestingly, a study using the maximum entropy model of brain dynamics found that the most probable brain states —in the case discussed here these would be the conscious states near the top— were characterised by common activation profiles, in that local, contiguous brain areas were frequently co-activated (Gu et al., 2018). This result makes sense in light of the aforesaid re-entrant activity, or neural closure, and suggests that many of those brain microstates that make up the “conscious” macrostate near the top are these co-activated networks involved in self-sustaining, intrinsic brain activity (section 2.2 and 3). Along this line of reasoning, it has been put forward that the units of function of the cerebral cortex are groups of neurons forming ensembles through Hebbian synaptic plasticity, in virtue of the recurrence of the anatomical connectivity (Yuste, 2018). So we have converging evidence for an extensive recurrent anatomical circuitry that fosters re-entrant functional connectivity which results, when meso/macroscale recordings are obtained from the brain, in large numbers of configurations of connectivity during conscious states.

Generally speaking this maximisation of energy distribution is a natural tendency. Just like gas molecules tend to occupy the maximal volume available, energy will redistribute in the widest manner for no particular reason but because that is the most probable outcome (Perez Velazquez, 2009). The diverse natural phenomena and their specific mechanisms are details as to how the optimal energy distribution is achieved, and from the variety of these mechanisms and phenomena our concepts of order/disorder and stochasticity/determinism emerge in attempts to describe them.

Figure 4. Configurations of connections among cell networks viewed from the perspective of energy distribution. Each dot represents a neural network and the lines their connectivity that define microstates, with the macrostate represented as the circle surrounding the microstates. For either no connectivity or all-to-all connections, the number of configurations is low (only 1), at the right and left hand side of the inverted U curve, whereas at the top the maximal number of configurations is found. This maximisation is given by a certain number of allowed connections, neither too many (moving towards the right of the curve) nor too few (towards the left of the curve); in this particular case when there are 4 networks the connectivity that gives the maximum configurations is 3 (for clarity, not all configurations are shown in the macrostate at the top). Shown as well are connectivity of 0, 1, 5 and 6 (from left to right). Considering neural connections as pathways for energy distribution, the y axis can be thought of as the configurations of energy distribution. In the original publications the y axis represented the entropy associated with the number of possible configurations, and the x axis the number of brain signals that were found “connected”, and the experimental data placed conscious states near the top and unconscious ones to the left or the right of the top (Guevara Erra et al., 2016; Mateos et al., 2017).

Figure 4. Configurations of connections among cell networks viewed from the perspective of energy distribution. Each dot represents a neural network and the lines their connectivity that define microstates, with the macrostate represented as the circle surrounding the microstates. For either no connectivity or all-to-all connections, the number of configurations is low (only 1), at the right and left hand side of the inverted U curve, whereas at the top the maximal number of configurations is found. This maximisation is given by a certain number of allowed connections, neither too many (moving towards the right of the curve) nor too few (towards the left of the curve); in this particular case when there are 4 networks the connectivity that gives the maximum configurations is 3 (for clarity, not all configurations are shown in the macrostate at the top). Shown as well are connectivity of 0, 1, 5 and 6 (from left to right). Considering neural connections as pathways for energy distribution, the y axis can be thought of as the configurations of energy distribution. In the original publications the y axis represented the entropy associated with the number of possible configurations, and the x axis the number of brain signals that were found “connected”, and the experimental data placed conscious states near the top and unconscious ones to the left or the right of the top (Guevara Erra et al., 2016; Mateos et al., 2017).

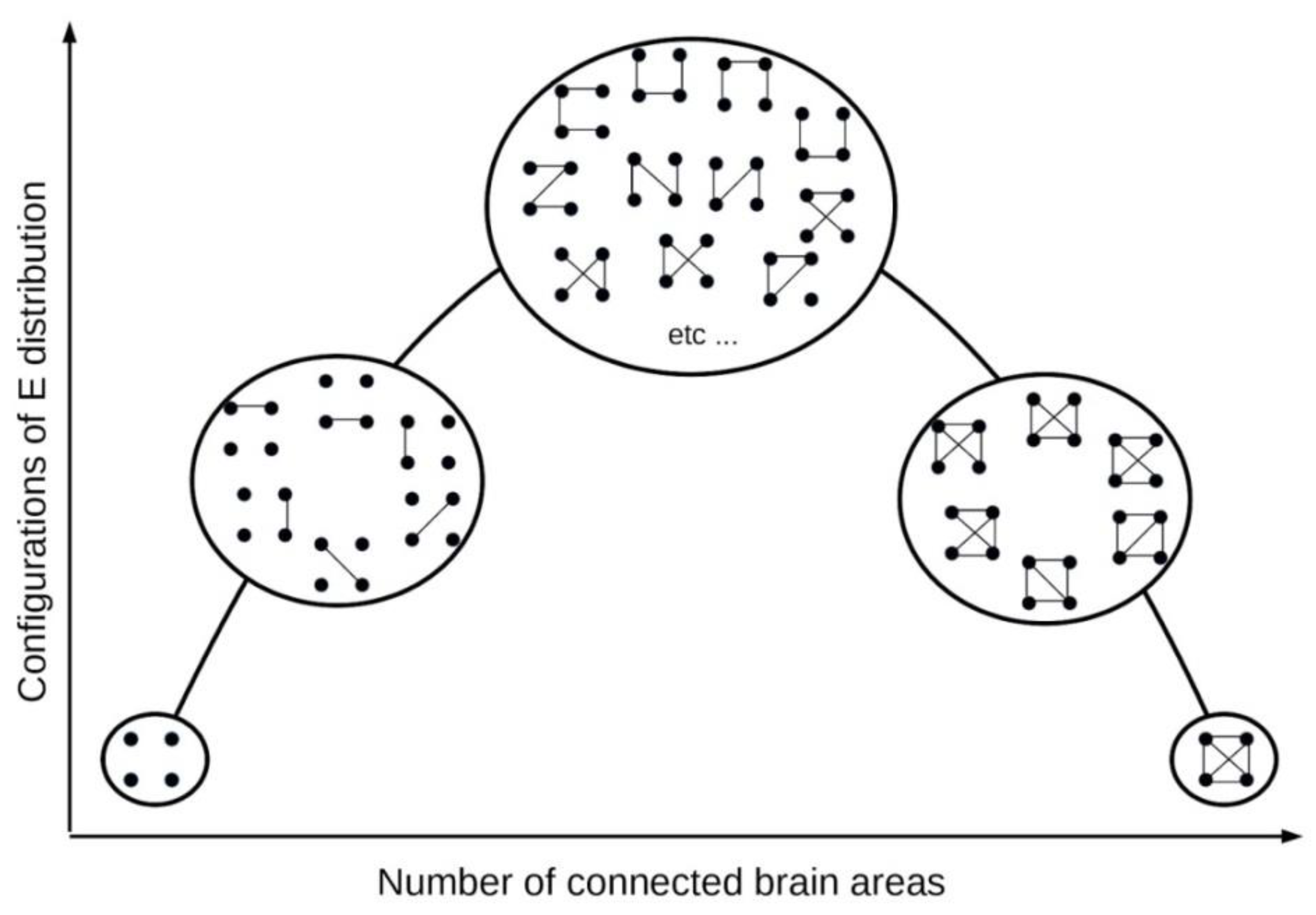
While the main advantage of using the energy perspective is that it is less ambiguous than the possible arbitrariness of the entropic viewpoint, there is still a problem: even physicists do not know what energy is. Efforts at obtaining precise and strict definitions of energy have not yielded too much success, the definitions proposed being inherently circular (see chapter 12, pp. 250 in Nunez, 2012). This is because energy is a fundamental property of natural phenomena, and these fundamental aspects are always hard to define in a general manner, nonetheless, it is fair to note that the notion of energy in biology and other sciences is normally associated with work produced leading to biological functions and therefore the need for a precise and strict definition of energy is not that crucial. Something similar occurs in the attempt to define consciousness or life, fundamental notions that have not obtained a definition everybody can agree on, and thus the advice to circumvent this problem (if indeed it is a problem) by defining them enumerating their features (Perez Velazquez, 2020; Guevara Erra et al., 2020). Perhaps, then, we should not worry too much about being unable to know the essential nature of some of these fundamentals because the key point is to capture aspects of the phenomenon that may help in the understanding. And along these lines just look at what physicists answered to the question posed by a reporter about what an elementary particle is, in her own words: “When I recently asked a dozen particle physicists what a particle is, they gave remarkably diverse descriptions. They emphasized that their answers don’t conflict so much as capture different facets of the truth” (Natalie Wolchover, What is a particle? published in Quantamagazine, November 12, 2020). Maybe the important matter is not so much what these fundamentals are, but what they do, as Paul Dirac remarked: “When you ask what are electrons and protons I ought to answer that this question is not a profitable one to ask and does not really have a meaning. The important thing about electrons and protons is not what they are but how they behave” (P. Dirac, in a Public Lecture in the Indian Science Congress, Baroda, 1955). Thus, Dirac’s words offer a way out of this conundrum about using strict definitions.

Please note that the purpose of all these comments that have appeared in several sections on the perils of applying entropy to life processes is not to deny the worth of theories like Prigogine’s dynamic changes in entropy to characterise and understand the evolution of irreversible processes, of which biology is almost all about. The dynamic changes in entropy may allow for a better understanding of the evolution of a system in some particular studies where, due to the conservation of energy, the energy perspective may not provide adequate views.

Going one step further in the simplification sought in this line of reasoning to find general principles of nervous system function, it should be considered that, in the final analysis, the distribution of energy in a system is due to interactions among the system’s constituents. Events occur in nature due to the interactions, as already recognised in antiquity: “No collision would take place and no impact of atom on atom would be created, thus nature would never have created anything”, these words coming from Lucretius in the first century BC (De Rerum Natura, Book II). At different levels of description these interactions trading energy give rise to diverse emergent properties, as depicted in Figure 5.

6. Pathological states as reduced fluctuations in energy distribution: a hypothesis

We have seen how variability in the configurations of neuronal connectivity is associated with conscious states, which supports the proposal that fluctuations of the order parameters used to describe a system become macroscopic variables to which diverse analytical methods can be applied (Haken, 2006). The order parameter considered in this text has been connectivity, or synchronization. And more specifically, fluctuations in neural activity can be promoted to a principle of brain organization. And because this activity can be thought of as energy transactions, this view may open an avenue for a thermodynamics of nervous systems. The origins of classical thermodynamics stem from measurements of heat and work. But heat, like work, is only a form of energy transfer, energy in transit (Callen, 1985, Le Bellac et al., 2004). When correlations in neuronal activity are measured, be it as synchrony, connectivity and so on, in reality these measurements represent energy in transit too. Therefore it is conceivable that a thermodynamics of nervous systems, or another system/organ where connections/interactions between cells can be measured, can be developed from these observables (Perez Velazquez et al., 2019).

In any event, the functional importance of the organization of energetic processing in the brain has been proposed by some authors (Pepperell, 2018), which is consistent with older proposals that postulated that the flow of energy through a system acts to organise the system (Morowitz, 1968), and that biological information is, in the final analysis, the energy flow (Smith, 2008) as metabolic pathways offer channels for energy to flow and cellular communication provides further conduits for that flow. The tendency to maximise those conduits found in natural phenomena, not only in the biological but also in the inorganic (Perez Velazquez, 2009), results in increasing the possibilities of diverse configurations into more states to create better channels for energy flow (Morowitz and Smith, 2007). All this is an expression of the multiple interactions among units in a system and among different systems. The notion that living processes make the energy flux through the system a maximum has been voiced since times past, of course so far as compatible with constraints (Lotka, 1922). Therefore, maximising the energy flow/distribution in the function of the brain could be the sufficient factor accountable for the emergence of conscious awareness (the necessary factor is to have enough energy, as explained in 3.1) and in general for a healthy brain. Using this perspective, other works have interpreted the formation of memory traces as activated neural paths for energy dispersal, advancing the idea that a memory persists in the pattern of a specific flow of energy in a neural circuit (Varpula et al., 2013), a thought consistent with the previously discussed re-entrant activity (section 5) where contiguous brain areas are frequently co-activated.

And what does the dispersal of energy in many gradients do? For living organisms that possess brains with many electrochemical energy gradients it means that they can process a large variety of inputs, hence affords more adaptability in a fast changing environment. Can we envisage what it may do for other parts of the organism? If in the case of brains appropriate brain function requires an efficient web of neural connections, which, interpreted from the perspective expounded in this text, is equivalent to saying that brains tend to a fluctuating and widespread energy distribution among all those microstates via maximization of the number of configurations, we venture the hypothesis that, beyond the nervous system, in other pathologies affecting different organs, less fluctuations in energy gradients/distribution is the cause of those pathological states. A neural example is Parkinson’s disease, where the rhythmic activity going through thalamus and cortex (and through other areas as well, but let’s keep it simple) that is responsible for the tremor can be considered a stable energy gradient, and the success of deep brain stimulation consists in destabilizing that energy channel so that the rhythmic synchronous activity diminishes and the tremor is almost abolished. In traumatic brain injury, studies have revealed that the temporal and spatial variability of phase synchronization among electroencephalographic signals increased as patients recovered and emerged from coma, and this variability correlated with clinical outcome, so this view represents a novel prognostic approach in the evaluation of traumatic brain injury (Nenadovic et al., 2008, 2014).

Beyond the nervous system, it is known that cardiac arrhythmias are caused by re-entrant activity that synchronises part of the cardiac muscle into abnormal rhythms, and cardiac electrical stimulation with pacemakers or similar devices, some using chaos control techniques, disturb that powerful electrochemical cardiac energy gradient thus relieving the arrhythmia. Specifically, a study of the electric field distribution in cardiac tissue found that just one electric pulse delivered to the core of the anatomical re-entry can abort arrhythmias (Takagi et al., 2004).

In cancer too, there is evidence for a concentration, so to speak, of energy in the tumour. It has been reported that cancer cells increase their metabolism to produce the energy and biomolecules necessary for their uncontrolled proliferation (Pattni et al., 2017). Thermogenesis, or elevated heat release, is also known to be a phenomenon of tumours, in fact it has been proposed that heat release may be a quantifiable trait of the metastatic process (Lemos et al., 2019). Hence, whereas this situation is quite different from the neural or cardiac systems where electrochemical energy gradients are evident, still the hypothesis may be advanced that dispersing the elevated resting energy of tumour cells to other neighbouring normal cells may decrease the probability to differentiate into malignant cells. Advances in engineering thermodynamics to assess and control heat exchange in organisms, especially related to controlling the energy available for tumours to grow, may offer avenues to diminish these pathological conditions (Lucia and Grisolia, 2022).

Thus the proposal is that less fluctuations in energy gradients/distribution is the cause of some pathological states. We are currently assessing the number of energy gradients in neuropathological unconscious states and in healthy conditions in an attempt to find some substantiation for this hypothesis. If it comes to be true in the end, those large and too stable energy gradients should be either abolished or made them brief to treat these pathologies.

For the sake of completion, it should be noted that the ideas behind how the information flow is related to energy flows have been treated in some studies (Marijuán et al., 2018) and have been the subject of special issues, e.g. ”Information and Energy/Matter" (Dodig-Crnkovic, 2012). As well, a recent interest in the consideration of the energy viewpoint has emerged, for instance in the free energy principle for biological systems (Friston, 2012) or the methodology of bond graphs models to consider energy transactions in biological processes (Gawthrop and Pan, 2022).

7. Concluding remarks

Brain activity and function, and in general all nervous system, is about large-scale patterns of coordinated cellular collective activity. The results we have examined at this meso/macroscopic level of description suggest that the common theme underlying some entropic measures in neurodynamics revolves around the well-known tendency of natural phenomena towards a maximal energy distribution —nothing more than the second principle of thermodynamics—, which in terms of the nervous system is manifested by maximisation of the number of configurations among the neural networks’ connectivity. Thus the brain reaches a steady state formed by many microstates (those configurations of functional connections), and depending on external and internal constraints including the neuroanatomical connectivity, the total energy available and the inputs the brain receives in diverse behavioural states —that is, depending on the context—, this steady state will have different features. Among these, the number of possible configurations of connections will differ, more abundant during conscious awareness and fewer during unconscious states both physiological (sleep) or pathological. In other, more classical words, it can be said that the embodied brains that are immersed in an environment seem to attempt to reach equilibrium, which is not possible due to the exchange of energy (information) with the surroundings.

From the perspective proposed here, considering neural connections as pathways for energy distribution so as to avoid the ambiguity of entropic results, it is all about the number of pathways in which energy can be dispersed. Thinking of entropy as an index of energy dispersal or dissipation, it is therefore plausible that energy is distributed in more pathways in healthy conditions and during conscious awareness. Thus the hypothesis was formulated that some pathologies may have as an underlying cause a lack of fluctuations in energy gradients/distribution, which can be investigated if the interactions among cells in the organ or system of interest can be measured using correlations of activity or any other method, as these measures represent energy in transit. So what at the macroscale may seem relatively stable steady states —those brain macrostates associated with different behavioral conditions— at the local, microscopic level variability, or fluctuations in the cell network connectivity, is found when assessed with the appropriate analytical techniques (section 3.1). This is the global and local perspectives: the microstates (local view) need to fluctuate hence be unstable/metastable, whereas the global macrostate remains stable. Therefore there should not be any paradox in these results, it all depends on the level of description. And this local creation and destruction of energy gradients is continuously maintained by self-sustaining cellular activity endowed by the recurrent loops and the “neuroglial closure” (Perez Velazquez, 2020).

We have described our perspective as a global principle, because, although we have focused on neuroscience to try to find rules governing the emergence of neural dynamic patterns, we think that the principle of the tendency to maximise the number of configurations of the interactions among a system’s constituents can be applied to other natural phenomena. As such, the current proposal is an extension of the idea that common principles of biological and nonbiological organization arise and evolve from a central theme captured by the process of energy transactions (Perez Velazquez, 2009). Biological processes support a widespread redistribution of energy/matter, as it is known that biological rates are limited by the rate of energy and matter distribution, requiring a minimization of the free energy and time required to distribute resources (West et al., 1997).

Another clarification that is fair to note is that whereas our narrative has focused on highly evolved nervous systems possessing brains, we always have to consider the continuum in the evolution of cognition and consciousness which developed in a graded, continuous fashion, as these are not static properties but dynamical processes such that the essential neural factors (neuroanatomical and biophysical features, etc.) are already present in primordial nervous systems. Thus, the suggestion that consciousness may be a general property present not only in highly evolved vertebrates (Feinberg and Mallatt, 2018). In fact, “primitive" creatures can be endowed with a sort of primordial cognition, as these entities possess some features of cognition like response to environmental changes, memory, and others; however, less complex nervous systems, in terms of numbers of neurons and combinations of network connections, do not allow these organisms to display what can be termed higher features of cognition like emotions or self-awareness. But even without nervous systems, there is information processing too —although not in the Shannon sense— for instance in microbes, afforded by cellular interactions but not of synaptic origin rather of other chemical nature: think of bacterial chemotaxis for instance (Slijepcevic, 2021). The nature of the interacting elements can in fact be considered accidental, the crucial point is that there is energy/matter transactions in those interactions that give rise to pattern formation, among these neural patterns or aggregation patterns of microbes (Ben-Jacob, 2009) like the well-known D. discoideum. In the final analysis, it is through the interactions among elements of a system, the interplay between the short and long range correlations in their activities, which result in the natural patterns we see around, including ecosystems and our societies.

And because those interactions involve energy transactions, then, it is the gradients of energy, the energy dissipation in a final state compared to an initial state, the driving force, and the entropy is the index of that dispersal (Lambert, 2002). After all, energy is a common currency of natural systems, and especially biological ones. Much of the experimental evidence and reflections about cognition and consciousness support the view that these are dynamic processes (Craik, 2020; Haken, 2006; Varpula et al., 2013; and many others), basically patterns of organised activity in the (embodied) nervous system, paraphrasing E. J. Ambrose's words that “life is basically a pattern of organized activity” (Ambrose, 1982). As well, postulating that cognition needs many energy gradients appearing and disappearing that are neither too large nor too stable is another way of saying that high and long-lasting synchronization (as occurs in coma, epileptic seizures or non-REM sleep) is generally not optimal for the brain functioning needed to process a myriad of inputs, which encapsulates the ideas about the need for the variability in neural connectivity leading to the integration/segregation of information that are common to several current theories of cognition as already described in section 3.

Let us emphasise again that we are not declaring that entropy plays no role in driving natural phenomena, rather what is meant is that entropy is a sort of arbitrary measurement that can be applied to many observables and hence the interpretation may vary (section 2.1). On the other hand, considering entropy as the dispersion or distribution of energy, then it is that dissipation of energy that can be thought of as the driving force of events. Hence, in reality one concept (more distribution of energy) is equivalent to the other (higher entropy), the main advantage using the energy perspective is that it is less ambiguous than the possible arbitrariness of the entropic viewpoint.

In sum, a necessary condition for cognition/consciousness (at least the high-level) to emerge is to possess enough energy, or cellular activity, and a sufficient condition is the multiplicity of configurations in which cell networks can communicate, the non-uniform energy distribution due to constant activity. These could be ideas whose development may reveal possible fundamental principles of brain organization from which cognition and conscious awareness emerge and how pathological states appear.