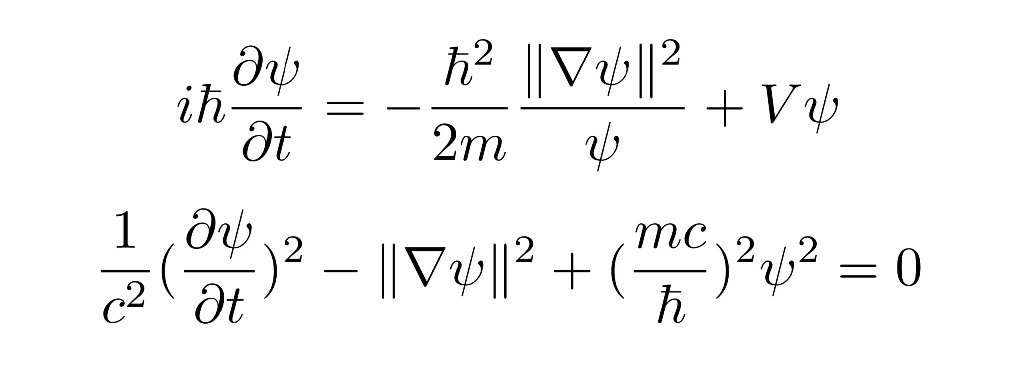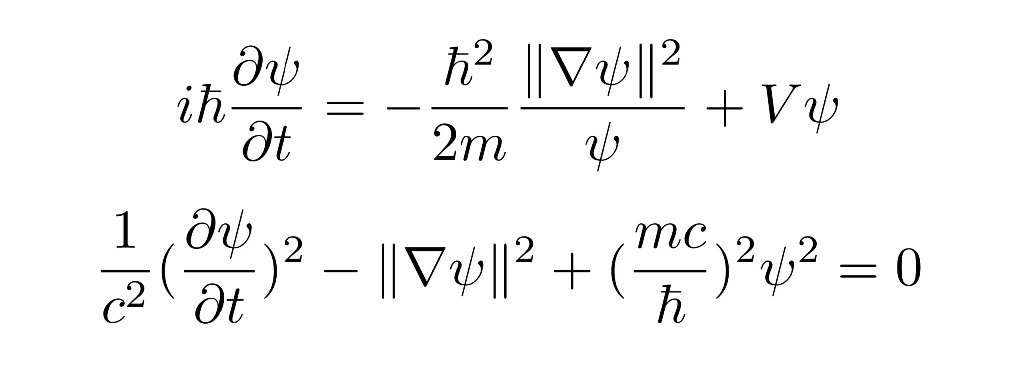Nonlinear Generalisation of Quantum Mechanics

According to our current understanding of quantum mechanics, a `measurement' violates unitarity. In other words as the act of measurement `resets' the probabilities described by the Schrödinger equation, in the very `moment' of the collapse of the wavefunction, conservation of probability does not hold. To make progress in our understanding of the measurement problem it is thus expected that one must encompass in a single equation both otherwise mutually-exclusive processes of measurement and unitary evolution. In this light, turning to the continuity equation, we realize the possibility that if we allow for existence of sources and sinks in the `fluid of probability' we get closer to such a theory by arriving at nonlinear generalizations of Schrödinger and Klein-Gordon equations. The generalized equations derived are then shown to satisfy all conditions that are expected from a proper generalization: simplification to their linear counterparts by a well-defined dynamical condition, and Galilean and Lorentz invariance.