Demonstration to Unify 4 Interactions in Particle Physics with the Zero‐Point Energy and Quantized Spacetime

1. Introduction

This study aims to explain the interrelationships of all the fields, including the static electromagnetic fields, gravity, and the weak and strong interactions by employing the concept of a quantized spacetime with a zero-point energy. That is, the aim of this paper is to demonstrate that the zero-point energy can describe the 4 interactions of the particle physics.

These 4 interactions have various phenomena. Thus, for example in this paper, electromagnetic fields and the weak interaction which describe the β collapse will be explained. As the gravity, we succeed to obtain the quantized Einstein’s gravity equation, using the electromagnetic fields. Furthermore, for the strong interaction, the mass of a pi-meson will be derived, employing the electromagnetic fields. Note that the electromagnetic fields which are common in the 4 interactions are derived only by the zero-point energy.

Let us discuss the background of this study. To unify the basic forces of nature has been pursued by many researchers, starting with Faraday. After his success in unifying the time-dependent electric and magnetic fields, he conducted many experiments under the assumption that the gravitational and electromagnetic fields must be unified, but he could not obtain a satisfactory result [1]. After discovering Hertz waves experimentally, Hertz also tried to unify Maxwell’s equations and Newtonian gravity to understand how gravity is transmitted [2]. This work was not understood by his generation, but its differential-geometry concept influenced Einstein. Einstein also tried to solve this problem. The concept he employed was to introduce an additional dimension to formulate a five-dimensional general relativity theory, hoping to unify gravity and the electromagnetic field. This is equivalent to the internal and external spaces of Kaluza-Klein theory [3], and it was hoped that the conservation laws governing general coordinate transformations in five dimensions might lead to gravity and the electromagnetic field. However, this theory is not complete.

The current standard model of elementary-particle physics has the same problem. That is, it does not contain the interaction due to gravity. Moreover, the standard model has other problems, which we summarize. Here let us discuss from reference [4]:

1)

the gravitational interaction: As mentioned, the standard model does not include the interaction due to gravity. The problem is that gravity is different from other interactions, in that an infinity of the gravitational field cannot be eliminated [5]. To solve this problem, super-string theories [6] are being investigated, but they currently cannot predict any physical phenomena. Another theory being investigated is loop quantum gravity [7]. This theory—like the present paper—introduces a quantized spacetime, but no concrete calculations have been performed.

2)

Relations between the basic interactions: The standard model claims that it describes the basic interactions, i.e., the electromagnetic force and the weak and strong interaction. However, the relations between them are not clear in this model. Even in Weinberg-Salam theory, the relationship between the weak interaction and the electromagnetic force is not clear. Moreover, the Weinberg angle in this theory cannot be predicted in the standard model.

3)

The charge is not constant: In the standard model, due to the existence of weak hypercharge, the charge is a continuous variable. However, at the elementary-particle level, the charge of each particle should be constant and quantized. As long as the Weinberg-Salam theory depends on weak hypercharge, the masses of the W and Z bosons must be obtained by another method.

4)

The problem of quantum corrections to the Higgs field: Only a little time has passed since the discovery of the Higgs boson. However, by employing the standard model, when quantum corrections involving the square of the mass are calculated, an ultraviolet infinity appears. Basically, in the standard model the combination of spontaneous symmetry-breaking and the Higgs field results in the masses of other particles. Because this is a QED model that deals with guages, it must explain why particles such as the W or Z gain mass. However, the standard model has a problem with the Higgs, and thus the basic story above is not complete. Many theories [8,9,10,11,12,13] have tried to solve this problem, but no measurements support them. Moreover, in the standard model, there are many undetermined parameters in the Higgs interaction or the Yukawa interaction.

5)

Dark Energy and Dark Matter: Recently it has been found that about 80% of the total energy of our universe consists of Dark Energy or Dark Matter. Many researchers believe that they will be explained at the level of elementary-particle physics, but nobody has been able to circumvent the fact that Einstein’s gravitational equation cannot be quantized.

Let us explain the contents of this paper.

This paper provides a basic theoretical concept to solve the abovementioned problems, and it claims that a sole source of energy—the zero-point energy—creates all the fields, including gravity, the electromagnetic field, and the weak and strong interactions when we introduce a quantized spacetime. Moreover, the relations between these fields are made clear at the level of quantum mechanics by this concept.

First, we introduce the concept of a quantized spacetime with a zero-point energy. In the process of quantizing gravity, we derive the relationships between the energies of a static electric field, gravitation, and a static magnetic field at the level of a quantized spacetime. Using these relations, we quantify Einstein’s gravitational equation. Next, we discuss the weak interaction. Specifically, using the zero-point energy, we calculate the radius and lifetime of the neutron. Moreover, we describe a β collapse from a different point of view than Fermi. In this process, another meaning of the neutrino appears. Furthermore, we calculate the masses of the W and Z bosons from a different point of view than Weinberg-Salam theory. Next, we calculate the pi-meson, which ties nucleons together in strong interactions.

In the Appendix, we derive spin and mass of a quark. Moreover, by employing the concept of a quantized spacetime, we interpret the meaning of a wave function and compared it with Einstein’s interpretation and Born’s interpretation. In this Appendix, moreover, the contraction of a wave packet will be discussed.

The significance of this paper is that it describes the above fields and their relationships with only the assumption of a quantized spacetime as the sole source of all the fields being the zero-point energy. Note that the common fields are the electromagnetic fields but they are obtained only by the zero-point energy. Moreover, the values this theory predicts agree with measurements. Furthermore, we obtain a quantized Einstein gravity equation. Moreover, by quantizing the Einstein’s gravity equation, we can solve the problem of singularity, which implies the infinity.

2. Theory

2-1. Gravity and Electromagnetic Field in the Quantum Level

The most important claim, and the significance of this paper, is that from the zero-point energy, all fields—including the electromagnetic field, gravity, and the week and strong interaction—are derived at the level of a quantum mechanics. As discussed later, the zero-point energy basically implies the time-independent static electromagnetic field energy, and thus all the fields concerning elementary particle physics are obtained from the electromagnetic fields. We present these derivations later.

Quantum field theory is common in elementary-particle physics. However, QED employs cut-offs to avoid the problems of troublesome infinities, which is inadequate for describing the real physical picture, because the internal infinities are purposely neglected. On the other hand, our claim is different: because QED deals with extremely local fields, i.e., points, this results in the problems of infinities and invalidates relativity theory. Moreover, QCD with color charges does not provide the valid mass of a quark, i.e., the mass is put in by hand. The mass of a quark in a nucleon must be three times that of an electron, as described in the Appendix.

Previously, loop quantum gravity theory employed the concept of quantized spacetime. However, the specific quantized space-length and time-span are unclear from that theory. In the present study, we instead focus on Dirac particles that obey the Dirac equation:

$$\mathrm{ħ}{\omega }_0=2\mathrm{m}{c}^2,$$

(1)

where ω_0, m, and c denote a constant angular frequency, the mass of an electron, and the speed of light, respectively

This equation can be rewritten as

$$\frac{1}{2}\mathrm{ħ}{\omega }_0=m{c}^2,$$

(2)

which implies that the zero-point energy creates the electron mass.

The zero-point energy is obtained from the Hamiltonian H of a harmonic oscillator when n=0:

$$\mathrm{H}=\left(\mathrm{n}+\frac{1}{2}\right)ħ{\omega }_0.$$

(3)

Because n = 0, a summation over variable n is not considered herein. However, we can define an angular frequency Ω = nω₀ ($\mathrm{ħ}\mathrm{n}{\omega }_0=ħ\Omega )$. Thus, the angular frequency ω₀ is constant, and thus the zero-point energy should be considered as a specific, universal constant energy. Moreover, it implies a vacuum energy gap, according to the Dirac equation. To conclude, the zero-point energy expresses the basic energy of the vacuum. Therefore, this study considers the electron mass as the sole and most basic parameter. That is, this equation produces the minimum quantized length ${\lambda }_0$ and time t₀ in terms of the spacetime:

$${\lambda }_0=\frac{\mathrm{ħ}}{2mc}$$

(4)

$$t_0=\frac{\mathrm{ħ}}{2m{c}^2}$$

(5)

Considering the Lorentz transformation, let us generalize the zero-point energy:,

$$\frac{1}{2}\mathrm{ħ}\omega =\frac{m{c}^2}{\sqrt{1-\frac{v^2}{c^2}}},$$

(6)

In this equation, the mass and rest energy imply a static electric field, and the velocity v implies indirectly the gravitational and magnetic fields in a quantized spacetime. We discuss the details later.

The Hamiltonian of a harmonic oscillator can be written again as

$$\mathrm{H}=\left(\mathrm{n}+\frac{1}{2}\right)ħ{\omega }_0.$$

(3)

In this equation, the first term implies a time-dependent electromagnetic field from the guage. (Many studies neglecting the zero-point energy have been investigated in quantum field theory. This theory has achieved partial success, but that success is derived by employing cut-offs and quantities being put in)

Considering this, the second term, which represents the zero-point energy of the vacuum, must imply time-independent static electromagnetic fields. Thus, the zero-point energy implies the electromagnetic field energy. We derive a more general constant quantized spacetime length and time:

$${\lambda }_c={\lambda }_0\sqrt{1-\frac{v^2}{c^2}}.$$

(7)

$$t_c=t_0\sqrt{1-\frac{v^2}{c^2}}.$$

(8)

The reason why spacetime must be quantized is that this solves the problem of the infinities that invalidates existing theories. Moreover, the quantization makes all the fields—including particles and forces—more clear, i.e, these fields are produced solely by the zero-point energy of the vacuum.

The zero-point energies are distinguished by the following two Dirac particles:

• The electron: this is described as

  $$\frac{1}{2}ħ\omega =m_e{c}^2$$

  (6)
  That is, this equation describes our spacetime (i.e., Minkowski space) and m_e is here the mass of an electron.
• Quarks: this describes the space in a nucleon as

  $$\frac{1}{2}ħ\omega =3m_A{c}^2,$$

  (7)

  here m_A denotes the mass of a quark in the nucleon. However, the important point is that both the equations above imply the static electromagnetic energy. In this sense, these energies are the same.

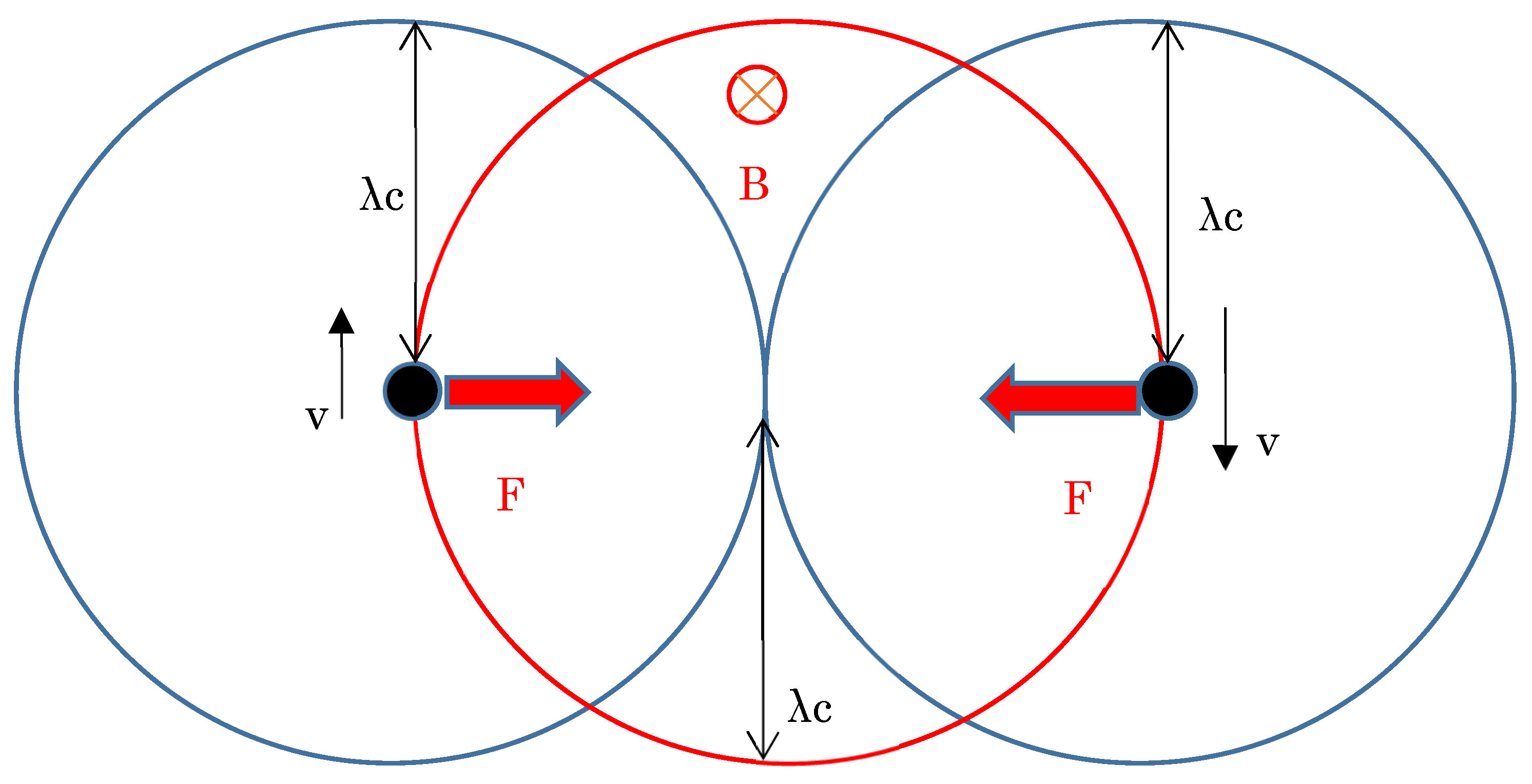
Figure 1 shows a schematic illustration of the force F in a quantized spacetime. In this figure, two quantized spacetimes are rotating. Each quantized space has an embedded up or down spin electron. The force F is the Lorentz-force from the static magnetic field, which is identified with the attractive gravity force F from the gravitational field. Based on the concept in this figure, we calculate the relation among the energies of a static electric field, a static magnetic field, and a gravity field.

Let us calculate the electrostatic energy at the level of quantum mechanics.

The electric energy is given by

$$u_E=\frac{1}{2}{\epsilon }_0\int E^{2}dv=\frac{1}{2}{\epsilon }_0{\int }_{r_e}^{\mathrm{\infty }}{\left(\frac{e}{4\pi {\epsilon }_0{r}^2}\right)}^{2}4\pi r^{2}dr.$$

(8)

This is tied to the mass of the electron:

$$u_E=\frac{1}{2}4\pi {\epsilon }_0{\left(\frac{e}{4\pi {\epsilon }_0}\right)}^2\frac{1}{r_e}=2\mathrm{m}{c}^2,$$

(9)

Note that there are two embedded electrons in Figure 1.

or

$$m=\frac{1}{2c^2}\frac{e^2}{4\pi {\epsilon }_0}\frac{1}{r_e}=\frac{1}{2}\frac{1}{c^2}{u}_E,$$

(10)

where E, r, ε_0, e, and u_E denote the static electric field, distance, the permittivity, and the electric-field energy

In turn, the gravitational and static magnetic-field energies at the level of quantum mechanics can be calculated in terms of the velocity v in Equation (6). In the following calculations, we include the rotational movements of the two electrons embedded in the quantized spacetime.

First, the kinetic energy equals that of the gravity field.

$$\frac{1}{2}m{v}^2=\left|u_G\right|,$$

(11)

Employing Newton’s law,

$$\frac{1}{2}m{v}^2=G\frac{m^2}{r},$$

(12-1)

where G denotes the gravitational constant.

Moreover,

$$u_G=-G\frac{m^2}{r},$$

(12-2)

From Equation (12-1), we obtain

$$v=\sqrt{\frac{2Gm}{r}},$$

(13)

where v is the rotational velocity in Figure 1:

$$v=r\omega ,$$

(14)

From Equation (13), the angular frequency is

$$\mathsf{\omega }=\sqrt{\frac{2Gm}{r^3}}.$$

(15)

We then introduce the zero-point energy:

$$\frac{1}{2}ħ\omega =m{c}^2.$$

(16)

Thus, using the above-mentioned equations, the energy of the gravitational field becomes conclusively

$$u_G=-2G^2\frac{m}{r^4}{\left(\frac{\mathrm{ħ}}{2c^2}\right)}^2,$$

(17)

Note that a general space is quantized in terms of λ_c

$$r=n{\lambda }_c,$$

(18)

From the previous calculations, we obtain the relation between u_G and u_E:

$$m=\frac{1}{2}\frac{1}{c^2}\frac{e^2}{4\pi {\epsilon }_0{r}_e}=\frac{1}{2c^2}{u}_E,$$

(19)

$$u_G=-G^2\frac{1}{r^4}\frac{1}{c^2}{u}_E{\left(\frac{\mathrm{ħ}}{2c^2}\right)}^2,$$

(20)

$$r=n{\lambda }_c,$$

(21)

Equation (20) implies a relation between u_G and u_E in a quantized spacetime. However, the static magnetic field energy u_B is given by the following in a quantized time-space:

$$\frac{1}{2}\mathrm{ħ}\omega =\frac{m{c}^2}{\sqrt{1-\frac{v^2}{c^2}}}\approx m{c}^2+\frac{1}{2}m{v}^2=\frac{1}{2}{u}_E+\left|u_B\right|=\frac{1}{2}{u}_E+\left|u_G\right|,$$

(22)

$$u_B=-G^2\frac{1}{r^4}\frac{1}{c^2}{u}_E{\left(\frac{\mathrm{ħ}}{2c^2}\right)}^2,u_B=u_G,$$

(23)

Let us calculate the velocity v, which is constant.

$$\frac{1}{2}\mathrm{ħ}\omega =\frac{1}{2}\mathrm{ħ}\frac{1}{{\lambda }_c}v=m{c}^2.$$

(16)

(Note that this equation embeds the Lorentz-contraction).

$$\mathrm{v}=\frac{2m{c}^2}{ħ}{\lambda }_c.$$

(24)

$$\mathrm{v}=\frac{2m{c}^2}{\mathrm{ħ}}{\lambda }_0\sqrt{1-\frac{v^2}{c^2}}.$$

(25)

$$\mathrm{v}=\frac{1}{\sqrt{2}}c=0.68c.$$

(26)

As we discussed later, the velocity of a neutrino can cause the quantum space-length λ_c to be changed to the order of size of a nucleon.

2-2. Quantization of the Einstein Gravity Equation

From the equation for quantized spacetime, we can combine the Einstein gravity equation with the derived equation, because both equations include the constant of gravitation G. The Einstein equation is

$$G_{\mu \nu }=\frac{8\pi G}{c^4}{T}_{\mu \nu }.$$

(27-1)

$$G_{\mu \nu }=R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }$$

(27-2)

where R_μν, T_μν, g_μν and R denote the Riemann curvature tensor, the energy flux tensor, the metric tensor, and the Ricci tensor.

As a result of substituting the gravitational constant G from Equation (23), we obtain

$$G_{\mu \nu }=\frac{16\pi }{c\mathrm{ħ}}\sqrt{-\frac{u_B}{u_E}}{\lambda }_c^2{T}_{\mu \nu }.$$

(28)

Herein, we assume the macroscopic tensor g_μν to be approximately the Minkowski tensor g_ij because, for a quantized spacetime, an analytical differential cannot be defined. That is, it implies merely a division by λ_c.. Moreover, the energy density is given by the zero-point energy:

$$\mathsf{\epsilon }=\frac{\frac{1}{2}\mathrm{ħ}\mathsf{\omega }}{{\lambda }_c^3}.$$

(29)

Thus, T_μν is approximated by the Minkowski tensor:

$$T_{\mu \nu }=\epsilon g_{ij}.$$

(30)

Considering the above, Einstein’s gravitational equation is transformed as

$$R_{\mu \nu }=(\frac{16\pi }{c\mathrm{ħ}}\sqrt{-\frac{u_B}{u_E}}\frac{\left|u_G\right|}{{\lambda }_c}+\frac{1}{2}R)g_{ij}.$$

(31)

As mentioned, the energy is given as the zero-point energy.

$$\left|u_G\right|=\frac{1}{2}ħ\omega .$$

(32)

Assuming the Ricci tensor 1/2R to be substantially smaller than the first term, we obtain

$$R_{\mu \nu }=\left(\frac{16\pi }{c\mathrm{ħ}}\sqrt{-\frac{u_B}{u_E}}\frac{1}{{\lambda }_c}\frac{1}{2}\mathrm{ħ}\omega \right)g_{ij}.$$

(33)

Moreover, considering the initial equation (23), the root in Equation (33) is out.

$$u_B=-G^2\frac{1}{r^4}\frac{1}{c^2}{u}_E{\left(\frac{\mathrm{ħ}}{2c^2}\right)}^2=-G^2\frac{1}{{\lambda }_c^4}\frac{1}{c^2}{u}_E{\left(\frac{\mathrm{ħ}}{2c^2}\right)}^2.$$

(34)

Considering this, we obtain

$$R_{\mu \nu }=\left(G\frac{8\pi }{c^4}\frac{1}{{\lambda }_c^3}\frac{1}{2}\mathrm{ħ}\omega \right)g_{ij}.$$

(35)

The equation (35) implies that, even when no macroscopic matter exists, the Riemann curvature tensor is not zero due to the zero-point energy.

2-3. Weak Interaction

The zero-point energy indicates a static electromagnetic field, and this energy also describes the weak interaction. Considering a static electric field,

$$\frac{1}{2}\mathrm{ħ}{\omega }_{ }=m{c}^2=\frac{1}{3}e\phi =\frac{1}{3}eE{r}_N$$

(36)

where φ and r_N denote the electrostatic potential and the radius of a neutron.

This equation implies an interaction between an electron and a quark. As shown in Figure 2, a neutron is composed of a proton and an electron. That is, an electron is distributed around the proton like a film. The important concept is that an electron generally behaves as a wave, not as a local point. This is a fact from basic quantum mechanics, while quantum field theory considers an extremely local point, which leads to the problems with infinities.

Thus,

$$\sigma ={\epsilon }_{0}E,$$

(37)

where σ denotes the surface density of a charge.

Therefore, we derive the approximate radius of the neutron as

$$r_N=\frac{e^2}{4\pi {\epsilon }_{0}m{c}^2}\times \frac{1}{3}.$$

(38)

As a result of calculations, we obtain

$$r_N=0.96\times {10}^{-15m}$$

(39)

Note that the electric-field interaction is that between a quark and an electron. Moreover, it is assumed that the charge of each quark is 1/3e.

Moreover, the value of this result is a little large. However, as discussed later, because the theoretical radius of a neutron obtained from another approach $\mathrm{i}\mathrm{s}0.7\times {10}^{-15}m$, we conclude that the calculated value is valid.

Let us calculate the lifetime of a neutron.

When an electron exists within a neutron, its wavelength is changed from the order of 10^-13 m, i.e., λ_c to the order of 10^-15 m. As discussed later, this does not contradict the quantized space length, due to the existence of the neutrino. However, this electron has the property of restoring a quantized space length. Thus, the neutron has a finite lifetime.

First, we assume the following proportionality:

$$r_N\left(t\right)=\alpha t{\lambda }_c,$$

(40)

where α is a constant having the unit and t is time, or

$$\mathsf{\alpha }\mathrm{t}=\frac{r_N\left(t\right)}{{\lambda }_c}.$$

(41)

In the above equation, we substitute the conditions:

$$\mathsf{\alpha }{t}_{\alpha }=\frac{r_N\left(t_{\alpha }\right)}{{\lambda }_c}\to \frac{{\lambda }_c}{{\lambda }_c}=1,$$

(42)

where t_α is considered the steady time. In this equation, for the time t_α, the length is restored to λ_c._.

Moreover, from Equation (41)

$$\mathsf{\alpha }\times 1=\frac{r_N\left(1\right)}{{\lambda }_c}\approx \frac{r_N}{{\lambda }_c}\approx 3.6\times {10}^{-3}$$

(43)

where for the radius r_N we substitute the value $0.7\times {10}^{-15}$m, which we discuss later and derive theoretically. Because the measured lifetime is about 12 minutes which is sufficiently long, we approximate that 1s is the initial time when a neutron form its radius of r_N.. Considering the number of the quark, the lifetime is thus

$$t_{\alpha }=3\times \left(2.7\times {10}^2\right)=810\mathrm{s}.$$

(44)

The measured value [15] is 885.7 s, which agrees sufficiently well.

Let us consider a β collapse and the masses of the W and Z bosons.

A β collapse was described by Fermi. He calculated it with QED and a neutrino, and he concluded that non-conservation of the kinetic energy of the electron was avoided by adding the neutrino energy. However, we claim that

• The mass of a neutrino is extremely small. Thus, even though it moves near the speed of light, its kinetic energy cannot contribute to the total energy. We claim instead that the existence of the neutrino has another reason in addition to the conservation of spin, as described later.
• As described later, the kinetic energy of an electron is constant, which gives the rest energy of the W in terms of a broken symmetry of space.
• The distribution of a β collapse does not indicate non-conservation of the kinetic energy of the electron but merely the probability density for an eigenfunction of the zero-point energy combined with an electron. Here, we employ Fourier transforms.

First, the total energy ε approximately is

$$K+\frac{1}{2}ħ\omega =\epsilon ,$$

(45)

where K denotes the kinetic energy of an electron.

The eigenfunction is obtained as the product of that of electron and the ground state of a photon, i.e., the zero-point energy.

$$\psi =\exp \left(\mathrm{i}\mathrm{b}\mathrm{x}\right)\times X_n,$$

(46)

where b is the constant wave number of an electron, and X_n denotes ground state of a harmonic oscillator.

From any basic quantum-mechanics text, X_n is given as

$$X_n=\sqrt{\frac{2M\omega }{\mathrm{ħ}}}\exp \left(-\frac{M\omega }{2\mathrm{ħ}}{x}^2\right),$$

(47)

where the mass M and the angular frequency ω will be given later.

Here, we Fourier transform this wave function using the following mathematical formulas:

$$F\left(\tau \right)=\left(-\alpha {\tau }^2\right)\leftrightarrow f\left(x\right)=\frac{1}{\sqrt{2\alpha }}exp(-\frac{x^2}{4\alpha }),$$

(48-1)

$$F[f\left(x\right)\mathit{exp}\left(-iCx\right)]=F\left(\tau +C\right).$$

(48-2)

When α is determined from Equation (47) and C is a constant, we obtain

$$F\left[\psi \right]=\mathrm{e}\mathrm{x}\mathrm{p}[-\frac{\mathrm{ħ}}{4M\omega }{\left(k-b\right)}^2].$$

(49)

To depict this distribution, we must determine the parameters M and ω.

To do this, we employ the zero-point energy of a quark, because the interaction is a static electric field between a quark and an electron, as discussed previously:

$$\frac{1}{2}\mathrm{ħ}\omega =3m_{A,}{c}^2{m}_A=3m,$$

(50)

where the mass m_A of a quark in a nucleon is theoretically given as three times that of an electron. For details, see the Appendix.

$$M=m_A=3m,\omega =\frac{9m{c}^2}{\mathrm{ħ}}\times 2,$$

(52)

To conclude,

$$F\left[\psi \right]=exp\left[-\frac{1}{4}\frac{1}{3m}\frac{1}{9m{c}^2}\frac{\mathrm{ħ}}{2}{\left(k-b\right)}^2\right],$$

(53)

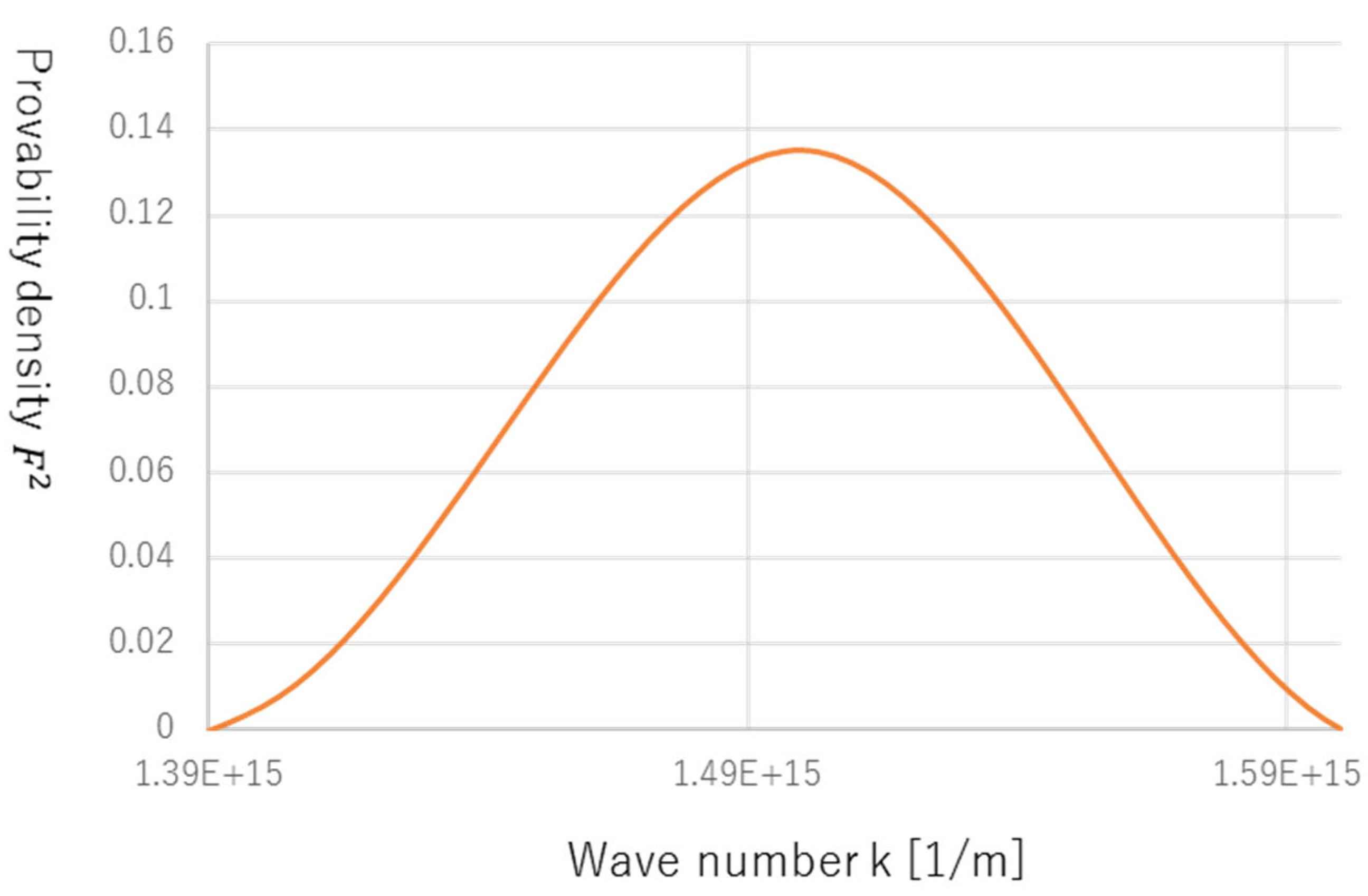
The result is shown in Figure 3. That is, the probability density of a neutron is F² for wave number k. This clearly shows that a β collapse is described by a Gaussian distribution.

Moreover, the kinetic energy of an electron is

$$K=\frac{{\mathrm{ħ}}^2{b}^2}{2m}=\mathrm{constant}$$

(54)

Considering the Feynman diagram [15], we assume that the constant kinetic energy of an electron gives the rest energy of W:

$$m_w{c}^2=\frac{{\mathrm{ħ}}^2{b}^2}{2m}.$$

(55)

When the mass of W in terms of measurements [15] is applied to this equation, the constant wave number implies the radius of a neutron as follows:

$$r_N\equiv \frac{1}{b}=0.7\times {10}^{-15}\mathrm{m}.$$

(56)

The equation is allowed to consider the radius of a neutron. Using this value, we calculated the lifetime of a neutron, which agrees well with the measurements. This implies that, from the initial state where an electron is attached around a proton, the electron conserves the wavelength 1/b. Because the wave number b of an electron is positive (not negative or zero), the symmetry of space is broken. Considering this logic is gone back, it implies that the mass of W boson was predicted.

Let us consider the mass of Z.

Considering the Feynman diagram [15], the mass difference between W and Z stems from the Coulombic attractive interaction F_E between an electron and a positron, which forms circular movements whose radius is λ_c . This implies that the electron and the positron have rotation as well as linear movement.

$$m_z{c}^2=\frac{e^2}{4\pi {\epsilon }_q{\lambda }_c}+m_W{c}^2.$$

(57)

As an important notation, in a nucleon, the perfect ferromagnetism is formed [16]. That is, B=H. Thus, the permittivity ε_q is varied:

$$\frac{1}{\sqrt{{\epsilon }_q\mu }}=c,\mu =1,$$

(58)

$${\epsilon }_q=1.0\times {10}^{-17}.$$

(59)

Employing this value, the first term for the attractive Coulombic interaction is calculated as:

$$\frac{e^2}{4\pi {\epsilon }_q}\frac{2mc}{ħ}=7.96GeV.$$

(60)

Considering the rest energy of W from the measurements, the rest energy of Z is given as:

$$m_z{c}^2=\left(7.96+80.5\right)GeV=88.4GeV.$$

(61)

The measurement is 91 GeV [15], and, thus, the agreement is sufficient.

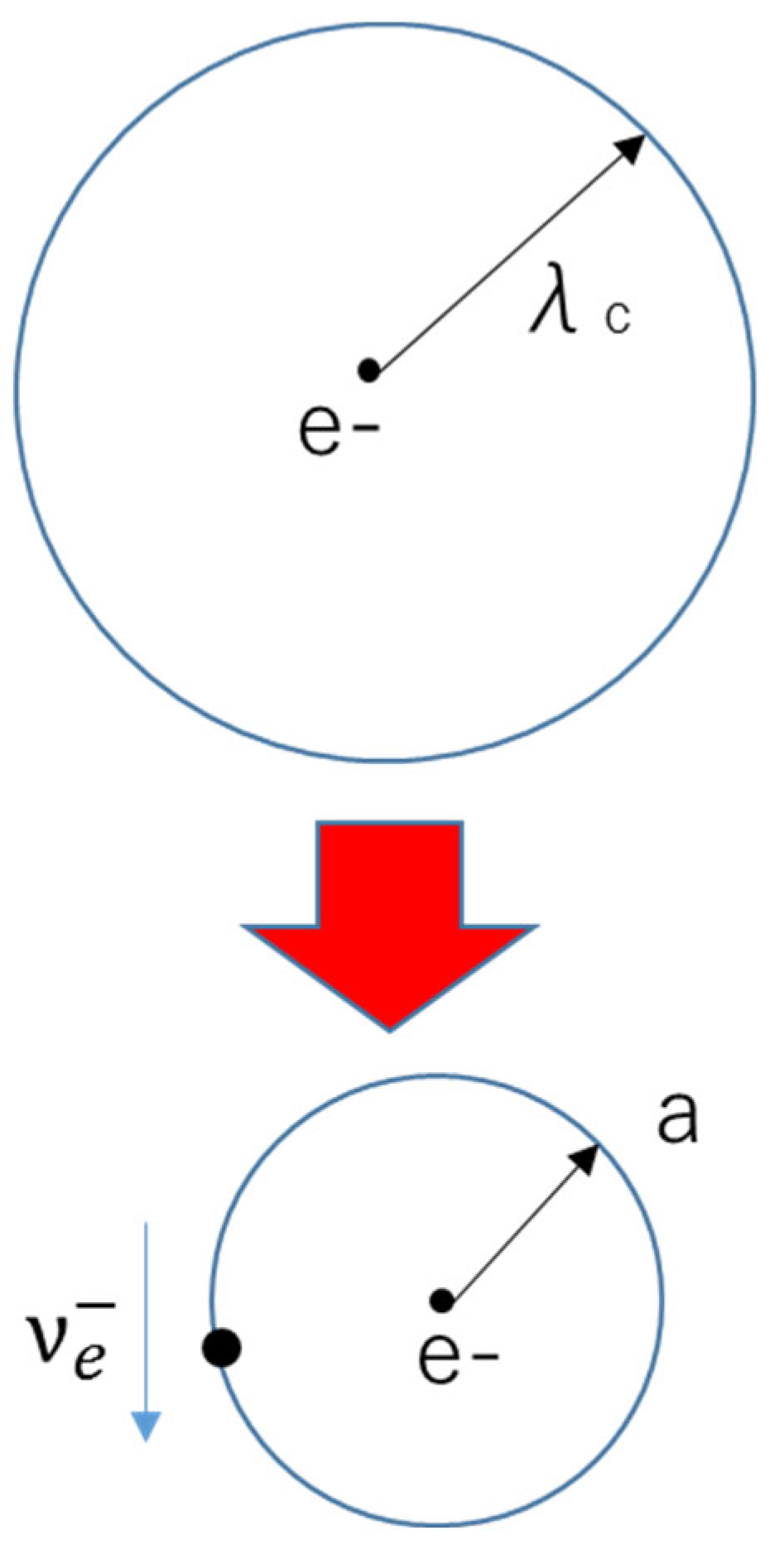
In turn, let us discuss the meaning of a neutrino.

The wave number b of an electron implies the radius of a neutron, which has 10^-15 m order and is smaller than λ_c.. However, this does not contradict the concept of a quantized space length λ_c, owing to the existence of a neutrino. Thus far, the velocity v in zero-point energy is kept constant at 0.68c. However, when an electron takes an accompanying neutrino, this velocity is changed, which leads to a larger Lorentz contraction, allowing for a quantized space (λ_c) change on the order of 10^-15m. Thus, electrons having a neutrino can exist in a nucleon:

$$r_N={\lambda }_c\sqrt{1-\frac{v_{\mu }^2}{c^2}},$$

(62)

where v_μ denotes the rotating velocity of a neutrino around an electron:

$$v_{\mu }=c\sqrt{1-\frac{r_N^2}{{\lambda }_c^2}}=0.993c.$$

(63)

As indicated in the result, the speed of a neutrino is approximately 99.3% of the speed of light. Because of this, if an experimenter were to apply a rough measurement, such a high speed could not be distinguished from the speed of light. Thus, to measure the speed of a neutrino, we need to apply an extremely accurate method of measurement. In Figure 4, a schematic of the above is shown.

2-3. Strong Interaction

In our previous paper [16], we described quarks’ interaction as static magnetic field energy, which resulted in the mass of a proton and a linear potential. The salient point was that this interaction was also derived from the zero-point energy and the linear attractive potential was obtained purely analytically (not numerically). Here, we discuss the pi-meson, which acts between two nucleons as a strong attractive interaction. In fact, this force is also derived from the zero-point energy, and this force is, indeed, the Lorentz force.

Figure 5 shows the schematic of two nucleons in which three quarks have rotation. Each rotation of two nucleons has the same angular frequency and rotational direction. Now we consider the motions of 1a and 1b quarks.

These quarks maintain constant distance, i.e., the radius r_c, and rotational velocity remain same. Considering this fact, we can employ a model in Figure 6. In this figure, quarks 1a and 1b move in the same direction with the same velocity. This model is analogized by two electric current leads, which exhibit an attractive force [17]. This force is the Lorentz force. We thus claim that the strong interaction between two nucleons is the Lorentz-force, which is derived from the zero-point energy.

Let us calculate the mass of a pi-meson considering this model. .

First, as discussed previously, the internal magnetic permeability of a nucleon is determined by the fact that it has the property of the perfect ferromagnetism. That is, B=H. Therefore, the Lorentz-force is:

$$F=\frac{1}{3}evH,$$

(64)

$$v=r_c\omega .$$

(65)

Here, the zero-point energy is considered as discussed previously:

$$\frac{1}{2}\mathrm{ħ}\omega =3m_A{c}^2,$$

(50)

where m_A is the mass of the quark in a nucleon, which is three times larger than that of an electron.

Thus,

$$v=r_c\frac{6m_A{c}^2}{\mathrm{ħ}}.$$

(66)

From [16], three quarks, each having the charge 1/3e, have rotations with an angular frequency ω, which results in a current I and magnetic field H. Thus, the central magnetic field is:

$$H=\frac{I}{2r_c},$$

(67)

$$I=\frac{1/3e}{T},$$

(68)

where T is the period of the rotations of the quarks.

Thus, the current is:

$$I=\frac{1}{3}e\frac{\omega }{2\pi }=\frac{1}{3}e\frac{1}{2\pi }\frac{6m_A{c}^2}{\mathrm{ħ}}.$$

(69)

From this current, the magnetic field is:

$$H=\frac{1}{4\pi }\frac{1/3e}{r_c}\frac{6m_A{c}^2}{\mathrm{ħ}}.$$

(70)

Thus, energy u is gained, which is an attractive force:

$$\mathrm{u}=-\int Fdr=-\frac{1}{3}evH{r}_c=-\frac{1}{36\pi }{e}^2{r}_c{\left(\frac{6m_A{c}^2}{\mathrm{ħ}}\right)}^2.$$

(80)

When substituting the physics constants,

$$\left|u\right|=21.9\times {10}^{-12}\mathrm{J}.$$

(81)

Thus, we obtain the mass of pi-meson m_m:

$$m_m=2.4\times {10}^{-28}\mathrm{k}\mathrm{g}.$$

(82)

This value agrees with the mass predicted by Yukawa [15].

3. Discussion

Existing elementary particle physics tends to add new concepts to solve problems. For example, when the problem of the exclusion principle in a nucleon arose, a new concept, the color charge, was added. However, while color charges have yet to be measured, a new theory was constructed using color charges to solve another problem. In this way, existing elementary particle physics went further in-depth and developed new confusions. Moreover, the Weinberg-Salam theory also added weak hypercharge as a new concept, and the authors introduced a continuous electrical charge. However, at the level of particle physics, a charge is quantized. While these views were adopted, the standard model had many undetermined parameters. To solve this problem, another new concept, known as the super-string, was added, a concept that has not predicted any measurable quantities in physics.

On the other hand, our attitude differs from the above. First, we have taken care to employ directly measurable physical phenomena instead of adding new concepts, and reconsider basic physics knowledge. In this way, the derived theory is simple and understandable and has a clear picture rooted in physics.

This study introduces a concept of quantized spacetimes with the zero-point energy and aims to explain all fields, including four forces and particles employing this concept. The basic assumption is only that a quantized spacetime is introduced. That is, other serious assumptions or conditions have not been introduced.

Under this concept of quantized spacetime with the zero-point energy, we could thus describe:

• Uniformity of the electromagnetic and gravitational fields on the microscopic scale with a quantized Einstein gravity equation;
• The weak field, with the radius and lifetime of a neutron, W and Z bosons, and β collapse. The key point is that the radius of a neutron has been derived by giving the measured mass of W; we use the radius of a neutron to predict the mass of W. Moreover, the mass of Z is calculated. These results agreed well with the measurements. We employed difference methods from the Weinberg-Salam theory. The reason is that:

  1)

  Weinberg-Salam theory employs weak hypercharge, and thus the charge is arbitrary and not quantized;

  2)

  The Weinberg angular was given such that the masses of W and Z agreed with the measurements [15]. The value of the Weinberg angular had no meaning in terms of physics.

• Moreover, we clarified the meaning of the existence of the neutrino in terms of a quantized spacetime. Considering the gravitational interaction between the electron and the neutrino, the mass of the electron in the β collapse apparently varies. Thus, strictly speaking:

  $$\frac{{ħ}^2{b}^2}{2\alpha m}=m_W{c}^2$$

  (54-2)

where α denotes the correction constant.

Thus, when the accurate mass of W and the wave number b, i.e., the radius of a neutron, are substituted, the correction constant, α, will be calculated. According to our hand calculations, α=0.95, approximately. Note that, from the measurements of neutrino oscillation, it was clarified that there are masses of neutrinos. However, considering our derivation, it is natural that the mass of a neutrino exists because it has gravitational interaction with the electron in the β collapse. We claim that it is more important to consider this interaction between the electron and the neutrino than to calculate the mass of the neutrino itself. However, if it can be considered that the gravitational interaction with a neutrino is identified as its measured mass, the mass can be determined with the following:

$$\frac{m{c}^2}{(m+m_{\nu })c^2}=\alpha .$$

(83)

When the correction constant α was substituted for the value 0.95, the mass, considering the gravitational interaction for a neutrino, is calculated as

$$m_{\nu }=4.5\times {10}^{-32}kg.$$

(84)

This mass including the gravity is about 5% for that of an electron.

We did not consider the Higgs field. The reasons are:

1)

To be sure, the Higgs mass was measured. However, it was not made completely clear whether it works as predicted by the standard model [4].

2)

As a more serious problem, the standard model treated cut-off Λ, which led to relatively low energy. However, when calculating quantum corrections concerning the square of the Higgs mass, there appeared a large quantum correction, proportional to ⋀². That is, under the quantum corrections, the standard model could not guarantee the small mass of the Higgs [4]. Basically, the standard model has a model from the QED, and, as a result of introducing very local gages, it was necessary to obtain the reason the particles gained mass. To solve this problem, in the standard model, the spontaneous break of symmetries and Higgs fields were suggested. However, as discussed above, the mass of Higgs had a serious problem, which implied that the standard model was incomplete. For this reason, many new theories have been suggested, though none are supported by measurements as described in the introduction in this paper. Nonetheless, until the Higgs is accurately described, we will not consider this field.

With our previous paper [16], a strong interaction was described between quarks. As a result, the mass of a proton, and the interaction between two nucleons, agreed well with the measurements using hand calculations. Moreover, the mass of a quark in a nucleon is clarified theoretically in the Appendix. Using this mass, the above calculations were achieved. On the other hand, the QCD has some problems:

1)

The concept of color charges has yet to be measured. Because the problem of the exclusion principle was solved by giving the spin of a quark theoretically instead of color charges, we claim that it was not necessary to add the concept of color charges. The color has not been expressly defined.

2)

In the QCD, the mass of a quark is given such that the hadrons’ masses are well-predicted.

3)

The QCD is a numerical calculation. This is a so-called ideal experiment, not pure theory.

To conclude, we can say that, using only the zero-point energy, we described the uniformity field including the gravity field, electromagnetic field, weak interaction, and strong interaction. However, in the present paper, we did not describe time-dependent electromagnetic fields. However, this was already well-described by quantum physics. Moreover, this paper describes only the first of three generations. As a future work, it will be necessary to consider them.

4. Summary

This paper describes how all fields in particle physics can be calculated using the concept of a quantized spacetime and the sole source of the zero-point energy.

The calculated values agreed well with the measurements. Moreover, we established new and concrete physical pictures in particle physics.

In the present work, we considered only the first of three generations. Thus, as the future works, the leptons and neutrinos of the other generations should be considered.