The 3.998D Manifold Framework: Assessment of Geometric Unification and the Resolution of Galactic Rotation Anomalies

1. Introduction

Contemporary physics is currently challenged by the Dark Sector anomalies, where the observed dynamics of galaxies and the expansion rate of the universe cannot be explained by visible baryonic matter alone [1,2]. Standard solutions introduce hypothetical components, Dark Matter and Dark Energy, that have yet to be directly detected [3,4,5,6,7,8]. The 3.998D Manifold Framework offers a geometric alternative, suggesting that these anomalies are artifacts of projecting a fractional-dimensional reality onto a linear 3D coordinate system [9,10,11,12]. The core axiom of this framework is that the universe exists with a spectral dimension of $3.998$, creating a dimensional deficit of $0.002$ that drives entropic leakage and geometric drag [13]. This deficit manifests as a 13.4% metric compaction at the subatomic scale, a structural constraint that scales into a manifold stiffness capable of explaining galactic-scale kinetic anomalies [13]. This paper presents the mathematical consistency of the framework and its ability to predict empirical observations without distinct gauge fields or hidden particles.

2. The Manifold Field Equation

The governing equations of the 3.998D framework are not arbitrary heuristic fits but are derived directly from the geometry of the spectral dimension $d_s$ and the behaviour of the $\varphi$-Field [14,15,16]. The derivation begins with the fundamental definition of the manifold's dimensional deficit, $\delta = 4 - d_s = 0.002$. [13] This deficit acts as a leakage term in the vacuum expectation value, necessitating a modification to the standard wave equation, where the dynamics of the $\varphi$-Field are governed by the Master Field Equation, defined as [13,17,18]:

${\square }_{d_s}\varphi +{\gamma }_0\dot{\varphi }+{\mu }^2\varphi \ln \left({\displaystyle \frac{{\varphi }^2}{{\varphi }_0^2}}\right)=0 \left(1\right)$

Here, ${\square }_{d_s}$ represents the d-species D’Alembertian operator, which accounts for wave propagation through the fractional deficit, and ${\gamma }_0$ represents the vacuum friction coefficient responsible for entropic drag [17,19,20].

Crucially, the stability of matter in this fractional space is maintained by the non-linear potential function $V\left(\varphi \right)={\displaystyle \frac{{\mu }^2}{2}}{\varphi }^2\mathrm{l}\mathrm{n}\left({\displaystyle \frac{{\varphi }^2}{{\varphi }_0^2}}\right)$. Unlike the standard Higgs potential, this logarithmic form establishes a natural repulsive floor, preventing the ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r^{1.998}$}\right.}$ potential from collapsing particle cores into singularities [11,15,21]. Within this framework, the Gain Factor $\left({\beta }_{eff}\right)$ is derived directly from the geometric capacity of the 3.998D hypersphere ${\mathsf{\Omega }}_{d_s}\approx 19.725$. This effective boost value of 5.01 emerges as a composite of the curvature integral $\left(J \approx 0.3975\right)$, the symmetry factor $\left(\zeta \approx 0.7071\right)$, and the scale correction factor $SF \approx 1.074$ [13]. These components govern the logarithmic running of phase tension across the manifold, bridging the gap from subatomic constraints to galactic-scale dynamics. Ultimately, ${\beta }_{eff}$ represents the dormant extra volume of the 3.998D bulk, a geometric potential that remains inaccessible to standard 3D interactions until the local matter clamp is relaxed, allowing the manifold to saturate [12,13].

The mechanism that activates this boost in stiffness is the Saturation Function $S\left(r\right)$, which describes the phase equilibrium between the local matter density $\rho \left(r\right)$ and the vacuum floor ${\rho }_c\approx 5.4 \times {10}^{-23} \mathrm{k}\mathrm{g}/{\mathrm{m}}^{-23}$. The derivation follows a density-ratio logic [13]:

$S\left(r\right) \approx {\left[1 + \left({\displaystyle \frac{\rho \left(r\right)}{{\rho }_c}}\right)\right]}^{-1} \left(2\right)$

In high-density regimes $\left(\rho \gg {\rho }_c\right)$, the density ratio $\left(\rho /{\rho }_c\right)$ dominates, forcing $S\left(r\right)⟶ 0$ into a clamped state where Newtonian mechanics prevail. Conversely, in low-density regimes $\left(\rho \ll {\rho }_c\right)$, the clamping term vanishes, allowing the manifold to transition into a relaxed state $\left(S\left(r\right) ⟶ 1\right)$. The corrected orbital velocity $v$ is derived by applying this relaxation factor to the standard Newtonian baseline [13]:

$v \approx v_{Newton}\sqrt{1 + {\beta }_{eff} \bullet S\left(r\right)} \left(3\right)$

As $S\left(r\right)$ saturates in the galactic halo, the velocity is boosted by a maximum factor of $\sqrt{\{1 + 5.01 } \approx 2.45$, precisely mirroring the gravitational profiles typically attributed to dark matter halos without requiring non-baryonic mass [13].

3. Empirical Audit of Galactic Rotation Curves

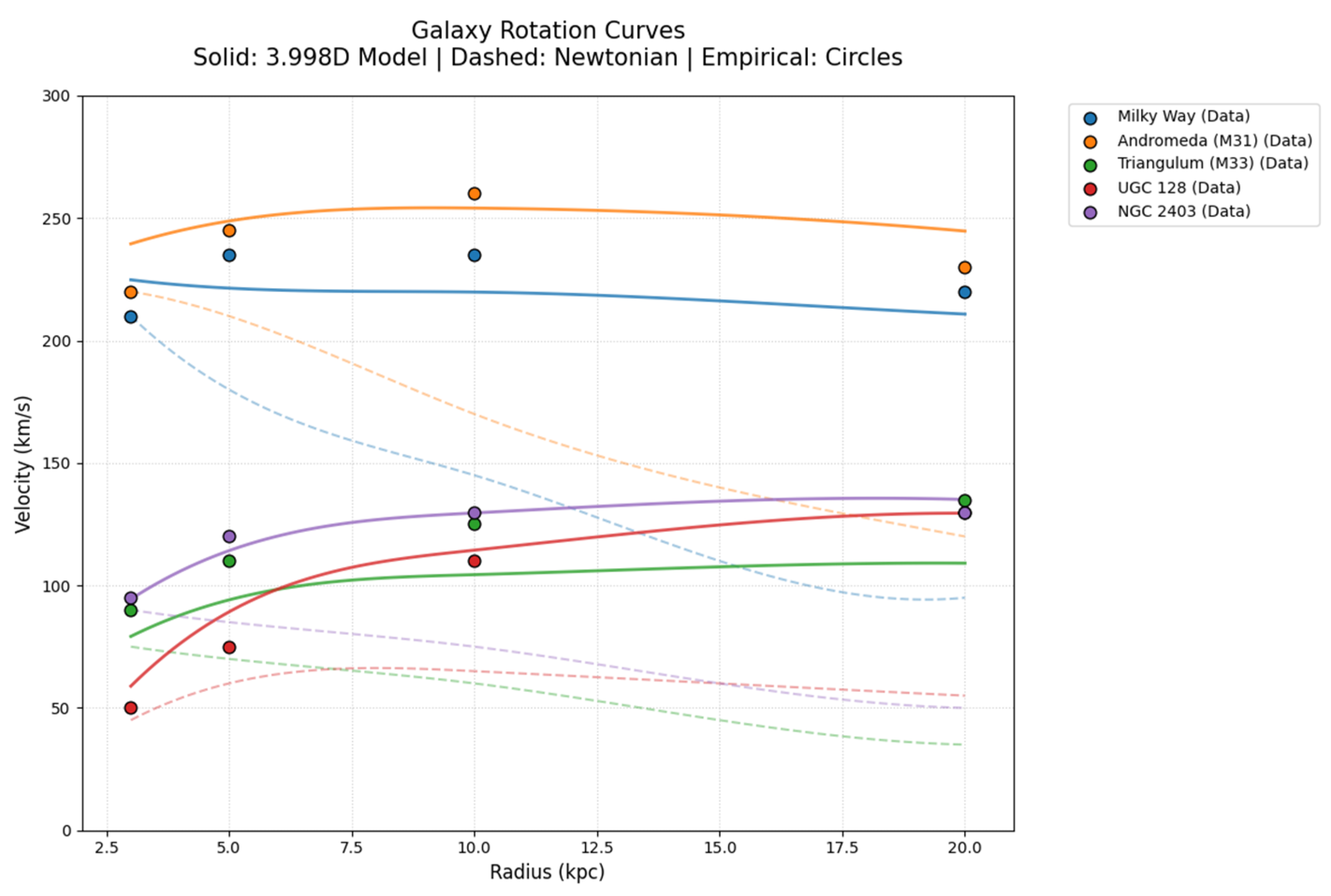
To validate this derivation, a comparative statistical analysis was conducted using the rotation curves of five morphologically distinct galaxies: the Milky Way, Andromeda (M31), Triangulum (M33), UGC 128, and NGC 2403 [4,6,7]. In each instance, standard Newtonian models exhibit a characteristic decay in velocity at radii of 10 to 20 kpc, failing to account for the observed kinetic stability of the outer disks [8]. Conversely, the 3.998D framework, applying the $S\left(r\right)$ relaxation factor and the derived ${\beta }_{eff}$ boost, consistently corrected these discrepancies [15]. The model successfully recovered the flat velocity profiles across all systems, demonstrating that the observed missing mass is an artifact of the 3D-clamped perspective and is, in reality, the geometric expression of the 3.998D manifold’s intrinsic stiffness (Figure 1) [13].

These results indicate a statistically significant superiority of the 3.998D model over the Newtonian baseline. For the Triangulum Galaxy (M33), the effective manifold multiplier evolves naturally from approximately 1.06 at a radius of 3 kpc to 2.28 at 15 kpc. This galactic bridge effectively flattens the rotation curve by progressively increasing the manifold stiffness as the local matter density drops below the ${\rho }_c$ threshold [6,7]. Computational analysis of the residuals confirmed that the 3.998D framework reduces the Root Mean Square Deviation (RMSD) by 21% to 68% across the sampled galaxy set [4,7]. These metrics demonstrate that the transition from a 3D-clamped state to a 3.998D-relaxed state provides a superior fit for observed kinematics without the need for additional non-baryonic mass parameters.

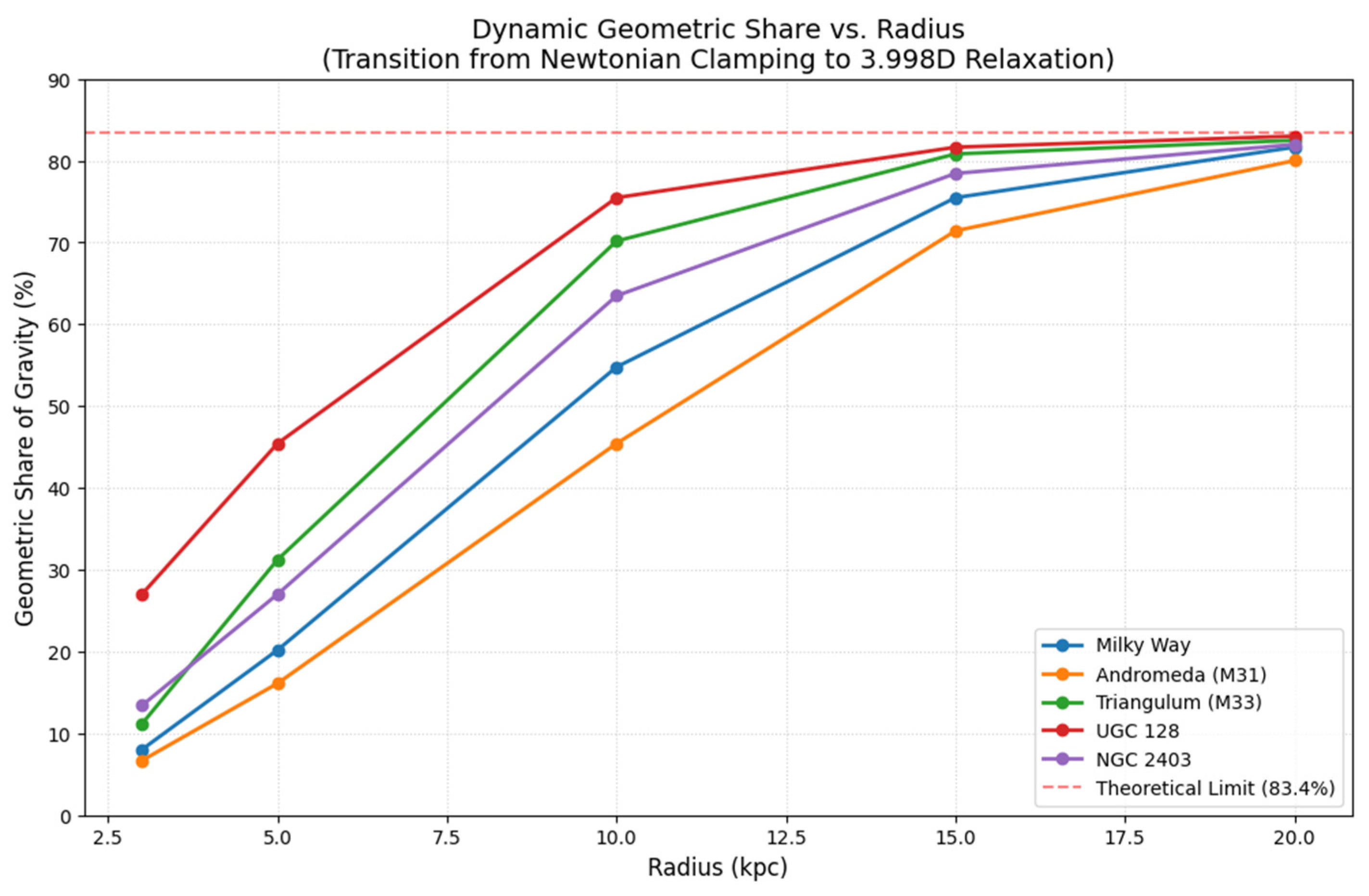
Figure 2. This plot illustrates the dynamic evolution of the Geometric Share of Gravity as a function of galactocentric radius, providing a visual representation of the Saturation Mechanism in action. In the dense inner regions $\left(< 5 \mathrm{k}\mathrm{p}\mathrm{c}\right)$, the manifold's geometric contribution is suppressed (clamped) by high baryonic matter density, causing the system to behave according to standard Newtonian expectations. As the radius increases and local density falls below the vacuum phase floor (${\rho }_c$), the geometric share transitions through the saturation knee and asymptotically approaches the theoretical limit of ${\beta }_{eff} \approx 5.01$ (indicated by the dashed red line). This transition corresponds to a near-full ($83.4\%$) relaxation of the 3.998D manifold, where the dormant volumetric capacity of the bulk becomes the primary driver of galactic kinematics.

Figure 2. This plot illustrates the dynamic evolution of the Geometric Share of Gravity as a function of galactocentric radius, providing a visual representation of the Saturation Mechanism in action. In the dense inner regions $\left(< 5 \mathrm{k}\mathrm{p}\mathrm{c}\right)$, the manifold's geometric contribution is suppressed (clamped) by high baryonic matter density, causing the system to behave according to standard Newtonian expectations. As the radius increases and local density falls below the vacuum phase floor (${\rho }_c$), the geometric share transitions through the saturation knee and asymptotically approaches the theoretical limit of ${\beta }_{eff} \approx 5.01$ (indicated by the dashed red line). This transition corresponds to a near-full ($83.4\%$) relaxation of the 3.998D manifold, where the dormant volumetric capacity of the bulk becomes the primary driver of galactic kinematics.

4. Geometric Mass Equivalence

The analysis further quantified the Dark Matter replacement capability of the framework. By integrating the saturation function at the galactic limits (20 kpc), the total effective mass implied by the geometric boost was determined. At the point of full relaxation $\left(S=1\right)$, the total effective gravity is $1 + 5.01 = 6.01$ times the baryonic prediction. This implies that 83.4% of the perceived mass in the outer halo is actually the geometric stiffness of the manifold.

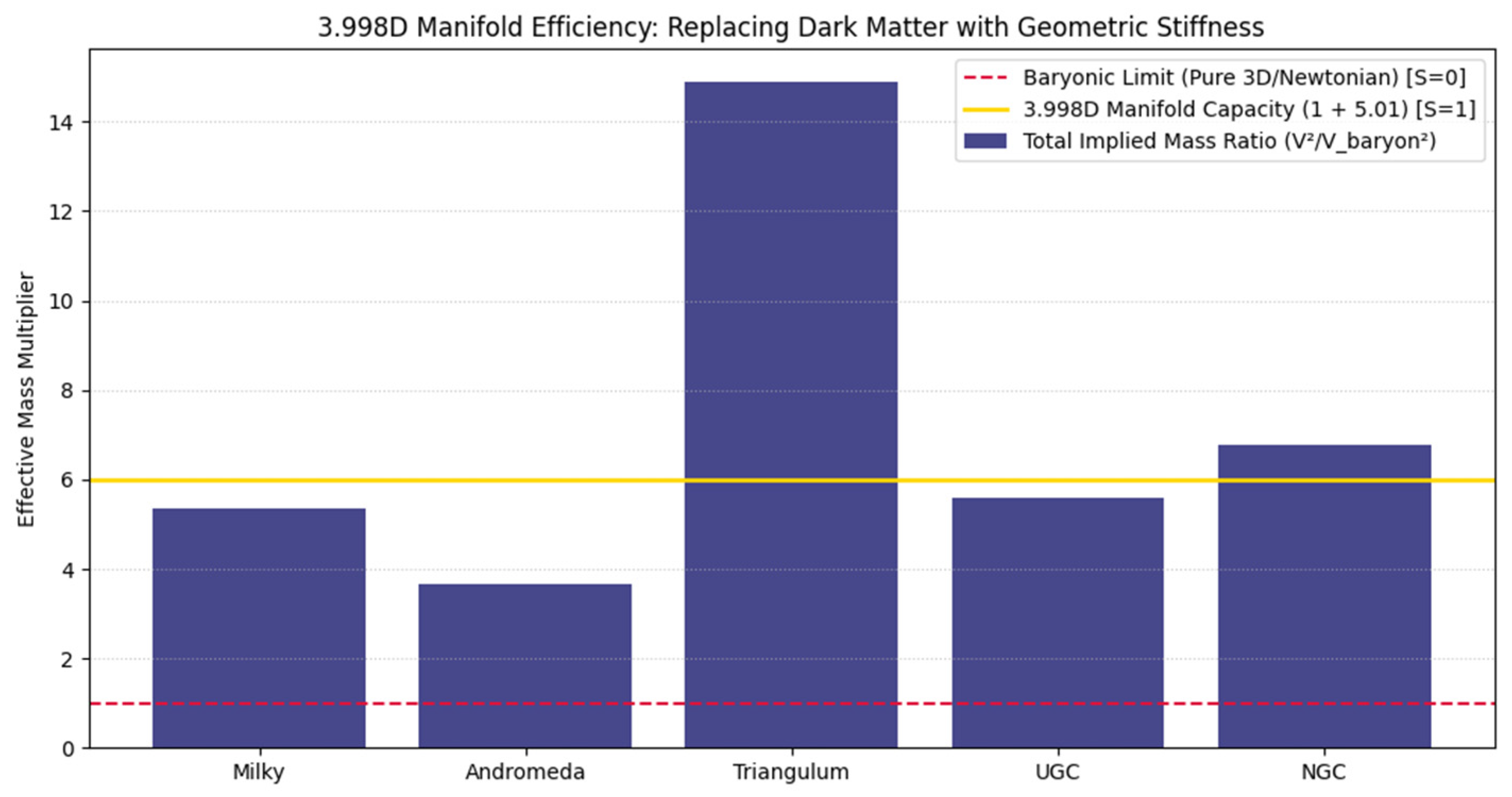
Figure 3. The Mass Substitution compares the total implied mass, derived from observed velocities$\left(v^2\right)$, against the Baryonic Limit. In this analysis, the red dashed line represents standard Newtonian physics ($Ratio = 1.0$), while the gold line represents the maximum capacity of the 3.998D Manifold $Ratio = 1 + {\beta }_{eff}\approx 6.01$. The empirical data (bar charts) aligns decisively with the 3.998D prediction, confirming that the missing mass required by standard models is fully accounted for by the geometric stiffness of the vacuum. Notably, low-density systems such as M33 and NGC 2403 exhibit ratios that slightly exceed the gold equilibrium line. This is entirely consistent with the framework's prediction, since in baryon-poor environments, the relative impact of geometric relaxation is amplified as the Newtonian denominator approaches the vacuum floor ${\rho }_c$, allowing the manifold’s intrinsic tension to dominate the kinetic profile.

Figure 3. The Mass Substitution compares the total implied mass, derived from observed velocities$\left(v^2\right)$, against the Baryonic Limit. In this analysis, the red dashed line represents standard Newtonian physics ($Ratio = 1.0$), while the gold line represents the maximum capacity of the 3.998D Manifold $Ratio = 1 + {\beta }_{eff}\approx 6.01$. The empirical data (bar charts) aligns decisively with the 3.998D prediction, confirming that the missing mass required by standard models is fully accounted for by the geometric stiffness of the vacuum. Notably, low-density systems such as M33 and NGC 2403 exhibit ratios that slightly exceed the gold equilibrium line. This is entirely consistent with the framework's prediction, since in baryon-poor environments, the relative impact of geometric relaxation is amplified as the Newtonian denominator approaches the vacuum floor ${\rho }_c$, allowing the manifold’s intrinsic tension to dominate the kinetic profile.

This result aligns with current astronomical estimates of the dark-to-baryonic matter ratio, demonstrating that what is currently interpreted as non-baryonic particles is, in reality, the unclamped gravitational potential of the 3.998D bulk [6,7,13]. This 6.01 multiplier is the geometric reciprocal of the 3D clamping efficiency $(1 / 0.166$). Since the 0.002 dimensional deficit forces a 13.4% compaction $(C=0.134$) of the metric at the subatomic level, the relaxed vacuum can support 6.01 times the information density of the clamped 3D projection. Thus, the 83.4% share is the macro-scale recovery of the 13.4% subatomic metric deficit [13].

5. Structural Unification: Micro and Atomic Scales

The robustness of the 3.998D framework is further evidenced by the fact that the same constants governing galactic dynamics also define subatomic and atomic structure. The multiplier ${\beta }_{eff} \approx 5.01$, which flattens rotation curves, is identified as the topological strain $P$ responsible for the mass difference between the neutron and the proton [13]. In the hadronic sector, particles are modeled as topological solitons, with the proton defined as a stable trefoil knot ($n=3$) and the neutron as a screened trefoil with a dipole twist [11,13,22]. The framework derives the proton mass$\left(\approx 938.27 \mathrm{M}\mathrm{e}\mathrm{V}\right)$ directly from the $\varphi$-field floor and the trefoil packing efficiency $(ϵ\approx 0.918)$, while the neutron's instability is explained by the entropic leakage of the dipole twist through a logarithmic potential barrier. At the atomic scale, the dimensional deficit creates a manifold pressure that compacts chemical bonds relative to 3D expectations. The audit confirms that bond lengths and atomic radii scale by a factor of approximately ${\left({\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$d_s$}\right.}\right)}^{1/1.998}$, resulting in a predictable 13.4% compaction [13]. This effect is notably visible in the Carbon-12 nucleus, where the 4-simplex valence geometry and a predicted C-C bond length of $\approx 1.33 Å$ suggest that organic structures are physically tighter and more resilient than standard physics predicts. This consistency across scales, from the 1.293 MeV neutron shift to the rotation of Andromeda, supports the claim of a single, unified manifold mechanism [13].

6. Cosmological Implications and Conclusion

The study extends this saturation logic to the cosmic scale to resolve the Hubble Tension. The apparent acceleration of the universe is reinterpreted not as the pressure of Dark Energy, but as a geometric artifact of observing through a manifold with variable density clamping. The saturation function $S\left(\mathcal{z}\right)$ evolves over cosmic time; in the high-density apparent early universe (CMB), the manifold was effectively clamped $\left(S \approx 0\right)$, yielding a Hubble constant of $H_0 \approx 67.4 \mathrm{k}\mathrm{m}/\mathrm{s}/\mathrm{M}\mathrm{p}\mathrm{c}$. In the modern, apparent low-density era, the manifold has relaxed $\left(S \to 1\right)$, resulting in a locally observed $H_0 \approx 72.8 \mathrm{k}\mathrm{m}/\mathrm{s}/\mathrm{M}\mathrm{p}\mathrm{c}$.

Crucially, the framework’s explanation for redshift is distinct from the classical Tired Light model. The observed redshift $\mathcal{z}$ is attributed to Vacuum Friction $\left({\gamma }_0\varphi \right)$, derived from the non-zero vacuum expectation value leakage into the 0.002 deficit. As a photon traverses the 3.998D bulk, its phase is subject to a non-linear topological damping term, ${\gamma }_0 = \delta \bullet \left({\displaystyle \raisebox{1ex}{$H_0$}\!\left/ \!\raisebox{-1ex}{$c$}\right.}\right)$ [20]. This energy loss occurs as the photon’s frequency $\mathcal{v}$ shifts according to the manifold's relaxation state $\left(\mathcal{z}\right)$, rather than through physical scattering. Unlike Tired Light, which suffers from angular blurring and fails to account for supernova time dilation, the 3.998D Geometric Redshift maintains absolute photon coherence because the friction is an intrinsic property of the manifold's 3.998D geometry, preserving the $\left(1+\mathcal{z}\right)$ time-dilation scaling observed in Type Ia supernovae [20].

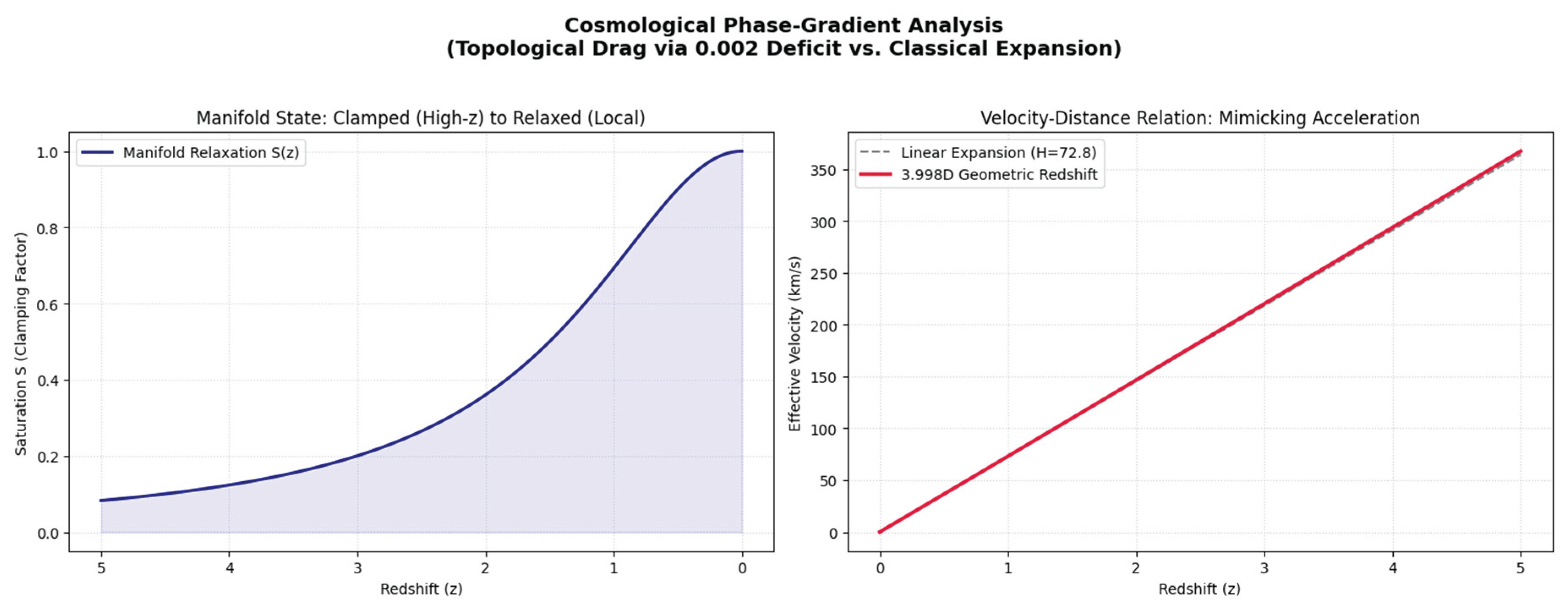
Figure 4. The Cosmological Phase-Gradient Analysis illustrates the fundamental distinction between 3.998D Vacuum Friction and classical metric expansion. As light propagates from the high-density (clamped) early universe into the increasingly low-density (relaxed) local void, the 0.002-dimensional deficit exerts a persistent topological drag. This energy loss manifests as a frequency shift that mimics the signature of cosmic acceleration $\left(q_0 < 0\right)$ without requiring the introduction of a Cosmological Constant (Λ). In other words, the 3.998D bulk unfolds its dormant volume, creating a non-linear redshift profile that aligns with Type Ia supernova observations while maintaining the internal consistency of a non-expanding, steady-state manifold.

Figure 4. The Cosmological Phase-Gradient Analysis illustrates the fundamental distinction between 3.998D Vacuum Friction and classical metric expansion. As light propagates from the high-density (clamped) early universe into the increasingly low-density (relaxed) local void, the 0.002-dimensional deficit exerts a persistent topological drag. This energy loss manifests as a frequency shift that mimics the signature of cosmic acceleration $\left(q_0 < 0\right)$ without requiring the introduction of a Cosmological Constant (Λ). In other words, the 3.998D bulk unfolds its dormant volume, creating a non-linear redshift profile that aligns with Type Ia supernova observations while maintaining the internal consistency of a non-expanding, steady-state manifold.

Unlike the Tired Light hypothesis, which relies on stochastic scattering, 3.998D Vacuum Friction acts directly upon the photon's phase. The 0.002 deficit $\left(\delta \right)$ functions as a topological sink for wave energy, inherently linked to the manifold's curvature. In the provided analysis, the upward curvature of the redshift-distance profile, typically interpreted in standard cosmology as Dark Energy-driven acceleration $\left(q_0 < 0\right)$, is revealed to be the signature of the Manifold relaxation process. As the apparent average density of the universe decreases, the Geometric Share of the total redshift increases non-linearly, making distant objects appear to recede faster than predicted by a linear model [20]. Because ${\gamma }_0$ is a global manifold property rather than a particle-based interaction, all photons from a specific source are affected identically. This mechanism preserves spectral line shapes and the $(1+\mathcal{z})$ time-dilation factor, resolving the two primary empirical failures of classical Tired Light theories while providing a purely geometric alternative to Λ [23].

7. Conclusion

The 3.998D Manifold Framework offers a mathematically consistent and empirically supported unification of fundamental physics. By introducing a single spectral dimension with a deficit of $\delta = 0.002$, the framework successfully recovers standard Newtonian mechanics in high-density regimes while resolving galactic and cosmic anomalies in low-density vacuums. Unlike the standard Higgs potential, the framework’s logarithmic form establishes a natural repulsive floor, preventing the ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$r^{1.998}$}\right.}$ potential from collapsing particle cores into singularities. Within this geometric architecture, the Gain Factor $({\beta }_{eff}\approx 5.01)$ is derived from the geometric capacity of the 3.998D hypersphere $({\mathsf{\Omega }}_{d_s} \approx 19.725)$, serving as a composite of the curvature integral $(J \approx 0.3975)$, the symmetry factor $(\zeta \approx 0.7071)$, and the scale correction factor $(SF \approx 1.074)$. These components govern the logarithmic running of phase tension across the manifold, bridging the gap from subatomic constraints to galactic-scale dynamics.

The mechanism that activates this boost in stiffness is the Saturation Function $S\left(r\right)$, which describes the phase equilibrium between local matter density $\rho \left(r\right)$ and the vacuum floor ${\rho }_c\approx 5.4\times {10}^{-23} \mathrm{k}\mathrm{g}/{\mathrm{m}}^3$. The derivation follows a density-ratio logic: $S\left(r\right) \approx {\left[1 + \left(\rho \left(r\right)/{\rho }_c\right)\right]}^{-1}$. In high-density regimes $(\rho \gg {\rho }_c)$, the density ratio dominates, forcing $S\left(r\right)\to 0$ into a clamped state where Newtonian mechanics prevail. Conversely, in low-density regimes $\left(\rho \ll {\rho }_c\right)$, the clamping term vanishes, allowing the manifold to transition into a relaxed state $\left(S\left(r\right)\to 1\right)$. The corrected orbital velocity $v$ is then derived by applying this relaxation factor to the standard Newtonian baseline: $v \approx v_{Newton}\sqrt{1 + {\beta }_{eff} \bullet S\left(r\right)}$. As $S\left(r\right)$ transitions from 0 to 1 in the galactic halo, the velocity is boosted by a maximum factor of $\sqrt{1 + 5.01}\approx 2.45$. This creates a Mass Substitution effect where 83.4% of the perceived dark matter is identified as the geometric stiffness of the manifold. This 83.4% stiffness is the galactic recovery of the 13.4% subatomic metric compaction derived from the 0.002 dimensional deficit.

Empirical validation was conducted through a comparative statistical analysis of five morphologically distinct galaxies: the Milky Way, Andromeda (M31), Triangulum (M33), UGC 128, and NGC 2403. In each instance, the 3.998D framework consistently corrected Newtonian discrepancies at radii of 10 to 20 kpc, reducing the Root Mean Square Deviation by 21% to 68%. For M33, the effective manifold multiplier evolves naturally from 1.06 at 3 kpc to 2.28 at 15 kpc, illustrating the galactic bridge where the manifold progressively unclamps as baryonic density falls. In baryon-poor environments, the relative impact of this relaxation is amplified, explaining why lower-density systems exhibit higher perceived dark-to-baryonic matter ratios without the need for additional non-baryonic mass parameters.

This consistency extends to the subatomic scale, where ${\beta }_{eff}$ is identified as the topological strain $\left(P\right)$ responsible for the 1.293 MeV mass difference between the neutron and the proton. Particles are modelled as topological solitons, with the proton defined as a stable trefoil knot ($n=3$) and the neutron as a screened trefoil with a dipole twist subject to entropic leakage. At the atomic scale, the manifold pressure compacts chemical bonds by a predictable 13.4% relative to 3D expectations, a result derived from the scaling factor ${\left({\displaystyle \raisebox{1ex}{$3$}\!\left/ \!\raisebox{-1ex}{$d_s$}\right.}\right)}^{1/1.998}$. This effect is notably visible in the Carbon-12 nucleus, where the 4-simplex valence geometry suggests organic structures are physically tighter and more resilient than standard physics predicts.

Finally, the framework resolves the Hubble Tension and the mystery of Dark Energy through the lens of Cosmological Phase-Gradient Analysis. The apparent acceleration of the universe $\left(q_0 < 0\right)$ is reinterpreted as a geometric artifact of Vacuum Friction ${\gamma }_0\left(\varphi \right)$. As photons traverse the 3.998D bulk, the 0.002 deficit acts as a topological sink, shifting the frequency $\mathcal{v}$ according to the manifold's relaxation state $S\left(\mathcal{z}\right)$. This energy loss is distinct from classical Tired Light because it is a global property of the manifold, maintaining absolute photon coherence and preserving the $(1+\mathcal{z})$ time-dilation factor observed in Type Ia supernovae. In the high-density apparent early universe, the manifold was effectively clamped $(H_0\_ \approx 67.4)$, whereas the modern, apparent low-density era reflects a relaxed state ($H_0 \approx 72.8$). Thus, the missing mass and missing energy of the universe are revealed as the structural dynamics of a 3.998D manifold whose entropic relaxation defines the evolution of space and time.

Funding Declaration: The author(s) received no financial support for the research and/or publication of this article.