Submitted:
13 January 2026
Posted:
15 January 2026
You are already at the latest version
Abstract
Keywords:
1. Introduction
- 1.
- As the coefficients of system faults and disturbances meet the counteraction assumption, SMO with compensating terms allocated in output states is designed, such that observed error of system states is convergent, and model system is stable via feedback control;
- 2.
- In the general situation when perturbations are randomly distributed, the similarity transform on system matrices is designed to retain the faults at observed port in the transformed system, and the observed error by SMO is stabilized to the neighborhood of origin, which is verified by Lyapunov function and Inequality transform.
- 3.
- The designed FDI method is applied on an airplane model with different disturbance conditions, and the effect of fault based control is validated in simulation results, including the convergence of observed error, the boundedness of state trajectory under fault and disturbance condition, and the fault detection responses.
2. Preliminary Results
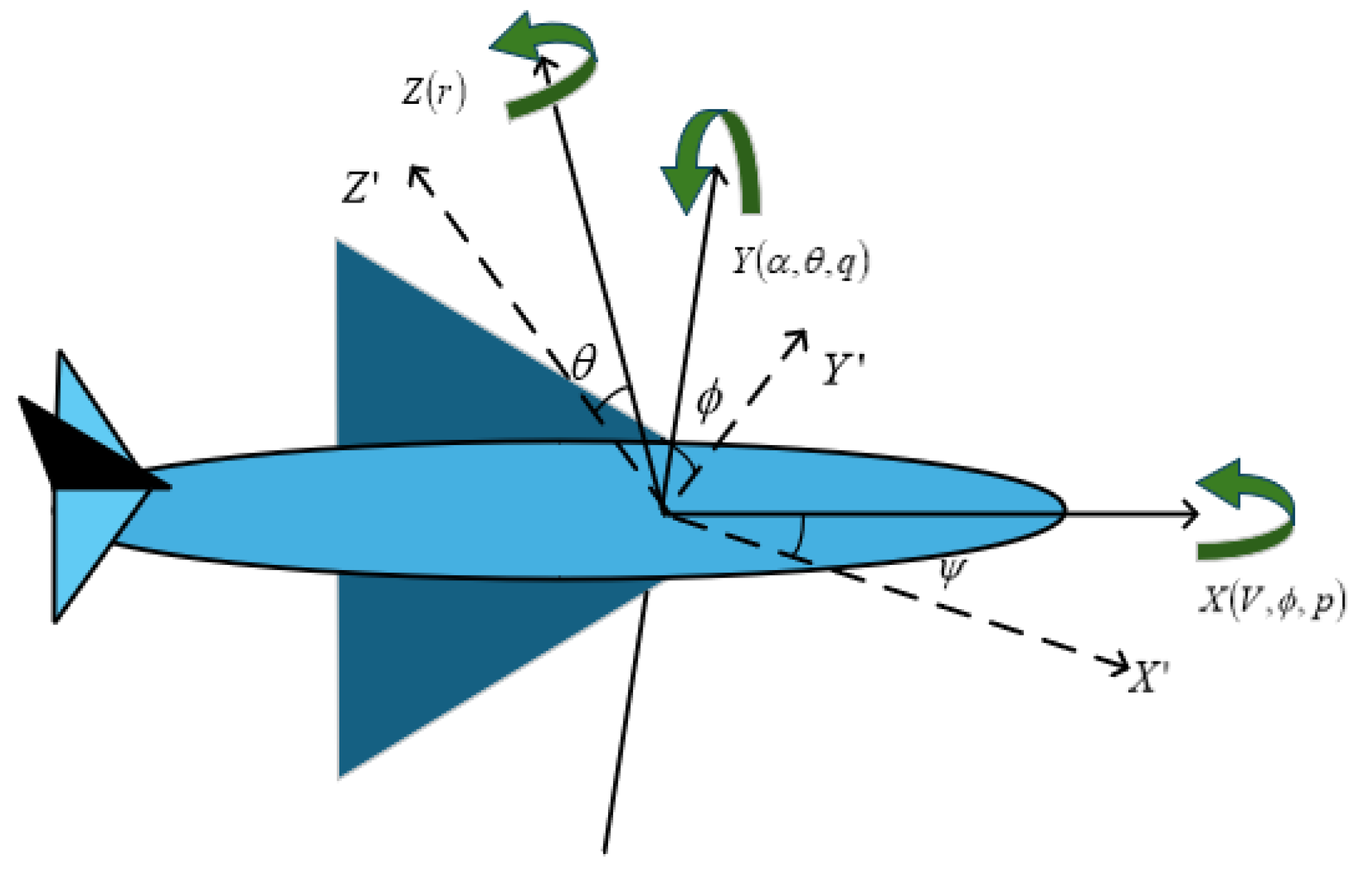
2.1. Airplane Model
2.2. Structural Decomposition of System
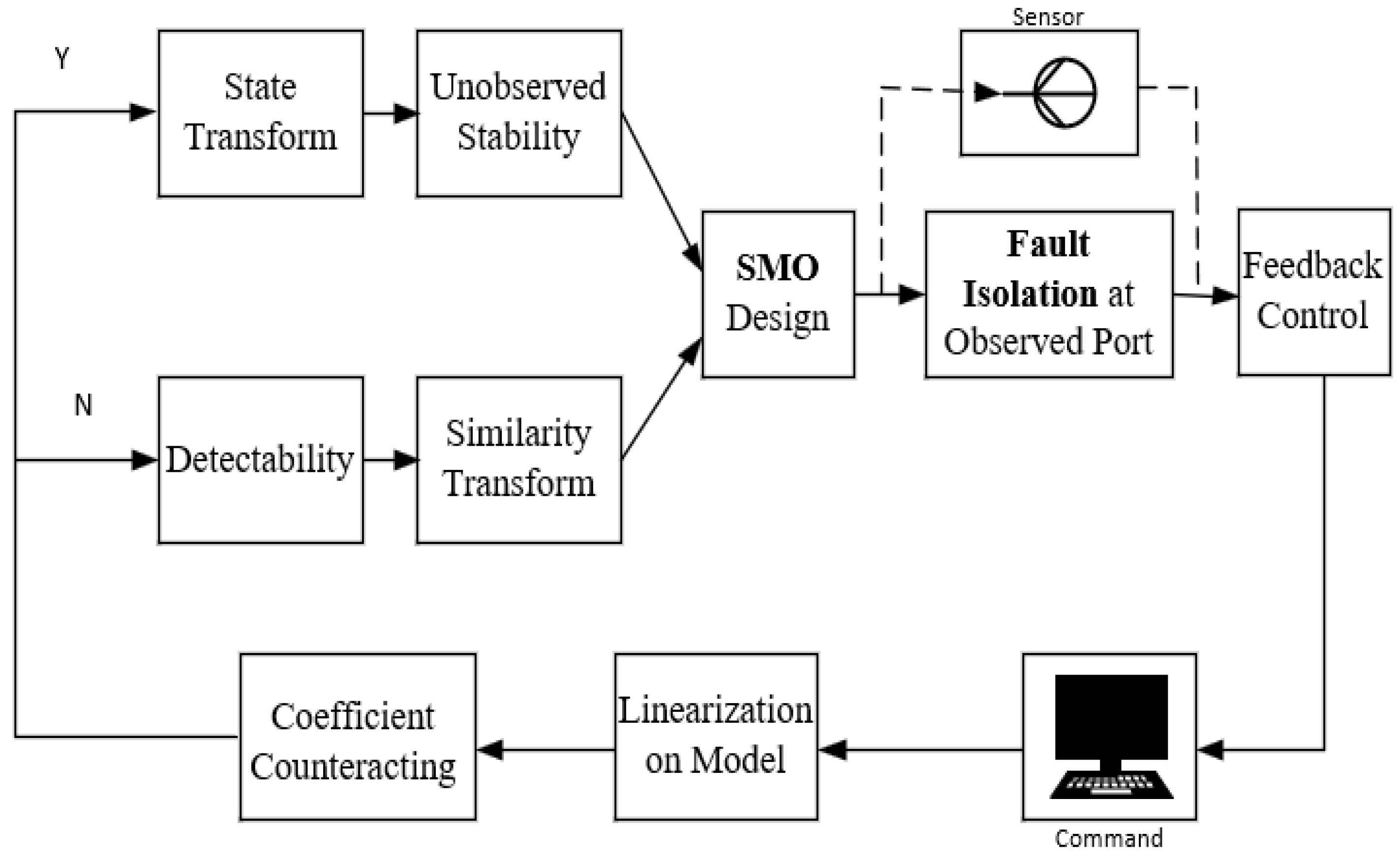
3. Main Results
3.1. Fault Isolation by Perturbation Counteracting
- 1.
- is Hurwitz;
- 2.
- is Hurwitz;
- 3.
- .
3.2. Fault Isolation with State Transform
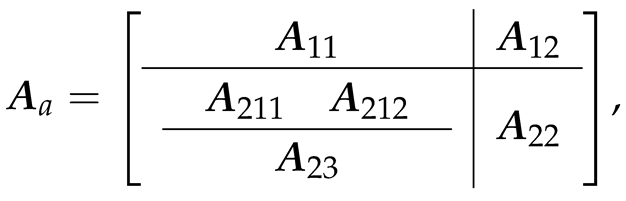
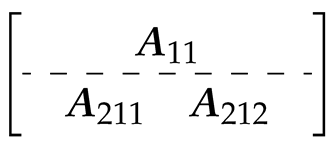
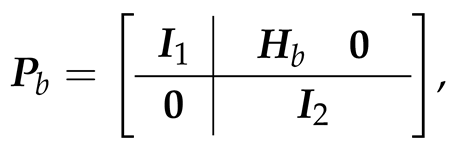
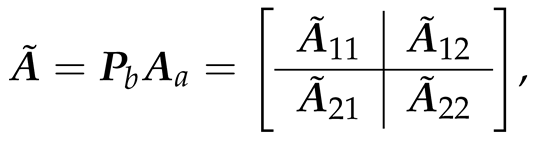
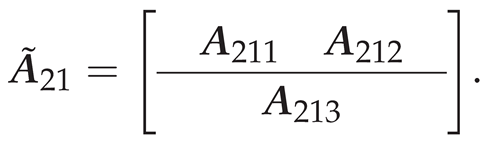
- 1.
- is Hurwitz matrix;
- 2.
- is Hurwitz matrix;
- 3.
- there exists positive definite matrix such that
- 4.
- the positive real number coefficient in (24) satisfies
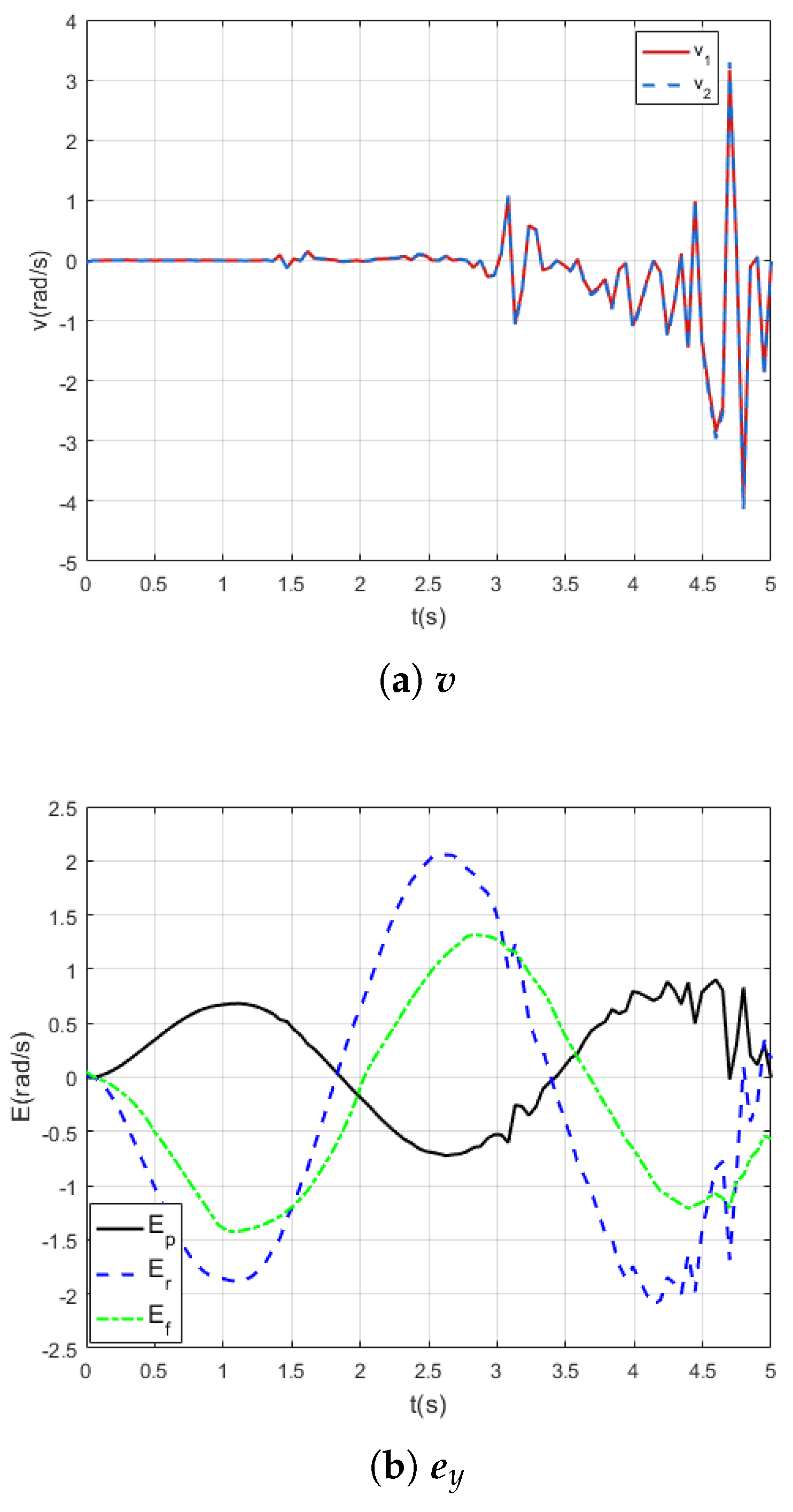
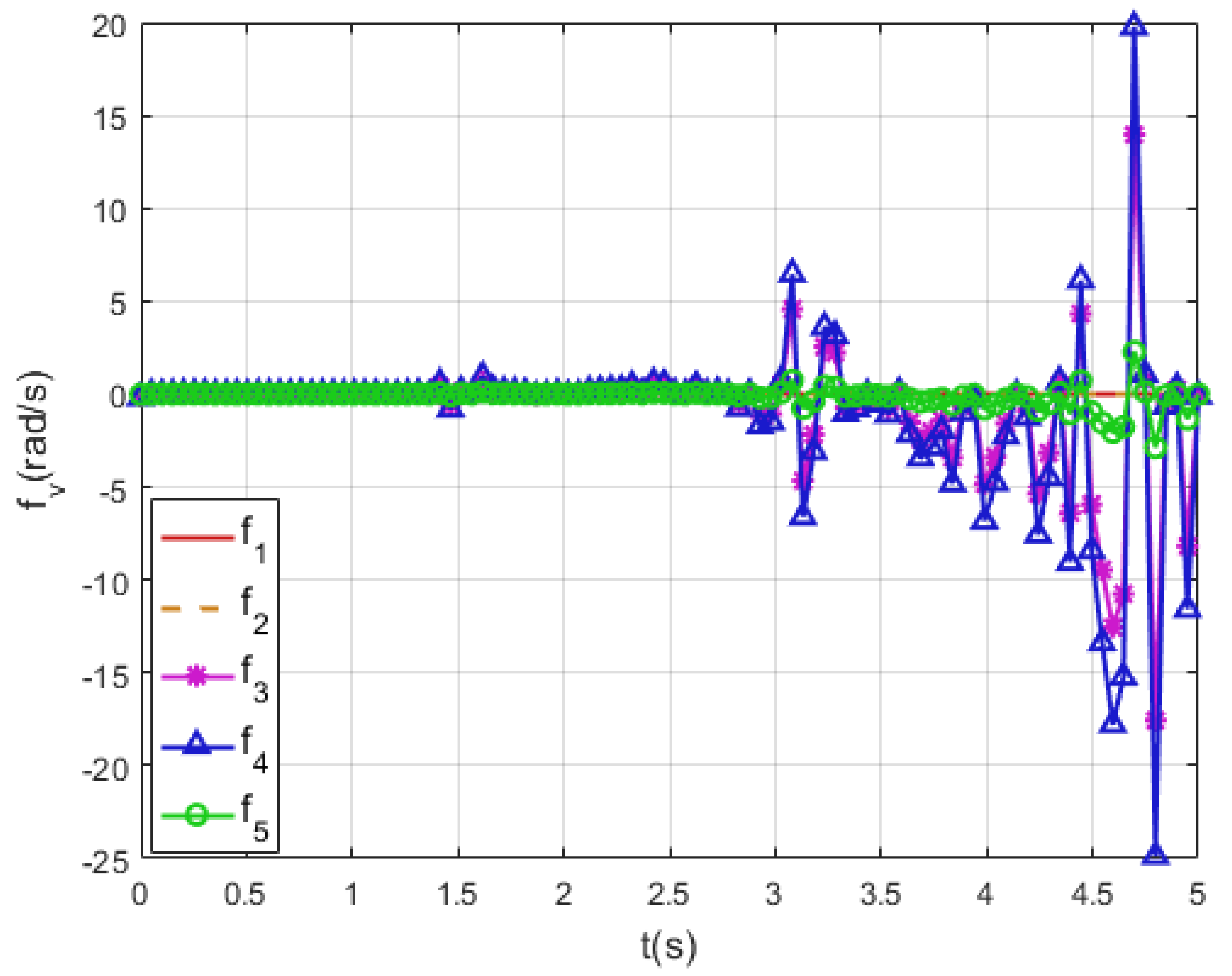
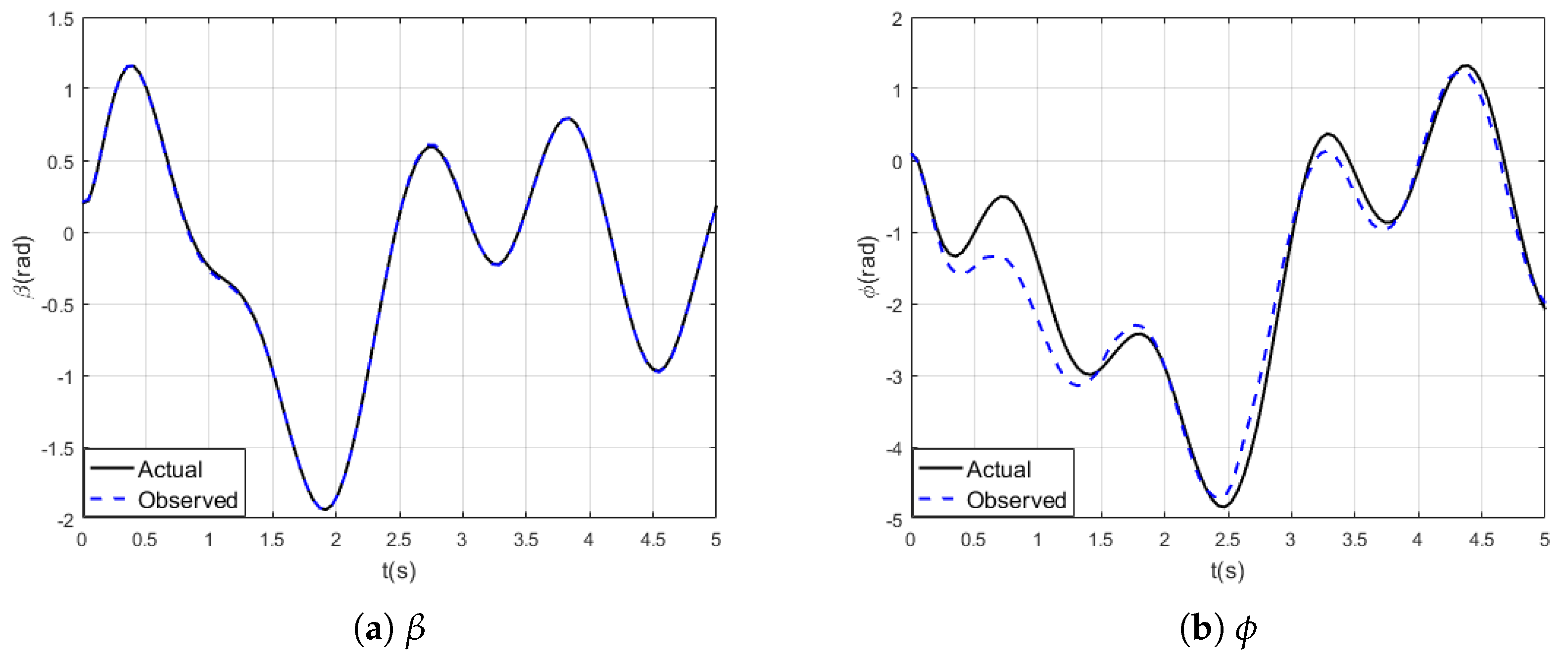
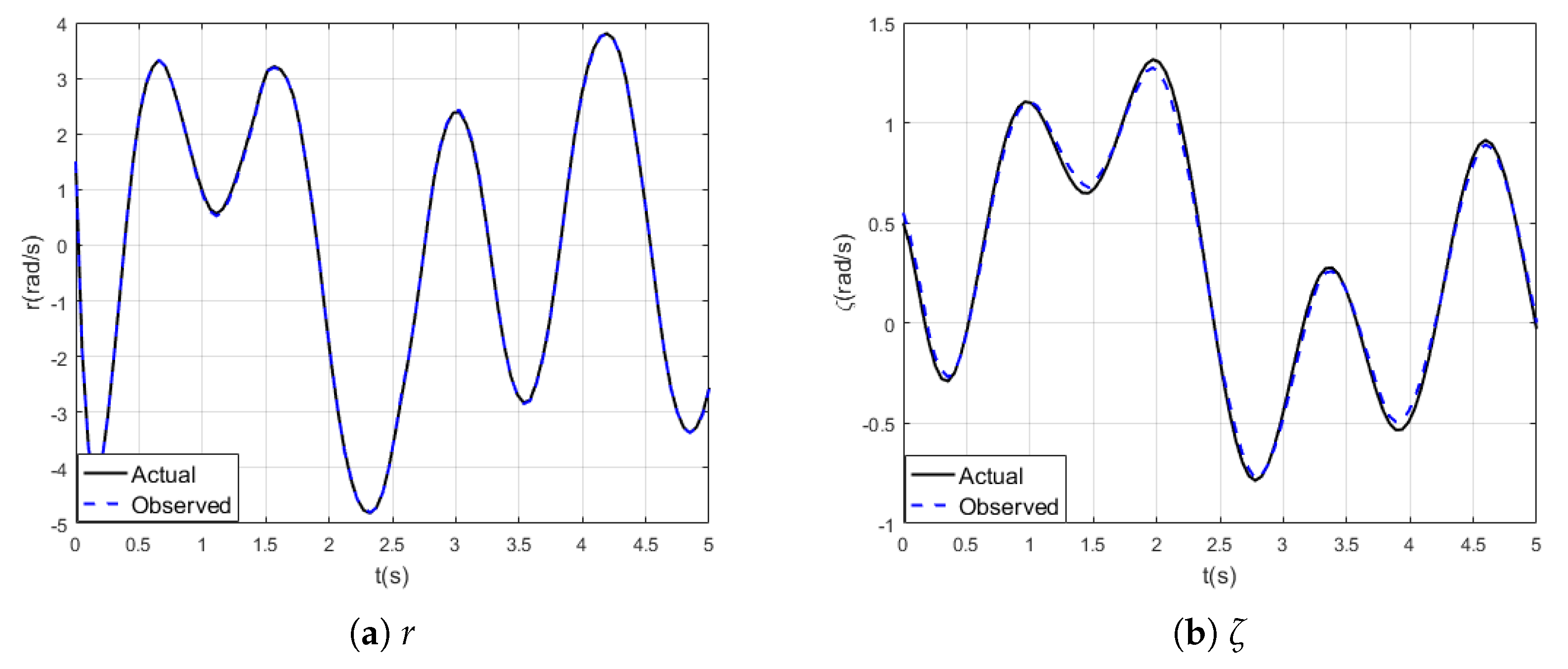
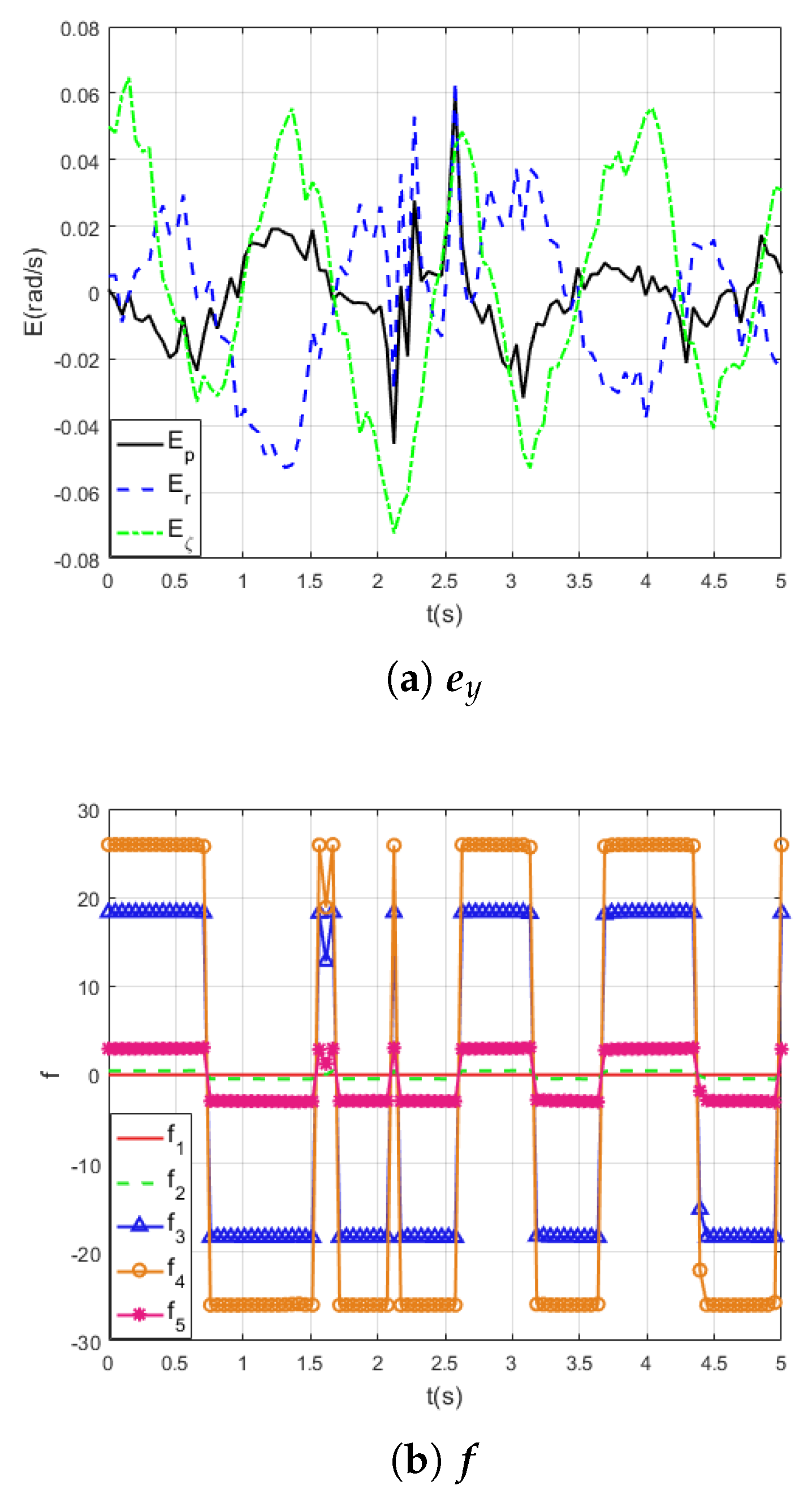
4. Simulation Results
4.1. Perturbations Counteraction
4.2. State Transform
5. Conclusion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, X.G.; Edwards, C. Sensor fault detection and isolation for nonlinear systems based on a sliding mode observer. International Journal of Adaptive Control and Signal Processing 2007, 21, 657–673. [Google Scholar] [CrossRef]
- Falcón, R.; Rios, H.; Dzul, A. A robust fault diagnosis for quad-rotors: A sliding-mode observer approach. IEEE/ASME Transactions on Mechatronics 2022, 27, 4487–4496. [Google Scholar] [CrossRef]
- Isermann, R. Fault-diagnosis systems: an introduction from fault detection to fault tolerance; Springer Science & Business Media: Berlin, 2005. [Google Scholar]
- Mekki, H.; Benzineb, O.; Boukhetala, D.; Tadjine, M.; Benbouzid, M. Sliding mode based fault detection, reconstruction and fault tolerant control scheme for motor systems. ISA Transactions 2015, 57, 340–351. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Pan, K.; Su, Q. Sensor fault detection and estimation for switched power electronics systems based on sliding mode observer. Applied Mathematics and Computation 2019, 353, 282–294. [Google Scholar] [CrossRef]
- Shahzad, E.; Khan, A.U.; Iqbal, M.; Saeed, A.; Hafeez, G.; Waseem, A.; Albogamy, F.R.; Ullah, Z. Sensor fault-tolerant control of microgrid using robust sliding-mode observer. Sensors 2022, 22, 2524. [Google Scholar] [CrossRef] [PubMed]
- Yan, X.G.; Edwards, C. Robust decentralized actuator fault detection and estimation for large-scale systems using a sliding mode observer. International Journal of Control 2008, 81, 591–606. [Google Scholar] [CrossRef]
- Chen, W.; Saif, M. A sliding mode observer-based strategy for fault detection, isolation, and estimation in a class of Lipschitz nonlinear systems. International Journal of Systems Science 2007, 38, 943–955. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K. On the development of discontinuous observers. International Journal of Control 1994, 59, 1211–1229. [Google Scholar] [CrossRef]
- Edwards, C.; Spurgeon, S.K.; Patton, R.J. Sliding mode observers for fault detection and isolation. Automatica 2000, 36, 541–553. [Google Scholar] [CrossRef]
- Yan, X.; Edwards, C. Robust sliding mode observer-based actuator fault detection and isolation for a class of nonlinear systems. International Journal of Systems Science 2008, 39, 349–359. [Google Scholar] [CrossRef]
- Floquet, T.; Barbot, J.P.; Perruquetti, W.; Djemai, M. On the robust fault detection via a sliding mode disturbance observer. International Journal of Control 2004, 77, 622–629. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Yan, X.G.; Mao, Z. Sliding mode observer based incipient sensor fault detection with application to high-speed railway traction device. ISA transactions 2016, 63, 49–59. [Google Scholar] [CrossRef] [PubMed]
- Brambilla, D.; Capisani, L.M.; Ferrara, A.; Pisu, P. Fault Detection for Robot Manipulators via Second-Order Sliding Modes. IEEE Transactions on Industrial Electronics 2008, 55, 3954–3963. [Google Scholar] [CrossRef]
- Shao, S.; Wheeler, P.W.; Clare, J.C.; Watson, A.J. Open-circuit fault detection and isolation for modular multilevel converter based on sliding mode observer. In Proceedings of the 2013 15th European Conference on Power Electronics and Applications (EPE), 2013; pp. 1–9. [Google Scholar]
- Tan, C.P.; Edwards, C. Sliding mode observers for robust detection and reconstruction of actuator and sensor faults. International Journal of Robust and Nonlinear Control: IFAC-Affiliated Journal 2003, 13, 443–463. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, K.L.V. A review of sliding mode observer based sensorless control methods for PMSM drive. IEEE Transactions on Power Electronics 2023, 38, 11352–11367. [Google Scholar] [CrossRef]
- Ding, H.; Zou, X.; Li, J. Sensorless control strategy of permanent magnet synchronous motor based on fuzzy sliding mode observer. IEEE Access 2022, 10, 36743–36752. [Google Scholar] [CrossRef]
- Edwards, C.; Alwi, H.; Tan, C.P. Sliding mode methods for fault detection and fault tolerant control with application to aerospace systems. International Journal of Applied Mathematics and Computor Science 2012, 22, 109–124. [Google Scholar] [CrossRef]
- Roger, P. Flight control systems: practical issues in design and implementation; Iet: London, UK, 2000. [Google Scholar]
- Callier, F.M.; Desoer, C.A. Linear system theory; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Yin, J.; Khoo, S. Continuous finite-time state feedback stabilizers for some nonlinear stochastic systems. International Journal of Robust and Nonlinear Control 2015, 25, 1581–1600. [Google Scholar] [CrossRef]
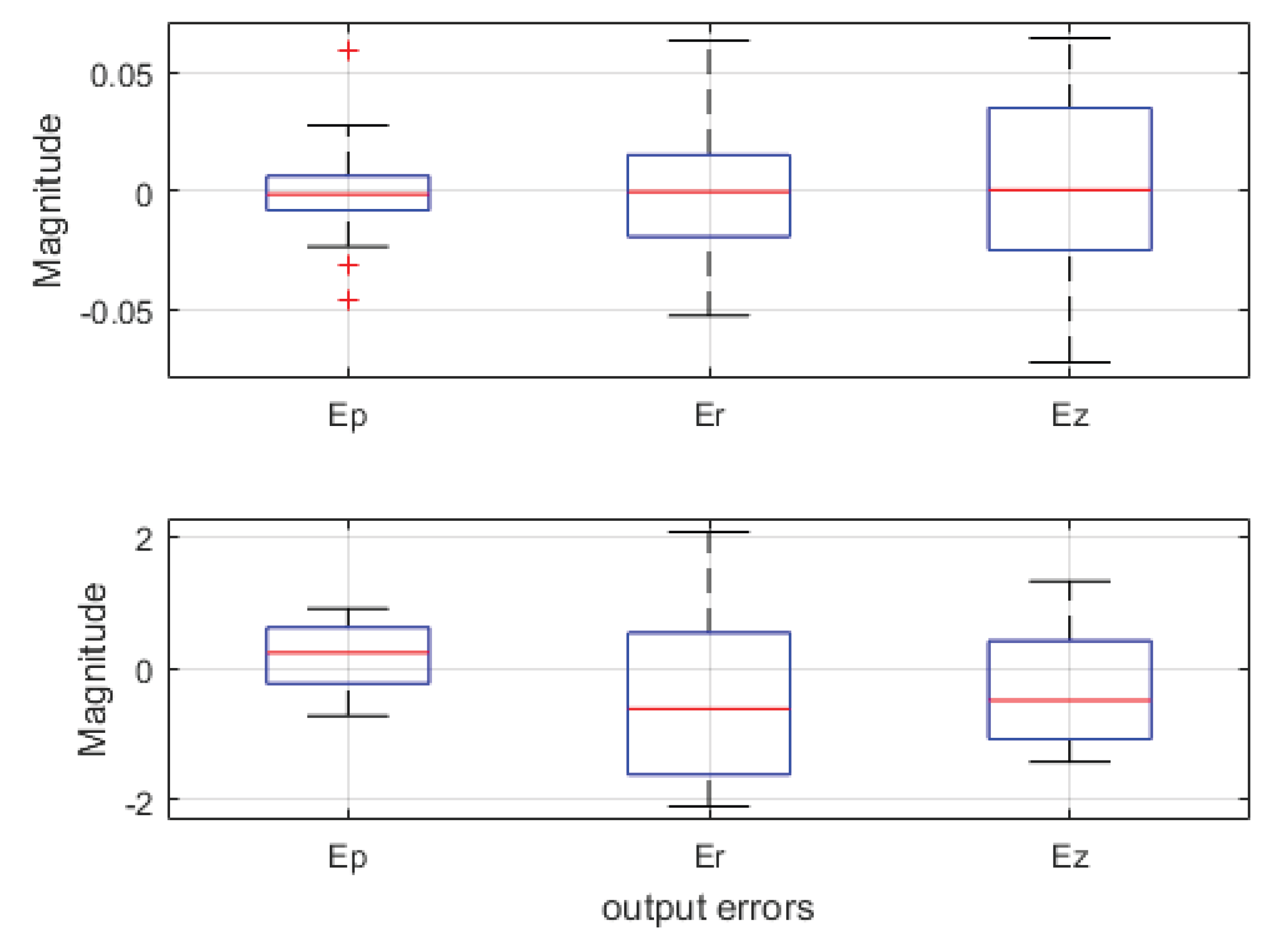
| 0.3 | 2.3 | ||||
|---|---|---|---|---|---|
| 1.2 | |||||
| 2.24 | |||||
| -0.4 | 2.59 | ||||
| 0.5 | 2.67 |
| mean | 0.1722 | -0.3769 | -0.2750 | -0.0007 | -0.0023 | 0.0024 |
| max | 0.9014 | 2.0628 | 1.3159 | 0.0595 | 0.0635 | 0.0647 |
| min | -0.7230 | -2.0954 | -1.4219 | -0.0454 | -0.0526 | -0.0723 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





