Quantum Information Copy Time and Gravity from Relative-Entropy Sources: Global Manuscript with Microscopic Control and Reproducible Artefacts

1. Notation and Standing Assumptions

We use natural units $c=\hslash =k_B=1$ unless stated otherwise. Reduced states are denoted ${\rho }_A{=}_{\overline{A}}\rho$ on a region A with complement $\overline{A}$. Relative entropy is $D(\rho \parallel \sigma ):=(\rho log\rho )-(\rho log\sigma )$, and the modular Hamiltonian of $\sigma$ is $K_{\sigma }:=-log\sigma$. We distinguish three layers of statements throughout: (i) Exact information-theoretic statements (data processing, modular identity, inequalities); (ii) Regime-dependent field-theoretic statements (locality of modular Hamiltonians for small causal diamonds / wedges); (iii) Microscopic proposals (discrete information-field UV completions), which are framed as testable programs rather than completed derivations.

2. Contribution Relative to Existing Literature

The operational part of this manuscript relies only on standard quantum information theory: CPTP contraction (data processing) and Pinsker-type inequalities. The gravity interface uses the modular identity for relative entropy and the entanglement-equilibrium strategy developed in the small-diamond setting. Our contribution is to consolidate these ingredients into a single referee-auditable package in which the same localized relative-entropy object appears on both sides: as an operational control functional for restricted distinguishability and as the variational functional entering entanglement-equilibrium closure. We emphasize that the gravitational step inherits the assumptions of the entanglement-equilibrium regime (local modular Hamiltonians, semiclassical control). The discrete information-field sector is presented as a concrete microscopic model class with explicit decision criteria (phase structure, IR universality diagnostics, and Lorentz-invariance naturalness targets), intended to guide nonperturbative tests.

3. Reproducibility and Artefact Policy

All figures embedded in this PDF are generated from the accompanying code. A single command python3 run_everything.py regenerates the figures and rebuilds the manuscript. In addition, V6 includes a dedicated supplementary derivations note (supplement_v6/supplement_v6_derivations.pdf) that provides (i) an explicit non-tautological time-indexed CPTP toy channel family, (ii) a worked semiclassical structure outline for small-region relative entropy, and (iii) a referee-auditable nonperturbative benchmark list. V7 additionally includes an explicit worked QFT example of the control functional: supplement_v7/supplement_v7_worked_example.pdf, computing $D({\rho }_T\parallel {\rho }_0)$ on a 2D CFT interval with a local modular Hamiltonian and showing the small-interval expansion.

A one-page referee map (REFEREE_MAP.pdf) provides “Claim → formal item → location” navigation.

4. Scope and Standards of Claim

QICT is primarily an operational program: it defines certifiability times for information under admissible locality and CPTP restrictions. The central closure idea is to isolate a single functional that (i) bounds restricted distinguishability and (ii) is the same functional that appears in entanglement-equilibrium derivations of gravitational dynamics in small causal diamonds. Exact statements (quantum information identities and inequalities) are separated from regime-dependent statements (local modular Hamiltonians in QFT; infrared universality claims for discrete models).

5. Operational Layer: Copy Time

Let A be a receiver-accessible region. Let $\mathfrak{F}$ be an admissible family of receiver CPTP maps encoding restricted access/locality. For reduced states ${\rho }_A\left(t\right)$ and ${\sigma }_A\left(t\right)$, define restricted distinguishability

$${\Delta }_{\mathfrak{F}}\left(t\right):=\underset{\Phi \in \mathfrak{F}}{sup}{\displaystyle \frac{1}{2}}{\parallel \Phi \left({\rho }_A\left(t\right)\right)-\Phi \left({\sigma }_A\left(t\right)\right)\parallel }_1.$$

(1)

Given $ϵ\in (0,1)$, define the operational copy time as the first-passage time

$${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}\left(ϵ\right):=inf\{t\ge 0:{\Delta }_{\mathfrak{F}}\left(t\right)\ge ϵ\}.$$

(2)

The goal is to control ${\Delta }_{\mathfrak{F}}$ by an intrinsic monotone functional compatible with CPTP contraction.

6. Fusion Functional: Localized Relative Entropy

Fix a reference reduced state ${\sigma }_A$ (vacuum-like or ground-state reduction). Define the localized relative entropy

$$D_A(\rho \parallel \sigma ):=D({\rho }_A\parallel {\sigma }_A).$$

(3)

6.1. Operational Control by Data Processing + Pinsker

For any CPTP $\Phi$, data processing implies $D(\Phi \left({\rho }_A\right)\parallel \Phi \left({\sigma }_A\right))\le D({\rho }_A\parallel {\sigma }_A)$. Combining with Pinsker’s inequality yields

$${\Delta }_{\mathfrak{F}}({\rho }_A,{\sigma }_A)\le \sqrt{{\displaystyle \frac{1}{2}}D({\rho }_A\parallel {\sigma }_A)}.$$

(4)

Thus $D_A$ upper-bounds the maximum restricted distinguishability and therefore constrains ${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}$ for any admissible $\mathfrak{F}$.

6.2. Exact Modular Representation

Let $K_{{\sigma }_A}:=-log{\sigma }_A$. Then the identity

$$D({\rho }_A\parallel {\sigma }_A)=\Delta \langle K_{{\sigma }_A}\rangle -\Delta S_A$$

(5)

is exact, where $\Delta \langle K\rangle :=\left({\rho }_{A}K\right)-\left({\sigma }_{A}K\right)$ and $\Delta S_A:=S\left({\rho }_A\right)-S\left({\sigma }_A\right)$.

7. Semiclassical Gravity Interface: Small Diamonds

In relativistic QFT, modular Hamiltonians become approximately local for wedges and for sufficiently small causal diamonds. In that regime, Eq. (5) connects D to stress-tensor expectation values and entanglement variations. Stationarity of the same functional $D({\rho }_D\parallel {\sigma }_D)$ under appropriate local variations provides the entanglement-equilibrium route to (linearized and then semiclassical) Einstein dynamics. The minimal interface claim here is structural: the same localized relative entropy that controls QICT distinguishability has the modular form used in entanglement-equilibrium closure.

8. Microscopic Demonstration (Reproducible Toy UV)

A microscopic local lattice toy model (TFIM chain) is used to compute reduced states, evaluate $D({\rho }_A\parallel {\sigma }_A)$ and ${\Delta }_A$, and verify Eqs. (4)–(5) numerically.

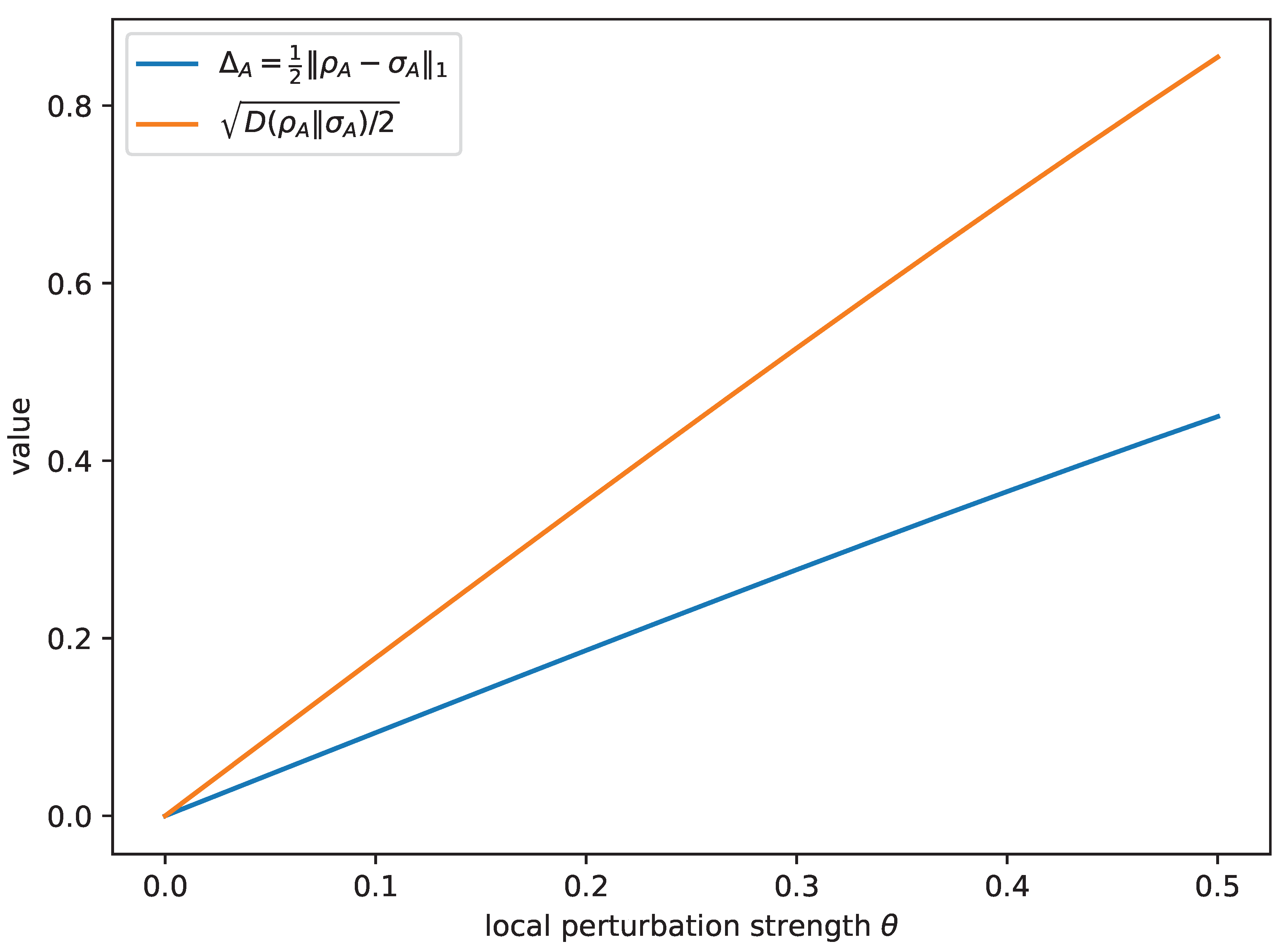
Figure 1. Toy UV: ${\Delta }_A$ and the Pinsker-type upper bound $\sqrt{D/2}$. Generated by code included in this package.

Figure 1. Toy UV: ${\Delta }_A$ and the Pinsker-type upper bound $\sqrt{D/2}$. Generated by code included in this package.

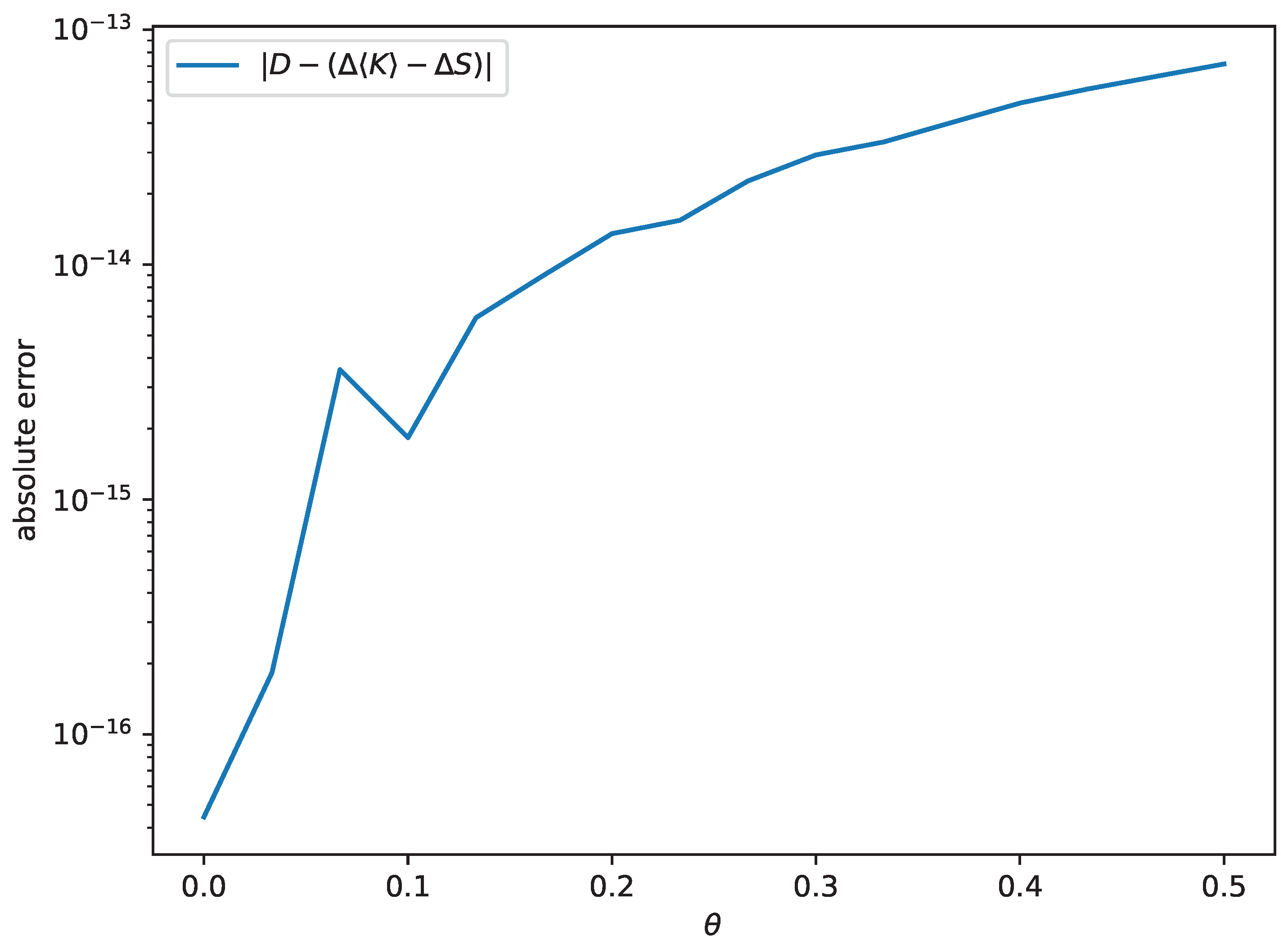
Figure 2. Toy UV: numerical check of the exact modular identity (5). Generated by code.

Figure 2. Toy UV: numerical check of the exact modular identity (5). Generated by code.

9. Discrete Information-Field Proposal (Microscopic Starting Point)

We include an explicit discrete information-field proposal in which the primitive variables live on a causal cell complex and geometry is derived from those variables. An exact gauge-invariant action defines discrete gravitational dynamics (Regge-type in the simplicial case). Classical GR is recovered as an infrared universality class if the coarse-graining flow admits an Einstein–Hilbert fixed point.

Figure 3. Schematic coarse-graining flow illustrating IR universality. In a full implementation, trajectories are extracted from lattice observables.

Figure 3. Schematic coarse-graining flow illustrating IR universality. In a full implementation, trajectories are extracted from lattice observables.

10. Nonperturbative Program and Measurable Targets

To raise the ultraviolet and infrared standing of the proposal beyond a referee-grade synthesis, the discrete information-field sector must be treated as a statistical field theory with explicit measure and coarse-graining. The high-yield deliverables are therefore: (i) a phase diagram identifying a macroscopic GR-like phase; (ii) scaling exponents and universality diagnostics near the putative Einstein–Hilbert fixed point; and (iii) quantitative QICT observables computed in the same ensemble, so that operational certifiability constraints and geometric dynamics are tested together rather than postulated in separate layers.

10.1. Microscopic Definition, Measure, and Gauge Constraints

A minimal microscopic definition consists of (a) a causal cell complex $\mathcal{K}$, (b) local information-field variables ${\mathcal{I}}_e$ on edges (or higher-cells) with a compact gauge group and local constraints (Gauss-type conditions), and (c) an action $S\left[\mathcal{I}\right]$ that is strictly local on $\mathcal{K}$ and gauge invariant. One then defines a partition function $Z=\int \mathcal{D}\mathcal{I}{e}^{-S\left[\mathcal{I}\right]}$ and a family of coarse-graining maps $\mathfrak{R}$ (block-spin / tensor-network renormalization) acting on $(\mathcal{K},\mathcal{I})$.

10.2. Observables

The minimal observable set is: (i) discrete curvature diagnostics (holonomy distributions and Regge deficit angles); (ii) long-distance two-point functions and spectral dimension; (iii) relative-entropy and modular-energy proxies for reduced regions (QICT outputs); (iv) Lorentz-violation-sensitive operators in the infrared effective action and their scaling. A practical implementation should publish raw Monte Carlo estimators and finite-size scaling plots to permit independent reproduction.

10.3. Decision Criteria for “GR Universality”

A conservative, referee-robust criterion is to require simultaneous evidence for: (a) an emergent local light-cone structure at large scales (approximate Lorentz invariance), (b) an effective action dominated by curvature invariants with Einstein–Hilbert form plus controlled higher-curvature terms, (c) stress-tensor Ward identities in the infrared, and (d) agreement of entanglement/relative-entropy stationarity relations with the same cutoff scheme used in the microscopic ensemble.

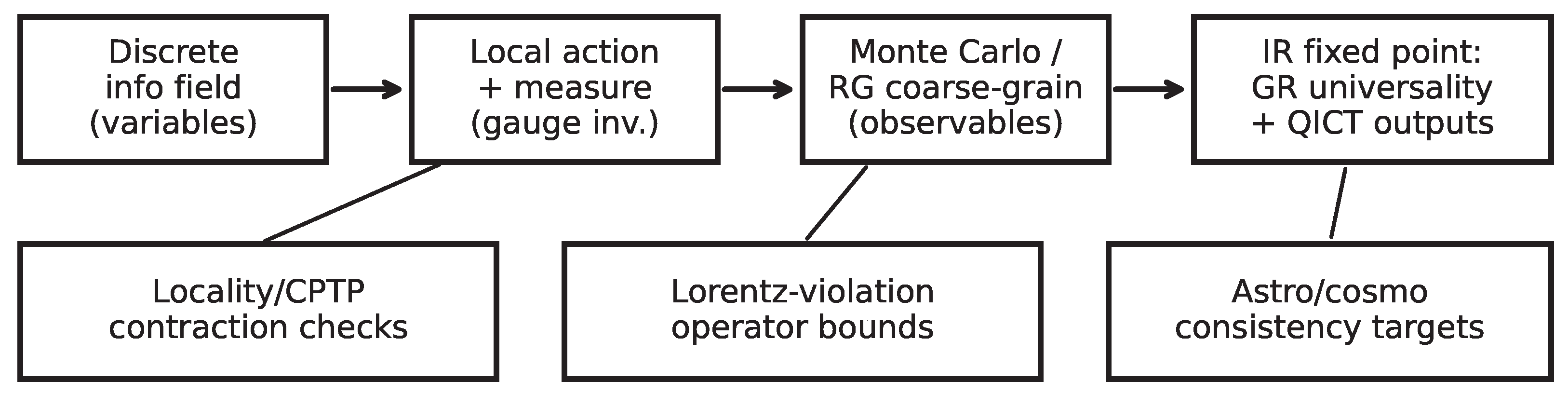
Figure 4. Nonperturbative closure pipeline: explicit microscopic definition → local action/measure → coarse-graining with measured observables → infrared universality diagnostics plus QICT outputs computed in the same ensemble.

Figure 4. Nonperturbative closure pipeline: explicit microscopic definition → local action/measure → coarse-graining with measured observables → infrared universality diagnostics plus QICT outputs computed in the same ensemble.

11. Lorentz Invariance, a Universal Update Time, and Naturalness

Any postulated universal update scale ${\tau }_0$ must be compatible with tight bounds on Lorentz-violating operators. The conservative stance is to treat ${\tau }_0$ as a regulator scale that can only enter the infrared effective action through Lorentz-covariant combinations, or else to demonstrate that Lorentz-violating operators are irrelevant under the coarse-graining flow. In effective-field-theory language, dimension-d Lorentz-violating operators have coefficients suppressed by powers of ${\Lambda }^{-(d-4)}$; without symmetry protection they may be radiatively generated. Therefore, a microscopic model aspiring to fundamental status must exhibit either (i) exact microscopic symmetries enforcing emergent Lorentz invariance or (ii) a dynamical mechanism (fixed-point attraction) rendering Lorentz-breaking operators irrelevant. This manuscript treats that requirement as a concrete test target rather than an assumption.

12. Quantitative Falsifiability Targets

The strongest near-term falsifiability route is to tie QICT-defined certifiability times to independently measurable information-propagation bounds in controlled many-body platforms (quantum simulators) and to compare the extracted control functional with relative-entropy predictions. On the gravitational side, the minimal interface is structural; stronger claims require explicit calculations of relative entropy in toy gravitational settings (e.g. perturbative semiclassical states) and consistency with known energy conditions and linearized gravity responses. For the discrete information-field proposal, falsifiability is through failure to realize a GR-like infrared phase or through unavoidable Lorentz-violation operators exceeding observational bounds.

13. Limitations and Concrete Next Checks

Exact results: data processing, Pinsker control, and the modular identity. Regime-dependent: local modular Hamiltonians in small diamonds and entanglement-equilibrium closure. Proposal-level: the discrete information-field UV completion, whose critical task is demonstrating the appropriate macroscopic phase and extracting scaling exponents (nonperturbatively), together with QICT observables computed in the same microscopic ensemble.

14. Prediction and Benchmark Inventory

To support community evaluation, we separate (A) operational predictions in controllable many-body platforms, (B) gravity-interface calculations in semiclassical settings, and (C) nonperturbative benchmarks for the discrete information-field sector. Items below are designed to be independently checkable; where a result is not yet computed in this bundle, it is stated as a benchmark target with a clear failure mode.

14.1. Operational (QICT) Predictions and Checks

• Restricted distinguishability bound: for any admissible receiver family $\mathfrak{F}$, ${\Delta }_{\mathfrak{F}}\le \sqrt{D/2}$ (exact). Benchmark: reproduce the bound in at least one interacting many-body simulator (e.g. cold atoms or superconducting qubits) by tomographic reduction on A and numerical evaluation of D.
• Copy-time scaling: in models with Lieb–Robinson bounds, the first-passage time ${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}\left(ϵ\right)$ should exhibit ballistic scaling with distance for fixed thresholds once $\mathfrak{F}$ encodes locality. Benchmark: extract ${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}$ versus distance in a finite chain and compare with LR velocities.

14.2. Gravity-Interface Calculations

• Small-diamond modular locality: compute $D({\rho }_D\parallel {\sigma }_D)$ for perturbative semiclassical excitations in a causal diamond D and verify the expected stress-tensor form of $\Delta \langle K\rangle$ in the same regularization scheme used for $\Delta S$.
• Entanglement-equilibrium stationarity: in the same setting, verify that stationarity of D under geometric variations reproduces the linearized Einstein response. This inherits the assumptions of the entanglement-equilibrium literature; the benchmark is an explicit worked example (to be added as a dedicated calculation note).

14.3. Nonperturbative Discrete Information-Field Benchmarks

• Phase structure: exhibit a macroscopic phase with stable long-distance dimension and curvature observables consistent with a continuum manifold limit.
• Universality diagnostics: extract critical exponents and show attraction toward an Einstein–Hilbert-type effective action in the IR, with controlled higher-curvature corrections.
• Lorentz-violation naturalness: demonstrate either symmetry protection or RG irrelevance of Lorentz-violating operators; failure is quantitative (operator coefficients exceed observational bounds in the inferred IR EFT).
• Joint computation of geometry and QICT observables: compute QICT-relevant relative entropies (or calibrated proxies) in the same microscopic ensemble that defines geometry; this is the decisive “fusion” benchmark at the nonperturbative level.

Table 1. Benchmarks and failure modes. “Exact” indicates statements proved without additional physical assumptions.

Layer	Deliverable (independent check)	Failure mode
Exact (QIT)	Data processing + Pinsker control; modular identity	Any counterexample to monotonicity/identity (none expected)
Operational (lab)	Measured ${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}\left(ϵ\right)$ scaling vs distance; compare to LR bounds	No consistent scaling or mismatch with locality constraints
Semiclassical	Explicit $D({\rho }_D\parallel {\sigma }_D)$ example with consistent regulator; linearized response	Regulator inconsistency; no agreement with known responses
Nonperturbative UV	Phase diagram; exponents; IR EFT form; Lorentz-operator suppression	No GR-like phase; wrong scaling; large Lorentz violation
Fusion in UV	Compute QICT observables within the same ensemble defining geometry	QICT observables decouple from geometric sector

Table 1. Benchmarks and failure modes. “Exact” indicates statements proved without additional physical assumptions.

Layer	Deliverable (independent check)	Failure mode
Exact (QIT)	Data processing + Pinsker control; modular identity	Any counterexample to monotonicity/identity (none expected)
Operational (lab)	Measured ${\tau }_{\mathrm{copy}}^{\left(\mathrm{op}\right)}\left(ϵ\right)$ scaling vs distance; compare to LR bounds	No consistent scaling or mismatch with locality constraints
Semiclassical	Explicit $D({\rho }_D\parallel {\sigma }_D)$ example with consistent regulator; linearized response	Regulator inconsistency; no agreement with known responses
Nonperturbative UV	Phase diagram; exponents; IR EFT form; Lorentz-operator suppression	No GR-like phase; wrong scaling; large Lorentz violation
Fusion in UV	Compute QICT observables within the same ensemble defining geometry	QICT observables decouple from geometric sector