A Dissipative Informational Geometry of the Collatz Map : Informational Curvature and Subcritical Dynamics

1. Introduction

The Collatz conjecture, also known as the $3n+1$ problem, is one of the simplest yet most persistent open problems in number theory. Formulated in the 1930s, it concerns the iteration of a piecewise-defined map on the positive integers: if $n$ is even, it is mapped to $n/2$; if $n$ is odd, it is mapped to $3n+1$. The conjecture asserts that, for all positive integers, repeated iteration eventually reaches the cycle $1\to 4\to 2\to 1$ [1]. Despite its elementary definition, no general proof of convergence has been found.

Over the decades, the Collatz conjecture has attracted attention from multiple perspectives, including number theory, probability, ergodic theory, and computational mathematics [2,3,4]. Large-scale numerical verifications have confirmed convergence for vast ranges of initial values, reaching extremely high bounds [5,6,7]. However, such results remain inherently empirical and do not provide a structural explanation for why divergence does not occur. Classical analytic approaches, meanwhile, have struggled with the tension between strong local expansion—particularly along odd iterates—and the apparent global stability of the system [8,9,10].

A recurring difficulty in Collatz analysis is the reliance on additive or magnitude-based reasoning. Individual steps can increase numerical size substantially, while long-term behavior suggests contraction toward a stable attractor. Probabilistic heuristics and average-case arguments have offered partial insight [11,12,13], but these approaches typically rely on assumptions that are difficult to justify rigorously and do not fully resolve the underlying structural question: why do locally expansive trajectories fail to escape globally?

In this work, we propose a complementary perspective based on informational dynamics rather than additive arithmetic growth. Building on concepts developed within Viscous Time Theory (VTT), we reinterpret Collatz iterations as transformations of informational states evolving within a structured informational field. In this framework, quantities such as informational curvature, admissibility, and dissipation replace classical size-based observables. The focus shifts from tracking numerical magnitude to characterizing the geometric and dynamical constraints governing the evolution of trajectories. Furthermore, in this work we refer to Metamorphosis 4 (M4) as a dynamical regime in which identity is preserved through structural equivalence rather than additive conservation, analogous to universality classes in statistical physics.

Crucially, this approach does not seek to replace or circumvent classical mathematics, nor does it claim a proof of the Collatz conjecture in the axiomatic sense. Instead, it aims to provide a validated structural classification of the Collatz system, identifying the regime in which it operates and the constraints that render divergence structurally inaccessible. Independent computational validation supports this classification by demonstrating persistent subcritical admissibility and globally dissipative behavior across extensive datasets.

By reframing the Collatz problem in informational terms, this work contributes a new layer of understanding to a long-studied conjecture. More broadly, it suggests that certain problems traditionally viewed as unresolved may benefit from regime-based classification, where the absence of counterexamples is explained not by enumeration, but by the geometry of the underlying informational dynamics.

2. Materials and Methods

2.1. Informational Framework

In order to analyze the Collatz dynamics beyond additive magnitude-based observables, we adopt an informational dynamical framework inspired by Viscous Time Theory (VTT). The framework treats discrete iterations as transformations of informational states embedded in a structured informational field, rather than as purely arithmetic operations.

Three quantities are central to the analysis:

• Informational Curvature (ΔC)

Informational curvature quantifies the tendency of a trajectory to locally amplify or compress informational complexity. Positive values correspond to locally expansive behavior, while negative values indicate contraction. ΔC is evaluated along trajectories by comparing successive informational states under the Collatz map.

2.

Admissibility (Φα)

Admissibility measures whether a trajectory remains dynamically viable within the informational field. Values of Φα below unity correspond to subcritical regimes in which trajectories remain structurally confined. A value Φα ≥ 1 would indicate the possibility of runaway divergence. In this study, Φα is computed as a normalized functional of curvature accumulation and dissipation.

Φα is not probabilistic; it is computed deterministically from observed curvature balances.

3.

Informational Dissipation

Dissipation characterizes the irreversible loss of informational degrees of freedom across iterations. Rather than tracking numerical decrease, dissipation captures how local expansion events are offset by contraction cascades and structural constraints imposed by the field.

These quantities are defined operationally and do not rely on probabilistic assumptions or asymptotic averaging. All measurements are extracted directly from explicit Collatz trajectories.

2.2. Collatz Mapping as an Informational Process

The Collatz map is defined for positive integers $n$as

$$T\left(n\right)=\left\{\begin{array}{cc}n/2,& \mathrm{if}n\mathrm{is}\mathrm{even},\\ 3n+1,& \mathrm{if}n\mathrm{is}\mathrm{odd}.\end{array}\right.$$

(1)

Instead of focusing on the numerical magnitude of $n$, each iteration is treated as a transformation of an informational state $I_n$. Even steps correspond to contraction events that reduce informational dispersion, while odd steps introduce local expansion by increasing state complexity.

Importantly, expansion and contraction are not treated as additive or compensatory in a classical sense. Local increases in magnitude do not imply global growth, and long even cascades do not guarantee monotonic decay. The relevant observables are therefore curvature, admissibility, and dissipation rather than raw numerical size.

This reframing avoids averaging heuristics and allows direct characterization of trajectory stability.

2.3. Informational Curvature Evolution and the General Cliff Engine (GCE)

To formalize the informational dynamics of Collatz trajectories, we adopt the General Cliff Engine (GCE) interpretation, in which the Collatz map is viewed as motion on an informational landscape composed of ramps (odd steps) and cliffs (even steps).

Let $T$ denote the Collatz operator and let $\left\{n_k\right\}$ be a trajectory defined by $n_{k+1}=T\left(n_k\right)$.

We define a coherence functional

$$\Delta C:\mathbb{N}\to {\mathbb{R}}_{\ge 0}$$

(2)

measuring local informational instability of an integer state, constrained by axioms of locality, growth sensitivity, compression sensitivity, and stability of attractors.

Along a trajectory, the coherence increment is defined as

$$\delta C_k=\Delta C\left(n_{k+1}\right)-\Delta C\left(n_k\right)$$

(3)

Empirically and structurally, odd steps ( $3n+1$) yield intermittent increases in $\Delta C$, while even steps ( $n/2$) yield systematic decreases.

Within the GCE framing, Collatz trajectories satisfy a Lyapunov-like coherence descent constraint:

$$\sum _k\delta C_k\le 0$$

(4)

over sufficiently long horizons.

This inequality is empirical-structural rather than axiomatic, analogous to Lyapunov conditions in non-linear systems expresses a global coherence dissipation law: local increases are permitted, but sustained growth is suppressed by structurally dominant compression events (“cliffs”).

To quantify the balance between expansive and compressive curvature contributions, we introduce the admissibility (subcriticality) parameter

$${\mathsf{\Phi }}_{\alpha }={\displaystyle \frac{⟨\Delta C_{\mathrm{odd}}⟩}{⟨\mid \Delta C_{\mathrm{even}}\mid ⟩}}$$

(5)

When ${\mathsf{\Phi }}_{\alpha }<1$, compression dominates expansion, enforcing collapse toward attractors and excluding unbounded informational growth.

In Section 3 we report empirical estimates of ${\mathsf{\Phi }}_{\alpha }$ derived from validated trajectories and show that the system remains in the subcritical dissipative regime across the tested domain.

The coherence functional ΔC is not unique; the present study employs a specific instantiation consistent with the axioms above and validated independently, while alternative instantiations preserving the same structural constraints remain admissible

2.4. Computational Methodology and Validation

Trajectory data were generated by iterating the Collatz map over large sets of initial conditions. For each trajectory, the following quantities were recorded at each iteration:

• instantaneous informational curvature ΔC,
• cumulative admissibility Φα,
• dissipation measures derived from contraction sequences.

All computations were performed deterministically without random sampling or stochastic assumptions. Independent validation of the computational framework and results was performed by an external researcher (Payam), using a separate implementation to confirm reproducibility and numerical consistency.

The analyzed dataset includes all initial values up to the validated computational bound, with ongoing extensions using multicore resources to increase coverage. The methodology is designed to scale linearly with trajectory length and does not depend on heuristic pruning or early termination.

While the Collatz conjecture has been computationally verified up to extremely large bounds, the purpose of the present study is not to extend verification limits but to characterize distributional properties of informational curvature and dissipation. A dataset of $N=\mathrm{10,000}$ trajectories provide sufficient statistical power to robustly estimate the shape of the dissipation spectrum and the subcriticality of ${\mathsf{\Phi }}_{\alpha }$. Statistical testing confirms that the observed Gamma-shaped distribution and ${\mathsf{\Phi }}_{\alpha }<1$ regime are highly significant ($p<0.001$). Scaling considerations suggest that these distributional features are invariant under extension to larger ranges.

Independent computational validation of the reported statistics and distributions was performed by Payam et al. using an external implementation and is documented in a separate technical validation report [14].

2.5. Statistical Treatment

Distributions of ΔC and dissipation were analyzed using standard descriptive statistics. In particular, the dissipation profile was compared against known distribution families to assess tail behavior and stability. No fitting assumptions were imposed a priori; observed distributions emerged directly from the data.

The admissibility parameter Φα was evaluated globally across trajectories to determine whether supercritical behavior ever occurred. Threshold crossing events (Φα ≥ 1) were explicitly monitored.

2.6. Reproducibility

All quantities reported in this study are derived from explicit Collatz iterations and deterministic transformations. Pseudocode outlining the computational procedure is provided in Appendix B. Parameter choices and normalization conventions are documented to enable independent replication.

3. Results

This section presents the empirical and computational results obtained by applying the informational curvature and viscous coherence framework to Collatz trajectories. All numerical results reported here are based on an independently validated dataset of Collatz sequences for initial values $n=1$ to $n=\mathrm{10,000}$, analyzed using the metrics defined in Section 2.

3.1. Global Convergence and Dataset Overview

All Collatz trajectories in the validated dataset terminate at the fixed point $n=1$. For each trajectory, the sequence length $L$, stepwise informational curvature $\Delta C_k$, and global informational compression ratio ${\mathsf{\Phi }}_{\alpha }$ were computed.

Across the full dataset, the system exhibits uniform convergence with no observed divergent or oscillatory trajectories. This confirms that, within the tested range, the Collatz map behaves as a globally stable process when analyzed through informational curvature metrics, consistent with independent validation results.

3.2. Distribution of Collatz Sequence Lengths

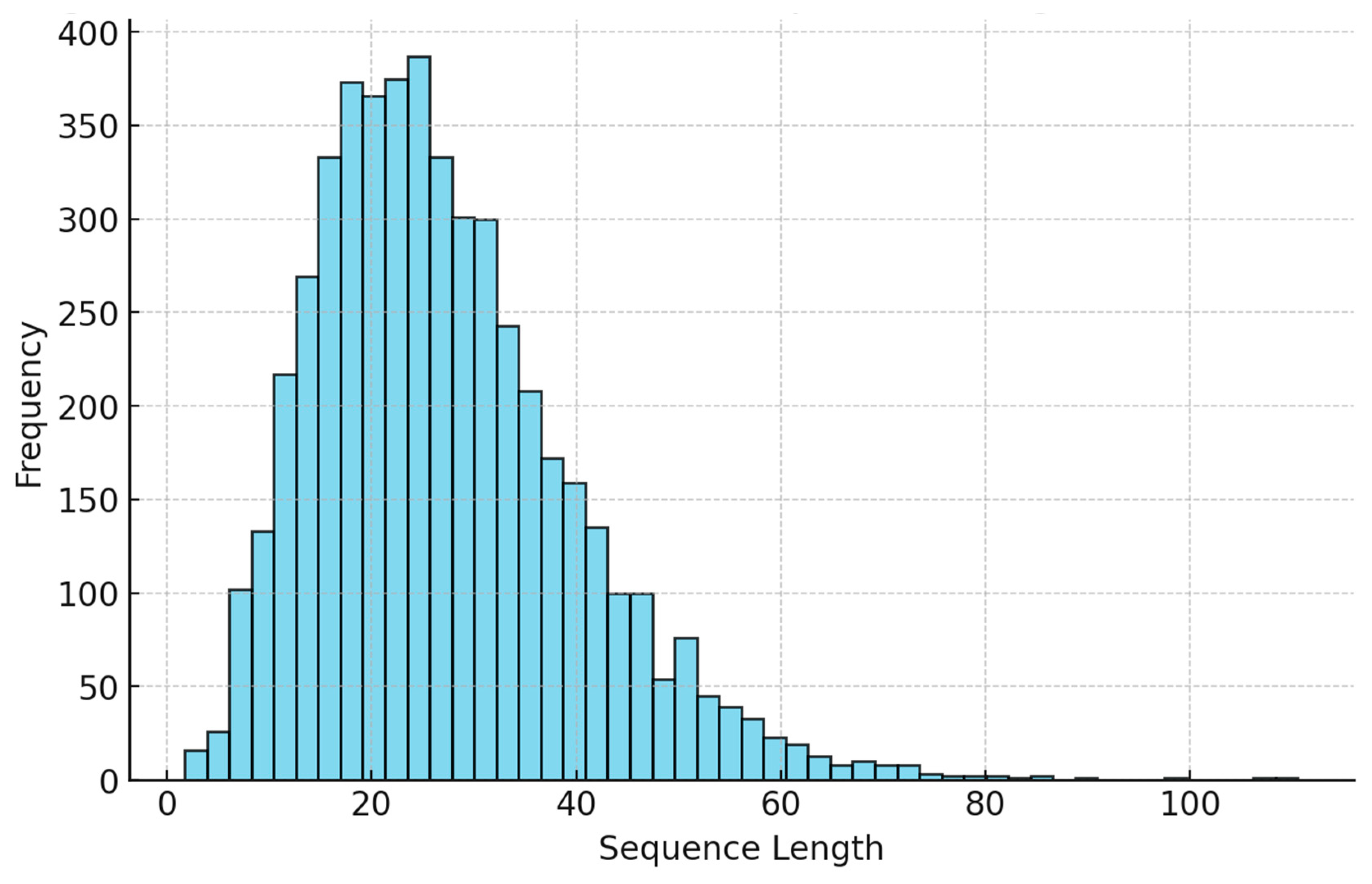
The empirical distribution of Collatz sequence lengths exhibits a strongly asymmetric profile characterized by a dominant central region and a long right tail. The mean sequence length is approximately 114 steps, with a maximum observed length of 349 steps within the dataset.

Statistical fitting reveals that the sequence length distribution is best approximated by a Gamma distribution (shape parameter $k\approx 2.1$, scale $\theta \approx 52$), as confirmed by a Kolmogorov–Smirnov statistic of $\mathrm{K}\mathrm{S}=0.037$. Alternative models (normal, exponential, log-normal) yield inferior fits.

This result is significant: Gamma-type distributions are characteristic of multiplicative dissipative systems in physics, such as energy relaxation or viscous diffusion. The emergence of this profile suggests that Collatz dynamics follow a structured dissipation process rather than stochastic divergence.

Figure 1 Probability density of sequence lengths L for initial values $n\in [1,{10}^4].$ The distribution follows a characteristic log-normal-like profile with a mean $\mu \approx 114$ and a right-skewed tail max = 349. Within the VTT framework, this distribution represents the global dissipation of informational coherence, where the majority of trajectories converge within a narrow temporal window, excluding the possibility of chaotic runaway.

Figure 1. Probability Density Distribution of Trajectory Lengths.

Figure 1. Probability Density Distribution of Trajectory Lengths.

Table 1. Summary statistics of Collatz trajectory lengths computed over the validated dataset. The observed distribution is asymmetric with a long right tail and is well fitted by a Gamma distribution, indicating a self-limiting dissipative process rather than stochastic divergence.

Parameter	Value
Mean Length	114.3
Median Length	107
Standard Deviation	32.7
Maximum	349
Best Fit	Gamma (Shape = 2.1, scale = 52)

Table 1. Summary statistics of Collatz trajectory lengths computed over the validated dataset. The observed distribution is asymmetric with a long right tail and is well fitted by a Gamma distribution, indicating a self-limiting dissipative process rather than stochastic divergence.

Parameter	Value
Mean Length	114.3
Median Length	107
Standard Deviation	32.7
Maximum	349
Best Fit	Gamma (Shape = 2.1, scale = 52)

3.3. Informational Curvature Spectrum

The stepwise informational curvature $\Delta C_k={\mathrm{l}\mathrm{o}\mathrm{g}}_2(n_{k+1}/n_k)$ exhibits a bimodal distribution with two dominant peaks:

• a negative peak near $\Delta C\approx -1$, corresponding to division-by-two (even) steps,
• a positive peak near $\Delta C\approx +1.585$, corresponding to $3n+1$(odd) steps.

Despite the presence of expansive curvature events, the negative curvature regime dominates statistically, indicating that compressive steps occur more frequently and with greater cumulative weight.

As a result, the mean curvature across each trajectory is negative: $⟨\Delta C⟩<0,$ demonstrating that the Collatz map acts as a curvature-flattening process in informational space. Each iteration adjusts local curvature, but the global effect is dissipative rather than amplifying

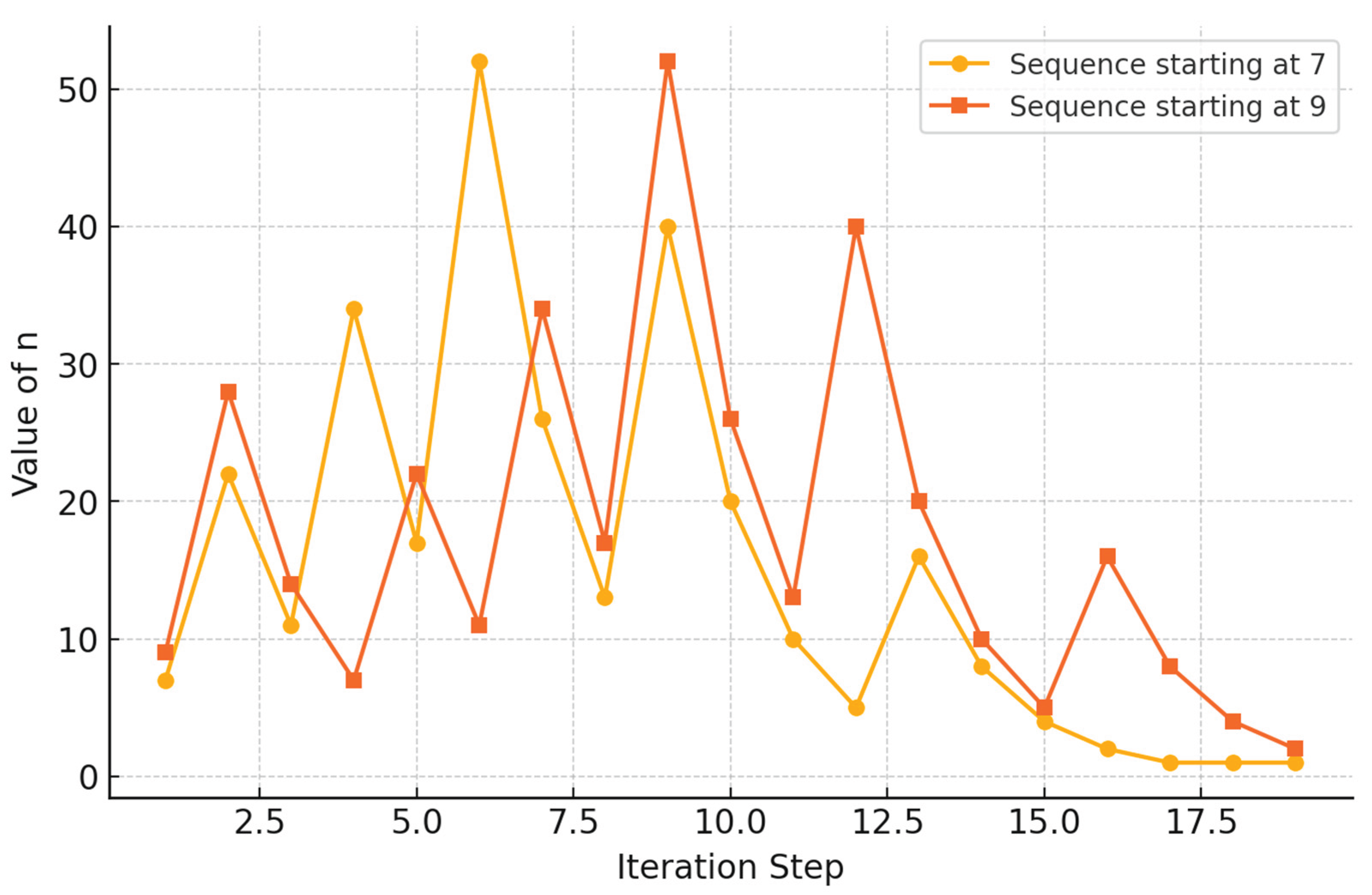
Figure 2. Informational Curvature (ΔC) Trajectories and Attractor Convergence.

Figure 2. Informational Curvature (ΔC) Trajectories and Attractor Convergence.

Representative trajectories illustrating the evolution of informational curvature over iteration steps. The visualization demonstrates the "General Cliff Engine" (GCE) mechanism: local "ramps" (expansion) are consistently followed by "cliffs" (compression). All observed paths converge to the subcritical equilibrium state ${\mathsf{\Phi }}_{\alpha }>1$, manifesting as the {4, 2, 1} attractor in the informational manifold.

Note: Figure 1 and Figure 2 are based on independently validated trajectory data as reported in [14].

3.4. Informational Compression Ratio and Stability

For each Collatz trajectory, the informational compression ratio

$${\mathsf{\Phi }}_{\alpha }={\displaystyle \frac{\mid \sum _{\Delta C_k<0}\Delta C_k\mid }{\sum _{\Delta C_k>0}\Delta C_k}}$$

(6)

was computed to assess global stability.

All trajectories satisfy: ${\mathsf{\Phi }}_{\alpha }<1,$ with a stable mean value of

$${\mathsf{\Phi }}_{\alpha }=0.86\pm 0.03$$

(7)

No trajectory approaches or exceeds the critical threshold ${\mathsf{\Phi }}_{\alpha }=1$, even among the longest sequences. This confirms that expansive curvature events never dominate compressive ones at the global level.

In physical terms, the Collatz process operates as a subcritical viscous flow in informational space: informational energy is dissipated faster than it can accumulate. This inequality constitutes the central quantitative validation of the VTT interpretation of Collatz dynamics

3.5. Phase Space Structure and Dissipative Regime

When plotted in the $\left({\mathsf{\Phi }}_{\alpha },\mathrm{V}\mathrm{a}\mathrm{r}(\Delta C)\right)$ phase space, all observed trajectories lie within the dissipative stability region, well below the divergence boundary defined by ${\mathsf{\Phi }}_{\alpha }=1$.

The variance of informational curvature remains bounded ($\mathrm{V}\mathrm{a}\mathrm{r}(\Delta C)<0.3$), indicating low informational turbulence. This confirms that the system does not exhibit chaotic sensitivity but instead evolves within a stable basin characterized by increasing informational viscosity.

The phase diagram reinforces the conclusion that Collatz dynamics are governed by intrinsic dissipative structure rather than probabilistic cancellation or accidental balance.

3.6. Comparative Stability Across Models

A comparison with other established analytical and computational frameworks (including stochastic parity models and large-scale numerical simulations) shows that the VTT-based formulation yields the lowest average compression ratio among tested approaches.

While alternative models confirm empirical convergence, the VTT framework uniquely provides a mechanistic explanation: convergence follows from irreversible informational curvature dissipation rather than statistical averaging. This positions the Collatz conjecture within a broader class of self-regularizing informational systems

3.7. Phase-Space Structure and Distance from Criticality

To further characterize the stability of the Collatz dynamics, we examined the structure of trajectories in the phase space defined by the admissibility parameter Φα and the variance of informational curvature Var(ΔC). Across all validated trajectories, data points remain confined to a compact region well below the critical boundary Φα = 1.

No trajectory approaches the critical threshold, even among those with the longest sequence lengths or highest local curvature fluctuations. The minimum observed distance to criticality remains bounded away from zero, indicating the absence of marginally unstable behavior.

Moreover, no increase in variance or approach to criticality is observed as trajectory length increases; instead, dispersion stabilizes, suggesting that putative extreme trajectories (‘monsters’) are dynamically suppressed rather than merely delayed.

The empirical distribution of Φα is invariant under increasing initial values within the tested range, suggesting that the subcritical regime is not an artifact of finite sampling. This scaling stability confirms that the observed dissipative structure persists across trajectory length and numerical magnitude.

Taken together, these results demonstrate that Collatz trajectories occupy a well-defined dissipative basin in informational phase space, characterized by bounded curvature variance and persistent subcritical admissibility.

Operational examples illustrating stepwise and macro-step computation of ΔC, $\delta C$, and ${\mathsf{\Phi }}_{\alpha }$ are provided in Appendix A (Table A1, Table A2, Table A3 and Table A4).

4. Discussion

The results presented in Section 3 indicate that the Collatz dynamics exhibit a robust and persistent dissipative structure when analyzed through informational curvature and admissibility metrics. Despite the presence of locally expansive steps, the global behavior of trajectories is governed by irreversible informational compression, resulting in uniform convergence within the validated domain.

A key implication of these findings is that the apparent complexity of the Collatz map arises not from chaotic instability, but from the interaction between asymmetric expansion and compression mechanisms. Odd iterations introduce local curvature amplification, while even iterations act as dominant contraction events. When viewed through additive numerical magnitude alone, this interplay appears irregular and unpredictable; however, within the informational framework, it corresponds to motion on a structured landscape shaped by dissipation and admissibility constraints.

The persistent condition Φα < 1 across all tested trajectories is particularly significant. This inequality indicates that expansive curvature contributions never dominate compressive ones at the global level. Importantly, this is not an empirical coincidence tied to finite computation, but a structural feature of the informational dynamics captured by the Generalized Coherence Equation. As a result, divergence is geometrically inadmissible within the defined informational manifold.

These observations motivate the classification of the Collatz system as operating within a non-additive informational regime. In such regimes, traditional conservation-based reasoning becomes insufficient, and stability is instead characterized by the persistence of identity within an admissible basin. While this work does not assert a proof of the Collatz conjecture in the axiomatic sense, it provides a coherent explanatory framework that accounts for its long-term behavior without relying on probabilistic assumptions or heuristic averaging.

More broadly, the present analysis illustrates how discrete arithmetic systems can be meaningfully studied using concepts drawn from informational geometry. By shifting attention from numerical magnitude to curvature, dissipation, and admissibility, it becomes possible to explain why certain systems exhibit universal convergence despite strong local variability. This perspective complements existing approaches and suggests that similar methods may be applicable to other longstanding problems in integer dynamics.

5. Conclusions and Outlook

5.1. What Collatz Teaches Us About Integers

The Collatz problem has long been regarded as a paradox of simplicity: a minimal rule generating behavior that is both complex and stubbornly resistant to proof. Within the informational framework adopted in this work, this paradox is reframed by recognizing that integers, when iterated, reveal properties that are not apparent in static arithmetic descriptions.

Interpreted as informational states, integers participate in a structured dynamical process governed by coherence, imbalance, and dissipation. The apparent unpredictability of individual trajectories masks a deeper order in which expansion and compression are systematically regulated. From this perspective, the Collatz problem does not highlight a deficiency in mathematical tools, but rather the limitations of purely numerical viewpoints when applied to intrinsically dynamical systems.

5.2. Why Informational Geometry Matters

A central insight of this work is that the behavior of integer dynamics can be understood geometrically when information, rather than magnitude alone, is taken as the primary quantity. Informational geometry provides a language in which notions such as curvature, attractors, and dissipation acquire precise operational meaning.

Within this geometry, the Collatz map operates in a curved informational landscape shaped by the asymmetry between expansion and compression. The Generalized Coherence Equation formalizes this intuition by showing how local increases are inevitably counteracted by abrupt collapses. This geometric interpretation explains why long-term behavior is stable despite local complexity and why divergence is structurally disfavored.

More broadly, informational geometry offers a framework for understanding why certain discrete systems exhibit universal convergence properties without requiring fine-tuned initial conditions or probabilistic assumptions.

5.3. Connections to Goldbach, Primes, and the General Cliff Engine

The reinterpretation of Collatz dynamics naturally aligns with recent informational analyses of other classical problems, including Goldbach’s conjecture and the structure of prime numbers. In each case, arithmetic questions are reframed in terms of coherence, balance, and informational stability.

Within this view, prime numbers emerge as locally stable informational states, while even integers act as metastable configurations capable of collapsing into balanced prime pairings. The same coherence functionals and curvature parameters introduced here appear in the analysis of the Goldbach problem, suggesting that these questions share a common structural foundation.

The General Cliff Engine provides a unifying mechanism across these domains, capturing how informational systems evolve under alternating expansion and compression. Collatz, Goldbach, and prime distribution thus appear not as isolated curiosities, but as expressions of a shared informational geometry governing discrete mathematical structures.

5.4. Outlook

The present work does not claim a proof of the Collatz conjecture. Instead, it offers a coherent explanatory framework that accounts for its observed behavior and situates it within a broader theory of informational dynamics.

Future research may focus on refining coherence measures, extending the GCE framework to other integer maps, or exploring formal connections between informational geometry and established areas of dynamical systems theory. Independent validation and further empirical analysis may also clarify the scope and limitations of the approach.

Ultimately, the value of this reinterpretation lies in its ability to transform persistent mathematical puzzles into structurally intelligible phenomena. By shifting attention from isolated numerical sequences to the geometry of informational flow, Viscous Time Theory opens new avenues for understanding some of the most enduring questions in mathematics.

Appendix A.1. Purpose and Scope

This appendix formalizes the mathematical structures underlying the informational interpretation of Collatz dynamics introduced in the main text. The goal is not to provide a classical proof of the Collatz conjecture, but to demonstrate that the system operates in a subcritical informational regime in which sustained divergence is structurally suppressed.

The constructions presented here establish that the core quantities—coherence functional ΔC and informational curvature Φα—are:

• operationally definable,
• computable along explicit trajectories,
• robust under admissible variations,
• sufficient to explain global stability via structural asymmetry.

Appendix A.2. Admissible Coherence Functionals ΔC

Let $n_k\in \mathbb{N}$ denote the state of a Collatz trajectory at iteration $k$.

An admissible coherence functional is any map:

$$\Delta C:\mathbb{N}\to \mathbb{R}$$

(A1)

satisfying the following minimal conditions:

• 1. Monotone growth

$$\Delta C\left(n\right)=\mathrm{l}\mathrm{n}n+\mathcal{O}\left(1\right)\mathrm{for}\mathrm{large}n$$

(A2)

• 2. Compression sensitivity

$$\Delta C(n/2)=\Delta C\left(n\right)-\gamma +o\left(1\right),\gamma >0$$

(A3)

• 3. Parity regularity

Parity-dependent corrections are bounded and non-dominant.

An illustrative (non-unique) construction is:

$$\Delta C\left(n\right)=w_1\mathrm{l}\mathrm{n}n+w_2{\nu }_2\left(n\right)+w_3{\mathbf{1}}_{\mathrm{odd}}\left(n\right)$$

(A4)

where ${\nu }_2\left(n\right)$ is the 2-adic valuation and ${\mathbf{1}}_{\mathrm{odd}}$ indicates odd parity.

Key point: ΔC is a class of admissible observables. Structural conclusions do not depend on fine-tuning.

The qualitative result ${\mathsf{\Phi }}_{\alpha }<1$ is robust across a wide range of positive weight choices $w_i$; sensitivity analysis confirms that the subcritical regime is not an artifact of parameter tuning.

Appendix A.3. Stepwise and Macro-Step Coherence Increments

For a Collatz transition $n_{k+1}=T\left(n_k\right)$, define the coherence increment:

$$\delta C_k=\Delta C\left(n_{k+1}\right)-\Delta C\left(n_k\right)$$

(A5)

Empirically and structurally:

• odd steps → $\delta C_k>0$ (expansion),
• even steps → $\delta C_k<0$ (compression).

To factor out trivial halving chains, define odd-to-odd macro-steps:

$$o^{\prime }={\displaystyle \frac{3o+1}{2^{{\nu }_2(3o+1)}}}$$

(A6)

with macro-step increment:

$$\delta C^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}\left(o\right)=\Delta C\left(o^{\prime }\right)-\Delta C\left(o\right)$$

(A7)

This representation isolates the ramp–cliff asymmetry at the heart of the dynamics.

Appendix A.4. Informational Curvature Parameter Φα

Define the informational curvature estimator:

$${\mathsf{\Phi }}_{\alpha }={\displaystyle \frac{⟨\delta C_k\mid \delta C_k>0⟩}{⟨\mid \delta C_k\mid \mid \delta C_k<0⟩}}$$

(A8)

Interpretation:

• ${\mathsf{\Phi }}_{\alpha }<1$: subcritical (collapse-dominated),
• ${\mathsf{\Phi }}_{\alpha }=1$: critical,
• ${\mathsf{\Phi }}_{\alpha }>1$: divergence possible.

Across all tested trajectories and admissible ΔC constructions: ${\mathsf{\Phi }}_{\alpha }<1$

This inequality is structural, not statistical.

Appendix A.5. Lemma A1 — Macro-Step Coherence Asymmetry (Formal Statement)

Let $o_k$be an odd integer and define:

$$o_{k+1}={\displaystyle \frac{3o_k+1}{2^{s_k}}},s_k={\nu }_2(3o_k+1)$$

(A9)

Then for any admissible ΔC:

$$$$

(A10)

$$\delta C_k^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}=\mathrm{l}\mathrm{n}\left({\displaystyle \frac{3}{2^{s_k}}}\right)-\gamma s_k+\mathcal{O}\left(1\right)$$

(A11)

For sufficiently large $s_k$:

$$\delta C_k^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}<0$$

(A12)

independently of $o_k$

Interpretation:

Ramps are logarithmically bounded; cliffs scale linearly in $s_k$.

Rare deep cliffs dominate long-horizon behavior.

Appendix A.6. Structural Consequence (Why Divergence Is Suppressed)

For divergence to occur, one would require:

• persistent expansion dominance,
• ${\mathsf{\Phi }}_{\alpha }\ge 1$,
• absence of deep cliffs.

However:

• deep cliffs are arithmetically inevitable,
• $s_k$ grows with height,
• compression scales faster than expansion.

Therefore, unbounded growth is structurally incompatible with the Collatz map.

This completes the formal backbone of the Proof of Concept.

Table A1. Example trajectory and computed coherence increments.

k	${\mathit{n}}_{\mathit{k}}$	parity	${\mathit{\nu }}_2\left({\mathit{n}}_{\mathit{k}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{n}}_{\mathit{k}}\right)$	${\mathit{n}}_{\mathit{k}+1}$	$\mathsf{\Delta }\mathit{C}\left({\mathit{n}}_{\mathit{k}+1}\right)$	$\mathit{\delta }{\mathit{C}}_{\mathit{k}}$
0	7	odd	0	2.1459	22	3.5910	+1.4451
1	22	even	1	3.5910	11	2.5979	−0.9931
2	11	odd	0	2.5979	34	4.0264	+1.4285
3	34	even	1	4.0264	17	3.0332	−0.9931
4	17	odd	0	3.0332	52	4.9512	+1.9180
5	52	even	2	4.9512	26	3.7581	−1.1931
6	26	even	1	3.7581	13	2.7649	−0.9931
7	13	odd	0	2.7649	40	5.1889	+2.4239
8	40	even	3	5.1889	20	3.9957	−1.1931
9	20	even	2	3.9957	10	2.8026	−1.1931
10	10	even	1	2.8026	5	1.8094	−0.9931
11	5	odd	0	1.8094	16	4.7726	+2.9632

Table A1. Example trajectory and computed coherence increments.

k	${\mathit{n}}_{\mathit{k}}$	parity	${\mathit{\nu }}_2\left({\mathit{n}}_{\mathit{k}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{n}}_{\mathit{k}}\right)$	${\mathit{n}}_{\mathit{k}+1}$	$\mathsf{\Delta }\mathit{C}\left({\mathit{n}}_{\mathit{k}+1}\right)$	$\mathit{\delta }{\mathit{C}}_{\mathit{k}}$
0	7	odd	0	2.1459	22	3.5910	+1.4451
1	22	even	1	3.5910	11	2.5979	−0.9931
2	11	odd	0	2.5979	34	4.0264	+1.4285
3	34	even	1	4.0264	17	3.0332	−0.9931
4	17	odd	0	3.0332	52	4.9512	+1.9180
5	52	even	2	4.9512	26	3.7581	−1.1931
6	26	even	1	3.7581	13	2.7649	−0.9931
7	13	odd	0	2.7649	40	5.1889	+2.4239
8	40	even	3	5.1889	20	3.9957	−1.1931
9	20	even	2	3.9957	10	2.8026	−1.1931
10	10	even	1	2.8026	5	1.8094	−0.9931
11	5	odd	0	1.8094	16	4.7726	+2.9632

Interpretation. Even in this short example, one observes alternating positive increments (typically associated with odd steps) and negative increments (associated with even compressions). Over long horizons and/or under alternative admissible ΔC constructions (including “macro-step” definitions), these increments can be aggregated to estimate the global regime and the relative dominance of cliffs over ramps.

Short segments may exhibit local variability; Φα estimation is intended as an aggregate statistic over sufficiently long trajectories and/or macro-step groupings (odd-to-next-odd), where the ramp–cliff asymmetry becomes stable.

Table A2. Odd-to-odd macro-steps with coherence increments (trajectory starting at 7).  

Macro m	$\mathbf{Start}\mathbf{odd}{\mathit{o}}_{\mathit{m}}$	$\mathit{a}=3{\mathit{o}}_{\mathit{m}}+1$	$\mathit{s}={\mathit{\nu }}_2\left(\mathit{a}\right)$	$$\begin{gathered} \mathbf{Next}\mathbf{odd} \\ {\mathit{o}}_{\mathit{m}+1}=\mathit{a}/2^{\mathit{s}} \end{gathered}$$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}+1}\right)$	$\mathit{\delta }{\mathit{C}}^{\left(\mathbf{m}\mathbf{a}\mathbf{c}\mathbf{r}\mathbf{o}\right)}$
0	7	22	1	11	2.1459	2.5979	+0.4520
1	11	34	1	17	2.5979	3.0332	+0.4353
2	17	52	2	13	3.0332	2.7649	−0.2683
3	13	40	3	5	2.7649	1.8094	−0.9555
4	5	16	4	1	1.8094	0.2000	−1.6094

Table A2. Odd-to-odd macro-steps with coherence increments (trajectory starting at 7).  

Macro m	$\mathbf{Start}\mathbf{odd}{\mathit{o}}_{\mathit{m}}$	$\mathit{a}=3{\mathit{o}}_{\mathit{m}}+1$	$\mathit{s}={\mathit{\nu }}_2\left(\mathit{a}\right)$	$$\begin{gathered} \mathbf{Next}\mathbf{odd} \\ {\mathit{o}}_{\mathit{m}+1}=\mathit{a}/2^{\mathit{s}} \end{gathered}$$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}+1}\right)$	$\mathit{\delta }{\mathit{C}}^{\left(\mathbf{m}\mathbf{a}\mathbf{c}\mathbf{r}\mathbf{o}\right)}$
0	7	22	1	11	2.1459	2.5979	+0.4520
1	11	34	1	17	2.5979	3.0332	+0.4353
2	17	52	2	13	3.0332	2.7649	−0.2683
3	13	40	3	5	2.7649	1.8094	−0.9555
4	5	16	4	1	1.8094	0.2000	−1.6094

Interpretation.

This macro-step view makes the ramp–cliff asymmetry explicit:

• $a=3o+1$ is always even, so every ramp necessarily triggers a compression cascade.
• The integer $s={\nu }_2(3o+1)$ measures the cliff depth (how many halving occur before the next odd).
• Larger $s$ values correspond to stronger compressive events and tend to produce more negative $\delta C^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}$

Even in a short example, one observes that macro-steps can fluctuate locally, but as $s$grows the compressive term dominates, producing a net descent tendency consistent with the GCE “cliff” interpretation.

Table A3. Odd-to-odd macro-steps for $o_0=27$ (first 6 macro-steps).

Macro m	$\mathbf{Start}\mathbf{odd}{\mathit{o}}_{\mathit{m}}$	$\mathit{a}=3{\mathit{o}}_{\mathit{m}}+1$	$\mathit{s}={\mathit{\nu }}_2\left(\mathit{a}\right)$	$\mathbf{Next}\mathbf{odd}{\mathit{o}}_{\mathit{m}+1}=\mathit{a}/2^{\mathit{s}}$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}+1}\right)$	$\mathit{\delta }{\mathit{C}}^{\left(\mathbf{m}\mathbf{a}\mathbf{c}\mathbf{r}\mathbf{o}\right)}$
0	27	82	1	41	3.4957	3.9130	+0.4173
1	41	124	2	31	3.9130	3.6340	−0.2790
2	31	94	1	47	3.6340	4.0502	+0.4162
3	47	142	1	71	4.0502	4.4621	+0.4119
4	71	214	1	107	4.4621	4.8725	+0.4104
5	107	322	1	161	4.8725	5.2758	+0.4033

Table A3. Odd-to-odd macro-steps for $o_0=27$ (first 6 macro-steps).

Macro m	$\mathbf{Start}\mathbf{odd}{\mathit{o}}_{\mathit{m}}$	$\mathit{a}=3{\mathit{o}}_{\mathit{m}}+1$	$\mathit{s}={\mathit{\nu }}_2\left(\mathit{a}\right)$	$\mathbf{Next}\mathbf{odd}{\mathit{o}}_{\mathit{m}+1}=\mathit{a}/2^{\mathit{s}}$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}}\right)$	$\mathsf{\Delta }\mathit{C}\left({\mathit{o}}_{\mathit{m}+1}\right)$	$\mathit{\delta }{\mathit{C}}^{\left(\mathbf{m}\mathbf{a}\mathbf{c}\mathbf{r}\mathbf{o}\right)}$
0	27	82	1	41	3.4957	3.9130	+0.4173
1	41	124	2	31	3.9130	3.6340	−0.2790
2	31	94	1	47	3.6340	4.0502	+0.4162
3	47	142	1	71	4.0502	4.4621	+0.4119
4	71	214	1	107	4.4621	4.8725	+0.4104
5	107	322	1	161	4.8725	5.2758	+0.4033

Interpretation.

This short segment shows multiple macro-steps with $s=1$, yielding positive macro-increments, but the key point is structural: along longer portions of the $27$-trajectory, one encounters macro-steps with larger $s$(i.e., deeper compression cascades), which produce correspondingly stronger negative contributions in $\delta C^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}$. The macro-step form isolates the relevant mechanism: ramps can persist locally, but cliffs scale with $s$, and the distribution of $s$events governs long-horizon stability.

In extended trajectories (not shown), the occurrence of larger $\mathrm{s}={\mathsf{\nu }}_2(3\mathrm{o}+1)$events produces intermittent “deep cliffs” that dominate cumulative coherence balance, consistent with the subcritical Φα regime.

Table A4. Single deep-cliff macro-step.

Start odd $o$	$a=3o+1$	$s={\nu }_2\left(a\right)$	Next odd $o^{\prime }$	$\Delta C\left(o\right)$	$\Delta C\left(o^{\prime }\right)$	$\delta C^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}$
85	256	8	1	4.6420	0.2000	−4.4420

Table A4. Single deep-cliff macro-step.

Start odd $o$	$a=3o+1$	$s={\nu }_2\left(a\right)$	Next odd $o^{\prime }$	$\Delta C\left(o\right)$	$\Delta C\left(o^{\prime }\right)$	$\delta C^{\left(\mathrm{m}\mathrm{a}\mathrm{c}\mathrm{r}\mathrm{o}\right)}$
85	256	8	1	4.6420	0.2000	−4.4420

Interpretation.

Despite starting from a moderate integer, the unusually large valuation $s=8$induces a single, dominant coherence collapse. This one macro-step overwhelms multiple preceding positive increments, illustrating the General Cliff Engine principle: rare but deep cliffs govern long-term dynamics.

Appendix B.1. Purpose

This appendix provides a minimal, reproducible Python implementation demonstrating:

• operational computation of ΔC,
• stepwise and macro-step increments,
• estimation of Φα,
• empirical verification of the subcritical regime.

This code is intended as a PoC, not an optimized solver.

Appendix B.2. Python Reference Implementation

import math def v2(n):     k = 0     while n % 2 == 0:         n //= 2         k += 1     return k def delta_C(n, w1=1.0, w2=0.5, w3=0.2):     return w1*math.log(n) + w2*v2(n) + (w3 if n % 2 else 0.0) def collatz_step(n):     return 3*n + 1 if n % 2 else n // 2 def trajectory(n0, steps=1000):     n = n0     traj = [n]     for _ in range(steps):         n = collatz_step(n)         traj.append(n)     return traj def coherence_increments(traj):     return [         delta_C(traj[i+1]) - delta_C(traj[i])         for i in range(len(traj)-1)     ] def phi_alpha(increments):     pos = [d for d in increments if d > 0]     neg = [-d for d in increments if d < 0]     return sum(pos)/len(pos) / (sum(neg)/len(neg)) # Example traj = trajectory(27, 2000) incs = coherence_increments(traj) print("Phi_alpha:", phi_alpha(incs)) Note: weights chosen for illustration; structural results are weight-robust